Complexation of Lanthanides(III) Ions with Terephthalic Acid in Aqueous Solutions by Potentiometric Titration Combined with Photoluminescence Spectroscopy
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
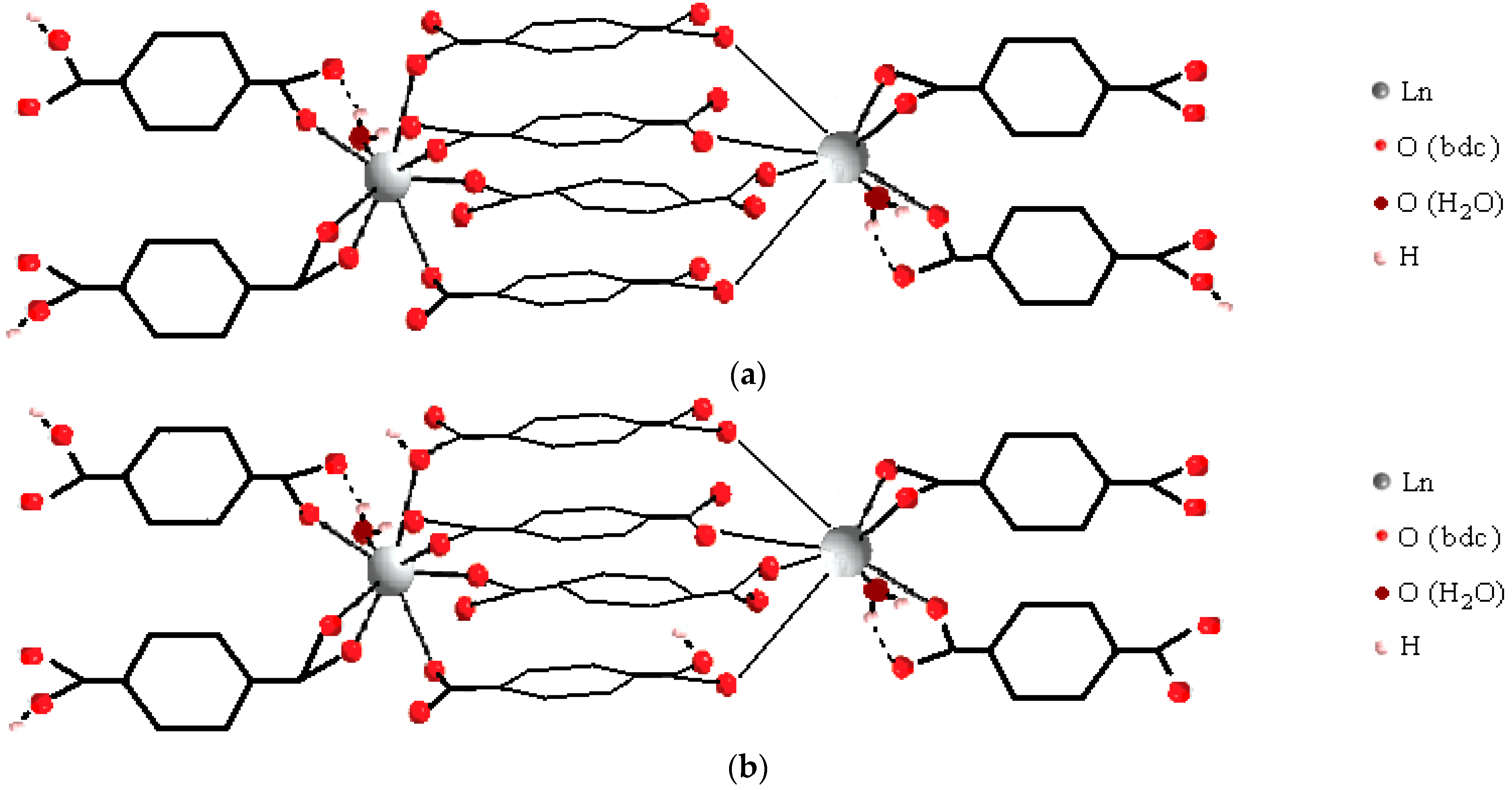
3.1. Initial Modeling
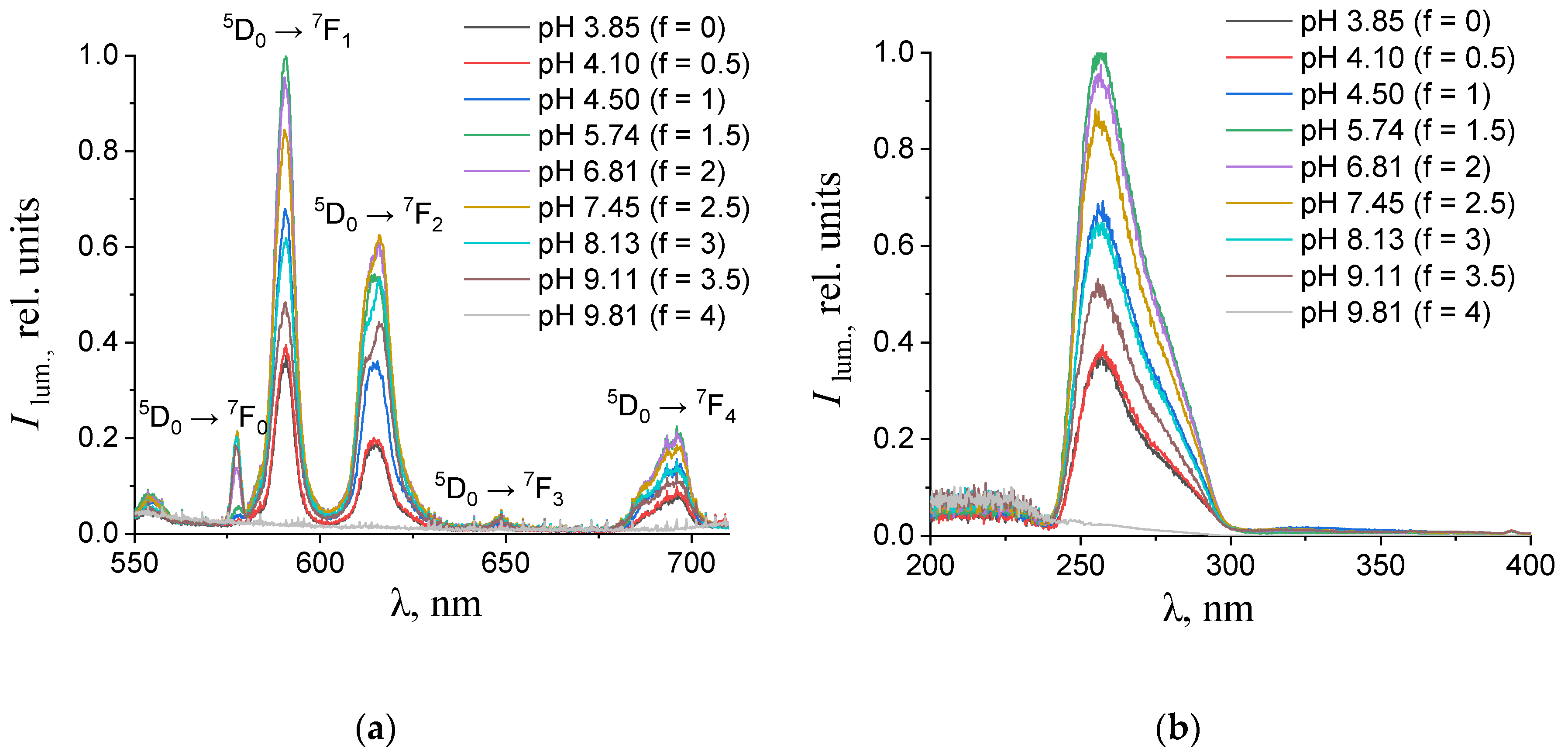
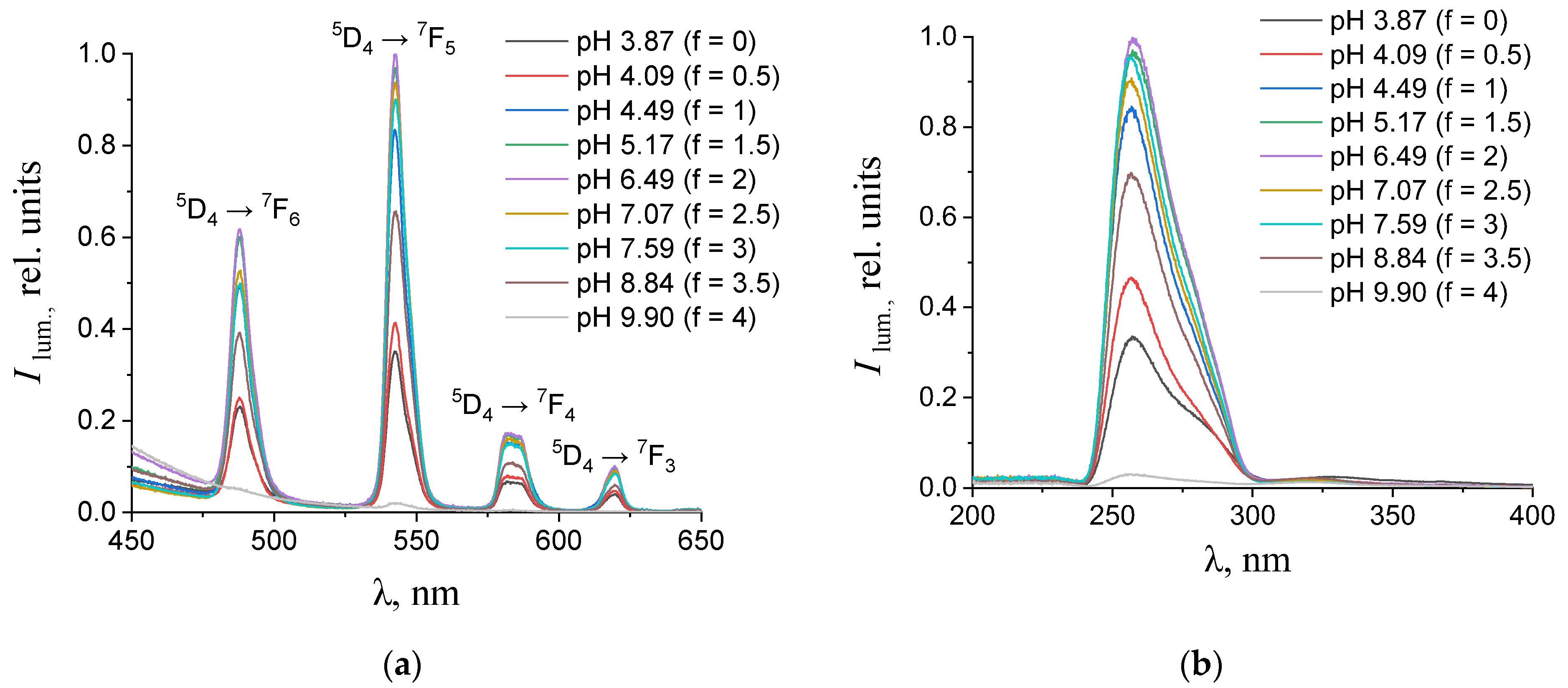
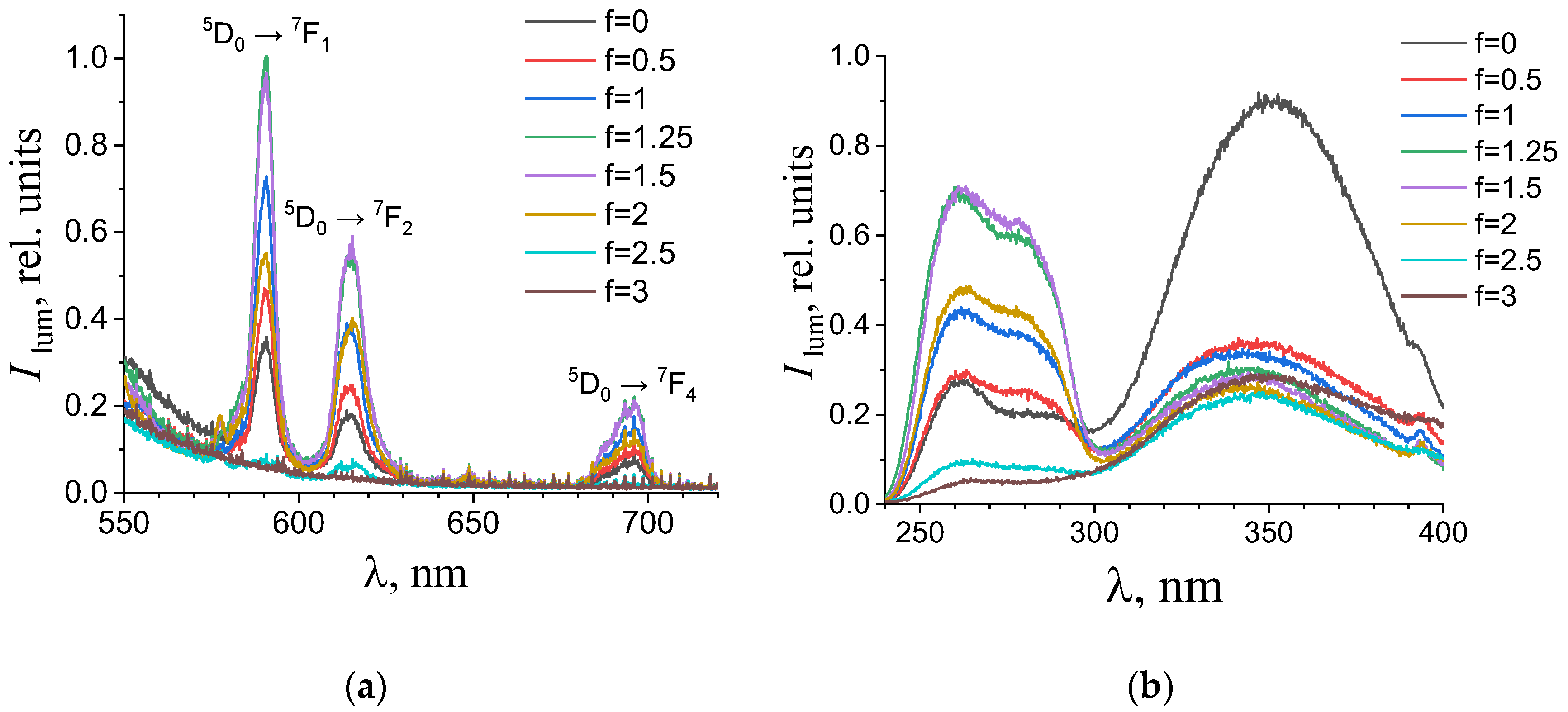
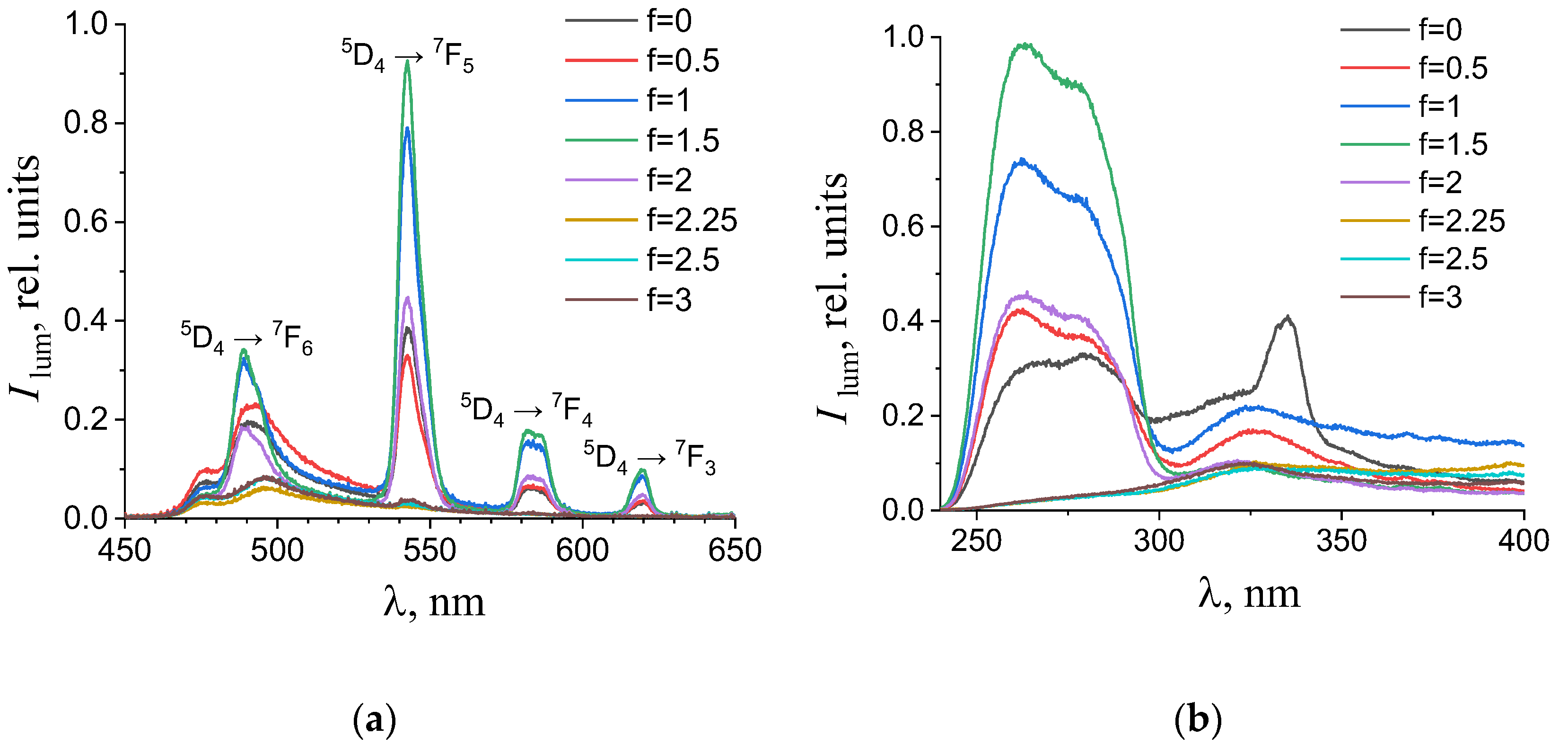
3.2. Photoluminescent Spectroscopy
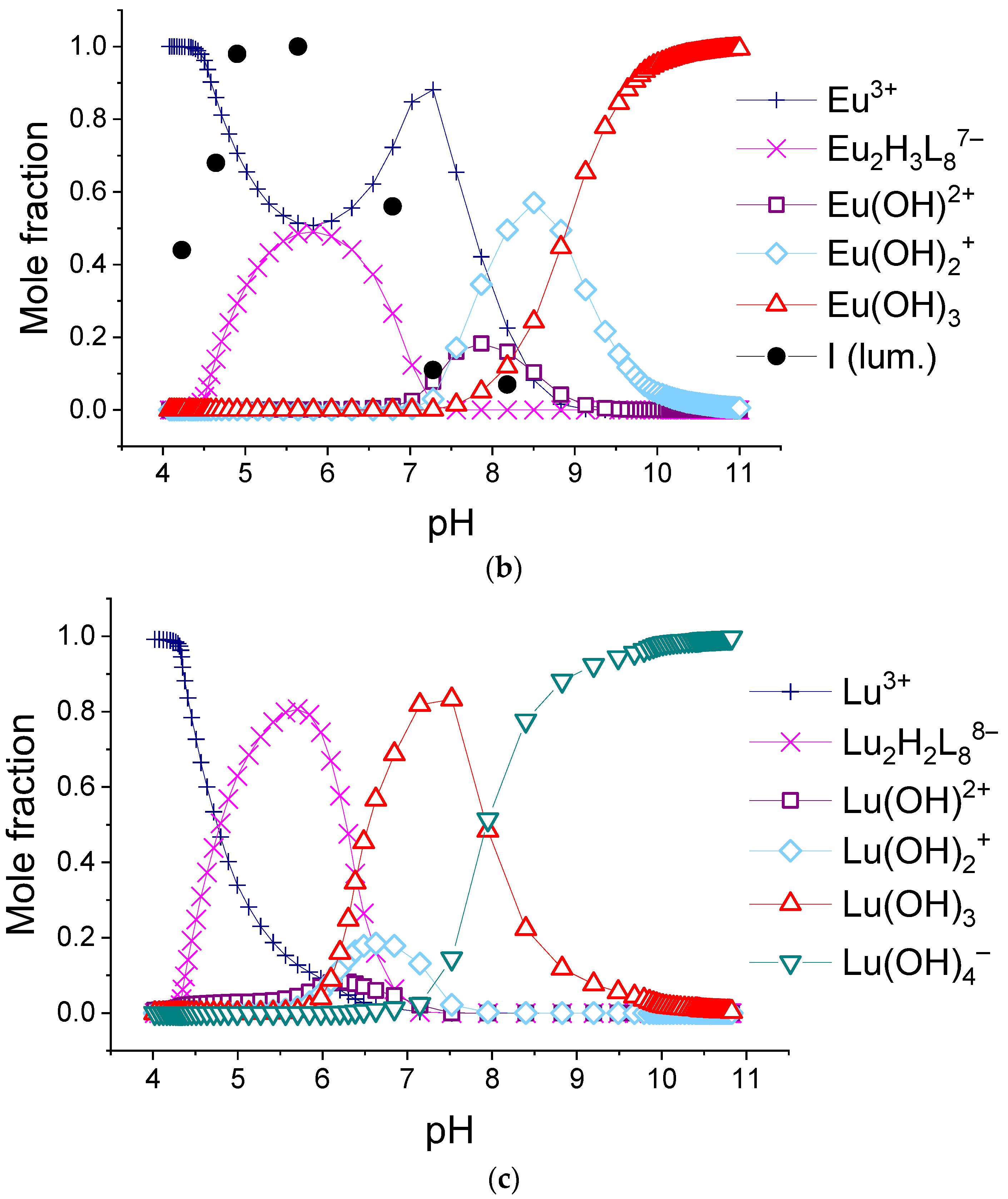
3.3. Equilibria Models in 1:8 Systems
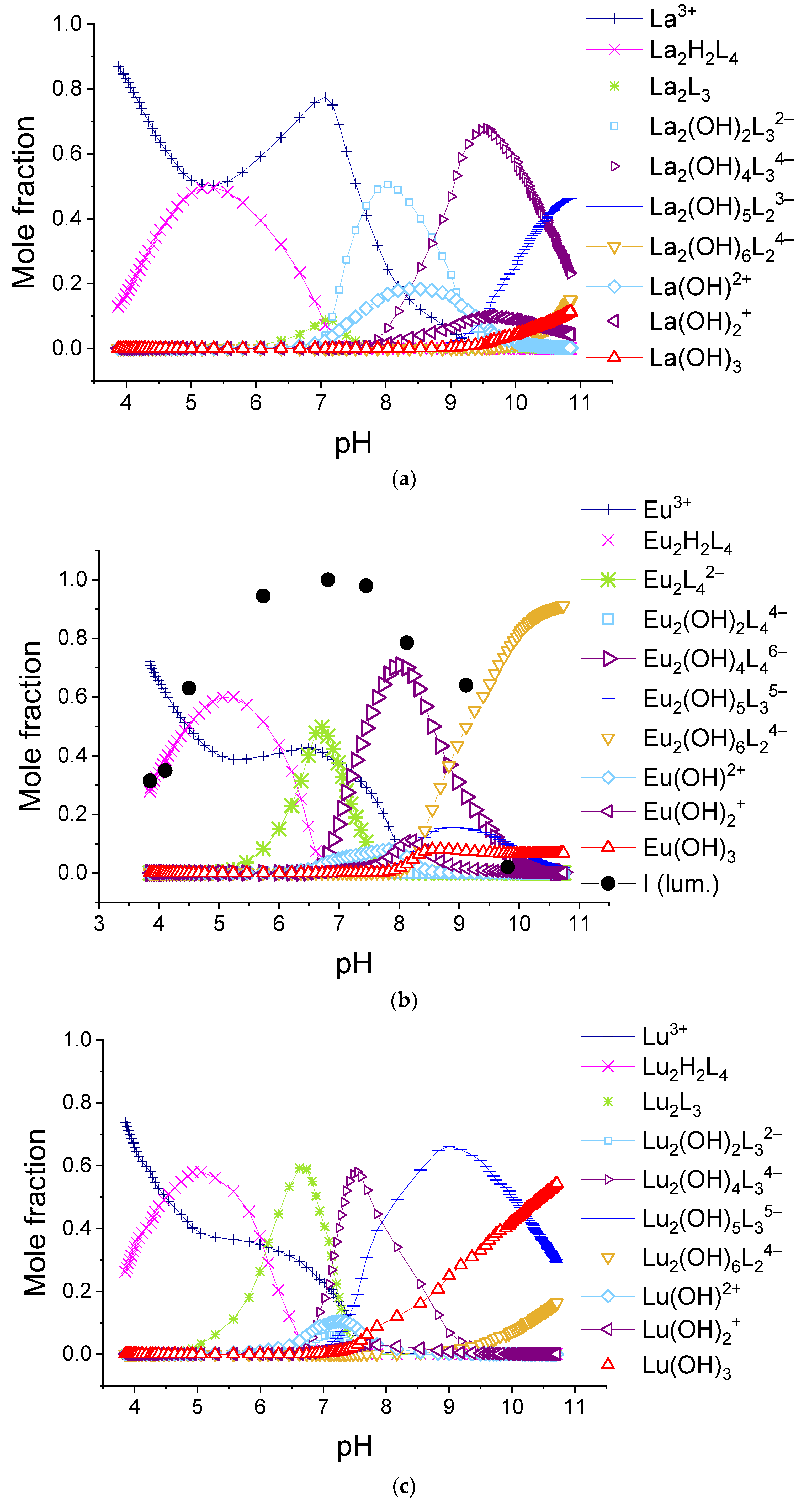
3.4. Equilibria Models in 1:2 Systems
3.5. The Summary of the Stability Constants
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MOF | Metal–organic framework |
| LED | Light emitting diod |
| REE | Rare-earth elements |
| 1,4-bdc | 1,4-benzene-dicarboxylic acid |
References
- Ning, X.; Chang, Y.; Zhou, Q.; Ding, S.; Gao, F. An Overview of the Design of Metal-Organic Frameworks-Based Fluorescent Chemosensors and Biosensors. Biosensors 2022, 12, 928. [Google Scholar] [CrossRef] [PubMed]
- Khairy, G.M.; Goda, R.M.; Anwar, Z.M.; Aboelngab, M.M.; Duerkop, A. Luminescent and time-resolved determination of gemifloxacin mesylate in pharmaceutical formulations and spiked blood plasma samples using a lanthanide complex as a probe. Anal. Methods 2024, 16, 2556–2568. [Google Scholar] [CrossRef] [PubMed]
- Barkanov, A.; Zakharova, A.; Vlasova, T.; Barkanova, E.; Khomyakov, A.; Avetissov, I.; Taydakov, I.; Datskevich, N.; Goncharenko, V.; Avetisov, R. NIR-OLED structures based on lanthanide coordination compounds: Synthesis and luminescent properties. J. Mater. Sci. 2022, 57, 8393–8405. [Google Scholar] [CrossRef]
- Zhang, Q.; O’Brien, S.; Grimm, J. Biomedical Applications of Lanthanide Nanomaterials, for Imaging, Sensing and Therapy. Nanotheranostics 2022, 6, 184–194. [Google Scholar] [CrossRef]
- Friedrich, S.; Sieber, C.; Drobot, B.; Tsushima, S.; Schmeide, K.; Stumpf, T.; Kretzschmar, J. Eu(III) and Cm(III) Complexation by the Aminocarboxylates NTA, EDTA, and EGTA Studied with NMR, TRLFS, and ITC—An Improved Approach to MoreRobust Thermodynamics. Molecules 2023, 28, 4881. [Google Scholar] [CrossRef]
- Heller, A.; Senwitz, C.; Foerstendorf, H.; Drobot, B.; Kretzschmar, J. Europium(III) Meets Etidronic Acid (HEDP): A Coordination Study Combining Spectroscopic, Spectrometric, and Quantum Chemical Methods. Molecules 2023, 28, 4469. [Google Scholar] [CrossRef]
- Gamov, G.A.; Zavalishin, M.N.; Pimenov, O.A.; Klochkov, V.V.; Khodov, I.A. La(III), Ce(III), Gd(III), and Eu(III) Complexation with Tris(hydroxymethyl)aminomethane in Aqueous Solution. Inorg. Chem. 2020, 59, 17783–17793. [Google Scholar] [CrossRef]
- Lytkin, A.I.; Chernikov, V.V.; Krutova, O.N.; Krutov, P.D. Thermodynamics of Complexation Reactions of Nd3+ and Eu3+ Ions with Glycyl-DL-Alanine, Glycyl-DL-Leucine, and Glycyl-DL Tyrosine in Aqueous Solution in the pH Range pH 1.6–7.5. Russ. J. Inorg. Chem. 2019, 64, 1451–1455. [Google Scholar] [CrossRef]
- Lytkin, A.I.; Krutova, O.N.; Chernikov, V.V.; Krutov, P.D.; Mokhova, Y.V. Thermodynamics of the Complexation of Nd3+, Eu3+, Gd3+, and Yb3+ Ions with Glycyl-Glycyl-Glycine in Aqueous Solutions in the pH Range 1.8–7.6. Russ. J. Phys. Chem. 2022, 96, 738–742. [Google Scholar] [CrossRef]
- Sheta, S.M.; Hamouda, M.A.; Ali, O.I.; Kandil, A.T.; Sheha, R.R.; El-Sheikh, S.M. Recent progress in high-performance environmental impacts of the removal of radionuclides from wastewater based on metal– organic frameworks: A review. R. Soc. Chem. Adv. 2023, 13, 25182–25208. [Google Scholar] [CrossRef]
- Weissman, S. Intramolecular energy transfer: The fluorescence of complexes of europium. J. Chem. Phys. 1942, 10, 214–217. [Google Scholar] [CrossRef]
- Daiguebonne, C.; Kerbellec, N.; Bernot, K.; Gérault, Y.; Deluzet, A.; Guillou, O. Synthesis, crystal structure, and porosity estimation of hydrated erbium terephthalate coordination polymers. Inorg. Chem. 2006, 45, 5399–5406. [Google Scholar] [CrossRef] [PubMed]
- Zehnder, R.; Renn, R.; Pippin, E.; Zeller, M.; Wheeler, K.; Carr, J.; Fontaine, N.; McMullen, N. Network dimensionality and ligand flexibility in lanthanide terephthalate hydrates. J. Mol. Struct. 2011, 985, 109–119. [Google Scholar] [CrossRef]
- Toikka, Y.; Badikov, A.; Bogachev, N.; Kolesnikov, I.; Skripkin, M.; Orlov, S.; Mereshchenko, A. Luminescent properties and thermal stability of (Lu0.98Eu0.02)2bdc3·10H2O metal–organic frameworks. Mend. Comm. 2024, 34, 634–636. [Google Scholar] [CrossRef]
- Feng, S. Poly[hexaaquabis(μ3-terephthalato)(μ2-terephthalato)diytterbium(III)]. Acta Cryst. 2010, 66, m33. [Google Scholar] [CrossRef]
- Daiguebonne, C.; Kerbellec, N.; Guillou, O.; Bünzli, J.-C.; Gumy, F.; Catala, L.; Mallah, T.; Audebrand, N.; Gérault, Y.; Bernot, K.; et al. Structural and luminescent properties of micro- and nanosized particles of lanthanide terephthalate coordination polymers. Inorg. Chem. 2008, 47, 3700–3708. [Google Scholar] [CrossRef]
- Reineke, T.; Eddaoudi, M.; Fehr, M.; Kelley, D.; Yaghi, O. From condensed lanthanide coordination solids to microporous frameworks having accessible metal sites. J. Am. Chem. Soc. 1999, 121, 1651–1657. [Google Scholar] [CrossRef]
- Nosov, V.; Toikka, Y.; Petrova, A.; Butorlin, O.; Kolesnikov, I.; Orlov, S.; Ryazantsev, M.; Kolesnik, S.; Bogachev, N.; Skripkin, M.; et al. Brightly luminescent (TbxLu1−x)2bdc3·nH2O MOFs: Effect of synthesis conditions on structure and luminescent properties. Molecules 2023, 28, 2378. [Google Scholar] [CrossRef]
- Janicki, R.; Mondry, A.; Starynowicz, P. Carboxylates of rare earth elements. Coord. Chem. Rev. 2017, 340, 98–133. [Google Scholar] [CrossRef]
- Makushova, G.N.; Voronshchikova, E.E. Complexation of Rare-earth elements with o-phthalic acid in aqueous solutions. Izv. Saratov Univ. Chem. Biol. Ecol. 2008, 8, 16–19. [Google Scholar]
- Stagg, W.R.; Andrews, B.L. Lanthanide Complexes with Phthalate Ligand. In Proceedings of the Tenth Rare Earth Research Conference, Carefree, AZ, USA, 30 April–3 May 1973; Volume 1, p. 342. [Google Scholar]
- Munshiyeva, M.K.; Usubaliyev, B.T.; Aliyeva, F.B.; Mamedova, S.R.; Jalaladdinov, F.F. Complexes of rare earth metals with 1,2-benzenedicarboxylic (o-phthalic) acid. Azerbaijan Chem. J. 2016, 3, 130–139. [Google Scholar]
- Yatsimirsky, K.B.; Kostromina, N.A.; Sheka, Z.A.; Davidenko, N.K.; Kriss, E.E.; Ermolenko, E.I. Chemistry of Complex Compounds of Rare-Earth Elements; Naukova dumka: Kyev, Ukraine, 1966; pp. 1–494. [Google Scholar]
- Mishustin, A.I. Estimate of the stability constants of trivalent actinide and lanthanide complexes with O-donor ligands in aqueous solutions. Russ. J. Inorg. Chem. 2010, 55, 800–807. [Google Scholar] [CrossRef]
- Wood, S.A. The aqueous geochemistry of the rare-earth elements: Critical stability constants for complexes with simple carboxylic acids at 25 °C and 1 bar and their application to nuclear waste management. Eng. Geol. 1993, 34, 229–259. [Google Scholar] [CrossRef]
- Kumar, S. Luminescence Studies of Eu3+ and UO22+ Complexes with Aromatic Carboxylic Acids in Acetonitrile Medium. Ph.D. Thesis, Indira Gandhi Centre for Atomic Research, Kalpakkam, India, 2016. [Google Scholar]
- Yun, S.; Kang, S.; Yun, S. Thermodynamics of complexation of lanthanides by some benzoic acid derivatives in aqueous solution. Thermochim. Acta 1999, 331, 13–19. [Google Scholar] [CrossRef]
- Moreau, P.; Colette-Maatouk, S.; Vitorge, P.; Gareil, P.; Reiller, P.E. Complexation of europium(III) by hydroxybenzoic acids: A time-resolved luminescence spectroscopy study. Inorganica Chim. Acta 2015, 432, 81–88. [Google Scholar] [CrossRef]
- Zheng, Y.-Z.; Speldrich, M.; Kogerler, P.; Chen, X.-M. The role of p–p stacking in stabilizing a,a-trans-cyclohexane-1,4 dicarboxylate in a 2D Co(II) network. CrystEngComm 2010, 12, 1057–1059. [Google Scholar] [CrossRef]
- Hudson, K.L.; Bartlett, G.J.; Diehl, R.C.; Agirre, J.; Gallagher, T.; Kiessling, L.L.; Woolfson, D.N. Carbohydrate−Aromatic Interactions in Proteins. J. Am. Chem. Soc. 2015, 137, 15152–15160. [Google Scholar] [CrossRef]
- Sonesson, A. On the Complex Chemistry of the Tervalent Rare Earth Ions. I. The Acetate Systems of Lanthanum, Cerium, Neodymium, and Gadolinium. Acta Chem. Scand. 1958, 12, 165–181. [Google Scholar] [CrossRef]
- Ermolenko, V.I. The oxibenzoates of neodymium. Russ. J. Inorg. Chem. 1964, 9, 48–55. [Google Scholar]
- Kereichuk, A.S.; Paramonova, V.I. The investigation of the complexation of europium(III) with oxalate ion by ion exchange method. Sov. Radiochem. 1963, 5, 464–473. [Google Scholar]
- Rudat, J. Enzymatische Decarboxylierung von Benzenpolycarbonsauren. Ph.D. Thesis, Rheinischen Friedrich-Wilhelms-Universitat Bonn, Bonn, Germany, 2006. [Google Scholar]
- Saitov, Y.E.; Guseva, P.B.; Toikka, Y.N.; Bogachev, N.A.; Skripkin, M.Y.; Mereshchenko, A.S. Complexation of Europium(III) and Terbium(III) Ions with Terephthalic Acid in Aqueous Solutions. Russ. J. Gen. Chem. 2024, 94, 591–599. [Google Scholar] [CrossRef]
- Merny, S.A.; Konyaev, D.S.; Kholin, Y.V. CLINP 2.1, Program for Robast Parametric Identification of Complexation Models, Chemical Faculty; V. N. Karazin Kharkov National University: Kharkov, Ukraine, 1999. [Google Scholar]
- Peppard, D.F.; Mason, G.V.; Hucher, T. Stability constants of certain lanthanide(III) and actinide(III) chloride and nitrate complexes. J. Inorg. Nucl. Chem. 1962, 24, 881–888. [Google Scholar] [CrossRef]
- Jordan, N.; Thoenen, T.; Starke, S.; Spahiu, K.; Brendler, V. A critical review of the solution chemistry, solubility, and thermodynamics of europium: Recent advances on the Eu3+ aqua ion and the Eu(III) aqueous complexes and solid phases with the sulphate, chloride, and phosphate inorganic ligands. Coord. Chem. Rev. 2023, 473, 214608. [Google Scholar] [CrossRef]
- Utochnikova, V.V.; Grishko, A.Y.; Koshelev, D.S.; Averin, A.A.; Lepnev, L.S.; Kuzmina, N.P. Lanthanide heterometallic terephthalates: Concentration quenching and the principles of the “multiphotonic emission”. Opt. Mater. 2017, 74, 201. [Google Scholar] [CrossRef]
- Binnemans, K. Interpretation of europium(III) spectra. Coord. Chem. Rev. 2015, 295, 1–45. [Google Scholar] [CrossRef]
- Utochnikova, V.V.; Kuzmina, N.P. Photoluminescence of lanthanide aromatic carboxylates. Russ. J. Coord. Chem. 2016, 42, 679–694. [Google Scholar] [CrossRef]
- Kalusniak, S.; Castellano-Hernández, E.; Yalçinŏglu, H.; Tanaka, H.; Kränkel, C. Spectroscopic properties of Tb3+ as an ion for visible lasers. Appl. Phys. B 2022, 128, 33. [Google Scholar] [CrossRef]
- Yakubovich, Y.Y.; Alekseev, V.G. Hydrolysis Constants of Tervalent Lanthanum and Lanthanides Ions in 0.1M KNO3 Solution. Russ. J. Inorg. Chem. 2012, 57, 984–988. [Google Scholar] [CrossRef]
- Stepanchikova, S.A.; Biteikina, R.P.; Shironosova, G.P.; Kolonin, G.P. An Experimental Study of Hydroxo Complex Formation in Basic and Near-Neutral Solutions of Rare-Earth Elements and Yttrium at 25 °C. Russ. Geol. Geophys. 2014, 55, 1188–1193. [Google Scholar] [CrossRef]
- Nazarenko, V.A.; Antonovich, V.P.; Nevskaya, E.M. Metal Ions Hydrolysis in Diluted Solutions; Atomizdat: Moscow, Russia, 1979; pp. 1–192. [Google Scholar]
- Nayan, R.; Dey, A.K. Protonated, hydroxo, and mixed protonated-hydroxo species in metal-ligand equilibria: Complexes of thorium(IV) with xylenol orange in aqueous solution solution. Transit. Metal. Chem. 1977, 2, 110–116. [Google Scholar] [CrossRef]
- Brown, C. Ekberg. Hydrolysis of Metal Ions; Wiley-VCH: Weinheim, Germany, 2016; pp. 1–917. [Google Scholar]
- Baes, C.F.; Mesmer, R.E. The Hydrolysis of Cations; Wiley: New York, NY, USA, 1976. [Google Scholar]
- Bandurkin, G.A.; Dzhurinsky, B.F.; Tananaev, I.V. About f-degeneracy in a series of rare-earth elements. Dokl. Chem. 1969, 189, 94–95. [Google Scholar]
- Demakov, P.A.; Sapchenko, S.A.; Samsonenko, D.G.; Dybtsev, D.N.; Fedin, V.P. Gadolinium break in a series of three-dimentional trans-1,4-cyclohexane dicarboxilates of rare earth elements. Rus. J. Struct. Chem. 2019, 60, 815–822. [Google Scholar] [CrossRef]
- Persson, I.; Angelo, P.D.; De Panfilis, S.; Sandstrçm, M.; Eriksson, L. Hydration of Lanthanoid(III) Ions in Aqueous Solution and Crystalline Hydrates Studied by EXAFS Spectroscopy and Crystallography: The Myth of the “Gadolinium Break”. Chem. Eur. J. 2008, 14, 3056–3066. [Google Scholar] [CrossRef] [PubMed]






| Ln | Ln2Hy(1,4-bdc)8y−10 | LnOH2+ | Ln(OH)2+ | Ln(OH)3 | Ln(OH)4− | S0 |
|---|---|---|---|---|---|---|
| La | 39.1, y = 3 | 5.86 [46] | 13.14 [44] | 16.97 [44] | - | 0.0195 |
| Ce | 39.2, y = 3 | 5.98 [46] | 13.78 [44] | 19.4 * | - | 0.0130 |
| Pr | 38.3, y = 3 | 6.14 [46] | 11.8 (Nd, [47]) | 16.34 [44] | - | 0.0199 |
| Nd | 38.3, y = 3 | 6.24 [46] | 11.8 [47] | 16.84 [47] | - | 0.0198 |
| Sm | 39.9, y = 3 | 6.40 [46] | 14.78 [44] | 18.76 [44] | - | 0.0196 |
| Eu | 38.6, y = 3 | 6.09 [43] | 12.3 [47] | 17.66 [43] | - | 0.0197 |
| Gd | 38.9, y = 3 | 6.64 [46] | 13.4 [47] | 19.19 (Eu, [44]) | - | 0.0132 |
| Tb | 38.4, y = 3 | 6.26 [43] | 13.4 (Gd, [47]) | 18.57 [43] | - | 0.0191 |
| Dy | 39.0, y = 3 | 6.92 [46] | 11.8 [48] | 19.03 [43] | - | 0.0183 |
| Ho | 39.3, y = 3 | 7.20 [46] | 11.65 [43] | 19.29 [43] | - | 0.0138 |
| Er | 40.0, y = 3 | 7.44 [46] | 11.85 [43] | 19.77 [43] | - | 0.0118 |
| Tm | 39.0, y = 3 | 7.64 [46] | 12.04 [43] | 20.03 [43] | - | 0.0131 |
| Yb | 40.1, y = 1 | 7.76 [46] | 15.52 ** | 23.28 ** | 28.5 * | 0.0185 |
| Lu | 40.5, y = 2 | 7.96 [46] | 15.92 ** | 23.88 ** | 29.5 * | 0.0168 |
| Ln | Ln2H2L4 | Ln2HL4 | Ln2Lz | Ln2(OH)2Lz | Ln2(OH)3L4 | Ln2(OH)4Lz | Ln2(OH)5Lz | Ln2(OH)6L2 | S0 |
|---|---|---|---|---|---|---|---|---|---|
| La | 22.16 | - | 14.87, z = 3 | 28.46, z = 3 | - | 38.83, z = 3 | 38.17, z = 2 | 40.93 | 0.0119 |
| Ce | 22.82 | - | 15.20, z = 3 | 28.47, z = 3 | - | 39.65, z = 3 | 39.08, z = 2 | 42.47 | 0.0090 |
| Pr | 22.57 | - | 21.14, z = 4 | 34.55, z = 4 | - | 40.96, z = 3 | 44.05, z = 3 | 43.75 | 0.0130 |
| Nd | 22.58 | - | 20.53, z = 4 | 33.19, z = 4 | 35.46 | - | - | 44.04 | 0.0144 |
| Sm | - | 22.21 | - | 33.90, z = 4 | - | 46.99, z = 4 | 47.46, z = 3 | 45.80 | 0.0157 |
| Eu | 23.20 | - | 21.57, z = 4 | 34.21, z = 4 | - | 49.15, z = 4 | 49.17, z = 3 | 49.93 | 0.0114 |
| Gd | 21.71 | - | 15.57, z = 3 | 27.42, z = 3 | - | 42.31, z = 3 | 44.63, z = 3 | 45.06 | 0.0137 |
| Tb | 21.89 | - | 21.15, z = 4 | 33.55, z = 4 | 41.77 | 49.49, z = 4 | 50.57, z = 3 | 50.64 | 0.0144 |
| Dy | 22.21 | - | 20.92, z = 4 | 32.97, z = 4 | - | 48.94, z = 4 | 50.01, z = 3 | 47.59 | 0.0088 |
| Ho | 22.09 | - | 20.89, z = 4 | 33.22, z = 4 | - | 49.38, z = 4 | 49.60, z = 3 | 49.92 | 0.0124 |
| Er | 22.27 | 21.31 | 20.53, z = 4 | 32.55, z = 4 | - | 47.82, z = 4 | - | 49.19 | 0.0133 |
| Tm | 22.26 | - | 16.60, z = 3 | 30.42, z = 3 | - | 44.09, z = 3 | 48.48, z = 3 | 51.01 | 0.0095 |
| Yb | 22.89 | - | 16.58, z = 3 | 30.65, z = 3 | - | 44.18, z = 3 | 50.53, z = 3 | 49.39 | 0.0118 |
| Lu | 23.06 | - | 17.38, z = 3 | 30.48, z = 3 | - | 44.91, z = 3 | 50.89, z = 3 | 49.86 | 0.0064 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guseva, P.B.; Badikov, A.R.; Butorlin, O.S.; Toikka, Y.N.; Orlov, S.N.; Ryazantsev, M.N.; Bogachev, N.A.; Skripkin, M.Y.; Mereshchenko, A.S. Complexation of Lanthanides(III) Ions with Terephthalic Acid in Aqueous Solutions by Potentiometric Titration Combined with Photoluminescence Spectroscopy. Chemistry 2025, 7, 57. https://doi.org/10.3390/chemistry7020057
Guseva PB, Badikov AR, Butorlin OS, Toikka YN, Orlov SN, Ryazantsev MN, Bogachev NA, Skripkin MY, Mereshchenko AS. Complexation of Lanthanides(III) Ions with Terephthalic Acid in Aqueous Solutions by Potentiometric Titration Combined with Photoluminescence Spectroscopy. Chemistry. 2025; 7(2):57. https://doi.org/10.3390/chemistry7020057
Chicago/Turabian StyleGuseva, Polina B., Alexander R. Badikov, Oleg S. Butorlin, Yulia N. Toikka, Sergey N. Orlov, Mikhail N. Ryazantsev, Nikita A. Bogachev, Mikhail Yu. Skripkin, and Andrey S. Mereshchenko. 2025. "Complexation of Lanthanides(III) Ions with Terephthalic Acid in Aqueous Solutions by Potentiometric Titration Combined with Photoluminescence Spectroscopy" Chemistry 7, no. 2: 57. https://doi.org/10.3390/chemistry7020057
APA StyleGuseva, P. B., Badikov, A. R., Butorlin, O. S., Toikka, Y. N., Orlov, S. N., Ryazantsev, M. N., Bogachev, N. A., Skripkin, M. Y., & Mereshchenko, A. S. (2025). Complexation of Lanthanides(III) Ions with Terephthalic Acid in Aqueous Solutions by Potentiometric Titration Combined with Photoluminescence Spectroscopy. Chemistry, 7(2), 57. https://doi.org/10.3390/chemistry7020057








