In this section, we discuss fitting factored regressions to a substantive data example in Blimp (version 3.0 [
11]). Below, we review how to factor the models and specify these factorizations with Blimp’s syntax. We include snippets of appropriate syntax and output from running the models to help familiarize readers with estimating and interpreting the results. In addition, we include the complete commented inputs, output, and data set in the
supplemental material. Overall, we will look at three analysis examples: (1) a single mediator model, (2) a mediator model with a moderator model, and (3) a latent mediator with a moderator model.
The three analysis examples use a data set that includes psychological correlates of pain severity for a sample of
individuals suffering from chronic pain. The main variables for the examples are a biological sex dummy code (0 = female, 1 = male), a binary severe pain indicator (0 = no, minor, or moderate pain, 1 = severe pain), a multi-item depression composite, and a multi-item scale measuring psychosocial disability (a construct capturing pain’s impact on emotional behaviors such as psychological autonomy, communication, and emotional stability), and we provide the variable definitions and missing data rates for these variables in
Table 1. The depression scale is the sum of seven 4-point rating scales, and the disability composite is the sum of six 6-point questionnaire items. The first two examples use the continuous sum scores, and the third example uses the item responses as indicators of a latent factor. The examples also include continuous measures of anxiety, stress, and perceived control over pain as auxiliary variables.
Before fitting the models, we will discuss the syntax for reading data into Blimp. The first ten lines of the Blimp script are below, which includes specifying four commands (denoted as capitalized names followed by a colon).
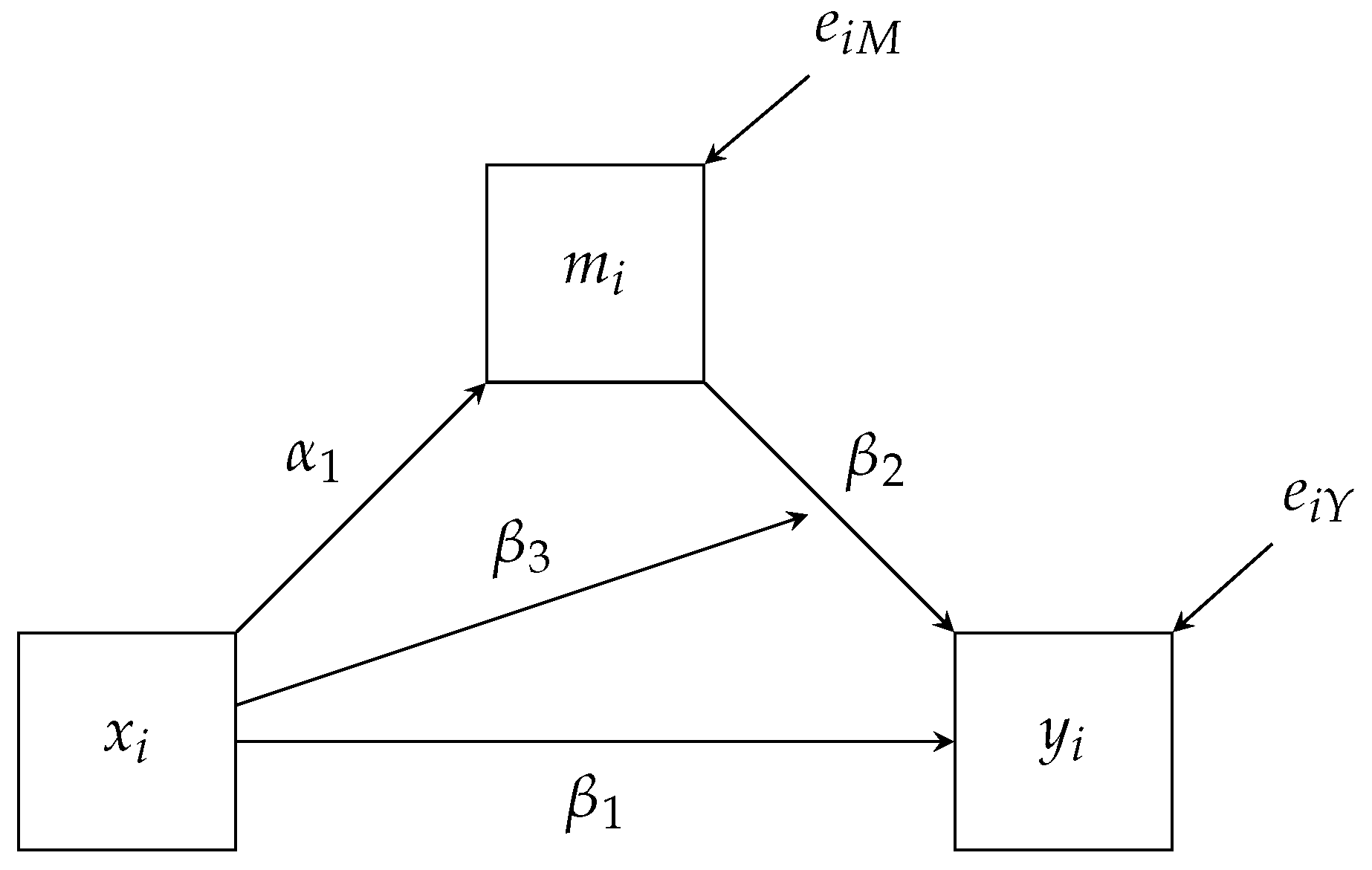
4.1. Fitting a Single Mediator Model
First, we will estimate is a single mediator model that investigates if depression (
depress) mediates the effect between pain severity (
severity) and the psychosocial disability construct (
disability) while controlling for biological sex (
male). We provide the path diagram for the model of interest in
Figure 3 with the mean structure excluded. To construct the factor regression, we first factor the joint distribution for
disability and
depress conditional on
severity and
male.
As already discussed, the factorization maps directly onto the path diagram. For example,
Figure 3 has three paths pointing towards
depress. These three paths match the same three variables that appear right of the pipe (i.e., ∣). Similarly, we have two paths pointing to
depress and the same two variables that appear right of the pipe above. These conditional distributions correspond to the two regression equations we expect from a mediation analysis, and we specify the models via the following Blimp syntax.
# Specify the single mediator model
MODEL:
# Single-Mediator model controlling for biological sex
disability ∼ depress@bpath severity male;
depress ∼ severity@apath male;
FIXED: male; # Specify no distribution for male
PARAMETERS: # Post compute the mediated effect
indirect = apath * bpath;
The
MODEL command signifies that we would like to specify our factored models. We list the first factorization,
disability conditional on
depress,
severity, and
male, on the first line. A tilde (∼) replaces the pipe in the factorization to specify the appropriate regression model. The
@ syntax denotes that we want the regression slope between
disability and
depress to be labeled as the
bpath. The second line after the
MODEL command specifies the second factorization,
depress conditional on
severity, and
male and has the
apath label. Both of these labeled paths are indicated in
Figure 3. Note, we did not specify any regressions for
male or
severity. By default, Blimp will specify a partially factored model for all predictors (i.e., who are never left of a tilde). Since
male is complete, there is no need to include any distributional assumptions about it, and we can indicate this using the
FIXED command. Thus, Blimp will by default will estimate the regression of
severity on
male for us. Alternatively, we could explicitly specify this model by including “
severity ∼ male” in the
MODEL command.
Finally, the PARAMETERS command allows us to specify quantities of interest. As we will see below, one of the advantages of using simulation methods to estimate the models is that we can easily take the sampled values and create quantities of interest. These quantities will have all the same summarizes as any other parameter (e.g., point estimate, uncertainty, and interval estimates). In this example, we are calculating the mediated effect, saved as the parameter called indirect, by multiplying the apath times the bpath.
In addition to the model syntax, we must specify various settings for the Markov chain Monte Carlo (MCMC) sampler that estimates the model. Below are the four main commands that need to be specified.
# Specify the MCMC sampler parameters
SEED: 398721; # Set a prng seed
BURN: 1000; # Set number of burn iterations
ITERATIONS: 10000; # Set number of post-burn iterations
CHAINS: 4; # Specify number independent of chains
First, the SEED command is an arbitrary positive integer used to replicate the results of the pseudo-random number generator. While many programs will have a default value if not specified, Blimp purposely requires one to be specified to ensure replicability. Second, the BURN command specifies the number of warm-up iterations the MCMC sampler runs. These iterations will be discarded and not summarized for the parameter summaries. We use the burn-in iterations to ensure convergence, that is, properly sampling from the posterior distributions for the parameters and imputations. We will discuss this more when we look at the output below. Thirdly, the ITERATIONS command requests the total number of post-burn iterations we want to be drawn and summarized as part of the MCMC estimation procedure. Fourthly, the CHAINS command specifies how many independent MCMC processes we want to run. In our example, we are requesting four to be run simultaneously with random starting values. Each chain will be run on a separate processor, allowing us better to utilize the computational power of a modern computer.
4.1.1. Adding Auxiliary Variables to the Model
To supplement the analysis model of interest (
Figure 3), we include additional auxiliary variables that will improve estimation with missing data. By adding these additional variables, we hope to better satisfy the missing data assumption about the incomplete observations [
33]. Therefore, we also include three continuous measures as auxiliary variables: anxiety (
anxiety), stress (
stress), and perceived control over pain (
control).
To include
anxiety,
stress, and
control into the model as auxiliary variables, we must not substantively change the meaning of the analysis model. We accomplish this by modeling the joint distribution of the auxiliary variables conditional on the predictors and outcomes. Just as we factored the analysis model, we take the joint distribution of the auxiliary variables conditional on the four variables from the analysis (two predictors and two outcomes) and factorize it into the following three conditional distributions.
Notably, we include the above factorization is in addition to the factorization that we have already specified for the analysis model. To specify this in Blimp, we replace the previous MODEL command with the following one that includes the factored auxiliary variables.
# Specify the single mediator model
MODEL:
# Single-Mediator model controlling for biological sex
disability ∼ depress@bpath severity male;
depress ∼ severity@apath male;
# Model for the Auxiliary Variables
anxiety ∼ stress control disability depress severity male;
stress ∼ control disability depress severity male;
control ∼ disability depress severity male;
The first two regressions in the syntax are the analysis model that we previously specified. The last three regressions are the three auxiliary models that we will use to better satisfy the missing data assumptions.
By including the auxiliary variables as outcomes regressed on the other variables in our model (i.e.,
disability,
depress, and
severity), we explicitly include the conditional distributions into the factorization without changing the meaning of our original analysis model’s densities. In other words, when we draw imputations on the missing variables, these factored regression densities will be a part of the sampling step. To illustrate, the distribution of
depress conditional on all other variables is proportional to the product of five densities.
Because specifying the auxiliary variable factorization can become tedious as we add more variables, Blimp offers syntax to quickly specify the command in one line.
# Specify auxiliary variable model with one line
anxiety stress control ∼ disability depress severity male;
The above syntax will produce the same exact auxiliary variable models above. In general, we can quickly specify these models by including every auxiliary variable to the left of the tilde and other variables to the right of the tilde.
4.1.2. Output from Single Mediator Model
For the first example, we will give a more broad overview of Blimp’s output, and in the later examples, we will only highlight the essential features that each example introduces. The full output for all models discussed in this article are provided in the
supplemental material. Once finished, Blimp’s output opens up with a header giving the software versioning and other information. This header is followed by algorithmic options discussing various aspects of the model, like specified default priors and starting values, and we recommend the interested readers consult the documentation [
11] for a discussion of those. The next output section is a table that provides the potential scale reduction factor (PSR or
[
25,
34]) for the burn-in iterations. The PSR factor represents a ratio of two estimates of the simulation’s posterior variability. As the MCMC algorithm converges to a stationary distribution (i.e., the distribution we are trying to sample from), the two estimates are expected to be equal, resulting in a
.
![Psych 04 00002 i001]()
Blimp calculates the PSR at twenty equally spaced intervals, where we discard the first half of the iterations and use the latter half. Blimp only prints out the highest PSR and the associated parameter number that produced this PSR. A parameter number is given to all estimated, fixed, or generated parameters in the output and, using the command
OPTIONS: labels will also print out a table displaying the numbers. As a general rule of thumb, we expect the MCMC sampler to converge once all PSR statistics are below approximately
to
[
25], and the table indicates that the algorithm quickly achieved this within the 1000 burn-in iterations requested.
The next section of the output is more diagnostic information about how well Blimp’s Metropolis sampler performed. As discussed earlier, Blimp uses a Metropolis step within the Gibbs sampler when drawing imputations from the factored distributions. These Metropolis steps require tuning parameters to be controlled so that the imputations are accepted approximately 50% of the time.
![Psych 04 00002 i002]()
Blimp monitors this throughout the process and always prints out one chain’s results by default. If the algorithm fails to tune correctly, an error will be displayed, alerting that more iterations are needed. The above output illustrates that the probability of the sampler accepting imputations for the three missing variables requiring a Metropolis step was approximately 50%.
Following both output sections of diagnostic information, Blimp prints out the sample size and missing data rates of all variables within the model.
![Psych 04 00002 i003]()
In general, this information allows us to double-check that Blimp read the data set correctly, and the output above matches the description of the data in
Table 1.
The next output section provides information about the statistical models that we specified. First, Blimp gives the number of parameters across all models. Blimp breaks this into three sections: estimated parameters in the specified models (referred to as an “Outcome Model” in Blimp), generated quantities we specified in the PARAMETERS command, and parameters that are used in the unspecified default models (referred to as a “Predictor Model” in Blimp).
![Psych 04 00002 i004]()
The above output indicates that in total, we have thirty estimated parameters in all specified models and two estimated parameters in the unspecified model for severity. The PREDICTORS section indicates that we have fixed male (i.e., made no distributional assumptions about the complete predictor) and estimated an ordinal probit model for the binary severity variable. The subsequent output then lists all five models that we specified in the syntax and the one generated parameter, indirect.
MODELS
[1] anxiety ∼ Intercept stress control disability depress severity male
[2] control ∼ Intercept disability depress severity male
[3] depress ∼ Intercept severity@apath male
[4] disability ∼ Intercept depress@bpath severity male
[5] stress ∼ Intercept control disability depress severity male
GENERATED PARAMETERS
[1] indirect = apath*bpath
By default, Blimp estimates an intercept for all manifest variables, indicated by the special variable name Intercept. This section serves as an overview of the regression equations and reflects the printing order of the models. We can see the three auxiliary models (i.e., regressions for anxiety, control, and stress) and two analysis models with the labeled paths. Finally, there is also a section showing how the generated parameters were computed—i.e., the indirect parameter was computed by multiplying the apath and bpath parameters.
Following the model information, the next section provides the posterior summaries for all specified models.
OUTCOME MODEL ESTIMATES:
Summaries based on 10,000 iterations using 4 chains.
To reiterate, Blimp defines an “Outcome Model” as any specified relationship in the syntax, including the auxiliary variable models we specified. After the header, Blimp prints the model’s output in the order listed in the Model Information section. For our discussion, we focus on the disability model’s output.
![Psych 04 00002 i005]()
By default, Blimp provides the posterior median, standard deviation, 95% intervals, PSR, and effective sample size (
N_EFF). For those unfamiliar with results from a Bayesian analysis, heuristically, we can think of the posterior median and standard deviation as analogous to the point estimate and standard error. Similarly, the 95% posterior interval is comparable to a confidence interval. The PSR is the same PSR we discussed earlier but now computed on all post-burn-in summaries. The effective sample size is a crude approximation of the “effective number of independent simulation draws” ([
25] p. 286) for each parameter. Typically speaking, these will be lower than the actual number of samples because of autocorrelation in the MCMC simulation procedure, and it is recommended that more iterations are needed if the effective sample size is less than ten per chain (e.g., less than 40 in our example; [
25] p. 287). The model’s output is sectioned into four main categories. The first two sections are the variance parameters and regression coefficients from the model. The next section is the standardized solutions for the regression coefficients. The final section provides the variance explained by the regression coefficients (i.e.,
) and the residual variance. For example, our regression coefficients explained about 20% of the variance, and we are 95% confident the value lies between
and
.
In addition to a summary table for each model’s output, Blimp provides a similar table for the generated indirect quantity.
![Psych 04 00002 i006]()
Just like the proportion of variance explained metrics, this quantity is computed based upon the parameters themselves. Therefore, we obtain posterior summaries, including a 95% posterior interval. The output above illustrates that our indirect effect for the regression of pain severity on disability (i.e., ) ranges from to with 95% confidence. The final section of the output is the ancillary model for severity regressed on male. This output also prints out the same posterior summaries but is not of substantive interest. Rather, the model serves to produce imputations for the incomplete predictor, severity.
4.2. Single Mediator Model with a Moderator
To continue with our single mediator example, suppose we are interested in investigating if biological sex (
male) moderates the A and B paths of the mediation model. The path diagram in
Figure 4 adds these two additional paths (labeled
amod and
bmod in the diagram) with the arrows pointing to the labeled A and B paths. Estimating this model in Blimp is a straightforward extension from the previous example. Notably, the factorization that we discussed in the previous example remains unchanged. What does change is the form of the two substantive models; that is, the models now include the products between
male and
severity or
depress. Below we provide the syntax to extend the mediation model to include the moderated A and B paths.
# Specify the mediation with moderated paths
MODEL:
# Single-Mediator model with male moderating a and b paths
disability ∼ depress@bpath severity male depress*male@bmod;
depress ∼ severity@apath male severity*male@amod;
# Specify auxiliary variable model with one line
anxiety stress control ∼ disability depress severity male;
FIXED: male; # Specify no distribution for male
PARAMETERS: # Post compute the mediated effect
indirect.female = (apath + (amod * 0)) * (bpath + (bmod * 0));
indirect.male = (apath + (amod * 1)) * (bpath + (bmod * 1));
indirect.diff = indirect.female - indirect.male;
The above code builds on the previous script. First, we have included the male by depress interaction into the regression and labeled the parameter bmod. Similarly, we have included the male by severity interaction and labeled the parameter amod. Importantly, with these two products added to our regression models, the missing observations in both depress and severity will now be imputed by taking into account the hypothesized nonlinear relationship. Said differently, the likelihoods in the factorizations will directly include the interaction when drawing imputations for missing observations. We have opted to label each moderated path to compute the indirect effects for both males and females. Just like the previous example, we use the PARAMETERS command to post compute the quantities after the sampler estimates the model. The first two lines of the PARAMETERS command computes the indirect effect for females and males, respectively. The third line illustrates that in Blimp, we can use these computed values to calculate the difference in indirect effects between the two groups.
In addition to manually computing the mediated effect for both males and females, Blimp can also produce the conditional regression equations (sometimes referred to as simple effects) for both interactions via the following syntax.
# Specify Simple command to obtain
# conditional regressions
SIMPLE:
severity | male;
depress | male;
CENTER: severity depress; # Center variables
The SIMPLE command (shown above) can be added on to the script to compute the conditional effect of severity or depress given male equals zero (i.e., females) and one (i.e., males). The variable to the left of the vertical bar is the focal variable, and to the right is the moderator. In our example, because we have specified male as ordinal, Blimp will produce the conditional intercept and slope for each value of the variable. Finally, in line with a typical interaction analysis, we have centered both severity and depress using the CENTER command. Note, by using the CENTER command, Blimp uses the Bayesian estimated mean to center for both variables. This approach allows us to fully capture the mean estimates’ uncertainty and is especially important when the variables are incomplete.
Single Mediator Model with a Moderator Output
Upon running the script, much of the output will be similar to the previously discussed output. This section highlights some of the main differences, and we provide the entire output in the
supplemental material. From the model information, the output now displays that we have centered both
severity and
depress when being used as a predictor.
CENTERED PREDICTORS
Grand Mean Centered: severity depress
MODELS
[1] anxiety ∼ Intercept stress control disability depress severity male
[2] control ∼ Intercept disability depress severity male
[3] depress ∼ Intercept severity@apath male severity*male@amod
[4] disability ∼ Intercept depress@bpath severity male depress*male@bmod
[5] stress ∼ Intercept control disability depress severity male
GENERATED PARAMETERS
[1] indirect.female = (apath+(amod*0))*(bpath+(bmod*0))
[2] indirect.male = (apath+(amod*1))*(bpath+(bmod*1))
[3] indirect.diff = indirect.female-indirect.male
Note, the centering only occurs when one of the variables is a regressor in a model, and Blimp uses the model parameter for the variable’s mean. In addition to centering, we have the new parameter labels from our analysis models and the generated parameters for the mediated effect for males, females, and the difference between the two groups.
Turning to the output for the disability model again, we present a truncated output table with the standardized coefficients section removed (i.e., where the vertical ellipsis are).
![Psych 04 00002 i007]()
As discussed, we can see that both depress and severity are centered at their overall means for this model; thus, substantively speaking, the interpretation of the intercept is an adjusted mean for the female’s group. In addition, we now have the depress by male interaction, which resulted in an approximately incremental 2% gain in variance explained when compared to the previous model.
Following the disability model, Blimp prints an additional table that provides the conditional effects that we requested with the SIMPLE command.
![Psych 04 00002 i008]()
The table consists of two sets of conditional regression equations. The conditional equations for disability predicted by severity only differ in the intercept because there is no male by severity interaction in this regression. The second set of equations, disability predicted by depress, are the intercepts and slopes holding all other predictors constant at zero (i.e., their means). As with all the generated quantities, the conditional slopes also include 95% posterior intervals that give us a sense of the uncertainty around the parameter. Comparing the female and male slopes, we can see that the interval does not include the other posterior median, which would suggest the slope differences are meaningful and most likely not due to sampling variability.
Finally, the requested generated parameters provide us with the indirect effects for females, males, and the difference between the two effects.
![Psych 04 00002 i009]()
These effects include all the same summaries as before, providing point estimates for each indirect effect and 95% posterior intervals. For example, the output above illustrates that the indirect effect for both males and female are most likely not zero; however, the difference between the two groups is still quite uncertain with the wide posterior interval ranging from to .
4.3. Adding Latent Variables to the Mediation Model
As discussed, factored regression can incorporate measurement models as well. To illustrate the syntax in Blimp, let us look at specifying latent variables for the two multi-item scales:
depress and
disability.
Figure 5 is the path diagram for this model, where the latent factor for depression is normally distributed with seven items as indicators (
dep1 to
dep7; represented by a set of ellipses in the path diagram), and the latent factor for disability is normally distributed with six items as indicators (
disab1 to
disab6). As with our previous path diagrams, we have excluded the mean structure from the diagram. In addition, we have fixed the first item for both factors to one for identification.
The structural model’s factorization is similar to that of the single mediator model. The main difference is we are now replacing
depress and
disability with their latent variables,
and
. In addition to the structural model, we now must also factor out the measurement model. Multiplying that factorization to the structural model gives us the full functional notation.
The first line of the factorization above is the structural model, where we are evaluating the mediated effect:
. The second and third lines are the measurement models for the disability and depression factors. Although we have used ellipses instead of writing out the full factored measurement model, all the item models follow the same form. These densities are obtained using the logic we discussed for Equations (
19) and (
20). Alternatively, we can directly look at the path diagram and deduce that the items are conditionally independent given the latent variables. Finally, because each item is an ordinal variable, we include them in Blimp’s
ORDINAL command; therefore, in line with traditional ordinal factor analysis, their regression models will follow an ordered probit specification. Using the factorization that we discussed above, we can specify our model via the following Blimp model syntax.
# Declare latent variables
LATENT: eta_dep eta_disab;
# Single-Mediator model with male moderating a and b paths
MODEL:
# Structural Models
eta_disab ∼ eta_dep@bpath severity male eta_dep*male@bmod;
eta_dep ∼ severity@apath male severity*male@amod;
# Measurement Models
dep1 ∼ eta_dep@1; dep2 ∼ eta_dep; dep3 ∼ eta_dep;
dep4 ∼ eta_dep; dep5 ∼ eta_dep; dep6 ∼ eta_dep;
dep7 ∼ eta_dep;
disab1 ∼ eta_disab@1; disab2 ∼ eta_disab; disab3 ∼ eta_disab;
disab4 ∼ eta_disab; disab5 ∼ eta_disab; disab6 ∼ eta_disab;
The LATENT command specifies two new latent variables to add to our data set, eta_dep and eta_disab. By declaring these variables, Blimp will allow us to use them in the MODEL command. As discussed previously, these variables have every observation missing, and each iteration, Blimp will produce imputations via data augmentation according to the model we specified. Mapping onto how we generally conceptualize SEM, we have broken the model syntax down into the structural and measurement parts. The structural part maps onto the same form we specified earlier for the single mediator model. The only difference is replacing the manifest scale scores with their respective latent variables, eta_dep and eta_disab. By default, Blimp excludes the intercept for any latent variable; thus, fixing it to zero for identification. Turning to the measurement model, we specify the regression equations for the two latent variables. In line with standard SEM conventions, we fix the first loading to one (i.e., disab1 and dep1) by using the @ symbol followed by a one. While this syntax matches both the factorization and how Blimp conceptualizes the model, the syntax also allows specifying measurement models concisely using a right-pointing arrow (->).
# Compact syntax to specify measurement models.
eta_dep -> dep1:dep7;
eta_disab -> disab1:disab6;
The above syntax has two essential features. First, as already mentioned, we use a colon (:) between the names to list all variables names between dep1 to dep7 and disab1 to disab6. Second, when using a right-pointing arrow (->) to predict variables using a factor, by default, Blimp will fix the first variable’s loading to one. Additionally, note that using this syntax still requires the latent variable to be specified via the LATENT command.
Although not shown in
Figure 5, we have also included
anxiety,
stress, and
control as auxiliary variables. In line with the previous example, we predict every auxiliary variable as a function of all the other manifest variables in our model. As discussed, this will allow for the imputations on the missing analysis variables to account for the relationship to the auxiliary variables.
MODEL:
# Specify auxiliary variable model with one line
anxiety stress control ∼ disab1:disab6 dep1:dep7 severity male;
FIXED: male; # Specify no distribution for male
PARAMETERS: # Post compute the mediated effect
indirect.female = (apath + (amod * 0)) * (bpath + (bmod * 0));
indirect.male = (apath + (amod * 1)) * (bpath + (bmod * 1));
indirect.diff = indirect.female - indirect.male;
SIMPLE: # Specify conditional regressions
severity | male;
eta_dep | male;
CENTER: severity; # Center variables
In addition to specifying the models for the auxiliary variables, we specify that male is fixed with no distribution and post compute the mediated effect for both groups and the difference between the two effects. Finally, we center severity and request for the conditional regression effects for our two focal predictors given the moderator, male.
Latent Single Mediator Model with a Moderator Output
As with the previous example, we highlight some of the main differences in the output and supply the entire output in the
supplemental material. The first difference is the number of iterations required for convergence. By including the two latent variables and their ordinal items, the model parameters have gone from a little over thirty to over one hundred free parameters. Therefore, we requested a burn-in of thirty thousand and sampled fifty thousand iterations across four independent chains.
![Psych 04 00002 i010]()
As we can see from the PSR output, our previous burn-in period of one thousand is insufficient to reduce the PSR to acceptable ranges. Increasing the burn-in to thirty thousand adequately reduces the maximum PSR value down well below the 1.05 value suggested by the literature. Therefore, we have reason to believe that the sampler has converged.
Turning to the model printout, we went from five to eighteen conditional models, adding the seven depression and six disability items.
![Psych 04 00002 i013]()
Blimp will list all latent variables first, followed by the manifest variables in alphabetical order. Notably, we see that Blimp conceptualizes an item’s model as the regression of the item onto the latent factor. For example, below is the output for the dep2 regression model.
![Psych 04 00002 i011]()
First, the output has an additional section for the estimated threshold parameters in the ordered probit model. These thresholds break up a normally distributed latent propensity into the observed categories. The loading, , is the regression slope for the imputed values of eta_dep, and the standardized coefficient is analogous to the standardized solution in any confirmatory factor analysis. In addition, because there is only one predictor, the proportion of variance explained by the coefficients is equivalent to the estimate of dep2’s reliability under a factor analytic approach. As with other values, Blimp provides the posterior interval for this measure, characterizing the precision in the reliability coefficient.
Moving to the latent disability factor, we provide the output with the standardized coefficients output truncated.
![Psych 04 00002 i012]()
This output illustrates how conceptually nothing has changed compared to using a manifest scale score. The output is no different from any other regression model in Blimp, with estimates of the residual variance, regression coefficients, standardized coefficients (not shown), and the proportion of variance explained. Similarly, the output includes the latent eta_dep by manifest male interaction, and the imputations on eta_dep are drawn in accordance to the nonlinearity. When comparing the above results to the previous example, the scaling of the regression slopes has changed because of the latent variable. Despite this, we can see that we are explaining about 10% more variance with the latent variable ( versus with manifest scale score), and this is one of the advantages of incorporating a model to account for the measurement error.
Although we have not presented it, Blimp also produces the conditional regression coefficients and the generated parameters for the latent mediation model. Intrinsically, Blimp does not treat a latent variable differently from a manifest variable. The imputations for either variable are drawn following the factorization discussed throughout the paper and can be saved into multiply imputed data sets.