Real Estate Valuations with Small Dataset: A Novel Method Based on the Maximum Entropy Principle and Lagrange Multipliers

Abstract

Accuracy in property valuations is a fundamental element in the real estate market for making informed decisions and developing effective investment strategies. The complex dynamics of real estate markets, coupled with the high differentiation of properties, scarcity, and opaqueness of real estate data, underscore the importance of adopting advanced approaches to obtain accurate valuations, especially with small property samples. The objective of this study is to explore the applicability of the Maximum Entropy Principle to real estate valuations with the support of Lagrange multipliers, emphasizing how this methodology can significantly enhance valuation precision, particularly with a small real estate sample. The excellent results obtained suggest that the Maximum Entropy Principle with Lagrange multipliers can be successfully employed for real estate valuations. In the case study, the average prediction error for sales prices ranged from 5.12% to 6.91%, indicating a very high potential for its application in real estate valuations. Compared to other established methodologies, the Maximum Entropy Principle with Lagrange multipliers aims to be a valid alternative with superior advantages.

1. Introduction

In real estate markets, accuracy in property valuations is a fundamental element for making informed decisions and effective investment strategies. The complex dynamics that characterize real estate markets, together with the high differentiation of properties, make the adoption of advanced approaches crucial to obtaining accurate valuations [1,2].

However, this is countered by a frequent scarcity of real estate data and opaqueness of related markets, problems that can be found in various territorial contexts. The causes of these phenomena can be traced back to a series of factors, including resistance to change in the real estate sector, the lack of standardization in registration practices, the absence of regulatory requirements that mandate complete disclosure of information, the limitations or incompleteness of information in public data, and the reticence of private individuals in disclosing transaction prices. The relevance of the negative impacts of all these factors is evident in the understanding of real estate markets, property valuations, and investment decisions within the real estate sector due to information asymmetries [2].

In this framework, the Principle of Maximum Entropy emerges as a powerful tool, offering a new paradigm to address the challenges of real estate valuations.

Entropy is a fundamental concept in information theory and is closely associated with the idea of measuring uncertainty or randomness in a system [3]. The Maximum Entropy Principle proposes to select the probability distribution that reflects the maximum uncertainty, given a set of observed constraints. In other words, it involves choosing a distribution that is as neutral as possible with respect to the known information. Applying this principle to the field of real estate valuations entails balancing the complexity and variety of data, allowing statistical models to adapt naturally, guided by the maximum possible entropy [4].

The Maximum Entropy approach moves away from assuming additional information not supported by observed data, providing valuations that are, by definition, the result of an inference process based on maximum uncertainty. In the real estate field, this approach allows you to flexibly integrate different sources of information, reflecting a variety of variables that can influence the value of a property.

When dealing with optimization problems with constraints, as in the case of the general formulation of Maximum Entropy Principle, the Lagrange multipliers are often used to incorporate these constraints into the objective function. The goal is to find the maximum of objective function subject to the given constraints. Thus, the integration of the Maximum Entropy Principle with Lagrange multipliers enables the handling of constraints in probability appraisal. This approach allows us to find the probability distribution that maximizes the entropy given the constrained knowledge of the system, ensuring consistency with the available information [5,6].

From a logical point of view, the proposed methodological approach, not unlike other procedures, leads to determining the market value or income of a property through a comparison with prices of properties that have similar characteristics to the one being estimated. A prerequisite is that the comparative real estate data occurred recently in relation to the time of the valuation. While it is logical to assume that a greater number of comparison data leads to a better estimate result, the conducted experimentation considers a small sample of real estate sales sufficient for arriving at a reliable estimated value. Under this last aspect, the approach effectively addresses the challenge posed by the scarcity of data that characterizes real estate markets. The method in question estimates the value of a property by comparing its characteristics with those of comparable properties, in accordance with the “similia similibus aestimentur” criterion [7].

One of the operational limits currently associated with the use of the proposed innovative approach, based on Maximum Entropy Principle and Lagrange multipliers, is the practical impossibility of obtaining the marginal prices of features that influence the market price of an examined property, and due to this limit, it is not suitable for real estate mass appraisal.

In conclusion, the objective of this study is to explore the applicability of the Maximum Entropy Principle to real estate valuations with the support of Lagrange multipliers, emphasizing how this methodology can significantly enhance the precision of valuations.

The research starts with a literature review of the concept of entropy and existing studies on its applications in the real estate field. Subsequently, a mathematical discussion of the Principle of Maximum Entropy integrated with Lagrange multipliers is presented, being a necessary and fundamental part of understanding the logic and functioning of the novel proposed method. After a brief description of the study’s territorial context and real estate sample, the new method is applied to forecast the market prices of a small sample of real estate data (eight total observations, including the subject to be estimated). Finally, some critical considerations and perspectives for further future developments in the research are formulated.

2. Literature Review

The word “entropy” first appeared in 1864 in the context of a thermodynamics treatise by Rudolf Clausius, where it represents a state function that quantifies the unavailability of a system to produce work (in variational form, it is equal to the ratio between the amount of heat absorbed or released reversibly and isothermally by the system at a certain temperature considered). In accordance with its original definition, entropy, therefore, indicates which processes can occur spontaneously: the evolution of a system always proceeds in the direction of increasing entropy [8].

In 1870, with the development of statistical mechanics, J.W. Gibbs gave a new meaning to entropy, linked to the possible molecular arrangements of a system of particles. The Gibbs entropy (S) is defined as [9]:

$$S=-k_B{{\displaystyle \sum }}_i{p}_{i}ln{p}_i$$

(1)

where k_B is the Boltzmann constant and p_i is the probability that the system is in the i-th microstate. Maximizing the entropy function (S), the system reaches its equilibrium state. Equation (1) can be regarded as the fundamental definition of entropy, as all other expressions of S can be derived from (1) but not vice versa.

Subsequently, Boltzmann reworked Gibbs’s concept, defining entropy as the measure of the number of possible microstates of a system, given its macroscopic thermodynamic properties [10].

In 1948, Shannon introduced the concept of information entropy, demonstrating how it was possible to quantify the information contained in a message emitted by a source. He completely disregarded the semantic content of the term entropy, considering the quantity of information solely in probabilistic terms. The information is quantified through a function that measures the uncertainty of X, namely entropy, defined as [3]:

$$H\left(p_1,p_2,\dots ,p_p\right)=-K{{\displaystyle \sum }}_{i=1}^p{p}_{i}log{p}_i$$

(2)

where K is a positive and arbitrary constant that depends on the logarithmic base, and (p₁, …, p_p) are the probabilities of a set of possible events. In this case, entropy measures the amount of uncertainty or information present in a random signal.

Starting in 1957, Jaynes dedicated himself to demonstrating the connection between the physical concept of entropy and that of information theory, developing the Principle of Maximum Entropy. Through this principle, Jaynes showed how it was possible to determine probability distributions of a configuration from partial information. The basic idea is to leverage the available information and impose that the sought distribution is the one that maximizes Shannon’s entropy, as a measure of uncertainty and information quantity [4].

Over time, the concept of entropy has been employed in applications across various scientific domains [11], including econometrics [12,13], decision-making under uncertainty [14,15], market behaviors [16], the performance of stakeholders connected to informational advantages [17,18], investments, asset and portfolio returns, financial time-series forecasting, and valuation of manufacturing yields [19,20,21].

From these studies, it is inferred that the reduction of entropy can represent a concept of fundamental importance in the economic domain. Indeed, low entropy can govern economic values [22,23] or measure the scarcity and value of economic goods [24]. Similarly, the economic value of a good, incorporating complex, indeterminate, and anthropic features, derives from the law of entropy [25].

International studies specifically focused on the application of the concept of entropy in the real estate field are very limited.

Brown [26] first investigated the effectiveness of entropy in explaining the inefficiency of the real estate market, followed by Chen et al. [27].

The paper by Ge and Du (2007) investigates the main variables that influence residential property values in the Auckland property market (New Zealand) and ranks the variables using the Entropy method [28].

Lam et al. proposed in 2008 a mathematical model for predicting housing prices in Hong Kong based on the integration of entropy and artificial neural networks [29]. Subsequently, in 2009, the same authors implemented artificial neural networks with support vector machines to enhance the accuracy of real estate assessments in Hong Kong and mainland China. The identification of key real estate variables, which could influence property prices, has been addressed through an entropy-based rating and weighting method aimed at providing objective and reasonable weights [30].

In 2009, Zhou et al. dealt with a complex problem of multi-objective decision making in the real estate venture capital sector, where the weight was assigned based on base points and maximum entropy [31].

Salois and Moss developed a dynamic information measure in 2011 to examine the informational content of farmland values and farm income in explaining the distribution of farmland values over time [32].

The primary goal of Gnat’s 2019 study was a proposal to modify the classical entropy measure, enhancing its ability to accurately reflect the specificity of assessing the homogeneity of valued areas in the context of property market analysis [33].

In 2020, Kostic and Jevremovic addressed the topic of property attractiveness, where property image features are used to describe specific attributes and examine the influence of visual factors on the price or duration of real estate listings. They considered a set of techniques for extracting visual features for efficient numerical inclusion in modern predictive algorithms, including Shannon’s entropy, center of gravity calculation, image segmentation, and the use of Convolutional Neural Networks. They concluded that the employed techniques can effectively describe visible features, thus introducing perceived attractiveness as a quantitative measure in predictive modeling of housing [34].

The study by Basse et al. (2020) utilizes the concept of transfer entropy to examine the relationship between the US National Association of Home Builders Index and the S&P CoreLogic Case-Shiller 20-City Composite Home Price Index. The empirical evidence suggests that the survey data can contribute to predicting US house prices [35].

The last work in chronological order is Özdilek’s addressing in 2023 the incorporation of entropy measurements into real estate valuation, modifying and integrating triadic estimates of price, cost, and income; his results have significantly improved the precision of value measurement [11].

The above studies, where entropy is applied to various aspects or issues of the real estate markets, all highlight a common theme: a significant improvement in the predictive accuracy of the measured values.

3. Methodology

The proposed model is based on constrained optimization with Lagrange multipliers. The problem involves maximizing an objective function, which is the opposite of the sum of Shannon entropy weighted by real estate prices, subject to normalization constraints and consistency moments.

The model design consists of the following phases:

• market analysis for the identification of recent sales of similar properties;
• verification of information, considering whether the observed prices adhere to the definition of the market value estimation criterion, and whether the transactions belong to the specific market segment to which the property being appraised belongs;
• selection of elements of comparison (property features);
• definition of the objective function based on Shannon’s Entropy, capable of incorporating the sum of products between the optimal weights of property features and the corresponding prices from the estimated sample data;
• setting variability and normalization constraints, as well as moments of consistency for real estate variables;
• definition of the Lagrangian function that includes the specified constraints, followed by the redefinition of the objective function that returns the sum of the Lagrangians;
• processing the solution and optimal value of the objective function, with the definition of weights for each optimal solution.

The foundational core of the proposed methodology lies in integrating the Maximum Entropy Principle with Lagrange multipliers. This integration provides a powerful approach to dealing complex optimization and inference problems, ensuring efficient handling of constraints, and preserving information with the maximum uncertainty allowed by the available data. In this way, the incorporation of additional information into the optimization problem is allowed, especially when dealing with complex problems featuring multiple constraints or when seeking a probability distribution that adheres to specific characteristics. To execute the model, access to a MATLAB environment or a similar computational platform is required [36].

Let us see in formal terms what applying the Maximum Entropy Principle with Lagrange multipliers involves [5,6,37].

Consider a system described by a set of state variables: {x₁, x₂, …, x_N} ≡ x, where each possible configuration has a certain probability of being observed. The probability of a state, in this case, cannot be thought of in a frequentist sense but rather should be understood as our knowledge of the system. Since one often deals with systems of very high dimensionality, with N being very large, it is convenient to study the distribution of suitable functions of the states.

Therefore, quantities related to the configuration are defined, f₁(x), f₂(x), …, f_K(x), which summarize some properties of a system, and whose average values 〈f_ν(x)〉_exp can be calculated. The distribution P(x) is then sought such that the average values of the K considered functions, 〈f_ν(x)〉_exp observed experimentally, coincide with their expected values 〈f_ν(x)〉_P with respect to the distribution.

The following expression for the entropy function is considered:

$$S\left[P\right]=-{{\displaystyle \sum }}_{x}P\left(x\right)lnP\left(x\right)$$

(3)

and the constrained maximization problem is solved, where the constraints are given by the partial information available, imposing:

$${\langle f_v\left(x\right)\rangle }_{exp}={\langle f_v\left(x\right)\rangle }_P\equiv {{\displaystyle \sum }}_{x}P\left(x\right)f_v\left(x\right)$$

(4)

with v = 0, …, K. Since the probability distribution must be normalized, the following technique is used: we choose f₀(x) = 1 and impose that it is equal to the experimental value 1. To solve the problem, Lagrange multipliers are used, introducing the K parameters {λ_μ} and the generalized entropy function:

$$S\left[P;\left\{{\lambda }_{\mu }\right\}\right]=S\left[P\right]-{{\displaystyle \sum }}_{\mu =0}^K{\lambda }_{\mu }\left[{\langle f_{\mu }\left(x\right)\rangle }_P-{\langle f_{\mu }\left(x\right)\rangle }_{exp}\right]$$

(5)

The optimization is then performed on S[P; {λ_μ}] with respect to the probability P(x) and the parameters, imposing two conditions.

A first condition:

$$0=\frac{\mathsf{\partial }S\left[P;\left\{{\lambda }_{\mu }\right\}\right]}{\mathsf{\partial }P\left(x\right)}=\frac{\mathsf{\partial }S\left[P\right]}{\mathsf{\partial }P\left(x\right)}-{{\displaystyle \sum }}_{\mu =0}^K{\lambda }_{\mu }\frac{\mathsf{\partial }{\langle f_{\mu }\left(x\right)\rangle }_P}{\mathsf{\partial }P\left(x\right)}=-lnP\left(x\right)-1-{{\displaystyle \sum }}_{\mu =0}^K{\lambda }_{\mu }{f}_{\mu }\left(x\right)$$

(6)

from which we obtain:

$$P_{me}\left(x\right)=\frac{1}{Z\left({\lambda }_v\right)}exp\left[-{{\displaystyle \sum }}_{\mu =1}^K{\lambda }_{\mu }{f}_{\mu }\left(x\right)\right]$$

(7)

with Z_me({λ_ν}) = S_x exp(−λ₀ − 1). Normalizing with respect to λ₀ is equivalent to normalizing the distribution, so it can be explicitly written as:

$$Z_{me}\left(\left\{{\lambda }_{\mu }\right\}\right)={{\displaystyle \sum }}_{x}exp\left[-{{\displaystyle \sum }}_{\mu =1}^K{\lambda }_{\mu }{f}_{\mu }\left(x\right)\right]$$

(8)

A second condition:

$$0=\frac{\mathsf{\partial }S\left[P;\left\{{\lambda }_{\mu }\right\}\right]}{\left\{\mathsf{\partial }{\lambda }_{\mu }\right\}}={\langle f_{\mu }\left(x\right)\rangle }_P-{\langle f_{\mu }\left(x\right)\rangle }_{exp}$$

(9)

from this, it can be seen that maximizing the generalized entropy with respect to the parameters {λ_ν} is equivalent to imposing that the averages of the considered functions measured experimentally coincide with the values predicted by the distribution. Writing explicitly 〈f_μ(x)〉_P and substituting in it the expression of P(x) found in (7), we have:

$${\langle f_{\mu }\left(x\right)\rangle }_{exp}=\frac{1}{Z\left({\lambda }_v\right)}{{\displaystyle \sum }}_x{f}_{\mu }\left(x\right)exp\left[-{{\displaystyle \sum }}_{\mu =1}^K{\lambda }_{\mu }{f}_{\mu }\left(x\right)\right]$$

(10)

Substituting the distribution P_me(x) into (5), we obtain the following expression for the generalized entropy:

$$S\left[P;\left\{{\lambda }_{\mu }\right\}\right]=lnZ\left(\left\{{\lambda }_v\right\}\right)+{{\displaystyle \sum }}_{\mu =0}^K{\lambda }_{\mu }{\langle f_{\mu }\left(x\right)\rangle }_{exp}$$

(11)

This last expression coincides with the logarithm of the probability that the model generates the observed data, namely the logarithm of the likelihood.

The Maximum Entropy Principle is based on the concept of distributional divergence of observed data and, therefore, does not guarantee the fulfillment of a result based on minimum variance, a preferential requirement in cases where estimating the value for predictive purposes is necessary. For this reason, Equation (3) may also be supplemented, as needed, with an additional optimization constraint based on the measurement of standard deviation or variance.

In practical terms, concerning the price variable in the context of real estate properties, a higher standard deviation could indicate greater variability in property prices, with some properties having significantly higher or lower prices than the average. On the other hand, a lower standard deviation might suggest that property prices are more homogeneous and closer to the mean. When using standard deviation as a constraint in an optimization problem, it is possible to adjust this parameter to model the desired tolerance regarding data variability. For instance, a constraint based on standard deviation could be employed to impose limits on the variability of weights assigned to variables in the optimized model. In analytical terms:

$${{\displaystyle \sum }}_{i=1}^h{w}_i{\left[Pric{e}_i-V^{*}\right]}^2\le {\sigma }^2$$

(12)

with i = 1, …, h, and where h represents the observed comparable properties, Price_i denotes the sales price of the i-th property, w_i corresponds to the optimal weights for each i-th property, V* is the estimated value of the subject determined by the optimal set of weights w_i.

All this can be interpreted as an additional penalty to the model based on the deviation of the price variable from its mean, fixing a desired value for a quantity associated with the standard deviation of real estate prices.

4. Empirical Demonstration: Materials and Results

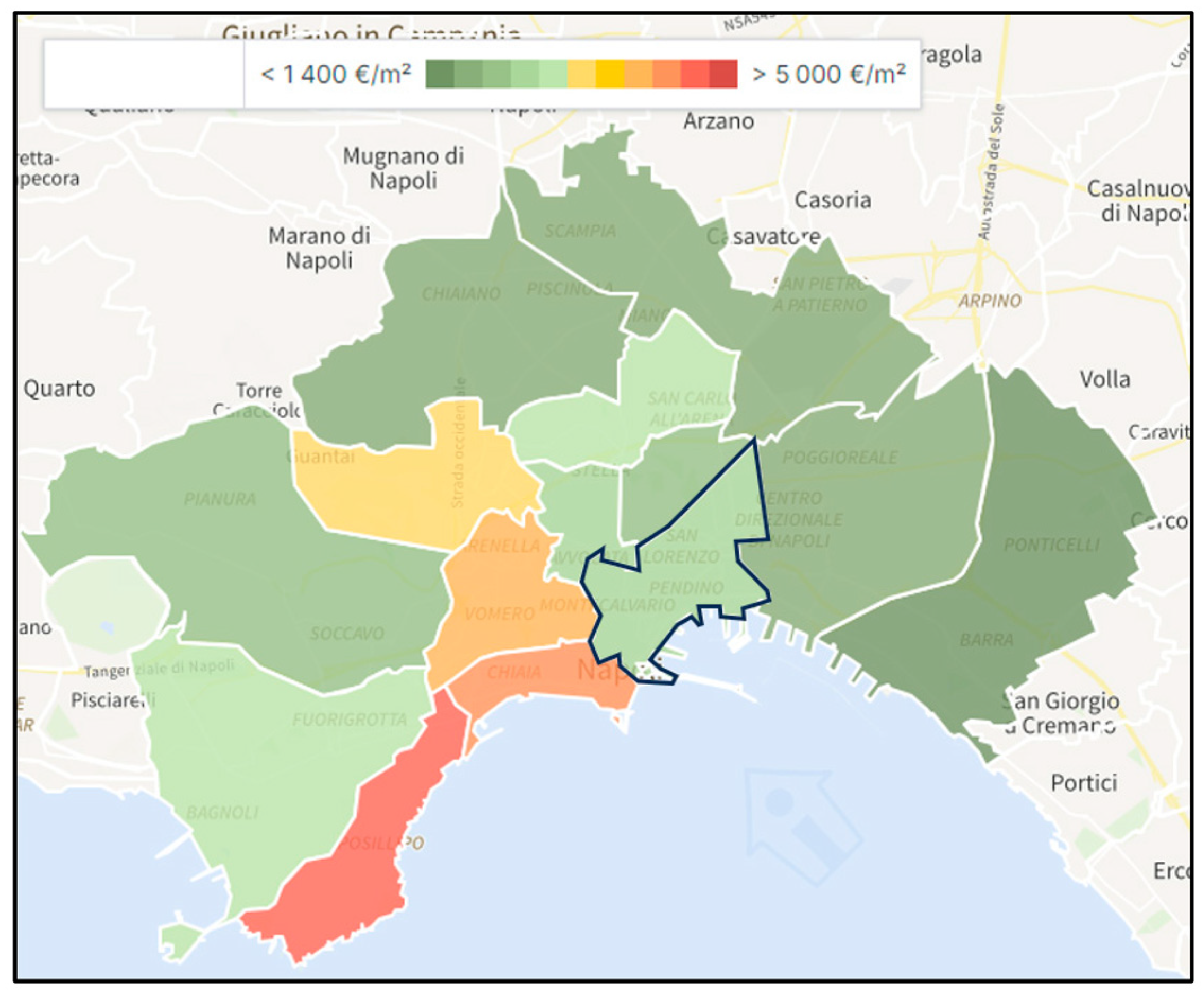
4.1. Context of the Dataset

Naples is an Italian city of approximately 910,000 inhabitants, the third largest in Italy by population, capital of the Campania Region, the metropolitan city of the same name and the center of one of the most populous and densely populated metropolitan areas in Europe [38]. Considered one of the great Italian and global tourist destinations, Naples is divided into 10 administrative municipalities of approximately one hundred thousand inhabitants each [39].

The average prices of residential properties in the city of Naples, updated to November 2023, are equal to €/sqm 2802, recording an increase of 3.47% compared to November 2022 (€/sqm 2708). In the last 2 years, the average price within the city of Naples reached its maximum in the month of October 2023, with a value of €2816 per square meter. The month in which the lowest price was requested was January 2022: an average of €2682 per square meter was requested for a property for sale [40]. The sample of comparables was drawn from the “Centre” area, where, in November 2023, residential properties for sale recorded an average offer price of €2304 per square meter, with an increase of 7.61% compared to November 2022 (€/sqm 2141) [40]. A general overview of the average real estate values for the residential segment of Naples is shown in Figure 1.

4.2. Data Specification

In accordance with phases 1 and 2 of the proposed model, the analysis of the reference real estate market segment has led to the identification of only eight real estate data points in the “Center” area of Naples. Specifically, the sample of real estate data consists of eight properties located in multi-story condominiums and sold in 2023 (last six months). These properties are situated in a homogeneous urban area in terms of qualification and distribution of key services. Only nonhomogeneous real estate characteristics were detected for each sampled unit and, in particular (see

Table 1. Real estate dataset.

Comparable	ROOMS	BATH	SUR	LEV	MAIN	PRICE
No. 1	4	1	130	3	2	490,000
No. 2	5	3	130	2	2	530,000
No. 3	5	2	125	1	1	595,000
No. 4	4	2	122	4	2	530,000
No. 5	5	1	150	2	1	560,000
No. 6	3	3	160	2	1	635,000
No. 7	4	2	110	3	1	530,000
No. 8	4	2	120	4	1	520,000

and

Table 2. Statistical description of real estate dataset.

Index	ROOMS	BATH	SUR	LEV	MAIN	PRICE
Mean	4.25	2.00	130.88	2.63	1.38	548,750.00
Std. Error	0.25	0.27	5.80	0.38	0.18	16,386.79
Median	4.00	2.00	127.50	2.50	1.00	530,000.00
Std. Deviation	0.71	0.76	16.40	1.06	0.52	46,348.83
Kurtosis	−0.23	−0.70	0.14	−0.94	−2.24	0.52
Asimmetry	−0.40	0.00	0.88	0.04	0.64	0.95
Minimum	3.00	1.00	110.00	1.00	1.00	490,000.00
Maximum	5.00	3.00	160.00	4.00	2.00	635,000.00
Confidence Level (95.0%)	0.59	0.63	13.71	0.89	0.43	38,748.59

):

• real estate sale price expressed in euro (PRICE);
• commercial area of housing unit expressed in square meters, i.e., the sum of the internal area plus eventual other secondary areas virtualized through specific coefficients used in the respective real estate market (SUR);
• number of floor levels of housing units (LEV);
• maintenance status (MAIN) expressed with a score scale: two if the housing unit is in optimal condition, one if maintenance status is good, and zero otherwise (mediocre status);
• number of rooms constituting the housing unit (ROOMS);
• number of bathrooms in the housing unit (BATH).

Other real estate characteristics, manifesting with the same modalities in all the sampled units, were excluded from the dataset.

4.3. Results

Having defined the real estate sample, the methodology based on the Maximum Entropy Principle integrated with Lagrange multipliers was applied, assuming that, alternatively and individually, each comparable in the real estate sample constitutes the subject for which the value is to be determined. This allowed for effective testing of the methodology and avoiding the randomness of the result obtained on a single subject.

All the elaborations were performed using MATLAB software vers. 9.0.0 [36].

For each subject, the solution and optimal value of the objective function were then processed, along with the definition of weights for each optimal solution. In general, to obtain the predicted probabilities for a specific observation, you can use the optimal weights obtained from the optimization process and then apply them to the prediction function. In the case of interest, optimal weights for the variables ROOMS, BATH, SUR, LEV, and MAIN were obtained during the optimization process (see

Table 3. Solutions for comparable no. 1 (if considered as subject).

Comparable	Optimal Weights (wi)					Optimal Solution (Oi)	Comparable Sale Price (Pi)	Contribution to the Estimated Value (Oi∙Pi)
	ROOMS	BATH	SUR	LEV	MAIN
8	0.0067	0.0235	0.0000	0.0078	0.0229	0.0610	€520,000.00	€31,720.00
2	0.0235	0.0826	0.0000	0.0275	0.0806	0.2143	€530,000.00	€113,579.00
3	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	€595,000.00	€0.00
4	0.0078	0.0275	0.0000	0.0092	0.0269	0.0714	€530,000.00	€37,842.00
5	0.0229	0.0806	0.0000	0.0269	0.0787	0.2091	€560,000.00	€117,096.00
6	0.0151	0.0531	0.0000	0.0177	0.0518	0.1377	€635,000.00	€87,439.50
7	0.0336	0.1182	0.0000	0.0394	0.1153	0.3065	€530,000.00	€162,445.00
Estimated Value for Comparable no. 1 (Sum of contributions Oi∙Pi)								€550,121.50
Optimal Value of objective function								−2.75 × 106

,

Table 4. Solutions for comparable no. 2 (if considered as subject).

Comparable	Optimal Weights (wi)					Optimal Solution (Oi)	Comparable Sale Price (Pi)	Contribution to the Estimated Value (Oi∙Pi)
	ROOMS	BATH	SUR	LEV	MAIN
1	0.0555	0.0737	0.0555	0.0171	0.0166	0.2184	€490,000.00	€107,016.00
8	0.0737	0.0978	0.0737	0.0227	0.0220	0.2898	€520,000.00	€150,696.00
3	0.0555	0.0737	0.0555	0.0171	0.0166	0.2184	€595,000.00	€129,948.00
4	0.0171	0.0227	0.0171	0.0053	0.0051	0.0673	€530,000.00	€35,669.00
5	0.0166	0.0220	0.0166	0.0051	0.0049	0.0652	€560,000.00	€36,512.00
6	0.0358	0.0475	0.0358	0.0110	0.0107	0.1408	€635,000.00	€89,408.00
7	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	€530,000.00	€0.00
Estimated Value for Comparable no. 2 (Sum of contributions Oi∙Pi)								€549,249.00
Optimal Value of objective function								−2.75 × 106

,

Table 5. Solutions for comparable no. 3 (if considered as subject).

Comparable	Optimal Weights (wi)					Optimal Solution (Oi)	Comparable Sale Price (Pi)	Contribution to the Estimated Value (Oi∙Pi)
	ROOMS	BATH	SUR	LEV	MAIN
1	0.0716	0.0573	0.0823	0.0000	0.0268	0.2381	€490,000.00	€116,669.00
2	0.0573	0.0459	0.0659	0.0000	0.0215	0.1905	€530,000.00	€100,965.00
8	0.0823	0.0659	0.0946	0.0000	0.0308	0.2736	€520,000.00	€142,272.00
4	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	€530,000.00	€0.00
5	0.0268	0.0215	0.0308	0.0000	0.0101	0.0892	€560,000.00	€49,952.00
6	0.0412	0.0329	0.0473	0.0000	0.0154	0.1368	€635,000.00	€86,868.00
7	0.0216	0.0173	0.0249	0.0000	0.0081	0.0719	€530,000.00	€38,107.00
Estimated Value for Comparable no. 3 (Sum of contributions Oi∙Pi)								€534,833.00
Optimal Value of objective function								−2.67 × 106

,

Table 6. Solutions for comparable no. 4 (if considered as subject).

Comparable	Optimal Weights (wi)					Optimal Solution (Oi)	Comparable Sale Price (Pi)	Contribution to the Estimated Value (Oi∙Pi)
	ROOMS	BATH	SUR	LEV	MAIN
1	0.0178	0.0349	0.0008	0.0000	0.0431	0.0966	€490,000.00	€47,334.00
2	0.0349	0.0684	0.0015	0.0000	0.0843	0.1891	€530,000.00	€100,223.00
3	0.0008	0.0015	0.0000	0.0000	0.0019	0.0042	€595,000.00	€2499.00
8	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	€520,000.00	€0.00
5	0.0431	0.0843	0.0019	0.0000	0.1040	0.2332	€560,000.00	€130,592.00
6	0.0260	0.0509	0.0011	0.0000	0.0628	0.1408	€635,000.00	€89,408.00
7	0.0621	0.1215	0.0027	0.0000	0.1498	0.3361	€530,000.00	€178,133.00
Estimated Value for Comparable no. 4 (Sum of contributions Oi∙Pi)								€548,189.00
Optimal Value of objective function								−2.74 × 106

,

Table 7. Solutions for comparable no. 5 (if considered as subject).

Comparable	Optimal Weights (wi)					Optimal Solution (Oi)	Comparable Sale Price (Pi)	Contribution to the Estimated Value (Oi∙Pi)
	ROOMS	BATH	SUR	LEV	MAIN
1	0.0654	0.0677	0.0188	0.0000	0.0586	0.2106	€490,000.00	€103,194.00
2	0.0677	0.0701	0.0195	0.0000	0.0607	0.2179	€530,000.00	€115,487.00
3	0.0188	0.0195	0.0054	0.0000	0.0168	0.0605	€595,000.00	€35,997.50
4	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	€530,000.00	€0.00
8	0.0586	0.0607	0.0168	0.0000	0.0525	0.1887	€520,000.00	€98,124.00
6	0.0421	0.0436	0.0121	0.0000	0.0377	0.1355	€635,000.00	€86,042.50
7	0.0580	0.0600	0.0167	0.0000	0.0520	0.1867	€530,000.00	€98,951.00
Estimated Value for Comparable no. 5 (Sum of contributions Oi∙Pi)								€537,796.00
Optimal Value of objective function								−2.69 × 106

,

Table 8. Solutions for comparable no. 6 (if considered as subject).

Comparable	Optimal Weights (wi)					Optimal Solution (Oi)	Comparable Sale Price (Pi)	Contribution to the Estimated Value (Oi∙Pi)
	ROOMS	BATH	SUR	LEV	MAIN
1	0.0099	0.0198	0.0045	0.0216	0.0270	0.0827	€490,000.00	€40,523.00
2	0.0198	0.0396	0.0090	0.0431	0.0539	0.1654	€530,000.00	€87,662.00
3	0.0045	0.0090	0.0020	0.0098	0.0123	0.0376	€595,000.00	€22,372.00
4	0.0216	0.0431	0.0098	0.0470	0.0588	0.1804	€530,000.00	€95,612.00
5	0.0270	0.0539	0.0123	0.0588	0.0736	0.2256	€560,000.00	€126,336.00
8	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	€520,000.00	€0.00
7	0.0369	0.0737	0.0168	0.0804	0.1006	0.3083	€530,000.00	€163,399.00
Estimated Value for Comparable no. 6 (Sum of contributions Oi∙Pi)								€535,904.00
Optimal Value of objective function								−2.68 × 106

,

Table 9. Solutions for comparable no. 7 (if considered as subject).

Comparable	Optimal Weights (wi)					Optimal Solution (Oi)	Comparable Sale Price (Pi)	Contribution to the Estimated Value (Oi∙Pi)
	ROOMS	BATH	SUR	LEV	MAIN
1	0.0760	0.0714	0.0316	0.0000	0.0421	0.2211	€490,000.00	€108,339.00
2	0.0714	0.0670	0.0297	0.0000	0.0395	0.2075	€530,000.00	€109,975.00
3	0.0316	0.0297	0.0131	0.0000	0.0175	0.0919	€595,000.00	€54,680.50
4	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	€530,000.00	€0.00
5	0.0421	0.0395	0.0175	0.0000	0.0233	0.1224	€560,000.00	€68,544.00
6	0.0468	0.0439	0.0194	0.0000	0.0259	0.1360	€635,000.00	€86,360.00
8	0.0760	0.0714	0.0316	0.0000	0.0421	0.2211	€520,000.00	€114,972.00
Estimated Value for Comparable no. 7 (Sum of contributions Oi∙Pi)								€542,870.50
Optimal Value of objective function								−2.71 × 106

and

Table 10. Solutions for comparable no. 8 (if considered as subject).

Comparable	Optimal Weights (wi)					Optimal Solution (Oi)	Comparable Sale Price (Pi)	Contribution to the Estimated Value (Oi∙Pi)
	ROOMS	BATH	SUR	LEV	MAIN
1	0.0622	0.0739	0.0051	0.0000	0.0546	0.1958	€490,000.00	€95,942.00
2	0.0739	0.0879	0.0060	0.0000	0.0649	0.2328	€530,000.00	€123,384.00
3	0.0051	0.0060	0.0004	0.0000	0.0045	0.0160	€595,000.00	€9520.00
4	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	€530,000.00	€0.00
5	0.0546	0.0649	0.0045	0.0000	0.0479	0.1718	€560,000.00	€96,208.00
6	0.0429	0.0509	0.0035	0.0000	0.0376	0.1349	€635,000.00	€85,661.50
7	0.0790	0.0939	0.0065	0.0000	0.0693	0.2487	€530,000.00	€131,811.00
Estimated Value for Comparable no. 8 (Sum of contributions Oi∙Pi)								€542,526.50
Optimal Value of objective function								−2.71 × 106

). In more operational terms, this means that to obtain a specific appraisal for a subject, the initialization vector of values needs to be adjusted to provide a starting point closer to the desired solution for optimization. Alternatively, it is possible to add tighter constraints for the moments of consistency, to require the system that the variables take on the desired values. Both options should lead to similar results if configured correctly.

After estimating the market value for each individual subject in correspondence to the optimal solution, the model was reapplied for each of them, considering the application of an exogenous nonlinear limit (upper limit of the standard deviation for the PRICE variable), in accordance with relation (12), significantly increasing the degree of estimation complexity. A constraint so imposed could have relevant meaning, for example, when there is nonsample information available, in terms of subjective upper or lower bounds on the final value estimate. With this aim, the constraint can be incorporated into the model to meet this requirement.

Table 11. Optimal solutions of the objective function for different standard deviation values.

Comparable	σ = €5000		σ = €10,000		σ = €20,000
	Estimated Value	% Error	Estimated Value	% Error	Estimated Value	% Error
1	€557,444.00	13.76%	€557,859.00	13.85%	€558,570.00	13.99%
2	€551,786.00	4.11%	€552,190.00	4.19%	€552,852.50	4.31%
3	€542,508.00	−8.82%	€542,801.00	−8.77%	€543,568.00	−8.64%
4	€551,787.00	4.11%	€552,144.50	4.18%	€552,860.50	4.31%
5	€547,492.50	−2.23%	€547,805.00	−2.18%	€548,520.50	−2.05%
6	€536,946.50	−15.44%	€661,361.50	4.15%	€806,879.50	27.07%
7	€551,781.50	4.11%	€552,141.50	4.18%	€552,913.00	4.32%
8	€553,210.50	6.39%	€553,517.00	6.45%	€554,237.00	6.58%

presents the optimal solution of the objective function imposing a specific upper limit on the standard deviation of the PRICE variable, set, for example, at €5000, €10,000, and €20,000.

In Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9 and Table 10, varying the sample estimate also changes the incidence of weights, expressing a “ranking” of real estate characteristics for the respective sample estimate considered each time. The sum of the products between the optimal feature weights and the corresponding prices was also incorporated into the objective function. However, the formulation of the objective function and constraints can be further customized to one’s specific needs.

The main results obtained from Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10 and Table 11 are summarized in

Table 12. Results summary.

Comparable	Sale Price	Maximum Entropy Basic Model		Best Fit (Basic/σ Upper Limit)
		% Error	Estimated Value	% Error	Estimated Value
1	€490,000	12.27%	€550,121.50	12.27%	€550,121.50
2	€530,000	3.63%	€549,249.00	3.63%	€549,249.00
3	€595,000	−10.11%	€534,833.00	−8.64%	€543,568.00
4	€530,000	3.43%	€548,189.00	3.43%	€548,189.00
5	€560,000	3.43%	€537,796.00	−2.05%	€548,520.50
6	€635,000	−15.61%	€535,904.00	4.15%	€661,361.50
7	€530,000	2.43%	€542,870.50	2.43%	€542,870.50
8	€520,000	4.33%	€542,526.50	4.33%	€542,526.50
Mean absolute % error		6.91%	Mean absolute % error	5.12%

, where observed real estate prices and corresponding values estimated by the model are reported, along with the percentage divergences between them. These divergences are categorized into two clusters: the Maximum Entropy “basic” model and the “best fit” model.

In the “basic” model, the results pertain to the definition of the objective function based on Shannon’s Entropy, as well as the Lagrangian function that includes constraints related to variability, normalization, and coherence moments for real estate variables. In the “best fit” column, improved results compared to the basic model are presented when an additional constraint is incorporated, namely an upper limit on the standard deviation concerning the “PRICE” variable.

In the basic model, the absolute percentage error ranges from a minimum of 2.43% to a maximum of 15.61%, with an average absolute error percentage of 6.91%. Regarding the “best fit” solution, the absolute percentage error varies from a minimum of 2.43% to a maximum of 12.27%, with an average absolute error percentage of 5.12%. In the latter case, the results show significant improvements, especially in cases where errors were higher in the basic model: for comparable three, the error changes from −10.11% to −8.64%. For comparable five, the error changes from 3.43% to −2.05%, and for comparable six, the error changes from −15.61% to −4.15%.

5. Discussion

The results obtained through the application of the proposed method are excellent and suggest that the Maximum Entropy Principle with Lagrange multipliers can be successfully used for real estate valuations. In the case study, the average prediction error for sales prices ranged from 5.12% to 6.91%, indicating a very high potential for its application in real estate valuations.

The proposed methodology has demonstrated particularly strong adaptability in cases where small real estate samples, consisting of a limited number of transaction data points, are necessary. This is due to spatial and temporal limitations in data collection, the atypicality and complexity of real estate, as well as challenges in certain national contexts (e.g., Italy) arising from difficulties in obtaining and verifying market prices. The most common purposes to which the model can be applied include real estate sale or purchase, mortgage or financing, inheritance or judicial divisions, legal disputes, regeneration and real estate development operations, leasing or rent, asset valuations, insurance, and regulatory compliance.

In practical circumstances, the real estate samples may be so small as to preclude the use of statistical tools designed for samples categorized as small or very small in the statistical sense [41,42].

In these latter circumstances, the so-called “Appraisal System” (or “General Appraisal System”, SGA) and the “Market Comparison Approach” (MCA) have traditionally represented the only paradigm capable of providing a quantitative measure of the value of a property [43]. Compared to these established methodologies, the Maximum Entropy Principle with Lagrange multipliers aims to be a valid alternative with superior advantages.

Among the drawbacks of SGA is the strong instability in solving the mathematical system that supports it in the presence of possible anomalies or outliers, with direct consequences on the estimation of marginal prices of real estate characteristics considered for comparison. In MCA, marginal prices are almost always determined empirically, so their estimation might not accurately reflect the dynamics of real estate market price formation. Unlike these limitations, the method proposed in this study does not require inferring marginal prices of real estate characteristics and demonstrates considerable stability from a computational perspective. This is because entropy is exploited as a tool for modeling: by using the Maximum Entropy method, it is possible to determine the probability of a configuration or set of real estate characteristics for the purpose of property valuation.

Future developments of the methodology certainly concern the minimum size of the real estate sample necessary to implement the methodology, the incorporation of qualitative features in the dataset (e.g., architectural, cultural or environmental resources, panoramic views, etc.), the study of constraints and parameters capable of optimizing the result computationally, and the potential integration with other statistical methodologies to explain the marginal prices of real estate characteristics considered in the model (e.g., hedonic price models).

6. Conclusions

In the dynamic landscape of the real estate sector, the accuracy of property valuations has become a crucial element for market operators, investors, and industry professionals. The increasing complexity of factors influencing property values requires a more sophisticated approach, where scientific research and the use of advanced computational tools become essential. This study aimed to explore the convergence between scientific research and the practical needs of real estate valuation, highlighting the importance of robust and accurate statistical models to address current and future challenges in the real estate sector.

Traditional real estate valuations, based on conventional approaches, can often underestimate the complexity of market dynamics, macroeconomic trends, and specific property characteristics. The need for more in-depth analysis is evident, pushing industry experts to increasingly turn to advanced statistical tools to obtain more reliable and informed estimates.

The Maximum Entropy Principle applied in this study allows deriving models substantially analogous to those of Statistical Mechanics, without the need to formulate any specific hypotheses to develop models describing the statistical behavior of an economic system. This is not the first time that economic sciences draw from the “hard” sciences, or vice versa, namely scientific disciplines that use quantitative, empirical, and often experimental methods to study natural phenomena. However, compared to the past, the current perspective is entirely new: no longer are universal laws sought to define the economic nature of a good according to a deterministic view of reality, but rather, there are some fundamental mechanisms that naturally emerge in a network of interconnected elements, regardless of the nature of the network itself. There are, in other words, some dynamics that repeat when there is a set of interacting units, be they humans, particles, or economic goods and systems. Often, in practice, recourse is made to mean-field models, which imply strong assumptions and simplifications, but in reality, the interactions between individual units of a system do not always have constant intensity.

In this context, the present research aims to represent a significant innovation in real estate valuation methodologies. Currently, the utilization of sophisticated statistical models and the integration of complex variables are crucial aspects for overcoming the limitations of traditional valuations.