A Finite Element Model for Trigger Finger
Abstract
:1. Introduction
2. Results
2.1. Outline of Results
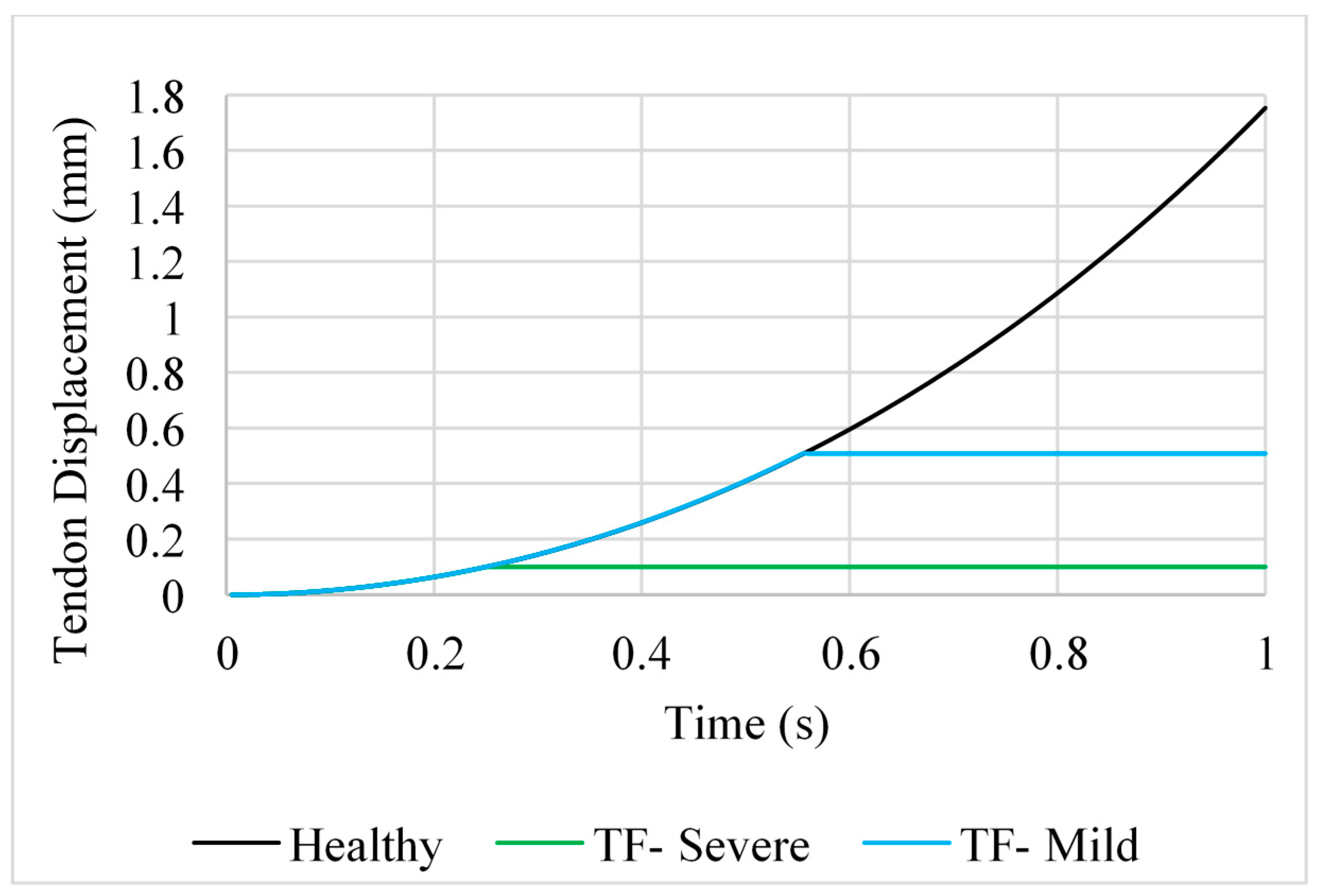
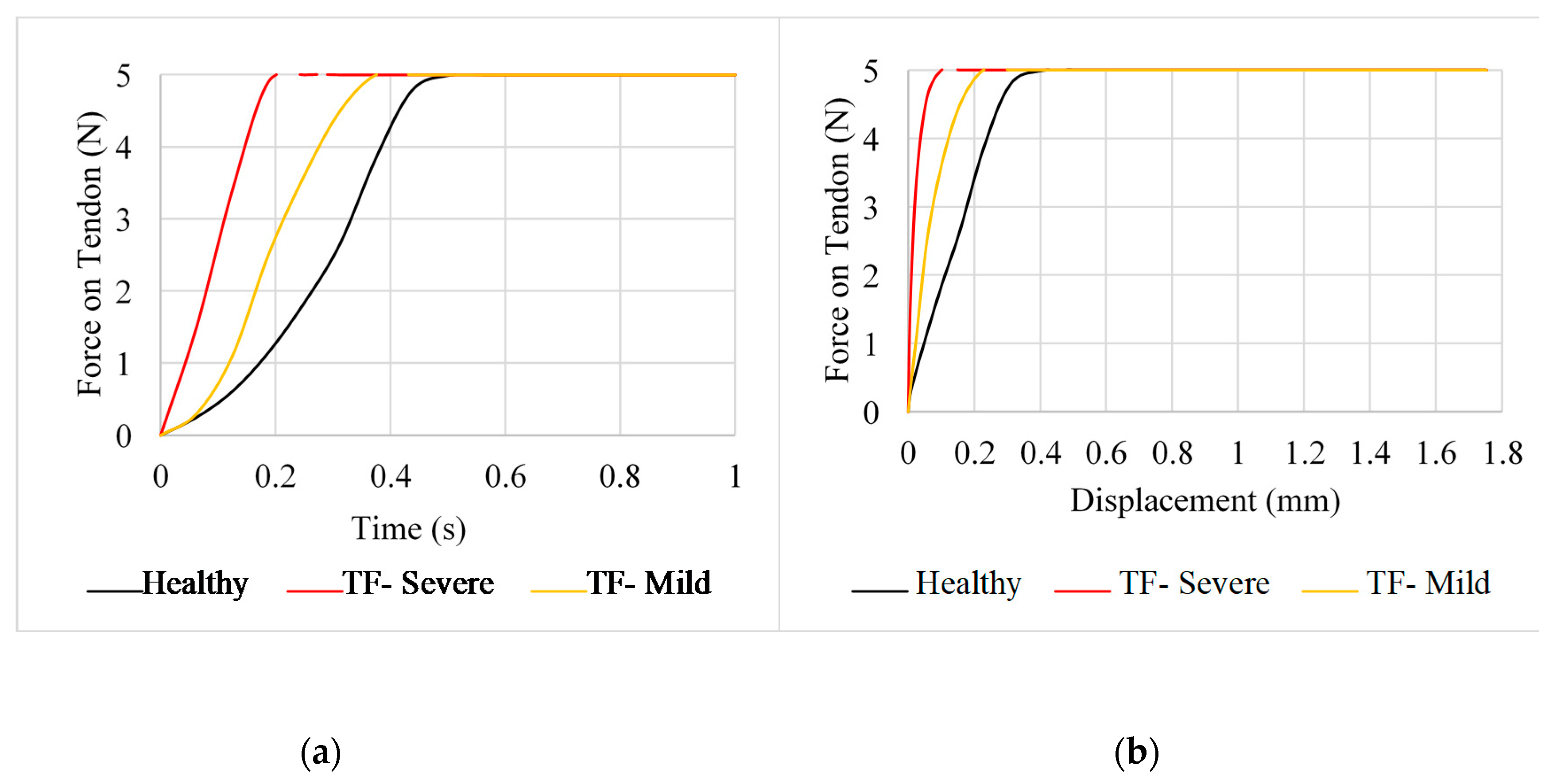
2.2. Position A—Extension
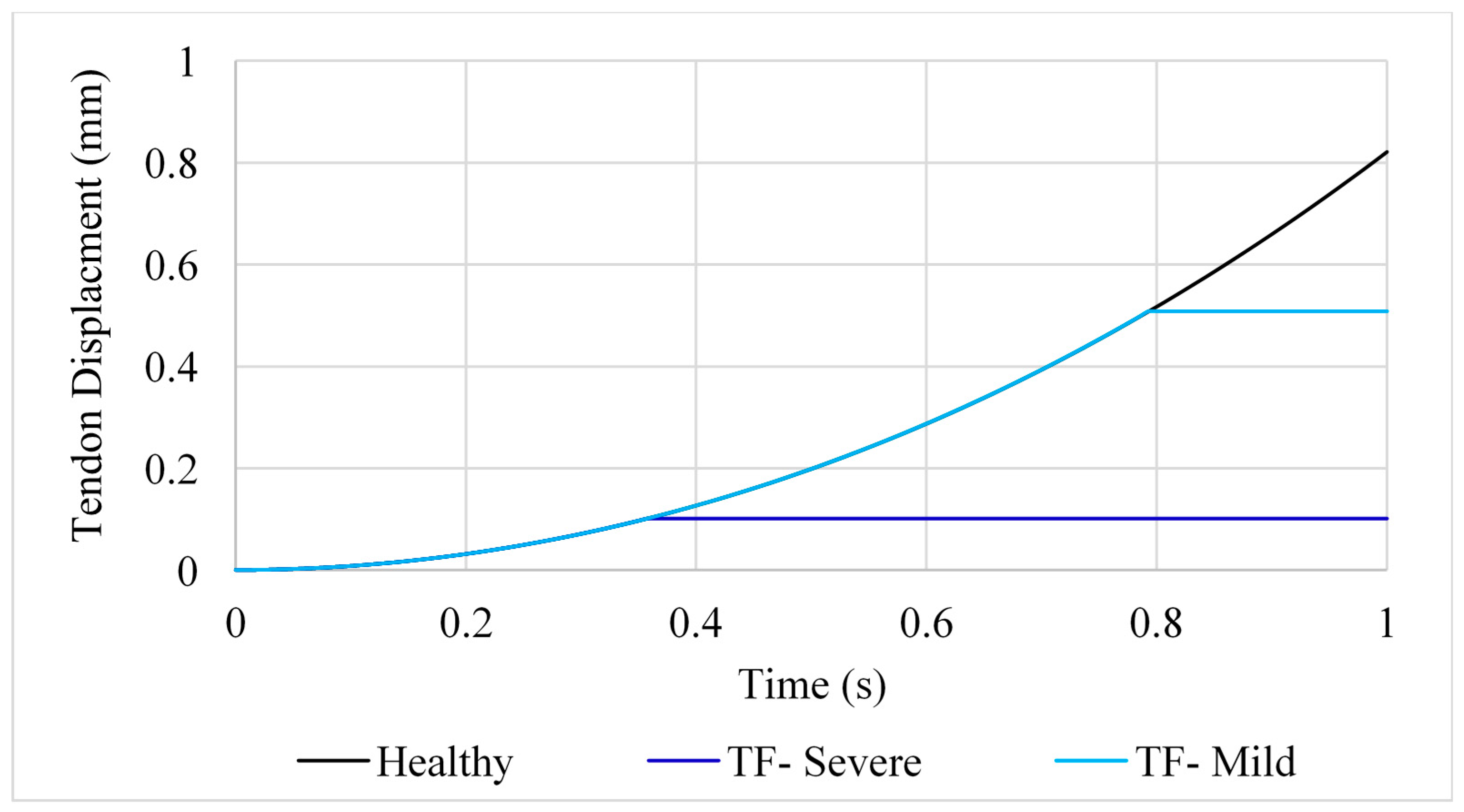
2.3. Position B—Abduction
2.4. Position C—Hyper-Extension
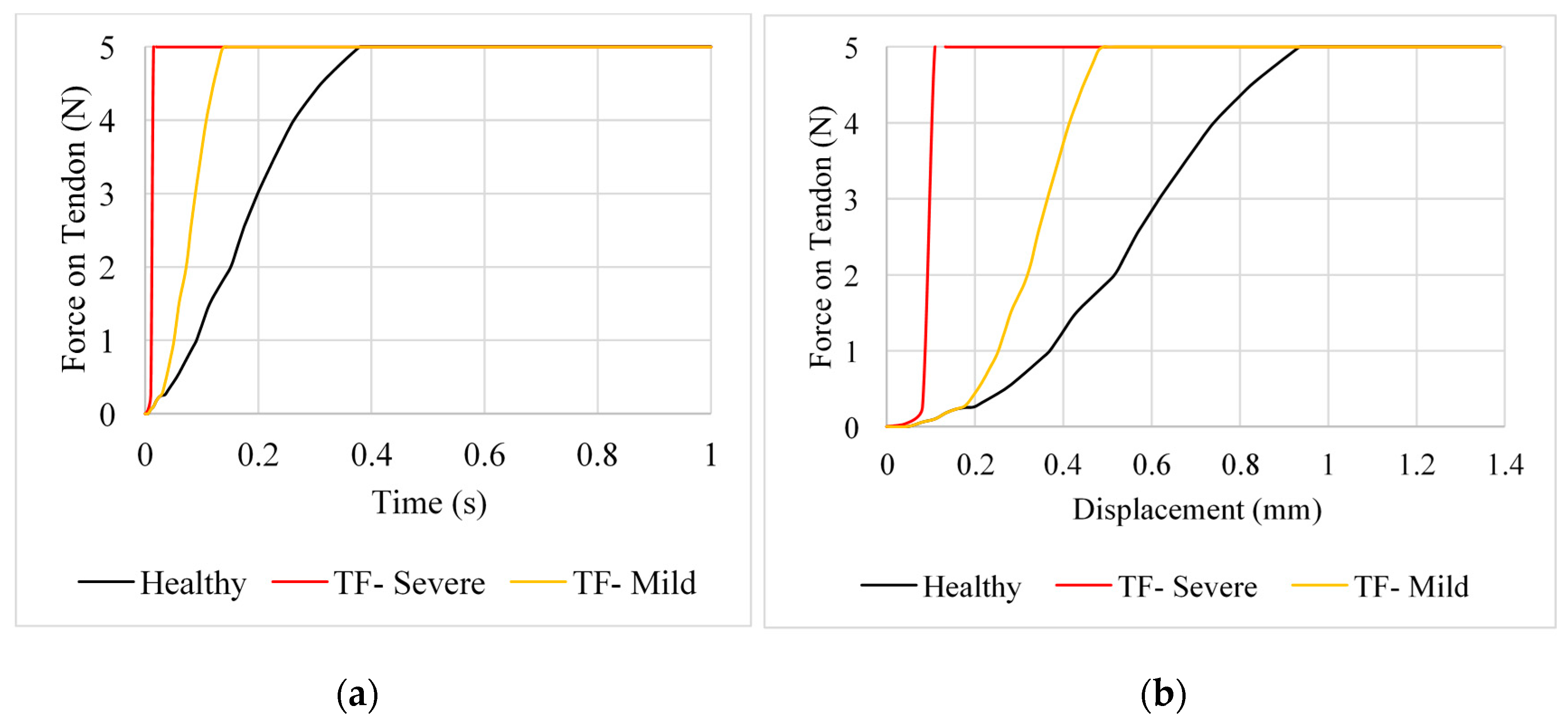
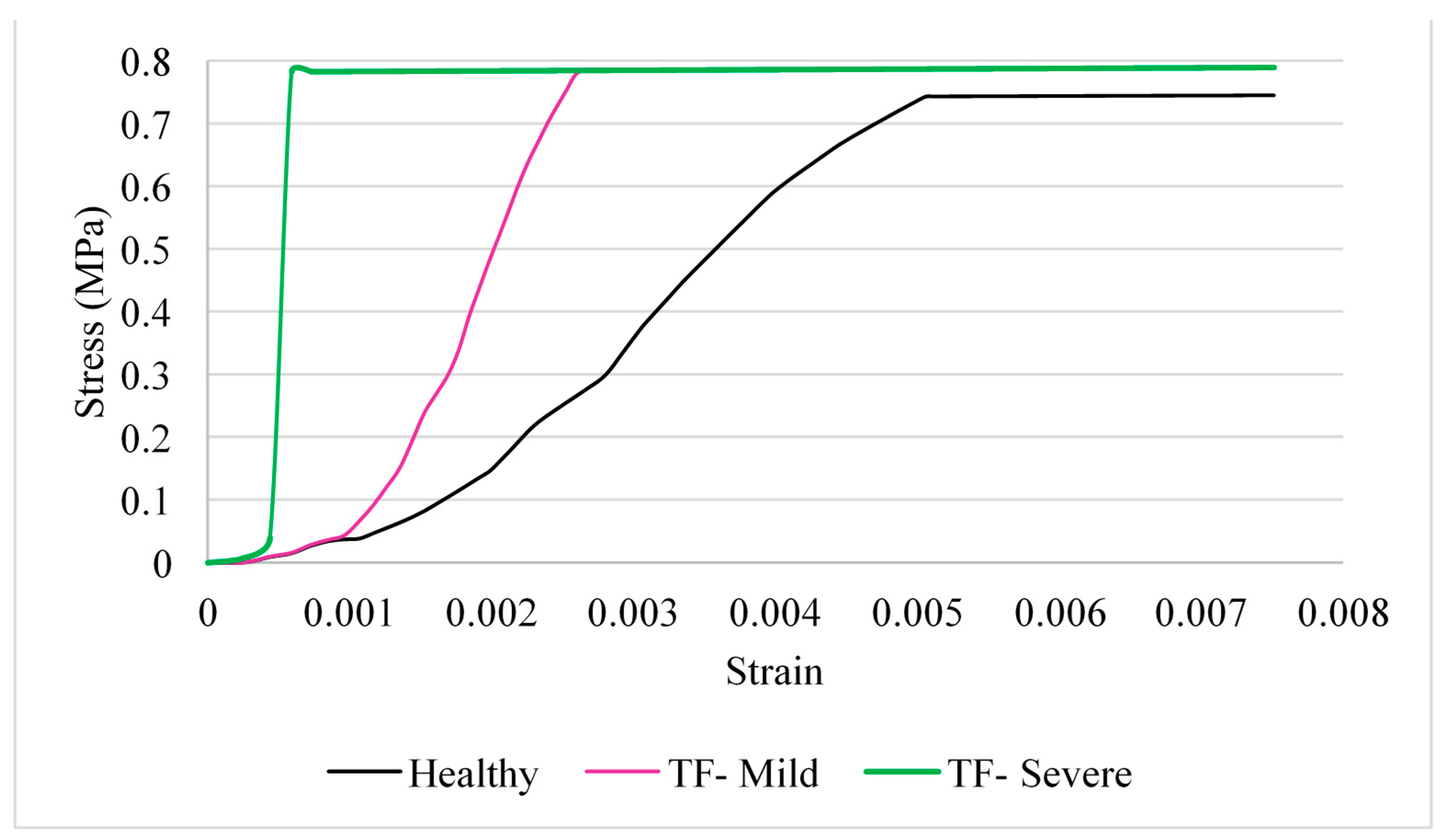
2.5. Cross-Sectional Area and Tension
3. Discussion
4. Materials and Methods
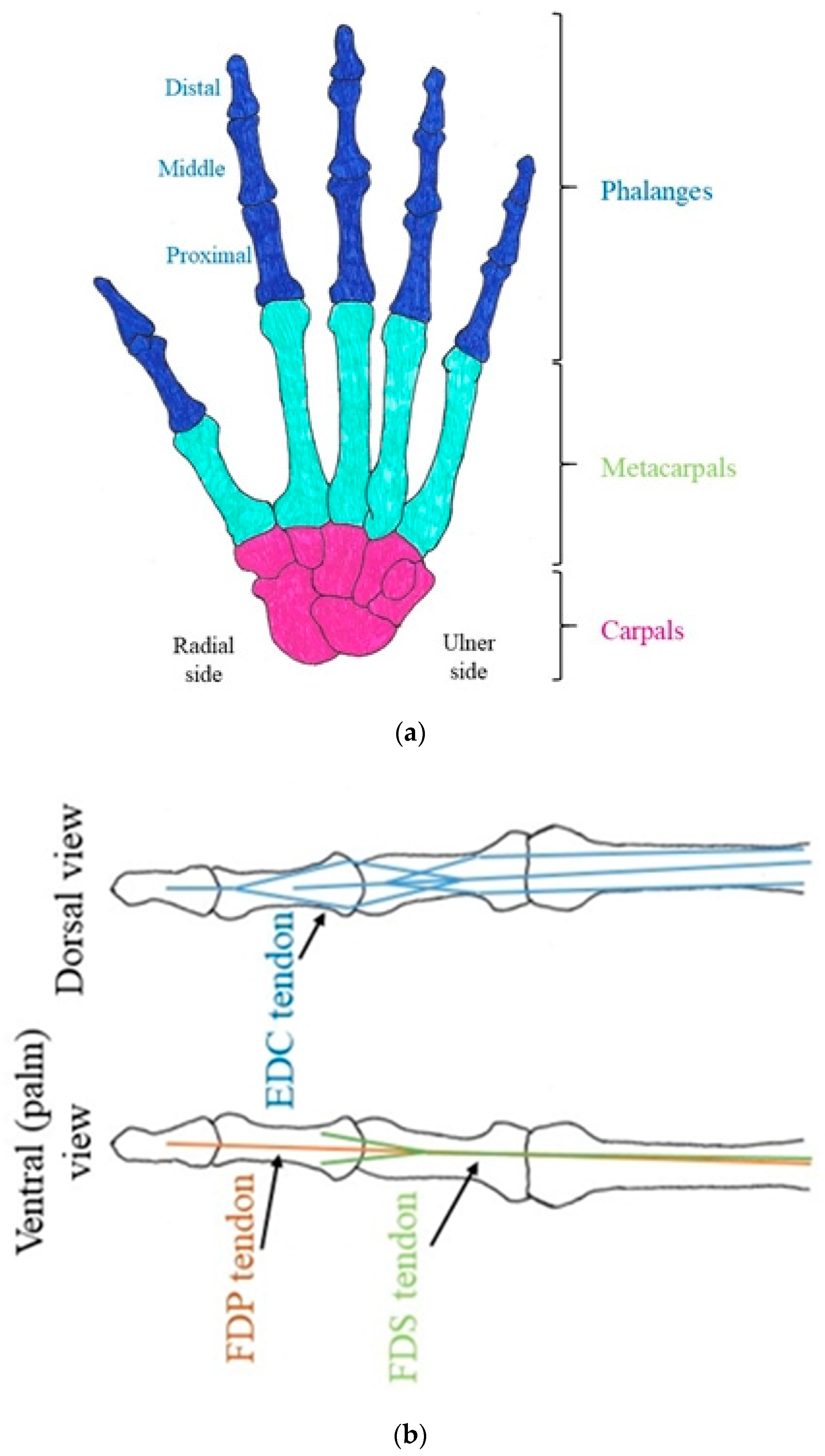
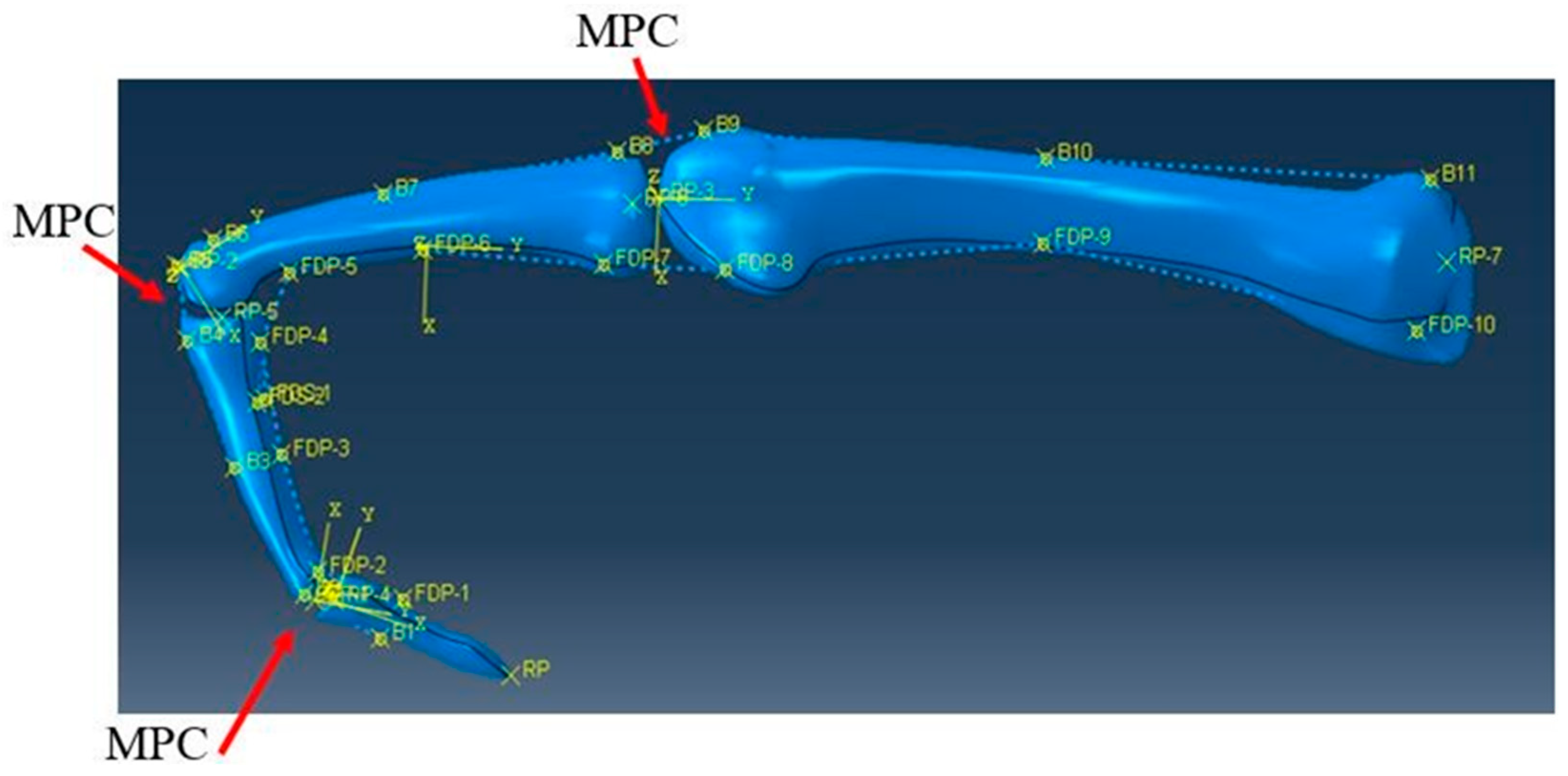
4.1. Geometry
4.2. Material Properties
4.3. Model Set-Up
4.3.1. Joint Orientation
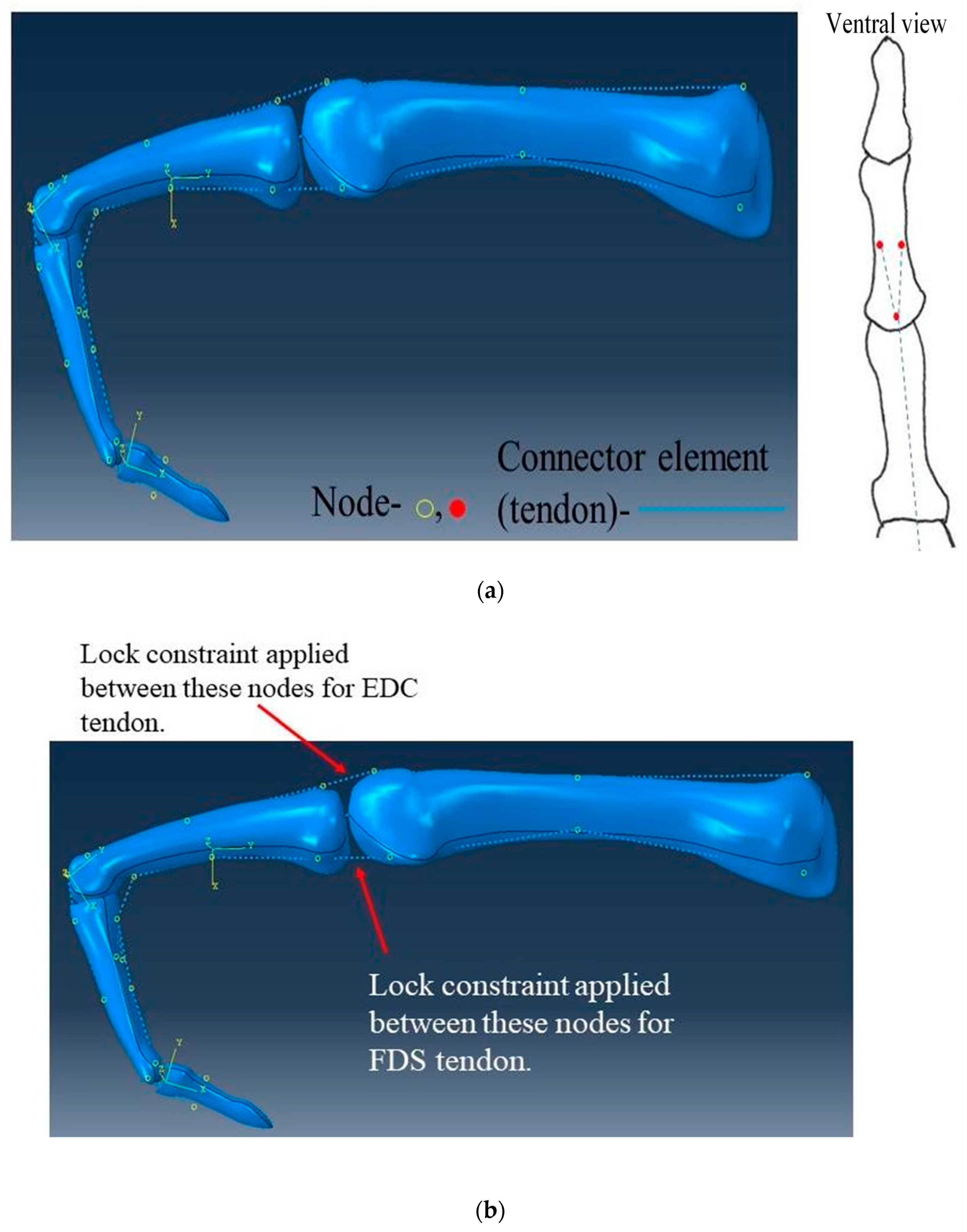
4.3.2. Tendon and Ligament Modelling
4.3.3. Boundary Conditions
4.4. Analysis
4.5. Mesh and Solution
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yun, Y.; Agarwal, P.; Deshpande, A.D. Accurate, robust, and real-time pose estimation of finger. J. Dyn. Syst. Meas. Control 2015, 137, 034505. [Google Scholar]
- Hu, D.; Ren, L.; Howard, D.; Zong, C. Biomechanical analysis of force distribution in human finger extensor mechanisms. BioMed. Res. Int. 2014, 2014, 743460. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Langer, D.; Maeir, A.; Michailevich, M.; Applebaum, Y.; Luria, S. Using the international classification of functioning to examine the impact of trigger finger. Disabil. Rehabil. 2016, 38, 2530–2537. [Google Scholar] [PubMed]
- Langer, D.; Maeir, A.; Michailevich, M.; Luria, S. Evaluating hand function in clients with trigger finger. Occup. Ther. Int. 2017, 2017, 9539206. [Google Scholar] [CrossRef]
- Lindner-Tons, S.; Ingell, K. An alternative splint design for trigger finger. J. Hand Ther. 1998, 11, 206–208. [Google Scholar] [CrossRef]
- Sbernardori, M.C.; Bandiera, P. Histopathology of the A1 pulley in adult trigger fingers. J. Hand Surg. 2007, 32, 556–559. [Google Scholar]
- Miyamoto, H.; Miura, T.; Isayama, H.; Masuzaki, R.; Koike, K.; Ohe, T. Stiffness of the first annular pulley in normal and trigger fingers. J. Hand Surg. 2011, 36, 1486–1491. [Google Scholar] [CrossRef]
- Doughlas, H.C.L.; Chin, D.H.; Jones, N.F. Repetitive motion hand disorders. J. Calif. Dent. Assoc. 2002, 30, 149–160. [Google Scholar]
- Makkouk, A.H.; Oetgen, M.E.; Swigart, C.R.; Dodds, S.D. Trigger finger: Etiology, evaluation, and treatment. Curr. Rev. Musculoskel Med. 2008, 1, 92–96. [Google Scholar]
- Colbourn, J.; Heath, N.; Manary, S.; Pacifico, D. Effectiveness of splinting for the treatment of trigger finger. J. Hand Ther. 2008, 21, 336–343. [Google Scholar] [CrossRef]
- Best, T.J. Post-traumatic stenosing flexor tenosynovitis. Can. J. Plast. Surg. 2003, 11, 143–144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- The British Society for Surgery of the Hand. Trigger Finger/Thumb. Available online: https://www.bssh.ac.uk/patients/conditions/18/trigger_fingerthumb (accessed on 10 March 2019).
- NHS Wales. Trigger Finger. Available online: https://www.nhsdirect.wales.nhs.uk/encyclopaedia/t/article/triggerfinger (accessed on 18 April 2019).
- NHS. Trigger Finger. Available online: https://www.nhs.uk/conditions/trigger-finger/ (accessed on 5 April 2019).
- Li, Z.M.; Zatsiorsky, V.M.; Latash, M.L. The effect of finger extensor mechanism on the flexor force during isometric tasks. J. Biomech. 2001, 34, 1097–1102. [Google Scholar] [CrossRef]
- Wilkinson, D.D.; Weghe, M.V.; Matsuoka, Y. An extensor mechanism for an anatomical robotic hand. In Proceedings of the International Conference on Robotics & Automation, Taipei, Taiwan, 14–19 September 2003; Volume 1, p. 243. [Google Scholar]
- Hirt, B.; Seyhan, H.; Wagner, M. Hand and Wrist Anatomy and Biomechanics: A Comprehensive Guide; Thieme Medical Publishers, Incorporated: New York, NY, USA, 2016. [Google Scholar]
- Amis, A. The mechanical properties of finger flexor tendons and development of stronger tendon suturing techniques. In Advances in the Biomechanics of the Hand and Wrist; Schuind, F., Garcia-Elias, M., An, K.N., Eds.; Springer: Boston, MA, USA, 1994; p. 41. [Google Scholar]
- Chen, P.; Lin, C.; Jou, I.M.; Chieh, H.F.; Su, F.C.; Kuo, L.C. One Digit Interruption: The altered force patterns during functionally cylindrical grasping tasks in patients with trigger digits. PLoS ONE 2013, 8, e83632. [Google Scholar] [CrossRef] [PubMed]
- Tung, W.L.; Kuo, L.C.; Lai, K.Y.; Jou, I.M.; Sun, Y.N.; Su, F.C. Quantitative evidence of kinematics and functional differences in different graded trigger fingers. Clin. Biomech. 2010, 25, 535–540. [Google Scholar] [CrossRef] [PubMed]
- Langer, D.; Luria, S.; Michailevich, M.; Maeir, A. Long-term functional outcome of trigger finger. J. Disabil. Rehabil. 2016, 40, 90–95. [Google Scholar]
- Vigouroux, L.; Quaine, F.; Labarre-Vila, A.; Moutet, F. Estimation of finger muscle tendon tensions and pulley forces during specific sport-climbing grip techniques. J. Biomech. 2006, 39, 2583–2592. [Google Scholar] [CrossRef]
- Lu, S.; Kuo, L.; Jou, I. Quantifying catch-and-release: The extensor tendon force needed to overcome the catching flexors in trigger fingers. J. Orthop. Res. 2013, 31, 1130–1135. [Google Scholar] [CrossRef]
- Weber, J.F.; Agur, A.M.R.; Fattah, A.Y.; Gordon, K.D.; Oliver, M.L. Tensile mechanical properties of human forearm tendons. J. Hand Surg. (Eur. Vol.) 2015, 40, 711–719. [Google Scholar] [CrossRef]
- Yang, T.; Lu, S.; Lin, W.; Zhao, K.; Zhao, C.; An, K.N.; Jou, I.M.; Lee, P.Y.; Kuo, L.C.; Su, F.C. Assessing finger joint biomechanics by applying equal force to flexor tendons in vitro using a novel simultaneous approach. PLoS ONE 2016, 11, e0160301. [Google Scholar]
- Tanaka, T.; Amadio, P.C.; Zhao, C.; Zobits, M.E.; An, K.N. Flexor digitorum profundus tendon tension during finger manipulation. J. Hand Ther. 2005, 18, 330–338. [Google Scholar] [CrossRef] [Green Version]
- Kursa, K.; Lattanza, L.; Diao, E.; Rempel, D. In vivo flexor tendon forces increase with finger and wrist flexion during active finger flexion and extension. Orthop. Res. 2006, 24, 763–769. [Google Scholar] [CrossRef] [PubMed]
- Edsfeldt, S.; Rempel, D.; Kursa, K.; Diao, E.; Lattanza, L. In vivo flexor tendon forces generated during different rehabilitation exercises. J. Hand Surg. 2015, 40, 705–710. [Google Scholar] [CrossRef]
- Barberio, C.G.; Chaudhry, T.; Power, D.M.; Tan, S.; Lawless, B.M.; Espino, D.M.; Wilton, J.C. Towards viscoelastic characterisation of the human ulnar nerve: An early assessment using embalmed cadavers. Med. Eng. Phys. 2019, 64, 15–22. [Google Scholar] [PubMed] [Green Version]
- Barberio, C.; Chaudhry, T.; Power, D.; Lawless, B.M.; Espino, D.M.; Tan, S.; Wilton, J.C. The effect of shoulder abduction and medial epicondylectomy on ulnar nerve strain. J. Musculoskelet Surg. Res. 2019, 3, 134–140. [Google Scholar] [CrossRef]
- Burton, H.E.; Williams, R.L.; Espino, D.M. Effects of freezing, fixation and dehydration on surface roughness properties of porcine left anterior descending coronary arteries. Micron 2017, 101, 78–86. [Google Scholar] [CrossRef] [PubMed]
- Burton, H.E.; Freij, J.M.; Espino, D.M. Dynamic viscoelasticity and surface properties of porcine left anterior descending coronary arteries. Cardiovasc. Eng. Technol. 2017, 8, 41–56. [Google Scholar] [CrossRef] [Green Version]
- Burton, H.E.; Cullinan, R.; Jiang, K.; Espino, D.M. Multiscale three-dimensional surface reconstruction and surface roughness of porcine left anterior descending coronary arteries. R. Soc. Open Sci. 2019, 6, 190915. [Google Scholar] [CrossRef] [Green Version]
- Constable, M.; Burton, H.E.; Lawless, B.M.; Gramigna, V.; Buchan, K.G.; Espino, D.M. Effect of glutaraldehyde based cross-linking on the viscoelasticity of mitral valve basal chordae tendineae. BioMed. Eng. Online 2018, 17, 93. [Google Scholar]
- Öhman, C.; Espino, D.M.; Heinmann, T.; Baleani, M.; Delingette, H.; Viceconti, M. Subject-specific knee joint model: Design of an experiment to validate a multi-body finite element model. Vis. Comput. 2011, 27, 153–159. [Google Scholar] [CrossRef]
- Lavecchia, C.E.; Espino, D.M.; Moerman, K.M.; Tse, K.M.; Robinson, D.; Lee, P.V.S.; Shepherd, D.E.T. Lumbar model generator: A tool for the automated generation of a parametric scalable model of the lumbar spine. J. R. Soc. Interface 2018, 15, 20170829. [Google Scholar] [CrossRef] [Green Version]
- Bahraseman, H.G.; Hassani, K.; Navidbakhsh, M.; Espino, D.M.; Sani, Z.A.; Fatouraee, N. Effect of exercise on blood flow through the aortic valve: A combined clinical and numerical study. Comput. Methods Biomech. Biomed. Eng. 2014, 17, 1821–1834. [Google Scholar] [CrossRef] [PubMed]
- Jewkes, R.; Burton, H.E.; Espino, D.M. Towards additive manufacture of functional, spline-based morphometric models of healthy and diseased coronary arteries: In vitro proof-of-concept using a porcine template. J. Funct. Biomater. 2018, 9, 15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sterling, S. Human Skeleton Used for a Parametric Gait Study. Available online: https://grabcad.com/library/human-skeleton-used-for-a-parametric-gait-study-1 (accessed on 10 November 2018).
- Jasuja, O.P.; Singh, G. Estimation of stature from hand and phalange length. J. indian Acad. Forensic Med. 2004, 26, 100–106. [Google Scholar]
- Pal, S. Mechanical properties of biological materials. In Design of Artificial Human Joints & Organs; Pal, S., Ed.; Springer: Boston, MA, USA, 2014; p. 23. [Google Scholar]
- Hooley, C.J.; McCrum, N.G.; Cohen, R.E. The viscoelastic deformation of tendon. J. Biomech. 1980, 13, 521–528. [Google Scholar] [CrossRef]
- Pradas, M.M.; Calleia, R.D. Nonlinear viscolelastic behaviour of the flexor tendon of the human hand. J. Biomech. 1990, 23, 773–781. [Google Scholar] [CrossRef]
- Proske, U.; Morgan, D.L. Tendon stiffness: Methods of measurement and significance for the control of movement. A review. J. Biomech. 1987, 20, 75–82. [Google Scholar] [CrossRef]
- Woo, S.L.; Johnson, G.A.; Smith, B.A. Mathematical modelling of ligaments and tendons. J. Biomech. Eng. 1993, 115, 468–473. [Google Scholar]
- Pring, D.J.; Amis, A.A.; Coombs, R.R. The mechanical properties of human flexor tendons in relation to artificial tendons. J. Hand Surg. Br. Eur. Vol. 1985, 10, 331–336. [Google Scholar] [CrossRef]
- Brook, N.; Mizrahi, J.; Shoham, M.; Daya, J. A biomechanical model of index finger dynamics. Med. Eng. Phys. 1995, 17, 54–63. [Google Scholar]
- Fok, K.S.; Chou, S.M. Development of a finger biomechanical model and its considerations. J. Biomech. 2010, 43, 701–713. [Google Scholar] [CrossRef]
- An, K.N.; Chao, E.Y.; Cooney, W.P.; Linscheid, R.L. Normative model of human hand for biomechanical analysis. J. Biomech. 1979, 12, 775–788. [Google Scholar] [CrossRef]
- Williams, M.; Temperley, D.; Murali, R. Radiology of the hand. Orthop. Trauma 2019, 33, 45–52. [Google Scholar] [CrossRef]
- Ward, S.R.; Loren, G.J.; Lundberg, S.; Lieber, R.L. High stiffness of human digital flexor tendons is suited for precise finger positional control. Neurophysiol 2006, 96, 2815–2818. [Google Scholar] [CrossRef]
- Boyer, M.I.; Meunier, M.D.; Lescheid, J.; Burns, M.E.; Gelberman, R.H.; Silva, M.J. The influence of cross-sectional area on the tensile properties of flexor tendons. J. Hand Surg. 2001, 26, 828–832. [Google Scholar] [CrossRef] [PubMed]
- Young, S.R.; Gardiner, B.; Mehdizadeh, A.; Rubenson, J.; Umberger, B.; Smith, D.W. Adaptive remodeling of achilles tendon: A multi-scale computational model. PLoS Comput. Biol. 2016, 12, e1005106. [Google Scholar] [CrossRef] [Green Version]
- Freij, J.M.; Burton, H.E.; Espino, D.M. Objective uniaxial identification of transition points in non-linear materials: Sample application to porcine coronary arteries and the dependency of their pre- and post-transitional moduli with position. Cardiovasc. Eng. Technol. 2019, 10, 61–68. [Google Scholar] [CrossRef] [Green Version]




| Tendon | Initial | Position A—Extension (mm2) | Position C—Hyper-Extension (mm2) | ||||
|---|---|---|---|---|---|---|---|
| Healthy | Mild | Severe | Healthy | Mild | Severe | ||
| FDP | 6.76 | 6.74 | - | - | 6.72 | - | - |
| FDS | 6.39 | - | 6.37 | 6.38 | - | 6.36 | 6.38 |
| EDC | 2.58 | - | 2.57 | 2.57 | - | - | - |
| Tendon | Position A—Extension (N) | Position C—Hyper-Extension (N) | ||||
|---|---|---|---|---|---|---|
| Healthy | Mild | Severe | Healthy | Mild | Severe | |
| FDP | 2.00 | - | - | 4.70 | - | - |
| FDS | - | 1.54 | 0.50 | - | 2.67 | 0.78 |
| EDC | - | 2.64 | 0.56 | - | - | - |
| Length (mm) | |||
|---|---|---|---|
| Distal | Middle | Proximal | Metacarpal |
| 24.1 | 34.5 | 56.1 | 104.7 |
| Property | Value |
|---|---|
| Young’s Modulus | 17 GPa |
| Poisson’s Ratio | 0.3 |
| Density | 1900 kg/m3 |
| Position | Diagram | Description |
|---|---|---|
| Initial | Radial view 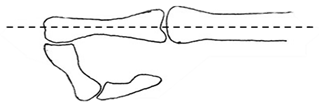 | Flexed |
| A | Radial view  | Extended from PIP joint (rotation about the z-axis) |
| B | Dorsal view 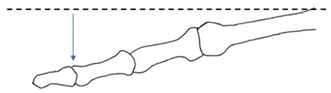 | Extended before abduction from MCP joint (rotation about the y-axis) |
| C | Radial view 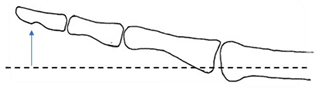 | Extended then hyperextended from MCP joint (rotated further about the z-axis) |
| Boundary Condition | Step | Type | Bone(s) | Value (Rotation in Radians) |
|---|---|---|---|---|
| Position A | ||||
| Initial | Initial | Encastre | Metacarpal Proximal phalanx | U1, U2, U3 = 0 UR1, UR2, UR3 = 0 |
| 1 | 1 | Displacement/rotation | Middle phalanx | UR3 = 1.68 |
| 2 | 1 | Displacement/rotation | Distal phalanx | UR3 = 1.06 |
| Position B | ||||
| Initial | Initial | Encastre | Metacarpal | U1, U2, U3 = 0 UR1, UR2, UR3 = 0 |
| 1 | 1 | Displacement/rotation | Middle phalanx | UR3 = 1.68 |
| 2 | 1 | Displacement/rotation | Distal phalanx | UR3 = 1.06 |
| 3 | 2 | Displacement/rotation | Proximal phalanx | UR2 = 0.7 |
| Position C | ||||
| Initial | Initial | Encastre | Metacarpal | U1, U2, U3 = 0UR1, UR2, UR3 = 0 |
| 1 | 1 | Displacement/rotation | Proximal phalanx | UR3 = 2.47 |
| 2 | 1 | Displacement/rotation | Distal phalanx | UR3 = 1.06 |
| A (mm2) | L0 (mm) | E (MPa) | |
|---|---|---|---|
| FDP | 6.76 | 185 | 1.5 |
| FDS | 6.38 | 149 | 1.5 |
| EDC | 2.58 | 180 | 1.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Relf, H.I.; Barberio, C.G.; Espino, D.M. A Finite Element Model for Trigger Finger. Prosthesis 2020, 2, 168-184. https://doi.org/10.3390/prosthesis2030015
Relf HI, Barberio CG, Espino DM. A Finite Element Model for Trigger Finger. Prosthesis. 2020; 2(3):168-184. https://doi.org/10.3390/prosthesis2030015
Chicago/Turabian StyleRelf, Helena I., Carla G. Barberio, and Daniel M. Espino. 2020. "A Finite Element Model for Trigger Finger" Prosthesis 2, no. 3: 168-184. https://doi.org/10.3390/prosthesis2030015
APA StyleRelf, H. I., Barberio, C. G., & Espino, D. M. (2020). A Finite Element Model for Trigger Finger. Prosthesis, 2(3), 168-184. https://doi.org/10.3390/prosthesis2030015





