Increase in Elastic Stress Limits by Plastic Conditioning: Influence of Strain Hardening on Interference Fits
Abstract
:1. Introduction
2. Problem Description
3. Materials and Methods
3.1. Problem-Solving through the Plastic Conditioning of Interference Fits—Basic Concept of the Procedure
3.2. Analytical Investigations (Two-Dimensional, Ideal Plastic Calculation Example)
3.3. Numerical Verification of the Analytical Investigations (Ideal Plastic)
3.4. The Influence of Strain-Hardening
4. Discussion of the Results of the FE Calculations with Hardening Material and Comparison with Ideal Plastic Investigations
5. Conclusions Regarding Engineering Practice and Industrial Applications
6. Summary and Outlook
7. Patents
Funding
Institutional Review Board Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Unit | Meaning |
| d | mm | Diameter coordinate (control variable) |
| DaA | mm | Outer diameter of the outer part |
| DF | mm | Joint diameter (nominal) |
| DiA | mm | Inner diameter of the outer part |
| DPA | mm | Plasticity diameter of the outer part |
| Dσr(GEH), Dσt(GEH) | MPa | Stress values at point D in the principal stress plane for von Mises yield criterion (GEH) |
| EA | MPa | Young’s modulus of the outer part |
| FGEH | MPa | Von Mises yield function |
| k | MPa | Critical value (yield strength in shear) |
| m | - | Factor for determining the angle of inclination |
| pi | MPa | Internal pressure of the disc |
| pE | MPa | Elastic joint pressure at the yield strength |
| pE, Kond | MPa | Elastic joint pressure after previous conditioning |
| pF | MPa | Joint pressure |
| pK | MPa | Conditioning pressure |
| pKond,max | MPa | Maximum joint pressure when undergoing conditioning |
| pN,lim | MPa | Yield pressure (elastic limit) of an outer part |
| QA | - | Diameter ratio of the outer part |
| ReL,A | MPa | Lower yield strength of the outer part |
| R+eL,A | MPa | Lower yield strength of the outer part after hardening |
| r | mm | Radius |
| SP | - | Safety against plastic deformation |
| SPA | - | Safety against plastic deformation of the outer part |
| S+PA | - | Safety against plastic deformation of the outer part after hardening |
| y | MPa | Intersection of the relief straight line with the ordinate (tangential residual stress after complete relief) |
| α | ° | Inclination angle for load line and relief straight line |
| εv | - | Equivalent strain |
| νA | - | Poisson’s ratio of the outer part |
| σr | MPa | Radial stress |
| σt | MPa | Tangential stress |
| σv | MPa | Equivalent stress |
| σv,G | MPa | Equivalent stress at point G |
| σv,G+ | MPa | Equivalent stress at point G+ |
| σv,lim | MPa | Equivalent limit stress |
| σ+v,lim | MPa | Equivalent limit stress after hardening of the material |
| σ1, σ2, σ3 | MPa | Principal stresses of the stress tensor |
| AT | Outer part of the PV | |
| ESZ | Plane stress state | |
| FE | Finite elements | |
| FEM | Finite element method | |
| GEH | Von Mises yield criterion | |
| PV | Interference fit | |
| MPV | Multiple interference fit | |
| SH | Shear stress hypothesis according to TRESCA | |
| IKAT | Institute of Construction and Drive Technology (TU Chemnitz) | |
| IKTD | Institute for Engineering Design and Industrial Design (University of Stuttgart) | |
References
- Kollmann, F.G. Die Auslegung elastisch-plastisch beanspruchter Querpressverbände. Forsch. Ing. 1978, 44, 1–11. [Google Scholar] [CrossRef]
- Kollmann, F.-G. Welle-Nabe-Verbindungen. Konstruktionsbücher, Band 32; Springer: Berlin/Heidelberg, Germany; New York, NY, USA; Tokyo, Japan, 1984. [Google Scholar]
- Leidich, E.; Lätzer, M. FVA-Nr. 566 I-Heft 993-Übertragungsfähigkeit von Klemmverbindungen Unter Besonderer Berücksichtigung Plastischer Verformungen; Abschlussbericht, Forschungsvereinigung Antriebstechnik e.V.: Frankfurt, Germany, 2011. [Google Scholar]
- Kovács, Á. Thermal stresses in a shrink fit due to an inhomogeneous temperature distribution. Acta Mech. 1994, 105, 173–187. [Google Scholar] [CrossRef]
- Mack, W. Spannungen im thermisch gefügten elastisch-plastischen Querpreßverband mit elastischer Entlastung. Ing.-Arch. 1986, 56, 301–313. [Google Scholar] [CrossRef]
- Schierz, M. Steigerung des Elastischen Potenzials von Pressverbindungen Durch Plastische Konditionierung der Fügepartner. Ph.D. Thesis, Technische Universität Chemnitz, Chemnitz, Germany, 2018. [Google Scholar]
- Schierz, M.; Leidich, E.; Ziaei, M. Plastisch konditionierte Pressverbindungen. In VDI (Hrsg) Welle-Nabe-Verbindungen; VDI-Berichte Nr.: 2018; VDI Verlag GmbH: Düsseldorf, Germany, 2018; Volume 2337, pp. 73–84. [Google Scholar]
- DIN 7190-1:2017; Pressverbände—Teil 1: Berechnungsgrundlagen und Gestaltungsregeln. DIN Deutsches Institut für Normung e.V.: Berlin, Germany, 2017.
- Schierz, M.; Leidich, E. FVA- Nr. 424 II—Heft 871-Erweiterung des Berechnungsprogramms PressFit®; Abschlussbericht, Forschungsvereinigung Antriebstechnik e.V.: Frankfurt, Germany, 2008. [Google Scholar]
- Schierz, M. FVA- Nr. 424 III—Heft 1170- Erweiterung des Berechnungsprogramms PressFit® für Elastisch und Elastisch-Plastisch Beanspruchte Mehrfachpressverbände (MPV); Abschlussbericht, Forschungsvereinigung Antriebstechnik e.V.: Frankfurt, Germany, 2015. [Google Scholar]
- DIN 7190-2:2017; Pressverbände—Teil 2: Berechnungsgrundlagen und Gestaltungsregeln für Kegelige, Selbsthemmende Pressverbände. DIN Deutsches Institut für Normung e.V.: Berlin, Germany, 2017.
- Schierz, M. Plastische Konditionierung von Pressverbindungen in der Antriebstechnik—Ein Verfahren mit Potenzial. Forsch. Ing. 2020, 84, 345–355. [Google Scholar] [CrossRef]
- Ulrich, D.; Binz, H. Elastisch-plastische Auslegung: Untersuchung von Pressverbindungen mit hohen Übermaßen. In VDI (Hrsg) Welle-Nabe-Verbindungen; VDI-Berichte Nr.: 2018; VDI Verlag GmbH: Düsseldorf, Germany, 2018; Volume 2337, pp. 279–282. [Google Scholar]
- Günther, C.; Leidich, E.; Hasse, A. Untersuchung der Gestaltfestigkeit hochbeanspruchter Hohlwellen-Pressverbindungen. In Proceedings of the Dresdner Maschinenelemente Kolloquium, Dresden, Germany, 26–27 December 2019; Sierke Verlag: Göttingen, Germany, 2019; pp. 381–392. [Google Scholar]



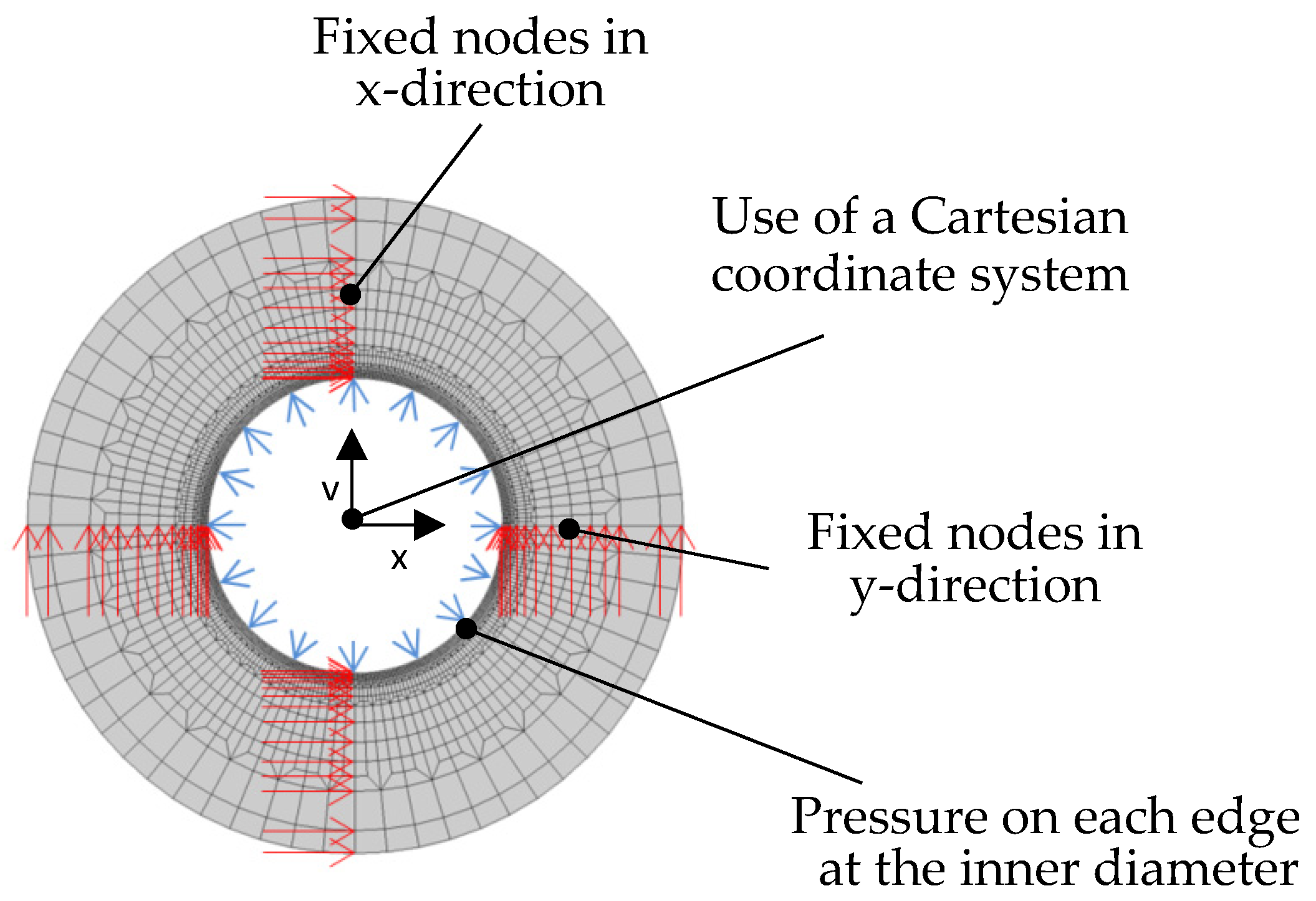
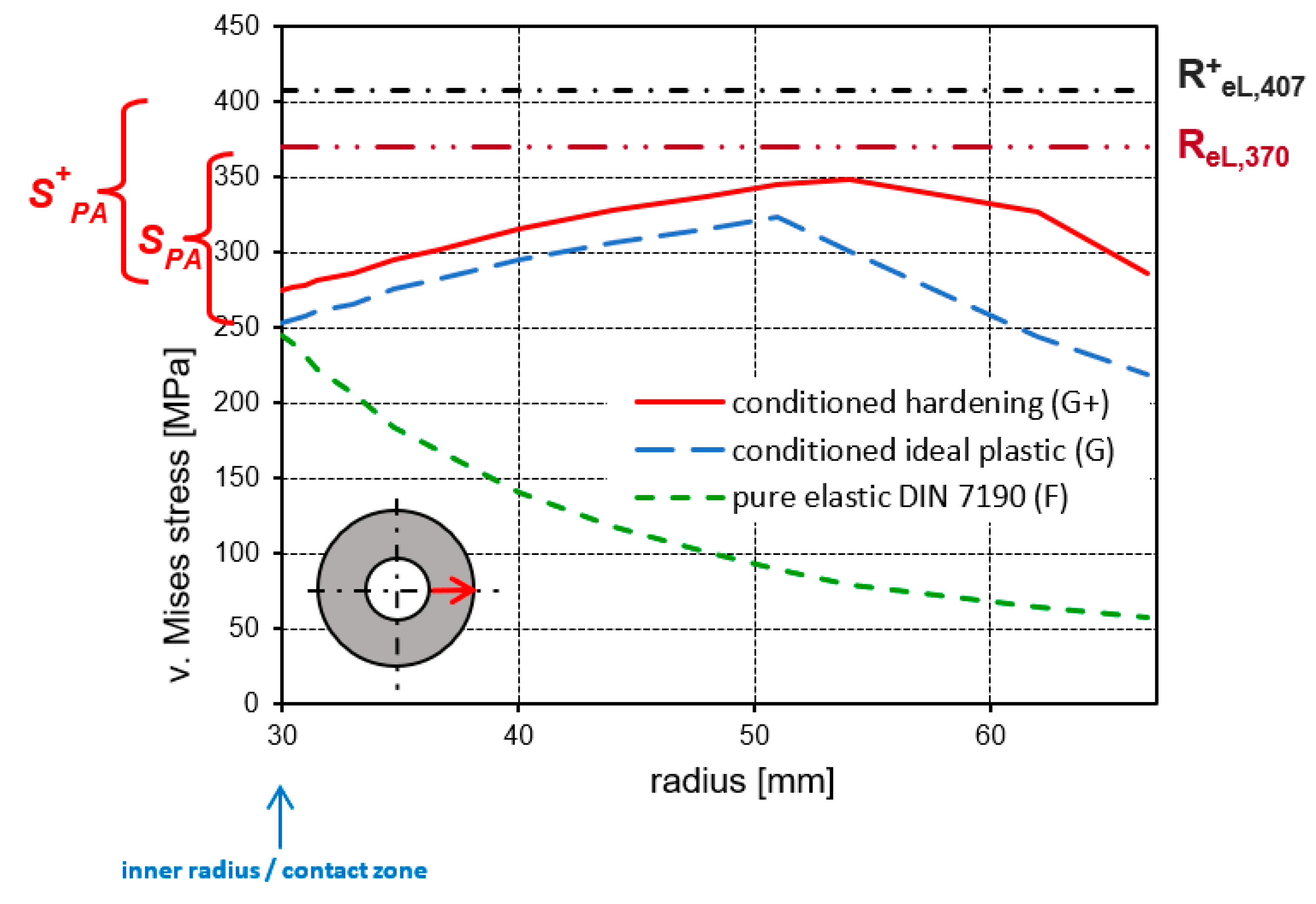
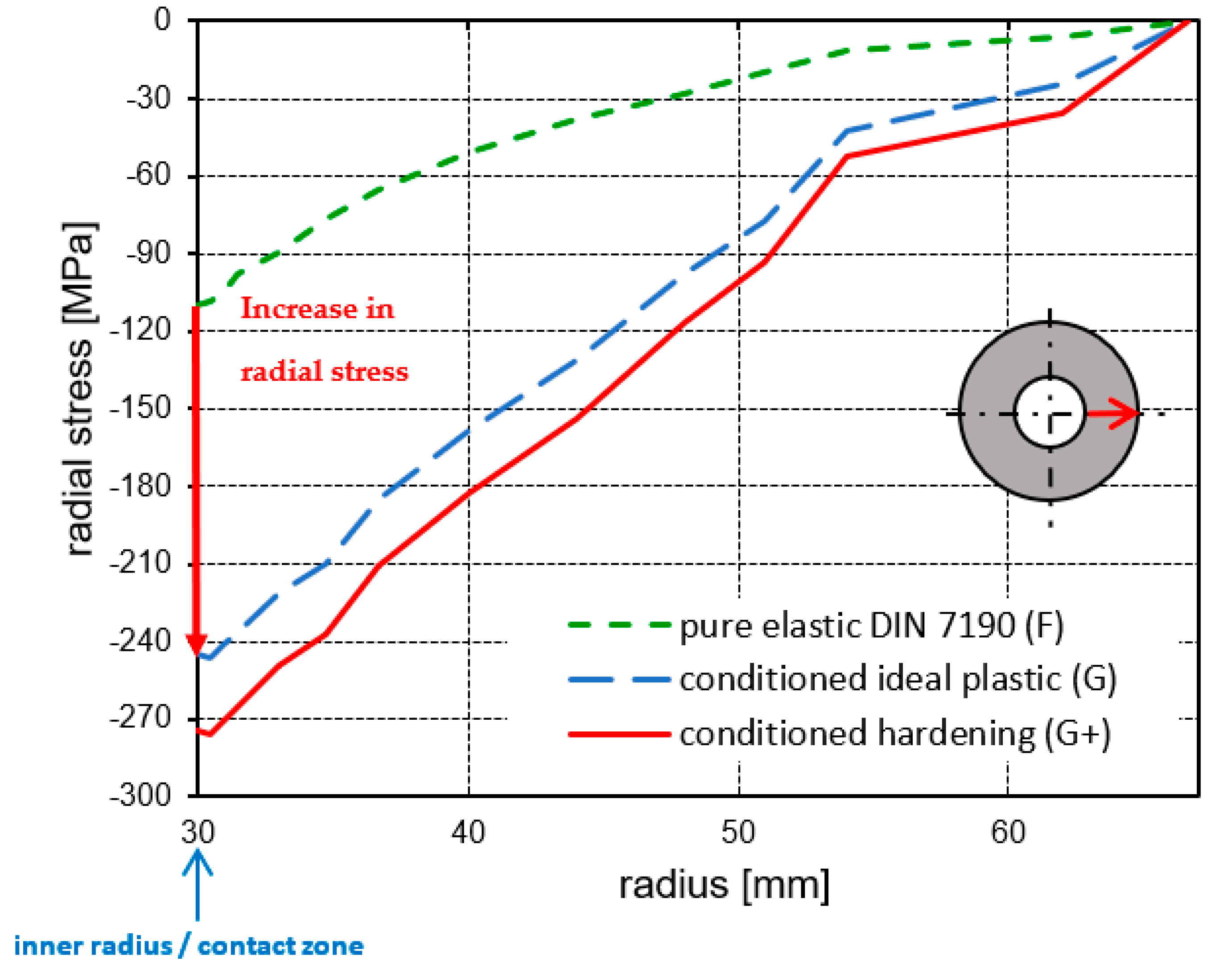

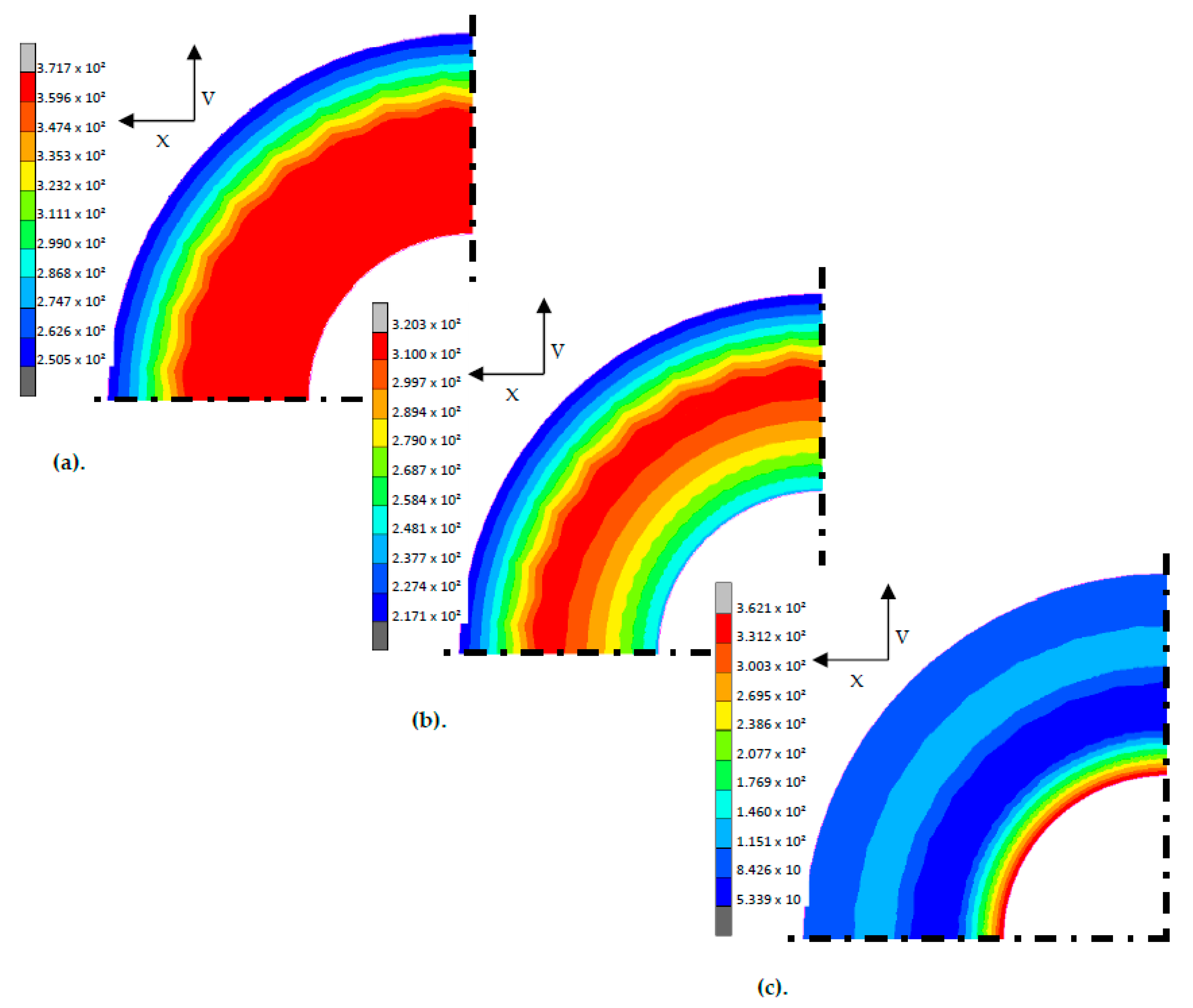



| Geometry Data | |||
| Hub outer diameter | DaA | 133.33 | mm |
| Hub inner diameter | DiA | 60.00 | mm |
| Hub diameter ratio | QA | 0.45 | - |
| Hub material | |||
| Designation | C 45 | ||
| Yield strength | ReL,A | 370 | MPa (ideal plastic) |
| Young’s modulus | EA | 205,000 | MPa |
| Poisson’s ratio | νA | 0.3 | - |
| Technological Data | |||
| Joint pressure for conditioning | pKond,max | 311 | MPa |
| Target safety against plastic deformation | SPA | 1.5 | - |
| Load Step | pi/MPa |
|---|---|
| 1 (Felast) | 113 |
| 2 (K) | 311 |
| 3 (D) | 0 |
| 4 (G) | 246 |
| σv | εv |
|---|---|
| (MPa) | (-) |
| 370.00 | 0.00171 |
| 390.00 | 0.00182 |
| 400.00 | 0.00189 |
| 410.00 | 0.01303 |
| 420.00 | 0.01417 |
| 430.00 | 0.01549 |
| 440.00 | 0.01665 |
| 470.00 | 0.02075 |
| 500.00 | 0.02543 |
| 530.00 | 0.03097 |
| 560.00 | 0.03775 |
| 590.00 | 0.04612 |
| 620.00 | 0.05967 |
| Load Step | pi/MPa |
|---|---|
| 1 (Felast) | 113 |
| 2 (K+) | 342 |
| 3 (D+) | 0 |
| 4 (G+) | 274 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schierz, M. Increase in Elastic Stress Limits by Plastic Conditioning: Influence of Strain Hardening on Interference Fits. Appl. Mech. 2022, 3, 375-389. https://doi.org/10.3390/applmech3020023
Schierz M. Increase in Elastic Stress Limits by Plastic Conditioning: Influence of Strain Hardening on Interference Fits. Applied Mechanics. 2022; 3(2):375-389. https://doi.org/10.3390/applmech3020023
Chicago/Turabian StyleSchierz, Mario. 2022. "Increase in Elastic Stress Limits by Plastic Conditioning: Influence of Strain Hardening on Interference Fits" Applied Mechanics 3, no. 2: 375-389. https://doi.org/10.3390/applmech3020023
APA StyleSchierz, M. (2022). Increase in Elastic Stress Limits by Plastic Conditioning: Influence of Strain Hardening on Interference Fits. Applied Mechanics, 3(2), 375-389. https://doi.org/10.3390/applmech3020023





