Multi-Scale Approach of HCF Taking into Account Plasticity and Damage: Application to LPBF Materials

Abstract

Laser additive manufacturing enables economical production of complex lightweight structures. To realize the potential benefits of additive manufacturing technology in industrial applications, the fatigue performance of parts additively manufactured materials must be modelized. The aim of this paper is to present a new modeling approach combining plasticity and damage, and appropriate for as-built Laser-Powder Bed Fusion (LPBF) structures. The model presented is an extension of the Dang Van criterion, including damage, defined as porosity in the case of LPBF. Attention is focused on the integration of damage in a fatigue criterion using the concept of elastic shakedown. Finally, the case of 316L will illustrate the results of the model by fatigue tests with deterministic defects.

1. Introduction

Additive manufacturing has now reached a sufficiently good maturity and robustness to fit with industrial criteria, with the use or not of post-building treatments (heat treatments, hot isostatic pressing). In the laser powder bed fusion (LPBF) process, a powder layer is spread on a building platform and a laser beam melts selectively around the deposited layer, each individual laser path being composed of a contour and a hatching phase. The platform is then lowered down by a 20 µm to 100 μm height and a new powder layer is applied. This single layer LPBF procedure is then repeated for a number of layers to reach the final 3D shape. At the end of the whole fusion stage, the built part is removed from the powder bed and de-powdered.

The most common defects observed systematically on LPBF are porosities (lacks-of-fusion LOF or blowholes) which can impact the material properties and specifically lower fatigue resistance. Such porosities are dependent on many process parameters (laser power, scan speed, hatch distance, etc.) which can be combined into volume energy density (J/mm³) parameters traducing the amount of laser energy injected into the built material. Additionally, the scan strategy (chess, stripes, etc.) also plays a major role versus the final porosity rate and residual stress distribution.

Classical fatigue mechanisms occurring on L-PBF parts are rather well documented in the literature [1]. For instance, it is well known that fatigue crack initiation in the case of LPBF is controlled by porosities, spatters and other microstructural heterogeneities. One of the specific trends of the LPBF process is the possibility of real-time detection and analysis of these defects during the process which is difficult for the casting process. The modeling of defects must be considered to adequately design components and to be able to estimate the final fatigue properties.

In High Cycle Fatigue (HCF), many multiaxial fatigue criteria can be found in the literature. Some of them are based on phenomenological approach such as the Sines [2] or Crossland [3] criterions. In terms of HCF of polycrystalline metallic materials, it is also widely accepted that meso-plasticity plays a key role in the initiation of fatigue cracks. The approach developed by Dang Van [4] consists of describing the plasticity at the mesoscopic scale by assuming that the Schmid yield criterion and linear isotropic hardening are appropriate; however, one limitation of this kind of criterion, is not taking into account defects in the theoretical framework.

Some criteria have already introduced the damage parameter in fatigue loading. Some of them coupled meso-plasticity and damage. Lemaitre [5,6] proposed an evolution of the initial approach based on thermodynamics and continuum mechanics; this approach [4] is often used for multiaxial random and non-proportional loading as presented by Jingran [7]. The Lemaitre’s damage law models are governed also by plasticity (through the accumulated plastic strain p) and enhanced by the stress level and triaxiality (through the elastic energy density denoted Y). The model is written in a rate form as:

$$\dot{\mathrm{D}}={\left(\frac{\mathrm{Y}}{\mathrm{S}}\right)}^{\mathrm{s}}\dot{\mathrm{p}}$$

(1)

Two damages parameters are introduced: the damage strength “S” and the damage exponent “s”.

Monchiet [8] has proposed an approach based on damage and mesoplasticity, but with the use of the Gurson model [9]. In this model, the damage is defined as a porosity and the variable f as the void fraction present in an elementary volume; this variable is connected to the development of a porosity present in the plastic shear bands located at the fatigue crack initiation zone. More precisely, authors tried to explain the effect of the mean stress. To introduce this latter effect, they considered the hydrostatic strain through a linear combination with the accumulated plastic strain, which is directly linked to the amplitude stress.

Koutiri [10] have proposed an approach based on Monchiet criterion [8] to take into account the effect of high mean stress (maximum stress close to the ultimate tensile strength) by researching the elastic shakedown of a yield function. The damage model used is the Gurson model with an extension of isotropic and kinematic hardening proposed by Monchiet [8]. In the first cycle, the maximum stress produces a damage, which is introduced in the variable f to obtain the maximum amplitude stress to achieve an elastic shakedown. The results show that in the first part of the Dang Van diagram, the area of the failure zone is similar whereas above the yield stress of the material, the induced damage changes the slope of the Dang Van line. More recently, Neves [11] estimated the fatigue life by using an incremental approach for ductile materials subjected to low cycle fatigue. In this approach, the life prediction is based on the evolution of the internal damage variable. They proposed an extension for the Gurson model capable of describing the gradual damage of the material as a function of the number of loading cycles with the use of the damage parameter f.

In all of these criteria, the variation of porosity obtained in a material is not considered. When a change of the porosity or any damage of the material is observed, the identification of the material parameters must be re-identified. Results for this last case, where porosity in material can change were not satisfactory enough, mainly because of the no integration of damage in the model.

The aim of the current study is to propose a new model to solve this issue. In order to properly consider the influence of defects in Dang Van Criterion, materials’ heterogeneities will be assimilated to material damage. It is first proposed to introduce the damage by a variable D parameter in the yield function, as defined by Lemaitre and Chaboche. In a second step, it will be possible to consider the elastic shakedown at both the mesoscopic and macroscopic scales as defined by Dang Van or Papadoulos [4,12]. The use of intermediate scale between the microscopic and macroscopic scale is one of the success of this kind of criteria.

This modeling approach will be confronted to recent fatigue tests, carried out on a 316L steel manufactured with the LPBF process, for which deterministic defects, including various predefined sizes and positions have been carefully generated and controlled [13].

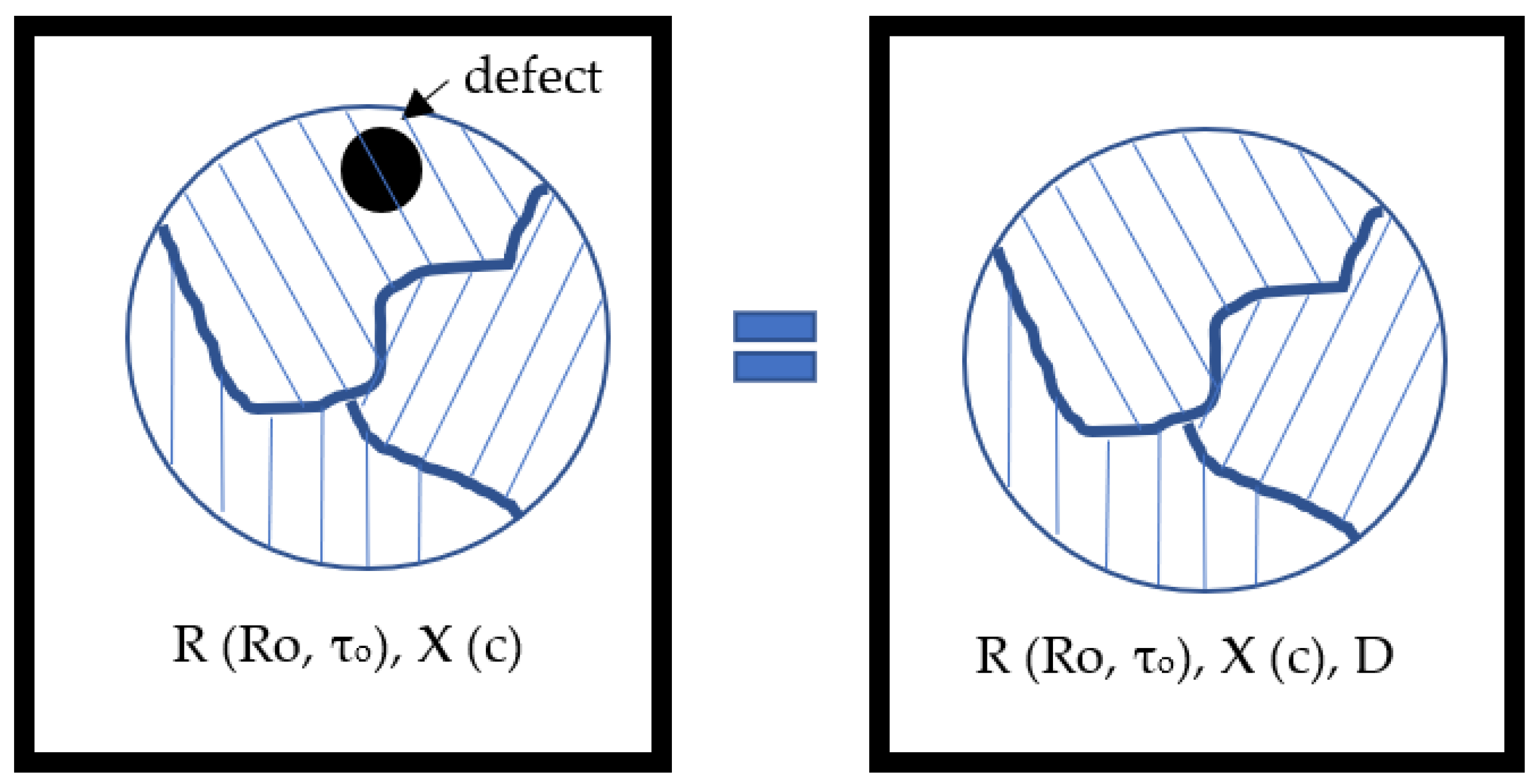
2. Integration of Damage

The aim of the modeling is to introduce the concept of damage in fatigue criteria based on the critical plane like Dang Van and Papadopoulos. In Figure 1, it can be observed a porosity in the material (with kinematic X and isotropic R hardening) and schematically the features of the modeling with the introduction of the damage D.

One way to modelized this defect is to use the theory of material damage. The definition given by Lemaitre [5,6] is the following: “Damage, in its mechanical sense in solid materials is the creation and growth of microvoids or microcracks which are discontinuities in a medium considered as continuous at a larger scale”. The defect as observed in initiation of fatigue cracks in L-PBF process can be assumed to be damage. In this way, the defect can be introduced in the plasticity law.

The criterion of fatigue crack initiation is linked to a threshold value of accumulated plastic strain at the mesoscopic scale, as defined by Papadopoulos:

$${\mathsf{\gamma }}_{\mathrm{cum} }\le {\mathsf{\gamma }}_{\mathrm{c}}$$

(2)

Based on the Dang Van’s original approach, the following three steps general framework has often been used in the literature to build a fatigue criterion:

-

Description of grain-scale plasticity;

-

Formulation of a local fatigue criterion;

-

Determination of a micro-macro model for macroscopic criterion.

The approach presented in this study not only considers these three aspects but also incorporates the effect of damage induced by a porosity located in the material. The size, position and geometry could be easily considered in the model proposed here; however, for a first evaluation, we will assume a spherical geometry of the defects.

In the Figure 2 representing the accumulated plastic strain versus the number of applied cycles, one can find the main possible cyclical behaviors:

-

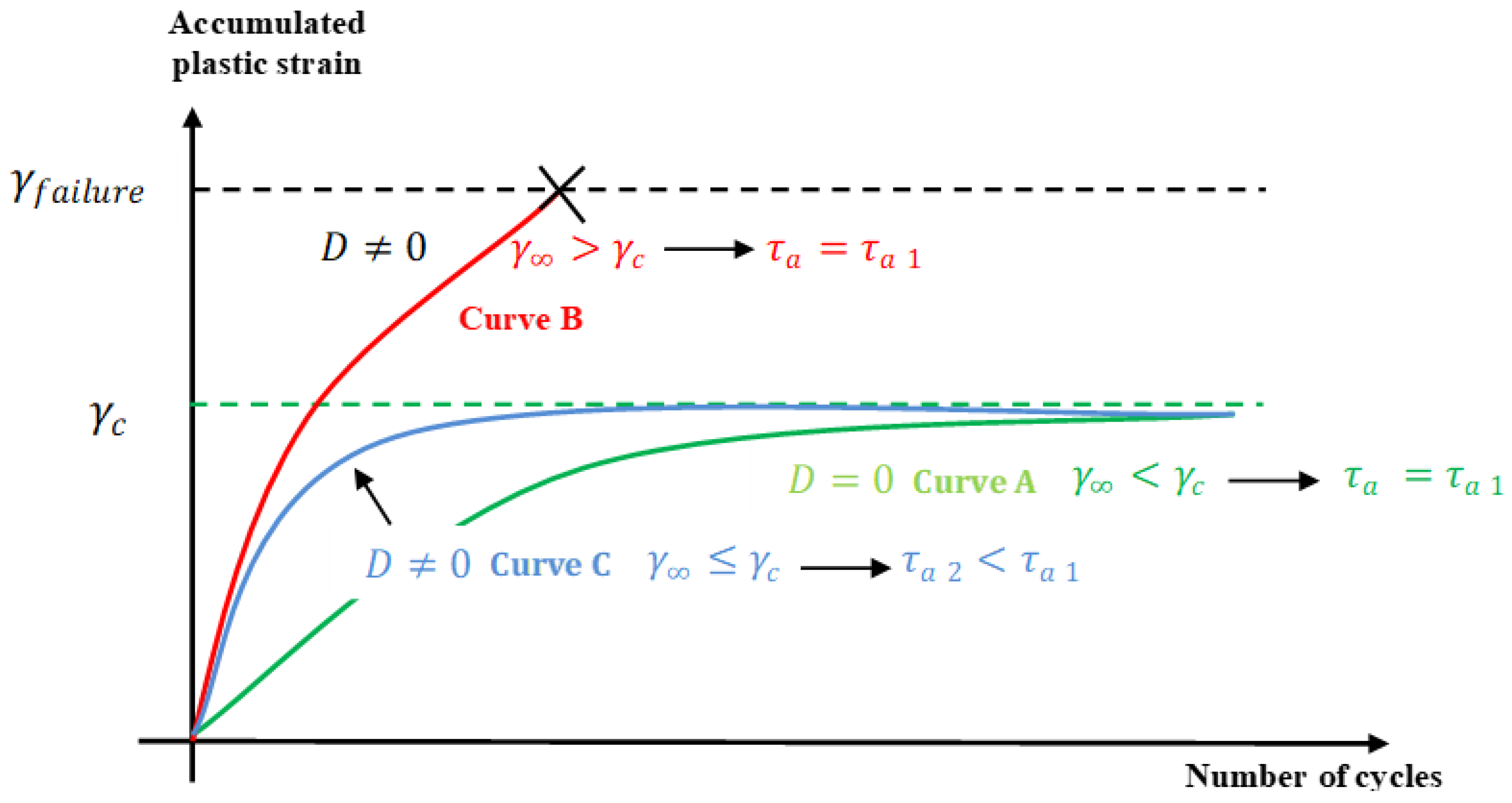
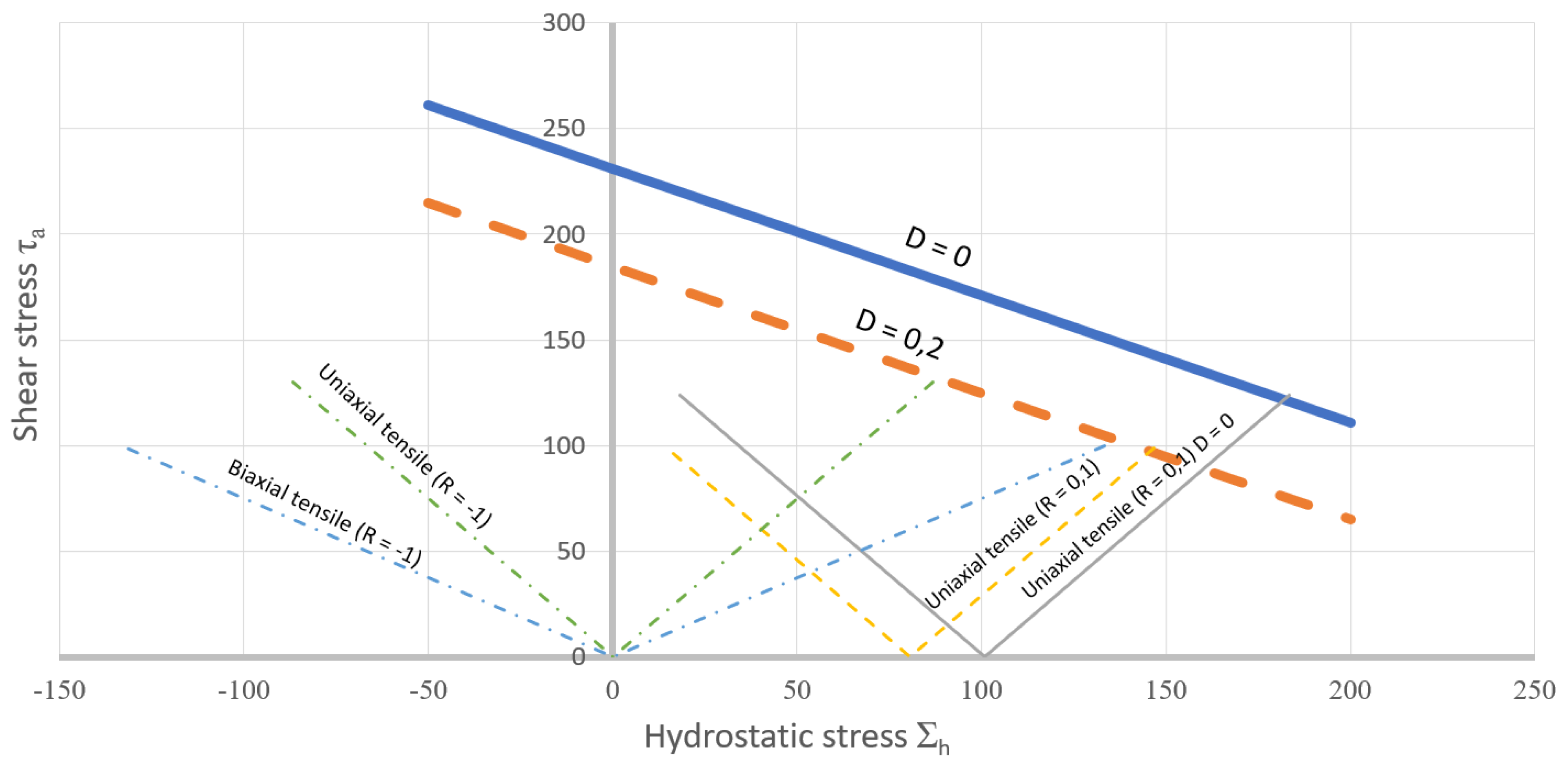
Curve A represents the case of a material without damage and without porosity. The damage D is equal to zero and the grain exhibits a purely elastic response (case of elastic shakedown). The failure is therefore excluded. The cumulative plastic slip in the crystal remains below the critical value of the crystal and the permissible shear constraint is less than ‘τ_a1’.

-

Curve B is a case where an initial porosity is present in the material. The applied shear constraint remains the same that for curve A. Because of this fraction of porosity, the cumulative plastic strain exceeds the critical threshold and initiation of fatigue crack appears. In this case, the elastic shakedown does not occur, and failure is unavoidable. Due to the damage, the materials’ durability decreases.

-

To achieve elastic shakedown with an initial damage, it is then necessary to limit the shear constraint to less than ‘τ_a1’. (Curve C).

The following introduces the basic principle of the modelling and the research of the elastic shakedown with the integration of damage in the yield function.

The yield function considered here was proposed by Lemaitre-Chaboche, with the damage variable D, extended to kinematic and isotropic hardening. The approach is similar, as proposed by Papadopoulos. The condition of elastic shakedown is not focused on the crystal but in the grain. The originality in this study is to observe the behavior of the grain by introducing damage. In this model, the effect due to the position of the porosity at the micro scale is negligible. It assumed here that the porosity and consequently the damage affect the evolution of accumulated plastic strain of the grain.

In this case, it was assumed that the damage, linked to the size, position and geometry of the porosity remains at the same value during the whole cyclic loading. The damage is here is defined by the impact of the defect and the decrease of the fatigue limit observed. The level of plasticity due to the porosity reached a higher value without the pore.

Here, we propose to follow the same framework defined by Dang Van and Papadopoulos. A presentation of the constitutive law is presented for the Dang Van criteria with an introduction of the damage. The plasticity loading function F at the grain scale is then determined by:

$$\mathrm{F}=\left(\frac{{\sigma }_{\mathrm{ij}}}{1-\mathrm{D}}-\mathrm{X}\right)-\mathrm{R}$$

(3)

where D is the damage parameter, X is the kinematic hardening and R is the isotropic hardening. We assume in this case a uniaxial loading for the calculations. A linear law is adopted for both hardenings:

$$\mathrm{X}=\mathrm{C} \mathsf{\gamma }$$

(4)

$$\mathrm{R}={\mathsf{\tau }}_{\mathrm{d}}={\mathsf{\tau }}_0+{\mathrm{R}}_{\mathrm{o}}{\mathsf{\gamma }}_{\mathrm{cum} }$$

(5)

where γ is the plastic slip strain at the moment, τ₀ is the elastic limit of the grain, Ro is the parameter of isotropic hardening, c is the parameter of kinematic hardening and γ_cum is the accumulated plastic strain.

As in the Dang Van criterion, the micro–macro model chosen in this study is based on the Lin–Taylor homogenization assumption in order to relate meso- and macroscopic mechanical fields. The model assumes equality between strain fields at the mesoscopic and macroscopic scale. The effect of the micro-macro model on the elastic shakedown has been well studied by Monchiet [8]. Three homogenization schemes have been tested: Sachs, Lin-Taylor and Kröner. It has been observed that the predictions of the fatigue behavior at the elastic shakedown are independent of the homogenization model.

For the research of the elastic shakedown, the knowledge of the constitutive laws associated to the yield stress is important to solve the function. All the following equations can be found in References [10,11].

$$\dot{\mathsf{\gamma }}=\dot{\mathsf{\lambda }}\frac{\partial \mathrm{F}}{\partial {\sigma }_{\mathrm{ij}}}$$

(6)

$${\dot{\mathsf{\epsilon }}}_{\mathrm{ij}}^{\mathrm{p}}=\dot{\mathsf{\lambda }}\frac{\partial \mathrm{F}}{\partial {\sigma }_{\mathrm{ij}}}$$

(7)

The plastic multiplier can be obtained by the first relation:

$$\dot{\mathsf{\lambda }}=\dot{\mathsf{\gamma }}\frac{{\mathsf{\tau }}_{\mathrm{d}}{}^2}{2{\sigma }_{\mathrm{ij}}}={\dot{\mathsf{\gamma }}}_{\mathrm{cum}}\frac{{\mathsf{\tau }}_{\mathrm{d}}{}^2}{2\left|{\sigma }_{\mathrm{ij}}\right|}$$

(8)

Constitutive laws concerning the isotropic and kinematic hardening are defined as follows:

$${\dot{\mathsf{\tau }}}_{\mathrm{d}}={\mathrm{R}}_{\mathrm{o}}{\dot{\mathsf{\gamma }}}_{\mathrm{cum}}$$

(9)

$$\dot{\mathsf{X}}=\mathrm{c}\dot{\mathsf{\gamma }}$$

(10)

In order to take into account the effect of damage, it is also necessary to use some specific formulations based on the elastic shakedown concept.

One of the criteria based on the critical plane notion is the Papadopoulos criterion defining a threshold value of accumulated plastic strain. In the current study, the variation of the accumulated plastic strain in the material will be addressed versus the damage intensity.

$${\mathsf{\gamma }}_{\mathrm{cum}}^{}\left(\mathrm{D}\right)\le {\mathsf{\gamma }}_{\mathrm{c}}$$

(11)

${\mathsf{\gamma }}_{\mathrm{cum}}^{*}$ is the maximal value of ${\mathsf{\gamma }}_{\mathrm{cum} }$ in the whole slip systems. In order to take into account, the effect of mean stress, as proposed by Dang Van, it is possible to consider the variation of the threshold value with the hydrostatic stress:

$${\mathsf{\gamma }}_{\mathrm{cum}}^{}\left(\mathrm{D}\right)\le {\mathsf{\gamma }}_{\mathrm{c}}-{\mathsf{\alpha }}^{\prime }{\sum }_{\mathrm{H},\max }^{}$$

(12)

Another way to take into account the effect of mean stress or multiaxial loading is the normal stress [14]. In this paper, it will be assumed in this study that the hydrostatic stress is not affected by the damage.

By introducing ${\mathrm{R}}_{\mathrm{o}}$ et ${\mathsf{\tau }}_0$, the criterion can be finally written:

$${\mathsf{\tau }}_0+{\mathrm{R}}_{\mathrm{o}}{\mathsf{\gamma }}_{\mathrm{cum}}^{}\left(\mathrm{D}\right)\le {\mathsf{\tau }}_0+{\mathrm{R}}_{\mathrm{o}}{\mathsf{\gamma }}_{\mathrm{c}}-{\mathrm{R}}_{\mathrm{o}}{\mathsf{\alpha }}^{\prime }{\sum }_{\mathrm{n},\max }^{}$$

(13)

Coefficients β and α are defined by Equations (13) and (14), and by considering the amplitude of the maximum cission (shear stress) in the elastic shakedown state τ_a (D), as a function of the damage D (Equation (15)), the criteria can be re-written as Equation (16).

$$\mathsf{\beta }={\mathsf{\tau }}_0+{\mathrm{R}}_{\mathrm{o}}{\mathsf{\gamma }}_{\mathrm{c}}$$

(14)

$$\mathsf{\alpha }={\mathrm{R}}_{\mathrm{o}}{\mathsf{\alpha }}^{\prime }$$

(15)

$${\mathsf{\tau }}_{\mathrm{a}} \left(\mathrm{D}\right)={ \mathsf{\tau }}_0+{\mathrm{R}}_{\mathrm{o}}{\mathsf{\gamma }}_{\mathrm{cum}}^{}\left(\mathrm{D}\right)$$

(16)

The criteria can be finally written as:

$${\mathsf{\tau }}_{\mathrm{a}} \left(1-\mathrm{D}\right)+\mathsf{\alpha }{\sum }_{\mathrm{h},\max }^{} \le \mathsf{\beta }$$

(17)

This criterion is based upon the critical plane approach, including the hydrostatic stress ${\sum }_{\mathrm{h},\max }^{*} \left(\mathrm{t}\right)$(t) as a function of time and the mesoscopic shear stress ${\mathsf{\tau }}_{\mathrm{a}} \left(1-\mathrm{D}\right)$ ($\overrightarrow{\mathrm{n}}$,t) (in the elastic shakedown state) on a plane defined by its normal vector, $\overrightarrow{\mathrm{n}}$. The definition is close to the dang Van criterion with an introduction of the damage; therefore, to avoid the fracture of the most strained grain, the criterion becomes:

$${\max }_{\overrightarrow{\mathrm{n}},\mathrm{t}} \left\{{\mathsf{\tau }}_{\mathrm{a} \left(\overrightarrow{\mathrm{n}},\mathrm{t}\right) }\left(1-\mathrm{D}\right)+\mathsf{\alpha }{\sum }_{\mathrm{h},\max }^{}\left(\mathrm{t}\right) \le \mathsf{\beta }\right\}$$

(18)

The material coefficients α et β are easily identifiable from fatigue limit in fully reversed tensile loading s₋₁ and torsion loading t₋₁. The value obtained is close to the Dang Van criteria with a new parameter which represents the damage.

On our case of LPBF process, the damage is linked to the porosity which decrease the fatigue limit. It is assumed to be a fixed quantity because the value of the porosity doesn’t change during the cyclic loading. In this case the mean stress and the damage is equal to 0. The analytical formulation of these two parameters are:

$$\mathsf{\alpha }=\frac{{\mathrm{t}}_{-1}-{\mathrm{s}}_{-1}/2}{{\mathrm{s}}_{-1}/3} \mathrm{et} \mathsf{\beta }={\mathrm{t}}_{-1}$$

(19)

3. Results

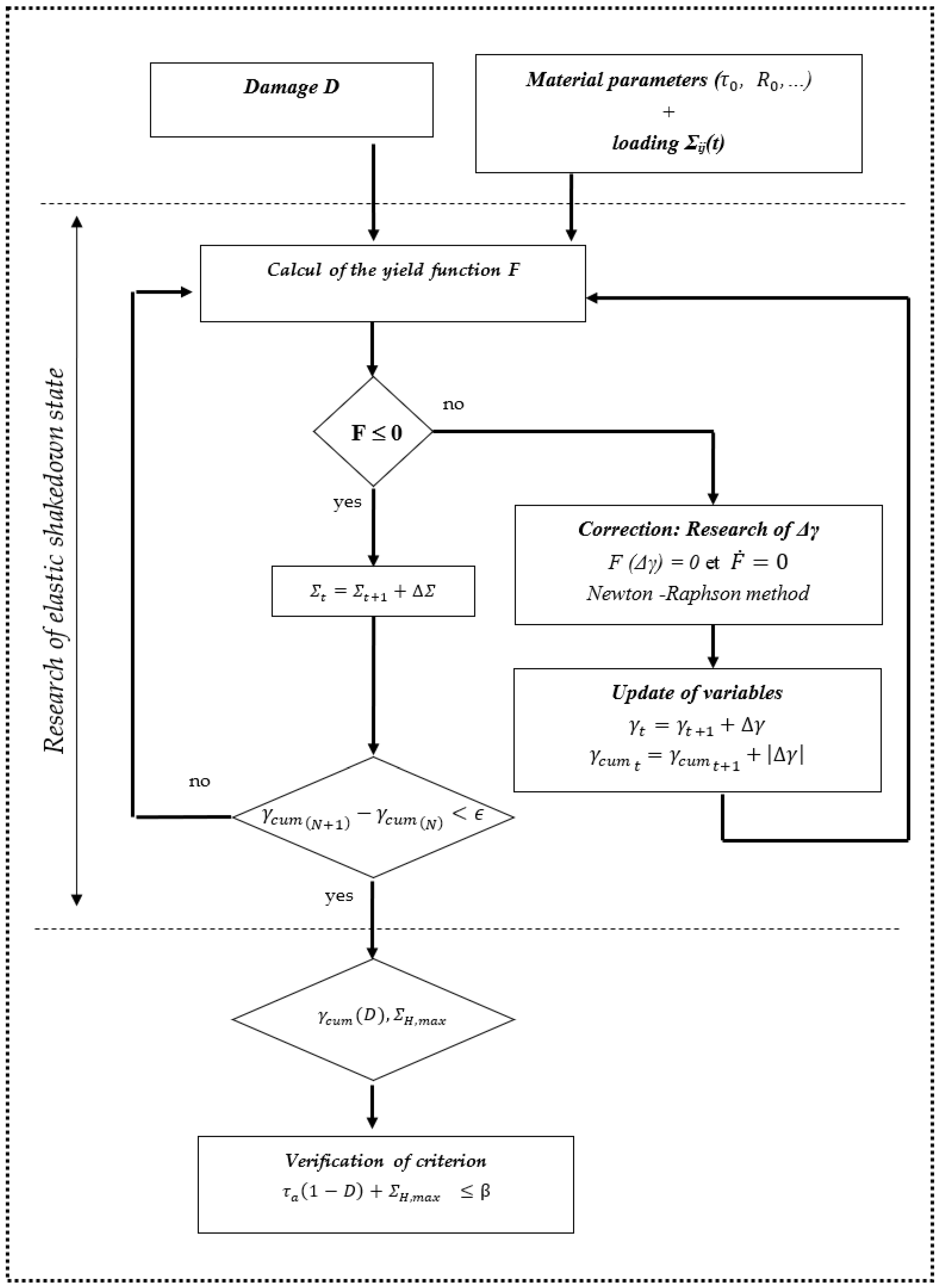
3.1. General Method

The coefficients used in the model are:

-

τ_o Elastic limit of the grain;

-

R_o Parameter of isotropic hardening;

-

c Parameter of kinematic hardening;

-

γ_c Critical accumulated plastic strain;

-

α et β Fatigue criterion parameters.

A sinusoidal loading can be defined as:

$${\sum }_{\mathrm{ij}}\left(\mathrm{t}\right)={\sum }_{\mathrm{ij},\mathrm{m}}+{\sum }_{\mathrm{ij},\mathrm{a}}\sin \mathsf{\omega }\mathrm{t}$$

(20)

${\sum }_{\mathrm{ij},\mathrm{m}}$ is defined as a mean stress and ${\sum }_{\mathrm{ij},\mathrm{a}}$ is the amplitude stress.

${\sum }_{\mathrm{ij},\mathrm{m}}$, ${\sum }_{\mathrm{ij},\mathrm{a}}$ and D are fixed. The next step is to reach the elastic shakedown. The condition is to find the good value of loading to satisfy the condition of critical accumulated plastic strain ${\mathsf{\gamma }}_{\mathrm{cum}}^{*}\left(\mathrm{D}\right)$. The different steps for obtaining this elastic shakedown state are presented in Figure 3. The numerical resolution is obtained by the Mathematica software (Wolfram Research, Champaign, IL, USA). The cyclic loading is divided in M steps:

$${\sum }_{\mathrm{ij},\mathrm{t}}={\sum }_{\mathrm{ij},\mathrm{a}}\sin \left(\frac{2\mathrm{t}\mathsf{\pi }}{\mathrm{M}}\right)+{\sum }_{\mathrm{ij},\mathrm{m}}$$

(21)

At each time, it is possible to check the plasticity condition defined by the yield function:

$$\mathrm{F}\le 0$$

(22)

If this condition is not satisfied, an increment of accumulated plastic strain $\Delta \mathsf{\gamma }$ is determined and applied in order to validate the yield function. The numerical resolution and the research of this value is obtained by the Newton-Raphson method, using a tangent operator ${\stackrel{=}{\mathrm{T}}}^{\mathrm{t}}$ determined by $\dot{\mathrm{F}}=0$.

The numerical integration is defined by the following equations:

$$\{\begin{array}{c}\Delta \mathsf{\gamma }={\stackrel{=}{\mathrm{T}}}^{\mathrm{t}}:\Delta {\displaystyle \sum ^{=}}\\ {\mathsf{\gamma }}^{\mathrm{t}}={\mathsf{\gamma }}^{\mathrm{t}-1}+\Delta \mathsf{\gamma } \end{array}$$

(23)

The accumulated plastic strain is directly deducted by:

$${\mathsf{\gamma }}_{\mathrm{cum}}^{\mathrm{t}}={\mathsf{\gamma }}_{\mathrm{cum}}^{\mathrm{t}-1}+\left|\Delta \mathsf{\gamma }\right|$$

(24)

The difference between the accumulated plastic strain at times t and t₋₁ is then calculated. When this difference is less than $\mathsf{ϵ}$, the shakedown state is reached. The last condition is to check that the accumulated plastic strain generated by the damage is below the critical accumulated plastic strain of the material.

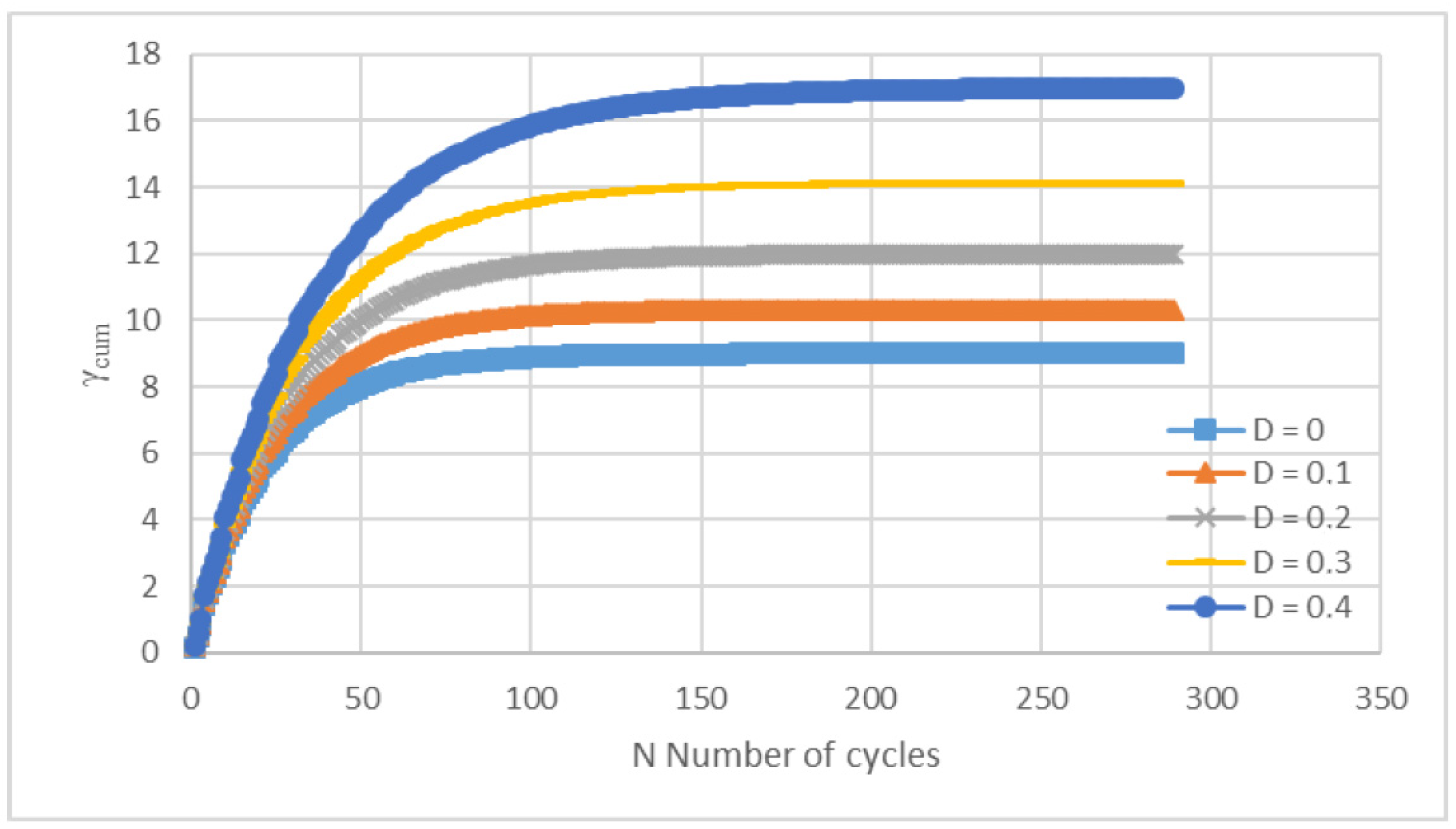
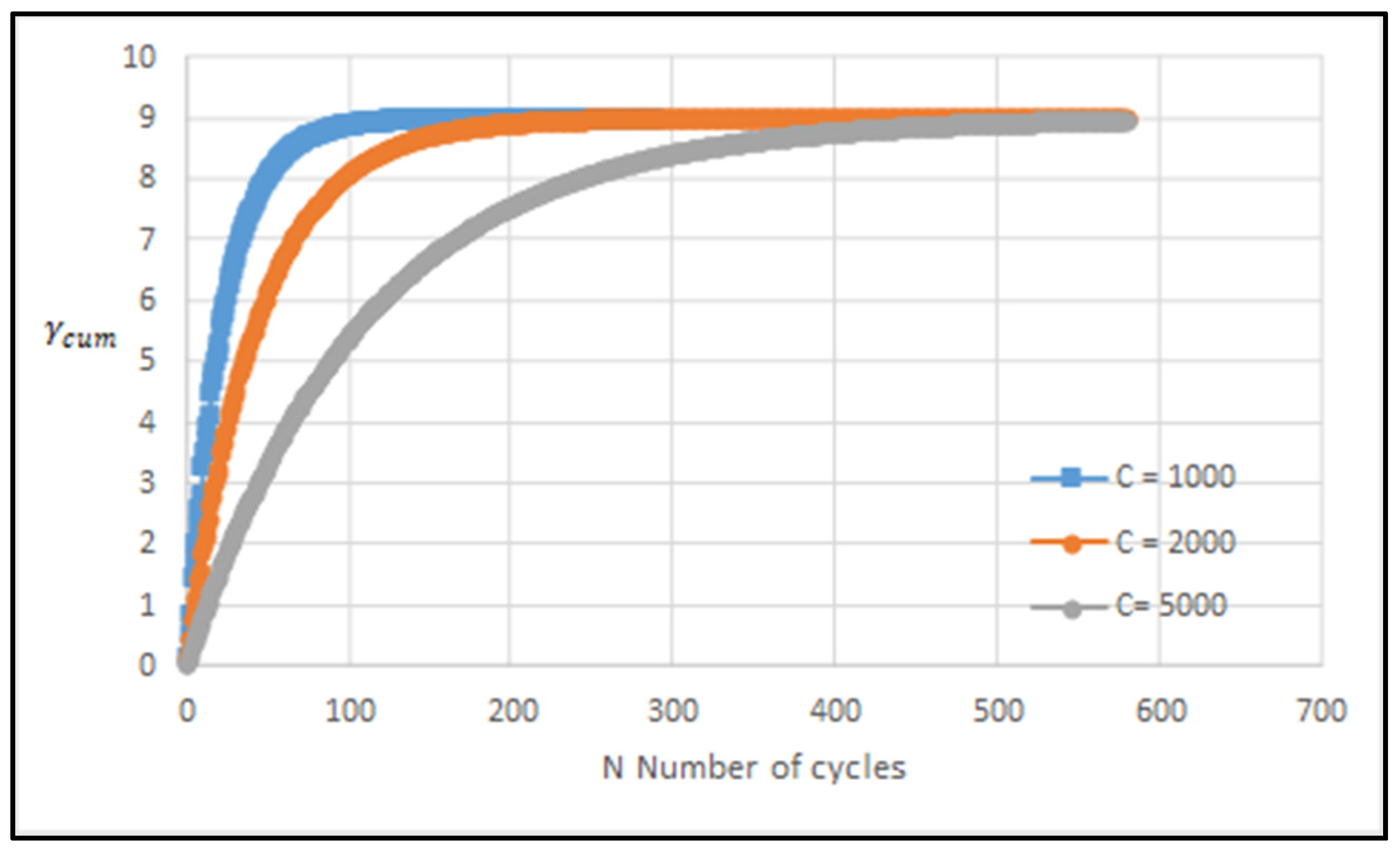
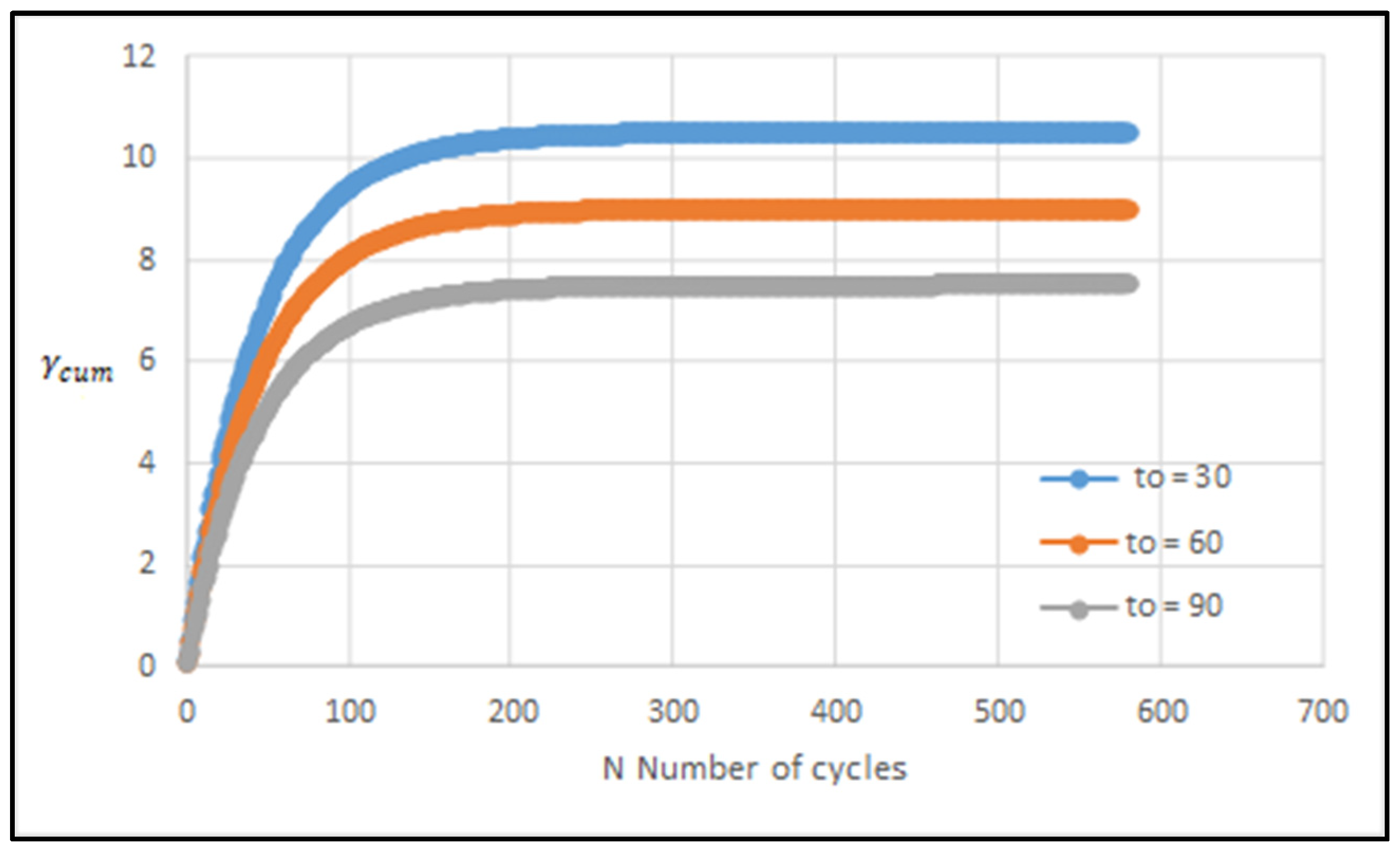
3.2. Testing of the Criterion

The criterion was tested by considering the influence of the different input parameters and determining the various responses of the elastic shakedown state. For this parametric study, the material properties of a steel, close to a 34Cr4, were assumed (

Table 1. Material properties at macroscopic scale.

s−1	t−1	α	β	${\mathsf{\sigma }}_{\mathbf{y}}$	${\mathsf{\sigma }}_{\mathbf{UTS}}$
400 MPa	240 MPa	0.2	240	700 MPa	900 MPa

and

Table 2. Material properties for the model at mesoscopic scale.

τo	Ro	c	γc
60 MPa	20 MPa	2000	9

). All of these parameters are taken from [14]. They are only used to have the behavior of the plasticity of the grain during the elastic shakedown.

The parameters, α and β, are assumed to be the fatigue limit of the steel for a load ratio equal to R = −1. For the other coefficients related to the mesoscopic scale, we use the values defined in the literature [8,15]:

Figure 4 shows the evolution of the plastic strain versus the shear stress during the number of cycles for a value of damage D. The loading defined here is an amplitude stress Σ_amp equal to 400 MPa in tensile loading. It can be clearly seen that the plastic shear strain tends to disappear after a number of cycles, thus providing an elastic shakedown. The different colors represent different number of cycles (0 cycle in blue to 300 cycles in purple when the elastic shakedown is reached).

To visualize the effect of the damage on the accumulated plastic strain, different values of the damage parameter D have been introduced to analyze the evolution of accumulated plastic strain. It be can clearly see in Figure 5 that the value of ${\mathsf{\gamma }}_{\mathrm{cum}}{}_{}$ increases with increased damage. It can be logically deduced that the material could be less resistant with the increase in damage. Similarly, for a given damage present in the material, the acceptable loading should be less important for the same durability.

For the same previously defined accumulated loading, Figure 6 shows the influence of kinematic hardening parameter “c” on the accumulated plastic strain. No effect is shown on the final accumulated plastic strain value γ_cum when reaching the elastic shakedown state; however, it is clearly observed that the elastic shakedown state is reached earlier with increasing “c” parameters. It means that a material, with a high kinematic parameter, reduced the time to reach the state of elastic shakedown. This phenomenon has also been observed by Borges [16]. They have done a parametric study of the effect of material properties on fatigue crack growth. A small effect of kinematic hardening parameters on crack closure was found. Finally, the increase of the number of load cycles between crack steps delivered a main reduction of crack closure but no effect of plastic crack tip opening displacement on models without contact of crack flanks.

To address the effect of the isotropic hardening, the accumulated plastic grain was reported versus the initial elastic limit of the grain “τ_o” (Figure 7) and the parameter of the isotropic hardening “R_o” (Figure 8).

For both parameters, increasing isotropic hardening (by increasing “τ_o” or “R_o”) decreases the accumulated plastic strain; therefore, for the same loading, plastic deformation is lower within grains, and the fatigue limit of the material increases. Consequently, the isotropic hardening plays an important role on the fatigue behavior of the material. Doquet and Haddar [17,18] have clearly shown in low cycle fatigue the beneficial effect of such an isotropic hardening effect on both 316 and 304 austenitic stainless steels. Consequently, a material with a high isotropic hardening parameter has a better fatigue limit due to his high properties. All of these conclusions, without damage has clearly been explained by Papadopoulos [12] where the accumulated plastic strain reached at the elastic shakedown does not depend on the kinematic hardening properties of the crystal; thus, the evaluation of the initial yield limit τ_o and the the parameter of the isotropic hardening “R_o” gives an evaluation without damage to the mesoscopic accumulated plastic strain.

Finally, it could be possible to draw the evolution of the global criterion, defined on the last Equation (18), for different levels of damage. The criterion is shown on a Dang Van diagram (shear stress vs. hydrostatic stress) for different values of D (0, 0.1, 0.2, 0.5) in Figure 9.

The initial value of shear stress decreases with increasing damage in the material. It is assumed here that the slope of the criterion line is the same, which means that the mean stress in the case of uniaxial stress or biaxial stress is not affected by the damage for a multiaxial loading. It is also assumed that the torsion limit decreases with increasing porosity and damage in the material.

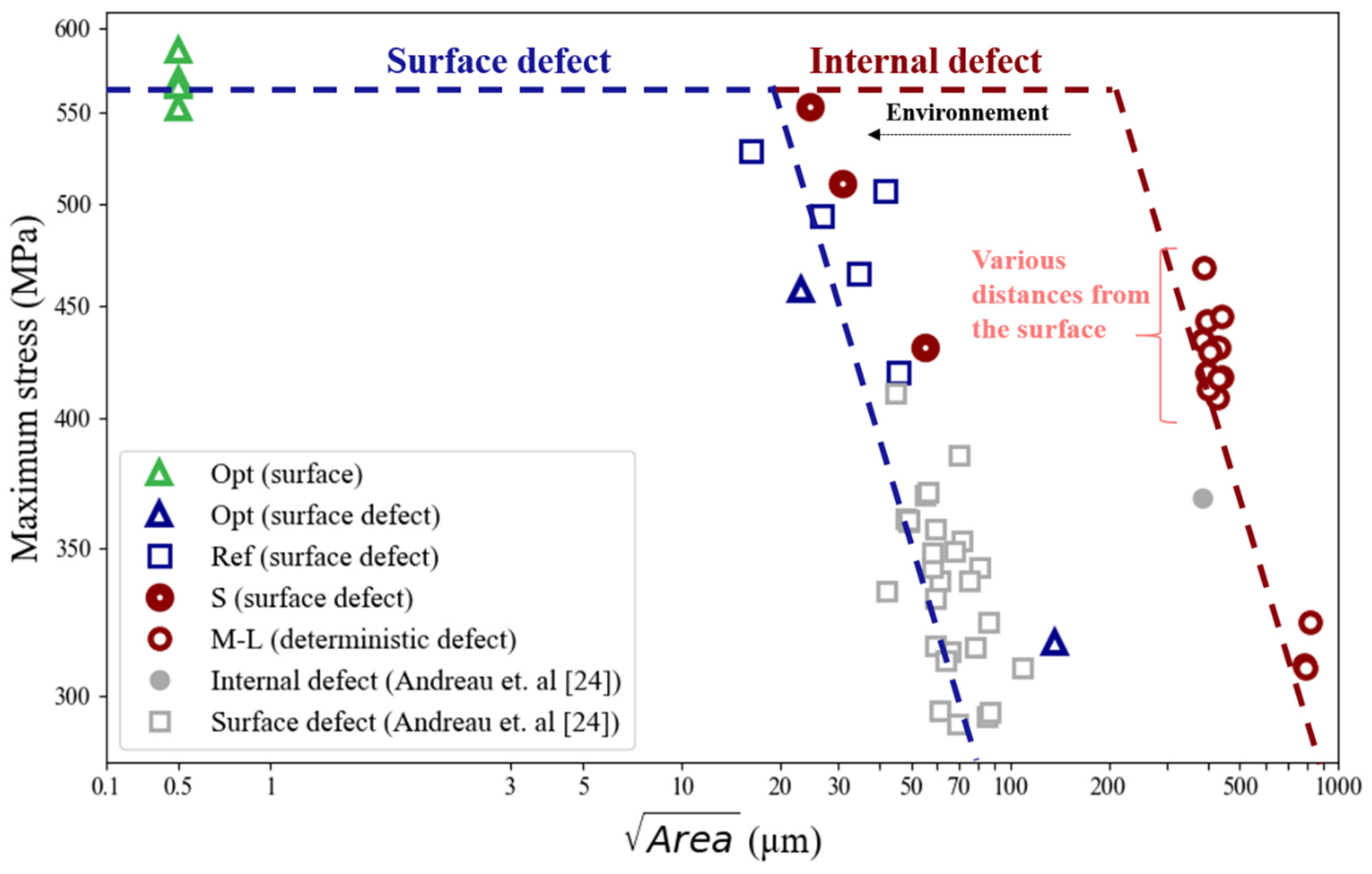
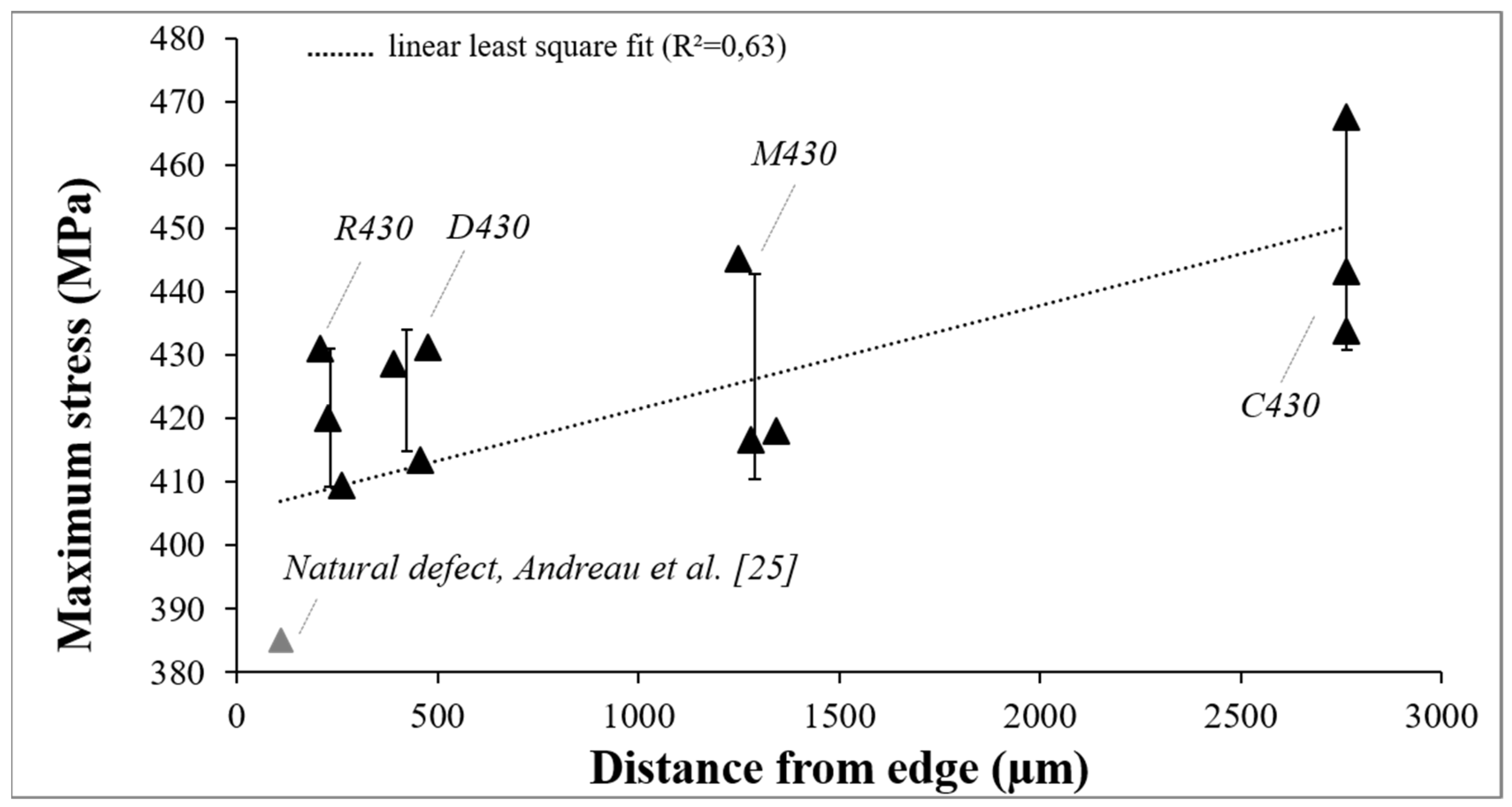
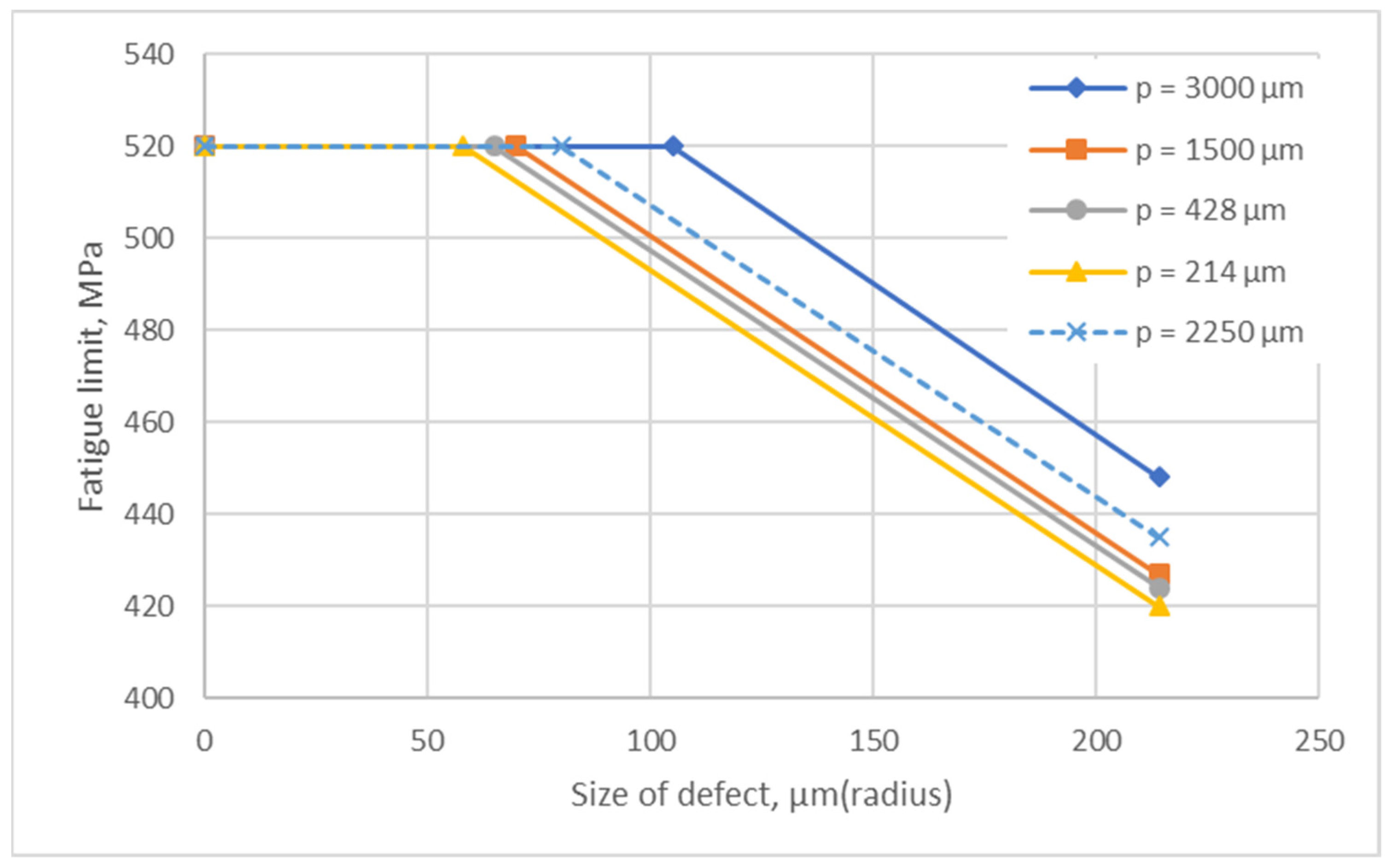
3.3. Application of Criterion: Case of 316L by LPBF Process with Deterministic Defects

In order to test the criterion detailed here above, based on Dang Van criterion but considering damage (porosity, particles, …), several fatigue tests were carried out recently on as-built LPBF specimens with deterministic defects by Andreau [13]. The aim of these tests is to characterize the damage variable D and to correlate this parameter with one deliberately induced porosity affecting the fatigue limit of the material. In Figure 10, it is clearly confirmed that the fatigue crack initiation directly occurs on the deterministic porosity designed during the CAD phase of fatigue samples.

One of the advantages of the LPBF process, is its ability to be able to control the position, geometry and size of the deterministic defect, in order to evaluate the damage which can be integrated in the criterion.

We propose to identify the criteria proposed in this paper to have classical material parameter:

-

Fully reversed tensile loading s₋₁;

-

Fully reversed torsion loading t₋₁.

With these two material parameters, it will be possible to have α and β, as presented in Equation (19).

The aim of this section is to propose a method to identify the parameter D for a porosity detected in the material. In order to correlate the porosity with the damage defined in the criteria, one way is to test different couple of size and position of deterministic defect using LPBF process.

Three sizes of defect and three positions are necessary to have the evolution of the fatigue limit for the material and consequently the evolution of the damage. Consequently, with an interpolation of the curve obtained, it will be possible to predict the fatigue limit of the material for a new set of size and position concerning a defect.

By determination of the fatigue limit (by any method as staircase or locati) for these specific specimens with controlled defects, and plotting the results on a (Kitagawa et al., 1976) diagram, it will be possible to extrapolate the results for any size and position and determining the parameter D.

The mechanisms observed, and the optimization of process parameters has been done previously. All the details of the LPBF manufacturing parameters and fatigue test conditions are available in the paper by Andreau et al. [13]. In the current paper, only a brief summary of the results and important data are presented.

The material is a stainless steel 316L built by the LPBF process, using SLM 125 HL machine from SLM Solutions Gmbh (Lubeck, Germany).

To characterize the effect of the deterministic defects in the fatigue behavior, some specimens of 6 mm diameter in the gauge section have been obtained from as-built cylinders. Machining was carried out in order to remove the deleterious surface finish and provide a R_a of 0.8. After machining, a 2 h 350 °C heat treatment was carried out under argon to relieve residual stresses.

Three sizes of defects (radii of 105, 214 and 424 μm) have been investigated. Figure 11 presents the fatigue results obtained for the different deterministic defects for 316L on a Kitagawa diagram [19]. Such a diagram clearly confirms that the fatigue behavior of as built 316L is depending on both size and position of the defects. For an internal defect location, the defect size threshold is higher than for a surface defect (around 25 μm for a surface defect versus 200 μm for an internal defect). Above this size defect threshold, a similar decrease of the fatigue limit occurs for both defect sizes. For this diagram, one limit of the criterion is that the effect of position is not represented. No statistical distribution of the porosity has been done due to the size of deterministic defect.

For the 316L LPBF, the influence of the defect position on the fatigue limit is shown to be relatively weak (Figure 12). For instance, for the same defect size (R = 214 μm) at 10⁶ cycles, the fatigue limit is equal to 450 MPa for a defect located in the center of the specimen (2800 µm for the surface) and 410 MPa for a defect close to the surface (C430, M430, D430, R430, respectively, means that the distance from defect center to surface is 3000 µm, 1715 µm, 645 µm and 430 µm).

Considering all the fatigue data obtained on samples with deterministic defects, it becomes possible to propose a relation between the fatigue limit and the damage, defined here by a porosity. For a macroscopic point of view, to define the evolution of the damage for a porosity rate, it could be necessary to define the definition of the damage, as expressed in Equation (18), and including defect size “ds” and position “p” of the defect:

$${\mathrm{S}}_{\mathrm{D}}\left(\mathrm{ds},\mathrm{p}\right)=\raisebox{1ex}{$\mathrm{S}$}\!\left/ \!\raisebox{-1ex}{$1-\mathrm{D}$}\right.$$

(25)

where S is equal to the fatigue limit of the material without defect, D is the damage variable, S_D is the fatigue limit with defect. With Figure 11 and Figure 12, it is possible to have the evolution of Sd with the size of the defect and the position. For this material, as said before, it appears that the effect of distance from edge is small. For other material, it could be different.

Two ways are possible to identify the damage parameters:

-

The first way is to create deterministic defects (by changing size and position) in many specimens and to achieve fatigue tests to determine the fatigue limit. This kind of identification is focused on one pore.

-

The second possibility is to test different porosity rate by changing for the LPBF process the process parameters. The fatigue limit obtained for this case is not focused here on one pore but for a statistic distribution of defects. That’s the simple way for a use case to connect the fatigue limit during the production of a part. It is possible to imagine that with some machine instrumentations to predict porosity during the process which can determine the damage.

The variation of fatigue limit with the size and position of the defects (the damage) is shown in Figure 13. As previously discussed, the effect of position is weak and the three lines for the positions to 214 μm, 428 μm and 1500 μm are close to each other. This specific fatigue behavior concerning the effect of the size and position of the defects for this material, 316 L, clearly show a non-sensibility to notch effect as presented by Andreau [13] due to a similar fatigue limit for different porosity rate. A similar experimental campaign with a material more sensitive to notch effect as aluminum alloy can help to better understand the effect of the size of defects, coupled with position.

We assumed in this diagram that the effect of size for the four positions (the slope of the diagrams above the size threshold) was the same. Interpolating these data, and using Equation (24), it becomes possible to predict the effect of any position (“p” in the diagram) and size. For instance, in Figure 13, the fatigue behavior can be predicted for a 2250 µm defect position (dotted line) and a defect size of 214 μm. The resulting maximum sustainable stress is equal to 440 MPa for a load ratio R equal to 0.1. The corresponding damage parameter, estimated by Equation (24), is equal to D = 0.2.

Such an approach could be easily used in combination with X-ray tomography, to provide a rather accurate estimation of the fatigue limit.

The value of tensile stress of the material for a load ratio R = −1 is around to 300 MPa as presented by [13,20]. The use of the Gerber criterion [21] is in agreement with the results obtained at R = 0.1. By assuming a torsion limit for a load ratio R = −1 equal to 0.7*s₋₁ as observed for many materials in the literature [22] it will be possible to predict the fatigue limit of the material in torsion.

After calculation of these two materials parameters, it is possible to draw the Dang Van line for a damage equal to D = 0 (Figure 14), and for a D = 0.2 damage using Equation (17) (for the same 214 μm defect size at a distance of 2250 μm from the surface). The use of Dang Van criterion also allows predicting the fatigue limit at 2.10⁶ cycles for different loadings. In the next figure, the loading paths for biaxial and uniaxial tensile loading with a stress ratio R = −1 are presented.

4. Conclusions

An extension of the Dang Van criterion was proposed to consider damage, and especially porosity, in the fatigue behavior. The proposed criterion uses the concept of elastic shakedown with the Lemaitre–Chaboche damage model. The search of elastic shakedown shows that with introducing a damage in the yield function, a stabilized condition is observed for the accumulated plastic strain; it is also possible to have the new Dang Van line for an evolution of the damage (modelized here by a porosity).

The result of the local criteria is similar to the initial Dang Van criteria with a new parameter D representing here the damage due to the presence of porosity.

The research of elastic shakedown show that there is no effect of kinematic hardening contrary to isotropic hardening which increases the fatigue strength of the material; it is clearly seen in the results that the damage increases the accumulated plastic strain.

The Dang Van criteria extended to damage is applied on a 316L material obtained by LPBF process. Two propositions are presented to identify the damage created by the porosity. The first focus on a deterministic defect and the second on a porosity rate. After determination of the evolution of the fatigue limit, depending on the size and position of the defect, it is possible to have the Dang Van line for a damage value D.

Finally, a new Dang Van line is obtained, and considers the damage in the fatigue behavior.

An example of application of the criterion was made on a 316L stainless steel built with LPBF additive manufacturing; it confirms that the porosity characteristics, in terms of size and position, changed the fatigue limit of the material, as exposed in the Kitagawa diagram. The extension proposed here, can open new opportunities such as the prediction of multiaxial loadings, which are not possible with a Kitagawa diagram. More widely, this kind of model, combined with in-situ monitoring of defects in LPBF machines or post-mortem x-ray tomography could be a solution to predict cyclic mechanical properties of the material, in any loading mode.