Delamination Behavior of Highly Stretchable Soft Islands Multi-Layer Materials
Abstract
1. Introduction
2. 3D Computational Model of Soft Islands Structures
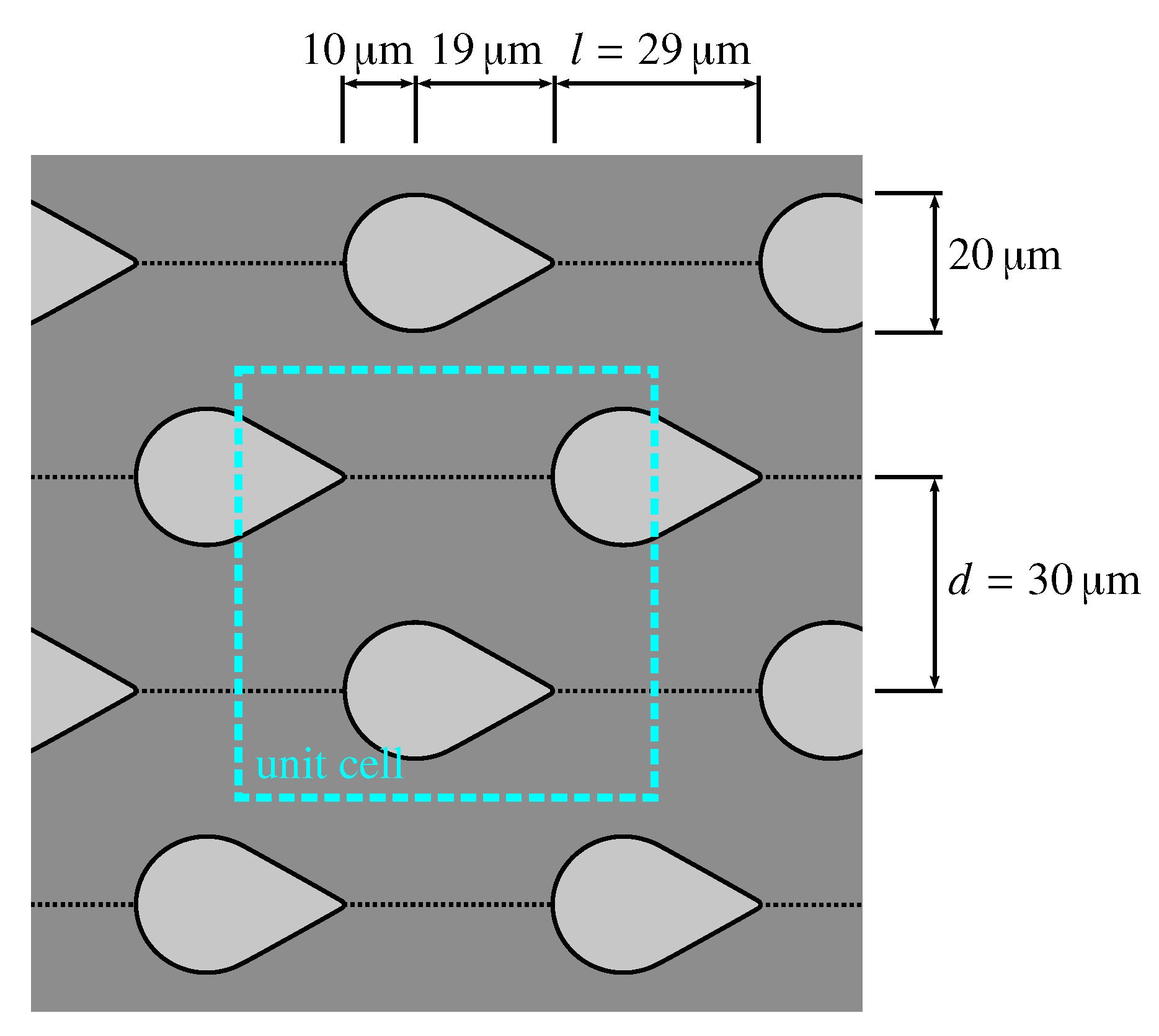
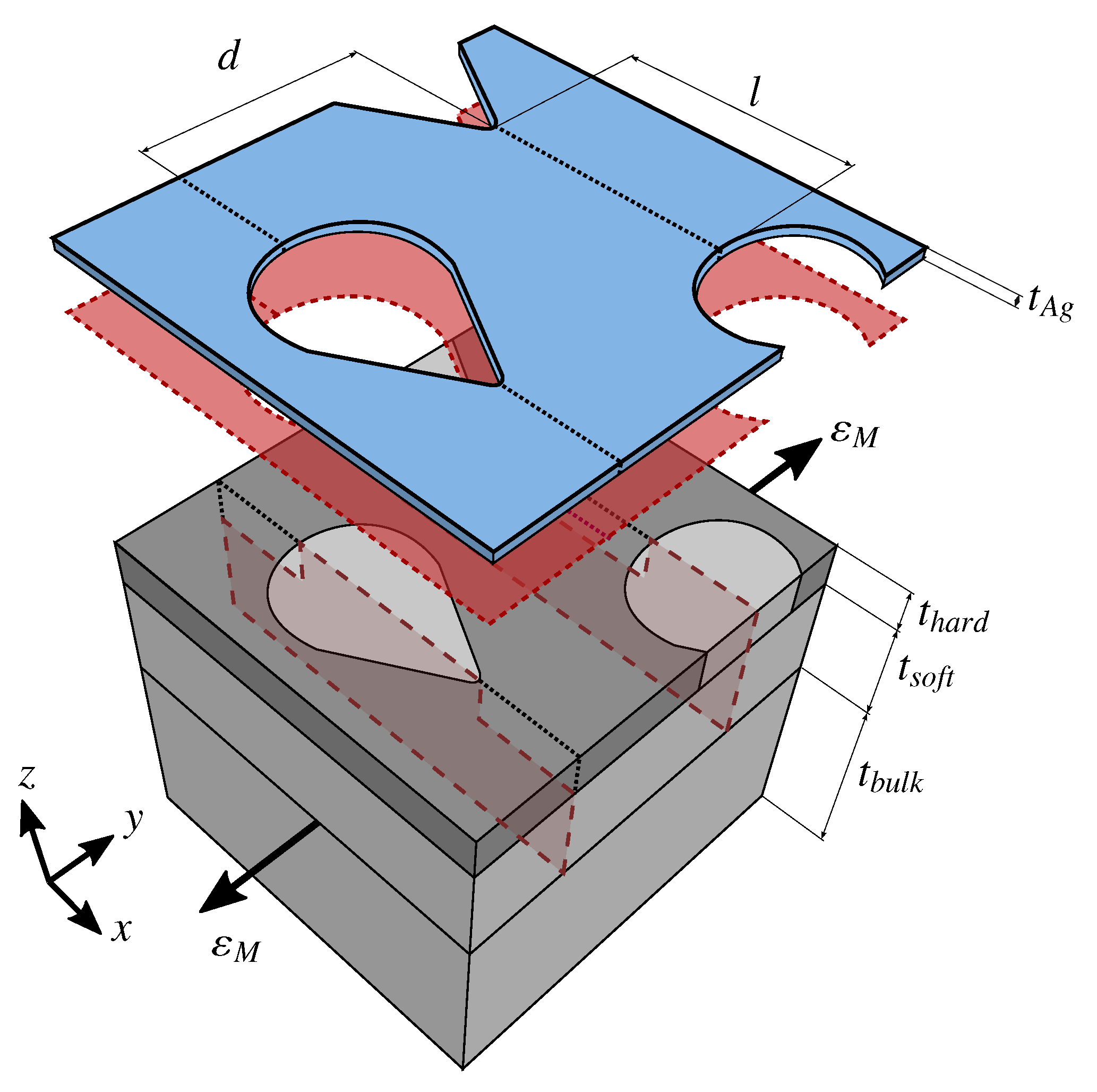
2.1. Representative Volume Element of Soft Island Composite
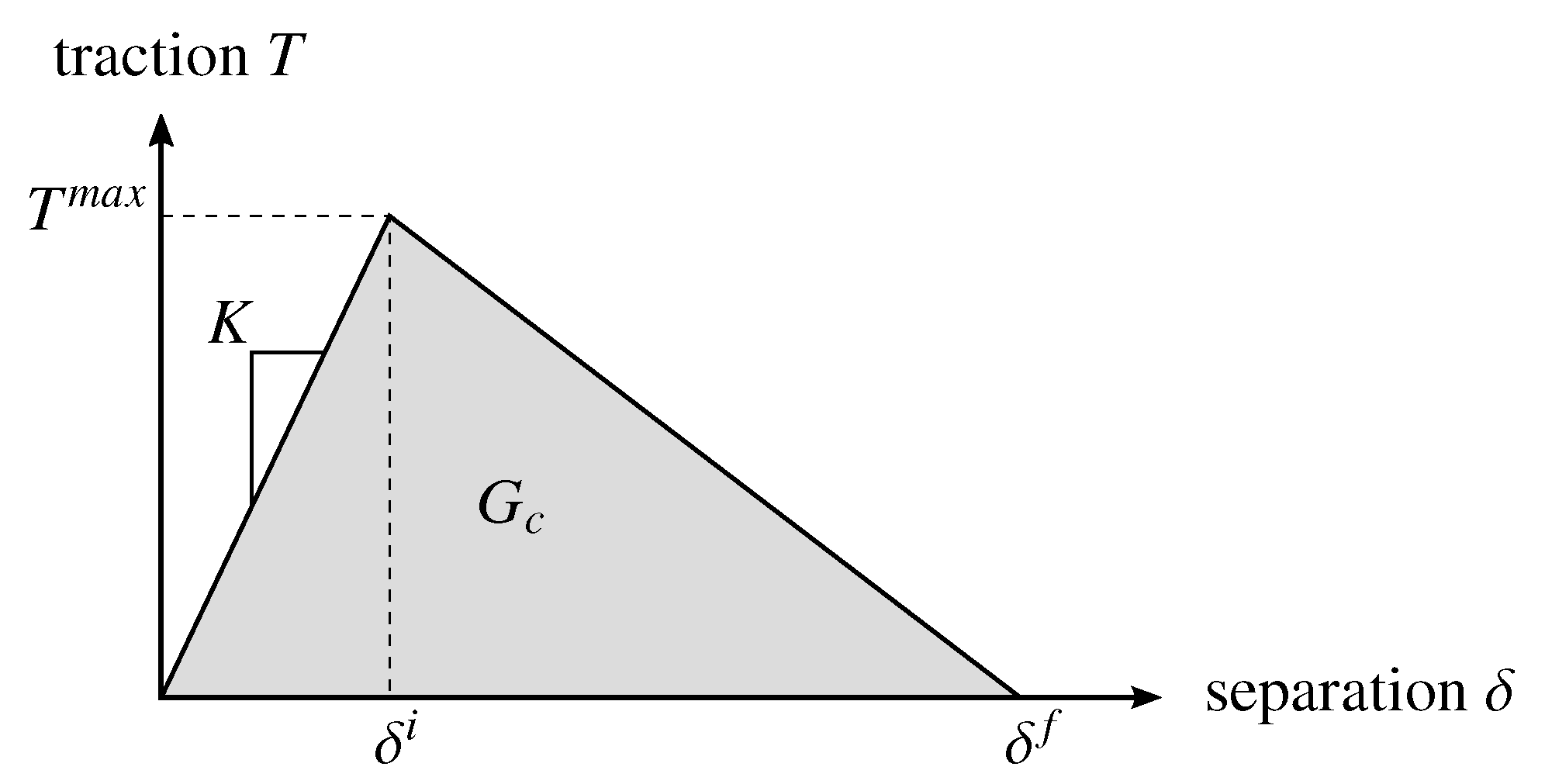
2.2. Cracking and Delamination
3. Results
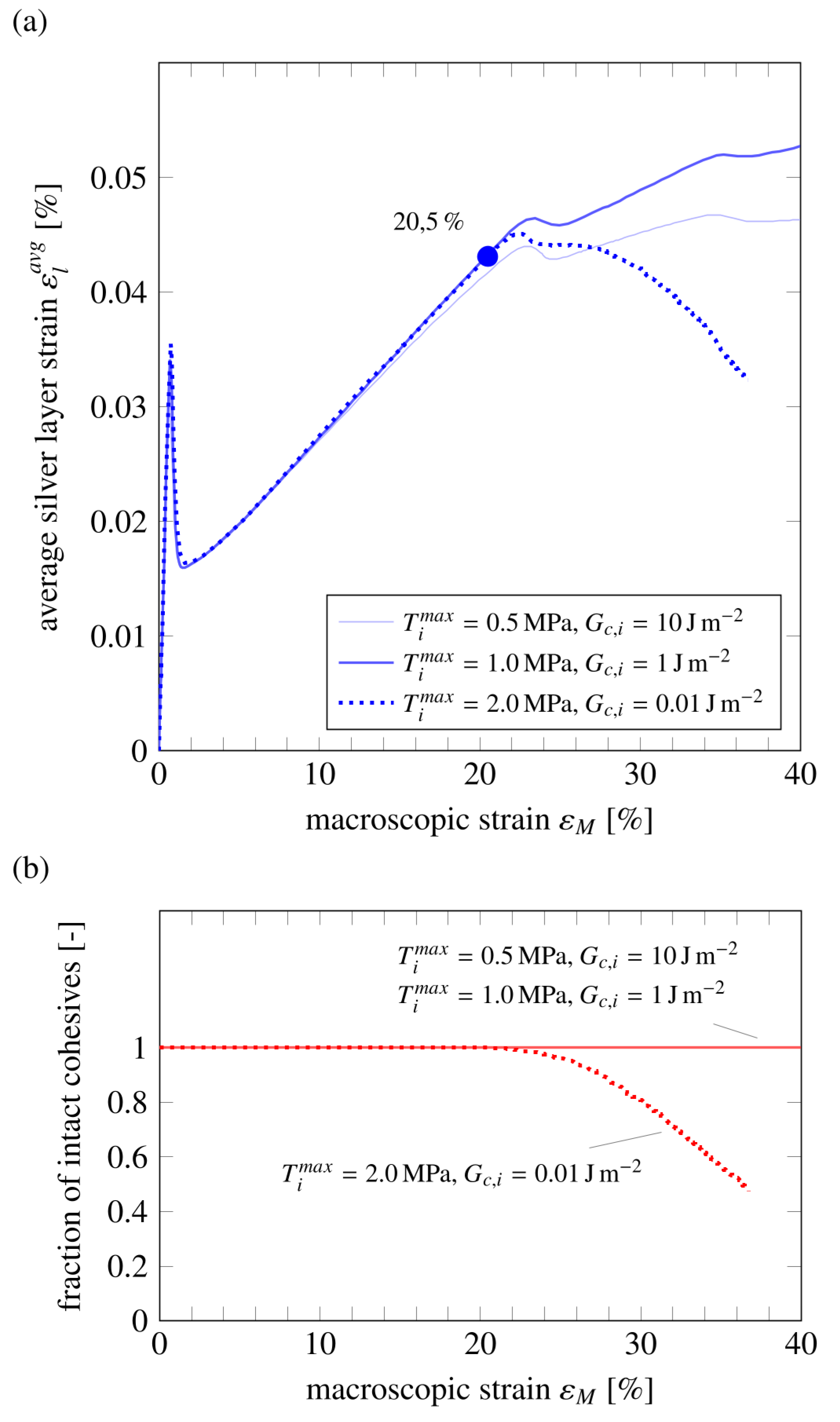
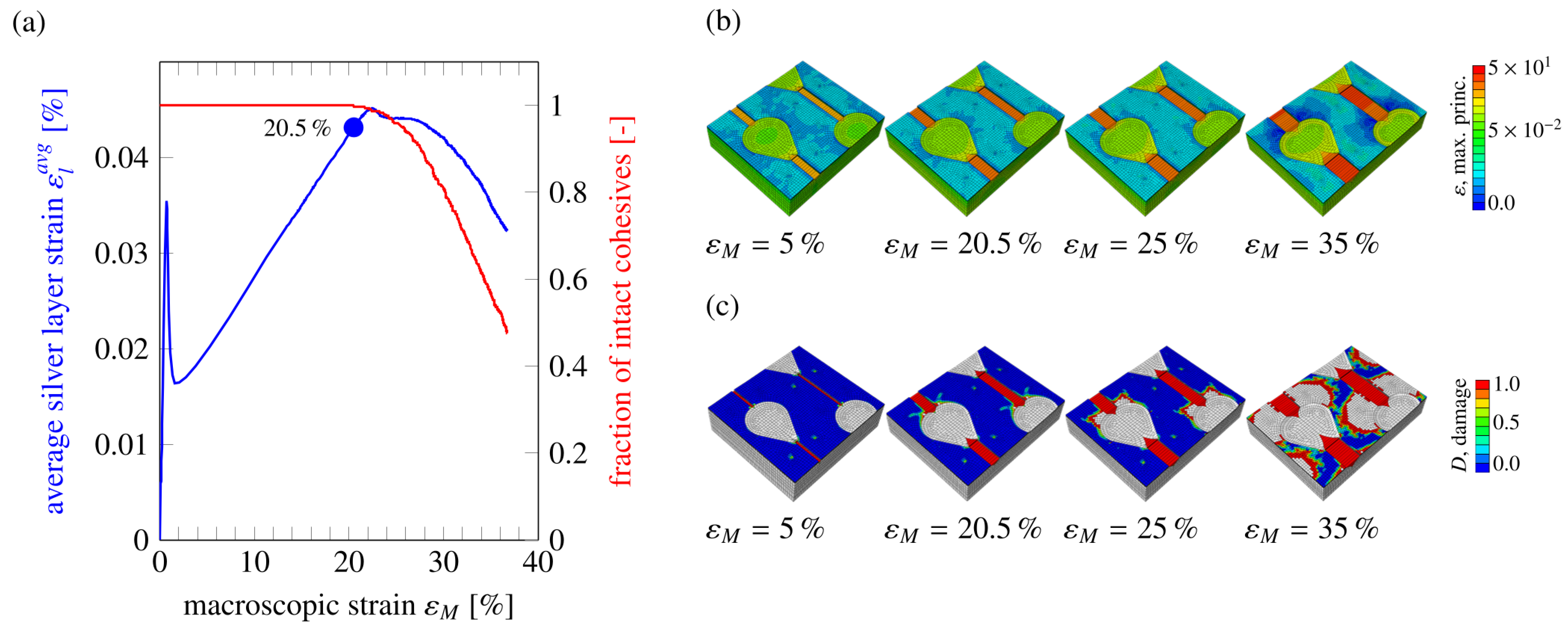
3.1. Delamination Behavior
3.2. Influence of Structure on Delamination
3.3. Influence of Interface Bonding on Delamination
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Finite Element Model Details and Cohesive Zone Model
References
- Fallegger, F.; Schiavone, G.; Lacour, S.P. Conformable Hybrid Systems for Implantable Bioelectronic Interfaces. Adv. Mater. 2020, 32, 1903904. [Google Scholar] [CrossRef] [PubMed]
- Chung, H.U.; Rwei, A.Y.; Hourlier-Fargette, A.; Xu, S. Skin-interfaced biosensors for advanced wireless physiological monitoring in neonatal and pediatric intensive-care units. Nat. Med. 2020, 26, 418–429. [Google Scholar] [CrossRef] [PubMed]
- Byun, J.; Lee, Y.; Yoon, J.; Lee, B.; Oh, E.; Chung, S.; Lee, T.; Cho, K.J.; Kim, J.; Hong, Y. Electronic skins for soft, compact, reversible assembly of wirelessly activated fully soft robots. Sci. Robot. 2018, 3, eaas9020. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.C.; Mun, J.; Kwon, S.Y.; Park, S.; Bao, Z.; Park, S. Electronic Skin: Recent Progress and Future Prospects for Skin-Attachable Devices for Health Monitoring, Robotics, and Prosthetics. Adv. Mater. 2019, 31, 1904765. [Google Scholar] [CrossRef]
- Kim, K.K.; Suh, Y.; Ko, S.H. Smart Stretchable Electronics for Advanced Human–Machine Interface. Adv. Intell. Syst. 2021, 3, 2000157. [Google Scholar] [CrossRef]
- Chitrakar, C.; Hedrick, E.; Adegoke, L.; Ecker, M. Flexible and Stretchable Bioelectronics. Materials 2022, 15, 1664. [Google Scholar] [CrossRef]
- Xue, Z.; Song, H.; Rogers, J.A.; Zhang, Y.; Huang, Y. Mechanically-Guided Structural Designs in Stretchable Inorganic Electronics. Adv. Mater. 2020, 32, 1902254. [Google Scholar] [CrossRef]
- Alcheikh, N.; Shaikh, S.; Hussain, M. Ultra-stretchable Archimedean interconnects for stretchable electronics. Extrem. Mech. Lett. 2018, 24, 6–13. [Google Scholar] [CrossRef]
- Polywka, A.; Jakob, T.; Stegers, L.; Riedl, T.; Görrn, P. Facile Preparation of High-Performance Elastically Stretchable Interconnects. Adv. Mater. 2015, 27, 3755–3759. [Google Scholar] [CrossRef]
- Yang, Y.; Duan, S.; Zhao, H. Advances in constructing silver nanowire-based conductive pathways for flexible and stretchable electronics. Nanoscale 2022, 14, 11484–11511. [Google Scholar] [CrossRef]
- Eda, A.; Yasuga, H.; Sato, T.; Sato, Y.; Suto, K.; Tachi, T.; Iwase, E. Large Curvature Self-Folding Method of a Thick Metal Layer for Hinged Origami/Kirigami Stretchable Electronic Devices. Micromachines 2022, 13, 907. [Google Scholar] [CrossRef] [PubMed]
- Polywka, A.; Stegers, L.; Krauledat, O.; Riedl, T.; Jakob, T.; Görrn, P. Controlled mechanical cracking of metal films deposited on polydimethylsiloxane (PDMS). Nanomaterials 2016, 6, 168. [Google Scholar] [CrossRef]
- Kowol, P.; Bargmann, S.; Görrn, P.; Wilmers, J. Strain relief by controlled cracking in highly stretchable multi-layer composites. Extrem. Mech. Lett. 2022, 54, 101724. [Google Scholar] [CrossRef]
- Huang, H.; Spaepen, F. Tensile testing of free-standing Cu, Ag and Al thin films and Ag/Cu multilayers. Acta Mater. 2000, 48, 3261–3269. [Google Scholar] [CrossRef]
- Xiang, Y.; Li, T.; Suo, Z.; Vlassak, J.J. High ductility of a metal film adherent on a polymer substrate. Appl. Phys. Lett. 2005, 87, 161910. [Google Scholar] [CrossRef]
- Hoefnagels, J.P.; Neggers, J.; Timmermans, P.H.; van der Sluis, O.; Geers, M.G. Copper-rubber interface delamination in stretchable electronics. Scr. Mater. 2010, 63, 875–878. [Google Scholar] [CrossRef]
- Kleinendorst, S.M.; Fleerakkers, R.; Cattarinuzzi, E.; Vena, P.; Gastaldi, D.; van Maris, M.P.; Hoefnagels, J.P. Micron-scale experimental-numerical characterization of metal-polymer interface delamination in stretchable electronics interconnects. Int. J. Solids Struct. 2020, 204–205, 52–64. [Google Scholar] [CrossRef]
- Li, K.; Shuai, Y.; Cheng, X.; Luan, H.; Liu, S.; Yang, C.; Xue, Z.; Huang, Y.; Zhang, Y. Island Effect in Stretchable Inorganic Electronics. Small 2022, 18, 2107879. [Google Scholar] [CrossRef]
- Li, H.; Wang, Z.; Lu, S.; Ma, Y.; Feng, X. Elastomers with Microislands as Strain Isolating Substrates for Stretchable Electronics. Adv. Mater. Technol. 2019, 4, 1800365. [Google Scholar] [CrossRef]
- Budzik, M.K.; Heide-Jørgensen, S.; Aghababaei, R. Fracture mechanics analysis of delamination along width-varying interfaces. Compos. Part B Eng. 2021, 215, 108793. [Google Scholar] [CrossRef]
- Bargmann, S.; Klusemann, B.; Markmann, J.; Schnabel, J.E.; Schneider, K.; Soyarslan, C.; Wilmers, J. Generation of 3D representative volume elements for heterogeneous materials: A review. Prog. Mater. Sci. 2018, 96, 322–384. [Google Scholar] [CrossRef]
- Johnston, I.D.; McCluskey, D.K.; Tan, C.K.; Tracey, M.C. Mechanical characterization of bulk Sylgard 184 for microfluidics and microengineering. J. Micromech. Microeng. 2014, 24, 035017. [Google Scholar] [CrossRef]
- Görrn, P.; Wagner, S. Topographies of plasma-hardened surfaces of poly(dimethylsiloxane). J. Appl. Phys. 2010, 108, 093522. [Google Scholar] [CrossRef]
- Mei, H.; Pang, Y.; Im, S.H.; Huang, R. Fracture, delamination, and buckling of elastic thin films on compliant substrates. In Proceedings of the 2008 11th Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems, Orlando, FL, USA, 28–31 May 2008; pp. 762–769. [Google Scholar]
- Momodu, D.Y.; Tong, T.; Zebaze Kana, M.G.; Chioh, A.V.; Soboyejo, W.O. Adhesion and degradation of organic and hybrid organic-inorganic light-emitting devices. J. Appl. Phys. 2014, 115, 084504. [Google Scholar] [CrossRef]
- Genesky, G.D.; Cohen, C. Toughness and fracture energy of PDMS bimodal and trimodal networks with widely separated precursor molar masses. Polymer 2010, 51, 4152–4159. [Google Scholar] [CrossRef]
- Neggers, J.; Hoefnagels, J.; van der Sluis, O.; Sedaghat, O.; Geers, M. Analysis of the dissipative mechanisms in metal–elastomer interfaces. Eng. Fract. Mech. 2015, 149, 412–424. [Google Scholar] [CrossRef]
- Oyewole, O.K.; Yu, D.; Du, J.; Asare, J.; Oyewole, D.O.; Anye, V.C.; Fashina, A.; Zebaze Kana, M.G.; Soboyejo, W.O. Micro-wrinkling and delamination-induced buckling of stretchable electronic structures. J. Appl. Phys. 2015, 117, 235501. [Google Scholar] [CrossRef]
- Meng, Q.; Chang, M. Interfacial crack propagation between a rigid fiber and a hyperelastic elastomer: Experiments and modeling. Int. J. Solids Struct. 2020, 188–189, 141–154. [Google Scholar] [CrossRef]
- van der Sluis, O.; Remmers, J.J.; Thurlings, M.; Welling, B.; Noijen, S.P. The Competition between Adhesive and Cohesive Fracture at Amicro-Patterned Polymer-Metal Interface. Key Engineering Materials. In Advances in Fracture and Damage Mechanics XII; Trans Tech Publications Ltd.: Bäch, Switzerland, 2014; Volume 577, pp. 225–228. [Google Scholar]
- van Tijum, R.; Vellinga, W.P.; De Hosson, J.T.M. Adhesion along metal–polymer interfaces during plastic deformation. J. Mater. Sci. 2007, 42, 3529–3536. [Google Scholar] [CrossRef]
- Li, T.; Suo, Z. Ductility of thin metal films on polymer substrates modulated by interfacial adhesion. Int. J. Solids Struct. 2007, 44, 1696–1705. [Google Scholar] [CrossRef]
- Lucchini, R.; Cattarinuzzi, E.; Maraghechi, S.; Gastaldi, D.; Adami, A.; Lorenzelli, L.; Vena, P. Delamination phenomena in aluminum/polyimide deformable interconnects: In-situ micro-tensile testing. Mater. Des. 2016, 89, 121–128. [Google Scholar] [CrossRef]
- Cornec, A.; Scheider, I.; Schwalbe, K.H. On the practical application of the cohesive model. Eng. Fract. Mech. 2003, 70, 1963–1987. [Google Scholar] [CrossRef]
- Park, K.; Paulino, G.H. Cohesive Zone Models: A Critical Review of Traction-Separation Relationships Across Fracture Surfaces. Appl. Mech. Rev. 2013, 64, 060802. [Google Scholar] [CrossRef]
- Bargmann, S.; Scheider, I.; Xiao, T.; Yilmaz, E.; Schneider, G.A.; Huber, N. Towards bio-inspired engineering materials: Modeling and simulation of the mechanical behavior of hierarchical bovine dental structure. Comput. Mater. Sci. 2013, 79, 390–401. [Google Scholar] [CrossRef]
- Ma, S.; Scheider, I.; Bargmann, S. Anisotropic constitutive model incorporating multiple damage mechanisms for multiscale simulation of dental enamel. J. Mech. Behav. Biomed. Mater. 2016, 62, 515–533. [Google Scholar] [CrossRef]
- van der Sluis, O.; Engelen, R.; Timmermans, P.; Zhang, G. Numerical analysis of delamination and cracking phenomena in multi-layered flexible electronics. Microelectron. Reliab. 2009, 49, 853–860. [Google Scholar] [CrossRef]
- Asur Vijaya Kumar, P.; Dean, A.; Reinoso, J.; Paggi, M. A multi phase-field-cohesive zone model for laminated composites: Application to delamination migration. Compos. Struct. 2021, 276, 114471. [Google Scholar] [CrossRef]
- Daniel, P.M.; Främby, J.; Fagerström, M.; Maimí, P. An efficient ERR-Cohesive method for the modelling of delamination propagation with large elements. Compos. Part A Appl. Sci. Manuf. 2023, 167, 107423. [Google Scholar] [CrossRef]
- Niazi, M.S.; Wisselink, H.H.; Meinders, T. Viscoplastic regularization of local damage models: Revisited. Comput. Mech. 2013, 51, 203–216. [Google Scholar] [CrossRef]


| Parameter | Value | |
|---|---|---|
| d | crack separation | 30 |
| l | crack length | 29 |
| silver layer thickness | 0.1 | |
| maximum cohesive traction | 2 | |
| critical strain energy release rate | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kowol, P.; Bargmann, S.; Görrn, P.; Wilmers, J. Delamination Behavior of Highly Stretchable Soft Islands Multi-Layer Materials. Appl. Mech. 2023, 4, 514-527. https://doi.org/10.3390/applmech4020029
Kowol P, Bargmann S, Görrn P, Wilmers J. Delamination Behavior of Highly Stretchable Soft Islands Multi-Layer Materials. Applied Mechanics. 2023; 4(2):514-527. https://doi.org/10.3390/applmech4020029
Chicago/Turabian StyleKowol, Philipp, Swantje Bargmann, Patrick Görrn, and Jana Wilmers. 2023. "Delamination Behavior of Highly Stretchable Soft Islands Multi-Layer Materials" Applied Mechanics 4, no. 2: 514-527. https://doi.org/10.3390/applmech4020029
APA StyleKowol, P., Bargmann, S., Görrn, P., & Wilmers, J. (2023). Delamination Behavior of Highly Stretchable Soft Islands Multi-Layer Materials. Applied Mechanics, 4(2), 514-527. https://doi.org/10.3390/applmech4020029






