Employment of Fracture Mechanics Criteria for Accurate Assessment of the Full Set of Elastic Constants of Orthorhombic/Tetragonal Mono-Crystalline YBCO
Abstract
:1. Introduction
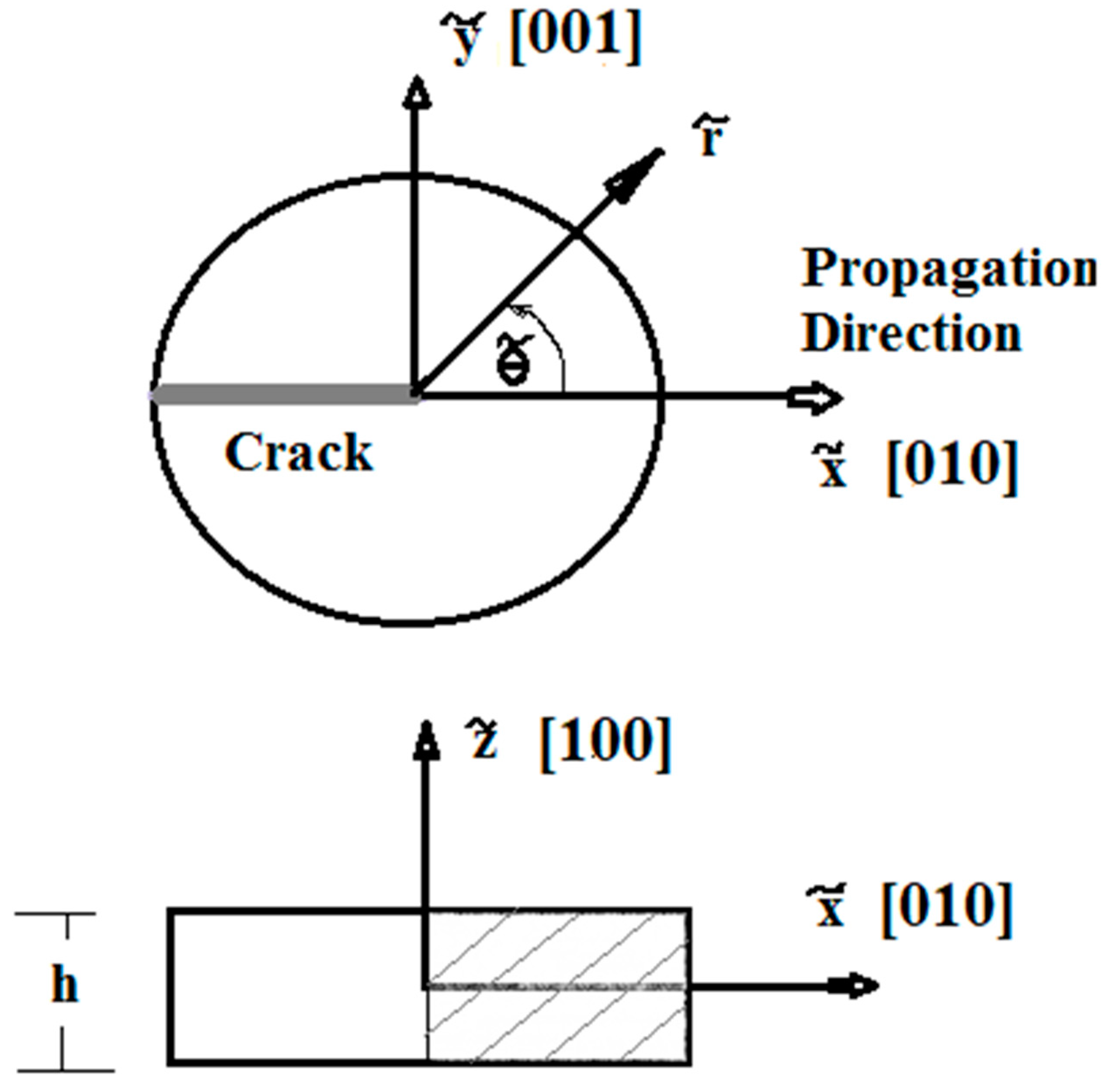
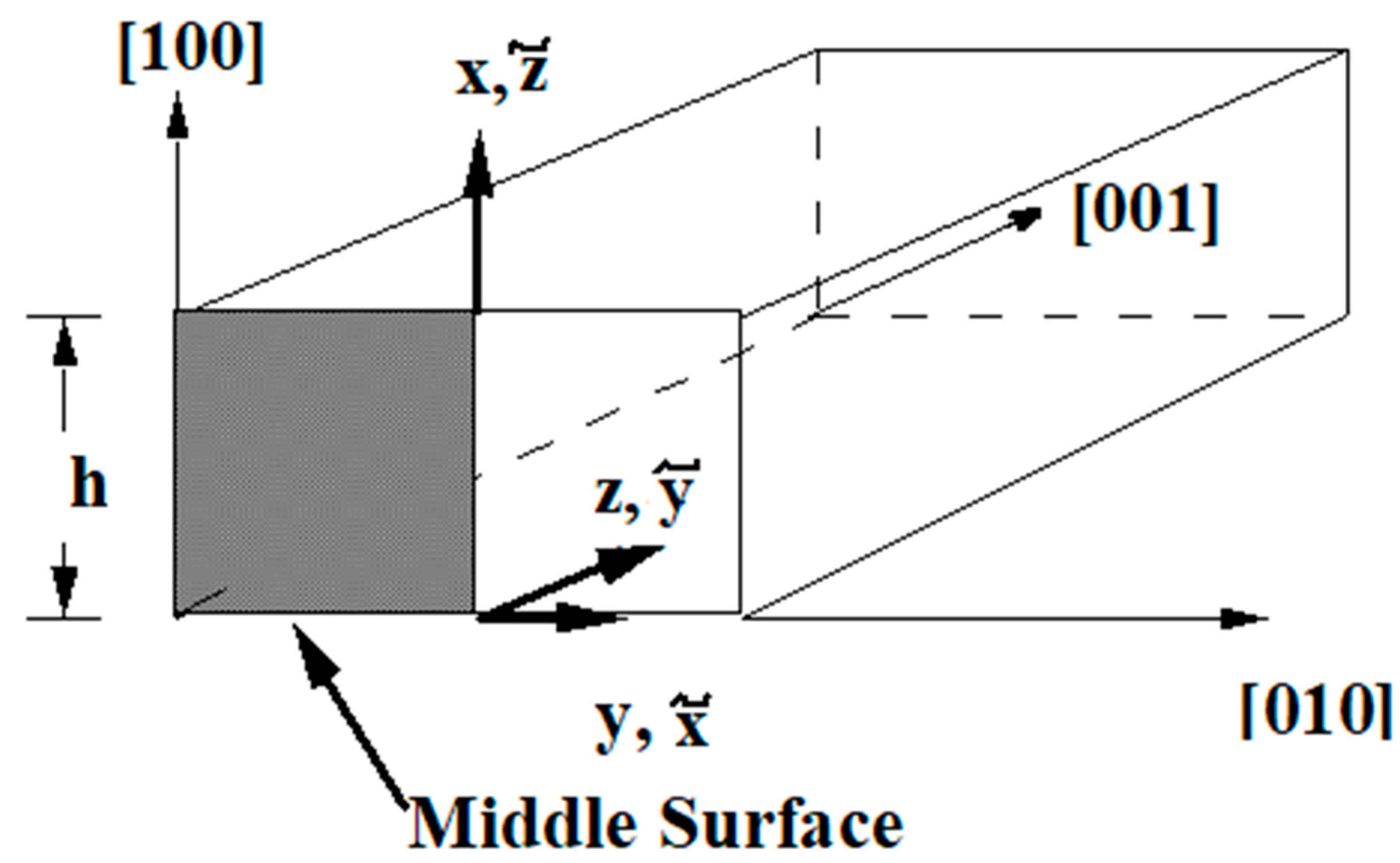
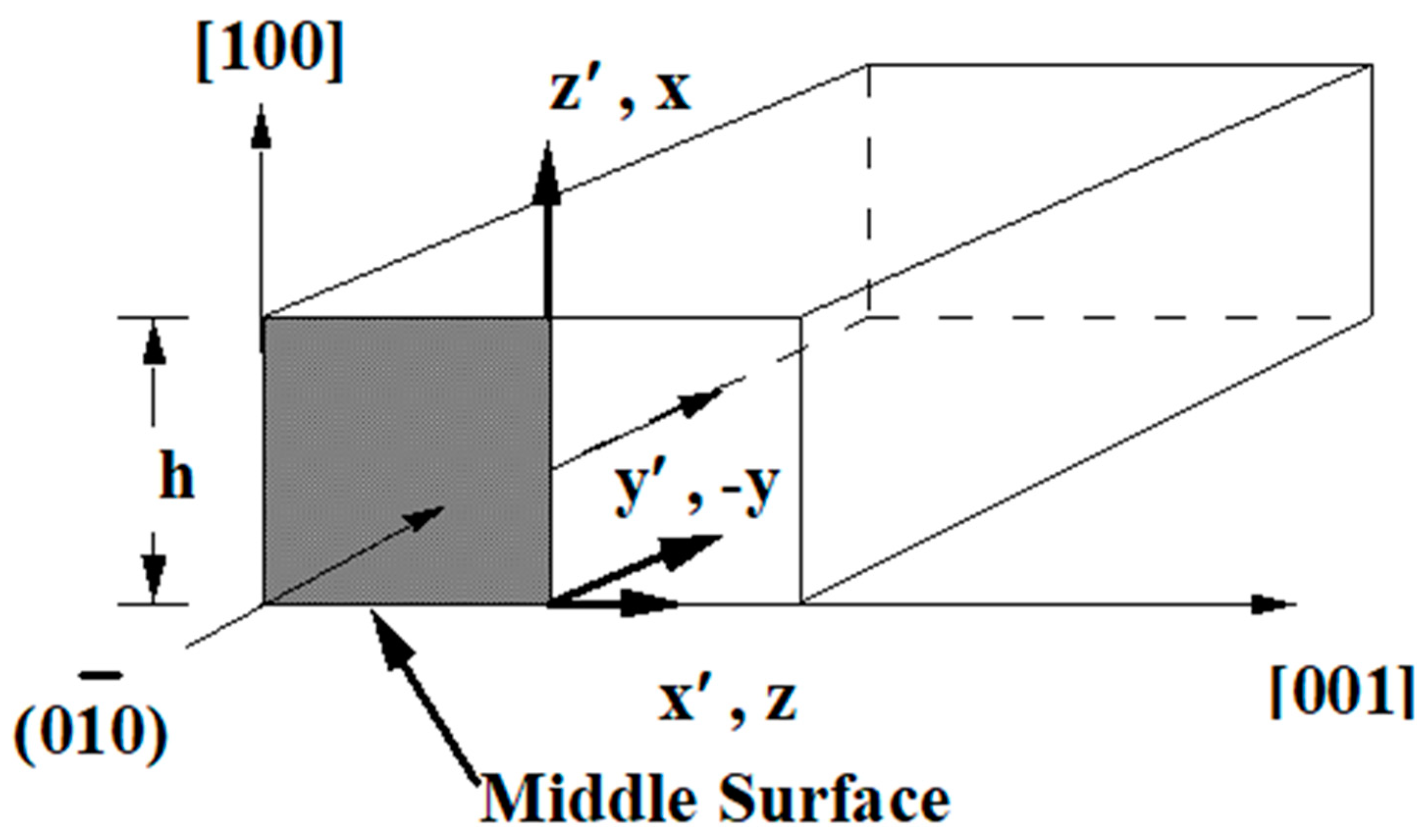
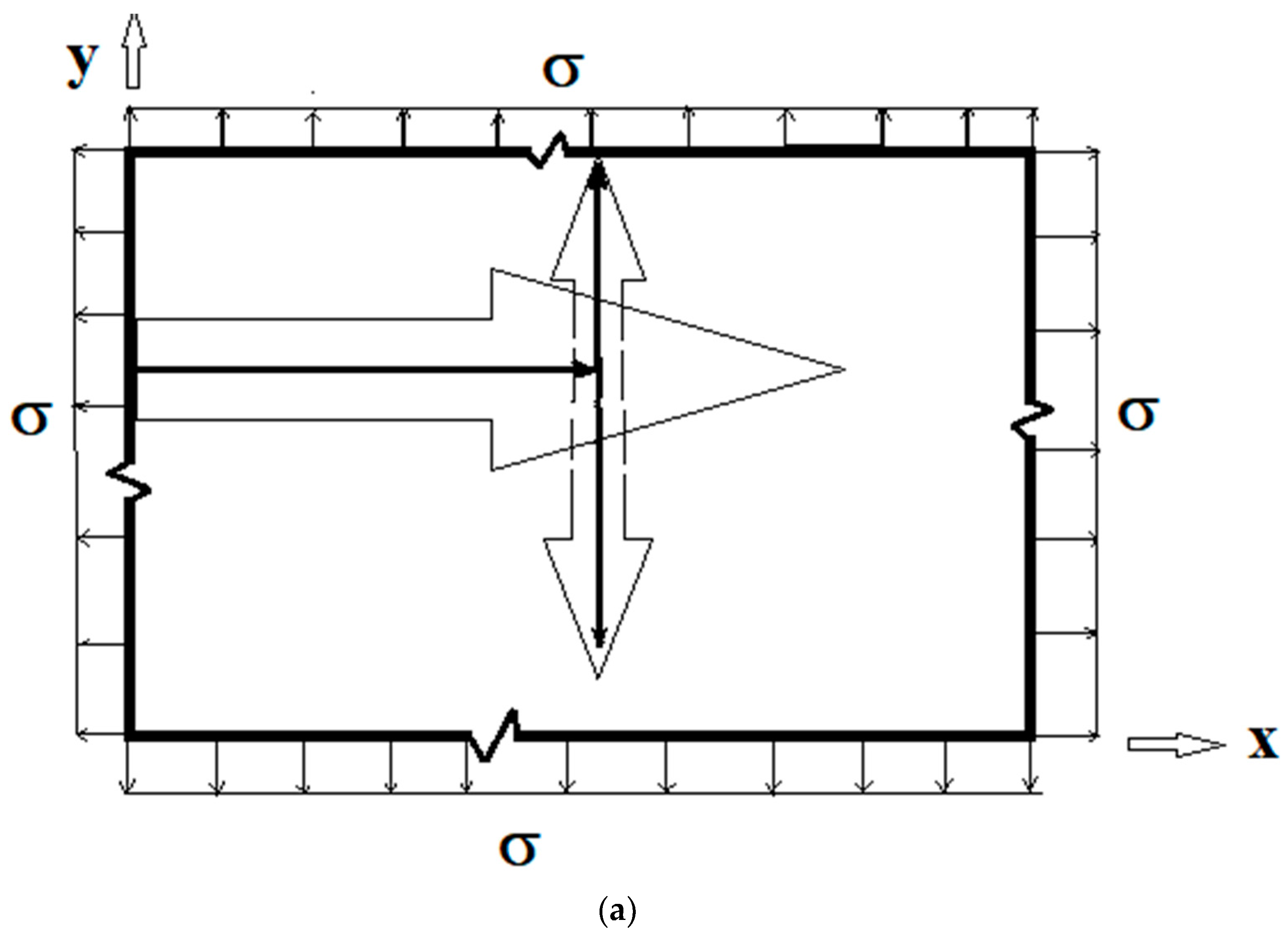
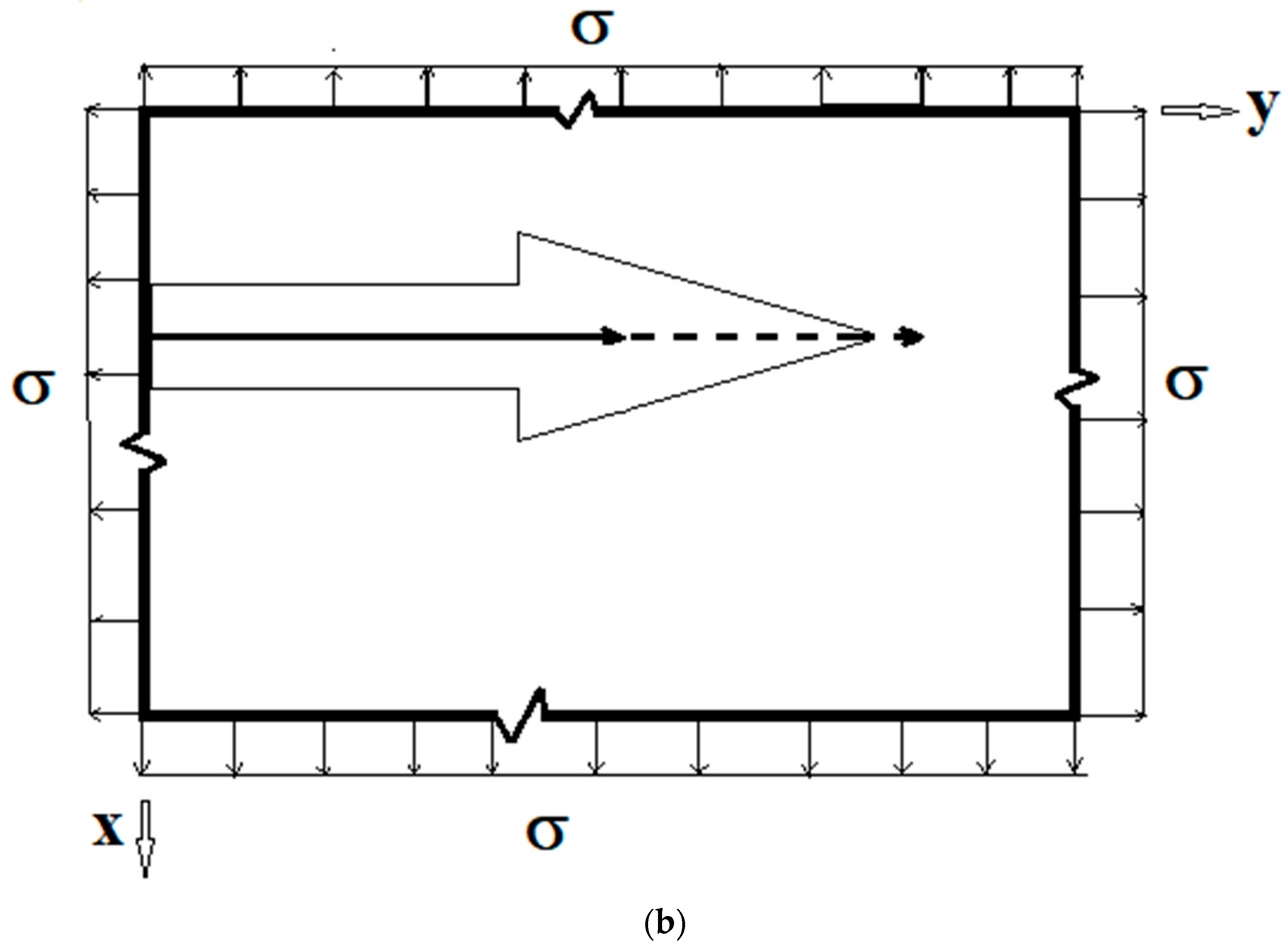
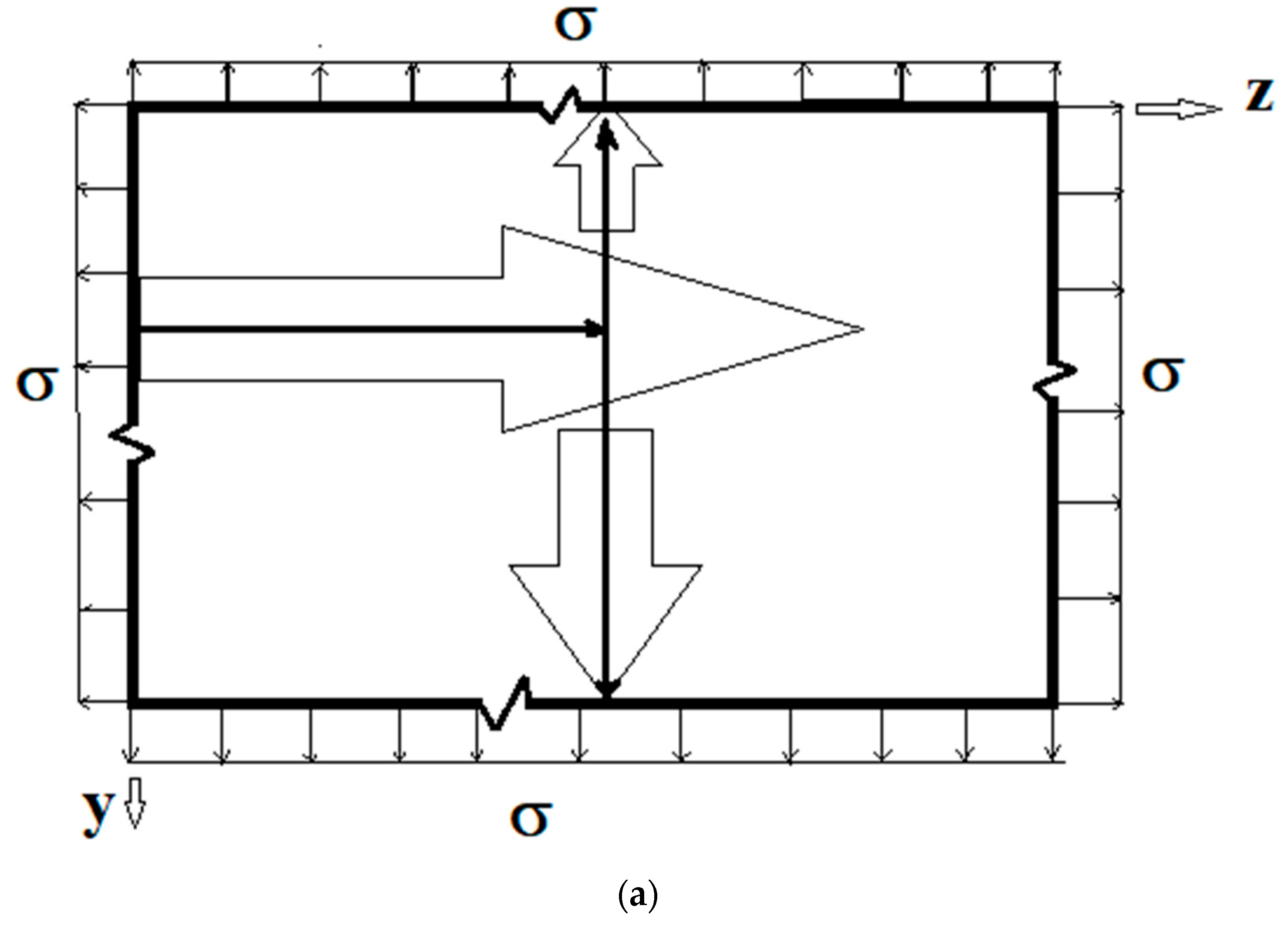
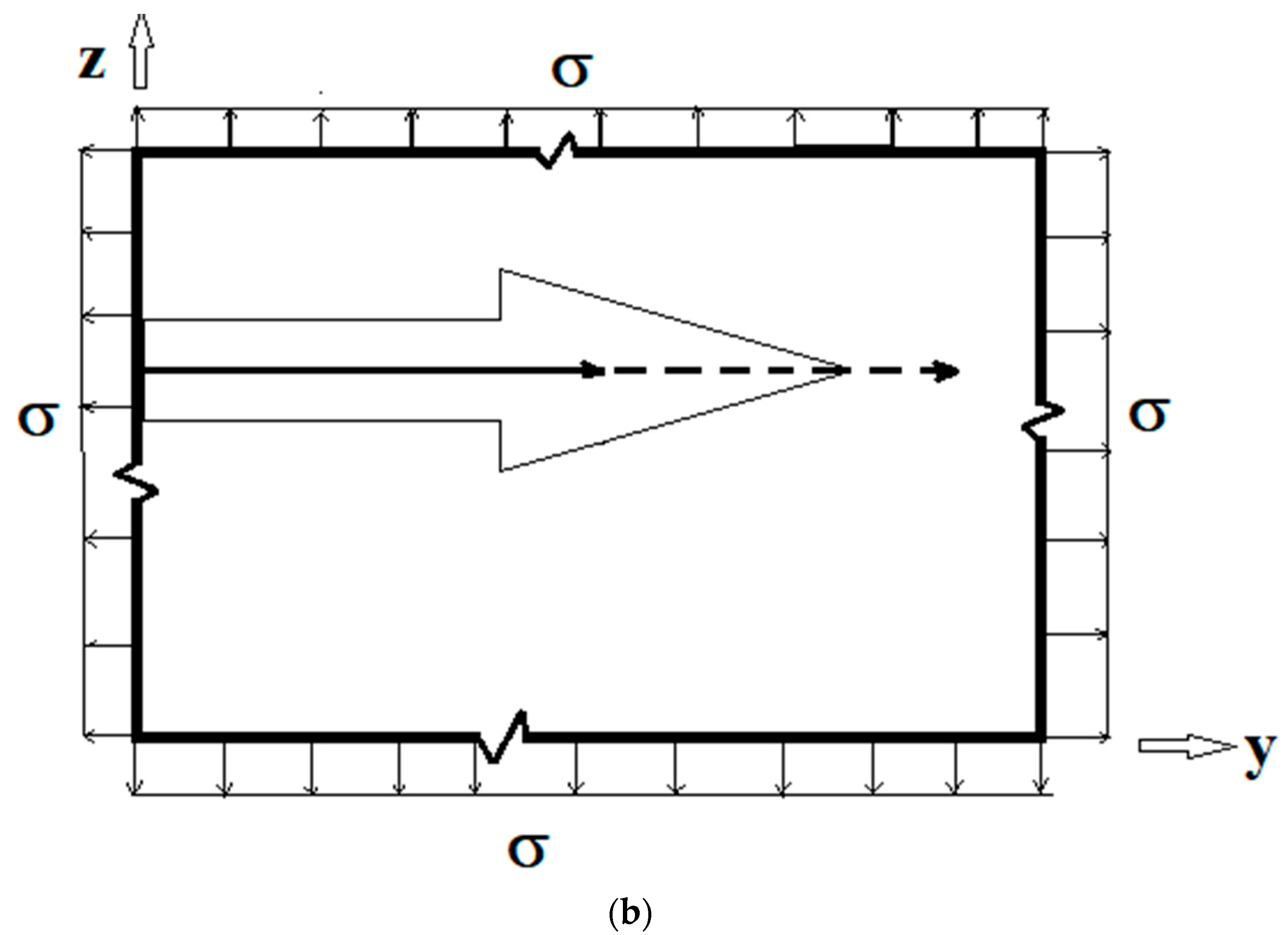
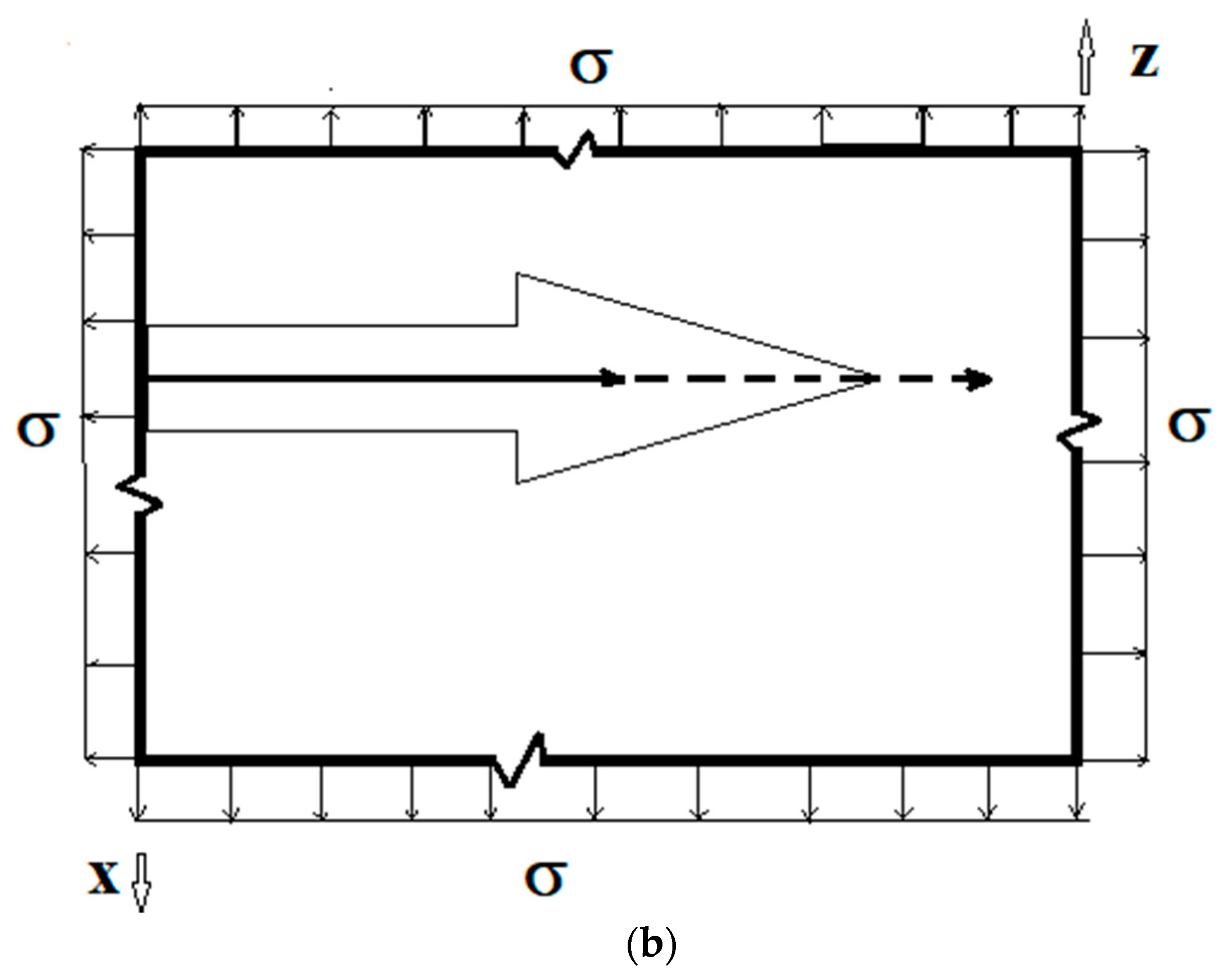
2. Formulation of the Problem
3. Singular Stress Fields in the Vicinity of a Crack Front Weakening an Orthotropic/Orthorhombic Lamina/Single Crystal under General Loading
4. Singular Stress Fields in the Vicinity of a (001)[100] Through-Crack Front Propagating under Mode I (Extension/Bending) and Mode II (Sliding Shear/Twisting) in [010] Direction
4.1. Case (a): Complex Roots
4.1.1. Symmetric (Mode I) Loading (Extension/Bending)
4.1.2. Skew-Symmetric (Mode II) Loading (Sliding Shear/Twisting)
4.2. Case (b): Imaginary Roots
4.2.1. Symmetric (Mode I) Loading (Extension/Bending)
4.2.2. Skew-Symmetric (Mode II) Loading (Sliding Shear/Twisting)
5. Plate Surface Boundary Conditions and Through-Thickness Distribution of Singular Stress Fields
5.1. Satisfaction of Traction-Free Boundary Conditions
5.2. Hyperbolic Cosine Distributed Far-Field Loading
6. Stress Intensity Factors and Energy Release Rates for a Through-Thickness Center-Crack (Modes I and II)
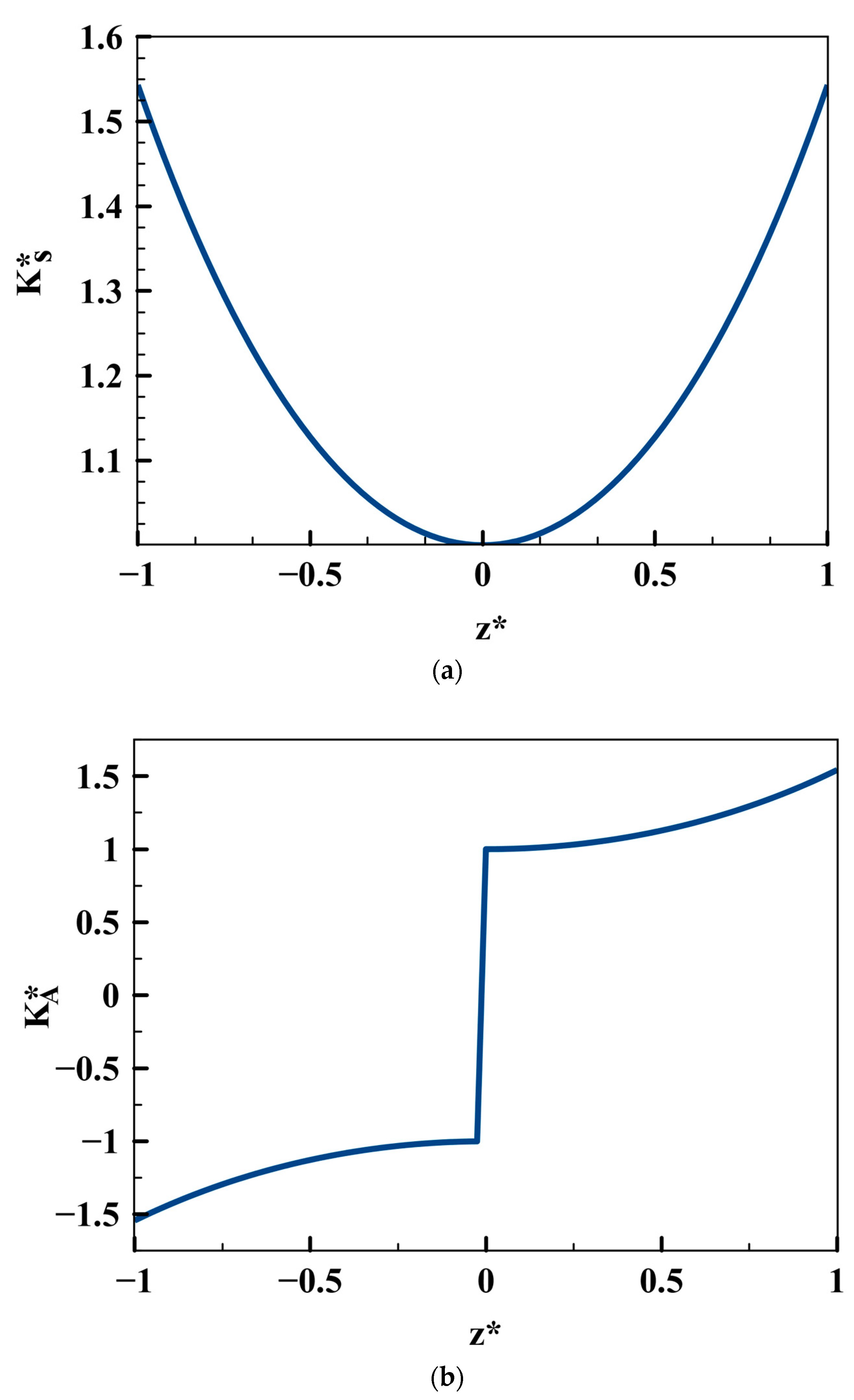
6.1. Through-Thickness Distribution of Stress Intensity Factors (Modes I and II)
6.2. Through-Thickness Distribution of Energy Release Rates (Modes I and II)
7. Necessary and Sufficient Conditions for Easy or Difficult Cleavage Planes
7.1. Crack Deflection Criterion, Based on the Relative Fracture Energy
7.2. Similarity/Dissimilarity of Present Solutions with Their Isotropic Counterpart
7.2.1. Isotropic Materials
7.2.2. Present Solution Involving Complex Roots
7.2.3. Present Solution Involving Imaginary Roots
8. Numerical Results and Discussion
9. Summary and Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Singular Stress Fields in the Vicinity of a (010)[001] Through-Crack Front Propagating under Mode I (Extension/Bending) and Mode II (Sliding Shear/Twisting) in [100] Direction
Appendix B. Singular Stress Fields in the Vicinity of a (00)[100] Through-Crack Front Weakening an Orthorhombic Single Crystal under Mode I (Extension/Bending) and Mode II (Sliding Shear/Twisting)
Appendix C. Singular Stress Fields in the Vicinity of a (00)[001] Through-Crack Front Propagating under Mode I (Extension/Bending) and Mode II (Sliding Shear/Twisting) in [010] Direction
Appendix D. Singular Stress Fields in the Vicinity of a (100)[010] Through-Crack Front Propagating under Mode I (Extension/Bending) and Mode II (Sliding Shear/Twisting) in [001] Direction
Appendix E. Singular Stress Fields in the Vicinity of a (001)[00]. Through-Crack Front Propagating under Mode I (Extension/Bending) and Mode II (Sliding Shear/Twisting) in [100] Direction
References
- Lei, M.; Sarrao, J.L.; Visscher, W.M.; Bell, T.M.; Thompson, J.D.; Migliori, A.; Welp, U.W.; Veal, B.W. Elastic constants of a monocrystal of superconducting YBa2Cu3O7−δ. Phys. Rev. B 1993, 47, 6154–6156. [Google Scholar] [CrossRef] [PubMed]
- Bednorz, J.G.; Muller, K.A. Perovskite-type oxides—The new approach to high-Tc superconductivity. Rev. Mod. Phys. 1988, 60, 585–600. [Google Scholar] [CrossRef]
- Walker, G. Technology: How SQUIDs Were Found Where Crystals Meet. New Scientist, Issue 1776, July 1991. Available online: https://www.newscientist.com/article/mg13117764-900-technology-how-squids-were-found-where-crystals-meet/ (accessed on 5 May 2003).
- Grimvall, G. The Electron-Phonon Interaction in Metals, Vol. XVI of Selected Topics in Solid State Physics; Wolhfarth, E.P., Ed.; North-Holland Publishing Company: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Allen, P.B. The electron-phonon coupling constant λ. In Handbook of Superconductivity; Poole, C.P., Jr., Ed.; Academic Press: New York, NY, USA, 1999; Chapter 9; pp. 478–483. [Google Scholar]
- Cook, R.F.; Dinger, T.R.; Clarke, D.R. Fracture toughness measurements of YBa2Cu3Oxsingle crystals. Appl. Phys. Lett. 1987, 51, 454–456. [Google Scholar] [CrossRef]
- Roa, J.J.; Capdevila, X.G.; Martínez, M.; Espiell, F.; Segarra, M. Nanohardness and Young’s Modulus of YBCO samples textured by Bridgman technique. Nanotechnology 2007, 18, 385701. [Google Scholar] [CrossRef]
- Konstantopoulou, K.; Roa, J.; Jiménez-Piqué, E.; Segarra, M.; Pastor, J.Y. Fracture micromechanisms and mechanical behavior of YBCO bulk superconductors at 77 and 300K. Ceram. Int. 2014, 40, 12797–12806. [Google Scholar] [CrossRef]
- Raynes, A.S.; Freiman, S.W.; Gayle, F.W.; Kaiser, D.L. Fracture toughness of YBa2Cu3O6+δsingle crystals: Anisotropy and twinning effects. J. Appl. Phys. 1991, 70, 5254–5257. [Google Scholar] [CrossRef]
- Goyal, A.; Funkenbusch, P.D.; Kroeger, D.M.; Burns, S.J. Anisotropic hardness and fracture toughness of highly aligned YBa2Cu3O7−δ. J. Appl. Phys. 1992, 71, 2363–2367. [Google Scholar] [CrossRef]
- Okudera, T.; Murakami, A.; Katagiri, K.; Kasaba, K.; Shoji, Y.; Noto, K.; Sakai, N.; Murakami, M. Fracture toughness evaluation of YBCO bulk superconductor. Physica C 2003, 392–396, 628–633. [Google Scholar] [CrossRef]
- Diko, P. Cracking in melt-grown RE–Ba–Cu–O single-grain bulk superconductors. Supercond. Sci. Technol. 2004, 17, R45–R58. [Google Scholar] [CrossRef]
- Congreve, J.V.J.; Shi, Y.; Huang, K.Y.; Dennis, A.R.; Durrell, J.H.; Cardwell, D.A. Characterisation of the mechanical failure and fracture mechanisms of single grain Y–Ba–Cu–O bulk superconductors. Supercond. Sci. Technol. 2019, 33, 015003. [Google Scholar] [CrossRef]
- Granozio, F.M.; di Uccio, U.S. Gibbs energy and growth habits of YBCO. J. Alloys Compd. 1997, 251, 56–64. [Google Scholar] [CrossRef]
- Lekhnitskii, S.G. Anisotropic Plates; Gordon and Breach: New York, NY, USA, 1968. [Google Scholar]
- Stroh, A.N. Dislocations and cracks in anisotropic elasticity. Philos. Mag. 1958, 3, 625–646. [Google Scholar] [CrossRef]
- Sih, G.C.; Paris, P.C.; Irwin, G.R. On cracks in rectilinearly anisotropic bodies. Int. J. Fract. Mech. 1965, 1, 189–203. [Google Scholar] [CrossRef]
- Suo, Z.; Bao, G.; Fan, B.; Wang, T. Orthotropy rescaling and implications for fracture in composites. Int. J. Solids Struct. 1991, 28, 235–248. [Google Scholar] [CrossRef]
- Lin, Y.Y.; Sung, J.C. Stress singularities at the apex of a dissimilar anisotropic wedge. ASME J. Appl. Mech. 1998, 65, 454–463. [Google Scholar] [CrossRef]
- Nazarov, S.A. Stress intensity factors and crack deviation conditions in a brittle anisotropic solid. J. Appl. Mech. Technol. Phys. 2005, 46, 386–394. [Google Scholar] [CrossRef]
- Nejati, M.; Ghouli, S.; Ayatollahi, M.R. Crack tip asymptotic fields in anisotropic planes: Importance of higher order terms. Appl. Math. Model. 2021, 91, 837–862. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. Three-dimensional singular stress field at the front of a crack and lattice crack deviation (LCD) in a cubic single crystal plate. Philos. Mag. 2010, 90, 2049–2113. [Google Scholar] [CrossRef]
- Kravchenko, V.V. Applied Quaternionic Analysis; Heldermann Verlag: Berlin, Germany, 2003. [Google Scholar]
- Stenger, F.; Chaudhuri, R.; Chiu, J. Sinc solution of boundary integral form fortwo-dimensional bi-material elasticity problems. Compos. Sci. Technol. 2000, 60, 2197–2211. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Xie, M. A novel eigenfunction expansion solution for three-dimensional crack problems. Compos. Sci. Technol. 2000, 60, 2565–2580. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. Eigenfunction expansion solutions for three-dimensional rigid planar inclusion problems. Int. J. Fract. 2003, 121, 95–110. [Google Scholar] [CrossRef]
- Xie, M.; Chaudhuri, R.A. Three-dimensional stress singularity at a bimaterial interface crack front. Compos. Struct. 1997, 40, 137–147. [Google Scholar] [CrossRef]
- Yoon, J.; Chaudhuri, R.A. Three-dimensional asymptotic antiplane shear stress fields at the front of interfacial crack/anticrack type discontinuities in trimaterial bonded plates. Compos. Struct. 2011, 93, 1505–1515. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Yoon, J. Three-dimensional asymptotic mode I/II stress fields at the front of interfacial crack/anticrack discontinuities in trimaterial bonded plates. Compos. Struct. 2012, 94, 351–362. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Xie, M. On three-dimensional asymptotic solution, and applicability of Saint–Venant’s principle to pie-shaped wedge and end face (of a semi-infinite plate) boundary value problems. Eng. Fract. Mech. 2015, 142, 93–107. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. On applicability and uniqueness of the correspondence principle to pie-shaped wedge (“wedge paradox”) with various boundary conditions. Eng. Fracture Mech. 2018, 127, 344–353. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Xie, M. A tale of two saints: St. Venant and “St. Nick—Does St. Venant’s principle apply to bi-material straight-edge and wedge-singularity problems? Compos. Sci. Technol. 2000, 60, 2503–2515. [Google Scholar] [CrossRef]
- Xie, M.; Chaudhuri, R.A. Three-dimensional asymptotic stress field at the front of a bimaterial wedge of symmetric geometry under antiplane shear loading. Compos. Struct. 2001, 54, 509–514. [Google Scholar] [CrossRef]
- Chiu, J.S.H.; Chaudhuri, R.A. Three-dimensional asymptotic stress field at the front of an unsymmetric bimaterial pie-shaped wedge under antiplane shear loading. Compos. Struct. 2002, 58, 129–137. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Xie, M. Free-edge stress singularity in a bimaterial laminate. Compos. Struct. 1997, 40, 129–136. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Chiu, S.-H.J. Three-Dimensional Asymptotic Stress Field in the Vicinity of an Adhesively Bonded Scarf Joint Interface. Compos. Struct. 2009, 89, 475–483. [Google Scholar] [CrossRef]
- Chiu, S.-H.J.; Chaudhuri, R.A. A three-dimensional eigenfunction expansion approach for singular stress field near an adhesively-bonded scarf joint interface in a rigidly-encased plate. Eng. Fract. Mech. 2011, 78, 2220–2234. [Google Scholar] [CrossRef]
- Yoon, J.; Chaudhuri, R.A. Three-dimensional asymptotic stress fields at the front of a trimaterial junction. Compos. Struct. 2012, 94, 337–350. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. Three-dimensional asymptotic stress field in the vicinity of the circumference of a penny shaped discontinuity. Int. J. Solids Struct. 2003, 40, 3787–3805. [Google Scholar] [CrossRef]
- Kaczy´nski, A.; Kozłowski, W. Thermal stresses in an elastic space with a perfectly rigid flat inclusion under perpendicular heat flow. Int. J. Solids Struct. 2009, 46, 1772–1777. [Google Scholar] [CrossRef]
- Willis, J.R. The penny shaped crack on an interface. Q. J. Mech. Appl. Math. 1972, 25, 367–385. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. Three-dimensional asymptotic stress field in the vicinity of the circumference of a bimaterial penny-shaped interfacial discontinuity. Int. J. Fract. 2006, 141, 211–225. [Google Scholar] [CrossRef]
- Folias, E.S. The 3D stress field at the intersection of a hole and a free surface. Int. J. Fract. 1987, 35, 187–194. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. Three-dimensional asymptotic stress field in the vicinity of the line of intersection of a circular cylindrical through/part–through open/rigidly plugged hole and a plate. Int. J. Fract. 2003, 122, 65–88. [Google Scholar] [CrossRef]
- Folias, E. On interlaminar stresses of a composite plate around the neighborhood of a hole. Int. J. Solids Struct. 1989, 25, 1193–1200. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. An eigenfunction expansion solution for three-dimensional stress field in the vicinity of the circumferential line of intersection of a bimaterial interface and a hole. Int. J. Fract. 2004, 129, 361–384. [Google Scholar] [CrossRef]
- Folias, E.S. On the stress singularities at the intersection of a cylindrical inclusion with the free surface of a plate. Int. J. Fract. 1989, 39, 25–34. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. Three-dimensional asymptotic stress field in the vicinity of the line of intersection of an inclusion and plate surface. Int. J. Fract. 2002, 117, 207–233. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. Three-dimensional asymptotic stress field in the vicinity of the circumferential tip of a fiber–matrix interfacial debond. Int. J. Eng. Sci. 2004, 42, 1707–1727. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. Three-dimensional singular stress field near a partially debonded cylindrical rigid fiber. Compos. Struct. 2006, 72, 141–150. [Google Scholar] [CrossRef]
- Chaudhuri, S.N.; Chaudhuri, R.A.; Benner, R.E.; Penugonda, M. Raman spectroscopy for characterization of interfacial debonds between carbon fibers and polymer matrices. Compos. Struct. 2006, 76, 375–387. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Chiu, S.-H.J. Three-dimensional asymptotic stress field at the front of an unsymmetric bimaterial wedge associated with matrix cracking or fiber break. Compos. Struct. 2007, 78, 254–263. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Chiu, S.-H.J. Three-dimensional singular stress field near the interfacial bond line of a tapered jointed plate either free-standing (notch) or (fully/partially) attached to a super-rigid inclusion (antinotch). Eng. Fract. Mech. 2012, 91, 87–102. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. Three-dimensional singular stress fields near the circumferential junction corner line of an island/substrate system either free-standing or fully/partially bonded to a rigid block. Eng. Fract. Mech. 2013, 107, 80–97. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. On through-thickness distribution of stress intensity factors and energy release rates in the vicinity of crack fronts. Eng. Fract. Mech. 2019, 216, 106478. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. Three-dimensional singular stress field at the front of a crack weakening a unidirectional fiber reinforced composite plate. Compos. Struct. 2011, 93, 513–527. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. On three-dimensional singular stress field at the front of a planar rigid inclusion (anticrack) in an orthorhombic mono-crystalline plate. Int. J. Fract. 2012, 174, 103–126. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. Three-dimensional mixed mode I+II+III singular stress field at the front of a (111)[2] × [10] crack weakening a diamond cubic mono-crystalline plate with crack turning and step/ridge formation. Int. J. Fract. 2014, 187, 15–49. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. On three-dimensional singular stress/residual stress fields at the front of a crack/anticrack in an orthotropic/orthorhombic plate under anti-plane shear loading. Compos. Struct. 2010, 92, 1977–1984. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. Three-dimensional stress/residual stress fields at crack/anticrack fronts in monoclinic plates under antiplane shear loading. Eng. Fract. Mech. 2012, 87, 16–35. [Google Scholar] [CrossRef]
- Yoon, J.; Chaudhuri, R.A. Three-dimensional singular antiplane shear stress fields at the fronts of interfacial crack/anticrack/contact type discontinuities in tricrystal anisotropic plates. Eng. Fract. Mech. 2013, 102, 15–31. [Google Scholar] [CrossRef]
- Eshelby, J.D.; Read, W.T.; Shockley, W. Anisotropic elasticity with application to dislocation theory. Acta Met. 1953, 1, 251–259. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. Comparison of stress singularities of kinked carbon and glass fibers weakening compressed unidirectional composites: A three-dimensional trimaterial junction stress singularity analysis. Philos. Mag. 2014, 94, 625–667. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Xie, M.; Garala, H.J. Stress singularity due to kink band weakening a unidirectional composite under compression. J. Compos. Mater. 1996, 30, 672–691. [Google Scholar] [CrossRef]
- Alexandrov, I.V.; Goncharov, A.F.; Stishov, S.M. State equation and compressibility of YBa2Cu3Ox high temperature supercon-ductor monocrystals under pressure to 20 GPa. Pis’ma Zh. Eksp. Teor. Fiz. 1988, 47, 357–360. [Google Scholar]
- Golding, B.; Haemmerle, W.H.; Schneemeyer, L.F.; Waszczak, J.V. Gigahertz ultrasound in single crystal superconducting YBa/sub 2/Cu/sub 3/O/sub 7/. In Proceedings of the IEEE 1988 Ultrasonics Symposium Proceedings, Chicago, IL, USA, 2–5 October 2003; Volume 2, pp. 1079–1083. [Google Scholar] [CrossRef]
- Reichardt, W.; Pintschovius, L.; Hennion, B.; Collin, F. Inelastic neutron scattering study of YBa2Cu3O7-x. Supercond. Sci. Technol. 1988, 1, 173–176. [Google Scholar] [CrossRef]
- Baumgart, P.; Blumenröder, S.; Erle, A.; Hillebrands, B.; Güntherodt, G.; Schmidt, H. Sound velocities of YBa2Cu3O7−δ single crystals measured by Brillouin spectroscopy. Solid State Commun. 1989, 69, 1135–1137. [Google Scholar] [CrossRef]
- Baumgart, P.; Blumenröder, S.; Erle, A.; Hillebrands, B.; Splittgerber, P.; Güntherodt, G.; Schmidt, H. Sound velocities of YBa2Cu3O7−δ and Bi2Sr2CaCu2Ox single crystals measured by Brillouin spectroscopy. Phys. C Supercond. Appl. 1989, 162–164 Pt 2, 1073–1074. [Google Scholar] [CrossRef]
- Saint-Paul, M.; Tholence, J.L.; Noel, H.; Levet, J.C.; Potel, M.; Gougeon, P. Ultrasound study on YBa2Cu3O7−δ and GdBa2Cu3O7−δ single crystals. Solid State Commun. 1989, 69, 1161–1163. [Google Scholar] [CrossRef]
- Saint-Paul, M.; Henry, J.Y. Elastic anomalies in YBa2Cu3O7−δ single crystals. Solid State Commun. 1989, 72, 685–687. [Google Scholar] [CrossRef]
- Zouboulis, E.; Kumar, S.; Chen, C.H.; Chan, S.K.; Grimsditch, M.; Downey, J.; McNeil, L. Surface waves on the a, b and c faces of untwinned single crystals of YBa2C3O7−δ. Phys. C Supercond. 1992, 190, 329–332. [Google Scholar] [CrossRef]
- Lin, S.; Lei, M.; Ledbetter, H. Elastic constants and Debye temperature of Y1Ba2Cu3Ox: Effect of oxygen content. Mater. Lett. 1993, 16, 165–168. [Google Scholar] [CrossRef]
- Migliori, A.; Visscher, W.M.; Brown, S.E.; Fisk, Z.; Cheong, S.W.; Alten, B. Elastic constants and specific-heat measurements on single crystals of La2CuO4. Phys. Rev. B 1990, 41, 2098–2102. [Google Scholar] [CrossRef]
- Migliori, A.; Visscher, W.M.; Wong, S.; Brown, S.E.; Tanaka, I.; Kojima, H.; Allen, P.B. Complete elastic constants and giant softening of c66 in superconducting La1.86Sr0.14CuO4. Phys. Rev. Lett. 1990, 64, 2458–2461. [Google Scholar] [CrossRef]
- Kunukkasseril, V.X.; Chaudhuri, R.A.; Balaraman, K. A method to determine 18 rigidities of layered anisotropic plates. J. Fibre Sci. Technol. 1975, 8, 303–318. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Balaraman, K. A novel method for fabrication of fiber reinforced plastic laminated plates. Compos. Struct. 2007, 77, 160–170. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Balaraman, K.; Kunukkasseril, V.X. A combined theoretical and experimental investigation on free vibration of thin symmetrically laminated plates. Compos. Struct. 2005, 67, 85–97. [Google Scholar] [CrossRef]
- Ledbetter, H.; Lei, M. Monocrystal elastic constants of orthotropic Y1Ba2Cu3O7: An estimate. J. Mater. Res. 1991, 6, 2253–2255. [Google Scholar] [CrossRef]
- Riddle, J.; Gumbsch, P.; Fischmeister, H.F. Cleavage Anisotropy in Tungsten Single Crystals. Phys. Rev. Lett. 1996, 76, 3594–3597. [Google Scholar] [CrossRef]
- Carslaw, H.S. Introduction to the Theory of Fourier Series and Integrals, 3rd ed.; Dover: New York, NY, USA, 1930. [Google Scholar]
- Wilcox, C.H. Uniqueness theorems for displacement fields with locally finite energy in linear elastostatics. J. Elast. 1979, 9, 221–243. [Google Scholar] [CrossRef]
- Sedov, L.I. Similarity and Dimensional Methods in Mechanics; Mir Publishers: Moscow, Russia, 1982. [Google Scholar]
- Perez, R.; Gumbsch, P. Directional Anisotropy in the cleavage fracture of silicon. Phys. Rev. Lett. 2000, 84, 5347–5350. [Google Scholar] [CrossRef]
- Kermode, J.R.; Albaret, T.; Sherman, D.; Bernstein, N.; Gumbsch, P.; Payne, M.C.; Csányi, G.; De Vita, A. Low-speed fracture instabilities in a brittle crystal. Nature 2008, 455, 1224–1227. [Google Scholar] [CrossRef]
- Newnham, R.E. Structure-Property Relations; Springer: New York, NY, USA, 1975. [Google Scholar]
- Pauling, L. The Chemical Bond; Cornell Univ. Press: Ithaca, NY, USA, 1967. [Google Scholar]
- Cotton, F.A.; Wilkinson, G. Advanced Inorganic Chemistry, 4th ed.; John Wiley & Sons: New York, NY, USA, 1980. [Google Scholar]
- Williams, A.; Kwei, G.H.; Von Dreele, R.B.; Raistrick, I.D.; Bish, D.L. Joint x-ray and neutron refinement of the structure of superconducting YBa2Cu3O7−x: Precision structure, anisotropic thermal parameters, strain, and cation disorder. Phys. Rev. B 1988, 37, 7960–7962. [Google Scholar] [CrossRef]
- Ledbetter, H. Elastic constants of polycrystalline Y1Ba2Cu3Ox. J. Mater. Res. 1992, 7, 2905–2907. [Google Scholar] [CrossRef]
- Lubenets, S.V.; Natsik, V.D.; Fomenko, L.S.; Kaufmann, H.-J.; Bobrov, V.S.; Izotov, A.N. Influence of oxygen content and structural defects on low-temperature mechanical properties of high-temperature superconducting single crystals and ceramics. Low Temp. Phys. 1997, 23, 678–683. [Google Scholar] [CrossRef]
- Streiffer, S.K.; Lairson, B.M.; Eom, C.B.; Clemens, B.M.; Bravman, J.C.; Geballe, T.H. Microstructure of ultrathin films ofYBa2Cu3O7−δ on MgO. Phys. Rev. B 1991, 43, 13007–13018. [Google Scholar] [CrossRef]
- Fowler, D.; Brundle, C.; Lerczak, J.; Holtzberg, F. Core and valence XPS spectra of clean, cleaved single crystals of YBa2Cu3O7. Electron Spectrosc. Relat. Phenom. 1990, 52, 323–339. [Google Scholar] [CrossRef]
- Tanaka, S.; Nakamura, T.; Tokuda, H.; Iiyama, M. Allinsitudeposition and characterization of YBa2Cu3O7−x thin films by low-energy electron diffraction and low-energy ion scattering spectroscopy. Appl. Phys. Lett. 1993, 62, 3040–3042. [Google Scholar] [CrossRef]
- Lin, C.T.; Liang, W.Y. Etch defects in YBa2Cu3O7−δ single crystals grown from flux. Physic. C 1994, 225, 275–286. [Google Scholar] [CrossRef]
- Lawn, B.R.; Wilshaw, T.R.; Rice, J.R. Fracture of Brittle Solids, 2nd ed.; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Anstis, G.R.; Chantikul, P.; Lawn, B.R.; Marshall, D.B. A critical evaluation of indentation techniques for measuring fracture toughness I. J. Am Ceramic Soc. 1981, 64, 533–538. [Google Scholar] [CrossRef]
- Roa, J.J.; Capdevila, X.G.; Segarra, M. Mechanical characterization at nanometric scale of ceramic superconductor composites. Int. J. Condens. Matter Adv. Mater. Supercond. Res. 2011, 10, 217–307. [Google Scholar]



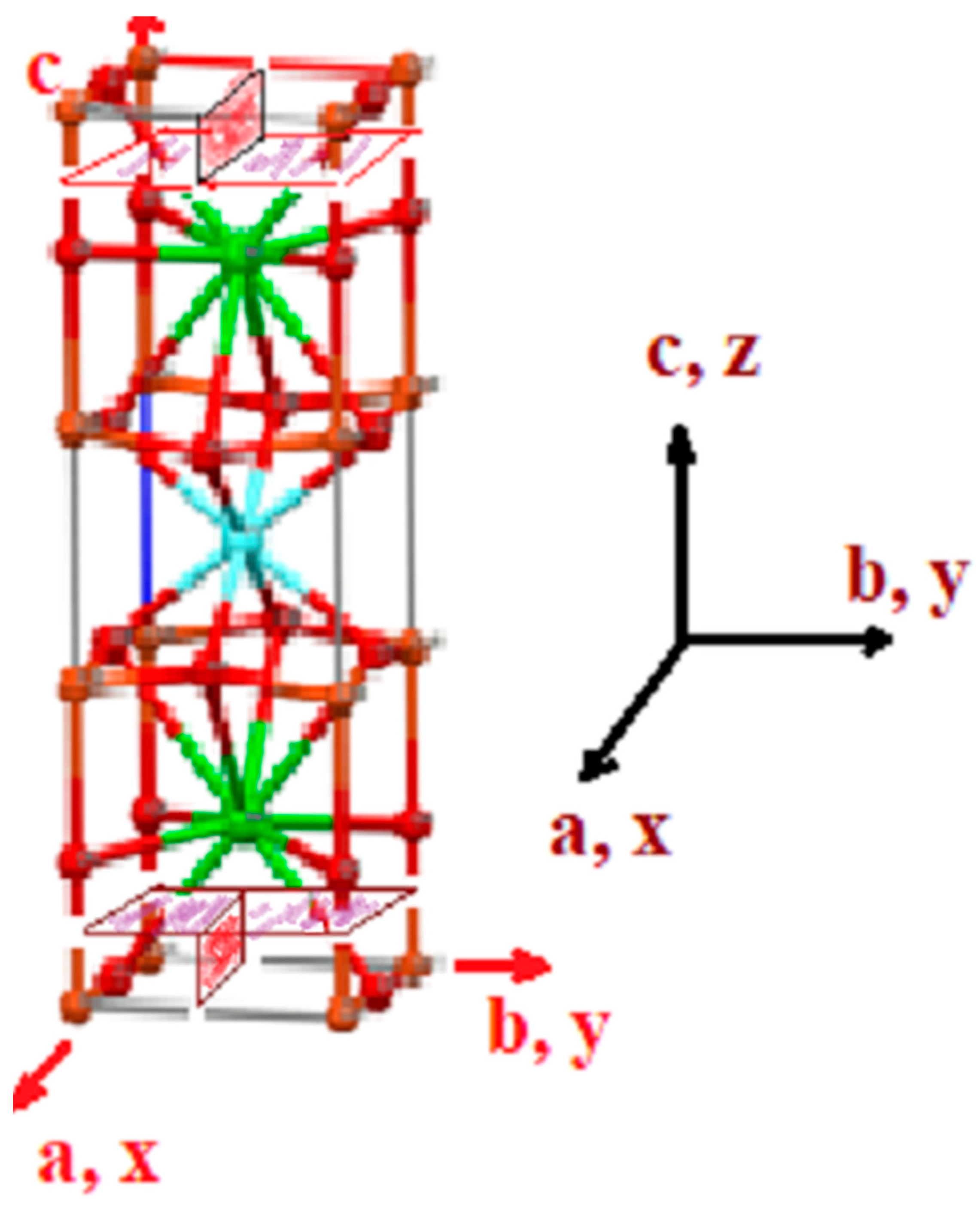

| Material (Technique) | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) |
|---|---|---|---|---|---|---|---|---|---|
| YBCO * [1] (Resonant Ultrasound) | 231.0 | 132.0 | 71.0 | 268.0 | 95.0 | 186.0 | 49.0 | 37.0 | 95.0 |
| YBCO ** [79] (Estimate) | 223.0 | 37.0 | 89.0 | 244.0 | 93.0 | 138.0 | 61.0 | 47.0 | 97.0 |
| YBCO *** (Inference) | 231.0 | 66.0 | 71.0 | 268.0 | 95.0 | 186.0 | 49.0 | 37.0 | 82.0 |
| YBCOT [67] (Neutron Scattering) | 230.0 | 100.0 | 100.0 | 230.0 | 100.0 | 150.0 | 50.0 | 50.0 | 85.0 |
| Material | A | κ | Roots | (010)[001] × [100] Cleavage System †: Easy or Difficult | |
|---|---|---|---|---|---|
| YBCO * | 1.6266 | 1.0771 | 2.624 | Complex | Difficult |
| YBCO ** | 0.9884 | 1.046 | 1.0321 | Imaginary | Easy |
| YBCO *** | 0.8971 | 1.0771 | 0.9406 | Imaginary | Easy |
| YBCOT | 1.3077 | 1.0 | 1.5097 | Complex | Difficult |
| Material | Roots | 0)[100] × [001] Cleavage System: Easy or Difficult | |||
|---|---|---|---|---|---|
| YBCO * | 0.7641 | 1.2003 | 0.8334 | Imaginary | Easy |
| YBCO ** | 1.3481 | 1.3298 | 2.1763 | Complex | Difficult |
| YBCO *** | 0.7641 | 1.2003 | 0.8334 | Imaginary | Easy |
| YBCOT | 1.1663 | 1.2382 | 1.586 | Complex | Difficult |
| Material | Roots | 00) [001] × [010 Cleavage System: Easy or Difficult | |||
|---|---|---|---|---|---|
| YBCO * | 1.6266 | 0.9284 | 2.2619 | Complex | Difficult |
| YBCO ** | 0.9884 | 0.956 | 0.9432 | Imaginary | Easy |
| YBCO *** | 0.8971 | 0.9284 | 0.817 | Imaginary | Easy |
| YBCOT | 1.3077 | 1.0 | 1.3086 | Complex | Difficult |
| Material | Roots | (100)[010] × [001] Cleavage System: Easy or Difficult | |||
|---|---|---|---|---|---|
| YBCO * | 0.543 | 1.1145 | 0.5232 | Imaginary | Easy |
| YBCO ** | 1.0877 | 1.2711 | 1.447 | Complex | Difficult |
| YBCO *** | 0.543 | 1.1145 | 0.5232 | Imaginary | Easy |
| YBCOT | 1.1663 | 1.2382 | 1.5863 | Complex | Difficult |
| Material | Roots | (001)[100] × [010] Cleavage System: Easy or Difficult | |||
|---|---|---|---|---|---|
| YBCO * | 0.7641 | 0.8331 | 0.5784 | Imaginary | Easy |
| YBCO ** | 1.3481 | 0.7521 | 1.2309 | Complex | Difficult |
| YBCO *** | 0.7641 | 0.8331 | 0.5784 | Imaginary | Easy |
| YBCOT | 1.1663 | 0.8076 | 1.0345 | Complex | Difficult |
| Material | Roots | 0] × [100] Cleavage System: Easy or Difficult | |||
|---|---|---|---|---|---|
| YBCO * | 0.543 | 0.8973 | 0.4213 | Imaginary | Easy |
| YBCO ** | 1.0877 | 0.7867 | 0.8954 | Complex | Difficult |
| YBCO *** | 0.543 | 0.8973 | 0.4213 | Imaginary | Easy |
| YBCOT | 1.1663 | 0.8076 | 1.0345 | Complex | Difficult |
| Cleavage System | (010)[001] × [100] | 0)[100] × [001] | 00)[001] × [010] | (100)[010] × [001] | (001)[100] × [010] | 0] × [100] |
|---|---|---|---|---|---|---|
| Fracture Toughness, Kc [9] (MPa ) | 0.59 ± 0.09 | 0.59 ± 0.09 | 0.47 ± 0.12 | 0.47 ± 0.12 | 0.32 ± 0.07 | 0.32 ± 0.07 |
| Fracture Energy, Gc (J/m2) | 1.50177 | 1.91945 | 1.02649 | 1.43075 | 0.73912 | 0.71163 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chaudhuri, R.A. Employment of Fracture Mechanics Criteria for Accurate Assessment of the Full Set of Elastic Constants of Orthorhombic/Tetragonal Mono-Crystalline YBCO. Appl. Mech. 2023, 4, 585-643. https://doi.org/10.3390/applmech4020032
Chaudhuri RA. Employment of Fracture Mechanics Criteria for Accurate Assessment of the Full Set of Elastic Constants of Orthorhombic/Tetragonal Mono-Crystalline YBCO. Applied Mechanics. 2023; 4(2):585-643. https://doi.org/10.3390/applmech4020032
Chicago/Turabian StyleChaudhuri, Reaz A. 2023. "Employment of Fracture Mechanics Criteria for Accurate Assessment of the Full Set of Elastic Constants of Orthorhombic/Tetragonal Mono-Crystalline YBCO" Applied Mechanics 4, no. 2: 585-643. https://doi.org/10.3390/applmech4020032
APA StyleChaudhuri, R. A. (2023). Employment of Fracture Mechanics Criteria for Accurate Assessment of the Full Set of Elastic Constants of Orthorhombic/Tetragonal Mono-Crystalline YBCO. Applied Mechanics, 4(2), 585-643. https://doi.org/10.3390/applmech4020032




