Modelling of Low-Voltage Varistors’ Responses under Slow-Front Overvoltages
Abstract
1. Introduction
2. Review of Surge Degradation
3. Experimental Work
3.1. Degradation of MOVs under Slow Front AC Switching Surges
3.2. C-V Measurement and Barrier Height Calculation
3.3. Effects of Number of Surges on the Grain Height Response
- (Null hypothesis): ZnO grain heights of tested samples are from the same normal population distribution. Therefore, the calculated probability (p)-value at 95% confidence should be greater than the critical value α = 0.05.
- 2.
- (Alternate hypothesis): ZnO grain heights of tested samples are from non-normal population distribution. Therefore, the calculated probability (p)-value at 95% confidence should be less than the critical value α = 0.05.
- Null hypothesis: the MOV varistor grain barrier height group mean of the samples degraded under different numbers of surges must be equal:
- Alternate hypothesis: one of the MOV varistor grain barrier height group means of samples degraded under different numbers of surges are not equal:
- Statistical test: null hypothesis is rejected if
- Calculate the sum of squares among the groups.
- Calculate sum of squares within the groups.
- Calculate the mean square values among and within groups.
- Then, compute the F statistic value.
3.4. Modelling of Grain Barrier Height Response Using Regression Analysis
- (Null hypothesis): , there is no linear relationship between the number of surges and the average grain barrier height response, and therefore the grain barrier height is independent of the number of surges.
- (Alternate hypothesis): , there is a linear relationship between the number of surges and the average grain barrier height, and therefore the grain barrier height changes are caused by the applied number of surges.
- Statistical test: null hypothesis is rejected if
4. Results and Analysis
4.1. Degradation Analysis
4.1.1. Percentage Change in Average Reference Voltages
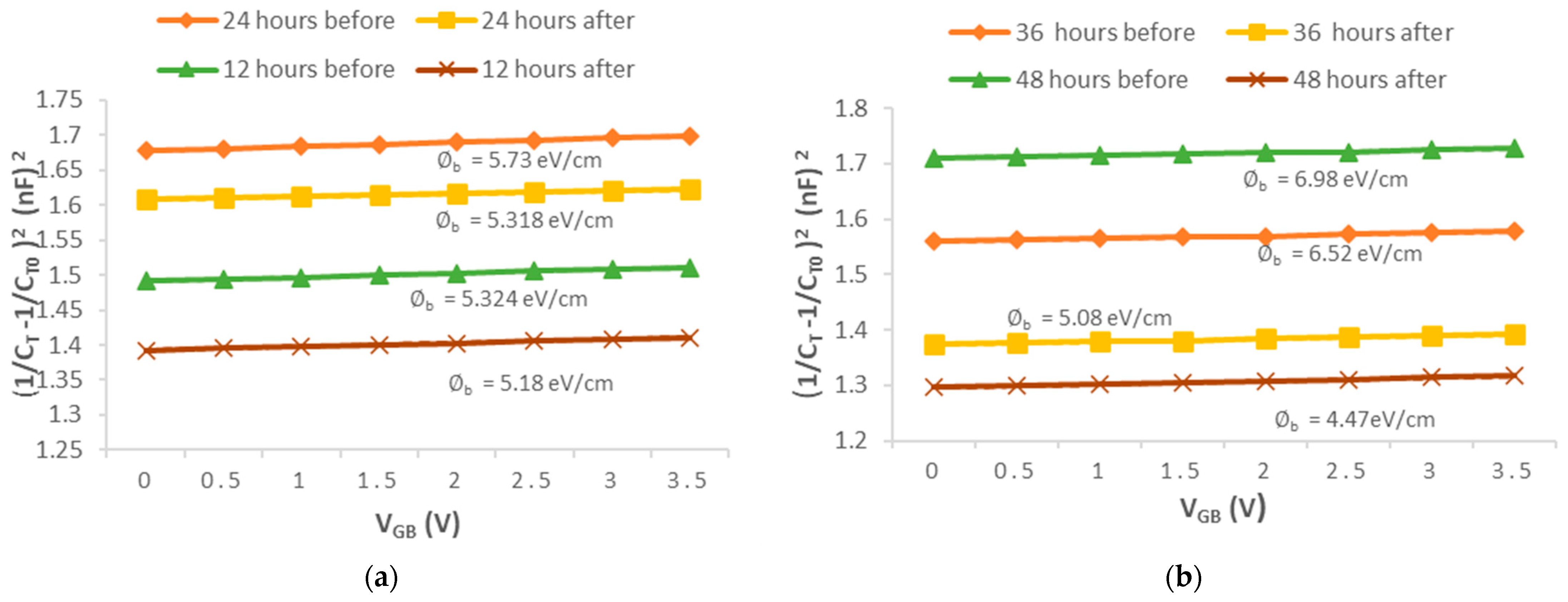
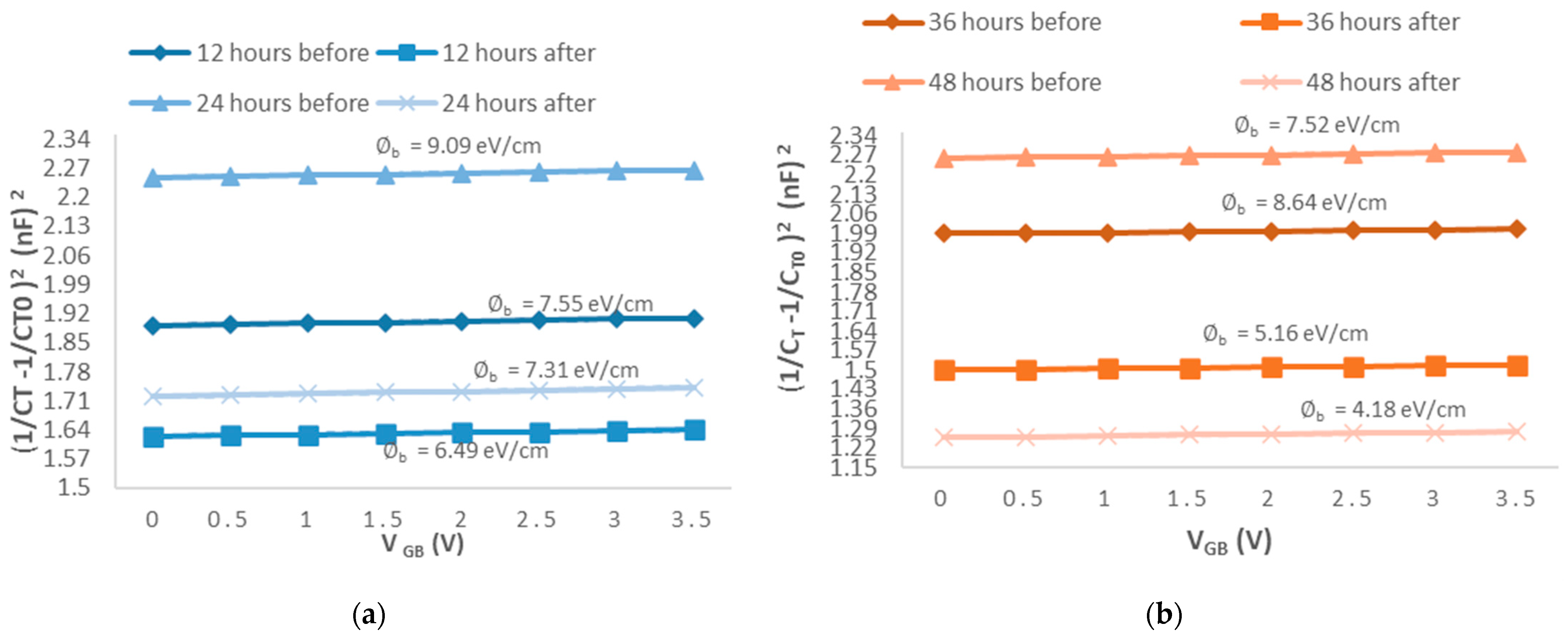
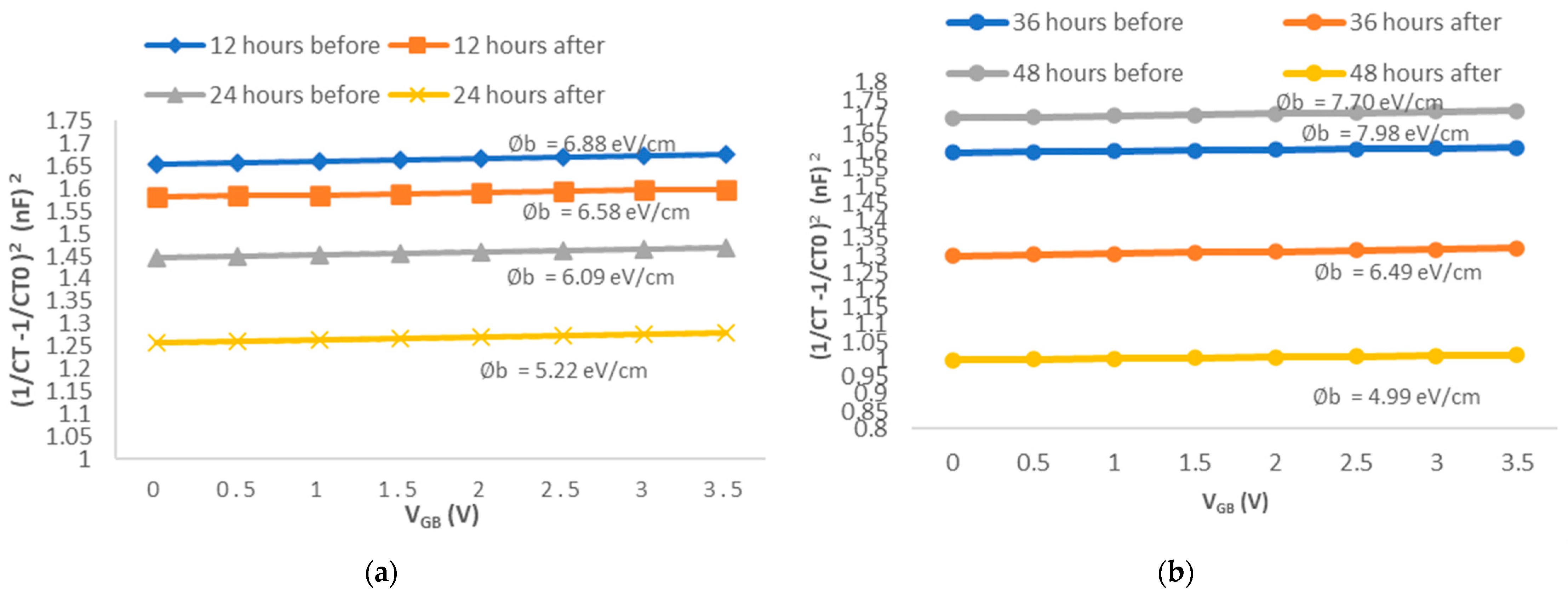
4.1.2. C-V Characteristics and Grain Barrier Height
4.2. Effects of Number of Surges on the MOV Average Grain Barrier Height
4.2.1. MOV Grain Barrier Height Adherence to Normal Results
4.2.2. F-Statistical Results
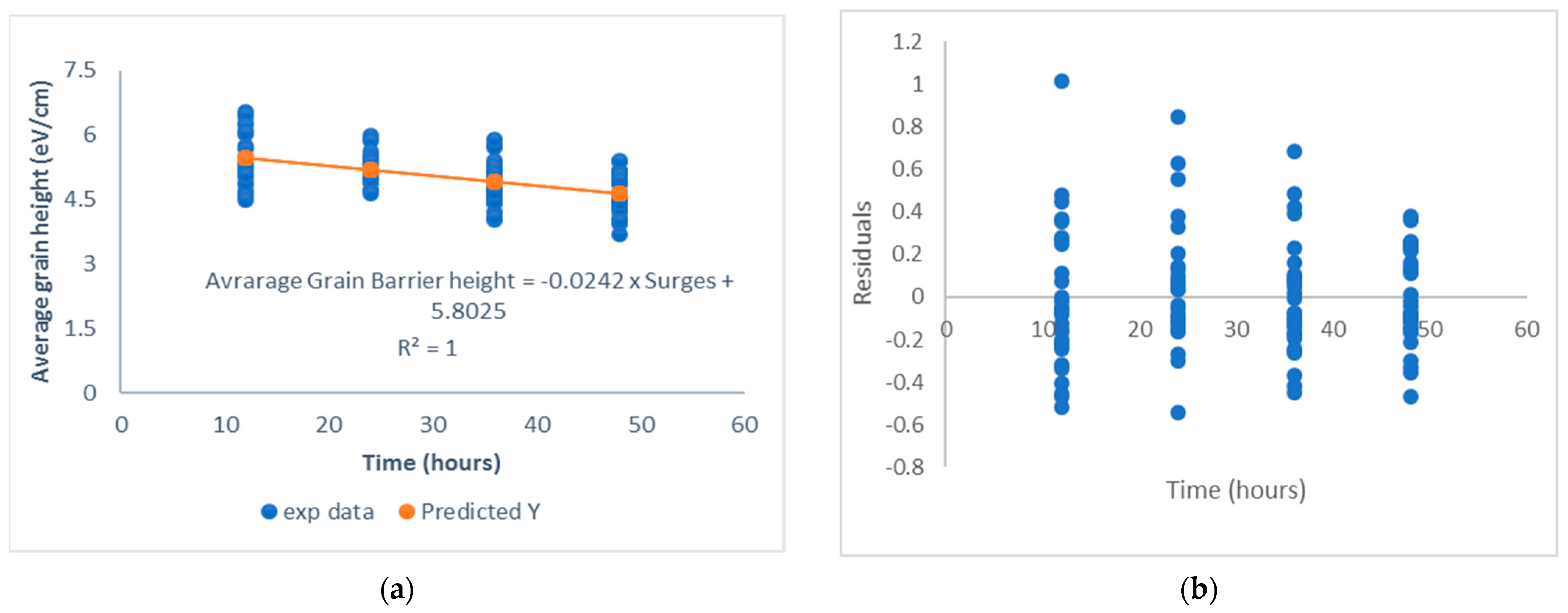
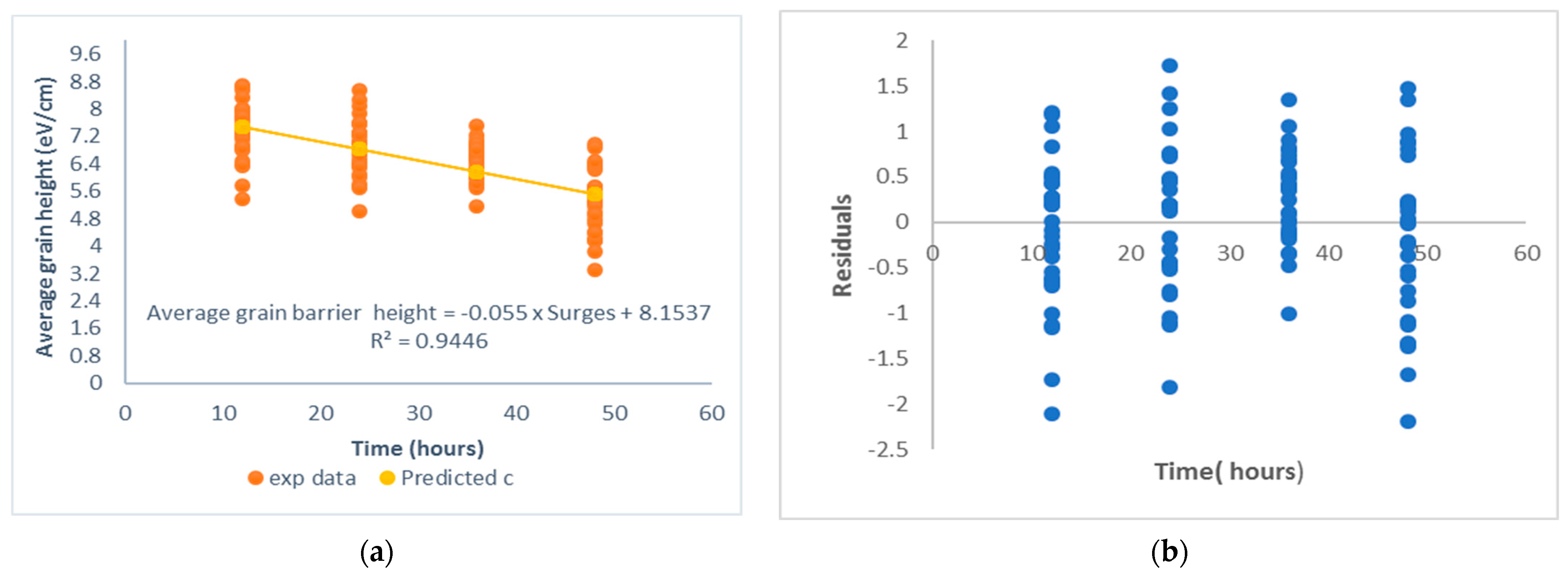
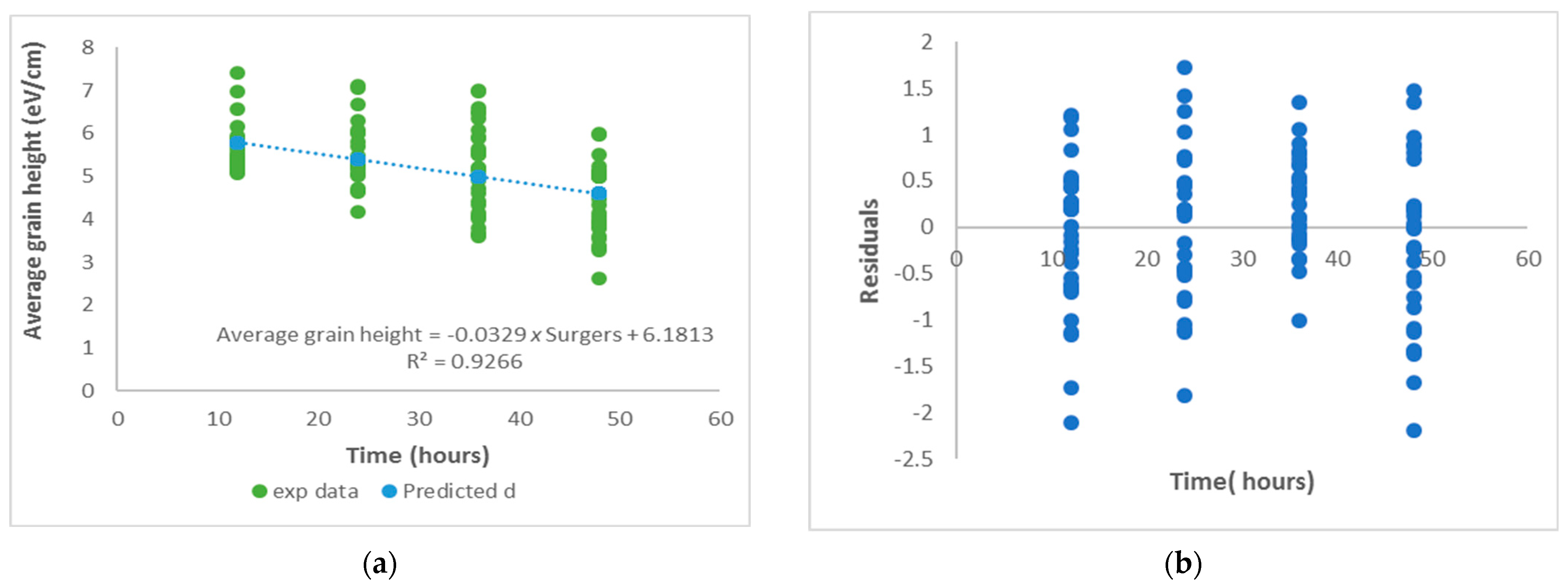
4.3. Regression Models
5. Summary
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Reddy, B.S.; Verma, A.R. Protection of Digital Telecom Exchanges against Lightning Surges and Earth Faults. IEEE Trans. Ind. Appl. 2015, 51, 5305–5311. [Google Scholar] [CrossRef]
- Greenwood, A. Electrical Transients in Power Systems; New York Wiley: New York, NY, USA, 1991. [Google Scholar]
- Thione, L. General Report of group 33 (Overvoltages and Insulation Coordination). Electra 1985, 99, 79–93. [Google Scholar]
- Grebe, T. Why power factor correction capacitors may upset adjustable speed drives. Power Qual. May/June 1991, 3, 14–18. [Google Scholar]
- Shipp, D.D.; Dionise, T.J.; Lorch, V.; MacFarlane, B.G. Transformer failure due to circuit-breaker-induced switching transients. IEEE Trans. Ind. Appl. Mar. 2011, 47, 707–718. [Google Scholar] [CrossRef]
- Miyazaki, T.; Ishii, T.; Okabe, S.A. Field Study of Lightning Surges Propagating into Residences. IEEE Trans. Electromagn. Compat. 2010, 52, 921–928. [Google Scholar] [CrossRef]
- IEEE Standards C62.34; Performance of Low-Voltage Surge-Protective Devices (Secondary Arresters). IEEE: Piscataway, NJ, USA, 1996; pp. 1–24.
- Gupta, T.K. Application of Zinc Oxide Varistors. J. Am. Ceram. Soc. 1990, 73, 1817–1840. [Google Scholar] [CrossRef]
- Khanmiri, D.T.; Ball, R.; Mosesian, J.; Lehman, B. Degradation of low voltage metal oxide varistors in power supplies. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 2122–2126. [Google Scholar]
- Khanmiri, D.T.; Ball, R.; Lehman, B. Degradation Effects on Energy Absorption Capability and Time to Failure of Low Voltage Metal Oxide Varistors. IEEE Trans. Power Deliv. 2017, 32, 2272–2280. [Google Scholar] [CrossRef]
- Pengfei, M.; Xiao, Y.; Wu, Y.; Xie, Q.; He, J.; Hu, J. Stable electrical properties of ZnO varistor ceramics with multiple additives against the AC accelerated aging process. Ceramic Int. 2019, 45, 11105–11108. [Google Scholar]
- Li, S.T.; He, J.Q.; Lin, J.J.; Wang, H.; Liu, W.F.; Liao, Y.L. Electrical-Thermal Failure of Metal–Oxide Arrester by Successive Impulses. IEEE Trans. Power Deliv. 2016, 31, 2538–2545. [Google Scholar] [CrossRef]
- Wang, M.; Xin, R.; Zhou, Q.; Li, Z.; Yang, H.; Jiang, H.; Yan, Y.; Ruan, X.; Yu, W.; Jin, L.; et al. High improvement of degradation behavior of ZnO varistors under high current surges by appropriate Sb2O3 doping. J. Eur. Ceram. Soc. 2021, 41, 436–442. [Google Scholar] [CrossRef]
- He, J.; Liu, J.; Hu, J.; Zeng, R.; Long, W. Non-uniform ageing behavior of individual grain boundaries in ZnO varistor Ceramics. J. Eur. Ceram. Soc. 2011, 31, 1451–1456. [Google Scholar] [CrossRef]
- Mardira, K.P.; Saha, T.K.; Sutton, R.A. Effects of electrical degradation on the microstructure of metal oxide varistor. In 2001 IEEE/PES Transmission and Distribution Conference and Exposition. Developing New Perspectives (Cat. No. 01CH37294); IEEE: Manhattan, NY, USA, 2001; Volume 1, pp. 329–334. [Google Scholar]
- Wang, G.; Kim, W.H.; Lee, J.H.; Kil, G.S. Condition monitoring and deterioration of metal oxide varistor. J. Electr. Eng. 2018, 69, 352–358. [Google Scholar] [CrossRef]
- Zhang, C.; Li, C.; Lv, D.; Zhu, H.; Xing, H. An Experimental Study on the Effect of Multiple Lightning Waveform Parameters on the Aging Characteristics of ZnO Varistors. Electronics 2020, 9, 930. [Google Scholar] [CrossRef]
- Mizukoshi, A.; Ozawa, J.; Shirakawa, S.; Nakano, K. Influence of Uniformity on Energy Absorption Capabilities of Zinc Oxide Elements as Applied in Arresters. IEEE Trans. Power Appar. Syst. 1983, PAS-102, 1384–1390. [Google Scholar] [CrossRef]
- Kan, M.; Nishiwaki, S.; Sato, T.; Kojima, S.; Yanabu, S. Surge discharge capability and thermal stability of a metal oxide surge arrester. IEEE Trans. Power Appar. Syst. 1983, PAS-102, 282–288. [Google Scholar] [CrossRef]
- He, J. Metal Oxide Varistors: From Microstructure to Macro-Characteristics; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Einzinger, R. Metal oxide varistors. Annu. Rev. Mater. Sci. 1987, 17, 299–321. [Google Scholar] [CrossRef]
- Plata, A.M.; Ponce, M.A.; Rios, J.M.; de la Rosa, F.; Castano, V.M. Degradation of ZnO based surge arresters under field conditions. IEE Proc. Sci. Meas. Technol. 1996, 143, 291–297. [Google Scholar] [CrossRef]
- Zhao, H.; Hu, J.; Chen, S.; He, J. Microstructure and Electrical Properties of Ga2O3 Doping on ZnO Varistor Ceramics with Different Sintering Temperature. In Proceedings of the 2016 IEEE International Conference on Dielectrics, Montpellier, France, 3–7 July 2016; pp. 260–263. [Google Scholar]
- Wang, M.H.; Tang, Q.H.; Yao, C. Electrical properties and AC degradation characteristics of low voltage ZnO varistors doped with Nd2O3. Ceram. Int. 2010, 36, 1095–1099. [Google Scholar] [CrossRef]
- Cheng, X.; Lu, Z.; Liu, X.; Yi, W.; Chen, Z.; Wang, X. Improvement of surge current performances of ZnO varistor ceramics via C3N4-doping. J. Eur Ceramic Society. J. Eur. Ceram. Soc. 2020, 40, 2390–2395. [Google Scholar] [CrossRef]
- Tao, M.; Bui, A.; Dorlanne, O.; Loubiere, A. Different “single grain junctions” within a ZnO varistor. J. Appl. Phys. 1987, 61, 1562–1567. [Google Scholar] [CrossRef]
- Wong, J. Barrier voltage measurement in metal oxide varistors. J. Appl. Phys. 1979, 47, 4971–4974. [Google Scholar] [CrossRef]
- Meshkatoddini, M.R. Statistical study of the thin metal-oxide varistor ceramics. Aust. J. Basic Appl. Sci. 2010, 4, 751–763. [Google Scholar]
- Górecki, T.; Smaga, L. A comparison of tests for the one-way ANOVA problem for functional data. Comput. Stat. 2015, 30, 987–1010. [Google Scholar] [CrossRef]
- Alassaf, M.; Qamar, A.M. Improving sentiment analysis of Arabic tweets by One-Way ANOVA. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 2849–2859. [Google Scholar] [CrossRef]
- D’agostino, R.B.; Belanger, A.; D’Agostino, R.B., Jr. A Suggestion for Using Powerful and Informative Tests of Normality. Am. Stat. 1990, 44, 316–321. [Google Scholar]
- Kim, T.K.; Park, J.H. More about the basic assumptions of t-test: Normality and sample size. Korean J. Anesthesiol. 2019, 72, 331–335. [Google Scholar] [CrossRef] [PubMed]
- Midway, S.; Robertson, M.; Flinn, S.; Kaller, M. Comparing multiple comparisons: Practical guidance for choosing the best multiple comparisons test. PeerJ 2020, 8, e10387. [Google Scholar] [CrossRef]
- Nanda, A.; Mohapatra, B.B.; Mahapatra, A.P.K.; Abiresh Prasad Kumar Mahapatra, A.P.K.; Mahapatra, A.P.K. Multiple comparison test by Tukey’s honestly significant difference (HSD): Do the confident level control type I error. IJAMS Int. J. Stat. Appl. Math. 2021, 6, 59–65. [Google Scholar] [CrossRef]
- Kim, H.Y. Statistical notes for clinical researchers: Simple linear regression 3–residual analysis. Restor. Dent. Endod. 2019, 4, e11. [Google Scholar] [CrossRef]
- Nel, T.; Clarke, C.E.; Hardie, A.G. Evaluation of simple and multivariate linear regression models for exchangeable base cation conversion between seven measurement techniques on South African soils. Geoderma Reg. 2020, 30, e00571. [Google Scholar] [CrossRef]
- Alita, D.; Putra, A.D.; Darwis, D. Analysis of classic assumption test and multiple linear regression coefficient test for employee structural office recommendation. IJCCS (Indones. J. Comput. Cybern. Syst.) 2021, 15, 1–5. [Google Scholar] [CrossRef]

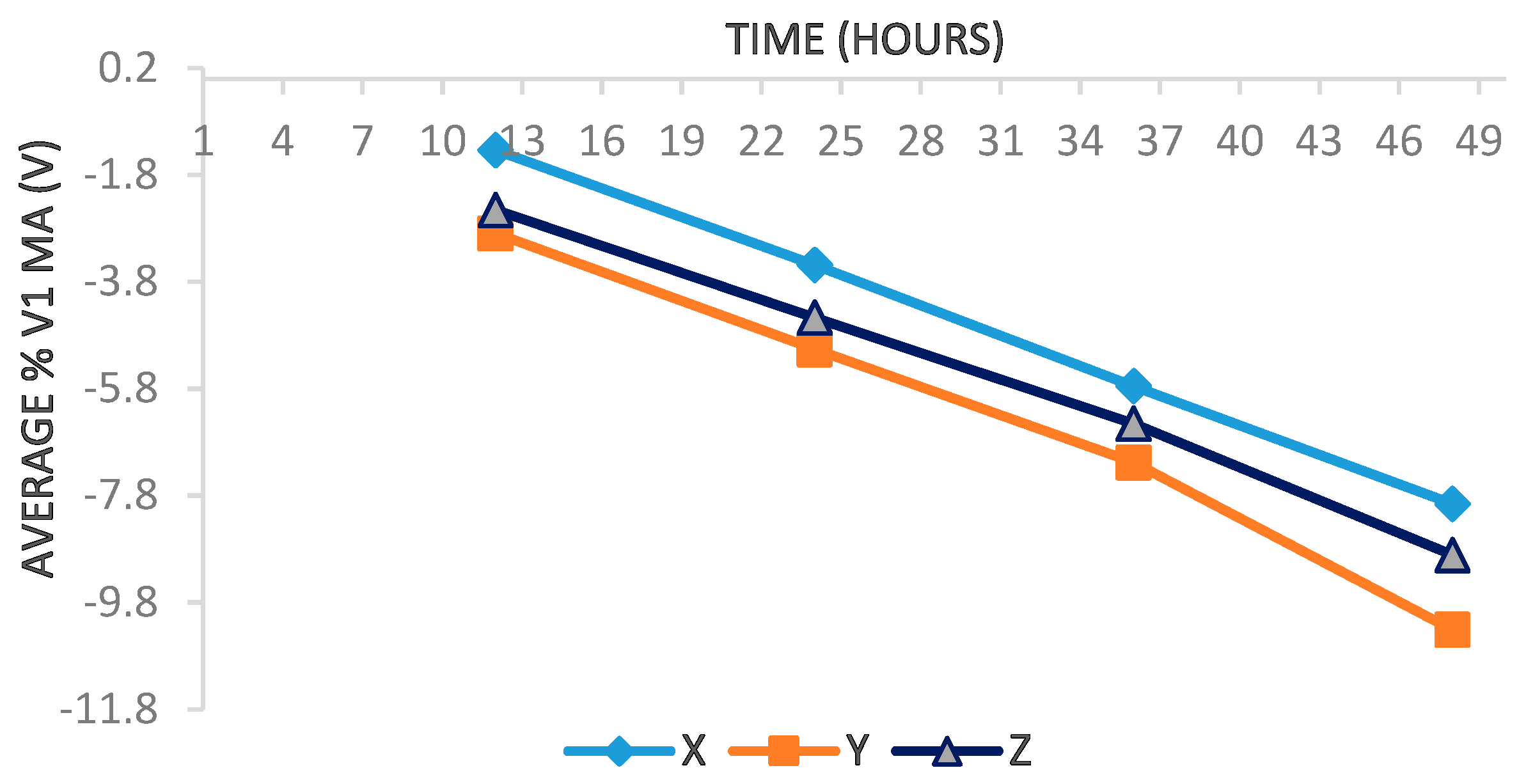
| 12 h | 24 h | 36 h | 48 h | |
|---|---|---|---|---|
| Manufacturer X | −1.33 | −3.48 | −5.75 | −7.95 |
| Manufacturer Y | −2.89 | −5.06 | −7.18 | −10.31 |
| Manufacturer Z | −2.45 | −4.47 | −6.45 | −8.91 |
| (eV/cm) before | (eV/cm) after | (%) | |
|---|---|---|---|
| Manufacturer X | |||
| 12 | 5.878 | 5.466 | 6.8 |
| 24 | 6.1377 | 5.304 | 13.12 |
| 36 | 5.8975 | 4.902 | 16.54 |
| 48 | 6.0754 | 4.631 | 23.57 |
| Manufacturer Y | |||
| 12 | 8.937 | 7.374 | 16.75 |
| 24 | 8.698 | 6.876 | 20.38 |
| 36 | 9.508 | 6.444 | 32.09 |
| 48 | 9.041 | 5.318 | 40.32 |
| Manufacturer Z | |||
| 12 | 6.076 | 5.674 | 6.46 |
| 24 | 6.427 | 5.483 | 13.75 |
| 36 | 7.028 | 5.148 | 26.51 |
| 48 | 7.196 | 4.468 | 37.35 |
| p-Value | |||||
|---|---|---|---|---|---|
| Manufacturer X | |||||
| 12 | 1.5056 | 0.4325 | 2.4538 | 2.4538 | 0.293 |
| 24 | 1.2646 | 0.5098 | 1.8588 | 1.8588 | 0.3948 |
| 36 | 1.111 | 0.3275 | 1.3415 | 1.3415 | 0.5113 |
| 48 | −0.21 | −1.0091 | 1.0623 | 1.0623 | 0.5879 |
| Manufacturer Y | |||||
| 12 | 1.2218 | 0.3695 | 1.6293 | 1.6293 | 0.4428 |
| 24 | −0.1883 | −0.0981 | 0.0451 | 0.0451 | 0.9777 |
| 36 | −0.5378 | 0.4996 | 0.5388 | 0.5388 | 0.7638 |
| 48 | −0.3958 | −0.5404 | 0.4487 | 0.4487 | 0.799 |
| Manufacturer Z | |||||
| 12 | 2.161 | 1.1318 | 0.9491 | 0.9491 | 0.052 |
| 24 | 1.7285 | 1.0002 | 3.9882 | 3.9882 | 0.1361 |
| 36 | 0.3887 | −2.033 | 4.2854 | 4.2854 | 0.1173 |
| 48 | −0.3907 | −0.7805 | 0.7618 | 0.7618 | 0.6833 |
| Source of Variation | SS | Df | MS | p-Value | ||
|---|---|---|---|---|---|---|
| Manufacturer X | ||||||
| Among Groups | 13.9695 | 3 | 4.32 | 13.74567 | 9.88 | 2.682809 |
| Within Groups | 36.487 | 116 | 0.31 | |||
| Total | 49.456 | 119 | ||||
| Manufacturer Y | ||||||
| Among Groups | 69.21657 | 3 | 23.07219 | 37.8962 | 3.81 | 2.682809 |
| Within Groups | 70.62382 | 116 | 0.608826 | |||
| Total | 139.8404 | 119 | ||||
| Manufacturer Z | ||||||
| Among Groups | 25.27437 | 3 | 8.424789 | 12.18309 | 5.48 | 2.682809 |
| Within Groups | 80.21572 | 116 | 0.691515 | |||
| Total | 105.4901 | 119 | ||||
| Groups (Hours) | p Value < 0.005 | Results | ||
|---|---|---|---|---|
| Manufacturer X | ||||
| 12 and 24 | 1.397 | 2.048 | 0.173170368 | Non-significantly different |
| 12 and 36 | 4.077 | 2.048 | 0.0003414 | Significantly different |
| 12 and 48 | 5.233 | 2.048 | 1.1455 | Significantly different |
| 24 and 36 | 2.379 | 2.040 | 0.024379054 | Non-significantly different |
| 24 and 48 | 4.76 | 2.048 | 5.31122 | Significantly different |
| 36 and 48 | 1.961 | 2.048 | 0.059821666 | Non-significantly different |
| Manufacturer Y | ||||
| 12 and 24 | 2.2739 | 2.048 | 0.0308 | Significantly different |
| 12 and 36 | 5.414 | 2.048 | 8.94831 | Significantly different |
| 12 and 48 | 8.128 | 2.048 | 7.53 | Significantly different |
| 24 and 36 | 2.068 | 2.048 | 0.0479 | Significantly different |
| 24 and 48 | 6.936 | 2.048 | 1.53339 | Significantly different |
| 36 and 48 | 5.104 | 2.048 | 2.08652 | Significantly different |
| Manufacturer Z | ||||
| 12 and 24 | 6.102 | 2.048 | 1.39154 | Significantly different |
| 12 and 36 | 1.987 | 2.048 | 0.0567 | Non-significantly different |
| 12 and 48 | 6.102 | 2.048 | 1.39154 | Significantly different |
| 24 and 36 | 1.288 | 2.048 | 0.208 | Non-significantly different |
| 24 and 48 | 5.284 | 2.048 | 1.27789 | Significantly different |
| 36 and 48 | 4.204 | 2.048 | 0.000242741 | Significantly different |
| Regression Statistics | ||||
|---|---|---|---|---|
| Manufacturer X | Manufacturer Y | Manufacturer Z | ||
| Multiple R | 0.988541 | 0.971919 | 0.962617 | |
| R Square | 0.977214 | 0.944626 | 0.926631 | |
| Adjusted R Square | 0.965821 | 0.916939 | 0.889947 | |
| Standard Error | 0.070187 | 0.252744 | 0.1758 | |
| Observations | 120 | 120 | 120 | |
| Coefficients | Standard Error | t Stat | p-value | |
| Manufacturer X | ||||
| Intercept | 5.8025 | 0.085961 | 67.50185 | 0.000219 |
| Surges | −0.02423 | 0.002616 | −9.26139 | 0.011459 |
| Manufacturer Y | ||||
| Intercept | 8.153682 | 0.309547 | 26.34066 | 0.001438 |
| Surges | −0.05502 | 0.009419 | −5.84108 | 0.028081 |
| Manufacturer Z | ||||
| Intercept | 6.1813 | 0.215311 | 28.70877 | 0.001211 |
| surges | −0.03293 | 0.006552 | −5.0259 | 0.037383 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muremi, L.; Bokoro, P.N.; Doorsamy, W. Modelling of Low-Voltage Varistors’ Responses under Slow-Front Overvoltages. Electron. Mater. 2023, 4, 62-79. https://doi.org/10.3390/electronicmat4020006
Muremi L, Bokoro PN, Doorsamy W. Modelling of Low-Voltage Varistors’ Responses under Slow-Front Overvoltages. Electronic Materials. 2023; 4(2):62-79. https://doi.org/10.3390/electronicmat4020006
Chicago/Turabian StyleMuremi, Lutendo, Pitshou N. Bokoro, and Wesley Doorsamy. 2023. "Modelling of Low-Voltage Varistors’ Responses under Slow-Front Overvoltages" Electronic Materials 4, no. 2: 62-79. https://doi.org/10.3390/electronicmat4020006
APA StyleMuremi, L., Bokoro, P. N., & Doorsamy, W. (2023). Modelling of Low-Voltage Varistors’ Responses under Slow-Front Overvoltages. Electronic Materials, 4(2), 62-79. https://doi.org/10.3390/electronicmat4020006








