Transmission Dynamics and Short-Term Forecasts of COVID-19: Nepal 2020/2021
Abstract
:1. Introduction
2. Materials and Methods
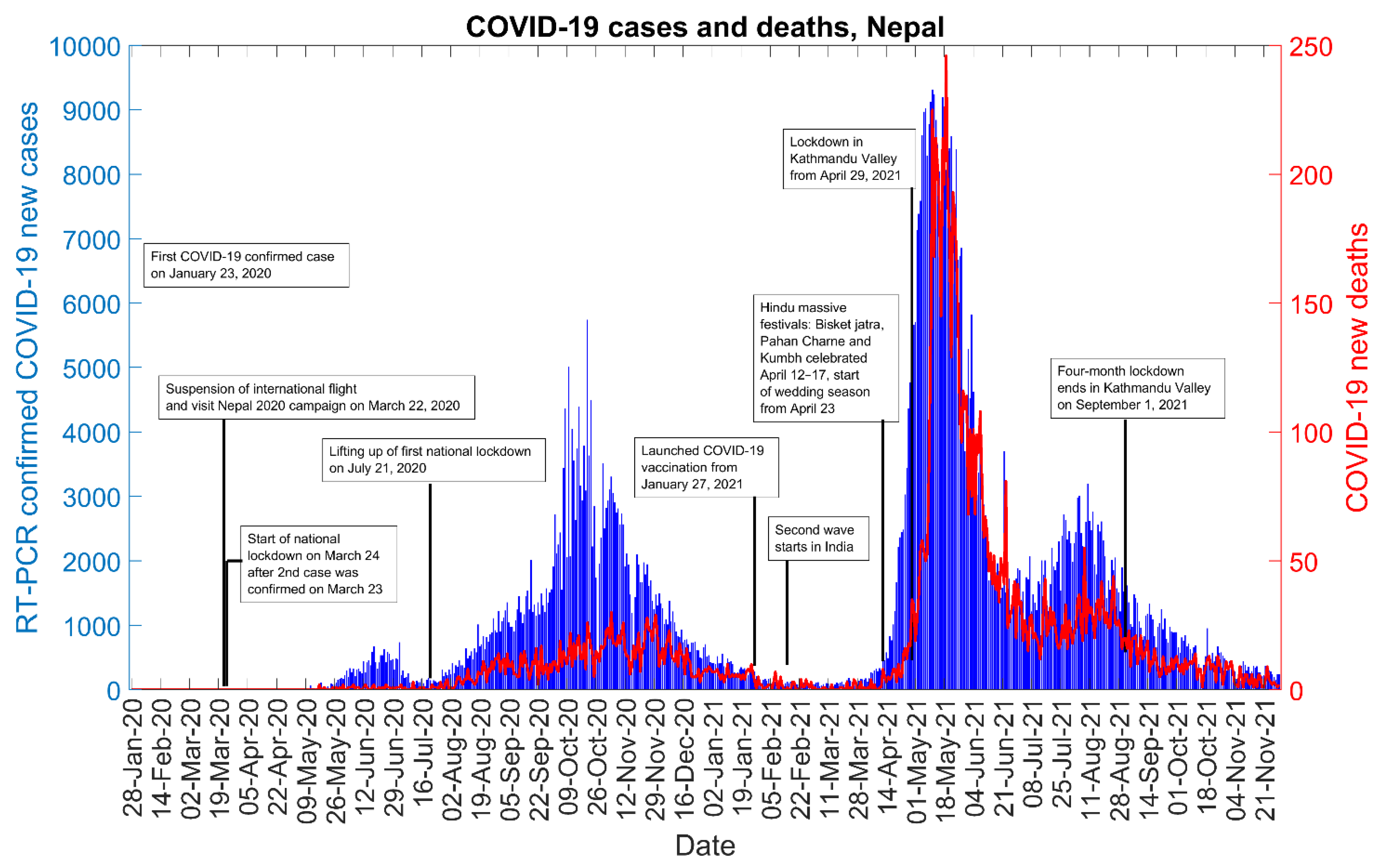
2.1. Setting
2.2. Data
2.3. Modeling Framework for Forecast Generation
2.3.1. Generalized Logistic Growth Model
2.3.2. Richards Growth Model
2.3.3. Sub-Epidemic Model
2.4. Model Calibration and Forecasting Approach
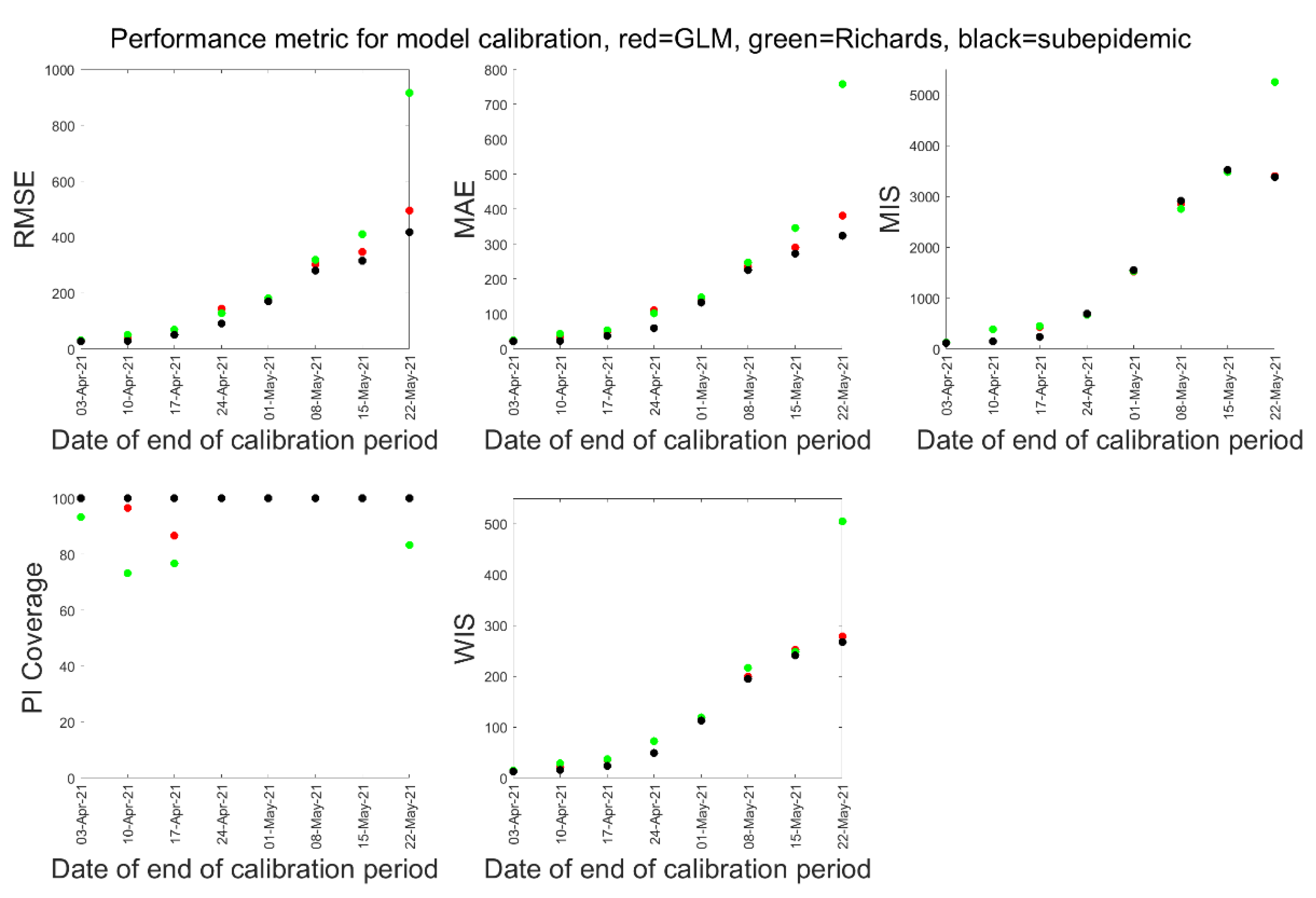
2.5. Performance Metrics
2.6. Reproduction Number
2.7. Estimating Reproduction Number () Using GGM
2.8. Estimating Instantaneous Reproduction Number ()
3. Results
3.1. Model Calibration and Forecasting Performance
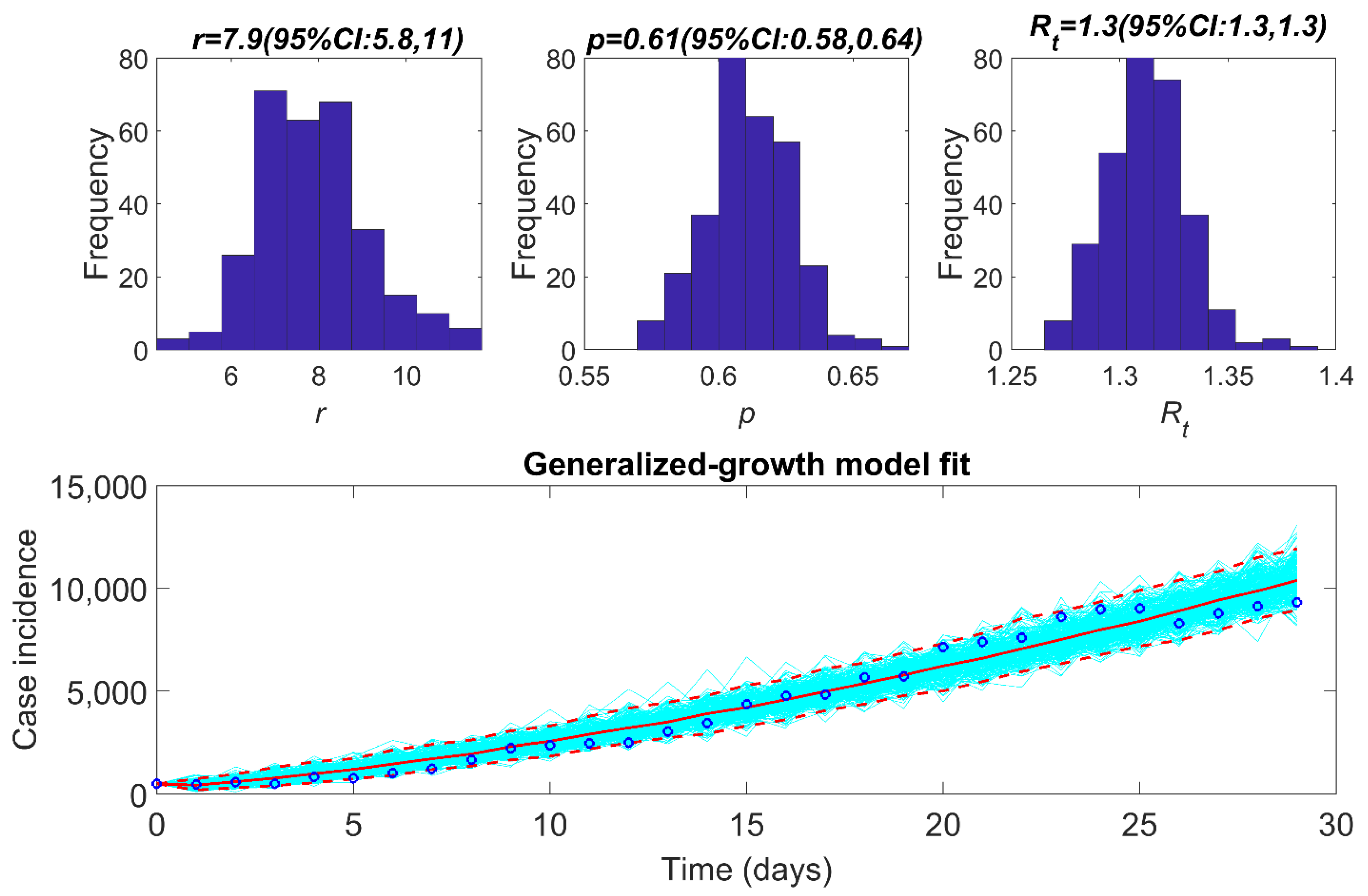
3.2. Estimate of Reproduction Number, from Case Incidence Data Using GGM
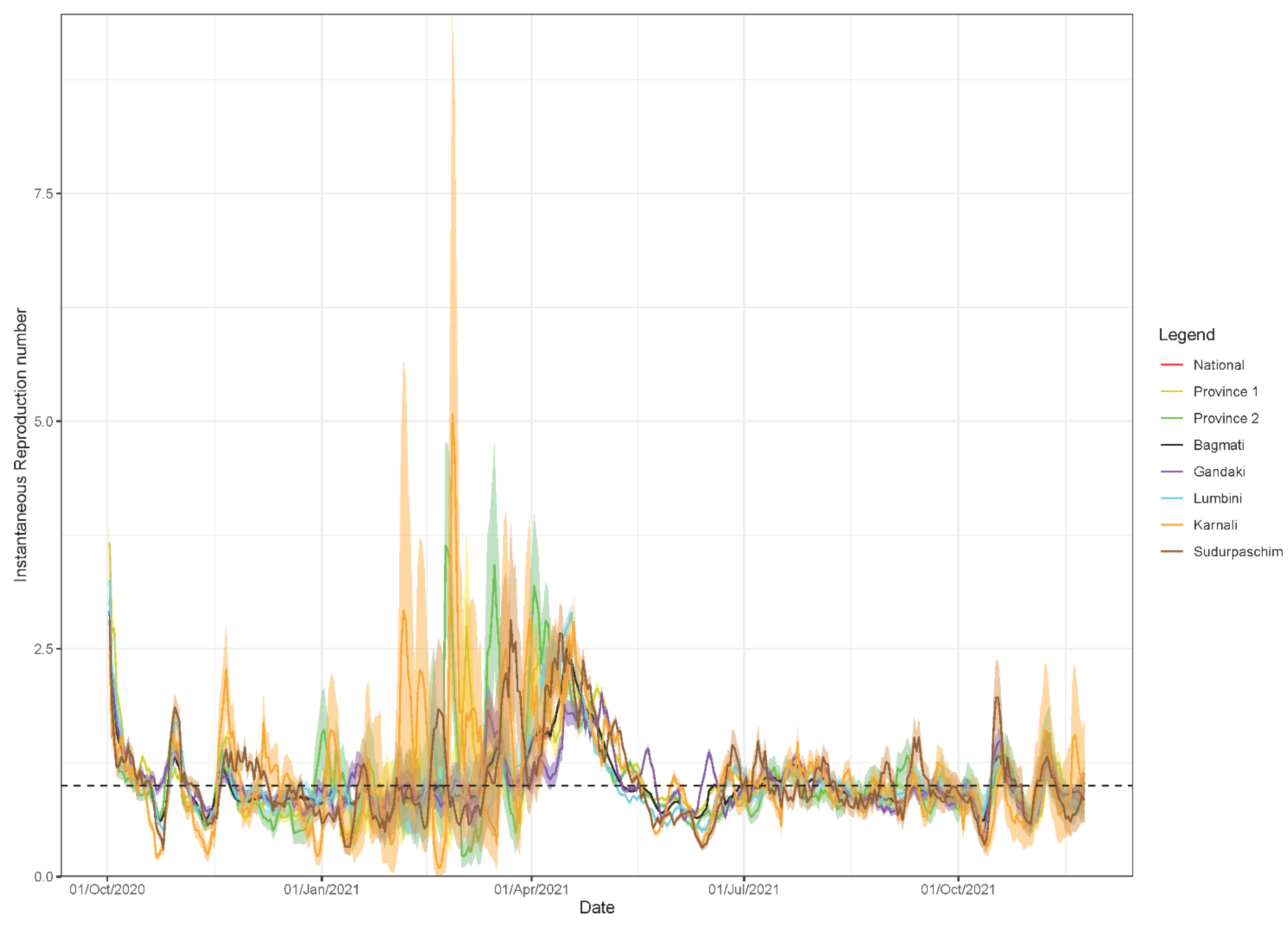
3.3. Estimate of Instantaneous Reproduction Number,
3.4. Analysis of Mobility Data
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Demographia World Urban Areas. June 2021. Available online: http://www.demographia.com/db-worldua.pdf (accessed on 30 August 2021).
- Kugelman, M. How COVID-19 Has Shaped South Asia. Foreign Policy 2021. Available online: https://foreignpolicy.com/2021/07/15/covid-19-pandemic-south-asia-bangladesh-india-nepal-hotspot/ (accessed on 30 August 2021).
- Pecho-Silva, S.; Barboza, J.J.; Navarro-Solsol, A.C.; Rodriguez-Morales, A.J.; Bonilla-Aldana, D.K.; Panduro-Correa, V. SARS-CoV-2 Mutations and Variants: What do we know so far? Microbes Infect. Chemother. 2021, 1, e1256. [Google Scholar] [CrossRef]
- WHO. COVID-19 Weekly Epidemiological Update-37; WHO: Geneva, Switzerland, 2021. [Google Scholar]
- COVID Variants: What You Should Know. Available online: https://www.hopkinsmedicine.org/health/conditions-and-diseases/coronavirus/a-new-strain-of-coronavirus-what-you-should-know (accessed on 22 October 2021).
- WHO. COVID-19 Dashboard; WHO: Geneva, Switzerland, 2021. [Google Scholar]
- MoHP Nepal. COVID-19 Situation Update 30 November 2021; MoHP Nepal: Kathmandu, Nepal, 2021. [Google Scholar]
- Dhakal, S.; Karki, S. Early epidemiological features of COVID-19 in Nepal and public health response. Front. Med. 2020, 7, 524. [Google Scholar] [CrossRef]
- Hollingsworth, J.; Jeong, S.; Thapa, A. Nepal’s cases skyrocket, prompting concern the country’s outbreak could mimic India’s. CNN. 6 May 2021. Available online: https://edition.cnn.com/2021/05/06/asia/nepal-covid-outbreak-intl-hnk-dst/index.html (accessed on 22 May 2021).
- Dalal, S. Relations between India and Nepal in Covid-19 situation. J. Hist. Archaeol. Anthropol. Sci. 2020, 5, 175–181. Available online: https://medcraveonline.com/JHAAS/JHAAS-05-00232.pdf (accessed on 9 April 2021).
- BW Business World. Nepal Re-Opens Border with India with Restrictions. Available online: http://www.businessworld.in/article/Nepal-re-opens-border-with-India-with-restrictions/29-01-2021-371457/ (accessed on 9 April 2021).
- Alam, J. Virus Surge, Vaccine Shortages Spread beyond India’s Borders. Available online: https://apnews.com/article/india-europe-business-global-trade-coronavirus-e95f0515b68ed20ea1f0a53bdea3ffae (accessed on 21 May 2021).
- The Guardian. ‘It’s as If There’s No Covid’: Nepal Defies Pandemic Amid a Broken Economy. Available online: https://www.theguardian.com/global-development/2021/feb/11/its-as-if-theres-no-covid-nepal-defies-pandemic-amid-a-broken-economy (accessed on 9 April 2021).
- Majority of Those Infected in Chitwan Attended Wedding, Bratabandha and Feasts. Kantipur Health. Available online: https://www.kantipurhealth.com/archives/5055 (accessed on 9 April 2021).
- Ethirajan, A. As India Halts Vaccine Exports, Nepal Faces Its Own Covid Crisis. BBC News. Available online: https://www.bbc.com/news/world-asia-57055209 (accessed on 21 May 2021).
- Adhikari, D. Nepal Struggles with a Surge in COVID-19 Cases. Devex-International Development News. Available online: https://www.devex.com/news/nepal-struggles-with-a-surge-in-covid-19-cases-99953 (accessed on 21 May 2021).
- Nepal: Act to Avert Looming Covid-19 Disaster. Human Rights Watch. Available online: https://www.hrw.org/node/378679/printable/print (accessed on 22 May 2021).
- Jewell, N.P.; Lewnard, J.A.; Jewell, B.L. Predictive mathematical models of the COVID-19 pandemic: Underlying principles and value of projections. JAMA 2020, 323, 1893–1894. [Google Scholar] [CrossRef] [PubMed]
- Chowell, G.; Hincapie-Palacio, D.; Ospina, J.; Pell, B.; Tariq, A.; Dahal, S.; Moghadas, S.; Smirnova, A.; Simonsen, L.; Viboud, C. Using phenomenological models to characterize transmissibility and forecast patterns and final burden of Zika epidemics. PLoS Curr. 2016, 8. [Google Scholar] [CrossRef]
- Pell, B.; Kuang, Y.; Viboud, C.; Chowell, G. Using phenomenological models for forecasting the 2015 Ebola challenge. Epidemics 2018, 22, 62–70. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Election Commission. Provincial Map of Nepal. Available online: https://www.election.gov.np/uploads/Pages/1564381682_np.pdf (accessed on 9 April 2021).
- Aljazeera. Hundreds of Nepalese Stuck at India Border Amid COVID-19 Lockdown. Available online: https://www.aljazeera.com/news/2020/4/1/hundreds-of-nepalese-stuck-at-india-border-amid-covid-19-lockdown (accessed on 9 April 2021).
- Government of Nepal. Covid-19 Situation Reports; Ministry of Health and Population: Kathmandu, Nepal, 2020–2021.
- Google. Covid-19 Community Mobility Report for Nepal. Available online: https://www.google.com/covid19/mobility/ (accessed on 3 December 2021).
- Shanafelt, D.W.; Jones, G.; Lima, M.; Perrings, C.; Chowell, G. Forecasting the 2001 foot-and-mouth disease epidemic in the UK. EcoHealth 2018, 15, 338–347. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roosa, K.; Lee, Y.; Luo, R.; Kirpich, A.; Rothenberg, R.; Hyman, J.M.; Yan, P.; Chowell, G. Short-term forecasts of the COVID-19 epidemic in Guangdong and Zhejiang, China: 13–23 February 2020. J. Clin. Med. 2020, 9, 596. [Google Scholar] [CrossRef] [Green Version]
- Roosa, K.; Lee, Y.; Luo, R.; Kirpich, A.; Rothenberg, R.; Hyman, J.; Yan, P.; Chowell, G. Real-time forecasts of the COVID-19 epidemic in China from 5 to 24 February 2020. Infect. Dis. Model. 2020, 5, 256–263. [Google Scholar]
- Richards, F. A flexible growth function for empirical use. J. Exp. Bot. 1959, 10, 290–301. [Google Scholar] [CrossRef]
- Chowell, G.; Tariq, A.; Hyman, J.M. A novel sub-epidemic modeling framework for short-term forecasting epidemic waves. BMC Med. 2019, 17, 164. [Google Scholar] [CrossRef] [Green Version]
- Chowell, G. Fitting dynamic models to epidemic outbreaks with quantified uncertainty: A primer for parameter uncertainty, identifiability, and forecasts. Infect. Dis. Model. 2017, 2, 379–398. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.-S.; Wu, J.; Yang, Y. Richards model revisited: Validation by and application to infection dynamics. J. Theor. Biol. 2012, 313, 12–19. [Google Scholar] [CrossRef]
- Banks, H.T.; Hu, S.; Thompson, W.C. Modeling and Inverse Problems in the Presence of Uncertainty; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Roosa, K. Comparative Assessment of Epidemiological Models for Analyzing and Forecasting Infectious Disease Outbreaks. Ph.D. Thesis, Georgia State University, Atlanta, GA, USA, 2020. [Google Scholar]
- Roosa, K.; Chowell, G. Assessing parameter identifiability in compartmental dynamic models using a computational approach: Application to infectious disease transmission models. Theor. Biol. Med. Model. 2019, 16, 1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gneiting, T.; Raftery, A.E. Strictly proper scoring rules, prediction, and estimation. J. Am. Stat. Assoc. 2007, 102, 359–378. [Google Scholar] [CrossRef]
- Kuhn, M.J.K. Applied Predictive Modeling, 1st ed.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Cramer, E.Y.; Lopez, V.K.; Niemi, J.; George, G.E.; Cegan, J.C.; Dettwiller, I.D.; England, W.P.; Farthing, M.W.; Hunter, R.H.; Lafferty, B. Evaluation of individual and ensemble probabilistic forecasts of COVID-19 mortality in the US. medRxiv 2021. [Google Scholar] [CrossRef]
- Bracher, J.; Ray, E.L.; Gneiting, T.; Reich, N.G. Evaluating epidemic forecasts in an interval format. PLoS Comput. Biol. 2021, 17, e1008618. [Google Scholar] [CrossRef]
- Inglesby, T.V. Public health measures and the reproduction number of SARS-CoV-2. JAMA 2020, 323, 2186–2187. [Google Scholar] [CrossRef]
- Pan, A.; Liu, L.; Wang, C.; Guo, H.; Hao, X.; Wang, Q.; Huang, J.; He, N.; Yu, H.; Lin, X. Association of public health interventions with the epidemiology of the COVID-19 outbreak in Wuhan, China. JAMA 2020, 323, 1915–1923. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ganyani, T.; Kremer, C.; Chen, D.; Torneri, A.; Faes, C.; Wallinga, J.; Hens, N. Estimating the generation interval for coronavirus disease (COVID-19) based on symptom onset data, March 2020. Eurosurveillance 2020, 25, 2000257. [Google Scholar] [CrossRef]
- Nishiura, H.; Chowell, G. Early transmission dynamics of Ebola virus disease (EVD), West Africa, March to August 2014. Eurosurveillance 2014, 19, 20894. [Google Scholar] [CrossRef] [Green Version]
- Nishiura, H.; Chowell, G. The effective reproduction number as a prelude to statistical estimation of time-dependent epidemic trends. In Mathematical and Statistical Estimation Approaches in Epidemiology; Springer: Berlin/Heidelberg, Germany, 2009; pp. 103–121. [Google Scholar]
- Paine, S.; Mercer, G.; Kelly, P.; Bandaranayake, D.; Baker, M.; Huang, Q.; Mackereth, G.; Bissielo, A.; Glass, K.; Hope, V. Transmissibility of 2009 pandemic influenza A (H1N1) in New Zealand: Effective reproduction number and influence of age, ethnicity and importations. Eurosurveillance 2010, 15, 19591. [Google Scholar] [CrossRef] [PubMed]
- Cori, A.; Ferguson, N.M.; Fraser, C.; Cauchemez, S. A new framework and software to estimate time-varying reproduction numbers during epidemics. Am. J. Epidemiol. 2013, 178, 1505–1512. [Google Scholar] [CrossRef] [Green Version]
- Fraser, C. Estimating individual and household reproduction numbers in an emerging epidemic. PLoS ONE 2007, 2, e758. [Google Scholar] [CrossRef]
- Xu, C.; Dong, Y.; Yu, X.; Wang, H.; Tsamlag, L.; Zhang, S.; Chang, R.; Wang, Z.; Yu, Y.; Long, R. Estimation of reproduction numbers of COVID-19 in typical countries and epidemic trends under different prevention and control scenarios. Front. Med. 2020, 14, 613–622. [Google Scholar] [CrossRef] [PubMed]
- Tariq, A.; Banda, J.M.; Skums, P.; Dahal, S.; Castillo-Garsow, C.; Espinoza, B.; Brizuela, N.G.; Saenz, R.A.; Kirpich, A.; Luo, R. Transmission dynamics and forecasts of the COVID-19 pandemic in Mexico, March-December 2020. PLoS ONE 2021, 16, e0254826. [Google Scholar] [CrossRef] [PubMed]
- Patrikar, S.; Kotwal, A.; Bhatti, V.; Banerjee, A.; Chatterjee, K.; Kunte, R.; Tambe, M. Incubation Period and Reproduction Number for novel coronavirus 2019 (COVID-19) infections in India. Asia Pac. J. Public Health 2020, 32, 458–460. [Google Scholar] [CrossRef] [PubMed]
- Marimuthu, S.; Joy, M.; Malavika, B.; Nadaraj, A.; Asirvatham, E.S.; Jeyaseelan, L. Modelling of reproduction number for COVID-19 in India and high incidence states. Clin. Epidemiol. Glob. Health 2021, 9, 57–61. [Google Scholar] [CrossRef]
- Shim, E.; Tariq, A.; Choi, W.; Lee, Y.; Chowell, G. Transmission potential and severity of COVID-19 in South Korea. Int. J. Infect. Dis. 2020, 93, 339–344. [Google Scholar] [CrossRef]
- Tariq, A.; Lee, Y.; Roosa, K.; Blumberg, S.; Yan, P.; Ma, S.; Chowell, G. Real-time monitoring the transmission potential of COVID-19 in Singapore, March 2020. BMC Med. 2020, 18, 1–14. [Google Scholar] [CrossRef]
- WHO Regional Office for South East Asia. COVID-19 Weekly Situation Report—Week 33; WHO Regional Office for South East Asia: New Delhi, India, 2021. [Google Scholar]
- CDC. Delta Variant: What We Know about the Science. Available online: https://www.cdc.gov/coronavirus/2019-ncov/variants/delta-variant.html (accessed on 30 August 2021).
- Poudel, A. Highly Infectious New AY.1 Variant of Coronavirus Found in Infected People. The Kathmandu Post. Available online: https://kathmandupost.com/health/2021/06/21/highly-infectious-new-ay-1-variant-of-coronavirus-found-in-swab-samples-of-infected-people (accessed on 30 August 2021).
- WHO. Nepal Story on COVID-19 Vaccine Deployment: A Good Start. Available online: https://www.who.int/about/accountability/results/who-results-report-2020-mtr/country-story/2020/nepal-story-on-covid-19-vaccine-deployment-a-good-start (accessed on 26 October 2021).
- 5 Million Doses of J&J Vaccine Arrive in Nepal. The Kathmandu Post. Available online: https://kathmandupost.com/health/2021/07/12/1-5-million-doses-of-j-j-vaccine-arrive-in-nepal (accessed on 26 October 2021).
- Country Analysis: Daily Cases and Deaths over Severity of Public Health and Social Measures (PHSM)-Nepal. Available online: https://experience.arcgis.com/experience/56d2642cb379485ebf78371e744b8c6a (accessed on 3 December 2021).
- Dramé, M.; Teguo, M.T.; Proye, E.; Hequet, F.; Hentzien, M.; Kanagaratnam, L.; Godaert, L. Should RT-PCR be considered a gold standard in the diagnosis of Covid-19? J. Med. Virol. 2020, 92, 2312–2313. [Google Scholar] [CrossRef]

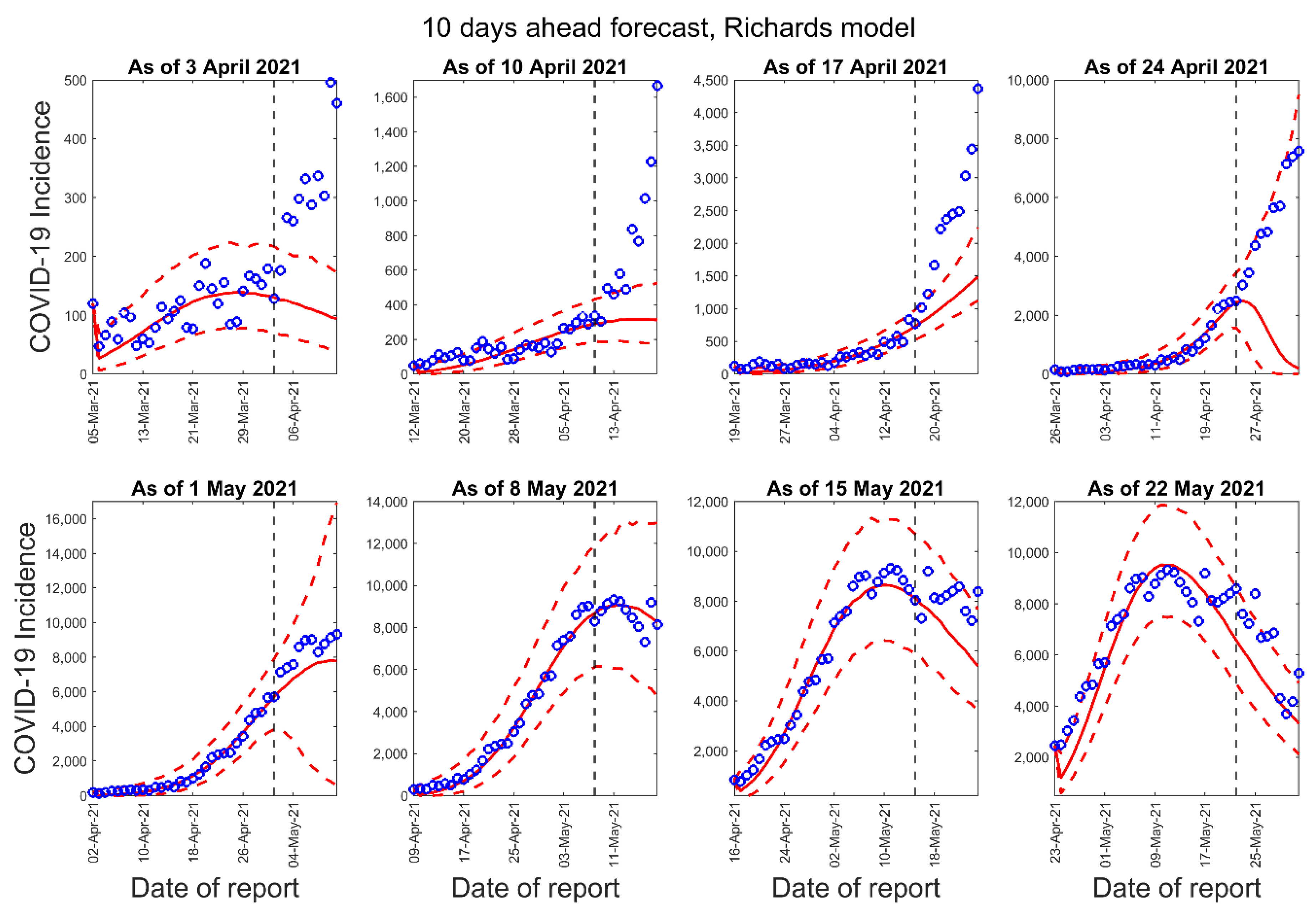
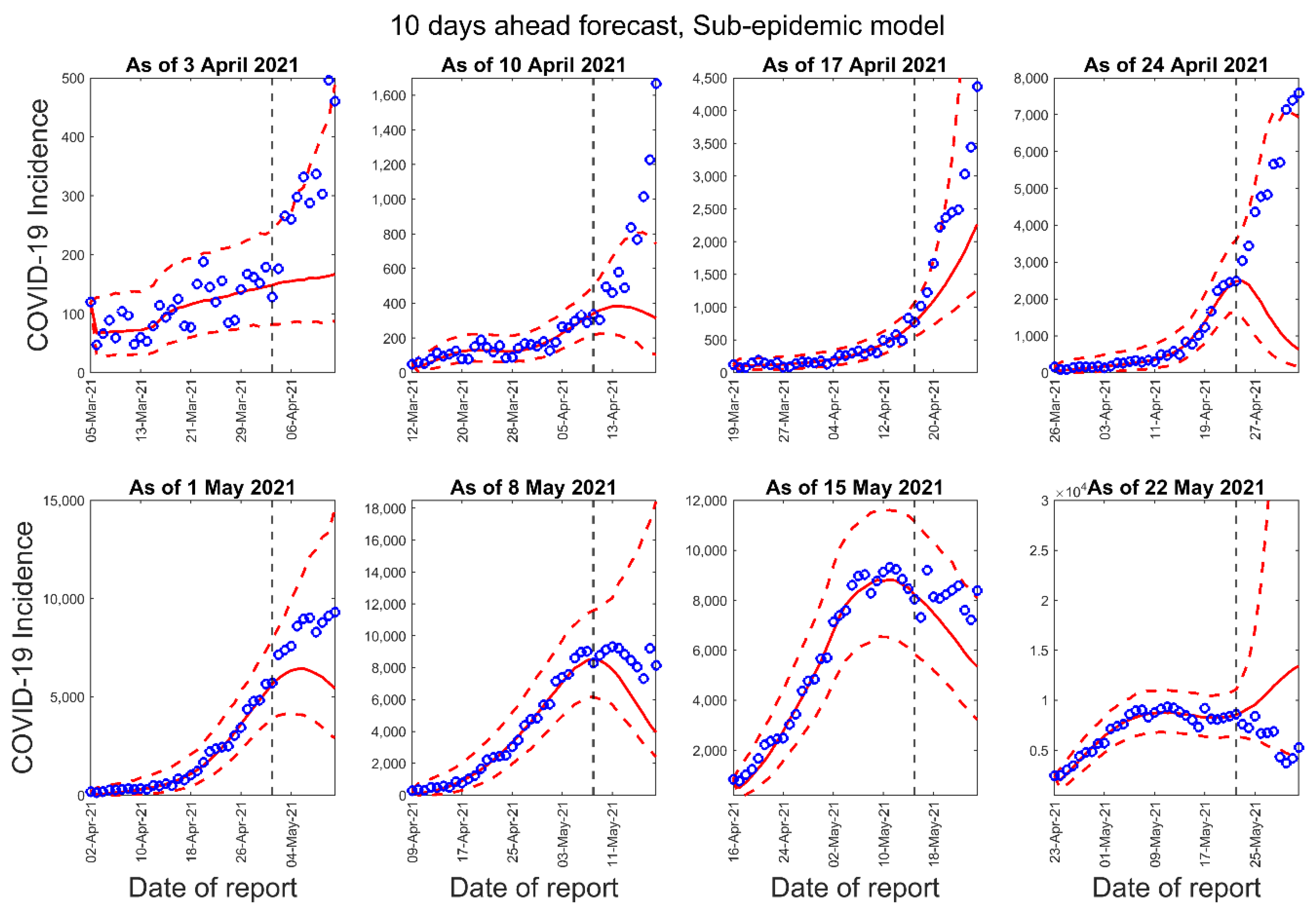


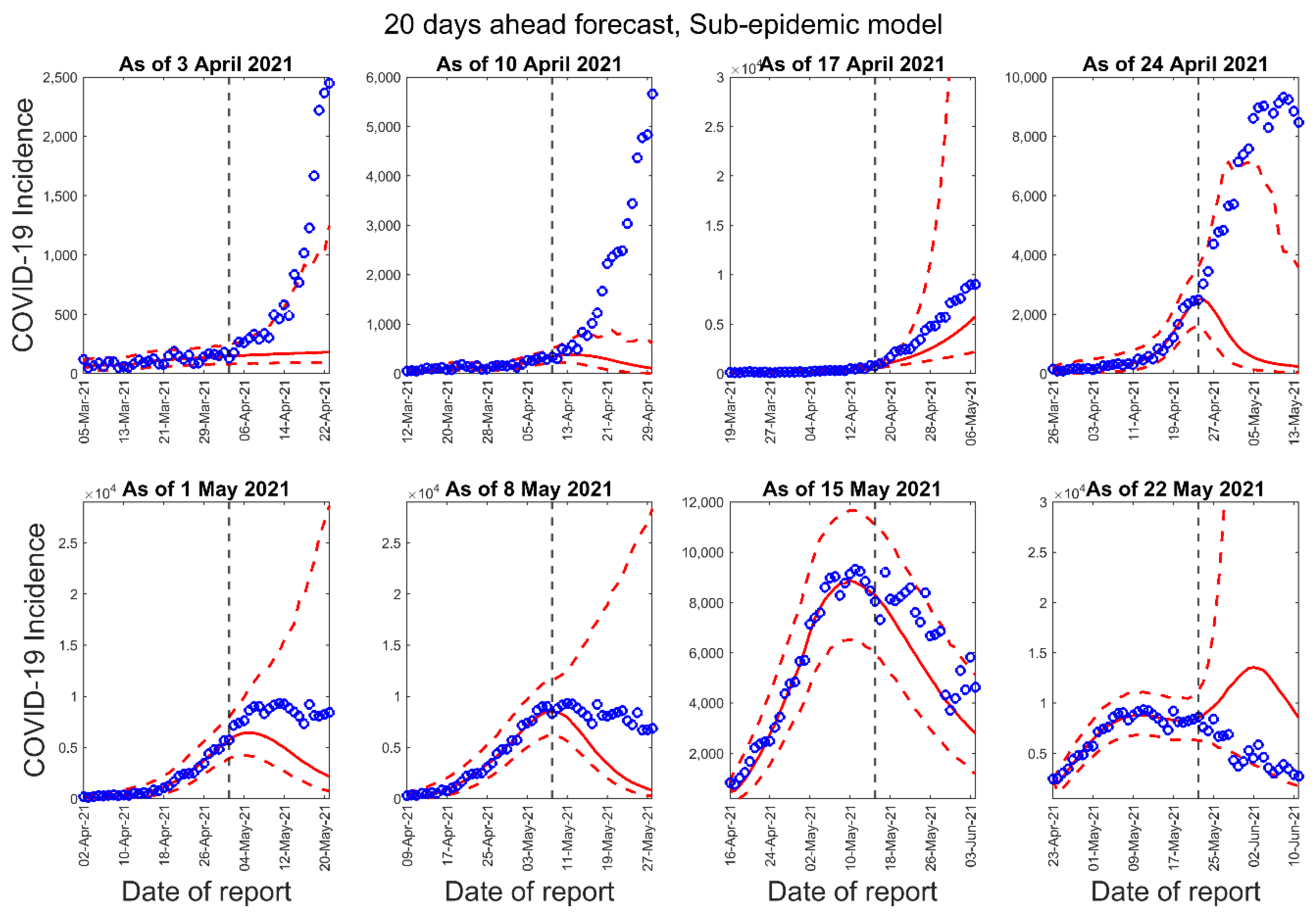



| Forecast Number | Calibration Period for the GLM, Richards, and Sub-Epidemic Model | Number of Days in the Calibration Period | Forecast Period for 10-Days Ahead Forecast | Forecast Period for 20-Days Ahead Forecast |
|---|---|---|---|---|
| 1 | 5 March 2021–3 April 2021 | 30 | 4 April 2021–13 April 2021 | 4 April 2021–23 April 2021 |
| 2 | 12 March 2021–10 April 2021 | 30 | 11 April 2021–20 April 2021 | 11 April 2021–30 April 2021 |
| 3 | 19 March 2021–17 April 2021 | 30 | 18 April 2021–27 April 2021 | 18 April 2021–7 May 2021 |
| 4 | 26 March 2021–24 April 2021 | 30 | 25 April 2021–4 May 2021 | 25 April 2021–14 May 2021 |
| 5 | 2 April 2021–1 May 2021 | 30 | 2 May 2021–11 May 2021 | 2 May 2021–21 May 2021 |
| 6 | 9 April 2021–8 May 2021 | 30 | 9 May 2021–18 May 2021 | 9 May 2021–28 May 2021 |
| 7 | 16 April 2021–15 May 2021 | 30 | 16 May 2021–25 May 2021 | 16 May 2021–4 June 2021 |
| 8 | 23 April 2021–22 May 2021 | 30 | 23 May 2021–June 1 2021 | 23 May 2021–11 June 2021 |
| 3 April 2021 | 10 April 2021 | 17 April 2021 | 24 April 2021 | 1 May 2021 | 8 May 2021 | 15 May 2021 | 22 May 2021 | |
|---|---|---|---|---|---|---|---|---|
| RMSE | ||||||||
| GLM | 183.77 | 580.17 | 1.51 × 103 | 1.57 × 103 | 2.41 × 103 | 805.31 | 1.93 × 103 | 1.23 × 103 |
| Richards | 228.92 | 615.59 | 1.51 × 103 | 4.68 × 103 | 1.13 × 103 | 580.1 | 1.61 × 103 | 1.68 × 103 |
| Sub-epidemic | 184.21 | 591.12 | 1.07 × 103 | 4.44 × 103 | 2.41 × 103 | 2.64 × 103 | 1.68 × 103 | 6.03 × 103 |
| MAE | ||||||||
| GLM | 163.17 | 446.36 | 1.32 × 103 | 1.28 × 103 | 2.23 × 103 | 549.5 | 1.74 × 103 | 891.01 |
| Richards | 206.49 | 472.57 | 1.31 × 103 | 4.02 × 103 | 1.09 × 103 | 425.69 | 1.47 × 103 | 1.44 × 103 |
| Sub-epidemic | 163.14 | 431.97 | 934.05 | 3.88 × 103 | 2.26 × 103 | 2.30 × 103 | 1.53 × 103 | 5.18 × 103 |
| MIS | ||||||||
| GLM | 3.34 × 103 | 1.30 × 104 | 3.18 × 104 | 7.35 × 102 | 1.12 × 104 | 1.06 × 104 | 6.14 × 103 | 7.67 × 103 |
| Richards | 5.37 × 103 | 1.26 × 104 | 3.44 × 104 | 5.80 × 103 | 1.02 × 104 | 7.12 × 103 | 7.37 × 103 | 1.18 × 104 |
| Sub-epidemic | 5.97 × 103 | 7.06 × 103 | 3.40 × 103 | 9.49 × 103 | 7.76 × 103 | 1.01 × 104 | 6.25 × 103 | 4.96 × 104 |
| PI-Coverage | ||||||||
| GLM | 10 | 10 | 10 | 100 | 100 | 100 | 90 | 80 |
| Richards | 10 | 30 | 10 | 100 | 100 | 100 | 90 | 60 |
| Sub-epidemic | 80 | 60 | 90 | 80 | 100 | 100 | 90 | 70 |
| WIS | ||||||||
| GLM | 132.41 | 401.63 | 1.12 × 103 | 625.49 | 1.22 × 103 | 600.13 | 1.05 × 103 | 625.39 |
| Richards | 179.84 | 412.37 | 1.13 × 103 | 2.88 × 103 | 723.83 | 440.77 | 919.38 | 9.74 × 102 |
| Sub-epidemic | 114.41 | 341.45 | 538.37 | 2.74 × 103 | 1.33 × 103 | 1.37 × 103 | 8.97 × 102 | 3.30 × 103 |
| 3 April 2021 | 10 April 2021 | 17 April 2021 | 24 April 2021 | 1 May 2021 | 8 May 2021 | 15 May 2021 | 22 May 2021 | |
|---|---|---|---|---|---|---|---|---|
| RMSE | ||||||||
| GLM | 985.56 | 2.39 × 103 | 3.65 × 103 | 3.80 × 103 | 4.03 × 103 | 2.37 × 103 | 2.08 × 103 | 1.11 × 103 |
| Richards | 1.06 × 103 | 2.50 × 103 | 3.81 × 103 | 7.07 × 103 | 1.18 × 103 | 937.85 | 1.57 × 103 | 1.68 × 103 |
| Sub-epidemic | 988.99 | 2.57 × 103 | 2.28 × 103 | 6.80 × 103 | 3.97 × 103 | 4.54 × 103 | 1.69 × 103 | 7.00 × 103 |
| MAE | ||||||||
| GLM | 673.39 | 1.79 × 103 | 3.06 × 103 | 3.18 × 103 | 3.65 × 103 | 1.85 × 103 | 1.88 × 103 | 898.59 |
| Richards | 745.56 | 1.87 × 103 | 3.16 × 103 | 6.42 × 103 | 1.08 × 103 | 739.33 | 1.39 × 103 | 1.50 × 103 |
| Sub-epidemic | 675.72 | 1.90 × 103 | 1.96 × 103 | 6.20 × 103 | 3.65 × 103 | 4.06 × 103 | 1.49 × 103 | 6.47 × 103 |
| MIS | ||||||||
| GLM | 2.34 × 103 | 6.56 × 104 | 7.29 × 104 | 2.60 × 104 | 2.41 × 104 | 1.65 × 104 | 6.27 × 103 | 5.89 × 103 |
| Richards | 2.69 × 104 | 6.67 × 104 | 9.18 × 104 | 9.11 × 103 | 1.78 × 104 | 7.67 × 103 | 7.37 × 103 | 1.47 × 104 |
| Sub-epidemic | 1.07 × 103 | 6.07 × 104 | 2.44 × 104 | 7.86 × 104 | 1.38 × 104 | 1.64 × 104 | 6.02 × 103 | 3.81 × 105 |
| PI-Coverage | ||||||||
| GLM | 5 | 5 | 5 | 100 | 100 | 100 | 95 | 85 |
| Richards | 5 | 10 | 5 | 95 | 100 | 100 | 85 | 45 |
| Sub-epidemic | 45 | 30 | 95 | 35 | 100 | 100 | 90 | 85 |
| WIS | ||||||||
| GLM | 639.32 | 1.73 × 103 | 2.60 × 103 | 1.64 × 103 | 2.19 × 103 | 1.17 × 103 | 1.14 × 103 | 575.45 |
| Richards | 719.45 | 1.79 × 103 | 2.78 × 103 | 4.93 × 103 | 895.16 | 534.59 | 899.52 | 1.05 × 103 |
| Sub-epidemic | 556.18 | 1.75 × 103 | 1.16 × 103 | 4.98 × 103 | 2.32 × 103 | 2.77 × 103 | 9.12 × 102 | 7.12 × 103 |
| Region | Reproduction Number (95% CI) | Growth Rate (95% CI) | Deceleration of Growth Parameter (95% CI) |
|---|---|---|---|
| National | 1.3 (1.3, 1.3) | 7.9 (5.8, 11) | 0.61 (0.58, 0.64) |
| Province 1 | 1.5 (1.4, 1.6) | 1.2 (0.77, 1.8) | 0.72 (0.67, 0.79) |
| Province 2 | 1.3 (1.2, 1.3) | 3.1 (2.1, 4.4) | 0.58 (0.53, 0.63) |
| Bagmati | 1.3 (1.3, 1.4) | 6.6 (4.0, 9.7) | 0.61 (0.56, 0.66) |
| Gandaki | 1.5 (1.3, 1.8) | 1.2 (0.53, 2.2) | 0.73 (0.63, 0.84) |
| Lumbini | 1.2 (1.2, 1.3) | 8.7 (4.1, 16) | 0.53 (0.46, 0.61) |
| Karnali | 1.2 (1.1, 1,4) | 6.1 (1.4, 15) | 0.51 (0.36, 0.68) |
| Sudurpaschim | 1.5 (1.3, 1.7) | 1.3 (0.59, 2.4) | 0.71 (0.61, 0.82) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dahal, S.; Luo, R.; Subedi, R.K.; Dhimal, M.; Chowell, G. Transmission Dynamics and Short-Term Forecasts of COVID-19: Nepal 2020/2021. Epidemiologia 2021, 2, 639-659. https://doi.org/10.3390/epidemiologia2040043
Dahal S, Luo R, Subedi RK, Dhimal M, Chowell G. Transmission Dynamics and Short-Term Forecasts of COVID-19: Nepal 2020/2021. Epidemiologia. 2021; 2(4):639-659. https://doi.org/10.3390/epidemiologia2040043
Chicago/Turabian StyleDahal, Sushma, Ruiyan Luo, Raj Kumar Subedi, Meghnath Dhimal, and Gerardo Chowell. 2021. "Transmission Dynamics and Short-Term Forecasts of COVID-19: Nepal 2020/2021" Epidemiologia 2, no. 4: 639-659. https://doi.org/10.3390/epidemiologia2040043
APA StyleDahal, S., Luo, R., Subedi, R. K., Dhimal, M., & Chowell, G. (2021). Transmission Dynamics and Short-Term Forecasts of COVID-19: Nepal 2020/2021. Epidemiologia, 2(4), 639-659. https://doi.org/10.3390/epidemiologia2040043









