Ticks on the Run: A Mathematical Model of Crimean-Congo Haemorrhagic Fever (CCHF)—Key Factors for Transmission
Abstract
:1. Introduction
- 1.
- What are the driving factors in CCHF transmission?
- 2.
- What critical density of ticks is necessary for a potential outbreak?
- 3.
- How to characterise the nature of CCHFV dissemination in the endemic areas?
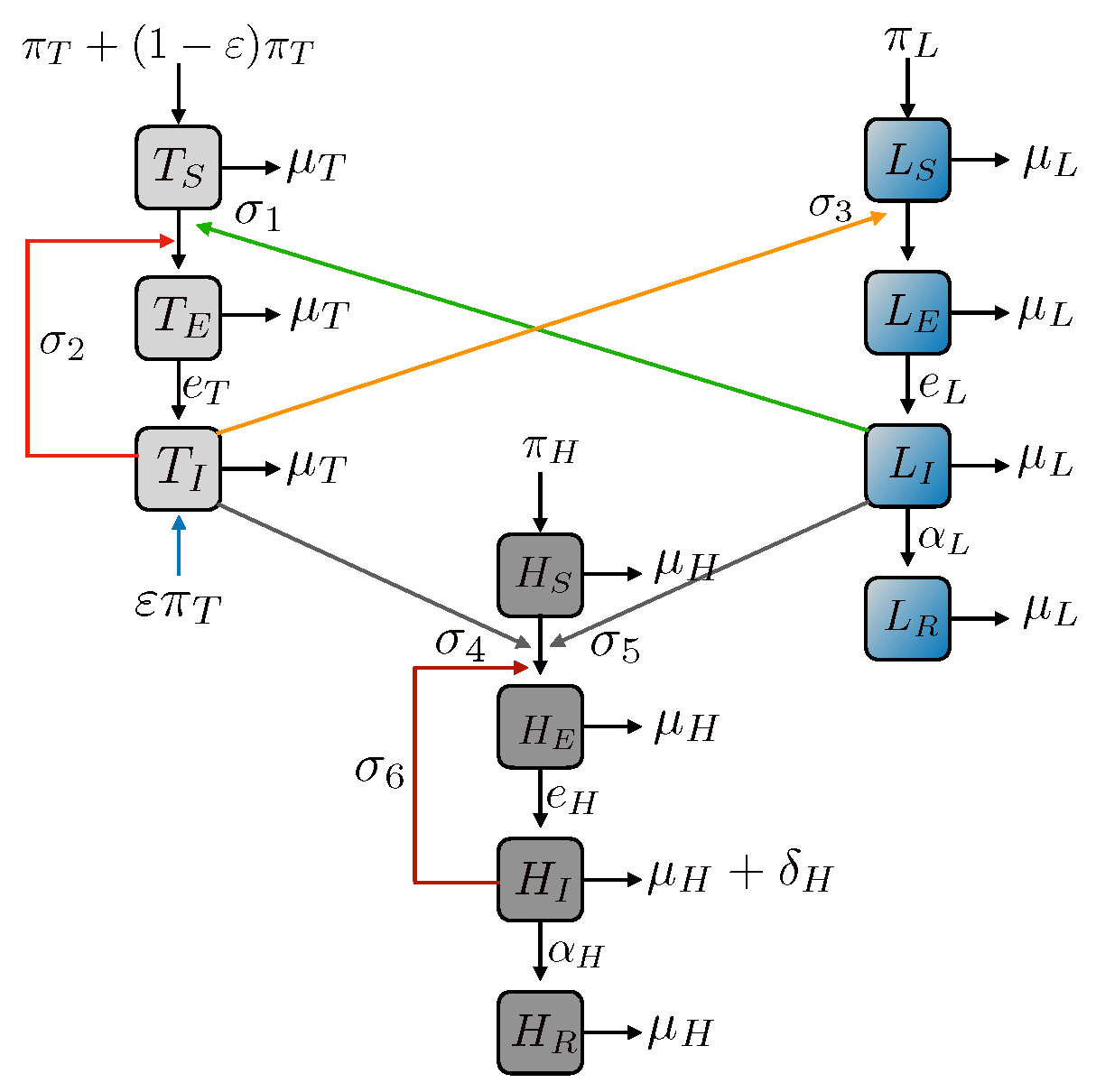
2. Model Formulations in Different Geographic Distributions
2.1. Inclusion of Human-to-Human Transmission
2.2. Tick-Human Model
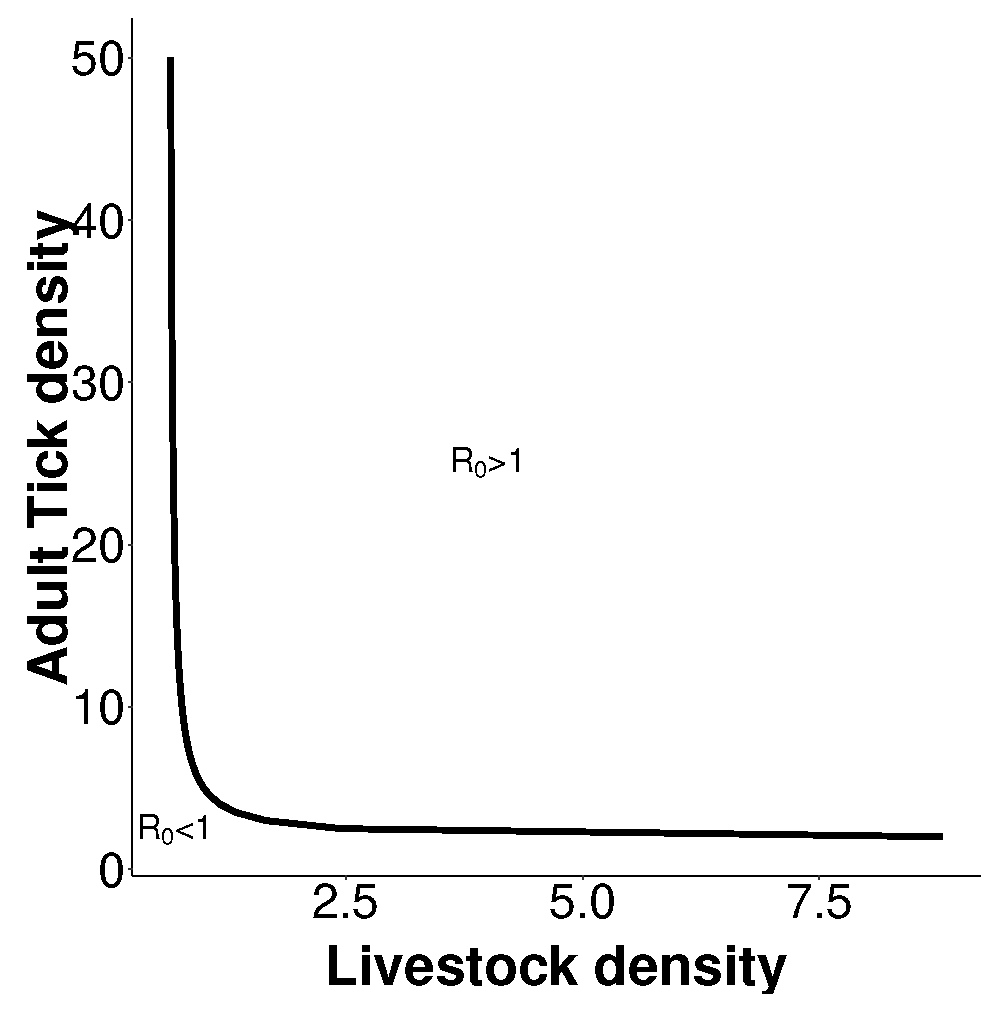
3. Basic Reproduction Number
4. Dynamics of the Model
5. Control Strategies in Different Geographic Locations
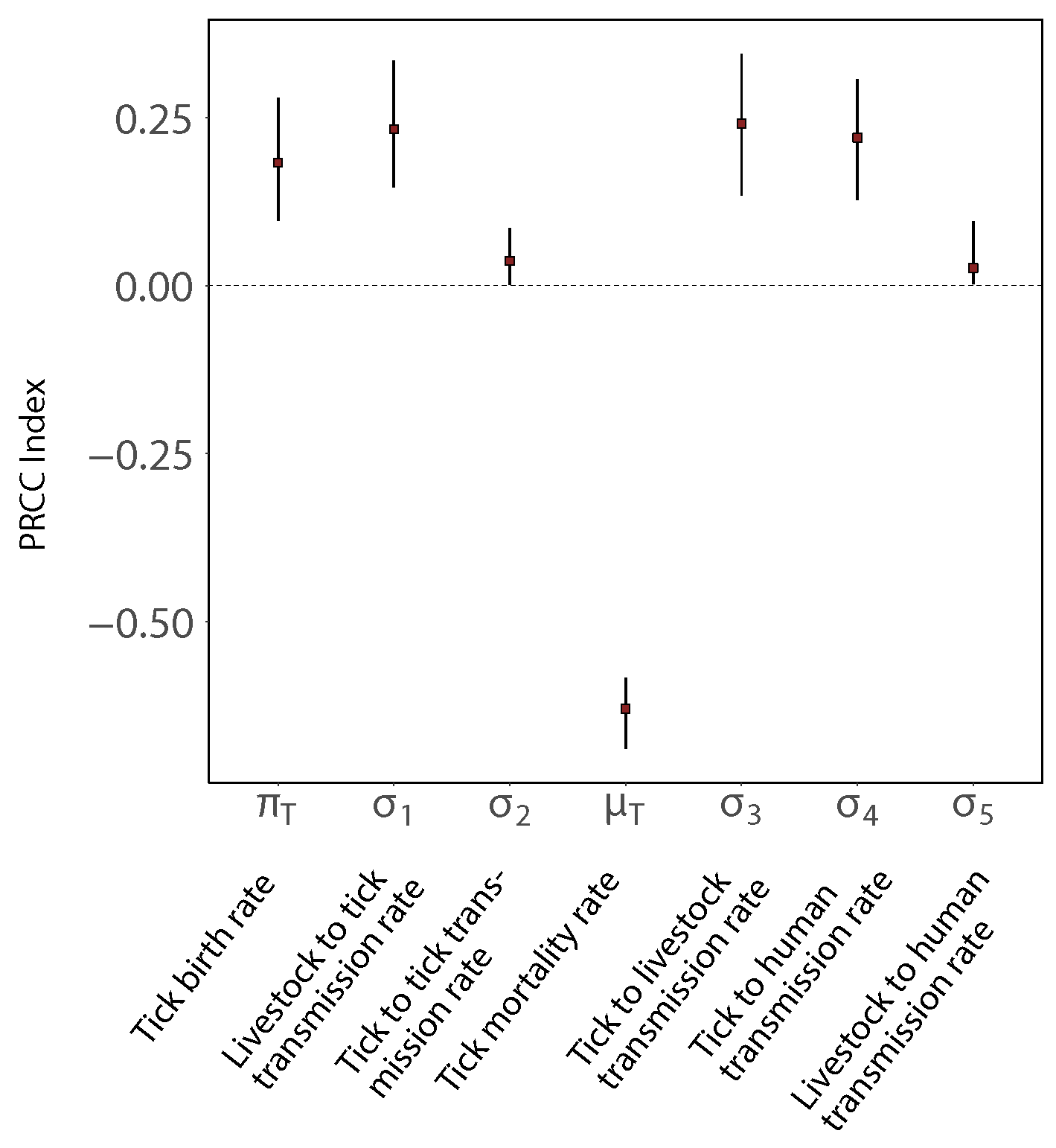
6. Sensitivity Analysis
Model Sensitivity Analysis
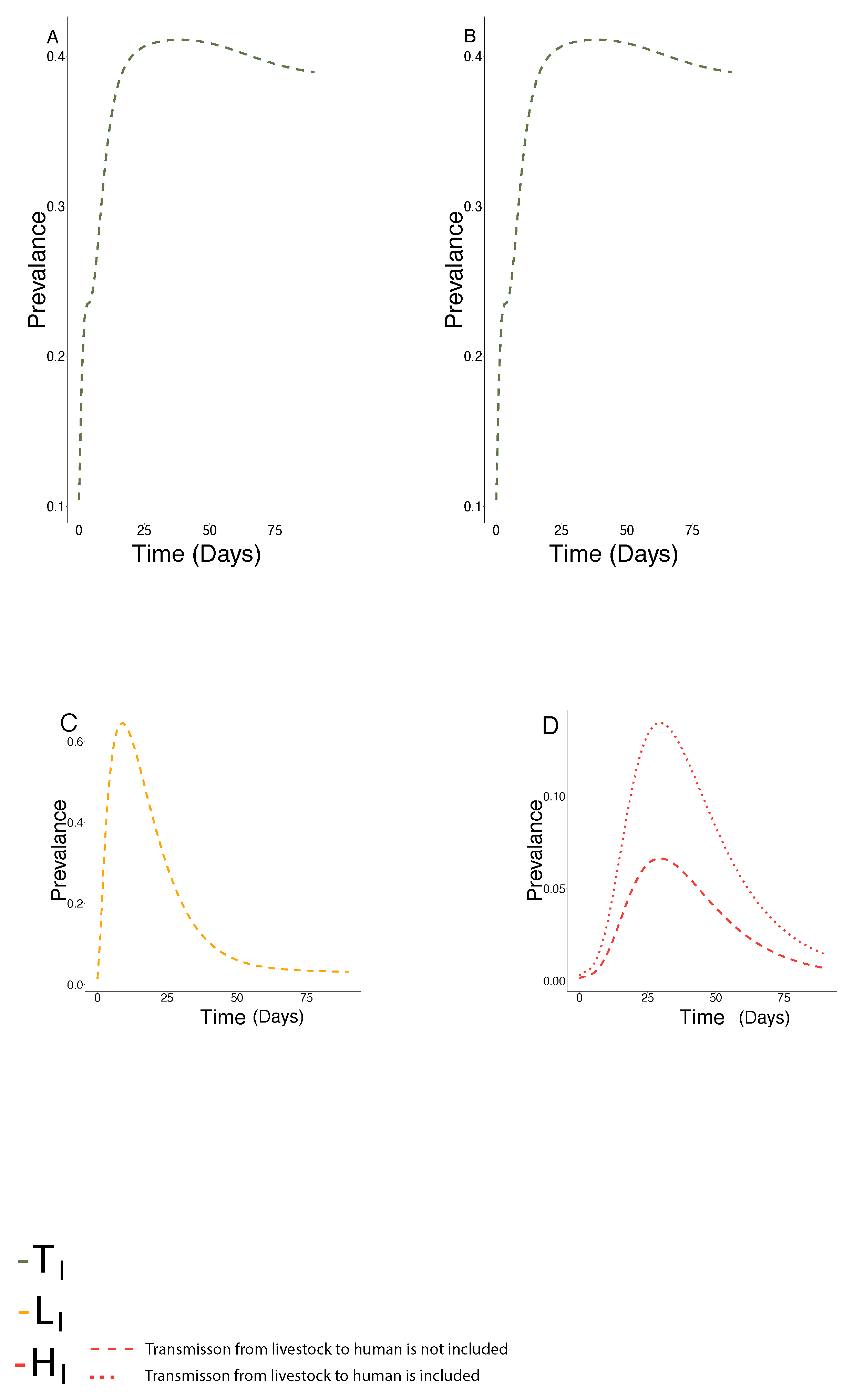
7. Fitting the Model to Outbreak Data
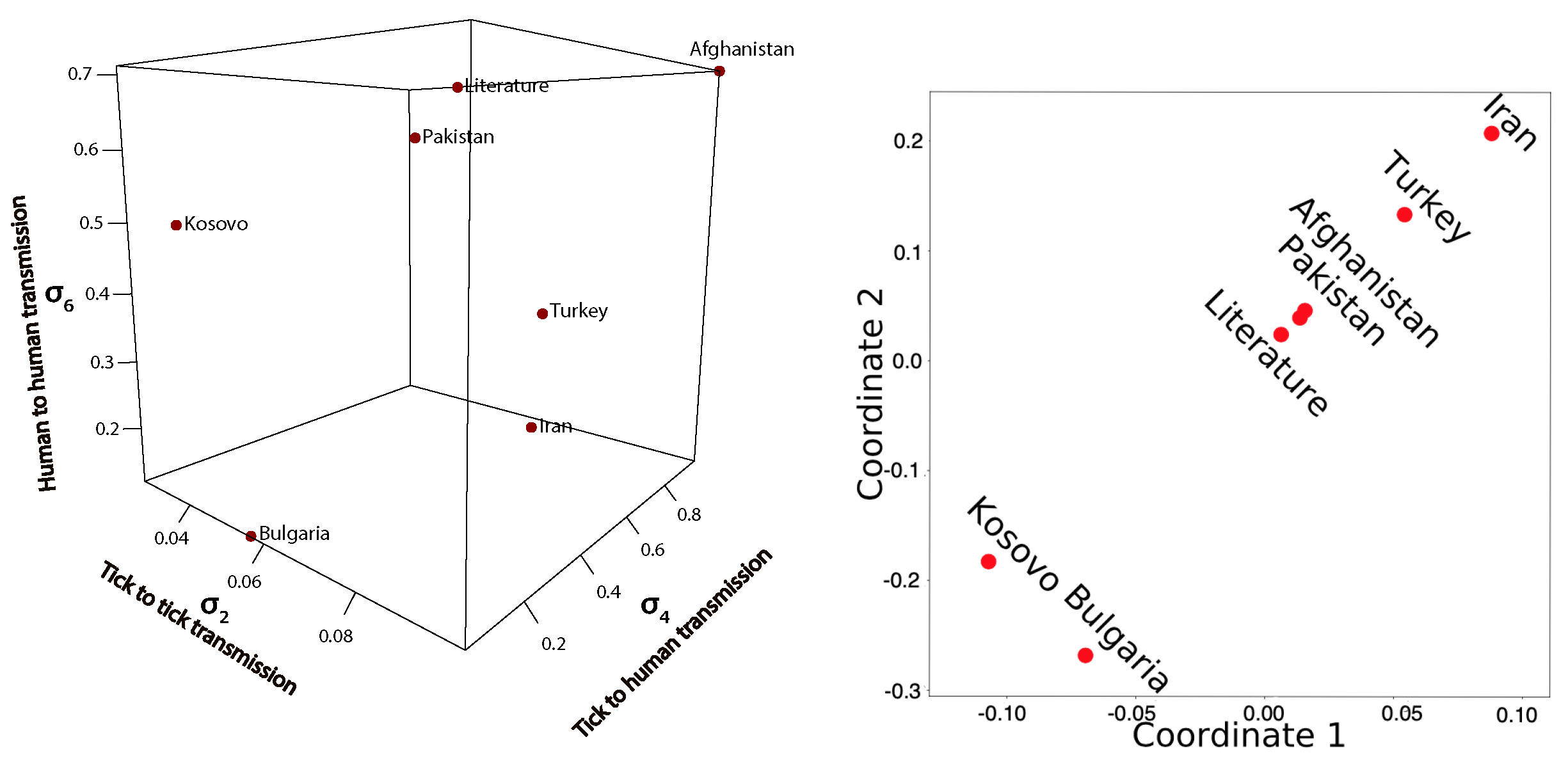
Comparison of Fitted Transmission Parameters
8. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Messina, J.P.; Pigott, D.M.; Golding, N.; Duda, K.A.; Brownstein, J.S.; Weiss, D.J.; Gibson, H.; Robinson, T.P.; Gilbert, M.; William Wint, G.R.; et al. The global distribution of Crimean-Congo hemorrhagic fever. Trans. R. Soc. Trop. Med. Hyg. 2015, 109, 503–513. [Google Scholar] [CrossRef] [PubMed]
- Gargili, A.; Estrada-Peña, A.; Spengler, J.R.; Lukashev, A.; Nuttall, P.A.; Bente, D.A. The role of ticks in the maintenance and transmission of Crimean-Congo hemorrhagic fever virus: A review of published field and laboratory studies. Antivir. Res. 2017, 144, 93–119. [Google Scholar] [CrossRef] [PubMed]
- Chumakov, M. A New Tick-Borne Virus Disease—Crimean Hemorrhagic Fever; Izd Otd Primorskoi Armii: Moscow, Russia, 1945. [Google Scholar]
- Woodall, J.; Williams, M.; Simpson, D.; Ardoin, P.; Lule, M.; West, R. The Congo group of agents. Rep. E Afr. Virus Res. Inst. (1963–1964) 1965, 14, 34–36. [Google Scholar]
- Chinikar, S.; Ghiasi, S.; Hewson, R.; Moradi, M.; Haeri, A. Crimean-Congo hemorrhagic fever in Iran and neighboring countries. J. Clin. Virol. 2010, 47, 110–114. [Google Scholar] [CrossRef] [PubMed]
- International Committee on Taxonomy of Viruses. 2018. Available online: https://talk.ictvonline.org/taxonomy/ (accessed on 11 August 2020).
- Spengler, J.R.; Estrada-Peña, A. Host preferences support the prominent role of Hyalomma ticks in the ecology of Crimean-Congo hemorrhagic fever. PLoS Neglected Trop. Dis. 2018, 12, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Matser, A.; Hartemink, N.; Heesterbeek, H.; Galvani, A.; Davis, S. Elasticity analysis in epidemiology: An application to tick-borne infections. Ecol. Lett. 2009, 12, 1298–1305. [Google Scholar] [CrossRef]
- Logan, T.M.; Linthicum, K.J.; Bailey, C.L.; Watts, D.M.; Moulton, J.R. Experimental Transmission of Crimean-Congo Hemorrhagic Fever Virus by Hyalomma Truncatum Koch. Am. J. Trop. Med. Hyg. 1989, 40, 207–212. [Google Scholar] [CrossRef]
- Gonzalez, J.; Camicas, J.; Cornet, J.; Faye, O.; Wilson, M. Sexual and transovarian transmission of Crimean-Congo haemorrhagic fever virus in Hyalomma truncatum ticks. Res. Virol. 1992, 143, 23–28. [Google Scholar] [CrossRef]
- WHO. World Health Organisation. Available online: http://applications.emro.who.int/docs/epi/2018/Epi_Monitor_2018_11_26.pdf?ua=1 (accessed on 2 May 2020).
- Zhang, Y.; Shen, S.; Fang, Y.; Liu, J.; Su, Z.; Liang, J.; Zhang, Z.; Wu, Q.; Wang, C.; Abudurexiti, A.; et al. Isolation, Characterization, and Phylogenetic Analysis of Two New Crimean-Congo Hemorrhagic Fever Virus Strains from the Northern Region of Xinjiang Province, China. Virol. Sin. 2018, 33, 74–86. [Google Scholar] [CrossRef]
- Sas, M.A.; Vina-Rodriguez, A.; Mertens, M.; Eiden, M.; Emmerich, P.; Chaintoutis, S.C.; Mirazimi, A.; Groschup, M.H. A one-step multiplex real-time RT-PCR for the universal detection of all currently known CCHFV genotypes. J. Virol. Methods 2018, 255, 38–43. [Google Scholar] [CrossRef]
- Estrada-Peña, A.; Vatansever, Z.; Gargili, A.; Ergönul, Ö. The trend towards habitat fragmentation is the key factor driving the spread of Crimean-Congo haemorrhagic fever. Epidemiol. Infect. 2010, 138, 1194–1203. [Google Scholar] [CrossRef] [PubMed]
- Atif, M.; Saqib, A.; Ikram, R.; Sarwar, M.R.; Scahill, S. The reasons why Pakistan might be at high risk of Crimean Congo haemorrhagic fever epidemic; a scoping review of the literature. Virol. J. 2017, 14, 63. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bente, D.A.; Forrester, N.L.; Watts, D.M.; McAuley, A.J.; Whitehouse, C.A.; Bray, M. Crimean-Congo hemorrhagic fever: History, epidemiology, pathogenesis, clinical syndrome and genetic diversity. Antivir. Res. 2013, 100, 159–189. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Spengler, J.R.; Bergeron, É.; Rollin, P.E. Seroepidemiological Studies of Crimean-Congo Hemorrhagic Fever Virus in Domestic and Wild Animals. PLoS Neglected Trop. Dis. 2016, 10, e0004210. [Google Scholar] [CrossRef] [Green Version]
- Schuster, I.; Mertens, M.; Mrenoshki, S.; Staubach, C.; Mertens, C.; Brüning, F.; Wernike, K.; Hechinger, S.; Berxholi, K.; Mitrov, D.; et al. Sheep and goats as indicator animals for the circulation of CCHFV in the environment. Exp. Appl. Acarol. 2016, 68, 337–346. [Google Scholar] [CrossRef] [Green Version]
- Hoch, T.; Breton, E.; Vatansever, Z. Dynamic Modeling of Crimean Congo Hemorrhagic Fever Virus (CCHFV) Spread to Test Control Strategies. J. Med Entomol. 2018, 55, 1124–1132. [Google Scholar] [CrossRef] [Green Version]
- Papa, A.; Maltezou, H.C.; Tsiodras, S.; Dalla, V.G.; Papadimitriou, T.; Pierroutsakos, I.; Kartalis, G.N.; Antoniadis, A. A case of Crimean-Congo haemorrhagic fever in Greece. Eurosurveillance 2008, 13, 843–847. [Google Scholar] [CrossRef] [Green Version]
- Pascucci, I.; Domenico, M.D.; Dondona, G.C.; Gennaro, A.D.; Polci, A.; Dondona, A.C.; Mancuso, E.; Cammà, C.; Savini, G.; Cecere, J.G.; et al. Assessing the role of migratory birds in the introduction of ticks and tick-borne pathogens from African countries: An Italian experience. Ticks Tick-Borne Dis. 2019, 10, 101272. [Google Scholar] [CrossRef]
- Jameson, L.J.; Medlock, J.M. Results of HPA tick surveillance in Great Britain. Vet. Rec. 2009, 165, 154. [Google Scholar] [CrossRef]
- Chitimia-Dobler, L.; Schaper, S.; Rieß, R.; Bitterwolf, K.; Frangoulidis, D.; Bestehorn, M.; Springer, A.; Oehme, R.; Drehmann, M.; Lindau, A.; et al. Imported Hyalomma ticks in Germany in 2018. Parasites Vectors 2019, 12, 134. [Google Scholar] [CrossRef] [Green Version]
- Estrada-Peña, A.; D’Amico, G.; Fernández-Ruiz, N. Modelling the potential spread of Hyalomma marginatum ticks in Europe by migratory birds. Int. J. Parasitol. 2021, 51, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Spengler, J.R.; Bergeron, É.; Spiropoulou, C.F. Crimean-Congo hemorrhagic fever and expansion from endemic regions. Curr. Opin. Virol. 2019, 34, 70–78. [Google Scholar] [CrossRef] [PubMed]
- Oehme, R.; Bestehorn, M.; Wölfel, S.; Chitimia-Dobler, L. Hyalomma marginatum in Tübingen, Germany. Syst. Appl. Acarol. 2017, 22, 1–6. [Google Scholar] [CrossRef]
- Hansford, K.M.; Carter, D.; Gillingham, E.L.; Hernandez-Triana, L.M.; Chamberlain, J.; Cull, B.; McGinley, L.; Phipps, L.P.; Medlock, J.M. Hyalomma rufipes on an untraveled horse: Is this the first evidence of Hyalomma nymphs successfully moulting in the United Kingdom? Ticks Tick-Borne Dis. 2019, 10, 704–708. [Google Scholar] [CrossRef] [PubMed]
- Okely, M.; Anan, R.; Gad-Allah, S.; Samy, A.M. Mapping the environmental suitability of etiological agent and tick vectors of Crimean-Congo Hemorrhagic Fever. Acta Tropica 2019, 203, 105319. [Google Scholar] [CrossRef] [PubMed]
- Switkes, J.; Nannyonga, B.; Mugisha, J.; Nakakawa, J. A mathematical model for Crimean-Congo haemorrhagic fever: Tick-borne dynamics with conferred host immunity. J. Biol. Dyn. 2016, 10, 59–70. [Google Scholar] [CrossRef] [Green Version]
- Cooper, B.S. Mathematical Modeling of Crimean-Congo Hemorrhagic Fever Transmission; Springer: Dordrecht, The Netherlands, 2007; Chapter 15; pp. 187–203. [Google Scholar]
- Hoch, T.; Breton, E.; Josse, M.; Deniz, A.; Guven, E.; Vatansever, Z. Identifying main drivers and testing control strategies for CCHFV spread. Exp. Appl. Acarol. 2016, 68, 347–359. [Google Scholar] [CrossRef]
- Al-Abri, S.S.; Abaidani, I.A.; Fazlalipour, M.; Mostafavi, E.; Leblebicioglu, H.; Pshenichnaya, N.; Memish, Z.A.; Hewson, R.; Petersen, E.; Mala, P.; et al. Current status of Crimean-Congo haemorrhagic fever in the World Health Organization Eastern Mediterranean Region: Issues, challenges, and future directions. Int. J. Infect. Dis. 2017, 58, 82–89. [Google Scholar] [CrossRef] [Green Version]
- Belobo, J.T.E.; Kenmoe, S.; Kengne-Nde, C.; Emoh, C.P.D.; Bowo-Ngandji, A.; Tchatchouang, S.; Sowe Wobessi, J.N.; Mbongue Mikangue, C.A.; Tazokong, H.R.; Kingue Bebey, S.R.; et al. Worldwide epidemiology of Crimean-Congo Hemorrhagic Fever Virus in humans, ticks and other animal species, a systematic review and meta-analysis. PLoS Neglected Trop. Dis. 2021, 15, 1–19. [Google Scholar] [CrossRef]
- Bolzoni, L.; Rosà, R.; Cagnacci, F.; Rizzoli, A. Effect of deer density on tick infestation of rodents and the hazard of tick-borne encephalitis. II: Population and infection models. Int. J. Parasitol. 2012, 42, 373–381. [Google Scholar] [CrossRef] [Green Version]
- Rosà, R.; Pugliese, A. Effects of tick population dynamics and host densities on the persistence of tick-borne infections. Math. Biosci. 2007, 208, 216–240. [Google Scholar] [CrossRef] [PubMed]
- Eisen, L.; Lane, R.S. Lyme Borreliosis: Biology, Epidemiology and Control; CABI: Wallingford, UK, 2002. [Google Scholar]
- Rosà, R.; Pugliese, A.; Norman, R.; Hudson, P.J. Thresholds for disease persistence in models for tick-borne infections including non-viraemic transmission, extended feeding and tick aggregation. J. Theor. Biol. 2003, 224, 359–376. [Google Scholar] [CrossRef]
- Hoch, T.; Monnet, Y.; Agoulon, A. Influence of host migration between woodland and pasture on the population dynamics of the tick Ixodes ricinus: A modelling approach. Ecol. Model. 2010, 221, 1798–1806. [Google Scholar] [CrossRef]
- Mpeshe, S.C.; Haario, H.; Tchuenche, J.M. A Mathematical Model of Rift Valley Fever with Human Host. Acta Biotheor. 2011, 59, 231–250. [Google Scholar] [CrossRef]
- Sutton, A.J.; Karagenc, T.; Bakirci, S.; Sarali, H.; Pekel, G.; Medley, G.F. Modelling the transmission dynamics of Theileria annulata: Model structure and validation for the Turkish context. Parasitology 2012, 139, 441–453. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shayan, S.; Bokaean, M.; Shahrivar, M.R.; Chinikar, S. Crimean-Congo Hemorrhagic Fever. Lab. Med. 2015, 46, 180–189. [Google Scholar] [CrossRef] [Green Version]
- Papa, A.; Bino, S.; Llagami, A.; Brahimaj, B.; Papadimitriou, E.; Pavlidou, V.; Velo, E.; Cahani, G.; Hajdini, M.; Pilaca, A.; et al. Crimean-Congo Hemorrhagic Fever in Albania, 2001. Eur. J. Clin. Microbiol. Infect. Dis. 2002, 21, 603–606. [Google Scholar] [CrossRef]
- Kriesel, A.; Meyer, M.; Peterson, G. Mathematical Modeling of Tick-Borne Encephalitis in Humans. J. Undergrad. Res. Minn. State Univ. Mankato 2009, 9, 9. [Google Scholar]
- Mondal, M.K.; Hanif, M.; Biswas, M.H.A. A mathematical analysis for controlling the spread of Nipah virus infection. Int. J. Model. Simul. 2017, 37, 185–197. [Google Scholar] [CrossRef]
- Ergönül, Ö. Crimean-Congo haemorrhagic fever. Lancet Infect. Dis. 2006, 6, 203–214. [Google Scholar] [CrossRef]
- Izadi, S.; Salehi, M.; Holakouie-Naieni, K.; Chinikar, S. The risk of transmission of Crimean-Congo hemorrhagic fever virus from human cases to first-degree relatives. Jpn. J. Infect. Dis. 2008, 61, 494–496. [Google Scholar] [PubMed]
- Pshenichnaya, N.Y.; Sydenko, I.S.; Klinovaya, E.P.; Romanova, E.B.; Zhuravlev, A.S. Possible sexual transmission of Crimean-Congo hemorrhagic fever. Int. J. Infect. Dis. 2016, 45, 109–111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Garrison, A.R.; Smith, D.R.; Golden, J.W. Animal Models for Crimean-Congo Hemorrhagic Fever Human Disease. Viruses 2019, 11, 590. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vorou, R. Crimean-Congo hemorrhagic fever in southeastern Europe. Int. J. Infect. Dis. 2009, 13, 659–662. [Google Scholar] [CrossRef] [Green Version]
- Mourya, D.T.; Yadav, P.D.; Gurav, Y.K.; Pardeshi, P.G.; Shete, A.M.; Jain, R.; Raval, D.D.; Upadhyay, K.J.; Patil, D.Y. Crimean Congo hemorrhagic fever serosurvey in humans for identifying high-risk populations and high-risk areas in the endemic state of Gujarat, India. BMC Infect. Dis. 2019, 19, 104. [Google Scholar] [CrossRef] [Green Version]
- Atkinson, B.; Chamberlain, J.; Jameson, L.J.; Logue, C.H.; Lewis, J.; Belobrova, E.A.; Valikhodzhaeva, M.; Mullojonova, M.; Tishkova, F.H.; Hewson, R. Identification and analysis of Crimean-Congo hemorrhagic fever virus from human sera in Tajikistan. Int. J. Infect. Dis. 2013, 17, e1031–e1037. [Google Scholar] [CrossRef] [Green Version]
- Yilmaz, G.R.; Buzgan, T.; Irmak, H.; Safran, A.; Uzun, R.; Cevik, M.A.; Torunoglu, M.A. The epidemiology of Crimean-Congo hemorrhagic fever in Turkey, 2002–2007. Int. J. Infect. Dis. 2009, 13, 380–386. [Google Scholar] [CrossRef] [Green Version]
- Diekmann, O.; Heesterbeek, J.A.P.; Metz, J.A.J. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990, 28, 365–382. [Google Scholar] [CrossRef] [Green Version]
- van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Ergonul, O.; Battal, I. Potential Sexual Transmission of Crimean-Congo Hemorrhagic Fever Infection. Jpn. J. Infect. Dis. 2014, 67, 137–138. [Google Scholar] [CrossRef] [Green Version]
- Gozel, M.G.; Bakir, M.; Oztop, A.Y.; Engin, A.; Dokmetas, I.; Elaldi, N. Investigation of Crimean-Congo Hemorrhagic Fever Virus Transmission from Patients to Relatives: A Prospective Contact Tracing Study. Am. Soc. Trop. Med. Hyg. 2014, 90, 160–162. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nguyen, A.; Mahaffy, J.; Vaidya, N.K. Modeling transmission dynamics of lyme disease: Multiple vectors, seasonality, and vector mobility. Infect. Dis. Model. 2019, 4, 28–43. [Google Scholar] [CrossRef] [PubMed]
- Heesterbeek, J.; Roberts, M. The type-reproduction number T in models for infectious disease control. Math. Biosci. 2007, 206, 3–10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shuai, Z.; Heesterbeek, J.A.P.; van den Driessche, P. Extending the type reproduction number to infectious disease control targeting contacts between types. J. Math. Biol. 2013, 67, 1067–1082. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Iooss, B.; Saltelli, A. Introduction to Sensitivity Analysis; Springer International Publishing: Cham, Switzerland, 2017; Chapter 26; pp. 1103–1122. [Google Scholar]
- Iooss, B.; Janon, A.; Pujol, G.; Boumhaout, k.; Veiga, S.D.; Delage, T.; Fruth, J.; Gilquin, L.; Guillaume, J.; Le Gratiet, L.; et al. Sensitivity: Global Sensitivity Analysis of Model Outputs. 2018. Available online: https://cran.r-project.org/web/packages/sensitivity/sensitivity.pdf (accessed on 2 May 2020).
- Carnell, R. lhs: Latin Hypercube Samples. 2019. Available online: https://cran.r-project.org/web/packages/lhs/index.html (accessed on 3 April 2020).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- MATLAB. Version 9.6 (R2019a); The MathWorks Inc.: Natick, MA, USA, 2019.
- Fajs, L.; Humolli, I.; Saksida, A.; Knap, N.; Jelovšek, M.; Korva, M.; Dedushaj, I.; Avšič, T. Prevalence of Crimean-Congo Hemorrhagic Fever Virus in Healthy Population, Livestock and Ticks in Kosovo. PLoS ONE 2014, 9, 1–6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Service, U.F.A. USDA Foreign Agricultural Service. Available online: https://apps.fas.usda.gov/newgainapi/api/report/ (accessed on 3 April 2020).
- Kamalzadeh, A.; Rajabbaigy, M.; Kiasat, A. Livestock production systems and trends in livestock Industry in Iran. J. Agric. Soc. Sci. 2008, 4, 1813–223504. [Google Scholar]
- Food and Agriculture Organization of the United Nations. Available online: http://www.fao.org/ag/againfo/resources/en/publications/sector_briefs/lsb_TUR.pdf (accessed on 4 May 2020).
- Estrada-Peña, A.; Ruiz-Fons, F.; Acevedo, P.; Gortazar, C.; de la Fuente, J. Factors driving the circulation and possible expansion of Crimean–Congo haemorrhagic fever virus in the western Palearctic. J. Appl. Microbiol. 2013, 114, 278–286. [Google Scholar] [CrossRef] [Green Version]
- Kasi, K.K.; Sas, M.A.; Sauter-Louis, C.; von Arnim, F.; Gethmann, J.M.; Schulz, A.; Wernike, K.; Groschup, M.H.; Conraths, F.J. Epidemiological investigations of Crimean-Congo haemorrhagic fever virus infection in sheep and goats in Balochistan, Pakistan. Ticks Tick-Borne Dis. 2020, 11, 101324. [Google Scholar] [CrossRef]
- Leblebicioglu, H.; Sunbul, M.; Memish, Z.A.; Al-Tawfiq, J.A.; Bodur, H.; Ozkul, A.; Gucukoglu, A.; Chinikar, S.; Hasan, Z. Consensus report: Preventive measures for Crimean-Congo Hemorrhagic Fever during Eid-al-Adha festival. Int. J. Infect. Dis. 2015, 38, 9–15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abbas, T.; Xu, Z.; Younus, M.; Qayyum, A.; Riaz, M.T. Seasonality in hospital admissions of Crimean-Congo hemorrhagic fever and its dependence on ambient temperature—Empirical evidence from Pakistan. Int. J. Biometeorol. 2017, 61, 1893–1897. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.A.P.; Roberts, M.G. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface. 2010, 7, 873–885. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baghi, H.B.; Aghazadeh, M. Include Crimean-Congo haemorrhagic fever virus prevention in pre-travel advice. Travel Med. Infect Dis. 2016, 14, 634–635. [Google Scholar] [CrossRef] [PubMed]
- Hegde, N. Livestock Development for Sustainable Livelihood of Small Farmers. Asian J. Anim. Vet. Adv. 2019, 3, 1–17. [Google Scholar]

| Parameter | Description | Value or Range | Units | References |
|---|---|---|---|---|
| Birth rate of livestock population | Livestock/Time | [39] | ||
| Birth rate of human population | Human/Time | [39] | ||
| Birth rate of tick population | Tick/Time | [40] | ||
| Death term of livestock population | 1/Time | [39] | ||
| Death term of human population | 1/Time | [39] | ||
| Incubation period in tick | Time | [8,41] | ||
| Incubation period in livestock | Time | [8] | ||
| Incubation period in human | Time | [41] | ||
| Proportion of hatched infected ticks | Number | [43] | ||
| Recovery period of livestock | Time | [19] | ||
| Recovery period of the human population | Time | [41,42] | ||
| Transmission parameter: livestock to tick | Number | [43] | ||
| Transmission parameter: tick to tick | Number | [8] | ||
| Transmission parameter: tick to livestock | Number | [43] | ||
| Transmission parameter: tick to human | Number | [43] | ||
| Transmission parameter: livestock to human | Number | [39] | ||
| Transmission parameter: human to human | Number | [46] | ||
| CCHF-induced death | 1/Time | [18,41] | ||
| Mean number of eggs | Number | [8] | ||
| Strength of density-dependence in birth rate | 1/Tick Time | [34,35] | ||
| Detachment rate of tick | 1/Time | [8] | ||
| Contribution of the rodent population | Number | [35] | ||
| Contribution of the livestock population | Number | [35] | ||
| Transmission efficiency: livestock to tick | Number | [8] | ||
| Duration of the infective period | Time | [8] | ||
| Duration of attachment | Time | [8] | ||
| Rate of the average number of ticks feeding on livestock | Ticks/Time | [8] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhowmick, S.; Kasi, K.K.; Gethmann, J.; Fischer, S.; Conraths, F.J.; Sokolov, I.M.; Lentz, H.H.K. Ticks on the Run: A Mathematical Model of Crimean-Congo Haemorrhagic Fever (CCHF)—Key Factors for Transmission. Epidemiologia 2022, 3, 116-134. https://doi.org/10.3390/epidemiologia3010010
Bhowmick S, Kasi KK, Gethmann J, Fischer S, Conraths FJ, Sokolov IM, Lentz HHK. Ticks on the Run: A Mathematical Model of Crimean-Congo Haemorrhagic Fever (CCHF)—Key Factors for Transmission. Epidemiologia. 2022; 3(1):116-134. https://doi.org/10.3390/epidemiologia3010010
Chicago/Turabian StyleBhowmick, Suman, Khushal Khan Kasi, Jörn Gethmann, Susanne Fischer, Franz J. Conraths, Igor M. Sokolov, and Hartmut H. K. Lentz. 2022. "Ticks on the Run: A Mathematical Model of Crimean-Congo Haemorrhagic Fever (CCHF)—Key Factors for Transmission" Epidemiologia 3, no. 1: 116-134. https://doi.org/10.3390/epidemiologia3010010
APA StyleBhowmick, S., Kasi, K. K., Gethmann, J., Fischer, S., Conraths, F. J., Sokolov, I. M., & Lentz, H. H. K. (2022). Ticks on the Run: A Mathematical Model of Crimean-Congo Haemorrhagic Fever (CCHF)—Key Factors for Transmission. Epidemiologia, 3(1), 116-134. https://doi.org/10.3390/epidemiologia3010010






