Channel Modeling for In-Body Optical Wireless Communications †
Abstract
:1. Introduction
- The utilization of an ML-enabled mathematical framework for the extraction of analytical expressions for the absorption coefficients of the main constituents of tissues, namely oxygenated and de-oxygenated blood, water, fat, and melanin.
- Based on these expressions, we drew a general model that enabled the estimation of the absorption coefficient of any generic tissue (i.e., skin, muscle, etc.) based only on its constitution.
- The usability of this model was extended by incorporating the phenomenon of scattering in the analysis and, therefore, increasing the estimation accuracy of the attenuation due to the existence of generic tissues. This model is expected to have a great impact in the design and optimization of future medical devices that require the transmission of optical radiation inside the human body.
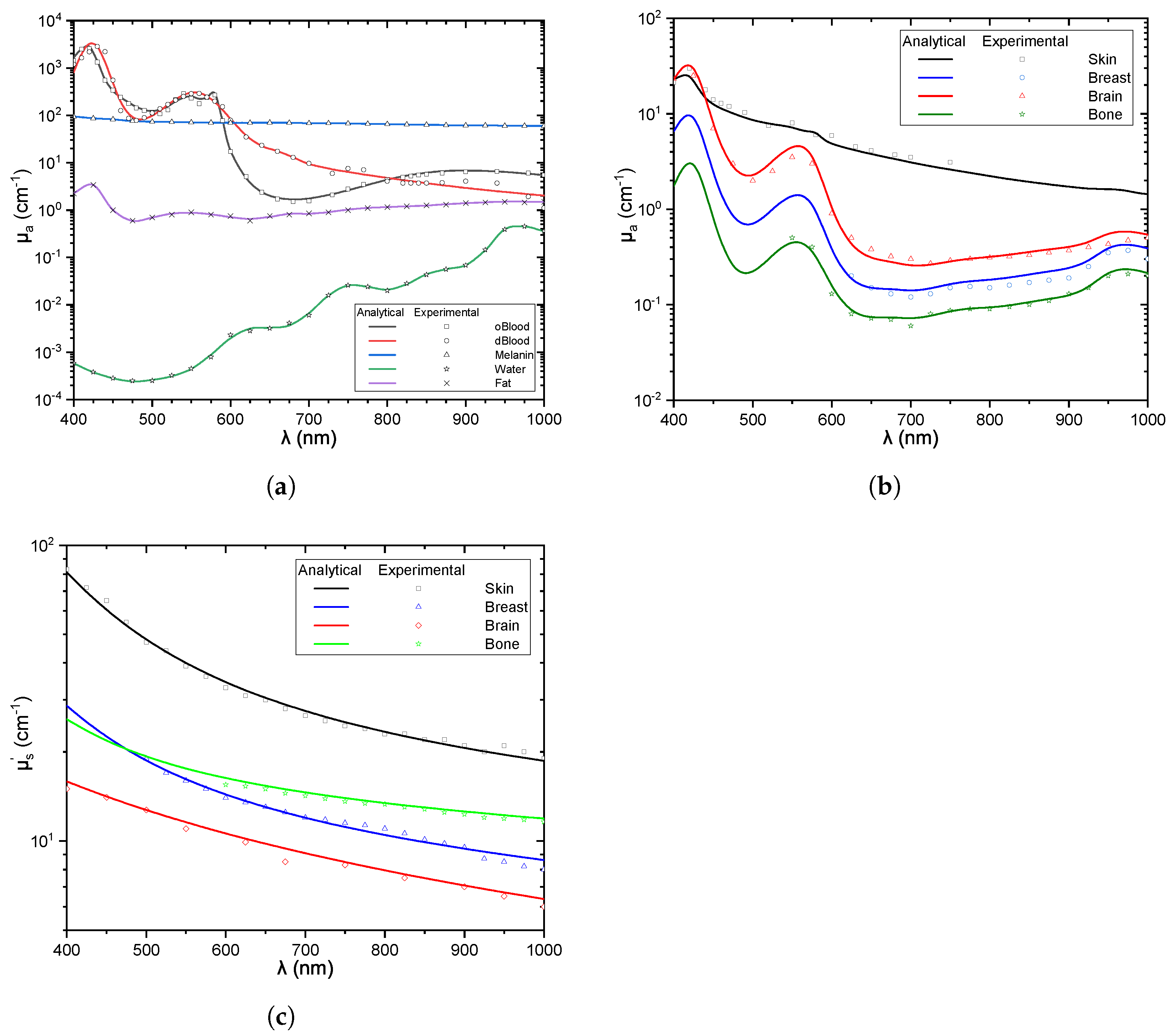
- We validated the extracted expression twofold. On the one hand, we fed experimental data into the ML algorithm to extract the mathematical expressions of the aforementioned coefficients and we drew the numerical results to visualize their performance. On the other hand, we compared the extracted numerical results against experimental data taken from different published papers and provided proof that they coincide. This twofold comparison illustrates the validity of the presented channel model.
- We provided the design with insightful discussions based on the pathloss variations, with regard to variable transmission wavelength, complex tissue types, and tissue thickness.
2. Channel Model
2.1. Absorption
| Algorithm 1 ML-based fitting mechanism |
|
2.2. Scattering
3. Results
3.1. Verification
3.2. Pathloss
4. Future Research Directions
- Stochastic channel modeling: As discussed in [2], transdermal and in-body optical wireless links suffer from wavelength-dependent particulate scattering. Within the skin, the main source of scattering is filamentous proteins (e.g., keratin in epidermis and collagen in dermis). Note that, since these particles are comparable to or larger than the wavelength, scattering can be approximated as a Mie solution to Maxwell’s equations. On the other hand, in in-body applications, tissues, such as membranes, striations in collagen fibrils, macromolecules, lysosomes, vesicles, mitochondria, and nuclei are the main scatterers. Note that membranes are usually lower than 1/10 of the wavelength, while all the other structures are comparable to the wavelength. Thus, scattering in tissues can be modeled as a mixture of Rayleigh and Mie processes. By taking into consideration the inhomogeneities in the body content in light-absorbing and scattering, which lead to a variation of the reflective index along the transmission path, it becomes evident that the received power is expected to randomly fluctuate. To model this phenomenon, experimentally verified ray-tracing investigations that capitalize the models presented in the current contribution need to be conducted. Furthermore, except for line-of-sight links, non-line-of-sights scenarios, where diffusion may be the key player, also need to be investigated.
- Theoretical investigation: Several different use cases, such as cochlear, gastric, cortical, retinal, foot drop implants, etc., have been identified [2]. However, only for a small number of them, a link budget analysis that supports their feasibility and reveals the architectural requirements that need to be accounted for has been conducted [6,7]. This motivates the use of the presented contribution as a building block towards the performance assessment of existing and envisioned designs and system models, as well as networks. In particular, for low-distance links, in the orders of some cm, where the strength of line-of-sight components are expected to be considerably larger than the one of non-line-of-sight, due to the high directionality of the links, the channel variation from its expected values will be relatively low. As a result, the presented channel model will provide a very accurate estimation of the received signal strength.
- Design and development of communication, energy harvesting, and neural stimulation modules: In order to select the optimal transmission and reception parameters and equipment, design energy and spectral efficient transmission waveforms, and reception filters and processes, develop low-complexity channel and error correction codes, devise suitable energy harvesting modules, and utilize energy transfer and harvesting policies, a low-complexity channel model that captures the inherent characteristics of the propagation medium is required. In more detail, and as illustrated in Section 3, the presented channel model can aid in identifying optimal transmission wavelengths, as well as transmission windows for different applications. This identification provides guidelines for the architecture designer concerning the LS and PD that should be used, as well as to the industry concerning the characteristics of the aforementioned units that need to be developed. By taking into account the channel characteristics, which in general are wavelength- and distance-dependent, suitable transmission waveform, codes, constellation, reception filters and detection processes that contribute to the maximization of the system’s energy efficiency can be developed and theoretically studied. Additionally, wavelength splitting strategies that ensure uninterrupted and reliable operation can be designed and optimized. Finally, combining the presented channel model with optogenetic stimulation, a highly efficient cell stimulation technique that offers improved spectral coding of sound information due to its higher temporal confinement, aspires great promise for the development of novel architectures capable of achieving unprecedented performance.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kaloxylos, A.; Gavras, A.; Camps Mur, D.; Ghoraishi, M.; Hrasnica, H. AI and ML—Enablers for Beyond 5G Networks. Zenodo 2020. [Google Scholar] [CrossRef]
- Boulogeorgos, A.A.A.; Trevlakis, S.E.; Chatzidiamantis, N.D. Optical wireless communications for in-body and transdermal biomedical applications. IEEE Commun. Mag. 2021, 59, 119–125. [Google Scholar] [CrossRef]
- Trevlakis, S.E.; Boulogeorgos, A.A.A.; Karagiannidis, G.K. On the impact of misalignment fading in transdermal optical wireless communications. In Proceedings of the 7th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 7–9 May 2018. [Google Scholar] [CrossRef]
- Trevlakis, S.; Boulogeorgos, A.A.A.; Karagiannidis, G. Signal Quality Assessment for Transdermal Optical Wireless Communications under Pointing Errors. Technologies 2018, 6, 109. [Google Scholar] [CrossRef] [Green Version]
- Trevlakis, S.E.; Boulogeorgos, A.A.A.; Karagiannidis, G.K. Outage Performance of Transdermal Optical Wireless Links in the Presence of Pointing Errors. In Proceedings of the IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Kalamata, Greece, 25–28 June 2018. [Google Scholar] [CrossRef]
- Trevlakis, S.E.; Boulogeorgos, A.A.A.; Sofotasios, P.C.; Muhaidat, S.; Karagiannidis, G.K. Optical wireless cochlear implants. Biomed. Opt. Express 2019, 10, 707. [Google Scholar] [CrossRef] [PubMed]
- Trevlakis, S.E.; Boulogeorgos, A.A.A.; Chatzidiamantis, N.D.; Karagiannidis, G.K. All-Optical Cochlear Implants. IEEE Trans. Mol. Biol. Multi-Scale Commun. 2020, 6, 13–24. [Google Scholar] [CrossRef]
- Zhao, J.; Ding, H.S.; Hou, X.L.; Zhou, C.L.; Chance, B. In vivo determination of the optical properties of infant brain using frequency-domain near-infrared spectroscopy. J. Biomed. Opt. 2005, 10, 024028. [Google Scholar] [CrossRef]
- Yaroslavsky, A.N.; Schulze, P.C.; Yaroslavsky, I.V.; Schober, R.; Ulrich, F.; Schwarzmaier, H.J. Optical properties of selected native and coagulated human brain tissues in vitro in the visible and near infrared spectral range. Phys. Med. Biol. 2002, 47, 2059–2073. [Google Scholar] [CrossRef]
- van der Zee, P.; Essenpreis, M.; Delpy, D.T. Optical properties of brain tissue. In Photon Migration and Imaging in Random Media and Tissues; Chance, B., Alfano, R.R., Eds.; SPIE: Bellingham, WA, USA, 1993. [Google Scholar] [CrossRef]
- Bashkatov, A.N.; Genina, E.A.; Kochubey, V.I.; Tuchin, V.V. Optical properties of human cranial bone in the spectral range from 800 to 2000 nm. In Saratov Fall Meeting 2005: Optical Technologies in Biophysics and Medicine VII; Tuchin, V.V., Ed.; SPIE: Bellingham, WA, USA, 2006. [Google Scholar] [CrossRef]
- Ugryumova, N.; Matcher, S.J.; Attenburrow, D.P. Measurement of bone mineral density via light scattering. Phys. Med. Biol. 2004, 49, 469–483. [Google Scholar] [CrossRef]
- Sandell, J.L.; Zhu, T.C. A review of in-vivo optical properties of human tissues and its impact on PDT. J. Biophotonics 2011, 4, 773–787. [Google Scholar] [CrossRef] [Green Version]
- Pifferi, A.; Swartling, J.; Chikoidze, E.; Torricelli, A.; Taroni, P.; Bassi, A.; Andersson-Engels, S.; Cubeddu, R. Spectroscopic time-resolved diffuse reflectance and transmittance measurements of the female breast at different interfiber distances. J. Biomed. Opt. 2004, 9, 1143. [Google Scholar] [CrossRef] [Green Version]
- Spinelli, L.; Torricelli, A.; Pifferi, A.; Taroni, P.; Danesini, G.M.; Cubeddu, R. Bulk optical properties and tissue components in the female breast from multiwavelength time-resolved optical mammography. J. Biomed. Opt. 2004, 9, 1137. [Google Scholar] [CrossRef] [PubMed]
- Tseng, T.Y.; Chen, C.Y.; Li, Y.S.; Sung, K.B. Quantification of the optical properties of two-layered turbid media by simultaneously analyzing the spectral and spatial information of steady-state diffuse reflectance spectroscopy. Biomed. Opt. Express 2011, 2, 901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salomatina, E.; Jiang, B.; Novak, J.; Yaroslavsky, A.N. Optical properties of normal and cancerous human skin in the visible and near-infrared spectral range. J. Biomed. Opt. 2006, 11, 064026. [Google Scholar] [CrossRef] [PubMed]
- Shimojo, Y.; Nishimura, T.; Hazama, H.; Ozawa, T.; Awazu, K. Measurement of absorption and reduced scattering coefficients in Asian human epidermis, dermis, and subcutaneous fat tissues in the 400- to 1100-nm wavelength range for optical penetration depth and energy deposition analysis. J. Biomed. Opt. 2020, 25, 1. [Google Scholar] [CrossRef]
- Jacques, S.L. Optical properties of biological tissues: A review. Phys. Med. Biol. 2013, 58, R37–R61. [Google Scholar] [CrossRef]
- Trevlakis, S.E.; Boulogeorgos, A.A.A.; Chatzidiamantis, N.D.; Karagiannidis, G.K.; Lei, X. Electrical vs Optical Cell Stimulation: A Communication Perspective. IEEE Access 2020, 8, 192259–192269. [Google Scholar] [CrossRef]
- Saidi, I.S.; Jacques, S.L.; Tittel, F.K. Mie and Rayleigh modeling of visible-light scattering in neonatal skin. Appl. Opt. 1995, 34, 7410. [Google Scholar] [CrossRef]
- Frontin, J.B.; Anthony, B.W. Quantifying dermatology: Method and device for user-independent ultrasound measurement of skin thickness. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 5743–5748. [Google Scholar]
- Coddington, A.; Levinson, N. Theory of Ordinary Differential Equations; International Series in Pure and Applied Mathematics; McGraw-Hill Companies: New York, NY, USA, 1955. [Google Scholar]
- Boulogeorgos, A.A.A.; Trevlakis, S.E.; Tegos, S.A.; Papanikolaou, V.K.; Karagiannidis, G.K. Machine Learning in Nano-Scale Biomedical Engineering. IEEE Trans. Mol. Biol.-Multi-Scale Commun. 2020, 7, 10–39. [Google Scholar] [CrossRef]
- Hale, G.M.; Querry, M.R. Optical Constants of Water in the 200-nm to 200-μm Wavelength Region. Appl. Opt. 1973, 12, 555. [Google Scholar] [CrossRef]
- Zolotarev, V.M.; Mikhailov, B.A.; Alperovich, L.I.; Popov, S.I. Dispersion and Absorption of Liquid Water in the Infrared and Radio Regions of the Spectrum. Opt. Spectrosc. 1969, 27, 430. [Google Scholar]
- Segelstein, D.J. The Complex Refractive Index of Water. Ph.D. Thesis, University of Missouri, Kansas City, MO, USA, 1981. [Google Scholar]
- Takatani, S.; Graham, M.D. Theoretical Analysis of Diffuse Reflectance from a Two-Layer Tissue Model. IEEE. Trans. Biomed. Eng. 1979, BME-26, 656–664. [Google Scholar] [CrossRef]
- Moaveni, M.K. A Multiple Scattering Field-Theory Applied to Whole Blood; University of Washington: Seattle, WA, USA, 1970. [Google Scholar]
- Schmitt, J. Optical Measurement of Blood Oxygen by Implantable Telemetry; Stanford University: Stanford, CA, USA, 1986. [Google Scholar]
- Zhao, Y.; Qiu, L.; Sun, Y.; Huang, C.; Li, T. Optimal hemoglobin extinction coefficient data set for near-infrared spectroscopy. Biomed. Opt. Express 2017, 8, 5151. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bashkatov, A.N. Optical Properties of the Subcutaneous Adipose Tissue in the Spectral Range 400–2500 nm. Opt. Spectrosc. 2005, 99, 836. [Google Scholar] [CrossRef]
- Jacques, S.L.; McAuliffe, D.J. The melanosome: Threshold temperature for explosive vaporization and internal absorption coefficient during pulsed laser irradiation. Photochem. Photobiol. 1991, 53, 769–775. [Google Scholar] [CrossRef] [PubMed]
- Zonios, G.; Dimou, A.; Bassukas, I.; Galaris, D.; Tsolakidis, A.; Kaxiras, E. Melanin absorption spectroscopy: New method for noninvasive skin investigation and melanoma detection. J. Biomed. Opt. 2008, 13, 014017. [Google Scholar] [CrossRef] [Green Version]
- Mourant, J.R.; Fuselier, T.; Boyer, J.; Johnson, T.M.; Bigio, I.J. Predictions and measurements of scattering and absorption over broad wavelength ranges in tissue phantoms. Appl. Opt. 1997, 36, 949. [Google Scholar] [CrossRef]
- Mourant, J.R.; Freyer, J.P.; Hielscher, A.H.; Eick, A.A.; Shen, D.; Johnson, T.M. Mechanisms of light scattering from biological cells relevant to noninvasive optical-tissue diagnostics. Appl. Opt. 1998, 37, 3586. [Google Scholar] [CrossRef]
- Lau, C.; Scepanovic, O.; Mirkovic, J.; McGee, S.; Yu, C.C.; Fulghum, S.; Wallace, M.; Tunnell, J.; Bechtel, K.; Feld, M. Re-evaluation of model-based light-scattering spectroscopy for tissue spectroscopy. J. Biomed. Opt. 2009, 14, 024031. [Google Scholar] [CrossRef]


| Variable | Name |
|---|---|
| B | Blood volume fraction |
| Cosine function | |
| Tissue thickness | |
| Exponential function | |
| F | Fat volume fraction |
| Rayleigh scattering factor | |
| g | Anisotropy factor |
| L | Pathloss |
| M | Melanin volume fraction |
| Absorption coefficient | |
| Scattering coefficient | |
| Reduced scattering coefficient | |
| Sine function | |
| W | Water volume fraction |
| dBlood | oBlood | Water | Fat | |
|---|---|---|---|---|
| - | - | - | ||
| 14 | ||||
| - | 73 | |||
| - | - | - | ||
| - | - | - | ||
| −25,880 | ||||
| - | ||||
| - | - | - | ||
| - | - | - | ||
| - | ||||
| - | ||||
| - | ||||
| 4668 | - | |||
| - | - | |||
| w | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trevlakis, S.E.; Boulogeorgos, A.-A.A.; Chatzidiamantis, N.D.; Karagiannidis, G.K. Channel Modeling for In-Body Optical Wireless Communications. Telecom 2022, 3, 136-149. https://doi.org/10.3390/telecom3010009
Trevlakis SE, Boulogeorgos A-AA, Chatzidiamantis ND, Karagiannidis GK. Channel Modeling for In-Body Optical Wireless Communications. Telecom. 2022; 3(1):136-149. https://doi.org/10.3390/telecom3010009
Chicago/Turabian StyleTrevlakis, Stylianos E., Alexandros-Apostolos A. Boulogeorgos, Nestor D. Chatzidiamantis, and George K. Karagiannidis. 2022. "Channel Modeling for In-Body Optical Wireless Communications" Telecom 3, no. 1: 136-149. https://doi.org/10.3390/telecom3010009
APA StyleTrevlakis, S. E., Boulogeorgos, A.-A. A., Chatzidiamantis, N. D., & Karagiannidis, G. K. (2022). Channel Modeling for In-Body Optical Wireless Communications. Telecom, 3(1), 136-149. https://doi.org/10.3390/telecom3010009








