Fingerprinting-Based Positioning with Spatial Side Information at the Positioning Device Solved via Feedforward and Convolutional Neural Networks: Survey and Feasibility Study Through System Simulations
Abstract
:1. Introduction
- The proposal to transfer the complexity and cost from the infrastructure side to a positioning device.
- Differentiation between uplink and downlink cases for fingerprinting-based positioning, relating Multiple-Input Multiple-Output (MIMO), massive MIMO, and intelligent surfaces.
- Differentiation between positioning data aggregation in the fingerprint and position domains.
- The proposal to collect the fingerprints at adjacent positions relative to a target position by means of a 2D sensor array located at the positioning device.
- The proposal to use 2D spatial side information from the fingerprints collected by the 2D sensor array to minimize the positioning error.
- The aggregation of the fingerprinting data from adjacent spatial positions prior to the mapping from the fingerprints to a position estimate.
- The conjecture that a pattern-matching method based on the classification of the discretized areas can be applied to estimating the position.
- Three pattern-matching methods for estimating the position by processing the fingerprints with spatial side information. Two methods are based on regression, implemented using FFNNs, and one method is based on the classification of fractions of the positioning area, implemented using a CNN. In turn, one method operates with data in the so-called position domain, and the other two methods operate with data in the so-called fingerprint domain.
- A feasibility study, for a given scenario and assumptions, using system simulations based on Monte Carlo methods.
- Benchmarking of cases without and with spatial side information.
- Benchmarking of the CNN-based method to determine whether it allows us to enhance the position estimates when compared with those from other methods.
Example of a Hybrid Positioning System
2. Basic Concepts and Work Scope
2.1. Acronyms Used in the Article
2.2. Fingerprinting-Based Positioning
2.3. Mobile-Device-Based Positioning
2.4. Positioning Data Aggregation Domains for Fingerprinting-Based Positioning
2.4.1. Position Estimates Without Positioning Data Aggregation
2.4.2. Position Estimates from Aggregated Positions in the Position Domain
2.4.3. Position Estimates from Aggregated Fingerprints in the Fingerprint Domain
2.5. Spatial Side Information
2.6. Data Aggregation Domains, Side Information, and Analogy to Communications Systems
2.7. Summary of the Key Assumptions and Scope
- We focus on fingerprinting-based positioning, with downlink transmission of the fingerprints and fingerprints processing on the positioning device side in 2D.
- The spatial side information on adjacent fingerprints at the positioning device is considered.
- The position is estimated considering positioning data aggregation in the position domain in one of the pattern-matching methods proposed and in the fingerprint domain in two of the pattern-matching methods proposed. However, our main interest is processing the fingerprints in the fingerprint domain before their input into the pattern-matching method.
- The collection of the fingerprints is assumed to be carried out using a two-dimensional sensor array (2D sensor array).
- The same 2D sensor array is used in the training and testing phases.
- An actual description of how the 2D sensor array should be built it is out of our scope. Each sensor, in charge of sampling fingerprints, may be an antenna or a receiver with a built-in antenna. Thus, it may be composed of an antenna array or a receiver array. We do not consider the actual antenna design aspects related to the construction of the 2D sensor array. In this context, we work only with the numeric modules of what would be the equivalent of the received signal strength, ignoring the effects of the constructive/destructive phases of the radio-waves, the optimal antenna spacing, the effect on the antenna spacing and the Signal-to-Noise Ratio (SNR), and variable Angles of Arrival (AoAs) of the radio-waves with respect to the 2D sensor array’s position.
- We carry out positioning in 2D.
- We assume that the fingerprint source nodes (transmitters) belong to the positioning system infrastructure, are always present, and are located in stationary positions.
- It is assumed that the fingerprints are always collected in the same plane, at the same height. In practice, this assumption is not unrealistic considering that the 2D sensor array may not be suitable as a hand-held positioning device. This requirement could be satisfied in practice by mounting the 2D sensor array onto a trolley, robot, or machine operating at the same height.
- Perfect alignment of the 2D sensor array with the positioning area in the scenario considered will be assumed. Rotation and tilting of the 2D sensor array were not considered in our study.
- It is assumed that a subdivision of the tile (called a sub-tile) is the smallest granularity for discretizing the positioning area and the sample positions. These subdivisions are non-overlapping, of a square shape, and uniform in size.
- We utilize Monte Carlo methods to generate synthetic RSS fingerprints. We will assume an omnidirectional radiation pattern for the antennas of the transmitters, an LOS radio propagation channel model, and transmitters with a constant transmit power.
- The primary goal is to observe whether using the spatial side information on the RSS fingerprints by means of an ideal 2D sensor array produces any gain in terms of minimizing the positioning error.
- It is out of the scope of this article to evaluate the computing cost of the patternmatching methods proposed.
- It is not part of our claim that the use of pattern-matching methods based on feedforward and convolutional NNs will outperform any other method. These were selected, and used as a tool, based on the general performance of these in the fields of fingerprinting-based positioning and pattern matching in images. Furthermore, NNs were selected for the proposed pattern-matching methods because among all of the deep learning methods known, NNs possess a competitive learning capacity. Our main goal, as stated, is to observe whether the use of spatial side information brings a gain. If a gain, in terms of minimizing the error distance, is observed with some of the selected methods, future in-depth research on the selection of the most optimal pattern-matching methods can be considered. An initial contribution in this direction is provided by studying the pattern-matching methods proposed and comparing the results produced by them.
3. Literature Review and Related Work
3.1. Fingerprinting-Based Positioning Implementing Fingerprint Images Processed Using CNNs
| Ref. | Year | Fingerprints Used | Discretized Positioning Area Size | CNN Type | Fingerprint Image | Side Inform. |
|---|---|---|---|---|---|---|
| [89] | 2017 | CSI: amplitude | to m | 2D | 30 subcarriers by 30 time samples | (Yes) 3 |
| [90] | 2017 | CSI: AoA | m × path width | 2D | Matrix of AoA values | (Yes) 2 |
| [91] | 2017 | CSI: AoA, amplitude | m × path width | 2D | 30 subcarriers by 30 time samples | (Yes) 3 |
| [92] | 2018 | CSI: amplitude | Ref. points spaced at m | 2D | 30 subcarriers by 30 time samples | (Yes) 3 |
| [93] | 2018 | RSS and correlation coefficient | m m | 2D | Fingerp. arranged in a matrix | No |
| [94] | 2018 | RSS | Building/floor size. | 2D | Fingerp. arranged in a matrix | No |
| [95] | 2018 | RSS | Not specified | 2D | Fingerp. arranged in a matrix | No |
| [96] | 2018 | RSS | Building/floor (classification) | 2D | Fingerp. arranged in a matrix | No |
| [97] | 2018 | CSI | m m | 2D | From CSI wavelet transform | (Yes) 3 |
| [98] | 2019 | RSS | Ref. points spaced at m | 2D | Fingerp. arranged in a matrix | No |
| [99] | 2019 | RSS and kurtosis from RSS | m m and m m | 2D | 3D tensor (number of access points × time × fingerprint and kurtosis) | No |
| [100] | 2019 | RSS | m mean dist., outdoor | 2D | Fingerp. arranged in a matrix | No |
| [101] | 2019 | RSS | m m | 2D | Fingerp. arranged in a matrix | No |
| [102] | 2019 | RSS | m m | 2D | Fingerp. arranged in a matrix | No |
| [103] | 2019 | CSI: amplitude | m m | 2D | 90 subcarriers by 90 time samples | (Yes) 3 |
| [104] | 2019 | RSS with wavelet transform | m m (corridor of m divided into 21 areas) | 2D | 2D representation of RSS via wavelet transform | No |
| [105] | 2019 | RSS | m m | 2D | Fingerp. arranged in a matrix | No |
| [106] | 2019 | CSI: amplitude, phase difference | Ref. points spaced at m | 2D | 114 subcarriers by 114 time samples | (Yes) 3 |
| [107] | 2019 | CSI: amplit., phase | Ref. points from to m | 3D | Fingerp. arranged in a tensor | (Yes) 3 |
| [108] | 2019 | CSI | Ref. points spaced at m | 2D | Channel state matrix | (Yes) 3 |
| [109] | 2019 | Radio beams | From dataset; see [109] | 2D | Number of beams by time samples | (Yes) - |
| [30] | 2020 | Geomagnetic | m m | 2D | Fingerp. arranged in a matrix | No |
| [31] | 2020 | Geomagnetic | Room size | 2D | Fourier transform of fingerprints arranged in a matrix | No |
| [110] | 2020 | CSI: AoA | m × path width | 2D | 60 subcarriers by 60 time samples | (Yes) 3 |
| [111] | 2020 | CSI: amplitude, phase difference | to m | 2D | 30 subcarriers by 50 time samples | (Yes) 3 |
| [112] | 2020 | CSI: amplitude, phase | m m | 2D | Fingerp. arranged in a matrix of 30 subcarriers by 30 time samples | (Yes) 3 |
| [113] | 2020 | RSS and other | Reference points spaced on average from m to m | 2D | Fingerp. arranged in a matrix of the topology of the access points | No |
| [114] | 2020 | CSI: amplitude | Ref. points spaced at m | 2D | Fingerp. arranged in a matrix | (Yes) 3 |
| [115] | 2020 | RSS | m m | 2D | Fingerp. arranged in a matrix | No |
| [116] | 2020 | RSS | m m | 2D | Fingerp. arranged in a matrix | No |
| [117] | 2020 | RSS | 25 m m to 200 m m | 2D | Fingerp. arranged in a matrix | No |
| [118] | 2020 | RSS | to m [88] | 2D | Fingerp. arranged in a matrix | No |
| [119] | 2020 | RSS | m m | 2D | Fingerp. arranged in a matrix | No |
| [120] | 2020 | SNR | m m | 2D | Beam covariance matrix | Yes 32 |
| [121] | 2020 | Radio beams | From dataset; see [121] | 2D | Number of beams by time samples | (Yes) - |
| [122] | 2020 | Radio beams | From dataset; see [122] | 2D | Number of beams by time samples | (Yes) - |
| [123] | 2021 | CSI: amplitude differences | m m, m m, and m m | 2D | Fingerp. arranged in a matrix of 30 subcarriers by 30 time samples | (Yes) 3 |
| [124] | 2021 | RSS | m mean dist., outdoor | 2D | Fingerp. arranged in a matrix | No |
| [125] | 2021 | RSS | Bounding box with estimated position in 40 m m area | 2D | Fingerp. arranged in a matrix | No |
| [126] | 2021 | RSS | Not specified | 2D | Fingerp. arranged in a matrix | No |
| [127] | 2021 | RSS and phase difference | m m | 2D | Fingerp. arranged in a matrix | No |
| [128] | 2021 | CSI | m m | 2D | Amplitude feature map | (Yes) 3 |
| [129] | 2021 | CSI: AoA, amplitude | m × path width | 2D | 30 subcarriers by 30 time samples | (Yes) 3 |
| [130] | 2021 | Geomagnetic | Not specified | 2D | Sequence of fingerprints arranged in a matrix | Yes 700 |
| [131] | 2021 | Geomagnetic | m m | 2D | Sequence of fingerprints arranged in a matrix | Yes 10 |
| [132] | 2021 | RSS | Ref. points spaced between m and m | 2D | Fingerp. arranged in a matrix sorted by the spatial relationship of the access points | No |
| [133] | 2021 | CSI: amplitude | Not specified | 2D | Fingerp. arranged in a sub-window | Yes 16 |
| [134] | 2021 | RSS | m m, m m | 2D | Matrix of scaled diff. of fingerp. | No |
| [135] | 2021 | CSI: amplitude | Not specified | 2D | 30 subcarriers by 30 time samples | (Yes) 3 |
| [136] | 2021 | RSS | m m | 2D | Fingerp. arranged in a matrix | No |
| [137] | 2021 | RSS | Ref. points spaced at m | 2D | Fingerp. arranged in a matrix of the topology of the access points | No |
| [138] | 2022 | RSS | Ref. points spaced at m | 2D | Fingerp. arranged in a matrix of time and frequency | No |
| [139] | 2022 | RSS | m m to m m | 2D | Fingerp. arranged in a matrix of the topology of the access points | No |
| [140] | 2022 | CSI: phase | m m | 2D | 30 subcarriers by 30 time samples | (Yes) 3 |
| [141] | 2022 | CSI: amplitude | m m | 2D | 30 subcarriers by 200 time samples | No |
| [142] | 2022 | RSS and other | m m | 2D | Four measurements by time sampl. | No |
| [143] | 2022 | RSS | m m | 2D | Matrix of vertical–horizontal beams | No |
| [144] | 2022 | RSS | to m [88] | 2D | Fingerp. arranged in a matrix | No |
| [145] | 2022 | RSS | According to [87] | 2D | Fingerp. arranged in a matrix | No |
| [146] | 2022 | RSS | m m | 2D | Fingerp. arranged in a matrix | No |
| [147] | 2022 | RSS | Ref. points spaced m | 2D | From a rasterization function | No |
| [148] | 2022 | CSI | Ref. points at or m | 2D | 30 subcarriers by 36 time samples | (Yes) 3 |
| [149] | 2022 | RSS | m m | 2D | Vector of fingerp. sampled in time arranged as a matrix | No |
| [150] | 2022 | RSS | Ref. points spaced at m | 2D | Fingerp. arranged in a matrix | No |
| [151] | 2022 | CSI | Ref. points at approx. m | 2D | Not specified | No |
| [152] | 2022 | RSS | According to [87] | 2D | Fingerp. arranged in a matrix | No |
| [153] | 2022 | RSS | m m | 2D | Vector of fingerp. sampled in time and space arranged as a matrix | Yes 40 |
| [154] | 2022 | RSS | to m [88] | 2D | Fingerp. arranged in a matrix | Yes 2 |
| [155] | 2022 | RSS | to m [88] | 2D | Fingerp. arranged in a matrix | No |
| [156] | 2022 | RSS | m m | 2D | Vector of fingerp. sampled in time arranged as a matrix | No |
| [157] | 2023 | CSI: amplitude | Ref. points spaced at m | 2D | 256 subcarriers by 1000 time sampl. | No |
| [158] | 2023 | RSS | m m | 2D | Vector of fingerp. sampled in time arranged as a matrix | No |
| [159] | 2023 | RSS | Ref. points spaced at m | 2D | Matrix of row vectors of fingerp. | No |
| [160] | 2023 | RSS | Not specified | 2D | Fingerp. arranged in a matrix of the vertical–horizontal topology of the access points | No |
| [161] | 2023 | CSI: amplitude | Ref. points spaced at m | 2D | 60 subcarriers by 60 time samples | (Yes) 3 |
| [162] | 2023 | CSI: amplitude | m m | 2D | 30 subcarriers by 30 time samples | (Yes) 3 |
| [163] | 2023 | RSS | m m | 2D | Fingerp. arranged in a matrix | No |
3.2. Positioning Implementing Time-Series of Spatially Distributed Fingerprints
3.3. Other Works Using Spatial Side Information
3.4. Discussion on Research Works Using Spatial Side Information
3.5. Positioning with Discretization of the Positioning Areas and Classification-Based Models
4. Fingerprinting-Based Positioning with Spatial Side Information
4.1. Two-Dimensional Sensor Array
4.2. Discretized Area Fractions with Tiles
4.3. Positioning Process
- The training phase: In a given positioning area, we create an ideal grid-like arrangement of fixed tiles. Each fixed tile corresponds in its size to the size of the 2D sensor array and in the number and size of the sub-tiles to each sensor in the 2D sensor array. The 2D sensor array is aligned with a fixed tile to sample fingerprints with adjacent side information. Fingerprint samples are collected from each sensor in the 2D sensors array and assigned to a vector of fingerprints. In turn, the vector of fingerprints is associated with a sub-tile. The elements in the vector of fingerprints are the fingerprints obtained from each fingerprint source. For a number of fingerprint sources, the vector has elements. The fingerprints from the whole 2D sensor array are associated with a tile and assigned to a tensor of fingerprints, with the dimensions .Fingerprint samples from fixed tiles, along with the reference ground truth positions, are used to train a regression-based FFNN model with a given pattern-matching method. Alternatively, fingerprint samples from fixed tiles, along with the tile-class labels, are used to train a classification-based CNN model with a given pattern-matching method. The training of all of the models is based on supervised learning.
- The testing phase: A positioning device implementing a 2D sensor array is placed at some random position within the positioning area. The position of the 2D sensor array determines what is thought of as a moving tile. The 2D sensor array samples fingerprints with adjacent side information. As in the case of fixed tiles, fingerprint samples are collected from each sensor in the 2D sensor array, which are associated with a sub-tile and assigned to a vector of fingerprints, with elements obtained from each fingerprint source. The fingerprints from the whole 2D sensor array are associated with a moving tile and assigned to a tensor of fingerprints, with the dimensions . Finally, the position estimate is calculated using all of the pattern-matching methods constructed in the training phase, using as the input the tensor of fingerprints associated with the moving tile.
- Comparison of the results: This consists of comparing the performance among all of the proposed pattern-matching methods considered in terms of the error distance, , given by Equation (1).
4.4. Pattern-Matching Methods
4.4.1. Pattern-Matching Method 1-SingFingIn-PosOut
4.4.2. Pattern-Matching Method 2-SingFingIn-AggPosOut
4.4.3. Pattern-Matching Method 3-MultFingIn-PosOut
4.4.4. Pattern-Matching Method 4-MultFingIn-ClassOut
- ○
- Translation Invariance PropertyIt is unclear to us whether the so-called translation invariance property of CNNs is present and contributing to boosting the recognition of parts of a moving tile, which are translated parts of the overlapped fixed tiles. This translation invariance property is also discussed in terms of shift invariance [209]. It is under debate whether the architecture of CNNs alone, the introduction of multiple convolutional layers, the introduction of pooling layers, data augmentation, or a combination of the former contributes to the translation invariance property. In [210], translation invariance is discussed in terms of a local translation, enabled by pooling functions, for small translations in the input. In [211], it is concluded that for the processing of images, the invariance increases with the depth of the CNN. In [212], it is concluded that CNNs alone are not translation-invariant but that the main contribution to the invariance is the training with the help of data augmentation. It is argued that CNNs are not shift-invariant due to the presence of downsampling, introduced by layers like strided max-pooling [213,214].We implemented a CNN without pooling and without data augmentation in the translation domain (meaning that we augmented data by introducing a random shadow fading component into each sub-tile, but the base path loss component remained constant for the position of each sub-tile, and thus, there was no augmentation through translation in the fixed tiles used for training). Thus, according to the claim of some works in line with those cited above, our CNN does not benefit from the translation invariance property. Yet as a matter of fact, the CNN implemented manages to find with a high probability fixed tiles that resemble moving tiles. Given that the tile-classes from the fixed tiles present a variation in a pattern that can be considered almost continuous, it is unclear to us whether the good performance observed is because the fixed tiles are identified by moving tiles with a close resemblance and/or because the good performance is enabled by the translation invariance. A reasoning in line with the possible contribution of the translation invariance is based on the assumption that the pattern described by a fixed tile, notwithstanding the noise component introduced by the shadow fading, can be found in the parts of a moving tile regardless of the position of the pattern in the tile. Parts of these patterns can be at different positions in the moving tile compared with in a fixed tile. Then, if translation invariance exists, we would expect to observe that the parts of a moving tile can be identified with a higher probability in fixed tiles around the moving tile.
- ○
- Tile-class Probabilities and Data Aggregation DomainsIt is open to discussion whether the processing of the tile-class probabilities, along with the known tile center positions, is regarded as positioning data aggregation in the position domain. The input fingerprints are aggregated in the fingerprint domain by the CNN; therefore, there is not a one-to-one mapping from an individual fingerprint to each tile-class probability. Therefore, we do not treat this step as an aggregation in the position domain, in as much as we do not treat as aggregation in the position domain the last layers in the pattern-matching method 3-MultFingIn-PosOut, which ultimately aggregates the NN data to calculate the final output position estimate.
5. Feasibility Study Through System Simulations
- The creation of a scenario with transmitting base stations in downlink and the area intended for positioning;
- Tiling of the area intended for positioning (creation of the positioning area);
- The creation of datasets of synthetic fingerprints for fixed and moving tiles (as arrangements that are equivalent to samples of the 2D sensor array) with a radio channel model, published by a standardization body, for a frequency of GHz;
- Training of the NN model for a selected patternmatching method in the training phase;
- Estimation of the positions of moving tiles in the testing phase;
- Storage of the best-performing result.
5.1. Scenario for Simulations, Area Intended for Positioning, and Positioning Area
5.2. Generation of Datasets of Fingerprints
5.2.1. Validation Datasets
5.2.2. Generation of the Center Position Coordinates for Fixed Tiles
 of the main execution flow of the simulator presented in Section 5.6.1). The function returns as the output a data structure with an arrangement of the fixed tiles’ centers, for example, in the form of a vector, array, or list, for each coordinate, namely and . These data structures are used next to generate datasets of fixed tiles in the function and to define the area allowed for generating the datasets of moving tiles in the function . This function also calculates and returns as output the total number of tiles required to cover the whole positioning area, .
of the main execution flow of the simulator presented in Section 5.6.1). The function returns as the output a data structure with an arrangement of the fixed tiles’ centers, for example, in the form of a vector, array, or list, for each coordinate, namely and . These data structures are used next to generate datasets of fixed tiles in the function and to define the area allowed for generating the datasets of moving tiles in the function . This function also calculates and returns as output the total number of tiles required to cover the whole positioning area, .
| Pseudocode 1 Function for calculating the center positions for fixed tiles - FTileCenters() |
|
5.2.3. Generation of Fixed Tiles
| Pseudocode 2 Function for generating fixed tiles - FFixedTiles() |
|
 and
and  of the main execution flow of the simulator presented in Section 5.6.1). Figure 12 depicts an example of the output produced by this function for one batch, in which the area intended for positioning is fully covered by fixed tiles. The figure also depicts an example of one radio channel realization. Each sub-tile has a vector of fingerprint elements from the four base stations associated with it. In the figure, each sub-tile is color-coded with the RGB and opacity channels to represent the fingerprints from each one of the four base stations. In this example, , and mm.
of the main execution flow of the simulator presented in Section 5.6.1). Figure 12 depicts an example of the output produced by this function for one batch, in which the area intended for positioning is fully covered by fixed tiles. The figure also depicts an example of one radio channel realization. Each sub-tile has a vector of fingerprint elements from the four base stations associated with it. In the figure, each sub-tile is color-coded with the RGB and opacity channels to represent the fingerprints from each one of the four base stations. In this example, , and mm.5.2.4. Generation of Moving Tiles
| Pseudocode 3 Function for generating moving tiles - FMovingTiles() |
|
 and
and  of the main execution flow of the simulator presented in Section 5.6.1). Figure 13 depicts an example of the output produced by this function for 40 moving tiles (colored tiles). In the figure, the positioning area for this example is the grid that spans from position 1 m to 14 m along the x coordinates and from position 1 m to 6 m along the y coordinates. This positioning area is analogous to the one depicted in Figure 12 for fixed tiles. The grid is provided as a reference to observe the relative position of the moving tiles to the actual position of the fixed tiles. Each sub-tile of the moving tiles has a vector of fingerprint elements from the four base stations associated with it. In the figure, each sub-tile is color-coded with the RGB and opacity channels to represent the fingerprints from each one of the four base stations. In this example, , and mm.
of the main execution flow of the simulator presented in Section 5.6.1). Figure 13 depicts an example of the output produced by this function for 40 moving tiles (colored tiles). In the figure, the positioning area for this example is the grid that spans from position 1 m to 14 m along the x coordinates and from position 1 m to 6 m along the y coordinates. This positioning area is analogous to the one depicted in Figure 12 for fixed tiles. The grid is provided as a reference to observe the relative position of the moving tiles to the actual position of the fixed tiles. Each sub-tile of the moving tiles has a vector of fingerprint elements from the four base stations associated with it. In the figure, each sub-tile is color-coded with the RGB and opacity channels to represent the fingerprints from each one of the four base stations. In this example, , and mm.5.2.5. Generation of Individual Tiles
| Pseudocode 4 Function for generating an individual tile - FTile() |
|
5.3. Border Conditions in the Area Intended for Positioning in the Scenario
5.4. Radio Channel Model
5.5. Generalization for Moving Tiles and the Optimization Metric
5.6. Simulation Process
5.6.1. Main Execution Flow of the Simulator
- In step
, the input parameters for the simulation are set, and some of the main variables that are a function of these are initialized. A list of the parameters for simulation, with the corresponding values used in our simulations, is presented in Table 9. The main variables are listed in Table 10. The number of fingerprint sources, , is fixed for the considered scenario to four fingerprint sources. The side length of the sub-tile and the number of sub-tiles per side of the tile are the two main parameters that are used in the simulations to compare the results using different sub-tile and tile sizes. The pattern-matching model is trained with initial random weights. A loop takes care to perform a number of iterations with different initial random weights, given by the parameter , as discussed in Section 5.5. The reference percentile for the selection of the best model weights with the MTV dataset is given by the parameter , discussed in Section 5.5. The parameters for the radio channel model, namely the frequency, the standard deviation in the shadow fading, and the power loss coefficient, are given by the parameters f, , and , respectively. The side length of the tile is calculated using the number of sub-tiles multiplied by the side length of the sub-tile, as indicated in Table 10, and stored in the variable . Because a tile is equivalent in size to the 2D sensor array, is the side length of the 2D sensor array. The total number of sub-tiles in a tile is stored in the variable .
- In step
, the scenario is created. The base stations’ positions (referred to as node coordinates in
) are set according to Table 7. Then, the fixed tile centers are calculated using the function (Pseudocode 1) as a function of and . The number of fixed tiles for training and validation of the datasets FTT and FTV is stored in the variables and . These are determined by the number of fixed tile batches, given through the parameter in step
, and multiplied by the number of tiles that fit into the positioning area in the scenario, . In turn, is a function of the positioning area’s dimensions. The value of the variable is calculated and returned by the function . In contrast, moving tiles do not follow the grid-like pattern of the fixed tiles but are placed in random places. Therefore, the number of moving tiles in the MTV and MTT datasets is directly given through the parameters and in step
.
In order to present a simple and compact structure for the simulator, we avoid adding additional functions and parameters passing variables to the functions. Then, the definition of the scenario is in part distributed across the hard-coded scenario dimensions presented in the function (Pseudocode 1) and the base station positions hard-coded into the function (Pseudocode 4).
- In step
, the fixed tile centers returned by the function are used to create a table mapping each one of the fixed tiles that covers the positioning area to the respective center positions of the tile and to a suitable class label to identify the tile. This information is used in pattern-matching method 4-MultFingIn-ClassOut, which is a classification-based method.
- In steps
and
, the datasets of fixed tiles FTT and FTV, introduced in Section 5.2.3, are created by calling the function (Pseudocode 2). In steps
and
, the moving tile datasets MTV and MTT, introduced in Section 5.2.4, are created by calling the function (Pseudocode 3).
- In step
, the function is called. This function is in charge of implementing a selected NN structure for a given pattern-matching method and is in charge of performing the training of the NN model. For convenience and compactness in the description, this function also executes the testing phase, consisting of the actual calculation of the estimated positions for the given dataset of moving tiles for testing, MTT. In addition, the error distances for the estimated positions with the dataset MTT are calculated. This step is executed for each one of the four pattern-matching methods introduced in Table 6 (Section 4.4) independently. For simplicity, for the model training, we present the simulation flow description at a general level, suitable for use with any of the pattern-matching methods considered. Therefore, we omit defining the actual pattern-matching methods as part of the block diagram.
5.6.2. Generation of the Same Datasets of Fingerprints for the Different Pattern-Matching Methods
 to
to  of the main execution flow of the simulator with the same seeds in the pseudo-random number generators for each pattern-matching method. Another option is to simply execute steps
of the main execution flow of the simulator with the same seeds in the pseudo-random number generators for each pattern-matching method. Another option is to simply execute steps  to
to  only once and store the datasets for posterior use with each one of the pattern-matching methods.
only once and store the datasets for posterior use with each one of the pattern-matching methods.5.6.3. Execution Flow of the Model Training Function
 in Figure 14 is executed independently for each pattern-matching method, calling the function with the same input datasets for each method, as mentioned in the previous subsection. In our implementation, we created a tailored function for each pattern-matching method. As mentioned, for simplicity, we present the simulation flow description at the general level by describing a function that is common to all of the pattern-matching methods and thus suitable for use with any of the pattern-matching methods considered.
in Figure 14 is executed independently for each pattern-matching method, calling the function with the same input datasets for each method, as mentioned in the previous subsection. In our implementation, we created a tailored function for each pattern-matching method. As mentioned, for simplicity, we present the simulation flow description at the general level by describing a function that is common to all of the pattern-matching methods and thus suitable for use with any of the pattern-matching methods considered.- In step ①, the four datasets FTT, FTV, MTV, and MTT are formatted into the input and output formats required by the NN structure implementing the selected pattern-matching method. These input and output formats are indicated in Table 6 and depicted in Figure 10, explained for each pattern-matching method in Section 4.4, and detailed in relation to the NN structures used in each pattern-matching method in Section 5.8. In the case of the pattern-matching method 4-MultFingIn-ClassOut, the output tile-classes are vectorized (e.g., using one-hot encoding).
- In step ②, the mean and standard deviation of the fingerprints and reference positions are calculated from the FTT training dataset. Then, these are used in step ③ to normalize all the datasets, shifting the values of the RSSs and positions to the zero mean, and scaling these by the inverse of the respective standard deviation. Actually, there is no need to normalize the reference positions for the fourth pattern-matching method (4-MultFingIn-ClassOut). This method is based on classification of the tile-classes. Then, for this method, the tiles are vectorized into one-hot-encoded classes.
- In step ④, the NN structure for the selected pattern-matching method is defined and introduced in the simulation process. However, the selection of the actual NN structure is decided beforehand. This is indicated by the label Mechanism 1, and shown inside a box with a dashed line, to indicate that the selection of the actual NN structure is not part of the simulation process. The selection of the NN structure is discussed in Section 5.7.1.
- In step ⑤, the random initial weights are set. This step is part of an iterative process (introduced in Section 5.5) which has the purpose of generalizing the model for moving tiles. In our simulations, the weights for each layer in the NN are set to different random initial values by calling a function provided for this purpose, taking as input a seed value. In Keras, this is achieved by retrieving the layer weight initializers, and , and setting new weights through the method for every layer in the NN model with the retrieved initializers. In each iteration of the loop for the initial random weights, all of the pseudo-random number generators are initialized with a new and unique seed (which, for convenience, in our implementation is the iteration number plus a preselected seed offset). Step ⑤ is the beginning of a loop iterating among the random initial weights for iterations, ending at step ⑪.
- In step ⑥, the training of the NN model takes place using as training data the FTT dataset of fixed tiles. The first three pattern-matching methods considered are based on regression of the position coordinates. In these methods, the target training position varies with the method. For these methods, the reference center position coordinates of the sub-tiles, returned in the data structure by the function (Pseudocode 2), are used to set the target training position. For the methods 1-SingFingIn-PosOut and 3-MultFingIn-PosOut, the position of the central sub-tile in a tile is considered the reference target training position (the selection of the central sub-tile is discussed in Section 4.4.1). For the method 2-SingFingIn-AggPosOut, the position of each one of the sub-tiles is considered the target training position. The fourth pattern-matching method, 4-MultFingIn-ClassOut, is based on classification of the tiles. In this case, the one-hot-encoded vectorization of the tile-class label is used as the training target.It is noted that in methods 1-SingFingIn-PosOut and 3-MultFingIn-PosOut, the target training position can be the same as the target reference position for the calculation of the positioning error. However, in the method 2-SingFingIn-AggPosOut, in contrast to pattern-matching methods one and three, multiple sub-tile center position estimates are aggregated. Then, the final position estimate used by us is the center of the tile, given by the aggregation performed in Equations (2) and (3). Thus, in the method 2-SingFingIn-AggPosOut, the center of the tile is used as the reference position to calculate the positioning error. In this step, the best model weights among the training epochs are selected. A checkpoint function call-back is configured to retain the weights that minimize a cost or loss metric of the model among the training epochs. The metric is evaluated using the validation dataset for fixed tiles FTV. At the end of all of the training epochs, the weights that produced the minimum metric value, among the training epochs, are retrieved and returned as the solution for the model. This process is indicated by the label Mechanism 2.
- In step ⑦, the position estimates for all of the datasets are calculated. The position estimates of the dataset of moving tiles for validation, MTV, are of importance in step ⑨ to determining the best solution among different initial weights. The position estimates of the moving tile dataset for testing, MTT, actually should be calculated after the final weights of the model are selected. However, for convenience, the position estimates of the MTT dataset are calculated at this step and stored as a temporary result. Once the final weights of the model are selected, the corresponding temporary results are returned as the final and best result of the model.The first three pattern-matching methods are based on regression. These return a normalized position estimate for each input set or vector of fingerprints. In the case of the method 2-SingFingIn-AggPosOut, the output position estimates are aggregated (as discussed in Section 4.4.2) to produce a final position estimate. Then, in the first three pattern-matching methods, the output position estimate for each input set or vector of fingerprints is unnormalized. The fourth method, 4-MultFingIn-ClassOut, returns a vector of tile-class probabilities. In this case, the position is estimated as explained in Section 4.4.4, that is, calculated from the output tile-class probabilities and the mapping between the tile-classes and the center coordinates of the tiles.It is noted that the model was trained for fixed tiles. Then, when it is used with the moving tiles of the MTV and MTT datasets, this can be interpreted as a transfer learning approach. However, the final selection of the model is biased by the action performed in step ⑨, selecting the best model among the different initial weights by evaluating the error distance in the moving tiles for the validation, MTV, dataset.
- In step ⑧, the error distances are calculated for the MTV and MTT datasets, using unnormalized positions, with Equation (1). Here, Equation (1) takes as input the estimated position coordinates and the known ground truth reference position coordinates. In the methods 1-SingFingIn-PosOut and 3-MultFingIn-PosOut, the ground truth reference position coordinates are taken from the position of the tile which was defined as the center position of the central sub-tile (as discussed in Section 4.4.1). The reference center position coordinates of the sub-tiles are returned in the data structure by the functions and . In the pattern-matching methods 2-SingFingIn-AggPosOut and 4-MultFingIn-ClassOut, the ground truth reference position is the center of the tile. This is consistent with the final position estimate in these methods calculated from the aggregated sub-tile position estimates using Equations (2) and (3) in method two and from the mapping from the tile-class labels to the center positions of the fixed tiles using Equations (4) and (5) in method four.
- In step ⑨, the Cumulative Density Function (CDF) of the error distances resulting from the MTV dataset is calculated. This step is part of the iterative process of generalizing the model for moving tiles (introduced in Section 5.5). The goal is to select the model that generalizes best for moving tiles by selecting the model that minimizes the 95th percentile of the CDF of the error distances for all of the moving tiles in the MTV dataset among the model training iterations initiated with different random weights.In the first iteration of the loop started in step ⑤, the value of the error distance at the 95th reference percentile, , of the CDF is retained as the minimum error, and the error distances and model weights for this iteration are temporarily stored and kept as the best model in step ⑩. From the second iteration onward, the error distance at the 95th reference percentile is compared against the minimum error obtained in a previous iteration. If the error distance at this percentile is smaller than the minimum error obtained in a previous iteration, this value is retained as the minimum, and the error distances and model weights for the current iteration are temporarily stored and kept as the best model in step ⑩. The training process is repeated again, with different random initial weights, repeating the process from step ⑤ until the number of iterations (given in Table 9) is completed. The number of iterations is checked with the condition of step ⑪. For convenience, in step ⑩, the error distances obtained from the testing dataset of moving tiles, MTT, are also temporarily stored. The process described above is indicated by the label Mechanism 3.
- Finally, in step ⑫, the model weights that produced the smallest error distance at the given CDF percentile are kept as the best and final weights for the model. The best weights are used to calculate the error distances in the testing dataset of moving tiles, MTT. Actually, for convenience, the estimation of the positions and calculation of the error distances for the MTT dataset are carried out in steps ⑦ and ⑧, and the best results, along with the corresponding weights, are temporarily stored in step ⑩. In addition, the error distances resulting from the MTT dataset using the best weights are permanently stored in step ⑫ to perform later comparisons among the other pattern-matching methods and among different tile arrangements (introduced in Section 5.9). The details of the settings for each pattern-matching method are detailed in Section 5.8, and the results obtained are presented in the next section.
5.7. Mechanisms to Optimize the Models and Minimize the Error Distance
- 1.
- Selection of the NN structure.
- The goal is to select a suitable NN structure such that the model can deliver results with a minimum positioning error when compared to models implementing other NN structures.
- 2.
- Selection of the best model weights among training epochs.
- The goal is to select the model weights that minimize the positioning error, generalizing the model for fixed tiles.
- 3.
- Selection of the best weights among model training iterations with different initial random weights.
- The goal is to select the model weights that minimize the positioning error, generalizing the model for moving tiles.
5.7.1. Mechanism 1: Selection of the NN Structure
5.7.2. Mechanism 2: Selection of the Best Model Weights Among Training Epochs
5.7.3. Mechanism 3: Selection of the Best Model Weights with Different Initial Weights
5.8. NN Structure for Each Pattern-Matching Method and Model Training Details
5.8.1. NN Structure for Methods 1SingFingInPosOut and 2SingFingInAggPosOut
5.8.2. NN Structure for Pattern-Matching Method 3-MultFingIn-PosOut
5.8.3. NN Structure for Pattern-Matching Method 4-MultFingIn-ClassOut
5.8.4. Notes on the Model Training Hyperparameters
5.9. Execution of the Simulations
5.10. Consistency in the Comparison of the Results Among Scenarios with Different Tile Sizes
5.11. Software and Hardware Details
6. Results of the Simulations
6.1. Baseline Reference Performance
6.2. Results with Pattern-Matching Method 1-SingFingIn-PosOut
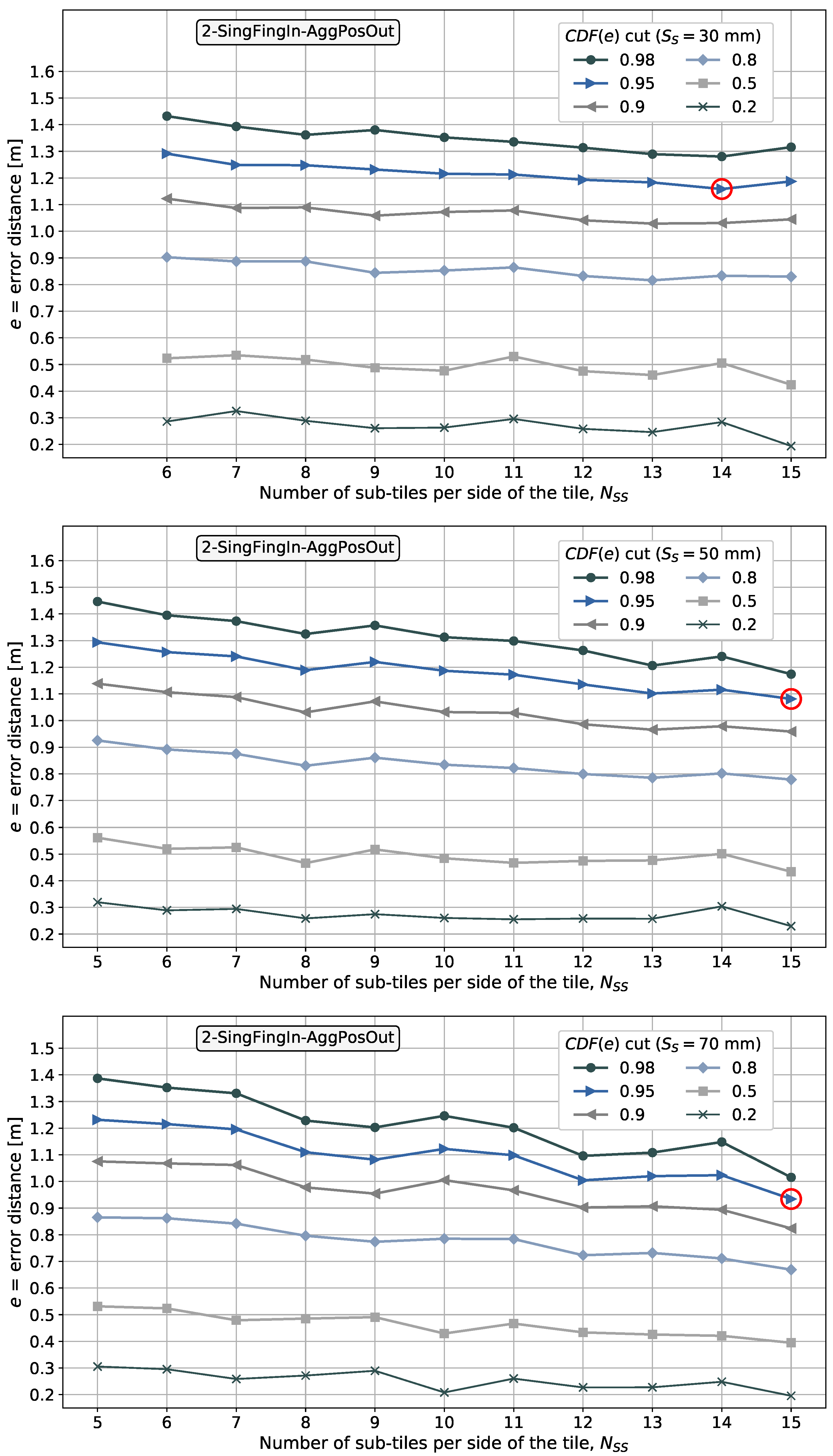
6.3. Results with Pattern-Matching Method 2-SingFingIn-AggPosOut
- sub-tiles per side of the tile, for mm;
- sub-tiles per side of the tile, for mm;
- sub-tiles per side of the tile, for mm.
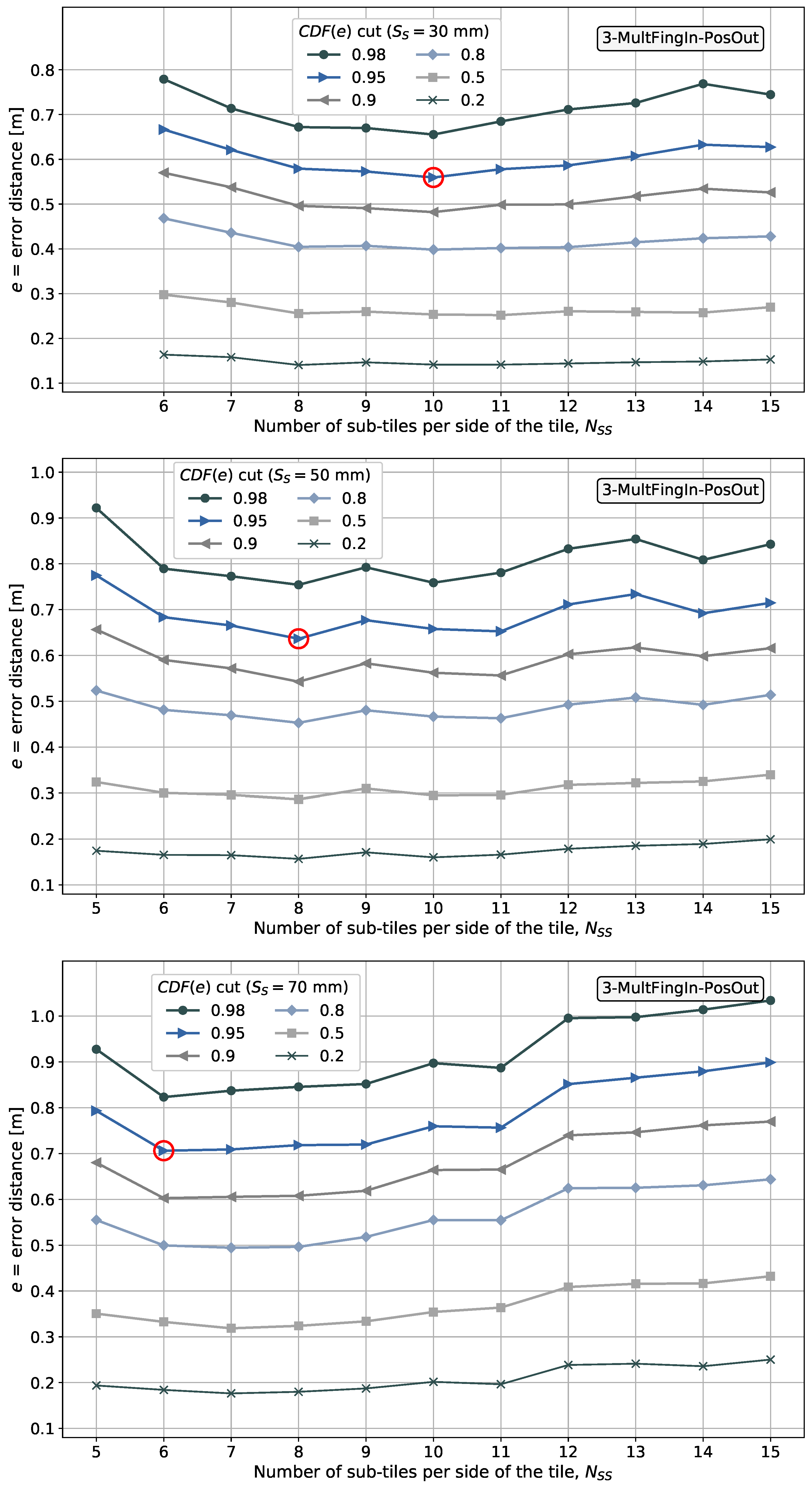
6.4. Results with Pattern-Matching Method 3-MultFingIn-PosOut
- sub-tiles per side of the tile, for mm;
- sub-tiles per side of the tile, for mm;
- sub-tiles per side of the tile, for mm.
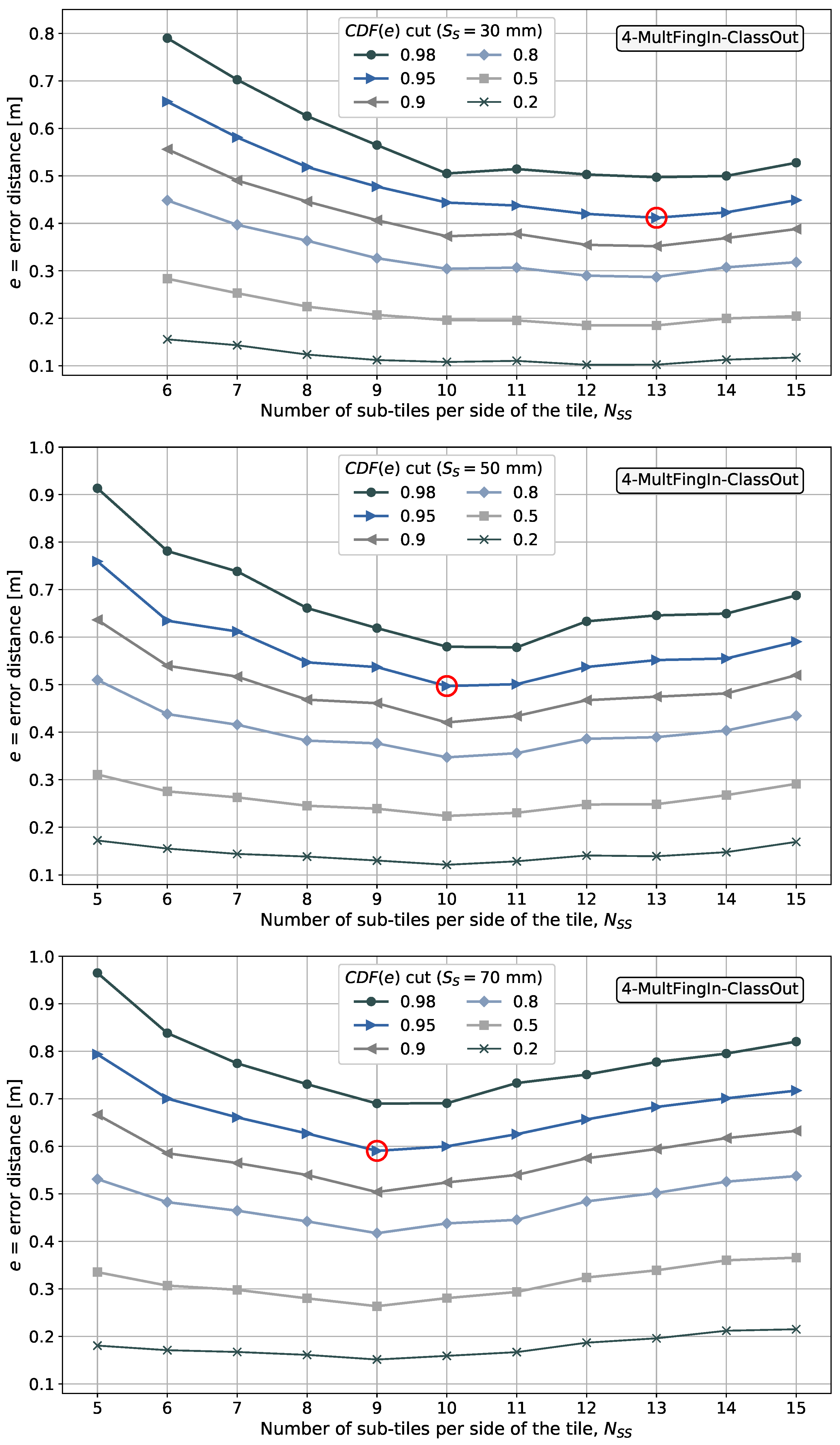
6.5. Results with Pattern-Matching Method 4-MultFingIn-ClassOut
- sub-tiles per side of the tile, for mm;
- sub-tiles per side of the tile, for mm;
- sub-tiles per side of the tile, for mm.

6.6. Comparison of the Results Among the Pattern-Matching Methods
- Comparison of the results obtained with the smallest 2D sensor array considered for different side lengths of the sub-tiles among the different pattern-matching methods;
- Comparison of the best results obtained that minimize the error distance for different side lengths of the sub-tiles among the different pattern-matching methods.
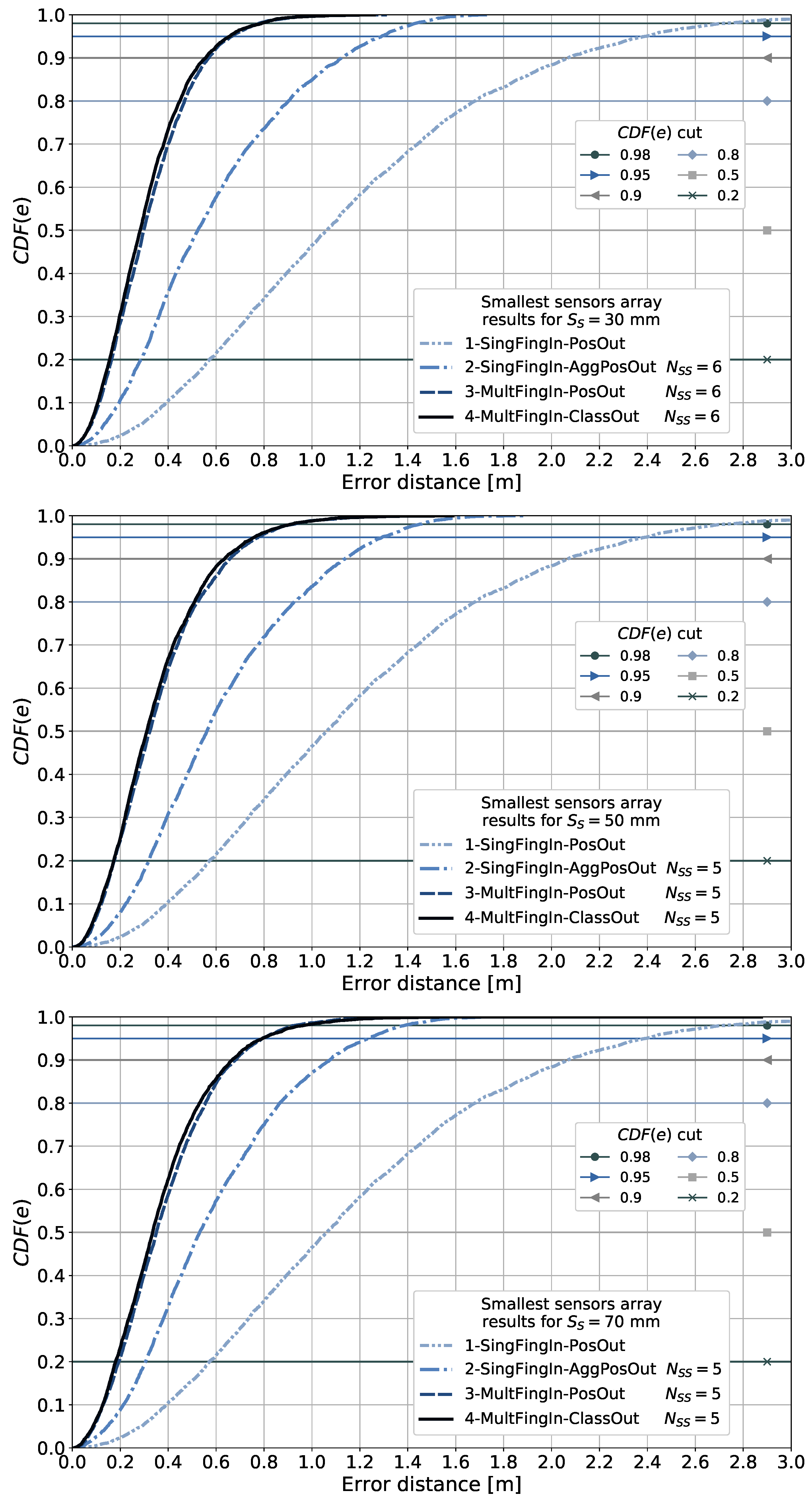
6.6.1. Comparison of the Results Obtained Using the Smallest 2D Sensor Array Considered
- mm with ;
- mm with ;
- mm with .
6.6.2. Comparison of the Best Results Obtained That Minimize the Error Distance
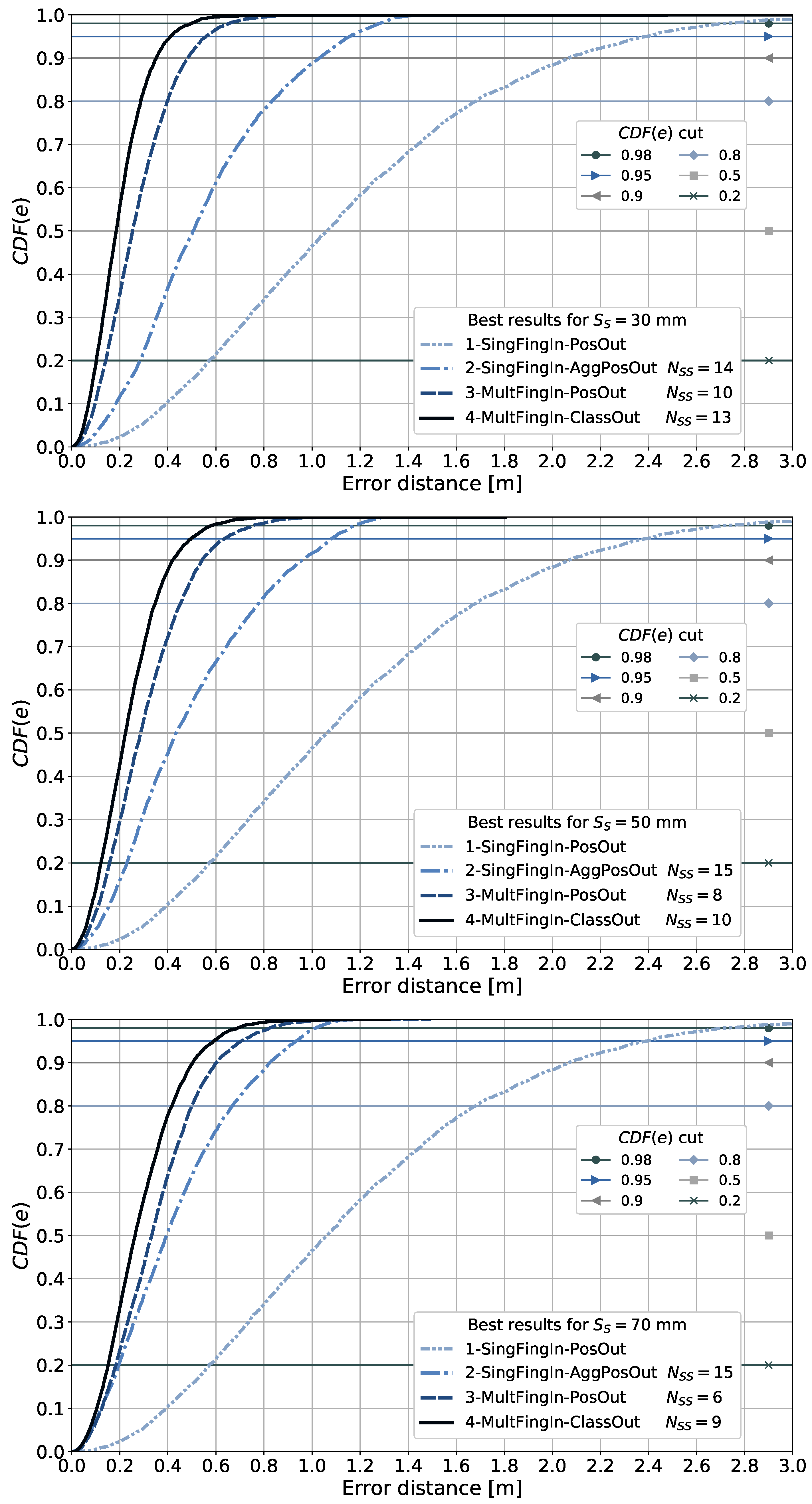
6.7. Pattern-Matching Method 4-MultFingIn-ClassOut Details
6.8. Observations for Cases with Spatial Side Information and Aggregation in the Fingerprint Domain
6.8.1. Lower Bound in Performance for the Smallest 2D Sensor Array Considered
6.8.2. Two-Dimensional Sensor Array Sizes and Positioning Errors for the Best Results
- ○
- Discussion About the Reduction in the Size of the 2D Sensor Array and ConstraintsThe observation mentioned above, discussing that at least 95 percent of the measurements have an error distance equal to or below the sampling resolution used by the 2D sensor array opens many research questions. For example, one line of thought suggests that the smaller the 2D sensor array, the smaller the positioning error. The reduction in the size of the 2D sensor array or tile is actually controlled by the combined result of reducing the side lengths of the sub-tiles, , and increasing the number of sub-tiles per side of the tile, . Thus, if this trend continues, near the limit, we would have a very small 2D sensor array with a large number of sensors. Decreasing the 2D sensor array further to the limit so that it converges to what is ideally a point on a 2D positioning plane, it can be thought that the minimization of the positioning error is not due to the availability of adjacent samples but due to the high number of samples collected at that point. However, note that this observation is associated with the assumed collection of training samples from every position delimited by fixed tiles, which in this case would be assumed for every single point on the positioning plane (and which at the limit will be an infinite number of points). Then, this view challenges the idea of benefiting from using spatial side information, suggesting that taking a high number of samples at a single point would produce better results than collecting samples at adjacent points. Yet this generates many questions. The instantaneous and simultaneous collection of samples using multiple sensors or receivers is not physically possible when all of the sensors converge to a single point. Then, we can think about using a single sensor or receiver and taking a high number of samples in the time domain, as has been suggested in some research works in the past. However, the initial observation was based on the assumption of the sampling of the entire positioning area. The sampling of the entire positioning area is realistically feasible if it is performed using a 2D sensor array with a size equivalent to a tile size of, say, above mm2. The sampling can be achieved using a certain mechanized process. One example could be sampling fingerprints using a robot driven by stepping motors. Another example could be using for the sampling the same machinery that needs the positioning information, taking overlapped samples, which will then be post-processed as training tiles. In contrast, it is not realistic to sample every point in the positioning area when the meaning of a point is defined in a mathematical sense, or even when it is defined as a very small discretized area. Another observation is that if there are no adjacent samples, it is not possible to perform the convolution operation in pattern-matching method 4-MultFingIn-ClassOut.Another line of thought is that in our assumptions, we did not consider the actual antenna design aspects related to the construction of the 2D sensor array, such as the effects and constraints of the inter-antenna spacing. These may counteract the performance gain experienced when reducing the 2D sensor array’s size in a real system. It was observed that for the system under consideration, there is a correlation between the reduction in the 2D sensor array’s size and the reduction in the positioning error. However, in reality, it could be expected that the physical arrangement of the sensors will introduce constraints that will counteract this trend. For example, in the case of implementing the 2D sensor array with an array of antennas, the inter-antenna spacing will add a constraint. In the case of implementing the 2D sensor array with a mechanical device sampling all of the positions equivalent to the sub-tiles, the precision of the mechanism and possible vibrations in the sequential sampling will add a constraint limiting the smallest possible size of the 2D sensor array. This consideration is discussed in Section 7.2.Yet, another line of thought is based on the idea that it would be beneficial to exploit the side information from adjacent positions as far as possible from the target position. This is based on the idea that the further apart the sensors are, the more the RSS level may vary enough to counteract the variations due to the fading. A possible research direction associated with this line of thought would be to study the use of side information collected using a kind of 2D sensor array with sparse sensors.
6.8.3. The Best Results and Border Conditions in the Positioning Area in the Scenario
6.9. Notes on the Computing Costs for the Proposed Pattern-Matching Methods
6.10. Reproducibility of the Results
7. Summary, Conclusions, and Discussion
7.1. Conclusions
7.1.1. Conclusions on the Use of Spatial Side Information
7.1.2. Conclusions on the Aggregation of Fingerprints in the Fingerprint Domain
7.2. Possible Limitations from the Assumptions
7.3. Discussion
7.4. Directions for Future Work
- Studying the effects of positioning considering the rotation along the vertical axis and tilting on the horizontal axes of the 2D sensor array.
- Modeling of the 2D sensor array as, for example, an antenna array, considering the effects of constructive and destructive waves for a given antenna spacing, the AoA of the radio-waves, etc.
- A performance evaluation of a 2D sensor array using datasets obtained from field measurements.
- Exploration of alternative pattern-matching methods or an enhancement to the proposed methods.
- The use of other tile arrangements.
- The use of overlapping fixed tiles.
- The use of any other tile format or shape. For example, an interesting tile format to consider would be hexagonal-shaped tiles.
- The use of spatial side information collected using a kind of 2D sensor array with sparse sensors—for example, distributed along the machinery or object(s) performing the positioning.
- Alternative mappings from the tile-classes to the positions using pattern-matching method 4-MultFingIn-ClassOut.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- De Lima, C.; Belot, D.; Berkvens, R.; Bourdoux, A.; Dardari, D.; Guillaud, M.; Isomursu, M.; Lohan, E.S.; Miao, Y.; Barreto, A.N.; et al. Convergent Communication, Sensing and Localization in 6G Systems: An Overview of Technologies, Opportunities and Challenges. IEEE Access 2021, 9, 26902–26925. [Google Scholar] [CrossRef]
- Pin Tan, D.K.; He, J.; Li, Y.; Bayesteh, A.; Chen, Y.; Zhu, P.; Tong, W. Integrated Sensing and Communication in 6G: Motivations, Use Cases, Requirements, Challenges and Future Directions. In Proceedings of the 2021 1st IEEE International Online Symposium on Joint Communications and Sensing, Dresden, Germany, 23–24 February 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, F.; Cui, Y.; Masouros, C.; Xu, J.; Han, T.X.; Eldar, Y.C.; Buzzi, S. Integrated Sensing and Communications: Toward Dual-Functional Wireless Networks for 6G and Beyond. IEEE J. Sel. Areas Commun. 2022, 40, 1728–1767. [Google Scholar] [CrossRef]
- Chepuri, S.P.; Shlezinger, N.; Liu, F.; Alexandropoulos, G.C.; Buzzi, S.; Eldar, Y.C. Integrated Sensing and Communications With Reconfigurable Intelligent Surfaces: From signal modeling to processing. IEEE Signal Process. Mag. 2023, 40, 41–62. [Google Scholar] [CrossRef]
- Liu, H.; Darabi, H.; Banerjee, P.; Liu, J. Survey of Wireless Indoor Positioning Techniques and Systems. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2007, 37, 1067–1080. [Google Scholar] [CrossRef]
- Al-Ammar, M.A.; Alhadhrami, S.; Al-Salman, A.; Alarifi, A.; Al-Khalifa, H.S.; Alnafessah, A.; Alsaleh, M. Comparative Survey of Indoor Positioning Technologies, Techniques, and Algorithms. In Proceedings of the 2014 International Conference on Cyberworlds, Santander, Spain, 6–8 October 2014; pp. 245–252. [Google Scholar] [CrossRef]
- Yassin, A.; Nasser, Y.; Awad, M.; Al-Dubai, A.; Liu, R.; Yuen, C.; Raulefs, R.; Aboutanios, E. Recent Advances in Indoor Localization: A Survey on Theoretical Approaches and Applications. IEEE Comm. Surv. Tutorials 2017, 19, 1327–1346. [Google Scholar] [CrossRef]
- Davidson, P.; Piché, R. A Survey of Selected Indoor Positioning Methods for Smartphones. IEEE Commun. Surv. Tutorials 2017, 19, 1347–1370. [Google Scholar] [CrossRef]
- Laoudias, C.; Moreira, A.; Kim, S.; Lee, S.; Wirola, L.; Fischione, C. A Survey of Enabling Technologies for Network Localization, Tracking, and Navigation. IEEE Commun. Surv. Tutorials 2018, 20, 3607–3644. [Google Scholar] [CrossRef]
- Zafari, F.; Gkelias, A.; Leung, K.K. A Survey of Indoor Localization Systems and Technologies. IEEE Commun. Surv. Tutorials 2019, 21, 2568–2599. [Google Scholar] [CrossRef]
- Kim Geok, T.; Zar Aung, K.; Sandar Aung, M.; Thu Soe, M.; Abdaziz, A.; Pao Liew, C.; Hossain, F.; Tso, C.P.; Yong, W.H. Review of Indoor Positioning: Radio Wave Technology. Appl. Sci. 2021, 11, 279. [Google Scholar] [CrossRef]
- Feng, X.; Nguyen, K.A.; Luo, Z. A survey of deep learning approaches for WiFi-based indoor positioning. J. Inf. Telecommun. 2022, 6, 163–216. [Google Scholar] [CrossRef]
- Zhuang, Y.; Zhang, C.; Huai, J.; Li, Y.; Chen, L.; Chen, R. Bluetooth Localization Technology: Principles, Applications, and Future Trends. IEEE Internet Things J. 2022, 9, 23506–23524. [Google Scholar] [CrossRef]
- Sartayeva, Y.; Chan, H.C.; Ho, Y.H.; Chong, P.H. A survey of indoor positioning systems based on a six-layer model. Comput. Netw. 2023, 237, 110042. [Google Scholar] [CrossRef]
- Naser, R.S.; Lam, M.C.; Qamar, F.; Zaidan, B.B. Smartphone-Based Indoor Localization Systems: A Systematic Literature Review. Electronics 2023, 12, 1814. [Google Scholar] [CrossRef]
- Pascacio, P.; Casteleyn, S.; Torres-Sospedra, J.; Lohan, E.S.; Nurmi, J. Collaborative Indoor Positioning Systems: A Systematic Review. Sensors 2021, 21, 1002. [Google Scholar] [CrossRef]
- Seguel, F.; Palacios-Játiva, P.; Azurdia-Meza, C.A.; Krommenacker, N.; Charpentier, P.; Soto, I. Underground mine positioning: A review. IEEE Sens. J. 2022, 22, 4755–4771. [Google Scholar] [CrossRef]
- Zhang, H.; Li, B.; Karimi, M.; Saydam, S.; Hassan, M. Recent Advancements in IoT Implementation for Environmental, Safety, and Production Monitoring in Underground Mines. IEEE Internet Things J. 2023, 10, 14507–14526. [Google Scholar] [CrossRef]
- Liu, S.; Liu, L.; Tang, J.; Yu, B.; Wang, Y.; Shi, W. Edge Computing for Autonomous Driving: Opportunities and Challenges. Proc. IEEE 2019, 107, 1697–1716. [Google Scholar] [CrossRef]
- Pham, Q.V.; Fang, F.; Ha, V.N.; Piran, M.J.; Le, M.; Le, L.B.; Hwang, W.J.; Ding, Z. A Survey of Multi-Access Edge Computing in 5G and Beyond: Fundamentals, Technology Integration, and State-of-the-Art. IEEE Access 2020, 8, 116974–117017. [Google Scholar] [CrossRef]
- Kim, G.; Choi, S.; Kim, A. Scan Context++: Structural Place Recognition Robust to Rotation and Lateral Variations in Urban Environments. IEEE Trans. Robot. 2022, 38, 1856–1874. [Google Scholar] [CrossRef]
- Xu, X.; Lu, S.; Wu, J.; Lu, H.; Zhu, Q.; Liao, Y.; Xiong, R.; Wang, Y. RING++: Roto-Translation Invariant Gram for Global Localization on a Sparse Scan Map. IEEE Trans. Robot. 2023, 39, 4616–4635. [Google Scholar] [CrossRef]
- Zhuang, Y.; Hua, L.; Qi, L.; Yang, J.; Cao, P.; Cao, Y.; Wu, Y.; Thompson, J.; Haas, H. A Survey of Positioning Systems Using Visible LED Lights. IEEE Commun. Surv. Tutorials 2018, 20, 1963–1988. [Google Scholar] [CrossRef]
- Tran, H.Q.; Ha, C. Fingerprint-Based Indoor Positioning System Using Visible Light Communication—A Novel Method for Multipath Reflections. Electronics 2019, 8, 63. [Google Scholar] [CrossRef]
- Lichtenegger, F.; Leiner, C.; Sommer, C.; Weiss, A.P.; Wenzl, F.P.; Salem, Z. Simulation of fingerprinting based Visible Light Positioning without the need of prior map generation. In Proceedings of the Illumination Optics VI, Online, 13–18 September 2021; Kidger, T.E., David, S., Eds.; International Society for Optics and Photonics, SPIE, 2021; Volume 11874, pp. 119–133. [Google Scholar] [CrossRef]
- Huilla, S.; Pepi, C.; Antoniou, M.; Laoudias, C.; Horsmanheimo, S.; Lembo, S.; Laukkanen, M.; Ellinas, G. Indoor Localization with Wi-Fi Fine Timing Measurements Through Range Filtering and Fingerprinting Methods. In Proceedings of the 2020 IEEE 31st Annual International Symposium on Personal, Indoor and Mobile Radio Communications, London, UK, 31 August–3 September 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Yu, L.; Laaraiedh, M.; Avrillon, S.; Uguen, B. Fingerprinting localization based on neural networks and ultra-wideband signals. In Proceedings of the 2011 IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), Bilbao, Spain, 14–17 December 2011; pp. 184–189. [Google Scholar] [CrossRef]
- Gettapola, K.I.; Ranaweera, R.R.W.M.H.D.; Godaliyadda, G.M.R.I.; Imara, M.N.F. Location based fingerprinting techniques for indoor positioning. In Proceedings of the 2017 6th National Conference on Technology and Management (NCTM), Malabe, Sri Lanka, 27 January 2017; pp. 175–180. [Google Scholar] [CrossRef]
- Aparicio, J.; Álvarez, F.J.; Hernández, Á.; Holm, S. A Survey on Acoustic Positioning Systems for Location-Based Services. IEEE Trans. Instrum. Meas. 2022, 71, 1–36. [Google Scholar] [CrossRef]
- Ashraf, I.; Kang, M.; Hur, S.; Park, Y. MINLOC:Magnetic Field Patterns-Based Indoor Localization Using Convolutional Neural Networks. IEEE Access 2020, 8, 66213–66227. [Google Scholar] [CrossRef]
- Galván-Tejada, C.E.; Zanella-Calzada, L.A.; García-Domínguez, A.; Magallanes-Quintanar, R.; Luna-García, H.; Celaya-Padilla, J.M.; Galván-Tejada, J.I.; Vélez-Rodríguez, A.; Gamboa-Rosales, H. Estimation of Indoor Location Through Magnetic Field Data: An Approach Based On Convolutional Neural Networks. ISPRS Int. J. -Geo-Inf. 2020, 9, 226. [Google Scholar] [CrossRef]
- Wang, X.; Gao, L.; Mao, S.; Pandey, S. CSI-Based Fingerprinting for Indoor Localization: A Deep Learning Approach. IEEE Trans. Veh. Technol. 2017, 66, 763–776. [Google Scholar] [CrossRef]
- Ashraf, I.; Hur, S.; Park, Y. Application of Deep Convolutional Neural Networks and Smartphone Sensors for Indoor Localization. Appl. Sci. 2019, 9, 2337. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, L.; Liu, Q.; Yin, Y.; Cheng, L.; Zimmermann, R. Fusion of Magnetic and Visual Sensors for Indoor Localization: Infrastructure-Free and More Effective. IEEE Trans. Multimed. 2017, 19, 874–888. [Google Scholar] [CrossRef]
- Sánchez-Rodríguez, D.; Quintana-Suárez, M.A.; Alonso-González, I.; Ley-Bosch, C.; Sánchez-Medina, J.J. Fusion of Channel State Information and Received Signal Strength for Indoor Localization Using a Single Access Point. Remote. Sens. 2020, 12, 1995. [Google Scholar] [CrossRef]
- Koweerawong, C.; Wipusitwarakun, K.; Kaemarungsi, K. Indoor localization improvement via adaptive RSS fingerprinting database. In Proceedings of the International Conference on Information Networking 2013 (ICOIN), Bangkok, Thailand, 28–30 January 2013; pp. 412–416. [Google Scholar] [CrossRef]
- Jan, R.H.; Lee, Y.R. An indoor geolocation system for wireless LANs. In Proceedings of the 2003 International Conference on Parallel Processing Workshops, Kaohsiung, Taiwan, 6–9 October 2003; pp. 29–34. [Google Scholar] [CrossRef]
- Ma, J.; Li, X.; Tao, X.; Lu, J. Cluster filtered KNN: A WLAN-based indoor positioning scheme. In Proceedings of the 2008 International Symposium on a World of Wireless, Mobile and Multimedia Networks, Newport Beach, CA, USA, 23–26 June 2008; pp. 1–8. [Google Scholar] [CrossRef]
- Teuber, A.; Eissfeller, B.; Pany, T. A Two-Stage Fuzzy Logic Approach for Wireless LAN Indoor Positioning. In Proceedings of the 2006 IEEE/ION Position, Location, And Navigation Symposium, San Diego, CA, USA, 25–27 April 2006; pp. 730–738. [Google Scholar] [CrossRef]
- Yim, J. Introducing a decision tree-based indoor positioning technique. Expert Syst. Appl. 2008, 34, 1296–1302. [Google Scholar] [CrossRef]
- Brunato, M.; Battiti, R. Statistical learning theory for location fingerprinting in wireless LANs. Comput. Netw. 2005, 47, 825–845. [Google Scholar] [CrossRef]
- Lembo, S.; Horsmanheimo, S.; Honkamaa, P. Indoor Positioning Based on RSS Fingerprinting in a LTE Network: Method Based on Genetic Algorithms. In Proceedings of the 2019 IEEE International Conference on Communications Workshops (ICC Workshops), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Wu, C.L.; Fu, L.C.; Lian, F.L. WLAN location determination in e-home via support vector classification. In Proceedings of the IEEE International Conference on Networking, Sensing and Control, Taipei, Taiwan, 21–23 March 2004; Volume 2, pp. 1026–1031. [Google Scholar] [CrossRef]
- Nessa, A.; Adhikari, B.; Hussain, F.; Fernando, X.N. A Survey of Machine Learning for Indoor Positioning. IEEE Access 2020, 8, 214945–214965. [Google Scholar] [CrossRef]
- Zhu, X.; Qu, W.; Qiu, T.; Zhao, L.; Atiquzzaman, M.; Wu, D.O. Indoor Intelligent Fingerprint-Based Localization: Principles, Approaches and Challenges. IEEE Commun. Surv. Tutorials 2020, 22, 2634–2657. [Google Scholar] [CrossRef]
- Roy, P.; Chowdhury, C. A Survey of Machine Learning Techniques for Indoor Localization and Navigation Systems. J. Intell. Robot. Syst. 2021, 101. [Google Scholar] [CrossRef]
- Miramá, V.F.; Díez, L.E.; Bahillo, A.; Quintero, V. A Survey of Machine Learning in Pedestrian Localization Systems: Applications, Open Issues and Challenges. IEEE Access 2021, 9, 120138–120157. [Google Scholar] [CrossRef]
- Singh, N.; Choe, S.; Punmiya, R. Machine Learning Based Indoor Localization Using Wi-Fi RSSI Fingerprints: An Overview. IEEE Access 2021, 9, 127150–127174. [Google Scholar] [CrossRef]
- 3GPP. Report on Specification Location Services (LCS); TR 25.923 V1.0.0 (1999-04); ETSI: Sophia Antipolis, France, 1999. [Google Scholar]
- 3GPP. Location Services (LCS); Technical Specification Service Description; Stage 1 (Release 16)—TS 22.071 V16.0.0 (2020-07); ETSI: Sophia Antipolis, France, 2020. [Google Scholar]
- 3GPP. Technical Specification Group Services and System Aspects; Functional Stage 2 Description of Location Services (LCS) (Release 16)—TS 23.271 V16.0.0 (2020-07); ETSI: Sophia Antipolis, France, 2020. [Google Scholar]
- 3GPP. Stage 2 Functional Specification of User Equipment (UE); Technical Specification Positioning in UTRAN (Release 16)—TS 25.305 V16.0.0 (2020-07); ETSI: Sophia Antipolis, France, 2020. [Google Scholar]
- Larsson, E.G.; Edfors, O.; Tufvesson, F.; Marzetta, T.L. Massive MIMO for next generation wireless systems. IEEE Commun. Mag. 2014, 52, 186–195. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, S.; Lin, Y.; Zheng, J.; Ai, B.; Hanzo, L. Cell-Free Massive MIMO: A New Next-Generation Paradigm. IEEE Access 2019, 7, 99878–99888. [Google Scholar] [CrossRef]
- Zhang, J.; Björnson, E.; Matthaiou, M.; Ng, D.W.K.; Yang, H.; Love, D.J. Prospective Multiple Antenna Technologies for Beyond 5G. IEEE J. Sel. Areas Commun. 2020, 38, 1637–1660. [Google Scholar] [CrossRef]
- Obakhena, H.; Imoize, A.; Anyasi, F.; Kavitha, K. Application of cell-free massive MIMO in 5G and beyond 5G wireless networks: A survey. J. Eng. Appl. Sci. 2021, 68, 13. [Google Scholar] [CrossRef]
- Hu, S.; Rusek, F.; Edfors, O. Beyond Massive MIMO: The Potential of Data Transmission With Large Intelligent Surfaces. IEEE Trans. Signal Process. 2018, 66, 2746–2758. [Google Scholar] [CrossRef]
- Savic, V.; Larsson, E.G. Fingerprinting-Based Positioning in Distributed Massive MIMO Systems. In Proceedings of the 2015 IEEE 82nd Vehicular Technology Conference (VTC2015-Fall), Boston, MA, USA, 6–9 September 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Vieira, J.; Leitinger, E.; Sarajlic, M.; Li, X.; Tufvesson, F. Deep convolutional neural networks for massive MIMO fingerprint-based positioning. In Proceedings of the 2017 IEEE 28th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Montreal, QC, Canada, 8–13 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Prasad, K.N.R.S.V.; Hossain, E.; Bhargava, V.K. Machine Learning Methods for RSS-Based User Positioning in Distributed Massive MIMO. IEEE Trans. Wirel. Commun. 2018, 17, 8402–8417. [Google Scholar] [CrossRef]
- Sun, X.; Wu, C.; Gao, X.; Li, G.Y. Fingerprint-Based Localization for Massive MIMO-OFDM System With Deep Convolutional Neural Networks. IEEE Trans. Veh. Technol. 2019, 68, 10846–10857. [Google Scholar] [CrossRef]
- Salihu, A.; Schwarz, S.; Pikrakis, A.; Rupp, M. Low-dimensional Representation Learning for Wireless CSI-based Localisation. In Proceedings of the 2020 16th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Thessaloniki, Greece, 12–14 October 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Wu, C.; Yi, X.; Wang, W.; You, L.; Huang, Q.; Gao, X.; Liu, Q. Learning to Localize: A 3D CNN Approach to User Positioning in Massive MIMO-OFDM Systems. IEEE Trans. Wirel. Commun. 2021, 20, 4556–4570. [Google Scholar] [CrossRef]
- Deng, J.; Tirkkonen, O.; Zhang, J.; Jiao, X.; Studer, C. Network-side Localization via Semi-Supervised Multi-point Channel Charting. In Proceedings of the 2021 International Wireless Communications and Mobile Computing (IWCMC), Harbin, China, 28 June–2 July 2021; pp. 1654–1660. [Google Scholar] [CrossRef]
- Hejazi, F.; Vuckovic, K.; Rahnavard, N. DyLoc: Dynamic Localization for Massive MIMO Using Predictive Recurrent Neural Networks. In Proceedings of the IEEE INFOCOM 2021—IEEE Conference on Computer Communications, Vancouver, BC, Canada, 10–13 May 2021; pp. 1–9. [Google Scholar] [CrossRef]
- Qiu, J.; Xu, K.; Shen, Z. Cooperative Fingerprint Positioning for Cell-Free Massive MIMO Systems. In Proceedings of the 2020 International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 21–23 October 2020; pp. 382–387. [Google Scholar] [CrossRef]
- Wei, C.; Xu, K.; Shen, Z.; Xia, X.; Xie, W.; Chen, L.; Xu, J. Joint AOA-RSS Fingerprint Based Localization for Cell-Free Massive MIMO Systems. In Proceedings of the 2020 IEEE 6th International Conference on Computer and Communications (ICCC), Chengdu, China, 11–14 December 2020; pp. 590–595. [Google Scholar] [CrossRef]
- Sánchez, J.R.; Edfors, O.; Liu, L. Positioning for Distributed Large Intelligent Surfaces using Neural Network with Probabilistic Layer. In Proceedings of the 2021 IEEE Globecom Workshops (GC Wkshps), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiang, T.; Yu, W. Localization with Reconfigurable Intelligent Surface: An Active Sensing Approach. IEEE Trans. Wirel. Commun. 2023, 23, 7698–7711. [Google Scholar] [CrossRef]
- Wu, T.; Pan, C.; Pan, Y.; Ren, H.; Elkashlan, M.; Wang, C.X. Fingerprint-Based mmWave Positioning System Aided by Reconfigurable Intelligent Surface. IEEE Wirel. Commun. Lett. 2023, 12, 1379–1383. [Google Scholar] [CrossRef]
- Chapre, Y.; Ignjatovic, A.; Seneviratne, A.; Jha, S. CSI-MIMO: An efficient Wi-Fi fingerprinting using Channel State Information with MIMO. Pervasive Mob. Comput. 2015, 23, 89–103. [Google Scholar] [CrossRef]
- Zeng, X.; Zhang, F.; Wang, B.; Liu, K.J.R. Massive MIMO for High-Accuracy Target Localization and Tracking. IEEE Internet Things J. 2021, 8, 10131–10145. [Google Scholar] [CrossRef]
- Gong, X.; Yu, X.; Liu, X.; Gao, X. Machine Learning-Based Fingerprint Positioning for Massive MIMO Systems. IEEE Access 2022, 10, 89320–89330. [Google Scholar] [CrossRef]
- Nguyen, C.L.; Georgiou, O.; Gradoni, G.; Di Renzo, M. Wireless Fingerprinting Localization in Smart Environments Using Reconfigurable Intelligent Surfaces. IEEE Access 2021, 9, 135526–135541. [Google Scholar] [CrossRef]
- Luo, X.; Meratnia, N. A Codeword-Independent Localization Technique for Reconfigurable Intelligent Surface Enhanced Environments Using Adversarial Learning. Sensors 2023, 23, 984. [Google Scholar] [CrossRef]
- Bahl, P.; Padmanabhan, V. RADAR: An in-building RF-based user location and tracking system. In Proceedings of the IEEE INFOCOM 2000—Conference on Computer Communications—Nineteenth Annual Joint Conference of the IEEE Computer and Communications Societies (Cat. No.00CH37064), Tel Aviv, Israel, 26–30 March 2000; Volume 2, pp. 775–784. [Google Scholar] [CrossRef]
- Hanzo, L.; Liew, T.H.; Yeap, B.L. Turbo Coding, Turbo Equalisation and Space-Time Coding for Transmission Over Fading Channels; Wiley: Chichester, UK, 2002. [Google Scholar]
- Goldsmith, A. Wireless Communications; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Konatowski, S.; Pieniȩżny, A.T. A comparison of estimation accuracy by the use of KF, EKF & UKF filters. WIT Trans. Model. Simul. 2007, 46, 779–789. [Google Scholar] [CrossRef]
- Wymeersch, H.; He, J.; Denis, B.; Clemente, A.; Juntti, M. Radio Localization and Mapping With Reconfigurable Intelligent Surfaces: Challenges, Opportunities, and Research Directions. IEEE Veh. Technol. Mag. 2020, 15, 52–61. [Google Scholar] [CrossRef]
- He, J.; Wymeersch, H.; Kong, L.; Silvén, O.; Juntti, M. Large Intelligent Surface for Positioning in Millimeter Wave MIMO Systems. In Proceedings of the 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 25–28 May 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, H.; Di, B.; Bian, K.; Han, Z.; Song, L. Towards Ubiquitous Positioning by Leveraging Reconfigurable Intelligent Surface. IEEE Commun. Lett. 2021, 25, 284–288. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, H.; Di, B.; Bian, K.; Han, Z.; Song, L. MetaLocalization: Reconfigurable Intelligent Surface Aided Multi-User Wireless Indoor Localization. IEEE Trans. Wirel. Commun. 2021, 20, 7743–7757. [Google Scholar] [CrossRef]
- Cai, C.; Deng, L.; Li, S. CSI-Based Device-Free Indoor Localization Using Convolutional Neural Networks. In Proceedings of the 2018 IEEE 4th International Conference on Computer and Communications (ICCC), Chengdu, China, 7–10 December 2018; pp. 753–757. [Google Scholar] [CrossRef]
- Yan, J.; Wan, L.; Wei, W.; Wu, X.; Zhu, W.P.; Lun, D.P.K. Device-Free Activity Detection and Wireless Localization Based on CNN Using Channel State Information Measurement. IEEE Sens. J. 2021, 21, 24482–24494. [Google Scholar] [CrossRef]
- Sun, W.; Yan, J. A CNN based localization and activity recognition algorithm using multi-receiver CSI measurements and decision fusion. In Proceedings of the 2022 International Conference on Computer, Information and Telecommunication Systems (CITS), Piraeus, Greece, 13–15 July 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Torres-Sospedra, J.; Montoliu, R.; Martínez-Usó, A.; Avariento, J.P.; Arnau, T.J.; Benedito-Bordonau, M.; Huerta, J. UJIIndoorLoc: A new multi-building and multi-floor database for WLAN fingerprint-based indoor localization problems. In Proceedings of the 2014 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Busan, Republic of Korea, 27–30 October 2014; pp. 261–270. [Google Scholar] [CrossRef]
- Mendoza-Silva, G.M.; Richter, P.; Torres-Sospedra, J.; Lohan, E.S.; Huerta, J. Long-Term WiFi Fingerprinting Dataset for Research on Robust Indoor Positioning. Data 2018, 3, 3. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Y.; Li, W.; Tao, X.; Zhang, P. ConFi: Convolutional Neural Networks Based Indoor Wi-Fi Localization Using Channel State Information. IEEE Access 2017, 5, 18066–18074. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Mao, S. CiFi: Deep convolutional neural networks for indoor localization with 5 GHz Wi-Fi. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Mao, S. ResLoc: Deep residual sharing learning for indoor localization with CSI tensors. In Proceedings of the 2017 IEEE 28th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Montreal, QC, Canada, 8–13 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Cai, C.; Deng, L.; Zheng, M.; Li, S. PILC: Passive Indoor Localization Based on Convolutional Neural Networks. In Proceedings of the 2018 Ubiquitous Positioning, Indoor Navigation and Location-Based Services (UPINLBS), Wuhan, China, 22–23 March 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Mittal, A.; Tiku, S.; Pasricha, S. Adapting Convolutional Neural Networks for Indoor Localization with Smart Mobile Devices. In Proceedings of the 2018 on Great Lakes Symposium on VLSI, Chicago, IL, USA, 23–25 May 2018; pp. 117–122. [Google Scholar] [CrossRef]
- Ibrahim, M.; Torki, M.; ElNainay, M. CNN based Indoor Localization using RSS Time-Series. In Proceedings of the 2018 IEEE Symposium on Computers and Communications (ISCC), Natal, Brazil, 25–28 June 2018; pp. 01044–01049. [Google Scholar] [CrossRef]
- Zhong, Z.; Tang, Z.; Li, X.; Yuan, T.; Yang, Y.; Wei, M.; Zhang, Y.; Sheng, R.; Grant, N.; Ling, C.; et al. XJTLUIndoorLoc: A New Fingerprinting Database for Indoor Localization and Trajectory Estimation Based on Wi-Fi RSS and Geomagnetic Field. In Proceedings of the 2018 Sixth International Symposium on Computing and Networking Workshops (CANDARW), Takayama, Japan, 27–30 November 2018; pp. 228–234. [Google Scholar] [CrossRef]
- Jang, J.W.; Hong, S.N. Indoor Localization with WiFi Fingerprinting Using Convolutional Neural Network. In Proceedings of the 2018 Tenth International Conference on Ubiquitous and Future Networks (ICUFN), Prague, Czech Republic, 3–6 July 2018; pp. 753–758. [Google Scholar] [CrossRef]
- Li, Q.; Qu, H.; Liu, Z.; Sun, W.; Shao, X.; Li, J. Wavelet Transform DC-GAN for Diversity Promoted Fingerprint Construction in Indoor Localization. In Proceedings of the 2018 IEEE Globecom Workshops (GC Wkshps), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Haider, A.; Wei, Y.; Liu, S.; Hwang, S.H. Pre- and Post-Processing Algorithms with Deep Learning Classifier for Wi-Fi Fingerprint-Based Indoor Positioning. Electronics 2019, 8, 195. [Google Scholar] [CrossRef]
- Njima, W.; Ahriz, I.; Zayani, R.; Terre, M.; Bouallegue, R. Deep CNN for Indoor Localization in IoT-Sensor Systems. Sensors 2019, 19, 3127. [Google Scholar] [CrossRef]
- Hernández, N.; Corrales, H.; Parra, I.; Rentero, M.; Llorca, D.F.; Sotelo, M. WiFi-based urban localisation using CNNs. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 1270–1275. [Google Scholar] [CrossRef]
- Sinha, R.S.; Hwang, S.H. Comparison of CNN Applications for RSSI-Based Fingerprint Indoor Localization. Electronics 2019, 8, 989. [Google Scholar] [CrossRef]
- Liu, Z.; Dai, B.; Wan, X.; Li, X. Hybrid Wireless Fingerprint Indoor Localization Method Based on a Convolutional Neural Network. Sensors 2019, 19, 4597. [Google Scholar] [CrossRef] [PubMed]
- Zhao, B.; Zhu, D.; Xi, T.; Jia, C.; Jiang, S.; Wang, S. Convolutional neural network and dual-factor enhanced variational Bayes adaptive Kalman filter based indoor localization with Wi-Fi. Comput. Netw. 2019, 162, 106864. [Google Scholar] [CrossRef]
- Soro, B.; Lee, C. Joint Time-Frequency RSSI Features for Convolutional Neural Network-Based Indoor Fingerprinting Localization. IEEE Access 2019, 7, 104892–104899. [Google Scholar] [CrossRef]
- Sinha, R.S.; Lee, S.M.; Rim, M.; Hwang, S.H. Data Augmentation Schemes for Deep Learning in an Indoor Positioning Application. Electronics 2019, 8, 554. [Google Scholar] [CrossRef]
- Li, H.; Zeng, X.; Li, Y.; Zhou, S.; Wang, J. Convolutional neural networks based indoor Wi-Fi localization with a novel kind of CSI images. China Commun. 2019, 16, 250–260. [Google Scholar] [CrossRef]
- Jing, Y.; Hao, J.; Li, P. Learning Spatiotemporal Features of CSI for Indoor Localization With Dual-Stream 3D Convolutional Neural Networks. IEEE Access 2019, 7, 147571–147585. [Google Scholar] [CrossRef]
- Xiang, C.; Zhang, S.; Xu, S.; Chen, X.; Cao, S.; Alexandropoulos, G.C.; Lau, V.K.N. Robust Sub-Meter Level Indoor Localization With a Single WiFi Access Point—Regression Versus Classification. IEEE Access 2019, 7, 146309–146321. [Google Scholar] [CrossRef]
- Gante, J.; Falcão, G.; Sousa, L. Enhancing Beamformed Fingerprint Outdoor Positioning with Hierarchical Convolutional Neural Networks. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 1473–1477. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Mao, S. Deep Convolutional Neural Networks for Indoor Localization with CSI Images. IEEE Trans. Netw. Sci. Eng. 2020, 7, 316–327. [Google Scholar] [CrossRef]
- Zhang, H.; Tong, G.; Xiong, N. Fine-grained CSI fingerprinting for indoor localisation using convolutional neural network. IET Commun. 2020, 14, 3266–3275. [Google Scholar] [CrossRef]
- Xun, W.; Sun, L.; Han, C.; Lin, Z.; Guo, J. Depthwise Separable Convolution based Passive Indoor Localization using CSI Fingerprint. In Proceedings of the 2020 IEEE Wireless Communications and Networking Conference (WCNC), Seoul, Republic of Korea, 25–28 May 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, Y.; Zhao, K.; Rao, W. DeepLoc: Deep neural network-based telco localization. In Proceedings of the 16th EAI International Conference on Mobile and Ubiquitous Systems: Computing, Networking and Services, Houston, TX, USA, 12–14 November 2020; pp. 258–267. [Google Scholar] [CrossRef]
- Xiao, Y.; Cui, Z.; Lu, X.; Wang, H. A passive Indoor Localization with Convolutional Neural Network Approach. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 1140–1145. [Google Scholar] [CrossRef]
- Sun, D.; Wei, E.; Yang, L.; Xu, S. Improving Fingerprint Indoor Localization Using Convolutional Neural Networks. IEEE Access 2020, 8, 193396–193411. [Google Scholar] [CrossRef]
- Ye, Q.; Fan, X.; Fang, G.; Bie, H.; Song, X.; Shankaran, R. CapsLoc: A Robust Indoor Localization System with WiFi Fingerprinting Using Capsule Networks. In Proceedings of the ICC 2020—2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Elawaad, K.; Ezzeldin, M.; Torki, M. DeepCReg: Improving Cellular-based Outdoor Localization using CNN-based Regressors. In Proceedings of the 2020 IEEE Wireless Communications and Networking Conference (WCNC), Seoul, Republic of Korea, 25–28 May 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Chen, H.; Wang, B.; Pei, Y.; Zhang, L. A WiFi Indoor Localization Method Based on Dilated CNN and Support Vector Regression. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 165–170. [Google Scholar] [CrossRef]
- Cao, J.; Zhang, X.; Lv, J.; Wu, X.; Yang, H. Research on Indoor Positioning Algorithm Based on Information Fusion. In Proceedings of the 2020 IEEE 5th International Conference on Signal and Image Processing (ICSIP), Nanjing, China, 23–25 October 2020; pp. 844–850. [Google Scholar] [CrossRef]
- Wang, P.; Koike-Akino, T.; Orlik, P.V. Fingerprinting-Based Indoor Localization with Commercial MMWave WiFi: NLOS Propagation. In Proceedings of the GLOBECOM 2020—2020 IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Gante, J.; Falcão, G.; Sousa, L. Deep Learning Architectures for Accurate Millimeter Wave Positioning in 5G. Neural Process. Lett. 2020, 51, 487–514. [Google Scholar] [CrossRef]
- Gante, J.; Sousa, L.; Falcao, G. Dethroning GPS: Low-Power Accurate 5G Positioning Systems Using Machine Learning. IEEE J. Emerg. Sel. Top. Circuits Syst. 2020, 10, 240–252. [Google Scholar] [CrossRef]
- Han, C.; Xun, W.; Sun, L.; Lin, Z.; Guo, J. DSCP: Depthwise Separable Convolution-Based Passive Indoor Localization Using CSI Fingerprint. Wirel. Commun. Mob. Comput. 2021, 2021, 1–17. [Google Scholar] [CrossRef]
- Montalvo, L.; Hernández, N.; Parra, I. A Comparison of Deep Learning Architectures for WiFi-based Urban Localisation. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 122–127. [Google Scholar] [CrossRef]
- Laska, M.; Blankenbach, J. DeepLocBox: Reliable Fingerprinting-Based Indoor Area Localization. Sensors 2021, 21, 2000. [Google Scholar] [CrossRef]
- Sinha, S.; Le, D.V. Completely Automated CNN Architecture Design Based on VGG Blocks for Fingerprinting Localisation. In Proceedings of the 2021 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Lloret de Mar, Spain, 29 November–2 December 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Peng, C.; Jiang, H.; Qu, L. Deep Convolutional Neural Network for Passive RFID Tag Localization Via Joint RSSI and PDOA Fingerprint Features. IEEE Access 2021, 9, 15441–15451. [Google Scholar] [CrossRef]
- Li, Q.; Qu, H.; Liu, Z.; Zhou, N.; Sun, W.; Sigg, S.; Li, J. AF-DCGAN: Amplitude Feature Deep Convolutional GAN for Fingerprint Construction in Indoor Localization Systems. IEEE Trans. Emerg. Top. Comput. Intell. 2021, 5, 468–480. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Mao, S. Indoor Fingerprinting With Bimodal CSI Tensors: A Deep Residual Sharing Learning Approach. IEEE Internet Things J. 2021, 8, 4498–4513. [Google Scholar] [CrossRef]
- Liu, N.; He, T.; He, S.; Niu, Q. Indoor Localization With Adaptive Signal Sequence Representations. IEEE Trans. Veh. Technol. 2021, 70, 11678–11694. [Google Scholar] [CrossRef]
- Abid, M.; Compagnon, P.; Lefebvre, G. Improved CNN-based Magnetic Indoor Positioning System using Attention Mechanism. In Proceedings of the 2021 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Lloret de Mar, Spain, 29 November–2 December 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Hernández, N.; Parra, I.; Corrales, H.; Izquierdo, R.; Ballardini, A.L.; Salinas, C.; García, I. WiFiNet: WiFi-based indoor localisation using CNNs. Expert Syst. Appl. 2021, 177, 114906. [Google Scholar] [CrossRef]
- Li, Q.; Liao, X.; Liu, M.; Valaee, S. Indoor Localization Based on CSI Fingerprint by Siamese Convolution Neural Network. IEEE Trans. Veh. Technol. 2021, 70, 12168–12173. [Google Scholar] [CrossRef]
- Li, D.; Xu, J.; Yang, Z.; Lu, Y.; Zhang, Q.; Zhang, X. Train Once, Locate Anytime for Anyone: Adversarial Learning based Wireless Localization. In Proceedings of the IEEE INFOCOM 2021—IEEE Conference on Computer Communications, Vancouver, BC, Canada, 10–13 May 2021; pp. 1–10. [Google Scholar] [CrossRef]
- Xu, C.; Wang, W.; Zhang, Y.; Qin, J.; Yu, S.; Zhang, Y. An Indoor Localization System Using Residual Learning with Channel State Information. Entropy 2021, 23, 574. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Sinha, R.S.; Hwang, S.H. Clustering-Based Noise Elimination Scheme for Data Pre-Processing for Deep Learning Classifier in Fingerprint Indoor Positioning System. Sensors 2021, 21, 4349. [Google Scholar] [CrossRef] [PubMed]
- Poulose, A.; Han, D.S. Hybrid Deep Learning Model Based Indoor Positioning Using Wi-Fi RSSI Heat Maps for Autonomous Applications. Electronics 2021, 10, 2. [Google Scholar] [CrossRef]
- Karakusak, M.Z.; Kivrak, H.; Ates, H.F.; Ozdemir, M.K. RSS-Based Wireless LAN Indoor Localization and Tracking Using Deep Architectures. Big Data Cogn. Comput. 2022, 6, 84. [Google Scholar] [CrossRef]
- Laska, M.; Blankenbach, J. Multi-Task Neural Network for Position Estimation in Large-Scale Indoor Environments. IEEE Access 2022, 10, 26024–26032. [Google Scholar] [CrossRef]
- Zhu, X.; Qu, W.; Zhou, X.; Zhao, L.; Ning, Z.; Qiu, T. Intelligent Fingerprint-Based Localization Scheme Using CSI Images for Internet of Things. IEEE Trans. Netw. Sci. Eng. 2022, 9, 2378–2391. [Google Scholar] [CrossRef]
- Guo, Y.; Yan, J. A CSI Based Localization and Identification Recognition Algorithm Using Multi-task Learning and Deep Residual Shrinkage Network. In Proceedings of the 2022 IEEE 22nd International Conference on Communication Technology (ICCT), Nanjing, China, 11–14 November 2022; pp. 1770–1776. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, K.; Zheng, Z.; Ji, W.; Huang, S.; Ma, D. Indoor Positioning with CNN and Path-Loss Model Based on Multivariable Fingerprints in 5G Mobile Communication System. Sensors 2022, 22, 3179. [Google Scholar] [CrossRef]
- Yang, C.H.; Lee, M.C.; Lin, C.H.; Lee, T.S. Beam Domain Based Fingerprinting Indoor Localization with Multiple Antenna Systems. In Proceedings of the 2022 IEEE 95th Vehicular Technology Conference: (VTC2022-Spring), Helsinki, Finland, 19–22 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Tiku, S.; Pasricha, S. Siamese Neural Encoders for Long-Term Indoor Localization with Mobile Devices. In Proceedings of the 2022 Design, Automation and Test in Europe Conference and Exhibition (DATE), Antwerp, Belgium, 14–23 March 2022; pp. 1215–1220. [Google Scholar] [CrossRef]
- Wang, L.; Tiku, S.; Pasricha, S. CHISEL: Compression-Aware High-Accuracy Embedded Indoor Localization With Deep Learning. IEEE Embed. Syst. Lett. 2022, 14, 23–26. [Google Scholar] [CrossRef]
- Ye, Q.; Bie, H.; Li, K.C.; Fan, X.; Gong, L.; He, X.; Fang, G. EdgeLoc: A Robust and Real-Time Localization System Toward Heterogeneous IoT Devices. IEEE Internet Things J. 2022, 9, 3865–3876. [Google Scholar] [CrossRef]
- Wu, S.; Huang, W.; Li, M.; Xu, K. A Novel RSSI Fingerprint Positioning Method Based on Virtual AP and Convolutional Neural Network. IEEE Sens. J. 2022, 22, 6898–6909. [Google Scholar] [CrossRef]
- Song, X.; Zhou, Y.; Qi, H.; Qiu, W.; Xue, Y. DuLoc: Dual-Channel Convolutional Neural Network Based on Channel State Information for Indoor Localization. IEEE Sens. J. 2022, 22, 8738–8748. [Google Scholar] [CrossRef]
- Hou, C.; Xie, Y.; Zhang, Z. An improved convolutional neural network based indoor localization by using Jenks natural breaks algorithm. China Commun. 2022, 19, 291–301. [Google Scholar] [CrossRef]
- Mazlan, A.B.; Ng, Y.H.; Tan, C.K. A Fast Indoor Positioning Using a Knowledge-Distilled Convolutional Neural Network (KD-CNN). IEEE Access 2022, 10, 65326–65338. [Google Scholar] [CrossRef]
- Kia, G.; Ruotsalainen, L.; Talvitie, J. A CNN Approach for 5G mm Wave Positioning Using Beamformed CSI Measurements. In Proceedings of the 2022 International Conference on Localization and GNSS (ICL-GNSS), Tampere, Finland, 7–9 June 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Sonny, A.; Kumar, A. Fingerprint Image-Based Multi-Building 3D Indoor Wi-Fi Localization Using Convolutional Neural Networks. In Proceedings of the 2022 National Conference on Communications (NCC), Mumbai, India, 24–27 May 2022; pp. 106–111. [Google Scholar] [CrossRef]
- Liu, J.; Jia, B.; Guo, L.; Huang, B.; Wang, L.; Baker, T. CTSLoc: An indoor localization method based on CNN by using time-series RSSI. Clust. Comput. 2022, 25, 2573–2584. [Google Scholar] [CrossRef]
- Zhang, G.; Hou, Z.; Li, Y.; Vucetic, B. Deep Learning-Based Indoor Localization Using Adjacent Received Signal Strength and Domain Knowledge. In Proceedings of the 2022 20th Mediterranean Communication and Computer Networking Conference (MedComNet), Paphos, Cyprus, 1–3 June 2022; pp. 25–30. [Google Scholar] [CrossRef]
- Hassen, W.F.; Mezghani, J. CNN based approach for Indoor Positioning Services using RSSI Fingerprinting Technique. In Proceedings of the 2022 International Wireless Communications and Mobile Computing (IWCMC), Dubrovnik, Croatia, 30 May–3 June 2022; pp. 778–783. [Google Scholar] [CrossRef]
- Wang, X.; Deng, X.; Zhang, H.; Liu, K.; Dai, P. LCSW: A Novel Indoor Localization System Based on CNN-SVM Model with WKNN in Wi-Fi Environments. In Neural Computing for Advanced Applications; Zhang, H., Chen, Y., Chu, X., Zhang, Z., Hao, T., Wu, Z., Yang, Y., Eds.; Springer: Singapore, 2022; pp. 162–176. [Google Scholar] [CrossRef]
- Guo, J.; Ho, I.W.H.; Hou, Y.; Li, Z. FedPos: A Federated Transfer Learning Framework for CSI-Based Wi-Fi Indoor Positioning. IEEE Syst. J. 2023, 17, 4579–4590. [Google Scholar] [CrossRef]
- Grira, H.; Chammakhi Msadaa, I.; Grayaa, K. Enhancing Fingerprinting Indoor Positioning Systems Through Hierarchical Clustering and GAN-Based CNN. In Proceedings of the 2023 IEEE Symposium on Computers and Communications (ISCC), Gammarth, Tunisia, 9–12 July 2023; pp. 1054–1057. [Google Scholar] [CrossRef]
- Yan, J.; Huang, Z.; Wu, X. Smartphone Based Indoor Localization Using Machine Learning and Multi-Source Information Fusion. IEEE Trans. Aerosp. Electron. Syst. 2023, 1–14. [Google Scholar] [CrossRef]
- Molina, M.C.; Ahriz, I.; Galle, C.; Terré, M. Enhancing Precision and Robustness in Indoor Localization Using Temporal and Spatial Features for BLE Fingerprinting. In Proceedings of the 2023 IEEE 14th Annual Ubiquitous Computing, Electronics and Mobile Communication Conference (UEMCON), New York, NY, USA, 12–14 October 2023; pp. 0472–0476. [Google Scholar] [CrossRef]
- Zhang, Y.; Fan, M.; Xu, C. Intelligent indoor localization based on CSI via radio images and deep learning. Meas. Sci. Technol. 2023, 34, 085002. [Google Scholar] [CrossRef]
- Liu, W.; Dun, Z. D-Fi: Domain adversarial neural network based CSI fingerprint indoor localization. J. Inf. Intell. 2023, 1, 104–114. [Google Scholar] [CrossRef]
- Ye, Q.; Fan, X.; Bie, H.; Puthal, D.; Wu, T.; Song, X.; Fang, G. SE-Loc: Security-Enhanced Indoor Localization with Semi-Supervised Deep Learning. IEEE Trans. Netw. Sci. Eng. 2023, 10, 2964–2977. [Google Scholar] [CrossRef]
- Jang, H.J.; Shin, J.M.; Choi, L. Geomagnetic Field Based Indoor Localization Using Recurrent Neural Networks. In Proceedings of the GLOBECOM 2017—2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Sahar, A.; Han, D. An LSTM-Based Indoor Positioning Method Using Wi-Fi Signals. In Proceedings of the 2nd International Conference on Vision, Image and Signal Processing, Las Vegas, NV, USA, 27–29 August 2018. [Google Scholar] [CrossRef]
- Shao, W.; Luo, H.; Zhao, F.; Ma, Y.; Zhao, Z.; Crivello, A. Indoor Positioning Based on Fingerprint-Image and Deep Learning. IEEE Access 2018, 6, 74699–74712. [Google Scholar] [CrossRef]
- Shao, W.; Luo, H.; Zhao, F.; Wang, C.; Crivello, A.; Tunio, M.Z. DePos: Accurate orientation-Free Indoor Positioning with Deep Convolutional Neural Networks. In Proceedings of the 2018 Ubiquitous Positioning, Indoor Navigation and Location-Based Services (UPINLBS), Wuhan, China, 22–23 March 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Lin, W.Y.; Huang, C.C.; Duc, N.T.; Manh, H.N. Wi-Fi Indoor Localization based on Multi-Task Deep Learning. In Proceedings of the 2018 IEEE 23rd International Conference on Digital Signal Processing (DSP), Shanghai, China, 19–21 November 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Xu, B.; Zhu, X.; Zhu, H. An Efficient Indoor Localization Method Based on the Long Short-Term Memory Recurrent Neuron Network. IEEE Access 2019, 7, 123912–123921. [Google Scholar] [CrossRef]
- Urano, K.; Hiroi, K.; Yonezawa, T.; Kawaguchi, N. An End-to-End BLE Indoor Location Estimation Method Using LSTM. In Proceedings of the 2019 Twelfth International Conference on Mobile Computing and Ubiquitous Network (ICMU), Kathmandu, Nepal, 4–6 November 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Elbes, M.; Almaita, E.; Alrawashdeh, T.; Kanan, T.; AlZu’bi, S.; Hawashin, B. An Indoor Localization Approach Based on Deep Learning for Indoor Location-Based Services. In Proceedings of the 2019 IEEE Jordan International Joint Conference on Electrical Engineering and Information Technology (JEEIT), Amman, Jordan, 9–11 April 2019; pp. 437–441. [Google Scholar] [CrossRef]
- Sun, H.; Zhu, X.; Liu, Y.; Liu, W. WiFi Based Fingerprinting Positioning Based on Seq2seq Model. Sensors 2020, 20, 3767. [Google Scholar] [CrossRef]
- He, T.; Niu, Q.; He, S.; Liu, N. Indoor Localization with Spatial and Temporal Representations of Signal Sequences. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Big Island, HI, USA, 9–13 December 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Bae, H.J.; Choi, L. Large-Scale Indoor Positioning using Geomagnetic Field with Deep Neural Networks. In Proceedings of the ICC 2019—2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Hoang, M.T.; Yuen, B.; Dong, X.; Lu, T.; Westendorp, R.; Reddy, K. Recurrent Neural Networks for Accurate RSSI Indoor Localization. IEEE Internet Things J. 2019, 6, 10639–10651. [Google Scholar] [CrossRef]
- Wu, L.; Chen, C.H.; Zhang, Q. A Mobile Positioning Method Based on Deep Learning Techniques. Electronics 2019, 8, 59. [Google Scholar] [CrossRef]
- Wang, R.; Luo, H.; Wang, Q.; Li, Z.; Zhao, F.; Huang, J. A Spatial–Temporal Positioning Algorithm Using Residual Network and LSTM. IEEE Trans. Instrum. Meas. 2020, 69, 9251–9261. [Google Scholar] [CrossRef]
- Yu, J.; Saad, H.M.; Buehrer, R.M. Centimeter-Level Indoor Localization using Channel State Information with Recurrent Neural Networks. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 1317–1323. [Google Scholar] [CrossRef]
- Belmonte-Hernández, A.; Hernández-Peñaloza, G.; Martín Gutiérrez, D.; Álvarez, F. Recurrent Model for Wireless Indoor Tracking and Positioning Recovering Using Generative Networks. IEEE Sens. J. 2020, 20, 3356–3365. [Google Scholar] [CrossRef]
- Chiang, T.H.; Sun, Z.H.; Shiu, H.R.; Lin, K.C.J.; Tseng, Y.C. Magnetic Field-Based Localization in Factories Using Neural Network With Robotic Sampling. IEEE Sens. J. 2020, 20, 13110–13118. [Google Scholar] [CrossRef]
- Bai, S.; Yan, M.; Wan, Q.; He, L.; Wang, X.; Li, J. DL-RNN: An Accurate Indoor Localization Method via Double RNNs. IEEE Sens. J. 2020, 20, 286–295. [Google Scholar] [CrossRef]
- Liu, Y.T.; Chen, J.J.; Tseng, Y.C.; Li, F.Y. Combining Auto-Encoder with LSTM for WiFi-Based Fingerprint Positioning. In Proceedings of the 2021 International Conference on Computer Communications and Networks (ICCCN), Athens, Greece, 19–22 July 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Khassanov, Y.; Nurpeiissov, M.; Sarkytbayev, A.; Kuzdeuov, A.; Varol, H.A. Finer-level Sequential WiFi-based Indoor Localization. In Proceedings of the 2021 IEEE/SICE International Symposium on System Integration (SII), Iwaki, Fukushima, Japan, 11–14 January 2021; pp. 163–169. [Google Scholar] [CrossRef]
- Zhang, M.; Jia, J.; Chen, J.; Deng, Y.; Wang, X.; Aghvami, A.H. Indoor Localization Fusing WiFi With Smartphone Inertial Sensors Using LSTM Networks. IEEE Internet Things J. 2021, 8, 13608–13623. [Google Scholar] [CrossRef]
- Qian, W.; Lauri, F.; Gechter, F. Supervised and semi-supervised deep probabilistic models for indoor positioning problems. Neurocomputing 2021, 435, 228–238. [Google Scholar] [CrossRef]
- Javed, A.; Ul Hassan, N. Low-Effort Deep Learning Method Trained through Virtual Trajectories for Indoor Tracking. In Proceedings of the 2021 IEEE 32nd Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Helsinki, Finland, 13–16 September 2021; pp. 1546–1551. [Google Scholar] [CrossRef]
- Wang, L.; Luo, H.; Wang, Q.; Shao, W.; Zhao, F. A Hierarchical LSTM-based Indoor Geomagnetic Localization Algorithm. IEEE Sens. J. 2021, 22, 1227–1237. [Google Scholar] [CrossRef]
- Zhang, Z.; Lee, M.; Choi, S. Deep-Learning-Based Wi-Fi Indoor Positioning System Using Continuous CSI of Trajectories. Sensors 2021, 21, 5776. [Google Scholar] [CrossRef] [PubMed]
- Tong, X.; Wan, Y.; Li, Q.; Tian, X.; Wang, X. CSI Fingerprinting Localization With Low Human Efforts. IEEE/ACM Trans. Netw. 2021, 29, 372–385. [Google Scholar] [CrossRef]
- Yu, C.; Shin, B.; Kang, C.G.; Lee, J.H.; Kyung, H.; Kim, T.; Lee, T. Smartphone based Indoor Localization Technology using 1D CNN-BLSTM. In Proceedings of the 2022 22nd International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 27 November–1 December 2022; pp. 911–915. [Google Scholar] [CrossRef]
- Jia, B.; Liu, J.; Feng, T.; Huang, B.; Baker, T.; Tawfik, H. TTSL: An indoor localization method based on Temporal Convolutional Network using time-series RSSI. Comput. Commun. 2022, 193, 293–301. [Google Scholar] [CrossRef]
- Ding, X.; Zhu, M.; Xiao, B. Accurate Indoor Localization Using Magnetic Sequence Fingerprints with Deep Learning. In Algorithms and Architectures for Parallel Processing; Lai, Y., Wang, T., Jiang, M., Xu, G., Liang, W., Castiglione, A., Eds.; Springer: Cham, Switzerland, 2022; pp. 65–84. [Google Scholar] [CrossRef]
- Abubakr, T.; Nasr, O.A. Novel LSTM-Based Approaches for Enhancing Outdoor Localization Accuracy in 4G Networks. IEEE Access 2023, 11, 140103–140115. [Google Scholar] [CrossRef]
- Tanaka, S.; Kondo, K. Improvement of Estimation Accuracy in BLE Indoor Position and Motion Direction Estimation System Using Bi-LSTM. In Proceedings of the 2023 IEEE 12th Global Conference on Consumer Electronics (GCCE), Nara, Japan, 10–13 October 2023; pp. 778–779. [Google Scholar] [CrossRef]
- Zhao, Y.; Gong, W.; Li, L.; Zhang, B.; Li, C. An Efficient and Robust Fingerprint-Based Localization Method for Multiflloor Indoor Environment. IEEE Internet Things J. 2024, 11, 3927–3941. [Google Scholar] [CrossRef]
- Feng, T.; Liu, Y.; Yu, Y.; Chen, L.; Chen, R. CrowdLOC-S: Crowdsourced seamless localization framework based on CNN-LSTM-MLP enhanced quality indicator. Expert Syst. Appl. 2024, 243, 122852. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A Search Space Odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2222–2232. [Google Scholar] [CrossRef]
- Shin, B.; Ho Lee, J.; Lee, T. Novel indoor fingerprinting method based on RSS sequence matching. Measurement 2023, 223, 113719. [Google Scholar] [CrossRef]
- Laska, M.; Blankenbach, J. Topology Preserving Input Image for Convolutional Neural Network Based Indoor Localization. In Proceedings of the 2021 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Lloret de Mar, Spain, 29 November–2 December 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Shin, H.G.; Choi, Y.H.; Yoon, C.P. Movement Path Data Generation from Wi-Fi Fingerprints for Recurrent Neural Networks. Sensors 2021, 21, 2823. [Google Scholar] [CrossRef] [PubMed]
- Whiton, R.; Chen, J.; Johansson, T.; Tufvesson, F. Urban Navigation with LTE using a Large Antenna Array and Machine Learning. In Proceedings of the 2022 IEEE 95th Vehicular Technology Conference: (VTC2022-Spring), Helsinki, Finland, 19–22 June 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, W.; Li, T.; Wang, W.; Tu, Z. Multiple Fingerprints-Based Indoor Localization via GBDT: Subspace and RSSI. IEEE Access 2019, 7, 80519–80529. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, W.; Xu, C.; Qin, J.; Yu, S.; Zhang, Y. SICD: Novel Single-Access-Point Indoor Localization Based on CSI-MIMO with Dimensionality Reduction. Sensors 2021, 21, 1325. [Google Scholar] [CrossRef]
- Nam, Y.H.; Ng, B.L.; Sayana, K.; Li, Y.; Zhang, J.; Kim, Y.; Lee, J. Full-dimension MIMO (FD-MIMO) for next generation cellular technology. IEEE Commun. Mag. 2013, 51, 172–179. [Google Scholar] [CrossRef]
- Kim, Y.; Ji, H.; Lee, J.; Nam, Y.H.; Ng, B.L.; Tzanidis, I.; Li, Y.; Zhang, J. Full dimension MIMO (FD-MIMO): The next evolution of MIMO in LTE systems. IEEE Wirel. Commun. 2014, 21, 26–33. [Google Scholar] [CrossRef]
- Gönültaş, E.; Lei, E.; Langerman, J.; Huang, H.; Studer, C. CSI-Based Multi-Antenna and Multi-Point Indoor Positioning Using Probability Fusion. IEEE Trans. Wirel. Commun. 2022, 21, 2162–2176. [Google Scholar] [CrossRef]
- Nabati, M.; Ghorashi, S.A. A real-time fingerprint-based indoor positioning using deep learning and preceding states. Expert Syst. Appl. 2023, 213, 118889. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Fawzi, A.; Frossard, P. Manitest: Are classifiers really invariant? arXiv 2015, arXiv:1507.06535. [Google Scholar] [CrossRef]
- Kauderer-Abrams, E. Quantifying Translation-Invariance in Convolutional Neural Networks. arXiv 2017, arXiv:1801.01450. [Google Scholar] [CrossRef]
- Zhang, R. Making Convolutional Networks Shift-Invariant Again. arXiv 2019, arXiv:1904.11486. [Google Scholar] [CrossRef]
- Chaman, A.; Dokmanić, I. Truly shift-invariant convolutional neural networks. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 3772–3782. [Google Scholar] [CrossRef]
- Comiter, M.Z.; Crouse, M.B.; Kung, H.T. A Data-Driven Approach to Localization for High Frequency Wireless Mobile Networks. In Proceedings of the GLOBECOM 2017—2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Caso, G.; De Nardis, L.; Lemic, F.; Handziski, V.; Wolisz, A.; Benedetto, M.G.D. ViFi: Virtual Fingerprinting WiFi-Based Indoor Positioning via Multi-Wall Multi-Floor Propagation Model. IEEE Trans. Mob. Comput. 2020, 19, 1478–1491. [Google Scholar] [CrossRef]
- Njima, W.; Chafii, M.; Chorti, A.; Shubair, R.M.; Poor, H.V. Indoor Localization Using Data Augmentation via Selective Generative Adversarial Networks. IEEE Access 2021, 9, 98337–98347. [Google Scholar] [CrossRef]
- Elasri, M.; Elharrouss, O.; Al-Maadeed, S.; Tairi, H. Image Generation: A Review. Neural Process. Lett. 2022, 54, 4609–4646. [Google Scholar] [CrossRef]
- Baraheem, S.S.; Le, T.N.; Nguyen, T.V. Image synthesis: A review of methods, datasets, evaluation metrics, and future outlook. Artif. Intell. Rev. 2023, 56, 10813–10865. [Google Scholar] [CrossRef]
- Andreini, P.; Bonechi, S.; Ciano, G.; Graziani, C.; Lachi, V.; Nikoloulopoulou, N.; Bianchini, M.; Scarselli, F. Multi-stage Synthetic Image Generation for the Semantic Segmentation of Medical Images. In Artificial Intelligence and Machine Learning for Healthcare: Volume 1: Image and Data Analytics; Springer International Publishing: Cham, Switzerland, 2023; pp. 79–104. [Google Scholar] [CrossRef]
- Wu, C.; Yang, Z.; Liu, Y.; Xi, W. WILL: Wireless Indoor Localization without Site Survey. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 839–848. [Google Scholar] [CrossRef]
- Lembo, S.; Horsmanheimo, S.; Somersalo, M.; Laukkanen, M.; Tuomimäki, L.; Huilla, S. Enhancing WiFi RSS fingerprint positioning accuracy: Lobe-forming in radiation pattern enabled by an air-gap. In Proceedings of the 2019 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Pisa, Italy, 30 September–3 October 2019; pp. 1–8. [Google Scholar] [CrossRef]
- TU-R P.1238-9; Propagation Data and Prediction Methods for the Planning of Indoor Radiocommunication Systems and Radio Local Area Networks in the Frequency Range 300 MHz to 100 GHz. ITU: Geneva, Switzerland, 2017.
- Keskar, N.S.; Mudigere, D.; Nocedal, J.; Smelyanskiy, M.; Tang, P.T.P. On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima. arXiv 2017, arXiv:1609.04836. [Google Scholar] [CrossRef]
- Hannan, P. The element-gain paradox for a phased-array antenna. IEEE Trans. Antennas Propag. 1964, 12, 423–433. [Google Scholar] [CrossRef]
- Von Ramm, O.T.; Smith, S.W. Beam Steering with Linear Arrays. IEEE Trans. Biomed. Eng. 1983, BME-30, 438–452. [Google Scholar] [CrossRef]
- Kummer, W. Basic array theory. Proc. IEEE 1992, 80, 127–140. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A System for Large-Scale Machine Learning. In Proceedings of the 12th USENIX Conference on Operating Systems Design and Implementation. USENIX Association, Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
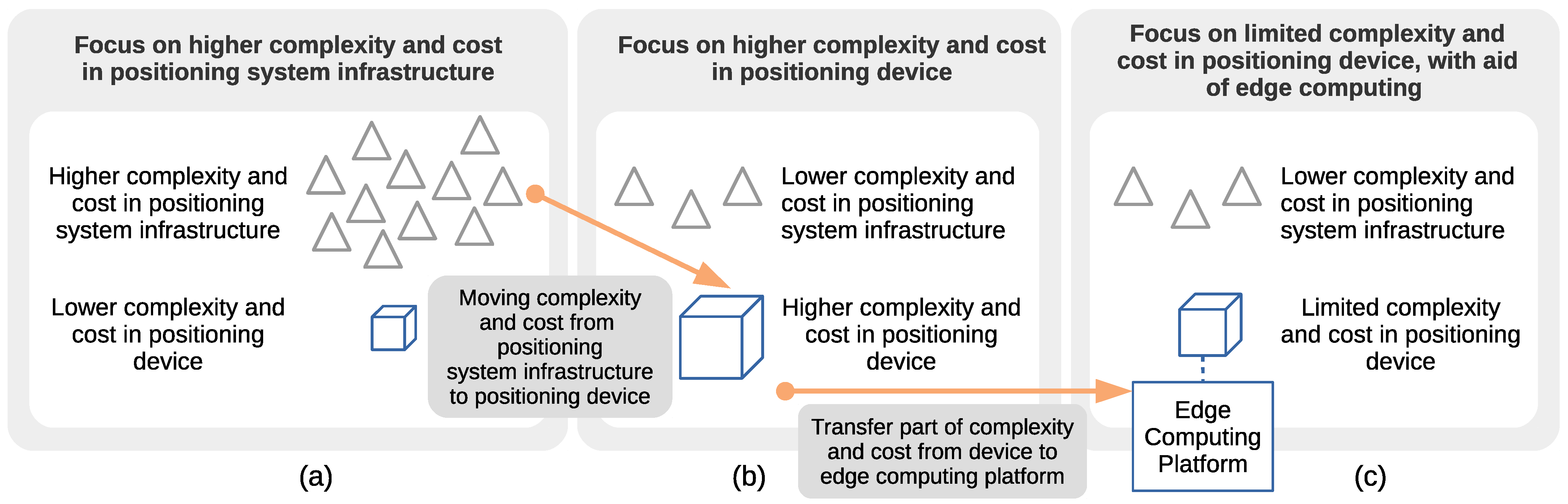
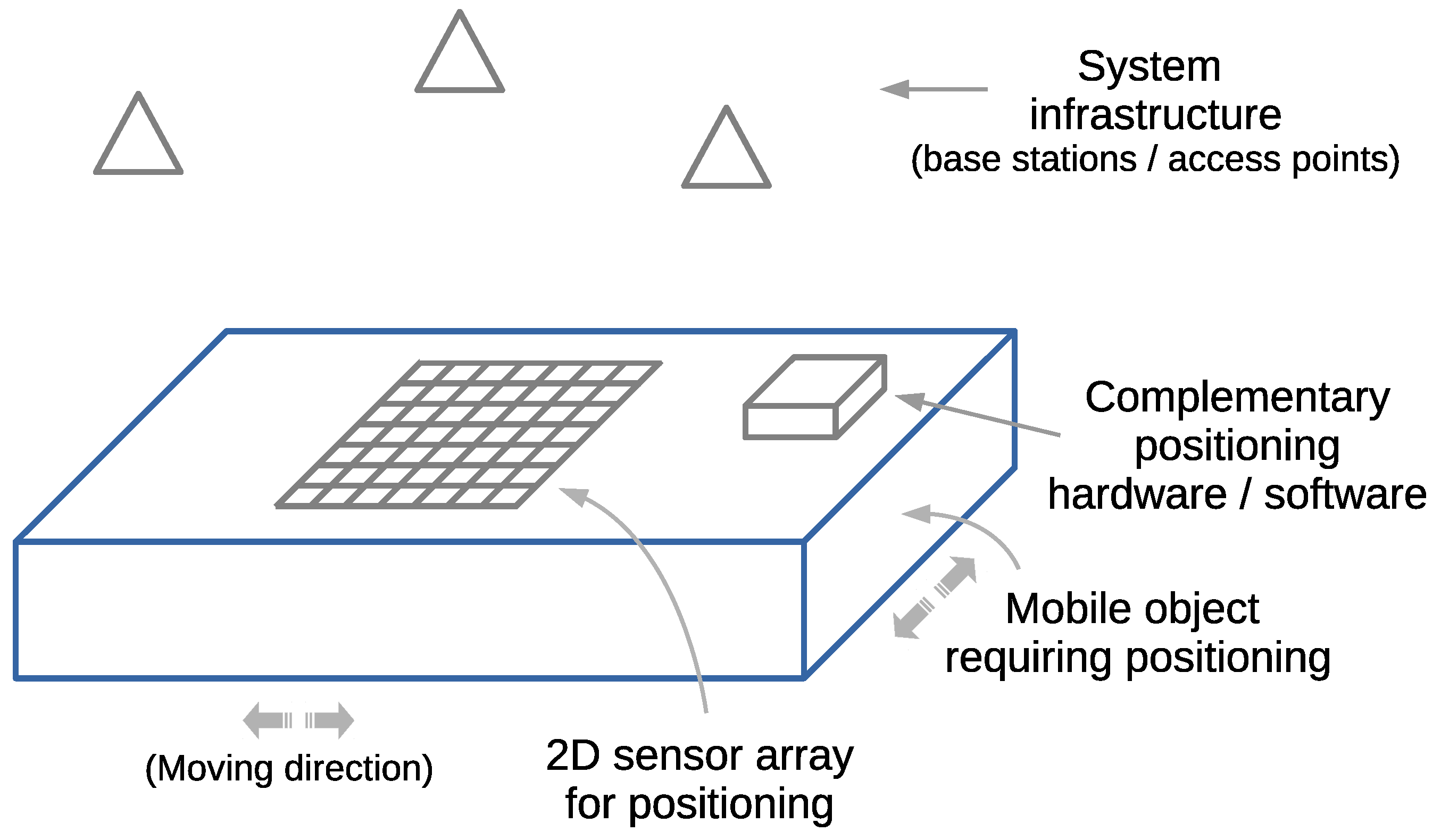
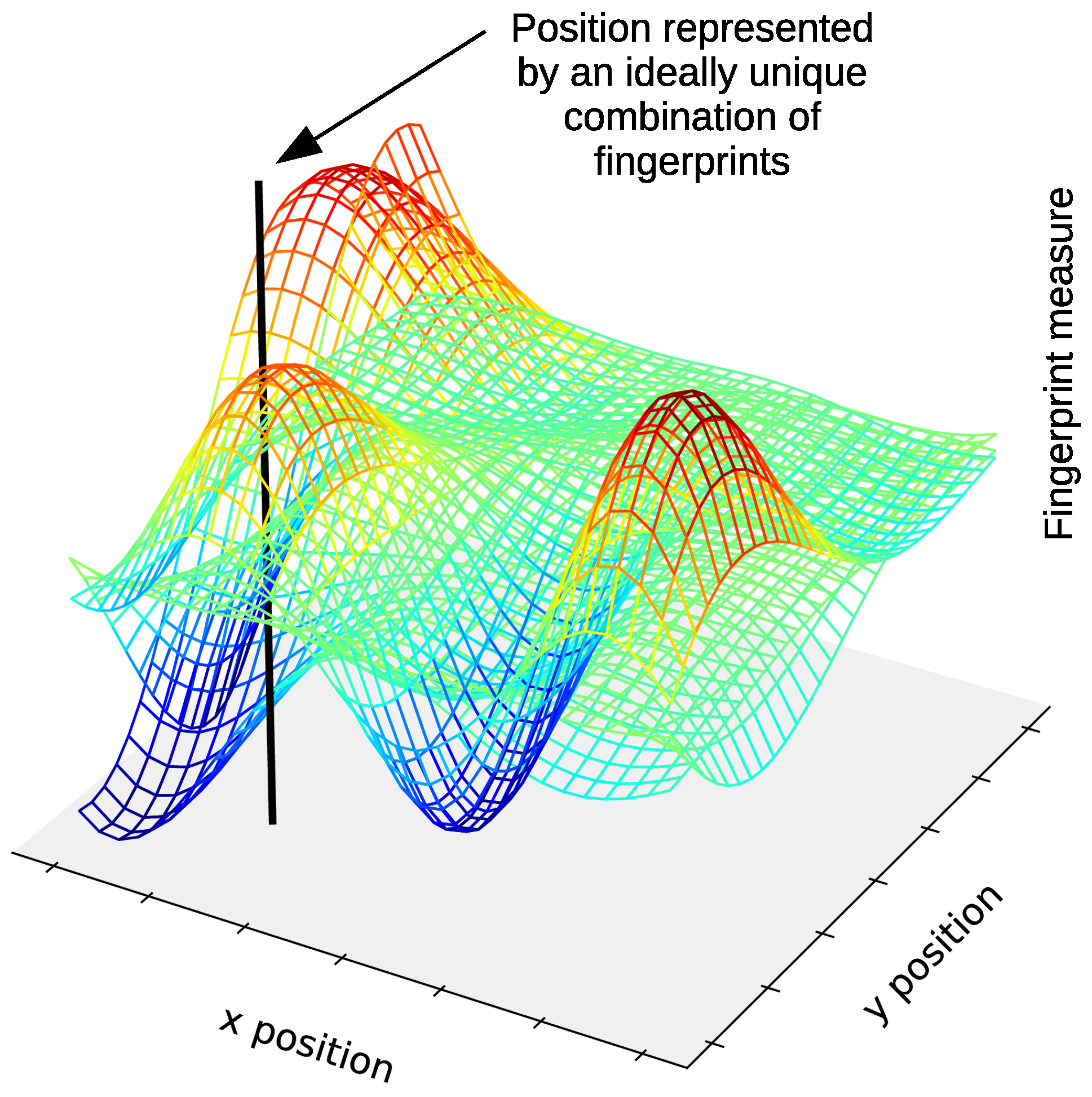
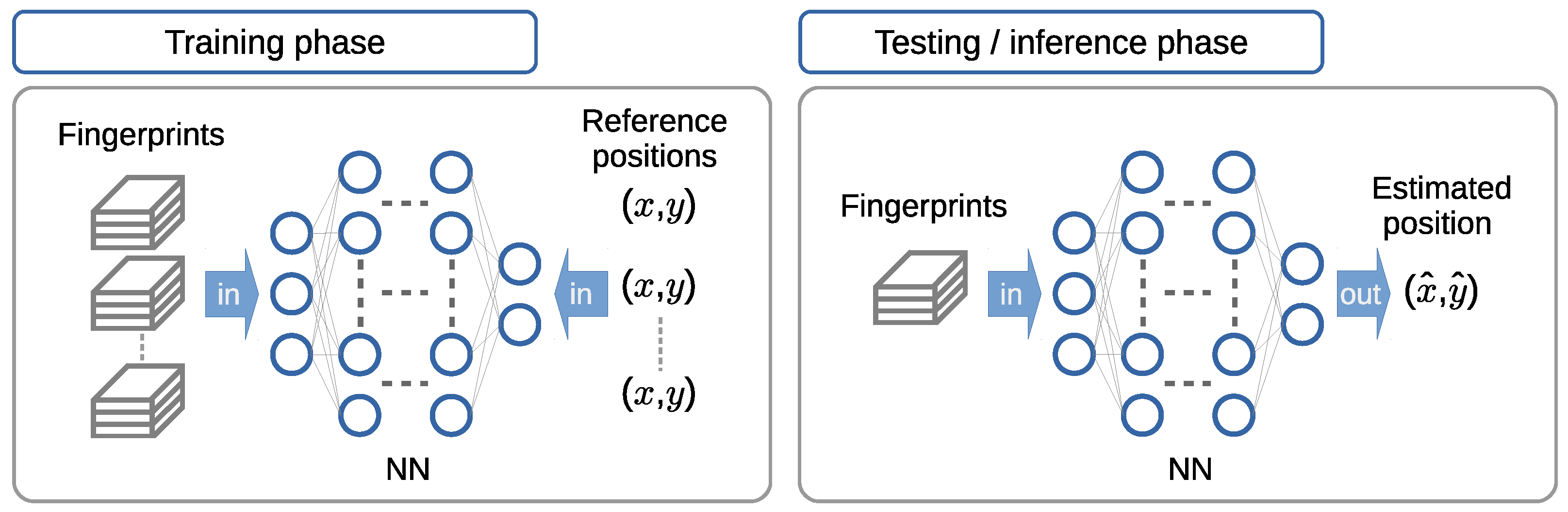
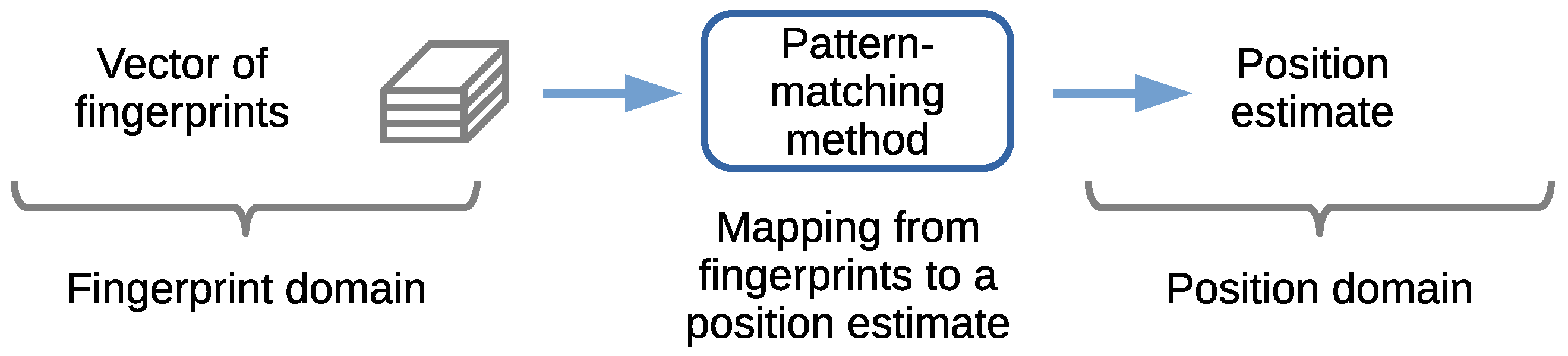
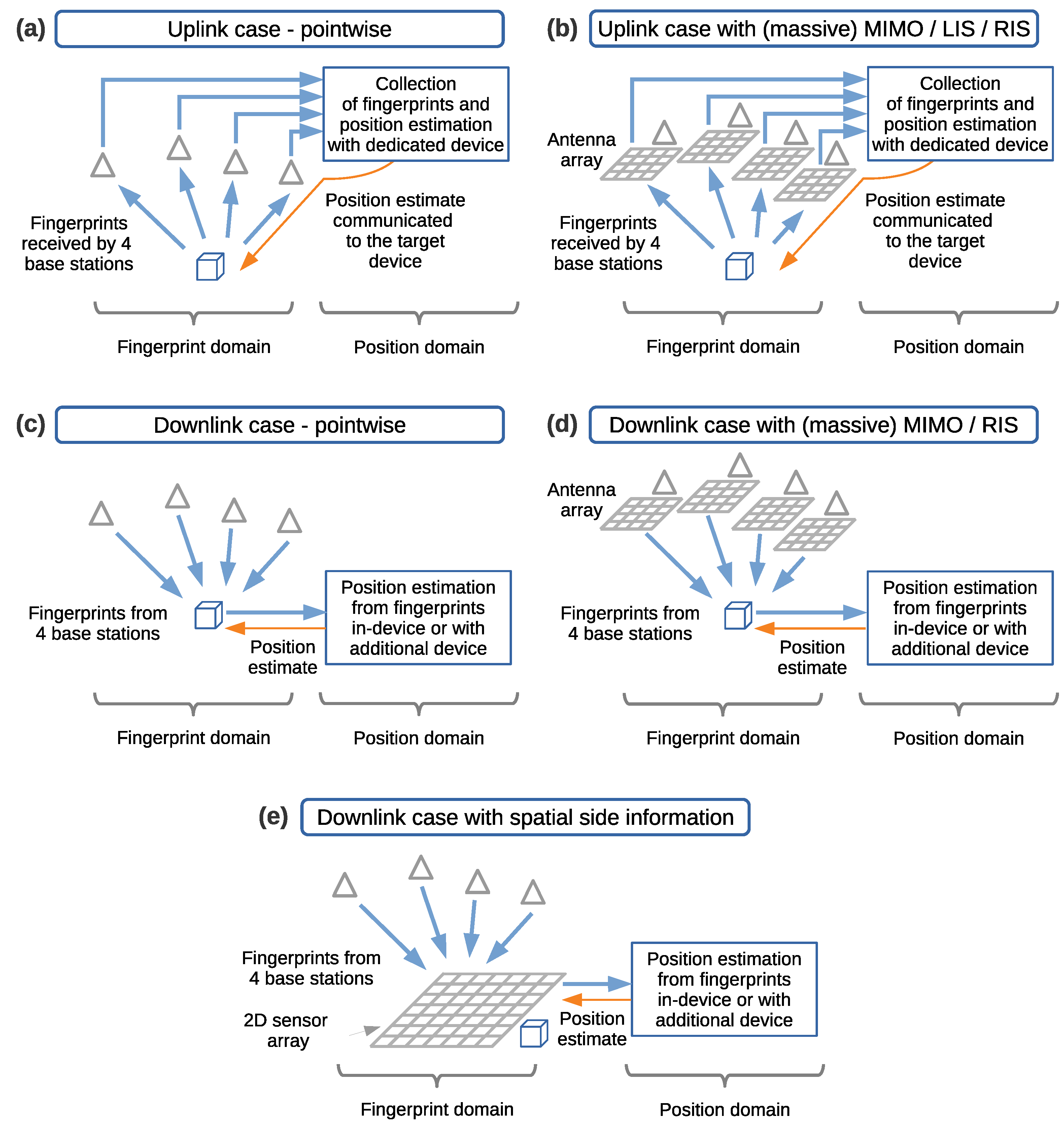

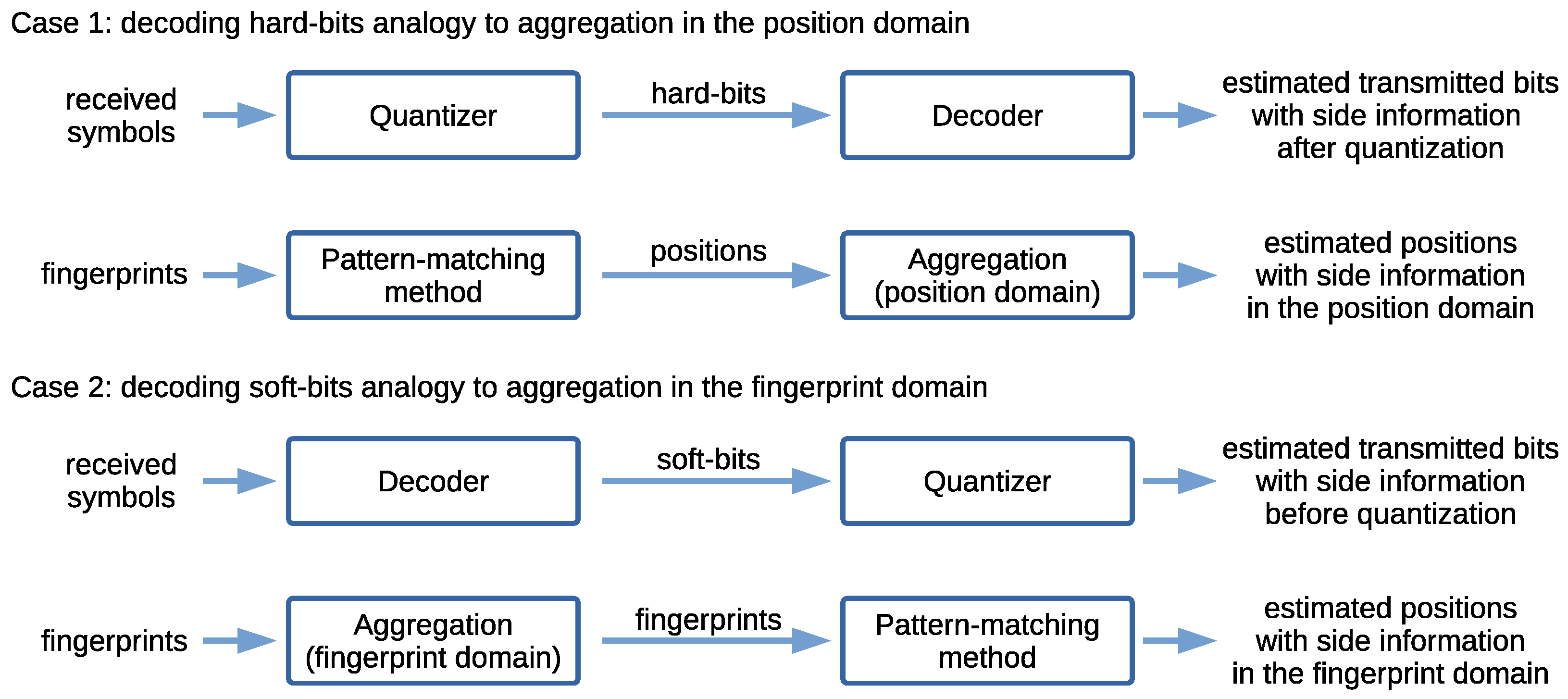



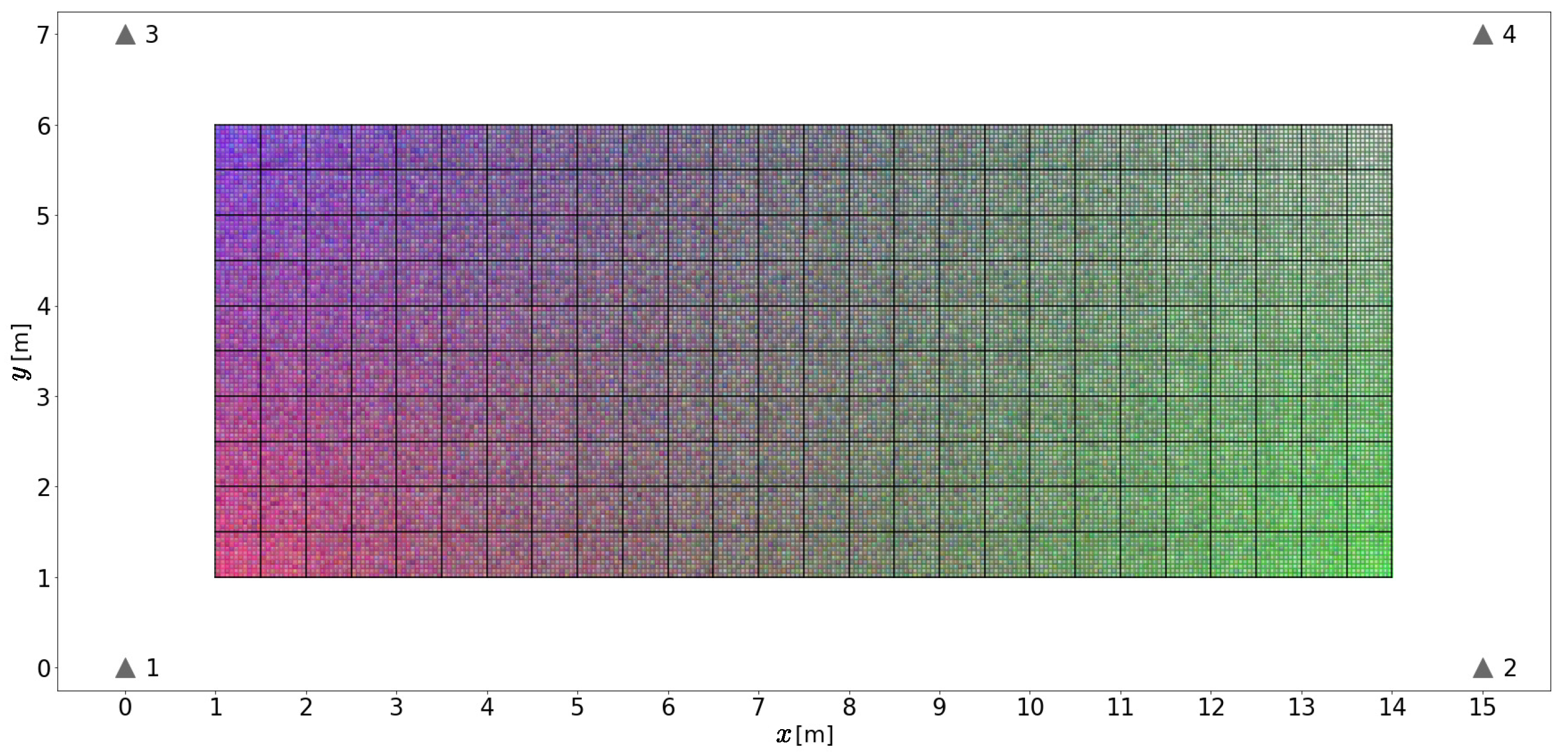



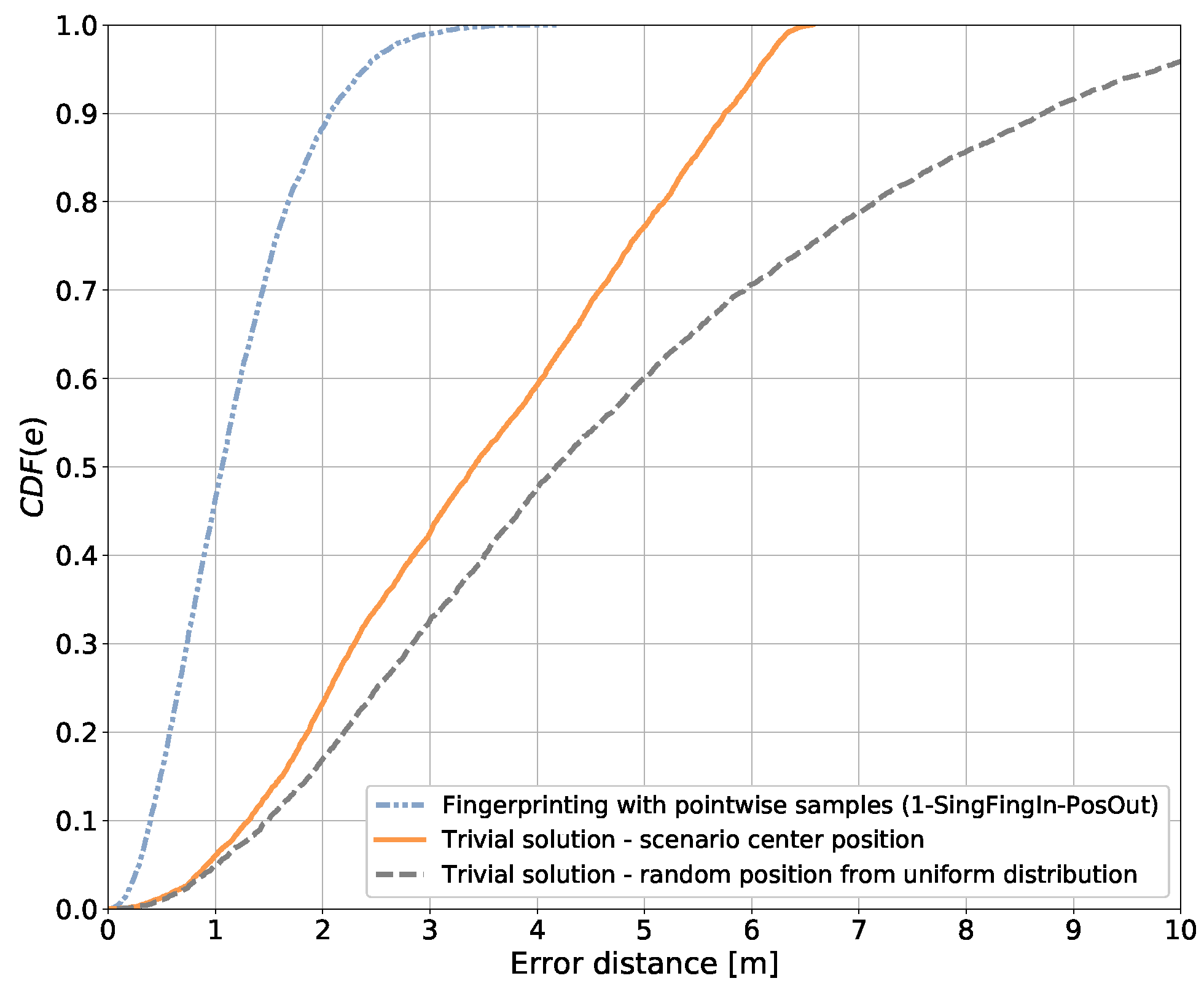
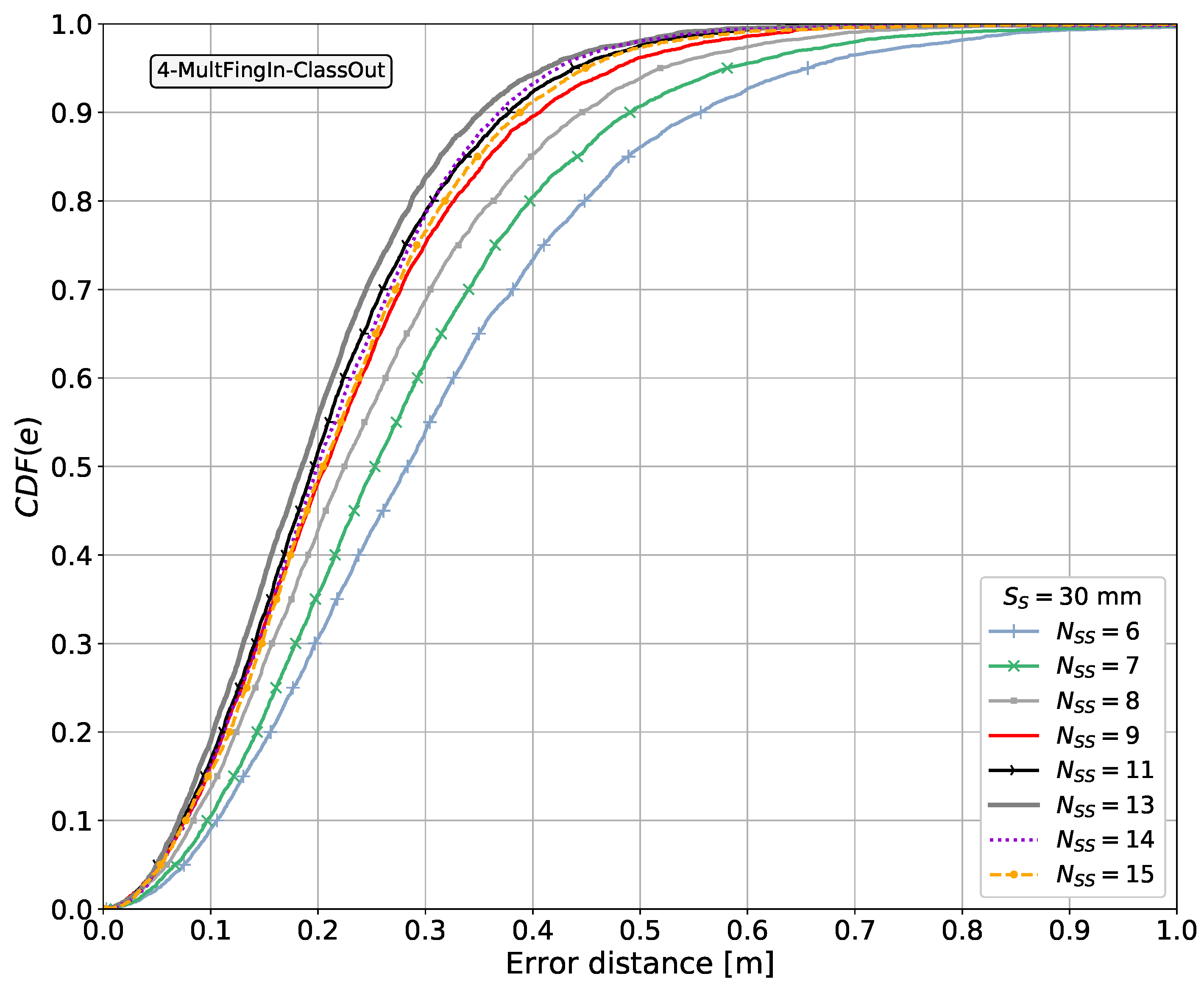


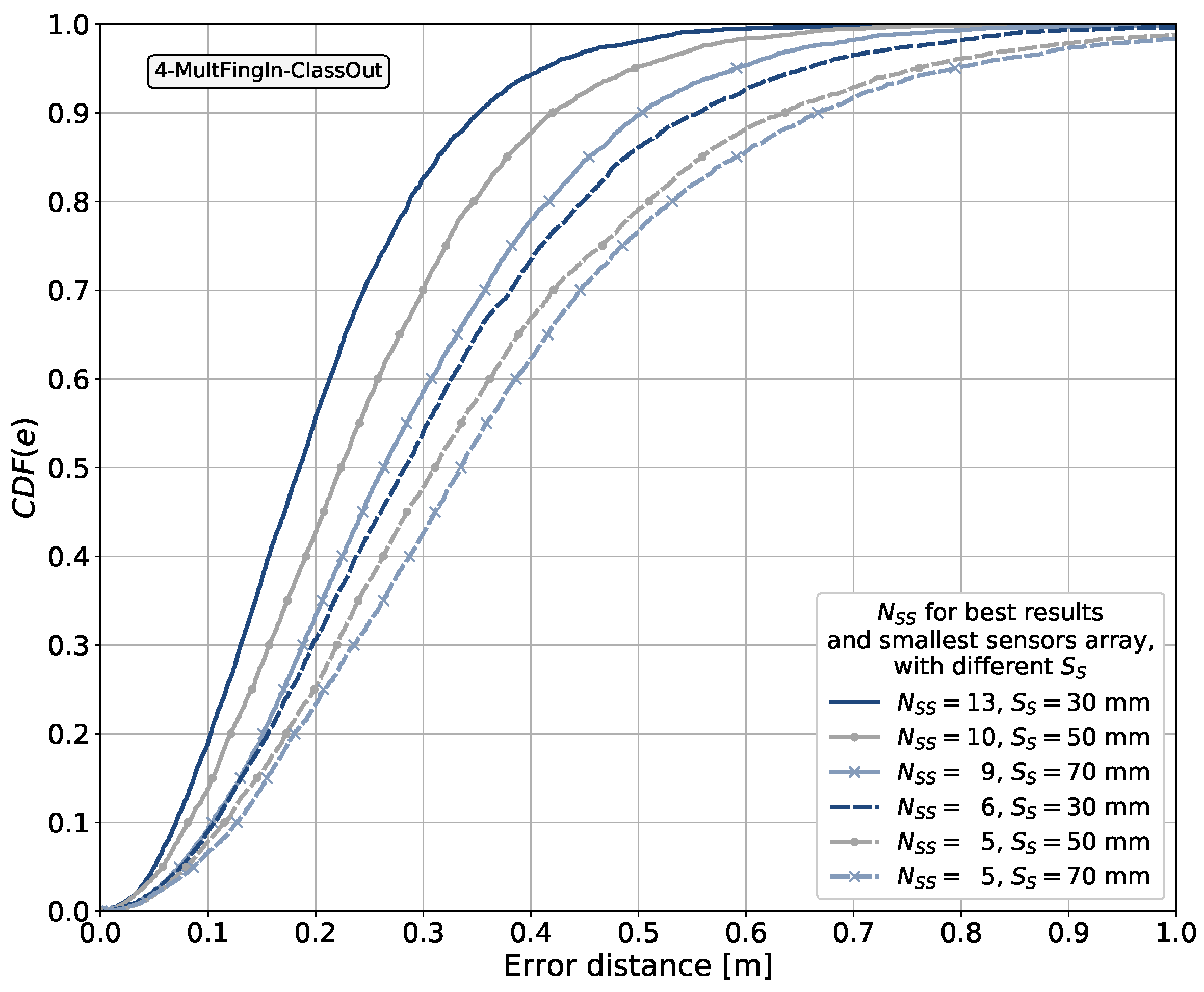
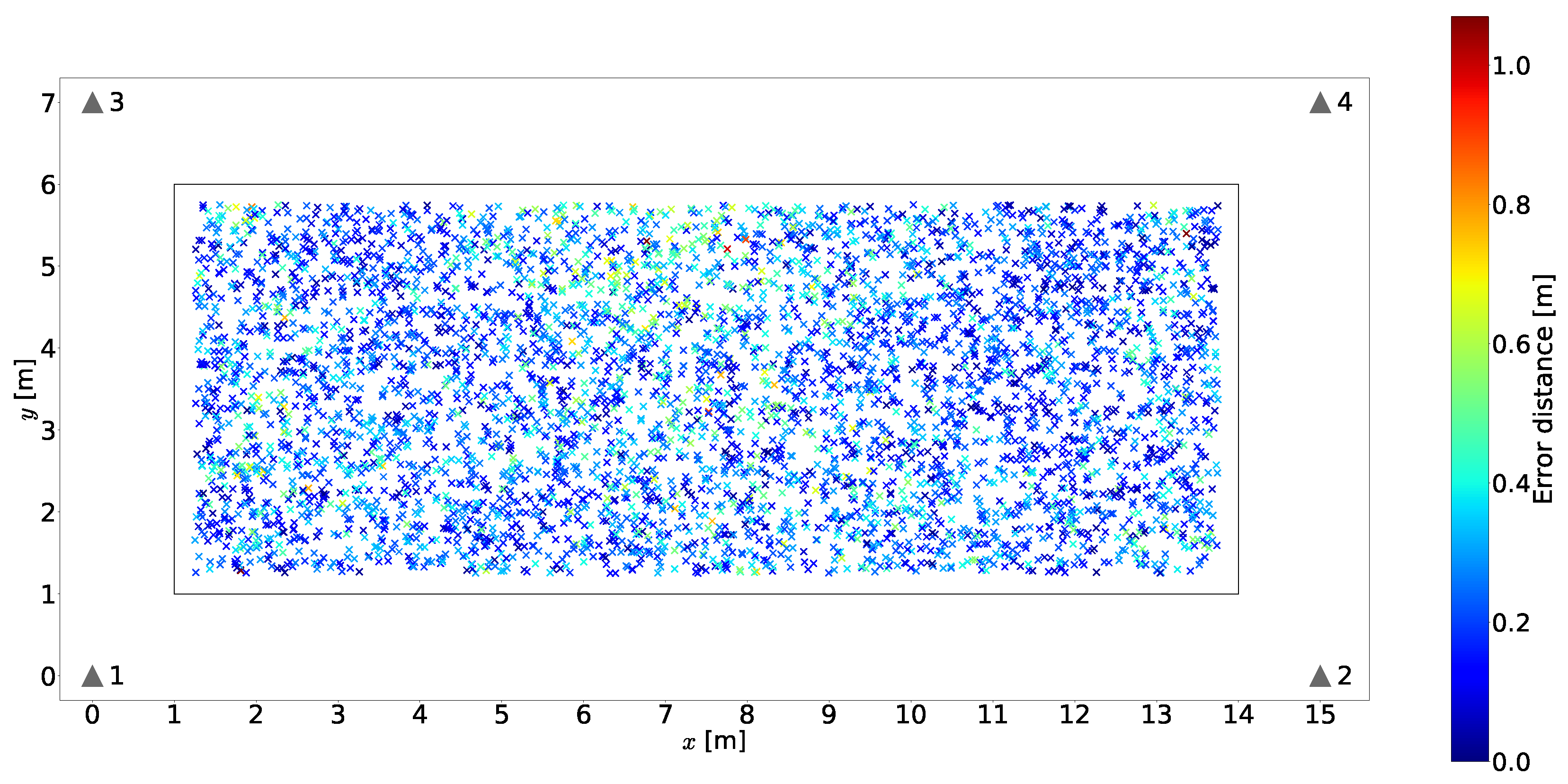
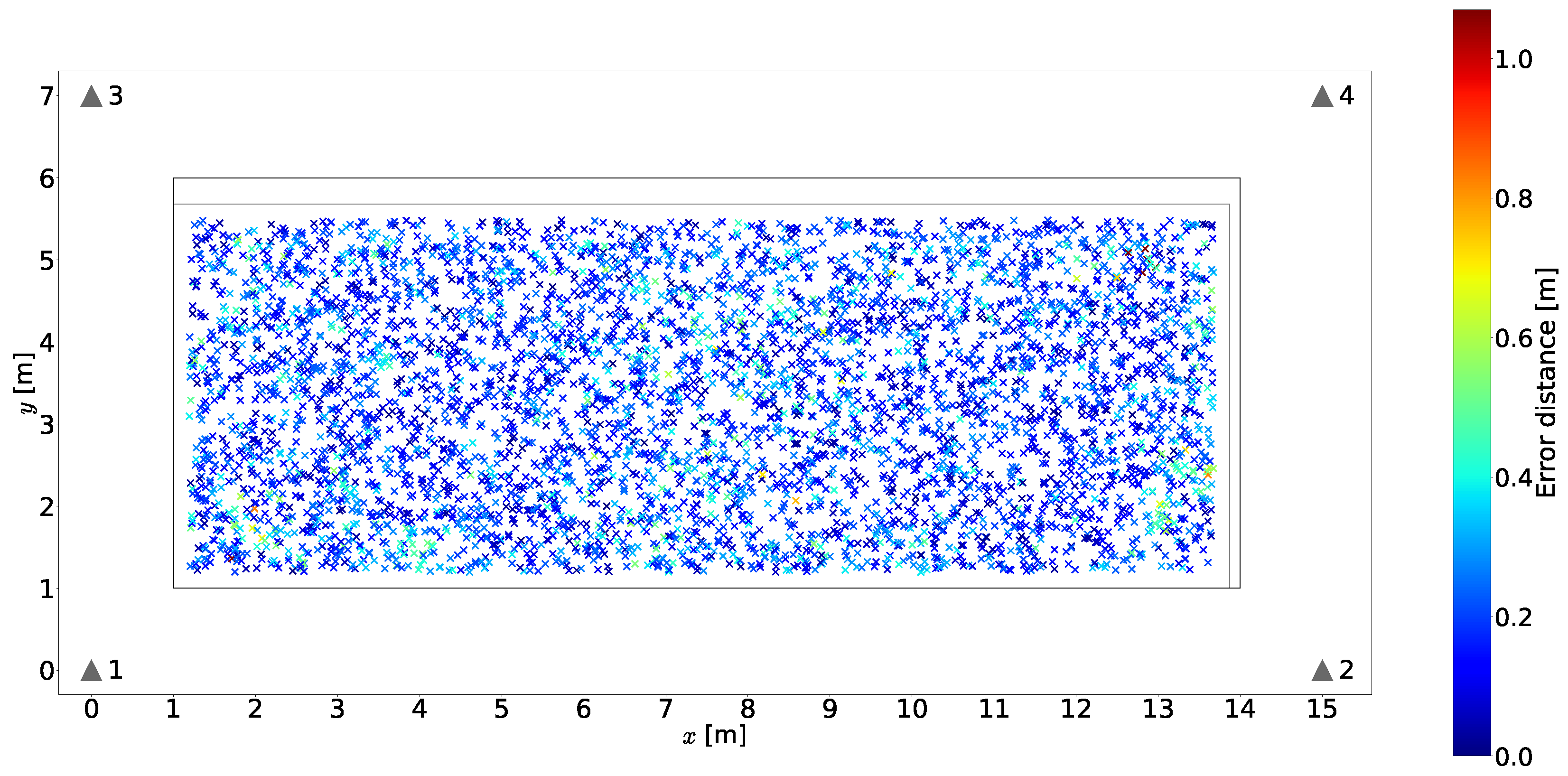
| Acronym | Description |
|---|---|
| 1D | One-dimensional/one-dimension |
| 2D | Two-dimensional/two-dimensions |
| 3D | Three-dimensional/three-dimensions |
| AoA | Angle of Arrival |
| CDF | Cumulative Distribution Function |
| CNN | Convolutional neural network |
| CSI | Channel State Information |
| FFNN | Feedforward neural network |
| FTM | Fine Timing Measurement |
| GNSS | Global Navigation Satellite System |
| ISAC | Integrated Sensing and Communications |
| kNN | k-Nearest Neighbors |
| LIS | Large Intelligent Surface |
| LOS | Line of Sight |
| LSTM | Long Short-Term Memory |
| MAE | Mean Absolute Error |
| MIMO | Multiple-Input Multiple-Output |
| (A)NN | (Artificial) neural network |
| RGB | Red–Green–Blue |
| RIS | Reconfigurable intelligent surface |
| RMSprop | Root Mean Square propagation |
| RNN | Recurrent neural network |
| RSS | Received signal strength |
| SNR | Signal-to-Noise Ratio |
| Case | Pattern-Matching Method | Aggregation Domain | |||
|---|---|---|---|---|---|
| Input (Fingerprints) | Output (Positions) | Number of Instances | Output Handling | ||
| 1 | Single set or vector | Single set or vector | One | None | (No aggregation) |
| 2 | Multiple sets or vectors | Multiple sets or vectors | One per input set | Aggregation | Positions |
| 3 | Multiple sets or vectors | Single set or vector | One | None | Fingerprints |
| Ref. | Year | Fingerprints Used | NN Type | Fingerprint Collection Method | # Side Inf. Dimensions |
|---|---|---|---|---|---|
| [164] | 2017 | Geomagnetic | RNN | Along a path | 1D |
| [165] | 2018 | RSS | LSTM | Along a path | 1D |
| [166] | 2018 | RSS, magnetic | 1D CNN | Along a path of m | 1D |
| [167] | 2018 | RSS, magnetic | 1D CNN | Along a path of m | 1D |
| [168] | 2018 | RSS | 1D CNN | Along a path, spaced at m | 1D |
| [169] | 2019 | RSS | LSTM | Three trajectory paths in an area of m m | 1D |
| [170] | 2019 | RSS | LSTM | Along a path | 1D |
| [171] | 2019 | RSS | LSTM | Along a path | 1D |
| [172] | 2019 | RSS | LSTM | Along a path | 1D |
| [173] | 2019 | Geomagnetic | LSTM | Along a path | 1D |
| [174] | 2019 | Geomagnetic | RNN and LSTM | Along a path, in two areas: m m and m m | 1D |
| [175] | 2019 | RSS | Six types of RNNs | Along a path, in an area of m m | 1D |
| [176] | 2019 | RSS | LSTM | Along a path, in only two or three steps | 1D |
| [177] | 2020 | RSS | LSTM | Along path of an estimated length of m | 1D |
| [178] | 2020 | SNR | RNN | Along a path, in an area of approx. m m | 1D |
| [179] | 2020 | RSS | LSTM | Along paths of different lengths | 1D |
| [180] | 2020 | Geomagnetic | RNN | Along a path | 1D |
| [181] | 2020 | RSS | RNN | Along a path | 1D |
| [113] | 2020 | RSS and other | LSTM | Along a path | 1D |
| [182] | 2021 | RSS | LSTM | Along a path of m, in an area of m m | 1D |
| [183] | 2021 | RSS | LSTM | Along a path | 1D |
| [184] | 2021 | RSS | LSTM | Along four paths of to m | 1D |
| [185] | 2021 | RSS | 1D CNN and RNN | Along a path | 1D |
| [186] | 2021 | RSS | 1D CNN | Along a trajectory of a random length | 1D |
| [187] | 2021 | Geomagnetic | LSTM | Along a path, positioning node every m, sequences with lengths of , , and m | 1D |
| [188] | 2021 | CSI | 1D CNN and LSTM | Along a path | 1D |
| [189] | 2021 | CSI | LSTM | Along a path, from simulation | 1D |
| [137] | 2021 | RSS | LSTM | Along a path | 1D |
| [153] | 2022 | RSS | 2D CNN | Along a path | 1D |
| [190] | 2022 | RSS | 1D CNN and LSTM | Trajectory generated from radio map | 1D |
| [191] | 2022 | RSS | CNN-based | Along a path | 1D |
| [192] | 2022 | Geomagnetic | 1D CNN and LSTM | Along a path | 1D |
| [193] | 2023 | RSS and other | LSTM | Along a path, outdoors | 1D |
| [194] | 2023 | RSS | LSTM | Along a path | 1D |
| [195] | 2024 | RSS | LSTM | Individually collected and arranged in a sequence | 1D |
| [196] | 2024 | RSS | 1D CNN and LSTM | Along a path | 1D |
| Parameter/Variable | Description |
|---|---|
| Number of sub-tiles per side of the tile | |
| (Number of sensors per side of the 2D sensor array) | |
| Total number of sub-tiles in a tile | |
| (Total number of sensors in the 2D sensor array) | |
| Total number of tiles to cover the whole positioning area | |
| Side length of sub-tile | |
| Side length of tile | |
| (Side length of the 2D sensor array) |
| Fingerprinting Pattern-Matching Method Mnemonic Name | Side Information [Positioning Data Aggregation Domain] | Input Data to the NN | Output Data from the NN [Oper. Type] | Position Calculation from the NN Output | NN Type (Implement. Structure) |
|---|---|---|---|---|---|
| 1-SingFingIn-PosOut | No side information [no aggregation] | Vector of fingerprints from center sub-tile | Position coordinates [regression] | None | Feedforward (Table: FFNN for pattern-matching methods 1-SingFingIn-PosOut and 2-SingFingIn-AggPosOut) |
| 2-SingFingIn-AggPosOut | Side information used at the output of the NN [position domain] | Vector of fingerprints from one of the sub-tiles | Position coordinates [regression] | Aggregation of position estimates | Feedforward (Table: FFNN for pattern-matching methods 1-SingFingIn-PosOut and 2-SingFingIn-AggPosOut) |
| 3-MultFingIn-PosOut | Side information used at the input of the NN [fingerprint dom.] | Tensor of fingerprints from sub-tiles (1D arrangement) | Position coordinates [regression] | None | Feedforward (Table: FFNN for pattern-matching method 3-MultFingIn-PosOut) |
| 4-MultFingIn-ClassOut | Side information used at the input of the NN [fingerprint dom.] | Tensor of fingerprints from sub-tiles (2D arrangement) | Class likelihood probability vector [classification] | Weighted sum of class probabilities multiplied by associated tile center positions | Convolutional (Table: CNN for pattern-matching method 4-MultFingIn-ClassOut) |
| Base Station Number | x Coordinates in Meters | y Coordinates in Meters |
|---|---|---|
| 1 | 0 | |
| 2 | 15 | 0 |
| 3 | 7 | |
| 4 | 15 | 7 |
| Acronym | Description |
|---|---|
| FTT | Fixed Tiles for Training |
| FTV | Fixed Tiles for Validation |
| MTV | Moving Tiles for Validation |
| MTT | Moving Tiles for Testing |
| Parameter | Description | Value |
|---|---|---|
| Number of fingerprint sources in the scenario | 4 fingerprint sources | |
| (Number of fingerprints in the vector/set | (4 fingerprints) | |
| of fingerprints) | ||
| Side length of the sub-tile | According to tile | |
| arrangement (Table: Tile arrangements) | ||
| Number of sub-tiles per side of the tile | According to tile | |
| arrangement (Table: Tile arrangements) | ||
| Number of fixed tile batches | 50 batches | |
| Number of moving tiles for validation | 5000 tiles | |
| Number of moving tiles for testing | 5000 tiles | |
| Number of training iterations | 120 iterations (minimum) | |
| Reference percentile for the selection of the | (95%) | |
| model weights with the MTV dataset | ||
| f | Frequency in the radio channel model | 2600 MHz |
| Standard deviation in the radio channel model | 3 [dB] | |
| Power loss coefficient in the radio channel model | 30 |
| Variable | Description | Value |
|---|---|---|
| Side length of tile (side length of the 2D sensor array) | ||
| Total number of sub-tiles in a tile | ||
| Total number of tiles to cover the positioning area | Returned by function | |
| (for method 4, it is equivalent to the number of classes) | (Pseudocode 1), listed in Table: Tile arrangements. | |
| Number of fixed tiles for training | 50 fixed tile batches of tiles each tiles | |
| Number of fixed tiles for validation | 50 fixed tile batches of tiles each tiles |
| Layer | Size | Activation Function | Notes |
|---|---|---|---|
| Dense | Hyperbolic tangent | Input: vector of fingerprints from a sub-tile. | |
| Dense | 32 | Hyperbolic tangent | - |
| Dense | 32 | Hyperbolic tangent | - |
| Dense | 32 | Rectified linear unit | - |
| Dense | 2 | Linear | Output: position coordinates. |
| Layer | Size | Activation Function | Notes |
|---|---|---|---|
| Dense | Hyperbolic tangent | Input: tensor of the fingerprints from | |
| sub-tiles (1D arrangement) by the size of | |||
| the set of fingerprints, . | |||
| Dense | 2048 | Hyperbolic tangent | - |
| Dense | 2048 | Hyperbolic tangent | - |
| Dense | 2048 | Hyperbolic tangent | - |
| Dense | 1024 | Hyperbolic tangent | - |
| Dense | 512 | Rectified linear unit | - |
| Dense | 2 | Linear | Output: position coordinates. |
| Layer | Size | Activation Function | Notes |
|---|---|---|---|
| Convolution | 2048 | Rectified linear unit | Input: tensor of fingerprints from |
| (2D) | sub-tiles (2D arrangement) by the size of | ||
| the set of fingerprints, . | |||
| Convolution kernel ; no padding; stride = 1. | |||
| Convolution | 2048 | Rectified linear unit | Convolution kernel ; no padding; stride = 1. |
| (2D) | |||
| Flatten | - | - | - |
| Dense | 2048 | Rectified linear unit | - |
| Dense | Softmax | Output: tile-class likelihood probability vector | |
| of size . |
| Tile Arrangement Mnemonic Name | [mm] | [mm] | Number of NN Parameters for Each Pattern-Matching Method | |||||
|---|---|---|---|---|---|---|---|---|
| 1-SingFingIn | 2-SingFingIn | 3-MultFingIn | 4-MultFingIn | |||||
| -PosOut | -AggPosOut | -PosOut | -ClassOut | |||||
| 6×6-30 | 30 | 6 | 180 | 1944 | 2358 | 2358 | 11,334,546 | 58,589,080 |
| 7×7-30 | 30 | 7 | 210 | 1403 | 2358 | 2358 | 11,458,774 | 78,452,091 |
| 8×8-30 | 30 | 8 | 240 | 1080 | 2358 | 2358 | 11,608,834 | 107,150,392 |
| 9×9-30 | 30 | 9 | 270 | 864 | 2358 | 2358 | 11,787,606 | 144,456,544 |
| 10×10-30 | 30 | 10 | 300 | 688 | 2358 | 2358 | 11,998,354 | 190,233,264 |
| 11×11-30 | 30 | 11 | 330 | 585 | 2358 | 2358 | 12,244,726 | 244,548,169 |
| 12×12-30 | 30 | 12 | 360 | 468 | 2358 | 2358 | 12,530,754 | 307,222,996 |
| 13×13-30 | 30 | 13 | 390 | 396 | 2358 | 2358 | 12,860,854 | 378,378,636 |
| 14×14-30 | 30 | 14 | 420 | 330 | 2358 | 2358 | 13,239,826 | 457,935,178 |
| 15×15-30 | 30 | 15 | 450 | 308 | 2358 | 2358 | 13,672,854 | 545,970,484 |
| 5×5-50 | 50 | 5 | 250 | 1040 | 2358 | 2358 | 11,233,654 | 44,153,872 |
| 6×6-50 | 50 | 6 | 300 | 688 | 2358 | 2358 | 11,334,546 | 56,015,536 |
| 7×7-50 | 50 | 7 | 350 | 518 | 2358 | 2358 | 11,458,774 | 76,638,726 |
| 8×8-50 | 50 | 8 | 400 | 384 | 2358 | 2358 | 11,608,834 | 105,724,288 |
| 9×9-50 | 50 | 9 | 450 | 308 | 2358 | 2358 | 11,787,606 | 143,317,300 |
| 10×10-50 | 50 | 10 | 500 | 260 | 2358 | 2358 | 11,998,354 | 189,356,292 |
| 11×11-50 | 50 | 11 | 550 | 207 | 2358 | 2358 | 12,244,726 | 243,773,647 |
| 12×12-50 | 50 | 12 | 600 | 168 | 2358 | 2358 | 12,530,754 | 306,608,296 |
| 13×13-50 | 50 | 13 | 650 | 140 | 2358 | 2358 | 12,860,854 | 377,854,092 |
| 14×14-50 | 50 | 14 | 700 | 126 | 2358 | 2358 | 13,239,826 | 457,517,182 |
| 15×15-50 | 50 | 15 | 750 | 102 | 2358 | 2358 | 13,672,854 | 545,548,390 |
| 5×5-70 | 70 | 5 | 350 | 518 | 2358 | 2358 | 11,233,654 | 43,084,294 |
| 6×6-70 | 70 | 6 | 420 | 330 | 2358 | 2358 | 11,334,546 | 55,281,994 |
| 7×7-70 | 70 | 7 | 490 | 260 | 2358 | 2358 | 11,458,774 | 76,110,084 |
| 8×8-70 | 70 | 8 | 560 | 184 | 2358 | 2358 | 11,608,834 | 105,314,488 |
| 9×9-70 | 70 | 9 | 630 | 140 | 2358 | 2358 | 11,787,606 | 142,973,068 |
| 10×10-70 | 70 | 10 | 700 | 126 | 2358 | 2358 | 11,998,354 | 189,081,726 |
| 11×11-70 | 70 | 11 | 770 | 96 | 2358 | 2358 | 12,244,726 | 243,546,208 |
| 12×12-70 | 70 | 12 | 840 | 75 | 2358 | 2358 | 12,530,754 | 306,417,739 |
| 13×13-70 | 70 | 13 | 910 | 70 | 2358 | 2358 | 12,860,854 | 377,710,662 |
| 14×14-70 | 70 | 14 | 980 | 65 | 2358 | 2358 | 13,239,826 | 457,392,193 |
| 15×15-70 | 70 | 15 | 1050 | 48 | 2358 | 2358 | 13,672,854 | 545,437,744 |
[mm] | Pattern-Matching Method | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2-SingFingIn-AggPosOut | 3-MultFingIn-PosOut | 4-MultFingIn-ClassOut | |||||||
| Small. | Number of | Small. | Number of | Small. | Number of | ||||
| NN Param. | [mm] | NN Param. | [mm] | NN Param. | [mm] | ||||
| 30 | 6 | 2358 (36 instances) | 180 | 6 | 11,334,546 | 180 | 6 | 58,589,080 | 180 |
| 50 | 5 | 2358 (25 instances) | 250 | 5 | 11,233,654 | 250 | 5 | 44,153,872 | 250 |
| 70 | 5 | 2358 (25 instances) | 350 | 5 | 11,233,654 | 350 | 5 | 43,084,294 | 350 |
[mm] | Pattern-Matching Method | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2-SingFingIn-AggPosOut | 3-MultFingIn-PosOut | 4-MultFingIn-ClassOut | |||||||
| Best | Number of | Best | Number of | Best | Number of | ||||
| NN Param. | [mm] | NN Param. | [mm] | NN Param. | [mm] | ||||
| 30 | 14 | 2358 (196 instances) | 420 | 10 | 11,998,354 | 300 | 13 | 378,378,636 | 390 |
| 50 | 15 | 2358 (225 instances) | 750 | 8 | 11,608,834 | 400 | 10 | 189,356,292 | 500 |
| 70 | 15 | 2358 (225 instances) | 1050 | 6 | 11,334,546 | 420 | 9 | 142,973,068 | 630 |
[mm] | Pattern-Matching Method | Difference in Error | |||||
|---|---|---|---|---|---|---|---|
| 3-MultFingIn-PosOut | 4-MultFingIn-ClassOut | Distance Between | |||||
| Error | Error | Error Dist. | Error | Error | Error Dist. | Methods 3-Mult- | |
| Distance | Distance | Difference | Distance | Distance | Difference | FingIn-PosOut | |
| at th | Norm. by | from Method | at th | Norm. by | from Method | and 4-MultFingIn- | |
| Percentile | Side Length | 1-SingFingIn- | Percentile | Side Length | 1-SingFingIn- | ClassOut at th | |
| [m] | of Tile [Tiles] | PosOut [m] | [m] | of Tile [Tiles] | PosOut [m] | Percentile [m] | |
| 30 | 0.5594 | 1.86 | 1.8406 | 0.4117 | 1.06 | 1.9883 | 0.1477 |
| 50 | 0.6364 | 1.59 | 1.7636 | 0.4970 | 0.99 | 1.9030 | 0.1394 |
| 70 | 0.7062 | 1.68 | 1.6938 | 0.5905 | 0.94 | 1.8095 | 0.1157 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lembo, S.; Horsmanheimo, S.; Ruponen, S.; Chen, T.; Tuomimäki, L.; Kemppi, P. Fingerprinting-Based Positioning with Spatial Side Information at the Positioning Device Solved via Feedforward and Convolutional Neural Networks: Survey and Feasibility Study Through System Simulations. Telecom 2025, 6, 15. https://doi.org/10.3390/telecom6010015
Lembo S, Horsmanheimo S, Ruponen S, Chen T, Tuomimäki L, Kemppi P. Fingerprinting-Based Positioning with Spatial Side Information at the Positioning Device Solved via Feedforward and Convolutional Neural Networks: Survey and Feasibility Study Through System Simulations. Telecom. 2025; 6(1):15. https://doi.org/10.3390/telecom6010015
Chicago/Turabian StyleLembo, S., S. Horsmanheimo, S. Ruponen, T. Chen, L. Tuomimäki, and P. Kemppi. 2025. "Fingerprinting-Based Positioning with Spatial Side Information at the Positioning Device Solved via Feedforward and Convolutional Neural Networks: Survey and Feasibility Study Through System Simulations" Telecom 6, no. 1: 15. https://doi.org/10.3390/telecom6010015
APA StyleLembo, S., Horsmanheimo, S., Ruponen, S., Chen, T., Tuomimäki, L., & Kemppi, P. (2025). Fingerprinting-Based Positioning with Spatial Side Information at the Positioning Device Solved via Feedforward and Convolutional Neural Networks: Survey and Feasibility Study Through System Simulations. Telecom, 6(1), 15. https://doi.org/10.3390/telecom6010015







