Lateral–Torsional Buckling of Externally Prestressed I-Section Steel Beams Subjected to Fire
Abstract
:1. Introduction
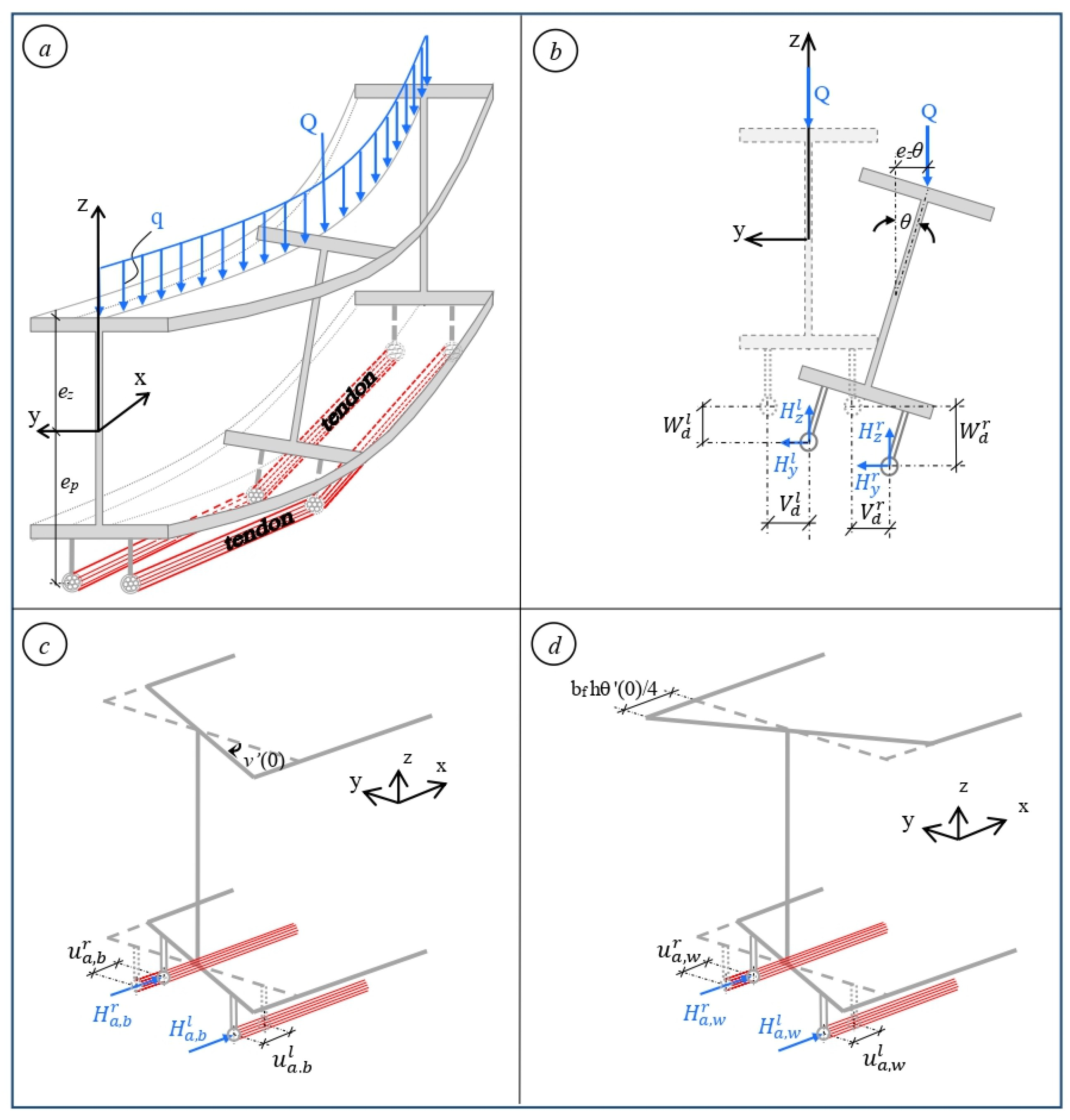
2. Analytical Formulation
- (1)
- The deviator and anchorages are rigid enough to prevent localised strain at the contact tendon–anchorage and tendon–deviator, even under remarkable prestresses. This is reasonable, due to the small dimensions and high strength of such elements, and allows us to focus on modelling how high temperatures affect the LTB of steel beams prestressed by protected and unprotected cables.
- (2)
- The cables are tensioned simultaneously at both ends by opposite forces, regardless of whether they have a bonded or unbonded deviator. Here, assuming tendon–deviator contact at one central point and simultaneous tensioning and blocking of cables at the anchors yields symmetrical tensions in the tendons. Conversely, if, for instance, tensioning is applied only at one end of the beam, this symmetry is not achieved.
- (3)
- To prevent local instability, the cross-sections are rigid in their own planes and Euler–Bernoulli beam theory still holds, as will be confirmed by nonlinear FEM simulations.
- (4)
- The temperature of the main member differs from that of the cables but is uniform within each element and varies over time.
2.1. Kinematics of Prestressed I-Section Beams
2.2. Variational Formulation
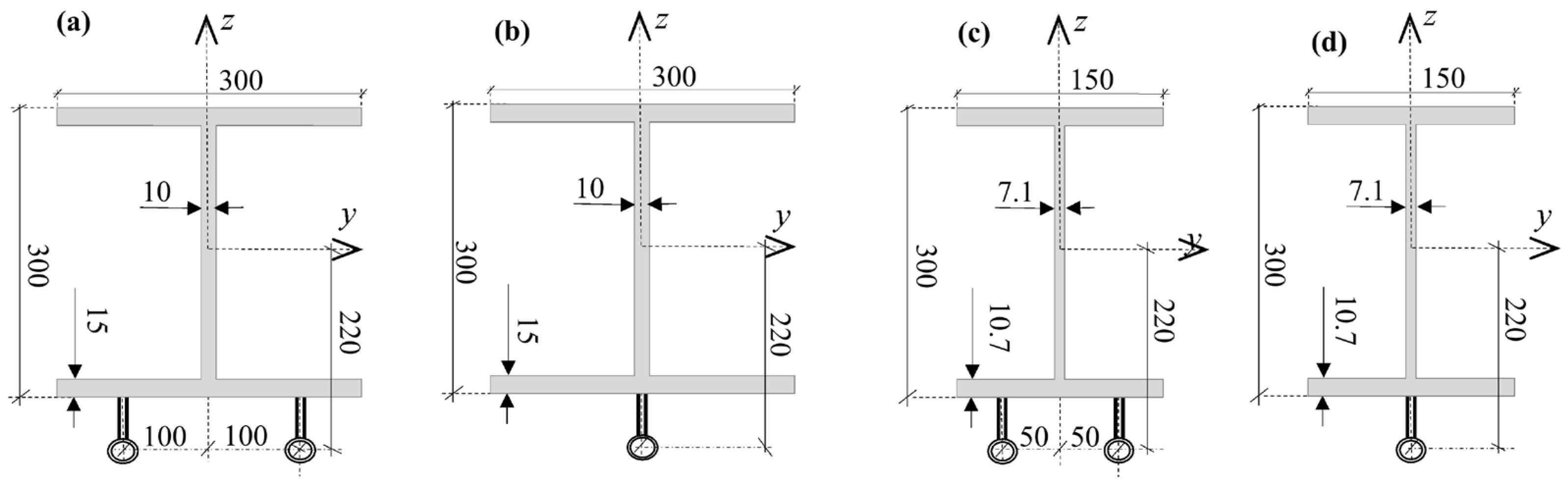
3. Results and Discussion
3.1. Prestressed Beams Under Mechanical Loading
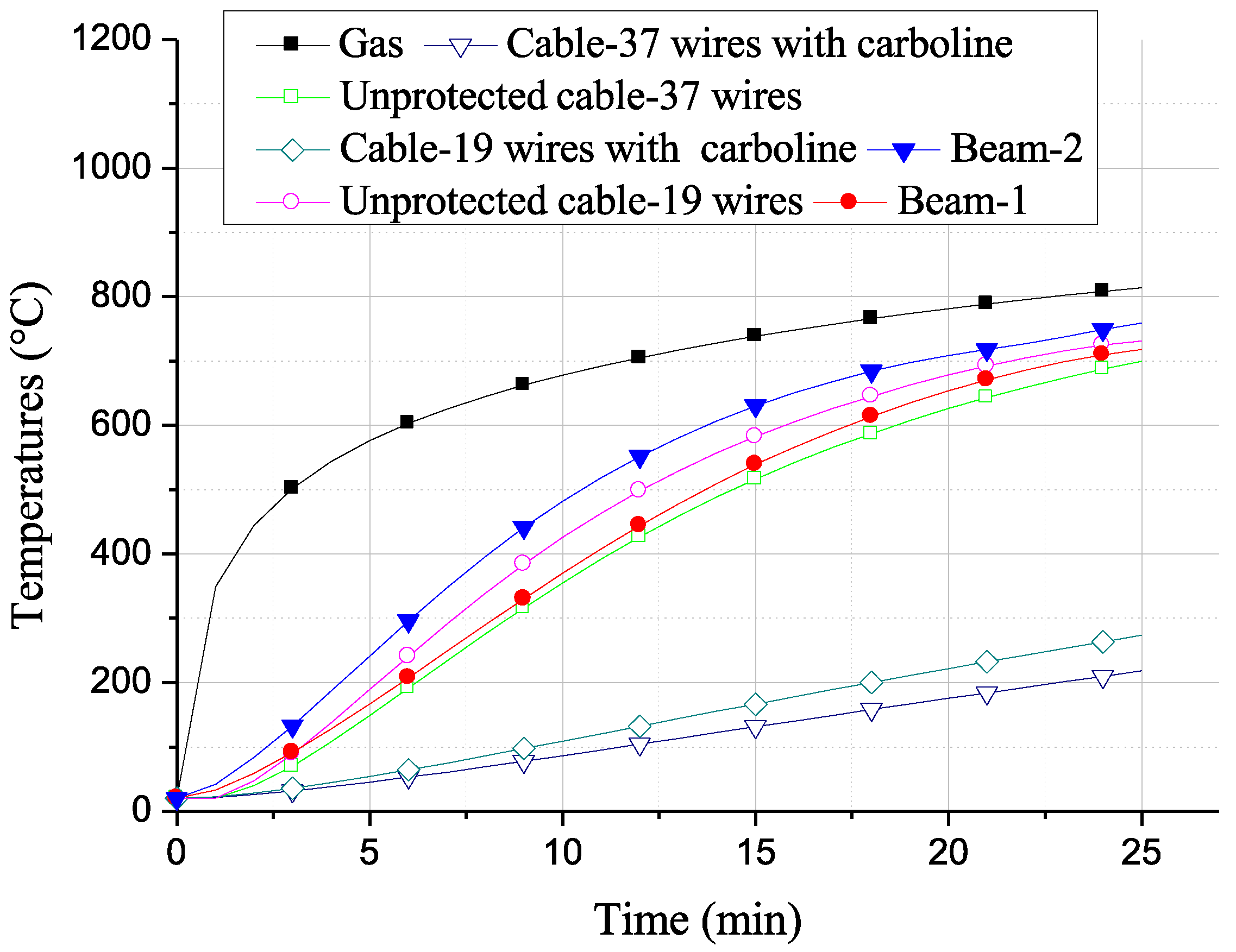
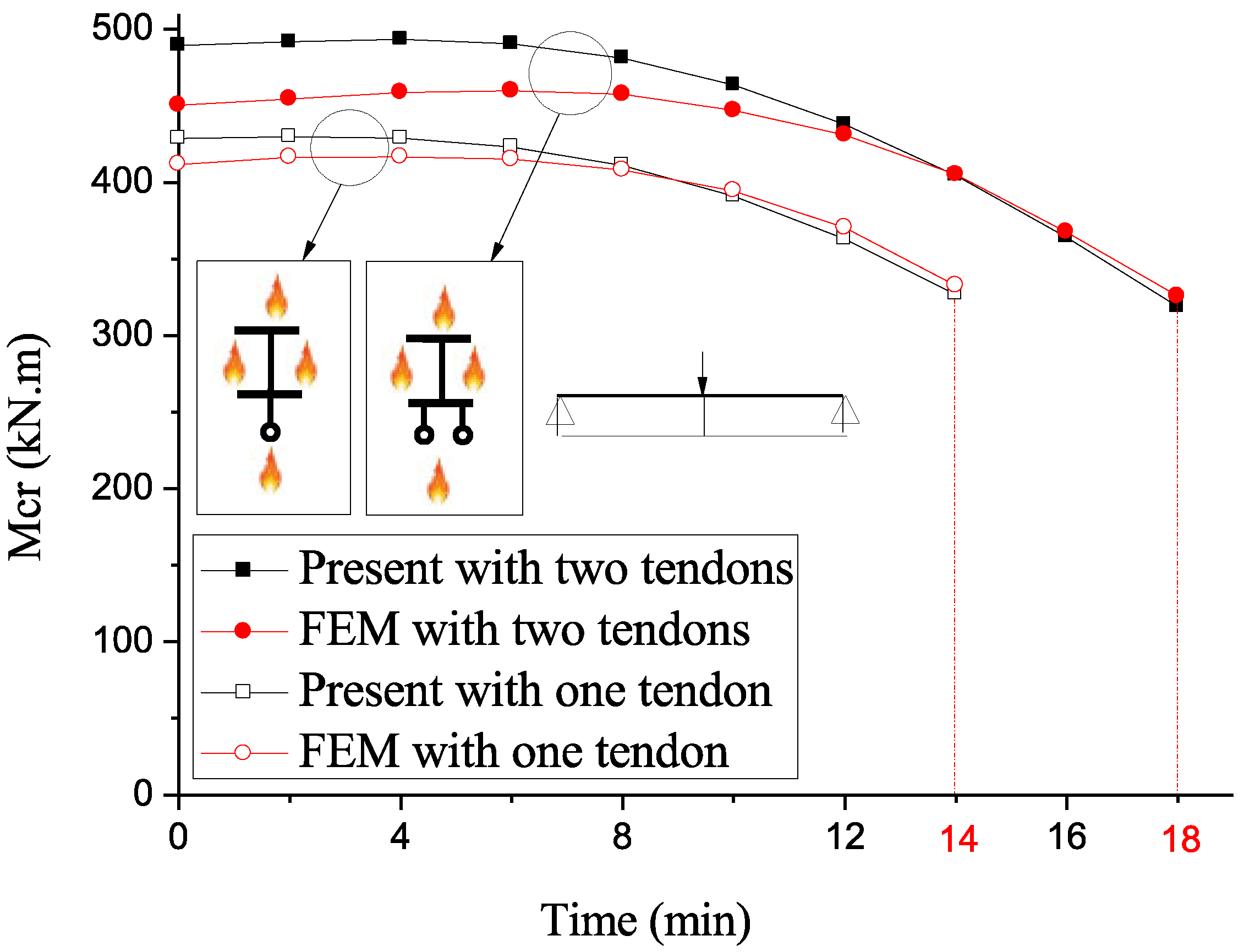
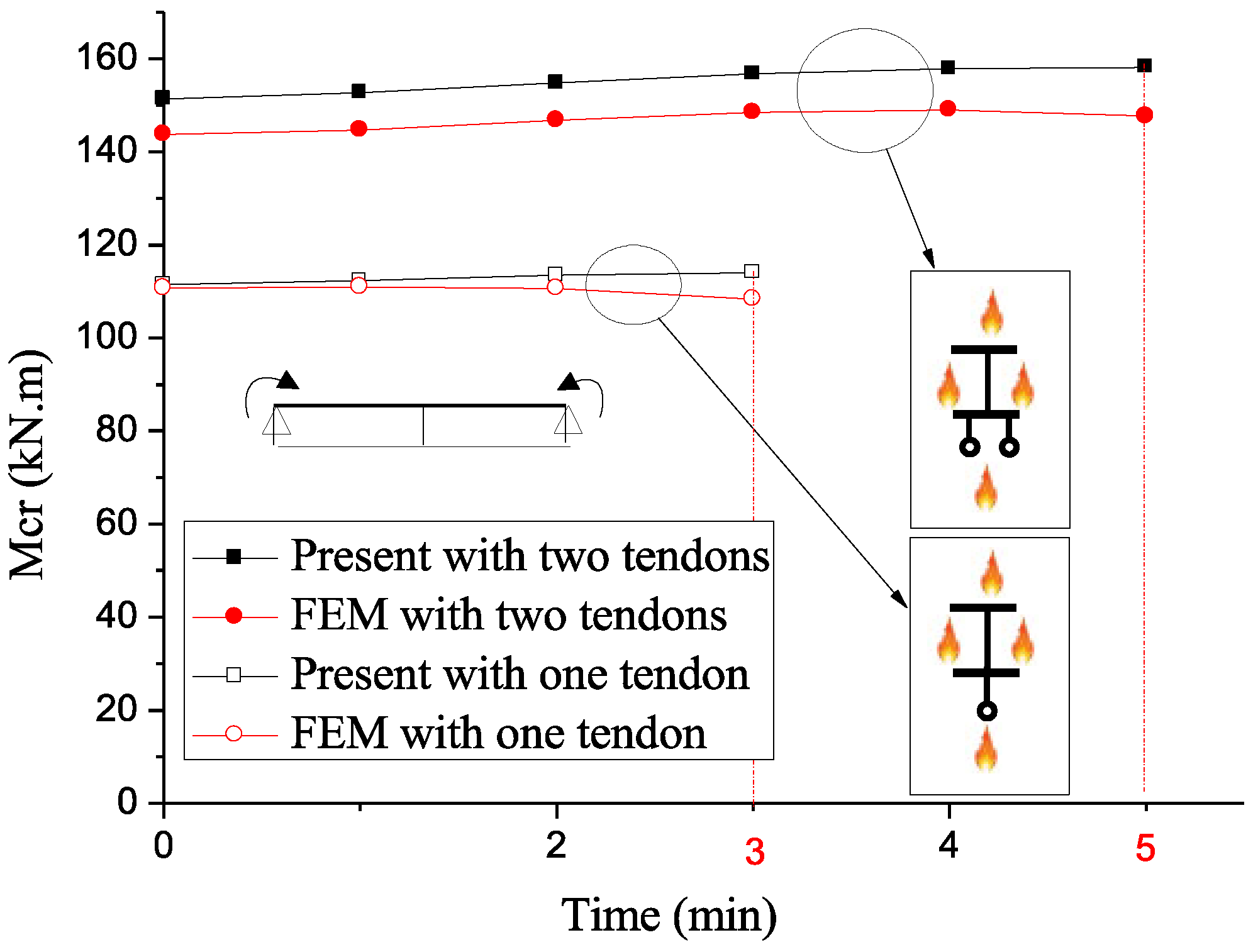
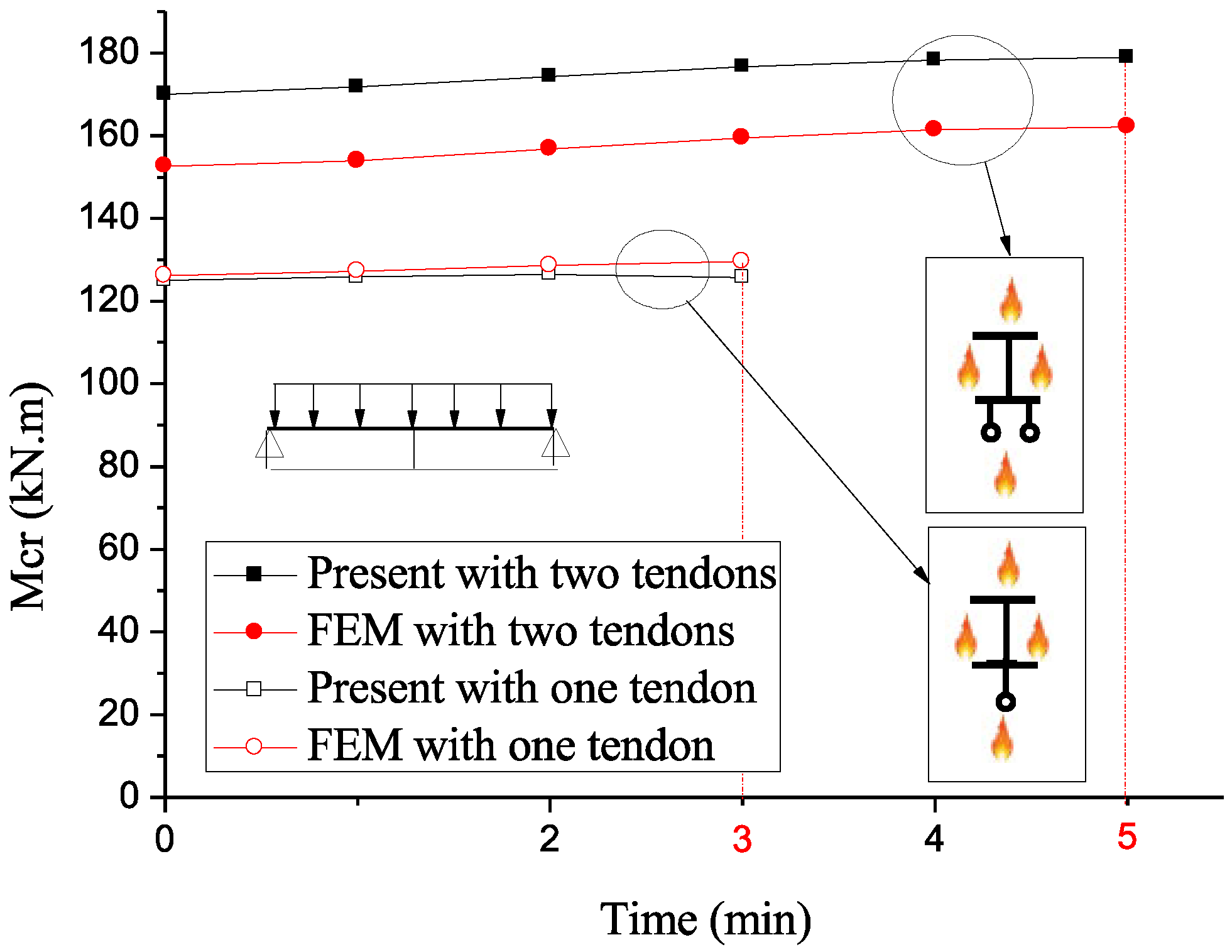
3.2. Prestressed Beams Under Thermomechanical Loading
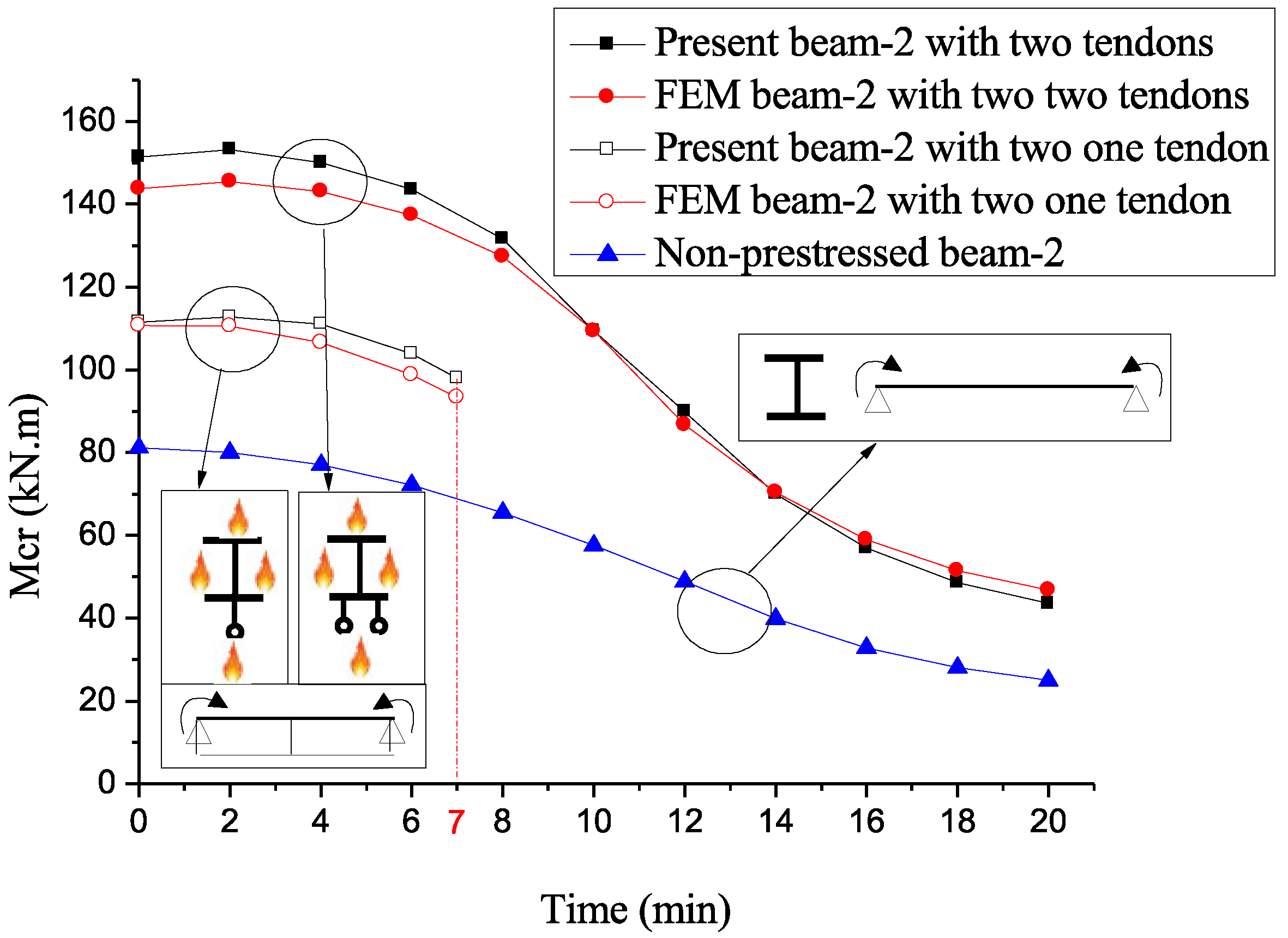
3.3. FEM Nonlinear Analysis
4. Final Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Torelli, G.; Mandal, P.; Gillie, M.; Tran, V.-X. A confinement-dependent load-induced thermal strain constitutive model for concrete subjected to temperatures up to 500 °C. Int. J. Mech. Sci. 2018, 144, 887–896. [Google Scholar] [CrossRef]
- Peng, F.; Xue, W. Calculating Method for Ultimate Tendon Stress in Internally Unbonded Prestressed Concrete Members. ACI Struct. J. 2019, 116, 225–234. [Google Scholar] [CrossRef]
- Oukaili, N.; Peera, I. Behavioral nonlinear modeling of prestressed concrete flexural members with internally unbonded steel strands. Results Eng. 2022, 14, 100411. [Google Scholar] [CrossRef]
- Corral, M.d.M.; Todisco, L. Structural design of a smart under-deck cable-stayed prestressed concrete viaduct: Theoretical basis and application to the Osormort viaduct. Struct. Concr. 2024, 25, 1528–1545. [Google Scholar] [CrossRef]
- He, Z.-Q.; Liu, Z. Stresses in External and Internal Unbonded Tendons: Unified Methodology and Design Equations. J. Struct. Eng. 2010, 136, 1055–1065. [Google Scholar] [CrossRef]
- Zona, A.; Ragni, L.; Dall’asta, A. Simplified method for the analysis of externally prestressed steel–concrete composite beams. J. Constr. Steel Res. 2009, 65, 308–313. [Google Scholar] [CrossRef]
- Lou, T.; Lopes, S.M.; Lopes, A.V. Numerical modeling of externally prestressed steel–concrete composite beams. J. Constr. Steel Res. 2016, 121, 229–236. [Google Scholar] [CrossRef]
- Moscoso, A.M.; Tamayo, J.L.; Morsch, I.B. Numerical simulation of external pre-stressed steel-concrete composite beams. Comput. Concr. 2017, 19, 191–201. [Google Scholar] [CrossRef]
- Almeida, M.M.d.R.; de Souza, A.S.C.; de Albuquerque, A.T.; Rossi, A. Parametric analysis of steel-concrete composite beams prestressed with external tendons. J. Constr. Steel Res. 2022, 189, 107087. [Google Scholar] [CrossRef]
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures—Part 1–1: General Rules and Rules for Buildings. European Committee for Standardisation (CEN): Brussels, Belgium, 2004.
- EN 1994-1-1:2004; Eurocode 4—Design of Composite Steel Concrete Structures, Part 1. 1: General Rules and Rules for Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2004.
- Chan, S.-L.; Shu, G.-P.; Lü, Z.-T. Stability analysis and parametric study of pre-stressed stayed columns. Eng. Struct. 2002, 24, 115–124. [Google Scholar] [CrossRef]
- Gupta, L.; Ronghe, G.; Naghate, M. Behaviour and stability of prestressed steel plate girder for torsional buckling. Steel Compos. Struct. 2003, 3, 65–73. [Google Scholar] [CrossRef]
- Abdelnabi, O.N. Stability of Externally Prestressed Steel Plate Girders. Master’s Thesis, Benha University, Calcutta, India, 2013. [Google Scholar]
- Wadee, M.A.; Gardner, L.; Osofero, A.I. Design of prestressed stayed columns. J. Constr. Steel Res. 2013, 80, 287–298. [Google Scholar] [CrossRef]
- Guo, Y.-L.; Fu, P.-P.; Zhou, P.; Tong, J.-Z. Elastic buckling and load resistance of a single cross-arm pre-tensioned cable stayed buckling-restrained brace. Eng. Struct. 2016, 126, 516–530. [Google Scholar] [CrossRef]
- Gosaye, J.; Gardner, L.; Wadee, M.A.; Ellen, M.E. Compressive behaviour and design of prestressed steel elements. Structures 2016, 5, 76–87. [Google Scholar] [CrossRef]
- Guo, Y.-L.; Zhou, P.; Bradford, M.A.; Pi, Y.-L.; Tong, J.-Z.; Fu, P.-P. Theoretical and numerical studies of elastic buckling and load resistance of double cross-arm pre-tensioned cable stayed buckling-restrained braces. Eng. Struct. 2017, 153, 674–699. [Google Scholar] [CrossRef]
- Yu, J.; Wadee, M.A. Mode interaction in triple-bay prestressed stayed columns. Int. J. Non-Linear Mech. 2017, 88, 47–66. [Google Scholar] [CrossRef]
- Belletti, B.; Gasperi, A. Behavior of Prestressed Steel Beams. J. Struct. Eng. 2010, 136, 1131–1139. [Google Scholar] [CrossRef]
- Zhang, W.-F. Symmetric and antisymmetric lateral–torsional buckling of prestressed steel I-beams. Thin-Walled Struct. 2018, 122, 463–479. [Google Scholar] [CrossRef]
- Mohri, F.; Bouzerira, C.; Potier-Ferry, M. Lateral buckling of thin-walled beam-column elements under combined axial and bending loads. Thin-Walled Struct. 2008, 46, 290–302. [Google Scholar] [CrossRef]
- Mohri, F.; Damil, N.; Potier-Ferry, M. Buckling and lateral buckling interaction in thin-walled beam-column elements with mono-symmetric cross sections. Appl. Math. Model. 2013, 37, 3526–3540. [Google Scholar] [CrossRef]
- Saoula, A.; Meftah, S.A.; Mohri, F.; Daya, E.M. Lateral buckling of box beam elements under combined axial and bending loads. J. Constr. Steel Res. 2016, 116, 141–155. [Google Scholar] [CrossRef]
- Kim, M.-Y.; Nanzad, N.; Hayat, U. Effects of un-bonded deviators on the out-of-plane buckling of steel H-beams pre-stressed by a straight tendon cable. Eng. Struct. 2020, 214, 110566. [Google Scholar] [CrossRef]
- Kim, M.-Y.; Hayat, U.; Mehdi, A.I. Lateral–torsional buckling of steel beams pre-stressed by straight tendons with a single deviator. Thin-Walled Struct. 2021, 163, 107642. [Google Scholar] [CrossRef]
- Kim, M.-Y.; Hayat, U.; Kim, S.-B.; Mehdi, A.I. Stabilizing effects of discrete deviators on LTB of mono-symmetric thin-walled beams pre-stressed by rectilinear tendon cables. Thin-Walled Struct. 2022, 176, 109329. [Google Scholar] [CrossRef]
- Mehdi, A.I.; Kim, M.-Y. LTB analysis of pre-stressed mono-symmetric thin-walled beams with deviators under non-uniform bending moments using a simplified FEM. Structures 2023, 47, 2331–2346. [Google Scholar] [CrossRef]
- Wu, K.; Wadee, M.A.; Gardner, L. Interactive buckling in prestressed stayed beam-columns. Int. J. Mech. Sci. 2020, 174, 105479. [Google Scholar] [CrossRef]
- Wu, K.; Wadee, M.A.; Gardner, L. Stability and ultimate behaviour of prestressed stayed beam-columns. Eng. Struct. 2019, 201, 109723. [Google Scholar] [CrossRef]
- Wu, K.; Xing, Z.; Li, H. Nonlinear stability and design of prestressed stayed columns in fire considering non-uniform temperature distribution. J. Build. Eng. 2023, 79, 1078. [Google Scholar] [CrossRef]
- Wu, K.; Xing, Z.; Li, G.; Chang, H. Fire Behavior of Prestressed Stayed Columns: Critical Temperature and Mode Transition. J. Struct. Eng. 2024, 150, 04024038. [Google Scholar] [CrossRef]
- ASCE Committee on Fire Protection. Structural Fire Protection. In Manuals and Reports on Engineering Practice No. 78; ASCE: New York, NY, USA, 1992. [Google Scholar]
- Franssen, J.-M.; Real, P.V. Fire Design of Steel Structures, 2nd ed.; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar] [CrossRef]
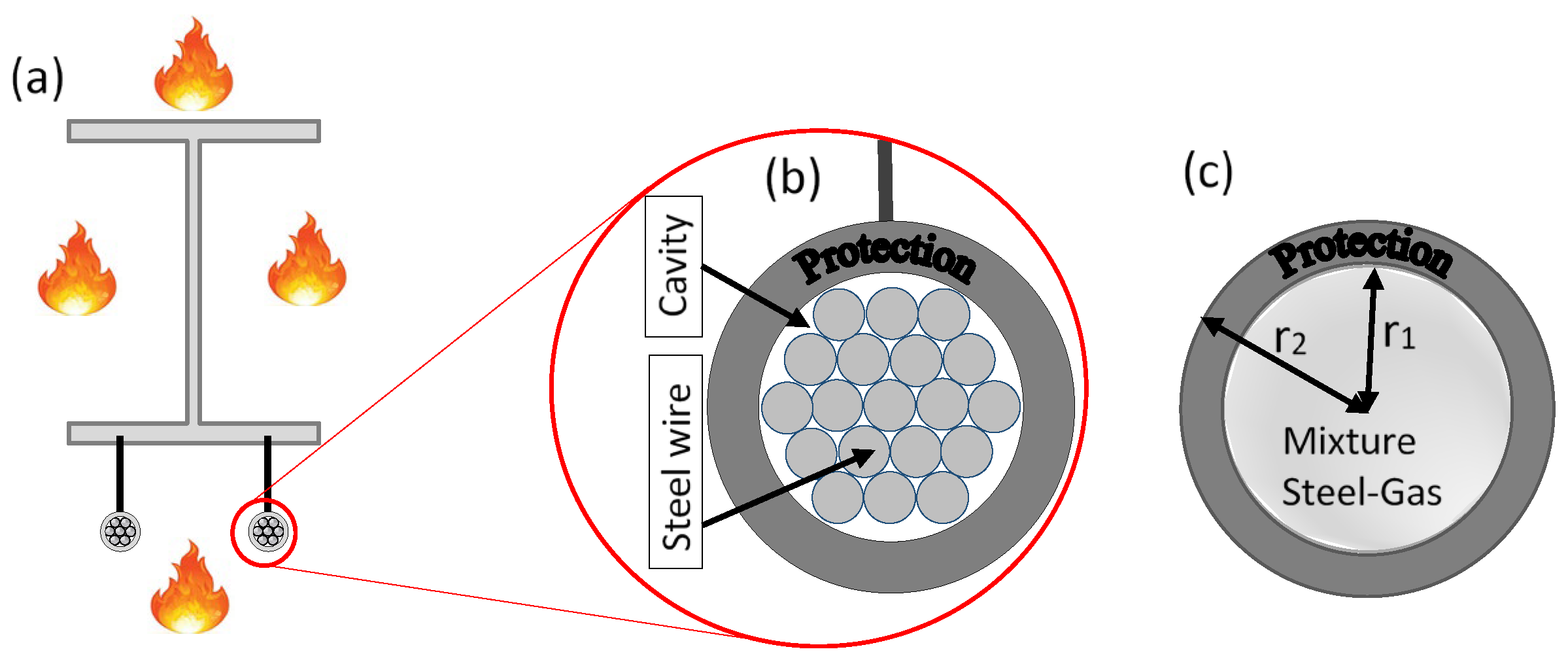
- Du, Y.; Peng, J.-Z.; Liew, J.R.; Li, G.-Q. Mechanical properties of high tensile steel cables at elevated temperatures. Constr. Build. Mater. 2018, 182, 52–65. [Google Scholar] [CrossRef]
- Du, Y.; Sun, Y.-K.; Jiang, J.; Li, G.-Q. Effect of cavity radiation on transient temperature distribution in steel cables under ISO834 fire. Fire Saf. J. 2019, 104, 79–89. [Google Scholar] [CrossRef]
- Vlasov, V.Z. Thin-Walled Elastic Beams; Russian Original Book: Moscow, Russia, 1940. [Google Scholar]
- Mohri, F.; Azrar, L.; Potier-Ferry, M. Flexural–torsional post-buckling analysis of thin-walled elements with open sections. Thin-Walled Struct. 2001, 39, 907–938. [Google Scholar] [CrossRef]
- Librescu, L.; Song, O. Thin-Walled Composite Beams Theory and Application; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- EN1993-1-1; Eurocode 3: Design of Steel Structures. Part 1–1: General Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2005.
- Ziane, N.; Ruta, G.; Meftah, S.A.; Doula, M.H.; Benmohammed, N. Instances of mixed buckling and post-buckling of steel RHS beams. Int. J. Mech. Sci. 2021, 190, 106013. [Google Scholar] [CrossRef]
- Dwaikat, M.; Kodur, V. Engineering Approach for Predicting Fire Response of Restrained Steel Beams. J. Eng. Mech. 2011, 137, 447–461. [Google Scholar] [CrossRef]
- Hirt, M.A.; Bez, R. Traité de Génie Civil de l’École Polytechnique Fédérale de Lausanne; Presses Polytechniques et Universitaire Romandes: Lausanne, Switzerland, 1994; Volume 10. [Google Scholar]
- Abaqus Standard User’s Manual, Version 6. Abaqus Standard User’s Manual, Version 6.4; Hibbit: Karlsson and Sorensen Inc.: Pawtucket, RI, USA, 2003. [Google Scholar]
- Ascione, L.; Feo, L. On the Non-Linear Statical Behaviour of Thin-Walled Elastic Beams of Open Cross-Section: A Numerical Approach. Int. J. Comput. Eng. Sci. 2001, 2, 513–536. [Google Scholar] [CrossRef]
- Simoncelli, M.; Zucca, M.; Stochino, F.; Bardhi, L. Structural behavior of steel storage racks under different fire scenarios. In Proceedings of the COMPDYN 2023, 9th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Athens, Greece, 12–14 June 2023. [Google Scholar] [CrossRef]
- Kodur, V.K.R.; Shakya, A.M. Effect of temperature on thermal properties of spray applied fire resistive materials. Fire Saf. J. 2013, 61, 314–323. [Google Scholar] [CrossRef]
- Ayrton, W.E.; Perry, J. On struts. Engineer 1886, 62, 464. [Google Scholar]


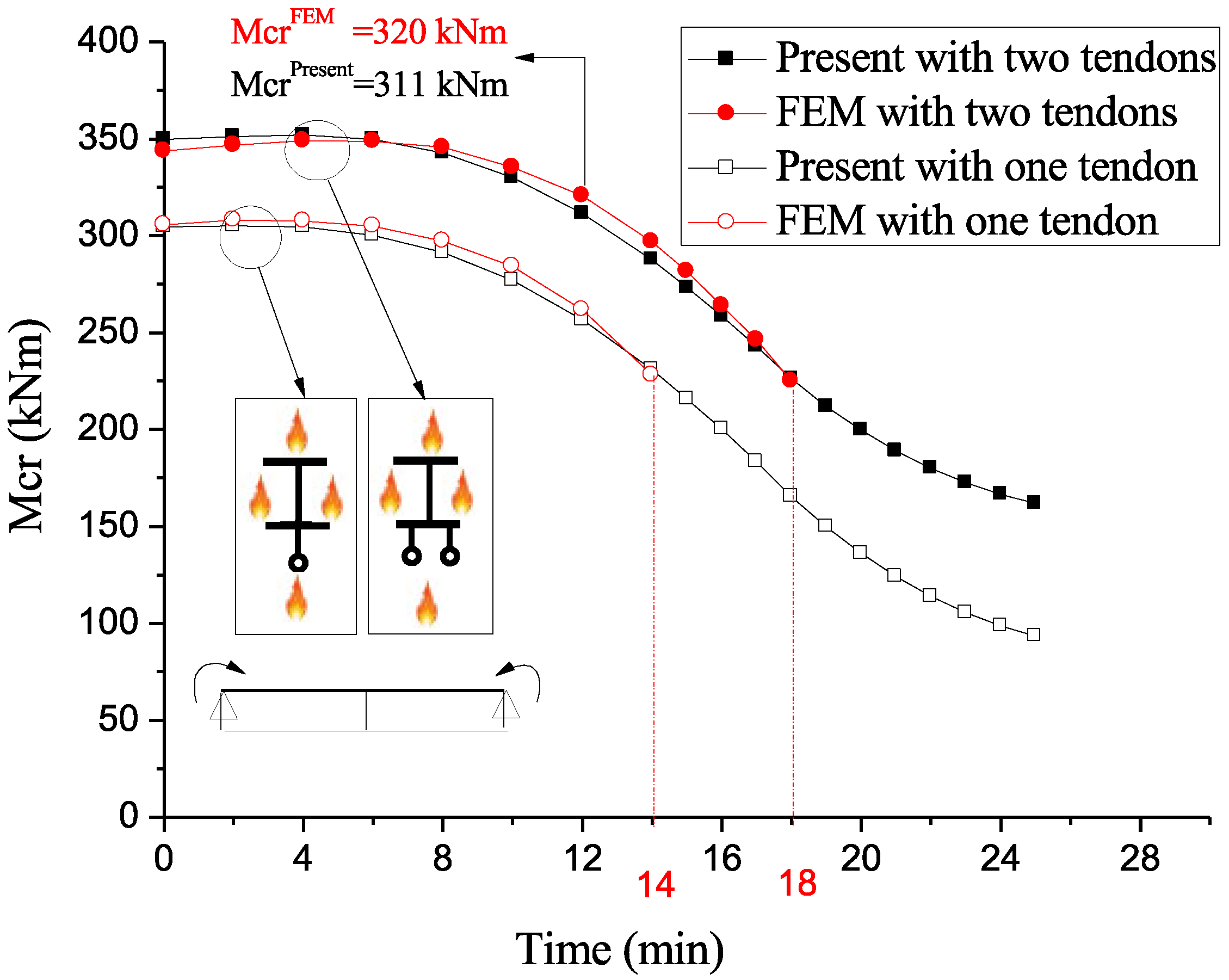
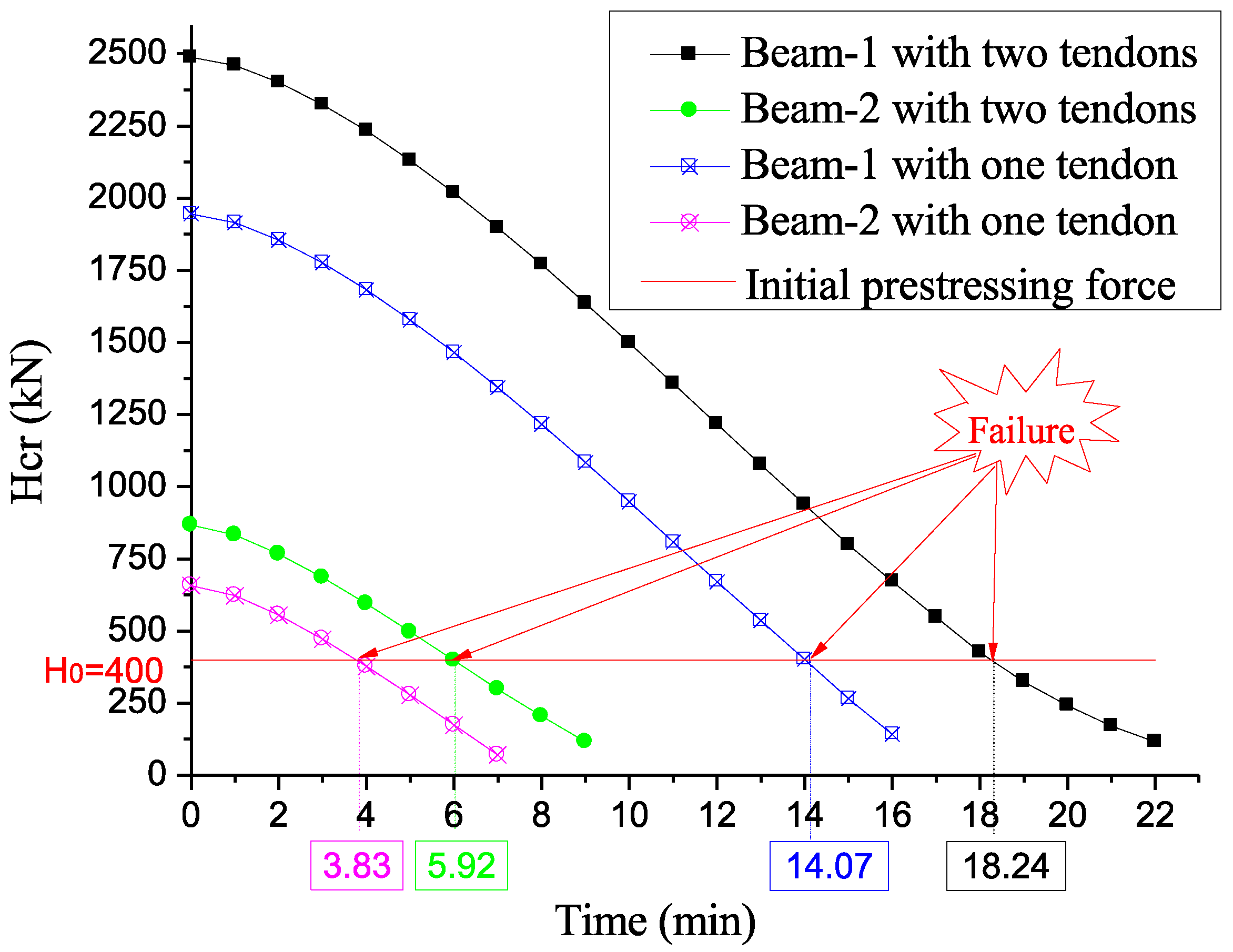
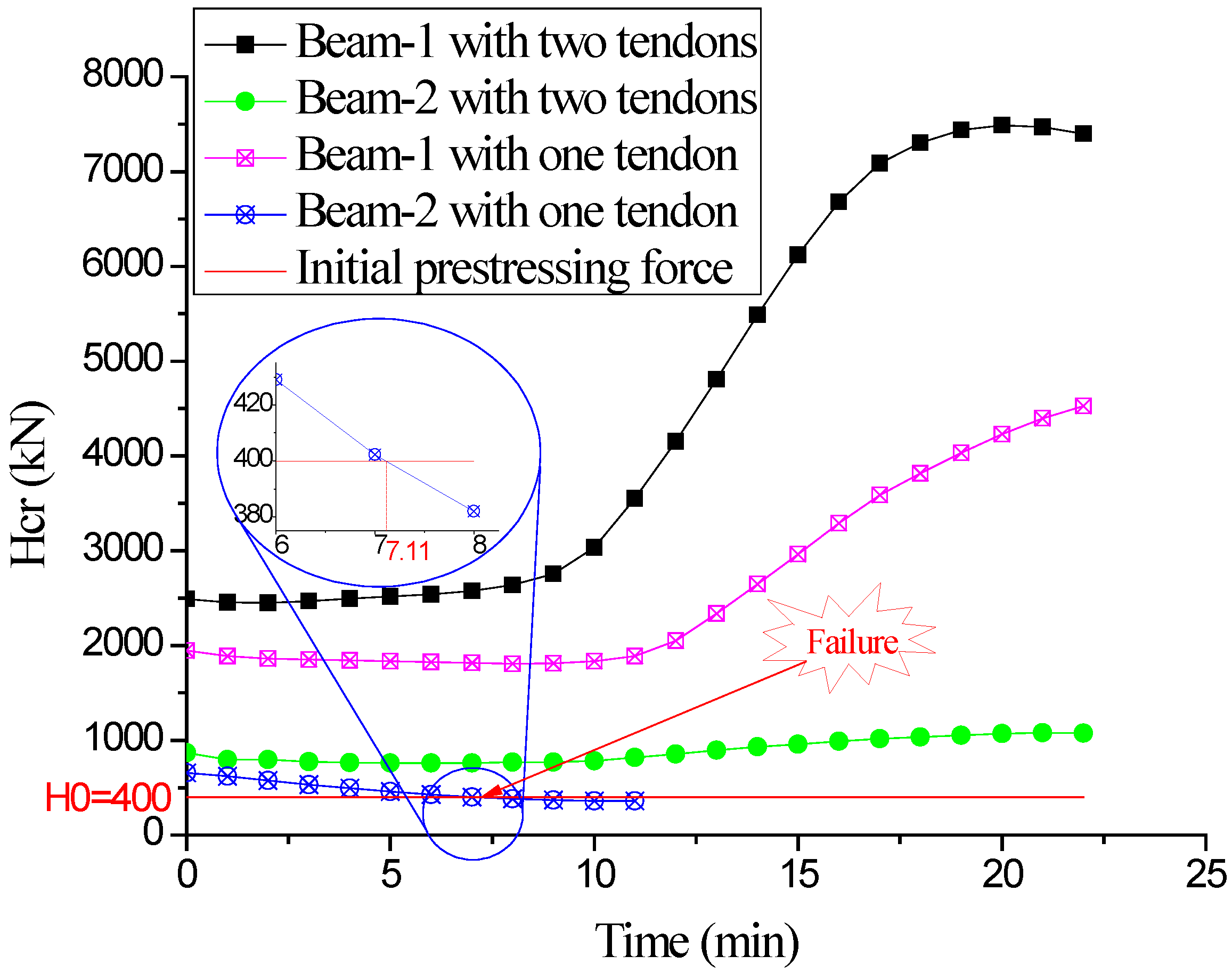
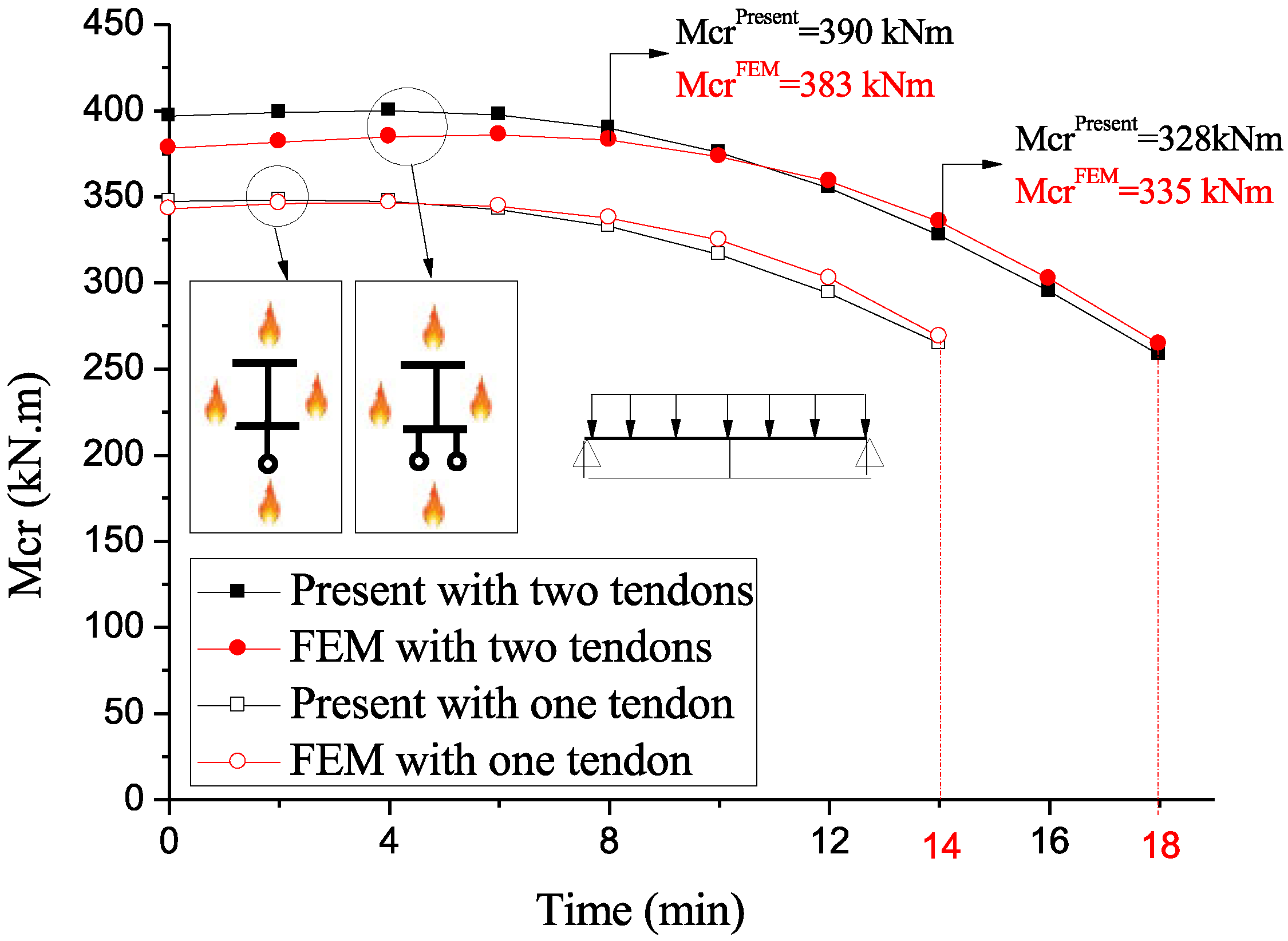

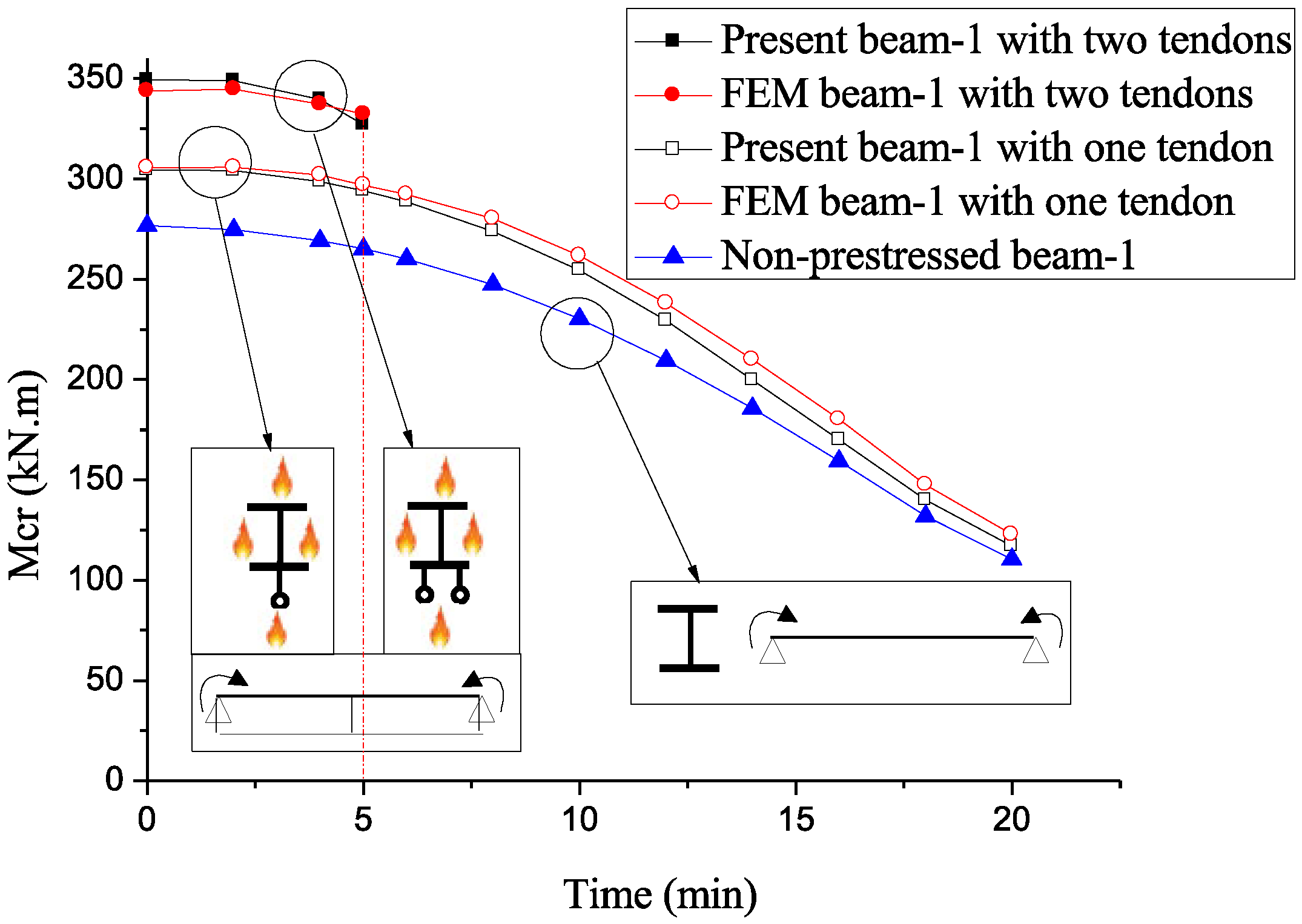
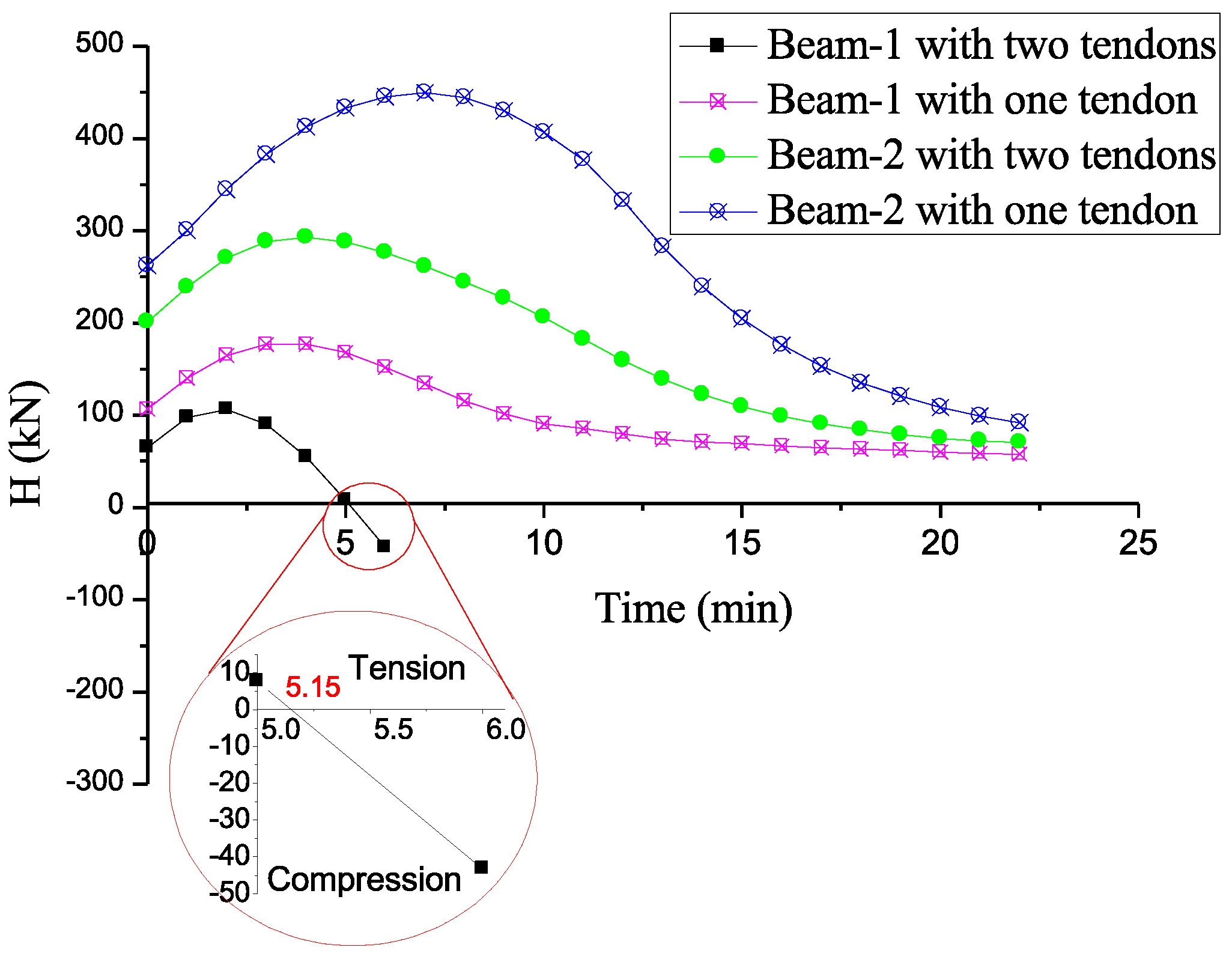


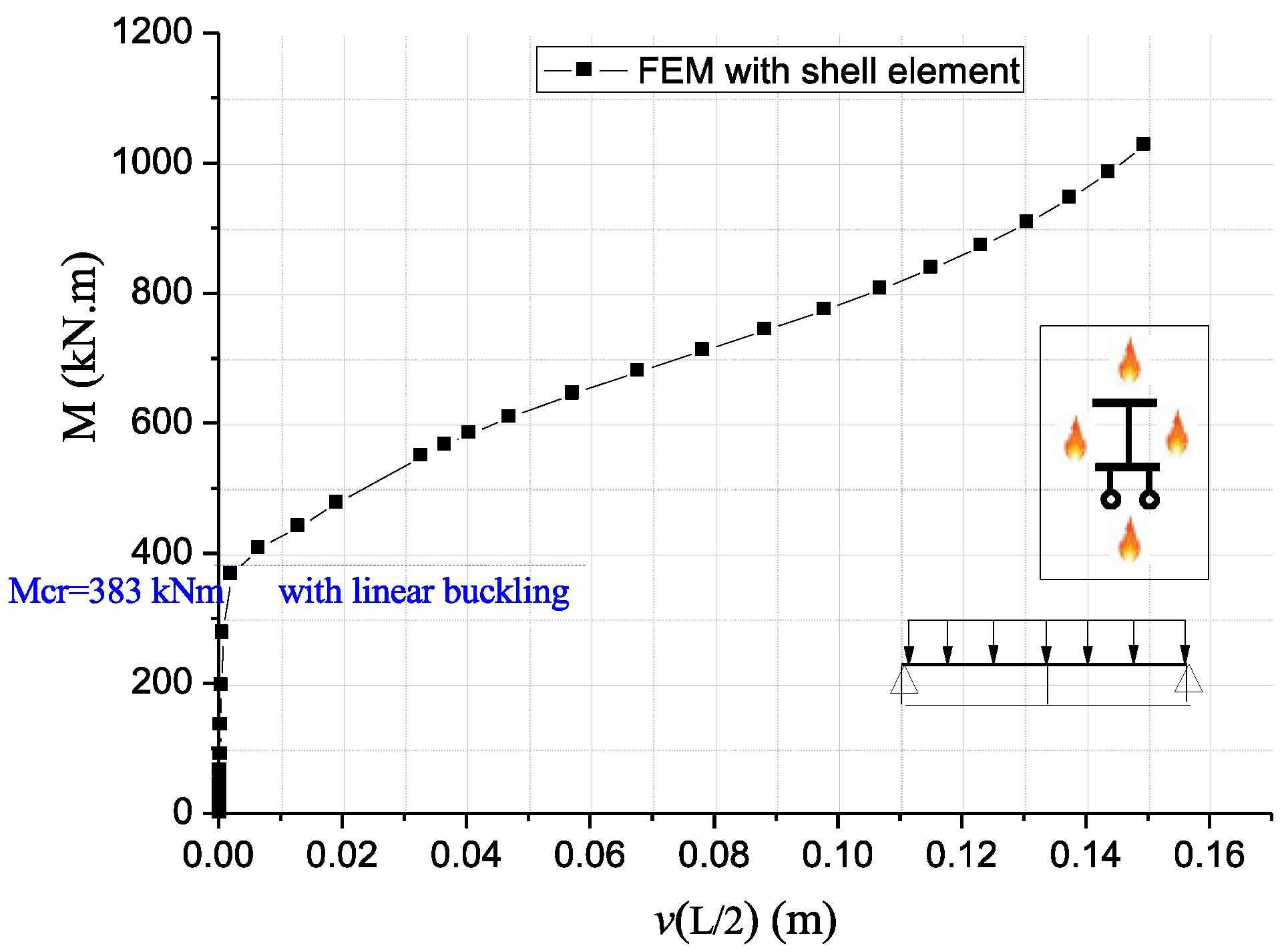



| Present | Kim [26] (Exact) | Kim [26] (FEM) | Kim [26] (Ritz) | ∆1 (%) | ∆2 (%) | ∆3 (%) | ||
|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | 277.43 | 276.06 | N/A | N/A | 0.50 | N/A | N/A |
| 200 | 0.0 | 296.93 | 296.70 | 295.97 | 297.01 | 0.08 | 0.32 | 0.03 |
| −280.52 | −280.20 | −279.43 | −280.49 | 0.11 | 0.39 | 0.01 | ||
| 0.1 | 332.93 | 319.19 | 325.82 | 327.47 | 4.30 | 2.18 | 1.67 | |
| −305.86 | −299.89 | −299.83 | −299.63 | 1.95 | 1.97 | 2.04 | ||
| 400 | 0.0 | 304.33 | 303.96 | 303.14 | 304.43 | 0.12 | 0.39 | 0.03 |
| −271.92 | −271.39 | −270.71 | −271.93 | 0.19 | 0.44 | 0.00 | ||
| 0.1 | 343.48 | 327.46 | 336.54 | 338.28 | 4.89 | 2.06 | 1.54 | |
| −301.08 | −292.61 | −292.55 | −295.13 | 2.81 | 2.83 | 1.98 |
| Present (Galërkin) | Kim [25] (Exact) | Kim [25] (FEM) | Kim [26] (Exact) | Kim [26] (FEM) | ∆1 (%) | ∆2 (%) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| No deviator | 0.11 | 1 | 1 | 821.46 | 821.44 | 819.56 | N/A | N/A | 0.00 | 0.23 | |
| 0 | 0.22 | 1 | 1 | 646.61 | 646.58 | 645.12 | N/A | N/A | 0.00 | 0.23 | |
| 0.22 | 2 | 2 | 1924.78 | N/A | N/A | 1924.6 | 1917.5 | 0.01 | 0.38 | ||
| 0.1 | 0.22 | 1 | 1 | 722.959 | N/A | N/A | 712.01 | 709.92 | 1.54 | 1.84 | |
| 0.22 | 2 | 2 | 1986.34 | N/A | N/A | 1925.9 | 1917.8 | 3.14 | 3.57 | ||
| 0.33 | 1 | 1 | 522.07 | 522.05 | 520.92 | N/A | N/A | 0.00 | 0.22 | ||
| With deviator | 0.11 | 2 | 2 | 2687.04 | 2686.8 | 2673.2 | N/A | N/A | 0.01 | 0.52 | |
| 0 | 0.22 | 2 | 2 | 1924.78 | 1924.6 | 1917.5 | N/A | N/A | 0.01 | 0.38 | |
| 0.22 | 2 | 1 | 2279.85 | N/A | N/A | 2287.5 | 2273.0 | 0.34 | 0.30 | ||
| 0.1 | 0.22 | 2 | 2 | 1986.34 | N/A | N/A | 1925.9 | 2069.9 | 3.14 | 4.21 | |
| 0.22 | 2 | 1 | 2479.21 | N/A | N/A | 2486.6 | 2476.3 | 0.30 | 0.12 | ||
| 0.33 | 2 | 2 | 1493.80 | 1493.7 | 1488.8 | N/A | N/A | 0.01 | 0.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahieddine, A.; Ziane, N.; Ruta, G.; Zahi, R.; Zidi, M.; Meftah, S.A. Lateral–Torsional Buckling of Externally Prestressed I-Section Steel Beams Subjected to Fire. CivilEng 2024, 5, 1110-1134. https://doi.org/10.3390/civileng5040054
Mahieddine A, Ziane N, Ruta G, Zahi R, Zidi M, Meftah SA. Lateral–Torsional Buckling of Externally Prestressed I-Section Steel Beams Subjected to Fire. CivilEng. 2024; 5(4):1110-1134. https://doi.org/10.3390/civileng5040054
Chicago/Turabian StyleMahieddine, Abdellah, Noureddine Ziane, Giuseppe Ruta, Rachid Zahi, Mohamed Zidi, and Sid Ahmed Meftah. 2024. "Lateral–Torsional Buckling of Externally Prestressed I-Section Steel Beams Subjected to Fire" CivilEng 5, no. 4: 1110-1134. https://doi.org/10.3390/civileng5040054
APA StyleMahieddine, A., Ziane, N., Ruta, G., Zahi, R., Zidi, M., & Meftah, S. A. (2024). Lateral–Torsional Buckling of Externally Prestressed I-Section Steel Beams Subjected to Fire. CivilEng, 5(4), 1110-1134. https://doi.org/10.3390/civileng5040054








