Arbitrary-Order Bernstein–Bézier Functions for DGFEM Transport on 3D Polygonal Grids

Abstract

In this paper, we present an arbitrary-order discontinuous Galerkin finite element discretization of the $S_N$ transport equation on 3D extruded polygonal prisms. Basis functions are formed by the tensor product of 2D polygonal Bernstein–Bézier functions and 1D Lagrange polynomials. For a polynomial degree p, these functions span ${\left\{x^a{y}^b\right\}}_{(a+b)\le p}\otimes {\left\{z^c\right\}}_{c\in (0,p)}$ with a dimension of $np(p+1)+(p+1)(p-1)(p-2)/2$ on an extruded n-gon. Numerical tests confirm that the functions capture exactly monomial solutions, achieve expected convergence rates, and provide full resolution in the thick diffusion limit.

1. Introduction

The linear Boltzmann transport equation, which we will simply call the transport equation, describes the transport of neutral particles (i.e., neutrons and photons) through background and multiplying media [1]. Some of the most prevalent discretization schemes are the discrete ordinates ($S_N$) in angle and multigroup in energy. Given an angular quadrature set, ${\{w_m,{\overrightarrow{\mathsf{\Omega }}}_m\}}_{m=1}^M$, the multigroup, $S_N$ transport equation for the angular flux of group g traveling in direction ${\overrightarrow{\mathsf{\Omega }}}_m$, denoted as ${\psi }_{m,g}\left(\overrightarrow{r}\right)\equiv {\psi }_g(\overrightarrow{r},{\overrightarrow{\mathsf{\Omega }}}_m)$, with isotropic scattering within an open, convex spatial domain $\mathcal{D}$, with boundary, $\partial \mathcal{D}$, is written as

$$\begin{array}{cc}\hfill {\overrightarrow{\mathsf{\Omega }}}_m·\overrightarrow{\nabla }& {\psi }_{m,g}\left(\overrightarrow{r}\right)+{\sigma }_{t,g}\left(\overrightarrow{r}\right){\psi }_{m,g}\left(\overrightarrow{r}\right)=\frac{1}{4\pi }\sum _{g^{\prime }=1}^G{\sigma }_s^{g^{\prime }\to g}\left(\overrightarrow{r}\right){\varphi }_{g^{\prime }}\left(\overrightarrow{r}\right)+q_{m,g}\left(\overrightarrow{r}\right),\hfill \end{array}$$

(1)

where the source term is given by

$$q_{m,g}\left(\overrightarrow{r}\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{4\pi }}{S}_g\left(\overrightarrow{r}\right),\hfill & \mathrm{Fixed}\text{-}\mathrm{Source}\hfill \\ {\displaystyle \frac{{\chi }_g}{4\pi k}}\sum _{g^{\prime }=1}^G\nu {\sigma }_{f,g^{\prime }}\left(\overrightarrow{r}\right){\varphi }_{g^{\prime }}\left(\overrightarrow{r}\right).\hfill & \mathrm{Eigenvalue}\hfill \end{array}\right.$$

(2)

${\sigma }_{t,g}$ is the total cross section of group g, ${\sigma }_s^{g^{\prime }\to g}$ is the scattering cross section from group $g^{\prime }$ to group g, $\nu {\sigma }_{f,g}$ is the fission neutron production term of group g, ${\chi }_g$ is the neutron fission spectrum of group g, $S_g$ is a distributed source, and the scalar flux of group g, is given by

$${\varphi }_g\left(\overrightarrow{r}\right)\equiv \underset{4\pi }{\int }d\mathsf{\Omega }{\psi }_g(\overrightarrow{r},\overrightarrow{\mathsf{\Omega }})\approx \sum _{m=1}^M{w}_m{\psi }_{m,g}\left(\overrightarrow{r}\right).$$

(3)

The discontinuous Galerkin finite element method (DGFEM) is a popular spatial discretization for Equation (1) [2,3,4]. Besides 1D, the use of DGFEM for transport has typically been reserved for meshes employing simplicial or tensor mesh cells. Stone and Adams [5] developed a discretization with linear precision for unstructured polygonal cells, which Bailey [6] later extended to unstructured polyhedral cells. Hackemack and Ragusa [7] analyzed quadratic serendipity functions on polygonal grids, which was further extended to extruded polygonal prisms [8]. Recently, utilizing the framework of Floater and Lai [9], Hackemack [10,11] analyzed arbitrary-order DGFEM $S_N$ and diffusion solutions on 2D polygonal grids using reduced-space polygonal Bernstein–Bézier functions. This work extends [10] to form arbitrary-order tensor-based functions on extruded polygonal prisms.

The remainder of this paper is as follows. In Section 2, we present the DGFEM discretization of the $S_N$ transport equation, followed by the employed 3D extruded basis functions in Section 3. Then, Section 4 presents numerical results demonstrating the expected precision and convergence properties of our DGFEM discretization. Finally, conclusions are presented in Section 5.

2. The DGFEM Transport Equation

In this section, we review the DGFEM discretization of the $S_N$ transport equation. First, we lay down an unstructured mesh, ${\mathbb{T}}_h\in {\mathbb{R}}^3$, over the spatial domain consisting of non-overlapping spatial elements to form a complete union over the spatial domain: $\mathcal{D}={\bigcup }_{K\in {\mathbb{T}}_h}K$. The angular flux unknown of Equation (1) is expanded using discontinuous functions over each mesh cell K:

$${\psi }_{m,g}\left(\overrightarrow{r}\right)\approx \sum _{j=1}^{N_K}{\psi }_{m,g,j}{u}_{m,g,j}\left(\overrightarrow{r}\right),\overrightarrow{r}\in K,$$

(4)

where $N_K$ is the number of basis functions on element K, and the functions are nonzero over a single element and discontinuous across the element interfaces. The scalar flux and source term can be expanded analogously. Multiplying Equation (1) by a test function u, integrating over element K, applying the divergence theorem, and using the standard upwind technique yields the following weak form over element K:

$$\begin{array}{cc}\hfill {〈({\overrightarrow{\mathsf{\Omega }}}_m·\overrightarrow{n})u,{\psi }_{m,g}〉}_{\partial K^{+}}-& {\left({\overrightarrow{\mathsf{\Omega }}}_m·\overrightarrow{\nabla }u,{\psi }_{m,g}\right)}_K+{\left({\sigma }_{t,g}u,{\psi }_{m,g}\right)}_K\hfill \\ \hfill & =\frac{1}{4\pi }\sum _{g^{\prime }=1}^G{\left({\sigma }_s^{g^{\prime }\to g}u,{\varphi }_{g^{\prime }}\right)}_K+{\left(u,q_{m,g}\right)}_K-{〈({\overrightarrow{\mathsf{\Omega }}}_m·\overrightarrow{n})u,{\psi }_{m,g}^{\uparrow }〉}_{\partial K^{-}}.\hfill \end{array}$$

(5)

In Equation (5), $\partial K^{\pm }$ represents the outflow/inflow boundary, $\partial K^{\pm }=\left\{\overrightarrow{r}\in \partial K|{\overrightarrow{\mathsf{\Omega }}}_m·{\overrightarrow{n}}_K\left(\overrightarrow{r}\right)\gtrless 0\right\}$; with ${\overrightarrow{n}}_K\left(\overrightarrow{r}\right)$ the outward unit normal, ${\psi }_m^{\uparrow }$ are the angular flux values on an inflow face taken from the upwind neighbor element, and the inner products

$${\left(v,w\right)}_K\equiv {\int }_{K}vwdr\mathrm{and}{〈v,w〉}_{\partial K}\equiv {\int }_{\partial K}vwds$$

(6)

correspond to integrations over the cell volume and faces, respectively, where $dr\in {\mathbb{R}}^3$ is within the cell and $ds\in {\mathbb{R}}^2$ is along the cell boundary.

The error of the discretized flux solution ${\varphi }_{hp}\in W_{\mathcal{D}}^{hp}$ with polynomial degree p, under the $L_2$-norm, can be written as

$$\left|\right|\varphi -{\varphi }_{hp}{\left|\right|}_{L_2}\le C\frac{h^{min(p+1,r)}}{{(p+1)}^r},$$

(7)

where h is the maximum diameter of all mesh elements, r is the regularity of the transport solution, and C is a constant independent of the mesh. Therefore, the convergence rates are limited by the solution regularity [3].

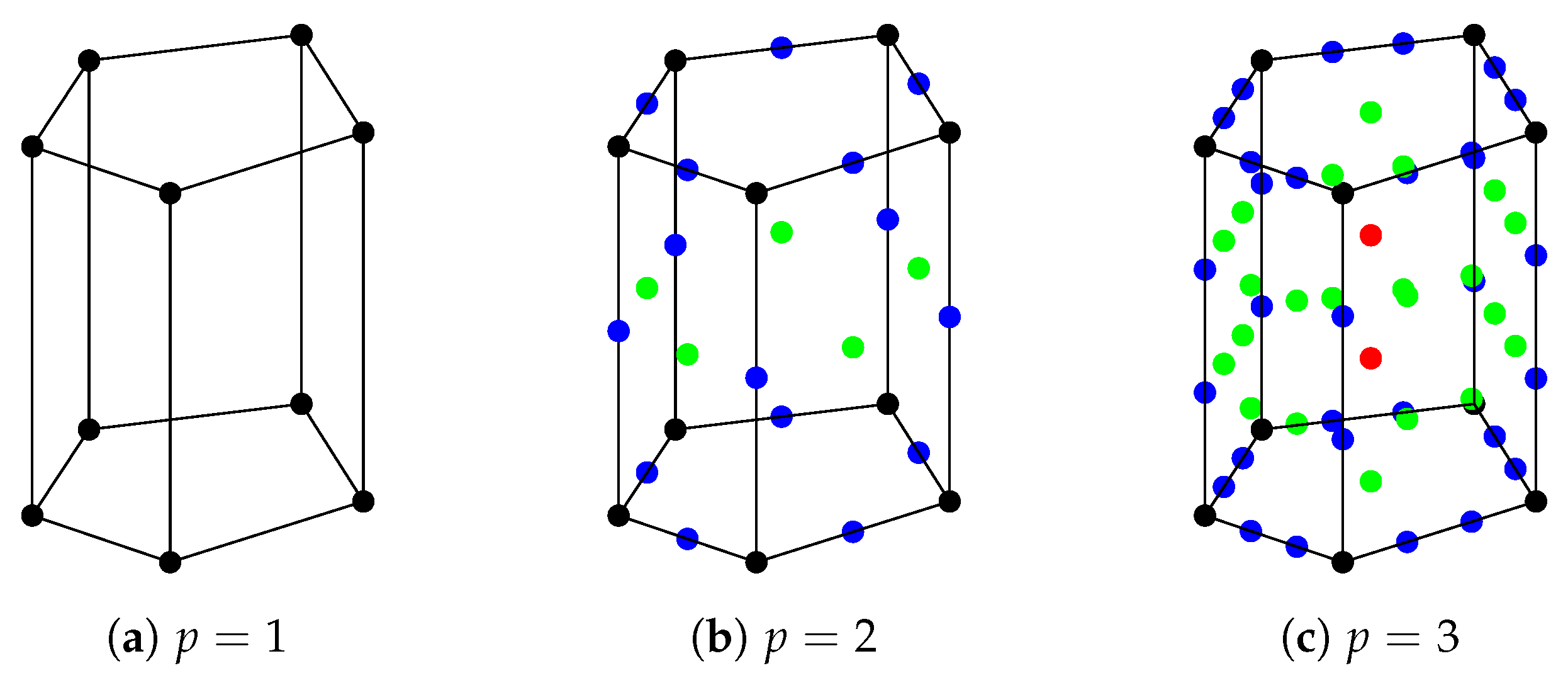
3. 3D Extruded Polygonal Basis Functions

In Section 2, we gave the DGFEM discretization of the $S_N$ transport equation but no definition to the test and trial functions. Now, we provide some details on the employed polygonal prism basis functions. Our extruded polygonal functions are formed from the tensor product of the 2D polygonal Bernstein–Bézier functions (we will refer to them as the $(x,y)$ radial functions) and the 1D Lagrange polynomials (we will refer to them as the z axial functions).

3.1. Brief Overview of 2D Polygonal Functions

We now provide a brief overview of the radial polygonal functions. In the interest of brevity, full details are not provided, and the interested reader should see the previous works of Floater and Lai [9] and Hackemack [10]. On a polygonal element, the reduced-space polygonal Bernstein–Bézier functions, $\left\{{\overrightarrow{\mathcal{B}}}_p\right\}$, are formed by a set of functions with support points on vertices, along edges, and within the interior. They reduce to the Lagrange fundamental polynomials on triangles. For a n-gon and a finite element space of degree p, there are n vertex functions, $p-1$ functions along each edge, and $\frac{(p-1)(p-2)}{2}$ interior functions for a total of $pn+\frac{(p-1)(p-2)}{2}$ functions. They span the ${\left\{x^a{y}^b\right\}}_{(a+b)\le p}$ space of functions. Figure 1 gives the distribution of the degrees of freedom on an example pentagon for polynomial degrees $p=1,2,3,4$.

3.2. Extrusion to Polygonal Prisms

With the radial functions given, we can now provide details on converting them into an arbitrary-order functional space compatible with extruded polygonal prisms. For polynomial degree p, the extruded 3D functions, $\left\{{\overrightarrow{\mathcal{E}}}_p\right\}$, are formed from the tensor product of the radial functions $\left\{{\overrightarrow{\mathcal{B}}}_p\right\}$ and the $(p+1)$ 1D Lagrange polynomials (denoted as $\left\{{\overrightarrow{\mathcal{L}}}_p\right\}$):

$${\overrightarrow{\mathcal{E}}}_p(x,y,z)={\overrightarrow{\mathcal{B}}}_p(x,y)\otimes {\overrightarrow{\mathcal{L}}}_p\left(z\right).$$

(8)

For a polygonal prism with lower and upper bounds of $z_B$ and $z_T$, respectively, the axial functions have evenly-spaced support points given by

$$z_i=z_B+\frac{i}{p}(z_T-z_B),i=0,...,p,$$

(9)

and the i-th axial function is given by

$${\mathcal{L}}_{p,i}\left(z\right)=\prod _{\begin{array}{c}j=0\\ j\ne i\end{array}}^p\frac{z-z_j}{z_i-z_j},i=0,...,p.$$

(10)

Since these extruded functions are taken as the tensor product of our radial and axial functions, their functional space is given by $\mathrm{span}\left({\overrightarrow{\mathcal{E}}}_p\right)=\left\{x^a{y}^b\right\}\otimes \left\{z^c\right\}$, where $\dim \left({\overrightarrow{\mathcal{E}}}_p\right)=np(p+1)+(p+1)(p-1)(p-2)/2$ (n still represents the number of vertices of the 2D polygon). The support points of the degrees of freedom are given in Figure 2 for an example pentagonal prism for polynomial degrees $p=1,2,3$. An analogous $p=4$ case compared to Figure 1 was not provided due to the excessive cluttering of the nodes.

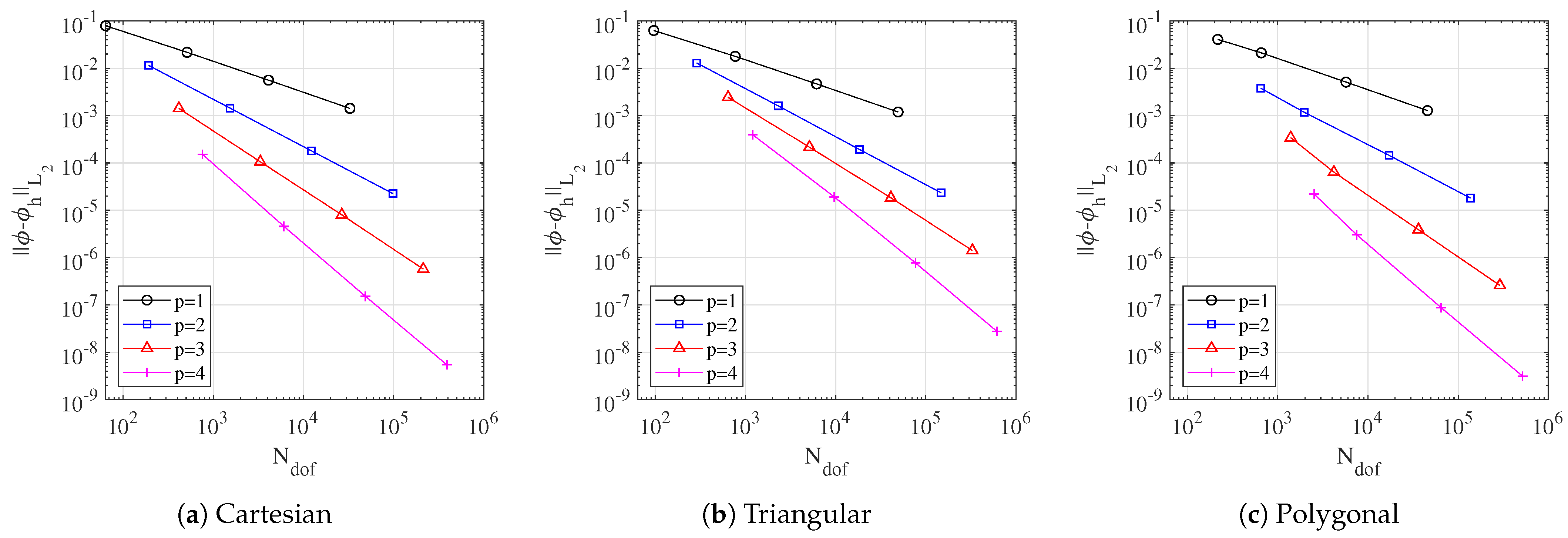
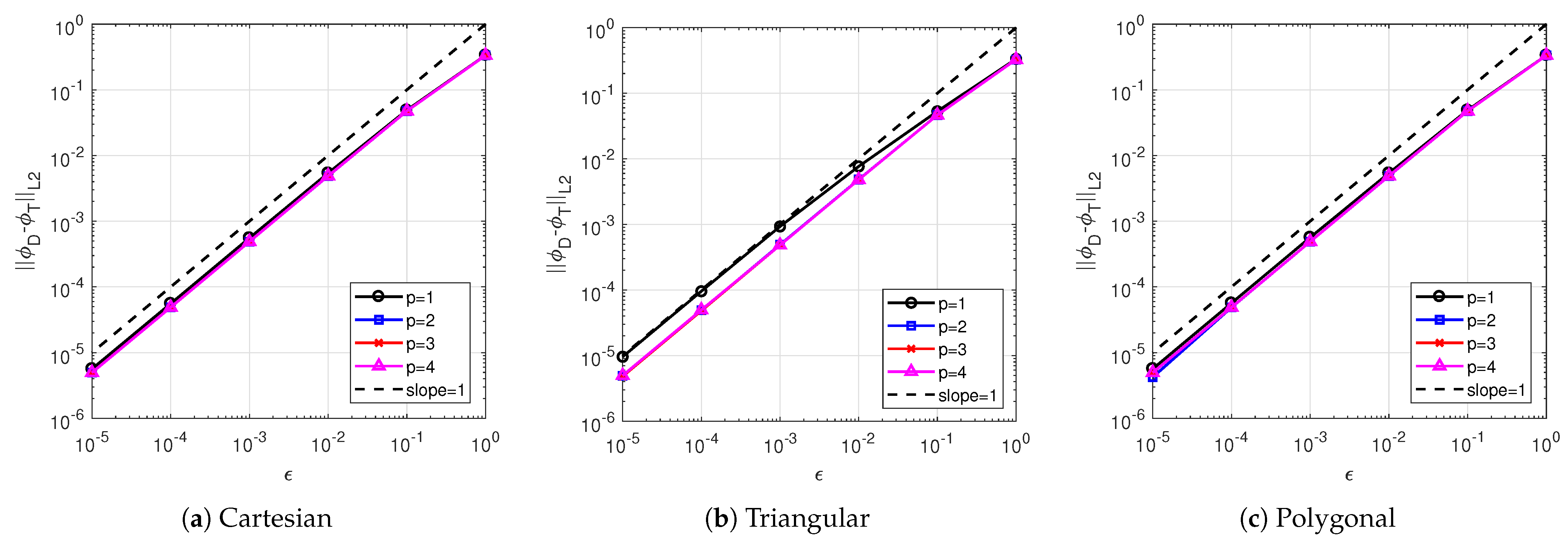
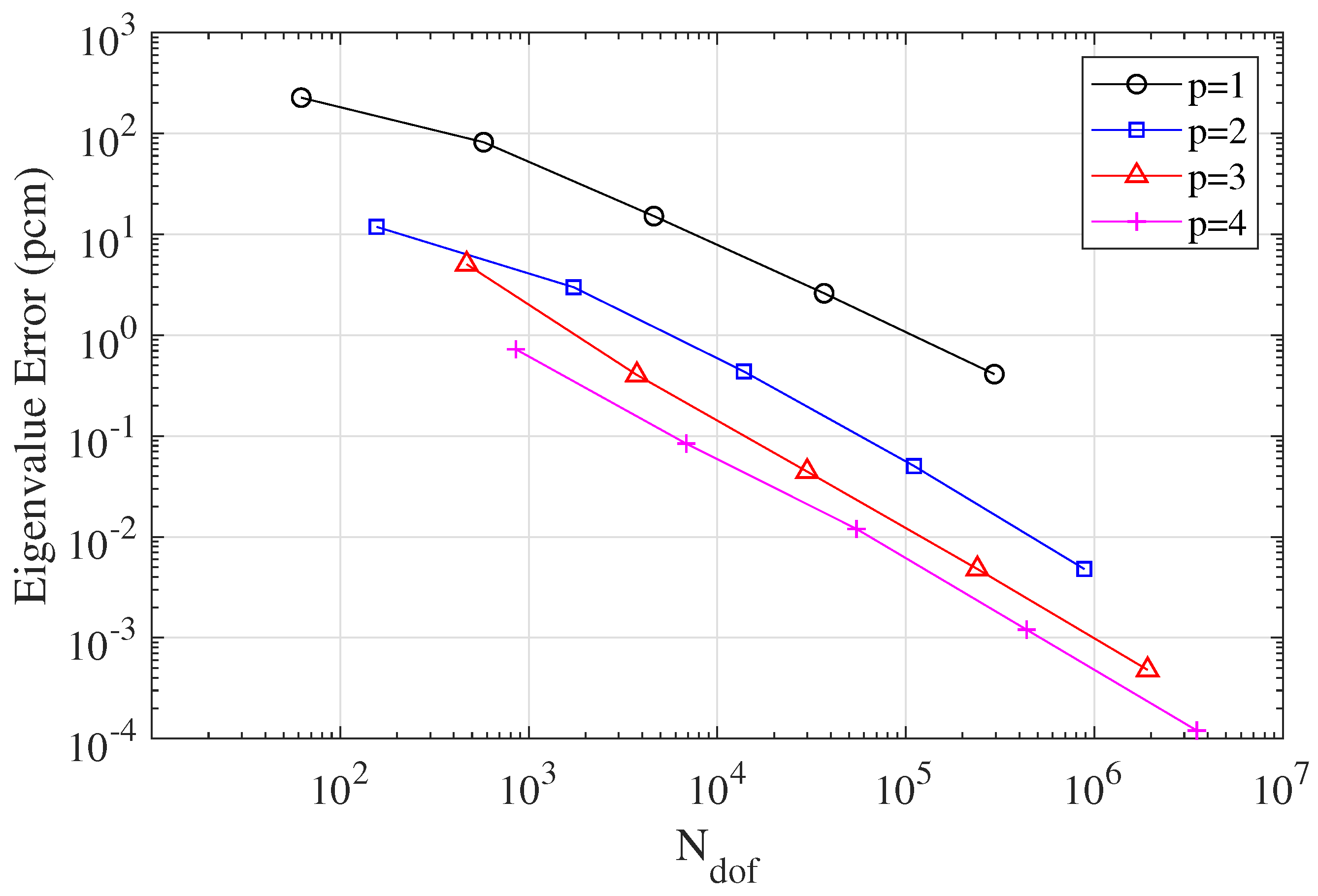
4. Numerical Results

4.1. Basis Function Verification

We first provide numerical experiments that verify properties of our extruded basis functions and the corresponding DGFEM transport solutions. We test three properties: (1) verify the DGFEM captures the proper interpolation space, (2) verify the DGFEM achieves proper convergence rates in h-type and p-type refinement, and (3) verify that the solutions maintain full resolution in the thick diffusion limit (TDL) [12].

We first test the interpolation properties and convergence rates of the $S_N$ solutions using the method of manufactured solutions (MMS). Our domain is ${[0,1]}^3$, with ${\sigma }_t=1$, ${\sigma }_s=0$, $S_8$ quadrature, and all vacuum boundaries. We define two functional forms to test interpolation, ${\psi }_p$, and convergence, ${\psi }_s$, properties given by

$$\begin{array}{cc}\hfill {\psi }_p(x,y,z)& =\sum _{c=0}^p\sum _{(a+b)\le p}{x}^a{y}^b{z}^c,\hfill \\ \hfill {\psi }_s(x,y,z)& =sin\left(k_x\pi x\right)sin\left(k_y\pi y\right)sin\left(k_z\pi z\right),\hfill \end{array}$$

(11)

with $k_x=1$, $k_y=2$, and $k_z=3$. Three extruded mesh types are utilized: Cartesian (hexahedra), triangular, and polygonal. The 2D polygonal meshes were generated with the PolyMesher software [13] before extrusion.

Table 1. $L_2$-norm of the error in the monomial solutions on the different mesh types.

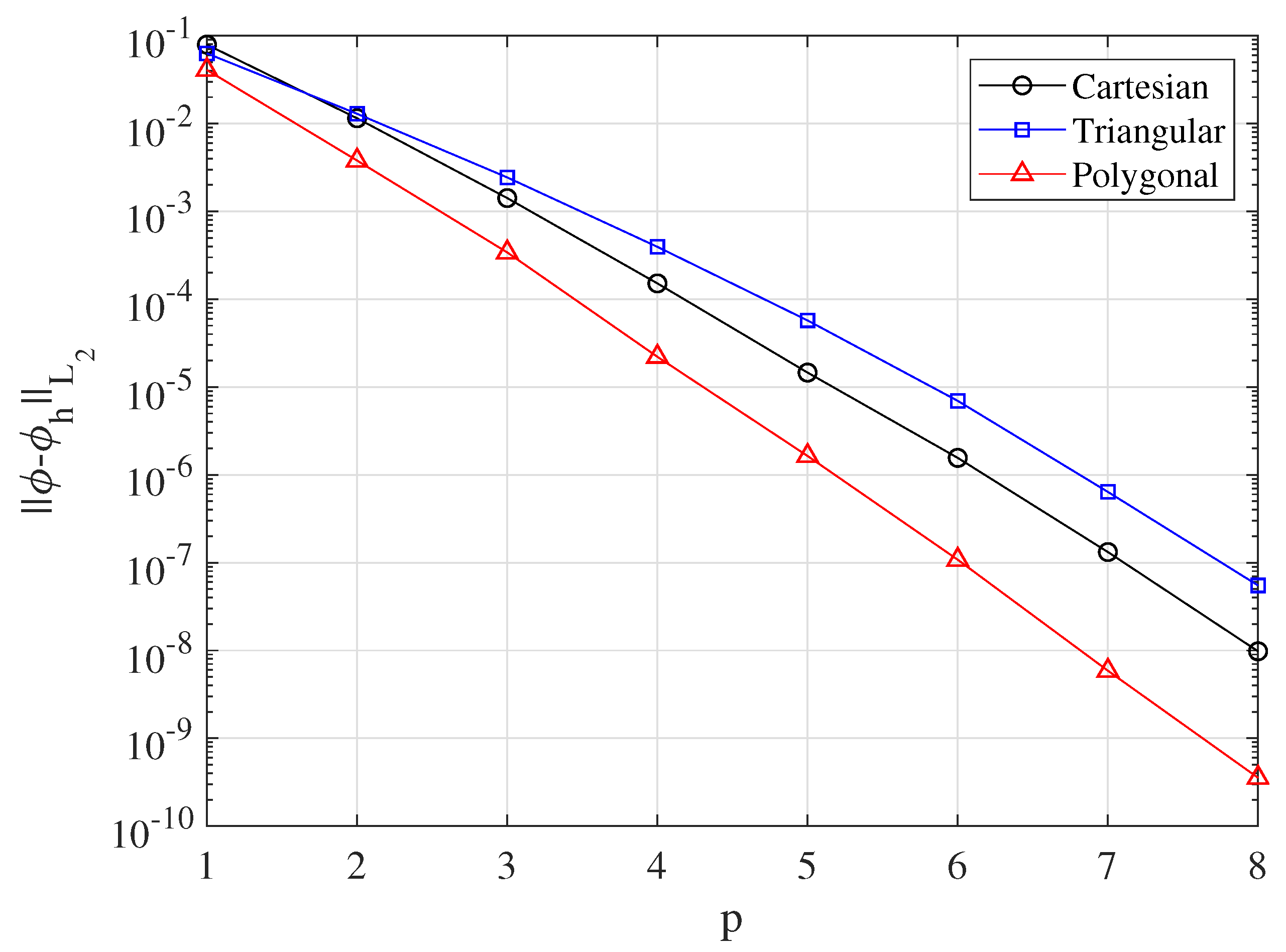
p	Cartesian	Triangular	Polygonal
1	8.97 × 10${}^{-16}$	8.10 × 10${}^{-16}$	8.81 × 10${}^{-16}$
2	3.86 × 10${}^{-15}$	2.66 × 10${}^{-15}$	5.36 × 10${}^{-15}$
3	7.52 × 10${}^{-15}$	5.71 × 10${}^{-15}$	9.24 × 10${}^{-15}$
4	1.33 × 10${}^{-14}$	9.89 × 10${}^{-15}$	5.50 × 10${}^{-14}$
5	5.74 × 10${}^{-14}$	4.97 × 10${}^{-14}$	8.88 × 10${}^{-14}$
6	1.04 × 10${}^{-13}$	8.80 × 10${}^{-14}$	2.19 × 10${}^{-13}$

gives the $L_2$-norm of the error for DGFEM orders of $p=1,...,6$. From the machine precision results, we can clearly see that the transport solutions fully-live within the functional space of the polygonal Bernstein–Bézier functions. The loss of exact precision is due to the magnitude of the functions to grow past unity with increasing polynomial degree. Next, Figure 3 and Figure 4 provide the convergence of the sinusoidal solution, ${\psi }_s$, under uniform h-refinement and p-refinement, respectively. Since $N_{dof}\propto h^{-3}$ in 3D, the slopes in Figure 3 approach $-(p+1)/3$ as expected. Additionally, since ${\psi }_s$ is analytic within $\overrightarrow{r}\in \mathcal{D}$, the exponential convergence of p-refinement in Figure 4 is expected.

Having verified the interpolation and convergence properties of our DGFEM scheme, we now confirm that our DGFEM transport solutions retain full resolution in the thick diffusion limit. From the work of Adams [12], it is known that a poor discretization of the $S_N$ transport equation (with full upwinding) leads to ‘locking’ into absurd transport solutions. Adams states that two properties of the DGFEM functions are needed for full resolution: (1) locality of the functions and (2) surface-matching (see Adams work for further details). The extruded polygonal prism functions of this work do possess these properties, and as such we expect full resolution.

In the TDL, the domain mean free path approaches infinity. If we fix the physical dimensions of the problem, we can then scale the cross sections and source to reflect the properties of the TDL. Introducing a scaling parameter, $ϵ$, we scale ${\sigma }_t$ as $1/ϵ$ and ${\sigma }_a$ and Q as $ϵ$. This leads to a scaled transport equation and corresponding diffusion equation given by

$$\overrightarrow{\mathsf{\Omega }}·\overrightarrow{\nabla }\psi +\frac{1}{ϵ}\psi =\left(\frac{1}{ϵ}-ϵ\right)\frac{\varphi }{4\pi }+\frac{ϵ}{4\pi }\mathrm{and}-\frac{ϵ}{3}{\nabla }^2\varphi +ϵ\varphi =ϵ,$$

(12)

respectively. The diffusion equation is discretized using a conforming Galerkin finite element method (CGFEM) with strongly-enforced homogeneous Dirichlet boundary conditions. As $ϵ\to 0$, the discretized transport solution, ${\varphi }_T$, will approach the discretized diffusion solution, ${\varphi }_D$, at a rate of $ϵ$ under the $L_2$-norm ($\left|\right|{\varphi }_D-{\varphi }_T{\left|\right|}_{L_2}$). This is confirmed in Figure 5.

4.2. Multigroup Pincell Problem

Our final numerical example is a 7 group pincell problem (with reflecting radial boundary conditions) that utilizes the geometry and cross sections of the ${\mathrm{UO}}_2$ pincells from the C5G7 benchmark problem [14]. The fuel region is formed from a 16-sided regular polygon where the fine mesh cells are formed by square tiling until the pin boundary is intersected. The convergence history of the error in k (given in units of pcm) are given in Figure 6. Superior convergence is realized for increasing polynomial degree but with diminishing returns. A significant reduction in error is realized going from linear to quadratic FEM.

5. Conclusions

In this paper, we have presented an arbitrary-order DGFEM discretization of the $S_N$ transport equation compatible with extruded polygonal grids. The basis functions are formed by a tensor product of 2D radial ($xy$) polygonal Bernstein–Bézier functions and 1D axial (z) Lagrange polynomials. On an extruded n-gon with polynomial degree p, there are $np+(p-1)(p-2)/2$ radial functions and $p+1$ axial functions, with their tensor product resulting in $np(p+1)+(p+1)(p-1)(p-2)/2$ total functions. These functions can exactly interpolate the $\left\{x^a{y}^b\right\}\otimes \left\{z^c\right\}$ space of functions, where $a+b\le p$ and $c=0,\dots ,p$. Due to the locality and surface matching properties of the functions across edges, these functions allow for transport solutions to maintain full resolution in the thick diffusion limit. Numerical testing also demonstrated the functions’ interpolation properties and appropriate convergence rates were observed. The methodology presented in this work can thus be used to compute $S_N$ solutions on 3D extruded polygonal prisms (e.g., reactor analysis calculations).