Fourth-Order Adjoint Sensitivity and Uncertainty Analysis of an OECD/NEA Reactor Physics Benchmark: I. Computed Sensitivities
Abstract
:1. Introduction
2. Fourth-Order Sensitivities of the PERP Leakage Response with Respect to the Benchmark’s Microscopic Total Cross Sections
- (i)
- The symbol indicates the integration of two elements, as defined in Equations (A1)−(A8) in the Appendix A.
- (ii)
- The indices and are used to index the parameters and , respectively, in the vector of parameters , which is defined as follows:The dagger in Equation (3) denotes “transposition”, denotes the group-averaged microscopic total cross section for isotope and energy group , and denotes the total number of microscopic total cross sections.
- (iii)
- The vectors denote the 1st-level, 2nd-level, 3rd-level, and 4th-level adjoint functions, respectively. Specifically:
- (1)
- denotes the 1st-level adjoint functions, which are the solutions of the 1st-Level Adjoint Sensitivity System (1st-LASS) as defined in Equations (A13) and (A14) in the Appendix A.
- (2)
- and denote the two 2nd-level adjoint functions, which are the solutions of the 2nd-Level Adjoint Sensitivity System (2nd-LASS) as defined in Equations (A15)−(A18) in the Appendix A.
- (3)
- , , and denote the four 3rd-level adjoint functions, which are the solutions of the 3rd-Level Adjoint Sensitivity System (3rd-LASS) as defined in Equations (A19)−(A26) in the Appendix A.
- (4)
- , denote the eight 4th-level adjoint functions, which are the solutions of the 4th-Level Adjoint Sensitivity System (4th-LASS) as defined in Equations (A27)−(A42) in the Appendix A.
- (iv)
- The vector is a diagonal matrix having non-zero elements of the form on its diagonal, i.e.,where denotes the macroscopic total cross section for energy group .
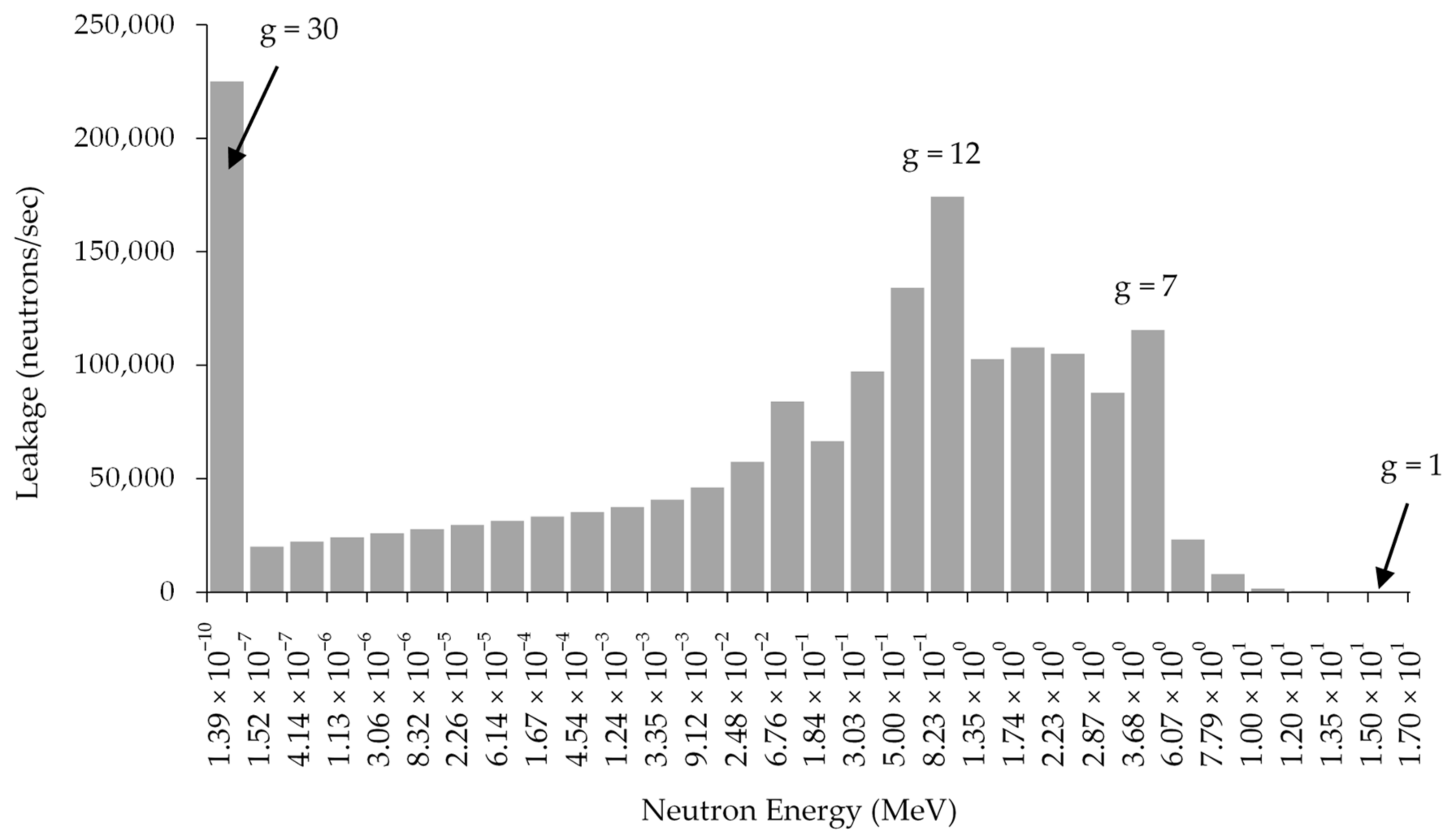
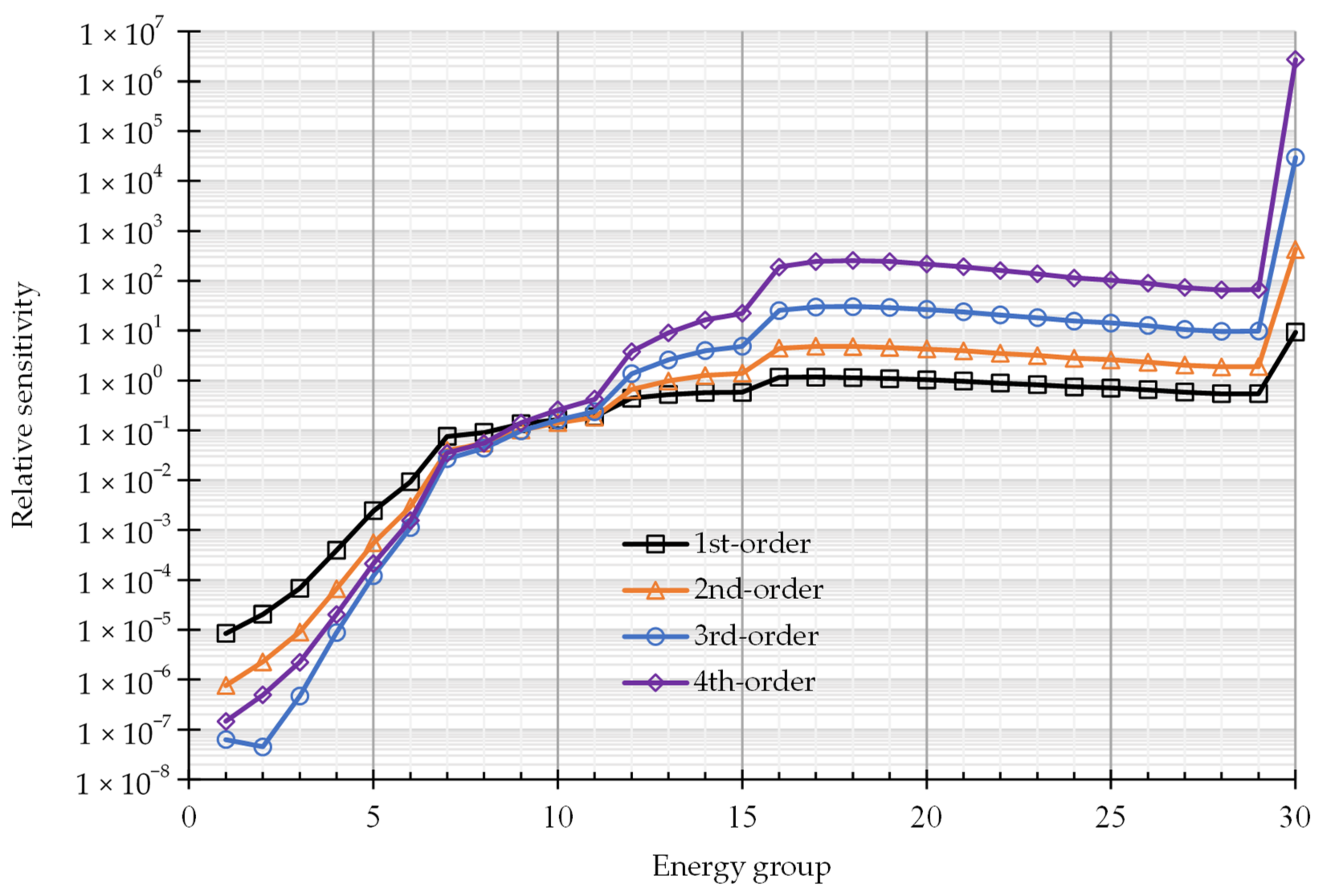
2.1. Numerical Results for Fourth-Order Unmixed Sensitivities and Comparison with the Corresponding 1st-, 2nd- and 3rd-Order Unmixed Sensitivities
- (i)
- the microscopic total cross section for the 12th-energy group (which comprises the energy interval from 0.823 MeV to 1.35 MeV) and the 16th-energy group (which comprises the energy interval from 67.6 KeV to 184 KeV) of isotope 239Pu (i.e., and ); and
- (ii)
- the 30th energy group (which comprises thermalized neutrons in the energy interval from 1.39 × 10−4 eV to 0.152 eV) of isotope 1H (i.e., ).
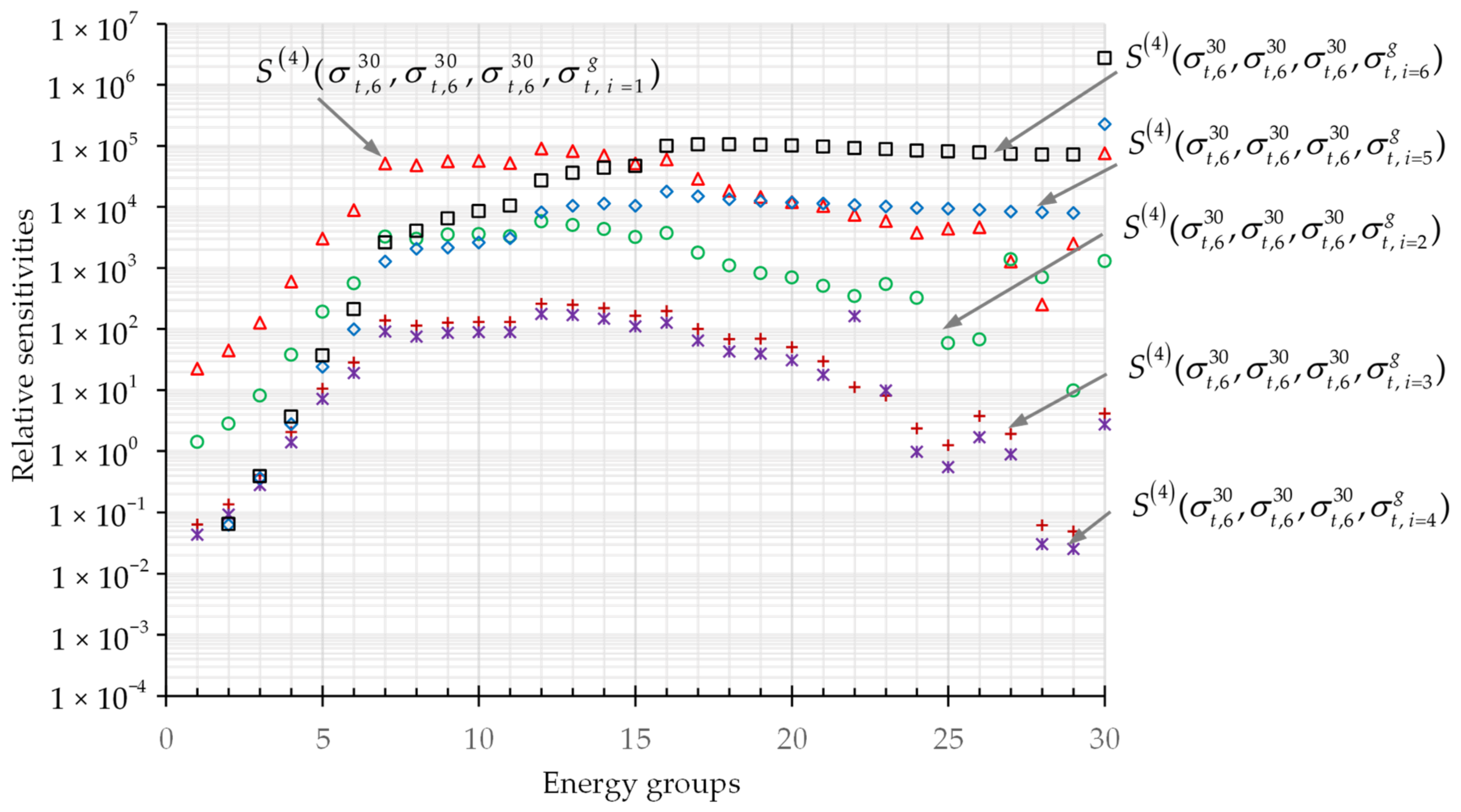
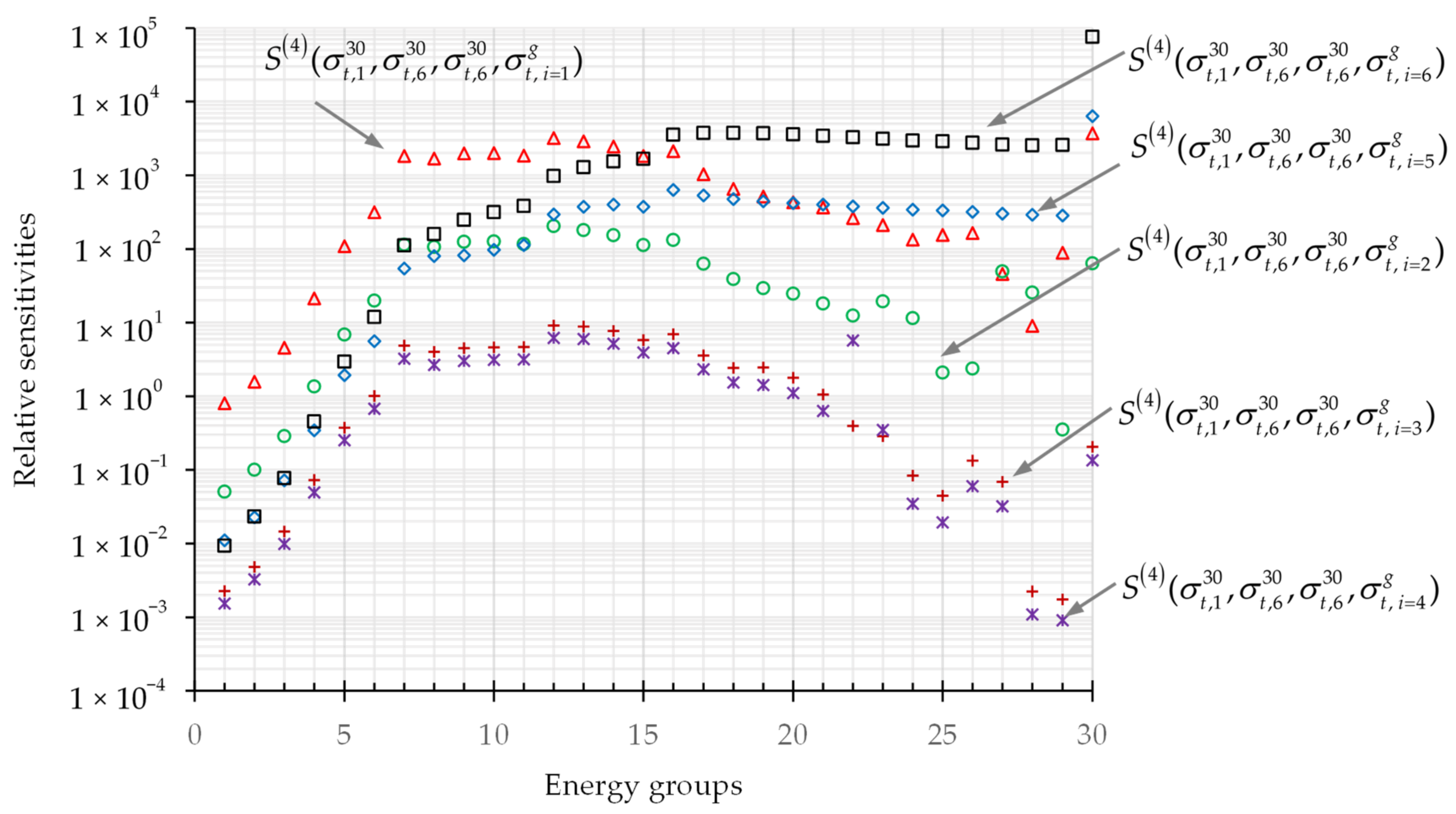
2.2. Numerical Results for Fourth-Order Mixed Sensitivities Corresponding to the Largest Third-Order Sensitivities
2.2.1. Fourth-Order Mixed Sensitivities
2.2.2. Fourth-Order Mixed Sensitivities
3. Verification of the 4th-Order Mixed Relative Sensitivities
3.1. Exact Verification of the 4th-Order Mixed Sensitivities Using the Inherent Symmetries within the 4th-CASAM
3.2. Approximate Verification of the 4th-Order Mixed Sensitivities Using Finite-Differences
- (i)
- the largest 4th-order mixed relative sensitivity depicted in Figure 4, i.e., , for the leakage response with respect to the microscopic total cross sections for group 30 of isotopes 5 (C) and 6 (1H); and
- (ii)
- the largest 4th-order mixed relative sensitivity depicted in Figure 5, i.e., , which occurs for group 30 of isotopes 1 (239Pu) and 6 (1H).
4. Finite-Difference Computations of the 4th-Order Unmixed Relative Sensitivities
- (i)
- the overall largest 4th-order unmixed relative sensitivity, namely, , which occurs for group 30 of isotope 6 (1H);
- (ii)
- the largest 4th-order unmixed relative sensitivity shown in Table 2, which is the sensitivity of the leakage response with respect to the microscopic total cross section for group 16 of isotope 1 (239Pu).
5. Comparison of Computational Requirements for the 4th-Order Sensitivities
- (i)
- To compute the 180 first-order sensitivities, one adjoint PARTISN large-scale computation is needed in order to obtain the 1st-level adjoint function . Thus, the CPU-time needed is ca. 24 s [for computing ] plus ca. 1 s for computing the integrals over this adjoint function. By comparison, ca. 270 min are needed to compute these 1st-order sensitivities using the FD-formula.
- (ii)
- To compute the distinct second-order sensitivities, adjoint PARTISN large-scale computations are needed to obtain the 2nd-level adjoint functions and . Thus, the CPU-time needed is ca. 2.4 h [for computing and ] plus ca. 3 min for computing the integrals over these adjoint functions. By comparison, ca. 810 h are needed to compute these 2nd-order sensitivities using the FD-formula.
- (iii)
- To compute the distinct third-order sensitivities, 32,940 adjoint PARTISN large-scale computations are needed to obtain the 3rd-level adjoint functions . Thus, the CPU-time needed is ca. 220 h [for computing ] plus ca. 0.6 h for computing the integrals over these adjoint functions. By comparison, 98,817 h are needed to compute these 3rd-order sensitivities using the FD-formula.
- (iv)
- To compute the distinct fourth-order sensitivities, 2,042,040 adjoint PARTISN large-scale computations are needed to obtain the 4th-level adjoint functions . Thus, the CPU-time needed is ca. 25,525 h [for computing ] plus ca. 50 h for computing the integrals over these adjoint functions. By comparison, ca. 1015 years are needed to compute these 4th-order sensitivities using the FD-formula.
6. Conclusions
- (1)
- The number of 4th-order unmixed relative sensitivities that have large values (e.g., greater than 1.0) is far greater than the number of large 1st-, 2nd- and 3rd-order sensitivities. The majority of the large sensitivities involve the isotopes 1H and 239Pu of the PERP benchmark, as shown in Table 2 and Table 7.
- (2)
- All of the important 4th-order relative sensitivities of the PERP leakage response with respect to the microscopic total cross sections have positive values. By comparison, all of the important 1st-order and 3rd-order relative sensitivities have negative values, while all of the important 2nd-order relative sensitivities have positive values.
- (3)
- For most energy groups for isotopes 1H and 239Pu, the values of the 4th-order unmixed relative sensitivities are significantly larger than the corresponding values of the 1st-, 2nd- and 3rd-order unmixed sensitivities. The overall largest 4th-order unmixed relative sensitivity is , which is around 291,000 times, 6350 times and 90 times larger than the corresponding largest 1st-order, 2nd-order and 3rd-order sensitivities, respectively.
- (4)
- All of the 1st-order through 4th-order unmixed relative sensitivities that involve the microscopic total cross sections of isotopes 240Pu, 69Ga, 71Ga and C have values of the order of 10−2 or less (except for isotope C at g = 30). For each of these isotopes, within the same energy group, the value of the 1st-order relative sensitivity is generally the largest, followed by the 2nd-order and 3rd-order sensitivities, while the 4th-order sensitivity is the smallest.
- (5)
- The majority of the 180 4th-order mixed relative sensitivities , which correspond to the largest unmixed 3rd-order sensitivity , have values greater than 1.0. Moreover, the mixed sensitivities and , which involve the microscopic total cross sections of isotopes 1 (239Pu) and 6 (1H), are larger than those involving the microscopic total cross sections of isotopes 2, 3 and 4 (i.e.,240Pu, 69Ga, and 71Ga).
- (6)
- The overall largest mixed 4th-order relative sensitivity is , involving the microscopic total cross sections for isotope 6 (1H) and isotope 5 (C) in the 30th energy (thermalized neutrons) group. The sensitivity is much larger than the largest 2nd-order and 3rd-order mixed sensitivities.
- (7)
- The numerical results obtained using the 4th-CASAM for the sensitivities and have been compared with the results obtained for these quantities by using finite difference formulas that were accurate to the second-order in the respective step-size(s). The finite-difference formulas turned out to be extremely sensitive to the step-size: when the step-sizes were too large or too small, the results produced by the finite-difference formulas were far off from the exact values of the derivatives and . This finding further highlights the importance of the 4th-CASAM framework for computing accurately and efficiently the 1st-, 2nd-, 3rd-, and 4th-order sensitivities of model responses with respect to model parameters.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Mathematical Expression for Computing the 4th-Order Sensitivities
References
- Cacuci, D.G. Second-Order Adjoint Sensitivity Analysis Methodology (2nd-ASAM) for Computing Exactly and Efficiently First- and Second-Order Sensitivities in Large-Scale Linear Systems: I. Computational Methodology. J. Comp. Phys. 2015, 284, 687–699. [Google Scholar] [CrossRef] [Green Version]
- Valentine, T.E. Polyethylene-reflected plutonium metal sphere subcritical noise measurements, SUB-PU-METMIXED-001. In International Handbook of Evaluated Criticality Safety Benchmark Experiments; NEA/NSC/DOC(95)03/I-IX; Nuclear Energy Agency: Paris, France, 2006. [Google Scholar]
- Cacuci, D.G.; Fang, R. Fourth-Order Adjoint Sensitivity Analysis of an OECD/NEA Reactor Physics Benchmark: I. Mathematical Expressions and CPU-Time Comparisons for Computing 1st-, 2nd- and 3rd-Order Sensitivities. Am. J. Comput. Math. 2021, 2, 94–132. [Google Scholar] [CrossRef]
- Cacuci, D.G.; Fang, R.; Favorite, J.A. Comprehensive Second-Order Adjoint Sensitivity Analysis Methodology (2nd-ASAM) Applied to a Subcritical Experimental Reactor Physics Benchmark: I. Effects of Imprecisely Known Microscopic Total and Capture Cross Sections. Energies 2019, 12, 4219. [Google Scholar] [CrossRef] [Green Version]
- Fang, R.; Cacuci, D.G. Comprehensive Second-Order Adjoint Sensitivity Analysis Methodology (2nd-ASAM) Applied to a Subcritical Experimental Reactor Physics Benchmark: II. Effects of Imprecisely Known Microscopic Scattering Cross Sections. Energies 2019, 12, 4114. [Google Scholar] [CrossRef] [Green Version]
- Cacuci, D.G.; Fang, R.; Favorite, J.A.; Badea, M.C.; Di Rocco, F. Comprehensive Second-Order Adjoint Sensitivity Analysis Methodology (2nd-ASAM) Applied to a Subcritical Experimental Reactor Physics Benchmark: III. Effects of Imprecisely Known Microscopic Fission Cross Sections and Average Number of Neutrons per Fission. Energies 2019, 12, 4100. [Google Scholar] [CrossRef] [Green Version]
- Fang, R.; Cacuci, D.G. Comprehensive Second-Order Adjoint Sensitivity Analysis Methodology (2nd-ASAM) Applied to a Subcritical Experimental Reactor Physics Benchmark: IV. Effects of Imprecisely Known Source Parameters. Energies 2020, 13, 1431. [Google Scholar] [CrossRef] [Green Version]
- Fang, R.; Cacuci, D.G. Comprehensive Second-Order Adjoint Sensitivity Analysis Methodology (2nd-ASAM) Applied to a Subcritical Experimental Reactor Physics Benchmark: V. Computation of Mixed 2nd-Order Sensitivities Involving Isotopic Number Densities. Energies 2020, 13, 2580. [Google Scholar] [CrossRef]
- Cacuci, D.G.; Fang, R.; Favorite, J.A. Comprehensive Second-Order Adjoint Sensitivity Analysis Methodology (2nd-ASAM) Applied to a Subcritical Experimental Reactor Physics Benchmark: VI. Overall Impact of 1st- and 2nd-Order Sensitivities on Response Uncertainties. Energies 2020, 13, 1674. [Google Scholar] [CrossRef] [Green Version]
- Cacuci, D.G.; Fang, R. Third-Order Adjoint Sensitivity Analysis of an OECD/NEA Reactor Physics Benchmark: I. Mathematical Framework. Am. J. Comput. Math. 2020, 10, 503–528. [Google Scholar] [CrossRef]
- Fang, R.; Cacuci, D.G. Third-Order Adjoint Sensitivity Analysis of an OECD/NEA Reactor Physics Benchmark: II. Computed Sensitivities. Am. J. Comput. Math. 2020, 10, 529–558. [Google Scholar] [CrossRef]
- Fang, R.; Cacuci, D.G. Third-Order Adjoint Sensitivity Analysis of an OECD/NEA Reactor Physics Benchmark: III. Response Moments. Am. J. Comput. Math. 2020, 10, 559–570. [Google Scholar] [CrossRef]
- Cacuci, D.G.; Fang, R. Fourth-Order Adjoint Sensitivity Analysis of an OECD/NEA Reactor Physics Benchmark: II. Mathematical Expressions and CPU-Time Comparisons for Computing 4th-Order Sensitivities. Am. J. Comput. Math. 2021, 11, 133–156. [Google Scholar] [CrossRef]
- Alcouffe, R.E.; Baker, R.S.; Dahl, J.A.; Turner, S.A.; Ward, R. PARTISN: A Time-Dependent, Parallel Neutral Particle Transport Code System; LA-UR-08-07258; Los Alamos National Laboratory: Los Alamos, NM, USA, 2008. [Google Scholar]
- Wilson, W.B.; Perry, R.T.; Shores, E.F.; Charlton, W.S.; Parish, T.A.; Estes, G.P.; Brown, T.H.; Arthur, E.D.; Bozoian, M.; England, T.R.; et al. SOURCES4C: A code for calculating (α,n), spontaneous fission, and delayed neutron sources and spectra. In Proceedings of the American Nuclear Society/Radiation Protection and Shielding Division 12th Biennial Topical Meeting, Santa Fe, NM, USA, 14–18 April 2002. [Google Scholar]
- Conlin, J.L.; Parsons, D.K.; Gardiner, S.J.; Gray, M.; Lee, M.B.; White, M.C. MENDF71X: Multigroup Neutron Cross-Section Data Tables Based upon ENDF/B-VII.1X.; Los Alamos National Laboratory Report LA-UR-15-29571; Los Alamos National Laboratory: Los Alamos, NM, USA, 2013. [Google Scholar] [CrossRef]
- Fang, R.; Cacuci, D.G. Fourth-Order Adjoint Sensitivity and Uncertainty Analysis of an OECD/NEA Reactor Physics Benchmark: II. Computed Response Uncertainties. J. Nucl. Eng. 2021. under review. [Google Scholar]

| Materials | Isotopes | Weight Fraction | Density (g/cm3) | Zones |
|---|---|---|---|---|
| Material 1 (Plutonium metal) | Isotope 1 (239Pu) | 9.3804 × 10−1 | 19.6 | Homogeneous sphere of radius = 3.794 cm, designated as “material 1” and assigned to zone 1. |
| Isotope 2 (240Pu) | 5.9411 × 10−2 | |||
| Isotope 3 (69Ga) | 1.5152 × 10−3 | |||
| Isotope 4 (71Ga) | 1.0346 × 10−3 | |||
| Material 2 (polyethylene) | Isotope 5 (C) | 8.5630 × 10−1 | 0.95 | Homogeneous spherical shell of inner radius = 3.794 cm and outer radius = 7.604 cm, designated as “material 2” and assigned to zone 2. |
| Isotope 6 (1H) | 1.4370 × 10−1 |
| g | 1st-Order | 2nd-Order | 3rd-Order | 4th-Order |
|---|---|---|---|---|
| 1 | −0.0003 | 0.0003 | −0.0003 | 0.00032 |
| 2 | −0.0007 | 0.0005 | −0.0005 | 0.00063 |
| 3 | −0.0019 | 0.0015 | −0.0015 | 0.0018 |
| 4 | −0.009 | 0.007 | −0.008 | 0.0098 |
| 5 | −0.046 | 0.043 | −0.054 | 0.083 |
| 6 | −0.135 | 0.162 | −0.267 | 0.552 |
| 7 | −0.790 | 1.987 | −7.294 | 35.17 |
| 8 | −0.726 | 1.768 | −6.270 | 29.19 |
| 9 | −0.843 | 2.205 | −8.454 | 42.66 |
| 10 | −0.845 | 2.177 | −8.247 | 41.15 |
| 11 | −0.775 | 1.879 | −6.691 | 31.39 |
| 12 | −1.320 | 4.586 | −23.71 | 162.05 |
| 13 | −1.154 | 4.039 | −20.96 | 143.67 |
| 14 | −0.952 | 3.435 | −18.29 | 128.58 |
| 15 | −0.690 | 2.487 | −13.18 | 91.99 |
| 16 | −0.779 | 3.487 | −23.10 | 202.03 |
| 17 | −0.364 | 1.578 | −10.07 | 84.76 |
| 18 | −0.227 | 0.995 | −6.428 | 54.71 |
| 19 | −0.181 | 0.789 | −5.063 | 42.86 |
| 20 | −0.155 | 0.601 | −3.431 | 25.74 |
| 21 | −0.137 | 0.479 | −2.480 | 16.85 |
| 22 | −0.099 | 0.297 | −1.313 | 7.624 |
| 23 | −0.081 | 0.205 | −0.777 | 3.894 |
| 24 | −0.051 | 0.123 | −0.438 | 2.055 |
| 25 | −0.060 | 0.138 | −0.473 | 2.149 |
| 26 | −0.063 | 0.158 | −0.581 | 2.807 |
| 27 | −0.017 | 0.022 | −0.039 | 0.095 |
| 28 | −0.003 | 0.002 | −0.0017 | 0.0019 |
| 29 | −0.035 | 0.072 | −0.226 | 0.939 |
| 30 | −0.461 | 1.353 | −5.980 | 35.05 |
| g | 1st-Order | 2nd-Order | 3rd-Order | 4th-Order |
|---|---|---|---|---|
| 1 | −2.060 × 10−5 | 1.052 × 10−6 | −6.857 × 10−8 | 5.127 × 10−9 |
| 2 | −4.117 × 10−5 | 2.089 × 10−6 | −1.358 × 10−7 | 1.018 × 10−8 |
| 3 | −1.192 × 10−4 | 6.055 × 10−6 | −3.948 × 10−7 | 2.983 × 10−8 |
| 4 | −5.638 × 10−4 | 2.947 × 10−5 | −1.994 × 10−6 | 1.586 × 10−7 |
| 5 | −2.894 × 10−3 | 1.730 × 10−4 | −1.370 × 10−5 | 1.316 × 10−6 |
| 6 | −8.513 × 10−3 | 6.485 × 10−4 | −6.744 × 10−5 | 8.802 × 10−6 |
| 7 | −4.958 × 10−2 | 7.836 × 10−3 | −1.806 × 10−3 | 5.467 × 10−4 |
| 8 | −4.574 × 10−2 | 7.026 × 10−3 | −1.571 × 10−3 | 4.613 × 10−4 |
| 9 | −5.318 × 10−2 | 8.769 × 10−3 | −2.120 × 10−3 | 6.747 × 10−4 |
| 10 | −5.345 × 10−2 | 8.711 × 10−3 | −2.087 × 10−3 | 6.586 × 10−4 |
| 11 | −4.909 × 10−2 | 7.547 × 10−3 | −1.703 × 10−3 | 5.064 × 10−4 |
| 12 | −8.364 × 10−2 | 1.842 × 10−2 | −6.032 × 10−3 | 2.613 × 10−3 |
| 13 | −7.145 × 10−2 | 1.548 × 10−2 | −4.974 × 10−3 | 2.111 × 10−3 |
| 14 | −5.953 × 10−2 | 1.342 × 10−2 | −4.466 × 10−3 | 1.962 × 10−3 |
| 15 | −4.267 × 10−2 | 9.506 × 10−3 | −3.114 × 10−3 | 1.344 × 10−3 |
| 16 | −4.864 × 10−2 | 1.052 × 10−6 | −5.606 × 10−3 | 3.059 × 10−3 |
| 17 | −2.236 × 10−2 | 2.089 × 10−6 | −2.328 × 10−3 | 1.202 × 10−3 |
| 18 | −1.358 × 10−2 | 6.055 × 10−6 | −1.383 × 10−3 | 7.051 × 10−4 |
| 19 | −1.021 × 10−2 | 2.947 × 10−5 | −9.170 × 10−4 | 4.392 × 10−4 |
| 20 | −8.914 × 10−3 | 1.730 × 10−4 | −6.590 × 10−4 | 2.853 × 10−4 |
| 21 | −6.716 × 10−3 | 6.485 × 10−4 | −2.947 × 10−4 | 9.841 × 10−5 |
| 22 | −4.676 × 10−3 | 7.836 × 10−3 | −1.364 × 10−4 | 3.723 × 10−5 |
| 23 | −7.458 × 10−3 | 7.026 × 10−3 | −6.187 × 10−4 | 2.872 × 10−4 |
| 24 | −4.371 × 10−3 | 8.769 × 10−3 | −2.703 × 10−4 | 1.079 × 10−4 |
| 25 | −8.131 × 10−4 | 8.711 × 10−3 | −1.170 × 10−6 | 7.178 × 10−8 |
| 26 | −9.171 × 10−4 | 7.547 × 10−3 | −1.776 × 10−6 | 1.245 × 10−7 |
| 27 | −1.862 × 10−2 | 1.842 × 10−2 | −4.965 × 10−2 | 1.295 × 10−1 |
| 28 | −9.671 × 10−3 | 1.548 × 10−2 | −3.722 × 10−2 | 1.186 × 10−1 |
| 29 | −1.364 × 10−4 | 1.342 × 10−2 | −1.385 × 10−8 | 2.268 × 10−10 |
| 30 | −7.909 × 10−3 | 9.506 × 10−3 | −3.016 × 10−5 | 3.031 × 10−6 |
| g | 1st-Order | 2nd-Order | 3rd-Order | 4th-Order |
|---|---|---|---|---|
| 1 | −9.214 × 10−7 | 2.104 × 10−9 | −6.132 × 10−12 | 2.050 × 10−14 |
| 2 | −1.974 × 10−6 | 4.804 × 10−9 | −1.497 × 10−11 | 5.381 × 10−14 |
| 3 | −6.012 × 10−6 | 1.541 × 10−8 | −5.068 × 10−11 | 1.932 × 10−13 |
| 4 | −3.036 × 10−5 | 8.545 × 10−8 | −3.114 × 10−10 | 1.334 × 10−12 |
| 5 | −1.587 × 10−4 | 5.204 × 10−7 | −2.260 × 10−9 | 1.191 × 10−11 |
| 6 | −4.353 × 10−4 | 1.696 × 10−6 | −9.018 × 10−9 | 6.019 × 10−11 |
| 7 | −2.107 × 10−3 | 1.415 × 10−5 | −1.386 × 10−7 | 1.784 × 10−9 |
| 8 | −1.717 × 10−3 | 9.897 × 10−6 | −8.307 × 10−8 | 9.152 × 10−10 |
| 9 | −1.912 × 10−3 | 1.133 × 10−5 | −9.845 × 10−8 | 1.126 × 10−9 |
| 10 | −1.956 × 10−3 | 1.166 × 10−5 | −1.022 × 10−7 | 1.181 × 10−9 |
| 11 | −1.943 × 10−3 | 1.182 × 10−5 | −1.055 × 10−7 | 1.241 × 10−9 |
| 12 | −3.756 × 10−3 | 3.714 × 10−5 | −5.464 × 10−7 | 1.063 × 10−8 |
| 13 | −3.522 × 10−3 | 3.762 × 10−5 | −5.957 × 10−7 | 1.246 × 10−8 |
| 14 | −2.987 × 10−3 | 3.371 × 10−5 | −5.624 × 10−7 | 1.238 × 10−8 |
| 15 | −2.182 × 10−3 | 2.485 × 10−5 | −4.163 × 10−7 | 9.187 × 10−9 |
| 16 | −2.551 × 10−3 | 3.733 × 10−5 | −8.089 × 10−7 | 2.315 × 10−8 |
| 17 | −1.262 × 10−3 | 1.893 × 10−5 | −4.187 × 10−7 | 1.220 × 10−8 |
| 18 | −8.411 × 10−4 | 1.371 × 10−5 | −3.289 × 10−7 | 1.039 × 10−8 |
| 19 | −8.605 × 10−4 | 1.790 × 10−5 | −5.485 × 10−7 | 2.213 × 10−8 |
| 20 | −6.458 × 10−4 | 1.050 × 10−5 | −2.506 × 10−7 | 7.859 × 10−9 |
| 21 | −3.919 × 10−4 | 3.949 × 10−6 | −5.856 × 10−8 | 1.141 × 10−9 |
| 22 | −1.489 × 10−4 | 6.668 × 10−7 | −4.408 × 10−9 | 3.832 × 10−11 |
| 23 | −1.104 × 10−4 | 3.859 × 10−7 | −2.008 × 10−9 | 1.380 × 10−11 |
| 24 | −3.199 × 10−5 | 4.778 × 10−8 | −1.059 × 10−10 | 3.094 × 10−13 |
| 25 | −1.726 × 10−5 | 1.136 × 10−8 | −1.118 × 10−11 | 1.456 × 10−14 |
| 26 | −5.147 × 10−5 | 1.046 × 10−7 | −3.139 × 10−10 | 1.235 × 10−12 |
| 27 | −2.586 × 10−5 | 4.825 × 10−8 | −1.331 × 10−10 | 4.823 × 10−13 |
| 28 | −8.496 × 10−7 | 1.192 × 10−10 | −2.523 × 10−14 | 7.064 × 10−18 |
| 29 | −6.754 × 10−7 | 2.747 × 10−11 | −1.682 × 10−15 | 1.364 × 10−19 |
| 30 | −2.542 × 10−5 | 4.111 × 10−9 | −1.002 × 10−12 | 3.237 × 10−16 |
| g | 1st-Order | 2nd-Order | 3rd-Order | 4th-Order |
|---|---|---|---|---|
| 1 | −6.266 × 10−7 | 9.730 × 10−10 | −1.928 × 10−12 | 4.385 × 10−15 |
| 2 | −1.345 × 10−6 | 2.230 × 10−9 | −4.734 × 10−12 | 1.159 × 10−14 |
| 3 | −4.103 × 10−6 | 7.176 × 10−9 | −1.611 × 10−11 | 4.190 × 10−14 |
| 4 | −2.069 × 10−5 | 3.967 × 10−8 | −9.849 × 10−11 | 2.874 × 10−13 |
| 5 | −1.072 × 10−4 | 2.374 × 10−7 | −6.966 × 10−10 | 2.479 × 10−12 |
| 6 | −2.906 × 10−4 | 7.557 × 10−7 | −2.683 × 10−9 | 1.195 × 10−11 |
| 7 | −1.397 × 10−3 | 6.218 × 10−6 | −4.037 × 10−8 | 3.443 × 10−10 |
| 8 | −1.149 × 10−3 | 4.436 × 10−6 | −2.492 × 10−8 | 1.838 × 10−10 |
| 9 | −1.295 × 10−3 | 5.202 × 10−6 | −3.063 × 10−8 | 2.374 × 10−10 |
| 10 | −1.327 × 10−3 | 5.368 × 10−6 | −3.192 × 10−8 | 2.501 × 10−10 |
| 11 | −1.318 × 10−3 | 5.439 × 10−6 | −3.296 × 10−8 | 2.630 × 10−10 |
| 12 | −2.549 × 10−3 | 1.710 × 10−5 | −1.707 × 10−7 | 2.253 × 10−9 |
| 13 | −2.375 × 10−3 | 1.711 × 10−5 | −1.828 × 10−7 | 2.579 × 10−9 |
| 14 | −2.005 × 10−3 | 1.521 × 10−5 | −1.705 × 10−7 | 2.523 × 10−9 |
| 15 | −1.481 × 10−3 | 1.145 × 10−5 | −1.302 × 10−7 | 1.950 × 10−9 |
| 16 | −1.662 × 10−3 | 1.585 × 10−5 | −2.237 × 10−7 | 4.172 × 10−9 |
| 17 | −8.176 × 10−4 | 7.950 × 10−6 | −1.139 × 10−7 | 2.152 × 10−9 |
| 18 | −5.318 × 10−4 | 5.479 × 10−6 | −8.310 × 10−8 | 1.660 × 10−9 |
| 19 | −4.939 × 10−4 | 5.898 × 10−6 | −1.037 × 10−7 | 2.403 × 10−9 |
| 20 | −3.976 × 10−4 | 3.979 × 10−6 | −5.847 × 10−8 | 1.129 × 10−9 |
| 21 | −2.344 × 10−4 | 1.413 × 10−6 | −1.253 × 10−8 | 1.461 × 10−10 |
| 22 | −2.170 × 10−3 | 1.416 × 10−4 | −1.364 × 10−5 | 1.727 × 10−6 |
| 23 | −1.337 × 10−4 | 5.659 × 10−7 | −3.568 × 10−9 | 2.970 × 10−11 |
| 24 | −1.322 × 10−5 | 8.156 × 10−9 | −7.470 × 10−12 | 9.013 × 10−15 |
| 25 | −7.518 × 10−6 | 2.154 × 10−9 | −9.232 × 10−13 | 5.234 × 10−16 |
| 26 | −2.313 × 10−5 | 2.112 × 10−8 | −2.848 × 10−11 | 5.034 × 10−14 |
| 27 | −1.201 × 10−5 | 1.041 × 10−8 | −1.333 × 10−11 | 2.243 × 10−14 |
| 28 | −4.131 × 10−7 | 2.818 × 10−11 | −2.901 × 10−15 | 3.949 × 10−19 |
| 29 | −3.512 × 10−7 | 7.429 × 10−12 | −2.365 × 10−16 | 9.973 × 10−21 |
| 30 | −1.665 × 10−5 | 1.764 × 10−9 | −2.815 × 10−13 | 5.958 × 10−17 |
| g | 1st-Order | 2nd-Order | 3rd-Order | 4th-Order |
|---|---|---|---|---|
| 1 | −9.992 × 10−6 | 1.066 × 10−6 | 1.038 × 10−7 | 2.827 × 10−7 |
| 2 | −2.017 × 10−5 | 2.185 × 10−6 | 4.236 × 10−8 | 4.551 × 10−7 |
| 3 | −6.373 × 10−5 | 7.901 × 10−6 | −3.833 × 10−7 | 1.722 × 10−6 |
| 4 | −2.996 × 10−4 | 3.873 × 10−5 | −3.872 × 10−6 | 6.870 × 10−6 |
| 5 | −1.597 × 10−3 | 2.359 × 10−4 | −3.370 × 10−5 | 3.870 × 10−5 |
| 6 | −4.403 × 10−3 | 6.521 × 10−4 | −1.175 × 10−4 | 7.664 × 10−5 |
| 7 | −3.698 × 10−2 | 9.376 × 10−3 | −3.113 × 10−3 | 1.981 × 10−3 |
| 8 | −4.631 × 10−2 | 1.447 × 10−2 | −5.744 × 10−3 | 3.688 × 10−3 |
| 9 | −4.502 × 10−2 | 1.114 × 10−2 | −3.553 × 10−3 | 1.709 × 10−3 |
| 10 | −5.135 × 10−2 | 1.368 × 10−2 | −4.754 × 10−3 | 2.369 × 10−3 |
| 11 | −5.645 × 10−2 | 1.633 × 10−2 | −6.262 × 10−3 | 3.304 × 10−3 |
| 12 | −1.345 × 10−1 | 6.055 × 10−2 | −3.799 × 10−2 | 3.192 × 10−2 |
| 13 | −1.529 × 10−1 | 8.249 × 10−2 | −6.342 × 10−2 | 6.411 × 10−2 |
| 14 | −1.504 × 10−1 | 8.573 × 10−2 | −7.064 × 10−2 | 7.609 × 10−2 |
| 15 | −1.299 × 10−1 | 6.928 × 10−2 | −5.391 × 10−2 | 5.477 × 10−2 |
| 16 | −2.074 × 10−1 | 1.415 × 10−1 | −1.429 × 10−1 | 1.902 × 10−1 |
| 17 | −1.665 × 10−1 | 9.779 × 10−2 | −8.554 × 10−2 | 9.874 × 10−2 |
| 18 | −1.439 × 10−1 | 7.678 × 10−2 | −6.114 × 10−2 | 6.431 × 10−2 |
| 19 | −1.310 × 10−1 | 6.625 × 10−2 | −5.004 × 10−2 | 4.995 × 10−2 |
| 20 | −1.212 × 10−1 | 5.905 × 10−2 | −4.297 × 10−2 | 4.133 × 10−2 |
| 21 | −1.129 × 10−1 | 5.347 × 10−2 | −3.780 × 10−2 | 3.532 × 10−2 |
| 22 | −1.036 × 10−1 | 4.747 × 10−2 | −3.247 × 10−2 | 2.934 × 10−2 |
| 23 | −9.589 × 10−2 | 4.280 × 10−2 | −2.851 × 10−2 | 2.509 × 10−2 |
| 24 | −8.693 × 10−2 | 3.756 × 10−2 | −2.422 × 10−2 | 2.063 × 10−2 |
| 25 | −8.213 × 10−2 | 3.496 × 10−2 | −2.220 × 10−2 | 1.862 × 10−2 |
| 26 | −7.550 × 10−2 | 3.142 × 10−2 | −1.949 × 10−2 | 1.597 × 10−2 |
| 27 | −6.727 × 10−2 | 2.701 × 10−2 | −1.617 × 10−2 | 1.279 × 10−2 |
| 28 | −6.224 × 10−2 | 2.437 × 10−2 | −1.422 × 10−2 | 1.097 × 10−2 |
| 29 | −5.995 × 10−2 | 2.298 × 10−2 | −1.312 × 10−2 | 9.896 × 10−3 |
| 30 | −7.847 × 10−1 | 3.016 × 100 | −1.745 × 101 | 1.340 × 102 |
| g | 1st-Order | 2nd-Order | 3rd-Order | 3rd-Order |
|---|---|---|---|---|
| 1 | −8.471 × 10−6 | 7.636 × 10−7 | 6.322 × 10−8 | 1.460 × 10−7 |
| 2 | −2.060 × 10−5 | 2.280 × 10−6 | 4.516 × 10−8 | 4.956 × 10−7 |
| 3 | −6.810 × 10−5 | 9.021 × 10−6 | −4.677 × 10−7 | 2.245 × 10−6 |
| 4 | −3.932 × 10−4 | 6.673 × 10−5 | −8.758 × 10−6 | 2.039 × 10−5 |
| 5 | −2.449 × 10−3 | 5.549 × 10−4 | −1.216 × 10−4 | 2.142 × 10−4 |
| 6 | −9.342 × 10−3 | 2.935 × 10−3 | −1.123 × 10−3 | 1.553 × 10−3 |
| 7 | −7.589 × 10−2 | 3.949 × 10−2 | −2.690 × 10−2 | 3.513 × 10−2 |
| 8 | −9.115 × 10−2 | 5.604 × 10−2 | −4.380 × 10−2 | 5.536 × 10−2 |
| 9 | −1.358 × 10−1 | 1.014 × 10−1 | −9.758 × 10−2 | 1.416 × 10−1 |
| 10 | −1.659 × 10−1 | 1.428 × 10−1 | −1.604 × 10−1 | 2.582 × 10−1 |
| 11 | −1.899 × 10−1 | 1.849 × 10−1 | −2.385 × 10−1 | 4.233 × 10−1 |
| 12 | −4.446 × 10−1 | 6.620 × 10−1 | −1.373 × 100 | 3.815 × 100 |
| 13 | −5.266 × 10−1 | 9.782 × 10−1 | −2.590 × 100 | 9.015 × 100 |
| 14 | −5.772 × 10−1 | 1.262 × 100 | −3.991 × 100 | 1.650 × 101 |
| 15 | −5.820 × 10−1 | 1.391 × 100 | −4.581 × 100 | 2.208 × 101 |
| 16 | −1.164 × 100 | 4.460 × 100 | −2.530 × 101 | 1.890 × 102 |
| 17 | −1.173 × 100 | 4.853 × 100 | −2.991 × 101 | 2.432 × 102 |
| 18 | −1.141 × 100 | 4.828 × 100 | −3.049 × 101 | 2.543 × 102 |
| 19 | −1.094 × 100 | 4.619 × 100 | −2.913 × 101 | 2.428 × 102 |
| 20 | −1.033 × 100 | 4.284 × 100 | −2.655 × 101 | 2.175 × 102 |
| 21 | −9.692 × 10−1 | 3.937 × 100 | −2.388 × 101 | 1.915 × 102 |
| 22 | −8.917 × 10−1 | 3.515 × 100 | −2.069 × 101 | 1.609 × 102 |
| 23 | −8.262 × 10−1 | 3.177 × 100 | −1.823 × 101 | 1.382 × 102 |
| 24 | −7.495 × 10−1 | 2.792 × 100 | −1.552 × 101 | 1.140 × 102 |
| 25 | −7.087 × 10−1 | 2.604 × 100 | −1.427 × 101 | 1.033 × 102 |
| 26 | −6.529 × 10−1 | 2.349 × 100 | −1.260 × 101 | 8.932 × 101 |
| 27 | −5.845 × 10−1 | 2.039 × 100 | −1.061 × 101 | 7.288 × 101 |
| 28 | −5.474 × 10−1 | 1.885 × 100 | −9.678 × 100 | 6.565 × 101 |
| 29 | −5.439 × 10−1 | 1.891 × 100 | −9.800 × 100 | 6.705 × 101 |
| 30 | −9.366 × 100 | 4.296 × 102 | −2.966 × 104 | 2.720 × 106 |
FD-Method | |||
|---|---|---|---|
| 0.125% × | 0.125% × | 3.066 × 105 | 34.6% |
| 0.50% × | 0.25% × | 2.423 × 105 | 6.34% |
| 0.50% × | 0.50% × | 2.818 × 105 | 23.6% |
| 1.00% × | 1.00% × | 6.784 × 105 | 197% |
| 3.00% × | 1.00% × | 2.124 × 106 | 832% |
| >3.0% × | >2.0% × | − | − |
FD-Method | |||
|---|---|---|---|
| 4.350 × 106 | 5659% | ||
| 0.125 × | 0.125 × | 7.521 × 104 | −0.44% |
| 7.471 × 104 | −1.10% | ||
| 9.283 × 104 | 22.9% | ||
| −1.835 × 104 | −124% | ||
| 4.007 × 106 | 5204% | ||
| − | − |
| Step-Size | FD-Method | |
|---|---|---|
| 0.125% × | −1.607 × 108 | −6010% |
| −7.488 × 106 | −375% | |
| 0.50% × | 2.239 × 106 | −17.7% |
| 0.60% × | 2.708 × 106 | −0.45% |
| 0.65% × | 2.838 × 106 | 4.3% |
| 0.75% × | 3.063 × 106 | 12.6% |
| 1.00% × | 3.574 × 106 | 31.4% |
| 2.00% × | 2.171 × 107 | 698% |
| − | − |
| Step-Size | FD-Method | |
|---|---|---|
| 0.50% × | −5.243 × 103 | −2695% |
| 1.00% × | −1.618 × 102 | −505% |
| 1.50% × | 8.035 × 101 | −60.2% |
| 1.75% × | 1.488 × 102 | −26.4% |
| 1.85% × | 1.929 × 102 | −4.51% |
| 3.00% × | 2.057 × 102 | 1.80% |
| 5.00% × | 2.137 × 102 | 5.77% |
| 10.0% × | 2.628 × 102 | 30.1% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, R.; Cacuci, D.G. Fourth-Order Adjoint Sensitivity and Uncertainty Analysis of an OECD/NEA Reactor Physics Benchmark: I. Computed Sensitivities. J. Nucl. Eng. 2021, 2, 281-308. https://doi.org/10.3390/jne2030024
Fang R, Cacuci DG. Fourth-Order Adjoint Sensitivity and Uncertainty Analysis of an OECD/NEA Reactor Physics Benchmark: I. Computed Sensitivities. Journal of Nuclear Engineering. 2021; 2(3):281-308. https://doi.org/10.3390/jne2030024
Chicago/Turabian StyleFang, Ruixian, and Dan Gabriel Cacuci. 2021. "Fourth-Order Adjoint Sensitivity and Uncertainty Analysis of an OECD/NEA Reactor Physics Benchmark: I. Computed Sensitivities" Journal of Nuclear Engineering 2, no. 3: 281-308. https://doi.org/10.3390/jne2030024
APA StyleFang, R., & Cacuci, D. G. (2021). Fourth-Order Adjoint Sensitivity and Uncertainty Analysis of an OECD/NEA Reactor Physics Benchmark: I. Computed Sensitivities. Journal of Nuclear Engineering, 2(3), 281-308. https://doi.org/10.3390/jne2030024







