Energy-Loss Straggling and Delta-Ray Escape in Solid-State Microdosimeters Used in Ion-Beam Therapy
Abstract
:1. Introduction
2. Materials and Methods
2.1. Method: Manipulation of the Collision Distributions
2.1.1. Vavilov’s Distribution
2.1.2. Kellerer’s Modified Distribution
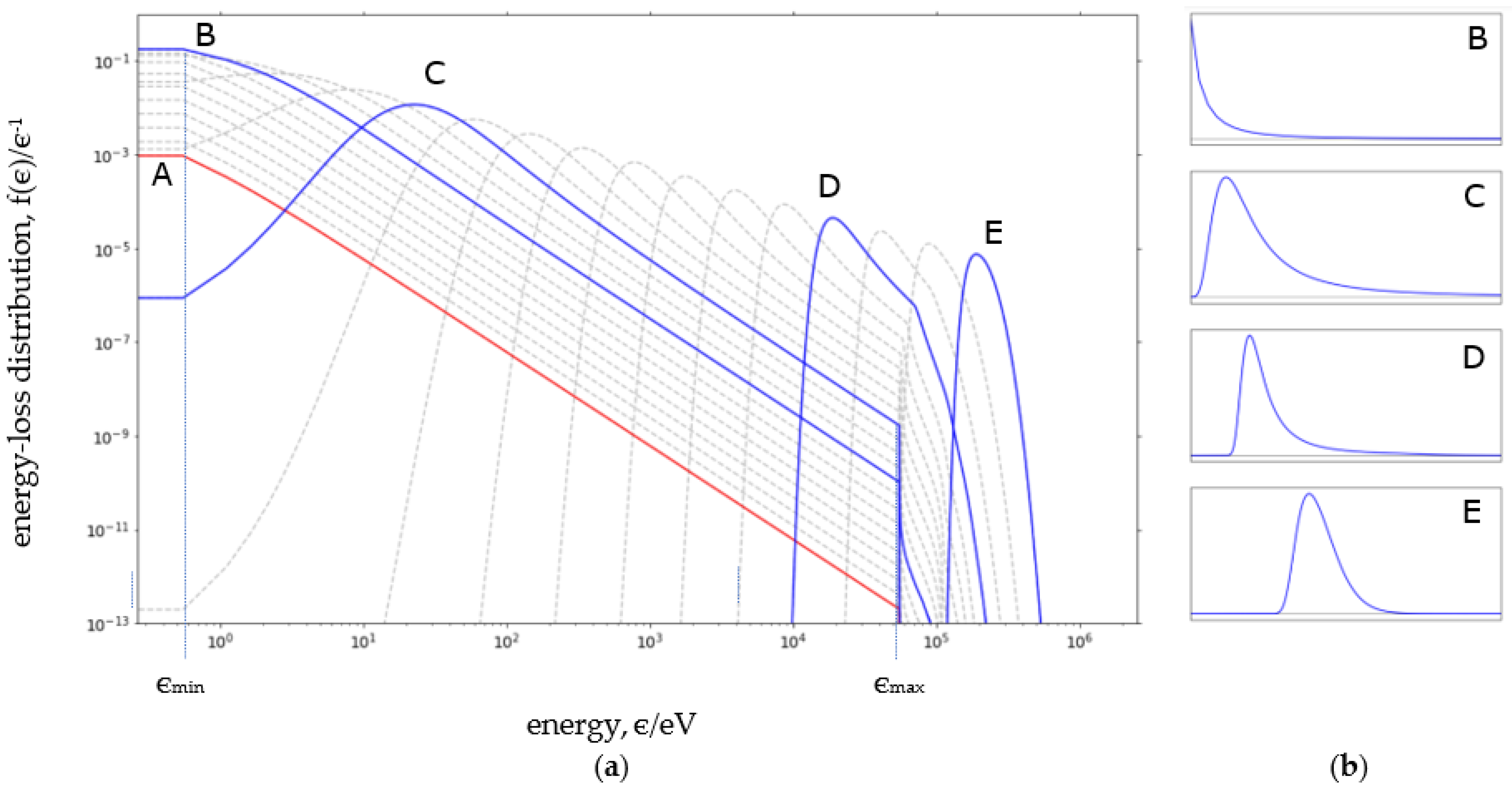
2.1.3. Energy Loss and Compound Poisson Process
Distribution of Energy Loss
- the probability of having a collision at a certain point is statistically independent of the probability of prior collisions;
- the energy lost in a single collision is negligible compared to the total energy of the ion;
- the mean energy lost in the thickness dm is the sum of the mean energy lost in each single sub-element of thickness d0.
Mean Energy of a Primary Collision
2.1.4. Kellerer’s Simplification
Generalization for Solid-State Detectors
Useful Parameters
2.1.5. From Energy Loss to Energy Imparted
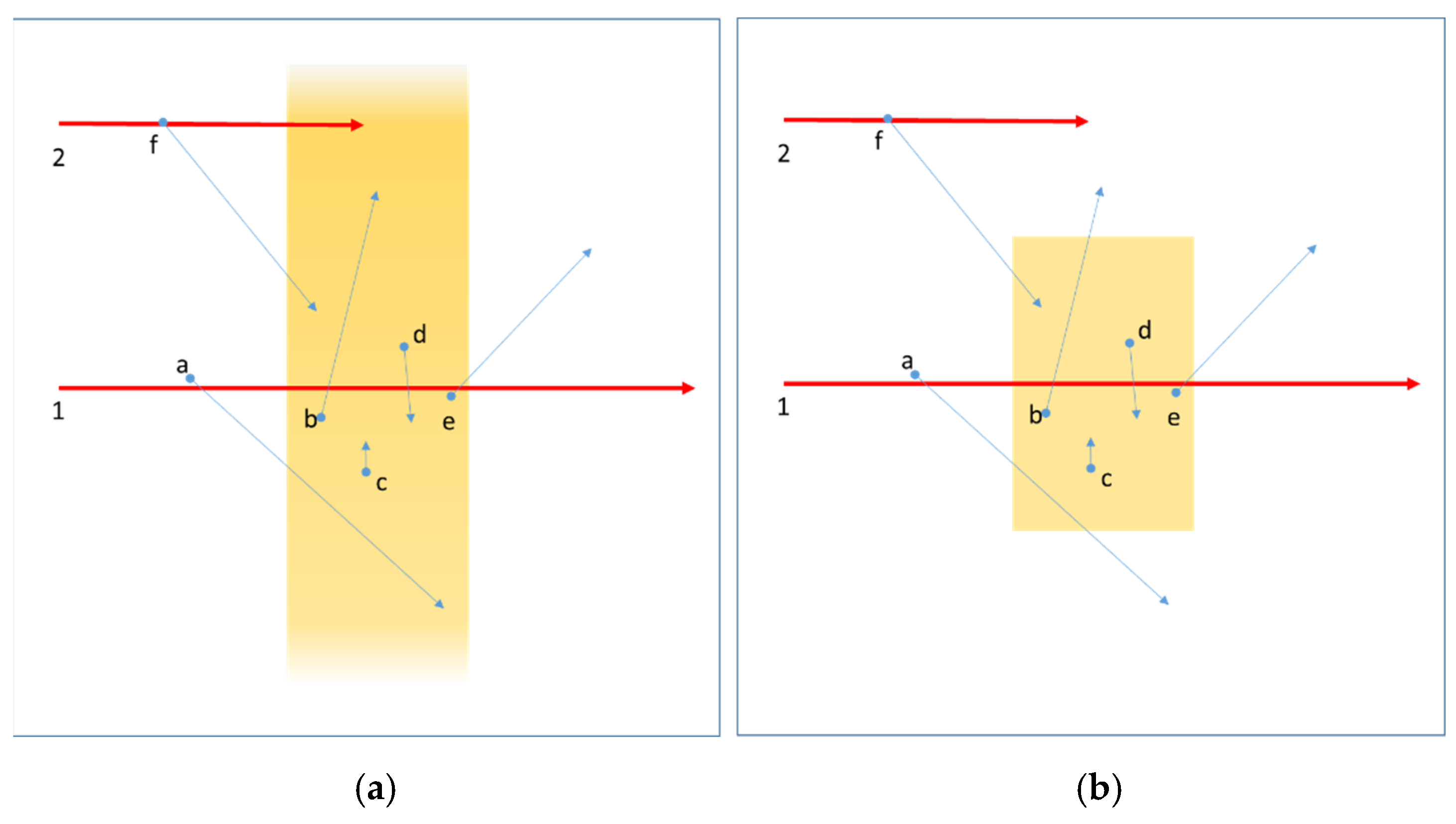
Escape-Modified Energy Distributions of Electronic Collisions
Simplification of the Escape-Modified Distributions
Further Considerations on the Energy Imparted and on the Escape of the Delta Rays
2.2. Method: Numerical Evaluations
2.2.1. Electronic Collision Distribution
- The maximum value єmax is obtained as a result of the formula for the relativistic solution in Equation (4), considering the energy of the primary ion;
- The value of єmin used in the discrete distribution is obtained using the approximate process according to Equation (14). This ensures that the calculated energy transferred per unit length matches the values provided by the selected electronic stopping power tables. The probability of collision in the interval 0 < є < єmin is given by the value P(0);
- The energy increment Δi, in the discrete representation of ωb,i, is chosen to be constant and equal to єmin;
- The value of δ1 calculated using the discrete sum:
- must be equal to the exact solution calculated with Equation (3). To ensure this, the value of ωb,i for the i-th bin is not calculated at the edge of the bin (єi or єi+1) but at a point within the interval (єi, єi+1) at a distance ∂є. Therefore, the discrete values, ωb,i, approximating the analytic function, ωb(є), are obtained as:
- The value of ∂є is chosen as the value that equals the values of δ1 calculated numerically and exactly:
- where ωb(єi + ∂є) = 1/(єi + ∂є)2 and, from Equation (1), ωb(є) = k0/є2 in the interval of energies (єmin,єmax). Therefore,
- The discrete distribution is normalized also taking into account the value ωb,0 which refers to the condition of no collision. Therefore:
2.2.2. Energy-Loss Distribution
- where the variance is given by .
2.2.3. Energy-Imparted Distribution
2.3. Material: The Ion Beam and the Microdosimeter
3. Results
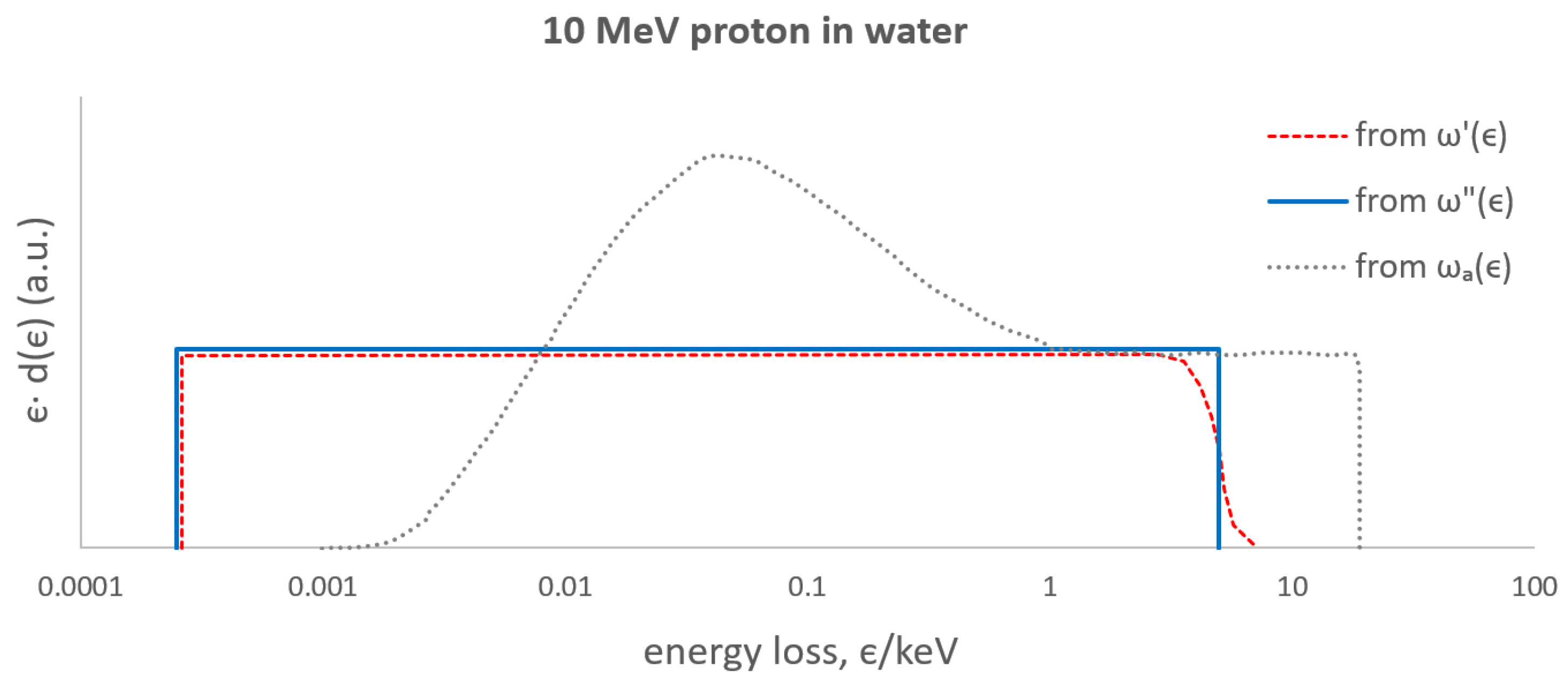
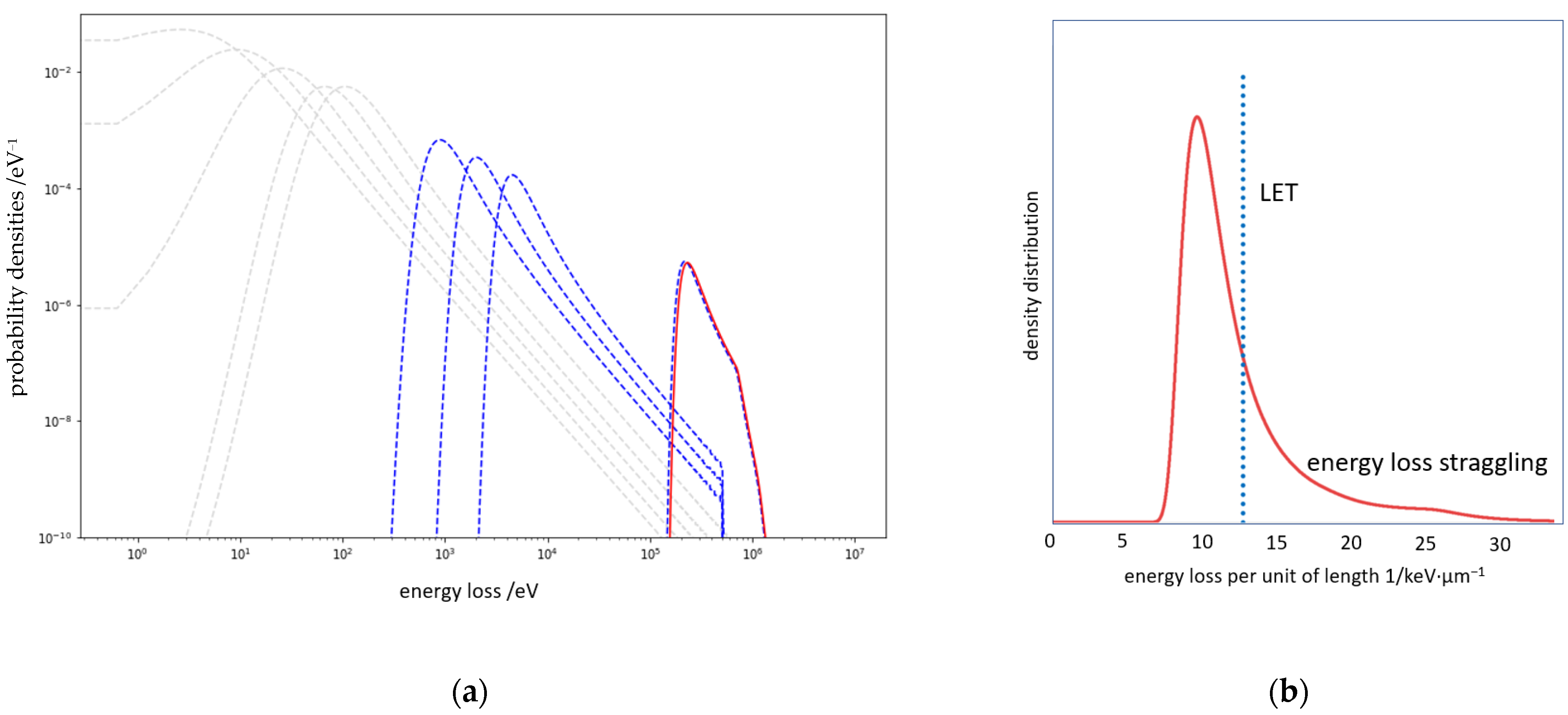
3.1. Energy-Loss Distribution
3.2. Energy-Imparted Distribution
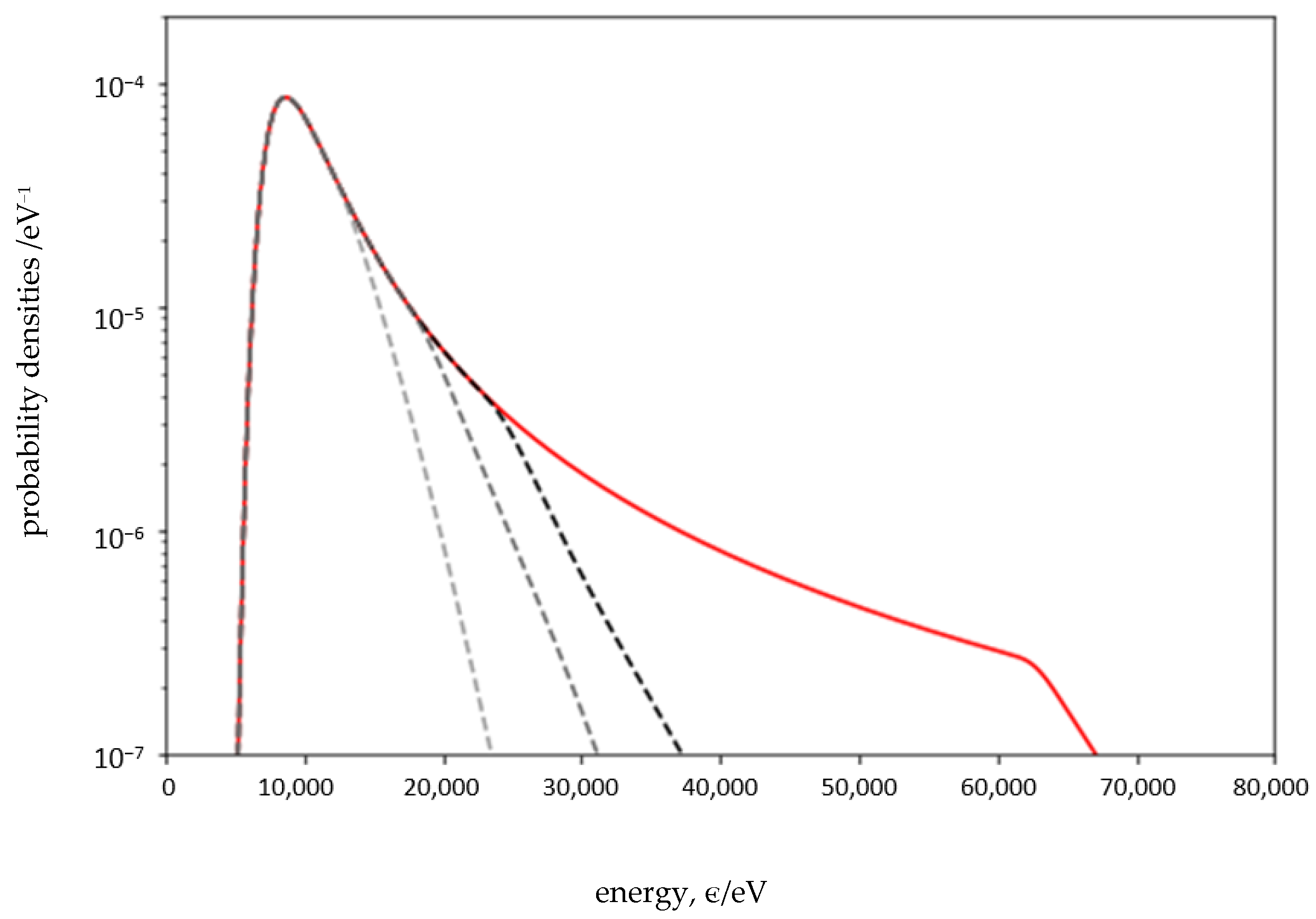
3.3. Comparison with Experimental Data
3.4. Mean Values
3.4.1. Mean Values of Energy Loss per Unit Length
3.4.2. Mean Values of Energy Imparted per Unit Length
3.4.3. Mean Values of Lineal Energy
3.4.4. Comparison of Mean Values
4. Discussion
4.1. LET Estimation
4.2. Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rossi, H.H. Specification of Radiation Quality. Radiat. Res. 1959, 10, 522–531. [Google Scholar] [CrossRef] [PubMed]
- Kellerer, A.M. Microdosimetry and the theory of straggling. In Biophysical Aspects of Radiation Quality, Second Panel Report; International Atomic Energy Agency: Vienna, Austria, 1968; pp. 89–104. ISBN 92-0-011068-1. [Google Scholar]
- Rutherford, E. The scattering of α and β particles by matter and the structure of the atom. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1911, 21, 669–688. [Google Scholar] [CrossRef]
- Landau, L. On the energy loss of fast particles by ionization. J. Phys. (USSR) 1944, 8, 201–205. [Google Scholar]
- Bohr, N. The Penetration of Atomic Particles through Matter; Matematisk-fysiske Meddelelser; Royal Danish Academy of Sciences and Letters: Copenhagen, Denmark, 1948; Volume 18, No. 8, pp. 63–73. [Google Scholar]
- Vavilov, P.V. Ionization losses of high-energy heavy particles. Soviet Phys. JETP 1957, 5, 749–751. [Google Scholar]
- Bichsel, H. Straggling and particle identification in silicon detectors. Nucl. Instrum. Meth. A 1970, 78, 277–284. [Google Scholar] [CrossRef] [Green Version]
- Bichsel, H. Energy loss and ionization of fast charged particles in a 20 μm silicon detector. Nucl. Instrum. Meth. A 1985, 235, 174. [Google Scholar] [CrossRef]
- Seltzer, M.; Berger, M.J. Energy loss straggling of protons and mesons. In Studies in Penetration of Charged Particles in Matter; Nuclear Science Series 39; National Academy of Sciences: Washington, DC, USA, 1964. [Google Scholar]
- Hancock, S.; James, F.; Movchet, J.; Rancoita, P.G.; VanRossum, L. Energy loss and energy straggling of protons and pions in the momentum range 0.7 to 115 GeV/c. Phys. Rev. A 1983, 28, 615–620. [Google Scholar] [CrossRef] [Green Version]
- Kellerer, A.M. Calculation of Energy Deposition Spectra. In Report of Panel on Biophysical Aspects of Radiation Quality; International Atomic Energy Agency: Vienna, Austria, 1968; pp. 57–74. [Google Scholar]
- Kellerer, A.M. Fundamentals of Microdosimetry. In The Dosimetry of Ionizing Radiation; Kase, K.R., Bjärngard, B.E., Attix, F.H., Eds.; Academic Press, Inc.: Cambridge, MA, USA, 1985; Volume I. [Google Scholar]
- Bohr, N., II. On the theory of the decrease of velocity of moving electrified particles on passing through matter. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1913, 25, 10–31. [Google Scholar] [CrossRef]
- Bolst, D.; Guatelli, S.; Tran, L.T.; Rosenfeld, A.B. The impact of sensitive volume thickness for silicon on insulator microdosimeters in hadron therapy. Phys. Med. Biol. 2020, 65, 035004. [Google Scholar] [CrossRef] [PubMed]
- Verona, C.; Cirrone, G.A.P.; Magrin, G.; Marinelli, M.; Palomba, S.; Petringa, G.; Verona Rinati, G. Microdosimetric measurements of a monoenergetic and modulated Bragg Peaks of 62 MeV therapeutic proton beam with a synthetic single crystal diamond microdosimeter. Med. Phys. 2020, 47, 5791–5801. [Google Scholar] [CrossRef] [PubMed]
- Berger, M.J.; Coursey, J.S.; Zucker, M.A.; Chang, J. NIST Standard Reference Database 124: Stopping-Power & Range Tables for Electrons, Protons, and Helium Ions. Available online: http://physics.nist.gov/Star (accessed on 2 March 2022).
- Booz, J.; Braby, L.; Coyne, J.; Kliauga, P.; Lindborg, L.; Menzel, H.-G.; Parmentier, N. ICRU Report 36, Microdosimetry. J. Int. Comm. Radiat. Units Meas. 1983, os19, r1983. [Google Scholar] [CrossRef]
- Kellerer, A.M. Criteria for the Equivalence of Spherical and Cylindrical Proportional Counters in Microdosimetry. Radiat. Res. 1981, 86, 277–286. [Google Scholar] [CrossRef] [Green Version]
- Tran, L.T.; Prokopovich, D.A.; Petasecca, M.; Lerch, M.L.; Kok, A.; Summanwar, A.; Hansen, T.E.; Da Via, C.; Reinhard, M.I.; Rosenfeld, A.B. 3D radiation detectors: Charge collection characterisation and applicability of technology for microdosimetry. IEEE Trans. Nucl. Sci. 2014, 61, 1537–1543. [Google Scholar] [CrossRef] [Green Version]
- Tran, L.T.; Chartier, L.; Prokopovich, D.A.; Bolst, D.; Povoli, M.; Summanwar, A.; Kok, A.; Pogossov, A.; Petasecca, M.; Guatelli, S.; et al. Thin Silicon Microdosimeter Utilizing 3-D MEMS Fabrication Technology: Charge Collection Study and Its Application in Mixed Radiation Fields. IEEE Trans. Nucl. Sci. 2018, 65, 467–472. [Google Scholar] [CrossRef] [Green Version]
- Bimbot, R.; Geissel, H.; Paul, H.; Schinner, A.; Sigmund, P.; Wambersie, A.; Deluca, P.; Seltzer, S.M. ICRU Report 73, Stopping of Ions Heavier Than Helium. J. Int. Comm. Radiat. Units Meas. 2005, 5, i-253. [Google Scholar] [CrossRef]
- Ziegler, J.F.; Ziegler, M.D.; Biersack, J.P. SRIM—The stopping and range of ions in matter. Nucl. Inst. Methods Phys. Res. B 2010, 268, 1818–1823. [Google Scholar] [CrossRef] [Green Version]
- Meouchi, C.; Barna, S.; Puchalska, M.; Tran, L.; Rosenfeld, A.; Verona, C.; Verona-Rinati, G.; Palmans, H.; Magrin, G. On the measurement uncertainty of microdosimetric quantities using diamond and silicon microdosimeters in carbon-ion beams. Med. Phys. 2022; in press. [Google Scholar]
- Conte, V.; Moro, D.; Grosswendt, B.; Colautti, P. Lineal energy calibration of mini tissue-equivalent gas-proportional counters (TEPC). In Proceedings of the AIP Conference Proceedings, Timisoara, Romania, 21–24 November 2013; Volume 1530, pp. 171–178. [Google Scholar]
- Parisi, A.; Boogers, E.; Struelens, L.; Vanhavere, F. Uncertainty budget assessment for the calibration of a silicon microdosimeter using the proton edge technique. Nucl. Inst. Methods Phys. Res. A 2020, 978, 164449. [Google Scholar] [CrossRef]
- Bianchi, A.; Mazzucconi, D.; Selva, A.; Colautti, P.; Parisi, A.; Vanhavere, F.; Reniers, B.; Conte, V. Lineal energy calibration of a mini-TEPC via the proton-edge technique. Radiat. Meas. 2021, 141, 106526. [Google Scholar] [CrossRef]
- Goodhead, D.T. Relationship of Microdosimetric Techniques to Applications in Biological Systems. In The Dosimetry of Ionizing Radiation; Kase, K.R., Bjärngard, B.E., Attix, F.H., Eds.; Academic Press: Cambridge, MA, USA, 1987; pp. 1–89. ISBN 9780124004023. [Google Scholar] [CrossRef]
- Kliauga, P.; Waker, A.J.; Barthe, J. Design of tissue equivalent proportional counters. Radiat. Prot. Dosim. 1995, 61, 309–322. [Google Scholar] [CrossRef]






| Parameter | Unit | Carbon Ions | |
|---|---|---|---|
| 279.8/MeV·u−1 | 207.8/MeV·u−1 | ||
| κ, (relativistic estimation) | 2.23 × 10−2 | 3.82 × 10−2 | |
| ξ¸ approximation of the mean total energy lost, through electronic collisions, in the detector | keV | 15.69 | 19.34 |
| єmax, maximum delta-ray energy (relativistic estimation) | eV | 7.04 × 105 | 5.06 × 105 |
| єmin, minimum delta-ray energy | eV | 6.41 × 10−1 | 6.34 × 10−1 |
| δ1, mean collision energy of the ion and electron in the medium | eV | 8.91 | 8.62 |
| dµ/dx, mean number of primary collisions per unit of length | nm−1 | 2.81 | 3.461 |
| µ, mean number of primary collisions in the SV | 2.81 × 104 | 3.46 × 104 | |
| d1, mean distance between primary collisions | nm | 3.56 × 10−1 | 2.89 × 10−1 |
| Sel/r, mass electronic stopping power from ICRU lookup tables [21] | keV·µm−1 | 10.79 | 12.86 |
| Sel/r, mass electronic stopping power from SRIM lookup tables [22] | keV·µm−1 | 10.43 | 12.45 |
(keV·μm−1) | (keV·μm−1) | (keV·μm−1) | (keV·μm−1) | |||
|---|---|---|---|---|---|---|
| LET 1 | 12.85 | 12.85 | ||||
| ya, 2 | 4.93 | 8.82 | 2.61 | 1.46 | ||
| yimp, 3 | 10.31 | 10.46 | 1.25 | 1.23 | ||
| yloss, | 12.83 | 14.49 | 1 | 0.89 |
| ȳF (keV·µm−1) | ȳD (keV·µm−1) | (keV·μm−1) | (keV·μm−1) | |||
|---|---|---|---|---|---|---|
| LET 1 | 10.79 | 10.79 | ||||
| yc, 2 | 4.55 | 7.46 | 2.37 | 1.44 | ||
| yimp, 3 | 8.45 | 8.60 | 1.28 | 1.25 | ||
| yloss, | 10.78 | 13.05 | 1 | 0.83 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magrin, G.; Barna, S.; Meouchi, C.; Rosenfeld, A.; Palmans, H. Energy-Loss Straggling and Delta-Ray Escape in Solid-State Microdosimeters Used in Ion-Beam Therapy. J. Nucl. Eng. 2022, 3, 128-151. https://doi.org/10.3390/jne3020008
Magrin G, Barna S, Meouchi C, Rosenfeld A, Palmans H. Energy-Loss Straggling and Delta-Ray Escape in Solid-State Microdosimeters Used in Ion-Beam Therapy. Journal of Nuclear Engineering. 2022; 3(2):128-151. https://doi.org/10.3390/jne3020008
Chicago/Turabian StyleMagrin, Giulio, Sandra Barna, Cynthia Meouchi, Anatoly Rosenfeld, and Hugo Palmans. 2022. "Energy-Loss Straggling and Delta-Ray Escape in Solid-State Microdosimeters Used in Ion-Beam Therapy" Journal of Nuclear Engineering 3, no. 2: 128-151. https://doi.org/10.3390/jne3020008
APA StyleMagrin, G., Barna, S., Meouchi, C., Rosenfeld, A., & Palmans, H. (2022). Energy-Loss Straggling and Delta-Ray Escape in Solid-State Microdosimeters Used in Ion-Beam Therapy. Journal of Nuclear Engineering, 3(2), 128-151. https://doi.org/10.3390/jne3020008






