Tritium Desorption Behavior and Microstructure Evolution of Beryllium Irradiated at Low Temperature Up to High Neutron Dose in BR2 Reactor
Abstract
:1. Introduction
2. Materials and Methods
3. Results
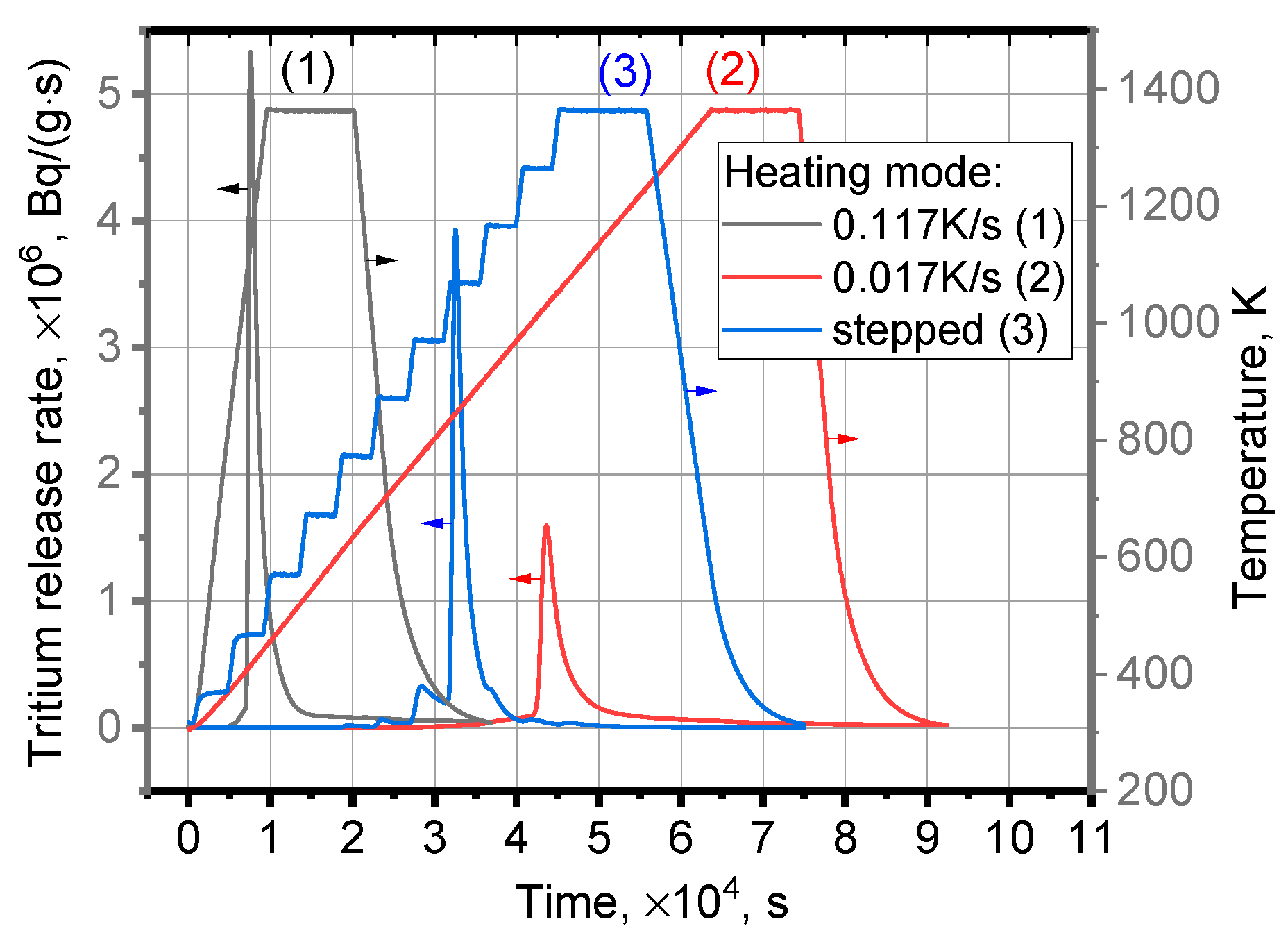
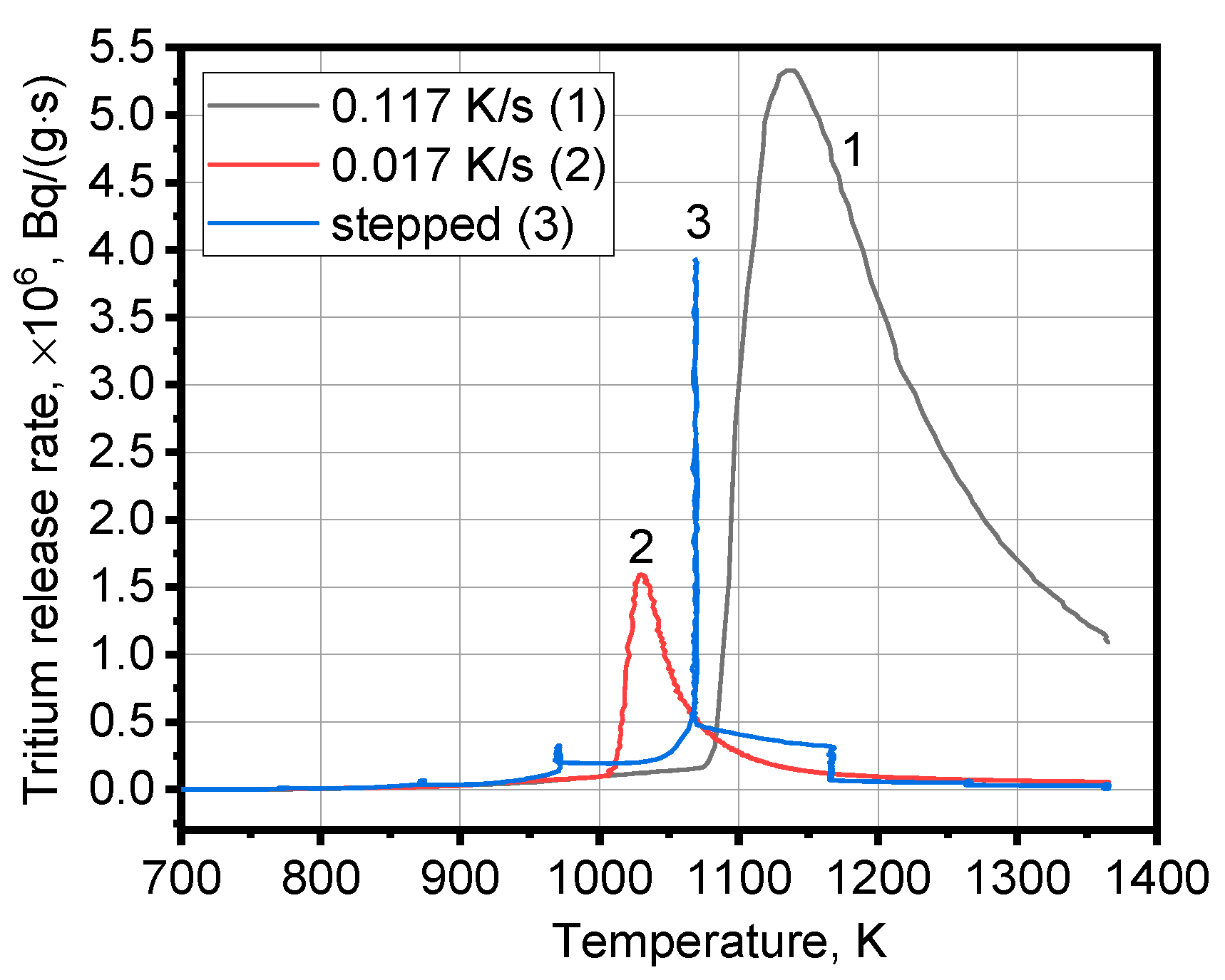
3.1. Tritium Release
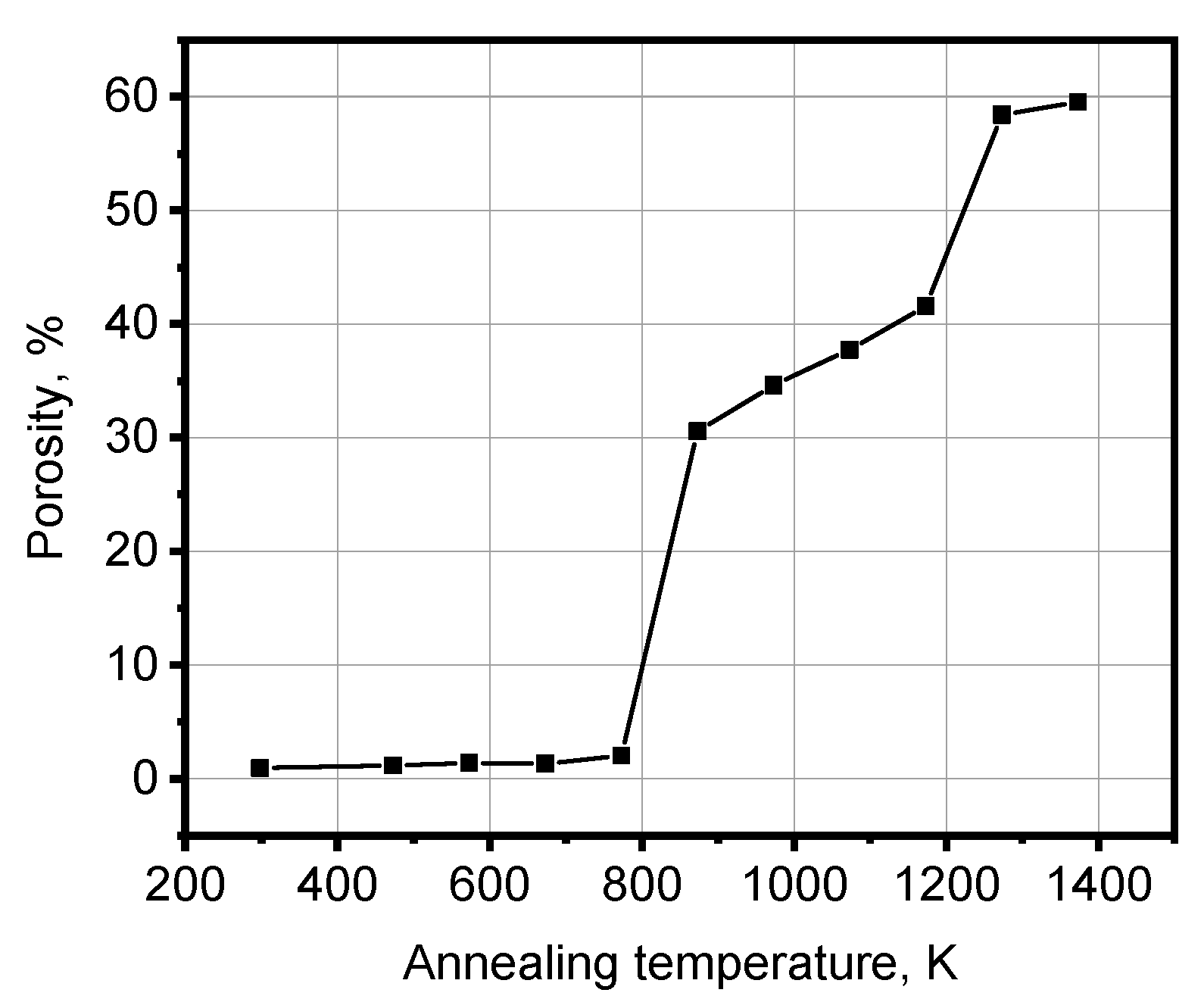
3.2. Optical Metallography
4. Discussion
4.1. Tritium Desorption Energy
4.2. Tritium Diffusion Coefficient
4.3. Evolution of Beryllium Microstructure after Low-Temperature Irradiation and Following High-Temperature Annealing
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sannen, L.; De Raedt, C.; Moons, F.; Yao, Y. Helium content and induced swelling of neutron irradiated beryllium. Fus. Eng. Des. 1994, 29, 470–474. [Google Scholar] [CrossRef]
- Leenaers, A.; Verpoucke, G.; Pellettieri, A.; Sannen, L.; Van den Berghe, S. Microstructure of long-term annealed highly irradiated beryllium. J. Nucl. Mater. 2008, 372, 256–262. [Google Scholar] [CrossRef]
- Van Renterghem, W.; Leenaers, A.; Van den Berghe, S. TEM investigation of long-term annealed highly irradiated beryllium. J. Nucl. Mater. 2008, 374, 54–60. [Google Scholar] [CrossRef]
- Scibetta, M.; Pellettieri, A.; Sannen, L. Experimental determination of creep properties of beryllium irradiated to relevant fusion power reactor doses. J. Nucl. Mater. 2007, 367–370, 1063–1068. [Google Scholar] [CrossRef]
- Melder, R.R.; Chakin, V.P.; Pokrovsky, A.S.; Shchuchkin, A.N. The SSC RIAR high-flux research reactors: Experience and possibilities of testing materials and mock-ups for fusion. Fus. Eng. Des. 2003, 69, 409–417. [Google Scholar] [CrossRef]
- Chakin, V.P. Radiation damage of beryllium blocks of the SM reactor. Phys. Metal Metallograph. 1999, 88, 200–204. [Google Scholar]
- Chakin, V.P.; Kupryanov, I.B.; Melder, R.R. State of beryllium after irradiation at low temperature up to extremely high neutron doses. J. Nucl. Mater. 2004, 329–333, 1347–1352. [Google Scholar] [CrossRef]
- Chakin, V.; Rolli, R.; Schneider, H.-C.; Moeslang, A.; Kurinskiy, P.; Van Renterghem, W. Pores and cracks in highly neutron irradiated beryllium. J. Nucl. Mater. 2011, 416, 3–8. [Google Scholar] [CrossRef]
- Federici, G.; Barabash, V.; Doerner, R.; Lorenzetto, P.; Matthews, G.; Raffray, A.R. Beryllium as a Plasma Facing Material for Near-Term Fusion Devices, Reference Module in Mater. Sc. Mater. Eng. 2016, refers Federici, G.; Doerner, R.; Lorenzetto, P.; Barabash, V. Beryllium as a Plasma-Facing Material for Near-Term Fusion Devices. Compreh. Nucl. Mater. 2012, 4, 621–666. [Google Scholar]
- Zmitko, M.; Vladimirov, P.; Knitter, R.; Kolb, M.; Leys, O.; Heuser, J.; Schneider, H.-C.; Rolli, R.; Chakin, V.; Pupeschi, S.; et al. Development and qualification of functional materials for the European HCPB TBM. Fus. Eng. Des. 2018, 136, 1376–1385. [Google Scholar] [CrossRef]
- Federici, G.; Boccaccini, L.; Cismondi, F.; Gasparotto, M.; Poitevin, Y.; Ricapito, I. An overview of the EU breeding blanket design strategy as an integral part of the DEMO design effort. Fus. Eng. Des. 2019, 141, 30–42. [Google Scholar] [CrossRef]
- Vladimirov, P.V.; Chakin, V.P.; Dürrschnabel, M.; Gaisin, R.; Goraieb, A.; Hernandez Gonzalez, F.A.; Klimenkov, M.; Rieth, M.; Rolli, R.; Zimber, N.; et al. Development and characterization of advanced neutron multiplier materials. J. Nucl. Mater. 2021, 543, 152593. [Google Scholar] [CrossRef]
- Gaisin, R.; Chakin, V.; Vladimirov, P.; Hernandez Gonzalez, F.A.; Udartsev, S.; Vechkutov, A.; Kolmakov, M. Industrial-scale Manufacturing Experience of Titanium Beryllide Block for DEMO Blanket Application. Fus. Eng. Des. 2020, 161, 111862. [Google Scholar] [CrossRef]
- Scaffidi-Argentina, F. Tritium and helium release from neutron irradiated beryllium pebbles from the EXOTIC-8 irradiation. Fus. Eng. Des. 2001, 58–59, 641–645. [Google Scholar] [CrossRef]
- Rabaglino, E.; Hiernaut, J.P.; Ronchi, C.; Scaffidi-Argentina, F. Helium and tritium kinetics in irradiated beryllium pebbles. J. Nucl. Mater. 2002, 307, 1424–1429. [Google Scholar] [CrossRef]
- Chakin, V.; Rolli, R.; Moeslang, A.; Klimenkov, M.; Kolb, M.; Vladimirov, P.; Kurinskiy, P.; Schneider, H.-C.; van Til, S.; Magielsen, A.J.; et al. Tritium release and retention properties of highly neutron-irradiated beryllium pebbles from HIDOBE-01 experiment. J. Nucl. Mater. 2013, 442, S483–S489. [Google Scholar] [CrossRef]
- Van Til, S.; Fedorov, A.V.; Stijkel, M.P.; Cobussen, H.L.; Mutnuru, R.K.; vd Idsert, P.; Zmitko, M. Tritium release from beryllium pebbles after high temperature irradiation up to 3000 appm He in the HIDOBE-01 experiment. J. Nucl. Mater. 2013, 442, S478–S482. [Google Scholar] [CrossRef]
- Chakin, V.; Rolli, R.; Klimenkov, M.; Zmitko, M. Tritium release and retention in beryllium pebbles irradiated up to 640 appm tritium and 6000 appm helium. J. Nucl. Mater. 2020, 542, 152521. [Google Scholar] [CrossRef]
- Chakin, V.; Rolli, R.; Gaisin, R.; Hoeppener-Kramar, U.; Nakamichi, M.; Zmitko, M. Tritium release and retention in beryllium and titanium beryllide after neutron irradiation up to damage doses of 23–38 dpa. Fus. Eng. Des. 2020, 161, 111938. [Google Scholar] [CrossRef]
- Chakin, V.; Rolli, R.; Vladimirov, P.; Moeslang, A. Tritium release from highly neutron irradiated constrained and unconstrained beryllium pebbles. Fus. Eng. Des. 2015, 95, 59–66. [Google Scholar] [CrossRef]
- Rabaglino, E.; Ronchi, C.; Cardella, A. Recent progress in the modelling of helium and tritium behaviour in irradiated beryllium pebbles. Fus. Eng. Des. 2003, 69, 455–461. [Google Scholar] [CrossRef]
- Redhead, P.A. Thermal desorption of gases. Vacuum 1962, 12, 203–211. [Google Scholar] [CrossRef]
- De Jong, A.M.; Niemantsverdriet, J.W. Thermal desorption analysis: Comparative test of ten commonly applied procedures. Surface Sci. 1990, 233, 355–365. [Google Scholar] [CrossRef]
- Falconer, J.L.; Madix, R.J. Flash desorption activation energies: DCOOH decomposition and CO desorption from Ni (100). Surf. Sci. 1975, 48, 393–405. [Google Scholar] [CrossRef]
- Booth, A.H. Calculation of electron trap depths from thermoluminescence maxima. Can. J. Chem. 1954, 32, 214. [Google Scholar] [CrossRef]
- Chan, C.-M.; Aris, R.; Weinberg, W.H. An analysis of thermal desorption mass spectra. I. Appl. Surf. Sci. 1978, 1, 360–376. [Google Scholar] [CrossRef]
- Vitins, A.; Kizane, G.; Matiss, A.; Pajuste, E.; Zubkovs, V. Tritium release behavior of beryllium pebbles after neutron irradiation between 523 and 823 K. J. Nucl. Mater. 2013, 442, S490–S493. [Google Scholar] [CrossRef]
- Macaulay-Newcombe, R.G.; Thompson, D.A.; Smeltzer, W.W. Thermal absorption and desorption of deuterium in beryllium and beryllium oxide. J. Nucl. Mater. 1992, 191–194 Pt A, 263–267. [Google Scholar] [CrossRef]
- Macaulay-Newcombe, R.G.; Thompson, D.A.; Smeltzer, W.W. Deuterium diffusion, trapping and release in ion-implanted beryllium. Fus. Eng. Des. 1991, 18, 419–424. [Google Scholar] [CrossRef]
- Tazhibaeva, I.L.; Shestakov, V.P.; Chikhray, E.V. Deuterium permeation through beryllium with surface element composition control. In Proceedings of the 18th Symposium on Fusion Technology, Karlsruhe, Germany, 22–26 August 1994; Newnes: Oxford, UK, 1994; pp. 427–431. [Google Scholar]
- Jones, P.M.S.; Gibson, R. Hydrogen in beryllium. J. Nucl. Mater. 1967, 21, 353–354. [Google Scholar] [CrossRef]
- Chakin, V.P.; Ostrovsky, Z.Y. Evolution of beryllium microstructure under high-dose neutron irradiation. J. Nucl. Mater. 2002, 307–311, 657–663. [Google Scholar] [CrossRef]
- Chakin, V.; Fedorov, A.; Gaisin, R.; Zmitko, M. Swelling of Highly Neutron Irradiated Beryllium and Titanium Beryllide. J. Nucl. Eng. 2022, 3, 398–408. [Google Scholar] [CrossRef]
- Klimenkov, M.; Chakin, V.; Moeslang, A.; Rolli, R. TEM study of beryllium pebbles after neutron irradiation up to 3000 appm helium production. J. Nucl. Mater. 2013, 443, 409–416. [Google Scholar] [CrossRef]




| Mode and Heating Rate, K/s | Weight, g | Approximate Diameter d, mm |
|---|---|---|
| Permanent at rate 0.117 | 0.0259 | 2.9915 |
| Permanent at rate 0.017 | 0.03115 | 3.1932 |
| Stepped at average rate 0.03 | 0.0347 | 3.2979 |
| Heating Mode | Peak Temperature Tm, K | Start of Tritium Release, K | Height of Peak, ×106, Bq/(g·s) | Peak Width at Half Height W1/2, K |
|---|---|---|---|---|
| Permanent at rate 0.117 K/s | 1136 | 800–870 | 5.34 | 141 |
| Permanent at rate 0.017 K/s | 1031 | 800–870 | 1.58 | 36 |
| Stepped at average rate 0.03 K/s | 1069 | 800–870 | 3.93 | 4 |
| Heating Rate Combination | Peak Temperatures Tm, K | tgα, 104 | Edes, eV | Edes/aver, eV |
|---|---|---|---|---|
| β1, β2 | 1136, 1031 | 1.9353 | 1.7 | 1.6 |
| β1, β3 | 1136, 1069 | 2.2465 | 1.9 | |
| β2, β3 | 1031, 1069 | 1.4374 | 1.2 |
| Heating Rate Combination | Peak Temperatures Tm, K | Edes, eV | Edes/aver, eV |
|---|---|---|---|
| β1, β2 | 1136, 1031 | 1.7 | 1.6 |
| β1, β3 | 1136, 1069 | 1.9 | |
| β2, β3 | 1031, 1069 | 1.2 |
| Heating Rate, K/s | Peak Temperature Tm, K | Y1/2 | Edes, eV | Edes/aver, eV |
|---|---|---|---|---|
| β1 | 1136 | 8.06 | 0.6 | 1.7 |
| β2 | 1031 | 28.64 | 1.1 | |
| β3 | 1069 | 267.25 | 3.5 |
| Heating Rate, K/s | Relative Heating Rate, 10−5, s−1 | Peak Temperature Tm, K | ν, 104, s−1 |
|---|---|---|---|
| 0.117 | 10.833 | 1136 | 2.02 |
| 0.017 | 1.5741 | 1031 | 1.92 |
| T, K | Mode | D, m2/s |
|---|---|---|
| 873 | stepped | 1.2318 × 10−12 |
| 973 | stepped | 7.4859 × 10−12 |
| 1073 | stepped | 1.788 × 10−10 |
| 1173 | stepped | 7.3514 × 10−11 |
| 1373 | permanent at 0.017 K/s | 1.6781 × 10−11 |
| 1373 | permanent at 0.117 K/s | 1.7275 × 10−11 |
| Mode | T, K | t, h | L, mm | R, mm |
|---|---|---|---|---|
| Heating to T with following exposure for t | 1273 | 100 | 1.45 | ~1.5 |
| 1373 | 3 | 0.29 | ||
| 1373 | 20 | 0.76 | ||
| 1373 | 100 | 1.7 | ||
| 1473 | 5 | 0.43 | ||
| 1473 | 50 | 1.37 | ||
| 1473 | 70 | 1.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chakin, V.; Rolli, R.; Gaisin, R.; van Renterghem, W. Tritium Desorption Behavior and Microstructure Evolution of Beryllium Irradiated at Low Temperature Up to High Neutron Dose in BR2 Reactor. J. Nucl. Eng. 2023, 4, 552-564. https://doi.org/10.3390/jne4030036
Chakin V, Rolli R, Gaisin R, van Renterghem W. Tritium Desorption Behavior and Microstructure Evolution of Beryllium Irradiated at Low Temperature Up to High Neutron Dose in BR2 Reactor. Journal of Nuclear Engineering. 2023; 4(3):552-564. https://doi.org/10.3390/jne4030036
Chicago/Turabian StyleChakin, Vladimir, Rolf Rolli, Ramil Gaisin, and Wouter van Renterghem. 2023. "Tritium Desorption Behavior and Microstructure Evolution of Beryllium Irradiated at Low Temperature Up to High Neutron Dose in BR2 Reactor" Journal of Nuclear Engineering 4, no. 3: 552-564. https://doi.org/10.3390/jne4030036
APA StyleChakin, V., Rolli, R., Gaisin, R., & van Renterghem, W. (2023). Tritium Desorption Behavior and Microstructure Evolution of Beryllium Irradiated at Low Temperature Up to High Neutron Dose in BR2 Reactor. Journal of Nuclear Engineering, 4(3), 552-564. https://doi.org/10.3390/jne4030036





