Neutron Yield Predictions with Artificial Neural Networks: A Predictive Modeling Approach

Abstract

The development of compact neutron sources for applications is extensive and features many approaches. For ion-based approaches, several projects with different parameters exist. This article focuses on ion-based neutron production below the spallation barrier for proton and deuteron beams with arbitrary energy distributions with kinetic energies from 3 $\mathrm{M}$$\mathrm{e}\mathrm{V}$ to 97 $\mathrm{M}$$\mathrm{e}\mathrm{V}$. This model makes it possible to compare different ion-based neutron source concepts against each other quickly. This contribution derives a predictive model using Monte Carlo simulations (an order of 50,000 simulations) and deep neural networks. It is the first time a model of this kind has been developed. With this model, lengthy Monte Carlo simulations, which individually take a long time to complete, can be circumvented. A prediction of neutron spectra then takes some milliseconds, which enables fast optimization and comparison. The models’ shortcomings for low-energy neutrons (<$0.1 \mathrm{M}\mathrm{e}\mathrm{V}$) and the cut-off prediction uncertainty ($\pm 3 \mathrm{M}\mathrm{e}\mathrm{V}$) are addressed, and mitigation strategies are proposed.

1. Introduction

Research with neutrons is increasingly limited to a few large-scale facilities due to the successive shutdown of European research reactors (as well as the not-far-off completion of the European Spallation Source ESS, the world’s brightest neutron source). The loss of reactors leads to a decrease in available beam time, as can be seen in Figure 1. Smaller facilities and institutes are developing compact neutron sources to continue their research with neutrons [1,2,3,4].

The loss of reactors causes a decline in the available beam time, as displayed in Figure 1. Compact neutron sources have the potential to establish themselves as a backup to large-scale neutron research facilities, as they can be commissioned more quickly and at smaller institutes. Utilizing these sources can increase the available beamtime and give more flexibility to neutron researchers.

Accelerator-based neutron sources, which we discuss here, are scalable. The miniaturization of accelerators generally means that only lower energies can be achieved compared to larger machines, reducing the neutron yield. This makes a trade-off necessary for conventional accelerators since the accelerator cannot become genuinely compact if high energies should be achieved, which increases the final neutron yield. Nuclear waste is less of an issue for particles with energies below the spallation threshold, leaving compactness as the remaining issue [5] (p. 1008 f). This reinforces the goal of keeping the energy below this threshold and aiming for more compact sources. An additional aspect of the design of a compact neutron source is the neutron energy. Higher neutron energies allow us to penetrate thicker materials and increase the number of applications for this source type, for example, in homeland security applications [6].

1.1. Physical Constraints

Most approaches to compact neutron sources are based on the acceleration of light ions (protons or deuterons) impinging on a low-mass target (e.g., lithium, beryllium [1], tantalum [2]) and have particle energies below the spallation threshold (<100 MeV/u) [5] (p. 1008 f). The projects mentioned in this article are based on projectile energies lower than that threshold [1,2,3,7,8].

A method that ensures comparability among these different projects and which is quick to evaluate is essential for developing, comparing, and improving compact neutron sources. Models and results created by the individual institutions for their systems are not necessarily comparable since different nuclear cross-section libraries and measurement methods are used. We developed a model based on simulations and deep learning to ensure this.

This model further allows the evaluation of compact neutron source concepts with non-mono energetic beams, for example, laser-driven ion acceleration via the Target Normal Sheath Acceleration mechanism (TNSA) [7]. TNSA ejects an exponential energy spectrum, which starkly contrasts the mono-energetic particles created by conventional accelerators.

1.2. Outline

The model presented in this work can be used to quickly evaluate neutron source characteristics such as neutron yield, neutron energy, and angular distribution over a wide range of ion energies for proton and deuteron projectiles for several converter materials. This model was originally devised as part of the thesis by B. Schmitz [9] and is here presented in more detail and with additional validations.

Data-driven modeling needs a large dataset of consistent experimental data distributed over the parameter range of interest. Due to insufficient data in the relevant energy range, Monte Carlo simulations were used as the basis for modeling. The simulation results are used to devise a surrogate model based on artificial neural networks to predict the double differential neutron yield with a fast inference of some microseconds. Bootstrap training was performed on the model to predict the uncertainty (refer to Section 2.4). Our model is then compared to experimentally measured neutron spectra and to the model of Wakabayashi et al. [10] to test its validity.

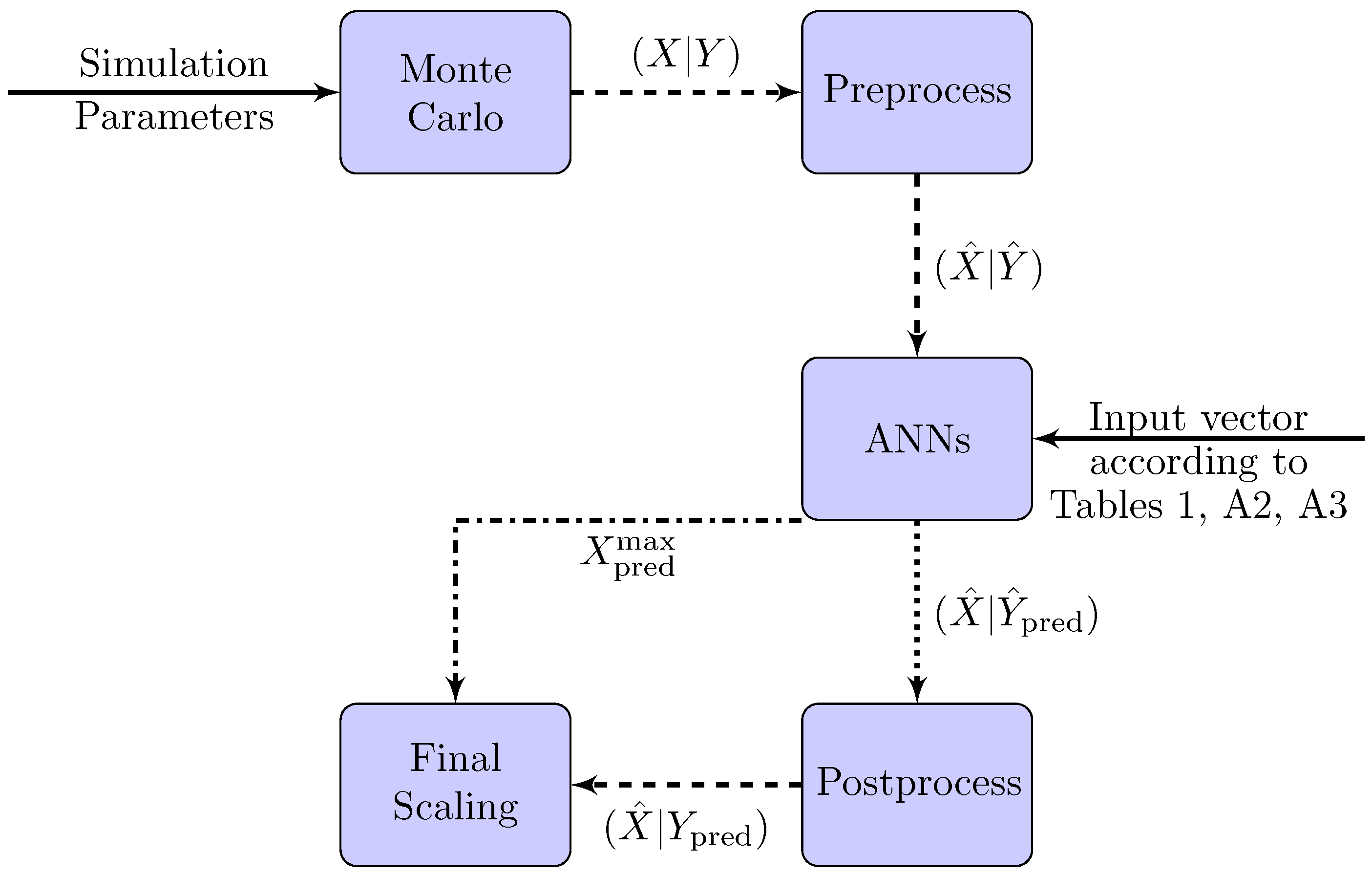
2. Methods

An overview of the steps to be taken is given in Figure 2. The details of the major steps are listed in the remainder of the section.

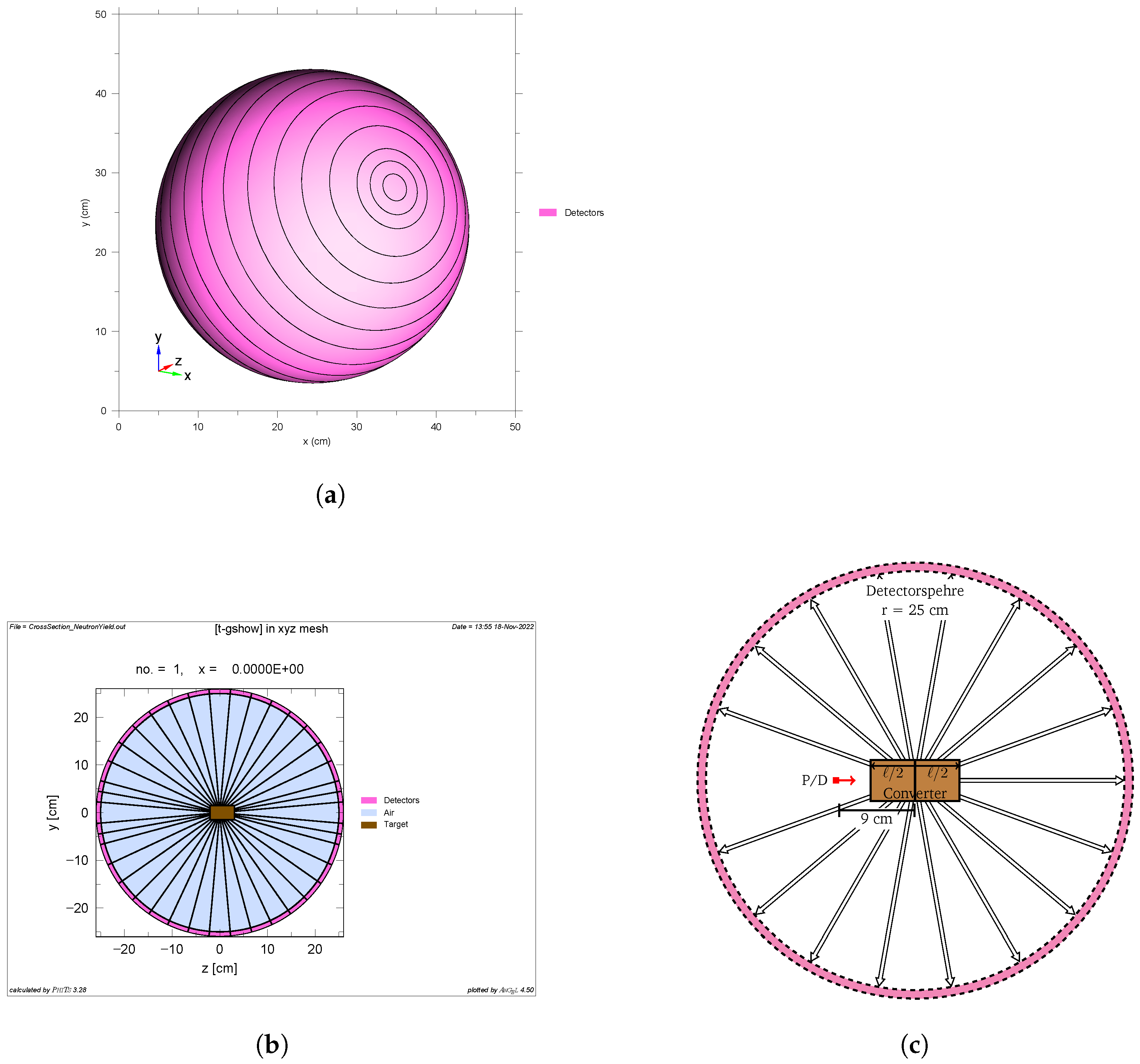
2.1. Monte Carlo Simulations

We simulated the neutron yield with Monte Carlo Simulations utilizing the PHITS [11] code in Version 3.28A with the FENDL [12] library in Version 3. The observable is the neutron count, which is determined by measuring the number of neutrons crossing a detector’s surface. We implemented several detectors as rings around the converter to resolve the angular distribution. This is illustrated in Figure 3.

We give the concrete parameters for the angle elements (center of the detector) $\Theta$ and its size $\Delta \Theta$ in Appendix A in

Table A1. Data for detectors implemented in the Monte Carlo model. Every second value is greyed to guide the eye.

	${\Theta }_{\mathbf{min}}$	${\Theta }_{\mathbf{max}}$	${\Theta }_{\mathbf{mean}}$	$\sigma \Theta$	Area	Ratio
	°	°	°	°	cm2	%
D01	−5	5	0.0	5.0	14.94	0.19
D02	5	10	7.5	2.5	44.72	0.57
D03	10	15	12.5	2.5	74.15	0.94
D04	15	25	20.0	5.0	234.12	2.98
D05	25	35	30.0	5.0	342.26	4.36
D06	35	45	40.0	5.0	440.00	5.60
D07	45	55	50.0	5.0	524.37	6.68
D08	55	65	60.0	5.0	592.81	7.55
D09	65	75	70.0	5.0	643.24	8.19
D10	75	85	80.0	5.0	674.12	8.58
D11	85	95	90.0	5.0	684.52	8.72
D12	95	105	100.0	5.0	674.12	8.58
D13	105	115	110.0	5.0	643.24	8.19
D14	115	125	120.0	5.0	592.81	7.55
D15	125	135	130.0	5.0	524.37	6.68
D16	135	145	140.0	5.0	440.00	5.60
D17	145	155	150.0	5.0	342.26	4.36
D18	155	165	160.0	5.0	234.12	2.98
D19	165	170	167.5	2.5	74.15	0.94
D20	170	175	172.5	2.5	44.72	0.57
D21	175	185	180.0	5.0	14.94	0.19

.

The ion beam is modeled as a cylindrical beam, starting at position $(0,0,-9)$. Its direction is aligned with $(0,0,1)$ and the radius is defined as $r_0=0.5 \mathrm{c}\mathrm{m}$. Energy and particle type of the incoming particles are subject to variation as indicated by

Table 1. Parameters of interest and their range. All parameters needed to set up the Monte Carlo simulations are listed here. Square brackets indicate each continuous interval, while categorical values are comma-separated. Steps indicate the number of possibilities (linearly divided) a parameter can take.

Quantity	Values	Steps
Projectile	Deuterons, Protons	2
Source Radius/cm	0.5	fix
$E_{\mathrm{kin}}$/MeV	$\left[3,97\right]$	56
Element	Li, LiF, Be, Va, Ta	5
Length/cm	$\left[0.002,10.445\right]$	356
Angle/°	$\left[0,180\right]$	21
Converter Radius/cm	2.4	fix

. The converter is given as a cylinder along the z-axis centered around $(0,0,0)$ with a radius $r=2.4 \mathrm{c}\mathrm{m}$. The length of the converter is variable and subject to change in this study. Its range is listed in Table 1.

We ensured the target was long enough to stop the full ion bunch inside the target for each energy.

Low-energy neutron absorption and moderation is an effect that has to be taken into account as well. We dealt with this by allowing converters to become longer than the ion stopping range. This is important for non-mono energetic ion beams such as TNSA. TNSA has an exponential energy distribution: if the high-energy part of the spectrum is fully stopped in a converter, then the low-energy part of the spectrum is stopped earlier, leaving more range for the created neutron to interact with the material. These neutrons have a lower final energy due to the moderation inside the remaining converter. If this is not incorporated, the model would overestimate the neutron yield at higher energies. For the parameters of interest, and throughout this study, we acquired 54,768 simulations. Each is generating energy-resolved neutron spectra for 21 distinct scattering angles.

2.2. Data Preparation

Data pre-processing is necessary to ensure the convergence of our model during training. We organized the data as follows: We labeled the categorical data features according to a binary representation of the values, commonly referred to as one-hot encoding. At the same time, we scaled the continuous data from 0 to 1 to its maximum value.

For the categorical data then follows: Each simulation using Deuterium gets assigned a 1, and each simulation using Hydrogen gets assigned a 0. Five different categorical values can only be represented in binary format if three bits are used. Then we can label the different converter materials as: ‘Li’–‘000’, ‘LiF’–‘001’, ‘Be’–‘010’, ‘Va’–‘011’, ‘Ta’–‘100’.

For the continuous parameters of the input features, namely Source Radius, $E_{\mathrm{kin}}$, Length, and Angle, we applied the mentioned normalization to the range of 0 to 1 by dividing each value by the defined maximum value of the parameter, as given in Table 1.

The observable is also a continuously distributed quantity. Since it varies by several orders of magnitude, four steps must be applied to prepare the data for training and ensure numerical convergence.

• We first resampled the data: The simulation output data were sampled logarithmically and are, therefore, relatively sparse in the higher energy end of the spectrum. With sparse data in the energy component and a decline in the particle count by several orders of magnitude, the stability of the surrogate in this area is in question. We circumvented this by linearly resampling the full spectrum. To acquire this resampling, we applied a cubic spline interpolation of the Monte Carlo output data. Both sets, the raw data and the resampled data, are merged, effectively doubling the number of data points. This resampling increases stability in the higher energy range while it keeps the spectral shape unchanged.
• We then rescaled the data using the relations given in Equation (1)

  $$\begin{array}{cc}\hfill \overline{Y}& ={log}_{10}\left(Y\right)\hfill \\ \hfill \widehat{Y}& =\overline{Y}/min\left(\overline{Y}\right)\hfill \end{array}$$

  (1)

  where $\widehat{Y}$ is the renormalized and Y is the raw data generated by the simulation.
  These two steps are necessary due to the numerical stability of the training process: not only the spareseness of data is problematic in surrogate training. Points with a (orders of magnitude) lower numerical value do contribute much less to the training process metrics than others. As a result, the training process is volatile, which we mitigated by these rescalings.
  As mentioned previously, the ion input energies are below the spallation threshold, and the unit of the spectral data Y is normalized to the reaction’s source particle. This implies that each data point is between 0 and smaller than 1. After both rescaling steps, the converted output data $\widehat{Y}$ of the simulation is normalized and ranges between 1 and the normalized maximal value.
• The spectrum also consists of energy information to the count rate. We normalized the resulting neutron’s energy $E_n$ by the neutron cut-off energy to get a scale from 0 to 1.

  $$\underset{\widehat{X}}{\underbrace{\widehat{E_n}}}=\underset{X}{\underbrace{E_n}}/max\left(E_n\right)$$

  (2)
  This results in the energy information range from 0 to 1 and allow us to use all spectra in the same training procedure. These maximum energy values are used later in a second model to predict the cut-off energy.

2.3. ANN Setup

Discontinuities are not smooth and can only be approximated with an even more extensive dataset. Since the physical spectrum has hard cut-off positions representing a discontinuity in the spectrum, we either needed even more data or used a more sophisticated approach. Therefore, we trained two models. The first predicts the normalized spectrum, while the second predicts the cut-off energy.

The networks are both fully connected feed-forward networks. For the spectrum, the node structure is as follows, where $x_s$ is an eight-dimensional input vector: $(x_s\to 200\to 200\to 200\to 200\to 200\to 200\to 200\to 1)$. For the cut-off energy of the spectrum, the node structure is as follows, where $x_c$ is a seven-dimensional input vector: $(x_c\to 260\to 180\to 180\to 340\to 180\to 180\to 340\to 340\to 180\to 1)$. More details about these input vectors are given in Appendix B.2. For both networks, the split between training and validation data is 90:10. The data for each epoch is taken from the training data and separated again 90:10 into the actual training data and the corresponding testing data.

Further optimization, such as dropout regularization, might acquire better results, but time constraints did not permit further topology optimization. The selected hyperparameters are given in Appendix B.1.

2.4. ANN Bootstrap

The simulation data have, due to their probabilistic nature, an uncertainty. We incorporated this uncertainty with a bootstrap method [13,14]. The raw data were randomly resampled in the range of uncertainty, which is Gaussian distribution, and calculated by PHITS. Taking the Gaussian distribution, we can resample the yield data N times:

$$Y_{\mathrm{res}}=\mathbf{G}\left(\mu =Y,\sigma ={\sigma }_Y\right),$$

(3)

where $\mathbf{G}$ is the Normal distribution. Applying the same procedure on each resampled spectrum yields $N+1$ different predictions, which deviate around the joined mean. For each set of input parameters, $N+1$ predictions are generated. The mean of these predictions is then the predicted value, while the standard deviation of those predictions is then the uncertainty of the prediction.

2.5. Ensuring Generality

Our surrogate $\mathfrak{F}$ maps the input parameters (converter shape, particle parameters) onto the spectrum (double differential yield). The simulated data are normalized to the incident particle. As a result, the model is also normalized. The model’s output must be multiplied by the corresponding particle count $N_p$ to determine the actual yield. We can further split non-monoenergetic ion spectra into mono-energetic slices and superpose the results; each summand depends on each slice’s ion energy $E_p$. Furthermore, since the data are binned, the bin width $\Delta E_p$ must also be considered.

The formal application $\mathfrak{F}$ is then given by

$$\begin{array}{cc}\hfill \frac{d^{2}Y}{d\Theta d{E}_n}& =\sum _{E_{\mathrm{p}}}{N}_{\mathrm{p}}\left(E_{\mathrm{p}}\right)·\widehat{\mathfrak{F}}\left(E_n,\Theta ,E_{\mathrm{p}},\ast \right)\Delta E_{\mathrm{p}}\hfill \end{array}$$

(4)

and with the infinitesimal limit for $\Delta E_p\to 0$:

$$\begin{array}{c}\hfill =\int N_{\mathrm{p}}\left(E_{\mathrm{p}}\right)·\widehat{\mathfrak{F}}\left(E_n,\Theta ,E_{\mathrm{p}},\ast \right)d{E}_{\mathrm{p}},\end{array}$$

(5)

where Y is the neutron yield, $\Theta$ the angle under which the observation is made, $E_n$ the energy of the neutron, $N_{\mathrm{p}}$ the number of incoming projectiles, $E_{\mathrm{p}}$ the energy of the projectile, and $\widehat{\mathfrak{F}}$ is the unit surrogate model, which is normalized to one projectile particle. ∗ denotes all other mentioned parameters from Table 1. $E_{\mathrm{p}}$ is sampled according to the needed precision; we used a bin width of $\Delta E_{\mathrm{p}}=1 \mathrm{M}\mathrm{e}\mathrm{V}$. Setting the model up like this enables us to apply and verify this model on mono-energetic spectra and laser-accelerated ions. This model ensures direct comparability between conventional accelerator-driven ion sources and laser-plasma-driven sources.

3. Results

Each network’s final mean squared error and the normalization factor used during preprocessing are displayed in

Table 2. Network metrics for all trained networks. Id 0 means the raw data are used. The other nine numbers indicate the nine resampled datasets. MSE is the mean squared error training metric, and Normalization indicates the normalization constant applied to each dataset after the logarithm was applied.

Id	MSE	Normalization
0	0.00128	−16.0505
1	0.00124	−16.2796
2	0.00128	−15.9784
3	0.00119	−16.6231
4	0.00114	−16.9578
5	0.00114	−16.8753
6	0.00125	−16.1653
7	0.00120	−16.5274
8	0.00140	−15.3819
9	0.00121	−16.4534

.

3.1. Validation against the Raw Simulation Data

The validity of the surrogate can be shown by plotting the surrogate’s results with the raw data curves. These curves are displayed in Figure 4 and Figure 5. Displayed are the full spectra created by the Monte Carlo code vs. the result created by our model, with its corresponding uncertainty.

We obtain important constraints of the surrogate regarding its validity from the comparison.

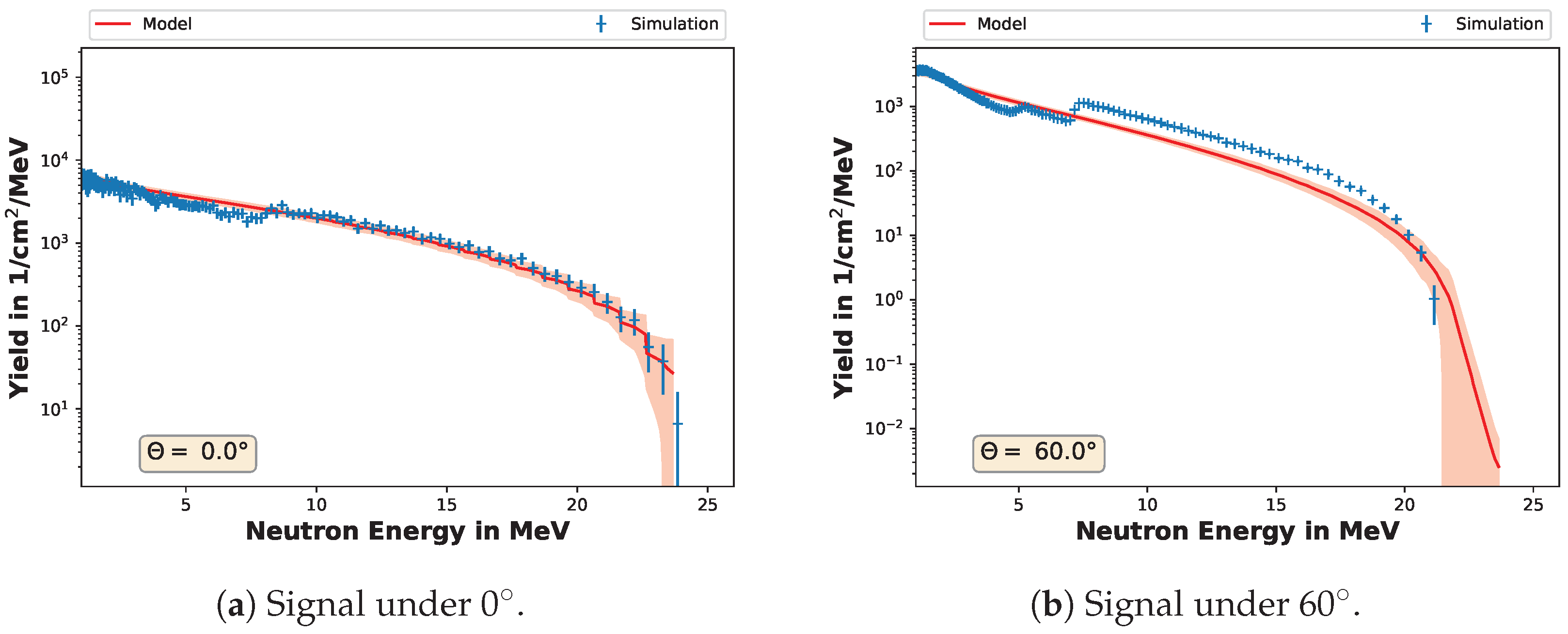
• The model predictions beyond the parameter range (see Table 1) are not physical.
• The model can predict the lowest energy neutrons, which cannot be seen in the Monte Carlo spectra. These values, however, have to be used with care: their uncertainty is very high, up to 100%, and the result does not reproduce measurement data correctly (see Section 3.2). The main reason for zero compatible count rates is the bulky target; the lowest neutrons created by low-energy projectiles cannot leave the target and are stuck there or scattered, so they are not counted in the detector. Therefore, the count rates in the simulation are low, meaning the statistical uncertainties are high.
• The characteristic high-energy peak in the forward direction, which occurs in the p-Li reaction due to the transition from Li-7 to the ground/excited state of Be-7, is suppressed (see Figure 4a). The model is based on regression. Due to this, it further suppresses fast signal peaks. It is, therefore, not capable of resolving these peaks.
• The cut-off energies mean squared error is approximately 9 $\mathrm{M}$$\mathrm{e}\mathrm{V}$². This implies an uncertainty of the cut-off energy of approximately $\pm 3$ $\mathrm{M}$$\mathrm{e}\mathrm{V}$.

If these limitations are taken into account, we can use the model to predict spectra over a large energy domain in milli seconds of time. How well this model fare against real-world experimental data is discussed and deployed in the following chapter.

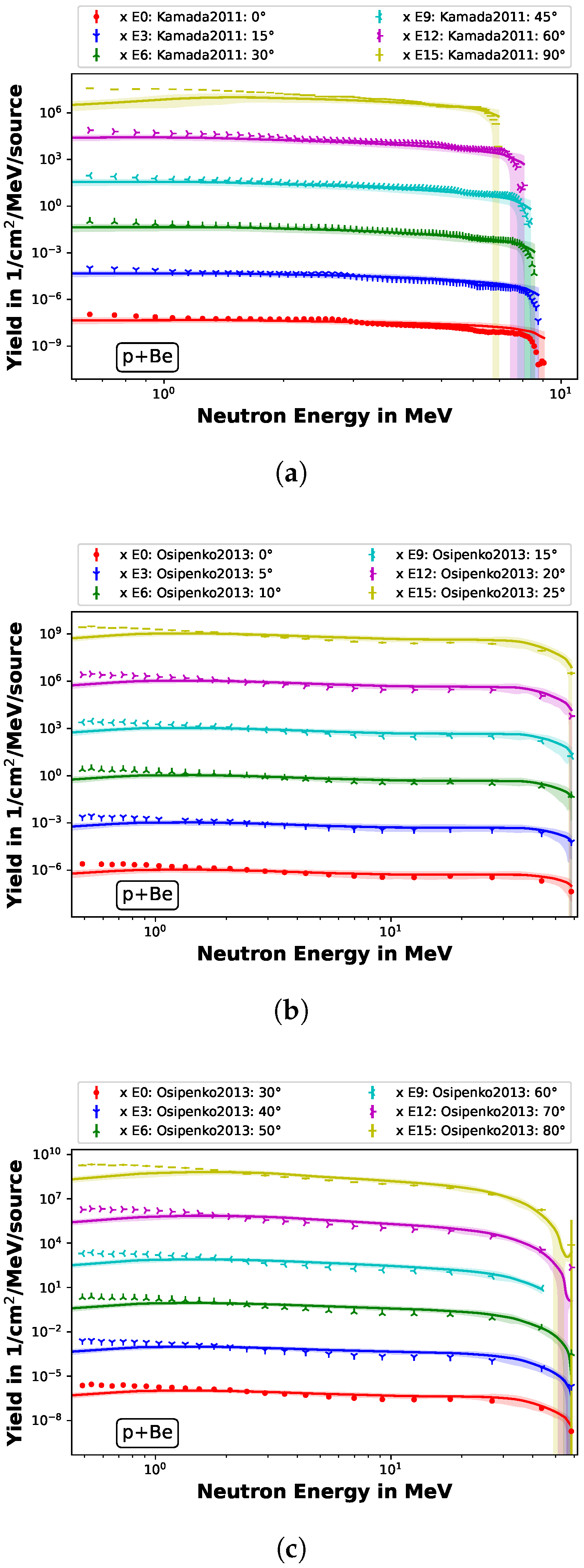
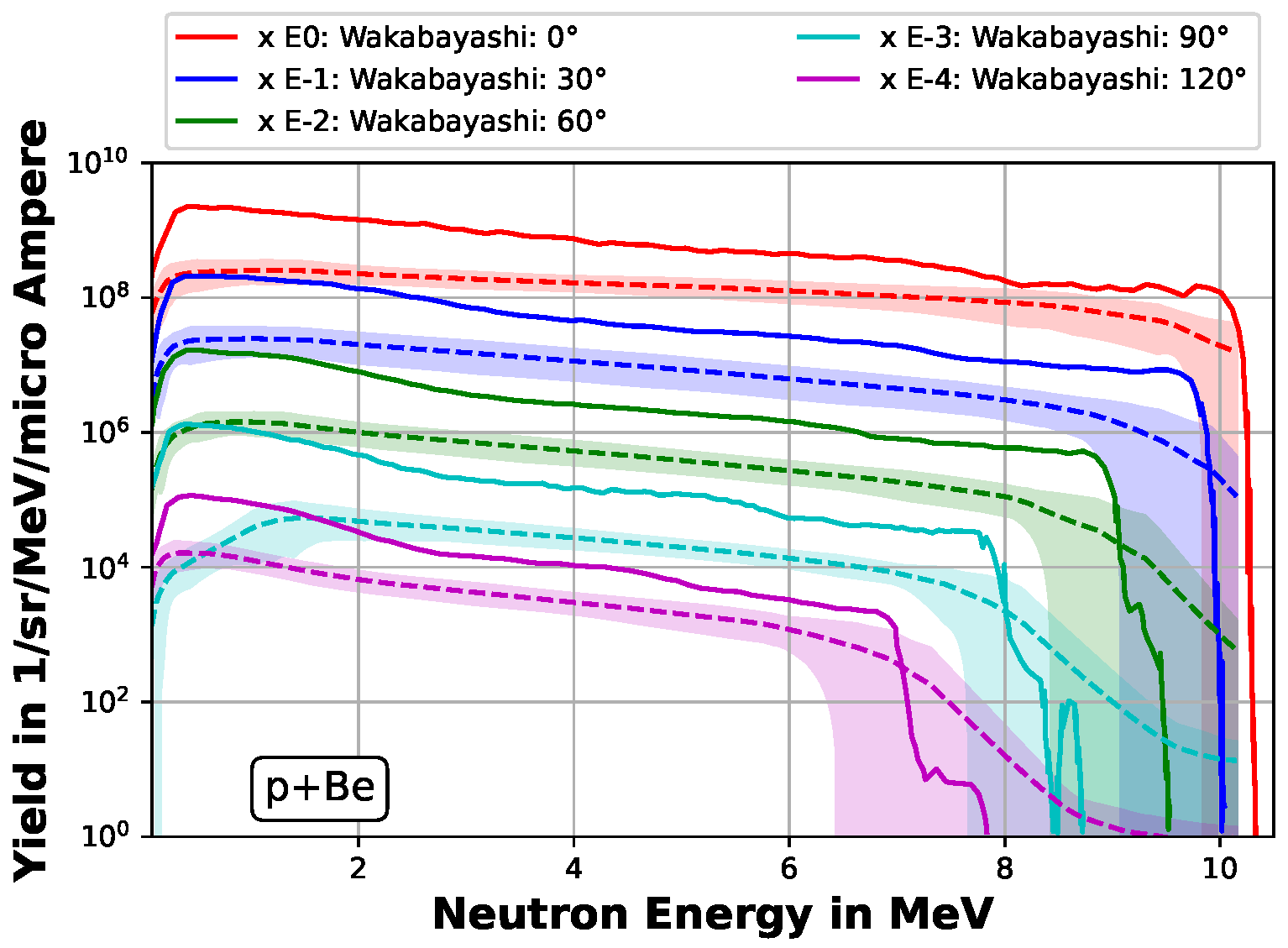
3.2. Validation against Experimental Data

The largest experimental data collection is the EXFOR database, hosted by the International Atomic Energy Agency (IAEA) [15,16]. Only a few datasets are comparable to the model derived here due to different experimental setups, the focus on cross-section measurements with thin targets, and energies of interest larger than 100 $\mathrm{M}$$\mathrm{e}\mathrm{V}$. We extracted the corresponding matching data and normalized it to the same units we used in our model.

It is visible that the model, displayed in Figure 6, deviates from the data in the low-energy region below $0.1$ $\mathrm{M}$$\mathrm{e}\mathrm{V}$. The dataset from Howard et al. taken in 2001 with $E_p=3 \mathrm{M}\mathrm{e}\mathrm{V}$ [17] could not be adequately reproduced and is therefore not displayed here. Both observations have the same reason: For low energy neutrons, the count rates in the Monte Carlo code were too low, and as such, the relative uncertainty is as high as 100%.

The model’s output can also be compared against other modeling approaches. We compare it here with the work from Wakabayashi et al. ([10], Figure 6). The data from the publication are compared with the results of our model in Figure 7.

We normalized our model to the same units as Wakabayashi’s model. The variation between experimental data, JENDL-based results, and the model in the corresponding publication already exceeds up to two orders of magnitude. Our model is continuously lower than the curves from Wakabayashi’s model because our model’s core is based on the JENDL database, resulting in a lower yield. Furthermore, the shape of the converter used in the experimental study is only described as a 2 $\mathrm{m}$$\mathrm{m}$ thick Beryllium disc without the radius information. Therefore, our model may further differ from Wakabayashi’s in the converter geometry, increasing the differences between the two models. JENDL was already continuously lower; we can, therefore, conclude that our model behaves indeed as it should. For the forward direction at 0°, we can ensure a good match in the geometry and, therefore, also acquire a spectrum that agrees with the model from Wakabayashi’s work. The larger the observation angle gets, the higher the spectra deviate. Due to the lower experimental yield, we would expect the Beryllium disc to have a radius larger than 24 $\mathrm{m}$$\mathrm{m}$.

3.3. Spectra for Different Conventional Setups

We can use the model to compare different setups. They vary in the number of particles and the corresponding input energies. Higher ion energy is expected to correlate with a higher neutron yield and higher cut-off energy of the spectrum. The number of neutrons is linearly dependent on the incoming particles due to the superposition principle.

The most progressed concepts and projects for compact neutron sources are based on conventional accelerators. We therefore extracted the relevant parameters from their design reports and used our model to compare those spectra against each other. The projects are the High Brightness Source project (HBS) from Jülich Center for Neutron Science [2], RIKEN accelerator-driven compact neutron systems (RANS) at RIKEN in Japan [1], SONATE at CEA-Saclay [3], and from the technical reports of the IAEA [8]. The parameters used for this evaluation are tabulated in

Table 3. Parameters for several conventional compact neutron sources based on ion accelerators. The sources are given in the text.

Name	Energy	Current	${\mathit{d}}_{\mathit{T}}$
Unit	MeV	10−4 A	cm
IAEA2	40	50	2.0
IAEA4	40	1250	2.0
RANS	7	1	0.03
HBS	70	1000	1.6
SONATE	20	1000	0.2

, and the model’s results are displayed in Figure 8a,b.

Differences in the spectrum result from the different particle energies and the observation angle. The number of incoming ions then scales this spectrum.

3.4. Spectra for Laser-Accelerated Protons

As mentioned previously, the laser-accelerated spectra are calculated by the superposition of several mono-energetic models which follow the composition of the full laser particle spectrum. We tested this on a simulation for the ion spectrum evaluated by Schmitz et al. [20]. The spectrum is analytically given as

$$\frac{dN}{dE}\left(E\right)=\frac{N_0}{E}exp\left(-\frac{E}{k_{B}T}\right),$$

(6)

where $N_0=3.7\times {10}^{11}$, $k_{B}T=7.4 \mathrm{M}\mathrm{e}\mathrm{V}$, and E the spectrum’s energy in the interval from 5 $\mathrm{M}$$\mathrm{e}\mathrm{V}$ to $25.5$ $\mathrm{M}$$\mathrm{e}\mathrm{V}$. We performed additional simulations for this proton spectrum and a corresponding beryllium target with a thickness of $5.02$ $\mathrm{m}$$\mathrm{m}$ and a radius of 24 $\mathrm{m}$$\mathrm{m}$. The results of the simulations, together with the corresponding model output, are displayed in Figure 9.

The model output is close to the simulation at 0°. At emission angles larger than 60°, the model prediction shows larger deviations from the simulated spectra, indicated by a jump in the spectrum at around 7 $\mathrm{M}$$\mathrm{e}\mathrm{V}$. With a larger angle, the neutron’s range inside the converter increases, as the transverse dimension of the target is much larger than the thickness of the target in beam direction (24 $\mathrm{m}$$\mathrm{m}$ vs. $5.02$ $\mathrm{m}$$\mathrm{m}$).

4. Conclusions

We presented a predictive surrogate model using an extensive Monte Carlo simulation dataset. This model can be deployed quickly and provides the core for quick evaluations of neutron yields. It increases the accessibility of neutron yield simulations and minimizes the need for experience and training for the complex Monte Carlo tools. Despite insufficient experimental data for data-driven modeling, we showed that our model reproduces experimental datasets if the experimental conditions come close to the model parameters.

Due to our simulation setup and its numerical feasibility, neutrons from projectile energies $E_p<5 \mathrm{M}\mathrm{e}\mathrm{V}$ have a large uncertainty if $E_n<0.1 \mathrm{M}\mathrm{e}\mathrm{V}$. We recommend not trusting the model in this region without an additional check via a Monte Carlo simulation. The uncertainty, which we calculate by the already explained bootstrapping method in Section 2.4 is a good indicator of the model’s validity.

The next step to improve this model is to investigate the geometry dependency in more detail and to improve the cut-off modeling for the neutron spectra. Both could be achieved by new experimental data or an extension of the simulation model.