Risk Contextualization for Nuclear Systems ^†

Abstract

Risk management strives to reach the standards of theoretical systematicity and empirical precision achieved in natural science models. To this end, a set of risk-informed and performance-based standards was developed in the form of statistically validated measures. The set enables the systematic extraction by deterministic and probabilistic analysis of potentially objective risk assessments and well-defined decisions. However, much of the data and models are subjectively influenced by the uncertainty of the context in which they are related and derived. Current risk analysis contains a large amount of risk-related information, but without the context of the models, its results lack sufficient predictive and explanatory power to be a solid basis for decisions. Therefore, to model the entire site of a multi-unit nuclear power plant as an integrated system connecting facility and activity, it is necessary to consider not only the technological conditions, but also the entire site context, including human, organizational, and environmental factors. An interface tool for dynamic deterministic-probabilistic safety analysis should be used to contextualize and complement existing risk indicators, but not to replace them. This article presents the possibilities of risk contextualization for nuclear systems through the symptom-based context quantification procedure of the Performance Evaluation Teamwork method.

1. Introduction

The probabilistic approach incorporates several assumptions, encompassing various uncertainties, that should be addressed as explicitly as possible [1]. Probabilistic safety assessment and management (PSAM) aims to encompass all risk contributors associated with the operation of facility and activity systems (FASs) to evaluate and comprehend their risk profile, facilitating risk-informed decisions. The outcomes are used to confirm that risk assessments align with the goals, criteria, and safety requirements by the regulator [2].

The comprehensive probabilistic safety analysis (PSA) model of an FAS, such as a nuclear power plant (NPP), must account for all potential influences: (1) all internal and external initiating events (IEs) and hazards arising from random failures, human actions (HAs), natural and man-made phenomena, for which an ‘exhaustive but limited’ list of initiators is compiled; (2) general or specific reliability data of the equipment; (3) certain operating modes, plant operating states (POSs), and conditions; (4) specific hazard sources; and (5) distinct configurations of the installations on the NPP site. These model elements are typically extracted, modeled, evaluated, and interpreted in various contexts for quantification using the same risk measures for different risk contributors. These contextual differences must be considered and, if possible, unified to understand and predict the risk and the myriad sequences of events and transitions between complex system states that require monitoring and analysis through integrated code simulations with specific boundary conditions and actual configurations. These event sequences must be verified, grouped, and limited to make the task feasible for PSA purposes. Detailed deterministic safety analyses (DSAs) should also be condensed to a set of representative event sequences and identified bounding cases with similar accident progressions to minimize uncertainty.

The stages of data selection, modeling, and evaluation in the model involve subjectively typed situations and averaging the context of their implementation. However, their interpretations for different configurations, reliability models, and situations imply heterogeneity of scope, limited details, and conservatism of initial and boundary conditions. Assuming an average homogeneous context of events during risk modeling, assessment, aggregation, and communication can distort both the risk profile and the risk-informed decision-making process. Increasing the elements for determining risk is justified, but it only heightens the need to gather data, which are ultimately re-collected through aggregation, context averaging, and subjective expert judgment. Therefore, risk must be contextualized to provide a more plausible secondary probabilistic dimension to the different configurations’ modes, conditions, and situations in which the FAS operates due to the various risk contributors. This contextualization, or the study of the context for its homogenization, can be achieved in different ways [3]. For instance, through causal modeling of scenarios in thermo-hydraulic (TH) simulation, specifying the significance of results according to given criteria, or by quantifying context based on the occurrence and recognition of combinations of typical symptoms of the object in different situations. Symptoms are the deterministic characteristics of the FAS as an object in a given situation perceived by the human as a subject through mental images. Their scenario-sensitive combination in their run, simulating a risk contributor, allows for deterministic-probabilistic modeling of symptom-based contexts. It includes symptoms from the past, present, and future, as illustrated in Figure 1.

Risk contextualization is the process of combining symptoms (contextual factors and conditions—CFCs) to provide a probabilistic description of the FAS state, reduce uncertainty in risk assessment, and specify the exact risk profile for more reliable risk-informed decision making [3]. According to the dictionary definition of ‘contextualization’, it involves placing the FAS in a context or situation within which it exists or occurs. The aim of this contextualization is to form a more accurate representation of risk, to contextualize and supplement existing risk metrics without replacing them. It supports risk characterization [4], information, understanding, communication, and integrated risk-informed decision making (IRIDM) [5].

Most sources of uncertainty need to be defined in the context in which they are considered. This relationship is most evident and can be derived from human reliability assessment (HRA) [6], but it can also be applied to probabilistic modeling of scenarios, phenomena, and dependencies [7]; data mining [8], living PSA, or dynamic risk monitoring (RM) [9]; multi-unit PSA, risk aggregation [6], ATHEANA error-forcing context [10], communication, and management.

A graphical overview summarizing the interrelation between aspects of the deterministic-probabilistic spiral of risk analysis and its contextualization is shown in Figure 2.

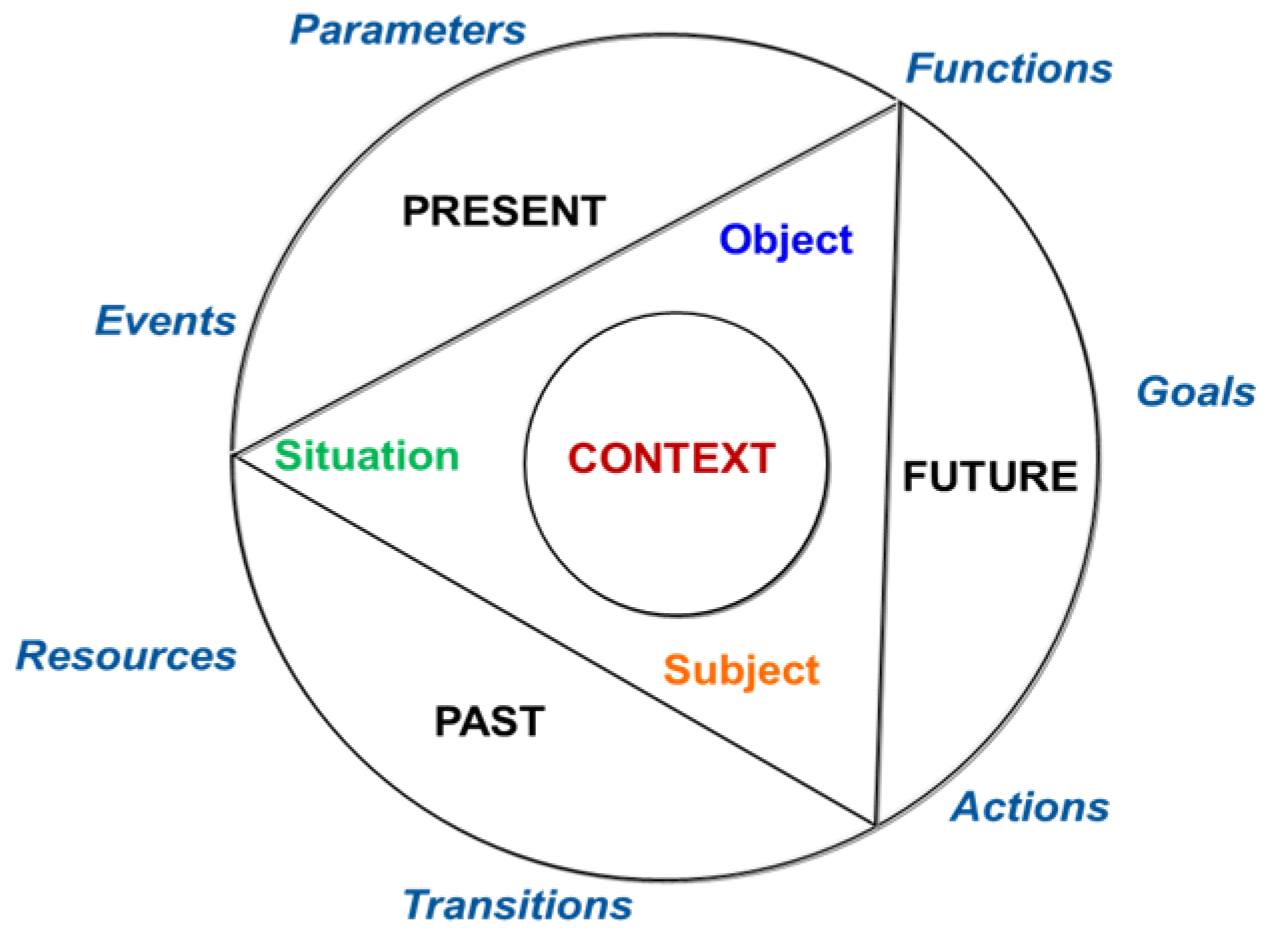
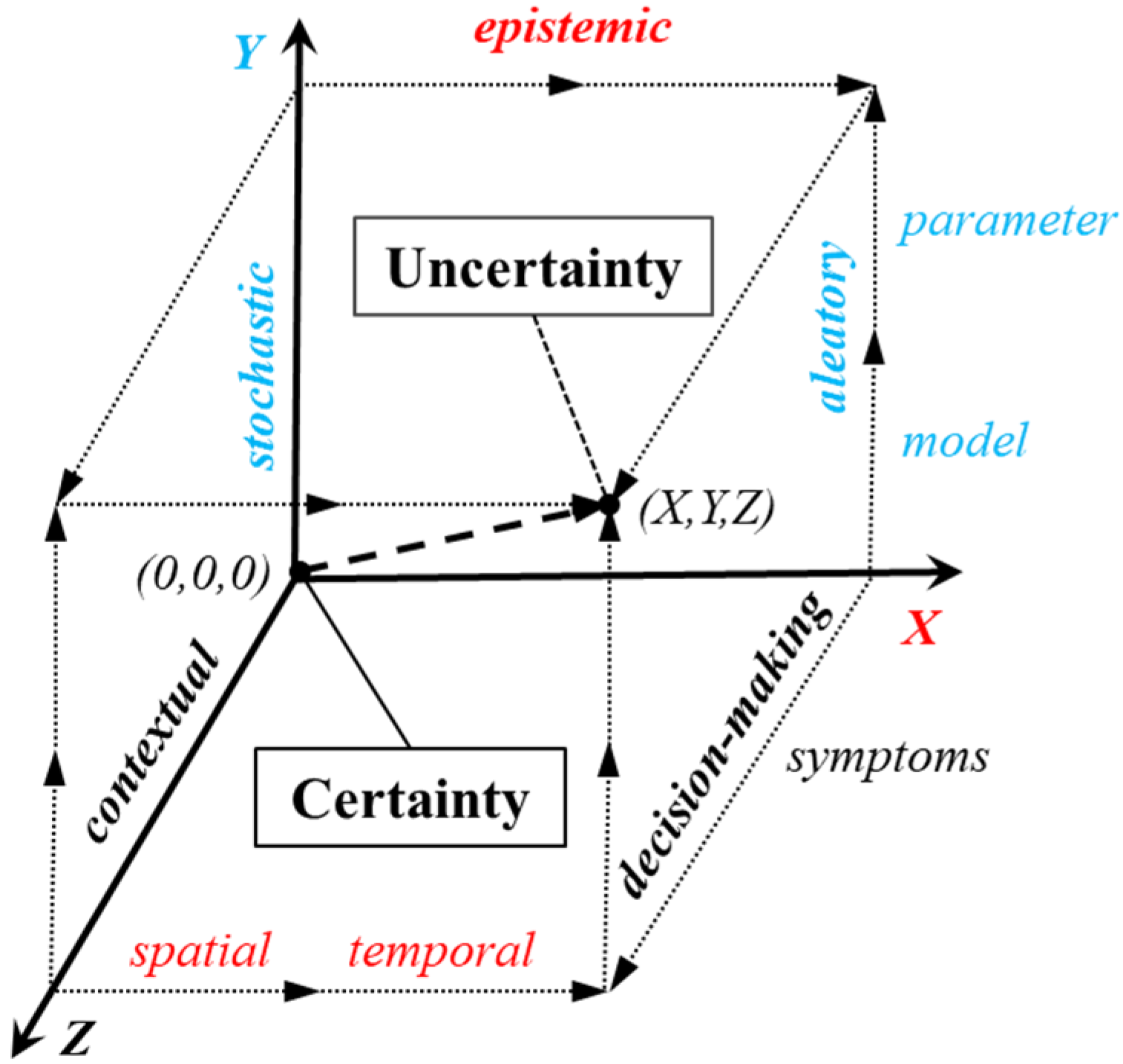
2. Symptom-Based Context and Uncertainty Vector

The definition of risk as a complete distribution of a set of triplets, R = {〈s_i|p_i|_Ci〉}, where s_i is an identification or description of a scenario i, p_i is the probability of that scenario, and c_i is a measure of the consequence of the scenario, is incomplete due to the inability of s_i, p_i, and c_i to be modeled and assessed properly in an exhaustive manner with sufficiently small uncertainty. Extending the definition of risk as the full distribution of a set of five elements, R = {〈s_i|p_i|c_i|u_i|g_i〉} (scenario, probability, outcome, significance/utility, group), does not always reduce the uncertainty of the risk.

Despite the desire to get closer to reality, the HRA and PSA models inevitably use different assumptions and idealizations of complex processes and phenomena, which predetermine the uncertainty of the end result. Uncertainty assessment is needed to review the risk profile, to have confidence in the representativeness of the results, and to support the communicating and decision-making processes.

The following categories could be considered as sources of uncertainty in the PSA/HRA model and data (see

Table 1. The categories of uncertainty.

Completeness	Objectiveness	Inference Cleanliness
Determined by the limitations of the methods used, the presence of various assumptions and simplifications in the models.	Determined by the limitations of the methods used, the presence of various assumptions and simplifications in the models.	Determined by the parametric uncertainty of the reliability indicators and risk metrics. A probability distribution is used to obtain different probabilities for various outcomes to occur.
Sources: scope and list of PIE and hazards, failures and HFEs, treatment of phenomena and dependency.	Sources: supporting documents and analyses of success criteria, assumptions, human actions, and model errors.	Sources: are the input parameters: number of actual requests, sample size, population definition, and data estimation models.

): completeness, objectiveness, and inference cleanliness.

Contextual awareness would be an appropriate way for uncertainty reduction in the PSA/HRA models. The real risk evaluated for a system must be based not only on the inherent unknowability in aleatory and epistemic factors but also on an indeterminate context in which the considered object and its image interact. Therefore, contextual quantification procedures can be viewed as a probabilistic tool for transforming reality and relative indifferences between alternatives to absolute indifferences between them in PSA models.

As a type distinct from aleatory and epistemic uncertainty, contextual uncertainty is conditional and aims to emphasize the importance of context in the decision-making process. A conceptual orthogonal framework for integrating different vectors of uncertainty—epistemic (X), aleatory (Y), and contextual (Z), is shown in [11]—Figure 3.

The expansion of risk-determining factors is justified, yet it primarily increases the quantitative demand for data collection, which is ultimately addressed through aggregation, context averaging, and subjective expert judgment, without achieving the necessary qualitative transformation. Most uncertainty sources must be defined within the specific context. This connection is most evident in HRA and can also be applied to probabilistic modeling of scenarios, phenomena, dependencies, data mining, living PSA, dynamic performance and RM, communication, and management.

Contextual or decision-making-related uncertainty can be easily projected and aggregated onto the (X, Y) plane, but this “epistemic-stochastic” or “black-and-white” uncertainty makes it more difficult to distinguish rational risks from irrational due to comparative ignorance and ambiguity aversion.

In order to better understand the value of the aggregated sum for the subjective probability amplitudes (SPAs) of risk communicating and decision making, it may be necessary to disaggregate uncertainty. As a result, some SPA measures, related to decision making, may be additive (constructive), while others may be subtractive (destructive). This means that their sum can be greater or less than 1, i.e., ‘conjunction fallacy’ (‘constructive interference’) or ‘disjunction fallacy’ (‘destructive interference’), of cognitive processes that can be observed. In these situations, the principle of superposition is valid only approximately.

Knight wrote that ‘We perceive the world before we react to it, and we react not to what we perceive, but always to what we infer’ [12]. A subject’s intervention is designed to change the future situation inferred from a present one. It involves perception and “two-fold inference”. Humans must infer what the future situation would be without intervention and what the change will be with it. And interpretation of failure events in context-free or subjectively judged situations by an expert introduces additional uncertainties.

They cannot be corrected by separately considering the dependencies only in the object or only in its images in the subject’s mind.

The reliability data collection also requires context-sensitive calibration. If the context during data mining is uncertain or quite generic, then the database availability does not mean good quality and data value, e.g., for HRA and PSA.

3. HRA Context for NPP Safety

3.1. HRA Development

HRA is a hybrid applied science at the intersection of PSA, reliability and resilience analyses, human factors (HFs), DSA, complex system simulation, cognitive systems engineering, psychometrics, psychology, ergonomics, neuroscience, etc. HRA seeks to apply scientific knowledge to reflect interactions and interferences within the FAS, assess the human error probability (HEP) of a human failure event (HFE), and design fault-tolerant, resilient interactions between humans, organizations, environments, and technology. HRA is linked to PSA, which includes at least two quantities: the severity of potential adverse consequences, the probability of each consequence’s occurrence, and possibly causal scenarios, utility, population groups, etc.

The context relates to the perception, understanding, control, safety, and management of natural phenomena, processes, and systems involving human participation. Thus, human resilience and HRA are directly dependent on context.

To enhance NPP safety, we must understand how human work is designed within the NPP context, how it is imagined, monitored, controlled, and executed, or expected to be executed, in situations of changing objects and their images. An object is developed, perceived, inferred, and managed by humans as its image (work tool) during design, construction, commissioning, operation, decommissioning, etc.

The technique for human error-rate prediction (THERP) is a method used in HRA to evaluate the HEP of an HFE during a specific task [13]. The THERP method provides the “thesis” or aim of first-generation HRA methods: to obtain an HEP of identified HFEs by reasoning and weighting internal and external holistic performance shaping factors (PSFs). HA can be distinguished in two sequential stages—cognitive (diagnosis) and executive (manual or response). Dougherty suggests changing first-generation HRA models like THERP and human cognitive reliability (HCR) correlation [8] with second-generation HRA models [14] due to the “unfinished business related to HRA, which includes identification, specification, and fitting of human cognition models to define error potential and context” of HA [14]. Hollnagel [15] notes that understanding HA in “second-by-second” dynamics requires detailed knowledge of HA’s objective context and its subjective image in the human mind. However, the temporal approach used in THERP, e.g., Swain’s TRC or its ‘improved’ version called the HCR correlation [8], is “virtually impervious to context” [14].

Most second-generation HRA methods make a formalistic substitution of THERP’s PSFs or their modifications with “contextual”, “influencing”, or “error-forcing” factors [10]. However, this did not significantly change HRA’s outcomes, as they also redefine context through expert judgment (guessing the anchor value) and by multiplying the PSF (guessing the influencing factors). This substitution exemplifies Dougherty’s observation [14] and insight that “the influential and contextual approaches may become indistinguishable at the quantification stage due to the lack of actual data”. The goal of new-generation HRA methods or “antithesis” is to consider context with its specificity, severity of consequences, multidimensional dynamics, and holistics of FAS states for each individual or group cognitive and executive response.

Some HRA concepts are indisputable; others result from group thinking inertia, misinterpretation, judgment heuristics, biases, and business interests. To overcome challenges based on subjective identification, quantification, reduction, data mining, and measuring of HFEs with expert judgment of PSFs and anchor values, a realistic symptom-based approach to describe the FAS context was proposed [11].

HRA ‘synthesis’ aims to obtain an HEP of an identified HFE in the holistic and dynamic FAS context based on specific symptoms’ recognition for any individual and group cognitive or executive response. A symptom’s impact is reasoned, measured, and weighted by internal and external global and local (“glocal”) symptoms for it.

3.2. Approaches to the Facility–Activity System Description, Modeling and Management

The following approaches could be identified and used to describe, model, and manage the complex systems, including facility and activity together:

• Person approach and system approach to modeling and managing HFE.

The first approach focuses on “the contribution of human errors on the system, their own psychological justification, accusations of forgetfulness, inattention, or moral weakness” [16].

The second approach focuses on the conditions, situations, and context in which a person deliberately and conscientiously performs actions to effectively manage the system and limit the consequences of operational risks. An extreme statement is ‘human error is never the root cause’. The system approach is preferable and practical for context-based HRA. It is not important “who blundered, but how & why the defenses failed”. Human performance needs to be considered as a variability of a whole system where humans interact with technology, other humans, organizations, and the environment (HFE ≡ FAS failure event).

2.

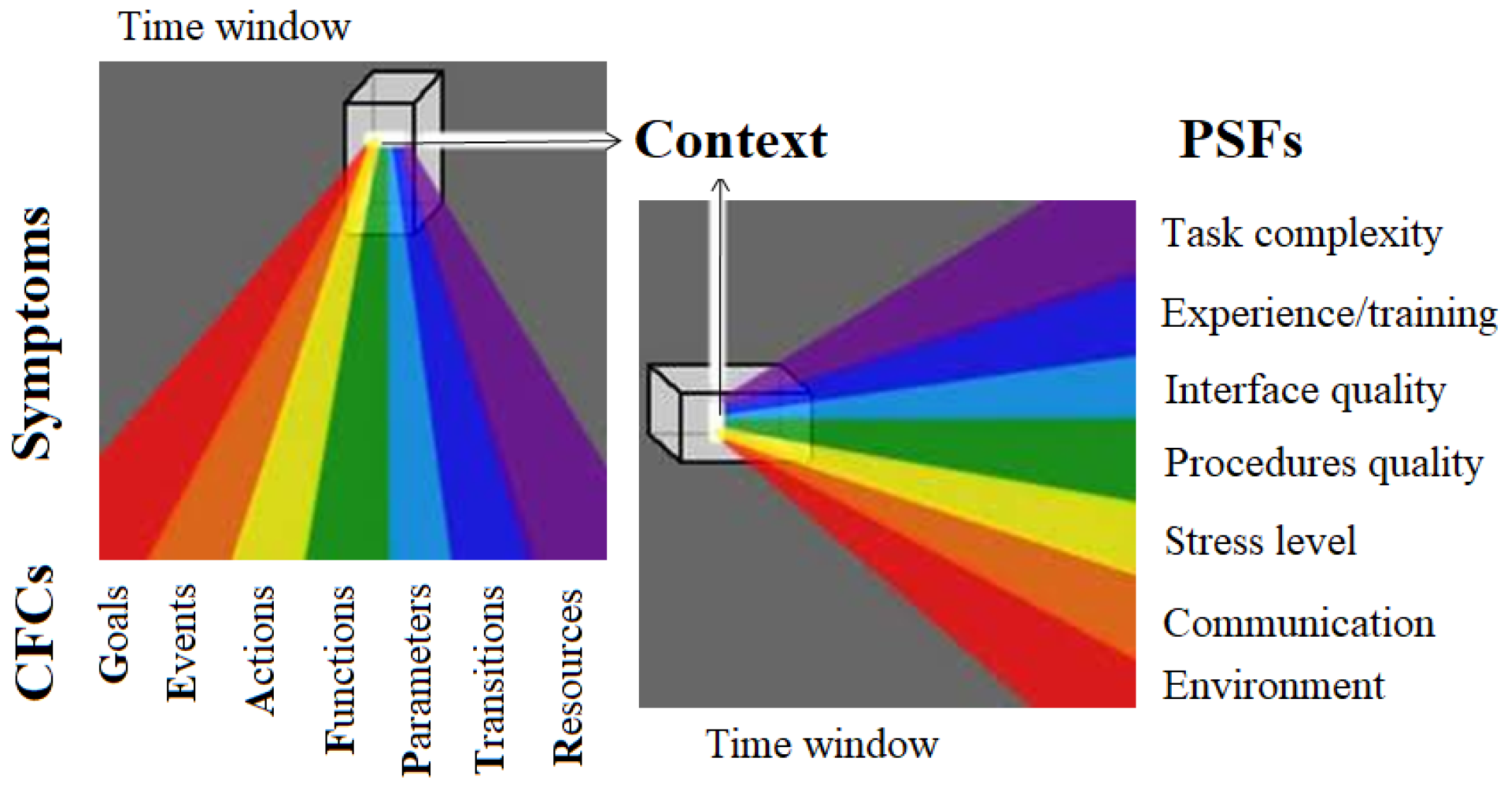
An approach to describing the FAS based on PSFs and an approach to describing the FAS variability of the system based on symptoms/CFCs are illustrated in Figure 4.

The symptom-based approach is preferable and more practical for a comprehensive, contextual, and dynamic description of FAS due to the following:

• extended application of the symptom-based approach to NPP accident management.
• The symptom-based approach is common in nuclear accident management. The IAEA NS-R-2 [17] establishes the following requirements for accident management: “The training of operating personnel shall ensure their familiarity with the symptoms of accidents beyond the design basis and with the procedures for accident management”. Later in IAEA SRS No. 48 [18], “symptom/state-based procedures” were justified. In IAEA NS-G-2.15 [19], a ‘symptom-based approach’ was also recommended: ‘2.14. The approach in accident management should be based on directly measurable plant parameters or parameters derived from these by simple calculations’.
• possibility for statistical entropy description of macroscopic FAS in addition to the microscopic causal description.

The dynamic interactions of the NPP are manifested by interference of symptoms (stimuli with meaning for operator). The FAS context could be presented by them on the macro level. To understand the root causes of human errors, we should search in depth at the micro level.

The holistic or macroscopic context qualification and quantification procedure is the first stage of a performance evaluation of teamwork (PET) method that models the most valuable FAS features in the accident progression obtained by PSA and DSA interaction [20]. It relies on combinations of recognizable symptoms for statistical description of the variability of FAS performance and provides a controllable framework of mental processes such as cognition and communication.

Macroscopic statistical description of the FAS context would help to identify the dynamic and holistic nature of the system’s behavior. A certain macroscopic state can be found in many microscopic accessible states. The basic idea of the distinction between macro- and microscopic levels is to change the set of microscopic accessible states with equivalent subsets of macroscopic states (bit states). It follows the Shannon theorem [21] regarding the entropy as the measure of information, and was the basis for the used, in the PET method, an analogy of energy and information. The mental process in the FAS is described at each moment by its microstates (quantum states). A specific quantum state represents the most detailed possible FAS description [7]:

• ability to solve theoretical questions about explored/unexplored mental processes;
• applicability for extending the definitions of images, errors, violations, holistics, and dynamics of context;
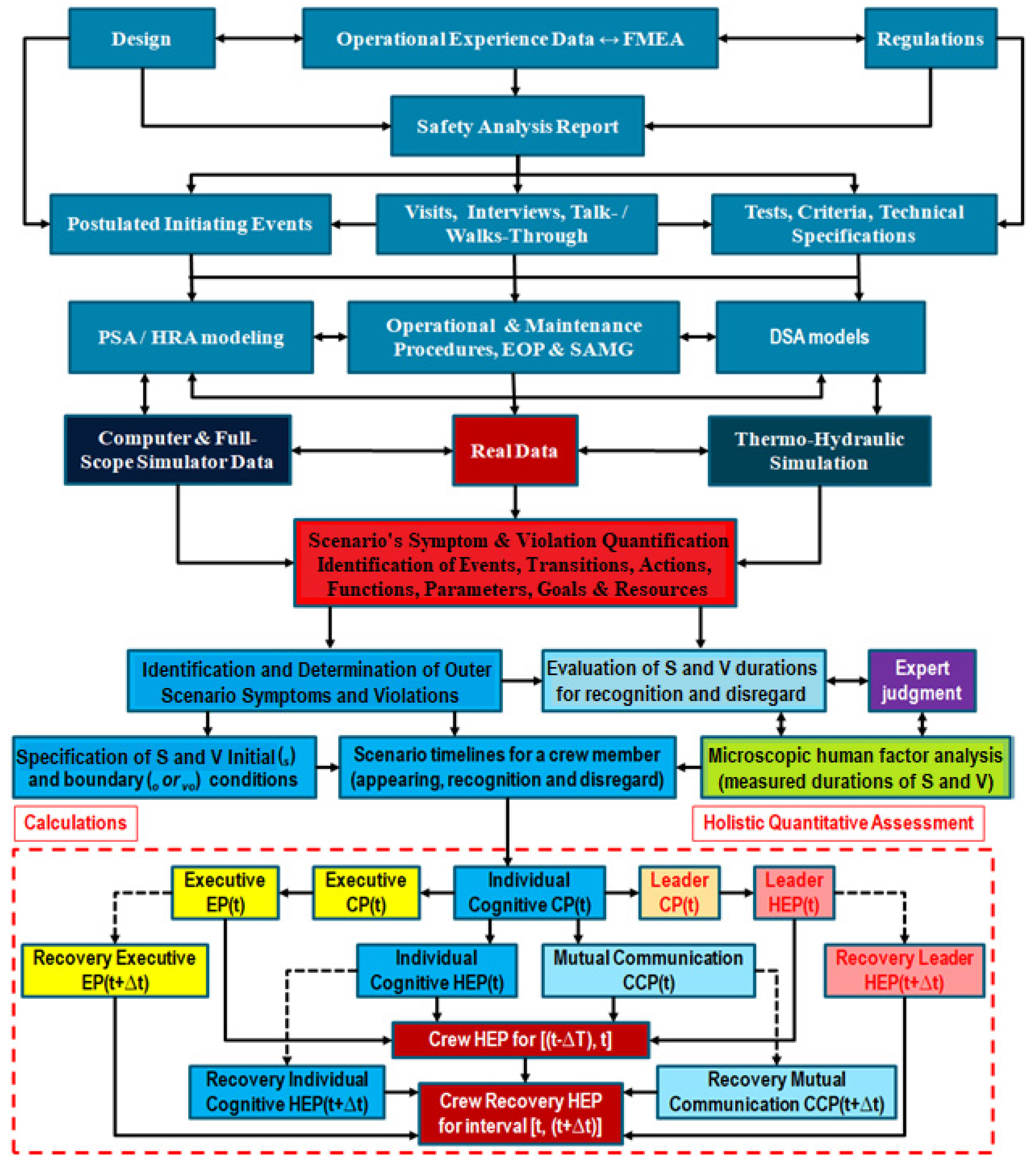
• the PET procedure for evaluation of context, cognition, communication, and decision-making error probabilities consists of eight steps, and its iterative and recursive character in the spiral evaluation steps are also presented in [7].

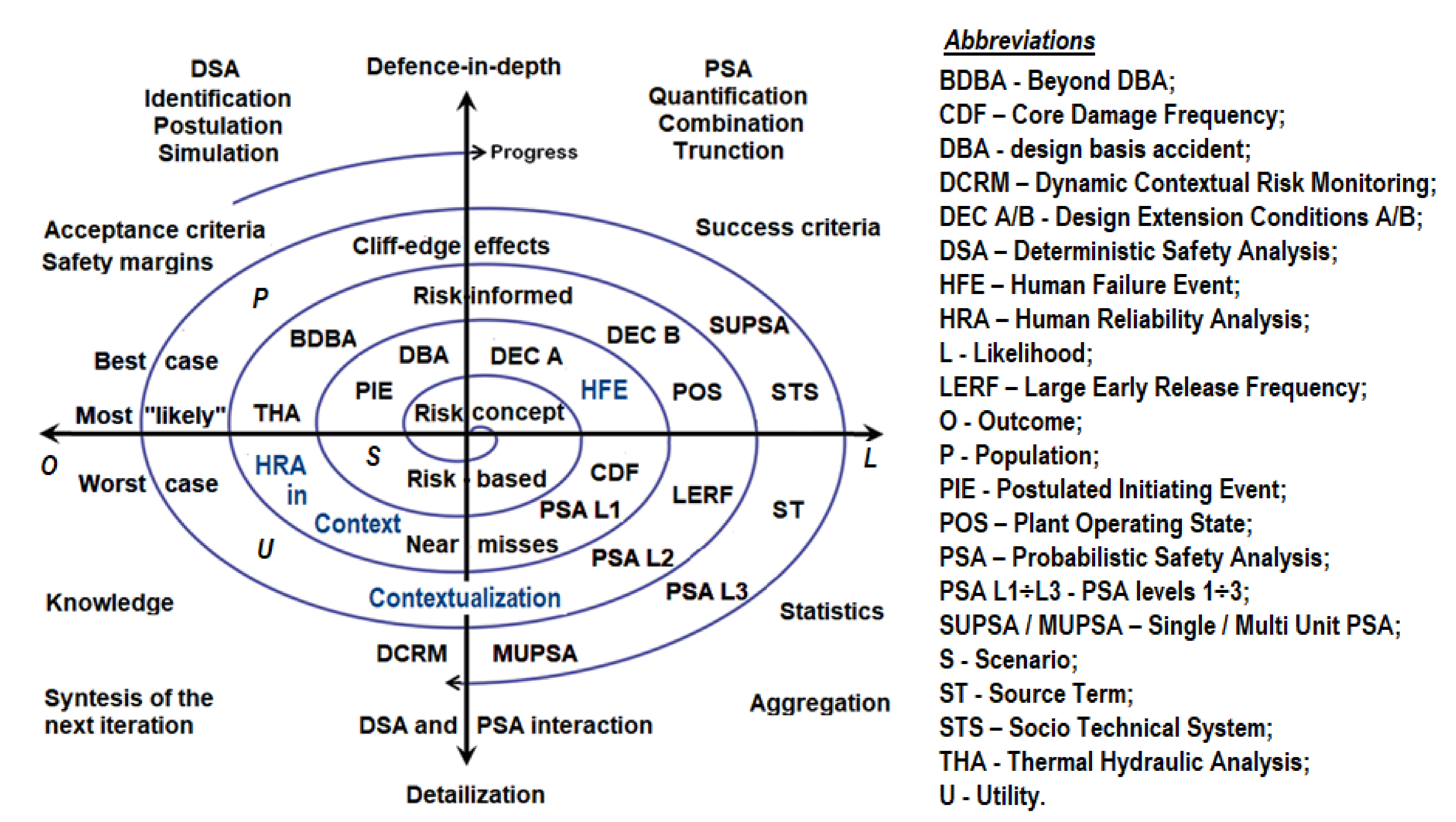
3.3. Description of the Scenario Context Qualification and Quantification Process

Insufficient exchange of information between designers, safety analysts, and technologists can lead to violated or unexpected contexts and inadequate risk assessment. If important symptoms of the description are omitted, then distortions in the context and risk assessment occur.

The timeline description and analysis of the accident scenario and tasks needs to be detailed and chronologized in order to improve the qualification and quantification process of the context probability (CP), error probability (EP), communication context probability (CCP), and HEP, as shown in Figure 5 [6].

4. Multi-Unit PSA Contextualization and Risk Aggregation

4.1. Multi-Unit PSA and Risk Aggregation Metrics

Single-unit and hazard PSA (SUPSA) for complex FASs as NPPs is usually based on static logical structures event and fault tree (ET–FT) models of a single reactor (R) without or with its spent fuel pools (SFPs). The DSA set of NPP sites most often includes modeling and simulation of the TH behaviors of single reactors and associated SFPs, and the operator responses to the accident scenario of internal and external events.

Following the Fukushima Daiichi disaster, special attention has been paid to multi-unit NPP sites, where a set of units, potential “hazards, and combinations thereof”’, impacts of inter-unit dependencies, shared systems, and common resources of on-site safety need to be addressed in PSA and DSA. This multi-unit PSA (MUPSA) considers the extended accident progression outside of the single reactor unit and requires explicit aggregation of risks of all potential on-site risk contributors.

The following expanded metrics of site risk are defined for an MUPSA with a frequency basis of accident events per site-year in [22] involving core damage frequency (CDF) or large early-release frequency (LERF) on one or more reactors:

• site CDF (SCDF) and site LERF (SLERF);
• multi-unit CDF (MUCDF) and multi-unit LERF (MULERF).

It should be borne in mind that the risk metrics must be scanned and selected without optimism or conservatism and correspond to the occurrence of real, severe accidents.

The various outcomes can be depicted on a Venn diagram shown in Figure 6. It shows a comparative scope of SCDF for a Kozloduy NPP (KNPP), Bulgaria, site with two Rs and two SFPs (four sources): 2⁴ − 1 = 15 disjunctive events need to be considered if all possible combinations need to be explicitly determined for calculating a site risk measure [22].

However, as shown in [6] for the three known major nuclear accidents (Three Mile Island, Chernobyl, and Fukushima Daiichi), the IE outcomes depend on scenario context. The over- or underestimation of the multi-source risk profile in risk aggregation could be avoided not only by moderately complicating of the integrated PSA model [22], but also by considering probabilistic measure of the IE scenario context, i.e., the contextualization of risk is necessary.

4.2. Contextual Challenges for Multi-Unit PSA and Risk Aggregation

All risk assessment tools look for dangerous relapses in the FAS dynamic holistic context. The main objective of the contextualization for MUPSA and risk aggregation on the NPP site is to account for all explicit and implicit dependencies between all units and hazards to minimize failures and risks, increase management effectiveness, and reduce decision-making uncertainties. These uncertainties and dependencies are determined in a situation for which an explicit probabilistic description of risk exists, based on static SUPSA of any single unit and hazard. This means that the MUPSA model should consider the scenario’s context and explicit aggregation of risks of as many facilities and hazards as possible at the NPP site: shared equipment, conditions, and organization; inadequate emergency procedures and guidelines (emergency operating procedure—EOP; severe accident management guideline—SAMG); hazard-induced and common cause failures (CCFs), and HFEs, during the scenario’s progression.

To correctly interface deterministic models (DMs) with probabilistic models (PMs), and to use them jointly for contextual MUPSA and HRA, there are three main challenges:

• How are the dynamic outputs of complex and time-consuming DM codes converted into PM input?
• How is the stochastic input in dynamic PSA or in contextual SUPSA or MUPSA models represented, and with what software tools?
• How are dependencies considered to reduce the transmitted and aggregated uncertainty from the DMs and PMs to the risk-informed outcomes and measures?

4.3. Suboptimal Safety Information Transfer

The DM codes provide the best physical description of the NPP processes and are the preferred tool for PM input preparation. Unfortunately, the combinations and variations of the input parameters and the obtained results are too numerous, making DMs impractical to cover all possible conditions and situations (contexts). Therefore, ways are sought to summarize and reduce the inputs and outputs of DMs for converting them to PM input for PSA by typing and grouping scenarios, simplifying models to reduce time and effort for modeling and calculation. An alternative option to such efforts is the probabilistic description and interpretation of the dynamic symptom-based context identifying the NPP events and processes for operators. This raises questions about how to optimize the interface and transfer of information between DSA and PSA to rationally use their capacity.

(i)

DSA capacity (C_DSA) includes the following:

• TH simulations of groups of postulated IEs (PIEs);
• Detailed dynamic TH models;
• Basis for full-scope simulators with multi-step procedures;
• FAS context can be modeled and defined much better than by expert judgment.

(ii)

PSA capacity (C_PSA) includes the following:

• Limited set/list of PIEs;
• Detailed static ET-FT models;
• Powerful software tools;
• Expertly judged HEPs for HFEs of the critical operator’s actions or tasks.

DSA capacity for PSA (C_DSA-PSA) is used only to formulate the ET–FT success criteria, where lists of PIEs and HFEs are used as the base set for TH analysis. The individual cognition, mutual communication, and group decision-making processes of designers, experts, and operators are not modeled in the DSA–PSA interface and consequently, the transfer rate from DSA to PSA (R_DSA-PSA) is small. A vast amount of DSA information about the FAS responses remains a side-product due to suboptimal transfer between DSA and PSA (C_DSA-PSA >> R_DSA-PSA). The optimal interface for an information transfer nearly without error requires C_DSA-PSA→R_DSA-PSA.

4.4. Features of Dynamic MUPSA Options

The two options of summarizing and reducing DM inputs and outputs for turning them into PM inputs for PSA have their advantages and disadvantages.

In the first option, the risk-informed safety margin characterization (RISMC) is to produce reduced-order models (ROMs) of the TH codes (RELAP5-3D, MELCOR) [11]. ROMs need to replace TH simulations completely in order to reduce high computational costs (time and number of runs), and their results should be interfaced to the used tools for stochastic or probabilistic modeling and selected codes for system analysis (RAVEN) instead of classical Boolean structures such as ETs–FTs [23].

The second option is to quantify the dynamic CP (t) for operators, crews in main control rooms (MCRs), emergency or technical support centers, local zones of single units, hazards, and site by the PET method [7]. CPs are used in parallel with the tree models for dynamic modulating of the PSA outcomes. The PET context quantification procedure relies on the change in time of the system macroscopic state and the counting of possible FAS-accessible states.

This option for dynamic contextual MUPSA explicitly considers timing and sequencing of symptoms appearing for all units simultaneously in a PSA–HRA framework. There are no limits for operator’s responses, outputs, and technological or logical interfaces between DMs and PMs. Explicitness of this option provides a clear idea of the possible decisions, prioritizations, and accident mitigation measures to be taken.

The PET approach employs both DMs and PMs in a single analysis framework for HRA, PSA, and accident analysis. In the DM set are included the following:

i.

TH behavior of the NPP (reports, TH code, or full-scope simulations);

ii.

External event study (such as flooding, tsunami, earthquake, etc.); and

iii.

Operator responses to the accident based on operational manuals.

DMs of the NPP (A, B, C) are performed by using TH codes which simulate the FAS behavior evolution. Scenario’s timeline could be traced by the counting of appearing, reported, recognized, and disregarded symptoms and violations in time. Such symptom-based tracing of the holistic dynamic context (including physical, psychological, organizational, environmental factors) of FAS agents (individual operators and crews) is applied on the NPP site. It is applied for qualification and quantification of their ‘‘situation awareness’’ in time and serves as a basis for dynamic contextual MUPSA, HRA, and accident analysis.

The CP (t) could be evaluated as a potential for erroneous action, wrong decision making, and failed or unsuccessful FAS behavior. It is based on operational recognized concepts (symptoms) for control obtained from TH or full-scope simulations in the accident progression. A dynamic symptom-based context quantification procedure could be used as a tool for DSA–PSA interfacing. This procedure is a part of the PET method for HRA and accident management [9,11].

Figure 7 shows the main features of the PET context vs. RISMC safety margin option.

5. Contextual Site PSA

5.1. Risk Metrics for Contextual Site PSA

The purpose of dynamic contextual MUPSA is to supplement, extend, and modulate the existing risk metrics and not to replace them as in [6]. The PET option uses standard SUPSA risk metrics (CDF and LERF). CP_ijk (t) is calculated for each accident sequence (k), group of PIEs (j), and single reactor/hazard (i). It considers dependencies, uncertainty, and ambiguity of statuses of units, hazards, and crews. It would not lead to overestimating multi-unit risk metrics and excluding any damage that was not underestimated originally, e.g., context-free or average SUPSA outcomes. Equation (1) can be used for a relationship between CDF (for SUPSA, upper S index) and SCDF (Site CDF, upper site index) in MUPSA on an NPP site:

$$\begin{array}{c}SCDF(t)={\sum }_{i=1}^I{\sum }_{j_i=1}^{J_i}{\sum }_{k_{ji}=1}^{K_{ji}}{\int }_{t_{ijk}}^{T_{ijk}}{\displaystyle \frac{{CP}^{Site}(t)\times {CDF}_{ijk}^S}{{CP}_{ijk}^S(t)}}\end{array},$$

(1)

where

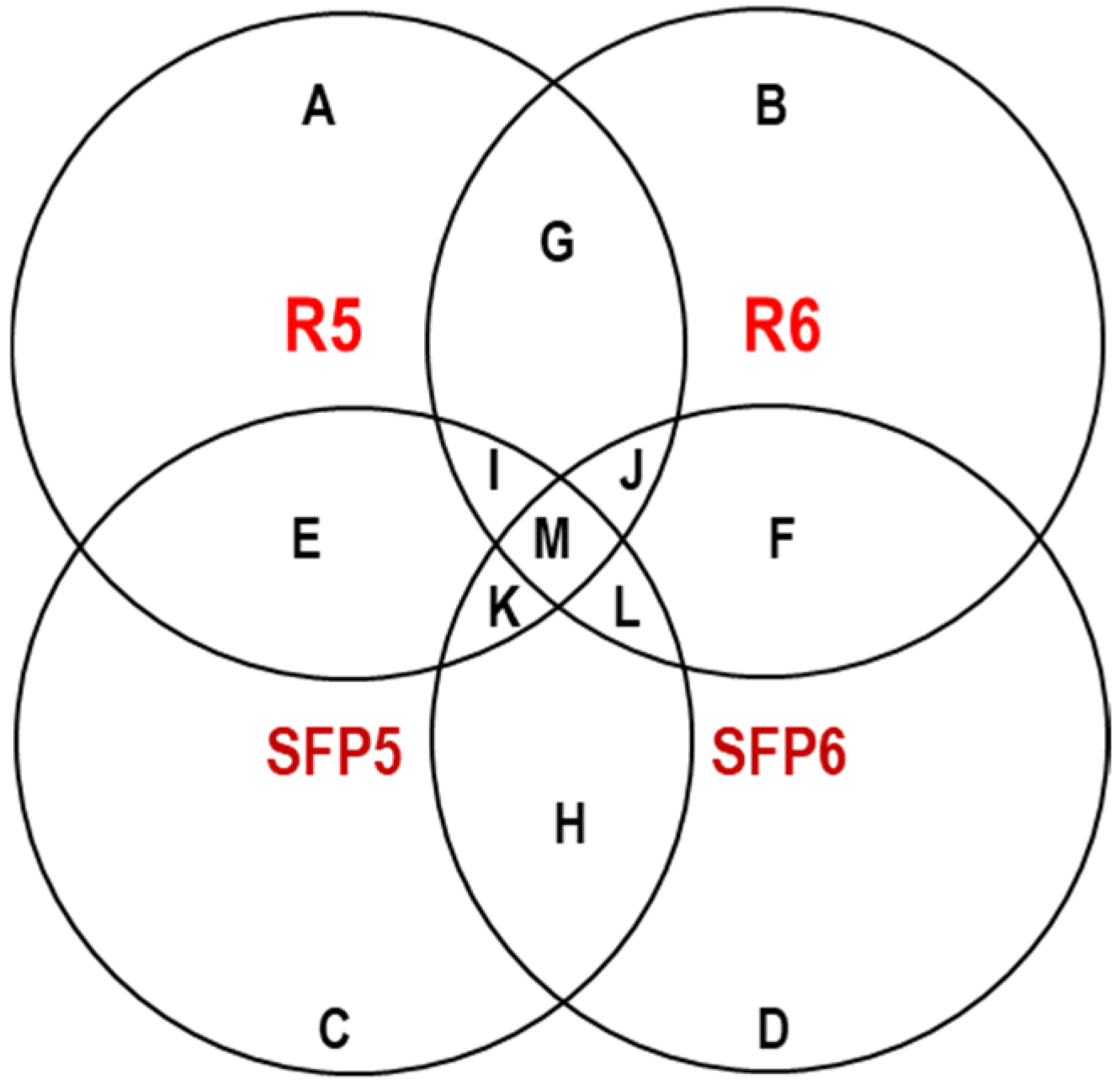
• i is the number of single units or hazards on the NPP site; I is the total number of units/hazards;
• j_i is the number of PIEs for i single units or hazards; j_i = 1…J_i, J_i is the total number of PIEs;
• k_ji is the number of sequences (scenarios) of j PIEs for i single units/hazards; k_ji = 1…K_ji; K_ji is the total number of sequences for j PIE_i.

The CDF evaluation by internal initiators is usually based on the analysis of ≈2 × 10¹ PIE groups and ≈10³ sequences leading to fuel damage. As a result of the quantification, about 10⁴ minimal cut sets for CDF could be received. In emergencies, the ‘sure choices’ over ‘choices that contain ambiguity’ alternatives to specific sequences must be compared in risk analysis. This includes not just accounting for failures of the structures, systems, and components (SSCs) but also needs to monitor the holistic context and take into account its impact on risk and “two-fold inference” perception. The contextual site PSA can be oriented both to a specific emergency sequence and general risk.

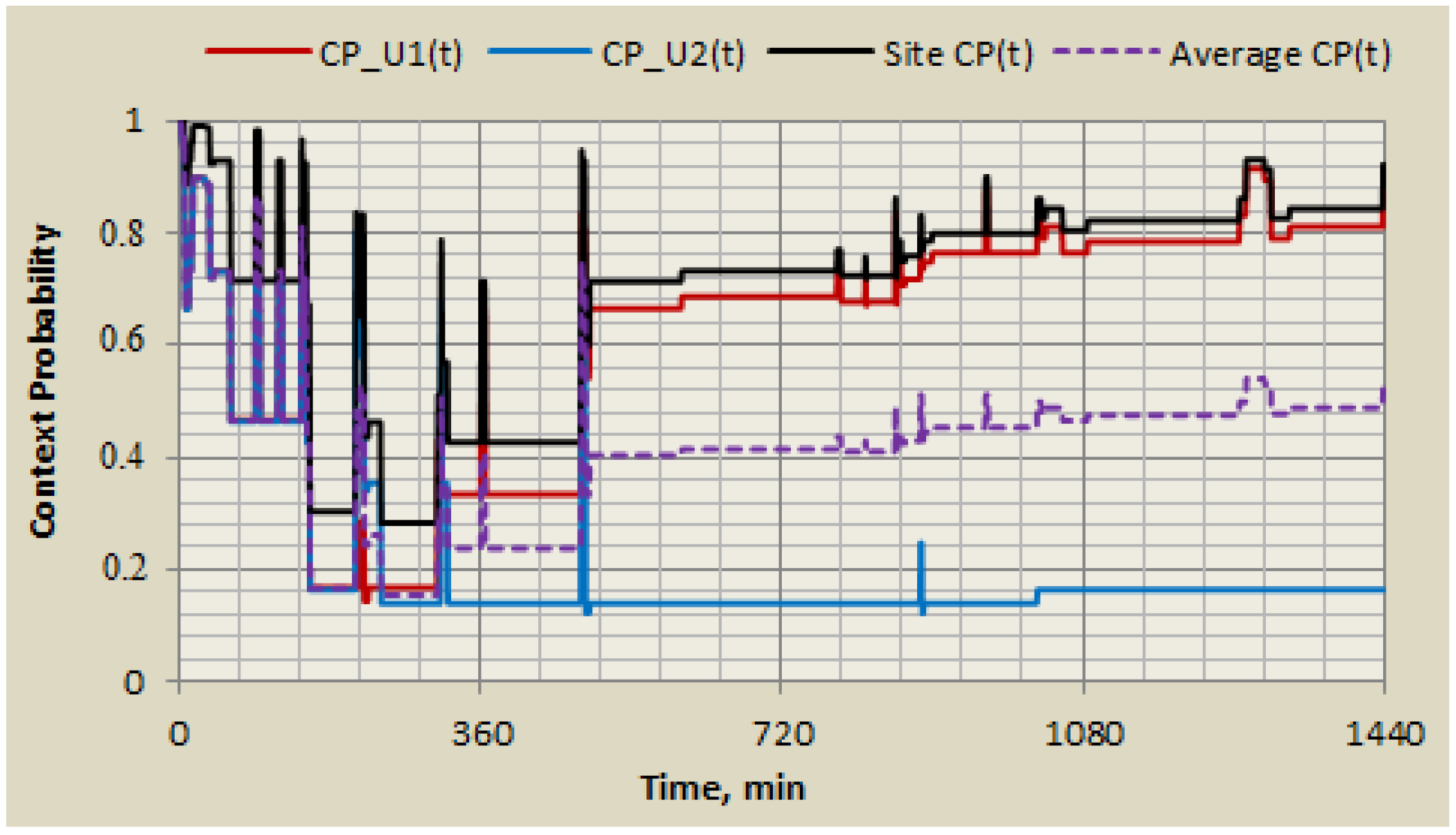
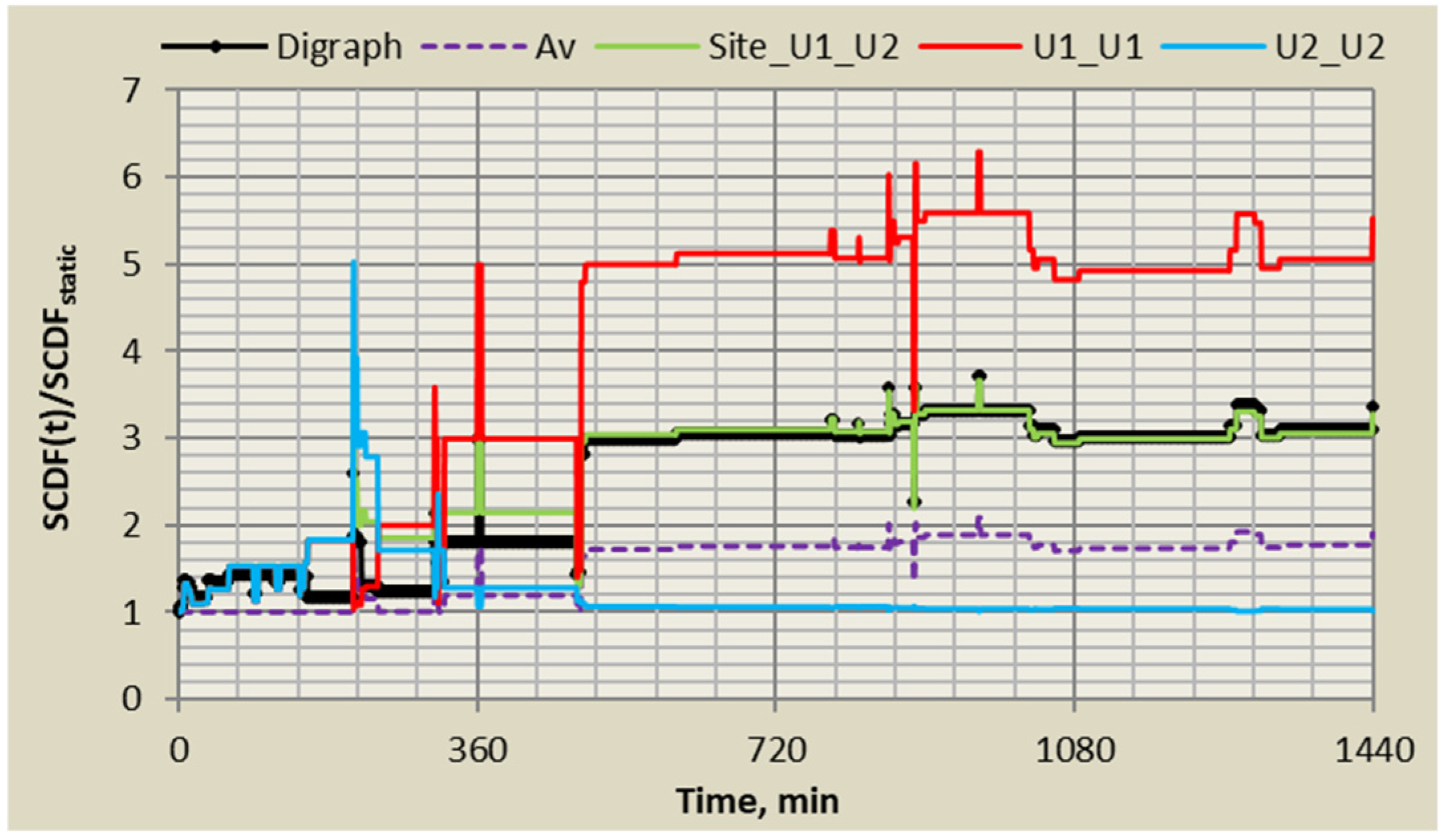
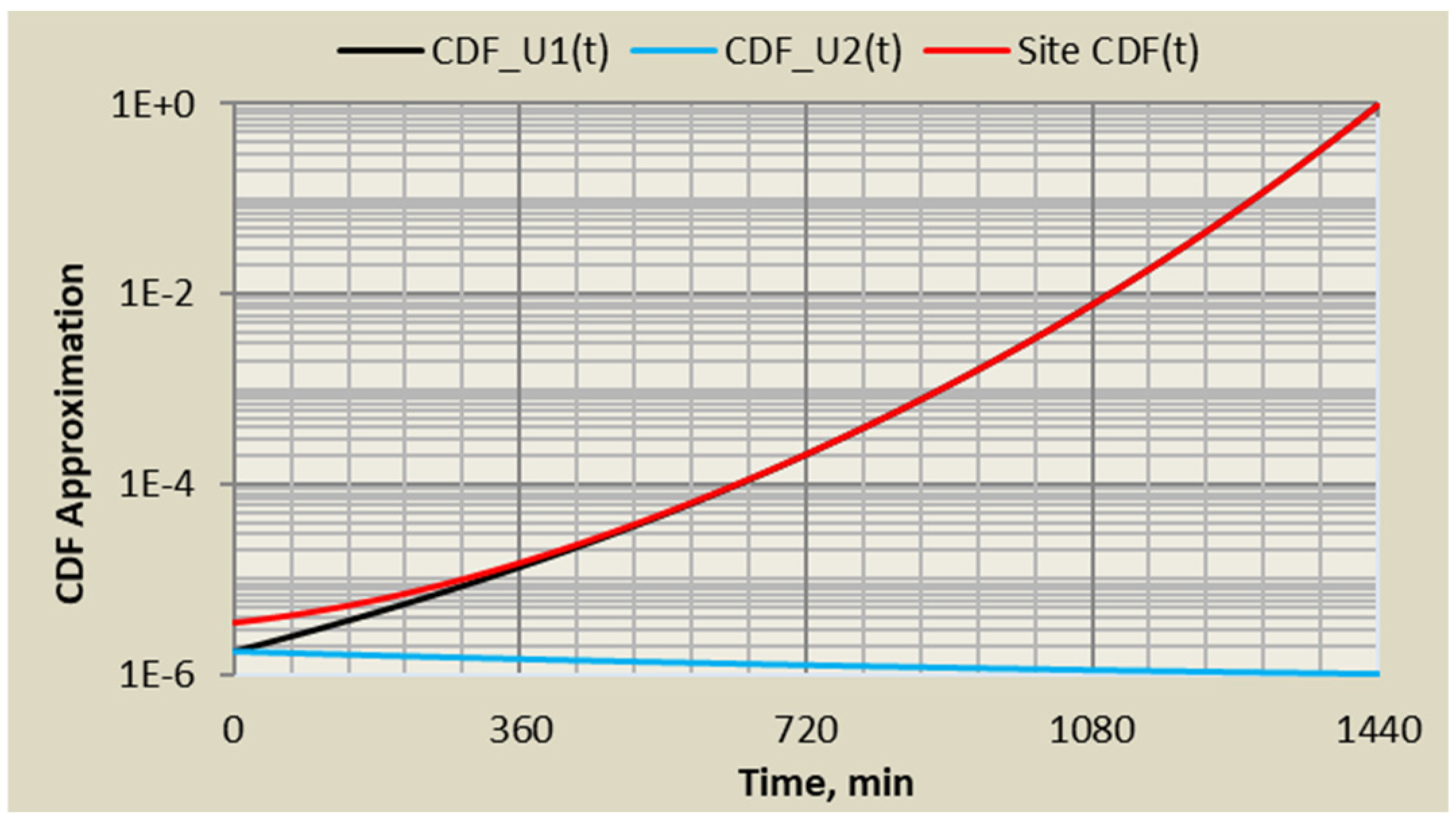
5.2. Example for a Contextual Site PSA

In the contextual site PSA example below, the deterministic data for PM are extracted out of the State-Of-the-Art Reactor Consequence Analyses (SOARCAs) project of the US NRC (2013), where a TH model with MELCOR 1.8.6 is used for simulation of the long-term station blackout (LTSBO) of the two-unit NPP “Surry” with pressurized water reactor (PWR). The ‘unmitigated’ unit 1 (U1) and ‘mitigated’ unit 2 (U2) LTSBO timelines are based on the results of TH and accident analyses, as described in [9].

A digraph decision-making model for a two-unit NPP “Surry” site is shown in [6]. However, only a simple sub-graph (7 nodes) of this model is used for calculation of the CP^Site (t) of the emergency operation facility (EOF) crew by CP_i^S (t) of the MCR1 and MCR2 crews.

Based on Equation (1), the following Equation (2) is for calculating the SCDF (t) on the NPP site in time for contextual MUPSA of LTSBO sequences:

$$\begin{array}{c}SCDF(t)={\sum }_{i=1}^I{\int }_{t_i}^{T_i}{\displaystyle \frac{{CP}^{Site}\left(t\right)\times {CDF}_i^S\left(t\right)}{{CP}_i^S(t)}}.\end{array}$$

(2)

Dynamic assessments of CP_i^S and CP^Site during the LTSBO for U1, U2, and NPP site are presented in Figure 8, for 24 h (1440 min). Figure 9 shows a comparison between dynamic curves of the relations between SCDF (t) and SCDF_static (≈2 × 10⁻⁶ per reactor-year) for 1440 min (24 h), obtained by the standard PSA level 1 model of the NPP “Surry” site, where ‘Digraph’, ‘Av’, and ‘Site_U1_U2’ are for a context with ‘mitigated’ and ‘unmitigated’ scenarios; ‘U1_U1’ and ‘U2_U2’ are for a context with two ‘unmitigated’ or ‘mitigated’ LTSBO scenarios accordingly.

It can be seen from Figure 9 that the difference between the ‘Digraph’ and ‘Site_U1_U2’ models results is negligible. It means that there is no need to use the full PET model to calculate the cognitive error probability (CEP) of MCR crews and the CCPs for mutual communication between crews. It can be replaced by a simple reliability formula (CP^Site = CP₁ + CP₂ − CP₁ × CP₂) to derive the approximate context of the NPP site (CP^site) from the aggregated contexts for the MCR1 (CP_U1) and MCR2 (CP_U2). However, this is not advisable when there are detailed contexts for other local operators and crews [6], and as shown in the Fukushima Daiichi accident analysis or for the HRA using the PET method [9].

The use of dynamic context assessment with the PET method is useful not only for dynamic contextual site PSA and weighing the severity of accident sequences and comparing and evaluating conservativeness of the PSA models (see [6]), but also for reducing the uncertainty and ambiguity of outcomes for dynamic and static risks. For example, in Figure 10 is shown the approximation of CDF (t) based on the LTSBO example, without taking into account the standard risk monitoring inputs (SSC statuses, changes in alignments, configurations, modes, and POSs).

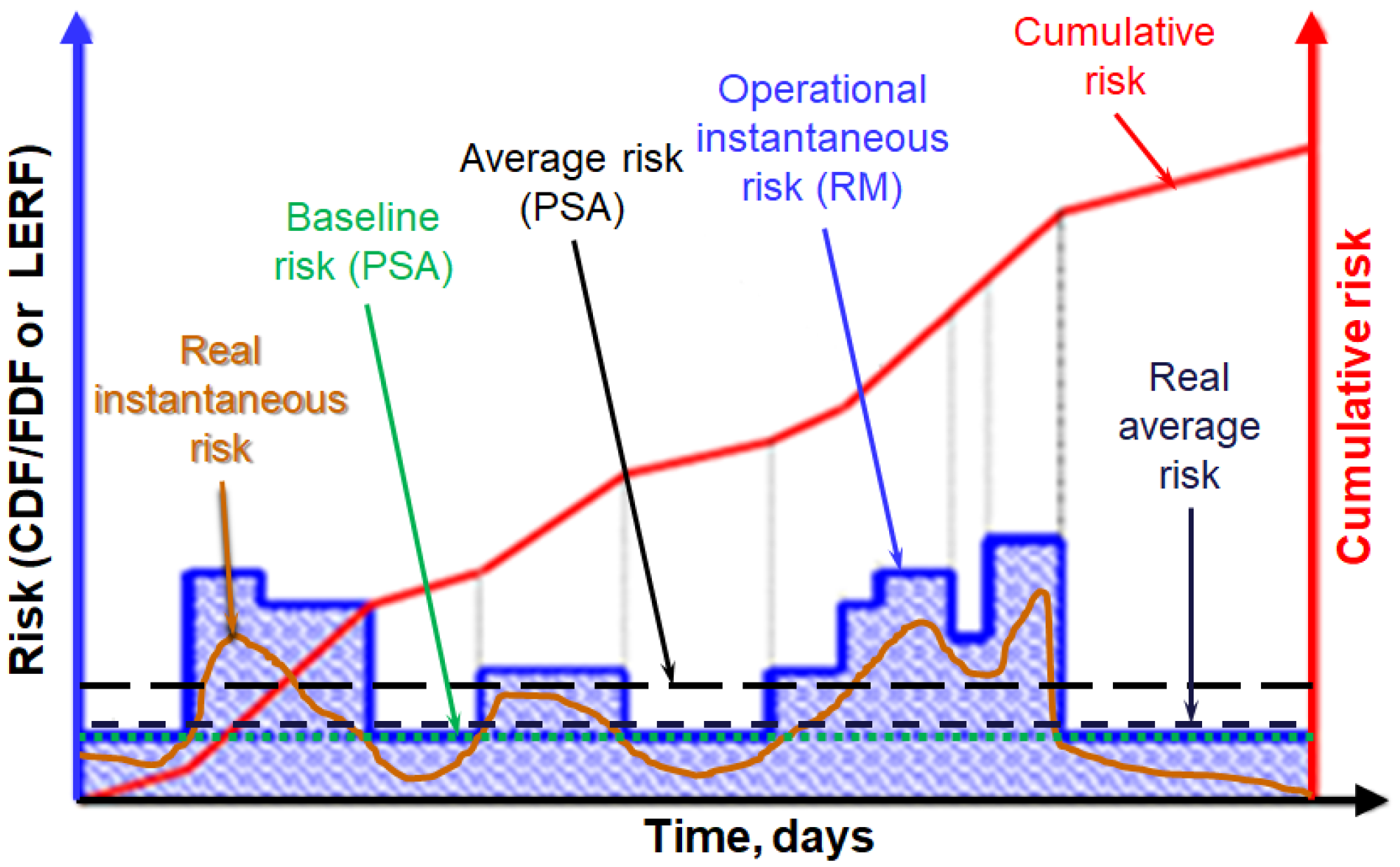
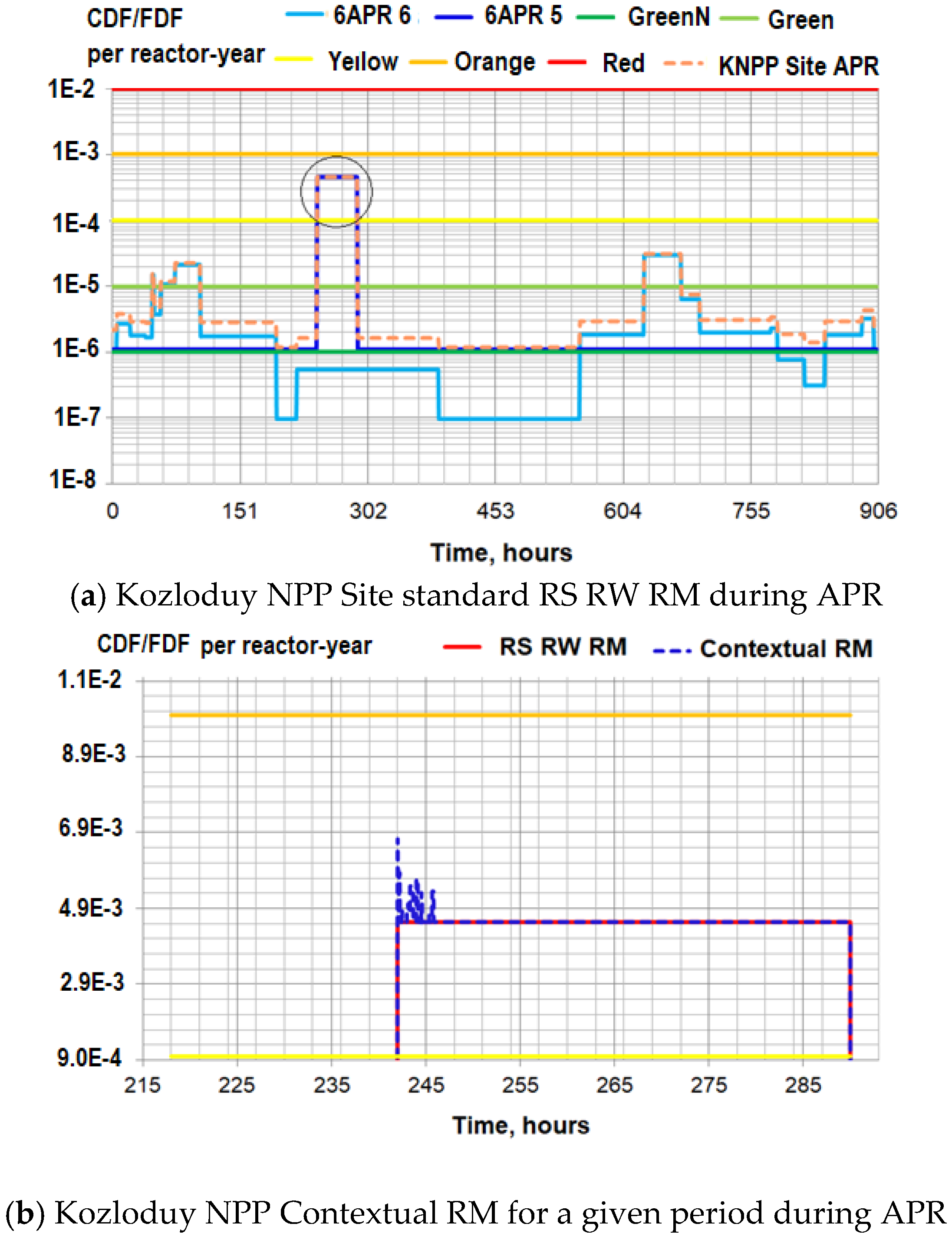
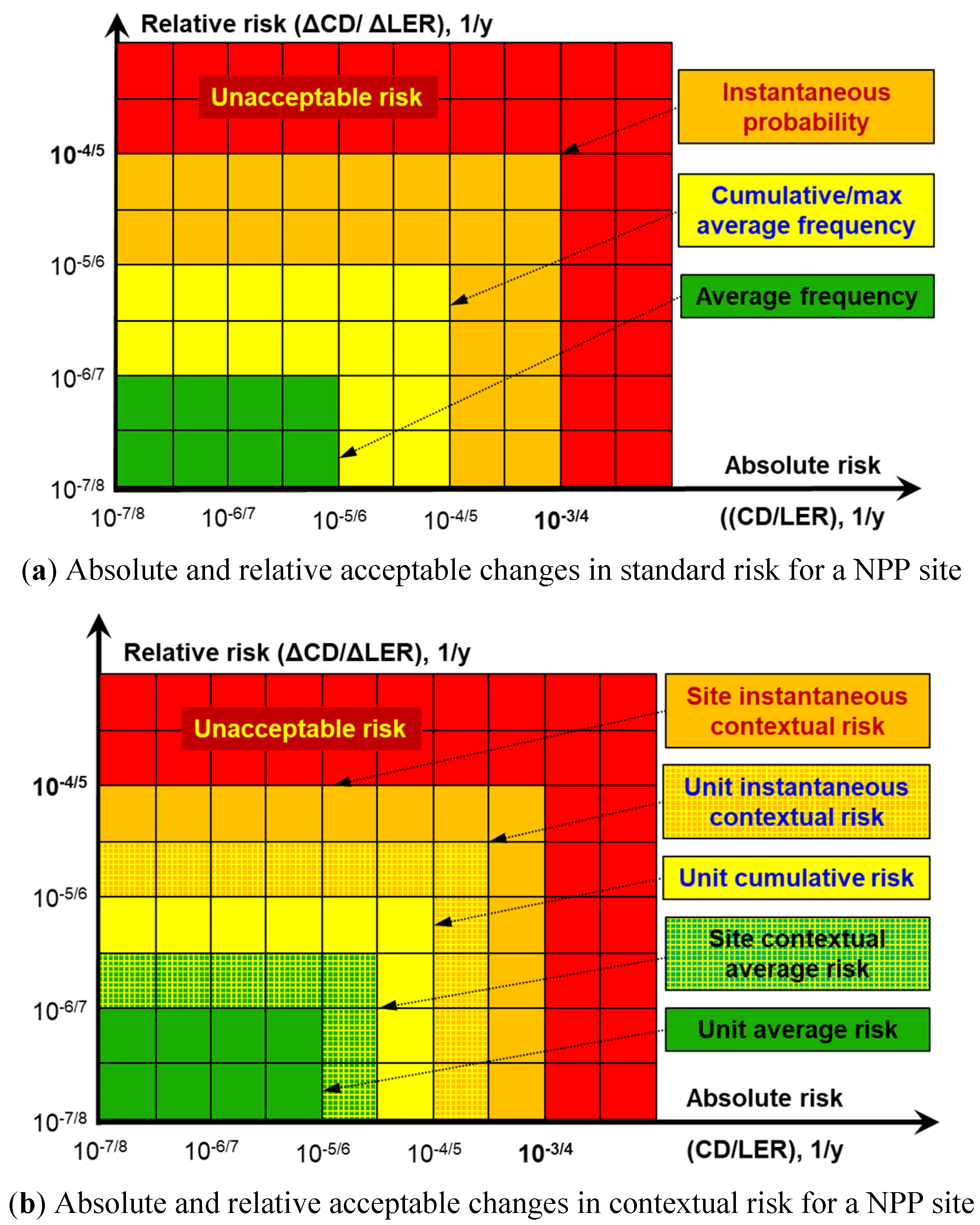
5.3. Dynamic Contextextual Risk Monitoring for Risk-Informed Decision Making and Applications

Advanced risk analysis needs multi-unit PSA and RM models that include dynamic contexts of as many NPP site facilities/hazards as possible: shared equipment, conditions and organization; inadequate EOPs and SAMGs; hazard-induced CCFs and HFEs during the scenario’s progression.

The IRIDM process application for the FAS requires performance and risk monitoring by reporting of all contexts, depending on the FAS life cycle. The following risk measures (CDF/FCF), as shown in Figure 11, can be calculated for use in risk-informed applications for the IRIDM.

Figure 12a,b show the differences and possibilities for decision making between the standard dynamic multi-unit RM by the Risk Spectrum Risk Watcher (RS RW) and its complementation by the contextual dynamic multi-unit RM during an annual planned repair (APR) of units 5 and 6 of the Kozloduy NPP in 2020.

Dynamic contextual risk monitoring (DCRM) should calculate actual and hypothetical curves of dynamic risk, planned schedule activities, defined allowed completion time (ACT) for restoration, compensation, and defense-in-depth (DiD). DCRM should take into account all explicit and implicit dependencies among all units, hazards, and impacts of important SSCs, environmental, human, organizational and testing factors, changes in FAS alignments, configurations, and operating modes in different POSs, in order to increase management effectiveness and minimize failures, errors, and uncertainty.

The DCRM must calculate the actual and hypothetical risk curves of planned maintenance, repair activities, ACTs and equipment restoration, in-depth corrective and compensatory protection measures, explicit and implicit dependencies, and changes in the SSCs, their configurations, tests, and modes of operation in different plant operating states of all NPP units, hazards, and impacts, and HF and organizational factors to increase safety, efficiency, and reduce the likelihood of wrong risk-informed decisions. The evaluation and use of dynamic risk fluctuations requires the introduction of different regulatory goals for acceptable static and dynamic risk changes for FASs as NPPs. Figure 13 shows examples of such goals formulated for a three-barrier average, cumulative and instantaneous risk measures that could be used for the standard and contextual IRIDM [9].

6. Conclusions

Quantification and representation of aleatory and epistemic uncertainties are already defined in current static and statistical PSAs. However, contextual uncertainties should better reflect the dynamics and determinism of the decision-making process in a particular FAS by qualifying and quantifying the operational context.

The IRIDM process for nuclear systems requires risk contextualization, which can be performed explicitly and implicitly by probabilistically modeling all NPP site dependencies and decision-maker contexts.

Site contextual RM should be performed in an integrated manner by including DSA and PSA aspects and considering the whole dynamic context in the event progression.

Development of an integrated system for dynamic contextual RM based on FAS performance during operation or simulation can help reduce the use of expert judgment for a balanced IRIDM process. The PET context quantification procedure for explicit and implicit dependency modeling and uncertainty reduction can be used as a valuable complement to site contextual PSA.

The proposed approach can be used to implement existing risk-informed decision-making methods by complementing static/statistical risk assessment with dynamic risk-informed and context-based assessment approach to better describe uncertainties and improve the interaction between PSA and DSA methods by better incorporating the latter methods into contextual evaluation.