A Vegetable Oil as Heat Transfer Fluid for Parabolic Trough Collector: Dynamic Performance Analysis under Ouagadougou Climate Conditions †
Abstract
:1. Introduction
2. Methodology
2.1. Parabolic Trough Collector Model
| Physical Model (See Figure 1) | Mathematical Model | |
|---|---|---|
| For the heat transfer fluid (HTF) energy balance: | (1) | |
| For the absorber pipe | (2) | |
| Similarly, the energy balance on the glass envelope is computed | (3) | |

2.2. Boundary and Initial Condition and Numerical Solution for the Proposed Model
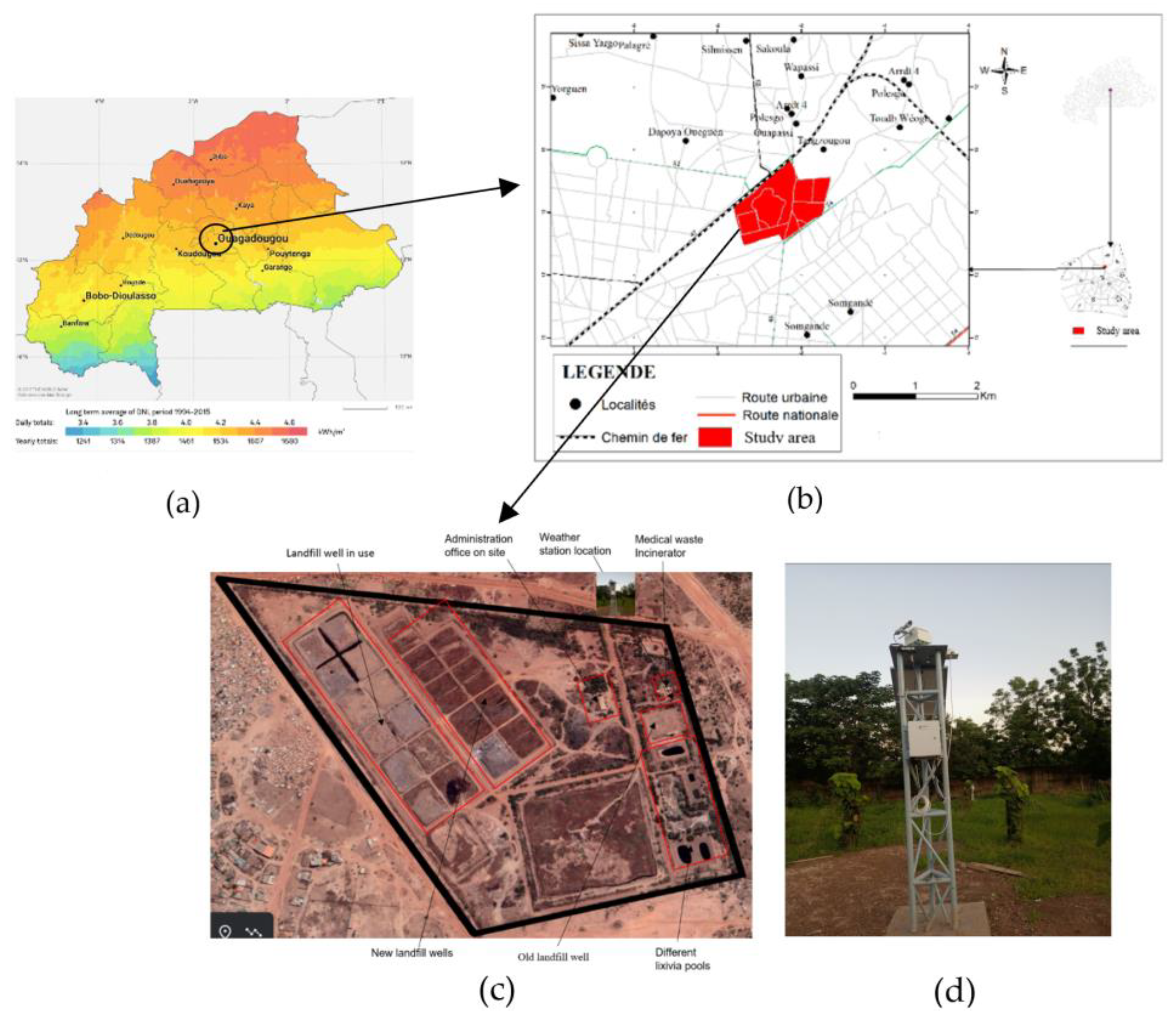
2.3. Study Area and Data Collection Materials
3. Results and Discussions
3.1. Model Validation
3.2. PTC Performance under Ouagdougou Climate Condition
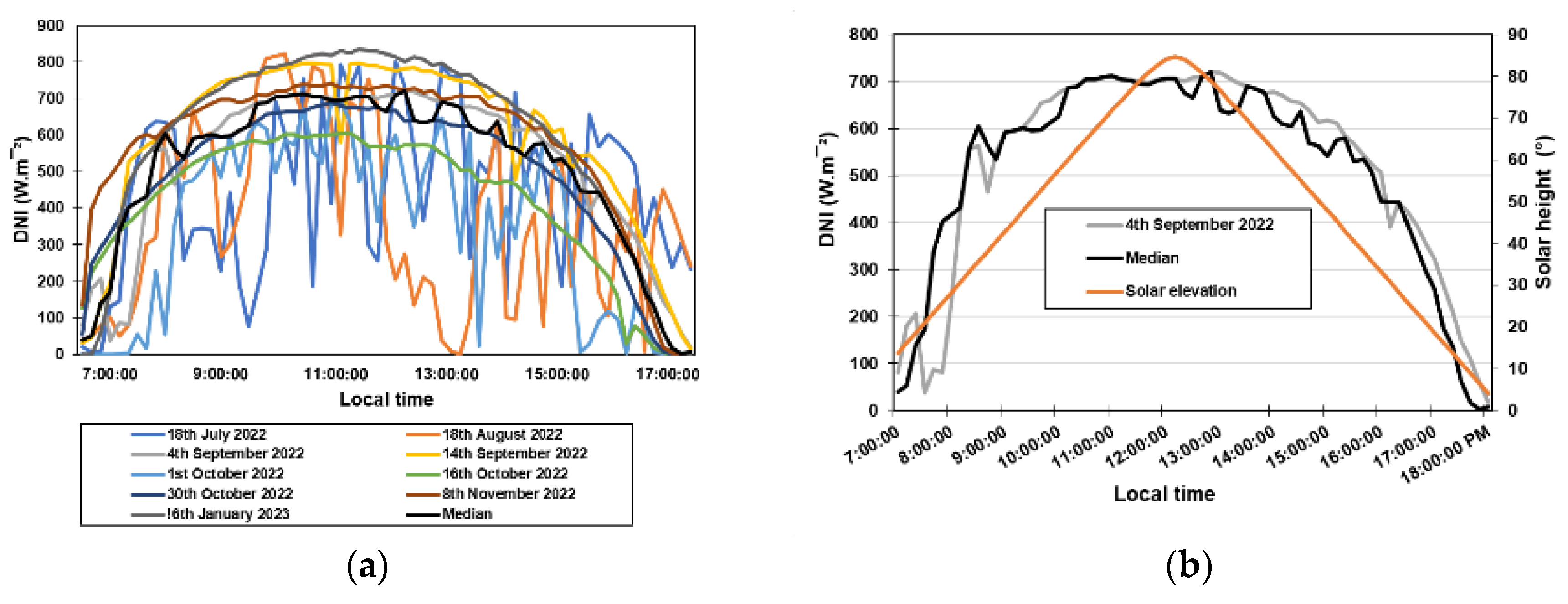
3.2.1. Direct Normal Irradiance for Some Days from July 2022 to January 2023
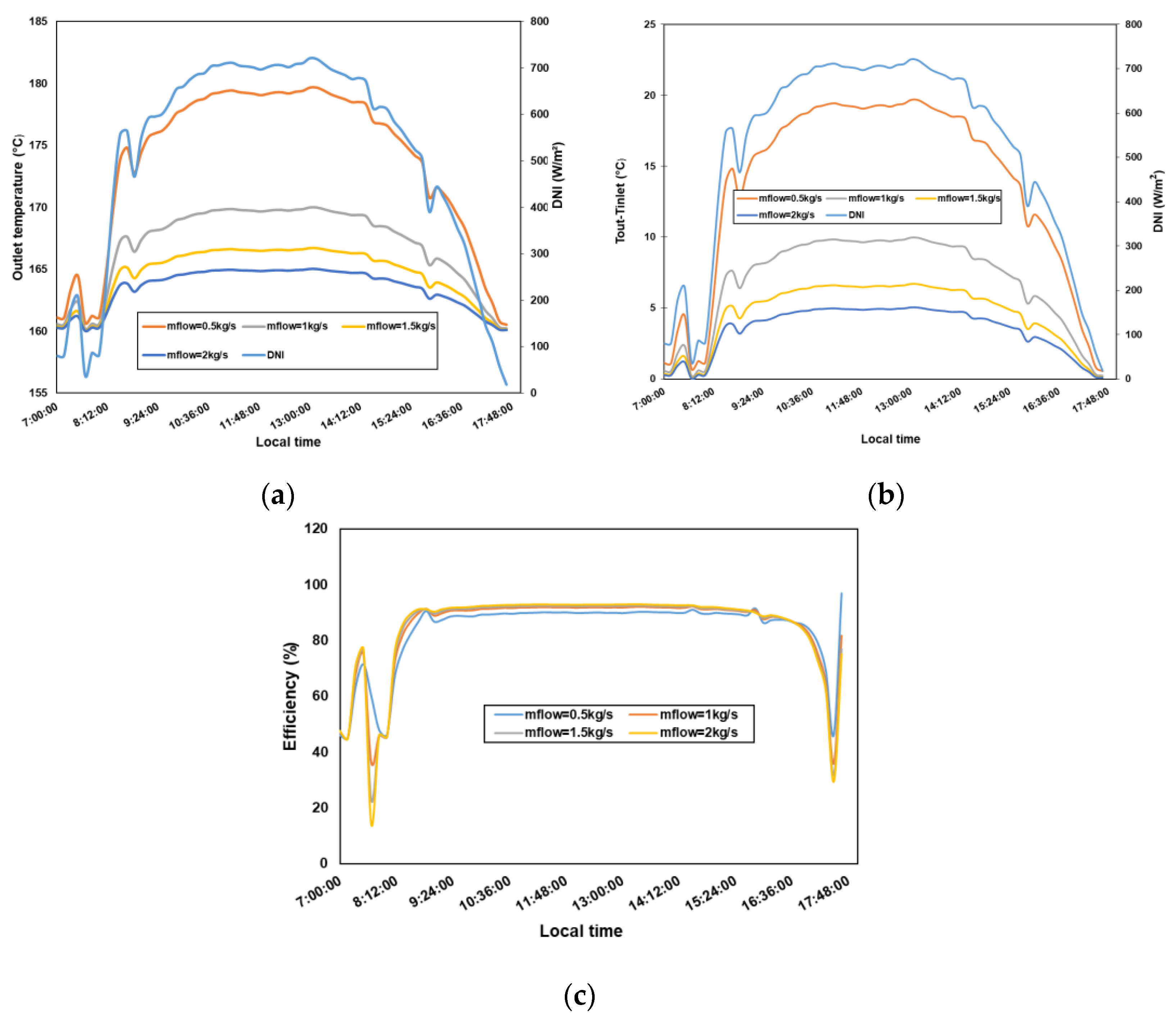
3.2.2. The Effect of Mass Flow Rate on Collector Performance
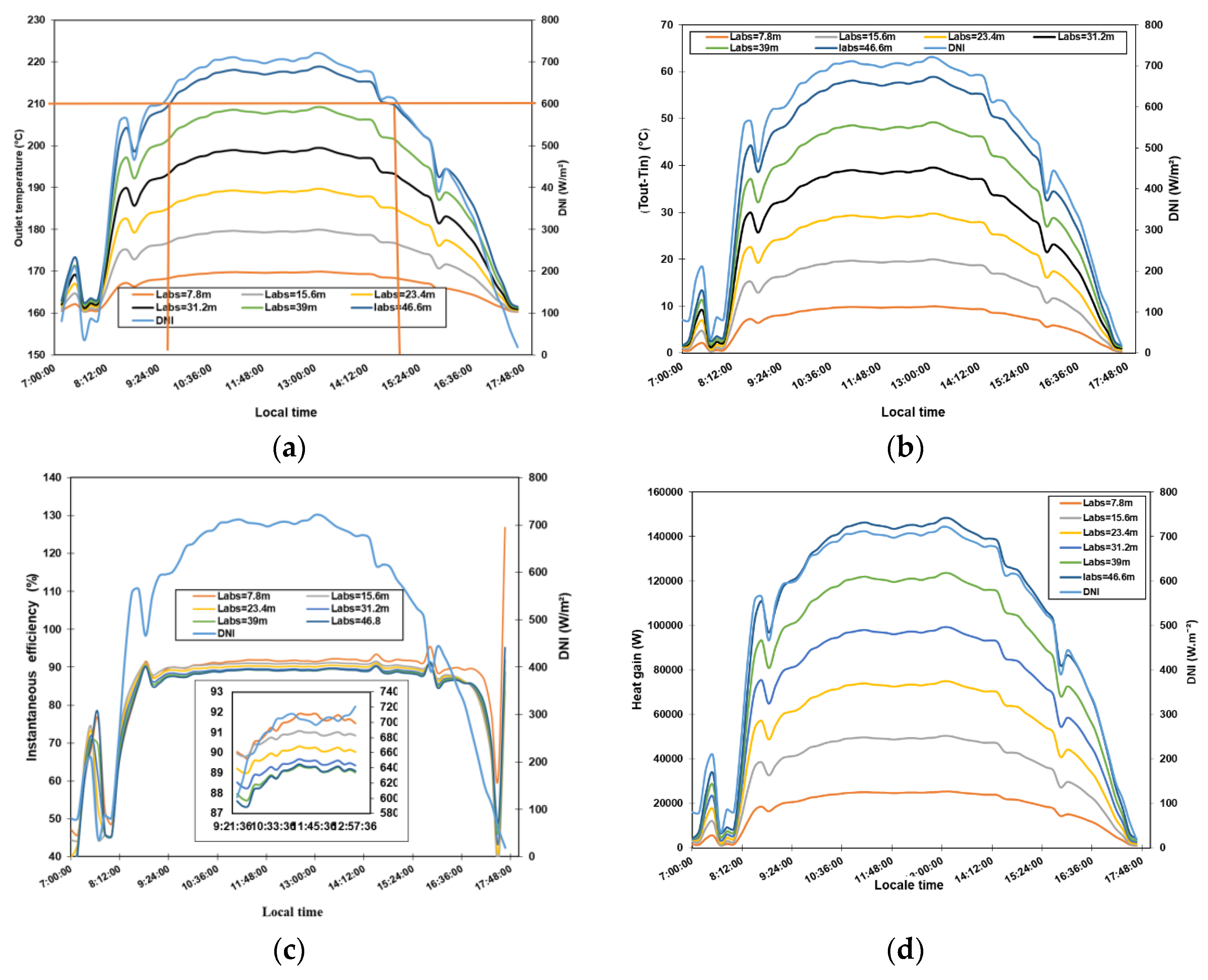
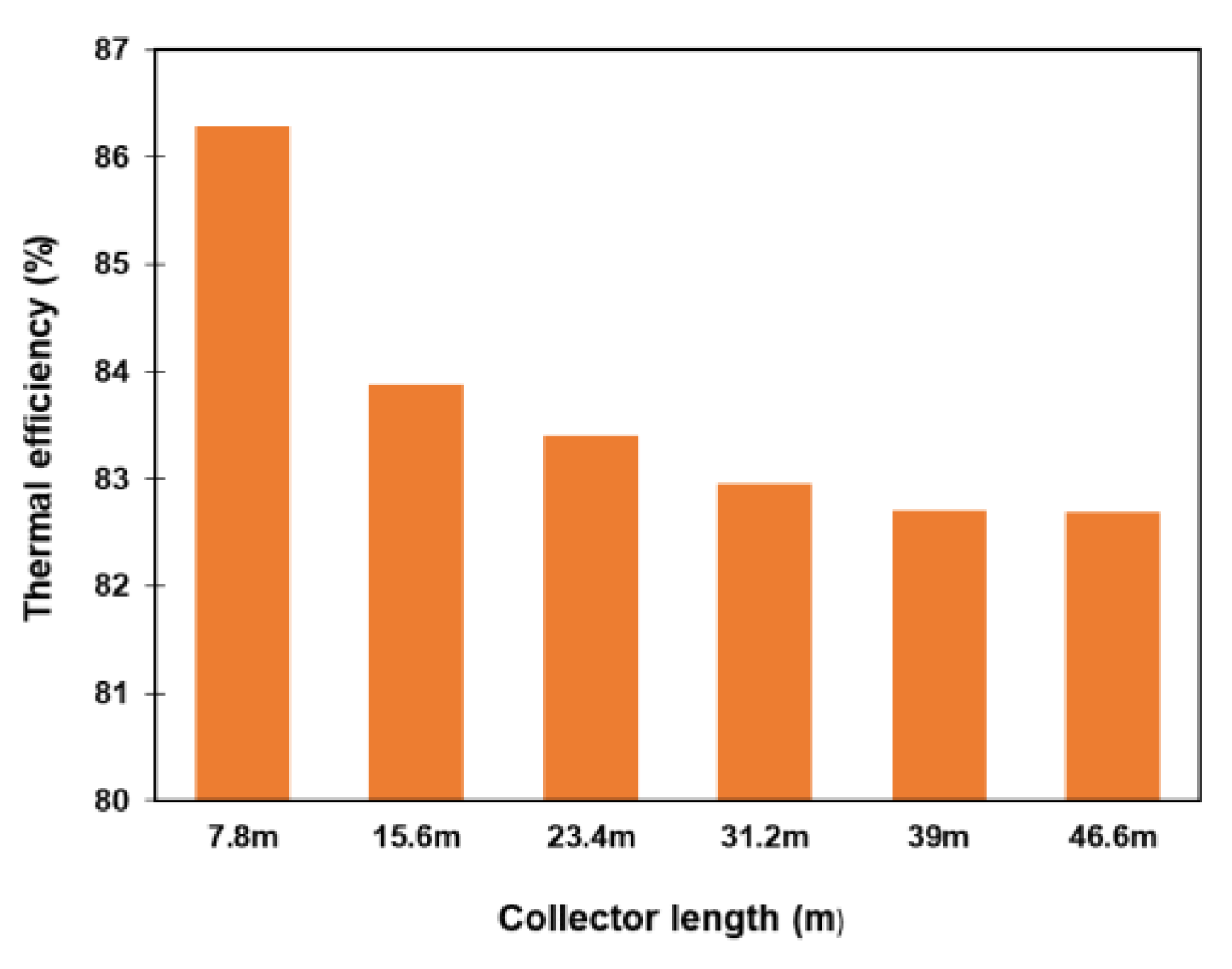
3.2.3. The Effect of Collector Length Rate on Collector Performance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Eltawil, M.A.; Zhengming, Z.; Yuan, L. A review of renewable energy technologies integrated with desalination systems. Renew. Sustain. Energy Rev. 2009, 13, 2245–2262. [Google Scholar] [CrossRef]
- Ummadisingu, A.; Soni, M.S. Concentrating solar power—Technology, potential and policy in India. Renew. Sustain. Energy Rev. 2011, 15, 5169–5175. [Google Scholar] [CrossRef]
- Boubou, B.; Muritala, I.K.; Makinta, B.; Tizane, D.; Christian, T.G.; Jacques, N.; Téré, D.; Antoine, B. Review on Thermocline Storage Effectiveness for Concentrating Solar Power Plant. Energy Power Eng. 2021, 13, 343–364. [Google Scholar] [CrossRef]
- Sattler, J.C.; Caminos, R.A.C.; Atti, V.; Ürlings, N.; Dutta, S.; Ruiz, V.; Kalogirou, S.; Ktistis, P.; Agathokleous, R.; Alexopoulos, S.; et al. Dynamic simulation tool for a performance evaluation and sensitivity study of a parabolic trough collector system with concrete thermal energy storage. AIP Conf. Proc. 2020, 2303, 160004. [Google Scholar] [CrossRef]
- Vignarooban, K.; Xu, X.; Arvay, A.; Hsu, K.; Kannan, A.M. Heat transfer fluids for concentrating solar power systems—A review. Appl. Energy 2015, 146, 383–396. [Google Scholar] [CrossRef]
- Padilla, R.V.; Demirkaya, G.; Goswami, D.Y.; Stefanakos, E.; Rahman, M.M. Heat transfer analysis of parabolic trough solar receiver. Appl. Energy 2011, 88, 5097–5110. [Google Scholar] [CrossRef]
- Babikir, M.H.; Njomo, D.; Barka, M.; Chara-dackou, V.S.; Kondji, Y.S.; Khayal, M.Y. Thermal modeling of a parabolic trough collector in a quasi-steady state regime Thermal modeling of a parabolic trough collector in a quasi-steady state regime. J. Renew. Sustain. Energy 2021, 13, 013703. [Google Scholar] [CrossRef]
- Haro, K.; Ouarma, I.; Sanogo, O.; Abdoulaye, C.; Tubreoumya, G.C.; Nana, B.; Bere, A.; Koulidiati, J. Evaluation de l’empreinte carbone d’une Installation de Stockage des Déchets Non Dangereux (ISDND): Cas du centre traitement et de valorisation des déchets (CTVD) sis à Polesgo (Ouagadougou). J. Phys. Soaphys 2019, 1, C19A5-1–C19A5-5. [Google Scholar] [CrossRef]
- Haro, K.; Ouarma, I.; Nana, B.; Bere, A.; Tubreoumya, G.C.; Kam, S.Z.; Laville, P.; Loubet, B.; Koulidiati, J. Assessment of CH4 and CO2 surface emissions from Polesgo’s landfill (Ouagadougou, Burkina Faso) based on static chamber method. Adv. Clim. Chang. Res. 2019, 10, 181–191. [Google Scholar] [CrossRef]
- Dudley, V.E.; Kolb, G.J.; Mahoney, A.R.; Mancini, T.R.; Matthews, C.W.; Sloan, M.; Kearney, D. Test Results: SEGS LS-2 Solar Collector; Report: SAND94-1884; Sandia National Laboratory: Albuquerque, Mexico, 1994; Volume 140. [Google Scholar]
- Bagré, B.; Boukar, M.; Muritala, I.K.; Mortey, E.M.; Ouarma, I.; Tera, S.; Korsaga, A.; Rabani, A. Modelling and Simulation of a Sustainable Thermal Energy Storage System for Concentrating Solar Power (CSP) Plant Using Eco-Materials. JP J. Heat Mass Transf. 2023, 31, 147–161. [Google Scholar] [CrossRef]
- Powell, K.M.; Edgar, T.F. Modeling and control of a solar thermal power plant with thermal energy storage. Chem. Eng. Sci. 2012, 71, 138–145. [Google Scholar] [CrossRef]
- Visser, C.J.; Malan, P.A.G.; Meyer, P.J.P. Modelling Heat And Mass Flow Through Packed Pebble Beds: A Heterogeneous Volume-Averaged Approach. Doctoral Dissertation, University of Pretoria, Pretoria, South Africa, 2008. [Google Scholar]
- Xu, C.; Wang, Z.; He, Y.; Li, X.; Bai, F. Sensitivity analysis of the numerical study on the thermal performance of a packed-bed molten salt thermocline thermal storage system. Appl. Energy 2012, 92, 65–75. [Google Scholar] [CrossRef]
| Boundary Conditions | Initial Conditions | ||
|---|---|---|---|
| (4) | (5) | ||
| (6) | (7) | ||
| Hot heat transfer fluid leaves the collector, an adiabatic condition for the fluid. | (8) | If DNI is less than the minimum sunshine value to heat up the fluid, the outlet temperature is less than | |
| Case | DNI (W m−2) | (°C) | (°C) | (Model) | (Exp) | Model Error (°C) | |
|---|---|---|---|---|---|---|---|
| 1 | 937.9 | 0.6206 | 297.8 | 317.46 | 19.66 | 19.1 | 2.932 |
| 2 | 933.37 | 0.678 | 102.2 | 122.237 | 20.037 | 21.8 | 8.087 |
| 3 | 920.9 | 0.5457 | 379.5 | 397.1 | 17.6 | 18.5 | 4.86 |
| 4 | 880.6 | 0.6205 | 299 | 317.27 | 18.27 | 18.2 | 0.38 |
| 5 | 909.5 | 0.6580 | 250.7 | 270.5 | 19.8 | 18.7 | 5.88 |
| 6 | 968.2 | 0.6536 | 151 | 173.35 | 22.35 | 22.3 | 0.224 |
| 7 | 982.3 | 0.6350 | 197.5 | 219.7 | 22.2 | 22 | 0.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bagré, B.; Kam, S.Z.; Gounkaou, Y.W.; Boukar, M.; Muritala, I.K.; Nomao, H.S.D.; Armand, K.; Beré, A.; Daho, T. A Vegetable Oil as Heat Transfer Fluid for Parabolic Trough Collector: Dynamic Performance Analysis under Ouagadougou Climate Conditions. Mater. Proc. 2022, 11, 6. https://doi.org/10.3390/materproc2022011006
Bagré B, Kam SZ, Gounkaou YW, Boukar M, Muritala IK, Nomao HSD, Armand K, Beré A, Daho T. A Vegetable Oil as Heat Transfer Fluid for Parabolic Trough Collector: Dynamic Performance Analysis under Ouagadougou Climate Conditions. Materials Proceedings. 2022; 11(1):6. https://doi.org/10.3390/materproc2022011006
Chicago/Turabian StyleBagré, Boubou, Sié Zacharie Kam, Yomi Woro Gounkaou, Makinta Boukar, Ibrahim Kolawole Muritala, Harouna Sani Dan Nomao, Korsaga Armand, Antoine Beré, and Tizane Daho. 2022. "A Vegetable Oil as Heat Transfer Fluid for Parabolic Trough Collector: Dynamic Performance Analysis under Ouagadougou Climate Conditions" Materials Proceedings 11, no. 1: 6. https://doi.org/10.3390/materproc2022011006
APA StyleBagré, B., Kam, S. Z., Gounkaou, Y. W., Boukar, M., Muritala, I. K., Nomao, H. S. D., Armand, K., Beré, A., & Daho, T. (2022). A Vegetable Oil as Heat Transfer Fluid for Parabolic Trough Collector: Dynamic Performance Analysis under Ouagadougou Climate Conditions. Materials Proceedings, 11(1), 6. https://doi.org/10.3390/materproc2022011006






