Measuring the Thickness of Metal Films: A Selection Guide to the Most Suitable Technique
Abstract
1. Introduction
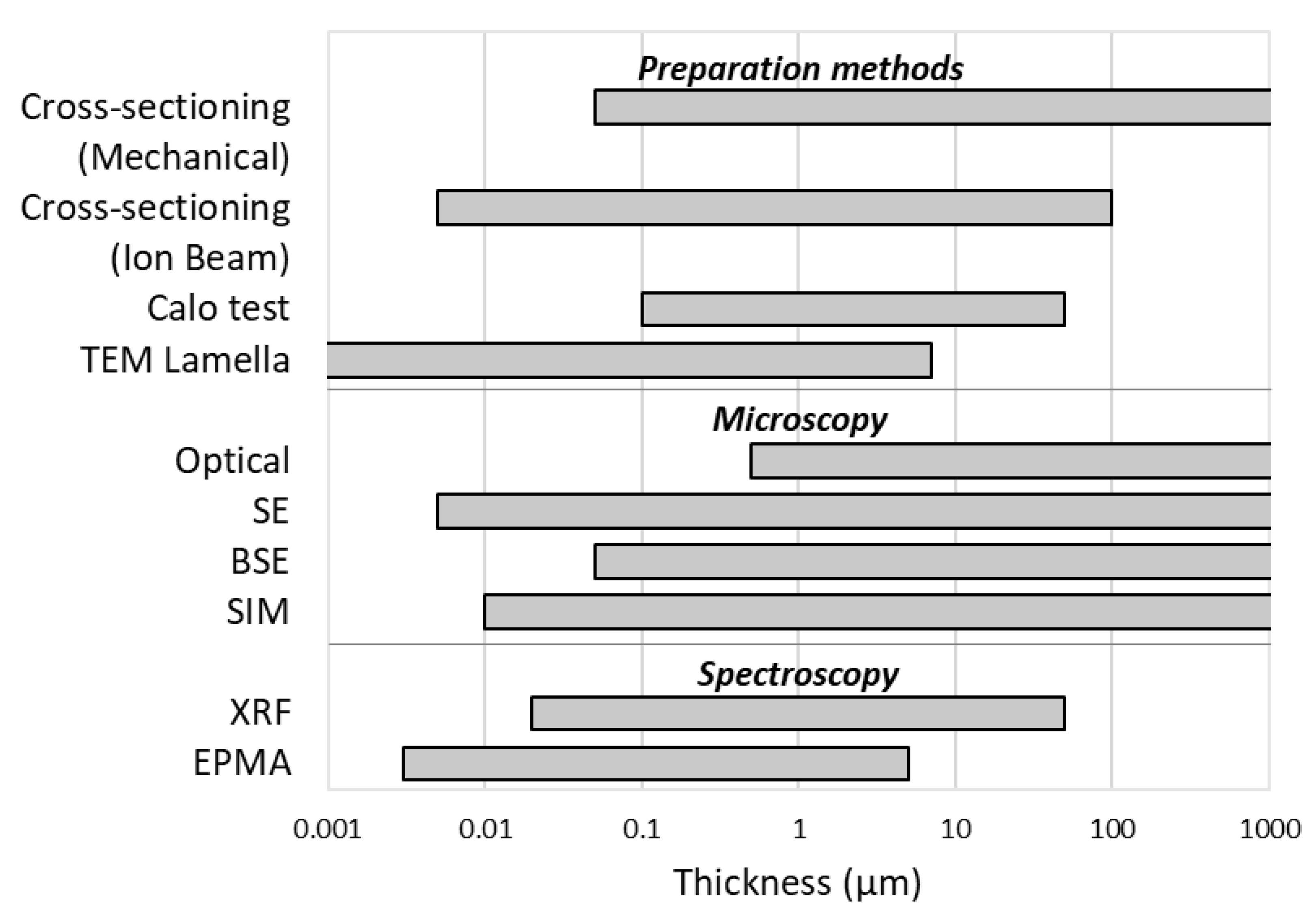
2. Destructive Techniques
2.1. Preparation Methods
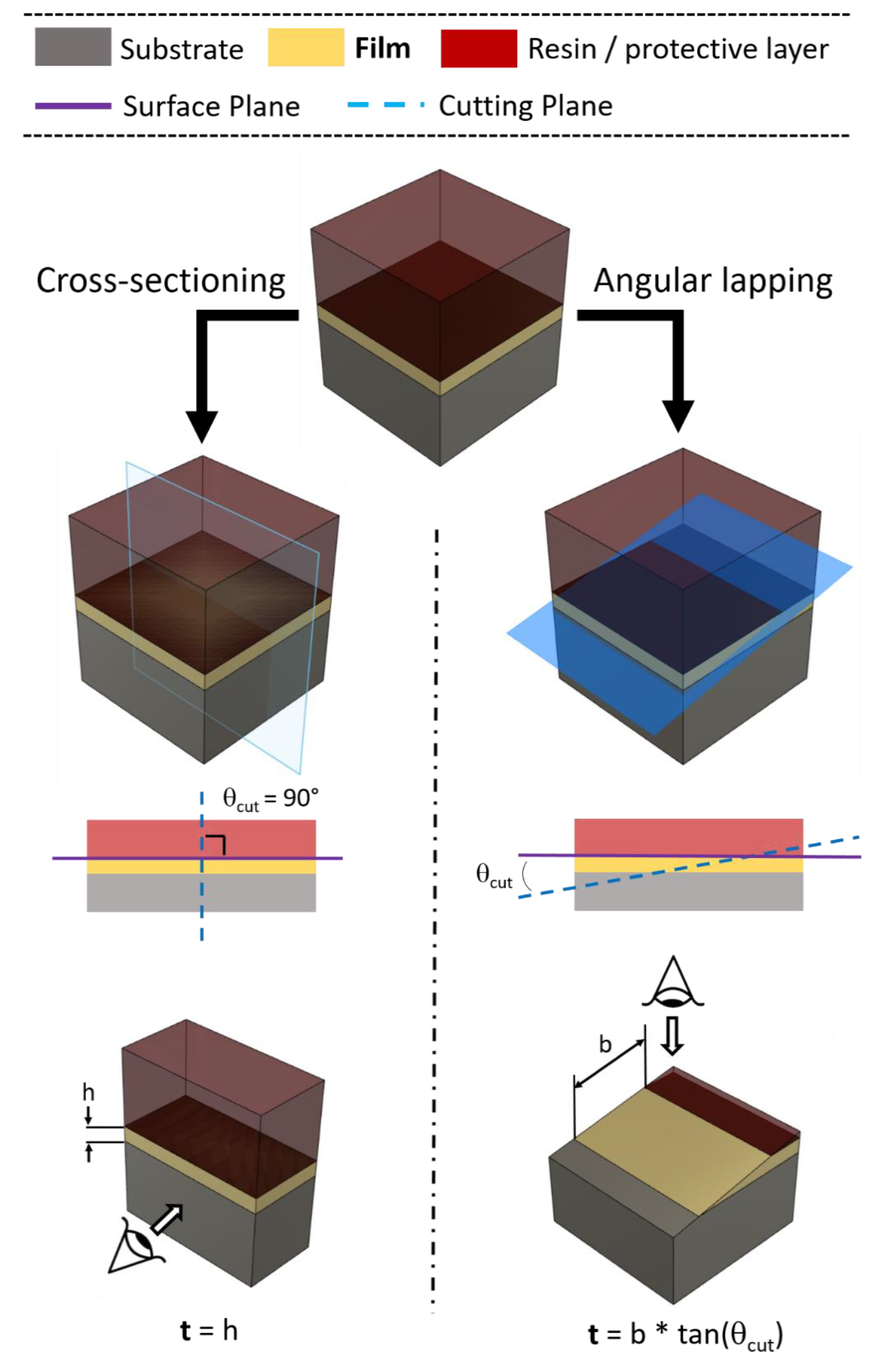
2.1.1. Mechanical Cross-Sectioning
2.1.2. Ion Beam Cross-Sectioning
2.1.3. Angle Lapping
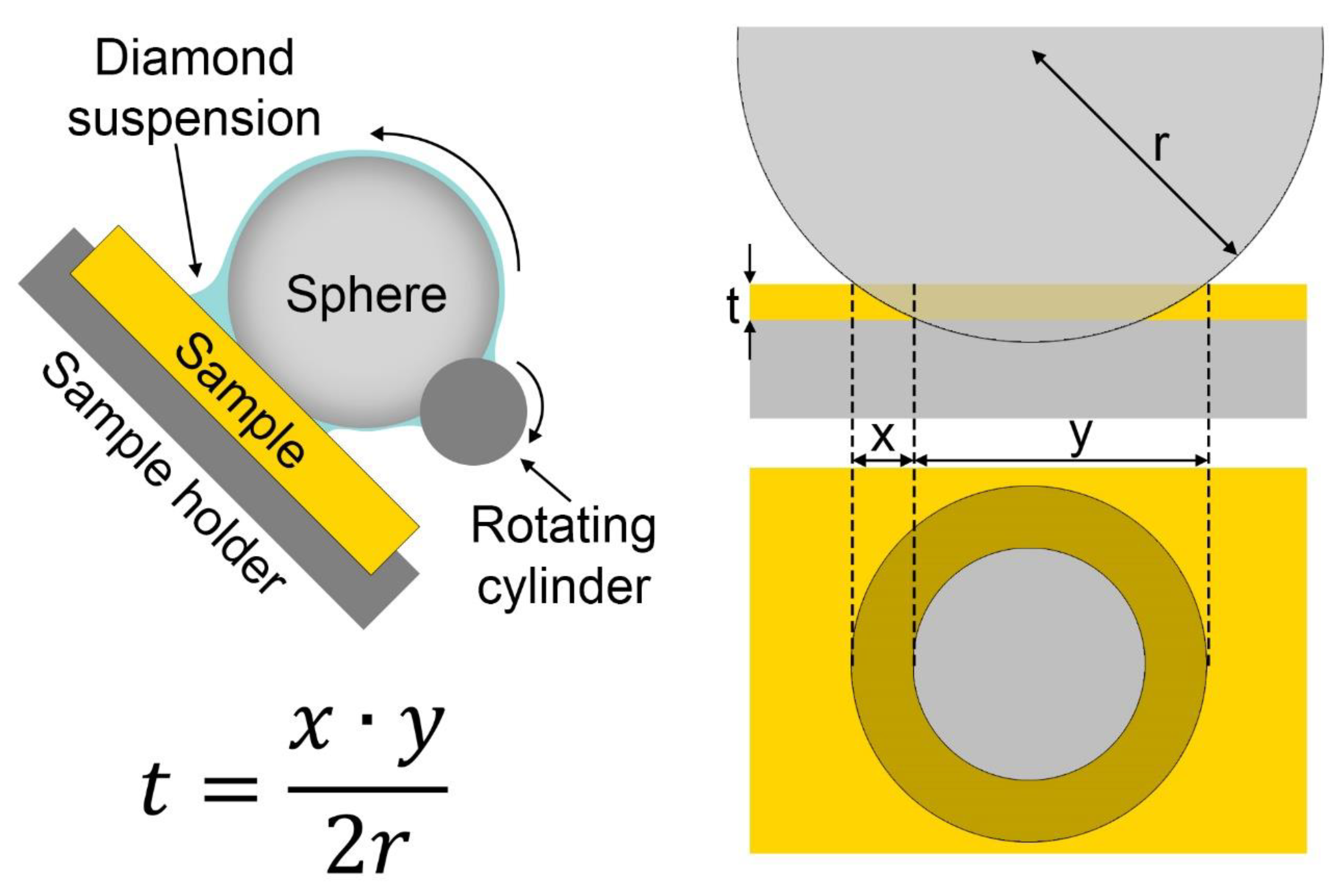
2.1.4. Calo Tester
2.1.5. TEM Lamella Preparation
2.2. Microscopic Analysis
2.2.1. Optical Microscopy
2.2.2. Electron Microscopy
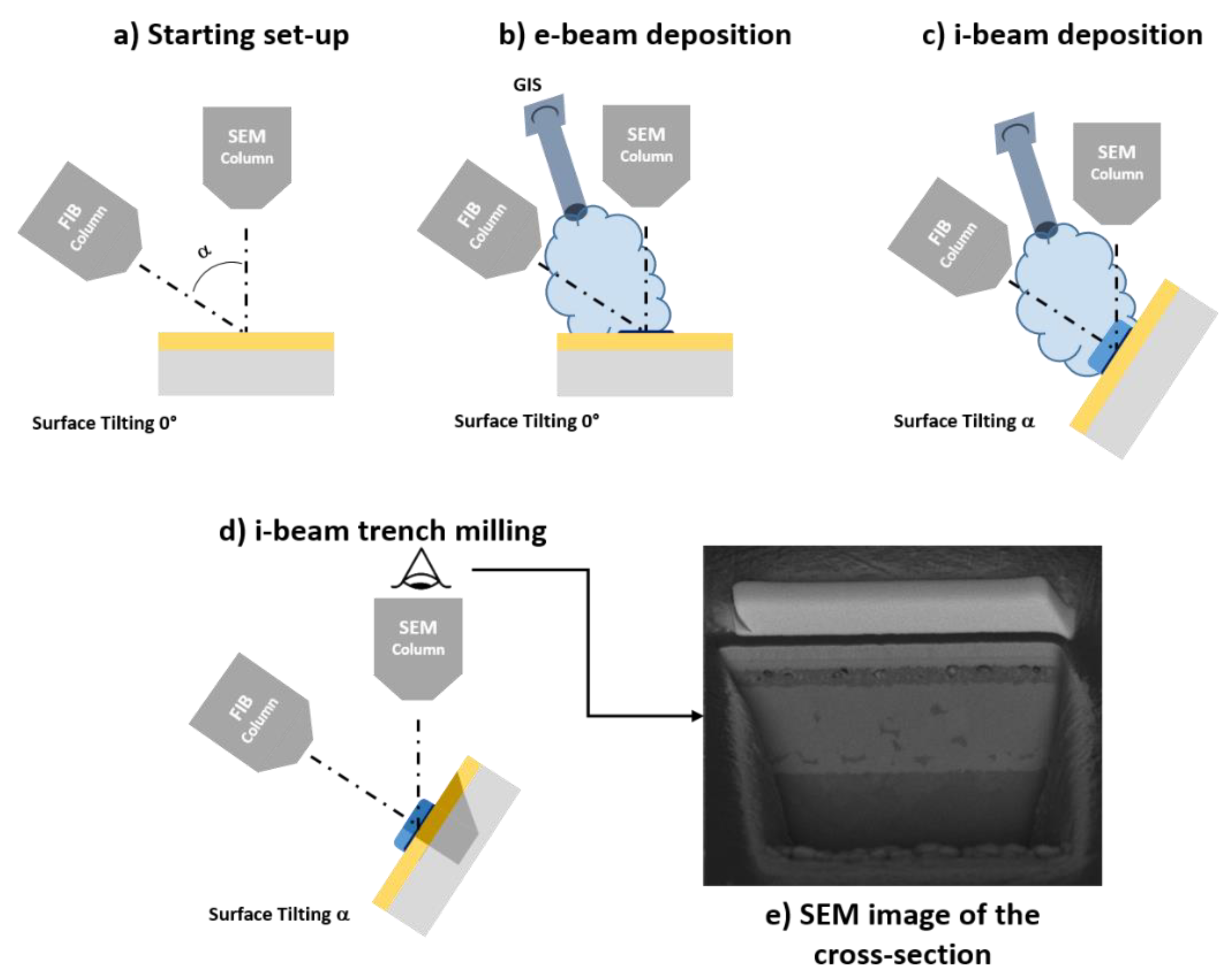
2.2.3. Focused Ion Beam Methods
2.2.4. Scanning Ion Microscopy
2.2.5. Data Analysis
3. Non-Destructive Techniques
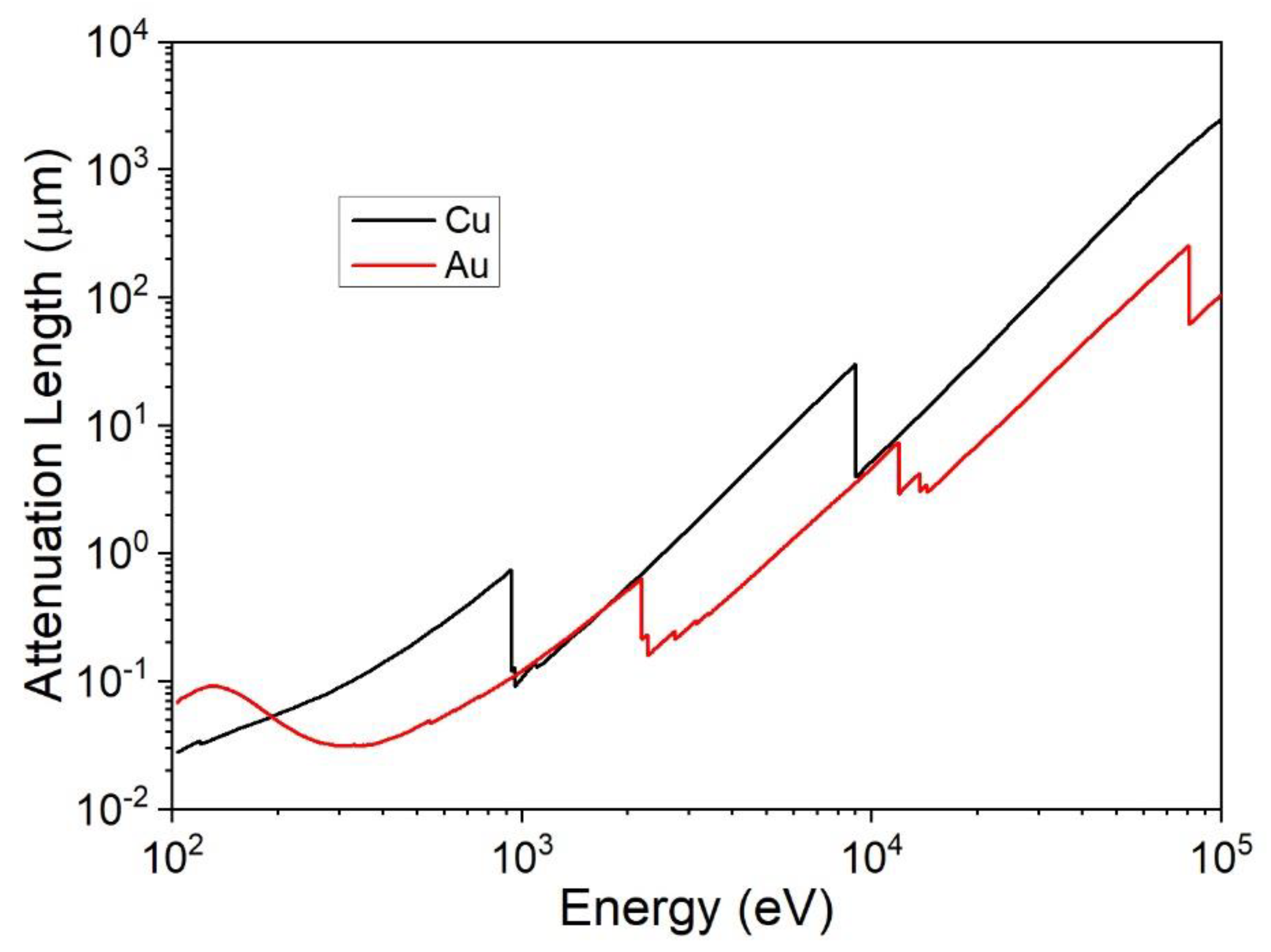
3.1. X-ray Fluorescence Spectroscopy
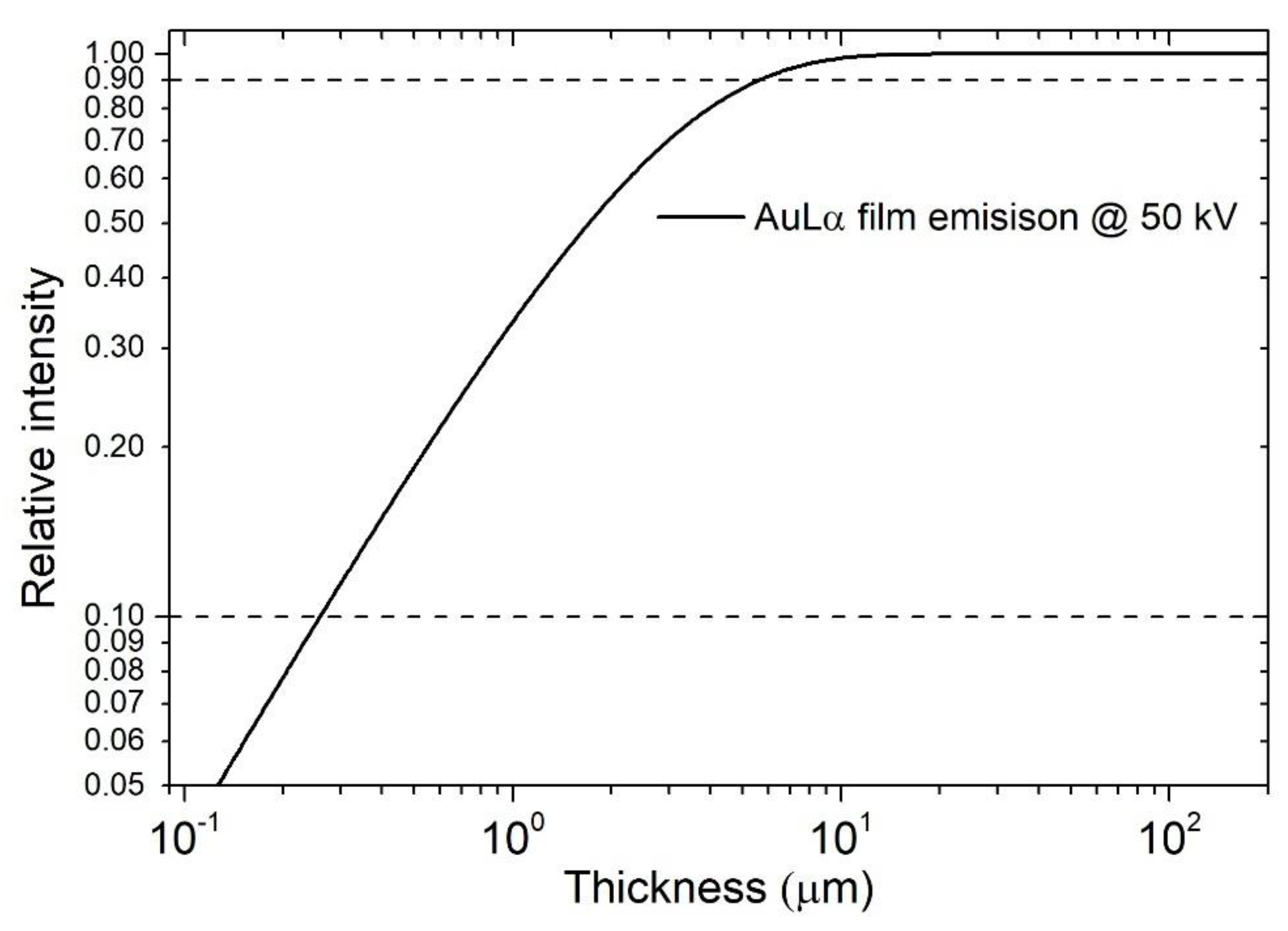
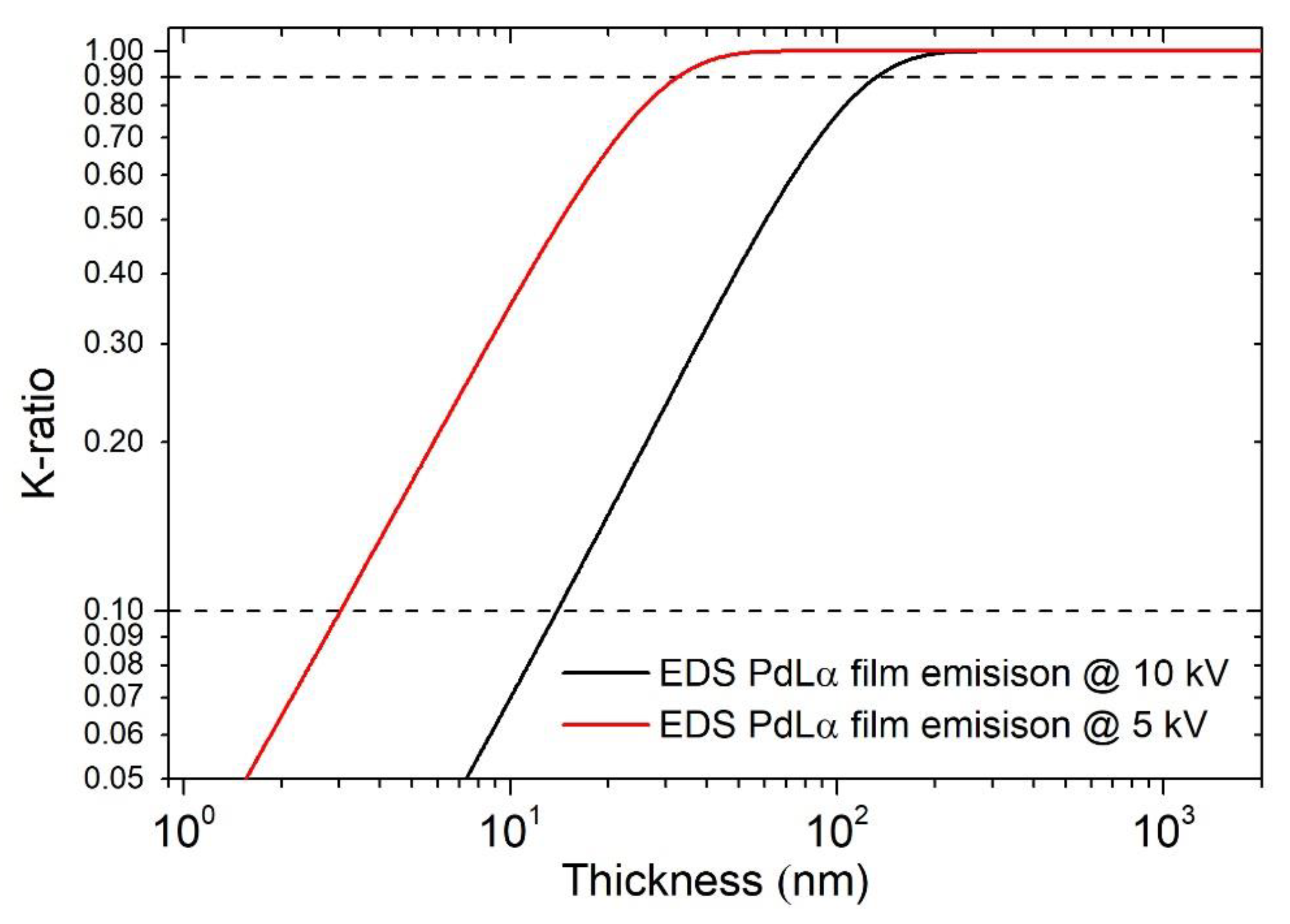
3.2. Electron Probe Microanalysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Whiteside, P.; Chininis, J.; Hunt, H. Techniques and Challenges for Characterizing Metal Thin Films with Applications in Photonics. Coatings 2016, 6, 35. [Google Scholar] [CrossRef]
- Nash, C.R.; Fenton, J.C.; Constantino, N.G.N.; Warburton, P.A. Compact chromium oxide thin film resistors for use in nanoscale quantum circuits. J. Appl. Phys. 2014, 116. [Google Scholar] [CrossRef]
- Lobo, R.F.M.; Pereira-da-Silva, M.A.; Raposo, M.; Faria, R.M.; Oliveira, O.N. In situ thickness measurements of ultra-thin multilayer polymer films by atomic force microscopy. Nanotechnology 1999, 10, 389–393. [Google Scholar] [CrossRef]
- Sitko, R. Quantitative X-ray fluorescence analysis of samples of less than “infinite thickness”: Difficulties and possibilities. Spectrochim. Acta Part B At. Spectrosc. 2009, 64, 1161–1172. [Google Scholar] [CrossRef]
- Lopes, F.; Cardozo Amorin, L.H.; da Silva Martins, L.; Urbano, A.; Roberto Appoloni, C.; Cesareo, R. Thickness Measurement of V2O5 Nanometric Thin Films Using a Portable XRF. J. Spectrosc. 2016, 2016, 1–7. [Google Scholar] [CrossRef]
- Criss, J.W.; Birks, L.S. Calculation Methods for Fluorescent X-Ray Spectrometry: Empirical Coefficients vs. Fundamental Parameters. Anal. Chem. 1968, 40, 1080–1086. [Google Scholar] [CrossRef]
- Giurlani, W.; Berretti, E.; Innocenti, M.; Lavacchi, A. Coating Thickness Determination Using X-ray Fluorescence Spectroscopy: Monte Carlo Simulations as an Alternative to the Use of Standards. Coatings 2019, 9, 79. [Google Scholar] [CrossRef]
- Pessanha, S.; Manso, M.; Antunes, V.; Carvalho, M.L.; Sampaio, J.M. Monte Carlo simulation of portable X-ray fluorescence setup: Non-invasive determination of gold leaf thickness in indo-Portuguese panel paintings. Spectrochim. Acta Part B At. Spectrosc. 2019, 156, 1–6. [Google Scholar] [CrossRef]
- Malarde, D.; Powell, M.J.; Quesada-Cabrera, R.; Wilson, R.L.; Carmalt, C.J.; Sankar, G.; Parkin, I.P.; Palgrave, R.G. Optimized Atmospheric-Pressure Chemical Vapor Deposition Thermochromic VO2 Thin Films for Intelligent Window Applications. ACS Omega 2017, 2, 1040–1046. [Google Scholar] [CrossRef]
- Krumrey, M.; Gleber, G.; Scholze, F.; Wernecke, J. Synchrotron radiation-based x-ray reflection and scattering techniques for dimensional nanometrology. Meas. Sci. Technol. 2011, 22. [Google Scholar] [CrossRef]
- Serafińczuk, J.; Pietrucha, J.; Schroeder, G.; Gotszalk, T.P. Thin film thickness determination using X-ray reflectivity and Savitzky-Golay algorithm. Opt. Appl. 2011, 41, 315–322. [Google Scholar]
- Sokolov, S.A.; Milovanov, R.A.; Sidorov, L.N. Determination of the Thickness of Thin Films Based on Scanning Electron Microscopy and Energy Dispersive X-Ray Analysis. J. Surf. Investig. X-ray Synchrotron Neutron Tech. 2019, 13, 836–847. [Google Scholar] [CrossRef]
- Goldstein, J.I.; Newbury, D.E.; Michael, J.R.; Ritchie, N.W.M.; Scott, J.H.J.; Joy, D.C. Scanning Electron Microscopy and X-Ray Microanalysis; Springer Publishing: New York, NY, USA, 2018; ISBN 978-1-4939-6674-5. [Google Scholar]
- Jablonski, A. Evaluation of procedures for overlayer thickness determination from XPS intensities. Surf. Sci. 2019, 688, 14–24. [Google Scholar] [CrossRef]
- Walton, J.; Alexander, M.R.; Fairley, N.; Roach, P.; Shard, A.G. Film thickness measurement and contamination layer correction for quantitative XPS. Surf. Interface Anal. 2016, 48, 164–172. [Google Scholar] [CrossRef]
- Cumpson, P.J. The Thickogram: A method for easy film thickness measurement in XPS. Surf. Interface Anal. 2000, 29, 403–406. [Google Scholar] [CrossRef]
- Alexander, M.R.; Thompson, G.E.; Zhou, X.; Beamson, G.; Fairley, N. Quantification of oxide film thickness at the surface of aluminium using XPS. Surf. Interface Anal. 2002, 34, 485–489. [Google Scholar] [CrossRef]
- Giurlani, W.; Innocenti, M.; Lavacchi, A. X-ray Microanalysis of Precious Metal Thin Films: Thickness and Composition Determination. Coatings 2018, 8, 84. [Google Scholar] [CrossRef]
- Kyser, D.F.; Murata, K. Quantitative Electron Microprobe Analysis of Thin Films on Substrates. IBM J. RES. Dev. 1974, 92, 352–363. [Google Scholar] [CrossRef]
- Roming, A.D.; Plimpton, S.J.; Michael, J.R.; Myklebust, R.L. Newbury DE Microbeam Analysis; San Francisco Press: San Francisco, CA, USA, 1990. [Google Scholar]
- Hill, J.M.; Royce, D.G.; Fadley, C.S.; Wagner, L.F.; Grunthaner, F.J. Properties of oxidized silicon as determined by angular-dependent X-ray photoelectron spectroscopy. Chem. Phys. Lett. 1976, 44, 225–231. [Google Scholar] [CrossRef]
- Benoit, M.; Bataillon, C.; Gwinner, B.; Miserque, F.; Orazem, M.E.; Sánchez-Sánchez, C.M.; Tribollet, B.; Vivier, V. Comparison of different methods for measuring the passive film thickness on metals. Electrochim. Acta 2016, 201, 340–347. [Google Scholar] [CrossRef]
- Passiu, C.; Rossi, A.; Weinert, M.; Tysoe, W.; Spencer, N.D. Probing the outermost layer of thin gold films by XPS and density functional theory. Appl. Surf. Sci. 2020, 507, 145084. [Google Scholar] [CrossRef]
- Tougaard, S. Surface nanostructure determination by x-ray photoemission spectroscopy peak shape analysis. J. Vac. Sci. Technol. A Vac. Surfaces Film. 1996, 14, 1415–1423. [Google Scholar] [CrossRef]
- Matthew, J. Surface Analysis by Auger and x-ray Photoelectron Spectroscopy; Briggs, D., Grant, J.T., Eds.; IMPublications: Chichester, UK; SurfaceSpectra: Manchester, UK, 2003; p. 900. ISBN 1-901019-04-7, 900 pp. Surf. Interface Anal. 2004, 36, 1647. [Google Scholar] [CrossRef]
- Elsener, B.; Rossi, A. XPS investigation of passive films on amorphous FeCr alloys. Electrochim. Acta 1992, 37, 2269–2276. [Google Scholar] [CrossRef]
- Rossi, A.; Elsener, B. XPS analysis of passive films on the amorphous alloy Fe70Cr10P13C7: Effect of the applied potential. Surf. Interface Anal. 1992, 18, 499–504. [Google Scholar] [CrossRef]
- Asami, K.; Hashimoto, K. An XPS study of the surfaces on Fe-Cr, Fe-Co and Fe-Ni alloys after mechanical polishing. Corros. Sci. 1984, 24, 83–97. [Google Scholar] [CrossRef]
- Jeynes, C.; Colaux, J.L. Thin film depth profiling by ion beam analysis. Analyst 2016, 141, 5944–5985. [Google Scholar] [CrossRef]
- Ho, S.M. Investigation of the electrical properties of metal chalcogenide thin films: A review. Der Pharma Chem. 2016, 8, 17–20. [Google Scholar]
- Hofmann, S.; Zhou, G.; Kovac, J.; Drev, S.; Lian, S.Y.; Lin, B.; Liu, Y.; Wang, J.Y. Preferential sputtering effects in depth profiling of multilayers with SIMS, XPS and AES. Appl. Surf. Sci. 2019, 483, 140–155. [Google Scholar] [CrossRef]
- Bardi, U.; Caporali, S.; Chenakin, S.P.; Lavacchi, A.; Miorin, E.; Pagura, C.; Tolstogouzov, A. Characterization of electrodeposited metal coatings by secondary ion mass spectrometry. Surf. Coat. Technol. 2006, 200, 2870–2874. [Google Scholar] [CrossRef]
- Bardi, U.; Chenakin, S.P.; Ghezzi, F.; Giolli, C.; Goruppa, A.; Lavacchi, A.; Miorin, E.; Pagura, C.; Tolstogouzov, A. High-temperature oxidation of CrN/AlN multilayer coatings. Appl. Surf. Sci. 2005, 252, 1339–1349. [Google Scholar] [CrossRef]
- Kalina, L.; Bílek Jr., V.; Bušo, M.; Koplík, J.; Másilko, J. Thickness determination of corrosion layers on iron using XPS depth profiling. Mater. Tehnol. 2018, 52, 537–540. [Google Scholar] [CrossRef]
- Scorciapino, M.A.; Navarra, G.; Elsener, B.; Rossi, A. Nondestructive Surface Depth Profiles from Angle-Resolved X-ray Photoelectron Spectroscopy Data Using the Maximum Entropy Method. I. A New Protocol. J. Phys. Chem. C 2009, 113, 21328–21337. [Google Scholar] [CrossRef]
- Olla, M.; Navarra, G.; Elsener, B.; Rossi, A. Nondestructive in-depth composition profile of oxy-hydroxide nanolayers on iron surfaces from ARXPS measurement. Surf. Interface Anal. 2006, 38, 964–974. [Google Scholar] [CrossRef]
- Smith, G.C.; Livesey, A.K. Maximum entropy: A new approach to non-destructive deconvolution of depth profiles from angle-dependent XPS. Surf. Interface Anal. 1992, 19, 175–180. [Google Scholar] [CrossRef]
- Skilling, J.; Bryan, R.K. Maximum entropy image reconstruction: General algorithm. Mon. Not. R. Astron. Soc. 1984, 211, 111–124. [Google Scholar] [CrossRef]
- Ishitani, T.; Yaguchi, T. Cross-sectional sample preparation by focused ion beam: A review of ion-sample interaction. Microsc. Res. Tech. 1996, 35, 320–333. [Google Scholar] [CrossRef]
- Mohamad Rashid, N.N.; Ahmad Junaidi, N.H.; Rahmah Aid, S. Interface Damage of Protective Layer in TEM Lamella Preparation for Highly Doped Ge Substrate. IOP Conf. Ser. Mater. Sci. Eng. 2019, 522, 012003. [Google Scholar] [CrossRef]
- Khamsehpour, B.; Davies, S.T. Angle lapping of multilayer structures for thickness measurements using focused ion beam micromachining. Semicond. Sci. Technol. 1994, 9, 249–255. [Google Scholar] [CrossRef]
- Gao, S.; Kang, R.K.; Guo, D.M.; Huang, Q.S. Study on the subsurface damage distribution of the silicon wafer ground by diamond wheel. Adv. Mater. Res. 2010, 126–128, 113–118. [Google Scholar] [CrossRef]
- International Organization for Standardization. Fine Ceramics (Advanced Ceramics, Advanced Technical Ceramics)—Determination of Coating Thickness by Crater-Grinding Method; ISO 26423:2009; ISO: Geneva, Switzerland, 2009. [Google Scholar]
- Vidakis, N.; Antoniadis, A.; Bilalis, N. The VDI 3198 indentation test evaluation of a reliable qualitative control for layered compounds. J. Mater. Process. Technol. 2003, 143–144, 481–485. [Google Scholar] [CrossRef]
- Randall, N. Finer particle size allows better coating characterization with the Calotest. Appl. Bull. 1997, 3–6. [Google Scholar]
- Demas, N.G.; Lorenzo-Martin, C.; Ajayi, O.O.; Erck, R.A.; Shareef, I. Measurement of Thin-film Coating Hardness in the Presence of Contamination and Roughness: Implications for Tribology. Metall. Mater. Trans. A 2016, 47, 1629–1640. [Google Scholar] [CrossRef]
- Rupetsov, V.; Minchev, R. Experimental Calo Tester for the Coating Thickness Measurement. In Proceedings of the XV International Scientific Conference, Smolyan, Bulgaria, 10–11 June 2016; pp. 188–192. [Google Scholar]
- Mayer, J.; Giannuzzi, L.A.; Kamino, T.; Michael, J. TEM sample preparation and FIB-induced damage. MRS Bull. 2007, 32, 400–407. [Google Scholar] [CrossRef]
- Schaffer, M.; Schaffer, B.; Ramasse, Q. Sample preparation for atomic-resolution STEM at low voltages by FIB. Ultramicroscopy 2012, 114, 62–71. [Google Scholar] [CrossRef]
- Özkan, D.; Kaleli, H.; Yüksek, L. Quantitative comparison of tribological performance of chromium- and zinc-phosphate-coated piston rings in tribotest rig. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2017, 231, 75–92. [Google Scholar] [CrossRef]
- Škarohlíd, J.; Ashcheulov, P.; Škoda, R.; Taylor, A.; Čtvrtlík, R.; Tomáštík, J.; Fendrych, F.; Kopeček, J.; Cháb, V.; Cichoň, S.; et al. Nanocrystalline diamond protects Zr cladding surface against oxygen and hydrogen uptake: Nuclear fuel durability enhancement. Sci. Rep. 2017, 7, 6469. [Google Scholar] [CrossRef]
- Vieira Junior, L.E.; Bendo, T.; Nieto, M.I.; Klein, A.N.; Hotza, D.; Moreno, R.; Rodrigues Neto, J.B. Processing of Copper Based Foil Hardened with Zirconia by Non-Deformation Method. Mater. Res. 2017, 20, 835–842. [Google Scholar] [CrossRef][Green Version]
- Nyyssonen, D.; Kirk, C.P. Optical microscope imaging of lines patterned in thick layers with variable edge geometry: theory. J. Opt. Soc. Am. A 1988, 5, 1270. [Google Scholar] [CrossRef]
- Sakai, Y.; Yamada, T.; Suzuki, T.; Ichinokawa, T. Contrast mechanisms of secondary electron images in scanning electron and ion microscopy. Appl. Surf. Sci. 1999, 144–145, 96–100. [Google Scholar] [CrossRef]
- Li, P.; Bao, S.X.; Zhang, D.Z.; Zhuang, L.B.; Ma, L.L. Application of Secondary Electron Composition Contrast Imaging Method in Microstructure Studies on Cathode Materials of TWT. Mater. Sci. Forum 2011, 689, 255–259. [Google Scholar] [CrossRef]
- Sohail, K.; Khan, I.U.; Shahzad, Y.; Hussain, T.; Ranjha, N.M. Ph-sensitive polyvinylpyrrolidone-acrylic acid hydrogels: Impact of material parameters on swelling and drug release. Brazilian J. Pharm. Sci. 2014, 50, 173–184. [Google Scholar] [CrossRef]
- Gierak, J. Focused ion beam technology and ultimate applications. Semicond. Sci. Technol. 2009, 24. [Google Scholar] [CrossRef]
- Kleyn, A.W. Ion-Surface Interactions--From Channeling to Soft-Landing. Science 1997, 275, 1440–1441. [Google Scholar] [CrossRef]
- Huh, Y.; Hong, K.J.; Shin, K.S. Amorphization Induced by Focused Ion Beam Milling in Metallic and Electronic Materials. Microsc. Microanal. 2013, 19, 33–37. [Google Scholar] [CrossRef] [PubMed]
- Williams, J.S. Ion Implantation and Beam Processing; Elsevier: Amsterdam, The Netherlands, 1984; ISBN 9780127569802. [Google Scholar]
- MoberlyChan, W.J.; Adams, D.P.; Aziz, M.J.; Hobler, G.; Schenkel, T. Fundamentals of focused ion beam nanostructural processing: Below, at, and above the surface. MRS Bull. 2007, 32, 424–432. [Google Scholar] [CrossRef][Green Version]
- Ishitani, T.; Tsuboi, H. Objective comparison of scanning ion and scanning electron microscope images. Scanning 1997, 19, 489–497. [Google Scholar] [CrossRef]
- Tseng, A.A. Recent developments in micromilling using focused ion beam technology. J. Micromech. Microeng. 2004, 14. [Google Scholar] [CrossRef]
- Van Kouwen, L. Introduction to focused ion beams, ion sources, and the nano-aperture ion source. In Advances in Imaging and Electron Physics; Elsevier: Amsterdam, The Netherlands, 2019; pp. 181–216. [Google Scholar]
- Joy, D.C. SEM for the 21st century-scanning ion microscopy. Electron. Device Fail. Anal. 2012, 14, 4–12. [Google Scholar] [CrossRef][Green Version]
- Eder, K.; Bhatia, V.; Van Leer, B.; Cairney, J.M. Using a Plasma FIB Equipped with Xe, N 2, O 2 and Ar for Atom Probe Sample Preparation—Ion Implantation and Success Rates. Microsc. Microanal. 2019, 25, 316–317. [Google Scholar] [CrossRef]
- Ernst, A.; Wei, M.; Aindow, M. A Comparison of Ga FIB and Xe-Plasma FIB of Complex Al Alloys. Microsc. Microanal. 2017, 23, 288–289. [Google Scholar] [CrossRef]
- Kant, K.; Losic, D. FIB Nanostructures; Springer International Publishing: New York, NY, USA, 2013; Volume 20, pp. 1–22. [Google Scholar] [CrossRef]
- An, B.-S.; Kwon, Y.; Oh, J.-S.; Shin, Y.-J.; Ju, J.; Yang, C.-W. Evaluation of ion/electron beam induced deposition for electrical connection using a modern focused ion beam system. Appl. Microsc. 2019, 49. [Google Scholar] [CrossRef] [PubMed]
- Tan, S.; Livengood, R.; Shima, D.; Notte, J.; McVey, S. Gas field ion source and liquid metal ion source charged particle material interaction study for semiconductor nanomachining applications. J. Vac. Sci. Technol. B Nanotechnol. Microelectron. Mater. Process. Meas. Phenom. 2010, 28, C6F15–C6F21. [Google Scholar] [CrossRef]
- Scipioni, L.; Stern, L.A.; Notte, J.; Sijbrandij, S.; Griffin, B. Helium ion microscope. Adv. Mater. Process. 2008, 166, 27–30. [Google Scholar] [CrossRef]
- Giannuzzi, L.A.; Michael, J.R. Comparison of channeling contrast between ion and electron images. Microsc. Microanal. 2013, 19, 344–349. [Google Scholar] [CrossRef]
- Passiu, C.; Rossi, A.; Bernard, L.; Paul, D.; Hammond, J.; Unger, W.E.S.; Venkataraman, N.V.; Spencer, N.D. Fabrication and Microscopic and Spectroscopic Characterization of Planar, Bimetallic, Micro- and Nanopatterned Surfaces. Langmuir 2017, 33, 5657–5665. [Google Scholar] [CrossRef]
- International Organization for Standardization. Surface Chemical Analysis—Auger Electron Spectroscopy and X-ray Photoelectron Spectroscopy—Determination of Lateral Resolution; ISO 18516; International Organization for Standardization: Geneva, Switzerland, 2006. [Google Scholar]
- Giurlani, W.; Zangari, G.; Gambinossi, F.; Passaponti, M.; Salvietti, E.; Di Benedetto, F.; Caporali, S.; Innocenti, M. Electroplating for Decorative Applications: Recent Trends in Research and Development. Coatings 2018, 8, 260. [Google Scholar] [CrossRef]
- Innocenti, M.; Giurlani, W.; Passaponti, M.; Luca, D.; Salvietti, E. Electrodeposition and innovative characterization of precious metal alloys for the Galvanic and Jewel industry. Substantia 2019, 3, 29–37. [Google Scholar] [CrossRef]
- International Organization for Standardization. Metallic Coatings—Measurement of Coating Thickness—X-ray Spectrometric Methods; ISO 3497:2000; International Organization for Standardization: Geneva, Switzerland, 2000. [Google Scholar]
- International ASTM. Standard Test Method for Measurement of Coating Thickness by X-Ray Spectrometry; ASTM B568-98; International ASTM: West Conshohocken, PA, USA, 1998. [Google Scholar]
- Takahara, H. Thickness and Composition Analysis of Thin Film Samples Using FP Method by XRF Analysis. Rigaku J. 2017, 33, 17–21. [Google Scholar]
- Boehm, S.; Bügler, M.J.L. Layer Thickness Analysis of Thin Metal Coatings with micro-XRF on SEM; Bruker Nano Analytics: Berlin, Germany, 2017. [Google Scholar]
- Axic Inc. Non-Destructive Composition and Thickness Analysis of Metal Films Using Combination EDS/WDS X-Ray Fluorescence Spectrometry. Axic Inc. application note, 1989. [Google Scholar]
- Brouwer, P. Theory of XRF—Getting Acquainted with the Principles; PANalytical BV: Almelo, The Netherland, 2010; ISBN 9090167587. [Google Scholar]
- Abdel-Fattah, T.M.; Wixtrom, A.; Arias, L.; Zhang, K.; Baumgart, H. Quantitative Analysis of X-ray Fluorescence Absorption and Emission for Thickness Determination of ALD-Grown Metal and Oxide Nanoscaled Films. J. Nanosci. Nanotechnol. 2017, 17, 5745–5750. [Google Scholar] [CrossRef]
- Hamann, D.M.; Bardgett, D.; Cordova, D.L.M.; Maynard, L.A.; Hadland, E.C.; Lygo, A.C.; Wood, S.R.; Esters, M.; Johnson, D.C. Sub-Monolayer Accuracy in Determining the Number of Atoms per Unit Area in Ultrathin Films Using X-ray Fluorescence. Chem. Mater. 2018, 30, 6209–6216. [Google Scholar] [CrossRef]
- Kataoka, Y. Standardless x-ray fluorescence spectrometry (Fundamental Parameter Method using Sensitivity Library). Rigaku J. 1989, 6, 33–40. [Google Scholar]
- Thomsen, V. Basic Fundamental Parameters in X-Ray Fluorescence. Spectroscopy 2007, 22, 46–50. [Google Scholar]
- Han, X.Y.; Zhuo, S.J.; Shen, R.X.; Wang, P.L.; Ji, A. Comparison of the quantitative results corrected by fundamental parameter method and difference calibration specimens in X-ray fluorescence spectrometry. J. Quant. Spectrosc. Radiat. Transf. 2006, 97, 68–74. [Google Scholar] [CrossRef]
- Pessanha, S.; Fonseca, C.; Santos, J.P.; Carvalho, M.L.; Dias, A.A. Comparison of standard-based and standardless methods of quantification used in X-ray fluorescence analysis: Application to the exoskeleton of clams. X-Ray Spectrom. 2018, 47, 108–115. [Google Scholar] [CrossRef]
- Nygård, K.; Hämäläinen, K.; Manninen, S.; Jalas, P.; Ruottinen, J.-P. Quantitative thickness determination using x-ray fluorescence: application to multiple layers. X-Ray Spectrom. 2004, 33, 354–359. [Google Scholar] [CrossRef]
- Vrielink, J.A.M.A.M.; Tiggelaar, R.M.M.; Gardeniers, J.G.E.G.E.; Lefferts, L. Applicability of X-ray fluorescence spectroscopy as method to determine thickness and composition of stacks of metal thin films: A comparison with imaging and profilometry. Thin Solid Films 2012, 520, 1740–1744. [Google Scholar] [CrossRef]
- Elam, W.T.T.; Shen, R.B.; Scruggs, B.; Nicolosi, J. Accuracy of Standardless FP Analysis of Bulk and Thin Film Samples Using a New Atomic Database. Adv. X-ray Anal. 2004, 47, 104–109. [Google Scholar]
- Ager, F.J.; Ferretti, M.; Grilli, M.L.; Juanes, D.; Ortega-Feliu, I.; Respaldiza, M.A.; Roldán, C.; Scrivano, S. Reconsidering the accuracy of X-ray fluorescence and ion beam based methods when used to measure the thickness of ancient gildings. Spectrochim. Acta Part B At. Spectrosc. 2017, 135, 42–47. [Google Scholar] [CrossRef]
- Kolbe, M.; Beckhoff, B.; Krumrey, M.; Ulm, G. Thickness determination for Cu and Ni nanolayers: Comparison of completely reference-free fundamental parameter-based X-ray fluorescence analysis and X-ray reflectometry. Spectrochim. Acta Part B At. Spectrosc. 2005, 60, 505–510. [Google Scholar] [CrossRef]
- Queralt, I.; Ibañez, J.; Marguí, E.; Pujol, J. Thickness measurement of semiconductor thin films by energy dispersive X-ray fluorescence benchtop instrumentation: Application to GaN epilayers grown by molecular beam epitaxy. Spectrochim. Acta Part B At. Spectrosc. 2010, 65, 583–586. [Google Scholar] [CrossRef]
- XRMC. Available online: https://github.com/golosio/xrmc/wiki (accessed on 30 July 2020).
- XMI-MSIM. Available online: https://github.com/tschoonj/xmimsim/wiki (accessed on 30 July 2020).
- Xraylib. Available online: https://github.com/tschoonj/xraylib/wiki (accessed on 30 July 2020).
- Schoonjans, T.; Brunetti, A.; Golosio, B.; Sanchez Del Rio, M.; Solé, V.A.; Ferrero, C.; Vincze, L. The xraylib library for X-ray-matter interactions. Recent developments. Spectrochim. Acta Part B At. Spectrosc. 2011, 66, 776–784. [Google Scholar] [CrossRef]
- Golosio, B.; Schoonjans, T.; Brunetti, A.; Oliva, P.; Masala, G.L. Monte Carlo simulation of X-ray imaging and spectroscopy experiments using quadric geometry and variance reduction techniques. Comput. Phys. Commun. 2014, 185, 1044–1052. [Google Scholar] [CrossRef]
- Schiavon, N.; de Palmas, A.; Bulla, C.; Piga, G.; Brunetti, A. An Energy-Dispersive X-Ray Fluorescence Spectrometry and Monte Carlo simulation study of Iron-Age Nuragic small bronzes (“Navicelle”) from Sardinia, Italy. Spectrochim. Acta Part B At. Spectrosc. 2016, 123, 42–46. [Google Scholar] [CrossRef]
- Brunetti, A.; Fabian, J.; La Torre, C.W.; Schiavon, N. A combined XRF/Monte Carlo simulation study of multilayered Peruvian metal artifacts from the tomb of the Priestess of Chornancap. Appl. Phys. A 2016, 122, 571. [Google Scholar] [CrossRef]
- Bottaini, C.E.; Brunetti, A.; Montero-Ruiz, I.; Valera, A.; Candeias, A.; Mirão, J. Use of Monte Carlo Simulation as a Tool for the Nondestructive Energy Dispersive X-ray Fluorescence (ED-XRF) Spectroscopy Analysis of Archaeological Copper-Based Artifacts from the Chalcolithic Site of Perdigões, Southern Portugal. Appl. Spectrosc. 2018, 72, 17–27. [Google Scholar] [CrossRef]
- Barcellos Lins, S.A.; Ridolfi, S.; Gigante, G.E.; Cesareo, R.; Albini, M.; Riccucci, C.; di Carlo, G.; Fabbri, A.; Branchini, P.; Tortora, L. Differential X-Ray Attenuation in MA-XRF Analysis for a Non-invasive Determination of Gilding Thickness. Front. Chem. 2020, 8, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Cesareo, R. Gold, gildings, and tumbaga from the Moche tomb of the Lady of Cao: An EDXRF test for the internal ratio method. X-Ray Spectrom. 2019, 48, 202–207. [Google Scholar] [CrossRef]
- Cesareo, R.; Franco Jordan, R.; Fernandez, A.; Bustamante, A.; Fabian, J.; del Pilar Zambrano, S.; Azeredo, S.; Lopes, R.T.; Ingo, G.M.; Riccucci, C.; et al. Analysis of the spectacular gold and silver from the Moche tomb ‘Señora de Cao’. X-Ray Spectrom. 2016, 45, 138–154. [Google Scholar] [CrossRef]
- Cesareo, R.; de Assis, J.T.; Roldán, C.; Bustamante, A.D.; Brunetti, A.; Schiavon, N. Multilayered samples reconstructed by measuring Kα/Kβ or Lα/Lβ X-ray intensity ratios by EDXRF. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2013, 312, 15–22. [Google Scholar] [CrossRef]
- Cesareo, R.; Bustamante, A.; Fabian, J.; Calza, C.; Dos Anjos, M.; Lopes, R.T.; Elera, C.; Shimada, I.; Curay, V.; Rizzutto, M.A. Energy-dispersive X-ray fluorescence analysis of a pre-Columbian funerary gold mask from the Museum of Sicán, Peru. X-Ray Spectrom. 2010, 39, 122–126. [Google Scholar] [CrossRef]
- Cesareo, R. Non-destructive EDXRF-analysis of the golden haloes of Giotto’s frescos in the Chapel of the Scrovegni in Padua. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2003, 211, 133–137. [Google Scholar] [CrossRef]
- Porcinai, S.; Ferretti, M. X-ray fluorescence-based methods to measure the thickness of protective organic coatings on ancient silver artefacts. Spectrochim. Acta Part B At. Spectrosc. 2018, 149, 184–189. [Google Scholar] [CrossRef]
- de Almeida, E.; Melquiades, F.L.; Marques, J.P.R.; Marguí, E.; de Carvalho, H.W.P. Determination of the polymeric thin film thickness by energy dispersive X-ray fluorescence and multivariate analysis. Spectrochim. Acta Part B At. Spectrosc. 2020, 167, 105818. [Google Scholar] [CrossRef]
- West, M.; Ellis, A.T.; Streli, C.; Vanhoof, C.; Wobrauschek, P. 2017 atomic spectrometry update—A review of advances in X-ray fluorescence spectrometry and its special applications. J. Anal. At. Spectrom. 2017, 32, 1629–1649. [Google Scholar] [CrossRef]
- Vanhoof, C.; Bacon, J.R.; Ellis, A.T.; Vincze, L.; Wobrauschek, P. 2018 atomic spectrometry update—A review of advances in X-ray fluorescence spectrometry and its special applications. J. Anal. At. Spectrom. 2018, 33, 1413–1431. [Google Scholar] [CrossRef]
- Vanhoof, C.; Bacon, J.R.; Ellis, A.T.; Fittschen, U.E.A.; Vincze, L. 2019 atomic spectrometry update—A review of advances in X-ray fluorescence spectrometry and its special applications. J. Anal. At. Spectrom. 2019, 34, 1750–1767. [Google Scholar] [CrossRef]
- Castaing, R. Application of Electron Probes to Local Chemical and Crystallographic Analysis. Ph.D. Thesis, University of Paris, Paris, France, 1951. [Google Scholar]
- Richter, S.; Pinard, P.T. Combined EPMA, FIB and Monte Carlo simulation: A versatile tool for quantitative analysis of multilayered structures. IOP Conf. Ser. Mater. Sci. Eng. 2016, 109, 012014. [Google Scholar] [CrossRef]
- Ortel, E.; Hertwig, A.; Berger, D.; Esposito, P.; Rossi, A.M.A.M.; Kraehnert, R.; Hodoroaba, V.D.V.-D.V.D. New Approach on Quantification of Porosity of Thin Films via Electron-Excited X-ray Spectra. Anal. Chem. 2016, 88, 7083–7090. [Google Scholar] [CrossRef]
- Eggert, F. EDX-spectra simulation in electron probe microanalysis. Optimization of excitation conditions and detection limits. Microchim. Acta 2006, 155, 129–136. [Google Scholar] [CrossRef]
- Armigliato, A. Thin film X-ray microanalysis with the analytical electron microscope. J. Anal. At. Spectrom. 1999, 14, 413–418. [Google Scholar] [CrossRef]
- Christien, F.; Pierson, J.F.; Hassini, A.; Capon, F.; Le Gall, R.; Brousse, T. EPMA–EDS surface measurements of interdiffusion coefficients between miscible metals in thin films. Appl. Surf. Sci. 2010, 256, 1855–1860. [Google Scholar] [CrossRef]
- Pascual, R.; Cruz, L.R.R.; Ferreira, C.L.L.; Gomes, D.T.T. Thin film thickness measurement using the energy-dispersive spectroscopy technique in a scanning electron microscope. Thin Solid Films 1990, 185, 279–286. [Google Scholar] [CrossRef]
- Benoit, D.; Bresse, J.-F.; Van’t dack, L.; Werner, H.; Wernisch, J. (Eds.) Microbeam and Nanobeam Analysis; Springer Vienna: Vienna, Austria, 1996; ISBN 978-3-211-82874-8. [Google Scholar]
- Waldo, R.A.; Militello, M.C.; Gaarenstroom, S.W. Quantitative thin-film analysis with an energy-dispersive x-ray detector. Surf. Interface Anal. 1993, 20. [Google Scholar] [CrossRef]
- Gauvin, R. Quantitative X-ray microanalysis of heterogeneous materials using Monte Carlo simulations. Microchim. Acta 2006, 155. [Google Scholar] [CrossRef]
- Sokolov, S.A.; Kelm, E.A.; Milovanov, R.A.; Abdullaev, D.A.; Sidorov, L.N. Non-destructive determination of thickness of the dielectric layers using EDX. In Proceedings of the SPIE—The International Society for Optical Engineering, Vienna, Austria, 19–23 September 2016; Lukichev, V.F., Rudenko, K.V., Eds.; Volume 10224, p. 1022426. [Google Scholar]
- Stenberg, G.; Boman, M. Thickness measurement of light elemental films. Diam. Relat. Mater. 1996, 5, 1444–1449. [Google Scholar] [CrossRef]
- Willich, P.; Obertop, D. Composition and thickness of submicron metal coatings and multilayers on Si determined by EPMA. Surf. Interface Anal. 1988, 13, 20–24. [Google Scholar] [CrossRef]
- Hunger, H.-J.; Baumann, W.; Schulze, S. A new method for determining the thickness and composition of thin layers by electron probe microanalysis. Cryst. Res. Technol. 1985, 20, 1427–1433. [Google Scholar] [CrossRef]
- Ares, J.R.; Pascual, A.; Ferrer, I.J.; Sánchez, C. A methodology to reduce error sources in the determination of thin film chemical composition by EDAX. Thin Solid Films 2004, 450. [Google Scholar] [CrossRef]
- Sempf, K.; Herrmann, M.; Bauer, F. First results in thin film analysis based on a new EDS software to determine composition and/or thickness of thin layers on substrates. In Proceedings of the EMC 2008 14th European Microscopy Congress, Aachen, Germany, 1–5 September 2008; Springer: Berlin, Germany, 2008; pp. 751–752. [Google Scholar]
- Hodoroaba, V.-D.; Kim, K.J.; Unger, W.E.S. Energy dispersive electron probe microanalysis (ED-EPMA) of elemental composition and thickness of Fe-Ni alloy films. Surf. Interface Anal. 2012, 44. [Google Scholar] [CrossRef]
- Canli, S. Thickness Analysis of Thin Films by Energy Dispersive X-Ray Spectroscopy; Middle East Technical University: Ankara, Turkey, 2010. [Google Scholar]
- Moller, A.; Weinbruch, S.; Stadermann, F.J.; Ortner, H.M.; Neubeck, K.; Balogh, A.G.; Hahn, H. Accuracy of film thickness determination in electron-probe microanalysis. Mikrochim. Acta 1995, 119, 41–47. [Google Scholar] [CrossRef]
- Procop, M.; Radtke, M.; Krumrey, M.; Hasche, K.; Schädlich, S.; Frank, W. Electron probe microanalysis (EPMA) measurement of thin-film thickness in the nanometre range. Anal. Bioanal. Chem. 2002, 374, 631–634. [Google Scholar] [CrossRef] [PubMed]
- Campos, C.S.; Coleoni, E.A.; Trincavelli, J.C.; Kaschny, J.; Hubbler, R.; Soares, M.R.F.; Vasconcellos, M.A.Z. Metallic thin film thickness determination using electron probe microanalysis. X-Ray Spectrom. 2001, 30, 253–259. [Google Scholar] [CrossRef]
- Libo, Z.; Shengxiang, B.; Rong, W.; Shilan, L.; Lili, M.; Dechun, L.; Zhuang, L.; Bao, S.; Wang, R.; Li, S.; et al. Thin film thickness measurement using electron probe microanalyzer. In Proceedings of the 2009 International Conference on Applied Superconductivity and Electromagnetic Devices, Chengdu, China, 25–27 September 2009; pp. 142–144. [Google Scholar]
- Osada, Y. Electron probe microanalysis (EPMA) measurement of aluminum oxide film thickness in the nanometer range on aluminum sheets. X-Ray Spectrom. 2005, 34, 92–95. [Google Scholar] [CrossRef]
- Merlet, C. Thin Film Quantification by EPMA: Accuracy of Analytical Procedure. Microsc. Microanal. 2006, 12, 842–843. [Google Scholar] [CrossRef]
- August, H.; Wernisch, J. A Method for Determining the Mass Thickness of Thin Films Using Electron Probe Microanalysis. Scanning 1987, 9, 145–155. [Google Scholar] [CrossRef]
- Shang, Y.; Guo, Y.; Liu, Z.; Xu, L. An EPMA software for determination of thin metal film thickness and it’s application. Acta Metall. Sin. 1997, 33, 443–448. [Google Scholar]
- Watanabe, M.; Horita, Z.; Nemoto, M. Absorption correction and thickness determination using the zeta factor in quantitative X-ray microanalysis. Ultramicroscopy 1996, 65, 187–198. [Google Scholar] [CrossRef]
- Bishop, H.E.; Poole, D.M. A simple method of thin film analysis in the electron probe microanalyser. J. Phys. D Appl. Phys. 1973, 6, 1142–1158. [Google Scholar] [CrossRef]
- Rinaldi, R.; Llovet, X. Electron Probe Microanalysis: A Review of the Past, Present, and Future. Microsc. Microanal. 2015, 21, 1053–1069. [Google Scholar] [CrossRef]
- Colby, J.W. Quantitative Microprobe Analysis of Thin Insulating Films. Adv. X-ray Anal. 1967, 11, 287–305. [Google Scholar] [CrossRef]
- HUNGER, H.J. Thin Film Analysis by X-Ray Microanalysis Using Gaussian f (p z) Curves. Scanning 1988, 10, 65–72. [Google Scholar] [CrossRef]
- STRATAGem—SAMx. Available online: http://www.samx.com/index.html.en (accessed on 30 July 2020).
- Kühn, J.; Hodoroaba, V.-D.; Linke, S.; Moritz, W.; Unger, W.E.S. Characterization of Pd-Ni-Co alloy thin films by ED-EPMA with application of the STRATAGEM software. Surf. Interface Anal. 2012, 44, 1456–1458. [Google Scholar] [CrossRef]
- Dumelié, N.; Benhayoune, H.; Balossier, G. TF_Quantif: A Quantification Procedure for Electron Probe Microanalysis of Thin Films on Heterogeneous Substrates; IOP Publishing: Bristol, UK, 2007; ISBN 9781600214554. [Google Scholar]
- Small World. Available online: http://www.small-world.net/efs.htm (accessed on 30 July 2020).
- Batanova, V.G.; Sobolev, A.V.; Kuzmin, D.V. Trace element analysis of olivine: High precision analytical method for JEOL JXA-8230 electron probe microanalyser. Chem. Geol. 2015, 419, 149–157. [Google Scholar] [CrossRef]
- ThinFilmID—Oxford Instruments. Available online: http://www.oxford-instruments.cn/OxfordInstruments/media/nanoanalysis/brochures and thumbs/ThinFilmID_Brochure.pdf (accessed on 30 July 2020).
- LayerProbe—Oxford Instruments. Available online: https://www.oxford-instruments.com/products/microanalysis/solutions/layerprobe (accessed on 30 July 2020).
- pyPENELOPE. Available online: http://pypenelope.sourceforge.net/ (accessed on 30 July 2020).
- Llovet, X.; Salvat, F. PENEPMA: A Monte Carlo Program for the Simulation of X-Ray Emission in Electron Probe Microanalysis. Microsc. Microanal. 2017, 23, 634–646. [Google Scholar] [CrossRef]
- Electron Beam Scattering Modeling. Available online: http://montecarlomodeling.mcgill.ca/ (accessed on 30 July 2020).
- Gauvin, R.; Lifshin, E.; Demers, H.; Horny, P.; Campbell, H. Win X-ray: A new Monte Carlo program that computes X-ray spectra obtained with a scanning electron microscope. Microsc. Microanal. 2006, 12, 49–64. [Google Scholar] [CrossRef]
- Gauvin, R.; Michaud, P. MC X-Ray, a new monte carlo program for quantitative X-ray microanalysis of real materials. Microsc. Microanal. 2009, 15, 488–489. [Google Scholar] [CrossRef]
- Llovet, X.; Merlet, C. Electron Probe Microanalysis of Thin Films and Multilayers Using the Computer Program XFILM. Microsc. Microanal. 2010, 16, 21–32. [Google Scholar] [CrossRef]
- CASINO. Available online: https://www.gel.usherbrooke.ca/casino/index.html (accessed on 30 July 2020).
- Demers, H.; Poirier-Demers, N.; Couture, A.R.; Joly, D.; Guilmain, M.; De Jonge, N.; Drouin, D. Three-dimensional electron microscopy simulation with the CASINO Monte Carlo software. Scanning 2011, 33, 135–146. [Google Scholar] [CrossRef]
- Hovington, P.; Drouin, D.; Gauvin, R. CASINO: A new Monte Carlo code in C language for electron beam interaction—Part I: Description of the program. Scanning 1997, 19, 1–14. [Google Scholar] [CrossRef]
- Drouin, D.; Couture, A.R.; Joly, D.; Tastet, X.; Aimez, V.; Gauvin, R. CASINO V2.42—A Fast and Easy-to-use Modeling Tool for Scanning Electron Microscopy and Microanalysis Users. Scanning 2007, 29, 92–101. [Google Scholar] [CrossRef] [PubMed]
- CalcZAF. Available online: http://www.probesoftware.com/Technical.html (accessed on 30 July 2020).
- Armstrong, J.T.; Donovan, J.; Carpenter, P. CALCZAF, TRYZAF and CITZAF: The Use of Multi-Correction-Algorithm Programs for Estimating Uncertainties and Improving Quantitative X-ray Analysis of Difficult Specimens. Microsc. Microanal. 2013, 19, 812–813. [Google Scholar] [CrossRef]
- Ritchie, N.W.M. NIST DTSA-II. Available online: http://www.cstl.nist.gov/div837/837.02/epq/dtsa2/ (accessed on 30 July 2020).
- Ritchie, N.W.m.M. Spectrum Simulation in DTSA-II. Microsc. Microanal. 2009, 15, 454–468. [Google Scholar] [CrossRef]
- Ritchie, N.W.M. Efficient Simulation of Secondary Fluorescence Via NIST DTSA-II Monte Carlo. Microsc. Microanal. 2017, 23, 618–633. [Google Scholar] [CrossRef] [PubMed]
- Salvat, F.; Fernández-Varea, J.M.; Sempau, J. PENELOPE—2006: A Code System for Monte Carlo Simulation of Electron and Photon Transport; OECD/NEA Data Bank: Paris, France, 2006; ISBN 9264023011. [Google Scholar]
- Katz, L.; Penfold, A.S. Range-energy relations for electrons and the determination of beta-ray end-point energies by absorption. Rev. Mod. Phys. 1952, 24, 28–44. [Google Scholar] [CrossRef]
- Cockett, G.H.; Davis, C.D. Coating thickness measurement by electron probe microanalysis. Br. J. Appl. Phys. 1963, 14, 813–816. [Google Scholar] [CrossRef]
- Matthews, M.B.; Kearns, S.L.; Buse, B. The Accuracy of Al and Cu Film Thickness Determinations and the Implications for Electron Probe Microanalysis. Microsc. Microanal. 2018, 24, 83–92. [Google Scholar] [CrossRef] [PubMed]
- Campos, C.S.; Vasconcellos, M.A.Z.; Llovet, X.; Salvat, F. Thickness Determination of Ultra-Thin Films on Si Substrates by EPMA. Microchim. Acta 2004, 145, 13–17. [Google Scholar] [CrossRef]
- Chininis, J.; Whiteside, P.; Hunt, H.K. Metal-clad waveguide characterization for contact-based light transmission into tissue. In Photonic Therapeutics and Diagnostics XII; Choi, B., Kollias, N., Zeng, H., Kang, H.W., Wong, B.J.F., Ilgner, J.F., Tearney, G.J., Gregory, K.W., Marcu, L., Skala, M.C., et al., Eds.; SPIE: Bellingham, WA, USA, 2016; Volume 9689, p. 968915. [Google Scholar]
- Stanford, J.A.; Teslich, N.; Donald, S.; Saw, C.K.; Gollott, R.; Dinh, L.N. Measurement of PuO2 film thickness by electron probe microanalysis (EPMA) calibration curve method. J. Nucl. Mater. 2020, 530, 151968. [Google Scholar] [CrossRef]
- Bastin, G.F.F.; Heijligers, H.J.M.M. A systematic database of thin-film measurements by EPMA Part I—Aluminum films. X-Ray Spectrom. 2000, 29, 212–238. [Google Scholar] [CrossRef]
- Bastin, G.F.; Heijligers, H.J.M. A systematic database of thin-film measurements by EPMA Part II - Palladium films. X-Ray Spectrom. 2000, 29, 373–397. [Google Scholar] [CrossRef]
- Merlet, C. Analytical Multilayer Model Revisited for High Atomic Numbers at Low Voltage. Microsc. Microanal. 2014, 20, 736–737. [Google Scholar] [CrossRef]
- Merlet, C. Quantitative X-ray Microanalysis of Multi-layered Specimens: Capability and Accuracy. Microsc. Microanal. 2013, 19, 1240–1241. [Google Scholar] [CrossRef]
- Pazzaglia, A.; Maffini, A.; Dellasega, D.; Lamperti, A.; Passoni, M. Reference-free evaluation of thin films mass thickness and composition through energy dispersive X-ray spectroscopy. Mater. Charact. 2019, 153, 92–102. [Google Scholar] [CrossRef]
- Darznek, S.A.; Kuzin, A.Y.; Mityukhlyaev, V.B.; Stepovich, M.A.; Todua, P.A.; Filippov, M.N. Measurement of the Thickness Nonuniformity of Nanofilms Using an Electron Probe Method. Meas. Tech. 2016, 59, 822–825. [Google Scholar] [CrossRef]


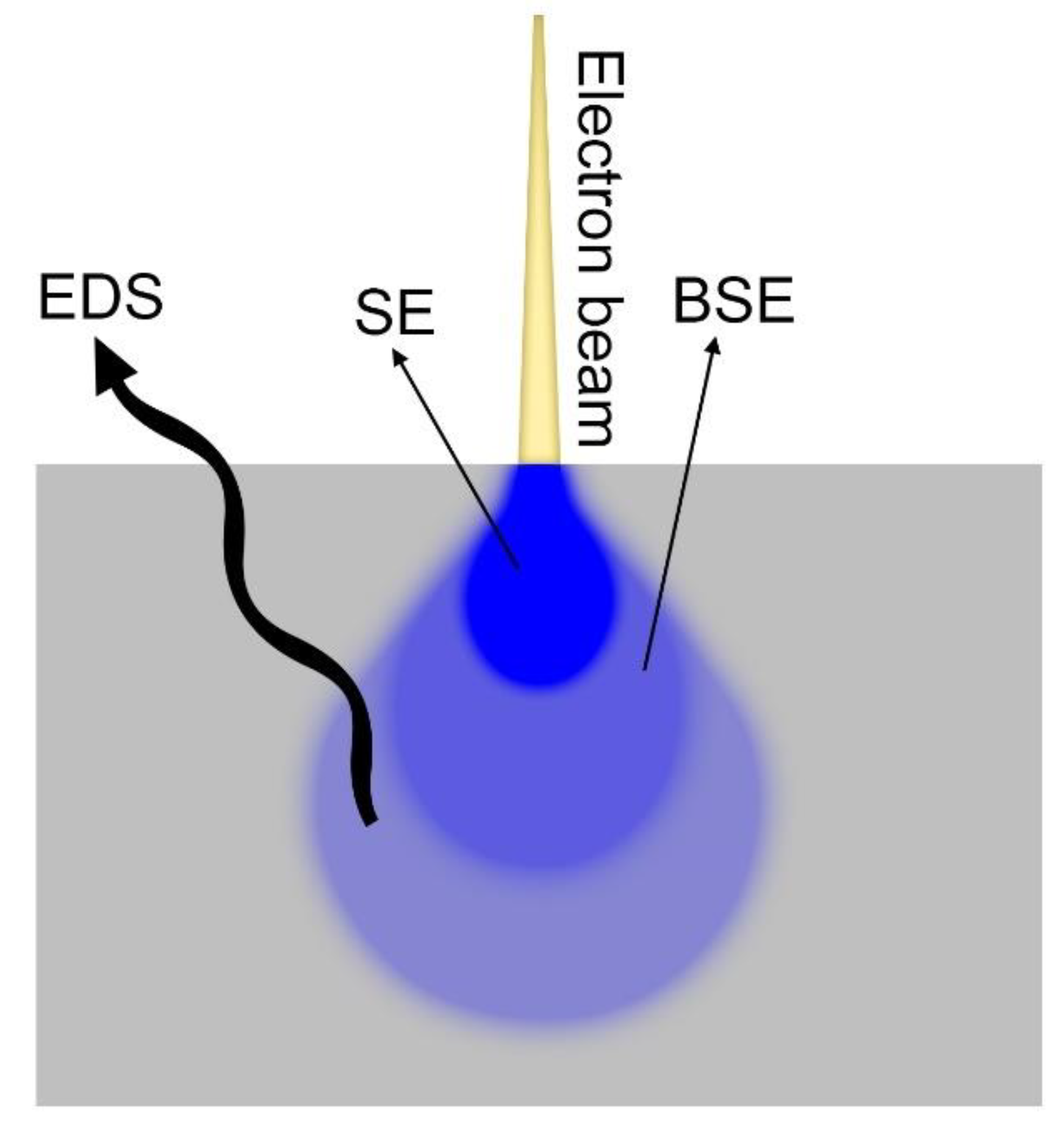

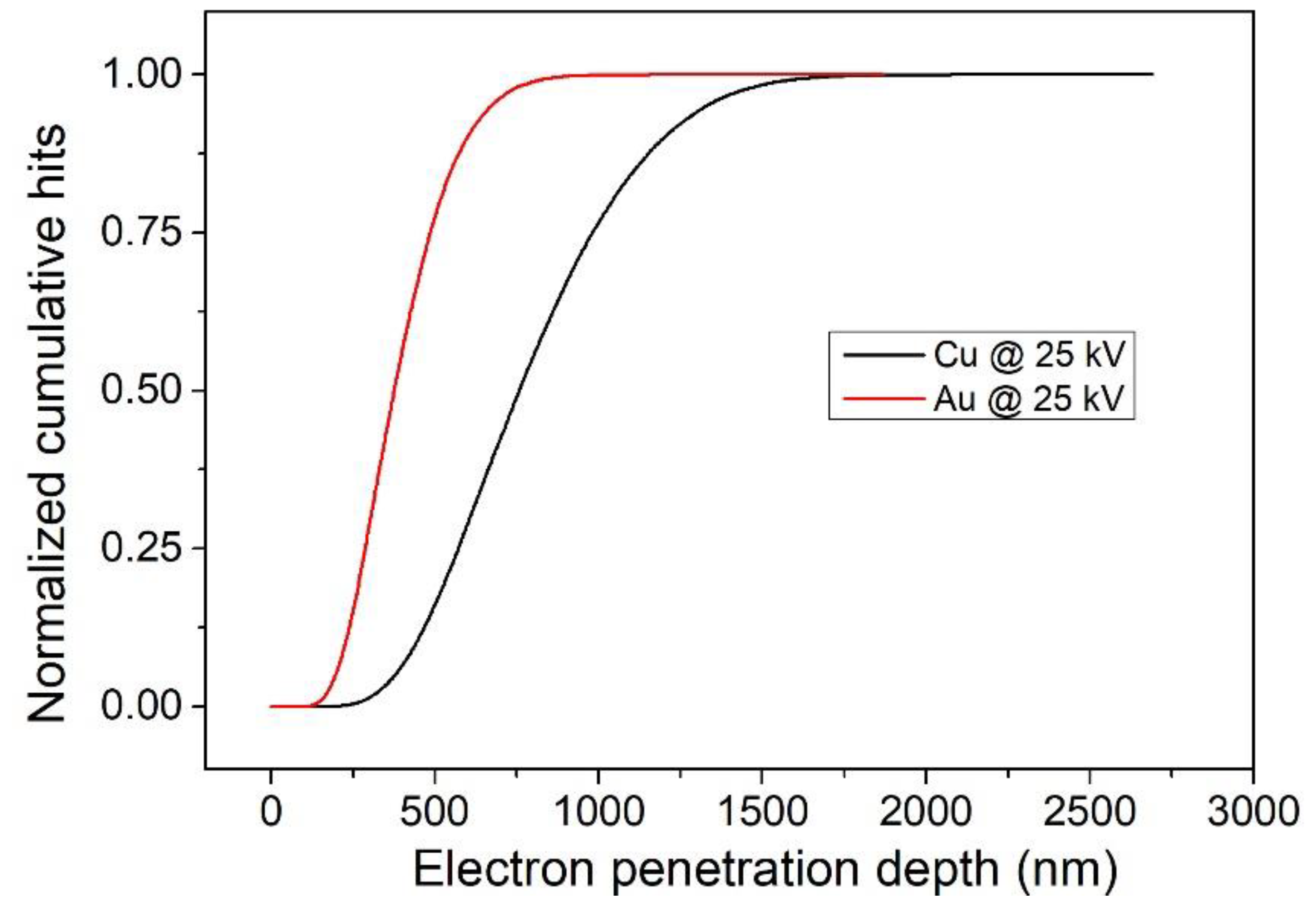

| 20 kV Beam Penetration Depth | SE | BSE | X-Ray |
|---|---|---|---|
| Al | 50 nm | 700 nm | 2000 nm |
| Au | 5 nm | 70 nm | 200 nm |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giurlani, W.; Berretti, E.; Innocenti, M.; Lavacchi, A. Measuring the Thickness of Metal Films: A Selection Guide to the Most Suitable Technique. Mater. Proc. 2020, 2, 12. https://doi.org/10.3390/CIWC2020-06823
Giurlani W, Berretti E, Innocenti M, Lavacchi A. Measuring the Thickness of Metal Films: A Selection Guide to the Most Suitable Technique. Materials Proceedings. 2020; 2(1):12. https://doi.org/10.3390/CIWC2020-06823
Chicago/Turabian StyleGiurlani, Walter, Enrico Berretti, Massimo Innocenti, and Alessandro Lavacchi. 2020. "Measuring the Thickness of Metal Films: A Selection Guide to the Most Suitable Technique" Materials Proceedings 2, no. 1: 12. https://doi.org/10.3390/CIWC2020-06823
APA StyleGiurlani, W., Berretti, E., Innocenti, M., & Lavacchi, A. (2020). Measuring the Thickness of Metal Films: A Selection Guide to the Most Suitable Technique. Materials Proceedings, 2(1), 12. https://doi.org/10.3390/CIWC2020-06823







