A Chemo-Mechanical Model of the Spreading of Endothelial Cells on the Lumen of Functionalized TEVGs †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mathematical Models
2.1.1. Integrins Balance
2.1.2. Cell Adhesion Mechanics
2.1.3. Laminar Blood Flow
2.1.4. Cell Structure Mechanical Behavior
2.1.5. Fluid-Structure Interaction on Cell Structure
2.2. Computational Approach
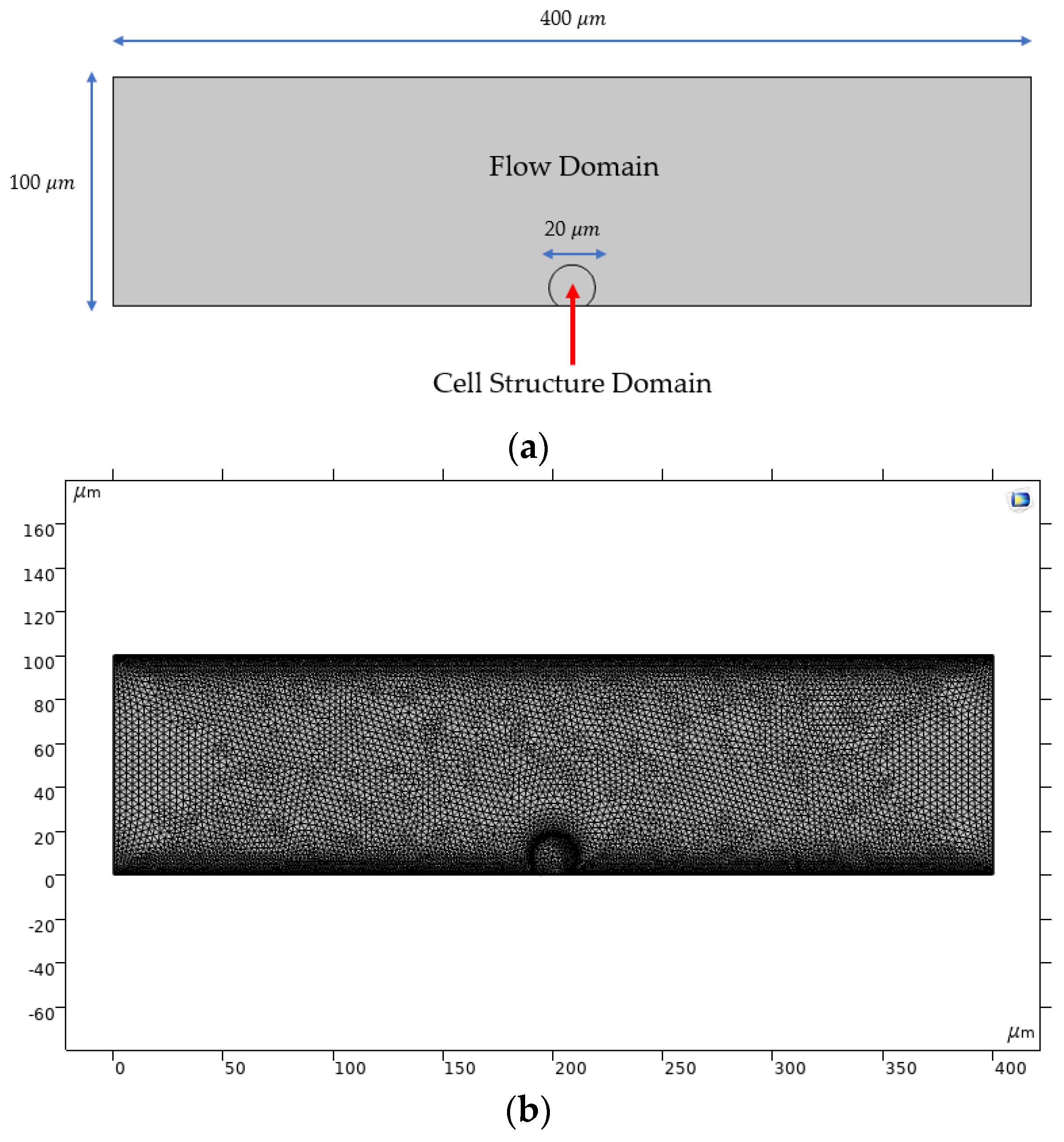
2.2.1. Computational Domain
2.2.2. Transport of Diluted Species
2.2.3. Laminar Flow
2.2.4. Solid Mechanics
2.2.5. Fluid-Structure Interaction
2.2.6. Simulations
3. Results
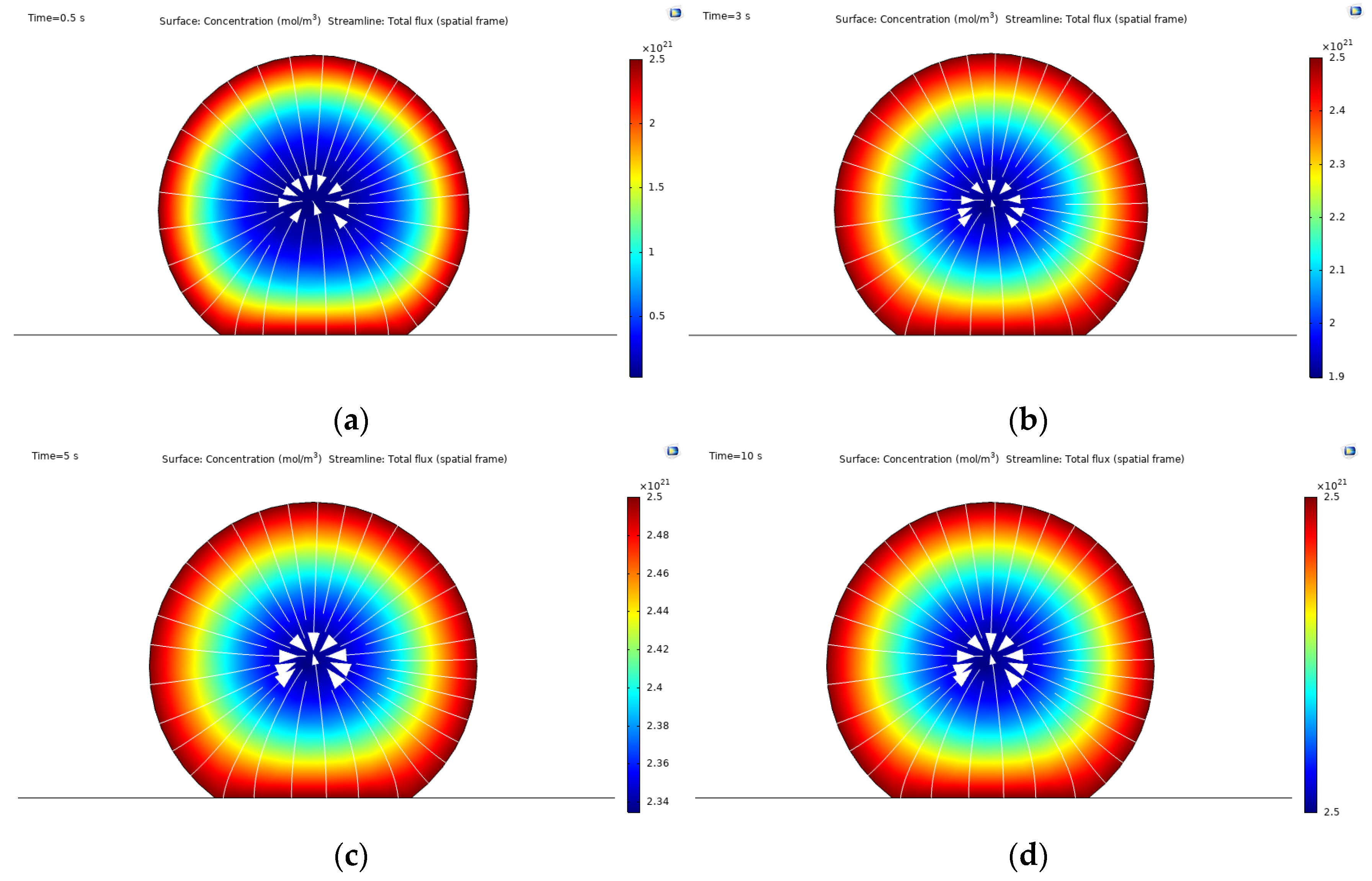
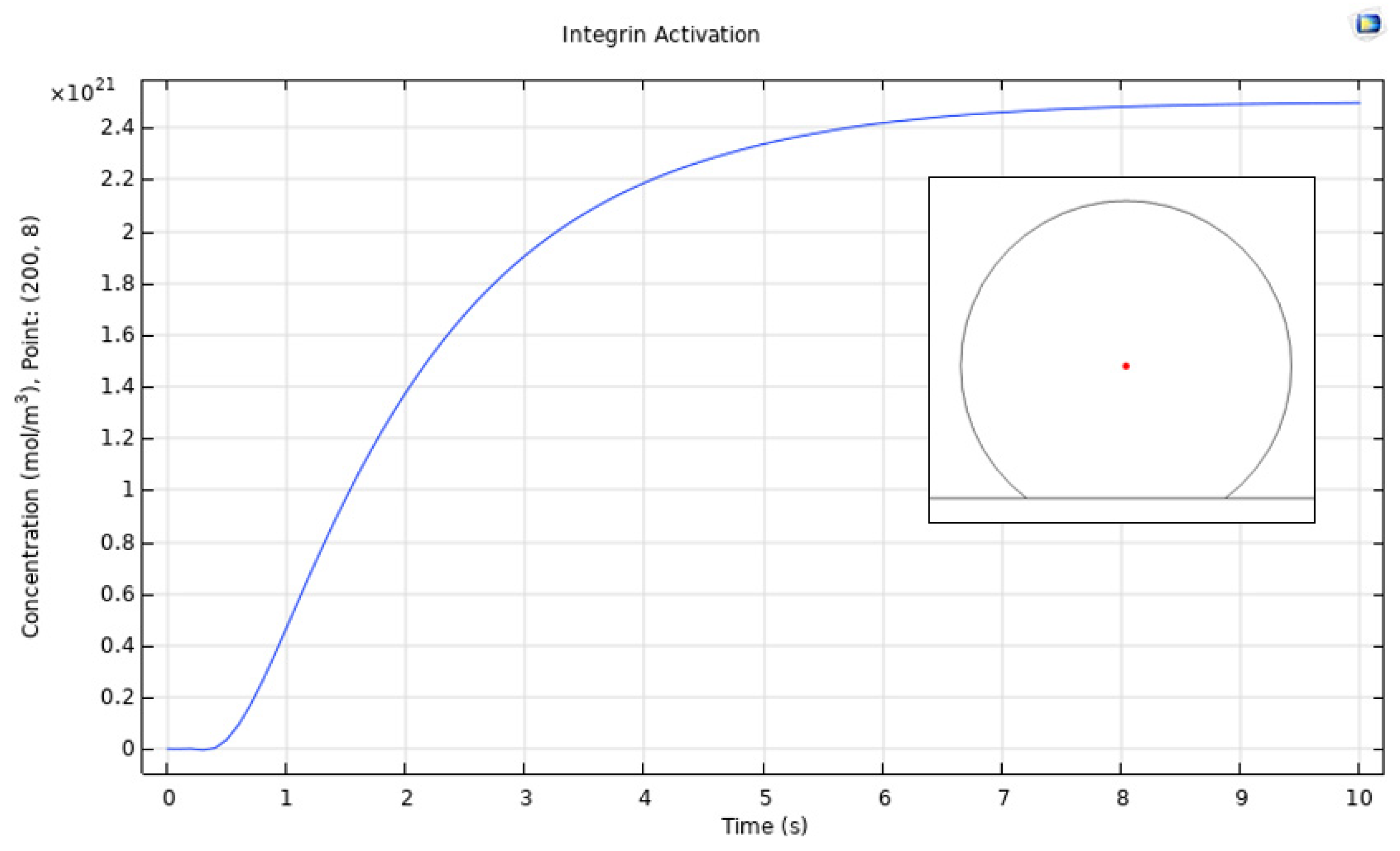
3.1. Integrin Activation
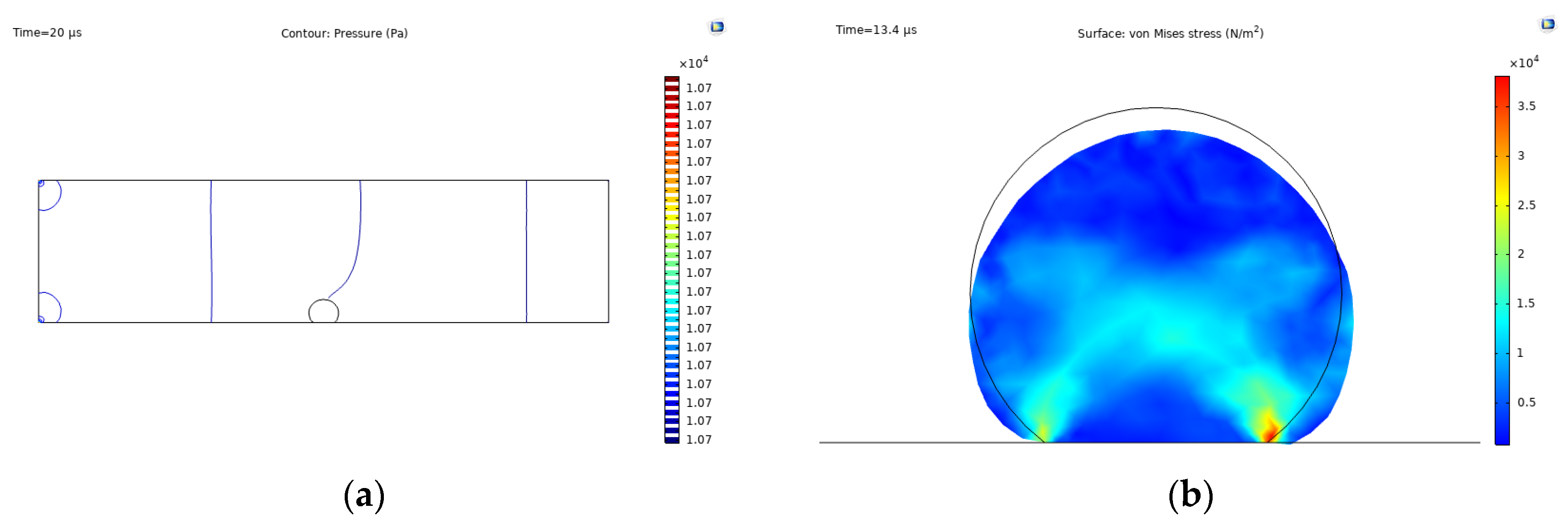
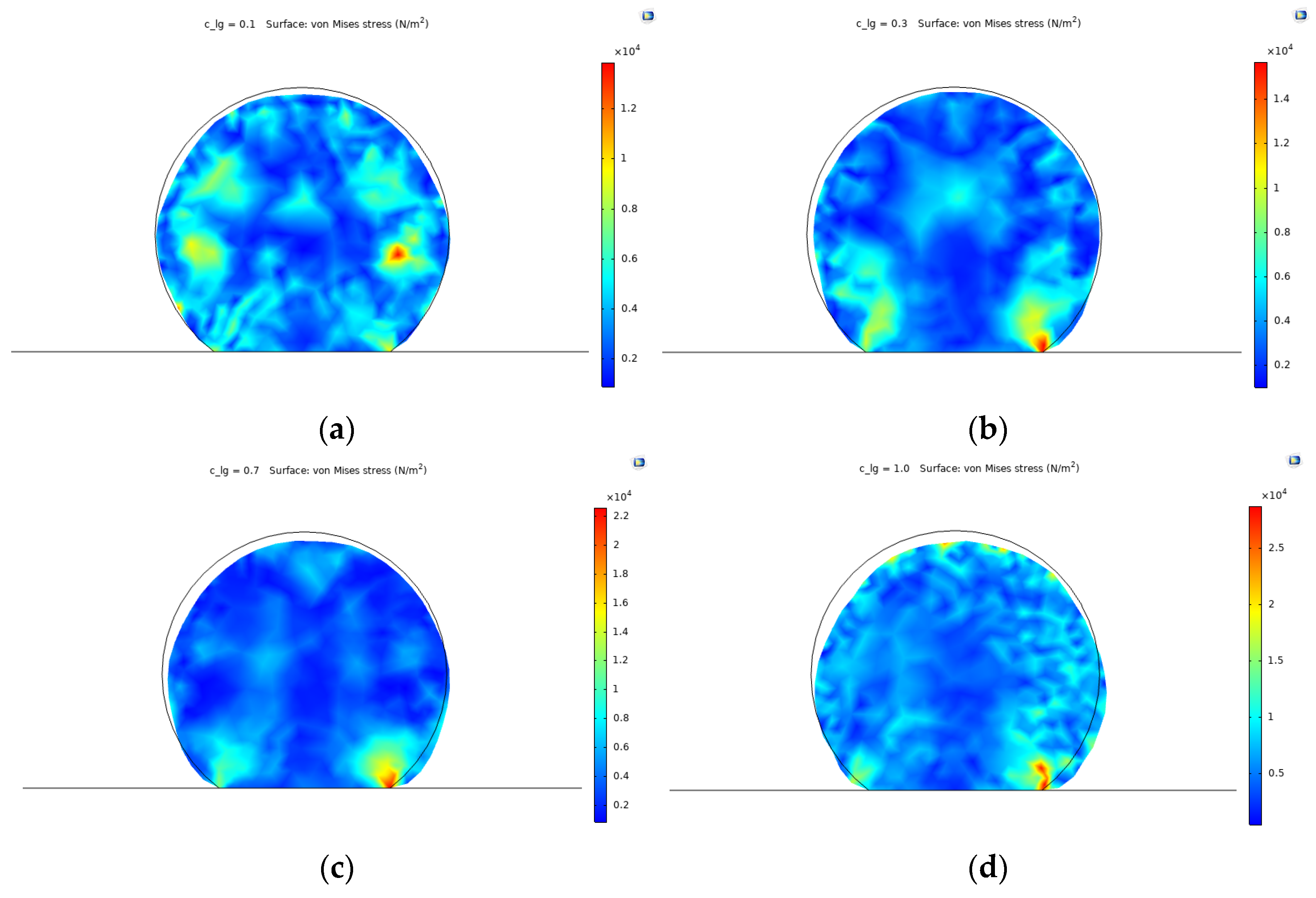
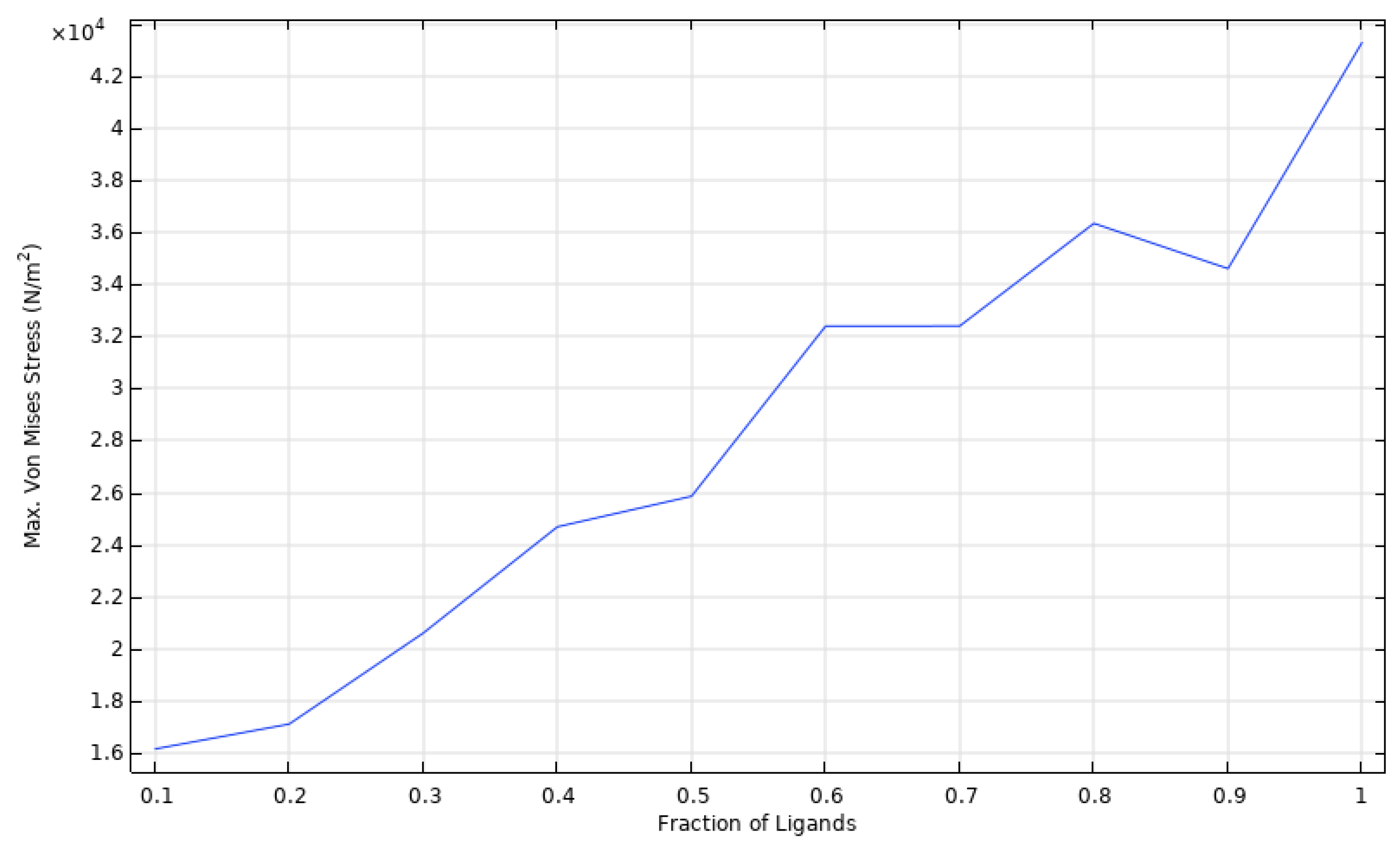
3.2. Cell Spreading and Attachment
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pashneh-Tala, S.; MacNeil, S.; Claeyssens, F. The Tissue-Engineered Vascular Graft—Past, Present, and Future. Tissue Eng. Part B Rev. 2016, 22, 68–100. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Liu, S.; Zhang, K.; Chen, J.; Huang, N. Endothelialization of implanted cardiovascular biomaterial surfaces: The development from in vitro to in vivo: Endothelialization of Implanted Cardiovascular Biomaterial Surfaces. J. Biomed. Mater. Res. 2014, 102, 3754–3772. [Google Scholar] [CrossRef] [PubMed]
- Sánchez, P.F.; Brey, E.M.; Briceño, J.C. Endothelialization mechanisms in vascular grafts. J. Tissue Eng. Regen. Med. 2018, 12, 2164–2178. [Google Scholar] [CrossRef] [PubMed]
- Mezu-Ndubuisi, O.J.; Maheshwari, A. The role of integrins in inflammation and angiogenesis. Pediatr. Res. 2020. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Fu, Y.; Gu, M.; Zhang, L.; Li, D.; Li, H.; Chien, S.; Shyy, J.Y.-J.; Zhu, Y. Activation of integrin α5 mediated by flow requires its translocation to membrane lipid rafts in vascular endothelial cells. Proc. Natl. Acad. Sci. USA 2016, 113, 769–774. [Google Scholar] [CrossRef] [PubMed]
- Ren, X.; Feng, Y.; Guo, J.; Wang, H.; Li, Q.; Yang, J.; Hao, X.; Lv, J.; Ma, N.; Li, W. Surface modification and endothelialization of biomaterials as potential scaffolds for vascular tissue engineering applications. Chem. Soc. Rev. 2015, 44, 5680–5742. [Google Scholar] [CrossRef] [PubMed]
- Vernerey, F.J.; Farsad, M. A mathematical model of the coupled mechanisms of cell adhesion, contraction and spreading. J. Math. Biol. 2014, 68, 989–1022. [Google Scholar] [CrossRef] [PubMed]
- Howard, J. Mass, Stiffness, and Damping of Proteins. In Mechanics of Motor Proteins and the Cytoskeleton; Sinauer Associates Inc.: Sunderland, MA, USA, 2001; Chapter 3; p. 30. [Google Scholar]
- Jean, R.P.; Chen, C.S.; Spector, A.A. Finite-element analysis of the adhesion-cytoskeleton-nucleus mechanotransduction pathway during endothelial cell rounding: Axisymmetric model. J. Biomech. Eng. 2005, 127, 594–600. [Google Scholar] [CrossRef]
- Dai, A.; Ye, F.; Taylor, D.W.; Hu, G.; Ginsberg, M.H.; Taylor, K.A. The Structure of a Full-length Membrane-embedded Integrin Bound to a Physiological Ligand. J. Biol. Chem. 2015, 290, 27168–27175. [Google Scholar] [CrossRef] [PubMed]
- Megali, G.; Pellicanò, D.; Cacciola, M.; Calarco, F.; De Carlo, D.; Laganà, F.; Morabito, F.C. Modeling Interface Response in Cellular Adhesion. In Proceedings of the COMSOL Conference 2009, Milan, Italy, 14–16 October 2009. [Google Scholar]
- Campbell, N.A.; Reece, J.B. Circulation and Gas Exchange. In Biology, 8th ed.; Wilbur, B., Ed.; Pearson Benjamin Cummings: San Francisco, CA, USA, 2008; p. 906. [Google Scholar]
- Vitello, D.J.; Ripper, R.M.; Fettiplace, M.R.; Weinberg, G.L.; Vitello, J.M. Blood Density Is Nearly Equal to Water Density: A Validation Study of the Gravimetric Method of Measuring Intraoperative Blood Loss. J. Vet. Med. 2015, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Shibeshi, S.S.; Collins, W.E. The rheology of blood flow in a branced arterial system. Appl. Rheol. 2005, 15, 398–405. [Google Scholar] [CrossRef] [PubMed]
- Dinnar, U. Cardiovascular Fluid Dynamics; CRC Press: Boca Raton, FL, USA, 1981; ISBN 978-0-8493-5573-8. [Google Scholar]
- Ding, Y.; Xu, G.-K.; Wang, G.-F. On the determination of elastic moduli of cells by AFM based indentation. Sci. Rep. 2017, 7, 45575. [Google Scholar] [CrossRef]
- Sato, M.; Levesque, M.J.; Nerem, R.M. An Application of the Micropipette Technique to the Measurement of the Mechanical Properties of Cultured Bovine Aortic Endothelial Cells. J. Biomech. Eng. 1987, 109, 27–34. [Google Scholar] [CrossRef] [PubMed]
- Félétou, M. Introduction, Part 1: Multiple Functions of the Endothelial Cells—Focus on Endothelium-Derived Vasoactive Mediators. In The Endothelium; Morgan & Claypool Life Sciences: San Rafael, CA, USA, 2011; Chapter 1. [Google Scholar]


| Parameter | Value | Units | Description | Ref. |
|---|---|---|---|---|
| 310.15 | Body temperature | n/a | ||
| 30 | Physiological average normal flow velocity | [12] | ||
| 1060 | Density of blood | [13] | ||
| 0.056 | Zero shear rate viscosity | [14] | ||
| 0.0035 | Infinite shear rate viscosity | [14] | ||
| 3.313 | s | Relaxation time constant | [14] | |
| 2000 | Shear rate | [15] | ||
| 0.3568 | ---- | Power law index of Carreau | [14] | |
| 400 | TEVG length | n/a | ||
| 50 | TEVG radius | n/a | ||
| 5 × 1015 | Total amount of available integrins | [7] | ||
| 1.5 × 10−4 | Stiffness of complex integrin-ligand | [7] | ||
| 184 | Young’s modulus of intima layer | n/a | ||
| 0.4 | ---- | Poisson ratio of intima layer | n/a | |
| 1211 | Density of intima layer | n/a | ||
| 1100 | Density of cell structure | [8] | ||
| 248 | Lamé parameter lambda for neo-Hookean model | n/a | ||
| 28 | Lamé parameter mu for neo-Hookean model | n/a | ||
| 80 | Young’s modulus of cell structure | [11,16] | ||
| 0.45 | ---- | Poisson ratio of cell structure | n/a | |
| 20 | Average cell diameter | [17] | ||
| 2 | Cell thickness | [18] | ||
| 10 × 10−12 | Mobility coefficient of integrins | [7] | ||
| 2000 | Cytoskeleton kinesins velocity | [8] | ||
| 53.1 | Contact angle of undeformed cell | n/a | ||
| 20 | Length of integrin-ligand complex upon binding | [10] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bermudez, J.S.; Rodriguez-Soto, M.A.; Riveros, A.; Suarez, N.; Muñoz-Camargo, C.; Cruz, J.C.; Sandoval, N.; Briceño, J.C. A Chemo-Mechanical Model of the Spreading of Endothelial Cells on the Lumen of Functionalized TEVGs. Mater. Proc. 2021, 4, 74. https://doi.org/10.3390/IOCN2020-07833
Bermudez JS, Rodriguez-Soto MA, Riveros A, Suarez N, Muñoz-Camargo C, Cruz JC, Sandoval N, Briceño JC. A Chemo-Mechanical Model of the Spreading of Endothelial Cells on the Lumen of Functionalized TEVGs. Materials Proceedings. 2021; 4(1):74. https://doi.org/10.3390/IOCN2020-07833
Chicago/Turabian StyleBermudez, Juan Sebastian, Maria A. Rodriguez-Soto, Alejandra Riveros, Natalia Suarez, Carolina Muñoz-Camargo, Juan C. Cruz, Nestor Sandoval, and Juan C. Briceño. 2021. "A Chemo-Mechanical Model of the Spreading of Endothelial Cells on the Lumen of Functionalized TEVGs" Materials Proceedings 4, no. 1: 74. https://doi.org/10.3390/IOCN2020-07833
APA StyleBermudez, J. S., Rodriguez-Soto, M. A., Riveros, A., Suarez, N., Muñoz-Camargo, C., Cruz, J. C., Sandoval, N., & Briceño, J. C. (2021). A Chemo-Mechanical Model of the Spreading of Endothelial Cells on the Lumen of Functionalized TEVGs. Materials Proceedings, 4(1), 74. https://doi.org/10.3390/IOCN2020-07833










