Abstract
The pillar stability factor (PSF) is calculated in three different mining stages for a sublevel open stoping mining project located in northern Botswana. Several three-dimensional finite element models were developed by varying the stope span. Pillar strength was estimated using the Lunder and Pakalnis equation and pillar stress was obtained from the numerical models. As mining progresses, both the first and second mining stages meet the rib pillar stability factor requirement for safe extraction. Geometrical improvements are suggested in the mining layout for the third mining stage to achieve the required PSF, which is based on international practices.
1. Introduction
The choice of an underground mining method is mainly influenced by the stability of the rock mass. Stable rock masses allow for self-supported (or unsupported) openings, in which the induced stresses are carried by the side walls and the pillars. Then, the ore can be extracted from the underground opening without the application of any supporting system. The main self-supporting mining methods are sublevel stoping and room and pillar [1].
Sublevel stoping is an open stoping, high-production, bulk mining method that is widely used in underground (hard-rock) metalliferous mining. This method allows for low cost, high recovery, and productivity, while providing operational safety to personnel and equipment. The most commonly used sublevel stoping mining methods are sublevel open stoping, long-hole open stoping, and vertical crater retreat (VCR). It is applicable to large, steeply dipping, regular competent ore bodies surrounded by competent host rock in both the hanging wall and the footwall. It has been used in ore bodies with a minimum strength of 50 MPa [2], a minimum width of 6 m [3] and a minimum dip of 50° [4].
Stopes are developed along the strike when the ore thickness is less than 15 m. Transverse stopes are used in wider (thicker) ore bodies which are aligned perpendicularly to the strike of the deposit with pillars left between the primary stopes [5].
In the absence of consolidated mine fill, sublevel stoping employs pillars to separate the individual stopes. The stopes, generated by the ore exploitation process, are bounded by crown, rib and sill pillars that serve as natural supports. The crown pillar provides support to the surrounding workings. The rib pillar separates adjacent stopes and thus limits the size of the stope along its length. The sill pillar serves as a base for the muck and for development of the ore extraction system.
Since the ore is extracted progressively from open stopes generated between pillars, the stability of large (mainly unreinforced) stope walls and crowns, as well as the stability of any exposed fill masses is critical to the success of the method [5].
Many researchers [6,7,8,9] have investigated and analyzed the design of the crown and the rib pillars numerically in 2D space, to evaluate the required geometrical dimensions for safe operation and to estimate the ore and rock mass response in underground metalliferous mines. The major factors which contribute to pillar stability are: (1) the depth of cover; (2) the excavation size; (3) the horizontal stresses; (4) rock mass properties; (5) backfilling; (6) reinforcement of the hanging wall; and (7) the orebody inclination (dip) [10,11].
This paper mainly focusses on the variation of the stope span dimension in a longitudinal sublevel open stoping (SLOS) operation, while the dimensions of the crown and rib pillars remain constant. The rib pillar stability of different SLOS layouts was analyzed and assessed with the aid of a three-dimensional finite element analysis software by RocScience. A parametric analysis is presented whereby the stope span parameter is varied and the resulting orebody rib pillar stresses are calculated at different depths and stages of mining sequence. The numerical results for each SLOS layout are compared to evaluate the proposed mining layouts, based on the required pillar stability factor (PSF), as suggested by international practices.
2. Geology
The study area is located within the Neoproterozoic-to Early Paleozoic Pan-African Ghantsi-Chobe Belt (GCB), which is part of the Kalahari Copper Belt (KCB) [12], extending from western Namibia into the northern part of Botswana along the north-western edge of the Paleoproterozoic Kalahari Craton [13]. Stratigraphically, the Late Mesoproterozoic [14] Kgwebe Volcanic Formation (KVF) forms the basement of the KCB in Botswana. The KVF comprises of inter-bedded meta-volcanic and meta-sedimentary rocks of about 2 km to 2.5 km thick. Overlying the KVF, is a 5000 m thick sequence of meta sedimentary rocks referred to as the Ghanzi Group [15]. The Ghanzi Group is comprised (from the oldest) of: (i) the Kuke Formation consisting of 500 m grey quartz arenite and red sandstone with a basal conglomerate [15]; (ii) the Ngwako Pan Formation (2 km thick), made up of a mudstone-rich matrix sandstone, which grades into a red sandstone with interbedded granular units [15]; (iii) the D’Kar Formation consisting of fine-grained sandstones, siltstones, mudstones with limestones [16], and; (iv) the Mamuno Formation, which is the youngest in the sequence, is a red sandstone with occasional mudstone and minor limestone [15]. Overlying the Mamuno Formation is the Cenozoic to recent Kalahari Group [14].
The Botswana portion of the KCB is host to numerous strata-bound Cu–Ag deposits/occurrences, which occur at the redox boundary between the oxidized Ngwako Pan and the reduced D’kar formations. The copper–silver mineralization, essentially comprises Ag-bearing Cu sulphides and Pb-Zn sulphides as accessories [17].
3. Case Study
3.1. Description
This case study considers a copper orebody, dipping at 60°, with an average thickness of 10 m, at an underground copper mine. In the area of interest, the orebody presents an excellent strike and depth continuity of mineralization and the whole thickness is mined. The footwall consists of a limestone unit, while the hanging wall is a thick unit of sandstone. The conventional SLOS mining method (Figure 1a) is used at an overburden depth of 85 m.
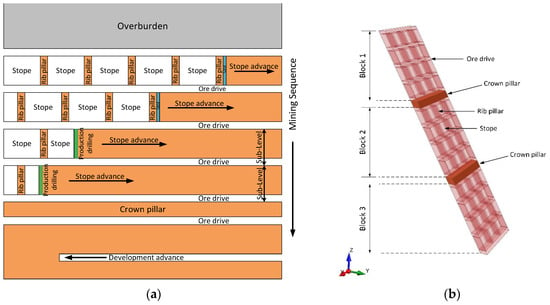
Figure 1.
(a) Section view along strike in the SLOS mining method. (b) The 3D layout of the mining area.
The mining area has been divided into three blocks (Figure 1b), based on the initial mine design; each block has a vertical height of 105 m. Each such block is mined by four sublevels, utilizing ore drives of 5 m height. The sublevel stopes are separated by rib pillars of 5 m strike length in a staggered pattern. Each stope has a dip height of 23.1 m and a width of 10 m, while the strike length (stope span) is under investigation and varies. The three blocks are separated by crown pillars of 11.5 m dip height and 10 m width.
3.2. Numerical Modeling
In this study, the numerical modeling was conducted using RS3 (developed and distributed by RocScience), assuming homogeneous isotropic rock materials and no discontinuities. Several numerical models were created based on the same initial SLOS layout. All the SLOS geometrical parameters were the same in each model, except for the stope span which varied to investigate its effect on the rib pillar stability.
The numerical model height is 600 m and the width is 700 m. The length along the strike depends on the stope span and varies between 90 m and 120 m (Figure 2a). The elastic–plastic Mohr–Coulomb model is used for the copper orebody, while the other rock layers were considered as elastic materials. The bottom of the numerical model is fixed, while the side boundaries are roller-supported to allow only vertical movement. The in-situ stress field was defined by the gravity field stress option, while the horizontal stresses were set equal in all directions. The horizontal to vertical stress ratio was set equal to 0.33. The model was meshed utilizing a graded mesh with 10-node tetrahedral elements which resulted to a total of 433,389 elements and 595,900 nodes. The initial mesh was improved by increasing the element density around the mining area, utilizing the mesh refinement procedure available in RS3. The RS3 models were solved in four stages: (1) the geostatic stage, in which the pre-mining in-situ stresses were initialized; (2) the Block 1 mining stage, in which all ore drives and stopes were excavated in the Block 1 mining area; (3) the Block 2 mining stage; (4) the Block 3 mining stage.
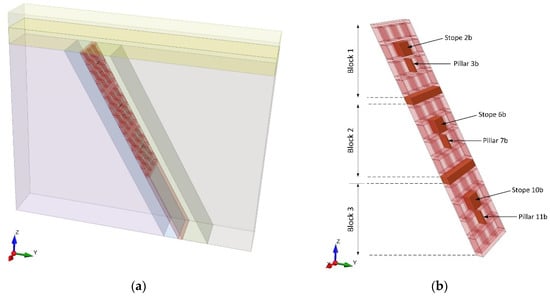
Figure 2.
(a) The numerical model for the three mining blocks in the SLOS method. (b) The stopes and rib pillars under investigation in each mining block.
The stope deformability and the pillar stability for each model were evaluated at specific selected stopes (Stope 2b, Stope 6b, and Stope 10b) and rib pillars (Pillar 3b, Pillar 7b, and Pillar 11b), in each Block at the middle vertical plane of the model, presented in Figure 2b.
4. Pillar Design Background
Pillar design is one of the most important issues in the field of ground control in underground self-supported mining operations. Traditional strength-based pillar design requires estimates of pillar stress and pillar strength [1]. The pillar stability factor (PSF) is then calculated by dividing pillar strength by pillar stress. The strength of a pillar is related to both its volume and its geometric shape. The effect of volume on strength can be readily understood in terms of a distribution of mining induced cracks, natural fractures and other defects in the rock mass.
The design of hard-rock pillars has not received the same research attention as coal pillar design. This is partly because fewer mines operate at depths sufficient to induce the stresses required to cause hard rocks to fail, and in hard-rock mining pillar and mining geometries may be irregular making it difficult to establish actual loads.
There have been several attempts to establish hard-rock pillar strength formulas, using the “back-calculation” approach [18,19,20,21,22]. The empirical formulation by Lunder and Pakalnis [23] (Equation (1)), which is based on a detailed pillar stability study combined with an extensive database of published pillar case histories (178), was utilized for pillar strength calculation in the present study:
where: is the uniaxial compression strength and
and is the square pillar width, is the pillar height. For a rectangular pillar with unequal side lengths (), the square pillar dimension in Equation (3) is substituted by the equivalent dimension given by:
In this study the pillar strength was calculated to be equal to 34.94 MPa, by applying Equations (1)–(4) and utilizing the geometrical parameters presented in Figure 3a.
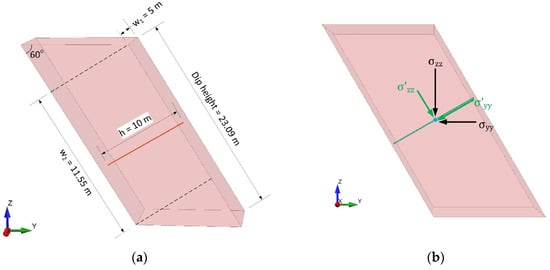
Figure 3.
(a) Rib pillar geometrical dimensions. (b) Stress transformation along the line query.
The pillar stress was numerically determined in each model. Consider a set of reference axes, x, y, and z, with the x-axis parallel to the strike, as shown in Figure 3b. In this study the pillar stress is calculated assuming plane problem state by utilizing transformation Equation (5), along the line query normal to the dip of the orebody, at the middle of the pillar.
5. Results and Discussion
In this study three numerical models were developed, based on the same SLOS mining layout with variations in the stope span (25 m, 30 m, and 35 m). This section discusses the influence of the stope span on the stope deformability and the rib pillar stability. The extraction ratio in the cases of 25 m, 30 m, and 35 m stope span are 82.1%, 83.8%, and 85.1%, respectively.
The mechanical characteristics of the selected stopes and pillars (Figure 2b) were evaluated along the line queries presented in Figure 4. More specifically the stope’s line query lies at the hanging wall parallel to the strike, at the middle of the dip height, while the pillar’s line query is normal to the dip of the orebody, at the middle of the pillar. The length of stope’s line query is equal to stope span in each model and the length of the pillar’s line query is equal to the orebody thickness (10 m).
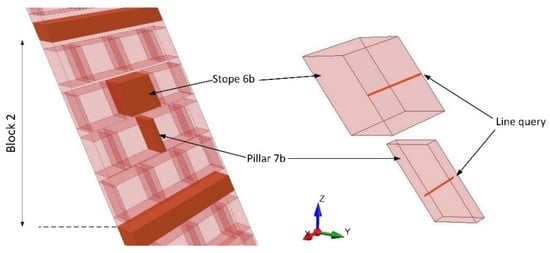
Figure 4.
Location of the line queries at the hanging wall of the stope and the middle of the rib pillar.
5.1. Stope Deformability
Figure 5a presents the variation of the total displacement along the Stope 6b hanging wall line query in the Block 3 mining stage, for three different stope spans, while Figure 5b shows the variation of the total displacement with respect to the stope span for each mining stage. It is evident that the total displacement increases with respect to the stope span and the mining stage.
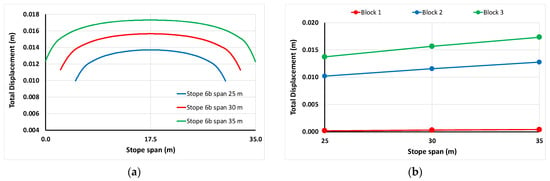
Figure 5.
Variation of the total displacement (a) along the Stope 6b hanging wall line query in the Block 3 mining stage, for three different stope spans and (b) at the middle of the Stope 6b hanging wall for each mining stage vs. the stope span.
5.2. Rib Pillar Behavior and Stability
Figure 6a presents the variation of normal stress along the thickness of Pillar 7b (0–10 m) and clearly shows that the pillar stress increases as the mining sequence progresses. In addition, the maximum value is observed at the middle of the pillar for mining stages 2 and 3. Pillar strength was calculated using Equation (1). The PSF was calculated utilizing the maximum value for each such curve.
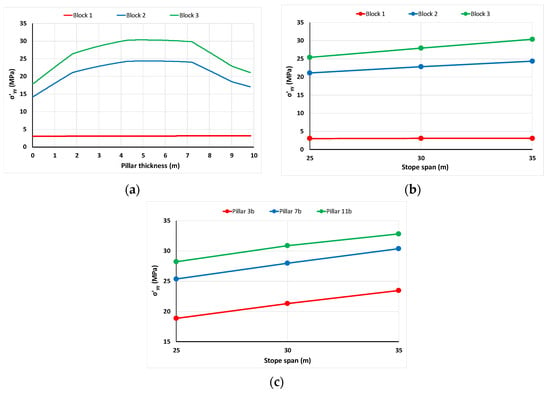
Figure 6.
Variation of the normal stress (a) along Pillar 7b for 35 m stope span and each mining stage, (b) at the middle of Pillar 7b for each mining stage vs. the stope span. (c) Variation of the normal stress at the middle of the three pillars for Block 3 mining stage vs. stope span.
Table 1 summarizes the normal stress at the middle of the pillars as well as the PSF calculated by Equation (1) for each mining stage and stope span. As expected, the PSF values decrease as the stope span increases and the mining sequence progresses. The maximum stress at the middle of the pillar increases with respect to the mining stage and the stope span (Figure 6b). This induced stress increases as the depth of the pillar under investigation increases (Figure 6c).

Table 1.
Summary of PSF for each mining stage and stope span.
6. Conclusions
The objective of this study was to numerically investigate the effect of the stope span, the mining depth and the mining sequence on the stability of rib pillars in a SLOS copper mining system, as well as to evaluate the three proposed SLOS mining layouts based on the required PSF. This investigation was completed using three-dimensional models in RS3.
As expected, the extraction ratio increases, while the PSF decreases as the stope span increases in all mining stages (Figure 7). Given that the required pillar stability factor for the entire mining sequence is 1.40 ± 0.05, it is obvious that this requirement is satisfied for both Block 1 and Block 2 mining stages (Figure 7a). In the Block 3 mining stage (Figure 7b), the PSF in Pillars 7b and 11b does not meet the requirement of PSF ≥ 1.40.
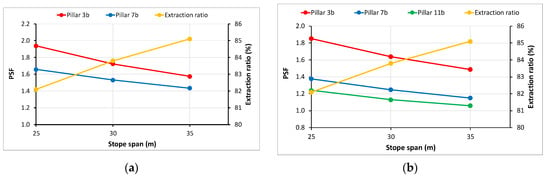
Figure 7.
Variation of PSF and extraction ratio with the stope span for the three pillars in (a) Block 2 and (b) Block 3 mining stage.
An increase in both the rib pillar’s strike length and the crown pillar’s height in Blocks 2 and 3, is recommended. Further numerical investigation is necessary to define these geometrical parameters for obtaining the required PSF. The results and conclusions drawn from this work should be extended by considering the stability of the stope roof. Pillar stability factors and roof stability characteristics should be jointly evaluated.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brady, B.H.G.; Brown, E.T. Pillar supported mining methods. In Rock Mechanics for Underground Mining; Springer: Berlin/Heidelberg, Germany, 2004; pp. 370–407. [Google Scholar]
- Haycocks, C.; Aelick, R.C. Sublevel Stoping. In SME Mining Engineering Handbook; Hartman, H.L., Ed.; Society for Mining, Metallurgy and Exploration, Inc.: Englewood, CO, USA, 1992; Volume 2, pp. 1717–1731. [Google Scholar]
- Tatiya, R.R. Surface and Underground Excavations—Methods, Techniques and Equipment; A.A. Balkema Publishers: Leiden, The Netherlands; New York, NY, USA; Philadelphia, PA, USA; Singapore, 2005; pp. 415–437. [Google Scholar]
- Pakalnis, T.R.; Hughes, P.B. Sublevel Stoping. In SME Mining Engineering Handbook, 3rd ed.; Darling, P., Ed.; Society for Mining, Metallurgy and Exploration, Inc.: Englewood, CO, USA, 2011; pp. 1355–1364. [Google Scholar]
- Villaescusa, E. Geotechnical Design for Sublevel Open Stoping; CRC Press, Taylor and Francis Group: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2014. [Google Scholar]
- Kumar, H.; Deb, D.; Chakravarty, D. Design of crown pillar thickness using finite element method and multivariate regression analysis. Int. J. Min. Sci. Technol. 2017, 27, 955–964. [Google Scholar] [CrossRef]
- Himanshu, V.K.; Tiwari, S.; Kushwaha, A.; Bhattacharjee, R. Elasto-plastic failure analysis for design of stoping dimension in underground metalliferous mine. NexGen Technol. Min. Fuel Ind. 2017, 1, 639–646. [Google Scholar]
- Mallı, T.; Yetkin, M.E.; Özfırat, M.K.; Kahraman, B. Numerical analysis of underground space and pillar design in metalliferous mine. J. Afr. Earth Sci. 2017, 134, 365–372. [Google Scholar] [CrossRef]
- Dzimunya, N.; Radhe, K.; William, C.M. Design and dimensioning of sublevel stoping for extraction of thin ore (<12 m) at very deep level: A case study of Konkola copper mines (kcm), Zambia. Math. Model. Eng. Probl. 2018, 5, 27–32. [Google Scholar] [CrossRef]
- Esterhuizen, G.S.; Dolinar, R.D.; Ellenberger, J.L.; Prosser, L.J. Pillar and Roof Span Design Guidelines for Underground Stone Mines; NIOSH, IC 9526: Pittsburgh, PA, USA, 2011. [Google Scholar]
- Esterhuizen, G.S.; Iannacchione, A.T. Effect of the Dip and Excavation Orientation on Roof Stability in Moderately Dipping Stone Mine Workings. In Proceedings of the 40th U.S. Symposium on Rock Mechanics (USRMS), Anchorage, AK, USA, 25–29 June 2005. [Google Scholar]
- Stanistreet, I.G.; Kukla, P.A.; Henry, G. Sedimentary basinal responses to a Late Precambrian Wilson Cycle: The Damara Orogen and Nama Foreland, Namibia. J. Afr. Earth Sci. 1991, 13, 141–156. [Google Scholar] [CrossRef]
- Kampunzu, A.B.; Armstrong, R.A.; Modisi, M.P.; Mapeo, R.B.M. Ion microprobe U-Pb ages on detrital zircon grains from the Ghanzi Group: Implications for the identification of a Kibaran-age crust in northwest Botswana. J. Afr. Earth Sci. 2000, 30, 579–587. [Google Scholar] [CrossRef]
- Carney, J.N.; Aldiss, D.T.; Lock, N.P. The Geology of Botswana, Geological Survey Department. Repub. Botsw. Bull. 1994, 37, 71–83. [Google Scholar]
- Modie, B.N. Geology and mineralisation in the Meso- to Neoproterozoic Ghanzi Chobe Belt of northwest Botswana. J. Afr. Earth Sci. 2000, 30, 467–474. [Google Scholar] [CrossRef]
- Modie, B.N.J. Depositional environments of the Meso- to Neoproterozoic Ghanzi-Chobe belt, northwest Botswana. J. Afr. Earth Sci. 1996, 22, 255–268. [Google Scholar] [CrossRef]
- Kelepile, T.; Bineli Betsi, T.; Franchi, F.; Shemang, E. Partitioning and distribution of silver in sediment-hosted Cu-Ag deposits: Evidence from the Ghanzi-Chobe Belt portion of the Kalahari Copper Belt. Ore Geol. Rev. 2020, 124, 103663. [Google Scholar] [CrossRef]
- Von Kimmelmann, M.R.; Hyde, B.; Madgwick, R.J. The use of computer applications at BCL Limited in planning pillar extraction and design of mining layouts. In ISRM Symposium: Design and Performance of Underground Excavations; Brown, E.T., Hudson, J.A., Eds.; British Geotechnical Society: London, UK, 1984; pp. 53–63. [Google Scholar]
- Krauland, N.; Soder, P.E. Determining pillar strength from pillar failure observations. Eng. Min. J. 1987, 188, 34–40. [Google Scholar]
- Potvin, Y.; Hudyma, M.R.; Miller, H.D.S. Design guidelines for open stope support. Can. Min. Metall. Bull. 1989, 82, 53–62. [Google Scholar]
- Sjoberg, J. Failure modes and pillar behaviour in the Zinkgruvan mine. In The 33rd U.S. Rock Mechanics Symposium, Sante Fe; Tillerson, J.A., Wawersik, W.R., Eds.; A.A. Balkema: Rotterdam, The Netherlands, 1992; pp. 491–500. [Google Scholar]
- Martin, C.D.; Maybee, W.G. The strength of hard-rock pillars. Int. J. Rock Mech. Min. Sci. 2000, 37, 1239–1246. [Google Scholar] [CrossRef]
- Lunder, P.J.; Pakalnis, R. Determination of the strength of hard-rock mine pillars. Can. Min. Metall. Bull. 1997, 90, 51–55. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).