Review of Deterministic and Probabilistic Wind Power Forecasting: Models, Methods, and Future Research
Abstract
:1. Introduction
- It offers a unique and wider view by reviewing the state of the art in both the deterministic and probabilistic wind power forecasting methodologies and by identifying their advantages and disadvantages.
- It provides comparative results among the models of the reviewed works, based on evaluation measures.
- It proposes future research goals of deterministic and probabilistic forecasting models, not only to improve the methodologies used in forecasting, but also to make both deterministic and probabilistic forecasting models more useful and helpful in energy markets and power systems.
- It aims to help researchers in having a view of possible expectations in research cases corresponding to the ones compared in the paper.
2. Evaluation of Wind Power Forecasts
2.1. Deterministic Forecasting
- Mean Absolute Error (MAE)
- Mean Squared Error (MSE)
- Root Mean Squared Error (RMSE)
2.2. Probabilistic Forecasting
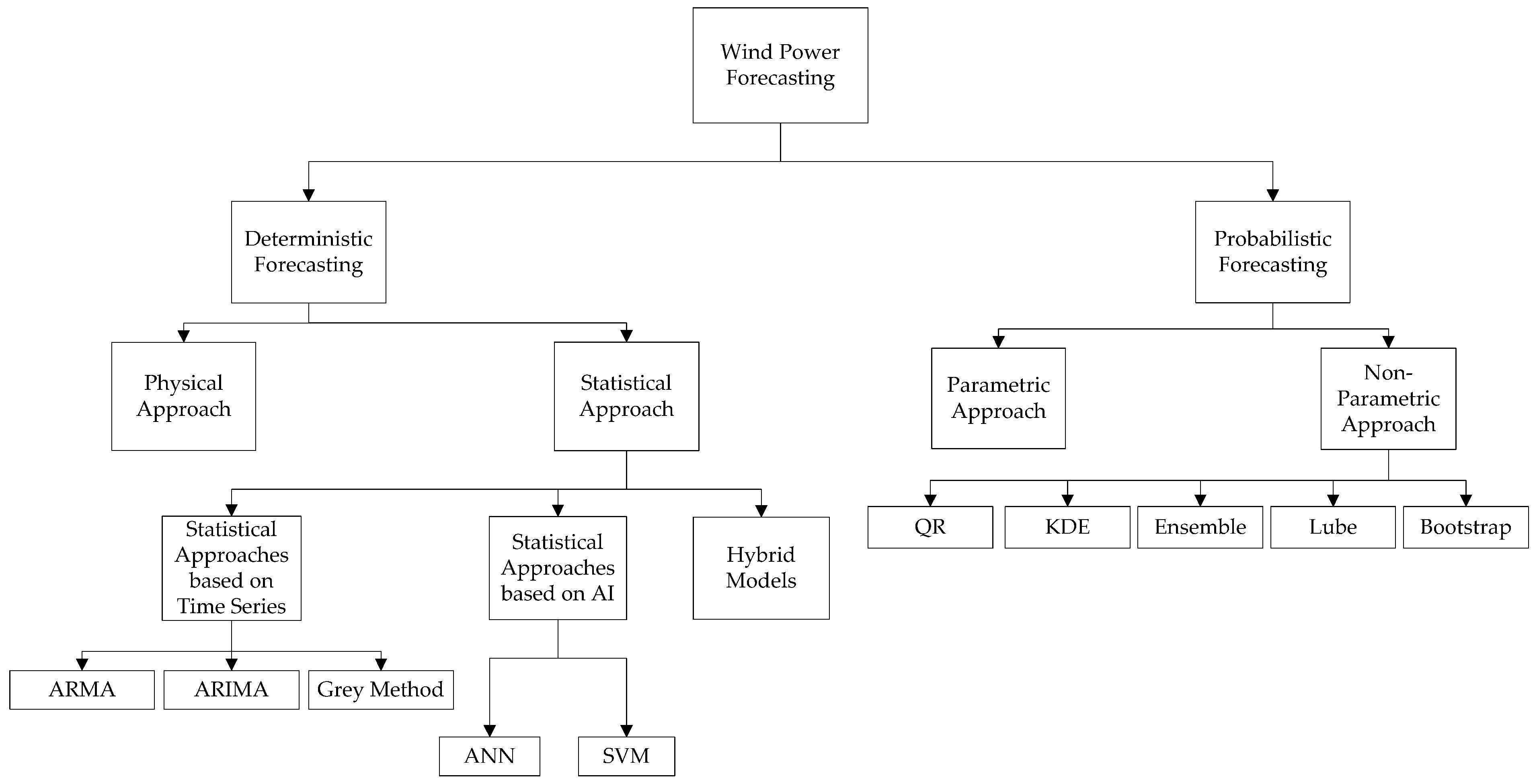
3. Wind Power Deterministic Forecasting
3.1. Physical Approach
3.2. Statistical Approach
3.2.1. Statistical Approaches Based on Time Series
ARMA and ARIMA
Grey Prediction Method
3.2.2. Statistical Approaches Based on Artificial Intelligence
Artificial Neural Network
Support Vector Machine
3.3. Hybrid Approach
4. Wind Power Probabilistic Forecasting
4.1. Parametric Approach
4.2. Non-Parametric Approach
4.2.1. Quantile Regression Method
4.2.2. Kernel Density Estimation
4.2.3. Ensemble Methods
4.2.4. Lower Upper Bound Estimation
4.2.5. Bootstrap
5. Recent Wind Power Forecasting Methodologies
6. Advantages of Using Deterministic and Probabilistic Forecasting Methods
- Probably the most important advantage of deterministic forecasts is the fact that they have been and are still used in the electricity markets all over the world. With the renewable energy being used more and more in the energy systems, the need for accurate and specific predictions is highly important, not only for the stability of power system, but also for trading electricity.
- Since they play a crucial role in electricity markets, deterministic models have been thoroughly researched over the years. Compared to probabilistic forecasting models, which are still at an early stage of research, researchers have been developing deterministic models in recent decades in order to optimize them and increase their accuracy.
- Another important advantage of deterministic forecasts is their simplicity compared to probabilistic forecasts. Not only are they faster to use and reproduce, but are also much easier to comprehend and evaluate. Simple error metrics are used to evaluate and compare deterministic forecasting methods, such as MAE, MAPE, MSE, and RMSE.
- The basic advantage of such models is the estimation of the uncertainty of the forecasted values. Unlike deterministic forecasts that give single valued outputs, probabilistic models offer an interval where various possible values for a specific time are given. As a result, they offer a wider view of the possible outcomes of the model researched.
- Probabilistic forecasts could also play an important role in energy markets in the future. Given the fact that the user not only knows a single value at a certain point in time but also knows possible higher or lower values as well, probabilistic forecasts could be used effectively in decision-making considering the uncertainty of future conditions.
7. Contributions of the Reviewed Works
8. Comparative Results of Reviewed Works
9. Discussion and Future Research
10. Conclusions
Funding
Conflicts of Interest
Abbreviations
| ACE | Average Coverage Error |
| AI | Artificial Intelligence |
| ANN | Artificial Neural Network |
| ARIMA | Auto Regressive Integrated Moving Average |
| ARMA | Auto Regressive Moving Average |
| CRPS | Continuous Ranked Probability Score |
| CWC | Coverage Width Criterion |
| ELM | Extreme Learning Machine |
| KDE | Kernel Density Estimation |
| LUBE | Lower Upper Bound Estimation |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| ME | Mean Error |
| MRE | Mean Relative Error |
| MSE | Mean Squared Error |
| NMAE | Nominal Mean Absolute Error |
| NN | Neural Network |
| NWP | Numerical Weather Prediction |
| Probability Density Function | |
| PI | Prediction Interval |
| PICP | PI Coverage Probability |
| PINAW | PI Normalized Average Width |
| PINC | PI Nominal Coverage |
| PINRW | PI Normalized Root-mean-square Width |
| QR | Quantile Regression |
| RMSE | Root Mean Squared Error |
| SVM | Support Vector Machine |
| WT | Wavelet Transform |
References
- Georgilakis, P.S. Technical challenges associated with the integration of wind power into power systems. Renew. Sustain. Energy Rev. 2008, 12, 852–863. [Google Scholar] [CrossRef] [Green Version]
- Tsikalakis, A.; Katsigiannis, Y.; Georgilakis, P.; Hatziargyriou, N. Impact of wind power forecasting error bias on the economic operation of autonomous power systems. Wind Energy 2009, 12, 315–331. [Google Scholar] [CrossRef] [Green Version]
- Giebel, G.; Brownsword, R.; Kariniotakis, G.; Denhart, M.; Draxl, C. The State-of-the-Art in Short-Term Prediction of Wind Power: A Literature Overview, 2nd ed. Available online: https://orbit.dtu.dk/en/publications/the-state-of-the-art-in-short-term-prediction-of-wind-power-a-lit (accessed on 10 October 2020).
- Pinson, P.; Chevallier, C.; Kariniotakis, G. Trading wind generation from short-term probabilistic forecasts of wind power. IEEE Trans. Power Syst. 2007, 22, 1148–1156. [Google Scholar] [CrossRef] [Green Version]
- Jabr, R. Adjustable robust OPF with renewable energy sources. IEEE Trans. Power Syst. 2013, 28, 4742–4751. [Google Scholar] [CrossRef]
- Wang, Q.; Guan, Y.; Wang, J. A chance-constrained two-stage stochastic program for unit commitment with uncertain wind power output. IEEE Trans. Power Syst. 2012, 27, 206–215. [Google Scholar] [CrossRef]
- Lei, M.; Shiyan, L.; Chuanwe, J.; Hongling, L.; Yan, Z. A review on the forecasting of wind speed and generated power. Renew. Sustain. Energy Rev. 2009, 13, 915–920. [Google Scholar] [CrossRef]
- Foley, A.M.; Leahy, P.G.; Marvuglia, A.; McKeogh, E.J. Current methods and advances in forecasting of wind power generation. Renew. Energy 2012, 37, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Soman, S.S.; Zareipour, H.; Malik, O.; Mandal, P. A review of wind power and wind speed forecasting methods with different time horizons. In Proceedings of the North American Power Symposium, Arlington, TX, USA, 26–28 September 2010. [Google Scholar]
- Wang, X.; Guo, P.; Huang, X. A Review of wind power forecasting models. Energy Procedia 2011, 12, 770–778. [Google Scholar] [CrossRef] [Green Version]
- Jung, J.; Broadwater, R.P. Current status and future advances for wind speed and power forecasting. Renew. Sustain. Energy Rev. 2014, 31, 762–777. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Wang, X. Review on probabilistic forecasting of wind power generation. Renew. Sustain. Energy Rev. 2014, 32, 255–270. [Google Scholar] [CrossRef]
- Wu, Y.K.; Po, E.S.; Jing, S.H. An overview of wind power probabilistic forecasts. In Proceedings of the IEEE PES Asia-Pacific Power and Energy Engineering Conference, Xi’an, China, 25–28 October 2016. [Google Scholar]
- Yan, J.; Liu, Y.; Han, S.; Wang, Y.; Feng, S. Review on uncertainty analysis of wind power forecasting. Renew. Sustain. Energy Rev. 2015, 52, 1322–1330. [Google Scholar] [CrossRef]
- Chen, N.; Qian, Z.; Nabney, I.T.; Meng, X. Wind power forecasts using Gaussian processes and numerical weather prediction. IEEE Trans. Power Syst. 2014, 29, 656–665. [Google Scholar] [CrossRef] [Green Version]
- De Giorgi, M.G.; Ficarella, A.; Tarantino, M. Assessment of the benefits of numerical weather predictions in wind power forecasting based on statistical methods. Energy 2011, 36, 3968–3978. [Google Scholar] [CrossRef]
- Box, G.; Jenkins, G.; Reinsel, G.; Ljung, G. Time Series Analysis: Forecasting and Control, 5th ed.; Wiley: New York, NY, USA, 2015; pp. 19–87. [Google Scholar]
- Rajagopalan, S.; Santoso, S. Wind power forecasting and error analysis using the autoregressive moving average modeling. In Proceedings of the IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009. [Google Scholar]
- Ling-ling, L.; Li, J.; He, P.; Wang, C. The use of wavelet theory and ARMA model in wind speed prediction. In Proceedings of the International Conference on Electric Power Equipment—Switching Technology, Xi’an, China, 23–27 October 2011. [Google Scholar]
- Gomes, P.; Castro, R. Wind speed and wind power forecasting using statistical models: AutoRegressive moving average (ARMA) and artificial neural networks (ANN). Int. J. Sustain. Energy Dev. 2012, 1, 41–50. [Google Scholar] [CrossRef]
- Cao, Y.; Liu, Y.; Zhang, D.; Wang, W.; Chen, Z. Wind power ultra-short-term forecasting method combined with pattern-matching and ARMA-model. In Proceedings of the IEEE PowerTech, Grenoble, France, 16–20 June 2013. [Google Scholar]
- Milligan, M.; Schwartz, M.; Wan, Y. Statistical wind power forecasting for U.S. wind farms. In Proceedings of the 17th Conf. Probability and Statistics in the Atmospheric Sciences American Meteorological Society Annual Meeting, Seattle, WA, USA, 11–15 January 2004. [Google Scholar]
- Abdelaziz, A.; Rahman, M.; El-Khayat, M.; Hakim, M. Short term wind power forecasting using autoregressive integrated moving average modeling. In Proceedings of the 15th International Middle East Power Systems Conference, Alexandria, Egypt, 23–25 December 2012. [Google Scholar]
- Wang, M.; Qiu, Q.; Cui, B. Short-term wind speed forecasting combined time series method and arch model. In Proceedings of the International Conference on Machine Learning and Cybernetics, Xi’an, China, 15–17 July 2012. [Google Scholar]
- Kavasseri, R.; Seetharaman, K. Day-ahead wind speed forecasting using f-ARIMA models. Renew. Energy 2009, 34, 1388–1393. [Google Scholar] [CrossRef]
- Deng, J. Introduction to grey system theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
- Huang, C.; Liu, Y.; Tzeng, W.; Wang, P. Short term wind speed predictions by using the Grey prediction model based forecast method. In Proceedings of the IEEE Green Technologies Conference, Baton Rouge, LA, USA, 14–15 April 2011. [Google Scholar]
- Tseng, F.; Yu, H.; Tzeng, G. Applied hybrid Grey model to forecast seasonal time series. Technol. Forecast. Soc. Chang. 2001, 67, 291–302. [Google Scholar] [CrossRef]
- Li, G.; Shi, L. On comparing three artificial neural networks for wind speed forecasting. Appl. Energy 2010, 87, 2313–2320. [Google Scholar] [CrossRef]
- Cadenas, E.; Rivera, W. Short term wind speed forecasting in La Venta, Oaxaca, Mexico, using artificial neural networks. Renew. Energy 2009, 34, 274–278. [Google Scholar] [CrossRef]
- Catalao, J.P.S.; Pousinho, H.M.I.; Mendez, V.M.F. An artificial neural network approach for short-term wind power forecasting in Portugal. In Proceedings of the 15th International Conference of Intelligent System Applications to Power Systems, Curitiba, Brazil, 8–12 November 2009. [Google Scholar]
- Xia, J.; Zhao, P.; Dai, Y. Neuro-fuzzy networks for short-term wind power forecasting. In Proceedings of the International Conference on Power System Technology, Hangzhou, China, 24–28 October 2010. [Google Scholar]
- Sun, Z.; Zhao, M. Short-term wind power forecasting based on VMD decomposition, ConvLSTM networks and error analysis. IEEE Access 2020, 8, 134422–134434. [Google Scholar] [CrossRef]
- Mohandes, M.; Halawani, T.; Rehman, S.; Hussain, A. Support vector machines for wind speed prediction. Renew. Energy 2004, 29, 939–947. [Google Scholar] [CrossRef]
- Zeng, J.; Qiao, W. Support vector machine-based short-term wind power forecasting. In Proceedings of the IEEE/PES Power Systems Conference and Exposition, Phoenix, AZ, USA, 20–23 March 2011. [Google Scholar]
- Thissen, U.; Brakel, R.; Weijer, A.; Melssen, W.; Buydens, L. Using support vector machines for time series prediction. Chemometr. Intell. Lab. Syst. 2003, 69, 35–49. [Google Scholar] [CrossRef]
- Liu, Y.; Shi, J.; Yang, Y.; Lee, W. Short-term wind-power prediction based on wavelet transform–support vector machine and statistic-characteristics analysis. IEEE Trans. Ind. Appl. 2012, 48, 1136–1141. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Niu, D.; Wang, H.; Fan, L. Short-term wind speed forecasting using wavelet transform and support vector machines optimized by genetic algorithm. Renew. Energy 2014, 62, 592–597. [Google Scholar] [CrossRef]
- Li, L.; Zhao, X.; Tseng, M.; Tan, R. Short-term wind power forecasting based on support vector machine with improved dragonfly algorithm. J. Clean. Prod. 2020, 242, 118447. [Google Scholar] [CrossRef]
- Catalão, J.P.S.; Pousinho, H.M.I.; Mendes, V.M.F. Short-term wind power forecasting in Portugal by neural networks and wavelet transform. Renew. Energy 2011, 36, 1245–1251. [Google Scholar] [CrossRef]
- Shi, J.; Guo, J.; Zheng, S. Evaluation of hybrid forecasting approaches for wind speed and power generation time series. Renew. Sustain. Energy Rev. 2012, 16, 3471–3480. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, F.; Zheng, X.; Li, Y. A hybrid EMD-SVM based short-term wind power forecasting model. In Proceedings of the IEEE PES Asia-Pacific Power and Energy Engineering Conference, Brisbane, QLD, Australia, 15–18 November 2015. [Google Scholar]
- Cadenas, E.; Rivera, W. Wind speed forecasting in three different regions of Mexico, using a hybrid ARIMA–ANN model. Renew. Energy 2010, 35, 2732–2738. [Google Scholar] [CrossRef]
- Abedinia, O.; Lotfi, M.; Bagheri, M.; Sobhani, B.; Shafie-khah, M.; Catalao, J.P.S. Improved EMD-based complex prediction model for wind power forecasting. IEEE Trans. Sustain. Energy 2020, 11, 2790–2802. [Google Scholar] [CrossRef]
- Liu, B.; Zhao, S.; Yu, X.; Zhang, L.; Wang, Q. A novel deep learning approach for wind power forecasting based on WD-LSTM model. Energies 2020, 13, 4964. [Google Scholar] [CrossRef]
- Viet, D.T.; Phuong, V.V.; Duong, M.Q.; Tran, Q.T. Models for short-term wind power forecasting based on improved artificial neural network using particle swarm optimization and genetic algorithms. Energies 2020, 13, 2873. [Google Scholar] [CrossRef]
- Kim, Y.; Hur, J. An ensemble forecasting model of wind power outputs based on improved statistical approaches. Energies 2020, 13, 1071. [Google Scholar] [CrossRef] [Green Version]
- Pinson, P.; Kariniotakis, G.; Nielsen, H.; Nielsen, T.; Madsen, H. Properties of quantile and interval forecasts of wind generation and their evaluation. In Proceedings of the European Wind Energy Conference & Exhibition, Athens, Greece, 27 February–2 March 2006. [Google Scholar]
- Pinson, P. Estimation of the uncertainty in wind power forecasting. Ph.D. Thesis, Ecole des Mines de Paris, Paris, France, 2006. [Google Scholar]
- Hodge, B.; Milligan, M. Wind power forecasting error distributions over multiple timescales. In Proceedings of the IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011. [Google Scholar]
- Pinson, P. Very short-term probabilistic forecasting of wind power with generalized logit-normal distributions. J. R. Stat. Soc. Ser. C 2012, 61, 555–576. [Google Scholar] [CrossRef]
- Tastu, J.; Pinson, P.; Trombe, P.; Madsen, H. Probabilistic forecasts of wind power generation accounting for geographically dispersed information. IEEE Trans. Smart Grid 2014, 5, 480–489. [Google Scholar] [CrossRef] [Green Version]
- Bofinger, S.; Luig, A.; Beyer, H. Qualification of wind power forecasts. In Proceedings of the Global Wind Power Conference, Paris, France, 2–5 April 2002. [Google Scholar]
- Zhang, Z.; Sun, Y.; Gao, D.; Lin, J.; Cheng, L. A Versatile probability distribution model for wind power forecast errors and its application in economic dispatch. IEEE Trans. Power Syst. 2013, 28, 3114–3125. [Google Scholar] [CrossRef]
- Bremnes, J. Probabilistic wind power forecasts using local quantile regression. Wind Energy 2004, 7, 47–54. [Google Scholar] [CrossRef]
- Wan, C.; Lin, J.; Wang, J.; Song, Y.; Dong, Z.Y. Direct quantile regression for nonparametric probabilistic forecasting of wind power generation. IEEE Trans. Power Syst. 2017, 32, 2767–2778. [Google Scholar] [CrossRef]
- Nielsen, H.; Madsen, H.; Nielsen, T. Using quantile regression to extend an existing wind power forecasting system with probabilistic forecasts. Wind Energy 2006, 9, 95–108. [Google Scholar] [CrossRef]
- Haque, A.; Nehrir, M.; Mandal, P. A Hybrid intelligent model for deterministic and quantile regression approach for probabilistic wind power forecasting. IEEE Trans. Power Syst. 2014, 29, 1663–1672. [Google Scholar] [CrossRef]
- Juban, J.; Fugon, L.; Kariniotakis, G. Uncertainty estimation of wind power forecasts: Comparison of probabilistic modelling approaches. In Proceedings of the European Wind Energy Conference, Brussels, Belgium, 31 March–3 April 2008. [Google Scholar]
- Hu, J.; Tang, J.; Lin, Y. A novel wind power probabilistic forecasting approach based on joint quantile regression and multi-objective optimization. Renew. Energy 2020, 149, 141–164. [Google Scholar] [CrossRef]
- Juban, J.; Siebert, N.; Kariniotakis, G. Probabilistic short-term wind power forecasting for the optimal management of wind generation. In Proceedings of the IEEE Power Tech, Lausanne, Switzerland, 1–5 July 2007. [Google Scholar]
- Zhang, Y.; Wang, J.; Luo, X. Probabilistic wind power forecasting based on logarithmic transformation and boundary kernel. Energy Convers. Manag. 2015, 96, 440–451. [Google Scholar] [CrossRef]
- Khorramdel, B.; Chung, C.; Safari, N.; Price, G.C.D. A fuzzy adaptive probabilistic wind power prediction framework using diffusion kernel density estimators. IEEE Trans. Power Syst. 2018, 33, 7109–7121. [Google Scholar] [CrossRef]
- Juban, J.; Fugon, L.; Kariniotakis, G. Probabilistic short-term wind power forecasting based on kernel density estimators. In Proceedings of the European Wind Energy Conference & Exhibition, Milan, Italy, 7–10 May 2007. [Google Scholar]
- Bessa, R.; Miranda, V.; Botterud, A.; Wang, J.; Constantinescu, E.M. Time adaptive conditional kernel density estimation for wind power forecasting. IEEE Trans. Sustain. Energy 2012, 3, 660–669. [Google Scholar] [CrossRef]
- Bessa, R.; Mendes, J.; Miranda, V.; Botterud, A.; Wang, J.; Zhou, Z. Quantile-copula density forecast for wind power uncertainty modeling. In Proceedings of the IEEE Powertech Conference, Trondheim, Norway, 19–23 June 2011. [Google Scholar]
- Jones, C.; Maron, J.; Sheather, S. A brief survey of bandwidth selection for density estimation. J. Am. Stat. Assoc. 1996, 91, 401–407. [Google Scholar] [CrossRef]
- Gneiting, T.; Raftery, A. Weather forecasting with ensemble methods. Science 2005, 310, 248–249. [Google Scholar] [CrossRef] [Green Version]
- Ren, Y.; Suganthan, P.; Srikanth, N. Ensemble methods for wind and solar power forecasting—A state-of-the-art review. Renew. Sustain. Energy Rev. 2015, 50, 82–91. [Google Scholar] [CrossRef]
- Pinson, P.; Madsen, H. Ensemble-based probabilistic forecasting at Horns Rev. Wind Energy 2009, 12, 137–155. [Google Scholar] [CrossRef] [Green Version]
- Sloughter, J.; Gneiting, T.; Raftery, A. Probabilistic wind speed forecasting using ensembles and Bayesian model averaging. J. Am. Stat. Assoc. 2010, 138, 1811–1821. [Google Scholar] [CrossRef] [Green Version]
- Pinson, P.; Kariniotakis, G. Conditional prediction intervals of wind power generation. IEEE Trans. Power Syst. 2010, 25, 1845–1856. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Li, G.; Wang, G.; Peng, J.; Jiang, H.; Liu, Y. Deep learning based ensemble approach for probabilistic wind power forecasting. Appl. Energy 2017, 188, 56–70. [Google Scholar] [CrossRef]
- Sun, M.; Feng, C.; Zhang, J. Multi-distribution ensemble probabilistic wind power forecasting. Renew. Energy 2020, 148, 135–149. [Google Scholar] [CrossRef]
- Wu, Y.K.; Wu, Y.C.; Hong, J.S.; Phan, L.H.; Quoc, D.P. Forecast of wind power generation with data processing and numerical weather prediction. IEEE Trans. Ind. Appl. 2021, 57, 36–45. [Google Scholar] [CrossRef]
- Khosravi, A.; Nahavandi, S.; Creighton, D.; Atiya, A. A lower upper bound estimation method for construction of neural network-based prediction intervals. IEEE Trans. Neural Netw. 2011, 22, 337–346. [Google Scholar] [CrossRef] [PubMed]
- Quan, H.; Srinivasan, D.; Khosravi, A. Short-Term Load and Wind Power Forecasting Using Neural Network-Based Prediction Intervals. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 303–315. [Google Scholar] [CrossRef] [PubMed]
- Kavousi-Fard, A.; Khosravi, A.; Nahavandi, S. A new fuzzy-based combined prediction interval for wind power forecasting. IEEE Trans. Power Syst. 2016, 31, 18–26. [Google Scholar] [CrossRef]
- Wu, Y.; Su, P.; Wu, T.; Hong, J.; Hassan, M. Probabilistic wind power forecasting using weather ensemble models. IEEE Trans. Ind. Appl. 2018, 54, 5609–5620. [Google Scholar] [CrossRef]
- Khosravi, A.; Nahavandi, S. Combined nonparametric prediction intervals for wind power generation. IEEE Trans. Sustain. Energy 2013, 4, 849–856. [Google Scholar] [CrossRef]
- Wan, C.; Xu, Z.; Pinson, P.; Dong, Z.Y.; Wong, K.P. Optimal prediction intervals of wind power generation. IEEE Trans. Power Syst. 2014, 29, 1166–1174. [Google Scholar] [CrossRef] [Green Version]
- Efron, B. Bootstrap Methods: Another Look at the Jackknife. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- Wan, C.; Xu, Z.; Pinson, P.; Dong, Z.Y.; Wong, K.P. Probabilistic forecasting of wind power generationusing extreme learning machine. IEEE Trans. Power Syst. 2014, 29, 1033–1044. [Google Scholar] [CrossRef] [Green Version]
- Khosravi, A.; Nahavandi, S.; Creighton, D. Prediction intervals for short-term wind farm power generation forecasts. IEEE Trans. Sustain. Energy 2013, 4, 602–610. [Google Scholar] [CrossRef]
- Hui, L.; Chengqing, Y.; Haiping, W.; Zhu, D.; Guangxi, Y. A new hybrid ensemble deep reinforcement learning model for wind speed short term forecasting. Energy 2020, 202, 117794. [Google Scholar]
- Miao, H.; Lei, Y.; Junshan, Z.; Vijay, V. A spatio-temporal analysis approach for short-term forecast of wind farm generation. IEEE Trans. Power Syst. 2014, 29, 1611–1622. [Google Scholar]
- Xiyun, Y.; Yanfeng, Z.; Yuwei, W.; Wei, L. Deterministic and probabilistic wind power forecasting based on bi-level convolutional neural network and particle swarm optimization. Appl. Sci. 2019, 9, 1794. [Google Scholar]
- Tascikaraoglu, A.; Sanandaji, B.; Poolla, K.; Varaiya, P. Exploiting sparsity of interconnections in spatio-temporal wind speed forecasting using wavelet transform. Appl. Energy 2016, 165, 735–747. [Google Scholar] [CrossRef] [Green Version]
- Afrasiabi, M.; Mohammadi, M.; Rastegar, M.; Afrasiabi, S. Advanced deep learning approach for probabilistic wind speed forecasting. IEEE Trans. Ind. Inform. 2021, 17, 720–727. [Google Scholar] [CrossRef]
- Wang, H.; Xue, W.; Liu, Y.; Peng, J.; Jiang, H. Probabilistic wind power forecasting based on spiking neural network. Energy 2020, 196, 117072. [Google Scholar] [CrossRef]
- Lin, Y.; Yang, M.; Wan, C.; Wang, J.; Song, Y. A multi-model combination approach for probabilistic wind power forecasting. IEEE Trans. Sustain. Energy 2019, 10, 226–237. [Google Scholar] [CrossRef]
- Dehnavi, S.D.; Shirani, A.; Mehrjerdi, H.; Baziar, M. New deep learning-based approach for the wind turbine output power modeling and forecasting. IEEE Trans. Ind. Appl. 2020. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Y.; Yan, J.; Han, S.; Li, L.; Long, Q. Improved deep mixture density network for regional wind power probabilistic forecasting. IEEE Trans. Power Syst. 2020, 35, 2549–2560. [Google Scholar] [CrossRef]
- Wang, J.; Niu, T.; Lu, H.; Yang, W.; Du, P. A novel framework of reservoir computing for deterministic and probabilistic wind power forecasting. IEEE Trans. Sustain. Energy 2020, 11, 337–349. [Google Scholar] [CrossRef]
- Tatsu, J.; Pinson, P.; Kotwa, E.; Madsen, H. Spatio-temporal analysis and modeling of short-term wind power forecast errors. Wind Energy 2011, 14, 43–60. [Google Scholar]
- Zhang, Y.; Wang, J. A distributed approach for wind power probabilistic forecasting considering spatio-temporal correlation without direct access to off-site information. IEEE Trans. Power Syst. 2018, 33, 5714–5726. [Google Scholar] [CrossRef]
- Taylor, J. Probabilistic forecasting of wind power ramp events using autoregressive logit models. Eur. J. Oper. Res. 2017, 259, 703–712. [Google Scholar] [CrossRef]
- Cui, M.; Zhang, J.; Wang, Q.; Krishnan, V.; Hodge, B.M. A data-driven methodology for probabilistic wind power ramp forecasting. IEEE Trans. Smart Grid 2017, 10, 1326–1338. [Google Scholar] [CrossRef]
| Approach | Reference |
|---|---|
| ARMA | [17,18,19,20,21,22,23] |
| ARIMA | [24,25] |
| Grey Method | [26,27,28] |
| ANN | [29,30,31,32,33] |
| SVM | [34,35,36,37,38,39] |
| Hybrid | [40,41,42,43,44,45,46,47] |
| Approach | Method | Reference |
|---|---|---|
| Parametric | Parametric | [49,50,51,52,53,54] |
| Non-Parametric | QR | [55,56,57,58,59,60] |
| KDE | [61,62,63,64,65,66,67] | |
| Ensemble | [68,69,70,71,72,73,74,75] | |
| LUBE | [76,77,78,79,80,81] | |
| Bootstrap | [82,83,84] |
| Reference | Published | Contribution |
|---|---|---|
| [34] | May 2004 | SVM was introduced for wind speed forecasting in order to examine its predictive abilities, compared to other NN models. |
| [30] | January 2009 | A comparison between four different ANN models for short-term wind speed forecasting was the main focus. Furthermore, selecting the appropriate parameters for the most suitable ANN model was also investigated. |
| [25] | May 2009 | The suitability of f-ARIMA models towards obtaining more accurate next hour wind speed forecasts is explored, due to their ability to include long range correlations. |
| [31] | November 2009 | An ANN model is proposed for short-term wind power forecasting in order to achieve high accuracy with low computational cost. |
| [29] | July 2010 | Three different types of NNs (FFBP, RBF and ADALINE) were used to investigate the behavior of different NNs while using multiple datasets and evaluation criteria. |
| [32] | October 2010 | A Neuro-fuzzy NN was proposed in order to create a powerful forecasting algorithm that could be integrated in an on-line wind power forecasting system. |
| [43] | December 2010 | Hybrid models based on ARIMA and ANN models were developed to forecast wind speed and wind power with increased accuracy. |
| [35] | March 2011 | An SVM-based model was proposed for short-term wind power forecasting. |
| [40] | April 2011 | A novel, hybrid model based on NN in combination with WT for short-term wind power forecasting was proposed, and its superiority in accuracy and computational cost over conventional forecasting models is shown. |
| [19] | October 2011 | The ARMA model along with the wavelet transform was used to enhance the accuracy of wind speed forecasts in order to reduce the negative effect of wind power to the power grid and supply system. |
| [37] | May 2012 | SVM models along with the wavelet transform were proposed in order to optimize the SVM model and improve its accuracy and computational cost. |
| [41] | June 2012 | The applicability of hybrid forecasting methodology for wind time series was investigated, in order to examine the hybrid models’ superiority over conventional forecasting models for wind speed and wind power forecasting. |
| [24] | July 2012 | An ARIMA-ARCH model was proposed in order to improve the accuracy of the ARMA methodology, taking into account the heteroscedasticity between the fluctuation of wind speed and the characteristics of the change of wind speed. |
| [19] | December 2012 | A comparison between two conventional statistical models, the ARMA model and the ANN, was researched, in order to evaluate their performance and applicability in wind forecasting. |
| [21] | June 2013 | To improve the ARMA model’s accuracy over the time, a combined ARMA-ARCH methodology was used for ultra-short-term forecasting. |
| [22] | November 2013 | The work investigated the efficiency of statistical time-series models in improving the accuracy of short-term forecasts. |
| [38] | February 2014 | A WT-SVM model was proposed and optimized by GA in order to further improve the efficiency and accuracy of the SVM model. |
| [42] | November 2015 | A hybrid EMD-SVM forecasting model was proposed, which improved the accuracy of the forecasts as well as reduced the non-stationary characteristics of the wind data on the predictive results. |
| [39] | January 2020 | A hybrid IDA-SVM model was proposed for short-term wind power forecasting. The systematic analysis with datasets in different seasons showed the increased accuracy of the proposed model. |
| [44] | February 2020 | A BaNN-based hybrid model was proposed for the forecasting process. A filtering and grouping model was also developed based on improved k-means for wind signal prediction. |
| [47] | March 2020 | Different statistical models were proposed and combined for short-term wind power forecasting, including ARIMAX, SVR and MCS power curve models. Via a spatial process, wind speed data from local NWP are adjusted for a specific wind farm and are further used as input for the forecasting process. |
| [46] | June 2020 | A double optimization approach was proposed based on NNs, PSO and GA. Based on these approaches, a WPF model was proposed, using data from a real power plant. |
| [33] | July 2020 | The proposed model used VMD to preprocess and decompose the wind power series. The ConvLSTM was used as the predictor engine in order to remove the noise and extract the spatio-temporal information of the sub-series. |
| [45] | September 2020 | A wind power forecasting model based on WD-LSTM and normalization was proposed to improve the prediction’s accuracy. Furthermore, the normalization and optimization of the input data further improved the predictive accuracy and the model’s convergence speed. |
| Reference | Published | Contribution |
|---|---|---|
| [53] | January 2002 | A phenomenological model was tested for the expected distribution of the forecast errors, in order to fully use the output of wind power forecasts. The application of an ANN was used to achieve bias free forecasts with reduced standard deviation. |
| [55] | March 2004 | A LQR model was used to specify the quantiles of the probability distribution of energy production in order to optimize the income function of the producer in energy markets. |
| [57] | December 2005 | Linear quantile regression together with spline bases were proposed to provide quantiles of the forecast error, using only predictable explanatory variables and indices. |
| [59] | March 2008 | A classification of different modeling approaches for probabilistic forecasting was proposed, in order to estimate the most efficient practices for using the available information for accurate on-line uncertainty estimation. |
| [70] | March 2009 | Focus was given to the methodology needed to converse meteorological variables to power generation data. Furthermore, the recalibration of the wind power ensembles to obtain accurate predictive densities was also studied. |
| [71] | March 2010 | Bayesian model averaging, a statistical ensemble postprocessing method that creates calibrated predictive probability density functions, was used to provide calibrated and sharp probabilistic forecasts. |
| [72] | April 2010 | Adaptive resampling approach was proposed in order to provide conditional interval forecasts, in order to successfully complement point forecasts with PIs and to avoid using a pre-assumed shape of the forecast error distribution. |
| [65] | June 2012 | A novel, robust, and time adaptive kernel density forecast algorithm was introduced in wind power forecasting. Apart from being a fully time adaptive model, it also adopted distinct kernels for different types of variables. |
| [51] | August 2012 | A generalized logit-normal distribution was introduced to deal with the non-linearity of wind power generation in wind power forecasting, as an efficient alternative of the conventional normal and beta distributions. |
| [84] | January 2013 | The application of two approaches for construction of PIs for wind farm power generation was proposed, in order to prove their efficiency in giving valid PIs, evading expensive forecasting tools. |
| [54] | March 2013 | The versatile probability distribution model was firstly formulated and its mathematical properties were presented. The model’s accuracy in solving a typical economic dispatch problem was analyzed. |
| [80] | September 2013 | An enhanced version of the nonparametric LUBE method was proposed, using multiple NN models to create PIs and then combining those PIs to obtain more reliable and informative PIs. |
| [81] | November 2013 | A hybrid intelligent algorithm based on interval forecasting approach was developed to produce prediction intervals based on the extreme learning machine and particle swarm optimization, in order to obtain optimal PIs without prior knowledge, statistical inference, or distribution assumption. |
| [83] | November 2013 | A new bootstrap-based ELM probabilistic wind power forecasting approach was proposed, considering the heteroscedasticity of wind power time series. The accuracy and speed of the model was also researched using only historical data. |
| [52] | December 2013 | A methodology was introduced and evaluated that allowed issuing probabilistic wind power forecasts optimally accounting for geographically dispersed information. The main focus was on time-adaptivity in order to reduce the computational cost. |
| [86] | January 2014 | A spatio-temporal analysis framework was proposed that analyzed the dynamics of wind generation by quantifying the statistical distribution and the level crossing rate. Wind power was modeled as a Markov chain and as a result the problem could be studied by Markovian state-space approaches. |
| [77] | February 2014 | A new problem formulation was proposed to create PIs. Furthermore, a new PI width evaluation index, suitable for training NN models, was used. A PSO-based LUBE method was implemented to increase the searching capability of the proposed methodology. |
| [58] | July 2014 | An accurate, efficient, and robust deterministic wind power forecasting model was developed, using a combination of a data filtering approach based on WT and a soft computing model based on FA network. Moreover, SQR was used to evaluate the effectiveness of the proposed deterministic model in a probabilistic sense. |
| [78] | January 2016 | A new fuzzy-based cost function was introduced to satisfy both PICP and PINAW criteria. BA was used for the first time to provide a solution for finding optimal lower and upper bounds of PIs. |
| [88] | March 2016 | An algorithm to determine the contribution of each meteorological station on the next forecasts was proposed. It was proved that combining WT with the proposed spatio-temporal method improved the forecasting model’s accuracy. |
| [73] | February 2017 | CNN was introduced to comprehensively extract the deep invariant structures and hidden high-level nonlinear features of any wind power frequency. A hybrid approach based on WT, CNN, and ensemble technique is proposed for the quantification of the wind power uncertainties. |
| [56] | July 2017 | A novel direct quantile regression approach was proposed for probabilistic forecasting using ELM and QR without prior knowledge, statistical inference, or distribution assumption. |
| [90] | February 2018 | A WPPF model was proposed based on SNN and LUBE, which did not require any prior knowledge or distribution assumption. Furthermore, a new PI optimization model was proposed based on the CPRS. The GSO was also implemented to solve the PI optimization model. |
| [91] | May 2018 | A novel MMC approach was proposed along with a two-step optimization framework. The comprehensive probabilistic combination model was applied for WPF. Evaluation in calibration and sharpness was presented in ten different farms. |
| [79] | December 2018 | The work combined local NWP with wind power generation data to achieve accurate wind power forecasts. Dimension reduction method was used to reduce the computational complexity. A complete hybrid CSS-LUBE model for probabilistic forecasting was developed that could simultaneously process both the historical and NWP data with low computational cost. |
| [87] | April 2019 | A forecasting model based on CNN and PSO was proposed. The wind data was preprocessed with VMD and PSR to give better suited data for CNN. |
| [60] | December 2019 | A joint QR model was proposed for the WPPF, which reduced the effect of the outlying observations and the occurrence of quantile curve crossings. Several conditional quantiles could be directly estimated. The MSSA algorithm was used for the optimization. |
| [94] | January 2020 | An advanced reservoir computing model, TWIESN, was introduced for deterministic and probabilistic WPF. Moreover, a hybrid selection strategy based on RReliefF algorithm and GCRT was selected for the system input. |
| [85] | May 2020 | The EWT method was used to preprocess wind speed time series. Deep NNs were used for the prediction process. The reinforcement learning algorithm was used to integrate three kinds of deep NNs. |
| [89] | July 2020 | A deep mixture density network (MDN) model was designed to provide statistical information in form of PDFs for look-ahead times. A deep network consisting of CNN and GRU was proposed. The reformulation of the MDN could directly construct predictive PDFs, thus gaining in computational cost. |
| [93] | July 2020 | An IDMDN model was proposed for wind power probabilistic forecasting in order to further improve the prediction results of conventional MDN and deep WPF models. |
| [75] | In press | A state-of-the-art methodology on hour-ahead WPPF was developed, that considered the effective preprocessing and postprocessing of the PI. NWP data were combined with measured wind speed data to improve the accuracy of the forecasts. The postprocessing of the PI was implemented to stabilize the forecasting model. |
| [92] | In press | A novel support vector machine model was introduced to improve the learning process of the wind farm active power. Furthermore, a novel FP algorithm was proposed in order to adjust the parameters of the support vectors. |
| Reference | Proposed Model | Compared Models | Parameters of Evaluation | Best Model |
|---|---|---|---|---|
| [20] | ARMA | ANN, Persistence | MAE, RMSE, MRE | ARMA had better performance than both ANN and Persistence |
| [21] | ARMA-Pattern Matching | ARMA | Real data, Relative tolerance | For 0–1 h forecasting horizon single ARMA had higher accuracy. For 1-6hour ARMA-Pattern Matching was better |
| [22] | Various ARMA models | Persistence | RMSE | All ARMA models surpassed the persistence model |
| [24] | ARIMA-ARCH | Single-ARIMA | MRE | ARIMA-ARCH was better with MRE = 11.2% over 17.4% of the single-ARIMA |
| [25] | f-ARIMA | Persistence, Single-ARIMA | DME, σ2, | f-ARIMA was overall better than single-ARIMA. Persistence was better for low wind speed excursions, while for higher ones f-ARIMA and ARIMA gave better results |
| [29] | FFBP, RBF, ADALINE | FFBP, RBF, ADALINE | MAE, MAPE, RMSE | For case 1, based on MAE and RMSE, FFBP was better; based on MAPE, ADALINE had better performance. In case 2, RBF surpassed the other two models. |
| [30] | Various ANN models | ANN1 (3 layers, 3 input, 3 hidden layers, 1output) ANN2(3 layers, 3 input, 2 hidden layers, 1output) ANN3(2 layers, 3 input, 1output) ANN4(2 layers, 2 input, 1output) | MAE, MSE | ANN 4(2 layers, 2 input, 1 output) was the bestmodel with a MAE of 0.0399 and MSE of 0.0016 |
| [31] | ANN | Persistence | MAPE | ANN model was better with a MAPE of 7.26% over 19.05% of the persistence model |
| [37] | WT-SVM | RBF-SVM | MRE, RMSE | WT-SVM outperformed RBF-SVM |
| [38] | WT-SVM-GA | Persistence, SVM-GA | MAE, MAPE | WT-SVM-GA outperformed the SVM-GA and persistence model |
| [35] | SVM | RBF-NN, Persistence | MAE, MAPE, Skill | For both very short-term and short-term forecasting SVM model had the best results |
| [39] | IDA-SVM | DA-SVM, GA-SVM, Grid-SVM, BPNN, GPR | NRMSE, NMAE, MAPE, R2 | The proposed model outperformed all the other models |
| [40] | WT-NN | Persistence, ARIMA, ANN | MAPE | WT-NN outperformed the rest of the models with a MAPE of 6.97% |
| [41] | ARIMA-ANN, ARIMA-SVM | ARIMA, ANN, SVM | MAE, RMSE | Based on MAE, for 1-step forecasting horizon, the ARIMA-ANN had the best results, while for 3-step to 9-step, the ANN and SVM models were better. Based on the RMSE, for 1-step and 7-step forecasting horizon, the best model was ARIMA-ANN, while for the rest, ANN and SVM had the best results |
| [42] | EMD-SVM | SVM | RMS | EMD-SVM had the best results with an RMS value of 15.63% while the SVM had 35.40% |
| [43] | ARIMA-ANN | ARIMA, ANN | ME, MAE, MSE | The ARIMA-ANN surpassed all the other models |
| [45] | WD-LSTM | BMA-EL, MRMLE-AMS, SVR-IDA | MAPE | The proposed model had a significantly improved MAPE value |
| [46] | PSO-PSO-ANN, GA-PSO-ANN | PSO-ANN, Adam-ANN | MSE, MAPE | Both models managed to outperform the PSO-ANN and the Adam-ANN models |
| Reference | Proposed Model | Compared Models | Parameters of Evaluation | Best Model |
|---|---|---|---|---|
| [55] | LQR Hirlam10, LQR climate | LQR Hirlam10, LQR climate | Sharpness | LQR Hirlam10 had better results from the LQR climate as it gave narrower PIs. |
| [56] | DQR | Persistence, BELM-normal, BELM-Beta, RBFNN | Reliability, Sharpness | Based on reliability, DQR had an APD of less than 2%. As for sharpness, DQR was 25% better than persistence model and 20% better than the RBFNN |
| [58] | Spline-QR-WT-FA-FF-SVM | Spline-QR-BPNN | Reliability, Sharpness, Skill score | Based on reliability, Spline-QR-WT-FA-FF-SVM had lower deviation overall. According to sharpness, the Spline-QR-BPNN gave better results; however based on the final skill score, the proposed model was overall better, especially for a confidence level of 5–35% |
| [59] | SQR, QRF, linear-QR, KDE | SQR, QRF, linear-QR, KDE | Reliability, Sharpness | According to reliability, the QRF and KDE models had close performance, better than the rest of the models. Based on sharpness evaluation, for less than 50% confidence level, all models were equal, but for more than 50%, SQR model had the best results, while linear-QR had the worst |
| [70] | Ensemble forecasts with AKD | Raw ensemble forecasts, ideal values | Reliability, Sharpness | The proposed model showed overall lower deviation and gave narrower PIs |
| [71] | Ensemble forecasts with BMA | Raw ensemble forecasts, Climatology model | CPRS, MAE | The proposed model outperformed the other two based on CPRS and MAE of the point forecasts of the median values of the PIs |
| [72] | 3 pointprediction methods (M1, M2, M3) with adaptive resampling | M1, M2, M3 | Reliability, Sharpness | All three models had a deviation of less than 1.5%. Based on sharpness results, for less than 5 h forecasting horizon, M1 model gave the most accurate results, while for more than 5 h, the M2 model was the most accurate |
| [73] | WT-CNN-Ensemble | Persistence, BR-QR, SVM-QR | ACE, IS, CPRS | The ACE value of the proposed model was improved by 50.84% than the SVM. The IS value was improved by 40.51% than the SVM. As for the CPRS, the proposed method showed the best results in all seasons. |
| [77] | LUBE-PSO | ARIMA, ES, naïve | PICP, PINAW, CWC | Based on CWC, the proposed model had a value of 72.57% while all other models had more than 75%. Furthermore, the LUBE-PSO model had a PINAW value of 72.57% while again the rest of the models were above 75%. As for the PICP, only the ES model, with 92.7% slightly surpassed the proposed model with 91.80% |
| [78] | LUBE-NN-MBA | PSO, BA | PICP, PINAW | In the first study, the proposed method outperformed the other two models. According to the PICP evaluation, the LUBE-NN-MBA had a value of 93.5%, while the BA model had a 90% and the PSO 83.8%. Based on the PINAW evaluation, the LUBE-NN-MBA had a value of 32.96%, while the BA model had a 33.7% and the PSO 38.22% |
| [79] | LUBE-CSS | Persistence | PICP, PINAW, CWC | For a confidence level of 50–90%, the proposed model was better than the persistence model |
| [83] | BELM | Persistence, Climatology, ESM, BELM-Beta | PICP, ACE | According to ACE evaluation, for 95–99% confidence level the value of the proposed model was less than 1%, surpassing the other models. Based on PICP evaluation, for 90−99% confidence level, the BELM model was better than the compared models |
| [84] | MBB-NN | LUBE-NN | PICP, PINAW, CWC | Based on the evaluation metrics, for forecasting horizon of less than 10 min, the MBB model gave better results, while for more than 15 min the LUBE model was more accurate |
| Method | Feature |
|---|---|
| Physical | Based on atmospheric conditions; directly connected to the stability of weather conditions |
| ARMA-ARIMA | Can predict future values of a time series through linear regression of the observed values of those time series |
| Grey Method | Powerful tool for forecasting with insufficient data |
| ANN | Evaluation and re-evaluation of input data and their weighed connections |
| SVM | Maps a set of data into high dimensional feature space through a nonlinear mapping process in order to simplify the linear regression process |
| Hybrid | Uses the advantages of combined methods to increase the accuracy of the forecasts |
| Method | Feature |
|---|---|
| Parametric | Assumes a specific distribution shape of the forecasts |
| KDE | Does not assume a specific distribution shape of the forecasts; requires large number of data |
| QR | Gives the uncertainty estimation in the form of predictive quantiles |
| LUBE | Simplifies the PI prediction in one step; low computational cost |
| Bootstrap | Resampling of original data; simplified PI construction |
| Ensemble | Diversity; uses NWP models; gives better results in short and mid-term forecasting |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bazionis, I.K.; Georgilakis, P.S. Review of Deterministic and Probabilistic Wind Power Forecasting: Models, Methods, and Future Research. Electricity 2021, 2, 13-47. https://doi.org/10.3390/electricity2010002
Bazionis IK, Georgilakis PS. Review of Deterministic and Probabilistic Wind Power Forecasting: Models, Methods, and Future Research. Electricity. 2021; 2(1):13-47. https://doi.org/10.3390/electricity2010002
Chicago/Turabian StyleBazionis, Ioannis K., and Pavlos S. Georgilakis. 2021. "Review of Deterministic and Probabilistic Wind Power Forecasting: Models, Methods, and Future Research" Electricity 2, no. 1: 13-47. https://doi.org/10.3390/electricity2010002
APA StyleBazionis, I. K., & Georgilakis, P. S. (2021). Review of Deterministic and Probabilistic Wind Power Forecasting: Models, Methods, and Future Research. Electricity, 2(1), 13-47. https://doi.org/10.3390/electricity2010002






