Experimental Characterization of an AC–DC Boost for Energy Harvesting Device Based on Magnetostrictive Materials †
Abstract
:1. Introduction
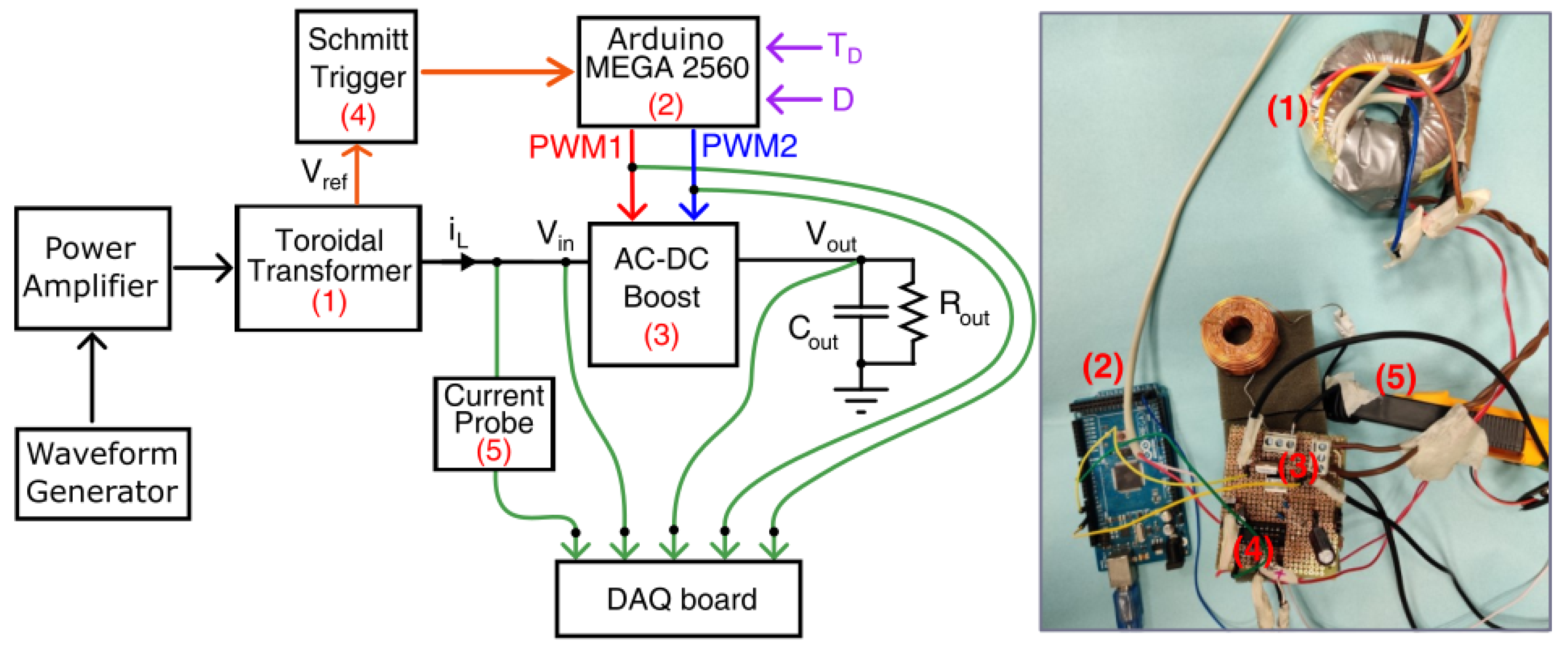
2. Experimental Setup
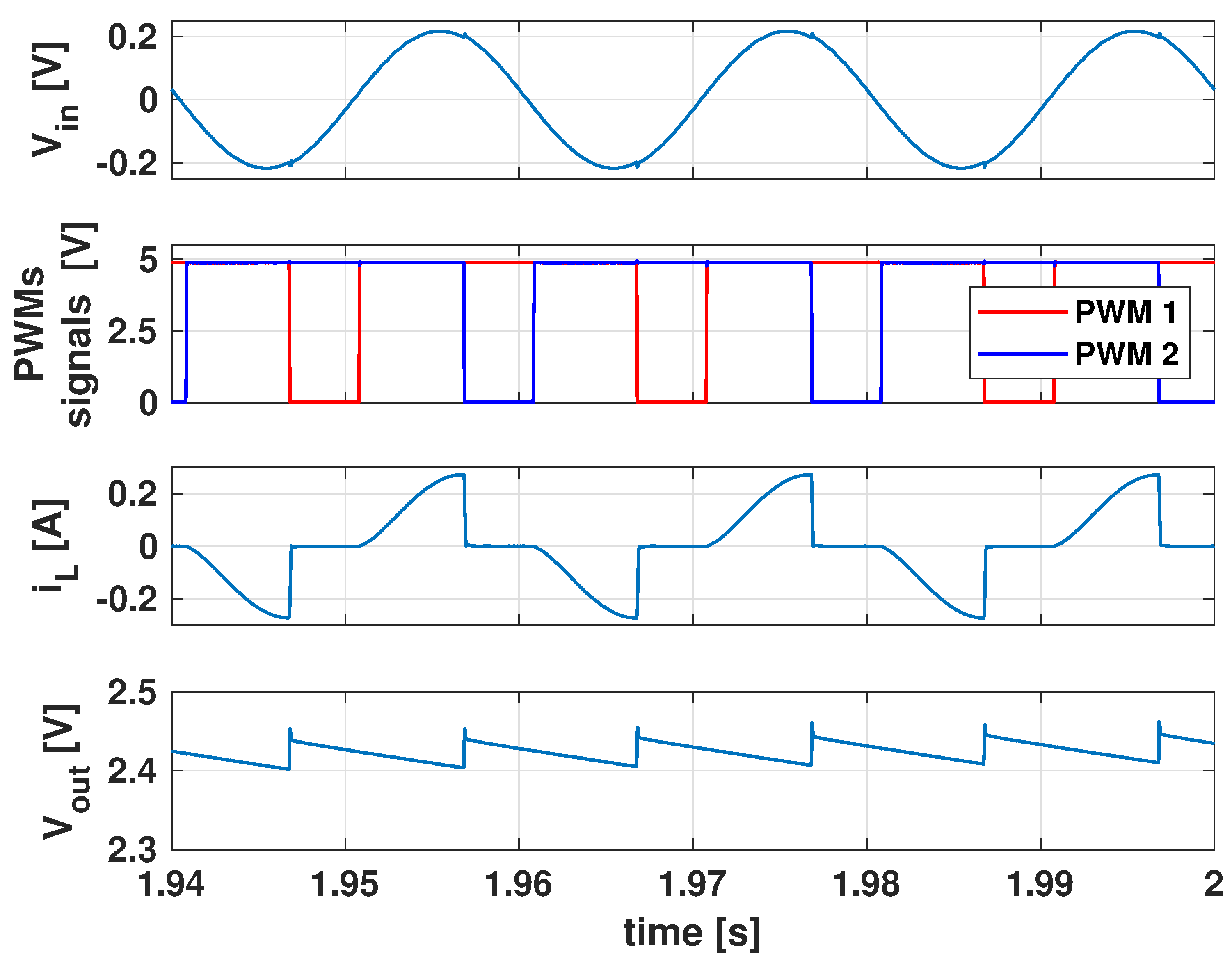
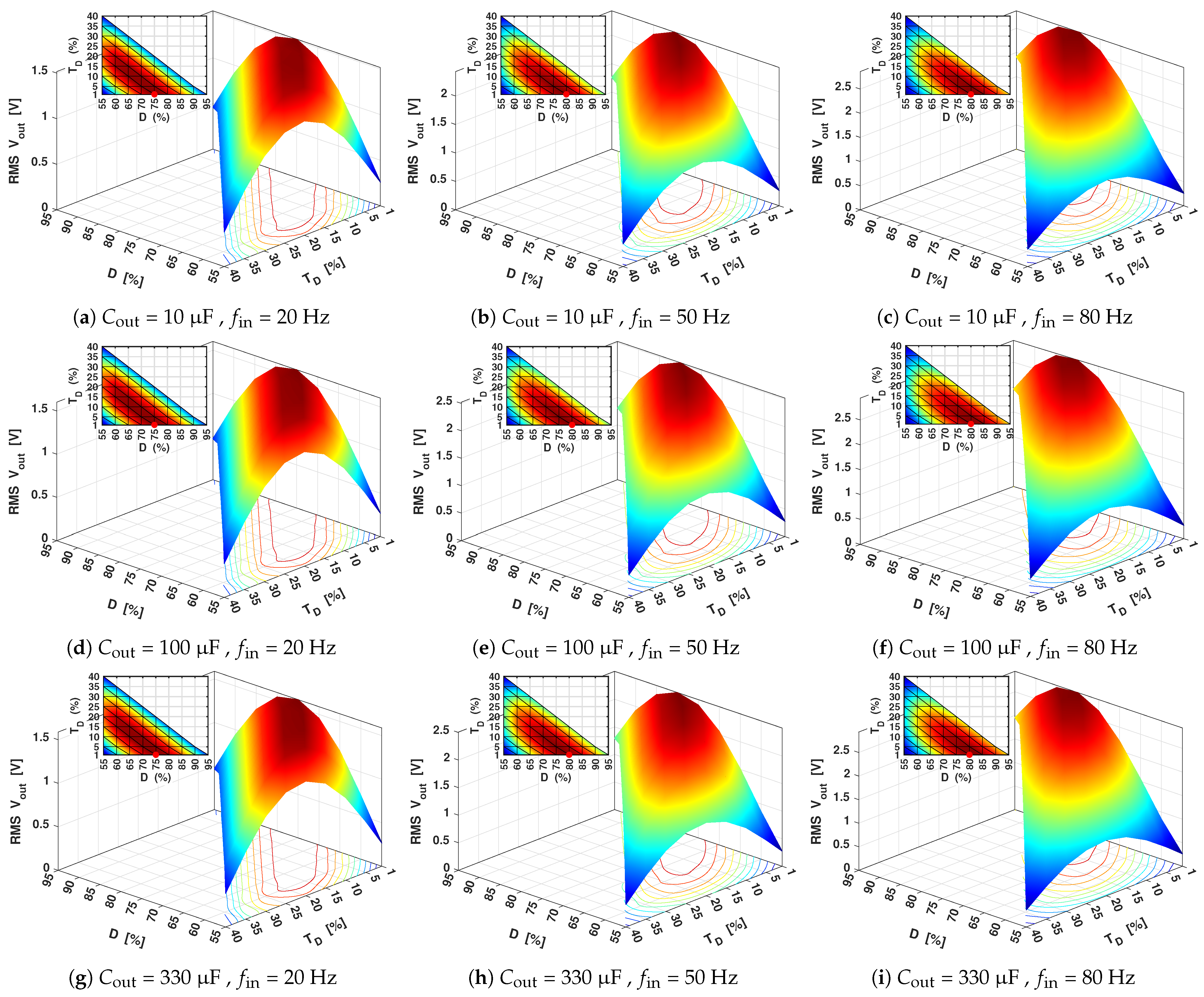
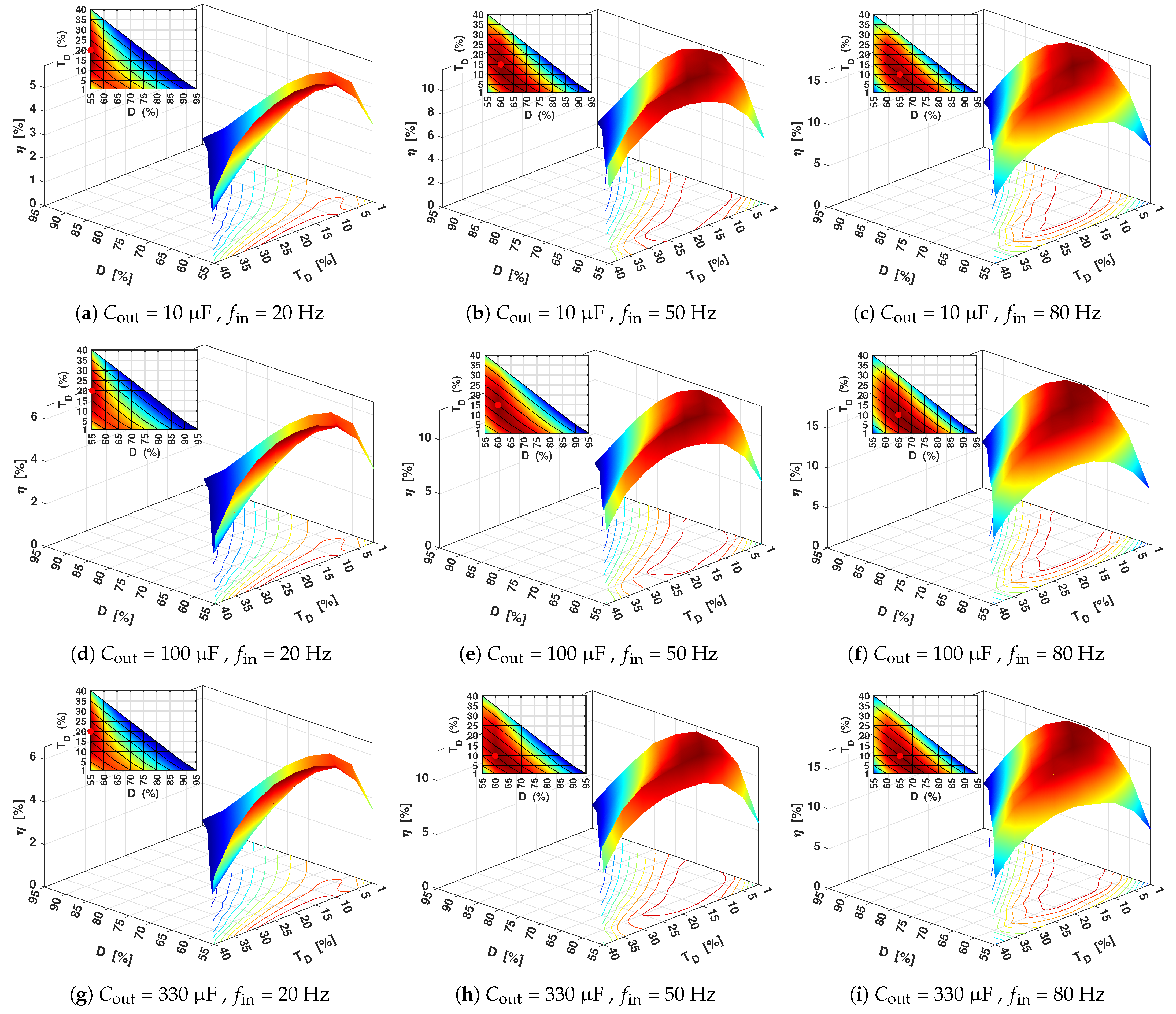
3. Measurements and Discussion
- , i.e., the inductor should be short-circuited on the AC input, and then charge in a certain time interval;
- , i.e., the delay and “ON” timing of the two PWM signals should belong to a time period T of the AC input ( of the time period T).
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EH | Energy Harvesting |
| IoT | Internet of Things |
| KEH | Kinetic Energy Harvester |
| WSN | Wireless Sensor Network |
| SHM | Structural Health Monitoring |
| PEI | Power Electronic Interface |
| FEM | Finite Element Method |
| D | Duty Cycle |
| Time Delay | |
| PWM | Pulse Width Modulation |
| DAQ | Data Acquisition |
| RMS | Root-Mean-Square |
| FoM | Figure of Merit |
| Ripple Factor | |
| Form Factor |
References
- Paradiso, J.; Starner, T. Energy scavenging for mobile and wireless electronics. IEEE Pervasive Comput. 2005, 4, 18–27. [Google Scholar] [CrossRef]
- Magno, M.; Spadaro, L.; Singh, J.; Benini, L. Kinetic energy harvesting: Toward autonomous wearable sensing for Internet of Things. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Capri, Italy, 22–24 June 2016; pp. 248–254. [Google Scholar] [CrossRef]
- Park, G.; Farinholt, K.M.; Farrar, C.R.; Rosing, T.; Todd, M.D. Powering Wireless SHM Sensor Nodes through Energy Harvesting; Springer: Boston, MA, USA, 2009; pp. 493–506. [Google Scholar] [CrossRef]
- Clemente, C.S.; Davino, D.; Loschiavo, V.P. Magnetostrictive materials and energy harvesting for structural health monitoring applications. IOP Conf. Ser. Mater. Sci. Eng. 2020, 949, 12012. [Google Scholar] [CrossRef]
- Zhu, D.; Beeby, S. Kinetic Energy Harvesting; Springer: New York, NY, USA, 2011; pp. 1–77. [Google Scholar] [CrossRef]
- Muscat, A.; Bhattacharya, S.; Zhu, Y. Electromagnetic Vibrational Energy Harvesters: A Review. Sensors 2022, 22, 5555. [Google Scholar]
- Sezer, N.; Koç, M. A comprehensive review on the state-of-the-art of piezoelectric energy harvesting. Nano Energy 2021, 80, 105567. [Google Scholar] [CrossRef]
- Deng, Z.; Dapino, M.J. Review of magnetostrictive vibration energy harvesters. Smart Mater. Struct. 2017, 26, 8347. [Google Scholar] [CrossRef]
- Engdahl, G. Handbook of Giant Magnetostrictive Materials; Academic Press: San Diego, CA, USA, 2000; pp. 1–386. [Google Scholar] [CrossRef]
- Narita, F.; Fox, M. A Review on Piezoelectric, Magnetostrictive, and Magnetoelectric Materials and Device Technologies for Energy Harvesting Applications. Adv. Eng. Mater. 2018, 20, 743. [Google Scholar] [CrossRef]
- Zucca, M.; Hadadian, A.; Bottauscio, O. Quantities affecting the behavior of vibrational magnetostrictive transducers. IEEE Trans. Magn. 2015, 51, 2359248. [Google Scholar] [CrossRef]
- Palumbo, S.; Rasilo, P.; Zucca, M. Experimental investigation on a Fe-Ga close yoke vibrational harvester by matching magnetic and mechanical biases. J. Magn. Magn. Mater. 2019, 469, 354–363. [Google Scholar] [CrossRef]
- Vocca, H.; Cottone, F. Kinetic Energy Harvesting. In ICT-Energy-Concepts Towards Zero; Fagas, G., Gammaitoni, L., Paul, D., Berini, G.A., Eds.; IntechOpen: Rijeka, Croatia, 2014; Chapter 3. [Google Scholar] [CrossRef]
- Clemente, C.S.; Davino, D.; Loschiavo, V.P. Analysis of a Magnetostrictive Harvester with a Fully Coupled Nonlinear FEM Modeling. IEEE Trans. Magn. 2021, 57, 1–4. [Google Scholar] [CrossRef]
- Clemente, C.S.; Davino, D. Modeling and characterization of a kinetic energy harvesting device based on galfenol. Materials 2019, 12, 3199. [Google Scholar] [CrossRef]
- Clemente, C.S.; Davino, D.; Iannone, I.; Loschiavo, V.P. Experimental verification of an AC-DC Boost towards non-periodic (AC) Energy Harvesting. In Proceedings of the 2022 IEEE 21st Mediterranean Electrotechnical Conference (MELECON), Palermo, Italy, 14–16 June 2022; pp. 1002–1006. [Google Scholar] [CrossRef]
- Szarka, G.D.; Stark, B.H.; Burrow, S.G. Review of power conditioning for kinetic energy harvesting systems. IEEE Trans. Power Electron. 2012, 27, 803–815. [Google Scholar] [CrossRef]
- Dwari, S.; Parsa, L. An efficient AC–DC step-up converter for low-voltage energy harvesting. IEEE Trans. Power Electron. 2010, 25, 2188–2199. [Google Scholar] [CrossRef]
- Dayal, R.; Dwari, S.; Parsa, L. Design and implementation of a direct AC–DC boost converter for low-voltage energy harvesting. IEEE Trans. Ind. Electron. 2011, 58, 2387–2396. [Google Scholar] [CrossRef]
- Turksoy, O.; Yilmaz, U.; Teke, A. Efficient AC-DC power factor corrected boost converter design for battery charger in electric vehicles. Energy 2021, 221, 119765. [Google Scholar] [CrossRef]
- Choetchai, P.; Thanachayanont, A. A Self-starting AC-to-DC Step-up Converter for Energy Harvesting Applications. Procedia Computer Science 2016, 86, 144–147. [Google Scholar] [CrossRef]
- Costanzo, L.; Schiavo, A.L.; Vitelli, M. Power Extracted from Piezoelectric Harvesters with Passive and Active AC/DC Stages. In Proceedings of the 2020 Fifteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 10–12 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Cheng, S.; Jin, Y.; Rao, Y.; Arnold, D.P. An Active Voltage Doubling AC/DC Converter for Low-Voltage Energy Harvesting Applications. IEEE Trans. Power Electron. 2011, 26, 2258–2265. [Google Scholar] [CrossRef]
- Iannone, I.; Clemente, C.S.; Davino, D.; Loschiavo, V.P. AC-DC Boost Modelling for Magnetostrictive Energy Harvesting. In Proceedings of the 2021 IEEE International Conference on Environment and Electrical Engineering and 2021 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I CPS Europe), Bari, Italy, 7–10 September 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Sahu, B.; Rincon-Mora, G. A high-efficiency, dual-mode, dynamic, buck-boost power supply IC for portable applications. In Proceedings of the 18th International Conference on VLSI Design held jointly with 4th International Conference on Embedded Systems Design, Kolkata, India, 3–7 January 2005; pp. 858–861. [Google Scholar] [CrossRef]
- Zhou, S.; Rincon-Mora, G. A high efficiency, soft switching DC-DC converter with adaptive current-ripple control for portable applications. IEEE Trans. Circuits Syst. II Express Briefs 2006, 53, 319–323. [Google Scholar] [CrossRef]
- Szarka, G.D.; Burrow, S.G.; Stark, B.H. Ultralow Power, Fully Autonomous Boost Rectifier for Electromagnetic Energy Harvesters. IEEE Trans. Power Electron. 2013, 28, 3353–3362. [Google Scholar] [CrossRef]
- Cervellini, P.; Antoszczuk, P.; Garcia Retegui, R.; Funes, M. Efficiency analysis on DCM interleaved boost power converters. In Proceedings of the 2017 17th Workshop on Information Processing and Control, RPIC 2017, Mar del Plata, Argentina, 20–22 September 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar] [CrossRef]
- Mitcheson, P.D.; Yeatman, E.M.; Rao, G.K.; Holmes, A.S.; Green, T.C. Energy Harvesting From Human and Machine Motion for Wireless Electronic Devices. Proc. IEEE 2008, 96, 1457–1486. [Google Scholar] [CrossRef]
- Blad, T.W.; Tolou, N. On the efficiency of energy harvesters: A classification of dynamics in miniaturized generators under low-frequency excitation. J. Intell. Mater. Syst. Struct. 2019, 30, 2436–2446. [Google Scholar] [CrossRef]
- Fuchs, E.; Masoum, M. Power Quality in Power Systems and Electrical Machines; Elsevier Inc.: Amsterdam, The Netherlands, 2008. [Google Scholar] [CrossRef]




| Circuit Element | Value | Model |
|---|---|---|
| 220 m | custom secondary winding of the toroidal transformer | |
| R | 700 m | - |
| L | 1 mH | - |
| D1, D2 | - | BAT46 |
| M1, M2 | - | IRF1404 |
| C | 10, 100, 330 F | - |
| R | 2.2 k | - |
| Article | [V] | [Hz] | R [] | L [H] | C [F] | R [] | max V [VRMS] | Voltage Gain [V/V] | [%] |
|---|---|---|---|---|---|---|---|---|---|
| [16] | 1 | 50 | 970 m | 1 m | 100 | 2.2 k | 9.96 | 10 | N/A |
| here | 0.155 | 20, 50, 80 | 700 m | 1 m | 10, 100, 330 | 2.2 k | 2.94 | 19 | 17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clemente, C.S.; Davino, D.; Iannone, I.; Loschiavo, V.P. Experimental Characterization of an AC–DC Boost for Energy Harvesting Device Based on Magnetostrictive Materials. Electricity 2024, 5, 24-35. https://doi.org/10.3390/electricity5010002
Clemente CS, Davino D, Iannone I, Loschiavo VP. Experimental Characterization of an AC–DC Boost for Energy Harvesting Device Based on Magnetostrictive Materials. Electricity. 2024; 5(1):24-35. https://doi.org/10.3390/electricity5010002
Chicago/Turabian StyleClemente, Carmine Stefano, Daniele Davino, Immacolato Iannone, and Vincenzo Paolo Loschiavo. 2024. "Experimental Characterization of an AC–DC Boost for Energy Harvesting Device Based on Magnetostrictive Materials" Electricity 5, no. 1: 24-35. https://doi.org/10.3390/electricity5010002
APA StyleClemente, C. S., Davino, D., Iannone, I., & Loschiavo, V. P. (2024). Experimental Characterization of an AC–DC Boost for Energy Harvesting Device Based on Magnetostrictive Materials. Electricity, 5(1), 24-35. https://doi.org/10.3390/electricity5010002









