Single-Stage LLC Resonant Converter for Induction Heating System with Improved Power Quality
Abstract
:1. Introduction
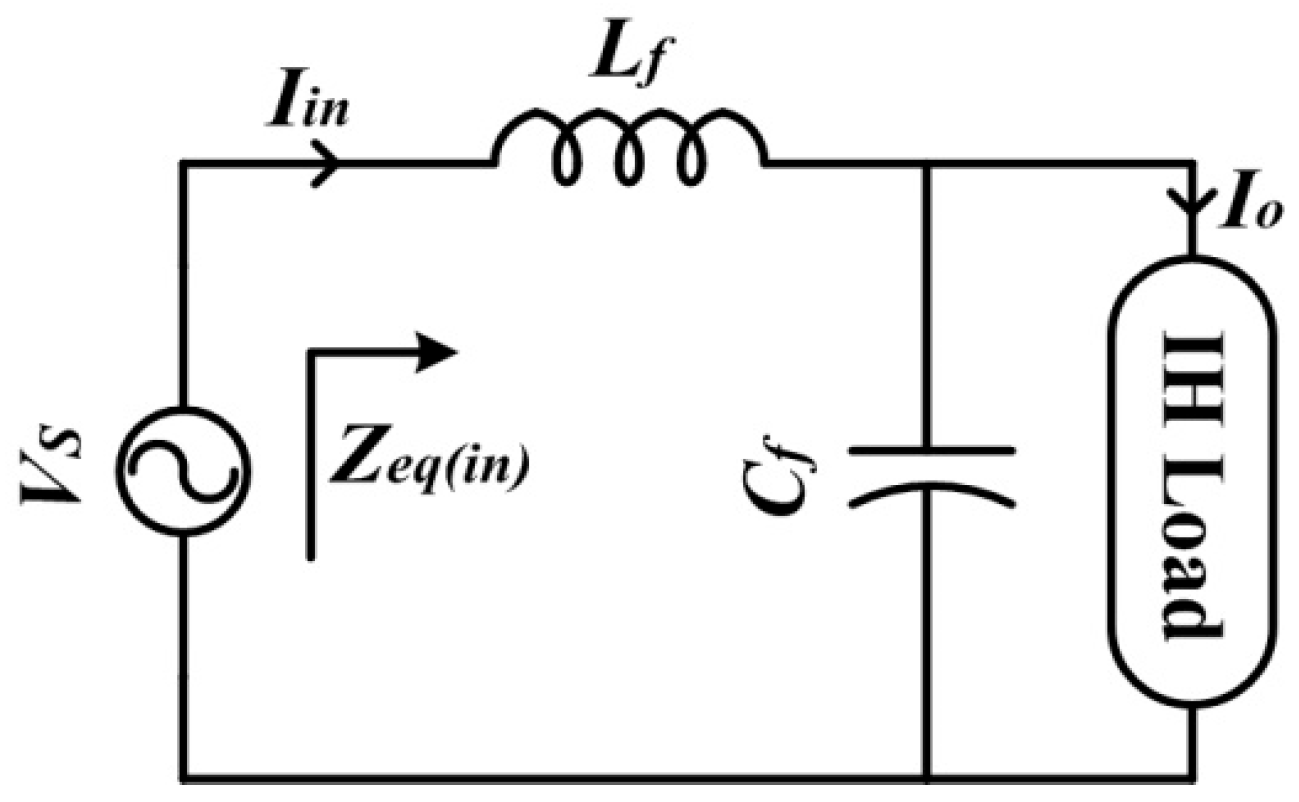
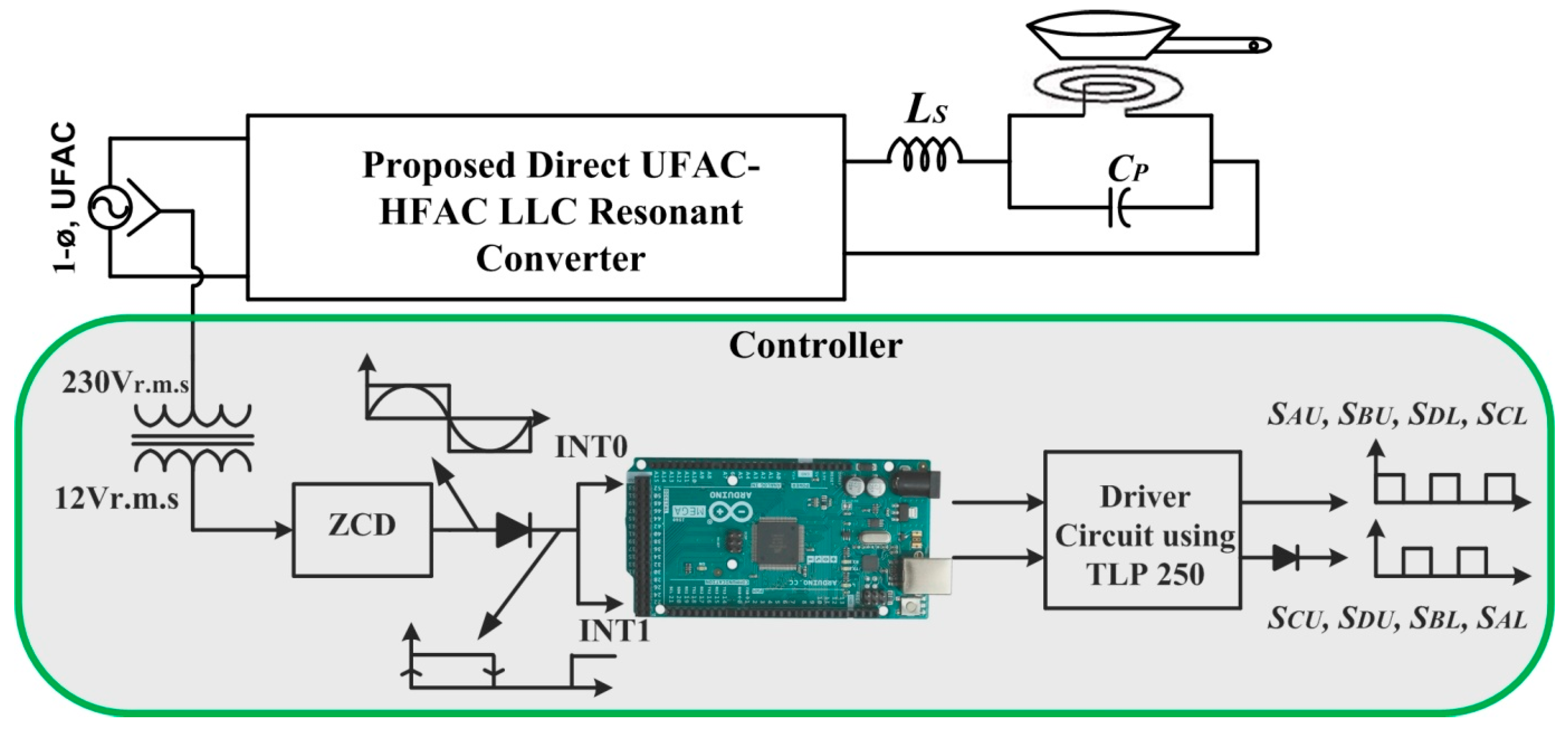
2. Proposed Direct AC–HFAC LLC Resonant Converter
2.1. Circuit Description
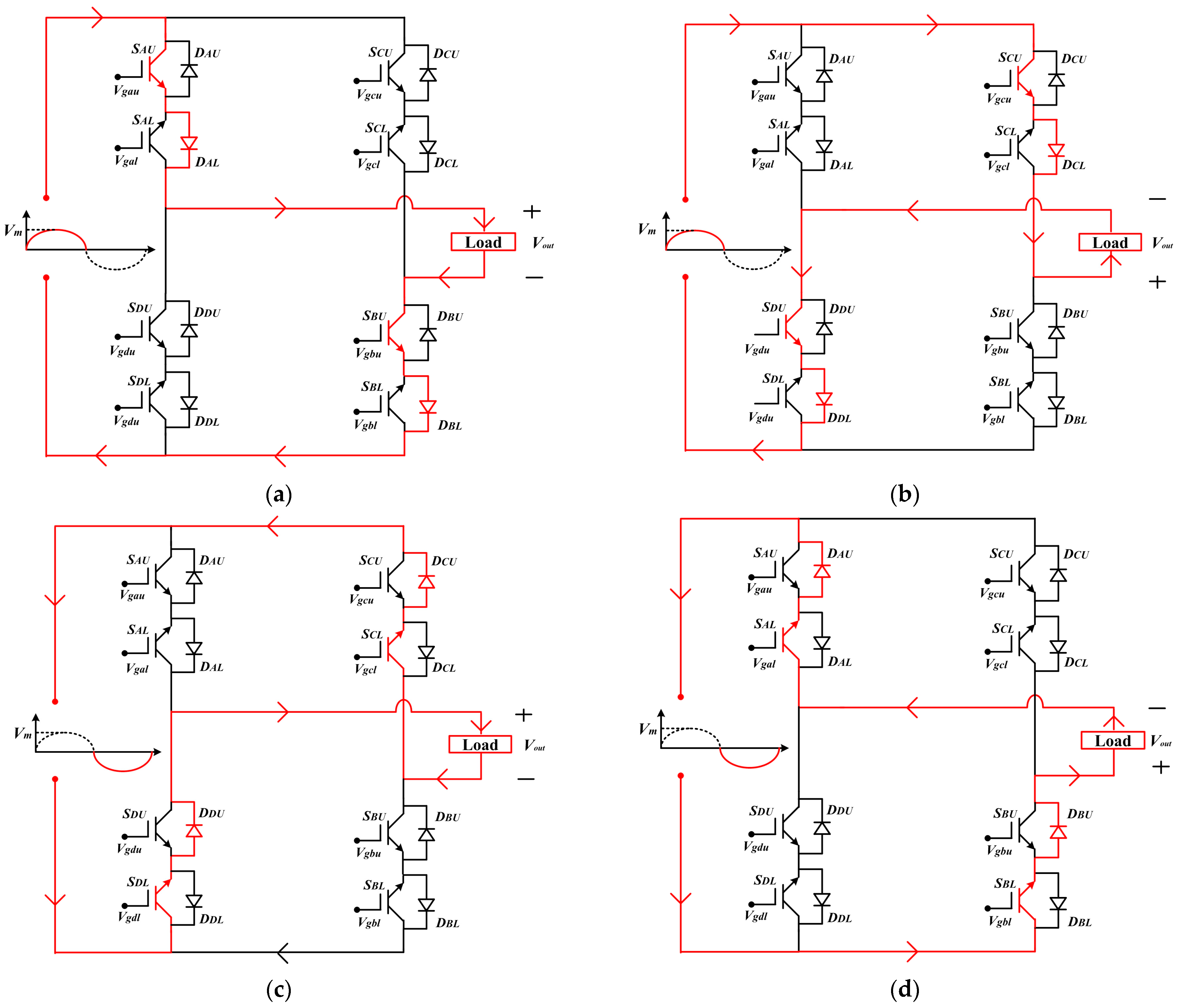
2.2. Modes of Operation
- Positive input half cycle, Vs > 0
- Negative input half cycle, Vs < 0
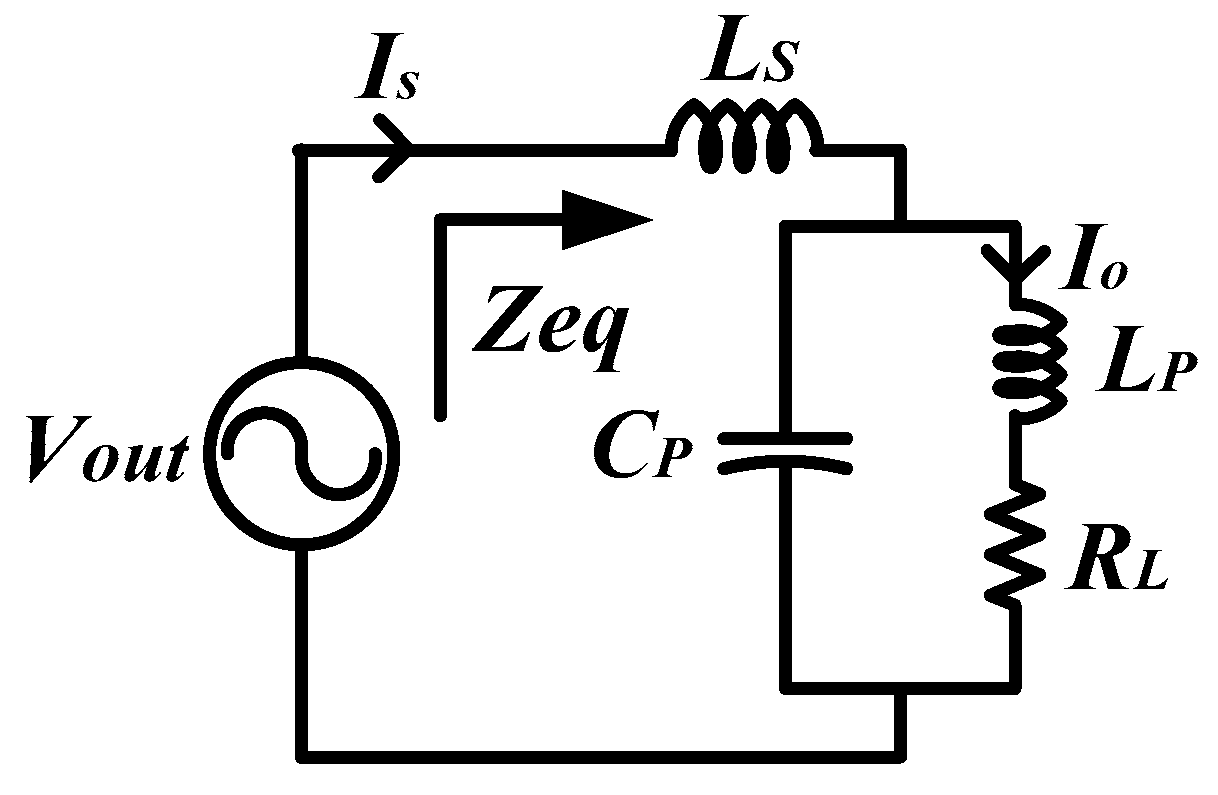
3. Mathematical Analysis of Proposed Topology
- (a)
- All components in the circuit are ideal.
- (b)
- The AC input voltage (Vs) is purely sinusoidal.
- (c)
- The effects of parasitic capacitance are neglected.
- (d)
- The load current is purely HF sinusoidal.
3.1. Calculation of Switching Frequency
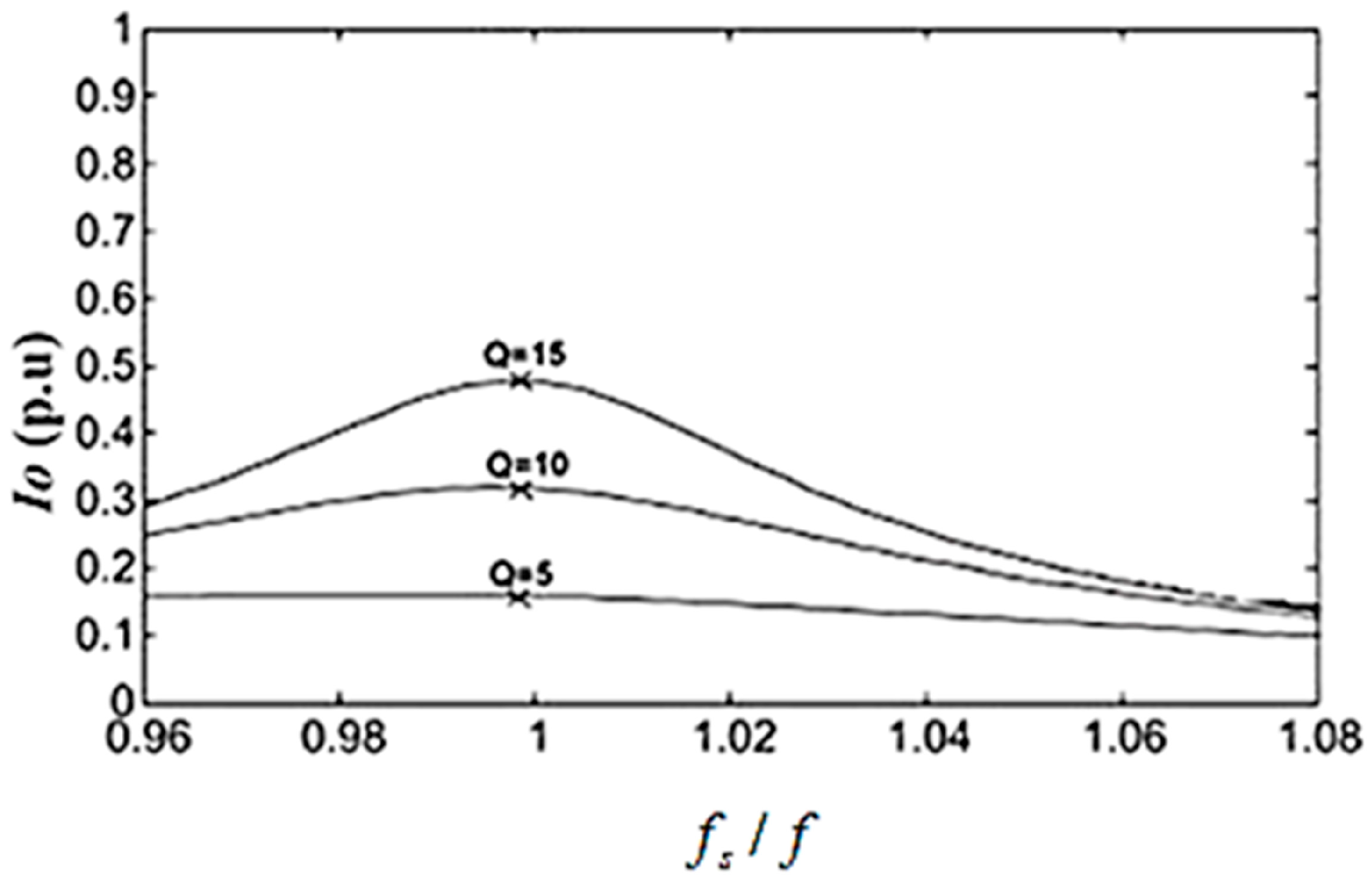
3.2. Quality Factor
3.3. Current Gain
3.4. Voltage Gain
3.5. Calculation of Output Power
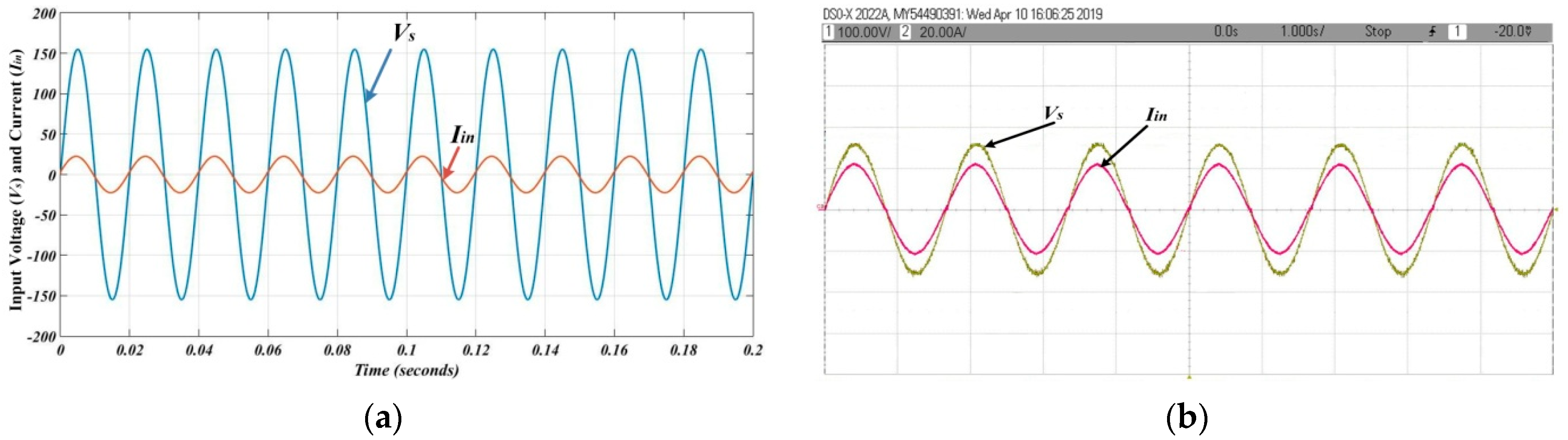
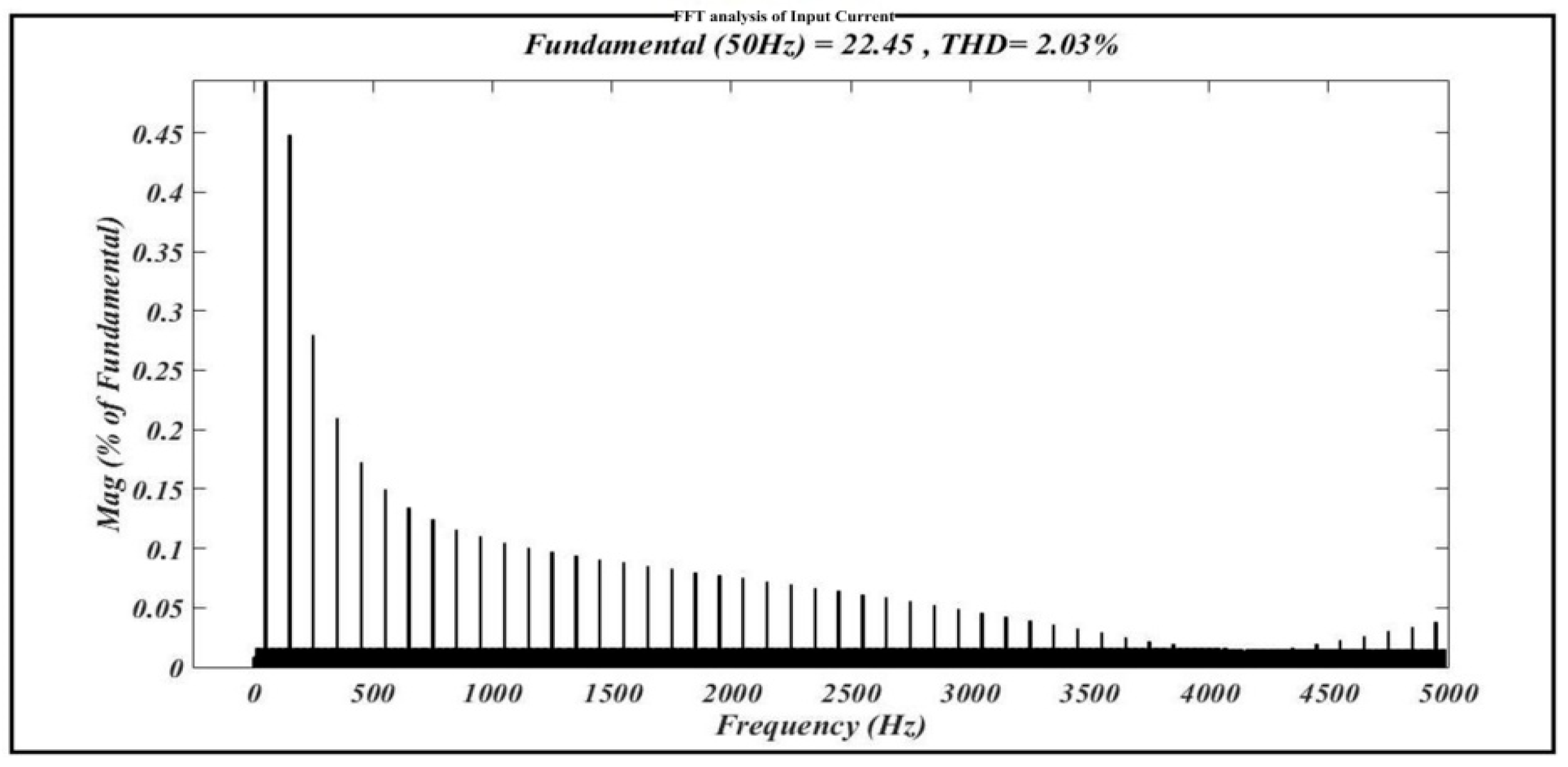
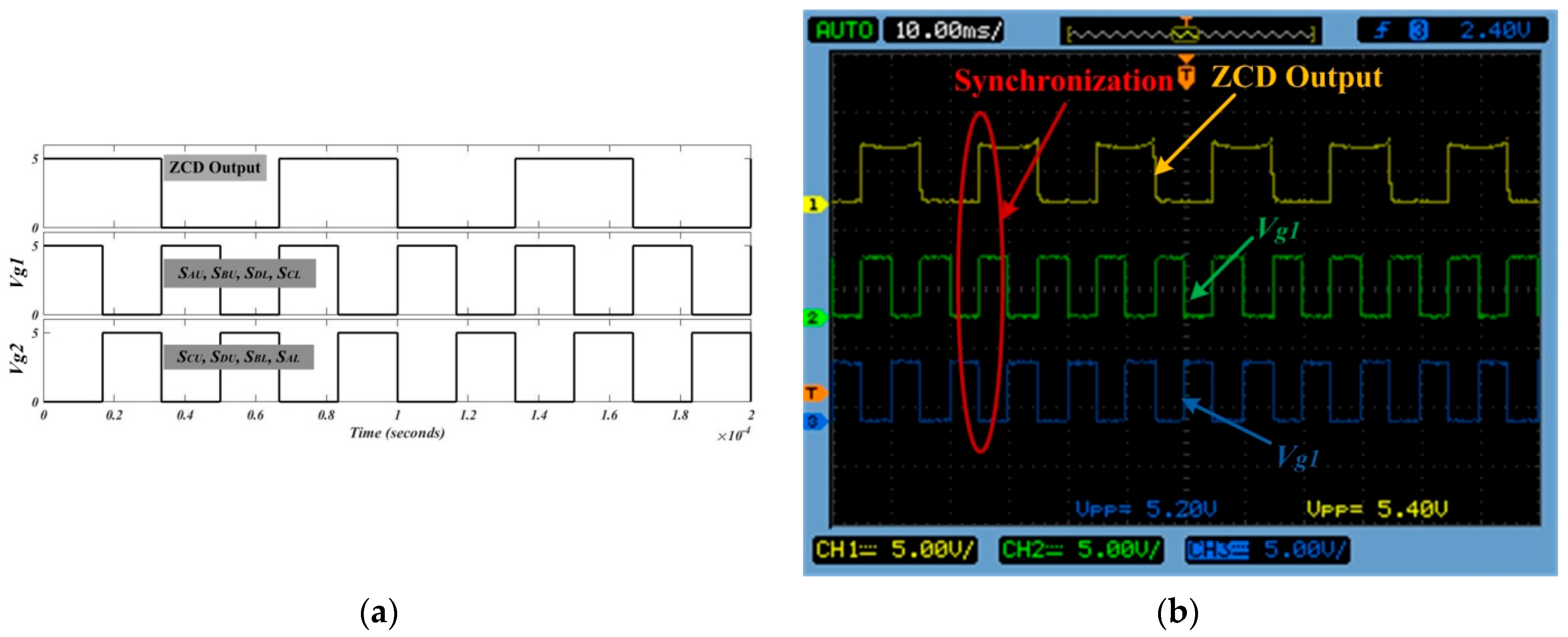
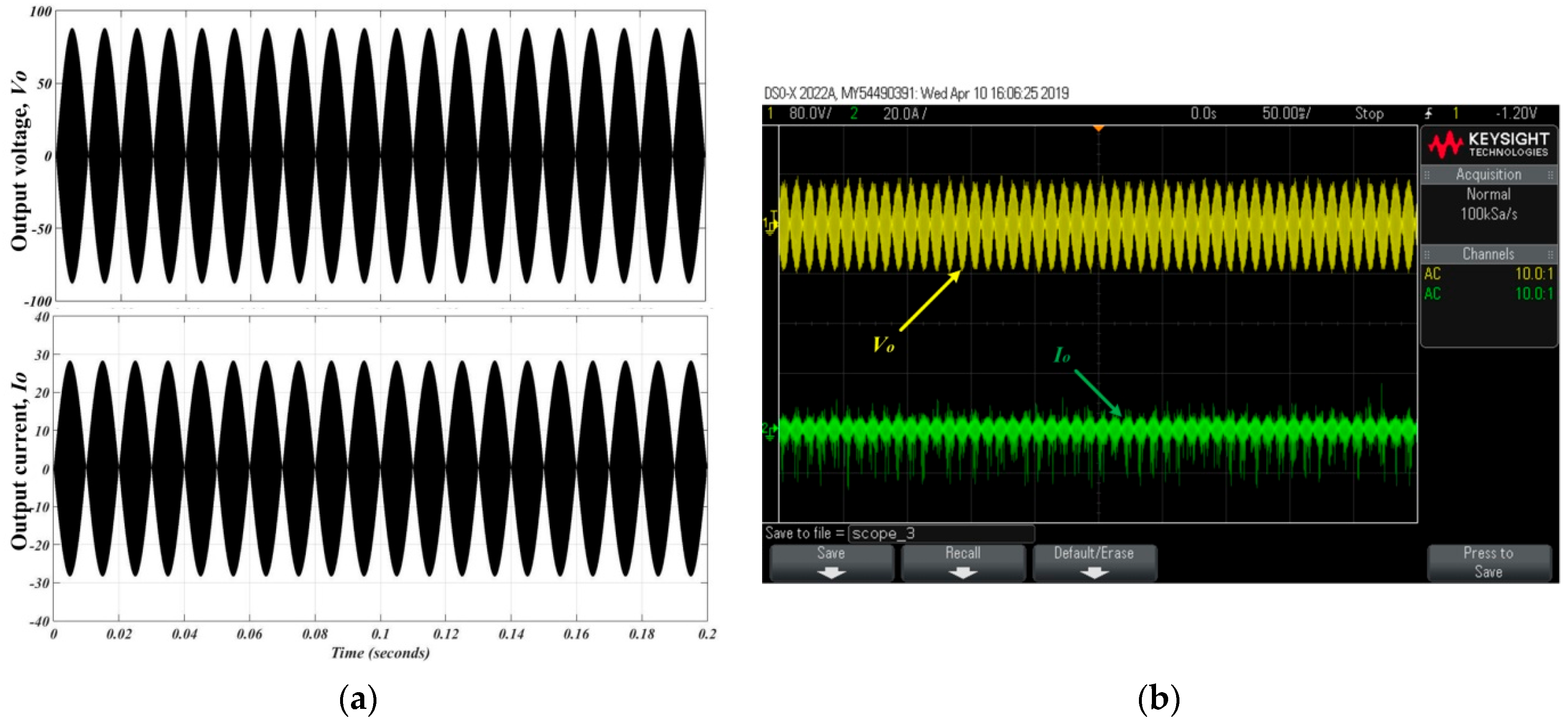
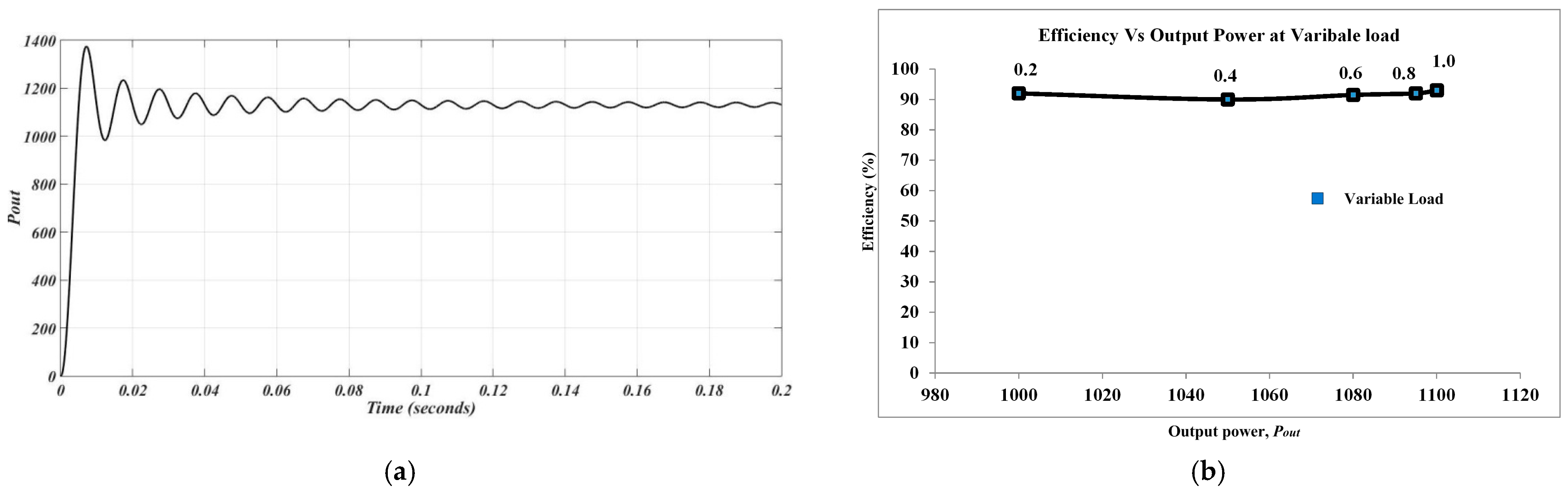
4. Results
5. Conclusions
- The presented topology converts utility grid-frequency AC to HF AC in a single stage and also maintains the input power factor close to unity simultaneously.
- The implemented control scheme is based on an embedded system having a simple configuration and is easy to implement.
- As LLC configuration is used, it reduces the current stress across the switches and also enables an intense current magnitude across the IH load simultaneously.
- Finally, the proposed topology not only lowers the THD of the input current but also blocks the HF component that receives back flows towards the utility side. Thus, the power quality of the input mains improves.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lucía, O.; Maussion, P.; Dede, E.J.; Burdío, J.M. Induction heating technology and its applications: Past developments, current technology, and future challenges. IEEE Trans. Ind. Electron. 2013, 61, 2509–2520. [Google Scholar] [CrossRef]
- Patil, M.; Choubey, R.K.; Jain, P.K. Influence of coil shapes on temperature distribution in induction heating process. Mater. Today: Proc. 2023, 72, 3029–3035. [Google Scholar] [CrossRef]
- Acero, J.B.L.B.J.; Alonso, R.; Burdio, J.M.; Barragán, L.A.; Puyal, D. Analytical equivalent impedance for a planar circular induction heating system. IEEE Trans. Magn. 2005, 42, 84–86. [Google Scholar] [CrossRef]
- Chaboudez, C.; Clain, S.; Glardon, R.; Rappaz, J.; Swierkosz, M.; Touzani, R. Numerical modelling of induction heating of long workpieces. IEEE Trans. Magn. 1994, 30, 5028–5037. [Google Scholar] [CrossRef]
- Ngoc, H.P.; Fujita, H.; Ozaki, K.; Uchida, N. Phase angle control of high-frequency resonant currents in a multiple inverter system for zone-control induction heating. IEEE Trans. Power Electron. 2011, 26, 3357–3366. [Google Scholar] [CrossRef]
- Musii, R.; Lis, M.; Pukach, P.; Chaban, A.; Szafraniec, A.; Vovk, M.; Melnyk, N. Analysis of Varying Temperature Regimes in a Conductive Strip during Induction Heating under a Quasi-Steady Electromagnetic Field. Energies 2024, 17, 366. [Google Scholar] [CrossRef]
- Millán, I.; Burdío, J.M.; Acero, J.; Lucía, O.; Llorente, S. Series resonant inverter with selective harmonic operation applied to all-metal domestic induction heating. IET Power Electron. 2011, 4, 587–592. [Google Scholar] [CrossRef]
- Dimitrov, B.; Hayatleh, K.; Barker, S.; Collier, G. Design, Analysis and Experimental Verification of the Self-Resonant Inverter for Induction Heating Crucible Melting Furnace Based on IGBTs Connected in Parallel. Electricity 2021, 2, 439–458. [Google Scholar] [CrossRef]
- Neogi, K.; Sadhu, M.; Das, N.; Sadhu, P.K.; Chakraborty, A.; Ganguly, A.; Banerjee, A. A new approach for the stability analysis of high-frequency series resonant inverter-fitted induction heater. Ain Shams Eng. J. 2019, 10, 185–194. [Google Scholar] [CrossRef]
- Aunsborg, T.S.; Duun, S.B.; Munk-Nielsen, S.; Uhrenfeldt, C. Development of a current source resonant inverter for high current MHz induction heating. IET Power Electron. 2022, 15, 1–10. [Google Scholar] [CrossRef]
- Yu, A.; Zeng, X.; Xiong, D.; Tian, M.; Li, J. An Improved Autonomous Current-Fed Push-Pull Parallel-Resonant Inverter for Inductive Power Transfer System. Energies 2018, 11, 2653. [Google Scholar] [CrossRef]
- Kim, N.G.; Jo, S.W.; Han, B.; Choi, H.H.; Kim, M. Highly efficient bidirectional current-fed resonant converter over a wide voltage gain range. IEEE Trans. Ind. Electron. 2020, 68, 10913–10927. [Google Scholar] [CrossRef]
- Miyamae, M.; Ito, T.; Matsuse, K.; Tsukahara, M. Performance of a high frequency quasi-resonant inverter with variable-frequency output for induction heating. In Proceedings of the 7th International Power Electronics and Motion Control Conference, Harbin, China, 2–5 June 2012; pp. 2877–2882. [Google Scholar]
- Mendonça, L.S.; Naidon, T.C.; Raposo, R.F.; Bisogno, F.E. An Unit-less Mathematical Model for Analysis and Design of Class-E Resonant Converters. In Proceedings of the 2019 IEEE 15th Brazilian Power Electronics Conference and 5th IEEE Southern Power Electronics Conference (COBEP/SPEC), Santos, Brazil, 1–4 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Gomes, R.; Vitorino, M.A.; Acevedo-Bueno, D.; Correa, M. Multi-Phase Resonant Inverter with Coupled Coils for AC/AC Induction Heating Application. IEEE Trans. Ind. Appl. 2019, 56, 551–560. [Google Scholar] [CrossRef]
- Devara, V.B.; Neti, V.; Maity, T.; Shunmugam, P. Capacitor-sharing two-output series-resonant inverter for induction cooking application. IET Power Electron. 2016, 9, 2240–2248. [Google Scholar] [CrossRef]
- Esteve, V.; Jordán, J.; Dede, E.J.; Bellido, J.L. Enhanced asymmetrical modulation for half-bridge series resonant inverters in induction heating applications. IET Power Electron. 2023, 16, 2482–2491. [Google Scholar] [CrossRef]
- Carretero, C.; Lucía, O.; Acero, J.; Burdío, J.M. Phase-shift control of dual half-bridge inverter feeding coupled loads for induction heating purposes. Electron. Lett. 2011, 47, 670–671. [Google Scholar] [CrossRef]
- Shen, J.; Ma, H.; Yan, W.; Hui, J.; Wu, L. PDM and PSM Hybrid Power Control of a Series-Resonant Inverter for Induction Heating Applications. In Proceedings of the 2006 1ST IEEE Conference on Industrial Electronics and Applications, Singapore, 24–26 May 2006; pp. 1–6. [Google Scholar]
- Burdio, J.M.; Barragan, L.A.; Monterde, F.; Navarro, D.; Acero, J. Asymmetrical voltage-cancellation control for full-bridge series resonant inverters. IEEE Trans. Power Electron. 2004, 19, 461–469. [Google Scholar] [CrossRef]
- Meziane, B.; Zeroug, H. Comprehensive Power Control Performance Investigations of Resonant Inverter for Induction Metal Surface Hardening. IEEE Trans. Ind. Electron. 2016, 63, 6086–6096. [Google Scholar] [CrossRef]
- Franco de Souza, A.; Ribeiro, E.R.; Vicente, E.M.; Tofoli, F.L. Experimental evaluation of active power factor correction techniques in a single-phase AC-DC boost converter. Int. J. Circuit Theory Appl. 2019, 47, 1529–1553. [Google Scholar] [CrossRef]
- Gonçalves, J.T.; Valtchev, S.; Melicio, R.; Gonçalves, A.; Blaabjerg, F. Hybrid three-phase rectifiers with active power factor correction: A systematic review. Electronics 2021, 10, 1520. [Google Scholar] [CrossRef]
- İnci, M.; Büyük, M.; Demir, M.H.; İlbey, G. A review and research on fuel cell electric vehicles: Topologies, power electronic converters, energy management methods, technical challenges, marketing and future aspects. Renew. Sustain. Energy Rev. 2021, 137, 110648. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, H.; Sangwongwanich, A.; Blaabjerg, F. Design for reliability of power electronic systems. In Power Electronics Handbook; Butterworth-Heinemann: Oxford, UK, 2018; pp. 1423–1440. [Google Scholar]
- Pérez-Tarragona, M.; Sarnago, H.; Lucía, Ó.; Burdío, J.M. Design and Experimental Analysis of PFC Rectifiers for Domestic Induction Heating Applications. IEEE Trans. Power Electron. 2018, 33, 6582–6594. [Google Scholar] [CrossRef]
- Espi-Huerta, J.M.; Santamaria, E.J.D.G.; Gil, R.G.; Castello-Moreno, J. Design of the L-LC Resonant Inverter for Induction Heating Based on Its Equivalent SRI. IEEE Trans. Ind. Electron. 2007, 54, 3178–3187. [Google Scholar] [CrossRef]
- Zgraja, J.; Lisowski, G.; Kucharski, J. Autonomous Energy Matching Control in an LLC Induction Heating Generator. Energies 2020, 13, 1860. [Google Scholar] [CrossRef]
- Chudjuarjeen, S.; Sangswang, A.; Koompai, C. LLC resonant inverter for induction heating with asymmetrical voltage-cancellation control. In Proceedings of the 2009 IEEE International Symposium on Circuits and Systems, Taipei, Taiwan, 24–27 May 2009; pp. 2874–2877. [Google Scholar]
- Kranprakon, P.; Sangswang, A.; Naetiladdanon, S. Model predictive control of LLC resonant inverter for induction furnace. In Proceedings of the 2017 International Electrical Engineering Congress (iEECON), Pattaya, Thailand, 8–10 March 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–4. [Google Scholar]
- Vishnuram, P.; Ramachandiran, G.; Sudhakar Babu, T.; Nastasi, B. Induction heating in domestic cooking and industrial melting applications: A systematic review on modelling, converter topologies and control schemes. Energies 2021, 14, 6634. [Google Scholar] [CrossRef]



| Converter Topology | Control Algorithm | Merits | Demerits |
|---|---|---|---|
| Two-output series resonant inverter with common capacitor | Pulse width modulation control |
|
|
| Full bridge converter | Pulse density modulation, frequency modulation, phase shift modulation |
|
|
| Single-stage boost full bridge resonant inverter | Phase shift PWM technique |
|
|
| Multi-modulated converters using full bridge topology | Deadband current control technique |
|
|
| Multi-frequency resonant converter | Deadband current control technique |
|
|
| Input Voltage (Vs) | Forward-Biased Switches | Modes | IGBTs/Diodes Status | Time Interval | Output Voltage (Vout) |
|---|---|---|---|---|---|
| Vs > 0 | (SAU, SBU, SCU, SDU) and (DAL, DBL, DCL, DDL) | Mode 1 | (SAU/DAL/SBU/DBL) ON (SCU/DCL/SDU/DDL) OFF | t0–t1 | Vout > 0 |
| Mode 2 | (SAU/DAL/SBU/DBL) OFF (SCU/DCL/SDU/DDL) ON | t1–t2 | Vout < 0 | ||
| Vs < 0 | (SAL, SBL, SCL, SDL) and (DAU, DBU, DCU, DDU) | Mode 3 | (SDL/DDU/SCL/DCU) ON (SBL/DBU/SAL/DAU) OFF | t2–t3 | Vout > 0 |
| Mode 4 | (SDL/DDU/SCL/DCU) OFF (SBL/DBU/SAL/DAU) ON | t3–t4 | Vout < 0 |
| Circuit Parameters | Operational Parameters | ||
|---|---|---|---|
| Parameters | Value | Parameters | Value |
| Input voltage (Vs) | 110 Vr.m.s | Output voltage (Vout) | 88 Vp |
| Series inductance (LS) | 56 μH | Output current (Iout) | 28 Vp |
| Induction coil (LP) | 52.7 μH | Average output power (Pout) | 1100 W |
| Workpiece resistance (RL) | 1 Ω | Switching frequency (fs) | 30 kHz |
| Resonant frequency (f) | 24 kHz | Input power factor | 0.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, A.; Goswami, A.; Sadhu, P.K.; Szymanski, J.R. Single-Stage LLC Resonant Converter for Induction Heating System with Improved Power Quality. Electricity 2024, 5, 211-226. https://doi.org/10.3390/electricity5020011
Kumar A, Goswami A, Sadhu PK, Szymanski JR. Single-Stage LLC Resonant Converter for Induction Heating System with Improved Power Quality. Electricity. 2024; 5(2):211-226. https://doi.org/10.3390/electricity5020011
Chicago/Turabian StyleKumar, Anand, Anik Goswami, Pradip Kumar Sadhu, and Jerzy R. Szymanski. 2024. "Single-Stage LLC Resonant Converter for Induction Heating System with Improved Power Quality" Electricity 5, no. 2: 211-226. https://doi.org/10.3390/electricity5020011
APA StyleKumar, A., Goswami, A., Sadhu, P. K., & Szymanski, J. R. (2024). Single-Stage LLC Resonant Converter for Induction Heating System with Improved Power Quality. Electricity, 5(2), 211-226. https://doi.org/10.3390/electricity5020011







