Optimal Placement and Sizing of Battery Energy Storage Systems for Improvement of System Frequency Stability †
Abstract
1. Introduction
1.1. Motivation
1.2. Related Works
1.3. Contributions of This Paper
- The proposal of a methodology based on optimization to locate (considering all power system buses) and size BESSs for the enhancement of the system frequency stability indices, i.e., the frequency nadir and RoCoF.
- The application of three metaheuristic optimization algorithms to solve the proposed optimization problem and selection of the best performing algorithm for the proposed method. The optimization is solved using the approach of co-simulation between DIgSILENT and MATLAB.
- The detailed analysis of the frequency stability indices under different scenarios, such as different large generator outages, RES penetrations, and load variations, in two test systems, i.e., the IEEE 9-bus system and the 39-bus system.
1.4. Paper Organization
2. Theoretical Background
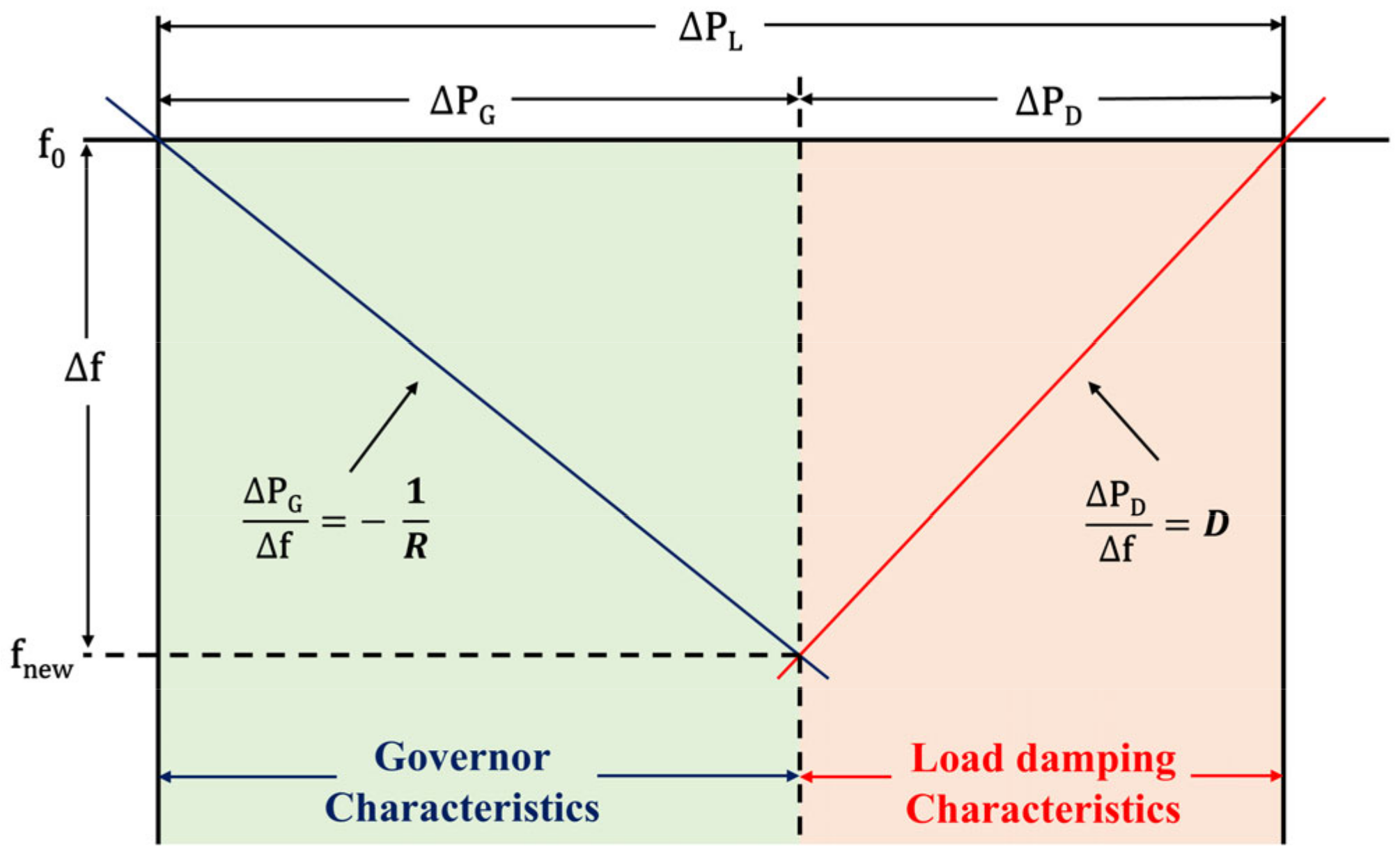
2.1. Frequency Stability Indices
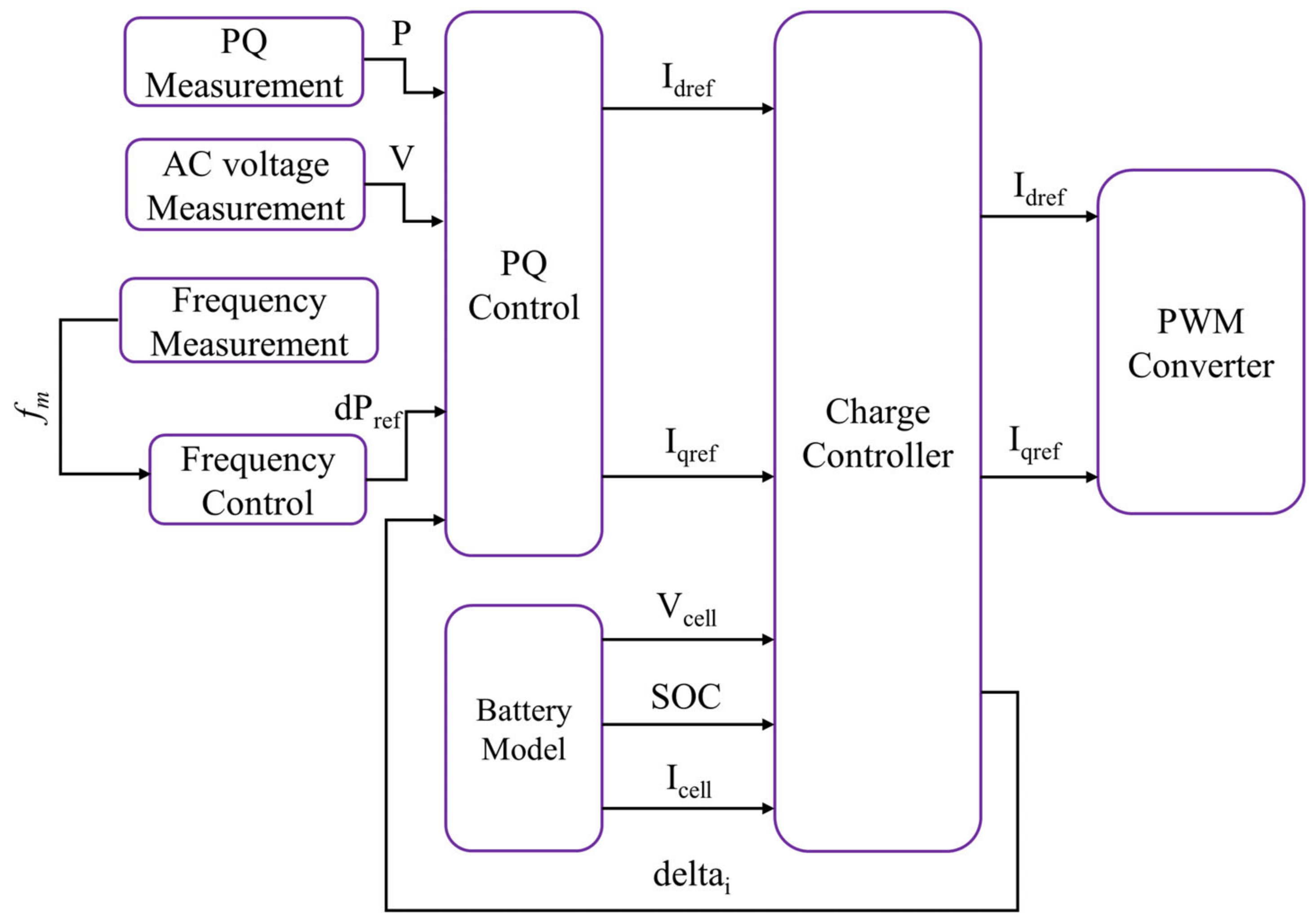
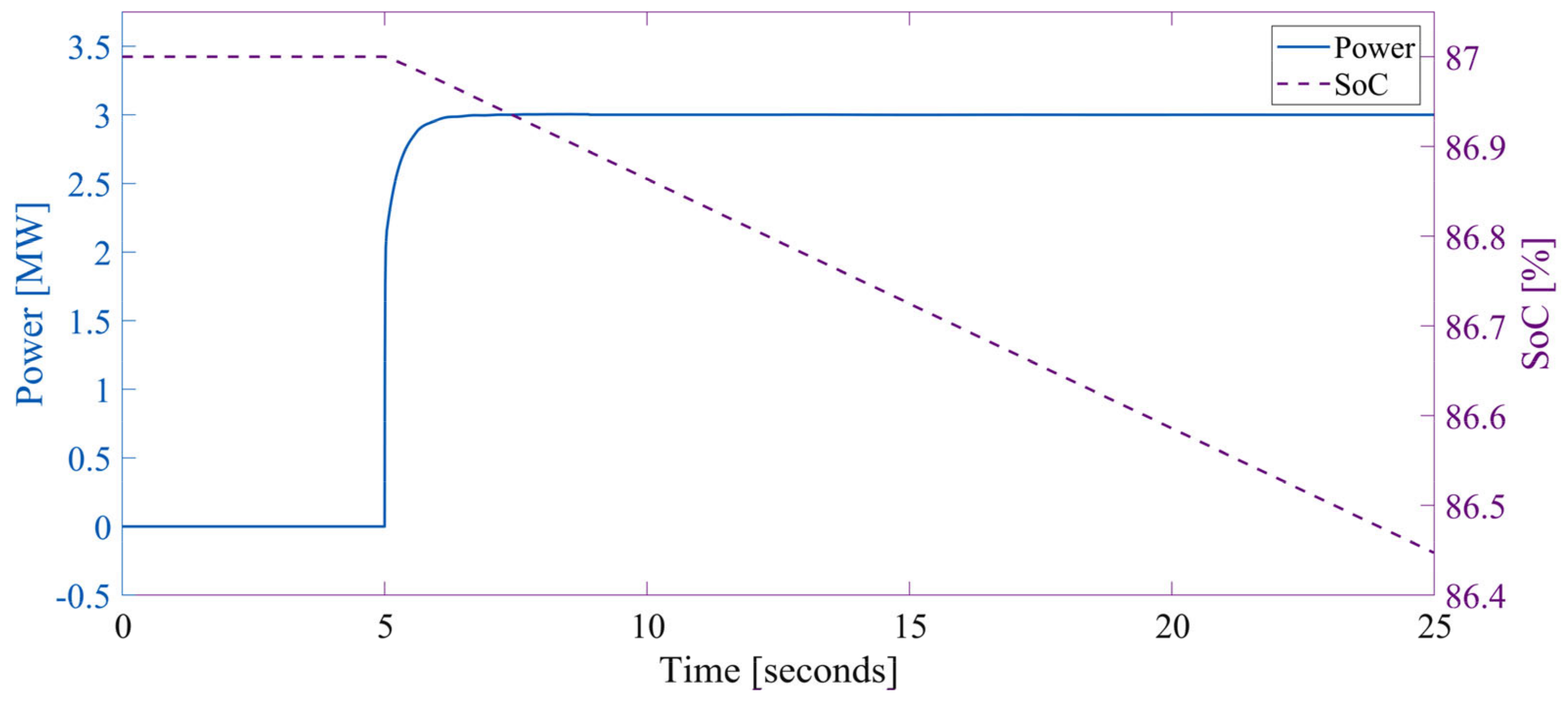
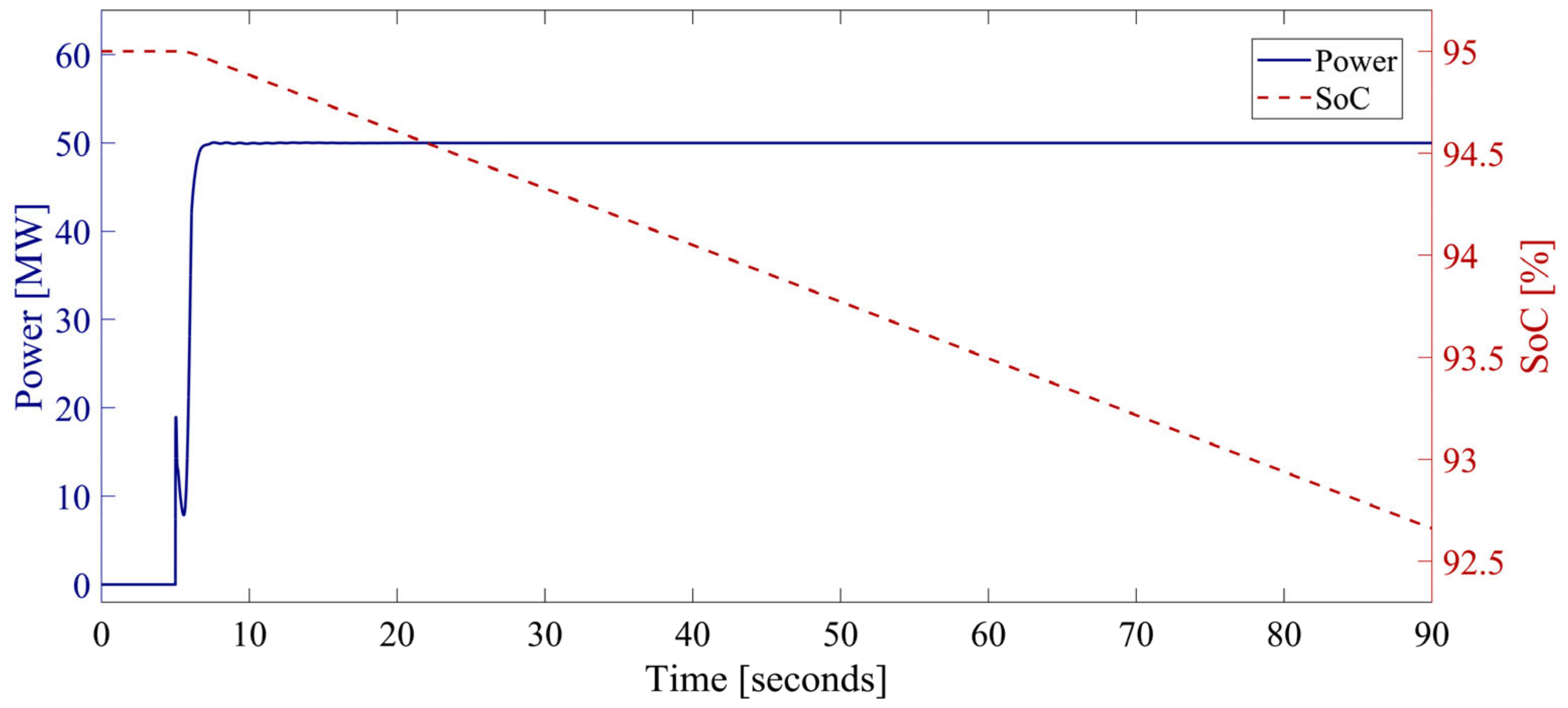
2.2. Battery Energy Storage Systems
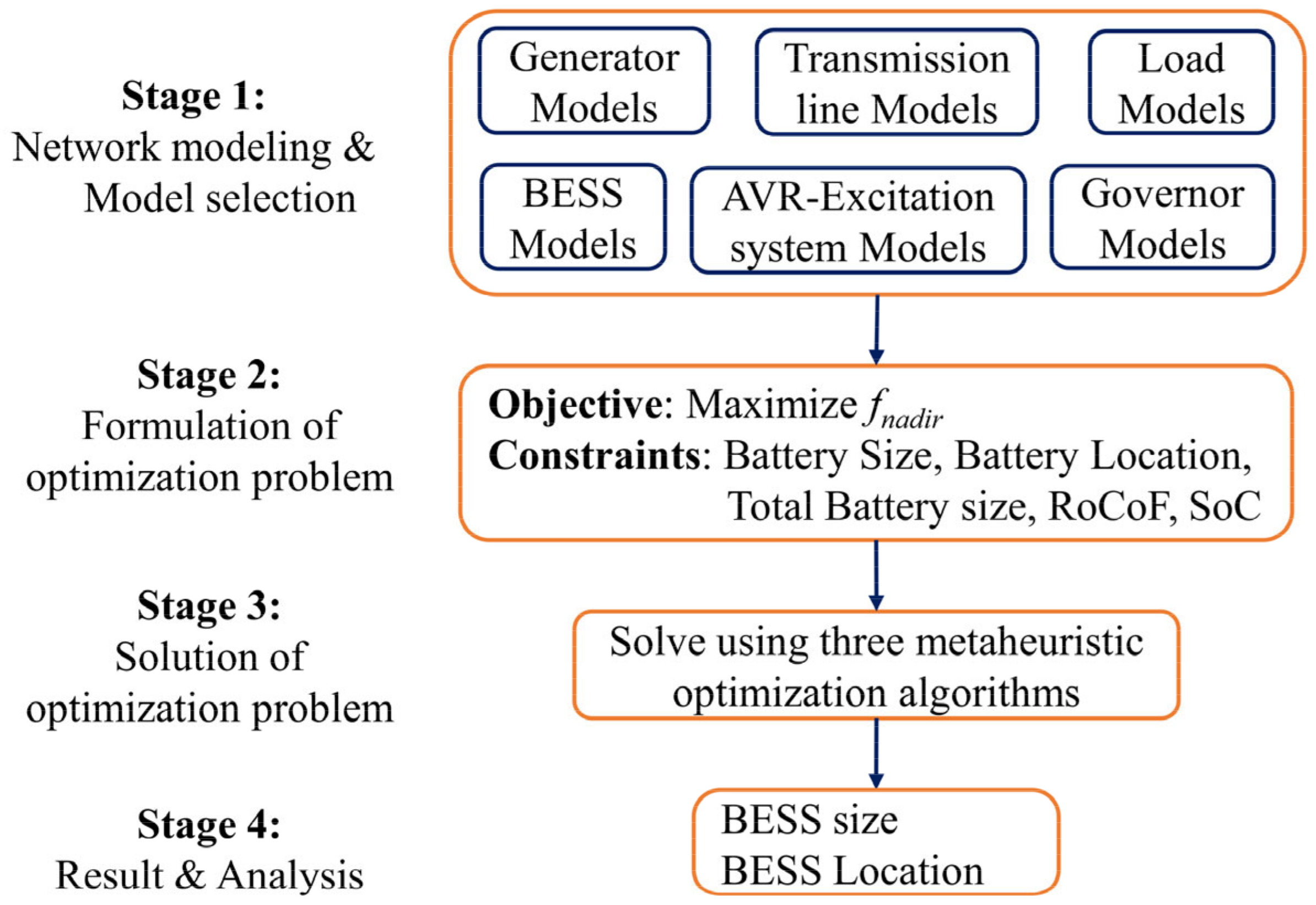
3. Proposed Methodology
3.1. Formulation of the Optimization Problem
3.2. Metaheuristic Optimization Algorithms
3.2.1. Particle Swarm Optimization
3.2.2. Firefly Algorithm
3.2.3. Bat Algorithm
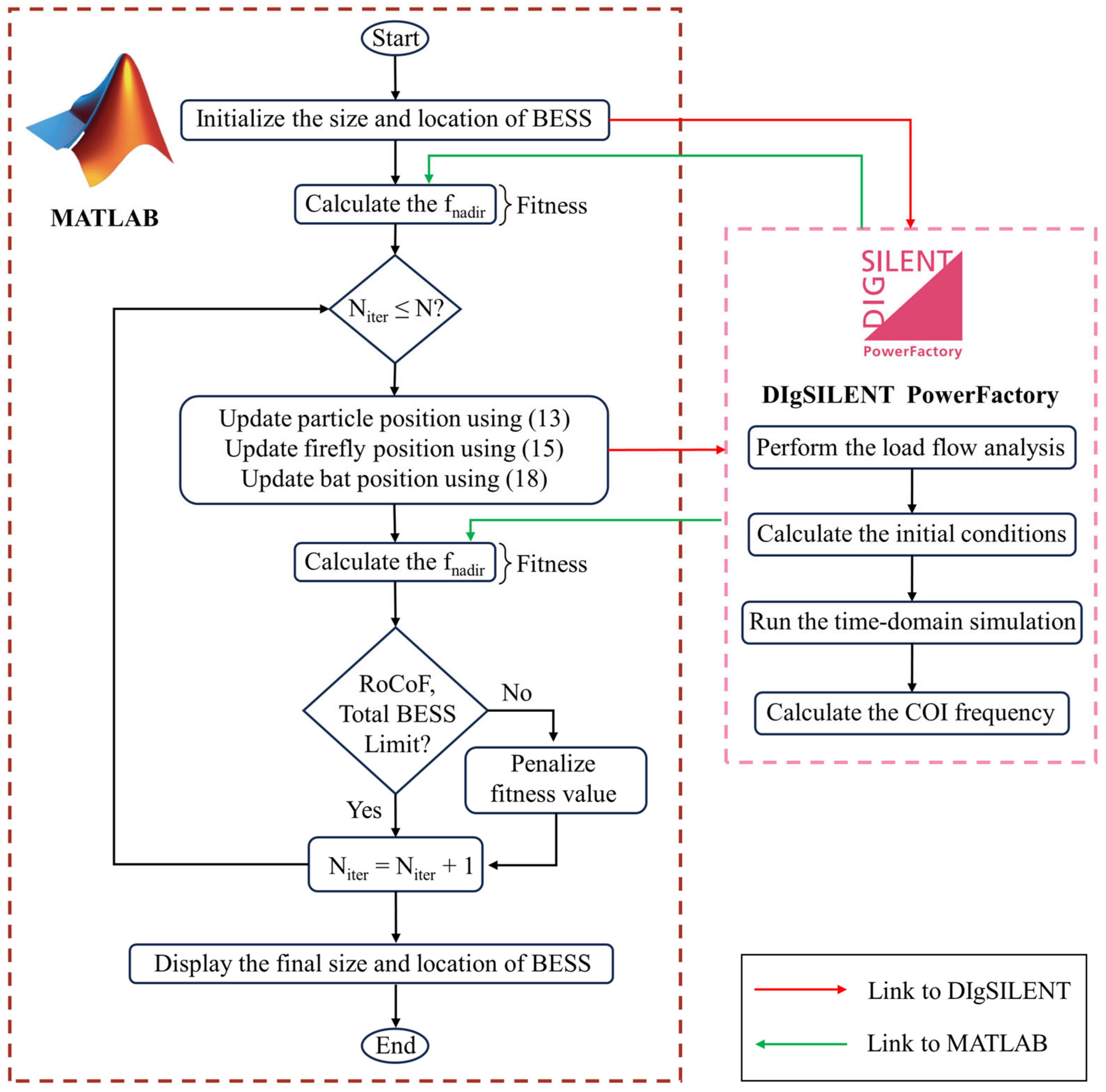
3.3. Solving the Optimization Problem
4. Results
4.1. Analysis of the IEEE 9-Bus System
4.1.1. Analysis under Contingency Condition
4.1.2. Analysis under Increased/Decreased Load Conditions
4.1.3. Analysis under Renewable Energy Resource Penetration
4.2. Analysis of the IEEE 39-Bus System
4.2.1. Analysis under Contingency Condition
4.2.2. Analysis under Increased/Decreased Load Conditions
4.2.3. Analysis under Renewable Energy Resource Penetration
5. Conclusions
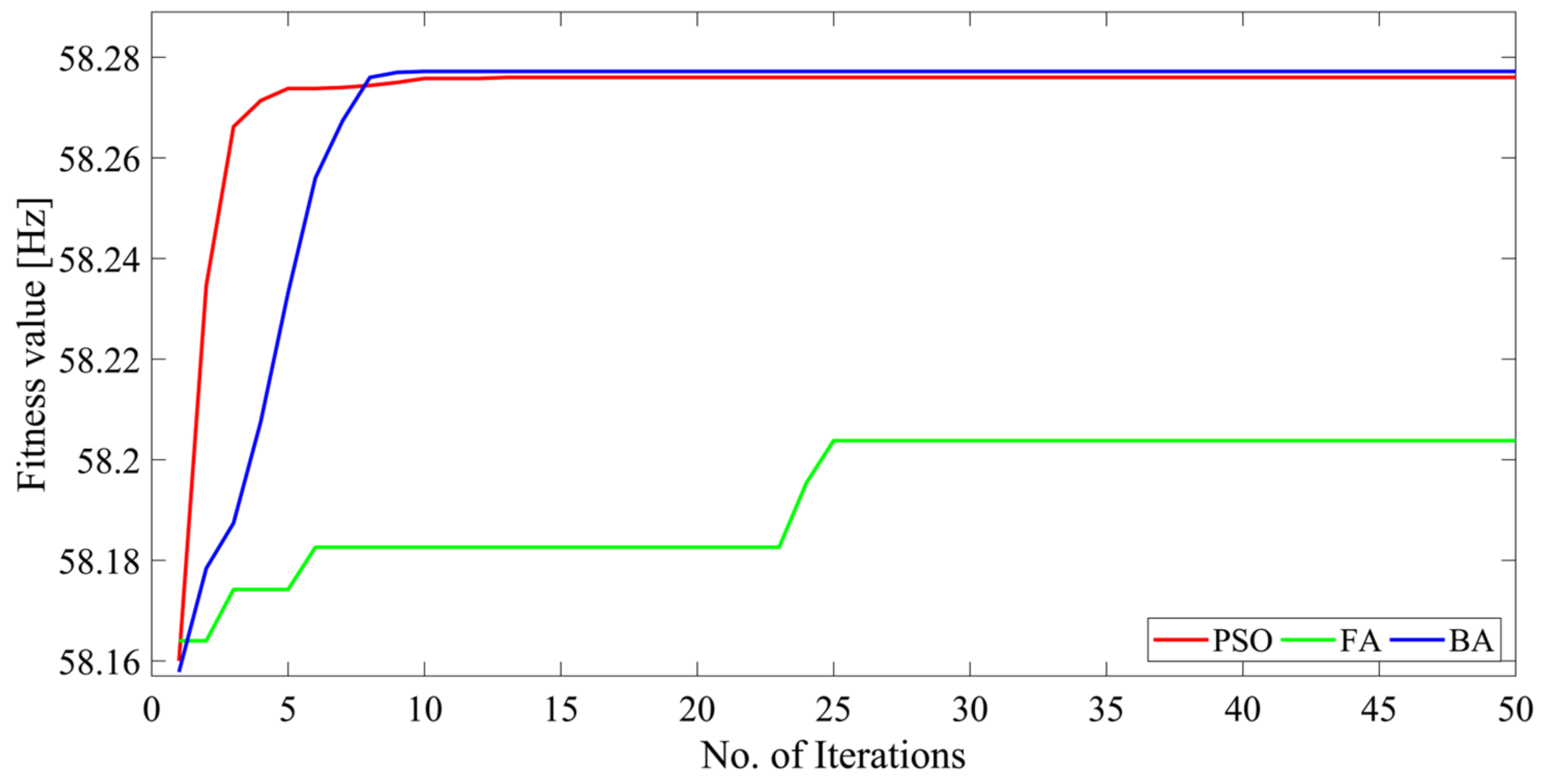
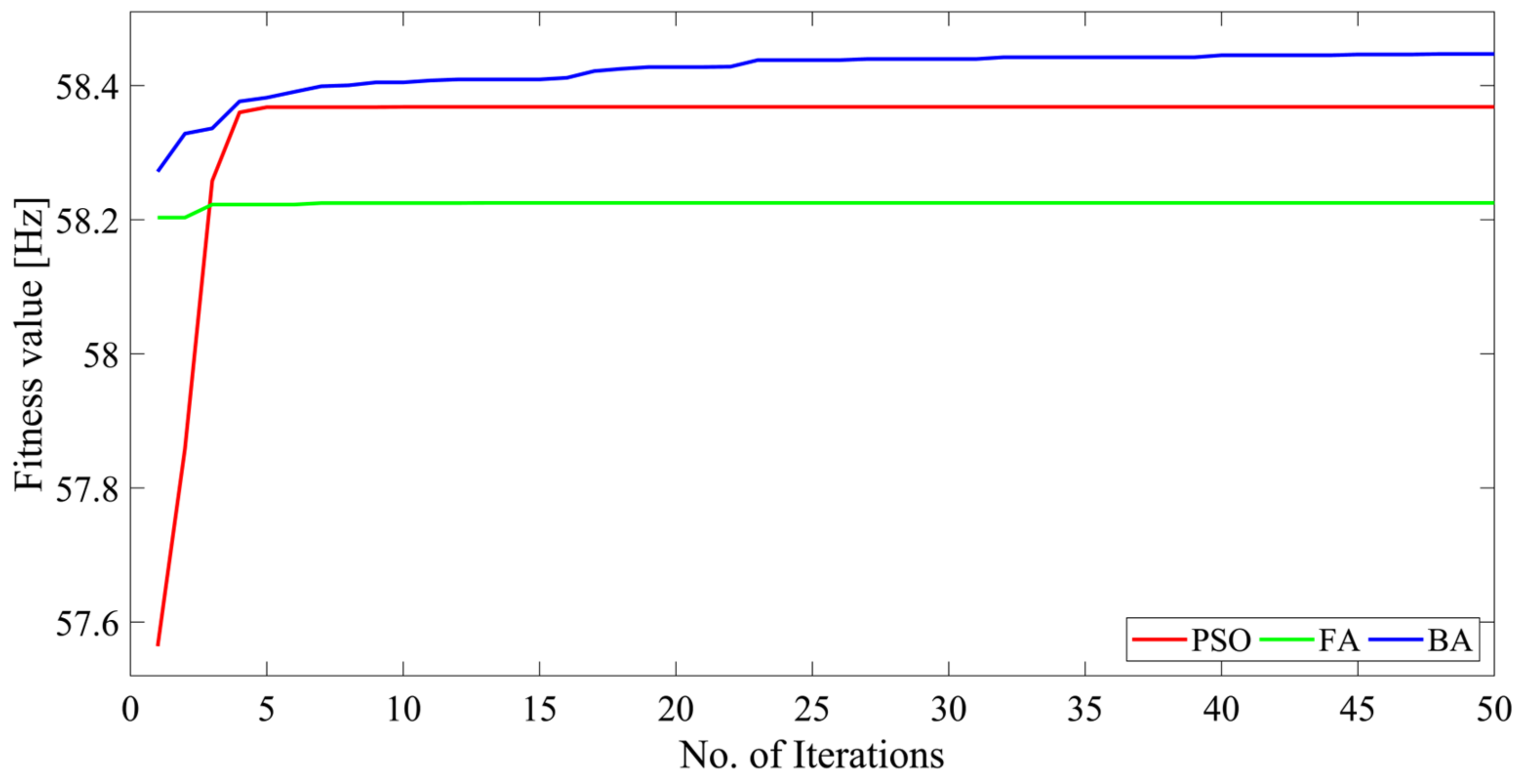
- The BA consistently exhibits the best performance compared to PSO and the FA, as demonstrated by its attainment of a mean fitness value of 58.2723 Hz in the IEEE 9-bus system, which is higher than 58.2681 Hz obtained with PSO, and 58.1926 Hz obtained with the FA in the IEEE 9-bus system. Similarly, the mean fitness value with the BA is 58.4220 Hz, 58.3395 Hz with PSO, and 58.2239 Hz with the FA, when tested with the proposed method in the IEEE 39-bus system.
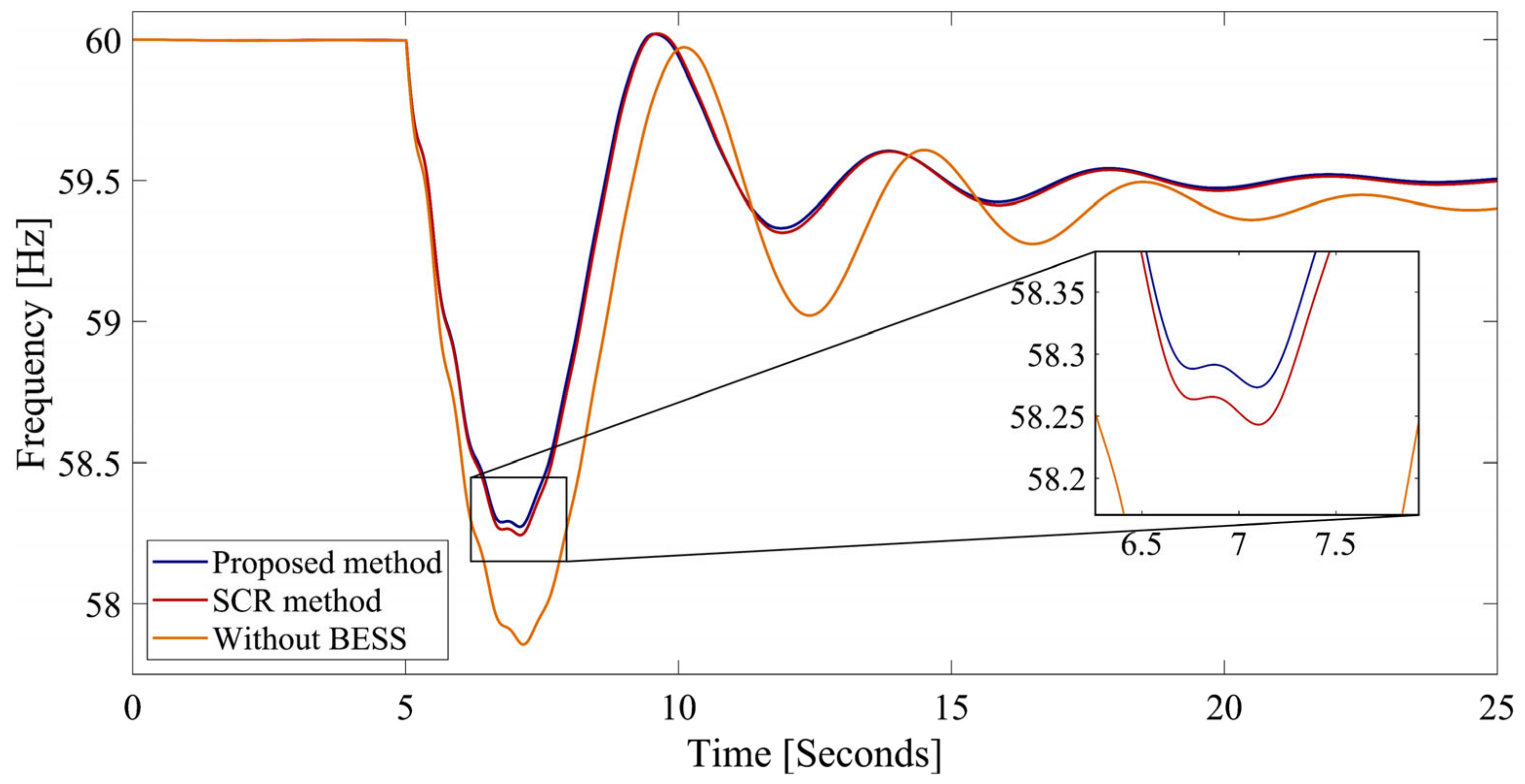
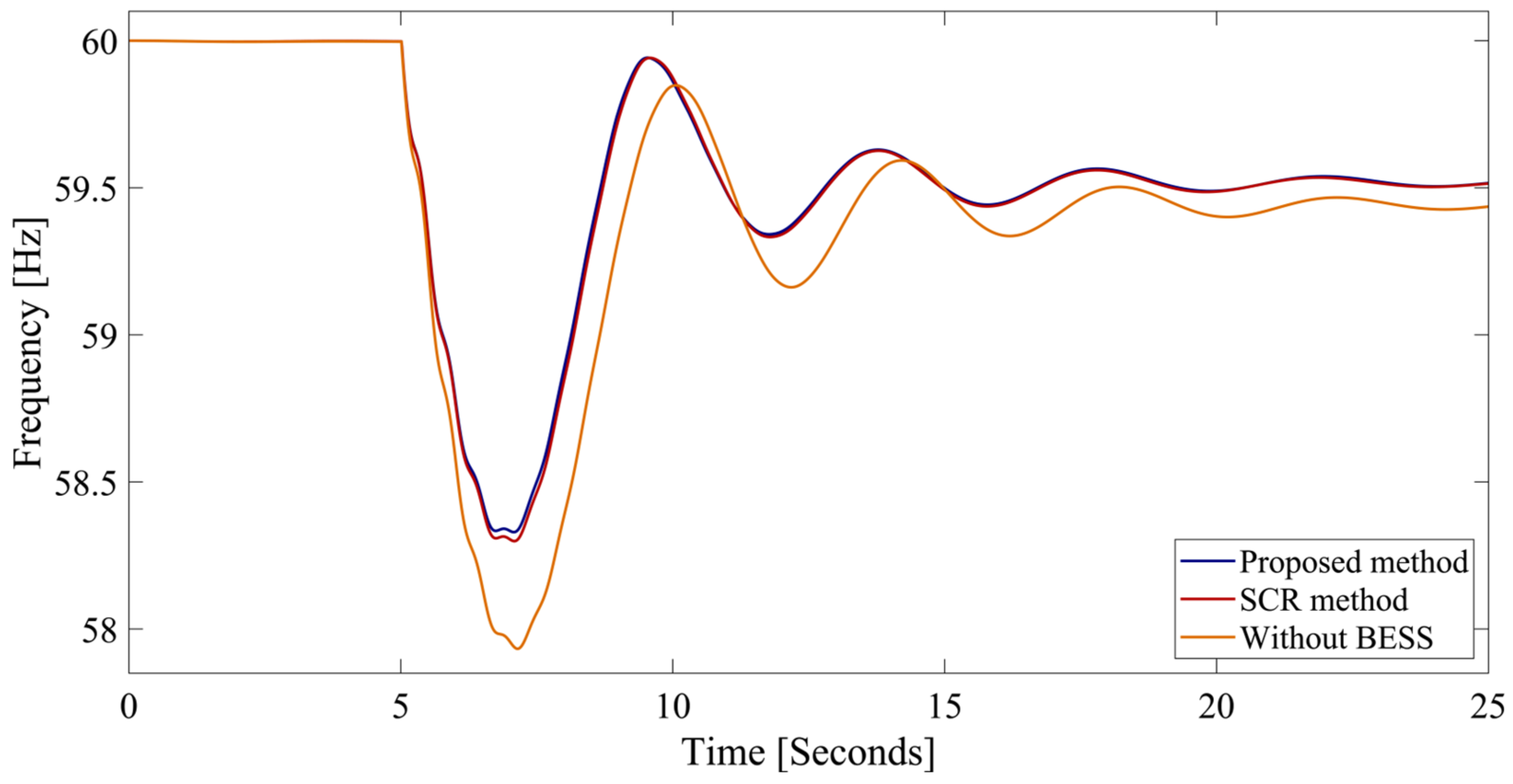
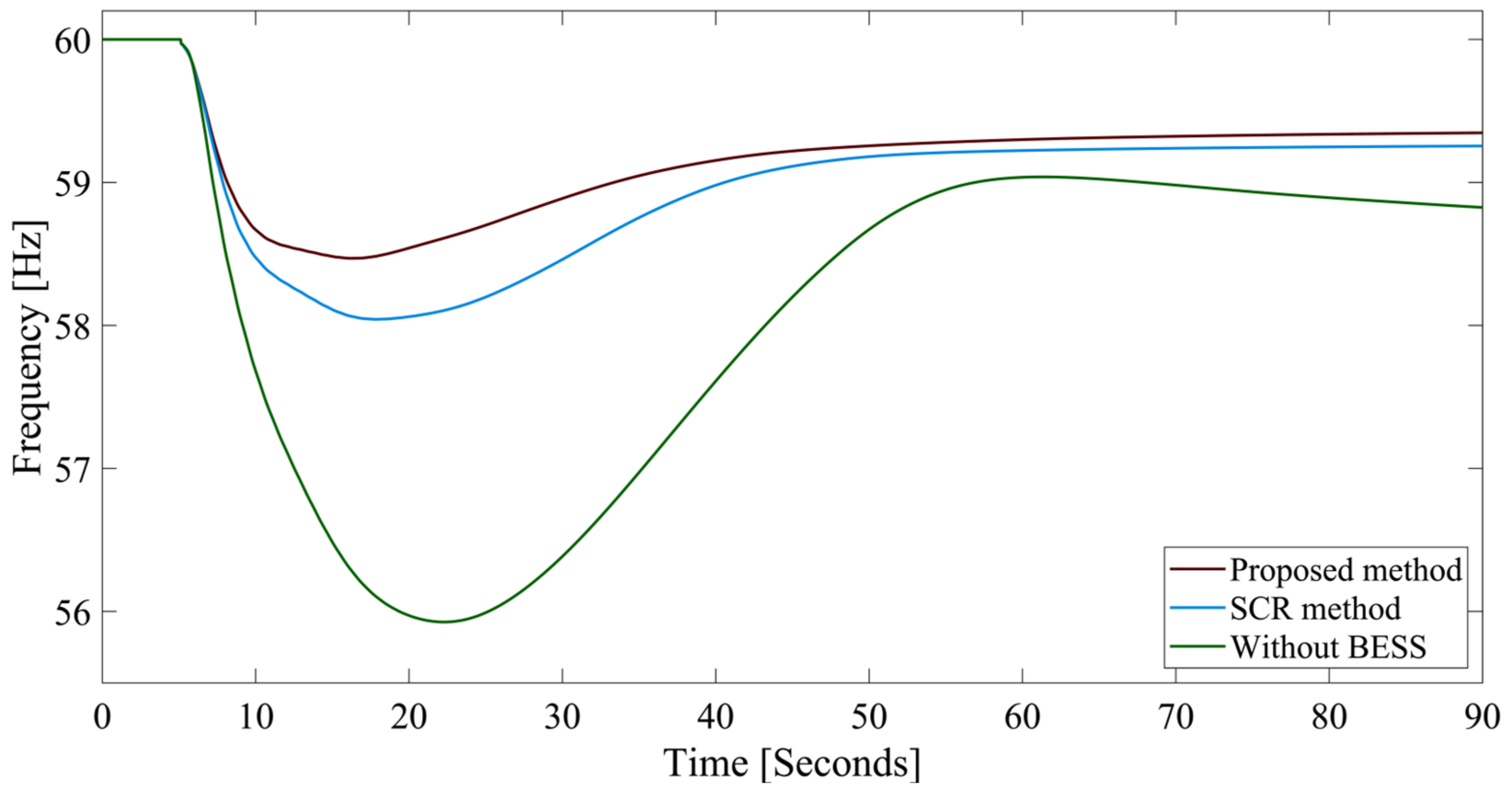
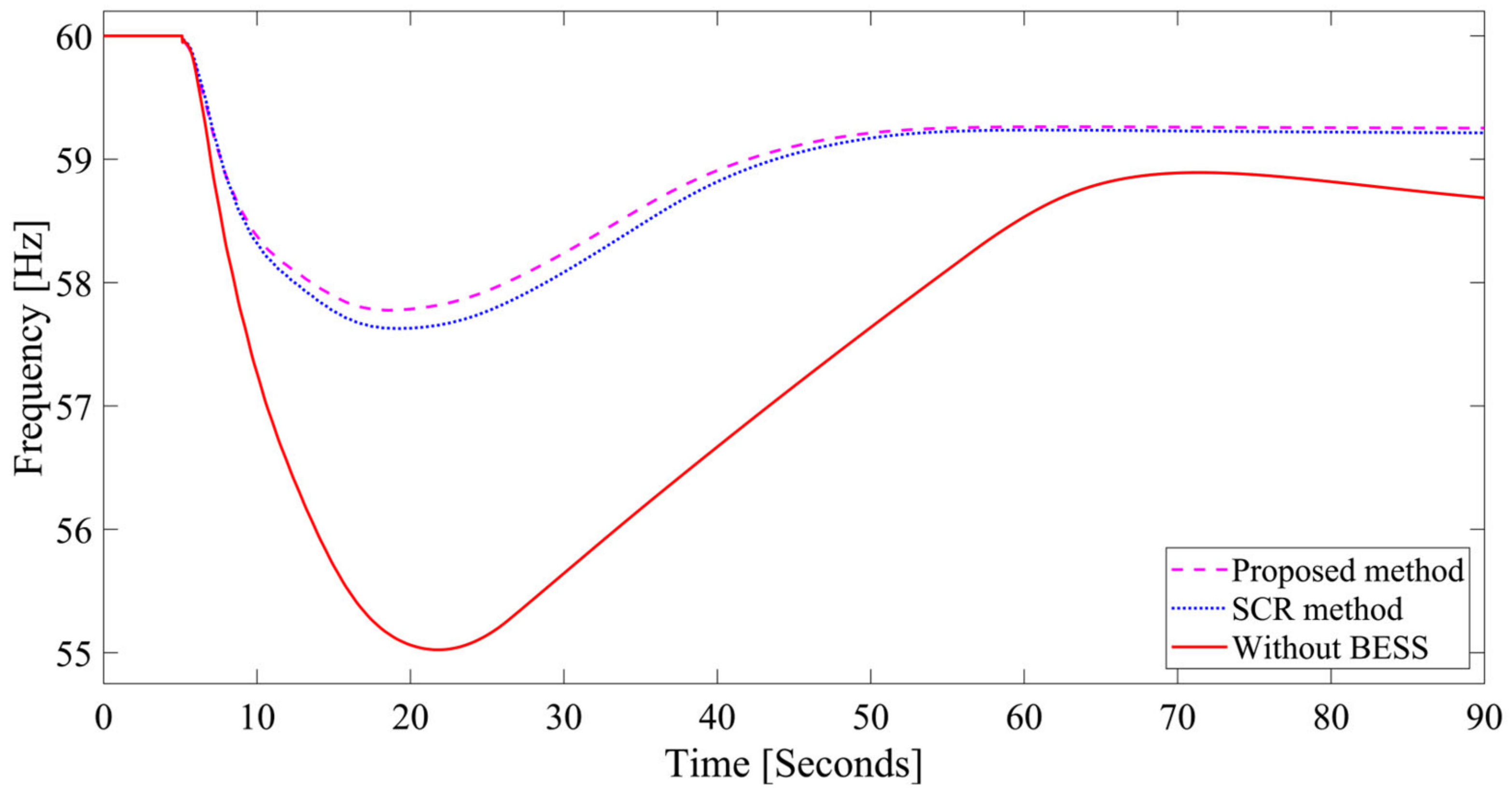
- The proposed method results in the value of 55.6914 Hz and the RoCoF value of 1.7855 Hz/s, which is better than the values of (55.6657 Hz) and RoCoF (1.7962 Hz) obtained using the compared method under outage of the largest generator in the IEEE 9-bus system.
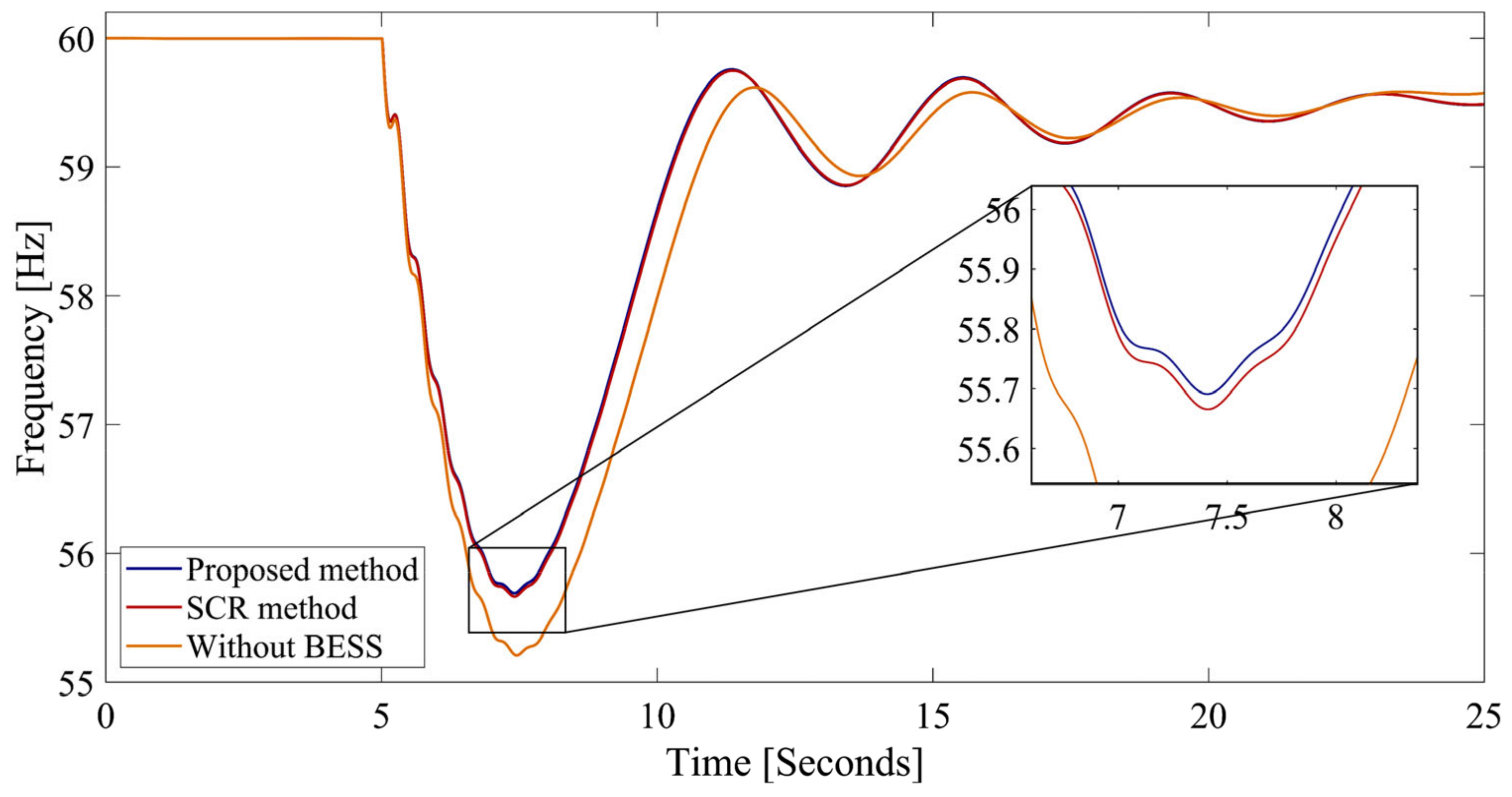
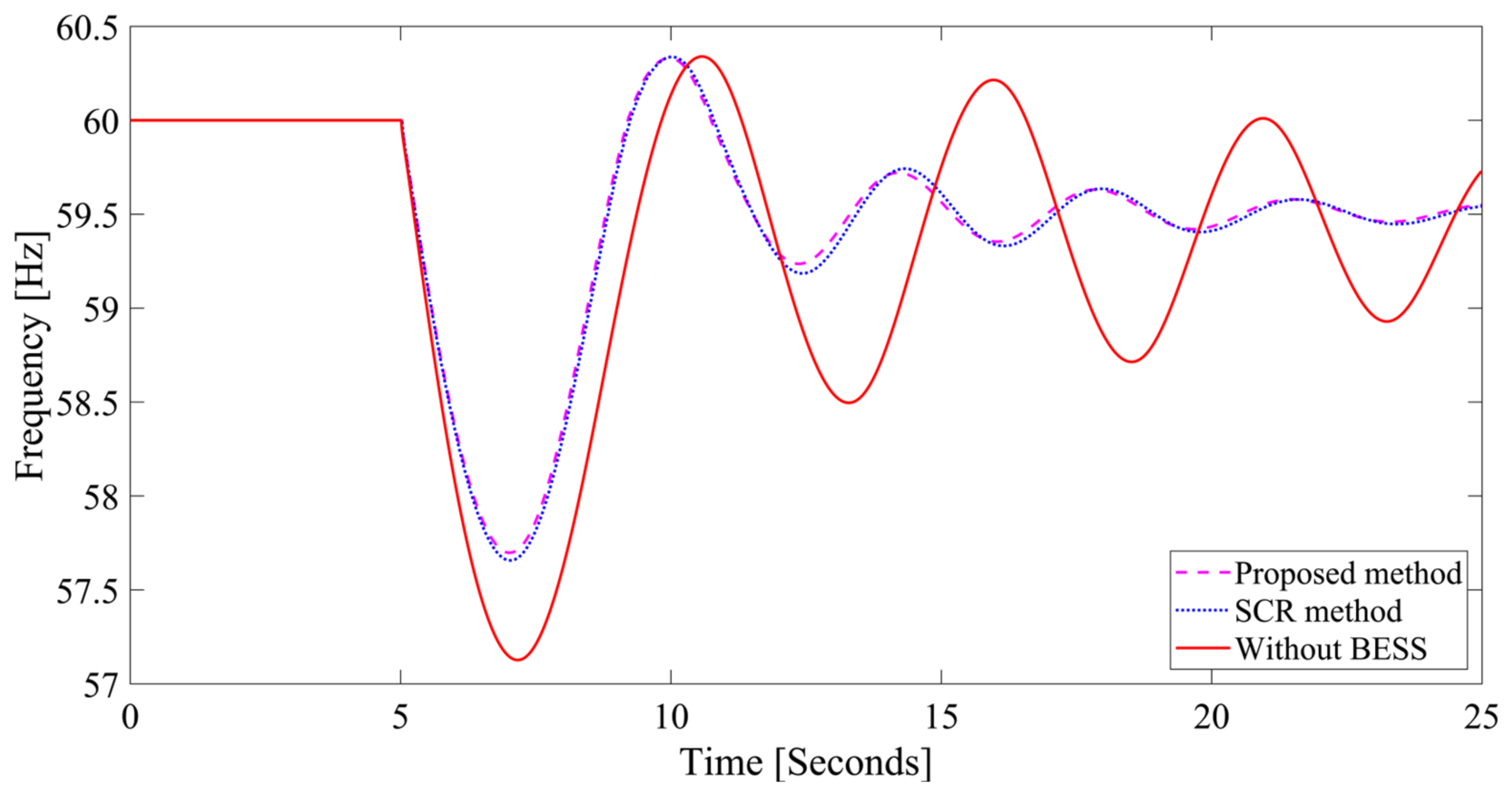
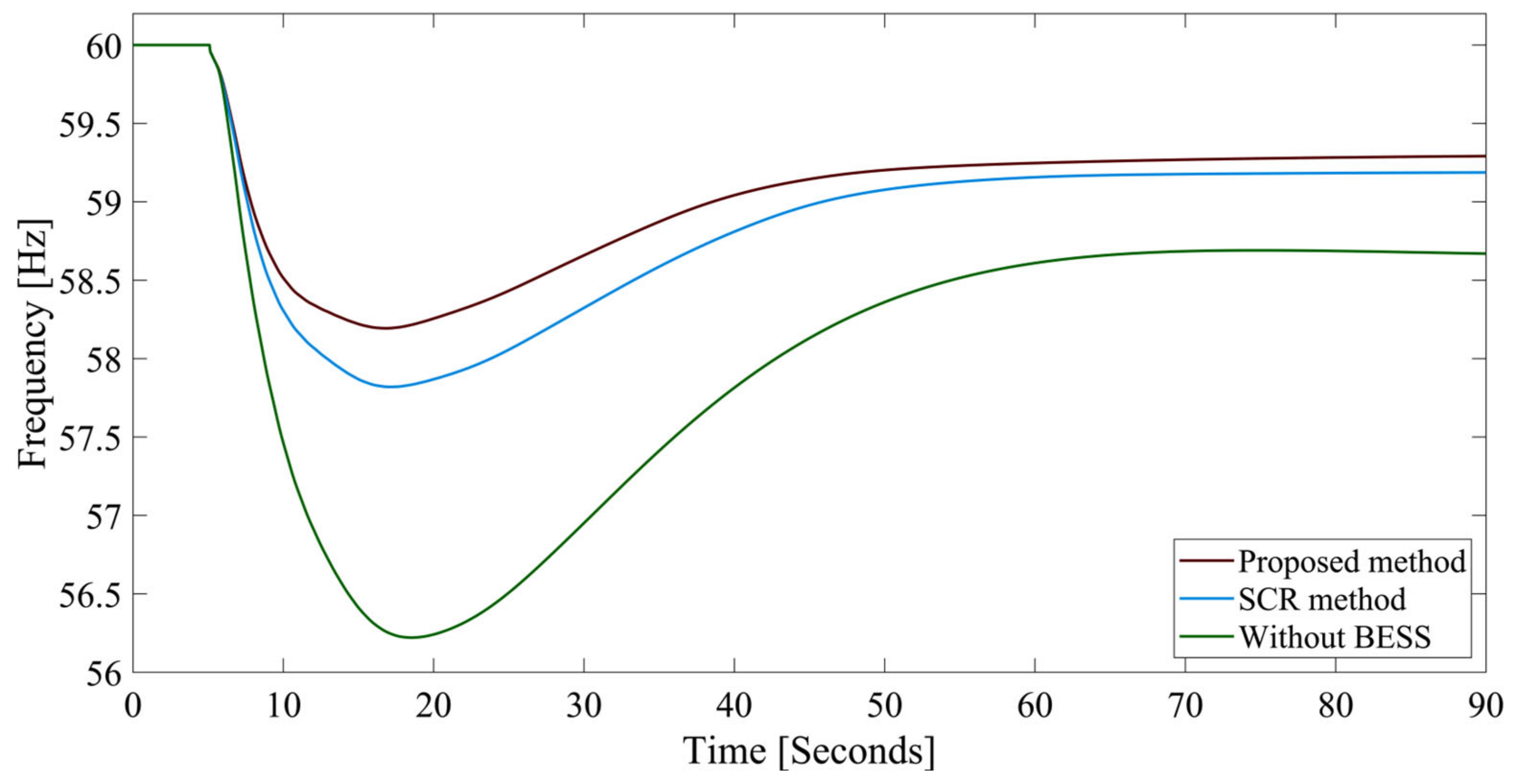
- The value of 55.9257 Hz and the value of 0.2365 Hz/s are observed when the largest generator, G 01, experiences an outage in the IEEE 39-bus system. Using the compared method, the and values are 58.0426 Hz and 0.1526 Hz/s, respectively. However, when the proposed method is applied, a better value of 58.4690 Hz and a better value of 0.1365 Hz/s are obtained.
- The proposed method demonstrated improved frequency stability indices under various scenarios, including variations in load conditions and the integration of wind turbine generation, as compared to other methods, when tested on both the IEEE 9-bus system and the IEEE 39-bus system.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| PV Controller | |||
| Parameters | Description | Units | Value |
| Tr | Filter time constant, active power | (s) | 0.01 |
| Trq | Filter time constant, reactive power | (s) | 0.1 |
| Kp | Proportional gain-id-PI control | (p.u.) | 2 |
| Tip | Integrator time constant—ip control | (s) | 0.2 |
| AC Deadband | Deadband for proportional gain | (p.u.) | 0 |
| Kq | Proportional gain-iq-PI control | (p.u.) | 1 |
| Tiq | Integrator time constant—iq control | (s) | 0.002 |
| id_min | Minimum discharging current | (p.u.) | −1 |
| iq_min | Minimum reactive current | (p.u.) | −1 |
| id_max | Maximum charging current | (p.u.) | 1 |
| iq_max | Maximum reactive current | (p.u.) | 1 |
| Battery Bank | |||
| Parameters | Description | Units | Value |
| Cbat | Battery capacity | MWh | 3 a, 50 b |
| SoCMin | Minimum state of charge | (%) | 0 |
| SoCMax | Maximum state of charge | (%) | 1 |
| SoCt−1 | Initial SoC | (%) | 87 a, 95 b |
| Frequency Controller | |||
| Parameters | Description | Units | Value |
| droop | Full active power within 1 Hz/2 Hz | 0.004 | |
| db | Deadband for frequency control | (p.u.) | 0.0004 |
| Particle Swarm Optimization Algorithm | |||
| Parameters | Description | Value | Range |
| n | Number of particles | 40 | |
| N_gen | Number of generations | 50 | |
| α | Learning factor | 0.2 | 0 ≤ α ≤ 2 |
| β | Learning factor | 0.5 | 0 < β < 2 |
| ω | Inertia weight | 0.5 | |
| Firefly Algorithm | |||
| Parameters | Description | Value | Range |
| n | Number of fireflies | 40 | |
| MaxGeneration | Number of pseudo time steps | 50 | |
| α | Randomness | 0.03 | 0 ≤ α ≤ 1 |
| γ | Absorption coefficient | 10 | |
| Bat Algorithm | |||
| Parameters | Description | Value | Range |
| n | Population size | 40 | 10 ≤ n ≤ 40 |
| N_gen | Number of generations | 50 | |
| A | Loudness | 0.1 | |
| r | Pulse rate | 0.9 | |
| Minimum emission frequency | 0 | ||
| Minimum emission frequency | 1 | ||
Appendix B
| Bus ID | Voltage Level (kV) | BESS Size (MW) |
|---|---|---|
| Bus 3 | 13.8 kV | 3.0 MW |
| Bus 4 | 230 kV | 3.0 MW |
| Bus 6 | 230 kV | 0.5 MW |
| Bus 7 | 230 kV | 3.0 MW |
| Bus 8 | 230 kV | 3.0 MW |
| Bus 9 | 230 kV | 3.0 MW |
| Bus ID | Voltage Level (kV) | BESS Size (MW) |
|---|---|---|
| Bus 02 | 345 kV | 50.0 MW |
| Bus 03 | 345 kV | 6.0 MW |
| Bus 19 | 345 kV | 47.0 MW |
| Bus 21 | 345 kV | 50.0 MW |
| Bus 24 | 345 kV | 50.0 MW |
| Bus 35 | 16.5 kV | 50.0 MW |
| Bus 37 | 16.5 kV | 50.0 MW |
References
- Kundur, P. Power System Stability and Control; McGraw-Hill, Inc.: New York, NY, USA, 2010. [Google Scholar]
- Hatziargyriou, N.; Milanovic, J.; Rahmann, C.; Ajjarapu, V.; Canizares, C.; Erlich, I.; Hill, D.; Hiskens, I.; Kamwa, I.; Pal, B.; et al. Definition and Classification of Power System Stability—Revisited & Extended. IEEE Trans. Power Syst. 2021, 36, 3271–3281. [Google Scholar] [CrossRef]
- Kebede, A.A.; Kalogiannis, T.; Van Mierlo, J.; Berecibar, M. A Comprehensive Review of Stationary Energy Storage Devices for Large Scale Renewable Energy Sources Grid Integration. Renew. Sustain. Energy Rev. 2022, 159, 112213. [Google Scholar] [CrossRef]
- Mitali, J.; Dhinakaran, S.; Mohamad, A.A. Energy Storage Systems: A Review. Energy Storage Sav. 2022, 1, 166–216. [Google Scholar] [CrossRef]
- Calero, F.; Cañizares, C.A.; Bhattacharya, K.; Anierobi, C.; Calero, I.; De Souza, M.F.Z.; Farrokhabadi, M.; Guzman, N.S.; Mendieta, W.; Peralta, D.; et al. A Review of Modeling and Applications of Energy Storage Systems in Power Grids. Proc. IEEE 2023, 111, 806–831. [Google Scholar] [CrossRef]
- Klyuev, R.; Bosikov, I.; Gavrina, O. Use of Wind Power Stations for Energy Supply to Consumers in Mountain Territories. In Proceedings of the 2019 International Ural Conference on Electrical Power Engineering (UralCon), Chelyabinsk, Russia, 1–3 October 2019; pp. 116–121. [Google Scholar]
- Facchini, L. The Numerical Simulation of Gaussian Cross-Correlated Wind Velocity Fluctuations by Means of a Hybrid Model. J. Wind Eng. Ind. Aerodyn. 1996, 64, 187–202. [Google Scholar] [CrossRef]
- Ilyushin, P.V.; Shepovalova, O.V.; Filippov, S.P.; Nekrasov, A.A. The Effect of Complex Load on the Reliable Operation of Solar Photovoltaic and Wind Power Stations Integrated into Energy Systems and into Off-Grid Energy Areas. Energy Rep. 2022, 8, 1515–1529. [Google Scholar] [CrossRef]
- Adrees, A.; Milanovic, J.V. Study of Frequency Response in Power System with Renewable Generation and Energy Storage. In Proceedings of the 2016 Power Systems Computation Conference (PSCC), Genoa, Italy, 20–24 June 2016; pp. 1–7. [Google Scholar]
- Silva-Saravia, H.; Pulgar-Painemal, H.; Mauricio, J.M. Flywheel Energy Storage Model, Control and Location for Improving Stability: The Chilean Case. IEEE Trans. Power Syst. 2017, 32, 3111–3119. [Google Scholar] [CrossRef]
- Poolla, B.K.; Bolognani, S.; Dorfler, F. Optimal Placement of Virtual Inertia in Power Grids. IEEE Trans. Automat. Contr. 2017, 62, 6209–6220. [Google Scholar] [CrossRef]
- Ramírez, M.; Castellanos, R.; Calderón, G.; Malik, O. Placement and Sizing of Battery Energy Storage for Primary Frequency Control in an Isolated Section of the Mexican Power System. Electr. Power Syst. Res. 2018, 160, 142–150. [Google Scholar] [CrossRef]
- Adrees, A.; Milanović, J. Effect of Load Models on Angular and Frequency Stability of Low Inertia Power Networks. IET Gener. Transm. Distrib. 2019, 13, 1520–1526. [Google Scholar] [CrossRef]
- Conte, F.; Massucco, S.; Paolone, M.; Schiapparelli, G.P.; Silvestro, F.; Zuo, Y. Frequency Stability Assessment of Modern Power Systems: Models Definition and Parameters Identification. Sustain. Energy Grids Netw. 2020, 23, 100384. [Google Scholar] [CrossRef]
- Tsany, F.N.; Widayat, A.A.; Aryani, D.R.; Jufri, F.H.; Ardita, I.M. Power System Stability Improvement Using Battery Energy Storage System (BESS) in Isolated Grid. IOP Conf. Ser. Earth Environ. Sci. 2020, 599, 012025. [Google Scholar] [CrossRef]
- Das, C.K.; Mahmoud, T.S.; Bass, O.; Muyeen, S.M.; Kothapalli, G.; Baniasadi, A.; Mousavi, N. Optimal Sizing of a Utility-Scale Energy Storage System in Transmission Networks to Improve Frequency Response. J. Energy Storage 2020, 29, 101315. [Google Scholar] [CrossRef]
- El-Bidairi, K.S.; Nguyen, H.D.; Mahmoud, T.S.; Jayasinghe, S.D.G.; Guerrero, J.M. Optimal Sizing of Battery Energy Storage Systems for Dynamic Frequency Control in an Islanded Microgrid: A Case Study of Flinders Island, Australia. Energy 2020, 195, 117059. [Google Scholar] [CrossRef]
- Ben Yosef, G.; Navon, A.; Poliak, O.; Etzion, N.; Gal, N.; Belikov, J.; Levron, Y. Frequency Stability of the Israeli Power Grid with High Penetration of Renewable Sources and Energy Storage Systems. Energy Rep. 2021, 7, 6148–6161. [Google Scholar] [CrossRef]
- Cao, Y.; Wu, Q.; Zhang, H.; Li, C. Optimal Sizing of Hybrid Energy Storage System Considering Power Smoothing and Transient Frequency Regulation. Int. J. Electr. Power Energy Syst. 2022, 142, 108227. [Google Scholar] [CrossRef]
- Alsharif, H.; Jalili, M.; Hasan, K.N. A Frequency Stability Analysis for BESS Placement Considering the Loads and Wind Farms Locations. In Proceedings of the 2022 IEEE PES 14th Asia-Pacific Power and Energy Engineering Conference (APPEEC), Melbourne, Australia, 20 November 2022; pp. 1–5. [Google Scholar]
- Akram, U.; Mithulananthan, N.; Shah, R.; Alzahrani, S. Design of Energy Storage for Frequency Stability in Low-Inertia Power Grid. IEEE Syst. J. 2023, 17, 4763–4774. [Google Scholar] [CrossRef]
- Ramos, A.F.; Ahmad, I.; Habibi, D.; Mahmoud, T.S. Placement and Sizing of Utility-Size Battery Energy Storage Systems to Improve the Stability of Weak Grids. Int. J. Electr. Power Energy Syst. 2023, 144, 108427. [Google Scholar] [CrossRef]
- Hosseini, S.A.; Toulabi, M.; Ashouri-Zadeh, A.; Ranjbar, A.M. Battery Energy Storage Systems and Demand Response Applied to Power System Frequency Control. Int. J. Electr. Power Energy Syst. 2022, 136, 107680. [Google Scholar] [CrossRef]
- Nassef, A.M.; Abdelkareem, M.A.; Maghrabie, H.M.; Baroutaji, A. Review of Metaheuristic Optimization Algorithms for Power Systems Problems. Sustainability 2023, 15, 9434. [Google Scholar] [CrossRef]
- Teng, F.; Strbac, G. Assessment of the Role and Value of Frequency Response Support from Wind Plants. IEEE Trans. Sustain. Energy 2016, 7, 586–595. [Google Scholar] [CrossRef]
- Adrees, A.; Milanović, J.V.; Mancarella, P. Effect of Inertia Heterogeneity on Frequency Dynamics of Low-inertia Power Systems. IET Gener. Transm. Distrib. 2019, 13, 2951–2958. [Google Scholar] [CrossRef]
- DIgSILENT PowerFactory Manual. Battery Energy Storing System Template. Application Guide. 2013. Available online: https://www.digsilent.de/en/ (accessed on 3 August 2023).
- Datta, U.; Kalam, A.; Shi, J. Battery Energy Storage System for Transient Frequency Stability Enhancement of a Large-Scale Power System. In Proceedings of the 2017 Australasian Universities Power Engineering Conference (AUPEC), Melbourne, VIC, Australia, 19–22 November 2017; pp. 1–5. [Google Scholar]
- Javadi, M.; Gong, Y.; Chung, C.Y. Frequency Stability Constrained BESS Sizing Model for Microgrids. IEEE Trans. Power Syst. 2023, 39, 1–13. [Google Scholar] [CrossRef]
- Yang, X. Engineering Optimization: An Introduction with Metaheuristic Applications, 1st ed.; Wiley: Hoboken, NJ, USA, 2010; ISBN 978-0-470-58246-6. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. A Discrete Binary Version of the Particle Swarm Algorithm. In Proceedings of the 1997 IEEE International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation, Orlando, FL, USA, 12–15 October 1997; Volume 5, pp. 4104–4108. [Google Scholar]
- Zhang, L.; Shan, L.; Wang, J. Optimal Feature Selection Using Distance-Based Discrete Firefly Algorithm with Mutual Information Criterion. Neural Comput. Applic. 2017, 28, 2795–2808. [Google Scholar] [CrossRef]
- Yang, X.-S. A New Metaheuristic Bat-Inspired Algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); González, J.R., Pelta, D.A., Cruz, C., Terrazas, G., Krasnogor, N., Eds.; Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2010; Volume 284, pp. 65–74. ISBN 978-3-642-12537-9. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Yang, X.-S. Binary Bat Algorithm. Neural Comput. Applic. 2014, 25, 663–681. [Google Scholar] [CrossRef]
- Illinois Center for a Smarter Electric Grid (ICSEG). Literature-Based Power Flow Test Cases; Illinois Center for a Smarter Electric Grid (ICSEG): Urbana, IL, USA, 2023. [Google Scholar]
- Gonzalez-Longatt, F.M.; Luis Rueda, J. (Eds.) PowerFactory Applications for Power System Analysis; Power Systems; Springer International Publishing: Cham, Switzerland, 2014; ISBN 978-3-319-12957-0. [Google Scholar]


| Refs. | BESSs | Method | Remarks | |
|---|---|---|---|---|
| Size | Location | |||
| [9,18,20] | √ | √ | Random | Unoptimized |
| [10] | √ | × | Eigenvalue | |
| [12,14] | √ | √ | Metaheuristics | Isolated microgrid |
| [16] | √ | × | One metaheuristic | Location obtained using sensitivity |
| [17] | √ | × | One metaheuristic | Isolated microgrid |
| [19] | √ | × | Mathematical optimization | |
| [21] | √ | √ | Iterative algorithm | Location based on linearization technique |
| [22] | √ | √ | One metaheuristic | Only weak buses are considered for placement |
| [23] | √ | √ | One metaheuristic | Simplified model, i.e., two-area model |
| Proposed method | √ | √ | Three metaheuristics | Detailed model, location, and sizing calculated using no linearization approximation |
| Performance Metrics | PSO | FA | BA |
|---|---|---|---|
| Mean | 58.2681 Hz | 58.1926 Hz | 58.2723 Hz |
| Median | 58.2772 Hz | 58.2038 Hz | 58.2760 Hz |
| Standard deviation | 0.0268 Hz | 0.0126 Hz | 0.0172 Hz |
| Average computation time | 40 min 52 s | 33 min 23 s | 23 min 24 s |
| Scenario | Outage of G3 | Outage of G2 | ||
|---|---|---|---|---|
| fnadir (Hz) | RoCoF (Hz/s) | fnadir (Hz) | RoCoF (Hz/s) | |
| Proposed method | 58.2732 | 0.8244 | 55.6914 | 1.7855 |
| SCR method | 58.2431 | 0.8347 | 55.6657 | 1.7962 |
| Without BESS | 57.8547 | 0.9909 | 55.2096 | 1.9526 |
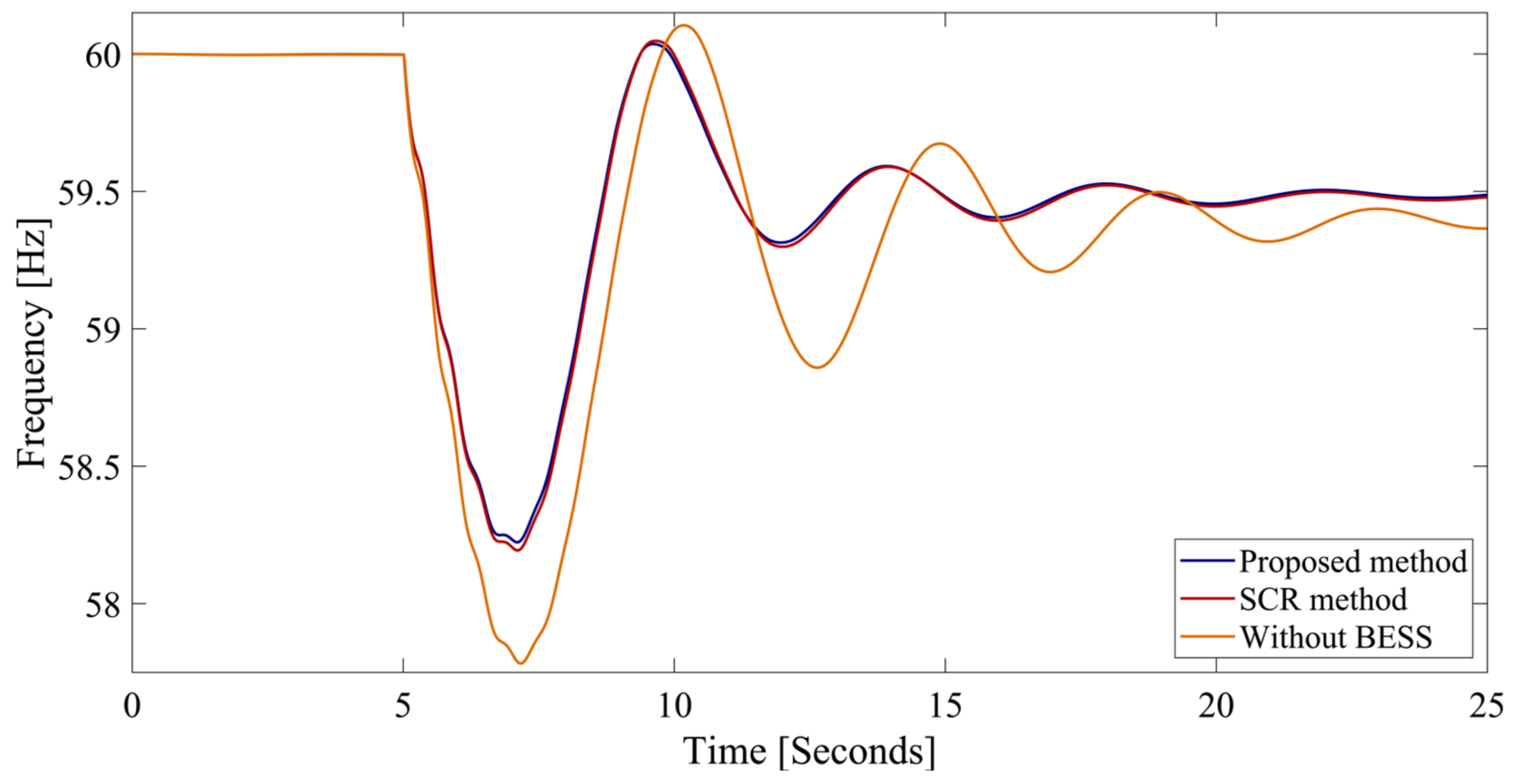
| Scenario | Decreased Load | Increased Load | RES Penetration | |||
|---|---|---|---|---|---|---|
| fnadir (Hz) | RoCoF (Hz/s) | fnadir (Hz) | RoCoF (Hz/s) | fnadir (Hz) | RoCoF (Hz/s) | |
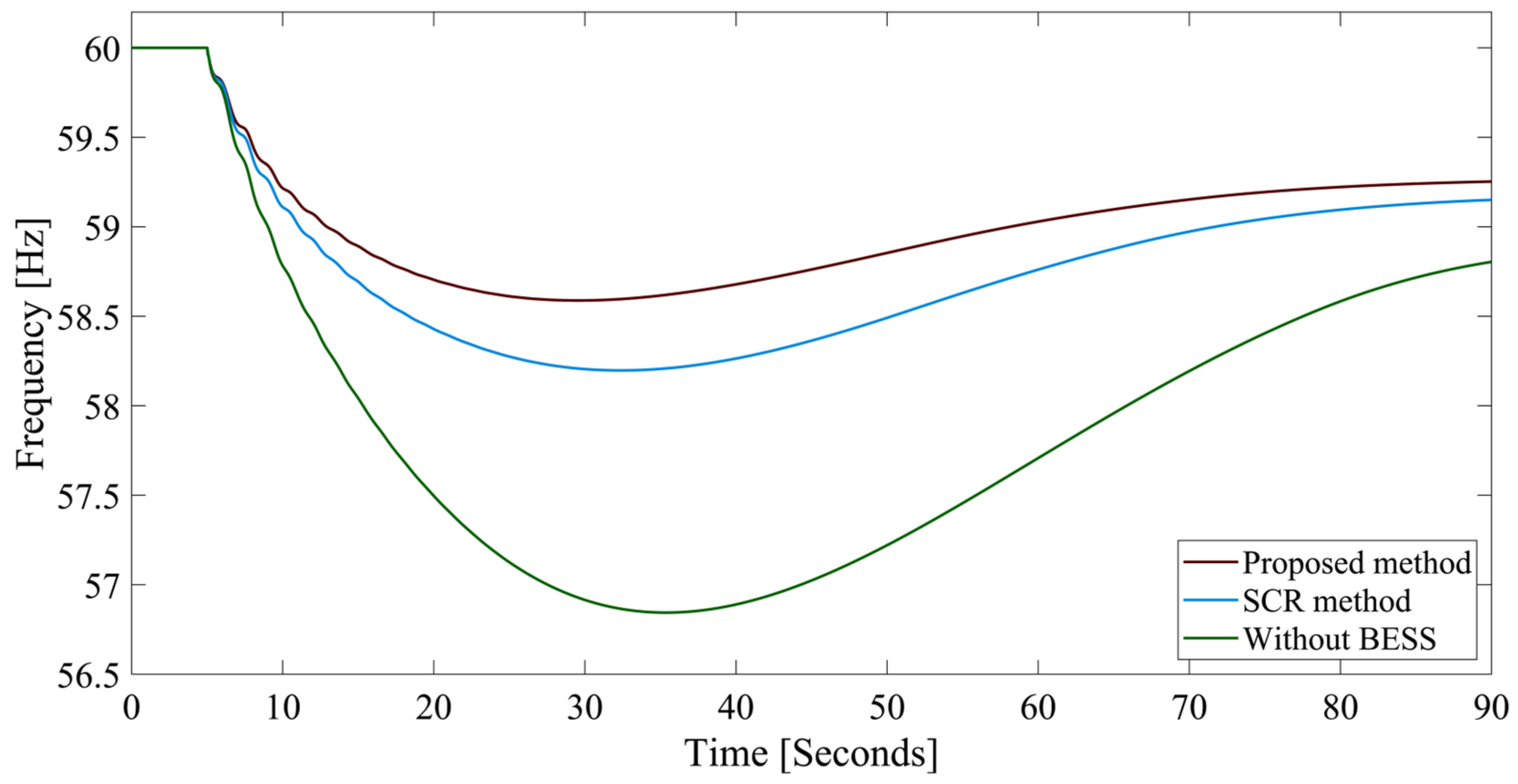
| Proposed method | 58.2233 | 0.8442 | 58.3293 | 0.8052 | 57.6977 | 1.1387 |
| SCR method | 58.1937 | 0.8542 | 58.2987 | 0.8121 | 57.6567 | 1.1476 |
| Without BESS | 57.7824 | 1.0196 | 57.9328 | 0.9592 | 57.1266 | 1.4007 |
| Performance Metrics | PSO | FA | BA |
|---|---|---|---|
| Mean | 58.3395 Hz | 58.2239 Hz | 58.4220 Hz |
| Median | 58.3682 Hz | 58.2250 Hz | 58.4380 Hz |
| Standard deviation | 0.1338 Hz | 0.0043 Hz | 0.0345 Hz |
| Average computation time | 1 h 14 min | 2 h 13 min | 1 h 33 min |
| Scenario | Outage of G 01 | Outage of G 09 | Outage of G 03 | |||
|---|---|---|---|---|---|---|
| fnadir (Hz) | RoCoF (Hz/s) | fnadir Hz) | RoCoF (Hz/s) | fnadir (Hz) | RoCoF (Hz/s) | |
| Proposed method | 58.4690 | 0.1365 | 58.5881 | 0.0576 | 59.2927 | 0.0401 |
| SCR method | 58.0426 | 0.1526 | 58.1974 | 0.0660 | 59.1060 | 0.0448 |
| Without BESS | 55.9257 | 0.2365 | 56.8440 | 0.1034 | 57.9580 | 0.0724 |
| Scenario | Decreased Load | Increased Load | RES Penetration | |||
|---|---|---|---|---|---|---|
| fnadir (Hz) | RoCoF (Hz/s) | fnadir (Hz) | RoCoF (Hz/s) | fnadir (Hz) | RoCoF (Hz/s) | |
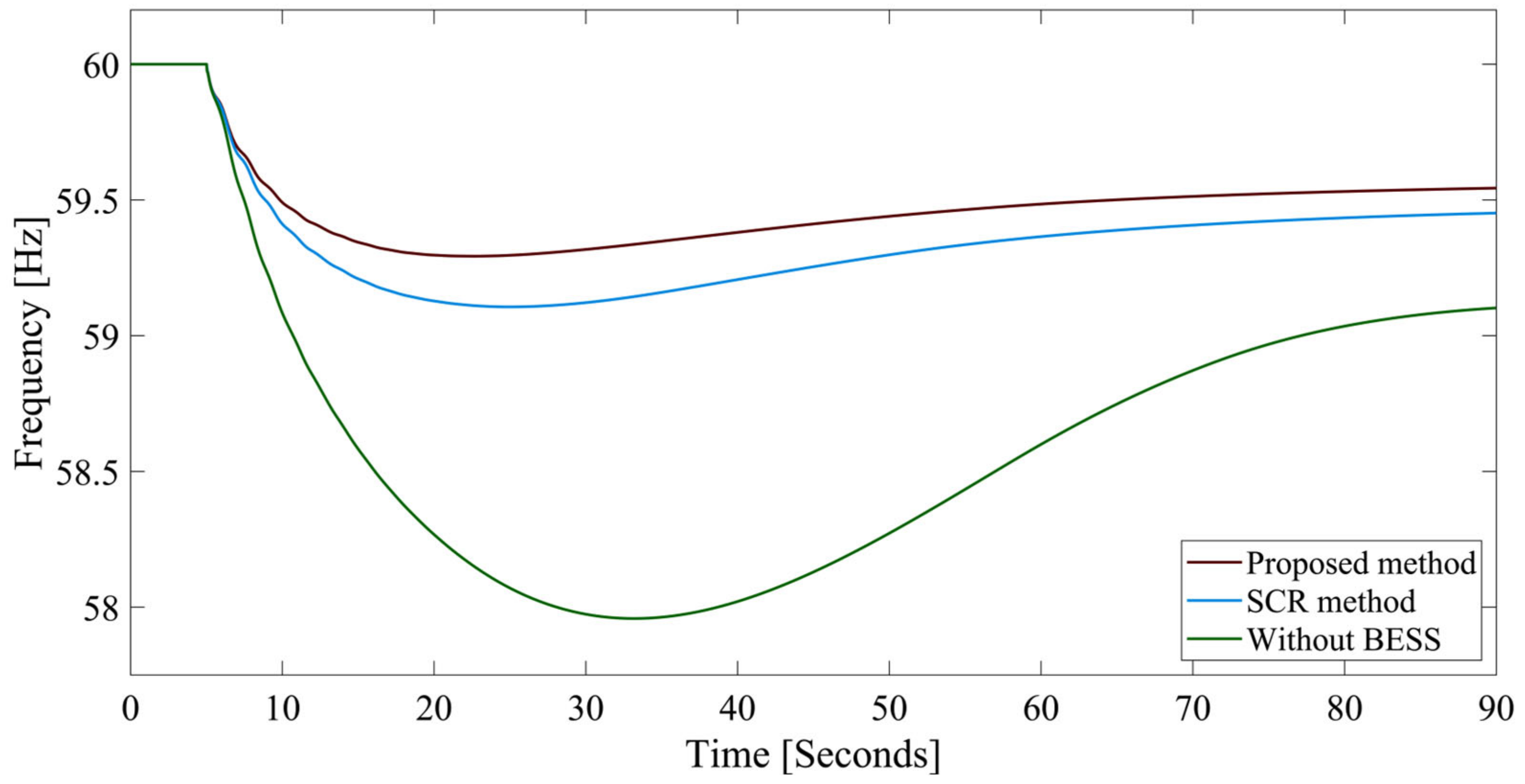
| Proposed method | 58.1935 | 0.1524 | 56.0335 | 0.2227 | 57.7762 | 0.1643 |
| SCR method | 57.8197 | 0.1809 | - | - | 57.6270 | 0.1677 |
| Without BESS | 56.2205 | 0.2795 | - | - | 55.0238 | 0.2974 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parajuli, A.; Gurung, S.; Chapagain, K. Optimal Placement and Sizing of Battery Energy Storage Systems for Improvement of System Frequency Stability. Electricity 2024, 5, 662-683. https://doi.org/10.3390/electricity5030033
Parajuli A, Gurung S, Chapagain K. Optimal Placement and Sizing of Battery Energy Storage Systems for Improvement of System Frequency Stability. Electricity. 2024; 5(3):662-683. https://doi.org/10.3390/electricity5030033
Chicago/Turabian StyleParajuli, Amrit, Samundra Gurung, and Kamal Chapagain. 2024. "Optimal Placement and Sizing of Battery Energy Storage Systems for Improvement of System Frequency Stability" Electricity 5, no. 3: 662-683. https://doi.org/10.3390/electricity5030033
APA StyleParajuli, A., Gurung, S., & Chapagain, K. (2024). Optimal Placement and Sizing of Battery Energy Storage Systems for Improvement of System Frequency Stability. Electricity, 5(3), 662-683. https://doi.org/10.3390/electricity5030033








