Standalone Operation of Inverter-Based Variable Speed Wind Turbines on DC Distribution Network

Abstract

This paper discusses the operation and control of a low-voltage DC (LVDC) isolated distribution network powered by distributed generation (DG) from a variable-speed wind turbine induction generator (WTIG) to supply unbalanced AC loads. The system incorporates a DC-DC storage converter to regulate network voltages and interconnect battery energy storage with the DC network. The wind turbines are equipped with a squirrel cage induction generator (IG) to connect a DC network via individual power inverters (WTIG inverters). Loads are unbalanced ACs and are interfaced using transformerless power inverters, referred to as load inverters. The DC-DC converter is equipped with a novel control strategy, utilizing a droop regulator for the DC voltage to stabilize network operation. The control system is modeled based on Clark and Park transformations and is developed for the load inverters to provide balanced AC voltage despite unbalanced load conditions. The system employs the perturbation and observation (P&O) method for maximum power point tracking (MPPT) to optimize wind energy utilization, while blade angle controllers maintain generator performance within rated power and speed limits under high wind conditions. System operation is analyzed under two scenarios: normal operation with varying wind speeds and the effects of load variations. Simulation results using PSCAD/EMTDC demonstrate that the proposed LVDC isolated distribution network (DC) achieves a stable DC bus voltage within ±5% of the nominal value, efficiently delivers balanced AC voltages with unbalanced levels below 2%, and operates with over 90% wind energy utilization during varying wind speeds, confirming LVDC network reliability and robustness.

1. Introduction

The growing adoption of renewable energy resources necessitates the development of advanced network architectures for efficient and reliable power distribution [1]. Low-voltage direct current (LVDC) systems have gained significant attention due to their ability to integrate distributed generation (DG) resources, such as wind turbines, and enhance power quality and system flexibility [2]. Multi-terminal LVDC isolated networks provide a promising solution for off-grid or remote locations where conventional AC grid access is unavailable or economically infeasible [3]. Renewable energy resources are used more where grid access is either unavailable or economically unfeasible [4]. Wind energy has experienced rapid global expansion with an annual expansion rate exceeding 30%, and using variable-speed wind turbines attracts considerable interest in the energy sector, as they increase power generation and reduce noise levels [5].

Several prior studies have explored various methodologies for LVDC network stability and power quality enhancement. For instance, adaptive fuzzy controllers for variable-speed wind turbines have been proposed to improve power regulation. However, these methods demand high computational resources, limiting their real-time applicability [6]. Other works introduce centralized optimal control strategies for DC voltage regulation, but they often rely on communication-dependent coordination, which reduces system resilience in isolated networks [7]. Bi-level robust scheduling techniques have also been studied for DC system security, yet these models primarily focus on frequency stability rather than voltage control under unbalanced loads [4]. To achieve maximum power tracking, ref. [6] proposes a duty cycle control and look-up table approach, which rely on the turbine operational characteristics relying on the turbine operational characteristics during or prior to execution. In a standalone wind turbine induction generator (WTIG), generated power directly supplies connected loads. Due to the fluctuating nature of wind speed, battery storage systems are often included in isolated WTIG to address discrepancies between load demand and power generation [7]. When wind power exceeds load demand, surplus energy charges the battery, while in situations where demand surpasses available wind power, the battery compensates for the load demand by supplying the additional energy [4]. A key challenge arises when the battery reaches full capacity, and excess power continues to be generated [8]. To address the challenge, the combined operation of standalone WTIG within a star-configured DC isolated distribution network is proposed, offering improved power quality, cost-effective scalability, and easier maintenance compared to AC distribution systems [9].

Reference [10] proposes an adaptive fuzzy controller for a wind turbine with variable pitch and speed. This method enhances the main controller by incorporating independent control strategies for each operational region, regardless of wind speed. Since this approach is independent of wind speed, it reduces the cost and computational burden of wind turbine control while enhancing power generation. Reference [11] introduces a voltage regulation approach that integrates centralized optimal control with adaptive droop control for droop-controlled DC distribution networks. This method employs bus injection power measurements to optimize the operational reference power of voltage source converters, thereby improving the voltage profile and equalizing the power loading rates among converters. Reference [12] proposes a bi-level robust scheduling strategy aimed at enhancing the security of DC systems by mitigating voltage fluctuations. This method optimizes the voltage source converter to adjust the reference voltage level dynamically. However, these methods focus on either voltage stability or frequency regulation, rather than addressing both simultaneously for comprehensive network stabilization. Reference [13] proposes a model predictive approach to control DC systems. This model detaches the power input to various frequency components and then shortens the high-frequency components. To effectively integrate inverter-based Distributed Energy Resources (DERs), challenges such as reduced system inertia and grid instability must be addressed. This necessitates the implementation of advanced control strategies, including droop control and virtual impedance, to maintain system stability. Inverter-based networks employ various techniques, such as hierarchical load frequency control, low-voltage ride-through (LVRT), and virtual impedance (VI), to enhance grid reliability under dynamic operating conditions [14]. In standalone wind energy systems, energy storage plays a crucial role in balancing power fluctuations and ensuring reliable operation. Battery-assisted inverters, such as quasi-Z source inverters (qZSIs), offer enhanced stability by mitigating wind power oscillations and maintaining a stable power supply [15]. To ensure stable operation, DGs must be designed with appropriate control parameters and system configurations. Mathematical modeling and dynamic analysis are essential in optimizing system design, enabling robust DG performance under varying grid conditions [16]. To achieve maximum power tracking, various control algorithms have been proposed for wind energy conversion systems (WECS). By regulating the supplied voltage frequencies to both stator and rotor terminals, DI-WRIG can operate in super-synchronous mode, enhancing power extraction efficiency under varying wind conditions [17].

While these approaches contribute to LVDC network development, they exhibit several drawbacks:

• Limited adaptability to load variations, particularly in networks supplying unbalanced AC loads.
• Complex centralized control schemes that increase communication overhead and computational burden.
• Lack of a decentralized and scalable voltage regulation strategy for isolated LVDC networks.

To ensure stable power delivery to unbalanced AC loads, the network requires an autonomous load inverter capable of regulating both voltage and frequency. The main contributions of this paper are as follows:

This paper addresses the research gaps by proposing a novel decentralized control strategy for an isolated LVDC distribution network powered by variable-speed wind turbines (WTIGs). This approach utilizes the following:

• Implementation of a droop control strategy for DC voltage regulation in isolated networks.
• Standalone operation and control of inverter-based variable-speed wind turbines, ensuring stable and efficient integration into DC microgrids.
• Utilization of an isolated DC distribution network for wind turbine integration, accounting for wind power fluctuations.
• Efficient energy management and battery storage utilization, where the battery system plays a critical role in DC voltage regulation and dynamic response to load and generation variations.
• Introducing a novel network architecture that serves as a promising and innovative solution for future power grids, enhancing resilience, flexibility, and reliability in renewable energy integration.
• Coordinated control of WTIG and storage converters to ensure continuous power supply under varying wind and load conditions.
• Improvement of power quality through balanced AC voltage regulation despite unbalanced loads.

Unlike existing approaches, the proposed system enhances stability, improves resilience, and achieves high wind energy utilization efficiency (over 90%), making it well suited for off-grid renewable energy applications. This paper presents a control system that utilizes Clarke and Park transformations for efficient load converter management. The perturbation and observation (P&O) method achieves maximum power point tracking (MPPT) without requiring prior knowledge of turbine power curves. Simulation results validate the proposed system, demonstrating its capability for coordinated power sharing between the battery and WTIG. A key feature of this design is its capability to manage excess power through battery storage under varying operational conditions.

The rest of the paper is structured as follows: Section 2 outlines the configuration of the LVDC isolated network. Section 3 presents the modeling of DC-side dynamics, Section 4 details the control strategies for the power converters and inverters, and Section 5 discusses the results. The research is then concluded in Section 6.

2. Standalone Distribution System Configuration

The configuration of a standalone star DC distribution system incorporating a wind turbine induction generator (WTIG), unbalanced AC loads, and a battery bank is illustrated in Figure 1. This configuration is tailored for small-scale, off-grid distribution systems, facilitating efficient power transfer among WTIG, load demand, and energy storage [18]. The DC buses comprise a WTIG, an AC-DC converter (WTIG inverter), unbalanced AC loads, and a power inverter (load inverter). The loads are 300 m apart, while the battery bank is strategically located at DC bus 0 via a storage converter to minimize power losses and enhance overall system efficiency. The battery is dimensioned to effectively accommodate fluctuating load demands across the DC network under different operating conditions [19].

The WTIG operates in parallel with the unbalanced AC loads, connecting to the DC bus through a dedicated WTIG inverter. The AC unbalanced loads are linked to the DC bus through their respective load inverters. The power balance of the DC network is regulated using a DC-DC converter and voltage regulator, and voltage levels are maintained within acceptable limits. The implemented control strategy facilitates efficient load sharing between multiple WTIGs and the energy storage system, ensuring stable operation under diverse conditions.

Unbalanced Load Characteristics

AC loads connected to DC distribution networks through inverters may exhibit phase imbalances in real-world operation. These unbalanced conditions result from asymmetric power demand across phases, causing voltage fluctuations and increased system losses. To quantify the degree of imbalance, the percentage of phase current asymmetry ($X\%$) is defined as follows:

$$X\%={\displaystyle \frac{|I_{\max }-I_{\min }|}{I_{\mathrm{avg}}}}\times 100,$$

(1)

where $I_{\max }$ and $I_{\min }$ are the maximum and minimum phase currents, respectively, and $I_{\mathrm{avg}}$ is the average phase current. In this study, three different levels of unbalance are considered:

• Mild Unbalance (5–10%): Characterized by small phase deviations that minimally impact system performance.
• Moderate Unbalance (10–20%): Characterized by noticeable phase asymmetry, which degrades power quality.
• Severe Unbalance (20–30%): Characterized by significant current imbalance, causing voltage fluctuations.

The inverter control strategy compensates for these imbalances to ensure stable power delivery and voltage regulation.

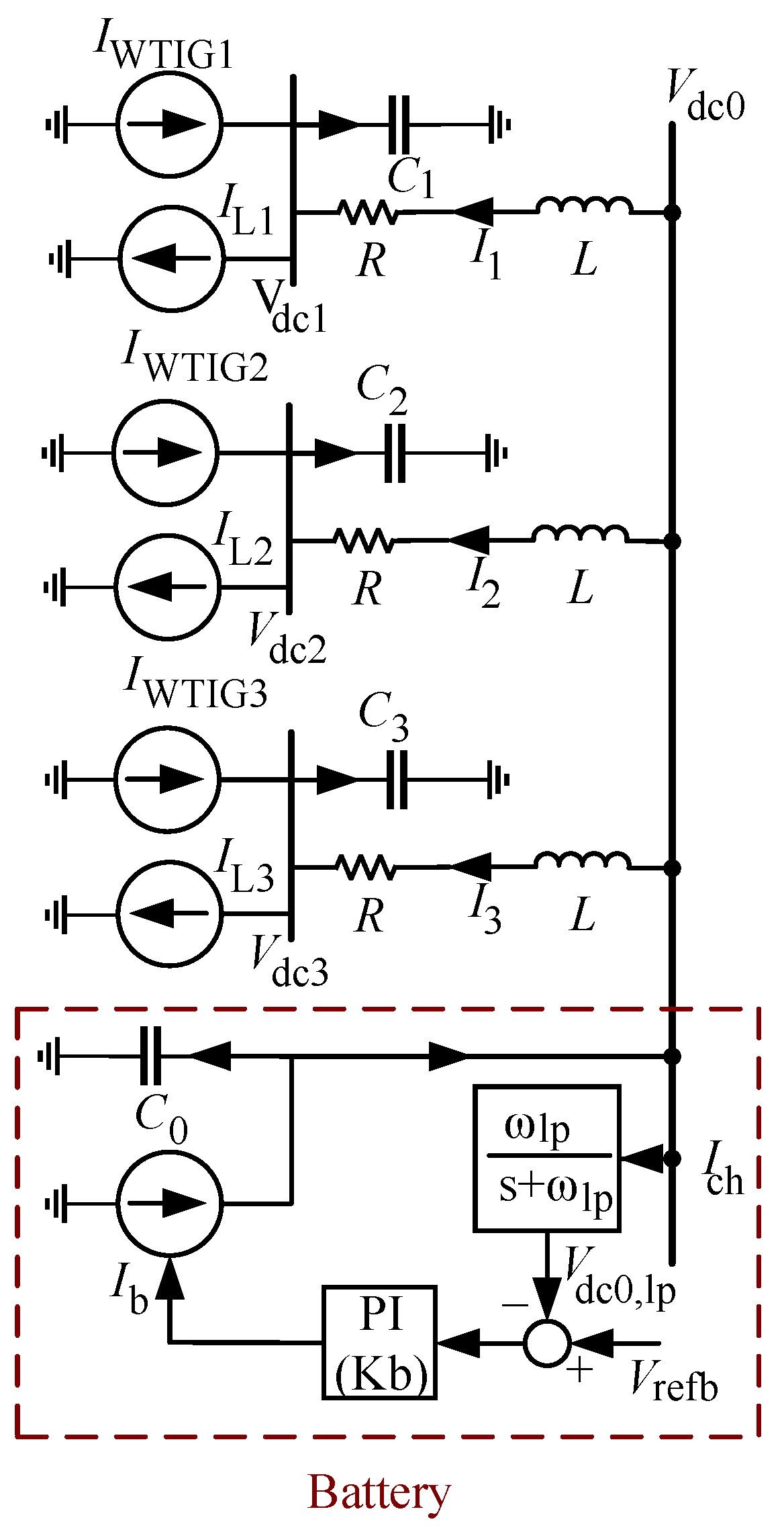
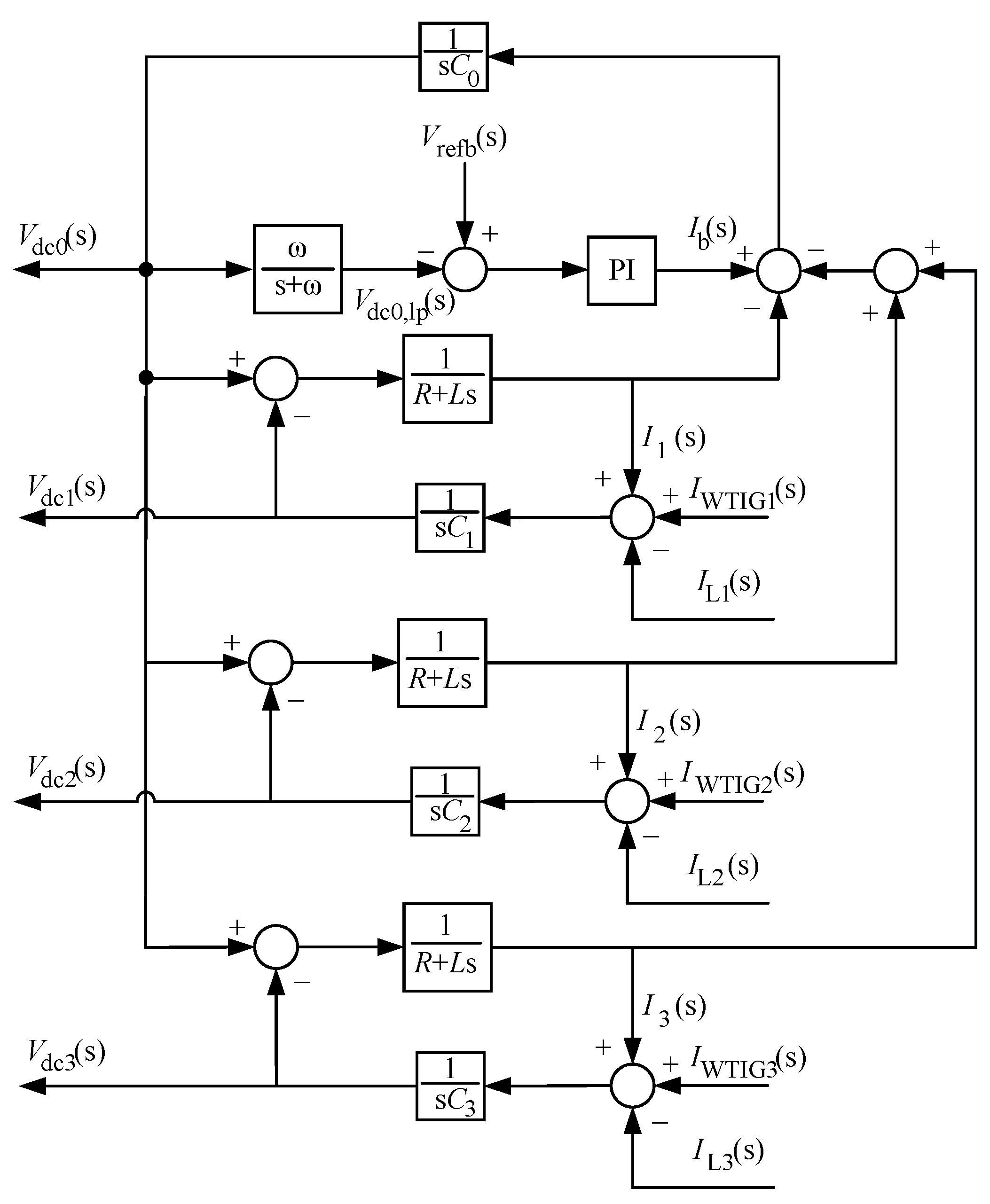
3. Modeling of DC Side Dynamic

The proposed system consists of multiple wind turbine induction generators (WTIGs), a battery energy storage system, and unbalanced AC loads connected through inverters, as shown in Figure 2. The DC-DC storage converter plays a key role in maintaining power balance within the LVDC distribution network. This section presents the mathematical modeling of the DC side, focusing on voltage regulation and power flow control. In this configuration, the DC-DC converter acts as a DC bus voltage-controlled current source, while the WTIG and load inverters operate under current-controlled mode. The storage converter control strategy utilizes a feedback loop mechanism that continuously monitors the DC bus voltage, $V_{dc0}$, and compares it to a predefined reference value. When the voltage of the DC bus drops, the storage system injects power into the DC network, with the WTIG supporting the load demand. Conversely, if the voltage exceeds the predefined threshold, the surplus energy in the network is redirected to recharge the battery storage system, thereby balancing the power flow. As shown in Figure 2, this control approach ensures system stability and maintains optimal voltage levels throughout the network. The battery storage system regulates the DC bus voltage using a droop control strategy. The relationship between the battery current, $I_b$, and the DC bus voltage deviation is given by the following:

$$\begin{array}{cc}\hfill & I_b\left(s\right)=K_b(V_{\mathrm{refb}}\left(s\right)-{\displaystyle \frac{\omega }{s+\omega }}{V}_{\mathrm{dc}0}\left(s\right)),\hfill \end{array}$$

(2)

where $K_b$ is the gain of the proportional-integral (PI) controller, $V_{\mathrm{ref},b}$ is the reference voltage, and $V_{\mathrm{dc},0}$ is the DC bus voltage. Here, $I_b$ represents the net battery current, which accounts for both charging and discharging states. The charging current $I_{ch}$ corresponds to the current flowing into the battery when storing excess power, while $I_{fb}$, represents the feedback current used in the droop control loop. The relationship between these currents is expressed as follows:

$$\begin{array}{cc}\hfill & I_b=I_{ch}-I_{fb}\hfill \end{array}$$

(3)

where $I_{ch}>$ 0 when the battery is charging, and $I_{fb}$ represents the regulated current fed back into the system for voltage stabilization. In (3), the term ${\displaystyle \frac{\omega }{s+\omega }}$ functions as a low-pass filter (LPF) that smooths voltage fluctuations. The power balance equation at the DC bus considers the total current contributions from the WTIG and load inverters. Thus, the total current injected into the DC bus is expressed as follows:

$$\begin{array}{cc}\hfill & I_b\left(s\right)=C_{0}s{V}_{\mathrm{dc}0}\left(s\right)+{\displaystyle \frac{V_{\mathrm{dc}0}\left(s\right)-V_{\mathrm{dc}1}\left(s\right)}{R+Ls}}+{\displaystyle \frac{V_{\mathrm{dc}0}\left(s\right)-V_{\mathrm{dc}2}\left(s\right)}{R+Ls}}+{\displaystyle \frac{V_{\mathrm{dc}0}\left(s\right)-V_{\mathrm{dc}3}\left(s\right)}{R+Ls}},\hfill \end{array}$$

(4)

Here, $C_0$ represents the equivalent capacitance of the DC bus, R and L denote the line resistance and inductance, respectively, and $V_{\mathrm{dc}1}$, $V_{\mathrm{dc}2}$, and $V_{\mathrm{dc}3}$ are the voltages of the connected buses. The DC network current distribution depends on the WTIG inverters ($I_{\mathrm{WTIG}i}$) and load inverters ($I_{L_i}$). The sum of generated and consumed currents is given by the following:

$$\begin{array}{cc}\hfill & I_{WTIG1}\left(s\right)+I_{WTIG2}\left(s\right)+I_{WTIG3}\left(s\right)-I_{L1}\left(s\right)-I_{L2}\left(s\right)-I_{L3}\left(s\right)=C_{1}s{V}_{dc1}\left(s\right)+C_{2}s{V}_{dc2}\left(s\right)+\hfill \\ \hfill & C_{3}s{V}_{dc3}\left(s\right)+{\displaystyle \frac{V_{dc1}\left(s\right)-V_{dc0}\left(s\right)}{R+Ls}}+{\displaystyle \frac{V_{dc2}\left(s\right)-V_{dc0}\left(s\right)}{R+L_s}}+{\displaystyle \frac{V_{dc3}\left(s\right)-V_{dc0}\left(s\right)}{R+Ls}}.\hfill \end{array}$$

(5)

In (5), the left-hand side represents the net current injected into the DC bus, while the right-hand side describes the DC bus voltage dynamics. The equation is verified for sign consistency with the current directions shown in Figure 2.

In the system model, several parameters define the performance and control of the DC-isolated distribution network. $I_b$ represents the output current of the battery storage system, $V_{refb}$ is the reference voltage, and $K_b$ is the gain of the PI controller for the storage converter. A low-pass filter (LPF) is used to reduce voltage ripple and enhance the stability of the controller by optimizing the pole placement [20]. The cutoff frequency of the LPF is a critical parameter that influences the filtering process. The output currents of the WTIG inverters are represented by $I_{WTIG1}$, $I_{WTIG2}$, and $I_{WTIG3}$, corresponding to inverter 1, inverter 2, and inverter 3, respectively. Similarly, the output currents of the load inverters are given by $I_{L1}$, $I_{L2}$, and $I_{L3}$, corresponding to load inverters 1, 2, and 3, respectively. The DC bus voltages are labeled as $V_{dc0}$, $V_{dc1}$, $V_{dc2}$, and $V_{dc3}$, representing the voltages at DC bus 0, bus 1, bus 2, and bus 3, respectively. Each DC bus has an equivalent capacitance $C_0$, $C_1$, $C_2$, and $C_3$ representing the combined capacitance of power converters and inverters connected in parallel at buses 0 through 3.

The cable lines connecting the different DC buses introduce resistance and inductance, denoted by R and L, respectively. These parameters are essential for modeling the electrical characteristics of the cables between DC bus 0, bus 1, bus 2, and bus 3, and they influence the overall power flow and stability of the network. Effective management of these electrical properties ensures balanced voltage levels and efficient power distribution. In Figure 2, the storage converter, acting as a current source, adjusts its operation based on DC bus voltage feedback. The WTIG and load inverters operate in current control mode to regulate power flow within predefined limits, ensuring balanced distribution across the network. The battery storage system dynamically responds to excess or deficient power by either absorbing or releasing energy, thereby stabilizing the system under varying load and generation conditions. This dynamic model enables efficient power management and stable voltage regulation, ensuring reliable operation of the DC-isolated distribution system under varying load and generation conditions.

Based on (3) through (5), Figure 3 shows the voltages $V_{dc0}$, $V_{dc1}$, $V_{dc2}$, and $V_{dc3}$, along with the reference voltage $V_{refb}$. It also depicts the output currents from the load inverters $I_{L1}$, $I_{L2}$, and $I_{L3}$, and the WTIG inverters $I_{WTIG1}$, $I_{WTIG2}$, and ($I_{WTIG3}$). This figure represents the fundamental operation of droop control for the DC bus, which regulates the storage converter performance. Figure 3 illustrates the dynamic characteristics of the DC network, demonstrating its operational framework under various conditions. This model is used to simulate and validate the behavior of the DC-isolated distribution system. The droop strategy of the storage converters is simulated based on system parameters, demonstrating its role in maintaining voltage stability across the network. For steady-state analysis, (3) can be reformulated to describe system behavior at equilibrium. These equations offer insight into the interactions between the load inverters, WTIG inverters, and the DC network, highlighting the need for balanced power flow and voltage regulation.

$$\begin{array}{cc}\hfill & I_b=\sum _{i=1}^3{I}_{Li}-\sum _{i=1}^3{I}_{WTIGi}.\hfill \end{array}$$

(6)

The proposed system ensures that each load demand is effectively matched to the capacity of its corresponding WTIG, resulting in efficient power distribution. This load-to-generator matching significantly reduces overall power losses in the system while improving energy utilization. Then, there are three scenarios:

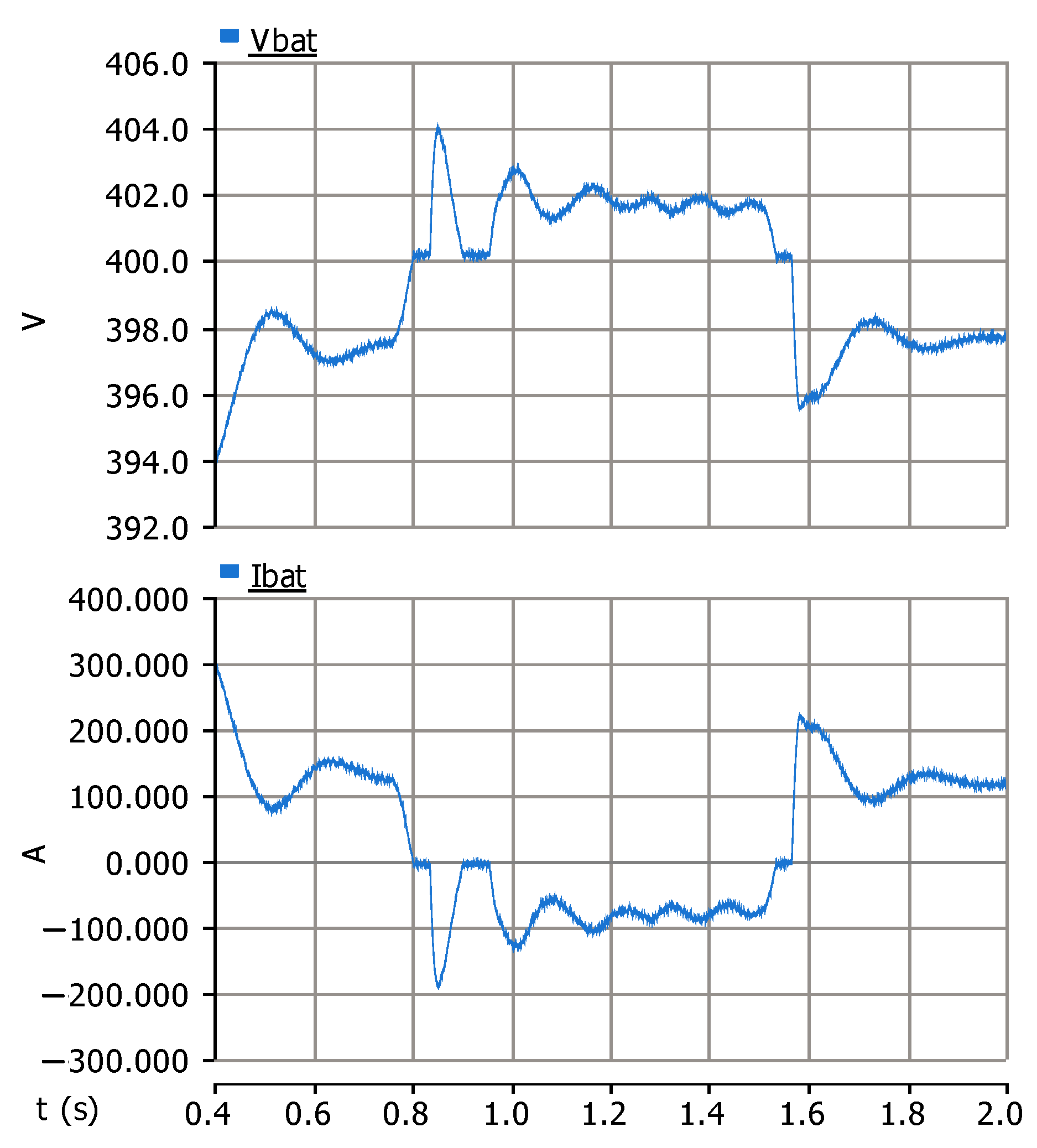
• If $I_b<0$, the power generated by inverter-based variable-speed wind turbine units increases, or the load consumption decreases. The surplus power in the DC network is transferred to the battery via the storage converter.
• If $I_b>0$, the power generated by variable-speed wind turbine units based on inverters decreases, or the load consumption increases. In this scenario, the battery supplies the required power via the storage converter.
• If $I_b=0$, the power generated by inverter-based variable-speed wind turbine units matches the load demand. Under this condition, no power is injected into or drawn from the battery via the storage converter.

In the proposed system, the storage converter’s DC power output is essential for maintaining power balance within the network. To ensure efficient voltage regulation, a voltage droop control strategy is implemented, where $k_b$ represents the droop gain. The steady-state droop characteristic of the DC-DC converter is described in [19]. The converter output current is regulated by adjusting the slope of the droop curve, as described in [21]. Voltage regulation is achieved through the battery, maintaining the DC bus voltage between 5% and 10%. When the voltage exceeds the reference value, WTIG power generation is curtailed to zero.

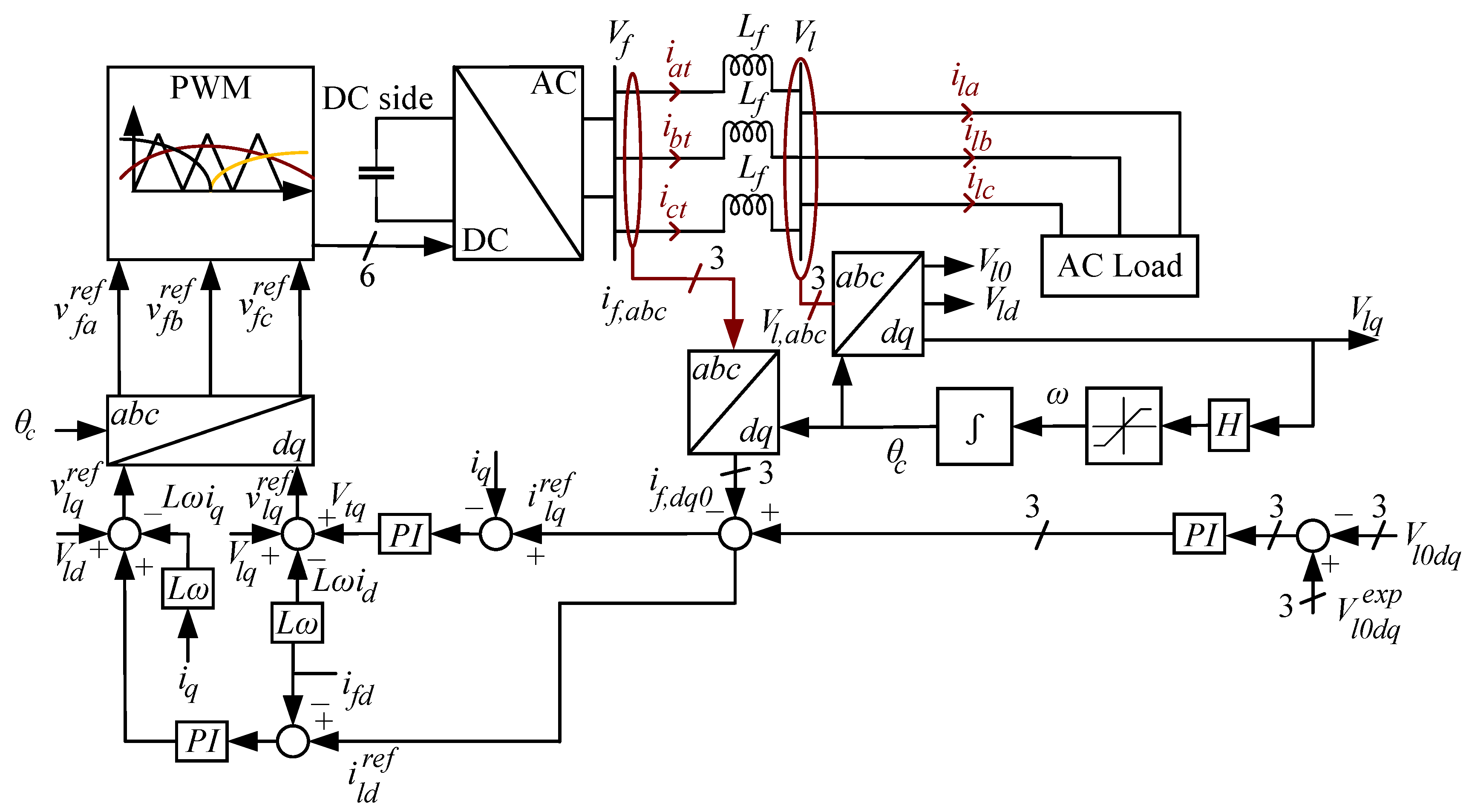
4. The Power Converters and Inverters Control Strategy

In this system, the storage converter regulates the DC bus voltage by dynamically distributing power between the network and the battery bank, based on load demand and WTIG power output. This paper presents control methods for storage converters, with the primary goal of maintaining the DC bus voltage within predefined limits. The WTIG inverter is designed to maximize wind energy extraction while regulating the induction generator speed. The load inverters implement a control strategy that accounts for both voltage and frequency to maintain AC load stability. Since these inverters do not directly regulate the DC bus voltage, they incorporate a voltage regulation mechanism to ensure a stable supply for the loads.

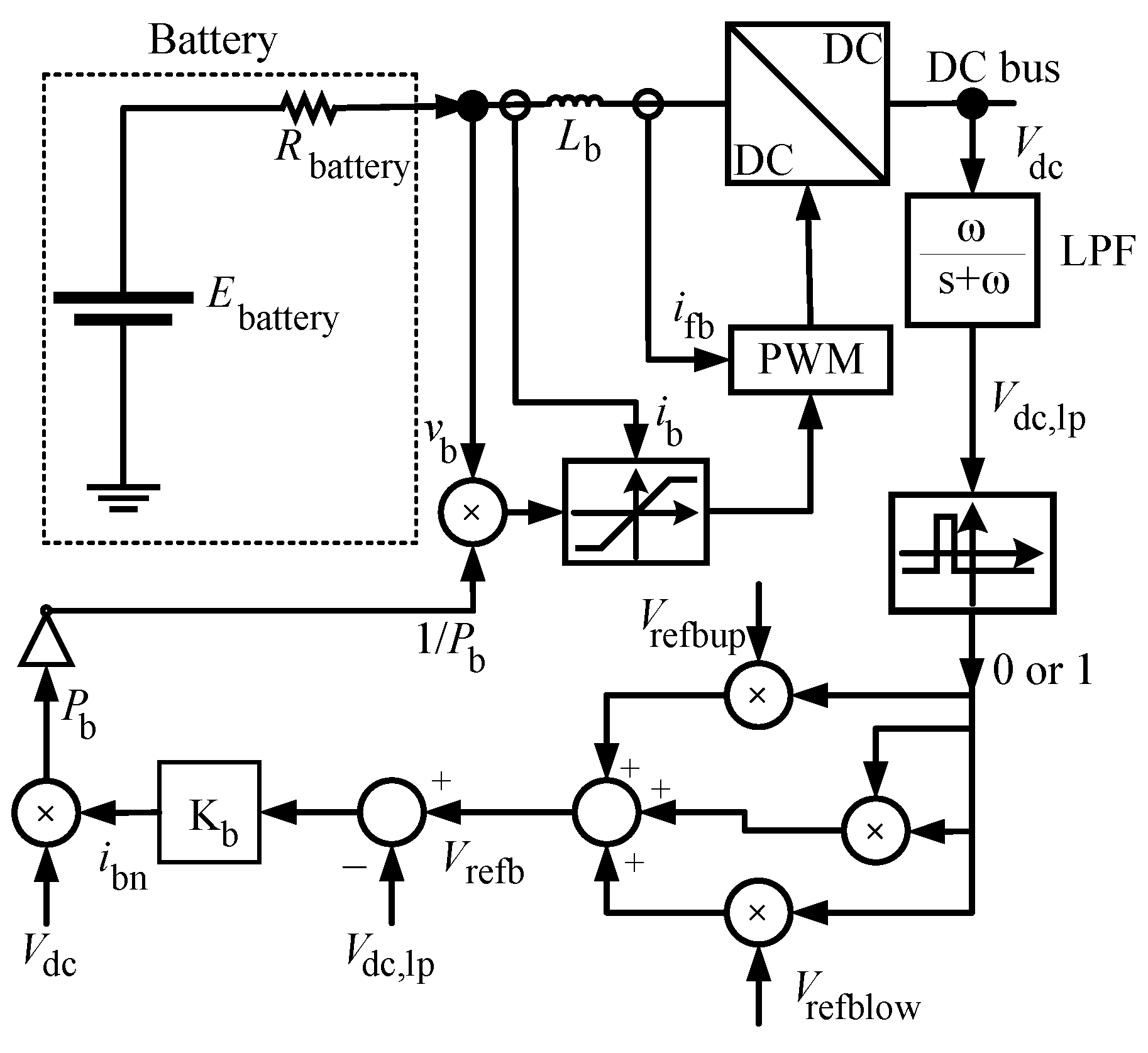
4.1. Energy Storage Units

The storage converter is modeled as a current source $i_{fb}$, regulating the real power for the bank of batteries and DC bus. The DC-DC system comprises a battery energy storage system represented by its Thevenin equivalent voltage $E_{battery}$ and resistance $R_{battery}$. As illustrated in Figure 4, the converter controller receives $v_b$, $i_b$, $i_{fb}$, $v_{dc}$, and the reference voltages $v_{refbup}$ and $v_{refblow}$ as input signals. The slope of the voltage droop characteristic determines the converter output current regulation. For proper operation of the battery storage bank, the DC bus voltage is maintained between the threshold values $v_{refbup}$ and $v_{refblow}$. Based on the proposed control strategy, the DC bus voltage is regulated within the acceptable limit of a 5% nominal droop.

Figure 4 shows the control strategy implemented for the DC-DC converter. The bidirectional DC-DC converter, modeled using IGBT switches, is controlled by a PWM current controller. A droop-based voltage regulator is implemented to control the DC bus voltage. The voltage error is processed by the droop controller, where the droop constant $k_b$ determines $i_{bn}$, the current injected into the DC bus. The injected power, $P_b$, is given by the product of $v_{dc}$ and $i_{bn}$. The DC voltage regulator follows the following equation:

$$\begin{array}{cc}\hfill & i_{bn}=k_b(V_{refb}-v_{dc,lp})\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & P_b=V_{dc}{i}_{bn}\hfill \end{array}$$

(8)

Using (7) and (8) [19],

$$\begin{array}{cc}\hfill & P_b=k_b{v}_{dc}(V_{dc,refb}-v_{dc,lp}).\hfill \end{array}$$

(9)

The DC bus voltage loop regulates the transition between the charging and discharging phases. When the DC bus voltage remains within the reference values $V_{refbup}$ and $V_{refblow}$, the power signal $P_b$ is zero, and no power is exchanged. If the voltage exceeds $V_{refbup}$, $P_b$ becomes negative, recharging the storage system with power from the WTIG. Conversely, if the voltage drops below $V_{refblow}$, $P_b$ becomes positive, discharging the battery bank to provide power to the network. The DC voltage regulator in the storage unit (Figure 4) governs $P_b$, where the reference current $i_{fb}^{ref}$ is derived from the droop control mechanism. This current serves as the input to the PWM control stage of the bidirectional DC-DC converter, adjusting the battery charge/discharge response based on the DC bus voltage deviation.

It is noteworthy to mention that the DC voltage regulator in the storage unit (Figure 4) governs $P_b$, where the reference current $i_{fb}^{ref}$ is derived from the droop control mechanism. This current serves as the input to the PWM control stage of the bidirectional DC-DC converter, adjusting the battery charge/discharge response based on the DC bus voltage deviation. The feedback current $I_{\mathrm{fb}}$ operates within predefined upper and lower limits, ensuring safe battery operation:

$$I_{\mathrm{dis}}\le I_{\mathrm{fb}}\le I_{\mathrm{ch}}$$

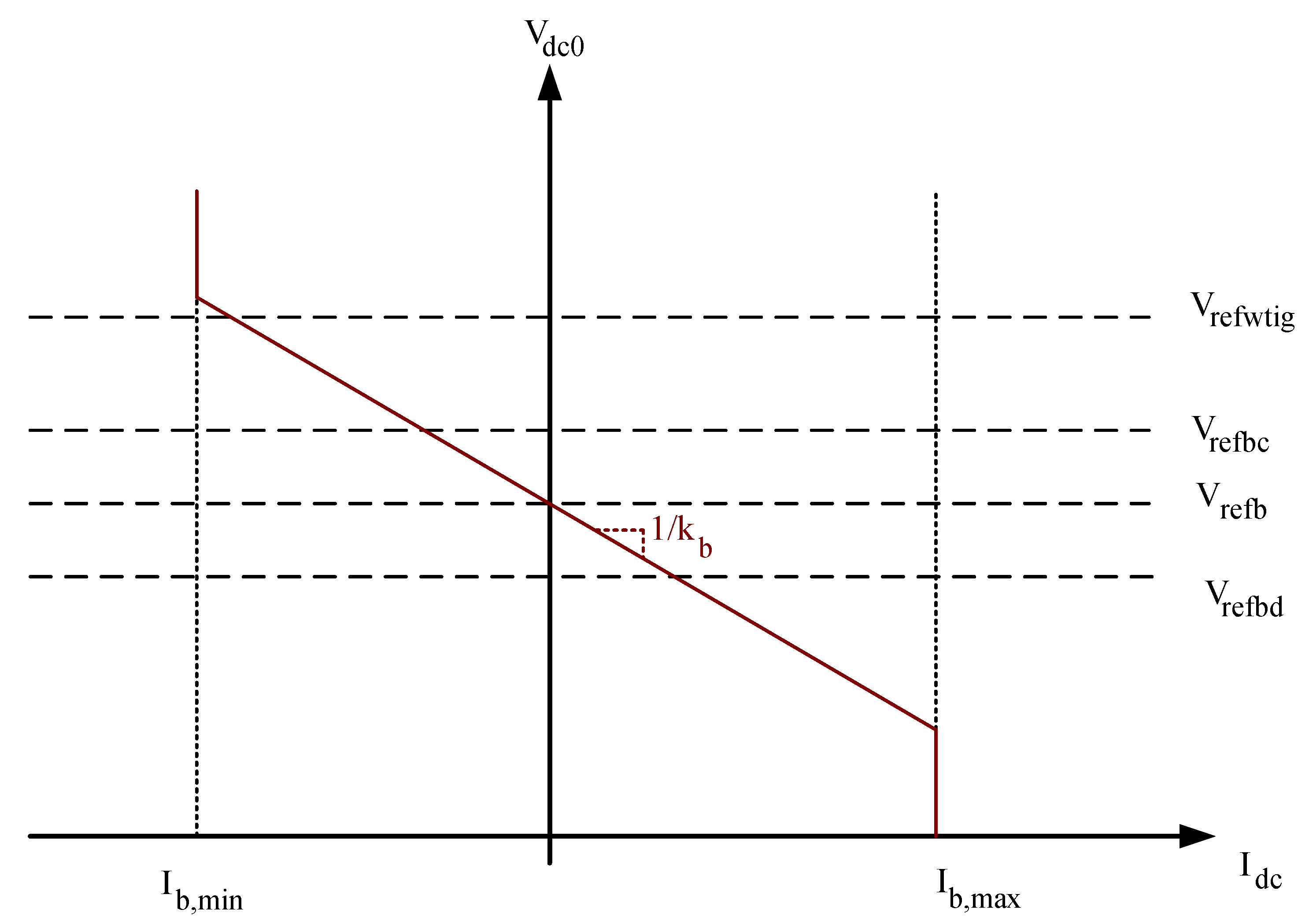
• $I_{\mathrm{ch}}$ (Upper Limit): Restricts the maximum charging current to prevent overcharging.
• $I_{\mathrm{dis}}$ (Lower Limit): Defines the discharge current threshold.

$$\begin{array}{cc}\hfill & i_{fb}^{ref}=-{\displaystyle \frac{P_b}{v_b}}\hfill \end{array}$$

(10)

To ensure stable operation of the DC distribution network, a voltage droop control strategy is employed to regulate the DC bus voltage. The proposed control strategy ensures the stable operation of an inverter-based wind energy system in a standalone DC distribution network. The system consists of three main control mechanisms:

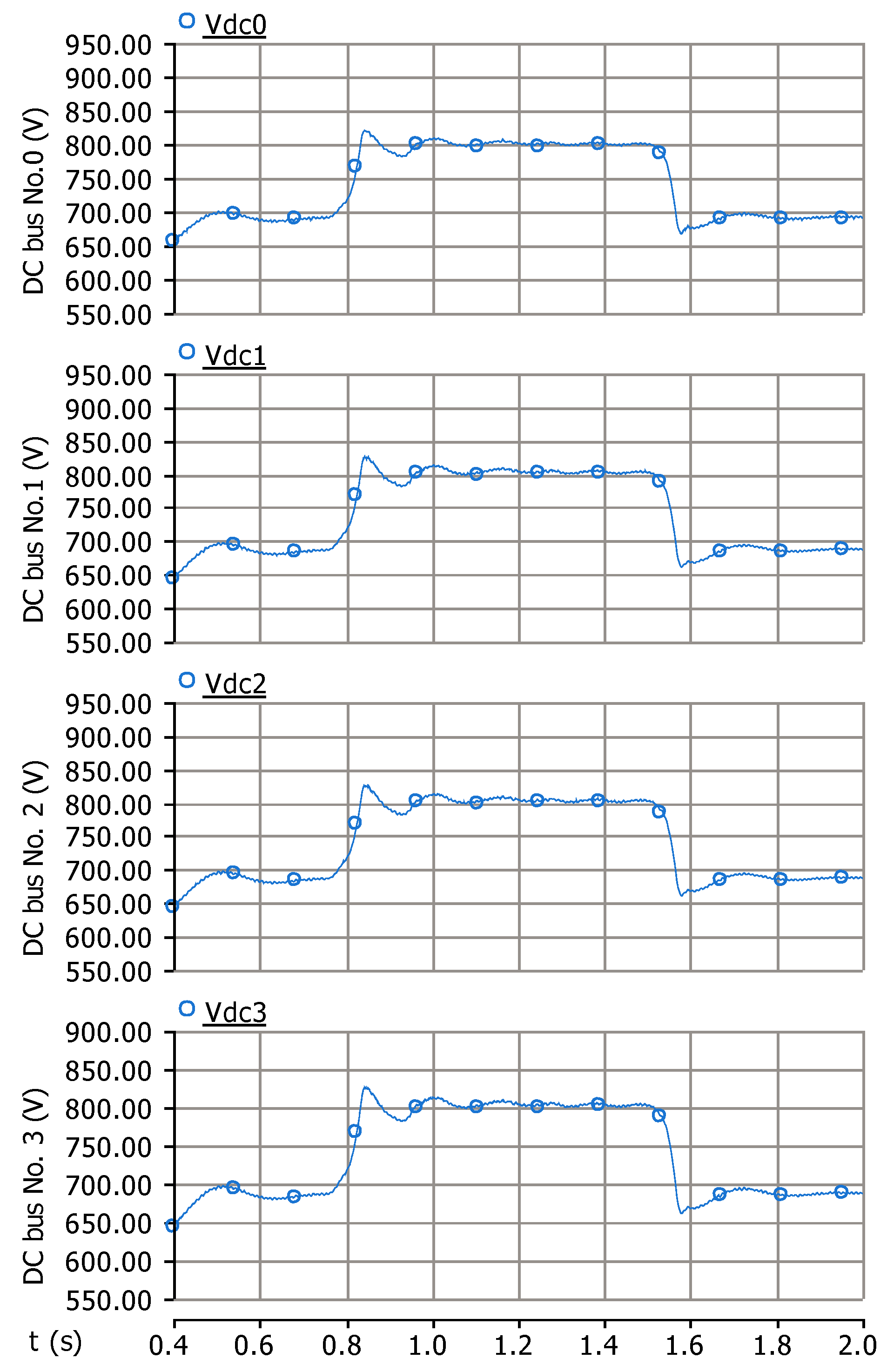
• DC Bus Voltage Regulation: Maintains voltage stability by dynamically regulating power exchange between the battery storage system and the network.
• Wind Turbine Power Control: Maximizes wind energy extraction while maintaining operational limits.
• Inverter-Based Load Management: Balances power delivery to unbalanced AC loads, ensuring a stable and reliable power supply.

This strategy eliminates the need for communication links between converters through local voltage-based power flow adjustments. The droop control method introduces a voltage deviation proportional to the output current. The droop control strategy regulates the DC bus voltage without requiring communication links between power sources. The relationship between the DC voltage deviation and the current injected by the storage system is represented as follows:

$$V_{\mathrm{dc},0}=V_{\mathrm{ref},b}-m{I}_b,$$

(11)

where:

• $V_{\mathrm{dc},0}$ is the DC bus voltage.
• $V_{\mathrm{ref},b}$ is the storage system’s reference voltage.
• $I_b$ is the output current of the storage converter, and
• m is the droop coefficient, which determines the slope of the voltage-current characteristic.

The droop coefficient m defines the extent to which the DC voltage decreases as load current increases. A higher droop coefficient results in a greater voltage deviation, which enhances system stability but may introduce higher voltage variations under dynamic load conditions. Figure 5 illustrates the voltage droop characteristic implemented in the system. In this figure, DC bus voltage is kept within two thresholds $V_{refbc}$ and $V_{refbd}$. Moreover, If the DC bus voltage exceeds the threshold $V_{refwtig}$, the power produced by WTIG is cancelled out. In this representation, $I_{dc}$ should not exceed $I_{b,min}$ and $I_{b,max}$.

The battery terminal voltage $v_b$ is constrained by current limits ($I_{b,\max }$ and $I_{b,\min }$) to manage the battery bank energy levels during charging and discharging. The hysteresis current control (HCC) system uses $i_{fb}^{ref}$ as the reference current and the filter current $i_{fb}$ to determine the switching strategy. This method enables the battery energy storage system to regulate the DC bus voltage by dynamically adjusting its charging and discharging rates.

4.2. WTIG Unit

This paper introduces a wind turbine unit utilizing a variable-speed wind turbine induction generator (WTIG). To maximize power extraction and reduce wind turbine noise, variable-speed wind turbines have gained significant attention in DC distribution networks. The proposed standalone distribution system utilizes three variable-speed wind turbines, each rated at 30 kW. To model the wind turbine, (12) describes the power extraction from wind, which is expressed as follows:

$$\begin{array}{cc}\hfill & P_w={\displaystyle \frac{1}{2}}\rho C_P(\lambda ,\beta )A{v}^3,\hfill \end{array}$$

(12)

where $P_w$ represents the mechanical power extracted from the wind turbine, air density is given by $\rho$ (kg/m³), the power coefficient is $C_p$, which depends on $\lambda$ and $\beta$, the rotor blade swept area is A, and wind speed is v (m/s). The power coefficient $C_p$ depends on the tip speed ratio ($\lambda$) and the blade pitch angle ($\beta$), which is defined by the following [22]:

$$\begin{array}{cc}\hfill & C_p(\lambda ,\beta )=\sum _{n=0}^4\sum _{n=0}^4{\alpha }_{ij}{\beta }^i{\lambda }^j,\hfill \end{array}$$

(13)

and

$$\begin{array}{cc}\hfill & \lambda =K_b(\omega /V_w).\hfill \end{array}$$

(14)

In this representation, the coefficient $C_p$ and the parameters ${\alpha }_{ij}$ are extracted from [22], $K_b$ is a constant, and $V_w$ represents the wind speed. The wind turbine model consists of wind speed, rotor radius, and air density as inputs, which are used to compute the tip speed ratio, a critical parameter for efficiency. This ratio is applied to the $C_p$-$\lambda$ curve, which determines the power coefficient, indicating the turbine’s efficiency in wind-to-mechanical energy conversion. A pitch angle controller dynamically adjusts blade angles using reference speed, power, and actual output, ensuring optimal operation under varying wind conditions. The turbine converts wind energy into mechanical power, generating torque to drive the gearbox. The gearbox increases the rotational speed to match the generator’s requirements, which then converts mechanical energy into electrical energy [23]. The inverter control system maintains power balance for unbalanced AC loads by dynamically adjusting output voltage and current. A phase-locked loop (PLL) synchronizes the inverter output with the load demand. The control reference for each inverter is determined as follows:

$$I_{\mathrm{inv},\varphi }={\displaystyle \frac{P_{L,\varphi }}{V_{\varphi }}},$$

(15)

where:

• $I_{\mathrm{inv},\varphi }$ represents the reference current for phase $\varphi$.
• $P_{L,\varphi }$ is the power demand of the load in phase $\varphi$, and
• $V_{\varphi }$ represents the instantaneous voltage of phase $\varphi$.

The inverter control logic mitigates load imbalances by dynamically adjusting the power supplied to each phase.

As shown in Figure 1, the wind turbine induction generator (WTIG) system connects to the DC network through a power inverter. Each converter functions as a voltage-sourced converter (VSC) and utilizes neutral-point clamped (NPC) capacitors [24]. The primary function of the WTIG inverter is to deliver wind turbine power to the DC distribution network. The controller design, outlined in Figure 6, is essential for optimizing performance. A variable-speed WTIG is used to enhance power generation and reduce wind turbine noise, coordinated with the controller for optimal performance. To precisely control the generator speed, a flux-oriented vector control method is applied [5]. As shown in Figure 6, the maximum power point tracking (MPPT) algorithm employs a perturbation and observation (P&O) method [25] to determine the optimal rotor speed reference for maximum power extraction. In this figure, $P_t$ and $W_t$ correspond to the turbine power and speed, respectively; W denotes the generator rotational speed [26]. The turbine speed is dynamically adjusted to maximize efficiency. The rated flux is represented as ${\displaystyle \frac{V}{w}}$, and $V_{abc}$ and $I_{dc}$ indicate the generator terminal voltage and the DC current through the converter, respectively.

The real and reactive power of the generator is regulated via the P and Q controllers, respectively. To prevent flux saturation in the generator or transformer and maintain proper gain in the torque control loop, the terminal voltage is modulated to remain proportional to the generator speed [5]. A phase-locked loop (PLL) synchronizes the off-grid voltage with the signals used for the control strategy. Figure 6 shows that the reference signals are compared to a triangular carrier wave to generate gate signals.

To ensure that power and speed stay within rated limits during high wind conditions, each turbine is equipped with a blade angle controller. The controller design is depicted in Figure 6. This figure presents key variables, including the mechanical speed (${\omega }_m$), reference speed (${\omega }_{ref}$), power demand ($P_{ref}$), generator output power ($P_g$), gain ($K_s$), proportional gain ($K_p$), integral gain ($K_i$), gain multiplier ($G_m$), actuator integral gain ($K_4$), and blade pitch angle ($\beta$) of the wind turbine. When wind speeds increase significantly, the blade angle controller adjusts the pitch angle ($\beta$) to keep power and speed within rated values. This adjustment follows the power coefficient curve [27] to ensure optimal performance under changing wind conditions.

4.3. AC Load Units

Figure 1 shows the load inverter positioned between the AC load and the DC bus. Load inverters function as voltage-source converters (VSCs), employing neutral-point clamping based on the $V-f$ control strategy. This configuration is defined using the load neutral point connection, modeled by voltage sources $v_{fa}^{ref}$, $v_{fb}^{ref}$, and $v_{fc}^{ref}$ (Figure 7) [28]. The load voltage frequency is maintained at 60 Hz through a phase-locked loop (PLL). In this representation, the voltages and currents for the load inverters and currents are represented by the following:

$$\left[\begin{array}{c}{v}_{fa}\\ v_{fb}\\ v_{fc}\end{array}\right]=\left[\begin{array}{c}{v}_{la}\\ v_{lb}\\ v_{lc}\end{array}\right]+\left[\begin{array}{ccc}{L}_f& 0& 0\\ 0& L_f& 0\\ 0& 0& L_f\end{array}\right]{\displaystyle \frac{d}{dt}}\left[\begin{array}{c}{i}_{fa}\\ i_{fb}\\ i_{fc}\end{array}\right],$$

(16)

where $v_{fa}$, $v_{fb}$, and $v_{fc}$ represent the phase-to-neutral voltages at the converter output, while $i_{fa}$, $i_{fb}$, and $i_{fc}$ indicate the phase currents. Likewise, $v_{la}$, $v_{lb}$, and $v_{lc}$ denote the phase-to-neutral voltages at the AC load. The d–q–0 frame voltages are expressed as

$$\left[\begin{array}{c}{v}_{ld}\\ v_{lq}\\ v_{l0}\end{array}\right]={\displaystyle \frac{2}{3}}\left[\begin{array}{ccc}cos\left(\omega t\right)& cos(\omega t-{120}^{\circ })& cos(\omega t+{120}^{\circ })\\ -sin\left(\omega t\right)& -sin(\omega t-{120}^{\circ })& -sin(\omega t+{120}^{\circ })\\ {\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{2}}\end{array}\right]\left[\begin{array}{c}{v}_{la}\\ v_{lb}\\ v_{lc}\end{array}\right].$$

(17)

The topology and control mechanisms for converters are shown in Figure 7. The power inverters for loads interface the DC bus with the AC unbalanced loads and utilize a V−f control method to regulate both the voltage and frequency of the AC loads. These converters do not include any feedback loop for voltage regulation of the DC bus. For the V−f control system, the following hold:

• The frequency ($\omega$) is managed by a Phase-Locked Loop (PLL), synchronized with the desired operating frequency.
• The phase voltages at the load ($v_{la}$, $v_{lb}$, and $v_{lc}$) are measured, followed by conversion to the synchronously rotating d–q–0 frame.

$$\left[\begin{array}{c}{v}_{d,desire}\\ v_{q,desire}\\ v_{0,desire}\end{array}\right]=\sqrt{{\displaystyle \frac{2}{3}}}\left[\begin{array}{c}0\\ 0.4\\ 0\end{array}\right].$$

(18)

For balanced and sinusoidal load phase voltages with constant amplitude and frequency, the reference load currents are calculated using a proportional–integral (PI) controller based on the error between the measured and expected values. Considering Figure 7, The reference currents of the load in the synchronous reference frame are given by [29].

$$\left[\begin{array}{c}{i}_{ld}^{ref}\\ i_{lq}^{ref}\\ i_{l0}^{ref}\end{array}\right]=\mathrm{PI}\left[\begin{array}{c}{v}_{ld}-v_{d,desire}\\ v_{lq}-v_{q,desire}\\ v_{l0}-v_{0,desire}\end{array}\right],$$

(19)

and thus the output signals from the PI controller are represented by the following equation:

$$\left[\begin{array}{c}{v}_{ld}^{ref}\\ v_{lq}^{ref}\\ v_{l0}^{ref}\end{array}\right]=\left[\begin{array}{c}{v}_{ld}\\ v_{lq}\\ v_{l0}\end{array}\right]+\mathrm{PI}\left[\begin{array}{c}{v}_{ld}-i_{fd}\\ v_{lq}-\sqrt{{\displaystyle \frac{8}{75}}}-i_{fd}\\ v_{l0}-i_{f0}\end{array}\right]+\left[\begin{array}{c}-\omega L_f{i}_{lq}\\ \omega L_f{i}_{ld}\\ 0\end{array}\right].$$

(20)

The voltages then transform into the a–b–c frame through inverse transformations:

$$\left[\begin{array}{c}{v}_{fa}^{ref}\\ v_{fb}^{ref}\\ v_{fc}^{ref}\end{array}\right]=\left[\begin{array}{ccc}cos\left(\omega t\right)& -sin\left(\omega t\right)& 1\\ cos(\omega t-{120}^{\circ })& -sin(\omega t-{120}^{\circ })& 1\\ cos(\omega t+{120}^{\circ })& -sin(\omega t+{120}^{\circ })& 1\end{array}\right]\left[\begin{array}{c}{v}_{fd}^{ref}\\ v_{fq}^{ref}\\ v_{f0}^{ref}\end{array}\right].$$

(21)

The voltage comparison with the carrier signal determines the appropriate switching pattern for each power inverter, ensuring proper operation.

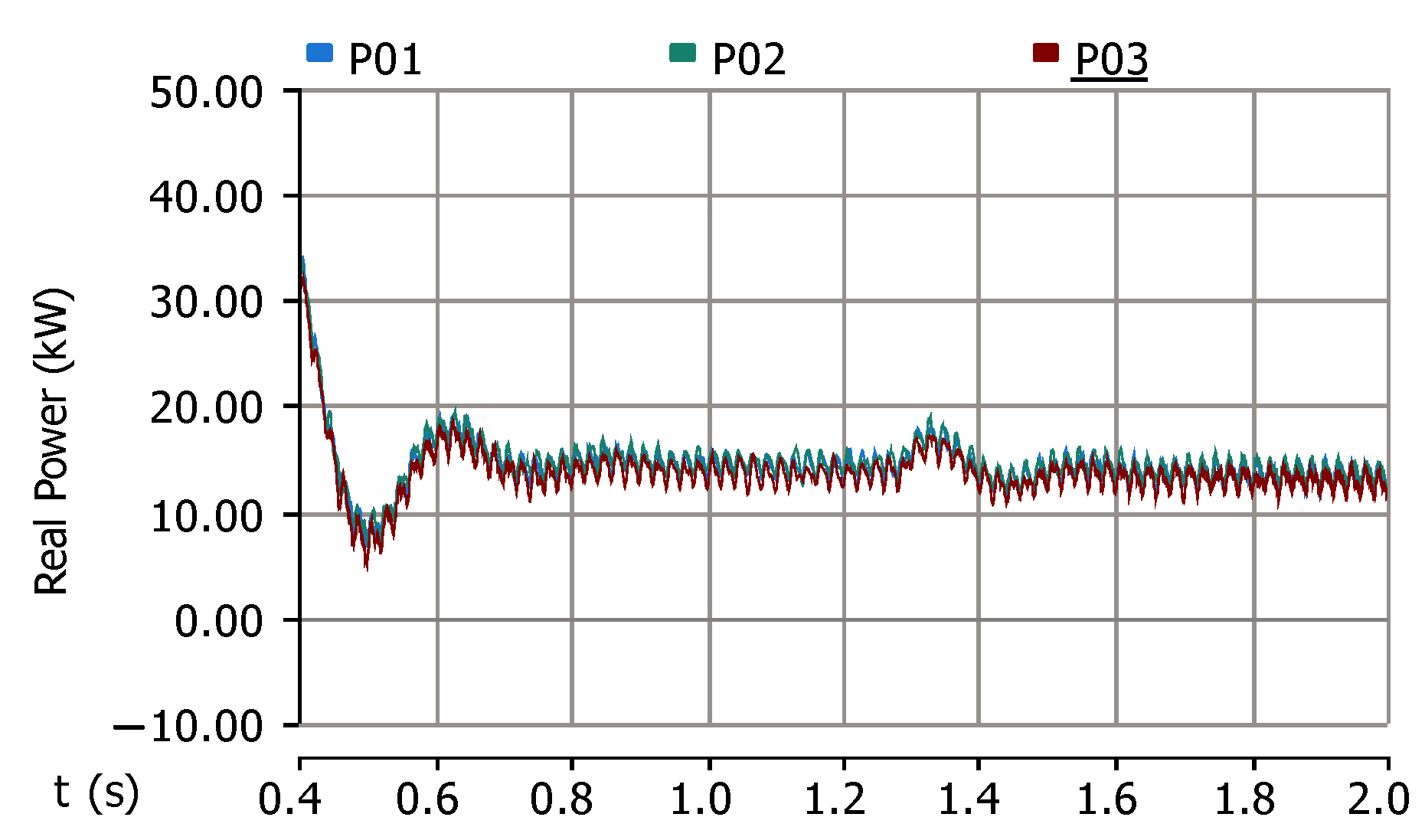
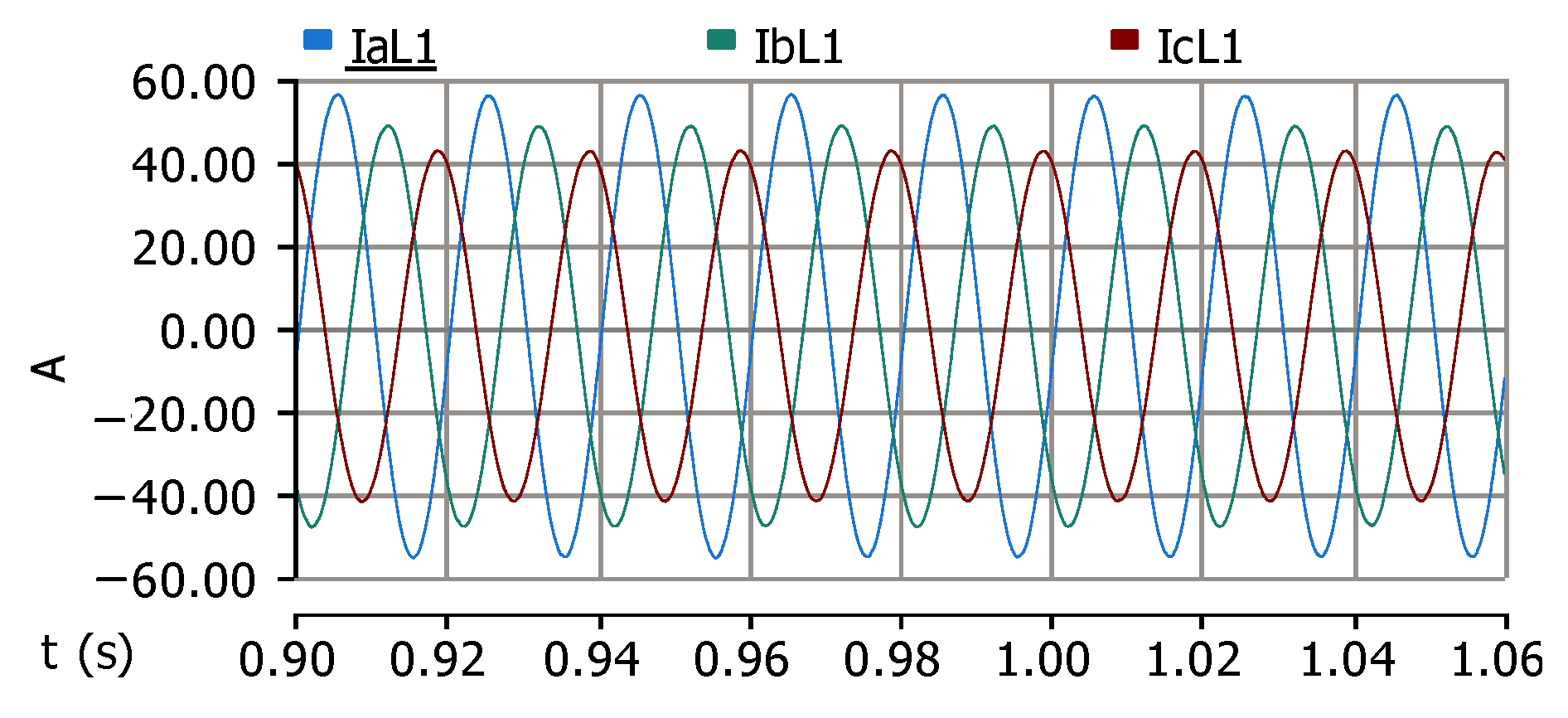
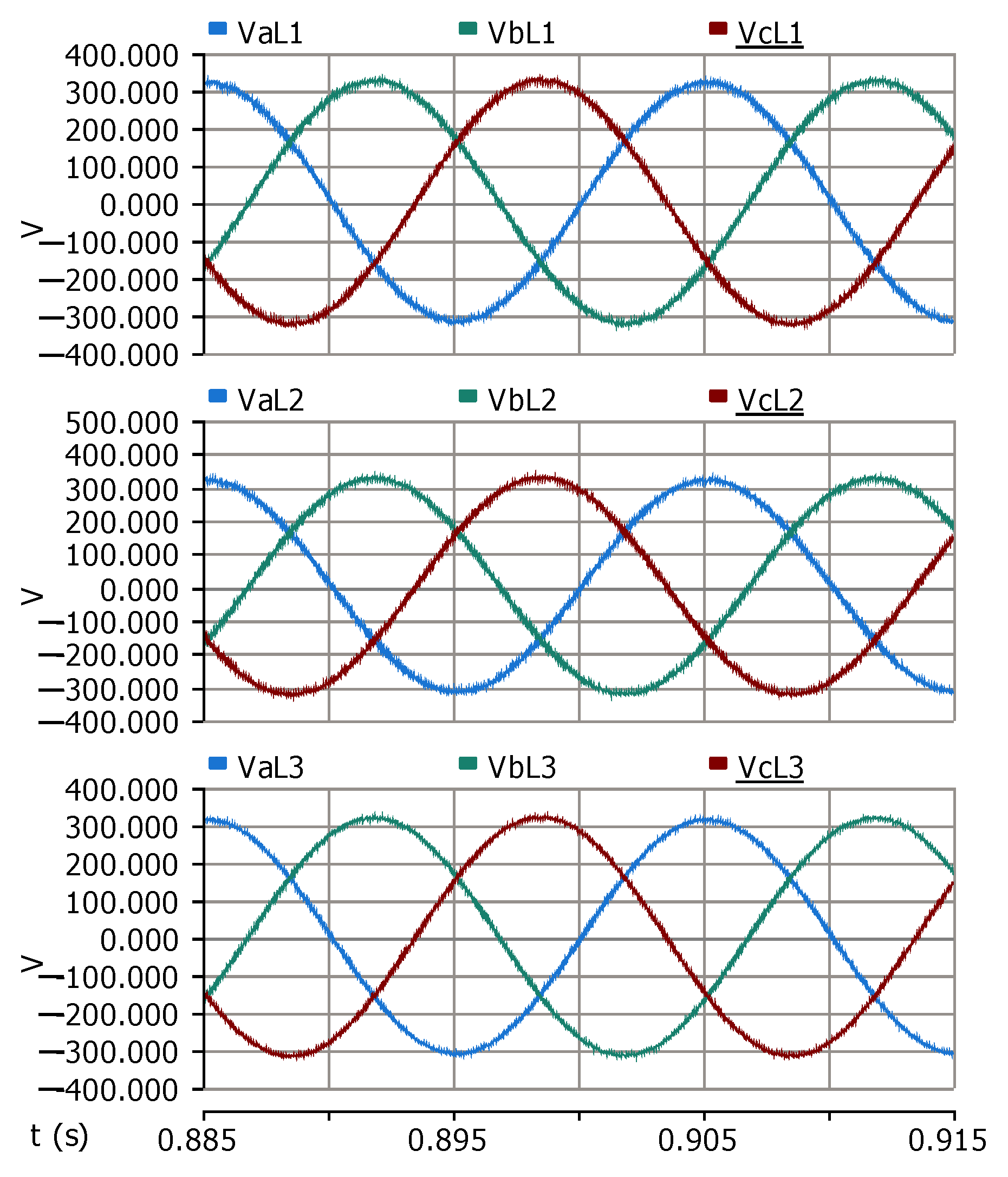
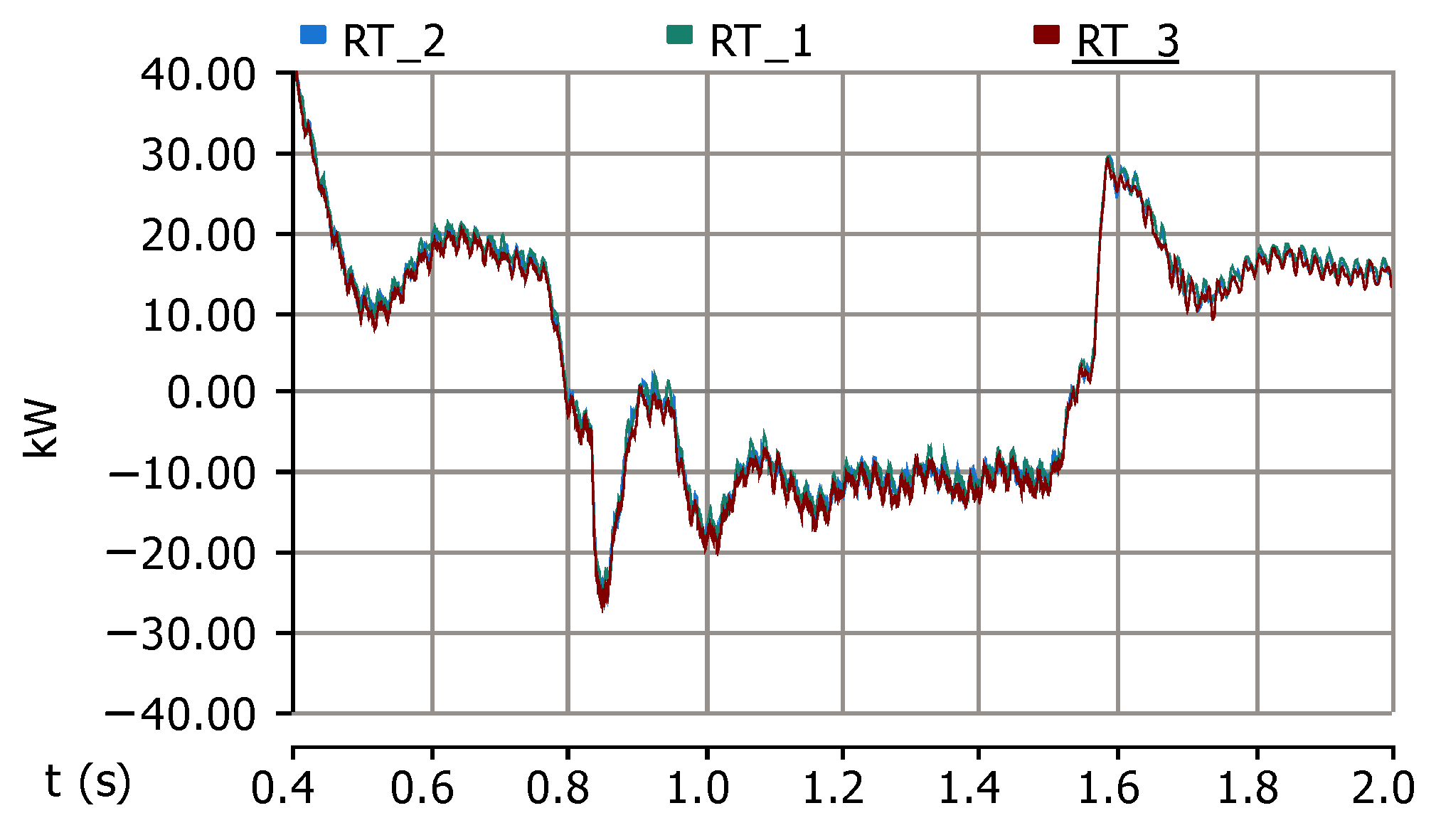
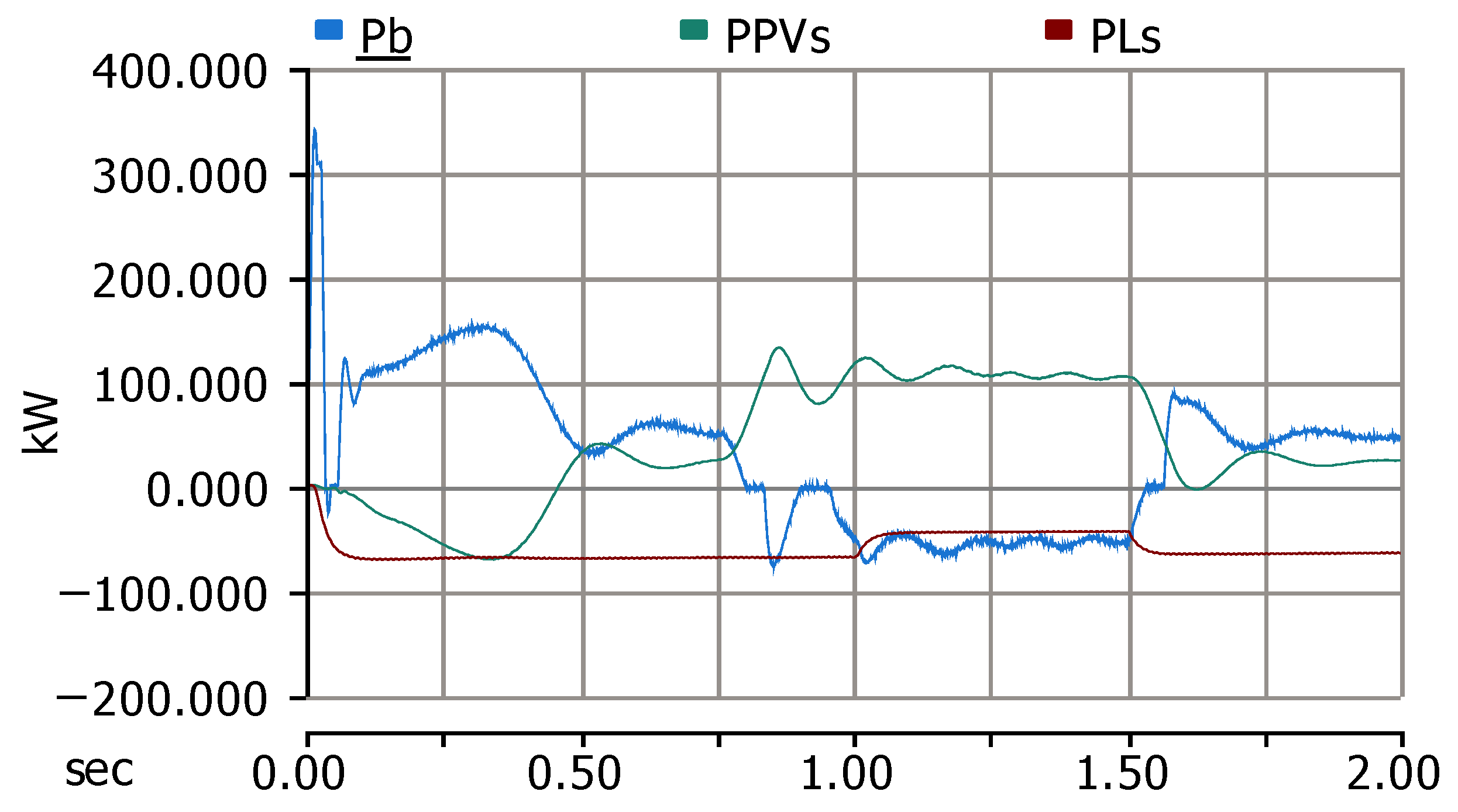
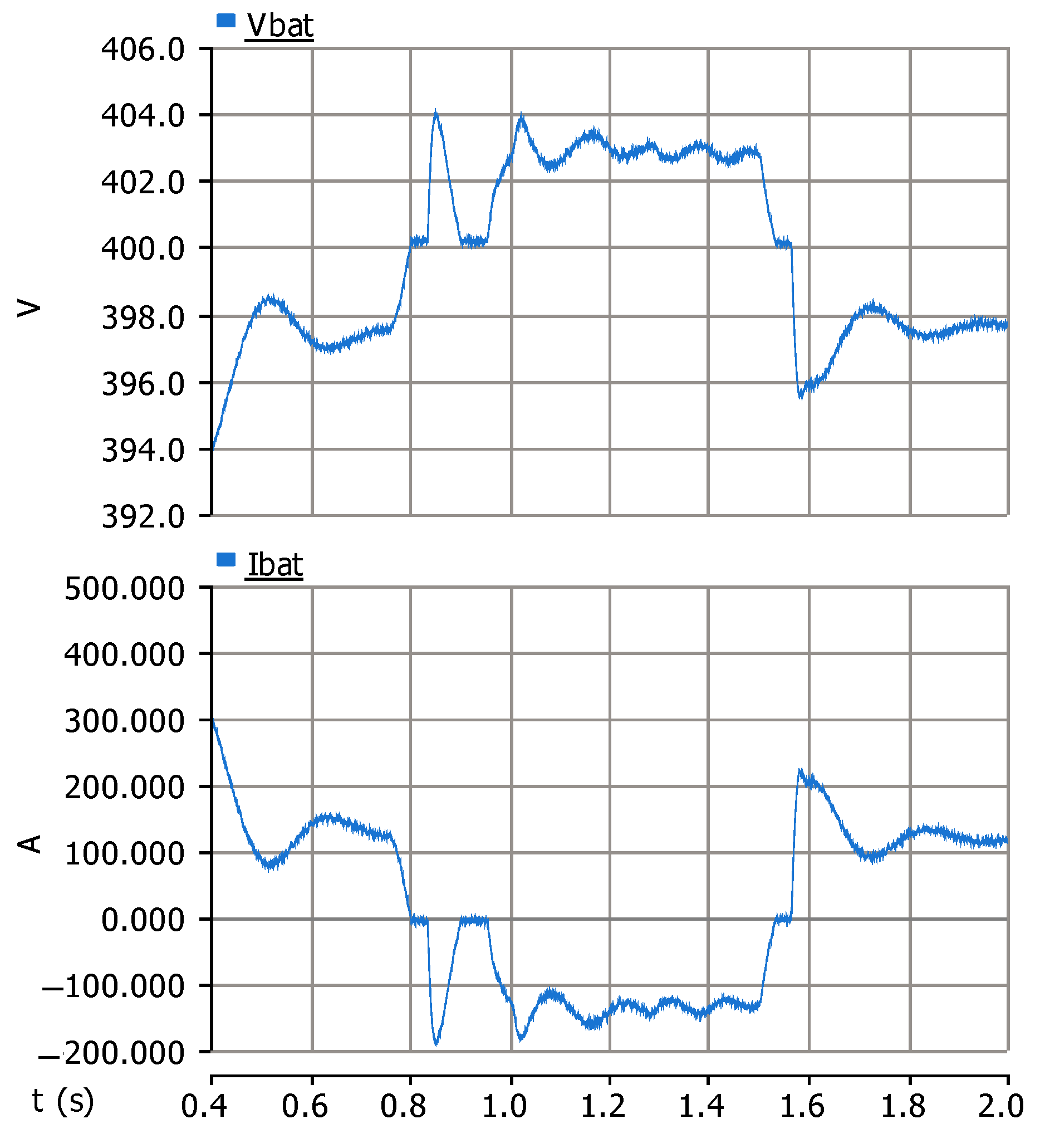
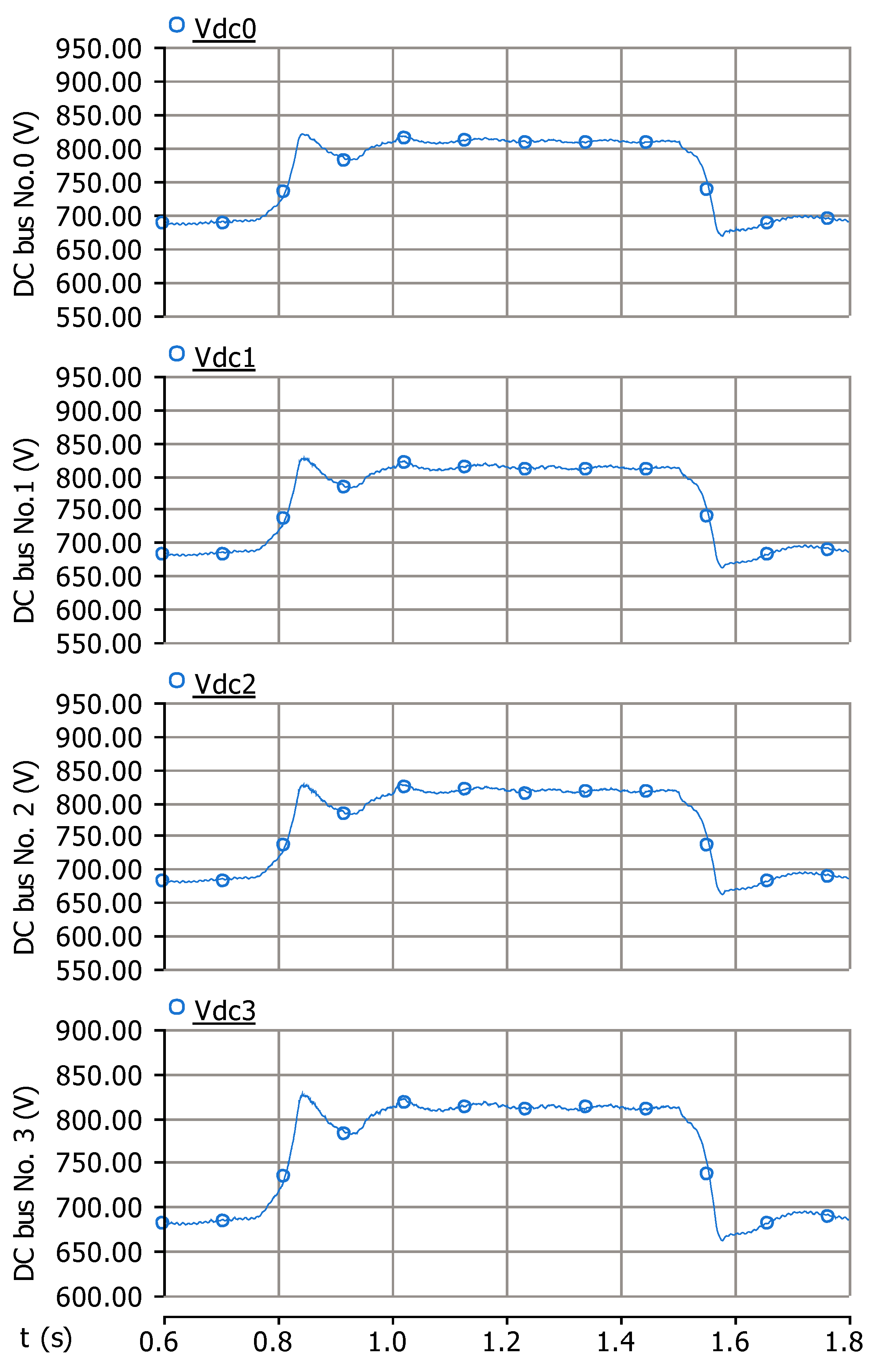
5. Simulation Results

The control strategies for the power electronic interfaces are implemented and modeled within PSCAD/EMTDC. Simulation results indicate that the designed system consistently delivers high-quality power to the loads connected to the grid. The assumed 100 kW storage converter operates within the system using a 750 V reference DC voltage with 5% nominal droop. The AC loads are assumed to have a rated power of 25 kW and 30 kW for the WTIG. Three operational scenarios are considered to evaluate the performance of the proposed system.

5.1. Scenario 1 (No Disturbance of Wind Turbine Operation)

In the first case scenario, the normal operation of the system without disturbances is considered. During this scenario, the average wind speed is constant at 8 m/s, and no disturbances are applied to the wind turbine. Figure 8 shows the real power ($P_b$), the total power generated by all WTIGs ($P_{WTIGs}=P_{WTIG1}+P_{WTIG2}+P_{WTIG3}$), and the power consumed by unbalanced AC loads ($P_{Ls}=P_{L1}+P_{L2}+P_{L3}$).

Figure 9 shows the voltage and current output of the battery storage system. The battery current ($I_{bat}$) increases during operation. The battery terminal voltage ($V_{bat}$) exhibits changes during the charging and discharging phases, attributed to the battery internal resistance.

Figure 10 indicates the voltage profiles of DC buses, which exhibit a voltage increase when the generated WT power increases, followed by a return to the nominal DC voltage. The DC bus voltages ($V_{dc0}$, $V_{dc1}$, $V_{dc2}$, and $V_{dc3}$) are presented in this figure.

Figure 11 illustrates the power transfer through the cables connecting each WTIG to the battery bank during the charging and discharging.

5.2. Scenario 2 (Wind Speed Variation)

In this scenario, the normal operation of the system is analyzed while considering variations in wind speed. During the simulation, the average wind speed, initially at 9 m/s, is increased to 12.5 m/s at $t=0.6$ s. Furthermore, at $t=1.4$ s, the average wind speed is reduced to 9 m/s. Figure 12 shows the real power ($P_b$), the total power generated by all WTIGs ($P_{WTIGs}=P_{WTIG1}+P_{WTIG2}+P_{WTIG3}$), and the power consumed by unbalanced AC loads ($P_{Ls}=P_{L1}+P_{L2}+P_{L3}$). Based on Figure 12, the proposed control strategy for the WTIGs ensures an adequate response to the changing wind conditions, and at high wind speeds, the power generated by the wind turbines exceeds the load demand, allowing surplus power to charge the battery bank. Conversely, when the wind turbine power output falls below the load demand at low wind speeds, the battery bank discharges to compensate for the energy deficit. Under all conditions, the MPPT algorithm efficiently extracts the needed power from the wind turbines.

Figure 13 illustrates the battery storage system voltage and current outputs in which $I_b$ increases during operation. $V_b$ exhibits fluctuation during the charging and discharging phases, attributed to the battery internal resistance. A larger battery helps reduce the observed ripple. The storage converter consistently supplies power to the DC network under various operating conditions, stabilizing DC voltages.

Figure 14 shows the voltage profiles of DC buses, which exhibit a voltage swell when the generated WT power increases, followed by a return to the nominal DC voltage. Additionally, the DC network experiences voltage sag when the WT power output decreases. As shown, the DC bus voltages ($V_{dc0}$, $V_{dc1}$, $V_{dc2}$, and $V_{dc3}$) (Figure 3).

Figure 15 reveals that the currents are non-sinusoidal.

Figure 16 displays the phase voltages ($V_{aL1}$, $V_{bL1}$, $V_{cL1}$), ($V_{aL2}$, $V_{bL2}$, $V_{cL2}$), and ($V_{aL3}$, $V_{bL3}$, $V_{cL3}$) remain balanced and sinusoidal. It is important to note that international standards typically mandate unbalanced levels below 2% [30].

Figure 17 illustrates the power transfer through the cables connecting each WTIG to the battery bank during the charging and discharging processes.

5.3. Scenario 3 (Load Variation)

In this scenario, one of the unbalanced AC loads (L2) is disconnected from the main system at $t=1$ s and reconnected at $t=1.5$ s. During this simulation, the average wind speed is set to 11 m/s. Figure 18 depicts the real power ($P_b$), the total power generated by all WTIGs ($P_{WTIGs}=P_{WTIG1}+P_{WTIG2}+P_{WTIG3}$), and the power consumed by the unbalanced AC loads ($P_{LS}=P_{L1}+P_{L2}+P_{L3}$).

Figure 19 illustrates the battery storage system instantaneous voltage and current profiles. It is evident that as the battery voltage decreases, the corresponding current increases. Additionally, when the unbalanced AC load (L2) is disconnected from the main system, the battery is charged until the wind speed drops. Under low wind speed conditions, the battery supports the main system by maintaining the DC bus voltages at their nominal levels. Furthermore, when the unbalanced AC load (L2) reconnects to the system at $t=1.5$ s, the battery resumes charging due to the high wind speed. However, as the wind speed declines, the battery discharges to stabilize the DC voltages, as observed towards the end of the simulation in Figure 19.

Figure 20 presents the voltage levels of DC buses No. 0, No. 1, No. 2, and No. 3. When the unbalanced AC load (L2) is disconnected from the system at $t=1$ s, the excess energy in the system causes the DC bus voltages to rise. Conversely, the DC bus voltages decrease when the AC load (L2) is reconnected at $t=1.5$ s.

The phase voltages at the terminals of the unbalanced AC loads, specifically ($V_{aL1}$, $V_{bL1}$, $V_{cL1}$), ($V_{aL2}$, $V_{bL2}$, $V_{cL2}$), and ($V_{aL3}$, $V_{bL3}$, $V_{cL3}$), similar to Scenario 1, are balanced and sinusoidal, maintaining constant amplitude and frequency. Wind energy utilization efficiency is a key performance metric for evaluating the effectiveness of the proposed system. The utilization rate is calculated as

$${\eta }_{\mathrm{wind}}={\displaystyle \frac{P_{\mathrm{WTIG},\mathrm{delivered}}}{P_{\mathrm{WTIG},\mathrm{generated}}}}\times 100,$$

(22)

where

• $P_{\mathrm{WTIG},\mathrm{generated}}$ represents the total power generated by the wind turbine induction generator (WTIG).
• $P_{\mathrm{WTIG},\mathrm{delivered}}$ is the actual power delivered to the DC bus and utilized by loads or stored in the battery.

Simulation results show that under typical operating conditions, the system achieves an average wind energy utilization efficiency of 91.3%. This efficiency is due to the optimized power management strategy, which minimizes curtailment and maximizes energy extraction.

It is noteworthy to mention that while the overall aerodynamic efficiency of wind turbines is typically below 40%, the electrical efficiency of the system, which refers to the effective conversion of generated power into usable electrical energy, exceeds 90%.

Table 1. Commonly used abbreviations.

Acronym	Definition
DG	Distributed Generation
WTIG	Wind Turbine Induction Generator
LPF	Low-Pass Filter
VSC	Voltage Source Converter
IGBT	Insulated Gate Bipolar Transistor
PWM	Pulse-Width Modulation
HCC	Hysteresis Current Control
MPPT	Maximum Power Point Tracking
PLL	Phase-Locked Loop

is the commonly used abbreviations and

Table 2. Definitions of key symbols.

Symbol	Definition
$a,b,c$	Phases in the three-phase a-b-c reference frame
$d,q,0$	Phases in the rotating d-q-0 coordinate system
$V_{\mathrm{ref},b}$	Reference voltage of the storage unit
$I_b$	Storage unit current (A)
$P_b$	DC power output from the storage unit (W)
$R_b$	Internal resistance of the storage system ($\Omega$)
$C_0$	Combined capacitance of converters at DC bus 0 (F)
$C_1$	Combined capacitance of converters at DC bus 1 (F)
$C_2$	Combined capacitance of converters at DC bus 2 (F)
$C_3$	Combined capacitance of converters at DC bus 3 (F)
R	Line resistance between DC buses ($\Omega$)
L	Line inductance between DC buses (H)
$K_b$	Control gain of the storage system regulator
$V_{\mathrm{dc},0}$	Voltage at DC bus 0 (V)
$V_{\mathrm{dc},1}$	Voltage at DC bus 1 (V)
$V_{\mathrm{dc},2}$	Voltage at DC bus 2 (V)
$V_{\mathrm{dc},3}$	Voltage at DC bus 3 (V)
$P_{\mathrm{WTIG},i}$	Power output of the ith wind turbine generator (W)
$I_{\mathrm{WTIG},i}$	Current from the ith WTIG inverter (A)
$P_{L,i}$	Power demand of the ith AC load (W)
$I_{L,i}$	Current supplied by the ith load inverter (A)
$P_{L,\mathrm{total}}$	Total power drawn by all loads (W)
$I_{\mathrm{ref},b}$	Desired current for the storage unit (A)
$V_{\mathrm{bat}}$	Battery terminal voltage (V)
$I_{\mathrm{ref},L,\varphi }$	Target current for phase $\varphi$ in a load inverter (A)
f	Frequency of system operation (Hz)
$V_{\varphi }$	Instantaneous voltage at phase $\varphi$ (V)
$I_{\varphi }$	Instantaneous current at phase $\varphi$ (A)

the definitions of key symbols.

6. Conclusions

Given the standalone (isolated) operation, DC distribution systems that are not connected to the AC grid present unique characteristics. These systems, commonly referred to as isolated DC distribution networks, face several challenges, including lower reliability and reduced power quality compared to AC-connected systems. Nevertheless, isolated DC distribution networks are well suited for integrating renewable distributed generation resources, such as wind turbine systems, and for independent operation (islanded operation). The integration of renewable energy sources within isolated DC distribution systems facilitates optimal load and generation sharing between sources and loads based on a droop-based power management system, ensuring the supply of loads with desirable power quality. Considering the variable nature of power generation from wind resources, the proposed system is designed to ensure power quality and transfer capability through its autonomous and integrated operation. In this study, the DC voltage control system within the storage converter, which effectively serves as the active power management system, is analyzed and designed. A comprehensive design methodology for the DC voltage control system is introduced, aiming to eliminate circulating currents within the system, stabilize the DC voltage within permissible limits, and achieve appropriate power distribution among source converters. Then, the performance of an isolated DC network powered by WTIG is examined. The proposed DC network supplies unbalanced AC loads, with battery energy storage used to regulate the DC bus voltage levels. Two operational scenarios are considered to evaluate the proposed system performance. The first scenario focuses on the system normal operation, accounting for variations in wind speed, while the second scenario investigates the impact of load variations on system behavior. Simulation results confirm that the proposed network maintains DC bus voltage stability within ±5% of the nominal value and achieves balanced AC voltage delivery with deviations below 2% under unbalanced load conditions. The system effectively adapts to wind speed variations (9–12.5 m/s) and manages load variations by dynamically charging or discharging the battery bank. The WTIG-based DC network demonstrates efficient power management, with wind energy utilization exceeding 90% in optimal conditions, ensuring reliable operation and robust performance for unbalanced AC loads.

As a continuation of this research, future work can focus on exploring additional operational scenarios and advancing toward real-world implementation in practical DC grids. This includes analyzing system performance under extreme wind fluctuations to assess stability, examining the effects of load reconnection dynamics on overall system behavior, and conducting a comparative evaluation of the proposed control strategy against conventional DC voltage regulation techniques.