1. Introduction
During abnormal events, it is very important to maintain a good level of service of water distribution networks (WDN), in terms of satisfying customer water demands. For this reason, the resilience of these systems is a key property [
1]. In 2005, the World Conference on Disaster Reduction (WCDR) highlighted the importance of the term resilience, in the context of disaster scenarios, and many authors proposed new methods to quantify the resilience [
2]. Ref. [
3] proposed an evaluation of the disaster resilience, based on dimensionless analytical functions related to the variation of functionality, obtaining a tool for disaster assessment in structural engineering. Successively, [
4] evaluated the performance of a WDN in the case of catastrophes using three indices: the number of users temporarily without water, the water level in the tank and the water quality.
In the framework of WDN, many definitions of resilience have been proposed over the years by different authors. Resilience has been used as a reliability indicator, together with other indexes. In the first developed approaches, the evaluation of the reliability of a WDN was made by the estimation of direct indicators, which required a high computational effort, due to the various scenarios and the complexity of real networks [
5,
6,
7,
8]. Successively, to reduce the computational time, reliability has been often expressed using indirect indexes. Many studies have been realized to understand which of the above-mentioned surrogate measures is the most appropriate, to better characterize the full reliability of the network depending on the considered problem.
The resilience index can be viewed either as a design parameter, aiming at maximizing resilience and minimizing investment costs, or as an operation parameter to consider how an existent network should be operated under crisis scenarios. The latter is considered as the main theme of this work, since the resilience assessment of an existing WDN is currently a main topic in the water research field. With this purpose, the resilience can be defined as the capability of a system to maintain and adapt its operational performance in the face of failures and other adverse condition
s [
9]. Recently, the Water Network Tool for Resilience (WNTR), an open source Python package designed to simulate and analyze resilience of WDN, has been developed [
10]. It integrates hydraulic and water quality simulation, a wide range of damage and response options, and different metrics into a single software framework for evaluating water network resilience.
The problem at hand is understanding how a network performs during critical scenarios and then prioritizing the operational choices that can improve its performance. Methodologies based on simulation and optimization tools can help water utilities in individuating how to operate their networks in these cases.
In the study, a methodology to guarantee the highest possible resilience during critical scenarios is also developed. After the evaluation of the network resilience during critical scenarios, the next step is to select how to operate the network. In particular, considering a pipe failure, the network resilience is maximized by changing valve statuses. This is formulated as an optimization problem, in which the decision variables are the valves to operate (open or closed), and the objective function is to maximize the network resilience, expressed as demand satisfaction rate. Gondwana [
11], a generic optimization tool for drinking water distribution networks, is used. Different objective functions are considered, in order to understand which is the most appropriate to improve network performance during critical scenarios. The methodology is tested on a real water distribution serving a city in The Netherlands. Different tests are realized, selecting 18 different critical scenarios and assessing resilience during the peak hour.
2. The Proposed Methodology
In the present paper, the resilience index is expressed through the demand satisfaction rate,
DSRs, defined as the ratio between the total available water that can be delivered to the consumers,
, under the scenario
, and the total water that is required by the consumers,
[
12]:
where,
is the water demand at node
i of the network,
is the actual delivered water to node
in the scenario
,
is the number of nodes in the network.The supplied water flow at each node is a function of the nodal pressure, evaluated as [
13]:
where,
is the actual head at node
and scenario
,
is the minimum head to allow any flow to the node, and
is the service head to fully satisfy nodal demand. The exponent
is usually set to 0.5 [
11]. In order to compute pressure driven demands, the pressure driven demand extension for EPANET (EPANET.pdd) developed by [
14] has been built in Gondwana. In this way, it is possible to compute, for each time step, the demand that is actually delivered to each node of the network during a critical event.
In order to investigate if it is possible to improve the network resilience under critical scenarios by changing its operational mode, the following methodology is performed:
Each critical scenario is created, considering one pipe failure.
The demand satisfaction rate is determined without changing valve statuses (current valve statuses), in order to get the initial resilience index of the WDN.
The valve statuses are changed using the numerical optimization technique implemented in Gondwana, in order to maximize the demand satisfaction rate, or in other words, to minimize the demand deficit. This is done considering the following objective functions:
Total demand: Maximization of total demand satisfaction rate summed over all nodes
n of the network and for the simulation period,
t, which is obtained by maximizing the following function:
Maximum demand: Maximization of the demand satisfaction rate at the node with highest demand deficit
ndef summed over all time steps of the simulation period, expressed as:
Maximum nodal demand: Maximization of the demand satisfaction rate of the highest demand deficit for each node
n evaluated over the entire simulation period, obtained through:
In each scenario, the simulation is done with each of the three objective functions, in order to compare the results and assess which one is more appropriate in the context of the problem.
3. Results
3.1. The Case Study
The proposed methodology is applied to a WDN serving a city in the Netherlands, with ca. 105 thousand inhabitants. The network supplies a total demand of 31,272 m
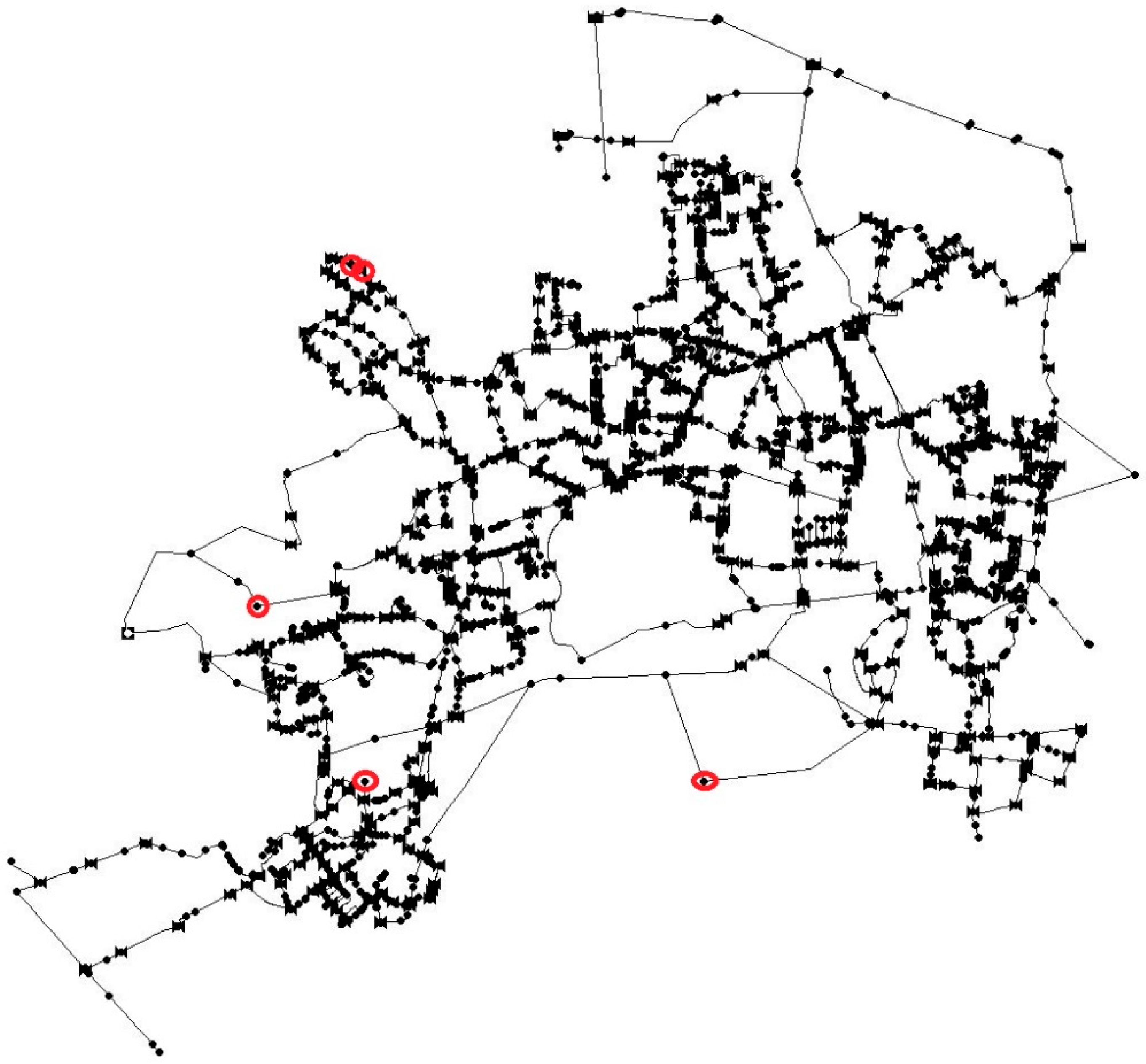
3/day. The elevation varies between 15–23 m, and pipes are made of plastic materials (84%), steel (12%) and concrete (4%). The hydraulic simulations are performed with the software EPANET, adopting the Darcy–Weisbach resistance formula. The network scheme, reported in
Figure 1, is composed of 4311 pipes, 5096 junctions, 5 reservoirs and 891 valves. In the model, three different demand patterns are assigned for considering different types of the consumptions.
3.2. The Considered Scenarios and the Performed Tests
Overall, 18 critical scenarios are considered, and each of them assumes one pipe out of service. To select the pipes for the failure scenarios, different criteria were considered, based on the diameter and length, highest flow, and proximity to the node with the highest base demand. The selected pipes are indicated in the network scheme of
Figure 1. Two kinds of tests are performed. The former refers to a situation in which it is assumed that the valve statuses in the network model are an accurate representation of the real valve statuses, and in this case all valves are assumed open. Then, the optimization model selects the valves to close. This is often not the case: in fact, water utilities in the Netherlands believe that about 1% of valves are in a different status than described in the model, due to unregistered network operations. In order to assess the resilience taking into consideration some uncertainty about valve statuses, the same computations are performed on different network models assuming 1% of closed valves randomly placed in the network. Then, the optimization model selects the valves to close for optimizing the resilience.
It is assumed that the events take place during an entire simulation period (00:00–24:00). In real-life situations, it is important to consider the actual start time of an event and its duration, and compute the resilience in this time period. In all nodes, a service pressure,
Hi,min, equal to 20 m is considered for the computation of the pressure delivered demand. This means that, for nodes with a pressure below 20 m, the volume of water that is actually delivered is less than the demand (Equation (2)). Gondwana uses a genetic algorithm (GA) for the optimization, and the GA parameters used are summarized in
Table 1.
3.3. Results
In presenting the results, the 18 different scenarios are sorted, starting from the worse one, i.e., the one with a higher percentage of unsatisfied demand in the initial situation,
DEFp0, evaluated during the peak hour, defined as:
Referring to the case in which it is assumed that all valves are open (Test1),
Table 2 summarizes the results obtained for the four most critical scenarios. It reports the improvement of the unsatisfied demand after the optimization process
.
The second column reports the node which is most affected by the critical scenario (represented in
Figure 2), while the third one indicates the percentage of unsatisfied demand in the current situation (i.e., before the optimization). The other three columns summarize the percentage decrease of the unsatisfied demand in the same node after the optimization, considering the three different objective functions. As shown in the table, the improvement after the optimization process is high only for the most critical scenario (failure of pipe number 2). The obtained improvement is similar for the three different analyzed objective functions.
Table 3. Percentage of unsatisfied demand in the initial condition and percentage improvement of the unsatisfied demand after the optimization for the Total Demand objective function (1% of closed valves)—shows the corresponding results relative to the case with 1% of valves initially closed (Test2). The four most critical scenarios are reported, and represented in
Figure 2, along with the percentage of improvement after the optimization of valve statuses, obtained by considering only the objective function total demand.
Comparing the results of the two different tests, the two worst cases of Test 1 are not present in the first four of the second one, while the scenarios with the rupture in pipes 7 and 25 are present in both. For those ones, the percentage of unsatisfied demand is higher in the case with 1% of closed valves, and the obtained improvement, even if small, is higher with respect the other case. The results indicate that the analyzed network has, in general, a high resilience to the pipe failure.
In order to give a more customer-oriented view of the improvement, the user connections affected by the critical scenarios above a given demand deficit threshold, before and after the optimization process, are counted. In
Table 4, the results are summarized, considering an initial situation with all open valves, and an initial situation with 1% of closed valves. A reduction of the unsatisfied user connects is observed after the optimization, and in particular it is very consistent for the 25% of the demand deficit relative to the Test2. In this case, the performance of the network is significantly improved after the optimization.
Considering that in every scenario the optimization consists in changing the valve statuses in order to reach a higher resilience,
Table 5 reports the number of times that every single valve is used for each objective function. In this way, it is possible to check which are the critical valves of the network, and so the ones that the water utility has to pay extra attention to. It can be noted that there are two valves operated many times with all the objective functions. In particular, for all cases, the most operated one is the valve 839.
4. Conclusions
In the present paper, a methodology to maximize the quality of the service during a pipe failure event has been studied. The obtained results prove that it is possible to make a WDN more resilient, in terms of unsatisfied demands, by changing the valve statuses. It has been applied to an over-dimensioned and highly looped network that has resulted in being already very resilient to failures.
The methodology can be used either during critical scenarios, or during maintenance works. It indicated also the valves operated more frequently during critical scenarios, which is a useful information for network management to preserve their functioning. Moreover, this is a useful information also in performing valve location designing analysis.
In future studies, the methodology will be applied to more complex networks, in particular divided into district meter areas (DMAs), where the resilience is lower due to the closure of boundary valves. In particular, it is expected that, in this case, the optimization of valve manipulations can furnish a great improvement.
Author Contributions
The methodology was developed by I.V. and further studied by A.G.; A.G. computed the results for the case study; K.v.L. developed the code in Gondwana for valve operation, assessment of resilience and pressure driven demand simulation; I.V., M.B., C.Q., A.L., R.G. and C.D.C. supervised the work. The paper was written by A.G., A.L. and C.D.C. All authors have read and agree to the published version of the manuscript.
Funding
The development of the methodology was funded through grant 402045/080 (BTO 2018-2023). It was also supported by the Erasmus Traineeship Programme of University of Cassino and Southern Lazio.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Makropoulos, C.; Nikolopoulos, D.; Palmen, L.; Kools, S.; Segrave, A.; Vries, D.; Koop, S.; Van Alphen, H.J.; Vonk, E.; Van Thienen, P.; et al. A resilience assessment method for urban water systems. Urban Water J. 2018, 15, 316–328. [Google Scholar] [CrossRef]
- Bruneau, M.; Chang, S.E.; Eguchi, R.T.; Lee, G.C.; O’Rourke, T.D.; Reinhorn, A.M.; Shinozuka, M.; Tierney, K.; Wallace, W.A.; Von Winterfeldt, D. A Framework to Quantitatively Assess and Enhance the Seismic Resilience of Communities. Earthq. Spectra 2003, 19, 733–752. [Google Scholar] [CrossRef]
- Cimellaro, G.P.; Reinhorn, A.M.; Bruneau, M. Framework for analytical quantification of disaster resilience. Eng. Struct. 2010, 32, 3639–3649. [Google Scholar] [CrossRef]
- Cimellaro, G.P.; Tinebra, A.; Renschler, C.; Fragiadakis, M. New Resilience Index for Urban Water Distribution Networks. J. Struct. Eng. 2016, 142, 4015014. [Google Scholar] [CrossRef]
- Gargano, R.; Pianese, D. Reliability as Tool for Hydraulic Network Planning. J. Hydraul. Eng. 2000, 126, 354–364. [Google Scholar] [CrossRef]
- Tanyimboh, T.T.; Tabesh, M.; Burrows, R. Appraisal of Source Head Methods for Calculating Reliability of Water Distribution Networks. J. Water Resour. Plan. Manag. 2001, 127, 206–213. [Google Scholar] [CrossRef]
- Ciaponi, C. Performance analysis in water supply. In Performance Indicators for the Planning, Design and Management of Water Supply; Ciaponi, C., Ed.; CSDU: Milano, Italy, 2009. [Google Scholar]
- Creaco, E.; Franchini, M. Fast network multi-objective design algorithm combined with an a posteriori procedure for reliability evaluation under various operational scenarios. Urban Water J. 2012, 9, 385–399. [Google Scholar] [CrossRef]
- Herrera, M.; Abrham, E.; Stoianov, I. A Graph-Theoretic framework for assessing the resilience of sectorized water distribution network. Water Res. Manag. 2016, 30, 1685–1699. [Google Scholar] [CrossRef]
- Klise, K.A.; Bynum, M.; Moriarty, D.; Murray, R. A software framework for assessing the resilience of drinking water systems to disasters with an example earthquake case study. Environ. Model. Softw. 2017, 95, 420–431. [Google Scholar] [CrossRef] [PubMed]
- Van Thienen, P.; Vertommen, I. Gondwana: A Generic Optimization Tool for Drinking Water Distribution Systems Design and Operation. Procedia Eng. 2015, 119, 1212–1220. [Google Scholar] [CrossRef]
- Creaco, E.; Fortunato, A.; Franchini, M.; Mazzola, M.R. Comparison between Entropy and Resilience as Indirect Measures of Reliability in the Framework of Water Distribution Network Design. Procedia Eng. 2014, 70, 379–388. [Google Scholar] [CrossRef]
- Wagner, J.M.; Shamir, U.; Marks, D.H. Water Distribution Reliability: Simulation Methods. J. Water Resour. Plan. Manag. 1988, 114, 276–294. [Google Scholar] [CrossRef]
- Morley, M.S.; Tricarico, C. Pressure Driven Demand Extension for Epanet (Epanetpdd); University of Exeter: Exeter, UK, 2008. [Google Scholar]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).