Evaluation of Impulse Oscillometry in Respiratory Airway Casts with Varying Obstruction Phenotypes, Locations, and Complexities
Abstract
:1. Introduction
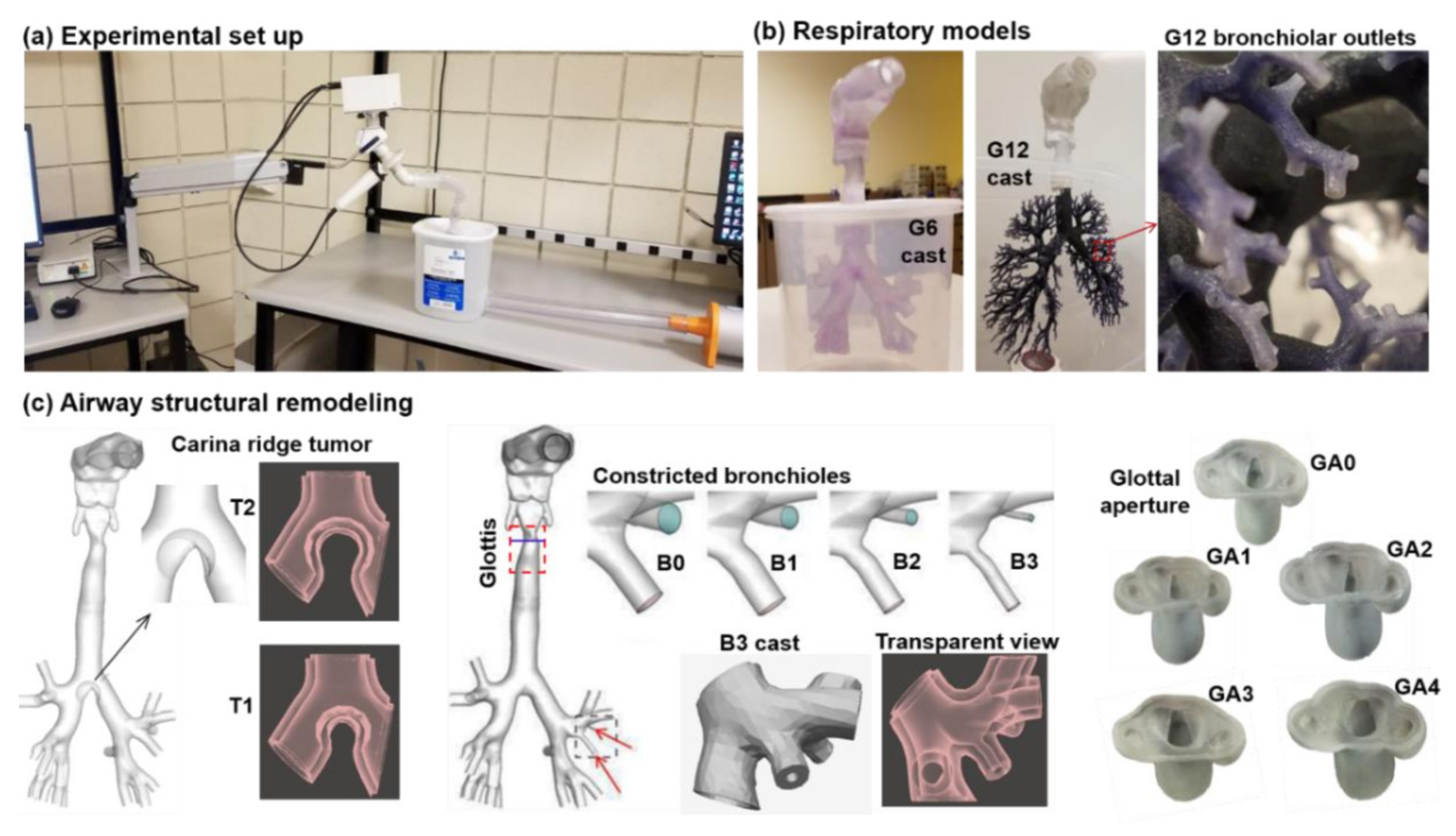
2. Materials and Methods
2.1. Study Design
2.2. IOS Testing Platform
2.2.1. Testing Procedures
2.2.2. IOS Governing Equations
2.3. Airway Models with Controlled Abnormalities
2.4. Experimental Pressure Measurements
2.5. Flow Simulations and Numerical Methods
3. Results
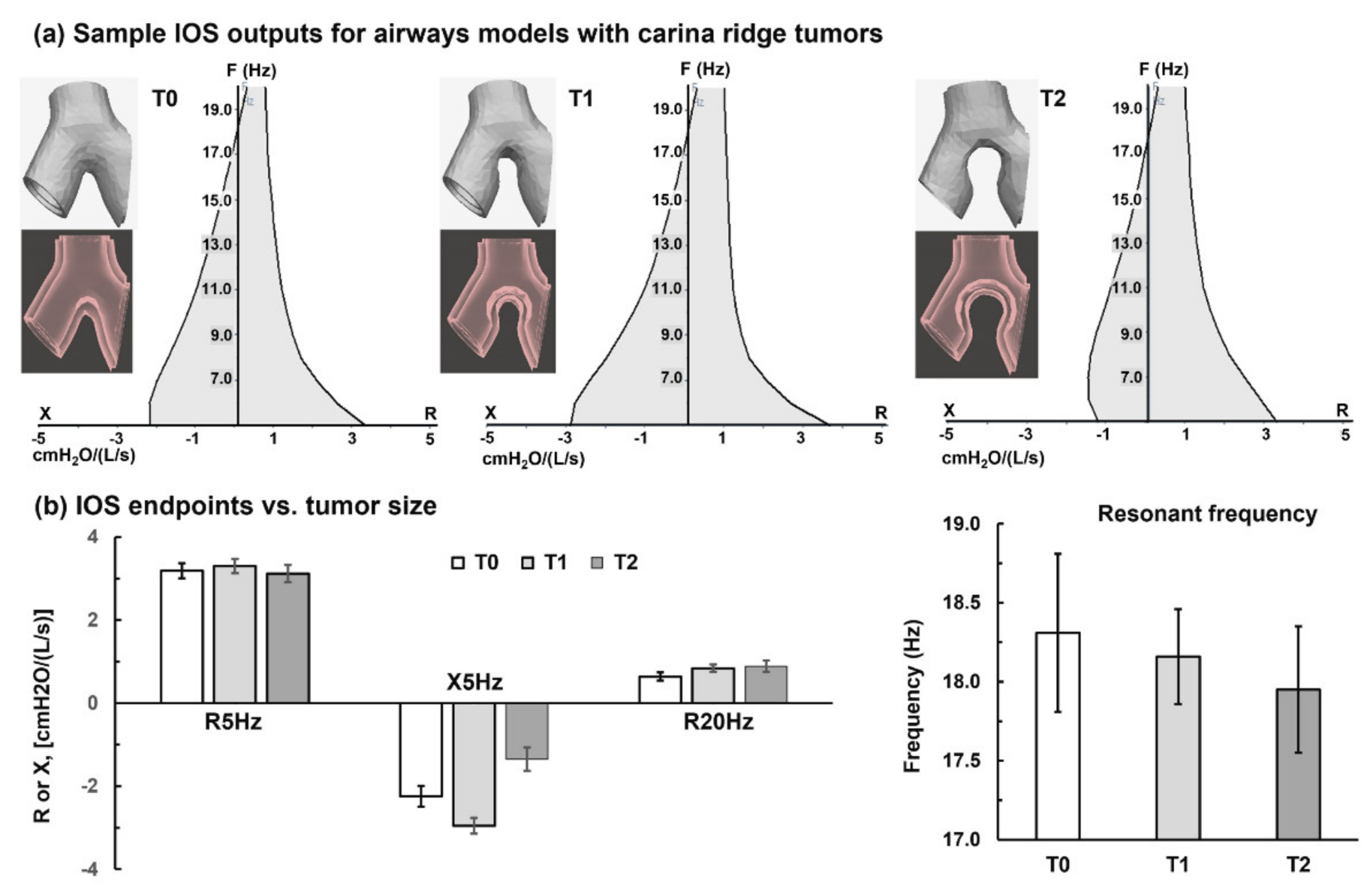
3.1. Carina Ridge Tumor
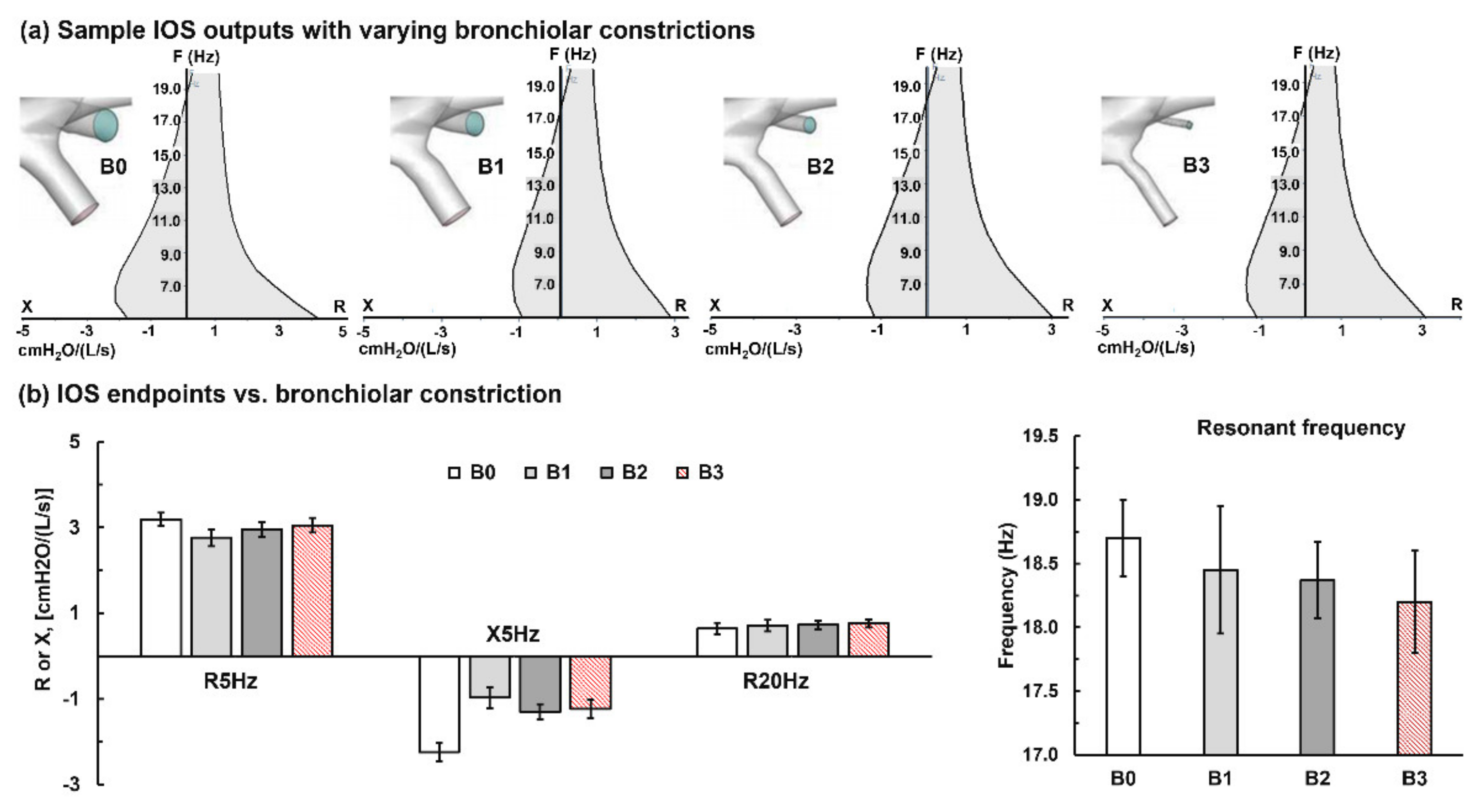
3.2. Bronchial Constrictions
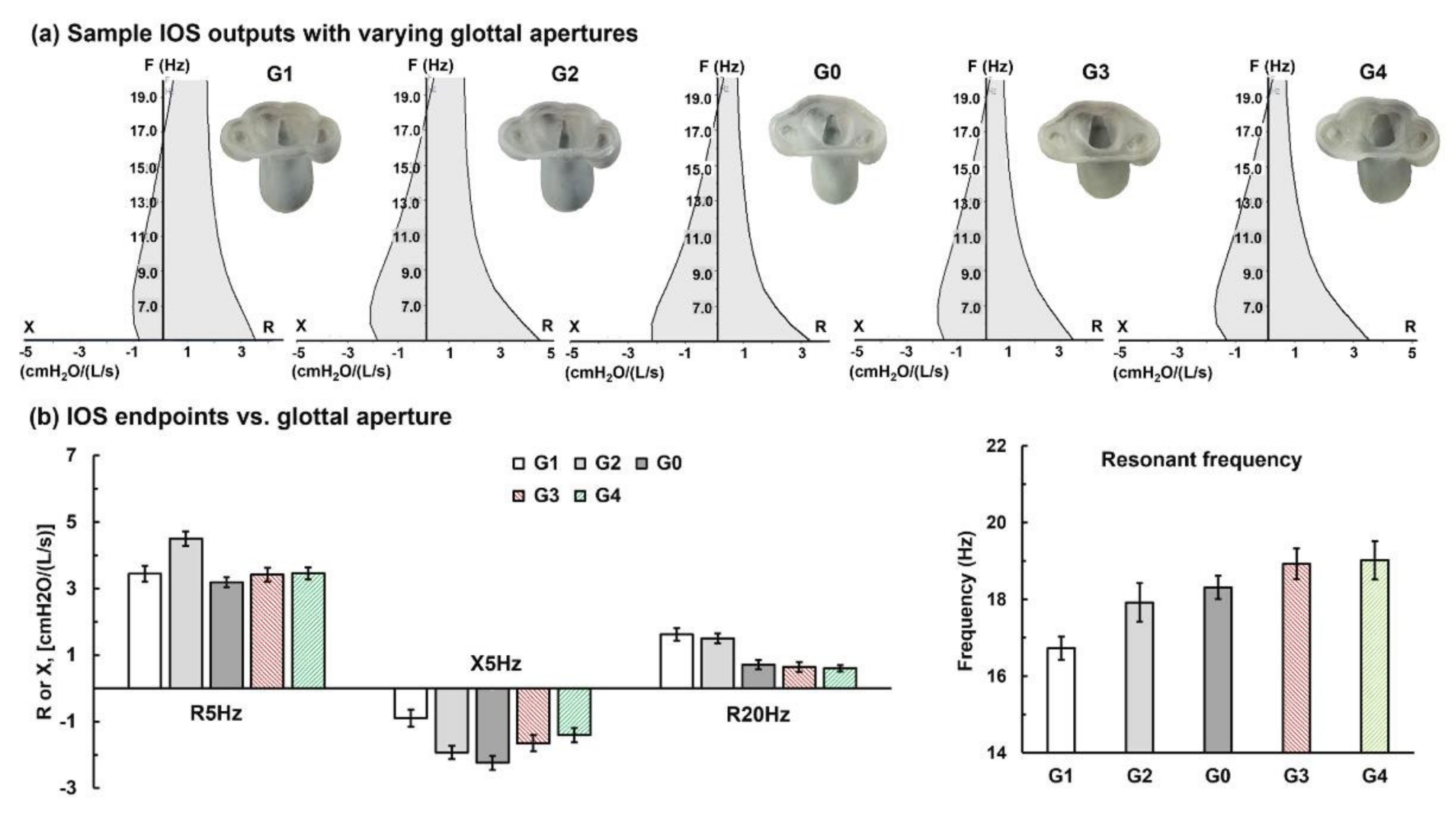
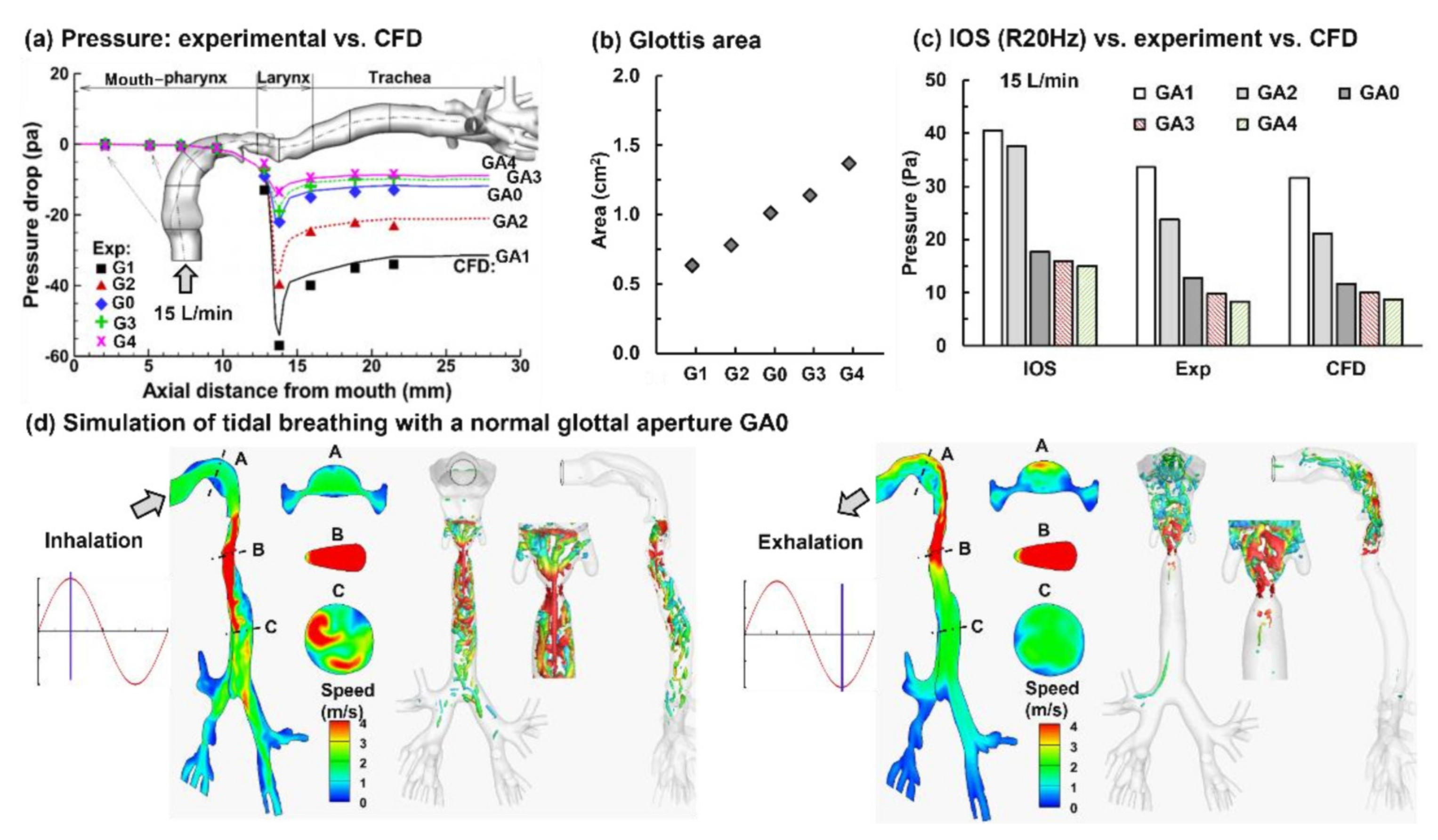
3.3. Glottal Aperture Effects
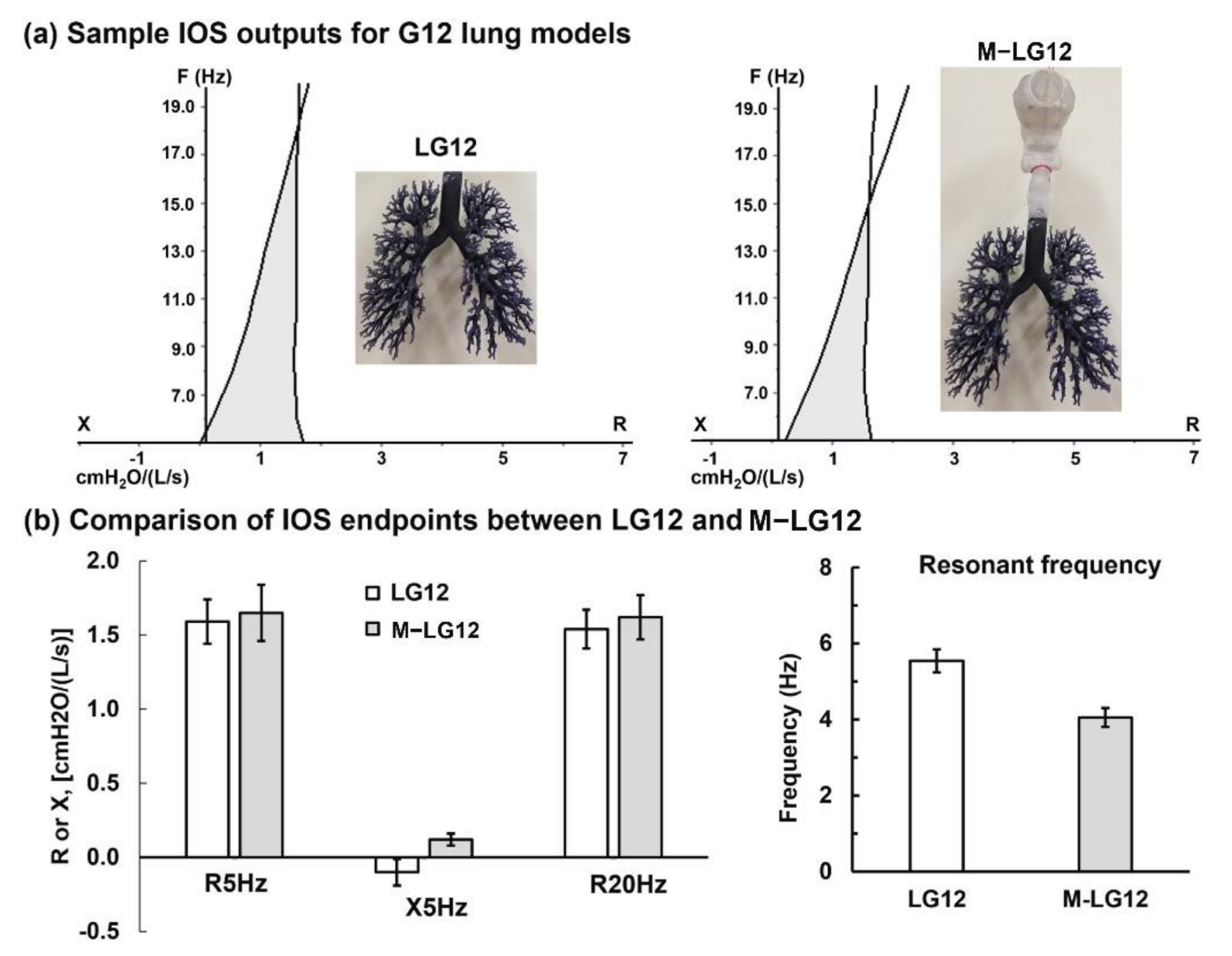
3.4. Lung Geometrical Complexity Effects: G6 vs. G12
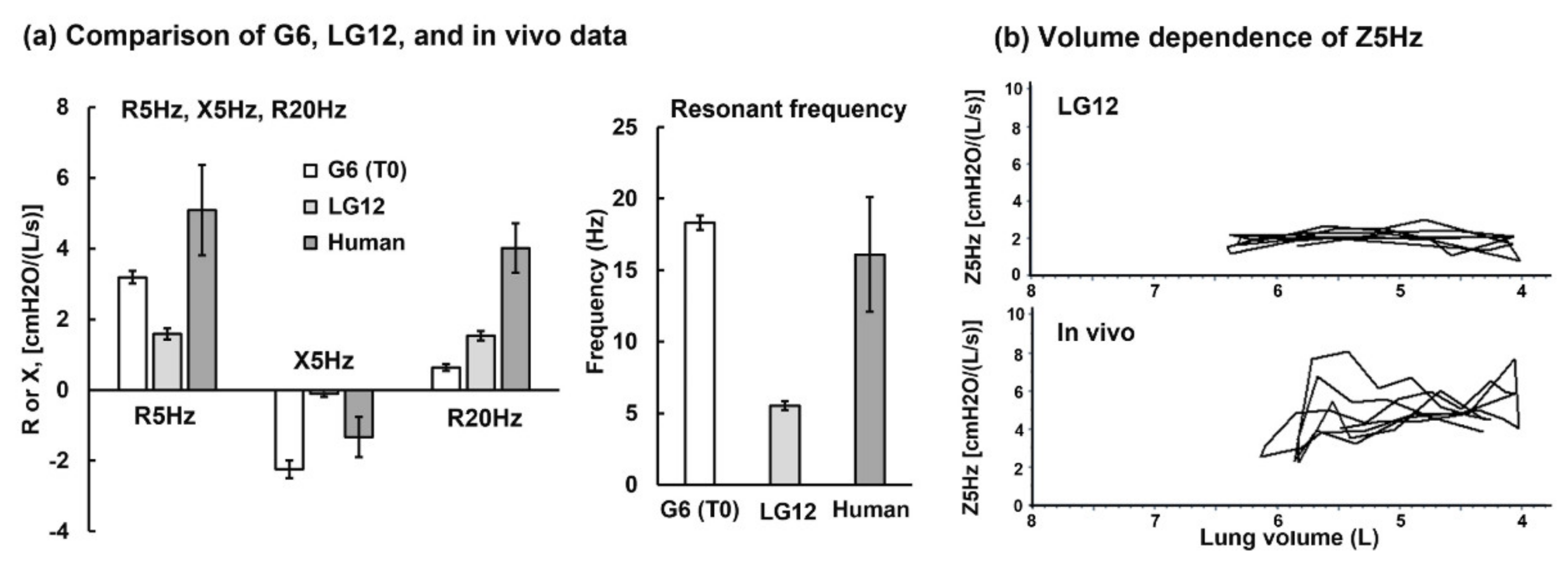
3.5. In Vitro Testing vs. Human Data
4. Discussion
4.1. How Well 3D Printed Casts Can Simulate Human Lungs?
4.2. CFD as a Complementary Tool in Understanding IOS Responses
4.3. Limitations and Future Studies
5. Conclusions
- The resonant frequency dropped with the increase in obstructions for all the three phenotypes of obstructions considered, possibly from neglect of the compliance-associated components.
- The R20Hz value increased with the increase in airway obstructions.
- R20Hz in the airway model with varying glottal apertures agreed reasonably well with complementary experimental measurements using TSI VelociCalc.
- The variations of R5Hz and X5Hz vs. airway obstructions were inconclusive in this study, indicating that 3D-printed rigid casts cannot test the compliance-related properties.
- Using 3D-printed airway casts to mimic IOS–lung interactions is still in its infancy. Factors that can significantly affect the physical realism of lung dynamics are still challenging to consider, such as elastic walls, small airway structures, and pulmonary compliance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Desai, U.; Joshi, J.M. Impulse oscillometry. Adv. Respir. Med. 2019, 87, 235–238. [Google Scholar] [CrossRef] [PubMed]
- Chaiwong, W.; Namwongprom, S.; Liwsrisakun, C.; Pothirat, C. Diagnostic ability of impulse oscillometry in diagnosis of chronic obstructive pulmonary disease. COPD 2020, 17, 635–646. [Google Scholar] [CrossRef] [PubMed]
- Martonen, T.; Fleming, J.; Schroeter, J.; Conway, J.; Hwang, D. In silico modeling of asthma. Adv. Drug Deliv. Rev. 2003, 55, 829–849. [Google Scholar] [CrossRef]
- Ruffin, R.E.; Dolovich, M.B.; Wolff, R.K.; Newhouse, M.T. The effects of preferential deposition of histamine in the human airway. Am. Rev. Respir. Dis. 1978, 117, 485–492. [Google Scholar]
- Mak, J.C.; Barnes, P.J. Autoradiographic visualization of muscarinic receptor subtypes in human and guinea pig lung. Am. Rev. Respir. Dis. 1990, 141, 1559–1568. [Google Scholar] [CrossRef]
- Carstairs, J.R.; Nimmo, A.J.; Barnes, P.J. Autoradiographic visualization of beta-adrenoceptor subtypes in human lung. Am. Rev. Respir. Dis. 1985, 132, 541–547. [Google Scholar]
- Brashier, B.; Salvi, S. Measuring lung function using sound waves: Role of the forced oscillation technique and impulse oscillometry system. Breathe 2015, 11, 57–65. [Google Scholar] [CrossRef]
- Bickel, S.; Popler, J.; Lesnick, B.; Eid, N. Impulse oscillometry: Interpretation and practical applications. Chest 2014, 146, 841–847. [Google Scholar] [CrossRef] [PubMed]
- King, G.G.; Bates, J.; Berger, K.I.; Calverley, P.; de Melo, P.L.; Dellacà, R.L.; Farré, R.; Hall, G.L.; Ioan, I.; Irvin, C.G.; et al. Technical standards for respiratory oscillometry. Eur. Respir. J. 2020, 55, 1900753. [Google Scholar] [CrossRef]
- Otis, A.B.; McKerrow, C.B.; Bartlett, R.A.; Mead, J.; McIlroy, M.B.; Selver-Stone, N.J.; Radford, E.P., Jr. Mechanical factors in distribution of pulmonary ventilation. J. Appl. Physiol. 1956, 8, 427–443. [Google Scholar] [CrossRef]
- Abdo, M.; Trinkmann, F.; Kirsten, A.M.; Pedersen, F.; Herzmann, C.; von Mutius, E.; Kopp, M.V.; Hansen, G.; Waschki, B.; Rabe, K.F.; et al. Small airway dysfunction links asthma severity with physical activity and symptom control. J. Allergy Clin. Immunol. Pract. 2021, 9, 3359–3368. [Google Scholar] [CrossRef] [PubMed]
- Hou, S.P.; Meskin, N.; Haddad, W.M. A general multicompartment lung mechanics model with nonlinear resistance and compliance respiratory parameters. In Proceedings of the American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 566–571. [Google Scholar]
- Guan, W.J.; Yuan, J.J.; Gao, Y.H.; Li, H.M.; Zheng, J.P.; Chen, R.C.; Zhong, N.S. Impulse oscillometry and spirometry small-airway parameters in mild to moderate bronchiectasis. Respir. Care 2016, 61, 1513–1522. [Google Scholar] [CrossRef]
- Handa, H.; Huang, J.; Murgu, S.D.; Mineshita, M.; Kurimoto, N.; Colt, H.G.; Miyazawa, T. Assessment of central airway obstruction using impulse oscillometry before and after interventional bronchoscopy. Respir. Care 2014, 59, 231–240. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yasuo, M.; Kitaguchi, Y.; Kinota, F.; Kosaka, M.; Urushihata, K.; Ushiki, A.; Yamamoto, H.; Kawakami, S.; Hanaoka, M. Usefulness of the forced oscillation technique in assessing the therapeutic result of tracheobronchial central airway obstruction. Respir. Investig. 2018, 56, 222–229. [Google Scholar] [CrossRef] [PubMed]
- Becker, H.D.; Slawik, M.; Miyazawa, T.; Gat, M. Vibration response imaging as a new tool for interventional-bronchoscopy outcome assessment: A prospective pilot study. Respir. Int. Rev. Thorac. Dis. 2009, 77, 179–194. [Google Scholar] [CrossRef] [PubMed]
- Wei, X.; Shi, Z.; Cui, Y.; Mi, J.; Ma, Z.; Ren, J.; Li, J.; Xu, S.; Guo, Y. Impulse oscillometry system as an alternative diagnostic method for chronic obstructive pulmonary disease. Medicine 2017, 96, e8543. [Google Scholar] [CrossRef]
- Porojan-Suppini, N.; Fira-Mladinescu, O.; Marc, M.; Tudorache, E.; Oancea, C. Lung function assessment by impulse oscillometry in adults. Ther. Clin. Risk Manag. 2020, 16, 1139–1150. [Google Scholar] [CrossRef]
- Rodriguez, E.; Bullard, C.M.; Armani, M.H.; Miller, T.L.; Shaffer, T.H. Comparison Study of Airway Reactivity Outcomes due to a Pharmacologic Challenge Test: Impulse Oscillometry versus Least Mean Squared Analysis Techniques. Pulm. Med. 2013, 2013, 618576. [Google Scholar] [CrossRef] [Green Version]
- Lipworth, B.J.; Jabbal, S. What can we learn about COPD from impulse oscillometry? Respir. Med. 2018, 139, 106–109. [Google Scholar] [CrossRef] [Green Version]
- Yasuo, M.; Kitaguchi, Y.; Tokoro, Y.; Kosaka, M.; Wada, Y.; Kinjo, T.; Ushiki, A.; Yamamoto, H.; Hanaoka, M. Differences Between Central Airway Obstruction and Chronic Obstructive Pulmonary Disease Detected with the Forced Oscillation Technique. Int. J. Chronic Obstr. Pulm. Dis. 2020, 15, 1425–1434. [Google Scholar] [CrossRef]
- Hira, H.; Munjal, J.; Zachariah, S.; Chauhan, M.; Singh, A. The site of airway obstruction among patients of emphysema: Role of impulse oscillometry. Lung India Off. Organ Indian Chest Soc. 2008, 25, 8–13. [Google Scholar] [CrossRef] [PubMed]
- Su, W.C.; Chen, Y.; Xi, J. A new approach to estimate ultrafine particle respiratory deposition. Inhal. Toxicol. 2019, 31, 35–43. [Google Scholar] [CrossRef] [PubMed]
- Longest, P.W.; Xi, J. Condensational growth may contribute to the enhanced deposition of cigarette smoke particles in the upper respiratory tract. Aerosol. Sci. Tech. 2008, 42, 579–602. [Google Scholar] [CrossRef]
- Cheng, K.H.; Cheng, Y.S.; Yeh, H.C.; Swift, D.L. Measurements of airway dimensions and calculation of mass transfer characteristics of the human oral passage. J. Biomech. Eng. 1997, 119, 476–482. [Google Scholar] [CrossRef] [PubMed]
- Xi, J.; Longest, P.W. Transport and deposition of micro-aerosols in realistic and simplified models of the oral airway. Ann. Biomed. Eng. 2007, 35, 560–581. [Google Scholar] [CrossRef] [PubMed]
- Cohen, B.S.; Sussman, R.G.; Lippmann, M. Ultrafine particle deposition in a human tracheobronchial cast. Aerosol. Sci. Tech. 1990, 12, 1082–1093. [Google Scholar] [CrossRef]
- Xi, J.; Kim, J.; Si, X.A.; Zhou, Y. Diagnosing obstructive respiratory diseases using exhaled aerosol fingerprints: A feasibility study. J. Aerosol. Sci. 2013, 64, 24–36. [Google Scholar] [CrossRef]
- Xi, J.; Kim, J.; Si, X.A.; Mckee, E.; Corley, R.A.; Kabilan, S.; Wang, S. CFD Modeling and Image Analysis of Exhaled Aerosols due to a Growing Bronchial Tumor: Towards Non-Invasive Diagnosis and Treatment of Respiratory Obstructive Diseases. Theranostics 2015, 5, 443–455. [Google Scholar] [CrossRef]
- Xi, J.; Zhao, W.; Yuan, J.E.; Kim, J.; Si, X.; Xu, X. Detecting lung diseases from exhaled aerosols: Non-Invasive lung diagnosis using ractal analysis and SVM classification. PLoS ONE 2015, 10, e0139511. [Google Scholar] [CrossRef] [Green Version]
- Xi, J.; Wang, Z.; Talaat, K.; Glide-Hurst, C.; Dong, H. Numerical study of dynamic glottis and tidal breathing on respiratory sounds in a human upper airway model. Sleep Breath 2018, 22, 463–479. [Google Scholar] [CrossRef] [Green Version]
- Kitaoka, H.; Koc, S.; Tetsumoto, S.; Koumo, S.; Hirata, H.; Kijima, T. 4D model generator of the human lung, “Lung4Cer”. In Proceedings of the 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; pp. 453–456. [Google Scholar]
- Kitaoka, H.; Nieman, G.F.; Fujino, Y.; Carney, D.; Di Rocco, J.; Kawase, I. A 4-dimensional model of the alveolar structure. J. Physiol. Sci. 2007, 57, 175–185. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kitaoka, H.; Tamura, S.; Takaki, R. A three-dimensional model of the human pulmonary acinus. J. Appl. Physiol. 2000, 88, 2260–2268. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Xi, J.; Simpson, J.; Irshad, H.; Cheng, Y.-S. Aerosol Deposition in a Nasopharyngolaryngeal Replica of a 5-Year-Old Child. Aerosol. Sci. Tech. 2013, 47, 275–282. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, M.; Xi, J.; Irshad, H.; Cheng, Y.-S. Nasal Deposition in Infants and Children. J Aerosol Med 2014, 26, 110–116. [Google Scholar] [CrossRef]
- Xi, J.; Yuan, J.E.; Zhang, Y.; Nevorski, D.; Wang, Z.; Zhou, Y. Visualization and quantification of nasal and olfactory deposition in a sectional adult nasal airway cast. Pharm. Res. 2016, 33, 1527–1541. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Xi, J.; Si, X.; Kim, J.; Su, G.; Dong, H. Modeling the pharyngeal anatomical effects on breathing resistance and aerodynamically generated sound. Med. Biol. Eng. Comput. 2014, 52, 567–577. [Google Scholar] [CrossRef]
- Xi, J.; Yuan, J.E.; Yang, M.; Si, X.; Zhou, Y.; Cheng, Y.-S. Parametric study on mouth–throat geometrical factors on deposition of orally inhaled aerosols. J. Aerosol. Sci. 2016, 99, 94–106. [Google Scholar] [CrossRef]
- Kalchiem-Dekel, O.; Hines, S.E. Forty years of reference values for respiratory system impedance in adults: 1977–2017. Respir. Med. 2018, 136, 37–47. [Google Scholar] [CrossRef] [Green Version]
- Kaczka, D.W.; Dellacá, R.L. Oscillation mechanics of the respiratory system: Applications to lung disease. Crit. Rev. Biomed. Eng. 2011, 39, 337–359. [Google Scholar] [CrossRef] [Green Version]
- Bates, J.H.; Irvin, C.G.; Farré, R.; Hantos, Z. Oscillation mechanics of the respiratory system. Compr. Physiol. 2011, 1, 1233–1272. [Google Scholar] [PubMed]
- Lundblad, L.K.A.; Robichaud, A. Oscillometry of the respiratory system: A translational opportunity not to be missed. Am. J. Physiol. Lung Cell Mol. Physiol. 2021, 320, L1038–L1056. [Google Scholar] [CrossRef] [PubMed]
- Williamson, P.A.; Clearie, K.; Menzies, D.; Vaidyanathan, S.; Lipworth, B.J. Assessment of small-airways disease using alveolar nitric oxide and impulse oscillometry in asthma and COPD. Lung 2011, 189, 121–129. [Google Scholar] [CrossRef] [PubMed]
- Hafez, M.R.; Abu-Bakr, S.M.; Mohamed, A.A. Forced oscillometry track sites of airway obstruction in bronchial asthma. Ann. Allergy Asthma Immunol. 2015, 115, 28–32. [Google Scholar] [CrossRef]
- Qi, G.S.; Zhou, Z.C.; Gu, W.C.; Xi, F.; Wu, H.; Yang, W.L.; Liu, J.M. Detection of the airway obstruction stage in asthma using impulse oscillometry system. J. Asthma Off. J. Assoc. Care Asthma 2013, 50, 45–51. [Google Scholar] [CrossRef]
- Wollmer, P.; Tufvesson, E.; Wennersten, A.; Malmqvist, U.; Engström, G.; Olsson, H.K.; Zaigham, S.; Frantz, S.; Nihlén, U. Within-session reproducibility of forced oscillometry. Clin. Physiol. Funct. Imaging 2021, 41, 401–407. [Google Scholar] [CrossRef]
- Zheng, S.; Hu, Y.; Chen, Z.; Wang, M.; Liao, W. Predicting asthma exacerbation by impulse oscillometry evaluation of small airway function and fractional exhaled nitric oxide in preschool children. Pediatr. Pulmonol. 2020, 55, 1601–1607. [Google Scholar] [CrossRef]
- Dawman, L.; Mukherjee, A.; Sethi, T.; Agrawal, A.; Kabra, S.K.; Lodha, R. Role of impulse oscillometry in assessing asthma control in children. Indian Pediatr. 2020, 57, 119–123. [Google Scholar] [CrossRef]
- Díaz Palacios, M.; Hervás Marín, D.; Giner Valero, A.; Colomer Hernández, N.; Torán Barona, C.; Hernández Fernández de Rojas, D. Correlation between impulse oscillometry parameters and asthma control in an adult population. J. Asthma Allergy 2019, 12, 195–203. [Google Scholar] [CrossRef] [Green Version]
- Oppenheimer, B.W.; Goldring, R.M.; Berger, K.I. Distal airway function assessed by oscillometry at varying respiratory rate: Comparison with dynamic compliance. COPD 2009, 6, 162–170. [Google Scholar] [CrossRef] [PubMed]
- Linhas, R.; Lima, F.; Coutinho, D.; Almeida, J.; Neves, S.; Oliveira, A.; Ladeira, I.; Lima, R.; Campainha, S.; Guimarães, M. Role of the impulse oscillometry in the evaluation of tracheal stenosis. Pulmonology 2018, 24, 224–230. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Xi, J.; Han, P.; Wongwiset, N.; Pontius, J.; Dong, H. Computational analysis of a flapping uvula on aerodynamics and pharyngeal wall collapsibility in sleep apnea. J. Biomech. 2019, 94, 88–98. [Google Scholar] [CrossRef] [PubMed]
- Shimoda, T.; Obase, Y.; Nagasaka, Y.; Kishikawa, R.; Iwanaga, T. Lung Sound Analysis and the Respiratory Cycle Dependence of Impulse Oscillometry in Asthma Patients. Intern. Med. Tokyo Jpn. 2019, 58, 47–52. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Andrade, D.S.M.; Ribeiro, L.M.; Lopes, A.J.; Amaral, J.L.M.; Melo, P.L. Machine learning associated with respiratory oscillometry: A computer-aided diagnosis system for the detection of respiratory abnormalities in systemic sclerosis. Biomed. Eng. Online 2021, 20, 31. [Google Scholar] [CrossRef]
- Walenga, R.L.; Babiskin, A.H.; Zhao, L. In Silico Methods for Development of Generic Drug-Device Combination Orally Inhaled Drug Products. CPT Pharmacomet. Syst. Pharmacol. 2019, 8, 359–370. [Google Scholar] [CrossRef] [Green Version]
- Xi, J.; Talaat, M.; Si, X.A.; Chandra, S. The application of statistical shape modeling for lung morphology in aerosol inhalation dosimetry. J. Aerosol Sci. 2021, 151, 105623. [Google Scholar] [CrossRef]
- Chandra, S.S.; Xia, Y.; Engstrom, C.; Crozier, S.; Schwarz, R.; Fripp, J. Focused shape models for hip joint segmentation in 3D magnetic resonance images. Med. Image Anal. 2014, 18, 567–578. [Google Scholar] [CrossRef]
- Heimann, T.; Meinzer, H.P. Statistical shape models for 3D medical image segmentation: A review. Med. Image Anal. 2009, 13, 543–563. [Google Scholar] [CrossRef]
- Castro-Mateos, I.; Pozo, J.M.; Cootes, T.F.; Wilkinson, J.M.; Eastell, R.; Frangi, A.F. Statistical shape and appearance models in osteoporosis. Curr. Osteoporos. Rep. 2014, 12, 163–173. [Google Scholar] [CrossRef] [PubMed]
- Fitzpatrick, C.; FitzPatrick, D.; Lee, J.; Auger, D. Statistical design of unicompartmental tibial implants and comparison with current devices. Knee 2007, 14, 138–144. [Google Scholar] [CrossRef]
- Hauser, R.; Smoliński, J.; Gos, T. The estimation of stature on the basis of measurements of the femur. Forensic Sci. Int. 2005, 147, 185–190. [Google Scholar] [CrossRef]
- Krishan, K.; Chatterjee, P.M.; Kanchan, T.; Kaur, S.; Baryah, N.; Singh, R.K. A review of sex estimation techniques during examination of skeletal remains in forensic anthropology casework. Forensic Sci. Int. 2016, 261, e161–e168. [Google Scholar] [CrossRef]
- Sella, G.; Hirsh, A.E. The application of statistical physics to evolutionary biology. Proc. Natl. Acad. Sci. USA 2005, 102, 9541–9546. [Google Scholar] [CrossRef] [Green Version]
- Bryan, R.; Nair, P.B.; Taylor, M. Use of a statistical model of the whole femur in a large scale, multi-model study of femoral neck fracture risk. J. Biomech. 2009, 42, 2171–2176. [Google Scholar] [CrossRef]
- Talaat, M.; Si, X.A.; Dong, H.; Xi, J. Leveraging statistical shape modeling in computational respiratory dynamics: Nanomedicine delivery in remodeled airways. Comput. Methods Programs Biomed. 2021, 204, 106079. [Google Scholar] [CrossRef]
- Si, X.A.; Talaat, M.; Su, W.C.; Xi, J. Inhalation dosimetry of nasally inhaled respiratory aerosols in the human respiratory tract with locally remodeled conducting lungs. Inhal. Toxicol. 2021, 33, 143–159. [Google Scholar] [CrossRef]
| G6 Cast (T0) | Ref | (ULN) | (LLN) | %Ref | Best | Tr1 | Tr2 | Tr3 | Tr4 | Tr5 |
|---|---|---|---|---|---|---|---|---|---|---|
| R5Hz cmH2O/(L/s) | 2.92 | 4.57 | 1.26 | 118 | 3.44 | 3.75 | 3.38 | 3.48 | 3.23 | 3.35 |
| R5Hz cmH2O/(L/s) | −0.01 | 1.64 | −1.67 | 7053 | −0.90 | −0.85 | −0.93 | −0.93 | −0.90 | −0.88 |
| R5Hz cmH2O/(L/s) | 2.51 | 3.82 | 1.19 | 1.62 | 1.62 | 1.82 | 1.62 | 1.53 | 1.55 | 1.59 |
| Fres. 1/s | 16.73 | 16.73 | 16.8 | 16.81 | 16.67 | 16.54 | 16.82 | |||
| LG12 cast | Ref | (ULN) | (LLN) | %Ref | Best | Tr1 | Tr2 | Tr3 | Tr4 | Tr5 |
| R5Hz cmH2O/(L/s) | 2.92 | 4.57 | 1.26 | 55 | 1.59 | 1.68 | 1.83 | 1.49 | 1.73 | 1.54 |
| R5Hz cmH2O/(L/s) | −0.01 | 1.64 | −1.67 | 768 | −0.10 | −0.14 | −0.05 | −0.11 | −0.08 | −0.09 |
| R5Hz cmH2O/(L/s) | 2.51 | 3.82 | 1.19 | 61 | 1.54 | 1.62 | 1.72 | 1.43 | 1.68 | 1.49 |
| Fres. 1/s | 5.54 | 5.76 | 5.32 | 5.61 | 5.46 | 5.52 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Si, X.; Xi, J.S.; Talaat, M.; Donepudi, R.; Su, W.-C.; Xi, J. Evaluation of Impulse Oscillometry in Respiratory Airway Casts with Varying Obstruction Phenotypes, Locations, and Complexities. J. Respir. 2022, 2, 44-58. https://doi.org/10.3390/jor2010004
Si X, Xi JS, Talaat M, Donepudi R, Su W-C, Xi J. Evaluation of Impulse Oscillometry in Respiratory Airway Casts with Varying Obstruction Phenotypes, Locations, and Complexities. Journal of Respiration. 2022; 2(1):44-58. https://doi.org/10.3390/jor2010004
Chicago/Turabian StyleSi, Xiuhua, Jensen S. Xi, Mohamed Talaat, Ramesh Donepudi, Wei-Chung Su, and Jinxiang Xi. 2022. "Evaluation of Impulse Oscillometry in Respiratory Airway Casts with Varying Obstruction Phenotypes, Locations, and Complexities" Journal of Respiration 2, no. 1: 44-58. https://doi.org/10.3390/jor2010004
APA StyleSi, X., Xi, J. S., Talaat, M., Donepudi, R., Su, W.-C., & Xi, J. (2022). Evaluation of Impulse Oscillometry in Respiratory Airway Casts with Varying Obstruction Phenotypes, Locations, and Complexities. Journal of Respiration, 2(1), 44-58. https://doi.org/10.3390/jor2010004







