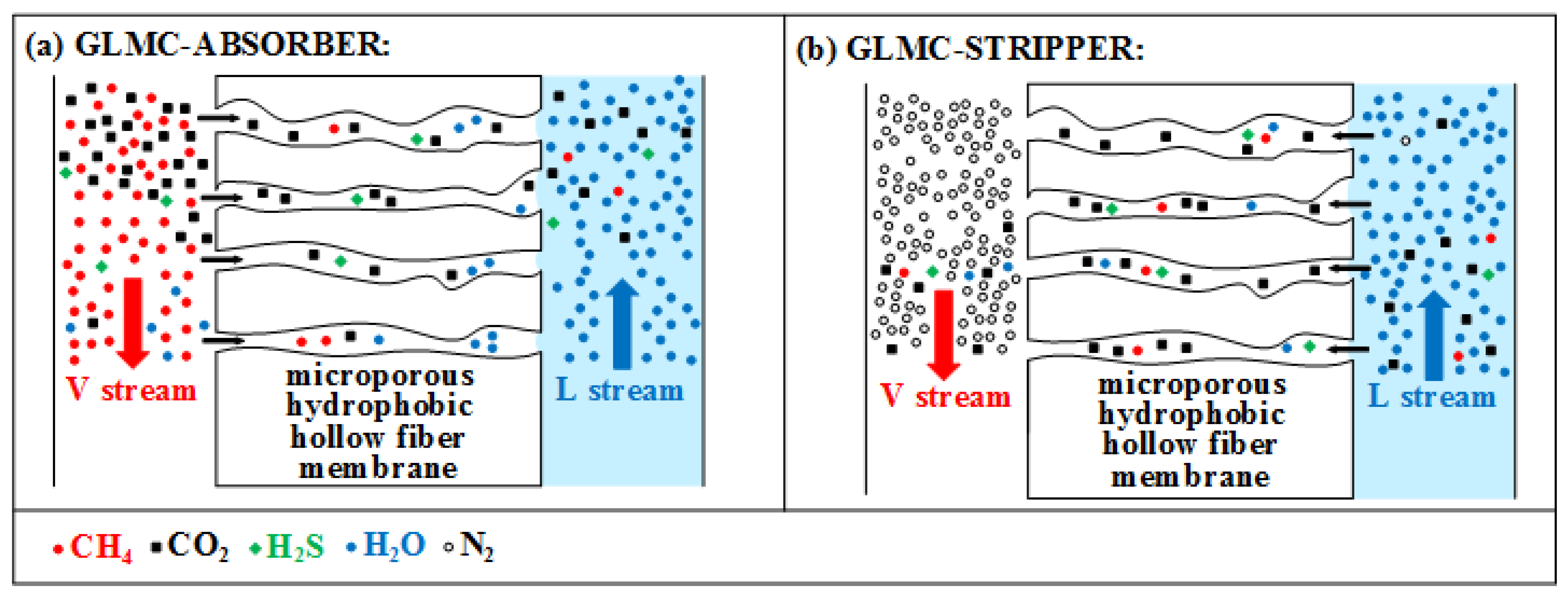
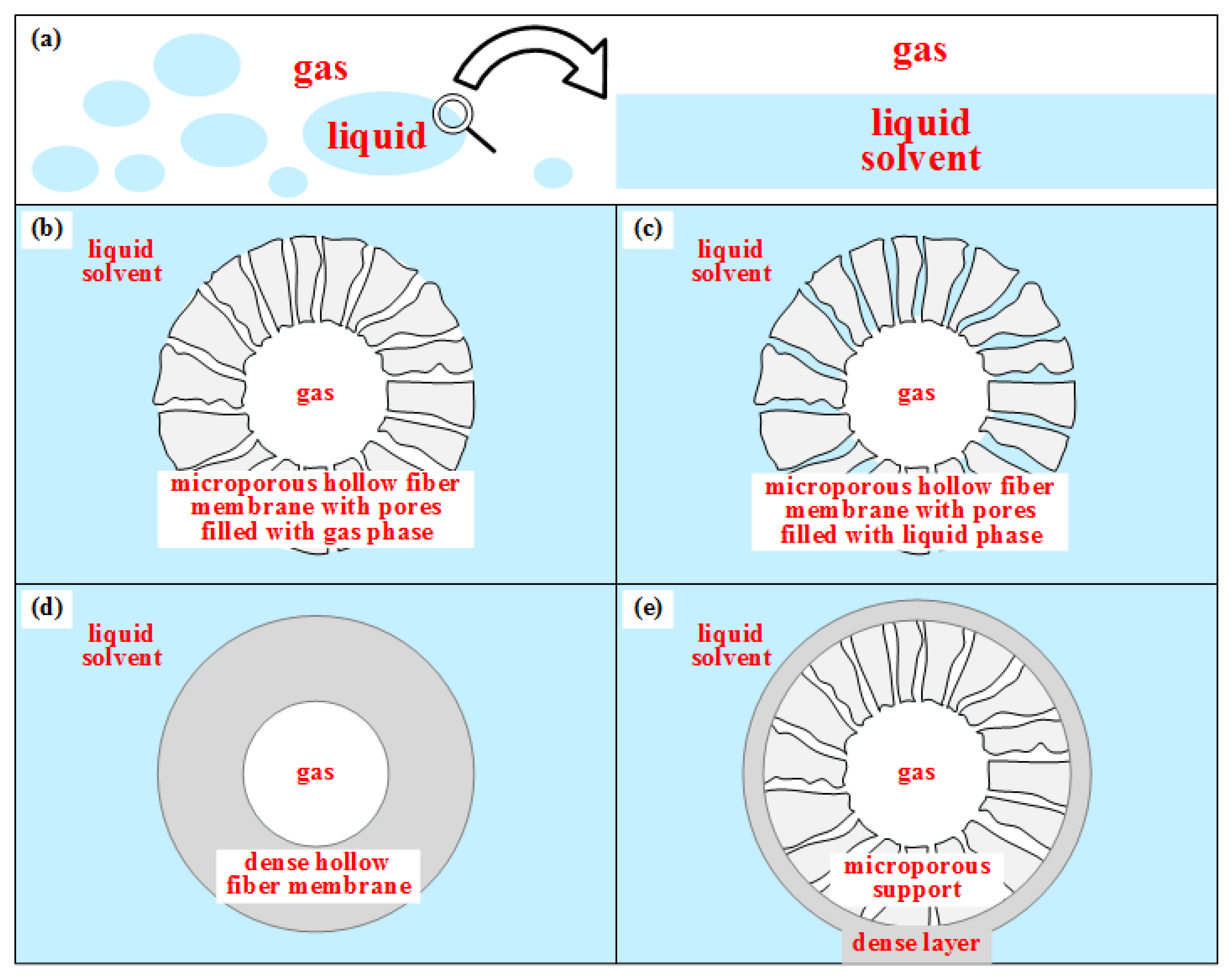
4.1. GLMC Modeling for CO2 Absorption from NG
As NG decarbonation is performed at high-pressure and frequently with concentrated aqueous-amine solvents highly deviating from ideal solution behavior, rigorous thermodynamic models must be used for property prediction, comprising an Equation-of-State (EOS) for the vapor phase and an activity coefficient model for the liquid phase. Moreover, mass, heat, and momentum transfers occur simultaneously and influence each other; i.e., related predictions must be accurate to ensure reliability in industrial scale conditions. Moreover, the multicomponent mass transfer must be considered as CO2/H2S simultaneous removal is necessarily entailing unavoidable transfers of CH4 and other hydrocarbons. Besides, H2O can move in both directions, V→L or L→V.
Dindore et al. [
129] modeled CO
2/H
2S mass transfer with chemical reaction in a cross-flow GLMC with aqueous-K
2CO
3 solvent. The model is simplified and does not include energy balance and thermal effects. Experiments were carried out with a CO
2-H
2S-N
2 gas mixture which deviates from NG behavior as CH
4 is considerably more soluble than N
2. Therefore CO
2/CH
4 selectivity and CH
4 losses were not evaluated.
The GLMC models for CO
2 removal from NG of Al-Marzouqi et al. [
65] (
Table 7, Equations (47), (48), (50), (51), (53), (55) and (56)) with water solvent and Al-Marzouqi et al. [
130] (
Table 7, Equations (47), (48), (50), (51), (53), (55) and (56)) with aqueous-MEA and aqueous-NaOH were developed for low-pressure GLMC. Faiz and Al-Marzouqi [
131] presented a low-pressure GLMC model (
Table 7, Equations (47), (50) and (55)) based on reaction kinetics for H
2S absorption in aqueous-Na
2CO
3, which is not suitable for high-pressure NG processing. Furthermore, NG purification requires CO
2/H
2S simultaneous removal. Faiz and Al-Marzouqi [
76] developed a low-pressure model (
Table 7, Equations (47), (48), (50), (51), (53), (55)–(60)) for CO
2/H
2S simultaneous removal with aqueous-MEA. Keshavarz et al. [
78] presented a simplified GLMC model (
Table 7, Equation (55),
Table 8, Equation (68)) for CO
2/H
2S simultaneous removal from CO
2-H
2S-N
2 gas mixture (CO
2 = 15 mol%, H
2S = 5 mol%, N
2 = 80 mol%) with aqueous-DEA. Unfortunately, low-pressure and isothermal behavior was considered an unrealistic situation in high-pressure CO
2/H
2S absorption from NG with aqueous-amines, which is a highly exothermic process. In addition, ideal gas behavior was also assumed.
Faiz and Al-Marzouqi [
132] developed the first GLMC modeling study at high-pressure (P ≤ 50 bar) for CO
2 removal from NG considering water and aqueous-amines solvents. The model (
Table 7, Equations (47), (48), (50), (51), (53), and (55)–(57)) consisted of differential equations in cylindrical coordinates for CO
2 mass transfer solved with COMSOL software and was validated with Marzouk et al. [
98] experiments. GLMC transfers of H
2S, CH
4, and water were not taken into account. The authors justified neglecting CH
4 transfer due to the low CH
4 solubility in aqueous solutions. However, this assumption is problematic because with physical solvents at high-pressure, CH
4 losses can reach 9–10%, while with chemical solvents, CH
4 losses are considerably smaller but never negligible. In addition, this model does not prescribe energy balance and head-loss calculations; i.e., heat effects and temperature/pressure changes were not predicted. Posteriorly, Faiz and Al-Marzouqi [
133] presented a low-pressure isothermal GLMC model (
Table 7, Equations (47), (48), (50), (51), (53), (55), and (56)) for CO
2/H
2S simultaneous removal from NG with aqueous-K
2CO
3 solvent. The authors implemented two serial GLMC modules to favor reaction kinetics so that all the H
2S and a small portion of CO
2 are removed in module #1 and the remaining CO
2 is removed in module #2. However, this low-pressure isothermal model is not compatible with real NG processing conditions.
Faiz et al. [
134] proposed a GLMC model (
Table 7, Equations (47), (48), (50), (51), (53), and (55)–(57)) taking into account the gas velocity change in the axial direction as CO
2 is removed from the gas initially with 10 mol% CO
2. The model was validated with experiments of [
97] and showed, for high CO
2 content in the gas feed, that the effect of gas velocity change is more evident since the gas velocity decreases significantly. The decrease in gas velocity implies a higher residence time, entailing higher CO
2 capture. Model predictions were in better agreement with the experimental data for chemical solvents, but they were not good for physical solvents. This study also contemplates a low-pressure GLMC NG purification.
Rezakazemi et al. [
82] studied CO
2/H
2S simultaneous GLMC removal from NG using aqueous-MDEA as solvent. A two-dimensional model was proposed (
Table 7, Equations (48), (51)–(53), (55), and (56)), considering axial and radial diffusion, convection, chemical reactions, and momentum equations. The model was solved with CFD techniques. However, the model was developed at low-pressure and ambient temperature, entailing oversimplified assumptions; namely: (i) isothermal GLMC profiles are unrealistic in a system with exothermic reactions of CO
2 with concentrated aqueous-MDEA; (ii) ideal gas behavior is not adequate at real operating conditions of high-pressure NG sweetening. The authors affirm that CH
4 does not dissolve in the solvent; another unrealistic outcome and water mass transfer was also ignored.
Boributh et al. [
135] developed a 1D GLMC model (
Table 6, Equation (37)) with water solvent for estimating the mass transfer area considering different GLMC module arrangements: single-stage module, two-stage parallel modules, two-stage serial modules with the separated liquid flow, and two-stage serial modules with combined liquid flow. In Boributh et al. [
136] (
Table 6, Equation (37)), the GLMC with water solvent model includes the effect of pore size distribution to predict MPW and CO2 mass transfer correctly. Boributh et al. [
137] proposed a GLMC model (
Table 6, Equation (37)) for the design of multistage GLMC schemes with aqueous-MEA solvent. Works [
135,
136,
137] modeled counter-current GLMC CO
2 removal from CO
2-CH
4 gas mixtures considering partial MPW. These works are similar, performed low-pressure case studies, and presented the same GLMC modeling simplifications: isothermal conditions, ideal gas behavior, and zero head-loss.
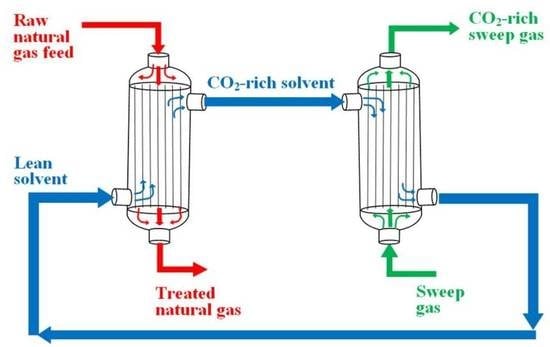
A new GLMC concept is found in Cai et al. [
138], which proposed to carry out both the acid–gas absorption and solvent regeneration in a single step, i.e., in the same GLMC cross-flow modules. The aim is to save space in offshore processing plants. In this concept, the solvent flows on the shell-side, while two types of HFM are used in the module. CO
2-rich NG flows in the microporous HFM at high-pressure (P = 50 bar), wherein CO
2/H
2S absorptions take place at the gas-liquid interface. Inside the GLMC module, there is also dense HFM, kept at low-pressure (P = 1 bar) so that the difference of pressure in relation to the solvent generates a stripping driving force which promotes solvent regeneration in the shell-side as CO
2/H
2S scape to the low-pressure HFM. Therefore, CO
2/H
2S absorption and solvent regeneration occur simultaneously in the GLMC module, theoretically resulting in better absorption efficiency as the solvent is kept with low acid-gas content while flowing through the GLMC module. The authors also suggest using baffles to improve mass transfer efficiency by increasing turbulence. Propylene carbonate was the physical solvent as it presents better CO
2 solubility in comparison with water. The use of physical solvents is recommended as chemical solvents demand heat-intensive regeneration and require more space on offshore rigs. Indeed, it is easy to understand that this GLMC concept would never work with chemical solvents because chemical solvents would necessarily require a GLMC-absorber and a separate solvent regeneration step. The GLMC model considers isothermal mass transfers through the microporous HFMs, through the dense HFMs, and on the shell side. The authors assumed isothermal conditions and neglected gas head-losses. Despite the new concept, this work did not trigger analogous works by other authors since then.
An important and disruptive contribution comes from Ghasem et al. [
60], as it was the first model to consider GLMC water vaporization and the respective heat effect, a phenomenon systematically ignored in the GLMC modeling literature, which prefers to assume isothermal GLMC modeling without water mass transfer, a fact that Ghasem et al. proved to be unrealistic. In [
60], GLMC CO
2 absorption from NG was performed using an aqueous-NaOH solvent. In comparison with previous works, a more complete GLMC model was developed (
Table 7, Equations (47), (49)–(51), (54), (56), and (61)–(67)). Instead of considering isothermal GLMC and neglecting pressure drop, the model [
60] considers mass, energy, and momentum balances. The work carried out experiments and results were compared with model predictions. Nonetheless, experiments were performed at atmospheric pressure with a raw NG composition of 10 mol% CO
2 and 90 mol% CH
4. Besides, in real NG processing, the high-pressure raw NG is water-saturated, so that water can transfer in both directions, a fact not considered in [
60]. Moreover, real raw NG contains H
2S and light hydrocarbons (C
2+).
After the good work in [
60], Ghasem et al. [
139] published a badly written article with several typos, including the article title and the titles of some sections. CO
2 absorption from NG was investigated experimentally and theoretically with a GLMC model comprising only material balances (
Table 7, Equations (47), (48), (51), (53), and (56)). Aqueous potassium glycinate was compared with aqueous-amine solvents showing superior results, a questionable outcome. The article is a mess: the text creates confusion among MEA, DEA, and MDEA all the time. Thereby, it is impossible to be sure of which aqueous-amine solvents were investigated.
A complete GLMC thermodynamic model is found in de Medeiros et al. [
33], which simulated an offshore high-pressure NG purification process for GLMC CO
2 removal with aqueous-MEA-MDEA. The GLMC model comprises a new acid-gas, water, and alkanolamines equilibrium model (AGWA model) [
140] capable of reproducing chemical absorption and desorption of CO
2 (and H
2S) in aqueous-amines, over a wide range of pressures, which was calibrated in terms of equilibrium constants with AGWA VLE data from the literature. The real species VLE is superimposed on the multi-reactive chemical equilibrium for the formation of fictitious species (non-ionic and non-volatile complexes), defining a reactive VLE or RVLE [
140]. The GLMC
V and
L flows are parallel and unidimensional (1D), assuming compressible two-phase plug-flow for
V and
L streams. The model also considered the mass transfer of CH
4, H
2O, and light hydrocarbons and was developed through rigorous mass, energy, and momentum balances for
V and
L streams, allowing heat and mass interfacial transfers, with shear and compressibility terms, and all properties of all phases rigorously calculated by the Peng–Robinson EOS (PR-EOS) and Soave–Redlich–Kwong EOS (SRK-EOS). This model was able to reproduce several interesting behaviors along the GLMC length as profiles of both streams, such as molar flowrates, species compositions, temperatures, pressures, fugacities, and CO
2/CH
4 selectivity [
33]. Model equations are shown in Equations (1) to (7).
Trans-membrane fluxes of real species “k”: Real species EMWR (Equivalent Moles Without Reaction) mass balances for V and L streams:
where
are trans-membrane fluxes of real species “
k”;
are trans-membrane mass transfer coefficients of species “
k”;
and
are the
V and
L fugacities of real species “
k”;
is the interfacial area per length;
and
are
V molar flowrate and the
L EMWR molar flowrate of real species “
k.”
Momentum balances for V and L:
where
is the GLMC shell internal diameter,
is GLMC inclination,
is the gravity acceleration,
is the number of real species,
and
are isobaric expansivity of
V and
L at RVLE,
and
are isothermal compressibility of
V and
L at RVLE,
and
are species “k” mol expansivity of
V and
L at RVLE,
and
are
V and
L temperatures,
and
are
V and
L absolute pressures,
and
are
V and
L flow velocities,
and
are
V and
L densities,
and
are sections of
V and
L flows,
and
are the shear stress on contact surfaces in
V and
L flows.
Energy balances for V and L:
where
and
are
V and
L molar isobaric heat capacities,
and
are the
V and
L EMWR molar masses,
and
are
V and
L mass flowrates,
is the HFM mass flux,
and
are external and internal heat transfer coefficients,
is the outside temperature,
and
are the PMP
EMWR energies of “
k” in
V and
L.
Faiz et al. [
141] described a 2D GLMC model (
Table 7, Equations (48), (50), (51), (53), and (55)–(57)) for H
2S removal from high-pressure NG with water solvent. Model predictions agreed perfectly with the experimental data only at low pressures. At high pressures, agreement with experimental data only occurred when the “pseudo-wetting” condition (3%) (MPW) was assumed. The model ignores the transfer of other species, energy balances, and head losses.
Razavi et al. [
79] modeled low-pressure GLMC CO
2 removal from NG with an aqueous di-isopropanol amine (DIPA) solvent. The 2D GLMC model (
Table 7, Equations (47), (48), (50)–(53), (55), and (56)) ignores thermal effects (isothermal GLMC), assumes ideal gas behavior, and considers only species mass balances without head-loss calculations.
Cai et al. [
142] modeled crossflow GLMC for CO
2 removal from NG. Experiments were performed and a CFD modeling was solved with ANSYS software. The model considers mass and momentum balances, without energy balance, in three-dimensional geometry. The study considered carbon capture from pure CO
2 with water solvent at P = 1 atm and T = 298 K, which are distant values from real NG processing conditions.
Abdolahi-Mansoorkhani and Seddighi [
80] investigated HFM improvements with the incorporation of montmorillonite nanoparticles for CO
2 removal from CO
2-CH
4 mixtures (CO
2 = 10 mol%, CH
4 = 90 mol%) using aqueous-MEA, aqueous-PZ, aqueous-TEA, and aqueous-EDA solvents. A 2D finite element modeling in cylindrical coordinates predicted GLMC behavior (
Table 7, Equations (47), (48), (50)–(53), and (55)–(60)). Despite the highly exothermic ChA with aqueous-amines, the model ignores energy balances, considering isothermal profiles without head-loss, ideal gas behavior, and VLE via Henry’s law. Besides, only CO
2 is transferred.
Nakhjiri et al. [
143] conducted experiments and developed a two-dimensional (2D) GLMC model (
Table 7, Equations (47), (48), (50), (51), (53) and (55)–(57)) for prediction of CO
2 removal from CO
2-CH
4 mixtures (CO
2 = 30 mol%, CH
4 = 70 mol%) with aqueous-MEA and aqueous-TEA. Predicted results were compared with experimental counterparts in both non-wetting and partial wetting (MPW) modes of operation. Model differential equations were solved with COMSOL software. This work did not unveil any noticeable novelty, as the isothermal low-pressure 2D model was developed with simplifications found in previously published works such as ideal gas behavior, Henry’s law for VLE, absence of H
2S and H
2O in raw NG, only CO
2 transference, and no head-loss. Nakhjiri et al. [
144] used almost the same equations (
Table 7, Equations (47), (48), (50), (51), (53), and (55)–(60)) of [
143], with the inclusion of aqueous-NaOH experiments, finding the following order of CO
2 removal performances: aqueous-MEA > aqueous-NaOH > aqueous-TEA. Model predictions were compared with data from [
95]. Nakhjiri and Heydarinasab [
145] studied GLMC CO
2 removal from a CO
2-CH
4 gas mixture (CO
2 = 10 mol%, CH
4 = 90 mol%) with aqueous ethylenediamine (EDA), aqueous 2-(1-piperazinyl)-ethylamine (PZEA) and aqueous potassium sarcosinate (PS) solvents using a model (
Table 7, Equations (47), (48), (50)–(53) and (55)–(57)) similar to [
143,
144] models, considering non-wetting mode of operation. Model predictions were compared with data from [
65] for validation, an awkward procedure since the experiments from [
65] were conducted with pure water solvent. Posteriorly, Nakhjiri et al. [
84] slightly improved their previous GLMC model [
143] by considering simultaneous CO
2/H
2S removal with aqueous-K
2CO
3 solvent, including momentum balance equations (
Table 7, Equations (47), (48), (50), (51), (53), (55)–(57) and (61)–(64)). However, all the remaining simplifications of [
143,
144,
145] were kept.
Mesbah et al. [
90] presented a theoretical study of GLMC CO
2 removal from CO
2-CH
4 gas mixtures using an aqueous-K
2CO
3 solvent containing a 2-methylpiperazine (2MPZ) promoter. Despite considering a complex chemical reaction scheme of CO
2 with aqueous-K
2CO
3-2MPZ, the 2D GLMC model (
Table 7, Equations (47), (48), (50)–(53) and (55)–(57)) is simplified with the following assumptions: isothermal profiles, low-pressure, ideal gas behavior, Henry’s law VLE, and only CO
2 is transferred. Awkwardly, the supposed model validation was performed with experimental data from [
143], which involved only aqueous-MEA and aqueous-TEA solvents.
Fougerit et al. [
146] performed an experimental and modeling study of GLMC CO
2 removal from CO
2-CH
4-H
2O gas mixtures covering a wide range of CO
2 contents, namely: NG sweetening (CO
2 = 5–10 mol%), post-combustion carbon capture (CO
2 = 10–15 mol%), biogas upgrading (CO
2 = 35–50 mol%). However, the authors ignored that each feed mixture needs different process conditions. Besides, the 1D mass transfer model is simplified: only CO
2 transference is considered, isothermal GLMC, ideal gas behavior, and low-pressure (P = 5.0 bar).
The GLMC decarbonation of coal-bed methane, an NG abundant in China, was studied by Zhang et al. [
147] with a 2D GLMC model (
Table 7, Equations (48), (50), (51), (53) and (55)–(57)) considering aqueous-MEA, aqueous-DEA, aqueous-TEA and aqueous 1-(2-hydroxyethyl)pyrrolidine solvents. The GLMC model is also simplified: low-pressure, ideal gas behavior, and isothermal GLMC profiles were adopted for ChA with aqueous-amine solvents. Pan et al. [
148] adopted the same GLMC model (
Table 7, Equations (48), (50), (51), (53), (55), and (56)) for the simultaneous CO
2/H
2S removal from coal-bed methane using aqueous-K
2CO
3 with potassium lysinate (PL) solvent. The pressure influence in the range 1 bar–50 bar on CO
2/H
2S transfers was studied (still under ideal gas behavior).
Ghasem [
149] experimentally studied GLMC CO
2 absorption from CO
2-CH
4 mixtures (CO
2 = 10 mol%, CH
4 = 90 mol%) and also the CO
2 stripping from the solvent. The solvent was 0.5 mol/L aqueous potassium glycinate in a closed loop with N
2 as stripping gas. Experimental results were compared with predictions of a GLMC model, which is 2D axisymmetric and transient, considering CO
2/CH
4 transports in GLMC-absorber, and CO
2/N
2 transports in GLMC-stripper. The model is simplified: it considers low-pressure, ideal gas behavior, isothermal profiles, VLE via Henry’s law, and lacks energy balance and head-loss calculations. H
2S and H
2O are absent. Ghasem [
150] investigated the influence of HFM bore size on the highly exothermic CO
2 removal from NG with aqueous-MEA, considering VLE via Henry’s law. In comparison with [
149], it was used a similar low-pressure 2D GLMC model at steady-state (
Table 7, Equations (47), (48), (50), (51), (53), (55) and (56)).
GLMC Modeling with Professional Process Simulators for CO2 Removal from NG
Implementation of GLMC modeling for carbon capture from NG in professional process simulators is crucial for rigorous GLMC modeling due to more accurate thermodynamic properties estimation [
128].
Among the few works implementing GLMC modeling in process simulators, there are studies on CO
2 removal from other sorts of gas streams (e.g., biogas and syngas). Kerber and Repke [
151] studied GLMC biogas purification, while Villeneuve et al. [
152,
153] studied carbon capture from post-combustion flue gas with GLMC implementation in Aspen Custom Modeler. Usman et al. [
154] developed a GLMC model for pre-combustion CO
2 capture in MATLAB. Posteriorly, Usman et al. [
155] integrated the MATLAB code with the HYSYS process simulator through the Cape-Open simulation compiler.
There are just a few works on GLMC modeling in process simulators for CO
2 removal from NG. Hoff et al. [
156] conducted laboratory-scale experiments on CO
2 removal from flue gas with aqueous-MEA and on high-pressure CO
2 removal from NG with aqueous-MDEA. The authors developed a 2D diffusion-reaction model to predict experimental absorption rates and concentration/temperature GLMC profiles. The model considers mass, energy, and momentum balances, and VLE was modeled via Henry’s law with activity coefficients to account for liquid phase non-ideality. The model equations—shown in Equations (8) to (16)—were solved via MATLAB.
Gas mass balance equations:
where
is the ideal gas constant,
is the specific GLMC inner surface area,
is the fraction of total area available to gas flow,
is the
V molar isobaric heat capacity of species “
k” and
is the heat rate.
Trans-membrane mass flux of species “k”:
where
is the partial pressure of “
k,”
is Henry’s law constant of “
k,”
is the concentration of “
k” at the liquid–membrane interface,
is the gas film mass transfer coefficient of “
k,”
and
are the internal and external HFM radiuses,
is the effective membrane diffusivity of “
k,”
is the molecular diffusivity of “
k,”
is membrane porosity,
is membrane tortuosity,
is
V heat transfer coefficient,
is the HFM heat transfer coefficient and
is the temperature at liquid-membrane interface.
Transport model for the liquid phase based upon mass and energy conservation:
where
is
L molar concentration of “
k,”
is the chemical reaction rate in terms of “
k,”
is the
L molar isobaric heat capacity,
is
L thermal conductivity, and
is the enthalpy of reaction.
Posteriorly, the model of Hoff et al. [
156] was improved for utilization in process simulators, including new thermodynamic models for aqueous-MEA and aqueous-MDEA/PZ, and solvent flow modeling inside HFM or in shell-side, besides improvements for gas and solvent head-loss calculation. In Hoff and Svendsen [
157], the GLMC model comprises an RVLE CO
2-water-amines system based on the Deshmukh–Mather approach [
158], employing a modified Debye–Hückel model similar to Kuranov et al. [
159]. The gas phase was modeled with PR-EOS and the trans-membrane fluxes were modified as shown in Equations (17) to (19).
where
,
,
,
,
,
,
,
,
,
are respectively, compressibility factor, gas film, membrane and liquid film mass transfer coefficients of “
k,” enhancement factor, combined diffusivity, membrane diffusivity, Knudsen diffusivity, diffusivity of membrane at liquid phase and partial liquid penetration, respectively.
In Hoff and Svendsen [
157], the following gas treatments were simulated: (i) low-pressure post-combustion carbon capture from offshore gas-turbines flue-gas to attain 90% capture with 30 w/w% aqueous-MEA in GLMC cross-flow modules installed in the process simulator SINTEF/NTNU CO2SIM; (ii) high-pressure (P = 70 bar) offshore sweetening of NG (CO
2 = 10 mol%) to CO
2 = 2.5 mol% using 30 w/w% aqueous-MDEA in GLMC parallel-flow modules installed in the process simulator Protreat; (iii) high-pressure (P = 70 bar) offshore sweetening of NG (CO
2 = 10 mol%) to LNG specification of CO
2 = 50 ppm-mol using 30 w/w% aqueous-MDEA with 5 w/w% PZ in GLMC parallel-flow modules installed in the process simulator Protreat. In comparison with packing columns, total equipment volume can be reduced to 25% using GLMC with liquid on the shell side. With liquid flowing inside HFM, the advantage reduces significantly. Authors highlighted that GLMC may significantly improve offshore CO
2 capture from gas–turbine flue-gas and for NG sweetening but pointed out the doubtful advantage of GLMC for post-combustion carbon capture due to a large number of required GLMC modules and high head-losses of
V and
L streams.
Quek et al. [
160] developed a predictive GLMC model for high-pressure NG sweetening. A temperature correction was calculated for the adiabatic GLMC to account for the ChA thermal effects. Model equations were implemented in gPROMS modeling language using a second-order centered finite difference scheme to discretize the differential equations. Model results attained good comparison with lab-scale experiments of CO
2 absorption from CH
4-CO
2 and N
2-CO
2 mixtures at P = 11 bar and from pilot-scale experiments on NG sweetening at P = 54 bar, both using 39 w/w% aqueous-MDEA with 5 w/w% PZ.
Quek et al. [
161] indicated limitations of their work [
160] since it fails to describe the gradual increase in temperature through the equipment, besides not considering solvent evaporation. Thus, an improvement of their GLMC model was carried out in [
161] via combining 1D and 2D mass balance equations to include MPW. Real gas behavior is implemented via PR-EOS. The GLMC model is shown in Equations (20) to (26).
Membrane-dry mass balance: Membrane-wet mass balance: Liquid mass balance:
where
and
are
V and
L average velocities,
is the average
V concentration of CO
2,
is
V CO
2 diffusivity,
is
L diffusivity of “
k,”
is the outer radius of the virtual cylindrical domain around each HFM,
is the gas-membrane interface at the pore-side,
is
L volumetric flowrate,
is the number of HFM within GLMC module and
is the fiber volume fraction (packing-ratio).
To predict solvent evaporation in counter-current GLMC [
161], the authors assumed a water-saturated gas at the GLMC outlet and used Raoult’s law to calculate H
2O content. However, there is some impertinency in this assumption, as the two premises for Raoult’s law are: (i) ideal gas vapor phase at low-pressure; (ii) ideal solution liquid phase with chemically similar species. As the GLMC has a gas phase at high pressure in VLE with a non-ideal solution with high ionic interaction between species, it would be much more adequate to use an equation-of-state for vapor fugacities, besides an excess Gibbs free energy local composition model for aqueous electrolyte systems. At the end of the article, the authors admitted that Raoult’s law is questionable. Moreover, an energy balance was performed [
161], considering the heat losses of solvent evaporation. As there is an inaccuracy in solvent loss prediction, this step is probably also inaccurate. Moreover, Henry’s law was employed to calculate liquid phase methane, ethane, and propane concentrations. These steps are shown in Equations (27) to (31).
L light hydrocarbons concentrations: Light hydrocarbons loss rate:where
is
V outlet mol fraction of “
k,”
and
are
L outlet/inlet mol fraction of “
k,”
is the saturation pressure of “
k,”
is
V mass flowrate of “
k,”
is
V molar mass of “
k,”
is
V average velocity and
is
L mass isobaric heat capacity.
Besides ignoring solvent head-loss [
161], the authors tried to convince us that gas head-loss can be safely neglected. On the other hand, several researchers, including Hoff and Svendsen [
157], proved exactly the opposite. The model was solved with gPROMS modeling language. Gas feed compositions were 20–24 mol% CO
2 in a N
2-CO
2 mixture (P = 54 bar, T = 293 K) in lab experiments and 5–18 mol% CO
2 NG (P = 54 bar, T = 298 K) in pilot runs. Solvent was 37 w/w% aqueous-MDEA with 6 w/w% PZ (P = 54.30 bar, T = 310–313 K) in lab experiments and 39 w/w% aqueous-MDEA with 5 w/w% PZ (T = 303–308 K) in pilot runs.
Quek et al. [
162] installed the GLMC model from [
161] in the process simulator gPROMS to perform the techno-economic assessment of the complete process for high-pressure NG sweetening and low-pressure regeneration in a closed-loop. Simulations predicted CO
2 absorption and light hydrocarbons losses, solvent evaporation, besides process energy consumption. Results were compared with data from a pilot plant in Malaysia with reasonable agreement. Raw gas composition was CO
2 = 5 mol%, CH
4 = 85 mol%, C
2H
6 = 7 mol%, C
3H
8 = 3 mol% at P = 54 bar, T = 298 K, and the fresh solvent was 39 w/w% aqueous-MDEA with 5 w/w% PZ (P = 54.3 bar, T = 303–308 K). Two solvent regenerations were considered: regeneration in stripping columns or semi-regeneration in low-pressure flash separators. Posteriorly, the design and scale-up of a commercial-scale GLMC was conducted with a semi-lean solvent at raw gas composition CO
2 = 24 mol%, CH
4 = 73 mol%, C
2H
6 = 2 mol%, C
3H
8 = 1 mol% (P = 54 bar, T = 298 K), while the semi-lean solvent was 39 w/w% aqueous-MDEA with 5 w/w% PZ (P = 54.3 bar, T = 318 K). CO
2 content was abated from 24 mol% to 6.5 mol%, which the authors considered excellent as they recommended the semi-lean regeneration with low-pressure flash to reduce energy consumption. However, it is widely known that the CO
2 target for NG sweetening usually ranges from 2 to 3 mol% [
14]; thereby, employing stripping columns for complete solvent regeneration is more adequate in this case.
Da Cunha et al. [
128] performed a technical evaluation of GLMC CO
2 removal from CO
2-rich NG using 30 w/w% aqueous-MEA through process simulations in Aspen HYSYS V8.8. The authors developed a GLMC model, with the driving force for CO
2 transfer predicted with CO
2 V and
L fugacity differences, rigorously calculated with thermodynamic resources of Aspen HYSYS V8.8 provided by the Acid-Gas package [
163] (based on Electrolyte-NRTL model) for liquid phase properties and PR-EOS for vapor properties [
164]. GLMC model equations consist of a non-linear algebraic system in Equations (32) to (34) solved by Newton-Raphson Method.
where
is the trans-membrane transfer rate of component “
k,”
is the trans-membrane mass transfer coefficient of “
k,”
is the transfer area of the GLMC battery,
and
are
V and
L CO
2 fugacities,
and
are
V and
L CO
2 molar fractions, and
and
are molar flowrates.
To perform process simulations in HYSYS, the authors created a GLMC HYSYS Unit Operation Extension (GLMC-UOE), in a similar procedure to Arinelli et al. [
165] for MP unit operation. GLMC-UOE was programmed in Visual Basic 6.0, which contains an HYSYS Type Library with commands to access HYSYS directly. After programming and compiling the code, an external DLL file was generated, which was installed through an EDF file as an available unit operation in the HYSYS palette usable in HYSYS flowsheets. The EDF file was programmed with the Aspen HYSYS Extension View Editor and also provided the GLMC-UOE property windows, where an HYSYS user interface is filled by the user with all the necessary simulation information. GLMC model equations were programmed to be solved by the Newton–Raphson Method.
GLMC-UOE [
128] is worthy of note because its present version already represents a new unit operation GLMC, which is implemented within an up-to-date professional simulation environment using full thermodynamics to calculate fluid properties and fugacities of real liquid and gas phases. Moreover, GLMC-UOE can be integrated into processing flowsheets comprising several other unit operations offered in the HYSYS palette, eventually constituting very complex process flowsheets.
4.2. GLMC Modeling for CO2 Stripping from the Solvent
Complete GLMC models for low-pressure CO
2 stripping from the solvent require the same framework of GLMC for CO
2 removal from NG, as described in the first paragraph of
Section 4.1.
Some GLMC models were developed for CO
2 stripping from physical solvents. Mehdipourghazi et al. [
166] investigated CO
2 stripping from the water via PVDF-HFM GLMC. The 2D model (
Table 7, Equations (48), (50)–(53), (55), and (56)) only considers isothermal CO
2 transfer. Lee et al. [
167] also studied vacuum-driven GLMC CO
2 stripping from water through experiments and using a 1D GLMC model (
Table 6, Equations (35)–(38)) to assess liquid flowrate, vacuum pressure, and pH. Bahlake et al. [
168] investigated GLMC CO
2/H
2S simultaneous stripping from the water via a 3D modeling approach whose differential equations were solved with COMSOL software. Sohaib et al. [
69] investigated two ionic liquids for post-combustion carbon capture via GLMC-absorber coupled to GLMC-stripper. A 2D dynamic model (
Table 7, Equations (48), (50)–(53), (55), and (56))was implemented based on low-pressure and low-temperature mass transfer equations. Vadillo et al. [
169] developed a 1D-2D GLMC model (
Table 7, Equation (55),
Table 8, Equation (68)) for vacuum-driven regeneration of the ionic–liquid 1-ethyl-3-methylimidazolium acetate [emin][Ac] solvent considering isothermal conditions. The best operating conditions were achieved at P = 0.4 bar and T = 310 K.
The literature has an evident interest in GLMC CO
2 stripping from aqueous-MEA. Ghadiri et al. [
170] used pure N
2 for CO
2 stripping in a GLMC modeling study. The 2D model (
Table 7, Equations (48), (53) and (55)–(57)) assumed isothermal and steady-state conditions, only CO
2 transference, and VLE via Henry’s law. CO
2 mass transfer predictions were compared with experimental data from [
113], with reasonable agreement. To remove CO
2 from 20 w/w% aqueous-MEA at T = 353 K, Wang et al. [
171] used vacuum-driven stripping with steam as a stripping agent on the shell side at
P = 20 kPa. The 1D-2D model (
Table 7, Equation (55),
Table 8, Equation (68)) is based on a system of steady-state continuity equations for each species with simultaneous diffusion and chemical reaction, considering isothermal operation and VLE via Henry’s law. Mohammed et al. [
172] developed a 2D GLMC model (
Table 7, Equations (48), (50)–(53), (55), and (56)) to investigate the effect of SiO
2 nanoparticles on CO
2 stripping from aqueous-MEA. Authors considered isothermal GLMC and VLE via Henry’s law. No energy balances or head-loss calculations were performed.
The following works were conducted in the context of post-combustion carbon capture. They are considered in the present review as low-pressure GLMC CO
2 stripping from the solvent is conducted similarly for both GLMC processes for carbon capture from NG and flue gas. Scholes [
173] used a simple model and a 1D rigorous model (
Table 6, Equations (35)–(37), (39), (40), (42), and (44)–(46)) with mass/energy balances and pressure drop calculation to study vacuum-driven CO
2 stripping from aqueous-MEA 30 w/w%, using steam as stripping-gas. The best stripping temperature was found between 90 °C and 105 °C. Above this temperature range, the solvent starts vaporizing, and below this range, the mass transfer driving force is drastically reduced. Scholes highlighted the trade-off between the reduction of stripping heat requirement against the vacuum pump power requirement. Zaidiza et al. [
174] developed a GLMC model for post-combustion CO
2 absorption with aqueous-MEA solvent and for the respective CO
2 stripping. The 1D adiabatic model (
Table 6, Equations (35)–(39) and (41)–(46)) considers the bidirectional mass transfer of all species (CO
2, H
2O, MEA); energy balances; and head-loss calculations via Hagen-Poiseuille equation for the HFM stream and via Happel equation [
175] for the shell-side. Model equations were presented with dimensional problems and inverted signs (e.g., Pa.s
−1 was the viscosity unit instead of Pa.s). Model assumptions include steady-state, ideal gas behavior, and VLE via Henry’s law. Water condensation/evaporation was considered at the liquid-membrane interface. The authors emphasize that GLMC-stripper needs HFM resistant to high temperatures (≈120 °C). Also, since water can be transferred in both directions, capillary condensation can occur, which would negatively influence mass transfer performance similarly to MPW.