Experimental and Molecular Dynamics Simulation of Interfacial Tension Measurements in CO2–Brine/Oil Systems: A Literature Review
Abstract
1. Introduction
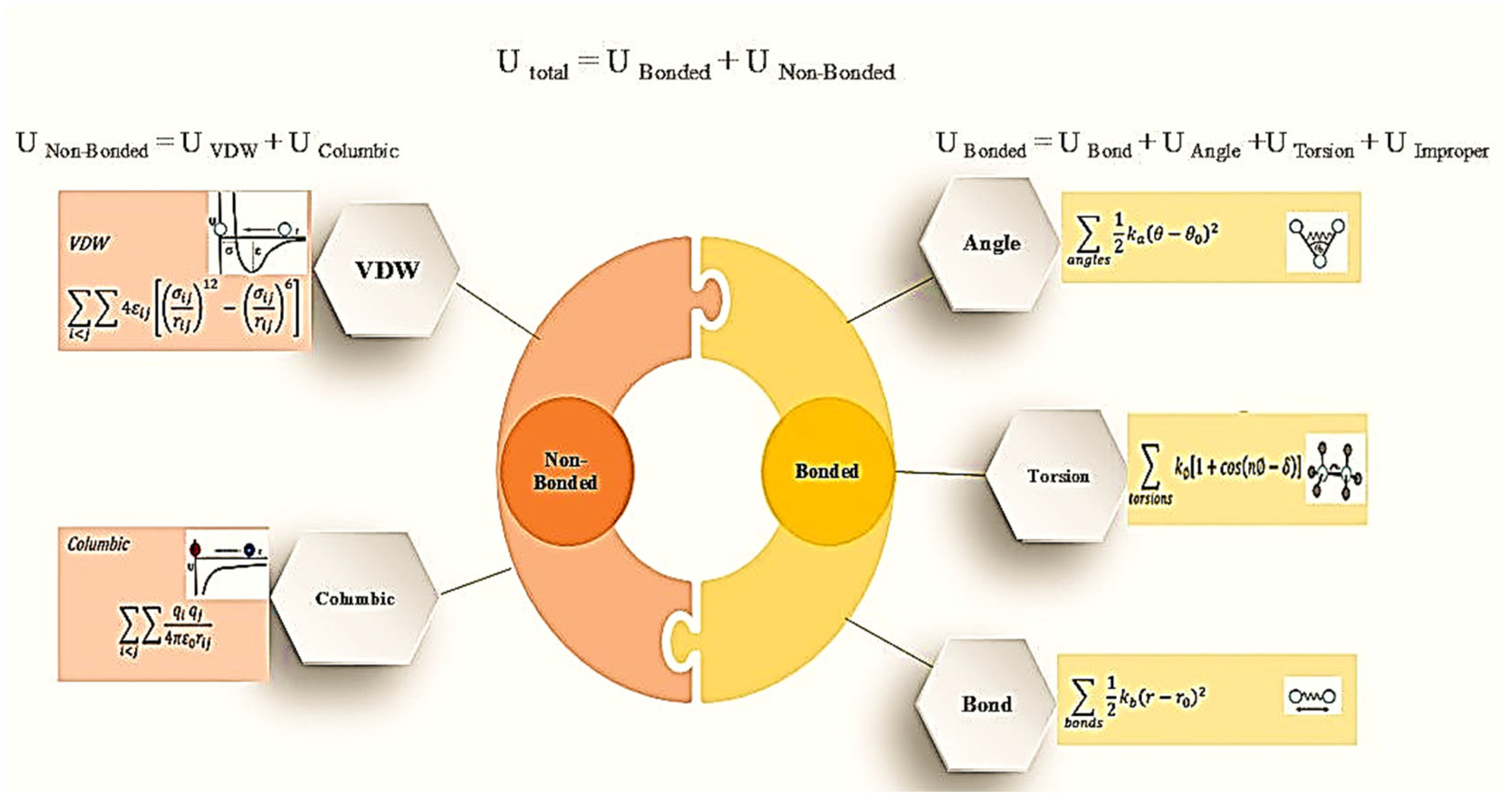
1.1. Molecular Dynamics
- Monte Carlo (MC): Introduced by Metropolis in 1953, the Monte Carlo method [4] is a non-quantum statistical technique. It converts a physical problem into a statistical one solved by random sampling. Averaging many simulation trials yields the desired property. It is conceptually simple: random moves are accepted or rejected according to an energy-based criterion. MC handles multicomponent, highly complex systems efficiently. The simulation in Monte Carlo does not accurately represent the actual movement of particles, so it can only display the static aspects of the system.
- Molecular Dynamics (MD): Alder and Wainwright developed the molecular dynamics simulation method in 1957 [5]. The molecular dynamics method utilizes the classical Newton’s equation of motion to simulate the movement of molecules. The study of molecular dynamics allows for the visualization of molecule motion and their interactions based on the forces at play between them. The fundamental concept of simulation involves the utilization of the traditional Newton equation of motion, Equation (1):
1.1.1. MD Concept and Scale
- Simulation Box
- Force field (FF)
- Ensemble
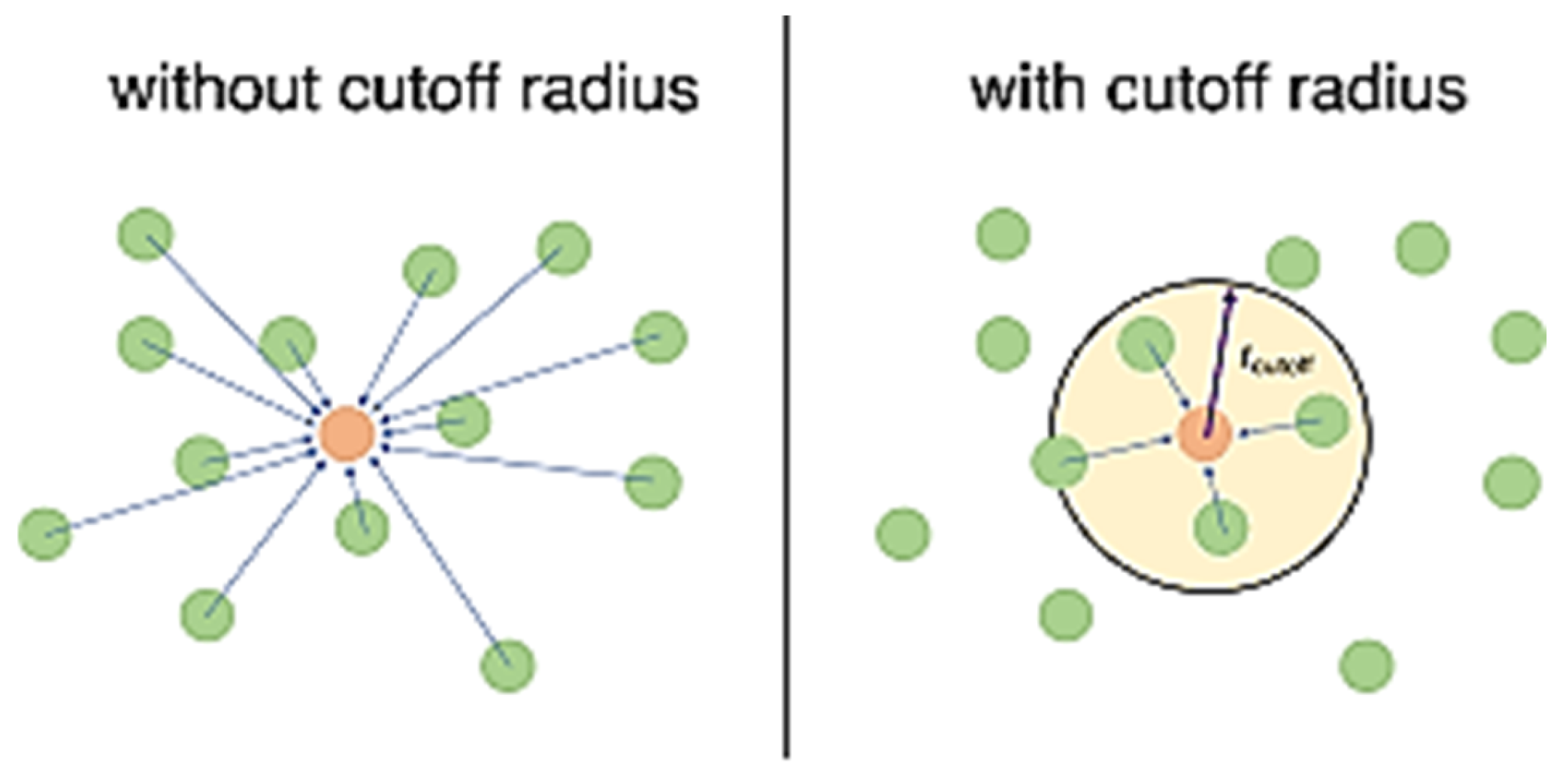
- Cut off radius
- Boundary condition
- ❖
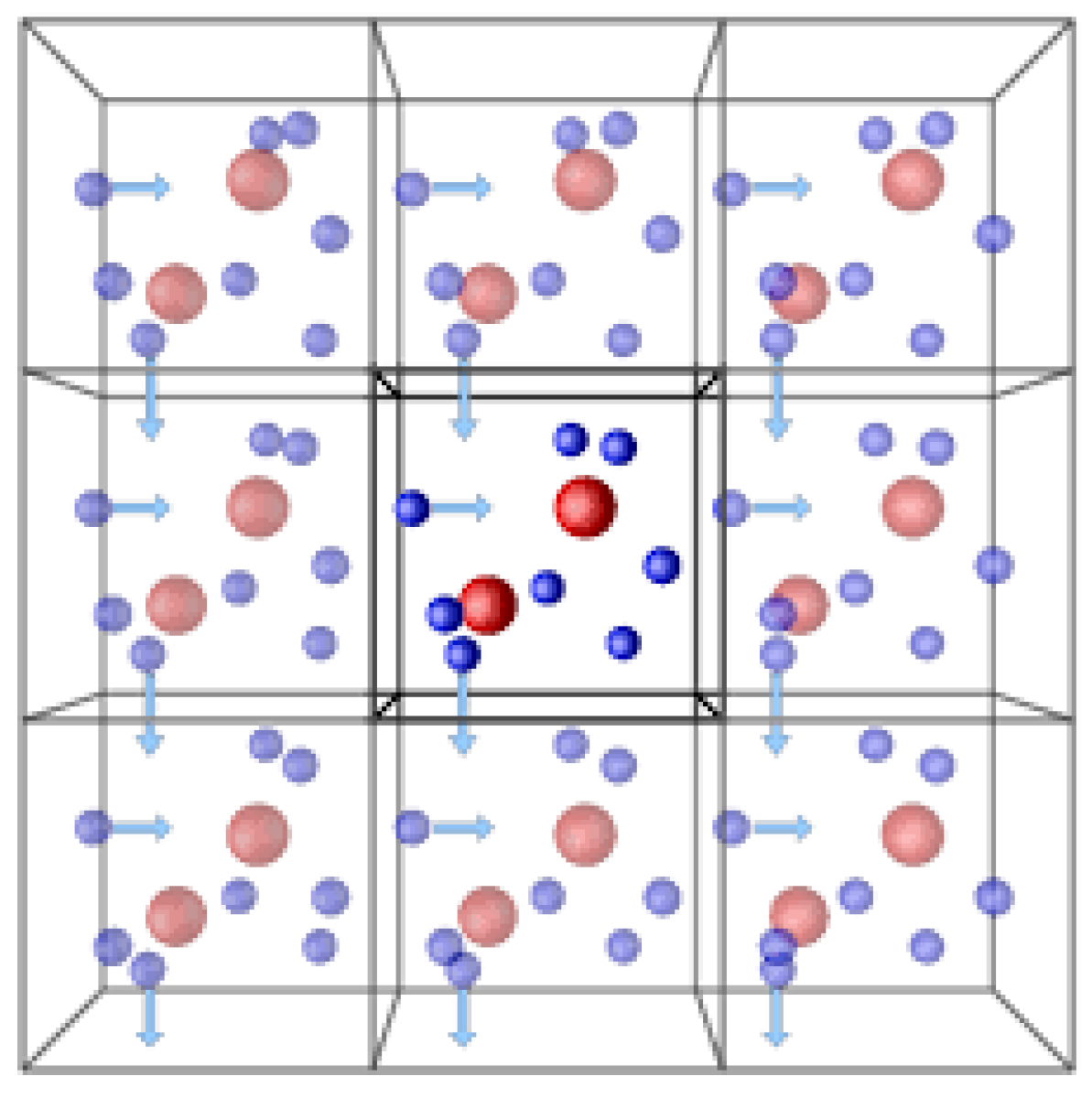
- Periodic Boundary Conditions (PBCs): This is the most widely used type. It essentially creates a repeating pattern of the simulation box. This creates the illusion of an infinitely repeating system and eliminates the unphysical effects introduced by a finite simulation box. PBCs are particularly useful for studying bulk properties of liquids, gases, and some solids. Figure 5 demonstrates the periodic boundary condition in three dimensions.
- ❖
- Fixed Boundaries: In this approach, the atoms at the edges of the simulation box are fixed in place. These fixed atoms can mimic the presence of a wall or a surface. However, fixed boundaries can introduce unphysical effects near the edges, as the real system would not have these abrupt stops. This method is sometimes used for studying thin films or interfaces, but with caution due to the potential artifacts.
1.1.2. MD Software
1.2. Molecular Structure of Oil and Injection Fluids
1.2.1. Different Types of Oil Structure
- Paraffin: The usual formula for paraffin, often known as n-alkanes, is CnH2n+2. Gases correspond to n = 1 to 4, liquids to n = 5 to 15, and solids (paraffin waxes) to n ≥ 15.
- Naphthene, which has the general formula CnH2n, produces saturated ring compounds when n is one of the following: 5, 6, or 7. A typical crude oil will contain 2% or more of the common components cyclopentane and cyclohexane, which are frequently observed in the methylated state.
- Aromatics: aromatics are hydrocarbons that are commonly classified as a minor category since they share a fourth bond with all carbons in at least one benzene ring (C6H6). Due to their ability to react and add hydrogen or other elements to their rings, they are known as undersaturated.
1.2.2. Injection Fluid Structures
1.3. Experimental Methodology of IFT Measurement
1.3.1. Force Tensiometry Methods
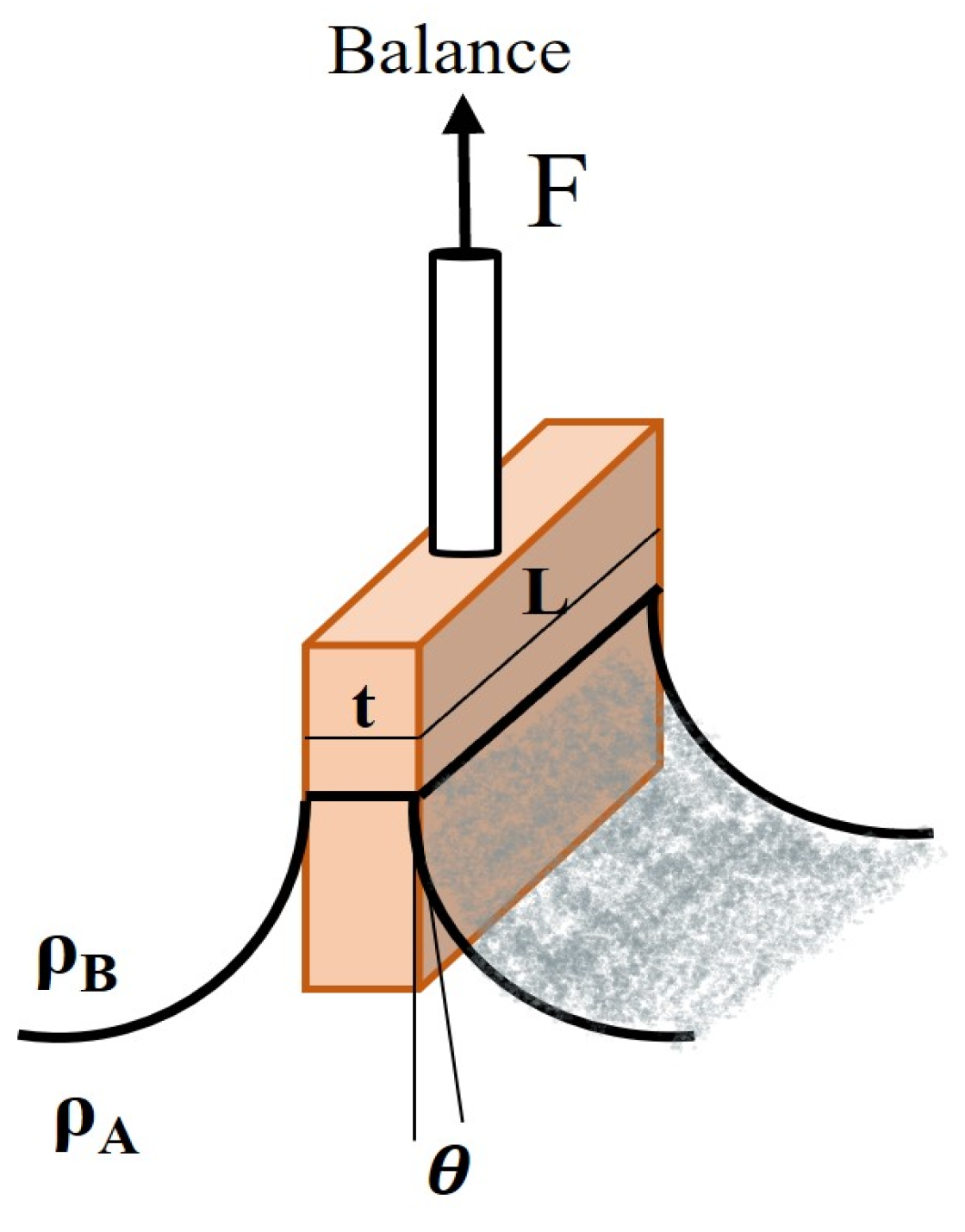
- Wilhelmy Plate Method: This method involves measuring the force required to pull a thin plate partially submerged in the liquid interface upwards, as demonstrated in Figure 8. The interfacial tension is calculated based on the measured force, plate dimensions, and contact angle. By measuring the mentioned force, the interfacial tension can be calculated using Equation (2), where p = 2 (L + t) [33].
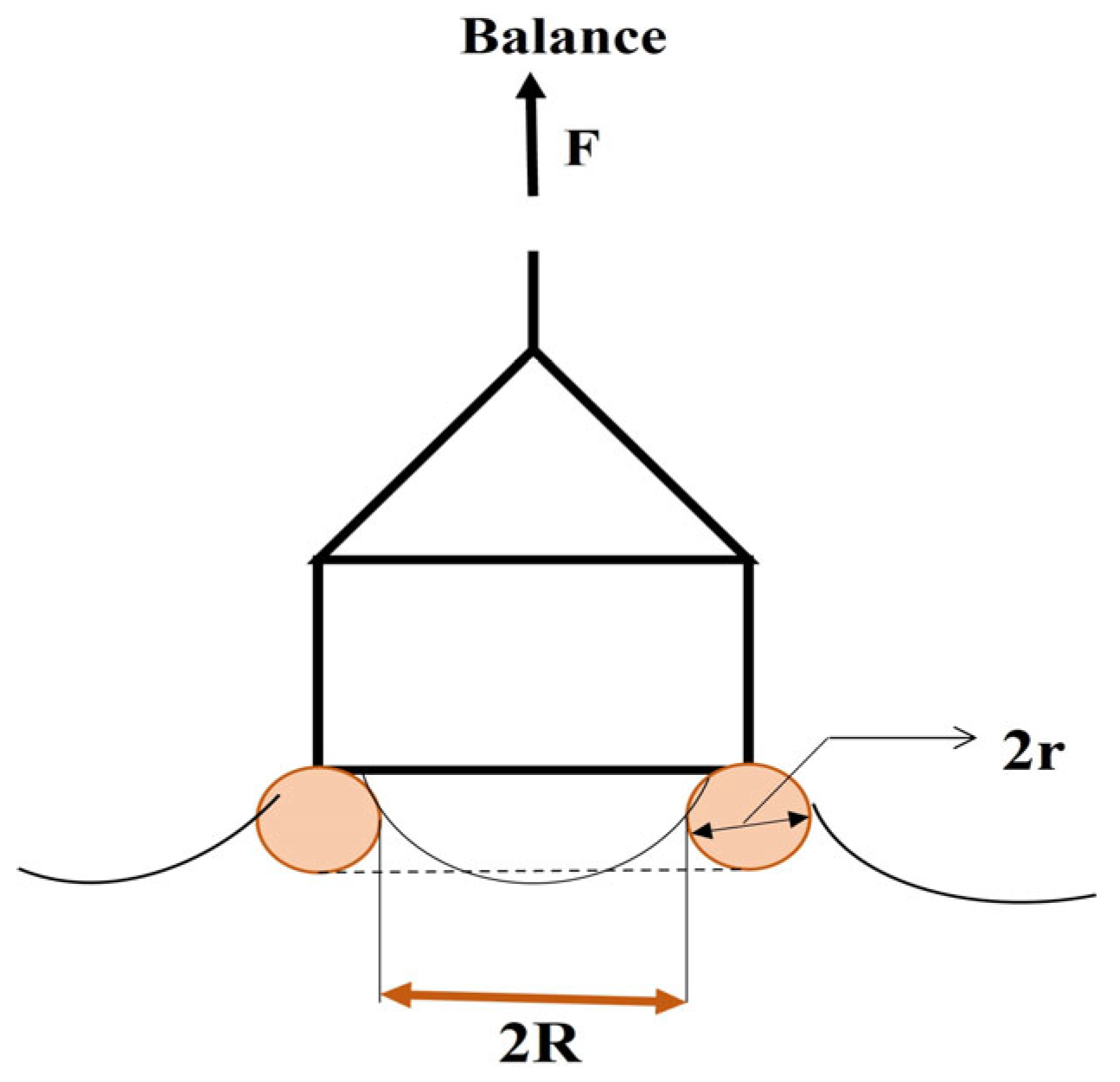
- Du Nouy Ring Method: This method involves measuring the force required to pull a wire ring partially submerged in the liquid interface upwards (Figure 9). The interfacial tension is related to this force through the ring’s geometry and the contact angle between the liquid and the ring. The ring circumference is equivalent to twice the perimeter (p) of the three-phase contact line in this case: p = 4 R. Equation (2) requires a correction factor (f) because more liquid is lifted during the ring’s separation from the interface [34]:
1.3.2. New Techniques (Based on Capillary Pressure)
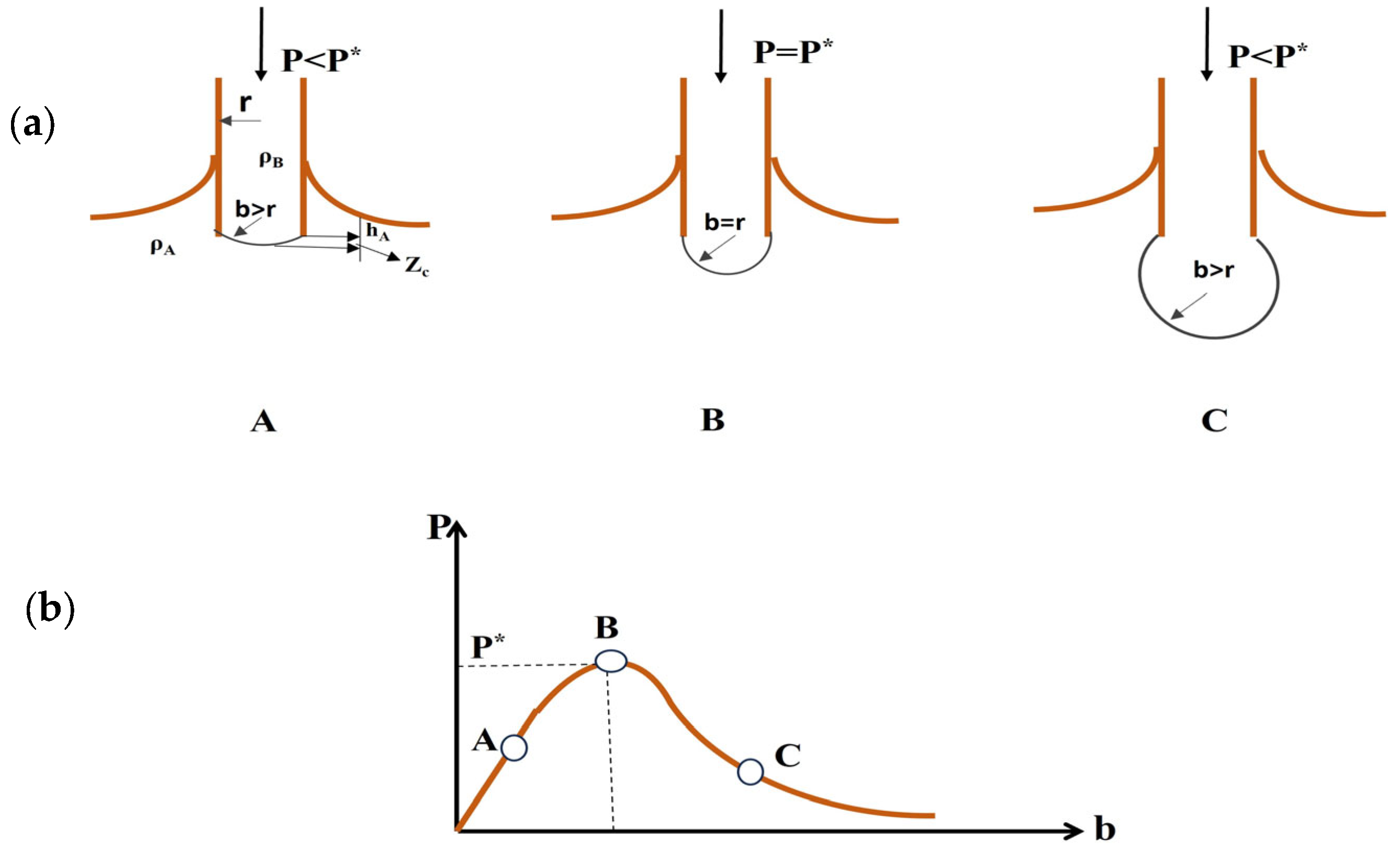
- Maximum Bubble Pressure Method: This method involves forcing a gas bubble to grow at the tip of a submerged tube. As the pressure inside the bubble increases, it counteracts the interfacial tension at the bubble’s surface (Figure 10). The pressure at which the bubble detaches from the tube is related to the interfacial tension. This method is particularly useful for studying high interfacial tension systems [36].
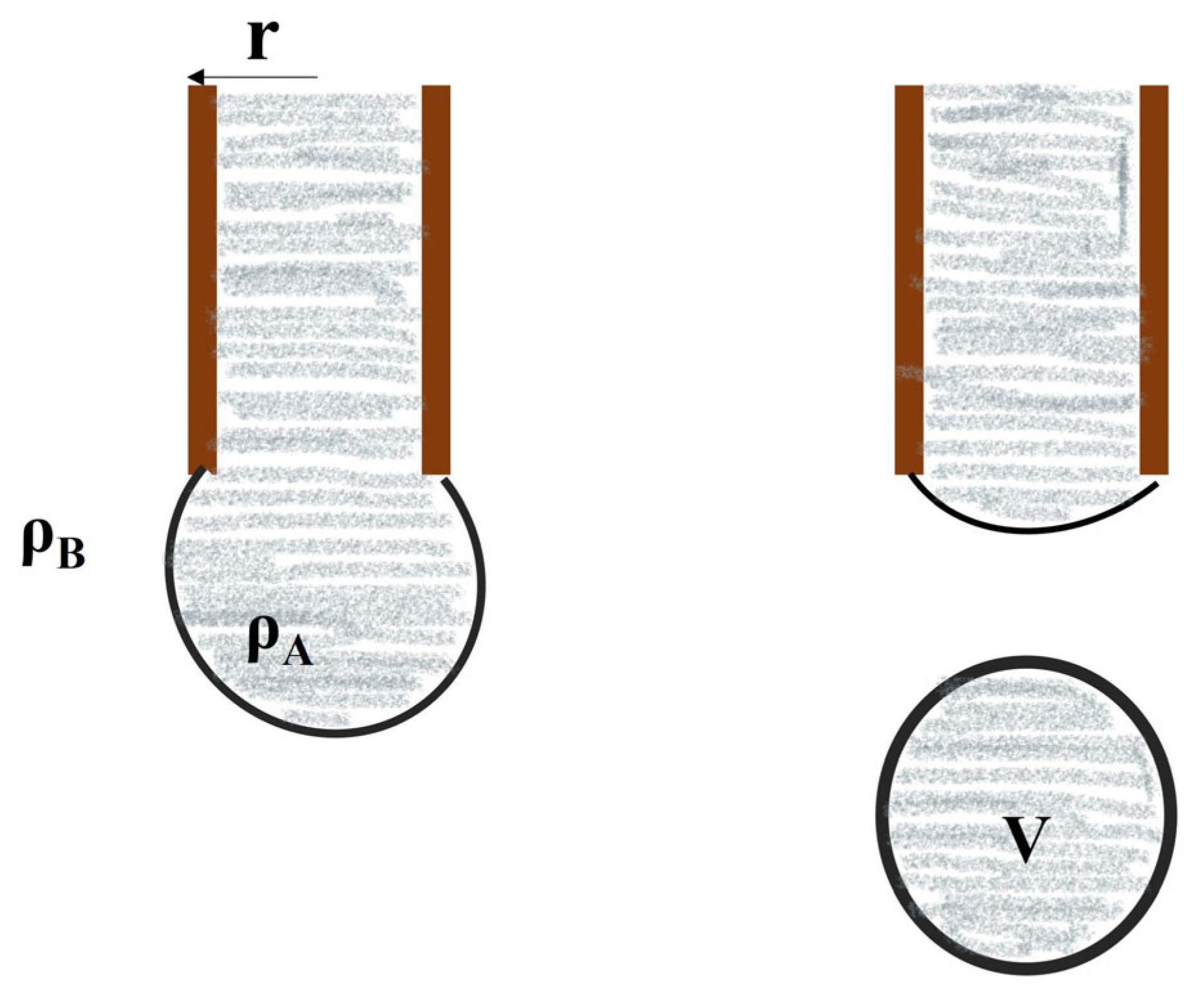
- Capillary Rise Method: This method utilizes the phenomenon where a liquid rises inside a narrow tube inserted vertically into the liquid, as shown in Figure 11. The height (h) to which the liquid rises depends on the interfacial tension (, the tube diameter (r or d), and the liquid’s density (. It is a relatively simple method, but it requires careful control of factors like tube cleanliness [37].
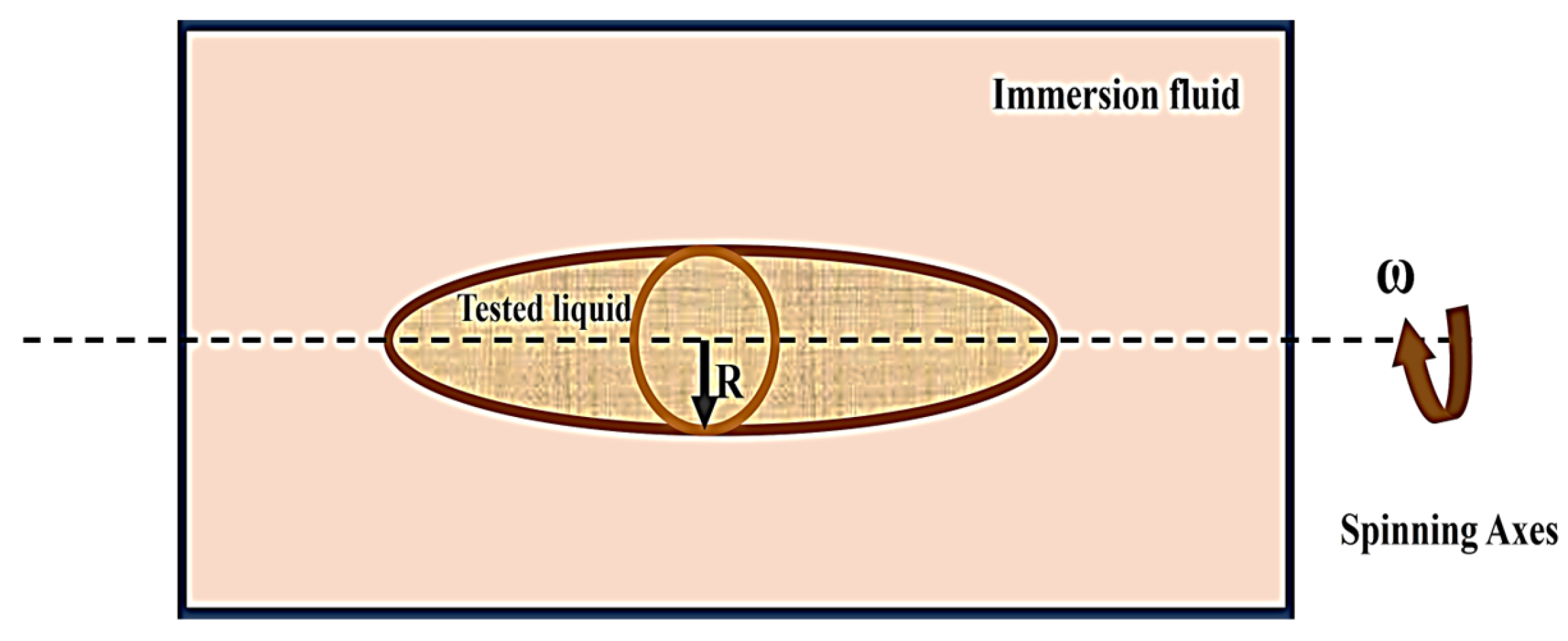
- Spinning drop method: The method of spinning drops involves evaluating the surface tension of a liquid by examining the characteristics and size of a droplet that appears on the surface of a different liquid during spinning under the mechanical equilibrium of interfacial force and centrifugal force (Figure 12) [38].
1.3.3. Optical Tensiometry Methods
- Drop Volume Method: This method involves determining the minimum volume of a drop required to detach from a tip (like a needle) due to its own weight. The interfacial tension is related to the drop volume and the tip geometry. This method is relatively simple but can be less accurate than other techniques. Figure 13 demonstrates the drop volume method for calculating IFT [39].
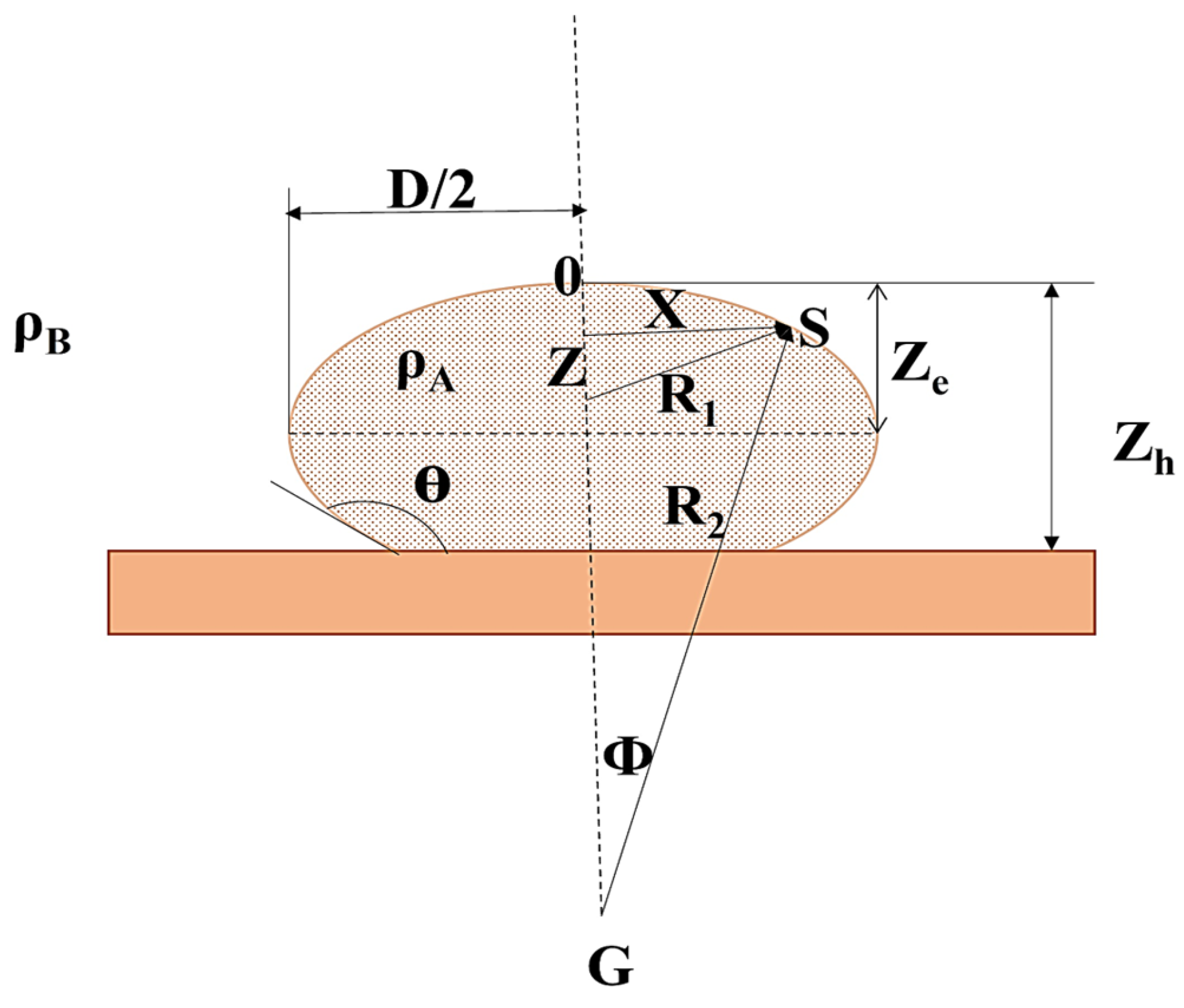
- Pendant Drop Method: This method is also known as axisymmetric drop shape analysis (ADSA). It involves analyzing the profile of a liquid drop suspended at the tip of a needle or pipette within another liquid, as shown in Figure 14. The software fits the drop shape into a theoretical model that incorporates interfacial tension. This method is advantageous because it allows for non-intrusive, continuous monitoring of interfacial tension [41,42,43].
- Sessile Drop Method: This method is similar to the pendant drop method, but instead of hanging from a tip, the liquid drop sits on a solid surface (Figure 15). The software analyzes the drop’s contact angle with the solid surface and its overall profile to determine the interfacial tension. This method is useful for studying solid–liquid interfaces [35].
1.3.4. Molecular Dynamics Simulation of IFT
2. Effective Parameters on IFT
- Temperature: Interfacial tension generally decreases with increasing temperature due to increased molecular motion and decreased intermolecular forces.
- Pressure: Interfacial tension between liquid and vapor phases is affected by pressure.
- Oil and injection fluids composition.
- Solvent properties:
- ❖
- Polarity and dielectric constant of the solvents.
- ❖
- Dispersion forces and hydrogen-bonding capabilities.
- ❖
- Miscibility and mutual solubility.
- Electrolyte concentration: The presence of ions can alter the interfacial tension due to electrostatic interactions and screening effects.
- External fields (e.g., electric or magnetic): Applied external fields can induce changes in the interfacial tension, particularly for systems involving charged or polarizable species.
3. Discussions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huhtamäki, T.; Tian, X.; Korhonen, J.T.; Ras, R.H. Surface-wetting characterization using contact-angle measurements. Nat. Protoc. 2018, 13, 1521–1538. [Google Scholar] [CrossRef]
- Marmur, A. Thermodynamic aspects of contact angle hysteresis. Adv. Colloid Interface Sci. 1994, 50, 121–141. [Google Scholar] [CrossRef]
- De Silva, G.; Ranjith, P.G.; Perera, M. Geochemical aspects of CO2 sequestration in deep saline aquifers: A review. Fuel 2015, 155, 128–143. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Alder, B.J.; Wainwright, T.E. Phase transition for a hard sphere system. J. Chem. Phys. 1957, 27, 1208. [Google Scholar] [CrossRef]
- Alipour, M.; Sakhaee-Pour, A. Application of Young-Laplace with size-dependent contact angle and interfacial tension in shale. Geoenergy Sci. Eng. 2023, 231, 212447. [Google Scholar]
- Feng, Z.; Xu, J.; Ren, Z.; Ma, R. Application of Molecular Simulation Technology in Improving Oil Recovery. IOP Conf. Ser. Earth Environ. Sci. 2021, 770, 012013. [Google Scholar]
- Zhou, K.; Liu, B. Molecular Dynamics Simulation: Fundamentals and Applications; Academic Press: San Diego, CA, USA, 2022. [Google Scholar]
- Alavi, S. Molecular Simulations: Fundamentals and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Badar, M.S.; Shamsi, S.; Ahmed, J.; Alam, M.A. Molecular dynamics simulations: Concept, methods, and applications. In Transdisciplinarity; Springer: New York, NY, USA, 2022; pp. 131–151. [Google Scholar]
- Mehana, M.; Kang, Q.; Nasrabadi, H.; Viswanathan, H. Molecular modeling of subsurface phenomena related to petroleum engineering. Energy Fuels 2021, 35, 2851–2869. [Google Scholar] [CrossRef]
- Rapaport, D.C. The Art of Molecular Dynamics Simulation; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Ghasemi, M.; Shafiei, A.; Foroozesh, J. A systematic and critical review of application of molecular dynamics simulation in low salinity water injection. Adv. Colloid Interface Sci. 2022, 300, 102594. [Google Scholar] [CrossRef] [PubMed]
- Siu, S.W.; Pluhackova, K.; Böckmann, R.A. Optimization of the OPLS-AA force field for long hydrocarbons. J. Chem. Theory Comput. 2012, 8, 1459–1470. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; MacKerell, A.D., Jr. CHARMM36 all-atom additive protein force field: Validation based on comparison to NMR data. J. Comput. Chem. 2013, 34, 2135–2145. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; He, X.; Vanommeslaeghe, K.; MacKerell, A.D., Jr. Extension of the CHARMM general force field to sulfonyl-containing compounds and its utility in biomolecular simulations. J. Comput. Chem. 2012, 33, 2451–2468. [Google Scholar] [CrossRef] [PubMed]
- Vanommeslaeghe, K.; MacKerell, A.D., Jr. Automation of the CHARMM General Force Field (CGenFF) I: Bond perception and atom typing. J. Chem. Inf. Model. 2012, 52, 3144–3154. [Google Scholar] [CrossRef]
- Sun, H. COMPASS: An ab initio force-field optimized for condensed-phase applications overview with details on alkane and benzene compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
- Maple, J.R.; Hwang, M.J.; Stockfisch, T.P.; Dinur, U.; Waldman, M.; Ewig, C.S.; Hagler, A.T. Derivation of class II force fields. I. Methodology and quantum force field for the alkyl functional group and alkane molecules. J. Comput. Chem. 1994, 15, 162–182. [Google Scholar] [CrossRef]
- Evans, D.J.; Holian, B.L. The nose–hoover thermostat. J. Chem. Phys. 1985, 83, 4069–4074. [Google Scholar] [CrossRef]
- Berendsen, H.J.; Postma, J.V.; Van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Andersen, H.C. Molecular dynamics simulations at constant pressure and/or temperature. J. Chem. Phys. 1980, 72, 2384–2393. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications; Academic Press: San Diego, CA, USA, 2002. [Google Scholar]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Riazi, M. Characterization and Properties of Petroleum Fractions; ASTM International: West Conshohocken, PA, USA, 2005. [Google Scholar]
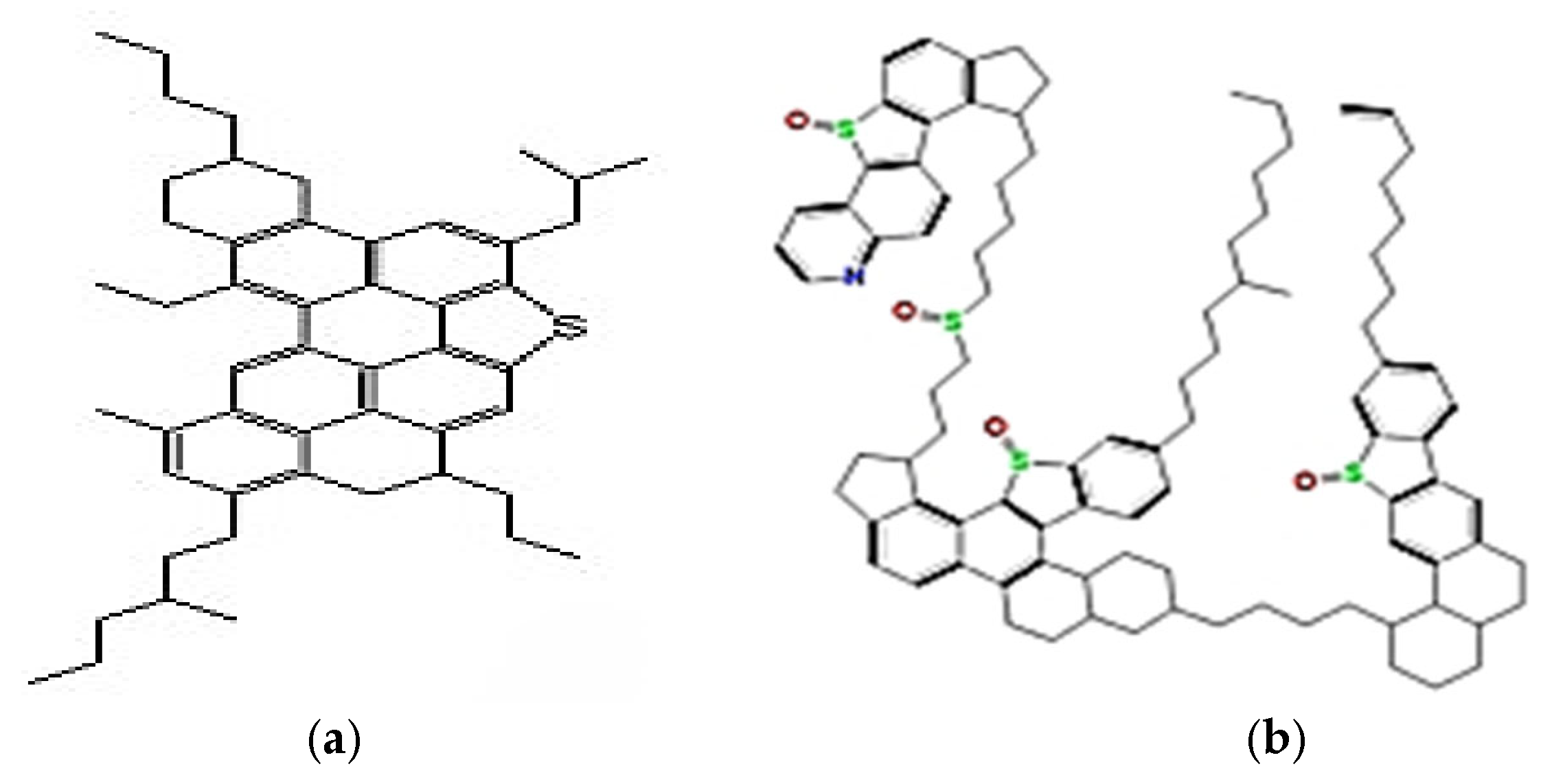
- Goual, L.; Sedghi, M.; Wang, X.; Zhu, Z. Asphaltene aggregation and impact of alkylphenols. Langmuir 2014, 30, 5394–5403. [Google Scholar] [CrossRef]
- Hassanzadeh, M.; Abdouss, M. A comprehensive review on the significant tools of asphaltene investigation. Analysis and characterization techniques and computational methods. J. Pet. Sci. Eng. 2022, 208, 109611. [Google Scholar] [CrossRef]
- Law, J.C.; Headen, T.F.; Jiménez-Serratos, G.; Boek, E.S.; Murgich, J.; Müller, E.A. Catalogue of plausible molecular models for the molecular dynamics of asphaltenes and resins obtained from quantitative molecular representation. Energy Fuels 2019, 33, 9779–9795. [Google Scholar] [CrossRef]
- Mullins, O.C. The modified Yen model. Energy Fuels 2010, 24, 2179–2207. [Google Scholar] [CrossRef]
- Yang, F.; Tchoukov, P.; Dettman, H.; Teklebrhan, R.B.; Liu, L.; Dabros, T.; Czarnecki, J.; Masliyah, J.; Xu, Z. Asphaltene subfractions responsible for stabilizing water-in-crude oil emulsions. Part 2: Molecular representations and molecular dynamics simulations. Energy Fuels 2015, 29, 4783–4794. [Google Scholar] [CrossRef]
- Kadaoluwa Pathirannahalage, S.P.; Meftahi, N.; Elbourne, A.; Weiss, A.C.; McConville, C.F.; Padua, A.; Winkler, D.A.; Costa Gomes, M.; Greaves, T.L.; Le, T.C. Systematic comparison of the structural and dynamic properties of commonly used water models for molecular dynamics simulations. J. Chem. Inf. Model. 2021, 61, 4521–4536. [Google Scholar] [CrossRef]
- Rusanov, A.I.; Prokhorov, V.A. Interfacial Tensiometry; Elsevier: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Wilhelmy, L. Ueber die Abhängigkeit der Capillaritäts-Constanten des Alkohols von Substanz und Gestalt des benetzten festen Körpers. Ann. Phys. 1863, 195, 177–217. [Google Scholar] [CrossRef]
- Du Noüy, P.L. A new apparatus for measuring surface tension. J. Gen. Physiol. 1919, 1, 521. [Google Scholar] [CrossRef]
- Drelich, J.; Fang, C.; White, C. Measurement of interfacial tension in fluid-fluid systems. Encycl. Surf. Colloid Sci. 2002, 3, 3158–3163. [Google Scholar]
- Sugden, S. XCVII.—The determination of surface tension from the maximum pressure in bubbles. J. Chem. Soc. Trans. 1922, 121, 858–866. [Google Scholar] [CrossRef]
- Rayleigh, L. On the theory of the capillary tube. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1916, 92, 184–195. [Google Scholar]
- Su, G.; Yang, L.; Liu, S.; Song, J.; Jiang, W.; Jin, X. Review on factors affecting nanofluids surface tension and mechanism analysis. J. Mol. Liq. 2024, 407, 125159. [Google Scholar] [CrossRef]
- Tate, T. XXX. On the magnitude of a drop of liquid formed under different circumstances. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1864, 27, 176–180. [Google Scholar] [CrossRef]
- Razafindralambo, H.; Blecker, C.; Delhaye, S.; Paquot, M. Application of the quasi-static mode of the drop volume technique to the determination of fundamental surfactant properties. J. Colloid Interface Sci. 1995, 174, 373–377. [Google Scholar] [CrossRef]
- Andreas, J.; Hauser, E.; Tucker, W. Boundary tension by pendant drops. J. Phys. Chem. 2002, 42, 1001–1019. [Google Scholar] [CrossRef]
- Stauffer, C.E. The measurement of surface tension by the pendant drop technique. J. Phys. Chem. 1965, 69, 1933–1938. [Google Scholar] [CrossRef]
- Misak, M.D. Equation for determining 1/H versus S values in computer calculations of interfacial tension by the pendant drop method. J. Colloid Interface Sci. 1968, 27, 141–142. [Google Scholar] [CrossRef]
- Jian, C.; Poopari, M.R.; Liu, Q.; Zerpa, N.; Zeng, H.; Tang, T. Reduction of water/oil interfacial tension by model asphaltenes: The governing role of surface concentration. J. Phys. Chem. B 2016, 120, 5646–5654. [Google Scholar] [CrossRef]
- Remesal, E.R.; Suárez, J.A.; Márquez, A.M.; Sanz, J.F.; Rincón, C.; Guitián, J. Molecular dynamics simulations of the role of salinity and temperature on the hydrocarbon/water interfacial tension. Theor. Chem. Acc. 2017, 136, 66. [Google Scholar] [CrossRef]
- Li, X.; Ross, D.A.; Trusler, J.M.; Maitland, G.C.; Boek, E.S. Molecular dynamics simulations of CO2 and brine interfacial tension at high temperatures and pressures. J. Phys. Chem. B 2013, 117, 5647–5652. [Google Scholar] [CrossRef]
- De Lara, L.S.; Michelon, M.F.; Miranda, C.R. Molecular dynamics studies of fluid/oil interfaces for improved oil recovery processes. J. Phys. Chem. B 2012, 116, 14667–14676. [Google Scholar] [CrossRef]
- Ghorbani, M.; Mohammadi, A.H. Effects of temperature, pressure and fluid composition on hydrocarbon gas-oil interfacial tension (IFT): An experimental study using ADSA image analysis of pendant drop test method. J. Mol. Liq. 2017, 227, 318–323. [Google Scholar] [CrossRef]
- Lashkarbolooki, M.; Riazi, M.; Ayatollahi, S. Investigation of effects of salinity, temperature, pressure, and crude oil type on the dynamic interfacial tensions. Chem. Eng. Res. Des. 2016, 115, 53–65. [Google Scholar] [CrossRef]
- Soleymanzadeh, A.; Rahmati, A.; Yousefi, M.; Roshani, B. Theoretical and experimental investigation of effect of salinity and asphaltene on IFT of brine and live oil samples. J. Pet. Explor. Prod. 2021, 11, 769–781. [Google Scholar] [CrossRef]
- Cumicheo, C.; Cartes, M.; Müller, E.A.; Mejía, A. Experimental measurements and theoretical modeling of high-pressure mass densities and interfacial tensions of carbon dioxide + n-heptane + toluene and its carbon dioxide binary systems. Fuel 2018, 228, 92–102. [Google Scholar] [CrossRef]
- Hemmati-Sarapardeh, A.; Ayatollahi, S.; Ghazanfari, M.-H.; Masihi, M. Experimental determination of interfacial tension and miscibility of the CO2–crude oil system; temperature, pressure, and composition effects. J. Chem. Eng. Data 2014, 59, 61–69. [Google Scholar] [CrossRef]
- Zolghadr, A.; Escrochi, M.; Ayatollahi, S. Temperature and composition effect on CO2 miscibility by interfacial tension measurement. J. Chem. Eng. Data 2013, 58, 1168–1175. [Google Scholar] [CrossRef]
- Qu, B.; Ma, X.; Dong, Z. Interfacial characterization and minimum miscible pressure study of CO2 flooding based on molecular dynamics. Improv. Oil Gas Recovery 2022, 6. [Google Scholar] [CrossRef]
- Li, N.; Zhang, C.-W.; Ma, Q.-L.; Jiang, L.-Y.; Xu, Y.-X.; Chen, G.-J.; Sun, C.-Y.; Yang, L.-Y. Interfacial tension measurement and calculation of (carbon dioxide + n-alkane) binary mixtures. J. Chem. Eng. Data 2017, 62, 2861–2871. [Google Scholar] [CrossRef]
- Pan, Z.; Trusler, J.M. Measurement and modelling of the interfacial tensions of CO2 + decane-iododecane mixtures at high pressures and temperatures. Fluid Phase Equilibria 2023, 566, 113700. [Google Scholar] [CrossRef]
- Samara, H.; Al-Eryani, M.; Jaeger, P. The role of supercritical carbon dioxide in modifying the phase and interfacial properties of multiphase systems relevant to combined EOR-CCS. Fuel 2022, 323, 124271. [Google Scholar] [CrossRef]
- Ahmadyar, S.; Samara, H. The effect of gas and liquid phase composition on miscibility through interfacial tension measurements of model oils in compressed CO2. J. Pet. Explor. Prod. Technol. 2025, 15, 31. [Google Scholar] [CrossRef]
- Yang, Z.; Li, M.; Peng, B.; Lin, M.; Dong, Z.; Ling, Y. Interfacial tension of CO2 and organic liquid under high pressure and temperature. Chin. J. Chem. Eng. 2014, 22, 1302–1306. [Google Scholar] [CrossRef]
- Naeiji, P.; Woo, T.K.; Alavi, S.; Ohmura, R. Molecular dynamics simulations of interfacial properties of the CO2–water and CO2–CH4–water systems. J. Chem. Phys. 2020, 153, 044701. [Google Scholar] [CrossRef]
- Chun, B.-S.; Wilkinson, G.T. Interfacial tension in high-pressure carbon dioxide mixtures. Ind. Eng. Chem. Res. 1995, 34, 4371–4377. [Google Scholar] [CrossRef]
- Hebach, A.; Oberhof, A.; Dahmen, N.; Kögel, A.; Ederer, H.; Dinjus, E. Interfacial tension at elevated pressures measurements and correlations in the water + carbon dioxide system. J. Chem. Eng. Data 2002, 47, 1540–1546. [Google Scholar] [CrossRef]
- Yang, D.; Tontiwachwuthikul, P.; Gu, Y. Interfacial interactions between reservoir brine and CO2 at high pressures and elevated temperatures. Energy Fuels 2005, 19, 216–223. [Google Scholar] [CrossRef]
- Akutsu, T.; Yamaji, Y.; Yamaguchi, H.; Watanabe, M.; Smith, R.L., Jr.; Inomata, H. Interfacial tension between water and high pressure CO2 in the presence of hydrocarbon surfactants. Fluid Phase Equilibria 2007, 257, 163–168. [Google Scholar] [CrossRef]
- Chiquet, P.; Daridon, J.-L.; Broseta, D.; Thibeau, S. CO2/water interfacial tensions under pressure and temperature conditions of CO2 geological storage. Energy Convers. Manag. 2007, 48, 736–744. [Google Scholar] [CrossRef]
- Bachu, S.; Bennion, D.B. Interfacial tension between CO2, freshwater, and brine in the range of pressure from (2 to 27) MPa, temperature from (20 to 125) °C, and water salinity from (0 to 334 000) mg L−1. J. Chem. Eng. Data 2009, 54, 765–775. [Google Scholar] [CrossRef]
- Shah, V.; Broseta, D.; Mouronval, G.; Montel, F. Water/acid gas interfacial tensions and their impact on acid gas geological storage. Int. J. Greenh. Gas Control 2008, 2, 594–604. [Google Scholar] [CrossRef]
- Bachu, S.; Bennion, D.B. Dependence of CO2-brine interfacial tension on aquifer pressure, temperature and water salinity. Energy Procedia 2009, 1, 3157–3164. [Google Scholar] [CrossRef]
- Chalbaud, C.; Robin, M.; Lombard, J.; Martin, F.; Egermann, P.; Bertin, H. Interfacial tension measurements and wettability evaluation for geological CO2 storage. Adv. Water Resour. 2009, 32, 98–109. [Google Scholar] [CrossRef]
- Aggelopoulos, C.; Robin, M.; Vizika, O. Interfacial tension between CO2 and brine (NaCl + CaCl2) at elevated pressures and temperatures: The additive effect of different salts. Adv. Water Resour. 2011, 34, 505–511. [Google Scholar] [CrossRef]
- Espinoza, D.N.; Santamarina, J.C. Water-CO2-mineral systems: Interfacial tension, contact angle, and diffusion—Implications to CO2 geological storage. Water Resour. Res. 2010, 46, W07537. [Google Scholar] [CrossRef]
- Georgiadis, A.; Maitland, G.; Trusler, J.M.; Bismarck, A. Interfacial tension measurements of the (H2O + CO2) system at elevated pressures and temperatures. J. Chem. Eng. Data 2010, 55, 4168–4175. [Google Scholar] [CrossRef]
- Bikkina, P.K.; Shoham, O.; Uppaluri, R. Equilibrated interfacial tension data of the CO2–water system at high pressures and moderate temperatures. J. Chem. Eng. Data 2011, 56, 3725–3733. [Google Scholar] [CrossRef]
- Li, X.; Boek, E.; Maitland, G.C.; Trusler, J.M. Interfacial Tension of (Brines + CO2):(0.864 NaCl + 0.136 KCl) at Temperatures between (298 and 448) K, Pressures between (2 and 50) MPa, and Total Molalities of (1 to 5) mol·kg−1. J. Chem. Eng. Data 2012, 57, 1078–1088. [Google Scholar] [CrossRef]
- Li, X.; Boek, E.S.; Maitland, G.C.; Trusler, J.M. Interfacial Tension of (Brines + CO2): CaCl2 (aq), MgCl2 (aq), and Na2SO4 (aq) at Temperatures between (343 and 423) K, Pressures between (2 and 50) MPa, and Molalities of (0.5 to 5) mol·kg−1. J. Chem. Eng. Data 2012, 57, 1369–1375. [Google Scholar] [CrossRef]
- Lun, Z.; Fan, H.; Wang, H.; Luo, M.; Pan, W.; Wang, R. Interfacial tensions between reservoir brine and CO2 at high pressures for different salinity. Energy Fuels 2012, 26, 3958–3962. [Google Scholar] [CrossRef]
- Banerjee, S.; Hassenklover, E.; Kleijn, J.M.; Cohen Stuart, M.A.; Leermakers, F.A. Interfacial tension and wettability in water–carbon dioxide systems: Experiments and self-consistent field modeling. J. Phys. Chem. B 2013, 117, 8524–8535. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Wang, S.; Li, S.; Liu, W.; Li, B.; Lv, Q.-C. Accurate determination of the CO2–brine interfacial tension using graphical alternating conditional expectation. Energy Fuels 2014, 28, 624–635. [Google Scholar] [CrossRef]
- Saraji, S.; Piri, M.; Goual, L. The effects of SO2 contamination, brine salinity, pressure, and temperature on dynamic contact angles and interfacial tension of supercritical CO2/brine/quartz systems. Int. J. Greenh. Gas Control 2014, 28, 147–155. [Google Scholar] [CrossRef]
- Al-Yaseri, A.; Sarmadivaleh, M.; Saeedi, A.; Lebedev, M.; Barifcani, A.; Iglauer, S. N2 + CO2 + NaCl brine interfacial tensions and contact angles on quartz at CO2 storage site conditions in the Gippsland basin, Victoria/Australia. J. Pet. Sci. Eng. 2015, 129, 58–62. [Google Scholar] [CrossRef]
- Liu, Y.; Mutailipu, M.; Jiang, L.; Zhao, J.; Song, Y.; Chen, L. Interfacial tension and contact angle measurements for the evaluation of CO2-brine two-phase flow characteristics in porous media. Environ. Prog. Sustain. Energy 2015, 34, 1756–1762. [Google Scholar] [CrossRef]
- Sarmadivaleh, M.; Al-Yaseri, A.Z.; Iglauer, S. Influence of temperature and pressure on quartz–water–CO2 contact angle and CO2–water interfacial tension. J. Colloid Interface Sci. 2015, 441, 59–64. [Google Scholar] [CrossRef]
- Arif, M.; Al-Yaseri, A.Z.; Barifcani, A.; Lebedev, M.; Iglauer, S. Impact of pressure and temperature on CO2–brine–mica contact angles and CO2–brine interfacial tension: Implications for carbon geo-sequestration. J. Colloid Interface Sci. 2016, 462, 208–215. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Li, H.A.; Okuno, R. Measurements and modeling of interfacial tension for CO2/CH4/brine systems under reservoir conditions. Ind. Eng. Chem. Res. 2016, 55, 12358–12375. [Google Scholar] [CrossRef]
- Zhao, L.; Ji, J.; Tao, L.; Lin, S. Ionic effects on supercritical CO2–brine interfacial tensions: Molecular dynamics simulations and a universal correlation with ionic strength, temperature, and pressure. Langmuir 2016, 32, 9188–9196. [Google Scholar] [CrossRef]
- Chow, Y.F.; Maitland, G.C.; Trusler, J.M. Interfacial tensions of the (CO2 + N2 + H2O) system at temperatures of (298 to 448) K and pressures up to 40 MPa. J. Chem. Thermodyn. 2016, 93, 392–403. [Google Scholar] [CrossRef]
- Arif, M.; Jones, F.; Barifcani, A.; Iglauer, S. Electrochemical investigation of the effect of temperature, salinity and salt type on brine/mineral interfacial properties. Int. J. Greenh. Gas Control 2017, 59, 136–147. [Google Scholar] [CrossRef]
- Liu, Y.; Tang, J.; Wang, M.; Wang, Q.; Tong, J.; Zhao, J.; Song, Y. Measurement of interfacial tension of CO2 and NaCl aqueous solution over wide temperature, pressure, and salinity ranges. J. Chem. Eng. Data 2017, 62, 1036–1046. [Google Scholar] [CrossRef]
- Pereira, L.M.; Chapoy, A.; Burgass, R.; Tohidi, B. Interfacial tension of CO2 + brine systems: Experiments and predictive modelling. Adv. Water Resour. 2017, 103, 64–75. [Google Scholar] [CrossRef]
- Yang, Y.; Narayanan Nair, A.K.; Sun, S. Molecular dynamics simulation study of carbon dioxide, methane, and their mixture in the presence of brine. J. Phys. Chem. B 2017, 121, 9688–9698. [Google Scholar] [CrossRef]
- Al-Anssari, S.; Barifcani, A.; Keshavarz, A.; Iglauer, S. Impact of nanoparticles on the CO2-brine interfacial tension at high pressure and temperature. J. Colloid Interface Sci. 2018, 532, 136–142. [Google Scholar] [CrossRef]
- Mutailipu, M.; Liu, Y.; Jiang, L.; Zhang, Y. Measurement and estimation of CO2–brine interfacial tension and rock wettability under CO2 sub-and super-critical conditions. J. Colloid Interface Sci. 2019, 534, 605–617. [Google Scholar] [CrossRef]
- Abdulelah, H.; Al-Yaseri, A.; Ali, M.; Giwelli, A.; Negash, B.M.; Sarmadivaleh, M. CO2/Basalt’s interfacial tension and wettability directly from gas density: Implications for Carbon Geo-sequestration. J. Pet. Sci. Eng. 2021, 204, 108683. [Google Scholar] [CrossRef]
- Yekeen, N.; Padmanabhan, E.; Abdulelah, H.; Irfan, S.A.; Okunade, O.A.; Khan, J.A.; Negash, B.M. CO2/brine interfacial tension and rock wettability at reservoir conditions: A critical review of previous studies and case study of black shale from Malaysian formation. J. Pet. Sci. Eng. 2021, 196, 107673. [Google Scholar] [CrossRef]
- Badizad, M.H.; Koleini, M.M.; Hartkamp, R.; Ayatollahi, S.; Ghazanfari, M.H. How do ions contribute to brine-hydrophobic hydrocarbon Interfaces? An in silico study. J. Colloid Interface Sci. 2020, 575, 337–346. [Google Scholar] [CrossRef] [PubMed]
- Kirch, A.; Celaschi, Y.M.; de Almeida, J.M.; Miranda, C.R. Brine–oil interfacial tension modeling: Assessment of machine learning techniques combined with molecular dynamics. ACS Appl. Mater. Interfaces 2020, 12, 15837–15843. [Google Scholar] [CrossRef]
- Chuntian, H.; Rongzuo, X.; Tran, C.; Andrew, Y.; Nikhil, J. Interfacial Properties of Asphaltenes at the Heptol–Brine Interface. Energy Fuels 2016, 30, 80–87. [Google Scholar]
- Barati-Harooni, A.; Soleymanzadeh, A.; Tatar, A.; Najafi-Marghmaleki, A.; Samadi, S.-J.; Yari, A.; Roushani, B.; Mohammadi, A.H. Experimental and modeling studies on the effects of temperature, pressure and brine salinity on interfacial tension in live oil-brine systems. J. Mol. Liq. 2016, 219, 985–993. [Google Scholar] [CrossRef]
- Alonso, G.; Gamallo, P.; Rincon, C.; Sayos, R. Interfacial behavior of binary, ternary and quaternary oil/water mixtures described from molecular dynamics simulations. J. Mol. Liq. 2021, 324, 114661. [Google Scholar] [CrossRef]
- Van Gunsteren, W.F.; Oostenbrink, C. Methods for classical-mechanical molecular simulation in chemistry: Achievements, limitations, perspectives. J. Chem. Inf. Model. 2024, 64, 6281–6304. [Google Scholar] [CrossRef] [PubMed]
- Barbhuiya, S.; Das, B.B. Molecular dynamics simulation in concrete research: A systematic review of techniques, models and future directions. J. Build. Eng. 2023, 76, 107267. [Google Scholar] [CrossRef]




| Software | Range of Application | Research Content | Merit | Defect | |
|---|---|---|---|---|---|
| 1 | Gaussian | Research on molecules | Mechanism of chemical reaction, impact of substituting elements, and simultaneous intermediate stages and transition structures | high level of accuracy in calculation | This only applies to minuscule systems because to calculation is laborious and time-consuming. |
| 2 | VASP | Research on Surface, Solid, and Atomic Structures | The theory of density functions provides a framework for solving the Kohn-Sham equation. | Swift computation performance and an effective algorithm for optimization | slow entrance |
| 3 | GROMACS | Investigation of molecular dynamics structures for numerous particle simulations | Solve the traditional Newton mechanical equation for a macromolecular structure. | Excellent functionality, quick computation times, and exceptional service for maintenance | Poor compatibility |
| 4 | AMBER | Investigation of conventional chemical molecular structures and systems of biology | - | highly built-in potential energy algorithms and simple molecular customization | Inadequate computational performance, snail-paced running, and costly purchase. |
| 5 | LAMMPS | molecular modeling investigation | Simulating particles in different states, including liquid, solid, and gas. Mimicking two or three-dimensional systems can be achieved with either a small or a large number of particles. | Sophisticated programming, excellent computational performance, and compatibility with the majority of potential energy models currently available | Lack of mapping output data, insufficient field parameters, inadequate maintenance, and unavailability of tools for creating molecular systems |
| 6 | Material Studio | Research for materials science | Predicting the characteristics of a material, creating structures of polymers, and modeling the scattering of X-rays. | Assists in working across a variety of devices, utilizes intelligent techniques, and is user-friendly. | Costly, not adept at distributing, and not very effective at multitasking. |
| 7 | CHARMM | Biological and chemical Structure investigation | - | The potential energy model has been quickly modified, allowing for easy customization and effective maintenance. | The software is slow and not efficient at processing math tasks, so a payment is required for its use. |
| 8 | NAMD | Biological and soft chemical substance investigation | - | Well-designed program, high compatibility and easy maintenance. | - |
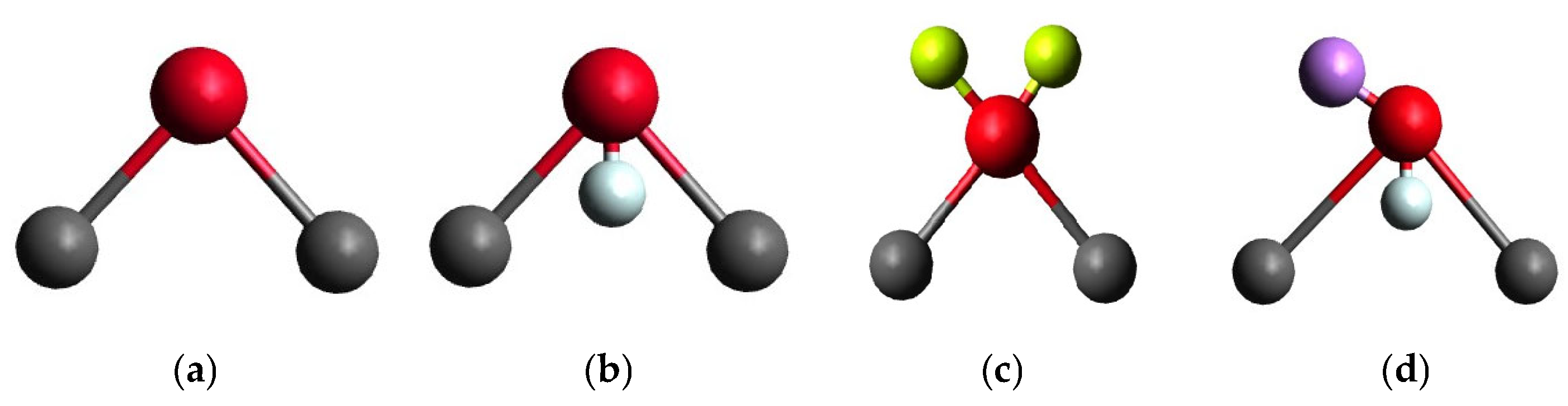
| No. | Name | Type | Flexibility | Density (g/cm3) | IFT (mN/m) | Published Year |
|---|---|---|---|---|---|---|
| 1 | SPC | 3-point | No | 0.972 ± 0.006 | 50.3 ± 0.2 | 1981 |
| 2 | TIP3P | 3-point | No | 0.980 ± 0.006 | 47.0 ± 0.2 | 1983 |
| 3 | TIP4P | 4-point | No | 0.994 ± 0.006 | 52.2 ± 0.2 | 1983 |
| 4 | TIPS3P | 3-point | No | 1.007 ± 0.006 | 51.1 ± 0.2 | 1985 |
| 5 | SPC/E | 3-point | No | 0.993 ± 0.006 | 57.6 ± 0.2 | 1987 |
| 6 | CVFF | 3-point | Yes | 0.978 ± 0.006 | 47.3 ± 0.4 | 1988 |
| 7 | TIP3P/Fw | 3-point | Yes | 1.027 ± 0.006 | 55.2 ± 0.4 | 1999 |
| 8 | TIP5P | 5-point | No | 0.985 ± 0.006 | 47.1 ± 0.2 | 2000 |
| 9 | TIP3P-Ew | 3-point | No | 0.996 ± 0.006 | 59.2 ± 0.2 | 2004 |
| 10 | TIP4P-Ew | 4-point | No | 0.996 ± 0.005 | 52.2 ± 0.2 | 2004 |
| 11 | TIP5P-Ew | 5-point | No | 1.003 ± 0.006 | 63.5 ± 0.2 | 2004 |
| 12 | TIP4P/2005 | 4-point | No | 0.997 ± 0.005 | 63.5 ± 0.2 | 2005 |
| 13 | TIP4P/Ice | 4-point | No | 0.993 ± 0.006 | 73.4 ± 0.2 | 2005 |
| 14 | SPC/Fw | 3-point | Yes | 1.007 ± 0.006 | 58.6 ± 0.4 | 2006 |
| 15 | SWM4-NDP | Polarizable | No | 0.990 ± 0.005 | 63.1 ± 0.5 | 2006 |
| 16 | TIP4P/2005f | 4-point | Yes | 0.996 ± 0.005 | 60.3 ± 0.4 | 2011 |
| 17 | TIP4P/ε | 4-point | No | 0.996 ± 0.006 | 64.6 ± 0.2 | 2014 |
| 18 | OPC | 4-point | No | 0.997 ± 0.005 | 70.1 ± 0.2 | 2014 |
| 19 | TIP3P-FB | 3-point | No | 0.990 ± 0.006 | 60.3 ± 0.2 | 2014 |
| 20 | TIP4P-FB | 4-point | No | 0.997 ± 0.006 | 64.7 ± 0.2 | 2014 |
| 21 | TIP4P-D | 4-point | No | 0.993 ± 0.006 | 70.8 ± 0.2 | 2015 |
| 22 | SPC/ε | 3-point | No | 0.991 ± 0.005 | 65.3 ± 0.2 | 2015 |
| 23 | OPC3 | 3-point | No | 0.991 ± 0.006 | 61.0 ± 0.2 | 2016 |
| 24 | a99SB-disp | 4-point | No | 0.996 ± 0.006 | 74.4 ± 0.2 | 2018 |
| 25 | TIP5P-2018 | 5-point | No | 0.997 ± 0.006 | 61.6 ± 0.2 | 2018 |
| 26 | TIP3P-ST | 3-point | No | 0.993 ± 0.005 | 63.8 ± 0.2 | 2019 |
| 27 | TIP4P-ST | 4-point | No | 0.999 ± 0.006 | 64.5 ± 0.2 | 2019 |
| 28 | FBA/ε | 3-point | Yes | 0.991 ± 0.005 | 68.0 ± 0.4 | 2020 |
| Method | Accuracy (mN/m) | Surfactant Solutions Compatibility | 2-Liquid Phases Compatibility | Viscous Liquids Compatibility | Commercial Accessibility |
|---|---|---|---|---|---|
| Wilhelmy plate | ~0.1 | Restricted | Adequate | Great | Available |
| Du Nouy ring | ~0.1 | Restricted | Reduced accuracy | Inappropriate | Available |
| Maximum bubble pressure | 0.1–0.3 | Great | Great | Inappropriate | Available |
| Capillary rise | Less than 0.1 | Great | Great (experimentally difficult) | Inappropriate | Available |
| Drop volume | 0.1–0.2 | Restricted | Adequate | Inappropriate | Available |
| Pendant drop | ~0.1 | Great | Great | Inappropriate | Available |
| Sessile drop | ~0.1 | Adequate | Great | Great | Available |
| No. | Oil Comp | Gas System | T (K) | P (MPa) | Method | Results | Ref |
|---|---|---|---|---|---|---|---|
| 1 | Heptol (0.0:1.0, 0.25:75, 0.5:0.5, 0.75:0.25, 1.0:0.0) | CO2 | 344.15 | 0.1–8 | Experimental + (SGT + SAFT VR Mie EOS model) | At a constant temperature, an increase in pressure causes an IFT reduction | [51] |
| 2 | 2 oil types (20.2 & 20.75 API) | CO2 | 313.15, 333.15, 353.5, and 373.15 | 0.68, 3.44, 6.89, 8.96, 11.72, 15.16 | Experimental | 1. As the temperature increases in the low-pressure area, the IFT decreases. 2. There was a change in trend at 6.89 MPa, and as the temperature increased, the IFT started to increase. The reason for this is that when the temperature goes up, CO2 dissolves more easily in crude oil. This makes the tension between the oil and water less when the pressure gets low. 3. At a constant temperature, IFT reduces due to pressure increase with two different trends, and these two different line connection points provide asphaltene offset | [52] |
| 3 | 3 types: heptane, hexadecane, Diesel fuel | CO2 | 313.15, 333.15, 353.5, 373.15, and 393.15 | 0–16 | Experimental | 1 Less pressure (up to 5. Increasing the temperature is found to be most effective for extracting CO2 oil at a low pressure (up to 5.17 MPa), as it reduces all interfacial tensions. 2. Regardless of the temperature, the IFT remains constant at 5. 17 MPa, forming a stable connection. Injecting carbon dioxide at this pressure is not advisable. 3. As the pressure increased, it was more effective to inject CO2 into reservoirs with lower temperatures due to the positive correlation between interfacial tension vs. temperature. | [53] |
| 4 | Alkanes & aromatic elements | CO2, N2, CH4 | 300, 350 | 0.1–30.397 | MD (LAMMPS) | 1. More favorable oil displacement when pressure and salt concentration increase because of IFT increase & aromatic molecules accumulate near the interface has been investigated. 2. Due to the increase in pressure and temperature, IFT for gases reduces, and gas diffusion in the oil increases. | [47] |
| 5 | n-decane | CO2 | 344 | 1–13 | MD (LAMMPS) | Interfacial tension decreases with increasing pressure | [54] |
| 6 | n-alkane | CO2 | 323.15, 353.15 | Up to 17.4 | Exp (Pendant drop) | 1. IFT decreases with an increase in pressure and temperature at lower pressures. 2. These trends reversed for higher pressure, which leads to an increase in MMP with temperature increase. 3. Heavier oil (long-chain n-alkane) leads to MMP. increase | [55] |
| 7 | decane-iododecane (mass fraction of 0%, 50%, 70%, 90% and 100%) | CO2 | 298, 313, 333, 353 | 1 up to the TC of the mixture | Exp (Pendant drop) | 1. Due to pressure and mass fraction of iododecane increasing the IFT decreases. 2. An increase in mass fraction in iododecane causes an increase in Tc of the mixture. 3. An overall average absolute deviation of 0.2 mN∙m−1 was reported between experimental data and the developed empirical model. | [56] |
| 8 | Model oil (45wt% of C16H34, 45wt% of C20 H42, 10wt% of C24H50) | CO2, CO2 +brine | 333.15 | Up to 25 | Exp (pendant drop) | 1. IFT decreases due to the pressure increase in both binary and ternary mixtures 2. In a ternary system, as pressure increases, the IFT decreases due to CO2 acting amphiphilic molecule between coexisting immiscible phases. 3. In the ternary mixture, the IFT reaches its maximum value at high salt concentrations. | [57] |
| 9 | n-decane, n-hexadecane, (n-decane + n-hexadecane) | CO2 | 313.15, 333.15 | 0.1–16 | Exp (pendant drop) | 1. Pressure increasing, temperature reduction, and larger chain length of hydrocarbon cause IFT reduction. 2. A light compound in flooding gas has a significant cosolvent effect, enhancing miscibility between large alkanes and CO2, as indicated by lower IFT and MMP values. | [58] |
| 10 | Organic liquid (Cyclohexane, ethanol, Octane, hexane) | CO2 | 308.15, 323.15, 333.15 | 3.6, 5.6, 6, 7.6 | Exp (pendant drop) | 1. As pressure increases and temperature reduces, CO2-organic liquid reduces. 2. Important factors influencing the IFT of CO2 and organic liquids are the intermolecular force that exists among their molecules and the organic liquid’s polarity and structure. | [59] |
| No. | Brine Com | Gas | T (K) | P (MPa) | Method | Results | Ref |
|---|---|---|---|---|---|---|---|
| 1 | NaCl, CaCl2 | CO2 | 303–393 | 2–50 | MD with GROMACS | 1. At every temperature, due to an increase in pressure, IFT decreases. 2. With salinity increases, IFT has a linear increasing trend. | [46] |
| 2 | pure water | CO2 | 275.15, 298.15 | up to 4 | MD with DL_POLY | Upon pressure increase, the IFT reduces due to the adsorption of more molecules at the interface. | [60] |
| 3 | Water | CO2 | 278.15–344.15 | 0.1–17 | Experimental (capillary rise method) | IFT decreases as pressure increases. | [61] |
| 4 | Water | CO2 | 278–333 | 0–25 | Experimental (Pendant drop method) | 1. Pressure has a greater impact on reducing IFT when the temperature is low. 2. IFT decreases with an increase in temperature at low pressures; vice versa, increasing the temperature under high pressure results in an increase in IFT. | [62] |
| 5 | Brine | CO2 | 300.15, 331.15 | 0–30 MPa | Experimental (Pendant drop method) | IFT increases as pressure reduction & temperature increase | [63] |
| 6 | Water | CO2 | 318.15 | 0–17 | Experimental (Pendant drop method) | As the pressure rises, the IFT reduces significantly before reaching a plateau at high pressure. | [64] |
| 7 | H2O + 20 g/L NaCl | CO2 | 308–383 | 5–45 | Experimental (Pendant drop method) | The IFT experiences a substantial decrease with increasing pressure, followed by a plateau and a slight decline as the temperature rises. Adding 20 g of salt to water doesn’t have a significant impact. | [65] |
| 8 | 0–334 010 mg·L−1 | CO2 | 293–398 | 2–27 | Experimental (Pendant drop method) | 1. At P < Pc, with pressure increase, the IFT reduces. 2. At temperature & pressure, as increase in salinity the IFT increases too. 3. At temperatures that are equal to or greater than Tc, due to temperature increases, the IFT increases too. | [66] |
| Water | CO2–H2S mixture (with 30 mol% H2S) | 313, 343,393 | 0–15 | Experimental (Pendant drop method) | Due to increasing H2S content, the IFT reduced sharply. | [67] | |
| 9 | (0–334,000 mg/L) formation brine | CO2 | 309–398 | 2–27 | Experimental (Pendant drop method) | Pressure increase and temperature decrease cause IFT reduction. | [68] |
| 10 | (0–334,000 mg/L) formation brine | CO2 | 293–398 | 2–27 | Experimental (Pendant drop method) | 1. A decrease in pressure results in a decrease in IFT, which then plateaus at higher pressure levels. 2. Salinity increases cause an increase in IFT. 3. At T < Tc, an increase in temperature causes the IFT to increase. At T = Tc, temperature increases cause noticeably reduced IFT. At T > Tc, the IFT stabilizes at a constant value asymptotically. | [66] |
| 11 | 0–2.75 mol/L NaCl | CO2 | 300.15, 344.15, 373.15 | 5–25 | Experimental (Pendant drop method) | Pressure causes the IFT to decrease and maintain a consistent level independent of salinity. The pressure needed to reach this plateau increases with the rising temperature. As the temperature increases, so does the IFT. IFT rises alongside the concentration of NaCl. | [69] |
| 12 | 0.045–2.7 mol/L CaCl2 | CO2 | 300.15, 344.15, 373.15 | 5–25 | Experimental (rising drop method) | As pressure increases, the IFT decreases, but then stabilizes once the pressure stops rising, regardless of the liquid’s saltiness. There is not much information available about how temperature influences IFT. An increase in salinity causes the IFT to rise. | [70] |
| 13 | Saltwater is produced by dissolving natural halite crystals in water. | CO2 | 296.5 ± 1.5 | 0.1–20 | Experimental (Sessile drop method) | As the pressure rises, the IFT experiences a sharp drop followed by a plateau. | [71] |
| 14 | Water | CO2 | 298–374 | 1–60 | Experimental (Pendant drop method) | IFT decreases as pressure rises. The change in IFT for isotherms at temperatures 297.9, 312.9, and 333.5 Kelvin can be split into two parts. The slope of the decrease in IFT at temperatures 343.3 and 374.3 shows a more gradual change. | [72] |
| 15 | NaCl (0.045–1.5 mol/L) & (0.045–1.5 mol/L) CaCl2 | CO2 | 300.15, 344.15, 373.15 | 5–25 | Experimental (rising drop method) | 1. There is a downward trend in the IFT, with the rate of decrease also diminishing for each temperature point. The IFT reaches a constant value as the pressure increases and the temperature changes. 2. From 300.15 < T < 344.15 & pressures P < P plateau, IFT increases 3. From 300.15 < T < 373.15, the IFT remains relatively constant. 4. An increase in salinity causes the IFT to rise. | [70] |
| 16 | Water | CO2 | 298.15–333.15 | 1.48–20.76 | Experimental (Pendant drop method) | 1. At low pressure, where CO2 CO2-rich phase is gaseous, an increase in pressure causes the IFT reduction. 2. At high pressure range where rich phase CO2 is liquid, IFT remains virtually unchanged. | [73] |
| 17 | NaCl + KCl (0.98–4.95 mol/kg) | CO2 | 298–448 | 2–50 | Experimental (Pendant drop method) | 1. Salinity effect: An increase in salt molality causes IFT to rise linearly. 2. Pressure effect: For P < Pc, an increase in pressure causes rapid IFT reduction afterwards, and IFT reduces gradually. 3. Temperature effect: There is a complex interrelationship between IFT & temperature. | [74] |
| 18 | CaCl2, MgCl2, Na2SO4 mixture (0.49–5.0 mol/kg) | CO2 | 343–423 | 2–50 | Experimental (Pendant drop method) | 1. An increase in salt molality causes IFT to rise linearly. 2. For P < Pc, an increase in pressure causes rapid IFT reduction afterwards, and IFT reduces gradually. 3. There is a higher IFT for divalent cations than monovalent cations. | [75] |
| 19 | brine (14,224.2 and 21,460.6 mg/L) | CO2 | 318.15, 370.68 | 0.1–36 | Experimental (Pendant drop method) | At higher pressures, the IFT reaches a plateau after a rapid reduction as the pressure rises. | [76] |
| 20 | Deionized water | CO2 | 283, 298, 313 | 3, 4, and 5 | Experimental (Pendant drop method) | The decrease in IFT is due to the increase in pressure and temperature reduction. | [77] |
| 21 | Brine | CO2 | 303–393 | 2–50 | MD | At any temperature, as pressure rises & salt molality reduces, IFT reduces. | [78] |
| 22 | Brine (0.2–5 m/L) | CO2+ SO2 (0–6 wt%) | 323.15–373.15 | 13.789–27.579 | Experimental (Captive bubble method) | IFT doesn’t change due to pressure variation, as temperature increases have a minimal reduction and a linear reduction trend as the concentration of SO2 increases. | [79] |
| Brine | CO2, N2 & CO2–N2 mix | 333 | 13 | Experimental (Pendant drop method) | IFTN2-brine > IFTCO2-brine ~ IFT N2/CO2-brine | [80] | |
| 23 | NaCl (0.102, 1 mol/L) | CO2 | 300.15, 308.15 & 313.15 | 3–9 | Experimental (Pendant drop method) | At high pressures and isotherms, IFT reduces and reaches a pseudo-plateau. At low pressure, the IFT increases as the temperature rises more quickly. | [81] |
| 24 | Water | CO2 | 296, 323 & 343 | 0.1–20 | Experimental (Pendant drop method) | For P < 10 MPa, as the pressure increases, IFT reduces sharply afterwards, with a slight reduction trend observed. An increase in temperature causes the IFT to rise. | [82] |
| 25 | NaCl (0–30 wt%) | CO2 | 308, 323 & 343 | 0.1–20 | Experimental (Pendant drop method) | An increase in temperature and salinity, pressure reduction, and the IFT increase. | [83] |
| 26 | NaCl (0–200,000 ppm) | CO2–CH4 mix | 350.15–530.15 | 0.1–34.66 | Experimental (Pendant drop method) | 1. CO2 presence: CH4-brine IFT reduction. 2. Pressure effect:—at low pressure, IFT linear reduction. -at high pressure: slightly reduced. 3. Salinity & temperature: IFT increases as these two factors increase. | [84] |
| 27 | brine (NaCl, CaCl2 & NaCl + CaCl2) | CO2 | 343 | 20 | MD | IFT alteration depends on cation valence. There is a linear correlation between IFT and ionic strength. | [85] |
| 28 | Water | N2,CO2 + N2 | 298.15–448.15 | 2–40 | Experimental (Pendant drop method) | As increasing pressure & temperature cause the CO2 + N2/H2O and N2/H2O IFTs to reduce | [86] |
| 29 | NaCl (0–30 wt%) | CO2 | 323 | 15 | Experimental (Pendant drop method) | A linear trend between IFT and salinity was observed. | [87] |
| 30 | CaCl2 & MgCl2 | CO2 | 323 | 0–20 | Experimental (Pendant drop method) | The decreasing pressure causes the IFT to lower gradually. The CO2/brine IFT increases sequentially with Mg2+ > Ca2+ > Na+ at a constant pressure, temperature, and salinity. | [83] |
| 31 | NaCl (0–1.8 mol/kg) | CO2 | 300–353 | 3–12 | Experimental (Pendant drop method) | 1. Salinity & temperature effect: An increase in these two factors causes IFT to rise. 2. Pressure effect: For P < Pc, an increase in pressure causes linear IFT reduction, and afterwards, IFT reduces gradually until it stabilizes. | [88] |
| 32 | NaCl (0.98, 1.98 mol/kg) | CO2 | 298–423 | ~69.51 | Experimental (Pendant drop method) | As pressure increases, the IFT decreases, but the rate of decrease gradually slows until it stabilizes. Salinities have a positive impact on interfacial tension. | [89] |
| NaCl (up to 14 wt%) | CO2 | 311–473 | Up to 100 | MD | An increase in temperature & pressure and a decrease in salinity cause an IFT reduction. | [90] | |
| 33 | Distilled water | CO2 | 296–343 | 0.1–20 | Experimental (Pendant drop method) | As the pressure increases, the interfacial tension also increases and then stabilizes. IFT decreases with temperature drops in low-pressure conditions. IFT increases with high pressure. | [91] |
| 34 | Brine (NaCl-CaCl2-KCl- MgCl2) | CO2 | 285–300 | Up to 9 | Experimental (Pendant drop method) | As the pressure increases, the interfacial tension also increases and then stabilizes. IFT decreases with temperature drops in low-pressure conditions. IFT increases with high pressure. IFT rises with both salinity & cation valence. | [92] |
| 35 | NaCl + KCl | CO2 | 298–373 | 3–15 | Experimental (Pendant drop method) | IFT rises with both salinity & temperature and reduces with pressure until it reaches a plateau. | [92] |
| 36 | NaCl + CaCl2 + MgCl2 + KCl | CO2 | 308, 333 | 4.48–20 | Experimental (Pendant drop method) | IFT reduces with pressure & rises with temperature. | [93] |
| 37 | NaCl (0–7 wt%) | CO2 | 353.15–453.15 | 8–22 | Experimental (Pendant drop method) | IFT reduces with pressure & rises with temperature and salinity. | [94] |
| No. | Oil Comp | Brine omp | T (K) | P (MPa) | Method | Results | Ref |
|---|---|---|---|---|---|---|---|
| 1 | Heptol (50:50) | 5, 15 wt% NaCl, CaCl2, Na2SO4 | 296.15 | 0.1 | MDS (LAMMPS) | Even though non-polar hydrocarbons lack a functional group for ion accumulation, ions gather at the interface between charge-neutral hydrocarbons and brine. This leads to fluid layers that are alternately positively and negatively charged, giving the appearance of an electrical double layer. The composition of contacting electrolytes controls the charged layer strength near non-polar hydrocarbons, with the interfacial charge density following the toluene > heptol > heptane trend. | [95] |
| 2 | Medium oil, light oil, heptane, toluene, heptol | Sulfate and chloride | 300 | 0.1 | MDS(LAMMPS) + Machine Learning (ML) | The ML with 2% to 9% error from experimental data has better results | [96] |
| 3 | Heptol (0–100:0–100) + (0–0.01) wt% asphaltene | DI water with 0.93 g of NaCl & 0.67 g of NaHCO3 | 298.15–358.15 | 0.1 | Experimental | 1. An increase in the concentration of asphaltenes decreases the IFT. 2. The IFT decreased at first but later increased due to the precipitation of asphaltenes. 3. As the temperature increases, IFTs decrease. | [97] |
| 4 | 2 oil types A,B | Reservoir brine | 298, 333, 374, 383 | 17.237, 20.684, 24.132, 27.579, 31.026 | Experimental & ML(LS-SVM) | 1. An increase in the temperature, pressure, and salinity of synthetic formation water results in a higher IFT for reservoir A. 2. The IFT of oil reservoir B increases with an increase in pressure and salinity but decreases with a temperature increase. 3. The model provides an authentic prediction of the experimental IFT data. | [98] |
| 5 | Dodecane &octane+ toluene & benzene | 0.0, 0.2,1, 2M NaCl | 295.15, 323.15 | 0.1 | MD with LAMMPS | 1. The IFT increases with salinity. 2. Temperatures rising cause IFT reductions. | [45] |
| 6 | Heptol (0:100, 100:00, 56:44, 20:80 volume ratio) +VO-79 asphaltene (50 ppm) | Pure water | 300 | 0.1 | MD with GROMACS | An increase in modeled asphaltene concentration causes an IFT reduction | [44] |
| 7 | Dodecane, toluene, resins (quinoline & 3-naphthenic acid) | Pure water | 300,600 | 0.1 | MD with LAMMPS | There is a correlation between the gathering of oil at the interface and the tension existing between oil layers. | [99] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salehi, N.; Kazemi, M.; Esmaeilbeig, M.A.; Helalizadeh, A.; Bahari Moghaddam, M. Experimental and Molecular Dynamics Simulation of Interfacial Tension Measurements in CO2–Brine/Oil Systems: A Literature Review. Gases 2025, 5, 23. https://doi.org/10.3390/gases5040023
Salehi N, Kazemi M, Esmaeilbeig MA, Helalizadeh A, Bahari Moghaddam M. Experimental and Molecular Dynamics Simulation of Interfacial Tension Measurements in CO2–Brine/Oil Systems: A Literature Review. Gases. 2025; 5(4):23. https://doi.org/10.3390/gases5040023
Chicago/Turabian StyleSalehi, Nadieh, Mohammad Kazemi, Mohammad Amin Esmaeilbeig, Abbas Helalizadeh, and Mehdi Bahari Moghaddam. 2025. "Experimental and Molecular Dynamics Simulation of Interfacial Tension Measurements in CO2–Brine/Oil Systems: A Literature Review" Gases 5, no. 4: 23. https://doi.org/10.3390/gases5040023
APA StyleSalehi, N., Kazemi, M., Esmaeilbeig, M. A., Helalizadeh, A., & Bahari Moghaddam, M. (2025). Experimental and Molecular Dynamics Simulation of Interfacial Tension Measurements in CO2–Brine/Oil Systems: A Literature Review. Gases, 5(4), 23. https://doi.org/10.3390/gases5040023







