Balancing Performance and Portability: A Study on CsI(Tl) Crystal Sizes for Real-Time Gamma-Ray Spectrum and Dose Monitoring
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Sequential Bayesian Estimation and Energy-Spectrum Unfolding
2.2. Dose-Rate Calculation
2.3. Response-Function Creation
- Using MCNP5 to model the experimental setup and perform simulations to create an initial response function for the measured energies;
- Using standard gamma-ray sources (137Cs, 22Na, and 60Co) to measure the full width at half maximum (FWHM) of energy peaks;
- Establishing a relationship between the measured FWHM and energy peaks to calculate the standard deviation (σ) for the Gaussian distribution, modelling the detector’s energy resolution;
- Applying the Gaussian distribution to blur (or “smear”) the MCNP5-derived response functions according to the detector’s energy resolution, accurately reflecting its response to gamma rays;
- Verifying the adjusted response functions against actual measurements for validation, then computing the response functions across the required energy range to form a comprehensive response matrix, which is used for the real-time unfolding of the gamma-ray energy spectrum according to Equation (1).
3. Results
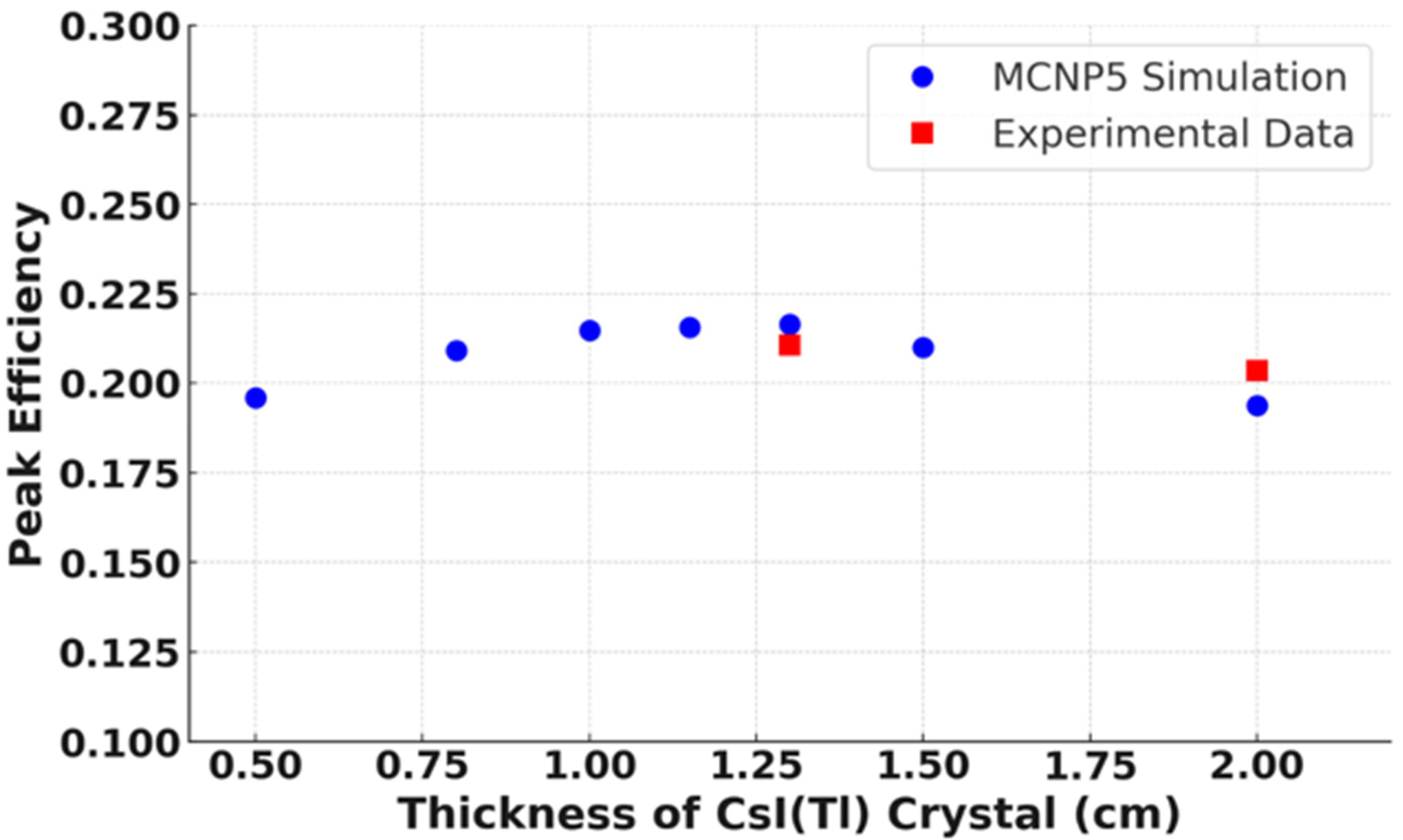
3.1. Detection Efficiency
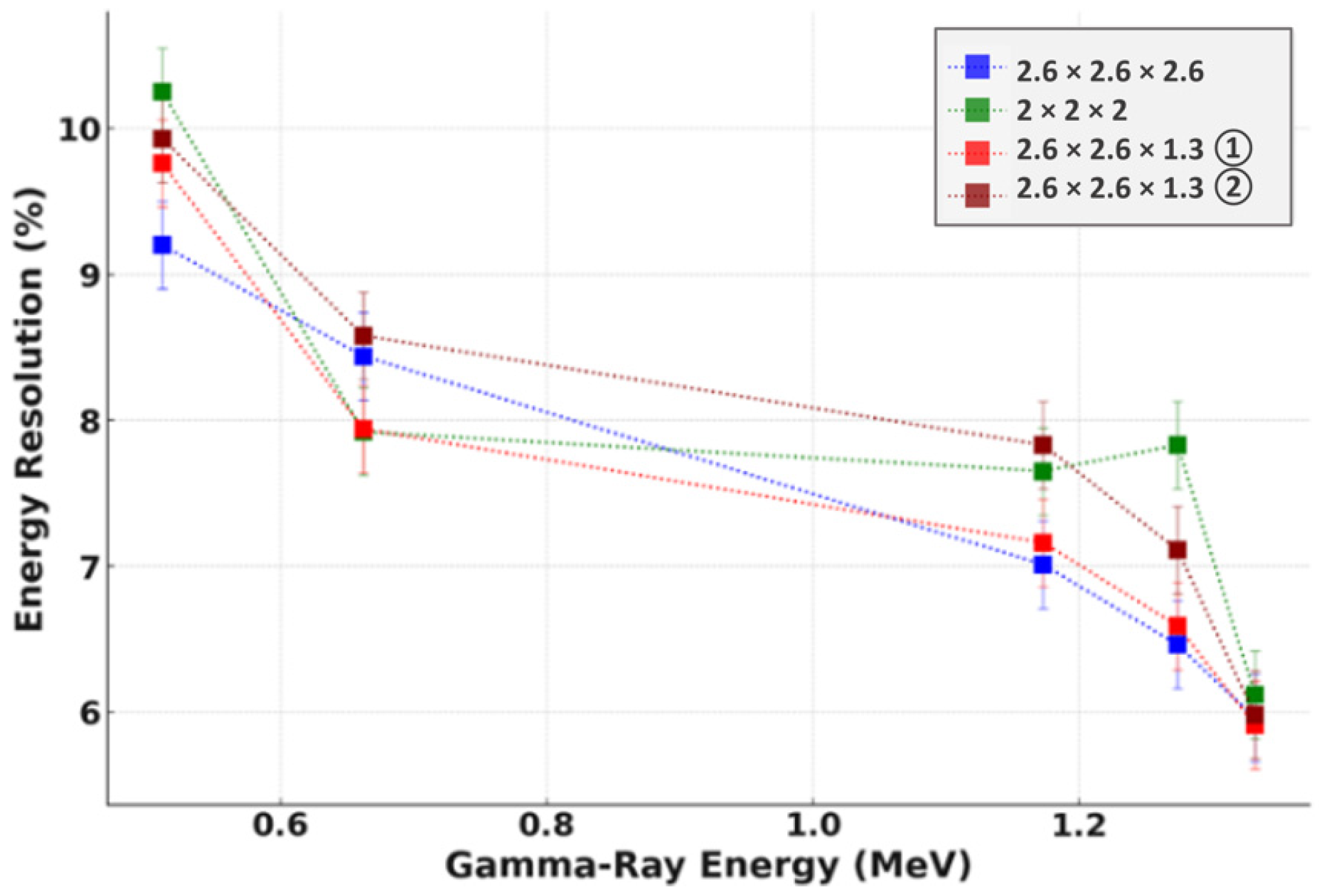
3.2. Energy Resolution
3.3. Pulse-Height Spectra Comparison
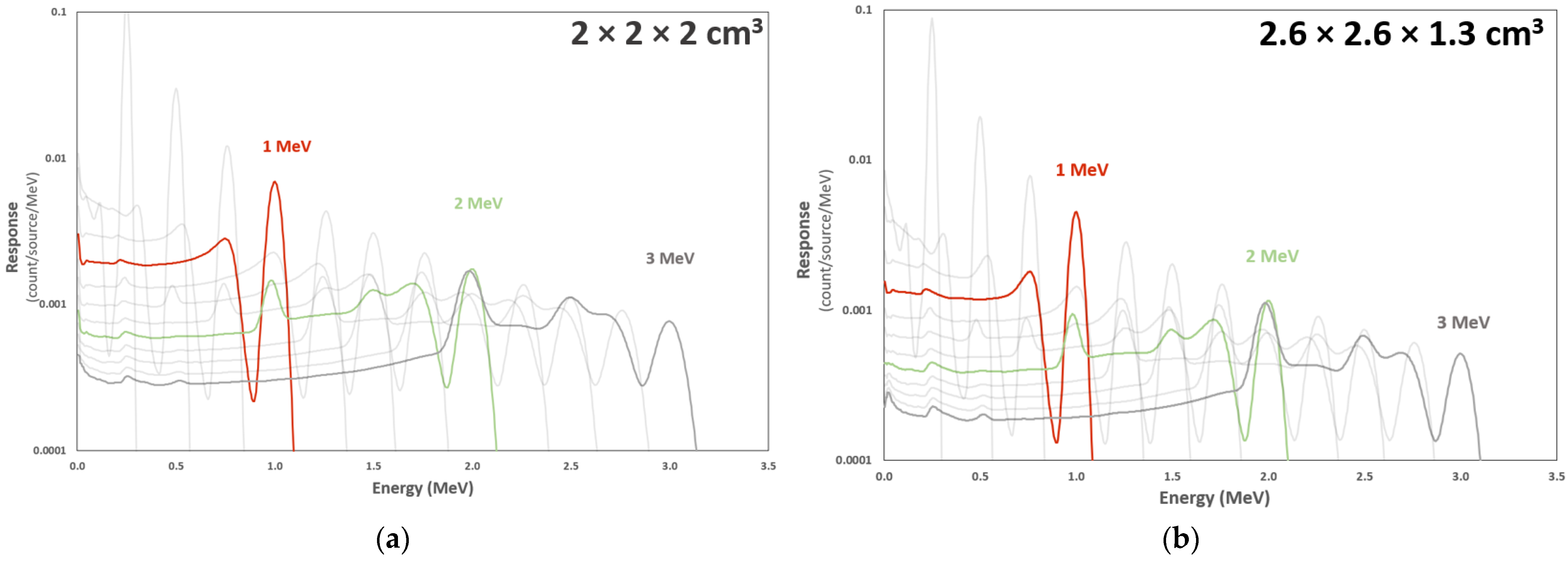
3.4. Response Functions
3.5. Dose-Rate Estimation in the Background
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Knoll, G.F. Radiation Detection and Measurement, 4th ed.; John Wiley: Hoboken, NJ, USA, 2010; ISBN 978-0-470-13148-0. [Google Scholar]
- ICRP. General Principles for the Radiation Protection of Workers, 1st ed.; ICRP Publication Radiation Protection; Pergamon Press: Oxford, UK, 1997; ISBN 978-0-08-042741-6. [Google Scholar]
- Tamam, N.; Salah, H.; Almogren, K.S.; Mahgoub, O.; Saeed, M.K.; Abdullah, Y.; Thanh Tai, D.; Omer, H.; Sulieman, A.; Bradley, D.A. Evaluation of Patients’ and Occupational Radiation Risk Dose during Conventional and Interventional Radiology Procedures. Radiat. Phys. Chem. 2023, 207, 110818. [Google Scholar] [CrossRef]
- Feng, C.-J.; Wu, C.-H.; Huang, Y.-H.; Chu, C.-H.; Lien, K.-Y.; Wang, Y.-C.; Lee, S.-H.; Hsu, S.-M. Results of the Performance Test for Quality Assessment of Personal Radiation Dosimetry Services Including the Influence of the Dosimeter Readout Frequency. Sci. Rep. 2022, 12, 20133. [Google Scholar] [CrossRef] [PubMed]
- Ortega, X.; Ginjaume, M. Advantages and Limitations of Electronic Devices for Primary Occupational Dosimetry. In Proceedings of the International ISOE Symposia, Tarragona, Spain, 5–7 April 2000; ISOE: Tarragona, Spain, 2000. [Google Scholar]
- Meier, J.; Kappadath, S.C. Characterization of the Energy Response and Backscatter Contribution for Two Electronic Personal Dosimeter Models. J. Appl. Clin. Med. Phys. 2015, 16, 423–434. [Google Scholar] [CrossRef] [PubMed]
- Nishimura, H.; Shinohara, M.; Miyoshi, T.; Voulgaris, N.; Kusaka, S.; Tamaki, S.; Sato, F.; Murata, I. Experimental Verification of Real-Time Gamma-Ray Energy Spectrum and Dose Monitor. Appl. Radiat. Isot. 2022, 185, 110226. [Google Scholar] [CrossRef] [PubMed]
- Radiation Solutions. Available online: https://www.radiationsolutionsonline.com/what-are-the-area-radiation-survey-and-radiation-survey-meter-requirements-for-fixed-gauges/ (accessed on 17 April 2024).
- Rizk, C.; Long, S.; Okyar, H.B.; Baradaran, S.; Al Fares, E.; Sangau, J.K.; Shah, B.R. Results of the joint Iaea/Arpansa intercomparison exercise on whole body dosemeters for photons in Asia and the Pacific Region. Radiat. Prot. Dosimetry 2019, 187, 418–425. [Google Scholar] [CrossRef] [PubMed]
- Qureshi, F.; Ramprasad, A.; Derylo, B. Radiation Monitoring Using Personal Dosimeter Devices in Terms of Long-Term Compliance and Creating a Culture of Safety. Cureus 2022, 14, e27999. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.J.; Jang, E.J.; Kim, K.S.; Bang, Y.J. Underestimation of Radiation Doses by Compliance of Wearing Dosimeters among Fluoroscopically-Guided Interventional Medical Workers in Korea. Int. J. Environ. Res. Public Health 2022, 19, 8393. [Google Scholar] [CrossRef] [PubMed]
- Piotrowski, I.; Dawid, A.; Kulcenty, K.; Suchorska, W.M. Use of Biological Dosimetry for Monitoring Medical Workers Occupationally Exposed to Ionizing Radiation. Radiation 2021, 1, 95–115. [Google Scholar] [CrossRef]
- Borrego, D.; Kitahara, C.M.; Balter, S.; Yoder, C. Occupational Doses to Medical Staff Performing or Assisting with Fluoroscopically Guided Interventional Procedures. Radiology 2020, 294, 353–359. [Google Scholar] [CrossRef]
- International Atomic Energy Agency. Occupational Radiation Protection; Proceedings Series; International Atomic Energy Agency: Vienna, Austria, 2022; ISBN 978-92-0-122522-1. [Google Scholar]
- Elshami, W.; Erdemir, R.U.; Abuzaid, M.M.; Cavli, B.; Issa, B.; Tekin, H.O. Occupational Radiation Dose Assessment for Nuclear Medicine Workers in Turkey: A Comprehensive Investigation. J. King Saud Univ. Sci. 2022, 34, 102005. [Google Scholar] [CrossRef]
- Koch, V.; Conrades, L.M.; Gruenewald, L.D.; Eichler, K.; Martin, S.S.; Booz, C.; D’Angelo, T.; Yel, I.; Bernatz, S.; Mahmoudi, S.; et al. Reduction of Radiation Dose Using Real-time Visual Feedback Dosimetry during Angiographic Interventions. J. Appl. Clin. Med. Phys. 2023, 24, e13860. [Google Scholar] [CrossRef]
- Hattori, K.; Inaba, Y.; Kato, T.; Fujisawa, M.; Yasuno, H.; Yamada, A.; Haga, Y.; Suzuki, M.; Zuguchi, M.; Chida, K. Evaluation of a New Real-Time Dosimeter Sensor for Interventional Radiology Staff. Sensors 2023, 23, 512. [Google Scholar] [CrossRef]
- Akber, A.A.; Wiggins, M.B. A Review of Dose Rate Meters as First Responders to Ionising Radiation. J. Radiat. Prot. Res. 2019, 44, 97–102. [Google Scholar] [CrossRef]
- Sarzi Amadè, N.; Bettelli, M.; Zambelli, N.; Zanettini, S.; Benassi, G.; Zappettini, A. Gamma-Ray Spectral Unfolding of CdZnTe-Based Detectors Using a Genetic Algorithm. Sensors 2020, 20, 7316. [Google Scholar] [CrossRef]
- Buzhan, P.; Karakash, A.; Teverovskiy, Y. Silicon Photomultiplier and CsI(Tl) Scintillator in Application to Portable H*(10) Dosimeter. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2018, 912, 245–247. [Google Scholar] [CrossRef]
- Kobayashi, M.; Sato, F.; Kusaka, S.; Murata, I. Feasibility Study on Real-Time γ-Ray Spectrum/Dose Measurement System. EPJ Web Conf. 2017, 153, 07014. [Google Scholar] [CrossRef]
- Brown, F.B.; Kiedrowski, B.C.; Bull, J.S. MCNP5-1.60 Release Notes; Los Alamos National Laboratory Tech. Rep; Los Alamos National Laboratory: Los Alamos, NM, USA, 2010. [Google Scholar]
- Voulgaris, N.; Miyoshi, T.; Tamaki, S.; Kusaka, S.; Murata, I. Development of real-time gamma-ray spectrum and dose monitor: Investigation of true real-time convergence. In Proceedings of the 37th Workshop on Radiation Detectors and Their Uses, High Energy Accelerator Research Organization (KEK). Tsukuba, Japan, 25–27 January 2023; pp. 30–42. Available online: https://www.i-repository.net/il/meta_pub/G0000128Lib_202325001 (accessed on 20 May 2024).
- Singh, I.; Singh, B.; Sandhu, B.S.; Sabharwal, A.D. Comparative Study for Intermediate Crystal Size of NaI(Tl) Scintillation Detector. Rev. Sci. Instrum. 2020, 91, 073105. [Google Scholar] [CrossRef] [PubMed]
- El Hamli, A.; Bazza, A.; Moussa, A.; Hamal, M.; Zerfaoui, M.; Ouchrif, M. Data and Simulation Studies on the Influence of Scintillation Crystal Dimensions on Spectrometric Parameters. Appl. Radiat. Isot. 2022, 181, 110053. [Google Scholar] [CrossRef] [PubMed]
- Wagner, A.; Tan, W.P.; Chalut, K.; Charity, R.J.; Davin, B.; Larochelle, Y.; Lennek, M.D.; Liu, T.X.; Liu, X.D.; Lynch, W.G.; et al. Energy Resolution and Energy–Light Response of CsI(Tl) Scintillators for Charged Particle Detection. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2001, 456, 290–299. [Google Scholar] [CrossRef]
- Jeong, M.; Van, B.; Wells, B.T.; D’Aries, L.J.; Hammig, M.D. Comparison between Pixelated Scintillators: CsI(Tl), LaCl 3(Ce) and LYSO(Ce) When Coupled to a Silicon Photomultipliers Array. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2018, 893, 75–83. [Google Scholar] [CrossRef]
- Wernick, M.N.; Aarsvold, J.N. Emission Tomography: The Fundamentals of PET and SPECT; Elsevier Academic Press: Amsterdam, The Netherlands; Boston, MA, USA, 2004; ISBN 978-0-12-744482-6. [Google Scholar]
- Mikhailik, V.B.; Kapustyanyk, V.; Tsybulskyi, V.; Rudyk, V.; Kraus, H. Luminescence and Scintillation Properties of CsI: A Potential Cryogenic Scintillator. Phys. Status Solidi B 2015, 252, 804–810. [Google Scholar] [CrossRef]
- Hawrami, R.; Ariesanti, E.; Farsoni, A.; Szydel, D.; Sabet, H. Growth and Evaluation of Improved CsI:Tl and NaI:Tl Scintillators. Crystals 2022, 12, 1517. [Google Scholar] [CrossRef]
- Yanagida, T. Inorganic Scintillating Materials and Scintillation Detectors. Proc. Jpn. Acad. Ser. B 2018, 94, 75–97. [Google Scholar] [CrossRef] [PubMed]
- Jasni, A.A.; Yap, Y.; Hashim, I.H.; Ahmad, N.E.; Ramlee, N. Two Dimensional Array of MPPC and CsI(Tl) for Radiation Monitoring Prototype. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1106, 012028. [Google Scholar] [CrossRef]
- Hamamatsu Photonics MPPC Array Module Documentation. Available online: https://www.hamamatsu.com/jp/en/product/optical-sensors/mppc/mppc_mppc-array/related_documents.html (accessed on 20 June 2024).
- ORTEC/AMETEK Nuclear Instrumentation, Nuclear Analysis Software, Radiation Detectors 575A Amplifier. Available online: https://www.ortec-online.com/products/electronic-instruments/amplifiers/575a (accessed on 20 June 2024).
- ORTEC/AMETEK MCA8000D Multichannel Analyzer. Available online: https://www.amptek.com/products/multichannel-analyzers/mca-8000d-digital-multichannel-analyzer (accessed on 20 June 2024).
- Gramuglia, F.; Frasca, S.; Ripiccini, E.; Venialgo, E.; Gâté, V.; Kadiri, H.; Descharmes, N.; Turover, D.; Charbon, E.; Bruschini, C. Light Extraction Enhancement Techniques for Inorganic Scintillators. Crystals 2021, 11, 362. [Google Scholar] [CrossRef]
- Vincent, K.N.; Mahapatra, S.; Poddar, I.; Verma, S. Improving the Resolution and Light Yield in CsI(Tl) Scintillators. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2023, 1056, 168624. [Google Scholar] [CrossRef]
- L’Annunziata, M.F. Handbook of Radioactivity Analysis, 2nd ed.; Academic Press: San Diego, CA, USA, 2003; ISBN 978-0-12-436603-9. [Google Scholar]
- Meyers, R.A. Encyclopedia of Physical Science and Technology, 3rd ed.; Academic Press: San Diego, CA, USA, 2002; ISBN 978-0-12-227410-7. [Google Scholar]
- Hussein, E.M.A. The Physical and Mathematical Aspects of Inverse Problems in Radiation Detection and Applications. Appl. Radiat. Isot. 2012, 70, 1131–1135. [Google Scholar] [CrossRef] [PubMed]
- Iwasaki, S. A New Approach for Unfolding PHA Problems Based Only on the Bayes Theorem. In Proceedings of the 9th International Symposium on Reactor Dosimetry, Prague, Czech Republic, 2–6 September 1996; Hamid, A., Bohumil, O., Eds.; American Society for Testing and Materials Euratom Working Group on Reactor Dosimetry & E.N. Society World Scientific: Prague, Czech Republic, 1996; pp. 245–252. [Google Scholar]
- Nauchi, Y.; Iwasaki, S. Convergence of Unfolded Spectrum with Response Function for Single Radiation Based on Bayes’ Theorem. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2014, 735, 437–443. [Google Scholar] [CrossRef]
- ICRP. Conversion Coefficients for Use in Radiological Protection against External Radiation, 1st ed.; ICRP Publication Radiation Protection; Pergamon Press: Oxford, UK, 1997; ISBN 978-0-08-042739-3. [Google Scholar]
- Nuclear Regulation Authority. Method for Measurement of Environmental Gamma-Rays with a Continuous Monitor, “Environmental Radioactivity and Radiation in Japan.”; The Series of Environmental Radioactivity Measuring Methods; Radiation Monitoring Division Radiation Monitoring Department Nuclear Regulation Authority: Tokyo, Japan, 2017. [Google Scholar]
- Moriuchi, S.; Tsutsumi, M.; Saito, K. Construction of Response Matrices for Various Cylindrical and Spherical NaI(Tl) Scintillation Detectors for Gamma Rays and the Test Results. Jpn. J. Health Phys. 2009, 44, 122–133. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Z.; Peeples, J.; Yu, H.; Gardner, R.P. Development of a Simple Detector Response Function Generation Program: The CEARDRFs Code. Appl. Radiat. Isot. 2012, 70, 1166–1174. [Google Scholar] [CrossRef]
- Hajheidari, M.T.; Safari, M.J.; Afarideh, H.; Rouhi, H. Experimental Validation of Response Function of a NaI(Tl) Detector Modeled with Monte Carlo Codes. J. Instrum. 2016, 11, P06011. [Google Scholar] [CrossRef]
- Mouhti, I.; Elanique, A.; Messous, M.Y.; Benahmed, A.; McFee, J.E.; Elgoub, Y.; Griffith, P. Characterization of CsI(Tl) and LYSO(Ce) Scintillator Detectors by Measurements and Monte Carlo Simulations. Appl. Radiat. Isot. 2019, 154, 108878. [Google Scholar] [CrossRef]
- Moszynski, M. Energy Resolution and Non-Proportionality of Scintillation Detectors. MRS Proc. 2007, 1038, 1038-O07-02. [Google Scholar] [CrossRef]
- Ferrulli, F.; Labalme, M.; Silari, M. Investigation of CLYC-6 for Thermal Neutron Detection and CLYC-7 for Fast Neutron Spectrometry. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2022, 1029, 166460. [Google Scholar] [CrossRef]
- Cheng, J.-H.; Wang, Z.; Lebanowski, L.; Lin, G.-L.; Chen, S. Determination of the Total Absorption Peak in an Electromagnetic Calorimeter. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2016, 827, 165–170. [Google Scholar] [CrossRef]
- Grozdanov, D.N.; Fedorov, N.A.; Bystritski, V.M.; Kopach, Y.N.; Ruskov, I.N.; Skoy, V.R.; Tretyakova, T.Y.; Zamyatin, N.I.; Wang, D.; Aliev, F.A.; et al. Measurement of Angular Distributions of Gamma Rays from the Inelastic Scattering of 14.1-MeV Neutrons by Carbon and Oxygen Nuclei. Phys. At. Nucl. 2018, 81, 588–594. [Google Scholar] [CrossRef]
- Pani, R.; Cinti, M.N.; De Notaristefani, F.; Pellegrini, R.; Bennati, P.; Betti, M.; Trotta, G.; Karimian, A.; Mattioli, M.; Garibaldi, F.; et al. Imaging Performances of LaCl/Sub 3/:Ce Scintillation Crystals in SPECT. In Proceedings of the IEEE Symposium Conference Record Nuclear Science 2004, Rome, Italy, 16–22 October 2004; IEEE: Rome, Italy, 2004; Volume 4, pp. 2283–2287. [Google Scholar]
- Moses, W.W.; Choong, W.-S.; Derenzo, S.E. Modeling Time Dispersion Due to Optical Path Length Differences in Scintillation Detectors. Acta Phys. Pol. B Proc. Suppl. 2014, 7, 725. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Voulgaris, N.; Nishimura, H.; Tamaki, S.; Kusaka, S.; Murata, I. Balancing Performance and Portability: A Study on CsI(Tl) Crystal Sizes for Real-Time Gamma-Ray Spectrum and Dose Monitoring. Radiation 2024, 4, 213-223. https://doi.org/10.3390/radiation4030016
Voulgaris N, Nishimura H, Tamaki S, Kusaka S, Murata I. Balancing Performance and Portability: A Study on CsI(Tl) Crystal Sizes for Real-Time Gamma-Ray Spectrum and Dose Monitoring. Radiation. 2024; 4(3):213-223. https://doi.org/10.3390/radiation4030016
Chicago/Turabian StyleVoulgaris, Nikolaos, Hikari Nishimura, Shingo Tamaki, Sachie Kusaka, and Isao Murata. 2024. "Balancing Performance and Portability: A Study on CsI(Tl) Crystal Sizes for Real-Time Gamma-Ray Spectrum and Dose Monitoring" Radiation 4, no. 3: 213-223. https://doi.org/10.3390/radiation4030016
APA StyleVoulgaris, N., Nishimura, H., Tamaki, S., Kusaka, S., & Murata, I. (2024). Balancing Performance and Portability: A Study on CsI(Tl) Crystal Sizes for Real-Time Gamma-Ray Spectrum and Dose Monitoring. Radiation, 4(3), 213-223. https://doi.org/10.3390/radiation4030016









