Abstract
Refractory high-entropy alloys (RHEAs) are strong candidates for use in high-temperature engineering applications. As such, the thermodynamic properties as a function of temperature for a variety of RHEA systems need to be studied. In the present work, thermodynamic quantities such as entropy, enthalpy, heat capacity at constant volume, and linear thermal expansion are calculated for three quaternary and three quinary single-phase, BCC RHEAs: AlMoNbV, NbTaTiV, NbTaTiZr, AlNbTaTiV, HfNbTaTiZr, and MoNbTaVW. First-principle calculations based on density functional theory are used for the calculations, and special quasirandom structures (SQSs) are used to represent the random solid solution nature of the RHEAs. A code for the finite temperature thermodynamic properties using the Debye-Grüneisen model is written and employed. For the first time, the finite temperature thermodynamic properties of all 24 atomic configuration permutations of a quaternary RHEA are calculated. At most, 1.7% difference is found between the resulting properties as a function of atomic configuration, indicating that the atomic configuration of the SQS has little effect on the calculated thermodynamic properties. The behavior of thermodynamic properties among the RHEAs studied is discussed based on valence electron concentration and atomic size. Among the quaternary RHEAs studied, namely AlMoNbV, NbTaTiZr, and NbTaTiV, it is found that the presence of Zr contributes to higher entropy. Additionally, at lower temperatures, Zr contributes to higher heat capacity and thermal expansion compared to the alloys without Zr, possibly due to its valence electron concentration. At higher temperatures, Al contributes to higher heat capacity and thermal expansion, possibly due its ductility. Among the quinary systems, the presence of Mo, W, and/or V causes the RHEA to have a lower thermal expansion than the other systems studied. Finally, when comparing the systems with the NbTaTi core, the addition of Al increases thermal expansion, while the removal of Zr lowers the thermal expansion.
1. Introduction
High-entropy alloys (HEAs) consist of four or more alloying components in roughly equiatomic proportions. They can form a single phase in the forms of face-centered cubic, body-centered cubic (BCC), or hexagonal close-packed [1]. HEAs take on the name high entropy because they exhibit unusually high entropy of mixing. If the entropy is sufficiently large, the entropy of mixing can suppress the enthalpy of formation of multiple phases, resulting in enhanced physical and mechanical properties [2,3,4].
Refractory alloys play an important role in industries including aerospace, defense, iron and steel, aluminum, glass, and power generation industries, as well as many others [5,6,7,8,9]. Whether it be a furnace for heating glass, melting Al, forging iron or steel, or a fired heater in the petrochemical industry, refractory alloys are needed so that the structures of these high-temperature processing units can withstand high levels of heat without compromising their structure [10,11]. Ni-base superalloys are a common refractory alloy that is used in industrial gas turbine applications [12,13]. Traditional metals used in refractory applications are Ni-base superalloys such as IN718 Waspaloy [14], IN939 [15]. It is possible that the traditional alloys could be replaced by refractory high entropy alloys (RHEAs) in the future [16,17]. When comparing RHEAs to conventional Ni-base superalloys, Yeh et al. [16], Patel et al. [17], and Naser-Zoshki et al. [14] showed how some RHEAs can have better hot hardness and yield strength than traditional Ni-base superalloys. BCC RHEAs have the potential of replacing traditional Ni-based super alloys due to their temperature-resistant qualities.
In order to characterize RHEAs at high temperatures, their thermodynamic behaviors at elevated temperatures must first be understood. For example, entropy affects the atom’s ability to move within that lattice structure, while enthalpy relates to the atomic bond strength within the alloy [1]. Thermal expansion is also an important property to consider in high-temperature environments due to the need of dimensional stability to resist deformation.
The goal of this work is to help bridge the gap between experimental techniques and computational methods by calculating thermodynamic properties as a function of temperature from first principles. The finite-temperature thermodynamic calculation methodology will be validated by comparing computational results with well-known and established experimental values, and applying this method to lesser-known RHEAs. Furthermore, a complete set of finite-temperature thermodynamic properties are calculated for all 24 atomic configuration permutations of a quaternary RHEA. To the best of the authors’ knowledge, this has not been performed before in the scientific literature. The negligible variation in resulting properties as a function of temperature will be highlighted.
The manuscript is organized as follows. First, in Section 1, an overview of the current literature with regards to the thermodynamic properties of RHEAs is given. In Section 2, the theory behind thermodynamic calculations is discussed, as well as an overview of the quasi-harmonic Debye model used for the finite-temperature thermodynamic properties. The computational details are also discussed, including the use of special quasirandom structures (SQSs) to represent the RHEAs. In Section 3, the computational methodology used in the present work is validated and the results of the thermodynamic property calculations for the NbTaTiZr, AlMoNbV, and NbTaTiV quaternary RHEAs, as well as the AlNbTaTiV, HfNbTaTiZr, and MoNbTaVW quinary RHEAs, are presented and discussed.
Literature Review
RHEAs were traditionally composed of refractory elements such as Mo, Nb, Ta, V, and W, but have more recently expanded to include one or more elements from the periodic table in Group IV (Ti, Zr, and Hf), Group V (V, Nb, and Ta), and/or Group VI (Cr, Mo, and W) [5]. Other non-refractory elements such as Al, Si, Co, and/or Ni may also be added [5]. In 2022, Hua et al. [18] reported on 100 RHEAs that have been discovered and published. More than seventeen elements were used, which could theoretically produce roughly 20,000 quaternary, quinary, senary, and septinary RHEAs. Clearly, computational approaches to calculate RHEA properties and understanding trends in RHEA behavior are needed.
With regards to the computational methods used, using first-principles calculations based on density functional theory to represent random solid solutions such as RHEAs is a challenge. The two most popular methods to represent the HEA random solid solution structure are special quasirandom structures (SQSs), as employed in the present work, and the coherent–potential approximation (CPA) method. Both have been used extensively in the scientific literature, for example, in [19,20,21,22,23,24,25,26,27,28,29]. The CPA method is a mean-field technique, where the effects of each of an HEA’s constituents are embedded into a “medium” that mimics the chemical disorder of an HEA [30]. A major advantage of CPA is that, due to the medium, only a single primitive unit cell is needed to run the DFT calculations, making them fast and less of a computational burden than other techniques [30]. The downside of the CPA technique is that it cannot represent local lattice distortions, chemical short-range order, or lattice vibrations [31]. In particular, the local chemical environment and the lattice vibrations are important considerations for calculation of thermodynamic properties as a function of temperature.
Since the lattice distortions and effects from lattice vibrations are necessary in the present work, SQSs are employed here. SQSs [32,33] solve the problem of needing a random solid solution by creating a structure that mimics the pair-correlation function of a perfectly random structure for the first several nearest neighbor shells, while using a finite number of atoms. However, the SQS method comes with an increased computational cost due to the larger supercell size and complex electronic structures associated with higher-order HEAs. Furthermore, when defects are present, it is typically necessary to average several atomic configuration permutations (meaning replacing all A atoms with B atoms, B atoms with C atoms, etc.) of the SQS together to capture the variations in the local environment surrounding the defect [22,24,34,35,36,37]. Other methods exist, such as random supercell sampling [20,38] and small sets of ordered structures (SSOSs) [39], but they are not widely adopted in the literature.
In this paper, several equiatomic quaternary and quinary RHEAs known to be single-phase BCC solid solutions are studied: AlMoNbV, NbTaTiZr, NbTaTiV, AlNbTaTiV, HfNbTaTiZr, and MoNbTaVW [5]. AlMoNbV is studied in the present work due to a previous first-principles study by Ge et al. [27], where similar thermodynamic properties and elastic properties are calculated using first-principles calculations and the CPA method already discussed. The work of Ge et al. provides an excellent opportunity to compare previous calculated data to the present work, in order to validate our computational methodology.
Notably, MoNbTaVW [3] and HfNbTaTiZr [40] are well-studied systems, with experimentation proving them to be single-phase BCC at lower temperatures and above 1273 K [5]. The high temperature single-phase stability makes these RHEAs excellent candidates for Ni-base superalloy alternatives. The HfNbTaTiZr RHEA has also been studied computationally by Song et al. [29], using first-principle calculations and the CPA to evaluate thermal expansion and entropy at both and elevated pressures. Sheikh et al. also studied HfNbTaTiZr as a proof of concept, theorizing that decreasing the number of s+d valence electrons can be used as a guide for designing new RHEAs [41,42,43]. NbTaTiZr has been studied by Yang et al. [28] using exact muffin-tin orbitals and the CPA to study the effects of varying the Ta/Ti ratio on the elastic and thermodynamic properties of the RHEAs and found higher concentrations of Ti as a replacement of Ta increases the ductility of the RHEA.
Yao et al. studied elastic and mechanical property results on body-centered cubic MoNbTaTiV [44] by using CALPHAD to calculate the mole fraction phase equilibrium versus temperature and DFT for various properties such as lattice parameter, elastic constants, enthalpy of formation, and other properties. Experimentally, they confirmed that arc-melting MoNbTaTiV formed a single BCC phase as-cast, as predicted by CALPHAD modeling. Melnick et al. completed a study on thirteen RHEAs based on W, Ta, Mo, Nb, V, Ti, Zr, Hf, and Cr [45]. They found that optimal compositions of HEAs were non-equiatomic. Liao et al. published their work on varying compositions of NbTiVZr based on first-principles calculation using virtual crystal approximation (VCA), showing that VCA is suitable for elastic and thermodynamic properties modeling [46], and found that BCC is the most stable structure in most situations, and that adding Nb and V increases BCC structure stability, while Ti and Zr decrease stability. Zheng et al. calculated the elastic properties of seventy different compositions of V-Mo-Nb-Ta-W for property optimization [47], and found that Mo and W produce high , B, E, and G values, while Nb and Ta have a relatively small influence on elastic properties. Dobbelstein et al. found that Ti25Nb50Ta25 and TiZrNbTa exist in a single-phase BCC solution with a coarse-grain microstructure, showing that laser metal deposition is a suitable processing tool [48]. Recently, Bhandari et al. published a paper on elastic properties of RHEAs predicted through machine learning, wherein their method was validated by comparing results of RHEAs to datasets. The RHEAs included MoNbTiVZr, MoNbTiZr, and NbTiVZr [49].
2. Materials and Methods
First-principle calculations based on density functional theory combined with the quasiharmonic approach yield accurate finite temperature properties of material systems [50,51]. The total Helmholtz free energy, , of any system can be calculated as shown in Equation (1) [50,51]
where is the vibrational contribution to the free energy, described by the quasi-harmonic Debye-Grüneisen model in the present work. is the static energy (without zero-point energy) at 0 K and volume V [50,51]. Other contributions, such as the thermal–electronic excitations at the Fermi level or magnetic contributions, can be added to Equation (1) as necessary.
In the present work, is calculated directly at 0 K using first-principle techniques.
2.1. Equation of State: Energy vs. Volume and Debye Model
In order to calculate thermodynamic properties as a function of temperature and volume, as given in Equation (1), a vibrational model is introduced. The first step is an energy vs. volume equation of state of the material at 0 K. The equation of state relates energy as a function of volume to the compressibility of the material, which is reciprocal to the bulk modulus through the equation at zero pressure, as shown in Equation (2) [51,52,53]
where a, b, c, and d are fitting parameters defined in by Shang et al. [51].
The Debye-Grüneisen model calculates the temperature at which the crystalline structure is at its highest mode of vibration [50,51,54,55]. This is undertaken because a crystalline structure will not have any phonons at 0 K, and as temperature is increased, phonons are created, and phonons will increase in energy as temperature increases. At a certain temperature, the phonons will reach a maximum energy threshold and any increase in temperature beyond that point will not be converted into phonons. That temperature is the Debye temperature that can be calculated by Equation (3) [50].
where is the Debye temperature and from Moruzzi et al.’s work [50]. = 231.04, as shown by Shang et al [51], where ℏ is reduced planks constant, and is Boltzmann’s constant, B is the bulk modulus in GPa, and M is the mass of the material being studied in atomic units. Equation (3) solves the Debye temperature which is needed to calculate Helmholtz free energy, and incorporates the vibrational contribution of energy to the system via Equation (1). The vibrational contribution to the system is defined in Equation (4) [51] as
where is the Debye function defined as and D varies between 0 and 1. D scales the phonon energy contribution to the system. Since the Debye temperature is a fixed value and calculates the maximum vibrational energy, the Debye function scales that value for any temperature below the Debye temperature. Once the vibrational contribution of the system is defined, the Helmholtz free energy can be calculated as shown in Equation (1).
2.2. Thermodynamic Properties
In this section, an overview of the calculated thermodynamic property theory and equations is given. Entropy as a function of V and T can be calculated by using Equation (5) [50,51]
where all elements of the equation have been defined above, including D and .
Now that entropy and enthalpy have been defined, and heat capacity is kept at a constant volume, can be considered. is the change in entropy with respect to temperature, as given in the following equation:
can be calculated via this derivative, or by using [56], where , and where n is the number of atoms, and is Avogadro’s number. These two equations for can be calculated separately and compared to check for precision. The present work reports from Equation (7).
Finally, the coefficient of thermal expansion (CTE) can be expressed as a linear, , or volumetric, , coefficient. CTE brings together both thermodynamic and elastic properties. CTE is an important property in RHEAs because thermally stable materials must be able to retain their structural dimensions and integrity at high temperatures. Linear thermal expansion, , is calculated through the relationship in Equation (8) as shown by [51]
where is the volume at equilibrium of the temperature of interest where P = 0 and volumetric thermal expansion is related to alpha such that , as shown by Wang [57].
2.3. Computational Details
The calculations in the present work were performed using the Vienna ab initio Simulation Package (VASP) [58,59], using the exchange–correlation functionals of Perdew–Burke–Ernzerhof within the generalized gradient approximation [60]. The behavior of core and valence electrons is described through the projector augmented-wave (PAW) method [61,62]. A plane–wave energy cutoff of 350 eV is employed for all calculations, which is recommended by the VASP manual at 1.3× higher than the default cutoff of any of the pure elements used in the calculation series. Dense k-point meshes of at least 20,000 point per reciprocal atom are used in conjunction with -centered meshes. The supercells were converged to at least 0.1 meV/atom during the VASP calculations, and all degrees of freedom of the system were allowed to relax. The blocked Davidson iterative scheme was used for the relaxation algorithm [63]. The partial occupancy of orbitals was smeared with the Methfessel–Paxton first-order method for relaxations [63] and the tetrahedron method with Blöchl corrections for accurate total energy calculations [64].
In order to represent the random solid nature of the RHEAs used in the present work, special quasirandom structures (SQSs) are employed [32]. SQSs use a finite number of atoms to represent the pair–correlation functions of a random solid solution. The mcsqs code as part of the Alloy Theoretic Automated Toolkit is used to generate the SQSs needed for both quaternary and quinary RHEAs [65]. Quaternary systems used a supercell of 40 or 60 atoms while the quinary RHEAs used 50 or 75 atom supercells.
There is an error associated with using SQSs to represent random solid solutions, since only a finite number of atoms are considered in the SQS. The quality of an SQS can be measured by calculating the energy associated with every permutation of atomic ordering (meaning all type “A” lattice sites are switched with type “B” lattice sites, until all combinations are made) and calculating the standard deviation of the energies [22]. In a perfect SQS, little-to-no variation in the ground-state energy should exist. Our group’s previous works have shown that, in defect-free BCC SQSs that represent HEAs, little variation among atomic permutations exists [37]. In Section 3.2, a full set of atomic configuration permutations is studied for the quaternary AlMoNbV system, in order to demonstrate that the SQSs used in the present work are sound and show little variation in the ground-state energies as a function of atomic configuration permutations. The quasi-harmonic Debye model is also applied to the 24 atomic configuration permutations, calculating all finite temperature thermodynamic properties for each of the AlMoNbV system’s 24 atomic configuration permutations.
3. Results and Discussion
3.1. Methodology Validation on BCC Ta and FCC Al
First, a validation of the finite-temperature thermodynamic calculation method is presented on the pure element systems of Ta and Al. By performing the calculations on well-studied pure elements first, the atomic complexity within the HEA environment is removed. The accuracy of the code written for the calculation of thermodynamic properties can be evaluated on simpler systems. Here, the validation is performed by comparing the calculated thermodynamic properties from the present work on pure BCC Ta and Al FCC systems to NIST-JANAF experimental values [66]. The results, as shown in Figure 1, include calculated (a) entropy and (b) enthalpy as a function of temperature up to the melting point of pure BCC Ta at 3358 K and 933 K for pure FCC Al from the present work (solid line), compared to experimental NIST-JANAF data (points). Enthalpy is normalized to 298.15 K such that H(298.15 K) = 0 kJ/mol, as is standard practice in the literature.
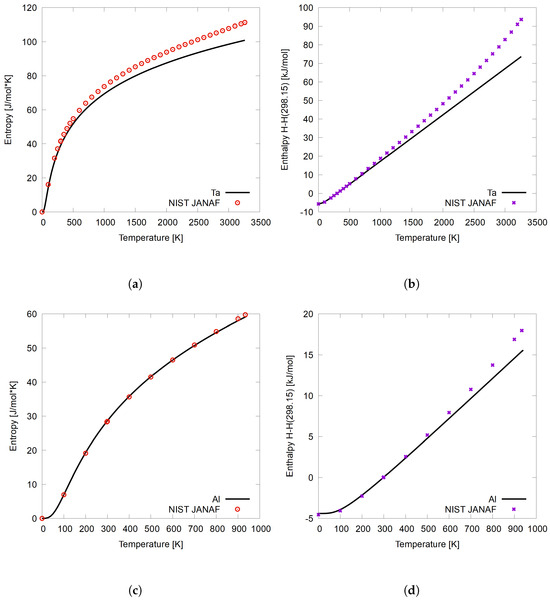
Figure 1.
Calculated (a) entropy and (b) enthalpy values as a function of temperature for pure Ta and calculated (c) entropy and (d) enthalpy as a function of temperature for pure Al. Calculated values are solid lines, and NIST-JANAF [66] data are points. Enthalpy is considered with reference to 298.15 K, where − .
Figure 1a,c illustrate the entropy of pure BCC Ta and pure FCC Al, respectively, calculated using the Debye-Grüneisen model in the present work, where entropy is found when by using Equation (5). In Figure 1a, the model of the present work represents the experimental entropy of BCC Ta well until about 300 K, at which point the model underestimates the experimental entropy. In Figure 1c, the model used in the present work represents the entropy of FCC Al well up to its melting temperature of 933 K. The discrepancy in the Ta data can be explained by the fact that the results from the present work are given without the thermal–electronic contribution to the total energy. The thermal–electronic contribution varies from metal to metal, and is based on the shape of the density of states around the Fermi level [51]. Including the thermal–electronic contribution was beyond the scope of the present work, but it would increase the overall Helmholtz free energy, as demonstrated in Equation (1) [27,51]. In Figure 1b,d, enthalpy is calculated from and compared to the same experimental datasets as entropy for Ta and Al, respectively. For Ta, the enthalpy is well reproduced until about 1000 K, at which point the model deviates from the experimental data due to the reasons already mentioned. Similar to the entropy plot, Figure 1d shows good agreement between the calculated enthalpy from the present work and the experimental data [66], with some deviations occurring below the melting temperature. In conclusion, the lack of thermal–electronic contribution will affect some systems more than others.
Overall, the computational methodology is validated through these comparisons. The experimental data are replicated adequately at lower temperatures. Furthermore, there is a 6% difference for Ta at 1600 K, which is about half of the melting temperature Ta. With regards to entropy, there is roughly a 1.2% difference for Al and a 9% difference for Ta just below the melting temperature. For enthalpy, at these same temperatures, there is a 7.8% difference at 500 K for Al, and a 14.7% difference just below the melting temperature. The calculated enthalpy of Ta has a 10.8% difference at 1600 K and a difference of 21.2% just below the melting temperature.
3.2. AlMoNbV—HEA Validation and Atomic Configuration Permutations
Since the Debye-Grüneisen model code written in the present work has been validated on pure Ta and Al, confirmation that the model works well for BCC RHEAs must be obtained. This confirmation is a two-step process on the quaternary HEA, AlMoNbV. As mentioned in Section 2, using DFT + SQS for calculation of HEA properties raises the question of how many atomic configurations are enough to accurately represent the HEA system. When an SQS is sufficiently large, one atomic configuration should be enough. To prove this, the ground state energy of every permutation that exists of AlMoNbV is calculated, by switching atom types of every species for every other atom type using the same 40 atom supercell. There is a total of 4! = 24 systems. All 24 of these ground state energy values and corresponding cell volumes are given in Table A1 of the Appendix A. It can be seen that the standard deviation of the energy amongst all 24 permutations is small, at 0.007 eV/atom. The standard deviation of the volume is also small. After the ground-state energy was calculated, the E-V EOS and the corresponding finite temperature thermodynamic properties on all 24 of the atomic configuration permutations were calculated via the quasiharmonic Debye-Grüneisen model, as outlined in Section 2.
The calculated properties are compared to the work of Ge et al. [27] in Figure 2 as (a) entropy as a function of temperature and (b) constant volume heat capacity, with as a function of temperature. Entropy is calculated from Equation (5), and constant volume heat capacity as defined by . In Figure 2, the solid red line is averaged properties for all 24 atomic configuration permutations of the AlMoNbV RHEA, including the Debye model. The black dashed line is the work of Ge et al [27]. For further validation of the quality of the SQS, the high (purple dotted-dashed line) and low (blue dotted line) entropy and constant-volume heat capacity data from the 24 atomic configuration permutations are included. Finally, it should be noted that the entropy in Figure 2a reported by Ge is vibrational entropy only, and is consistent with our set of calculations. Based on Ge et al.’s report that is dominated by electronic contributions, the authors assume that the results in Figure 2b are also the vibrational contribution only.
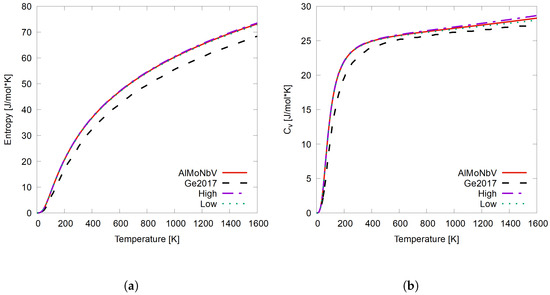
Figure 2.
(a) Entropy and (b) as a function of temperature from 0 to 1600 K comparing this work to the values Ge et al. [27] reported for the AlMoNbV RHEA. The red solid line is the average of the 24 permutations of the AlMoNbV system, while the purple dashed-dotted line is the highest dataset from the 24 permutations and the blue dotted line is the lowest dataset.
First, the finite temperature properties of the 24 atomic configurations permutations are discussed by comparing the range of calculated results. In Figure 2a, it can be seen that, when the average, highest, and lowest datasets for AlMoNbV out of the 24 atomic configuration permutations are used, no difference in the calculated entropy exists. This shows that the DFT + SQS + Debye method used is sound, and that multiple permutations of the SQS do not need to be averaged together to obtain an accurate representation of the thermodynamic properties of these RHEAs. Similar results are shown for in Figure 2b. While some small variations exist at higher temperatures, the average differences are on the order of 1.7 % from 1000 to 1600 K from the high and low values and are within the error associated with DFT calculations. Since the error between the highest and lowest atomic configuration permutation calculations is not more than 2% over the range of calculated values, as few as one atomic configuration permutation is needed to ensure accuracy and consistency between permutations. This method gives future researchers a method for efficiently calculating thermodynamic properties in RHEAs using the DFT + SQS + Debye method used in the present work.
Second, our calculated results of entropy and as a function of temperature are compared to the previous work of Ge et al. [27] for validation of the DFT + SQS + Debye model. It should be noted that Ge et al. performed DFT calculations based on the CPA, which is a mean-field technique, to obtain the thermodynamic properties. In the CPA, the effects of each element in the alloy are embedded in a “medium” that represents the effects of all elements at the same time [31]. As the method used by Ge et al. [27] is a very different process than DFT + SQS permutation and averaging technique employed in the present work, an excellent comparison opportunity exists. In Figure 2a,b, we see a strong comparison to the previously calculated work of Ge et al. [27]. For entropy, we see a maximum difference at the melting temperature of about 6–7% from our work compared to Ge et al.’s [27]. We note that, without the thermal–electronic contribution, our DFT + SQS method produces a larger entropy for the AlMoNbV RHEA than the CPA method used by Ge. For constant-volume heat capacity, which is essentially the rate of change of entropy, our results reproduce the results of Ge et al. nearly exactly. In conclusion, our DFT+SQS+Debye method produces accurate and consistent thermodynamics properties for RHEAs, and can be applied to systems that have not been previously studied in the literature but are found in the next section.
3.3. Thermodynamic Properties of RHEAs
3.3.1. Quaternary RHEAs
After validating the methodology on pure elements Ta and Al, as well as validating the methodology on the more complex system AlMoNbV, the results of quaternary systems AlMoNbV, NbTaTiV, and NbTaTiZr, are presented in this section. The thermodynamic properties as a function of temperature that are reported include entropy, enthalpy, , and , linear thermal expansion, from 0 K to 1800 K. For the sake of comprehensiveness, ground-state energies were averaged using a varying number of permutations. NbTaTiZr averaged 6 permutations, AlMoNbV averaged all 24 permutations, and NbTaTiV averaged 4 permutations. The results are shown in Figure 3. The results of NbTaTiZr are presented as a solid blue line, while those of AlMoNbV are presented by the orange dashed line, and those of NbTaTiV are presented as a dash-dotted green line.
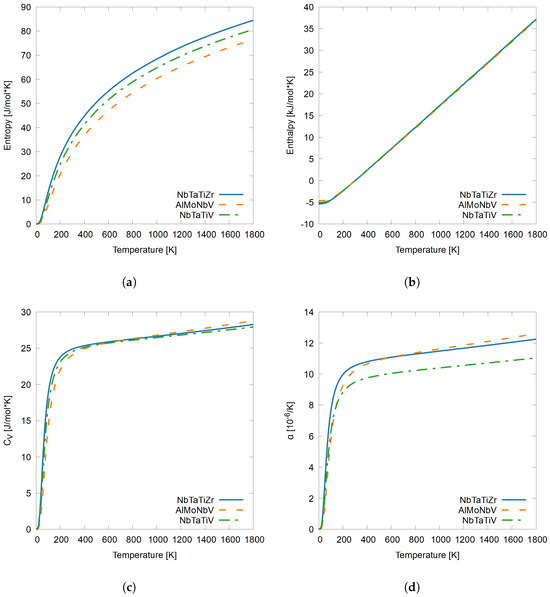
Figure 3.
(a) Entropy, (b) enthalpy, (c) , and (d) , linear thermal expansion as a function of temperature from 0 K to 1800 K of quaternary systems NbTaTiZr, AlMoNbV, NbTaTiV calculated in the present work [27].
First, entropy in Figure 3a is discussed. The system with the highest entropy is NbTaTiZr and the system with the lowest entropy is AlMoNbV. This may be an indication that the presence of the Ta/Ti elements increases the entropy of an RHEA as a function of temperature, while the presence of Al leads to a lower calculated entropy. The entropy of the NbTaTiZr system at 1800 K decreases to 4.5% when replacing Zr with V in the NbTaTiZr system. Second, enthalpy as a function of temperature is shown in Figure 3b for the quaternary HEAs. The calculated enthalpy of all three quaternary RHEAs are almost identical throughout the temperature range studied. It is possible that the inclusion of the thermal–electronic contribution could add some variation in the results. Third, constant volume heat capacity, , as a function of temperature is shown in Figure 3c. Contrary to entropy, the highest calculated is for AlMoNbV, and similarly to entropy NbTaTiZr, it has an overall higher than NbTaTiV. The variation in is lower than the variation in entropy between the NbTaTiZr and NbTaTiV systems, indicating a similar rate of change of entropy as temperature increases. This shows that systems with similar subsets of elements, in this case NbTaTi-X, behave similarly. There is only a 1.2% reduction in the calculated between the two systems by replacing Zr with V. The calculated of NbTaTiZr is in good agreement with the reported by Yang et al. [28]. Fourth and finally, linear thermal expansion, , calculated as a function of temperature is shown in Figure 3d. Linear thermal expansion has the most difference between NbTaTiZr and NbTaTiV of all of the thermodynamic properties studied, despite the similar shape of the curves. At 1800 K, there is a 9.9% reduction when replacing Zr with V in the NbTaTi-X systems. AlMoNbV has the lowest thermal expansion at lower temperatures, while increasing more rapidly as temperature increases. Around 600 K, of AlMoNbV displays the highest calculated thermal expansion as temperature increases to 1800 K.
The overall pattern observed from studying Figure 3 is that Zr contributes to higher thermodynamic properties in all four reported values: entropy, enthalpy, , and linear thermal expansion. This pattern may be due to the larger atom size compared to V. Zr has an atomic mass of 91.2 amu, while V has a mass of 50.9 amu, nearly a 56% reduction in mass from Zr to V. The pattern could also be attributed to the valence electron concentration (VEC) of Zr which is 4 [67].
Systems with lower VEC have more ductile properties, such as higher entropy, , and , which has been shown both in the literature and experimentally [41,42,43]. Furthermore, when comparing the quaternary RHEAs, it was found that V is a much more thermodynamically stable principle element in equiatomic systems. V in the NbTaTi-X system, when compared to Zr, yields a lower entropy, as well as lower thermal expansion. Replacing Ta and Ti with Al and Mo reduces the entropy of the system, but the Al in the system increases thermal expansion at higher temperatures. This suggests that Mo is structurally and thermodynamically more stable, which may be due to its VEC of 6 in HEAs, but the addition of Al overcomes the structural stability of Mo at higher temperatures.
3.3.2. Quinary RHEAs
Next, calculated thermodynamic properties for quinary RHEAs are presented. The calculated thermodynamic properties include entropy, enthalpy, , and , linear thermal expansion as a function of temperature from 0 K to 1800 K. The quinary systems studied are AlNbTaTiV, HfNbTaTiZr, and MoNbTaVW. In order to shed some light on the mechanisms driving the thermodynamic behavior, VEC is calculated following several previous works in the literature [67,68,69,70]. AlNbTaTiV, HfNbTaTiZr, and MoNbTaVW have a VEC of 4.4, 4.4, and 5.4, respectively, which is calculated by obtaining the total number of valence electrons of each species divided by the total number of elements in the system. All of the calculated results are presented in Figure 4, where the properties of AlNbTaTiV are presented as solid red lines, HfNbTaTiZr is presented in blue dashed double-dotted lines, and MoNbTaVW is presented in green dashed single-dotted lines. AlNbTaTiV thermodynamic values are from an average of two permutations, HfNbTaTiZr use two averaged permutations, and MoNbTaVW uses one set of permutations to calculate its thermodynamic values.
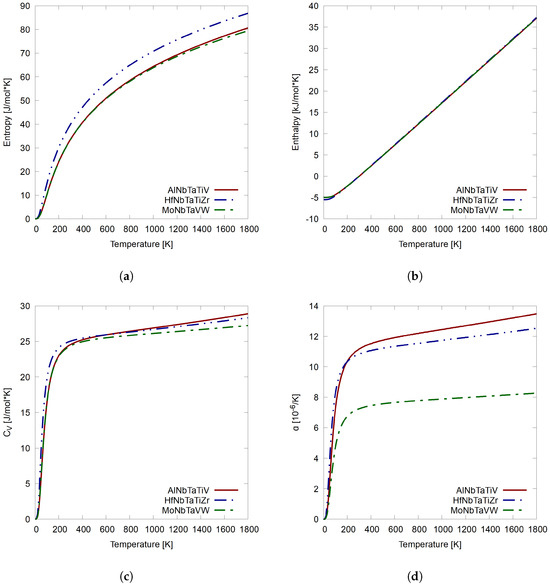
Figure 4.
(a) Entropy, (b) enthalpy, (c) , and (d) , linear thermal expansion, as a function of temperature from 0 K to 1800 K for quinary systems AlNbTaTiV, HfNbTaTiZr, and MoNbTaVW.
First, in Figure 4a, entropy as a function of temperature is given for the quinary RHEAs studied in the present work. The calculated data show HfNbTaTiZr as having the highest values and MoNbTaVW as having the lowest values. AlNbTaTiV and MoNbTaVW are almost identical over the entire temperature range. The biggest difference is at its highest calculated value of 1800 K, where there is only a 1.5% difference between systems. Between HfNbTaTiZr and MoNbTaVW, which are the highest and lowest values, there is a difference of 8.5% at the highest calculated temperature. Second, enthalpy as a function of temperature in Figure 4b shows that calculated enthalpy values are nearly identical for all three of the quinary RHEAs studied. The enthalpy results are congruent with the results of the quaternary system in the previous section. Third, in Figure 4c, as a function of temperature is examined. The values of AlNbTaTiV and MoNbTaVW are nearly identical, leading up to 400 K. AlNbTaTiV surpasses MoNbTaVW at higher temperatures, consistent with the variation in the entropy plot. At 1800 K, there is a difference between AlNbTaTiV and MoNbTaVW of 5.8%, while HfNbTaTiZr is consistently higher than MoNbTaVW. Finally, , linear thermal expansion, is given in Figure 4d. The largest difference in the thermodynamic values out of all the systems is . MoNbTaVW has the lowest thermal expansion out of all systems with a thermal expansion of 8.3 at 1800 K and AlNbTaTiV has the highest thermal expansion of all systems with a thermal expansion of 13.5 at 1800 K. The variation could be due to the VEC, where AlNbTaTiV has a lower VEC at 4.4, while MoNbTaVW has a VEC of 5.4. Similar to the quaternary results, V significantly decreases at higher temperatures unless combined with Al, which causes the system to expand at higher temperatures. Also, similar to the quaternary systems, replacing V with Zr significantly increases , although it does not increase as much as just adding Al to the system in conjunction with V.
The quinary systems show similar trends to the quaternary systems. Like the quaternary systems, elements such as Mo and Al reduce entropy and are more stable at lower temperatures, but the presence of Al at higher temperatures overcomes the stability of Mo. This is seen in AlNbTaTiV having the lowest at lower temperatures, but at high temperatures above 800 K it has the highest . This could be due to the thermal expansion of Al within the system. When comparing the quinary systems, the system with Al has the highest thermal expansion. While the element V within an HEA seems to drastically reduce thermal expansion when compared to similar systems with Zr, the addition of Al in a system with V significantly increases and overcomes the structural stability of V in thermal expansion. However, in the core system, XNbTaTiX has higher entropy with Hf and Zr than with Al and V. This could be due to the thermal stability of V. Zr and Al may have similar thermo-elastic properties to each other since the addition of Zr or Al significantly increases thermal expansion. However, Al contributes to more thermal expansion than Zr. This gives room for more research on RHEAs that have both Zr and Al, possibly having higher thermal expansion than the RHEAs researched in this work.
3.4. Comparing NbTaTiZr, NbTaTiV, and AlNbTaTiV
A final analysis is made on the three systems with the three elements, NbTaTi, in common. These three systems all three are closely related, because each RHEA is only one chemical species different from the others. Figure 5 shows the same set of results, entropy, enthalpy, constant volume heat capacity, and linear thermal expansion, comparing NbTaTiZr as a solid blue line, NbTaTiV as a green dash-dotted line, and AlNbTaTiV as a red dashed line. Figure 5a shows entropy as a function of temperature, and the addition of Al to the NbTaTiV system does not affect the entropy while substituting Zr for V in the NbTaTiV system increases the entropy of the system as temperature increases overall to a total of 4.5% at 1800 K. The enthalpy of all three systems, given in Figure 5b, are similar and consistent with previous results. In Figure 5c, the results for are shown. In general, the chemical variations between these three RHEAs do not yield much change in heat capacity. for NbTaTiZr is the highest until roughly 400 K, and at that point AlNbTaTiV increases more rapidly and retains the highest heat with 28.9 J/mol·K and is 3.3% higher than NbTaTiV without Al. Substituting Zr for V only increases the of the system by 1.2%. Finally, the most interesting and varying results from the thermodynamic properties are in the linear thermal expansion, given in Figure 5d. NbTaTiV has the lowest thermal expansion, but adding an equimolar amount of Al to the system increases the thermal expansion more than substituting Zr for V. When substituting Zr for V, the thermal expansion at 1800 K increases from 11.0 to 12.3 [/K], which is an 11% increase, while just adding an equimolar amount of Al to the NbTaTiV system increases the thermal expansion to 13.5 [/K], a 22.1% increase, which is twice as much as the substitution. The increase in thermal expansion may be due to the number of valence electrons of V, Zr, and Al. In Figure 5d, the thermal expansion given in order from lowest to highest is NbTaTiV, NbTaTiZr, and AlNbTaTiV. When looking at these three systems, all three have NbTaTi in common. The system which has the lowest thermal expansion is NbTaTiV, V has five valence electrons, which is a high VEC. The system with the median CTE is NbTaTiZr, this system compared to the system with V has a lower VEC, since Zr has less valence electrons, with only four electrons. The system with the highest CTE is AlNbTaTiV, and although this system has V just like NbTaTiV, it also has Al, which NbTaTiV does not, and Al has three valence electrons. This lowers the overall VEC of this system, increasing ductility.
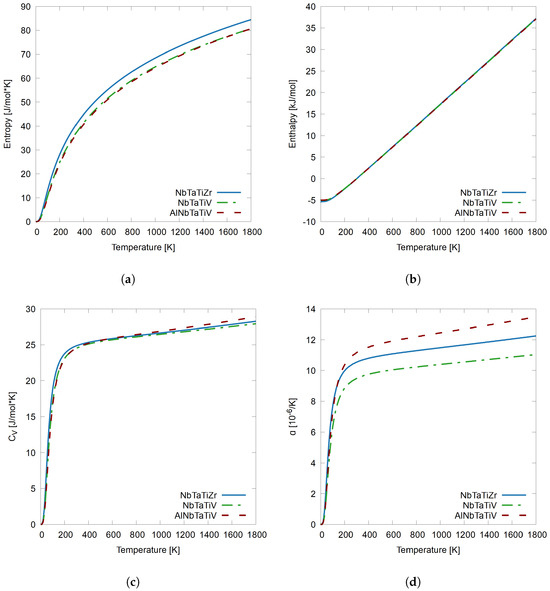
Figure 5.
(a) Entropy, (b) enthalpy, (c) , and (d) , linear coefficient of thermal expansion as a function of temperature from 0 K to 1800 K for systems NbTaTiZr, NbTaTiV, and AlNbTaTiV.
4. Conclusions
This paper focuses on calculating the thermodynamic properties of quaternary and quinary RHEAs as a function of temperature. DFT calculations are used for ground-state energy and then employs a modified Birch–Murnaghan equation of state for energy–volume relationships and the Debye model to expand the 0 K and 0 P calculations into finite temperature thermodynamic properties. The calculated properties in the work yield results that compare well to values in the literature for both pure element properties compared to experimental data, and to previous computational studies from RHEAs. After validating the methodology, three different quaternary RHEAs, namely AlMoNbV, NbTaTiV, and NbTaTiZr, and three different quinary RHEAs, namely AlNbTaTiV, HfNbTaTiZr, and MoNbTaVW, are analyzed and compared. From this work, the following conclusions can be drawn:
- Using DFT + SQS + Debye is a reliable method to use when calculating the finite temperature thermodynamic properties of an RHEA. This is because the difference between the highest and lowest calculated properties of entropy and heat capacity from all of the atomic configuration permutations of the quaternary system AlMoNbV vary by at most 1.7%. Only a few atomic permutation calculations are needed, depending on the number of chemical species in the alloy, which saves computational time and resources.
- The presence of Al and Zr elements with lower VEC in the RHEAs contributes to higher thermal expansion, while the presence of Mo, V, and W, elements with higher VEC contribute to lower thermal expansion, further validating the theory that lower VEC can lead to higher ductility in BCC refractory alloy design.
- In the RHEAs, the presence of Hf, an element with a VEC of four electrons, in the same way as other ductile metals such as Zr contributes to higher entropy and a higher compared to systems without Hf, especially at lower temperatures.
- At higher temperatures, Al contributes to the highest , which could be attributed to its capability for thermal expansion and low VEC of 3.
- V, Mo, and W elements with high VEC are the most structurally stable with the lowest thermal expansion, lowest , and entropy.
- The comparison of the compositionally similar systems as well as the comparison of quaternary and quinary systems offers valuable guidance for subsequent theoretical and experimental endeavors.
Author Contributions
Conceptualization, C.Z.H.; methodology, C.Z.H. and D.E.M.; validation, C.Z.H. and D.E.M.; formal analysis, D.E.M.; investigation, D.E.M.; writing—original draft preparation, C.Z.H. and D.E.M.; writing—review and editing, C.Z.H. and D.E.M.; visualization, D.E.M.; supervision, C.Z.H.; project administration, C.Z.H.; funding acquisition, C.Z.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the United States National Science Foundation with Award No. DMR-2046670 and the Department of Energy National Nuclear Security Administration with Award No. DE-NA0003988.
Data Availability Statement
The data presented in this manuscript are available upon email request from the corresponding author.
Acknowledgments
D. E. Moreno would like to thank William Hale for his assistance with code writing. C. Z. Hargather would like to thank S. L. Shang for stimulating discussions about the Debye model.
Conflicts of Interest
The authors declare no conflict of interest.
Correction Statement
This article has been republished with a minor correction to the Funding statement. This change does not affect the scientific content of the article.
Appendix A

Table A1.
The 24 permutations are shown with their ground-state energy (GSE). GSE values are at 0 K and 0 GPa in terms of eV/atom and the ground-state volume is in terms of (Å3/atom).
Table A1.
The 24 permutations are shown with their ground-state energy (GSE). GSE values are at 0 K and 0 GPa in terms of eV/atom and the ground-state volume is in terms of (Å3/atom).
| Type | GSE (eV/Atom) | (Å3/Atom) |
|---|---|---|
| AlMoNbV | −8.547 | 15.60 |
| AlMoVNb | −8.556 | 15.64 |
| AlNbMoV | −8.552 | 15.63 |
| AlNbVMo | −8.558 | 15.61 |
| AlVMoNb | −8.567 | 15.62 |
| AlVNbMo | −8.560 | 15.57 |
| MoAlNbV | −8.565 | 15.61 |
| MoAlVNb | −8.556 | 15.66 |
| MoNbAlV | −8.558 | 15.60 |
| MoNbVAl | −8.551 | 15.59 |
| MoVAlNb | −8.563 | 15.62 |
| MoVNbAl | −8.565 | 15.57 |
| NbAlMoV | −8.559 | 15.62 |
| NbAlVMo | −8.574 | 15.61 |
| NbMoAlV | −8.550 | 15.61 |
| NbMoVAl | −8.561 | 15.61 |
| NbVAlMo | −8.555 | 15.60 |
| NbVMoAl | −8.554 | 15.58 |
| VAlMoNb | −8.554 | 15.64 |
| VAlNbMo | −8.575 | 15.57 |
| VMoAlNb | −8.553 | 15.64 |
| VMoNbAl | −8.567 | 15.61 |
| VNbAlMo | −8.552 | 15.62 |
| VNbMoAl | −8.546 | 15.61 |
| AVG | −8.559 | 15.61 |
| STD | 0.007 | 0.023 |
| Max | −8.546 | 15.66 |
| Min | −8.575 | 15.57 |
References
- Miracle, D.B.; Senkov, O.N. A critical review of high entropy alloys and related concepts. Acta Mater. 2017, 122, 448–511. [Google Scholar] [CrossRef]
- Miracle, D.B.; Miller, J.D.; Senkov, O.N.; Woodward, C.; Uchic, M.D.; Tiley, J. Exploration and development of high entropy alloys for structural applications. Entropy 2014, 16, 494–525. [Google Scholar] [CrossRef]
- Senkov, O.N.; Wilks, G.; Scott, J.; Miracle, D.B. Mechanical properties of Nb25Mo25Ta25W25 and V20Nb20Mo20Ta20W20 refractory high entropy alloys. Intermetallics 2011, 19, 698–706. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Y.; Qiao, Y.; Chen, G. Novel microstructure and properties of multicomponent CoCrCuFeNiTix alloys. Intermetallics 2007, 15, 357–362. [Google Scholar] [CrossRef]
- Senkov, O.N.; Miracle, D.B.; Chaput, K.J.; Couzinie, J.P. Development and exploration of refractory high entropy alloys—A review. J. Mater. Res. 2018, 33, 3092–3128. [Google Scholar] [CrossRef]
- Senkov, O.; Wilks, G.; Miracle, D.; Chuang, C.; Liaw, P. Refractory high-entropy alloys. Intermetallics 2010, 18, 1758–1765. [Google Scholar] [CrossRef]
- Philips, N.; Carl, M.; Cunningham, N. New opportunities in refractory alloys. Metall. Mater. Trans. A 2020, 51, 3299–3310. [Google Scholar] [CrossRef]
- Kwon, S.K.; Park, J.S.; Park, J.H. Influence of refractory-steel interfacial reaction on the formation behavior of inclusions in Ce-containing stainless steel. ISIJ Int. 2015, 55, 2589–2596. [Google Scholar] [CrossRef]
- Abyzov, V. Refractory cellular concrete based on phosphate binder from waste of production and recycling of aluminum. Procedia Eng. 2017, 206, 783–789. [Google Scholar] [CrossRef]
- Graddy, G.E., Jr.; Weirauch, D.A., Jr. Refractories Used for Aluminum Processing. In Alumina Chemicals: Science and Technology Handbook; Wiley: Hoboken, NJ, USA, 1990; pp. 489–493. [Google Scholar]
- Antusch, S.; Reiser, J.; Hoffmann, J.; Onea, A. Refractory Materials for Energy Applications. Energy Technol. 2017, 5, 1064–1070. [Google Scholar] [CrossRef]
- Pollock, T.M.; Tin, S. Nickel-based superalloys for advanced turbine engines: Chemistry, microstructure and properties. J. Propuls. Power 2006, 22, 361–374. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, B.; Hu, D.; Jiang, K.; Liu, H.; Mao, J.; Jing, F.; Hao, X. Thermomechanical fatigue experiment and failure analysis on a nickel-based superalloy turbine blade. Eng. Fail. Anal. 2019, 102, 35–45. [Google Scholar] [CrossRef]
- Naser-Zoshki, H.; Kiani-Rashid, A.R.; Vahdati-Khaki, J. Design of a low density refractory high entropy alloy in non-equiatomic W–Mo–Cr–Ti–Al system. Vacuum 2020, 181, 109614. [Google Scholar] [CrossRef]
- Cutler, C.; Shaw, S. The interrelationship of γ’ size, grain size and mechanical properties in IN-939, a cast nickel-base superalloy. In Strength of Metals and Alloys; Elsevier: Amsterdam, The Netherlands, 1979; pp. 1357–1362. [Google Scholar]
- Yeh, J.W.; Lin, S.J. Breakthrough applications of high-entropy materials. J. Mater. Res. 2018, 33, 3129–3137. [Google Scholar] [CrossRef]
- Patel, K.; Sadeghilaridjani, M.; Pole, M.; Mukherjee, S. Hot corrosion behavior of refractory high entropy alloys in molten chloride salt for concentrating solar power systems. Sol. Energy Mater. Sol. Cells 2021, 230, 111222. [Google Scholar] [CrossRef]
- Hua, X.J.; Hu, P.; Xing, H.R.; Han, J.Y.; Ge, S.W.; Li, S.L.; He, C.J.; Wang, K.S.; Cui, C.J. Development and Property Tuning of Refractory High-Entropy Alloys: A Review. Acta Metall. Sin. English Lett. 2022, 2022, 1–35. [Google Scholar] [CrossRef]
- Zaddach, A.; Niu, C.; Koch, C.; Irving, D. Mechanical properties and stacking fault energies of NiFeCrCoMn high-entropy alloy. JOM 2013, 65, 1780–1789. [Google Scholar] [CrossRef]
- Zhang, Z.; Sheng, H.; Wang, Z.; Gludovatz, B.; Zhang, Z.; George, E.P.; Yu, Q.; Mao, S.X.; Ritchie, R.O. Dislocation mechanisms and 3D twin architectures generate exceptional strength-ductility-toughness combination in CrCoNi medium-entropy alloy. Nat. Commun. 2017, 8, 14390. [Google Scholar] [CrossRef]
- Huang, H.; Li, X.; Dong, Z.; Li, W.; Huang, S.; Meng, D.; Lai, X.; Liu, T.; Zhu, S.; Vitos, L. Critical stress for twinning nucleation in CrCoNi-based medium and high entropy alloys. Acta Mater. 2018, 149, 388–396. [Google Scholar] [CrossRef]
- Zhao, S.; Stocks, G.M.; Zhang, Y. Stacking fault energies of face-centered cubic concentrated solid solution alloys. Acta Mater. 2017, 134, 334–345. [Google Scholar] [CrossRef]
- Patriarca, L.; Ojha, A.; Sehitoglu, H.; Chumlyakov, Y. Slip nucleation in single crystal FeNiCoCrMn high entropy alloy. Scr. Mater. 2016, 112, 54–57. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhuang, Y.; Hu, A.; Kai, J.J.; Liu, C.T. The origin of negative stacking fault energies and nano-twin formation in face-centered cubic high entropy alloys. Scr. Mater. 2017, 130, 96–99. [Google Scholar] [CrossRef]
- Alkan, S.; Ojha, A.; Sehitoglu, H. Determination of latent hardening response for FeNiCoCrMn for twin-twin interactions. Acta Materialia 2018, 147, 149–164. [Google Scholar] [CrossRef]
- Niu, C.; LaRosa, C.R.; Miao, J.; Mills, M.J.; Ghazisaeidi, M. Magnetically-driven phase transformation strengthening in high entropy alloys. Nat. Commun. 2018, 9, 1363. [Google Scholar] [CrossRef] [PubMed]
- Ge, H.; Tian, F.; Wang, Y. Elastic and thermal properties of refractory high-entropy alloys from first-principles calculations. Comput. Mater. Sci. 2017, 128, 185–190. [Google Scholar] [CrossRef]
- Yang, M.; Shao, L.; Duan, J.M.; Chen, X.T.; Tang, B.Y. Temperature dependence of mechanical and thermodynamic properties of Ti (25+x) Zr25Nb25Ta (25-x)(x ≤ 20) refractory high entropy alloys: Influences of substitution of Ti for Ta. Phys. B Condens. Matter 2021, 606, 412851. [Google Scholar] [CrossRef]
- Song, H.; Tian, F.; Wang, D. Thermodynamic properties of refractory high entropy alloys. J. Alloy. Compd. 2016, 682, 773–777. [Google Scholar] [CrossRef]
- Yin, B.; Curtin, W.A. First-principles-based prediction of yield strength in the RhIrPdPtNiCu high-entropy alloy. NPJ Comput. Mater. 2019, 5, 14. [Google Scholar] [CrossRef]
- Ikeda, Y.; Grabowski, B.; Körmann, F. Ab initio phase stabilities and mechanical properties of multicomponent alloys: A comprehensive review for high entropy alloys and compositionally complex alloys. Mater. Charact. 2019, 147, 464–511. [Google Scholar] [CrossRef]
- Zunger, A.; Wei, S.H.; Ferreira, L.; Bernard, J.E. Special quasirandom structures. Phys. Rev. Lett. 1990, 65, 353. [Google Scholar] [CrossRef]
- Wei, S.H.; Ferreira, L.; Bernard, J.E.; Zunger, A. Electronic properties of random alloys: Special quasirandom structures. Phys. Rev. B 1990, 42, 9622. [Google Scholar] [CrossRef] [PubMed]
- Kaufman, J.L.; Pomrehn, G.S.; Pribram-Jones, A.; Mahjoub, R.; Ferry, M.; Laws, K.J.; Bassman, L. Stacking fault energies of nondilute binary alloys using special quasirandom structures. Phys. Rev. B 2017, 95, 094112. [Google Scholar] [CrossRef]
- Zhao, S.; Weber, W.J.; Zhang, Y. Unique challenges for modeling defect dynamics in concentrated solid-solution alloys. JOM 2017, 69, 2084–2091. [Google Scholar] [CrossRef]
- De Jong, M.; Qi, L.; Olmsted, D.L.; van de Walle, A.; Asta, M. Calculations of planar defect energies in substitutional alloys using the special-quasirandom-structure approach. Phys. Rev. B 2016, 93, 094101. [Google Scholar] [CrossRef]
- Strother, J.D.; Hargather, C.Z. Statistical data set for first-principles calculations of stacking fault energies in an AlNbTaTiV high entropy alloy. Data Brief 2021, 34, 106670. [Google Scholar] [CrossRef]
- Kivy, M.B.; Zaeem, M.A. Generalized stacking fault energies, ductilities, and twinnabilities of CoCrFeNi-based face-centered cubic high entropy alloys. Scr. Mater. 2017, 139, 83–86. [Google Scholar] [CrossRef]
- Jiang, C.; Uberuaga, B.P. Efficient ab initio modeling of random multicomponent alloys. Phys. Rev. Lett. 2016, 116, 105501. [Google Scholar] [CrossRef] [PubMed]
- Senkov, O.; Scott, J.; Senkova, S.; Meisenkothen, F.; Miracle, D.; Woodward, C. Microstructure and elevated temperature properties of a refractory TaNbHfZrTi alloy. J. Mater. Sci. 2012, 47, 4062–4074. [Google Scholar] [CrossRef]
- Qi, L.; Chrzan, D.C. Tuning Ideal Tensile Strengths and Intrinsic Ductility of bcc Refractory Alloys. Phys. Rev. Lett. 2014, 112, 115503. [Google Scholar] [CrossRef]
- Wang, J.; Bai, S.; Tang, Y.; Li, S.; Liu, X.; Jia, J.; Ye, Y.; Zhu, L. Effect of the valence electron concentration on the yield strength of Ti–Zr–Nb–V high-entropy alloys. J. Alloy. Compd. 2021, 868, 159190. [Google Scholar] [CrossRef]
- Sheikh, S.; Shafeie, S.; Hu, Q.; Ahlström, J.; Persson, C.; Veselý, J.; Zýka, J.; Klement, U.; Guo, S. Alloy design for intrinsically ductile refractory high-entropy alloys. J. Appl. Phys. 2016, 120, 164902. [Google Scholar] [CrossRef]
- Yao, H.; Qiao, J.; Hawk, J.; Zhou, H.; Chen, M.; Gao, M. Mechanical properties of refractory high-entropy alloys: Experiments and modeling. J. Alloy. Compd. 2017, 696, 1139–1150. [Google Scholar] [CrossRef]
- Melnick, A.; Soolshenko, V. Thermodynamic design of high-entropy refractory alloys. J. Alloy. Compd. 2017, 694, 223–227. [Google Scholar] [CrossRef]
- Liao, M.; Liu, Y.; Min, L.; Lai, Z.; Han, T.; Yang, D.; Zhu, J. Alloying effect on phase stability, elastic and thermodynamic properties of Nb-Ti-V-Zr high entropy alloy. Intermetallics 2018, 101, 152–164. [Google Scholar] [CrossRef]
- Zheng, S.; Wang, S. First-Principles Design of Refractory High Entropy Alloy VMoNbTaW. Entropy 2018, 20, 965. [Google Scholar] [CrossRef]
- Dobbelstein, H.; Gurevich, E.L.; George, E.P.; Ostendorf, A.; Laplanche, G. Laser metal deposition of compositionally graded TiZrNbTa refractory high-entropy alloys using elemental powder blends. Addit. Manuf. 2019, 25, 252–262. [Google Scholar] [CrossRef]
- Bhandari, U.; Ghadimi, H.; Zhang, C.; Yang, S.; Guo, S. Predicting elastic constants of refractory complex concentrated alloys using machine learning approach. Materials 2022, 15, 4997. [Google Scholar] [CrossRef]
- Moruzzi, V.L.; Janak, J.F.; Schwarz, K. Calculated thermal properties of metals. Phys. Rev. B 1988, 37, 790–799. [Google Scholar] [CrossRef]
- Shang, S.L.; Wang, Y.; Kim, D.; Liu, Z.K. First-principles thermodynamics from phonon and Debye model: Application to Ni and Ni3Al. Comput. Mater. Sci. 2010, 47, 1040–1048. [Google Scholar] [CrossRef]
- Shang, S.; Böttger, A. A combined cluster variation method and ab initio approach to the γ-Fe [N]/γ’-Fe4N1- x phase equilibrium. Acta Mater. 2005, 53, 255–264. [Google Scholar] [CrossRef]
- Teter, D.; Gibbs, G.V.; Boisen, M.B., Jr.; Allan, D.; Teter, M. First-principles study of several hypothetical silica framework structures. Phys. Rev. B 1995, 52, 8064. [Google Scholar] [CrossRef]
- Debye, P. Zur Theorie der spezifischen Wärmen. Ann. Der Phys. 1912, 344, 789–839. [Google Scholar] [CrossRef]
- Abrahams, S.C.; Hsu, F.S.L. Debye temperatures and cohesive properties. J. Chem. Phys. 1975, 63, 1162–1165. [Google Scholar] [CrossRef]
- Degueldre, C.; Tissot, P.; Lartigue, H.; Pouchon, M. Specific heat capacity and Debye temperature of zirconia and its solid solution. Thermochim. Acta 2003, 403, 267–273. [Google Scholar] [CrossRef]
- Wang, X.; Bai, X.; Xiao, W.; Liu, Y.; Li, X.; Wang, J.; Peng, C.; Wang, L.; Wang, X. Calculation of Thermal Expansion Coefficient of Rare Earth Zirconate System at High Temperature by First Principles. Materials 2022, 15, 2264. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Kresse, G.; Marsman, M.; Furthmüller, J. VASP the Manual. Available online: https://www.vasp.at/wiki/index.php/The_VASP_Manual (accessed on 11 July 2023).
- Blochl, P.E.; Jepsen, O.; Andersen, O.K. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B 1994, 49, 16223–16233. [Google Scholar] [CrossRef]
- Van de Walle, A.; Tiwary, P.; De Jong, M.; Olmsted, D.; Asta, M.; Dick, A.; Shin, D.; Wang, Y.; Chen, L.Q.; Liu, Z.K. Efficient stochastic generation of special quasirandom structures. Calphad 2013, 42, 13–18. [Google Scholar] [CrossRef]
- Chase, M. NIST-JANAF Thermochemical Tables, 4th ed.; American Institute of Physics: College Park, MD, USA, 1998. [Google Scholar]
- He, X.; Bai, Y.; Zhu, C.; Sun, Y.; Li, M.; Barsoum, M. General trends in the structural, electronic and elastic properties of the M3AlC2 phases (M= transition metal): A first-principle study. Comput. Mater. Sci. 2010, 49, 691–698. [Google Scholar] [CrossRef]
- Khazaei, M.; Arai, M.; Sasaki, T.; Estili, M.; Sakka, Y. Trends in electronic structures and structural properties of MAX phases: A first-principles study on M2AlC (M= Sc, Ti, Cr, Zr, Nb, Mo, Hf, or Ta), M2AlN, and hypothetical M2AlB phases. J. Phys. Condens. Matter 2014, 26, 505503. [Google Scholar] [CrossRef] [PubMed]
- Guo, S.; Ng, C.; Lu, J.; Liu, C. Effect of valence electron concentration on stability of fcc or bcc phase in high entropy alloys. J. Appl. Phys. 2011, 109, 103505. [Google Scholar] [CrossRef]
- Ikeda, Y.; Körmann, F.; Tanaka, I.; Neugebauer, J. Impact of chemical fluctuations on stacking fault energies of CrCoNi and CrMnFeCoNi high entropy alloys from first principles. Entropy 2018, 20, 655. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).