A Cautionary Note on Linear Measurements and Their Ratios in Taxonomy

Abstract

Statisticians work with figures, whereas scientists work with estimated quantities. Every direct (physical) measurement has some degree of uncertainty. Single numbers pose no problems, and an implied range can always be specified. Difficulties arise when those numbers or sets of numbers are used to calculate derived figures. Statistical measures such as ratios can be skewed if uncertainty about the actual measurements used to derive those quantities is not taken into account. This lack of consideration may lead to incorrect figures being used and calls into question the criteria used to diagnose, identify or delimit new species. In this case study, I use data gathered from the literature on different species of the clade Hydrachnidia (Acari, Parasitengona) to show how range ratios of important characters differ when uncertainty is considered. I outline the successive steps taken during the measuring process—from microscope calibration to the calculation of several statistical values from the direct measurements—and suggest some corrections. I anticipate that the results and recommendations presented here will be applicable to other taxonomic groups for which linear measurements play a central role in the description and identification of species.

1. Introduction

“For measurements to be meaningful, however, they must retain their connection to the theoretical and instrumental context from which they were derived.” Houle, Pélabon, Wagner and Hansen, 2011 [1].

One succinct definition of taxonomy is the study of “sorting relationship from variation”. A more detailed one is as follows: “Taxonomy implies the use of the current best evidence to demarcate species and their relationships” [2].

The task of preliminary taxonomic work is the qualitative and quantitative characterization of organisms, distinguishing them from other similar ones and selecting characters or criteria to easily diagnose or identify them. In other words “…identifying minimal groups based on diagnostic character differences…” [3]. After an introductory “sorting out” of the material during a sample campaign or in a museum collection, generally by groups that may be easily distinguished to the genus level, the work of the taxonomist is to provide basic data on the number and the distribution of qualitative characters and the measurement of continuous characters. These data may be considered the basic variables with which to build a further analysis on the relationship among specimens, species, taxa, etc. However, basic considerations regarding significant figures, precision, accuracy and types of errors on any measurement, although well treated in the statistical and zoological literature [4,5], are frequently overlooked in taxonomic studies in which basic data are obtained and used for a species diagnosis or taxon discrimination in a clade. However, problems compound when those basic data are then used as inputs to calculate derived statistics such as indexes, proportions and ratios.

In statistical reference works, the usual statistics of the arithmetic mean ($\overline{\mathit{x}}$), standard deviation (s) and coefficient of variation (c.v.) are most often included, along with others, depending on the data being analyzed. However, as these types of statistics are derived from direct measurements, scientists collecting these quantities should more carefully consider the implicit uncertainty in their original measurements and apply corrections for the final figures that they provide in their studies.

In the clade Hydrachnidia, basic statistics (e.g., $\overline{\mathit{x}}$ and s) are often calculated as criteria to distinguish and identify species. Range variation, ratios, proportion and indexes are commonly included with the series of linear measurements and basic statistics in taxonomic publications. In this context, ratios (division of two linear measurements), percentages of substructures within a functional structure (e.g., segments of a leg in an arthropod) and indexes (division of the figure of an anatomical element by a larger one) are frequently assumed to serve as better diagnostic characters for the identification or distinction of species compared with the original quantities. However, the use of ratios, percentages, indexes and other derived variables are confronted with serious problems related to their proper calculation and significant figures and the implied range of a measurement [4,5].

Ratios usually correspond to structures that do not have rigid isometric growth. If this were the case, it would be necessary only to obtain a single measure of each structure (e.g., length and width of an arachnid palp segment) and, once that first measurement is known, use the quotient as a predictor of the next measurement. However, variables included in a ratio are usually correlated to some degree and cannot be considered independent. Paraphrasing Jasieński and Bazzaz [6], “taxonomic researchers love ratios–statisticians loathe them.”

Ratios reported in a study would be more useful if they could be easily re-evaluated (or recalculated) for uncertainty by having the original measures used to derive them included in the same text. The problem arises in those publications in which ratios are assumed to have been validated and are used on a regular basis as diagnostic characters, but whose calculation cannot be easily checked for accuracy.

In the last few years, as a result of the European Fauna of Hydrachnidia (Acari, Parasitengona) project, a series of revisionary works, e.g., [7,8,9], and three important synthetic works have been published [10,11,12]. Some of the ranges, ratios and other statistics included in these works have been selected as diagnostic characters in species identification keys. The trend of using these statistics is increasing, as evidenced by recent publications on the taxonomy of this clade, e.g., [13,14].

In some publications of water mite species of Hydrachnidia (Parasitengona, Acari), e.g, [7,15], the authors provide the information on the direct measurements from which ratios and other statistics were derived. Using these previously gathered data, I recalculated these figures considering the degree of uncertainty and discuss these examples (and related references) with respect to the application of these figures in species discrimination or descriptions. I followed the workflow shown in Figure 1, going from the original data to the calculation of several statistics including data range, mean, standard variation, coefficient of variation and ratios, with a particular focus on how the last statistic should be properly calculated.

In many cases, I obtained wider ranges than those calculated by the authors of the original data. As a result, users of those works and diagnostic keys are warned not to use those figures as the only diagnostic character and to correct them when the data are available. Although all the presented examples involve species of Hydrachnidia, the shortcomings and recommendations shown by this case study would likely apply to other similar groups.

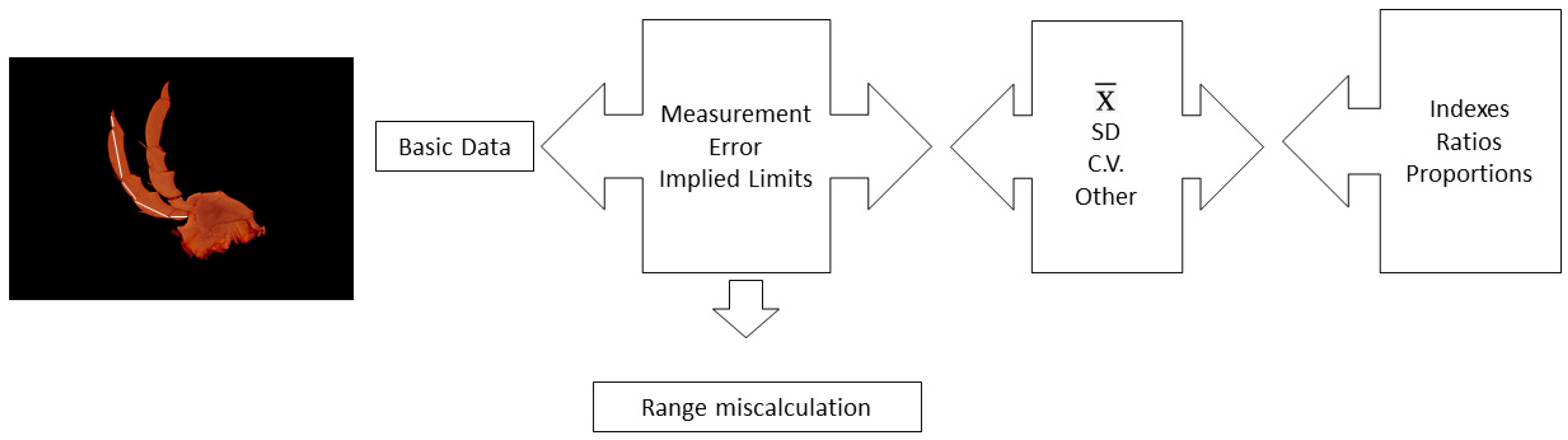
2. On the Origin of Data: Uncertainty and Implied Range

Two key concepts to consider in any measurement are precision and accuracy. An example of precision is given in Memories of My Life by Francis Galton [16] (pp. 315–316), who wrote while building a “Beauty Map” of the British Isles, “…classifying the girls I passed in streets or elsewhere as attractive, indifferent, or repellent. Of course, this was a purely individual estimate, but it was consistent, judging from the conformity of different attempts in the same population.” His “consistent” is what we know as precision: visiting the same location on different occasions always gave the same scores. However, Galton could not be accurate due to the lack of a universal reference standard for beauty. He was biased to his conception of beauty, and only judged females. Measurements of any kind may be precise if we always obtain the same figure on different occasions; however, absolute accuracy is elusive because we can never know the exact measure of an object.

Measurements of specimens of Hydrachnidia (or any microscopic organism) obtained through microscopic observations derive from two operations: (1) the calibrating factor resulting from the division of a length of a stage micrometer by the number of units covered by the ocular micrometer (or graticule), e.g., [17], and (2) a multiplication of the calibrating factor (the value of any division on the ocular micrometer for a specific microscope objective) by the number of divisions of the ocular micrometer that cover the linear distance of the morphological feature being measured (Figure 2).

Stage micrometers are produced with a certain level of error. For instance, stage micrometers sold by Edmund Optics Ltd. have a line width to 1.7 µm, whereas those from Edge Scientific have a line width to 2 µm. Many stage micrometers available through Amazon or AliExpress do not even specify a line width. In contrast, those from Graticules Optics Ltd. are calibrated by the National Physical Laboratory, and customers are provided with a Certificate of Calibration. Calibrating factors obtained from stage micrometers with finer line widths have lower levels of error.

The observed value of a measurement is the midpoint of its implied range that gives the extent of its uncertainty [4]. The body size of most water mite species is less than 1 mm, and measurements of their appendages must be obtained using microscopes. A general assumption in microscopy is that calibration with the largest number of stage micrometer divisions provides the highest degree of accuracy; however, this is not necessarily true, except for Plan Apochromat objectives [17,18].

To illustrate the degree of uncertainty, values of an ocular graticule were obtained using a stage micrometer from Muhwa Scientific (purchased through Amazon). The line width of this micrometer was not specified and a calibration certificate was not provided. Measurements were taken under a 10x/0.22 NA achromatic objective. The average of the significant numbers was 7.8 µm (last column,

Table 1. Example of the calibration of an ocular micrometer (graticule) using a 10x/0.22 NA microscope objective and a stage micrometer from Muhwa Scientific.

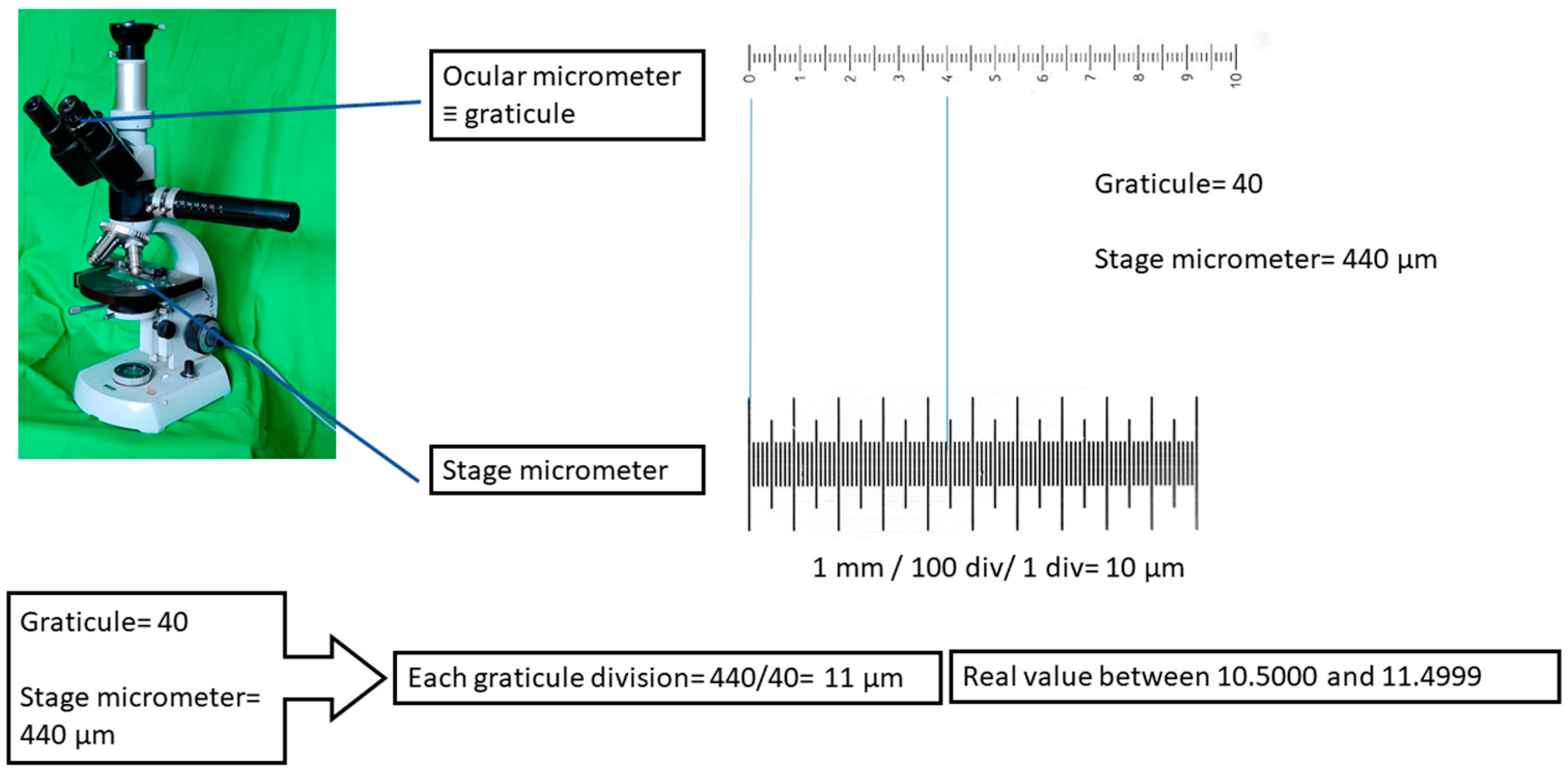
Stage Micrometer	Ocular Micrometer	Ocular 1 div	Significant Numbers
100 µm	13 div	7.69 µm	7.7 µm
150 µm	19 div	7.89 µm	7.9 µm
250 µm	32 div	7.81 µm	7.8 µm
350 µm	45 div	7.77 µm	7.8 µm
490 µm	63 div	7.77 µm	7.8 µm

); however, the true value of each ocular division was in the implied range of 8, that is, 7.500 to 8.499, which covers all measurements observed (it is easy to check that neither the implied range of 7.8 nor 7.9 covers all the observed values) (Table 1). This implied range gives the degree of uncertainty for this specific objective and microscope. Similar calculations may be obtained for any other objectives.

Nevertheless, based on optical principles, the resolution of a microscope is obtained according to the Rayleigh criterion:

d = 0.61 λ/NA

In the case above, the resolution limit is 1.5 µm, which is wider than the one calculated with the stage micrometer.

To use an example from the literature, in the initial dichotomic key of the species of the genus Eylais [10] (p. 314), one of the decisions divides species according to the width of the eye capsule, being either >1.5 µm or <1.5 µm. The implied limits overlap between 1.45000 and 1.54999 and, therefore, this character is not practical. In addition, there is no option for the exact value of 1.5. In another example from the same key for Eylais [10] (p. 315), the authors provide the following dichotomy for the length of the pharyngeal plate: ≥300 µm or <300 µm. In this case, there is a provision for the value 300 µm; however, as in the previous example, the real value of the measurement 300 µm lies between 299.500 µm and 300.499 µm, leading to some uncertainty. For instance, any real values above 299.5 µm and below 299.9 µm are included within the implied limits of a measure of 300 µm. Other characters in this key present the same situation [10] (p. 314).

Similar cases can also be found in other studies of Hydrachnidia. For instance, Di Sabatino et al. [8] distinguish between two species of Torrenticola by the ratio L/W: >1.5 for Torrenticola elliptica and <1.5 for T. meridionalis (though, other characters may also distinguish them). One can envision how this diagnostic character may lead to the misidentification of specimens or even the erection of a new species by a busy generalist taxonomist, particularly in cases when only one specimen is being assessed. To illustrate probable specimen misidentifications in these two species of Torrenticola, cytochrome c oxidase subunit I (COI) sequences available from GenBank were inputted into the BOLD system to find specimens with high sequence identities. When COI sequence OL870191.1, which is identified as belonging to T. elliptica, was inputted in BOLD, several specimens identified as T. elliptica were interspersed between other specimens identified as T. meridionalis. The same result occurred when COI sequence OL870276.1, identified as T. meridionalis, was used as the input (

Table 2. BOLD System results obtained using, as the input, a COI sequence of T. elliptica (OL870191.1; left column) versus one of T. meridionalis (OL870276.1; right column). Percent similarity is also indicated.

Torrenticola	elliptica	100	Torrenticola	meridionalis
Torrenticola	meridionalis	92.35	Torrenticola	meridionalis
Torrenticola	meridionalis	92.35	Torrenticola	meridionalis
Torrenticola	meridionalis	92.33	Torrenticola	meridionalis
Torrenticola	meridionalis	92.11	Torrenticola	meridionalis
Torrenticola	elliptica	91.9	Torrenticola	meridionalis
Torrenticola	meridionalis	91.9	Torrenticola	meridionalis
Torrenticola	meridionalis	91.9	Torrenticola	meridionalis
Torrenticola	meridionalis	91.74	Torrenticola	meridionalis
Torrenticola	meridionalis	91.74	Torrenticola	meridionalis
Torrenticola	meridionalis	91.71	Torrenticola	elliptica
Torrenticola	meridionalis	91.67	Torrenticola	elliptica
Torrenticola	elliptica	91.59	Torrenticola	meridionalis
Torrenticola	elliptica	91.59	Torrenticola	meridionalis
Torrenticola	meridionalis	91.59	Torrenticola	meridionalis
Torrenticola	meridionalis	91.55	Torrenticola	meridionalis
Torrenticola	meridionalis	91.51	Torrenticola	meridionalis
Torrenticola	meridionalis	91.51	Torrenticola	meridionalis
Torrenticola	meridionalis	91.47	Torrenticola	meridionalis
Torrenticola	meridionalis	91.46	Torrenticola	meridionalis

).

As of this writing, the sequences of several of the specimens of T. elliptica and T. meridonalis on this list remain private (last accessed: 14 October 2022); therefore, no further sequence analyses could be performed. It is unknown if the possible misidentifications may be due to the single use of a diagnostic character, as mentioned above, or some other reason.

2.1. Measurement of Variability in Species

Taxonomic decisions related to the species identification of a specimen are taken after an implicit or explicit evaluation of the variability of a species. Although taxonomists generally obtain a good idea of the usual variability of the species of a clade after years of study, their experience is not a “full-save” criterion for assigning a specimen to a species or erecting a new one. When more than one specimen is available for study, then some measure of variability is advisable. In this context, some statistical estimates are more informative than others. For instance, mean, standard deviation and coefficient of variation are three highly useful measures of variability, whereas range, ratios and indexes—although occasionally useful—generally present some problems.

2.2. Range Calculation

Range, or the difference between the lowest and the highest values of a measurement of a structure, is a weak indicator of variability. As pointed out by Van Valen [19], “the full observed range is very sensitive to sample size and is rarely very useful.” Range size indicates the representativeness of the central tendency measures, with central measures being more representative when the range is small. In addition, the difference should be calculated from the lowest implied limit of the lowest value to the highest implied limit of the highest value.

2.3. Mean and Standard Deviation

Nothing new can be said about arithmetic mean ($\overline{\mathit{x}}$) and standard deviation (s) that cannot be found in any statistical book, e.g., [5,20]. Basically, arithmetic mean should be the preferred term instead of “average” or simply “mean”, as other averages that can be considered include the mode, median and geometric mean.

2.4. Coefficient of Variation

This statistic is defined as:

$$\mathit{c}\mathit{v}=\mathbf{100}\frac{\mathit{s}}{\overline{\mathit{x}} }$$

It is commonly phrased as an answer to the question “Is a mouse as variable as an elephant?” [19,21]. The use of this coefficient may be considered in the context of a biological disparity problem rather than a biological diversity question [22], with the latter issue being more related to taxonomic investigation. The question that cv answers is about the relative variability of a species within a clade, e.g., species of a certain genus or species among different families, or the variability of characters within a species. There is no reason why this very informative statistic should not be included as another common statistic for variation, especially considering that means of linear measurement differ [19,23]. In taxonomic studies, the cv can be especially useful in the selection of characters that display little variability as diagnostic characters. After comparing hundreds of cv values for mammalian anatomical elements, Simpson et al. [4] found that “the great majority lie between 4 and 10, and 5 and 6 are good average values.” To illustrate the usefulness of this statistic for a species of water mite, the cv for characters of Torrenticola costaricense Goldschmidt, 2003, was added to a list of other statistics previously published for the species [24] (

Table 3. Statistics of characters of Torrenticola costaricense that were derived from the analysis of 46 male specimens. In the last column, I have added the cv values for these characters (for an explanation of the abbreviations of the characters, see [24]).

	Holotype	Mean	Min	Max	sd	cv
IdiosomaL	701	753	667	849	44.3	5.88
Idiosoma W	594	618	544	755	52.6	8.51
Idiosoma L/W	1.18	1.2	1.11	1.3	0.05	4.17
Cx-It L	314	314	284	358	14.5	4.62
Cx-III W	412	412	368	500	28.9	7.01
Cx-ItL/Cx-III W	0.76	0.75	0.67	0.82	0.04	5.33
Ds L	608	652	559	760	46.6	7.15
Dp L	574	618	525	706	44.8	7.25
Ds W	481	527	461	628	38.8	7.36
Ds L/W	1.27	1.24	1.16	1.29	0.03	2.42
Dp L/W	1.19	1.17	1.08	1.23	0.03	2.56
A-mplatelet L	184	189	159	218	13.1	6.93
A-mplatelet W	61	69	58	83	5.9	8.55
A-mplatelet L/W	3	2.69	2.44	3	0.1	3.72
Capitularbay L	164	164	135	181	10.2	6.22
Capitularbay W	69	76	64	102	8.1	10.66
Cb L/W	2.39	2.13	1.51	2.44	0.2	9.39
Distcb–gf	216	224	203	279	15.7	7.01
Cx-Im L	152	157	135	194	10.6	6.75
Cx-II + IIIm L	54	59	39	78	8	13.56
Cx-ItL/Cx-II/IIIm L	5.82	5.35	4	8.63	0.9	16.82
Cx-I/Cx-II + IIIm L	2.82	2.67	1.87	4.25	0.4	14.98

).

2.5. Ratios and Indexes

In a strict sense, index is the division of a dimension by a large one of the same structure, expressed as a percentage, and ratios are divisions between dimension of different structures [4]. In the taxonomy of Hydrachnidia, they are used indistinctly. Here, I primarily focus on ratios, although the considerations may also be applicable to proportions and indexes.

As previously mentioned, any value of a measured variable has an implied range. For instance, the length of chelicera, the given value of which is 210 μm, is actually between 209.5 μm and 210.5 μm (more precisely, this last value should be 210.499 to avoid overlapping with the lower limit of the value 211, but for simplification, it is rounded up to 210.5). The problem becomes even more complex if we want to calculate the range between two ratios.

A very common ratio used in water mite taxonomy is the ratio of the dorsal length of palp segments P-2 and P-4 (P-2/P-4). As an example of miscalculation in this group, I highlight the case of the species Atractides nodipalpis and Ignacarus salaries. Gerecke [25] measured 47 males of A. nodipalpis and obtained a minimum value for the length of P-2 of 74 μm and a maximum of 99 μm, and for P-4, a minimum of 99 μm and a maximum of 128 μm [25] (see Table 1). Calculated precisely considering the calibrating factor, the range of variation of the P-2/P-4 ratio is actually 0.57–1.0, which is much wider than the range of 0.63–0.84 published by Gerecke [25]. Likewise, in Gerecke [15], the ratio of the length of the second palp segment to that of the fourth segment of I. salaries is reported as P-2/P-4 = 0.80–0.86 [15] (p. 131). Previously, this author documented the dorsal length of the individual segments as P-2: 29.2–31.0 μm and P-4: 35.0–36.7 μm [14]. With these data, the ratio can be properly calculated after first transforming each figure to its implied range. The implied range of the lower value of P-2 is 29.15000 to 29.24999, and that for the higher value of P-2 is 30.95000 to 31.04999. For P-4, the implied lower limit range is 34.95000 to 35.04999, and the higher one is 36.65000 to 36.74999. Using these values, a corrected P-2/P-4 is calculated as 29.15000/36.74999 to 31.04999/34.95000, with the range being 0.79–0.88.

The idea of calculating range values of ratios of linear measurements (e.g., length and height or length and width), which is very common in the taxonomy of Hydrachnidia and other animal groups, is not based on isometric growth. If this were the case, then a single measure of length and height would be enough to derive either of these measures for another specimen using the ratio, assuming the other measurement is known.

To calculate a ratio, the following methodological steps should be taken:

• Single figures, before being used in a ratio, should be converted to their implied range.
• The lower limit of the first measurement should be divided by the higher limit of the second measurement.
• The higher limit of the first measurement should be divided by the lower limit of the second measurement.
• Although the ratio cannot have more significant figures than the measurement with the fewest significant figures, it may be acceptable to leave them.

Example: a structure that varies between 1.2 and 3.5 μm in length and 0.8 and 1.3 μm in width will have a L/W ratio range of 0.85 to 4.73 (and not 1.5 to 2.7).

A more detailed illustration of the calculation correcting for uncertainty due to measurement error and resulting differences in the range of ratios is shown in

Table 4. Length ratio range for the five palp segments of Hydrachna geographica Müller, 1776 [7] (p. 43), and their values corrected for uncertainty following the steps outlined above.

Palp Segment	Published Measurements of L/H (in μm)	Published Ratio Range	Corrected Ratio Range	Calculation Correcting for Uncertainty
P-1	400–420/590–640	0.66–0.68	0.62–0.71	400/640 = 0.62 420/590 = 0.71
P-2	670–710/370–380	1.81–1.87	1.76–1.92	670/380 = 1.76 710/370 = 1.92
P-3	850–930/190–195	4.47–4.77	4.35–4.89	850/195 = 4.35 930/190 = 4.89
P-4	250/110	2.27	2.27	250/110
P-5	100–110/50–60	1.67–2.20	1.64–2.23	100/60 = 1.67 110/50 = 2.2

. In this example, I use the values given by [7] (p. 43) (for the dorsal length of palp segments in the species Hydrachna geographica Müller, 1776. Given that the ratio between the dorsal length of P2 and P4 has been used as an important diagnostic character in the literature of Hydrachnidia, it is important that this value be properly calculated if it is to continue to fulfill that important role.

Indexes and proportions have the same problem as ratios and should be properly (re)calculated, and their sum should be 100%. However, these statistics do not as clearly convey information on size relationships as do ratios; therefore, it is better to avoid using them in taxonomic studies.

3. Conclusions

From our case study on the effect that the degree of uncertainty can have on derived statistical values, we conclude the following main points:

(1)

Primary data should always be made accessible either in the main publication or as supplementary material or, as is becoming more commonplace, in a research data repository. This point is very important: in order to (re)examine the accuracy of any statistical quantity, the data distribution must be known.

(2)

Any direct measurement has implicit uncertainty limits. In the case of microscopic animals, uncertainty derives from the primary error that occurs when calibrating the ocular micrometer with a stage micrometer, followed by secondary errors that can occur during the act of measuring itself.

(3)

Along with the traditional measures of variability (i.e., $\overline{\mathit{x}}$ and s), cv may be a useful tool for identifying characters with low variability that could potentially function as diagnostic characters.

(4)

Finally, the ratios of characters should be properly calculated by taking into consideration the degree of uncertainty, particularly if they are to be used in species diagnoses.