Eigenfemora—Age-at-Death Estimation in the Proximal Femur through an Image Processing Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample
2.2. Methods
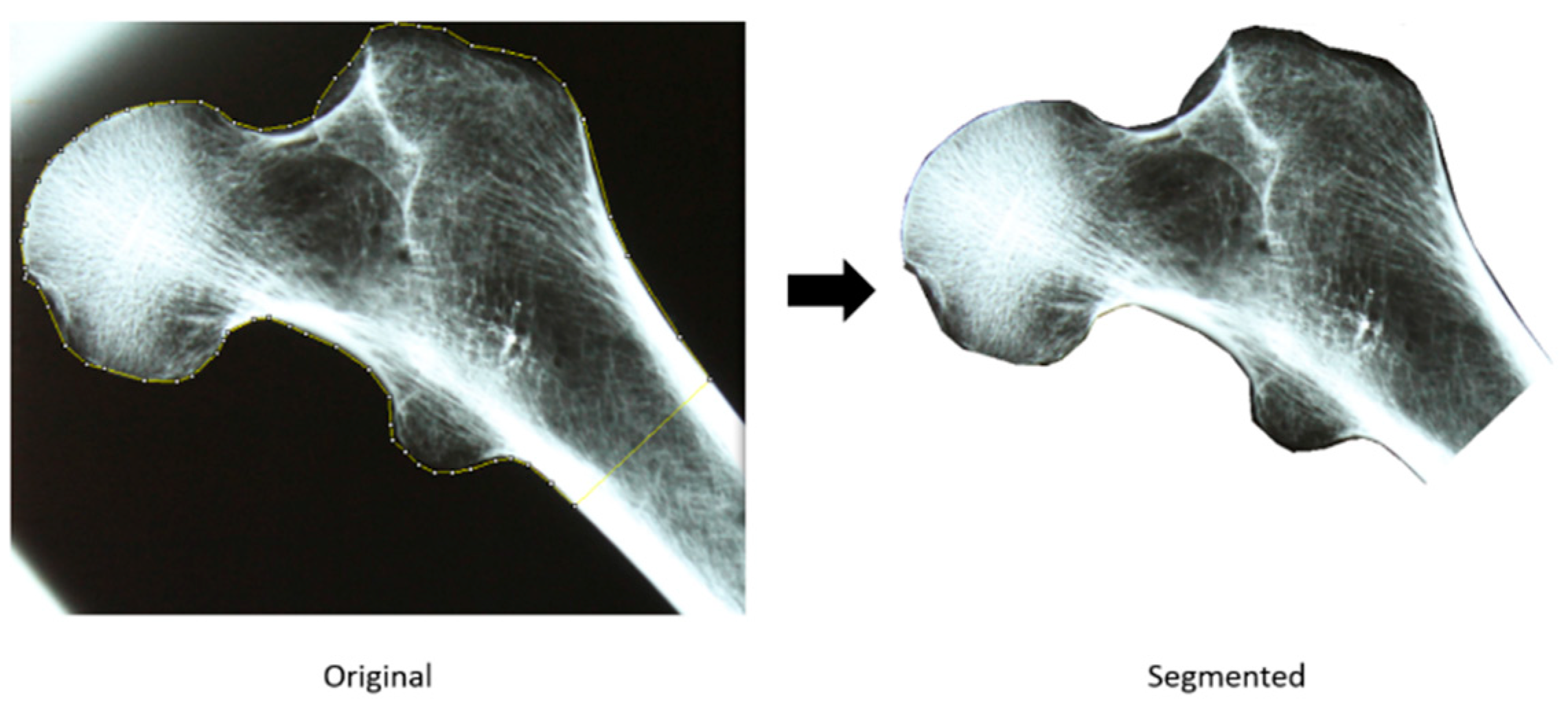
2.2.1. Acquisition and Segmentation
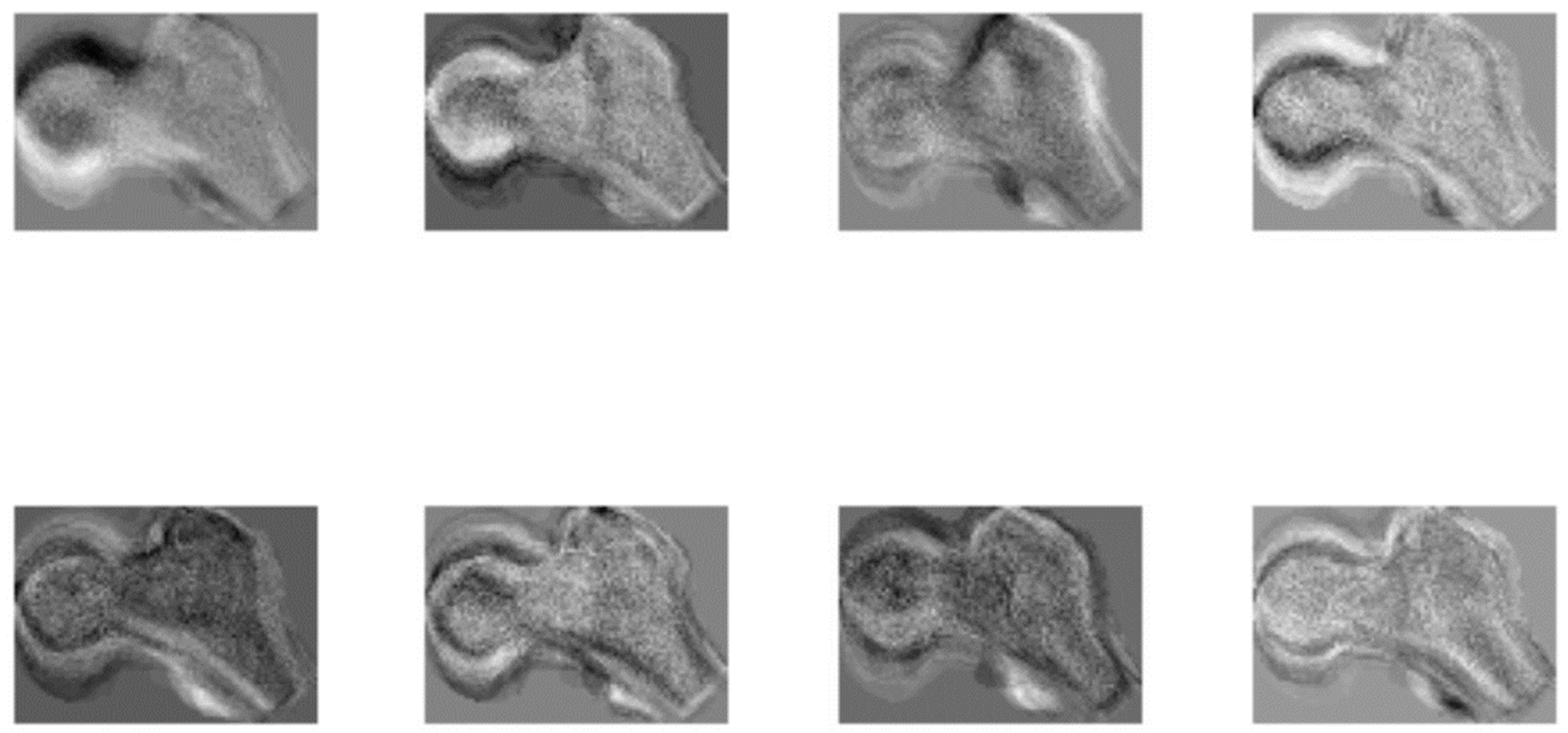
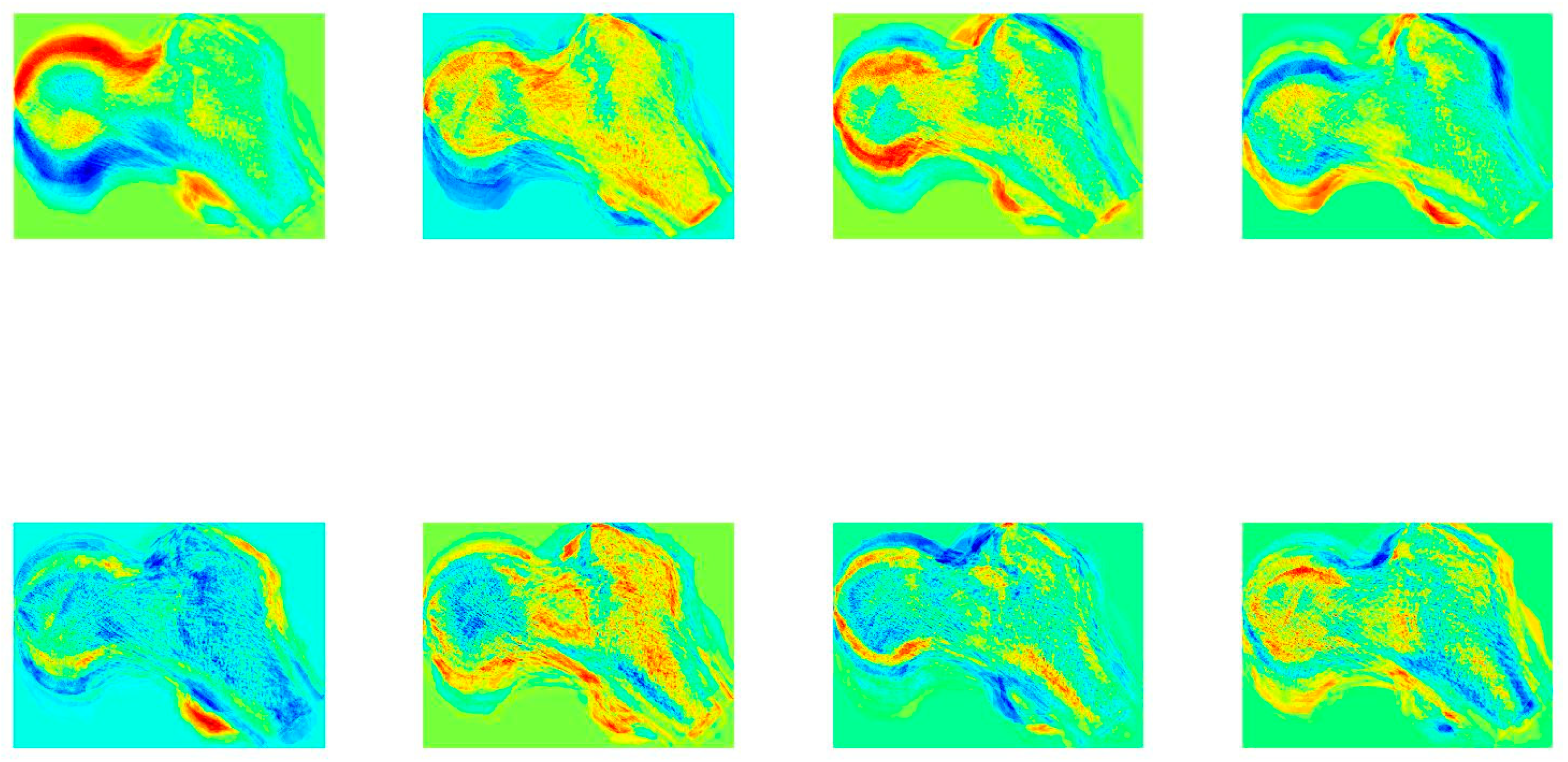
2.2.2. Age Estimation from the Femora Space with K-Nearest Neighbor Search
3. Results
4. Discussion
5. Final Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cunha, E.; Baccino, E.; Martrille, L.; Ramsthaler, F.; Prieto, J.; Schuliar, Y.; Lynnerup, N.; Cattaneo, C. The Problem of Aging Human Remains and Living Individuals: A Review. Forensic Sci. Int. 2009, 193, 1–13. [Google Scholar] [CrossRef]
- Márquez-Grant, N. An Overview of Age Estimation in Forensic Anthropology: Perspectives and Practical Considerations. Ann. Hum. Biol. 2015, 42, 306–320. [Google Scholar] [CrossRef]
- Navega, D.; Costa, E.; Cunha, E. Adult Skeletal Age-At-Death Estimation through Deep Random Neural Networks: A New Method and Its Computational Analysis. Biology 2022, 11, 532. [Google Scholar] [CrossRef]
- Komar, D.A.; Buikstra, J.E. Forensic Anthropology: Contemporary Theory and Practice; Oxford University Press: Oxford, UK, 2007; ISBN 9780195300291. [Google Scholar]
- Xanthopoulou, P.; Valakos, E.; Youlatos, D.; Nikita, E. Assessing the Accuracy of Cranial and Pelvic Ageing Methods on Human Skeletal Remains from a Modern Greek Assemblage. Forensic Sci. Int. 2018, 286, 266.e1–266.e8. [Google Scholar] [CrossRef]
- Ubelaker, D.H.; Khosrowshahi, H. Estimation of Age in Forensic Anthropology: Historical Perspective and Recent Methodological Advances. Forensic Sci. Res. 2019, 4, 1–9. [Google Scholar] [CrossRef]
- Hens, S.M.; Godde, K. A Bayesian Approach to Estimating Age from the Auricular Surface of the Ilium in Modern American Skeletal Samples. Forensic Sci. 2022, 2, 682–695. [Google Scholar] [CrossRef]
- Cappella, A.; Cummaudo, M.; Arrigoni, E.; Collini, F.; Cattaneo, C. The Issue of Age Estimation in a Modern Skeletal Population: Are Even the More Modern Current Aging Methods Satisfactory for the Elderly? J. Forensic Sci. 2017, 62, 12–17. [Google Scholar] [CrossRef]
- Navega, D.; Coelho, J.d.O.; Cunha, E.; Curate, F. DXAGE: A New Method for Age at Death Estimation Based on Femoral Bone Mineral Density and Artificial Neural Networks. J. Forensic Sci. 2018, 63, 497–503. [Google Scholar] [CrossRef]
- Garvin, H.M.; Passalacqua, N.V. Current Practices by Forensic Anthropologists in Adult Skeletal Age Estimation. J. Forensic Sci. 2012, 57, 427–433. [Google Scholar] [CrossRef]
- Bailey, C.; Vidoli, G. Age-at-Death Estimation: Accuracy and Reliability of Common Age-Reporting Strategies in Forensic Anthropology. Forensic Sci. 2023, 3, 179–191. [Google Scholar] [CrossRef]
- Ousley, S.D.; Hollinger, R.E. The Pervasiveness of Daubert. In A Companion to Forensic Anthropology; Dirkmaat, D.C., Ed.; Blackwell Publishing Ltd.: Chichester, UK, 2012; pp. 654–665. ISBN 9781405191234. [Google Scholar]
- Shen, Y.; Huang, X.; Wu, J.; Lin, X.; Zhou, X.; Zhu, Z.; Pan, X.; Xu, J.; Qiao, J.; Zhang, T.; et al. The Global Burden of Osteoporosis, Low Bone Mass, and Its Related Fracture in 204 Countries and Territories, 1990–2019. Front. Endocrinol. 2022, 13, 882241. [Google Scholar] [CrossRef]
- Aggarwal, A.; Pal, R.; Bhadada, S.K.; Ram, S.; Garg, A.; Bhansali, A.; Singh, P.; Thakur, J.S.; Singh, T.; Sachdeva, N.; et al. Bone Mineral Density in Healthy Adult Indian Population: The Chandigarh Urban Bone Epidemiological Study (CUBES). Arch. Osteoporos. 2021, 16, 17. [Google Scholar] [CrossRef]
- Curate, F.; Navega, D.; Cunha, E.; Coelho, J. d’Oliveira DXAGE 2.0—Adult Age at Death Estimation Using Bone Loss in the Proximal Femur and the Second Metacarpal. Int. J. Legal Med. 2022, 136, 1483–1494. [Google Scholar] [CrossRef]
- Curate, F.; Cunha, E. Femoral Cortical Bone in a Portuguese Reference Skeletal Collection. Antropol. Port. 2017, 34, 91–109. [Google Scholar] [CrossRef]
- Seeman, E. Structural Basis of Growth-Related Gain and Age-Related Loss of Bone Strength. Rheumatology 2008, 47, 2–8. [Google Scholar] [CrossRef]
- Riggs, B.L.; Melton, L.J.; Robb, R.A.; Camp, J.J.; Atkinson, E.J.; McDaniel, L.; Amin, S.; Rouleau, P.A.; Khosla, S. A Population-Based Assessment of Rates of Bone Loss at Multiple Skeletal Sites: Evidence for Substantial Trabecular Bone Loss in Young Adult Women and Men. J. Bone Miner. Res. 2008, 23, 205–214. [Google Scholar] [CrossRef]
- Schranz, D. Age Determination from the Internal Structure of the Humerus. Am. J. Phys. Anthropol. 1959, 17, 273–277. [Google Scholar] [CrossRef]
- Bascou, A.; Dubourg, O.; Telmon, N.; Dedouit, F.; Saint-Martin, P.; Savall, F. Age Estimation Based on Computed Tomography Exploration: A Combined Method. Int. J. Legal Med. 2021, 135, 2447–2455. [Google Scholar] [CrossRef]
- Dubourg, O.; Faruch-Bilfeld, M.; Telmon, N.; Maupoint, E.; Saint-Martin, P.; Savall, F. Correlation between Pubic Bone Mineral Density and Age from a Computed Tomography Sample. Forensic Sci. Int. 2019, 298, 345–350. [Google Scholar] [CrossRef] [PubMed]
- Paschall, A.; Ross, A.H. Biological Sex Variation in Bone Mineral Density in the Cranium and Femur. Sci. Justice 2018, 58, 287–291. [Google Scholar] [CrossRef] [PubMed]
- Dubourg, O.; Faruch-Bilfeld, M.; Telmon, N.; Savall, F.; Saint-Martin, P. Technical Note: Age Estimation by Using Pubic Bone Densitometry According to a Twofold Mode of CT Measurement. Int. J. Legal Med. 2020, 134, 2275–2281. [Google Scholar] [CrossRef] [PubMed]
- Bergot, C.; Bocquet, J.-P. Etude Systématique, En Fonction de l’âge, de l’os Spongieux et de l’os Cortical de l’humérus et Du Fémur. Bull. Mem. Soc. Anthropol. Paris 1976, 3, 215–242. [Google Scholar] [CrossRef]
- Szilvássy, J.; Kritscher, H. Estimation of Chronological Age in Man Based on the Spongy Structure of Long Bones. Anthropol. Anzeiger 1990, 48, 289–298. [Google Scholar] [CrossRef]
- Lespessailles, E.; Poupon, S.; Niamane, R.; Loiseau-Peres, S.; Derommelaere, G.; Harba, R.; Courteix, D.; Benhamou, C.L. Fractal Analysis of Trabecular Bone Texture on Calcaneus Radiographs: Effects of Age, Time since Menopause and Hormone Replacement Therapy. Osteoporos. Int. 2002, 13, 366–372. [Google Scholar] [CrossRef] [PubMed]
- Barrier, P.; Dedouit, F.; Braga, J.; Joffre, F.; Rougé, D.; Rousseau, H.; Telmon, N. Age at Death Estimation Using Multislice Computed Tomography Reconstructions of the Posterior Pelvis. J. Forensic Sci. 2009, 54, 773–778. [Google Scholar] [CrossRef]
- Ferrant, O.; Rougé-Maillart, C.; Guittet, L.; Papin, F.; Clin, B.; Fau, G.; Telmon, N. Age at Death Estimation of Adult Males Using Coxal Bone and CT Scan: A Preliminary Study. Forensic Sci. Int. 2009, 186, 14–21. [Google Scholar] [CrossRef]
- Curate, F.; Perinha, A.; Silva, A.M.; Cunha, E.; Umbelino, C.; Nogueira, C. Metacarpal Cortical Bone Loss and Osteoporotic Fractures in the Coimbra Identified Skeletal Collection. Int. J. Osteoarchaeol. 2019, 29, 73–81. [Google Scholar] [CrossRef]
- Virtama, P.; Helelä, T. Radiographic Measurements of Cortical Bone: Variations in a Normal Population between 1 and 90 Years of Age. Acta Radiol. 1969, 97, 1–268. [Google Scholar]
- Sinanoglu, A.; Kocasarac, H.D.; Noujeim, M. Age Estimation by an Analysis of Spheno-Occipital Synchondrosis Using Cone-Beam Computed Tomography. Leg. Med. 2016, 18, 13–19. [Google Scholar] [CrossRef]
- Turunen, M.J.; Prantner, V.; Jurvelin, J.S.; Kröger, H.; Isaksson, H. Composition and Microarchitecture of Human Trabecular Bone Change with Age and Differ between Anatomical Locations. Bone 2013, 54, 118–125. [Google Scholar] [CrossRef]
- Lochmüller, E.M.; Matsuura, M.; Bauer, J.; Hitzl, W.; Link, T.M.; Müller, R.; Eckstein, F. Site-Specific Deterioration of Trabecular Bone Architecture in Men and Women with Advancing Age. J. Bone Miner. Res. 2008, 23, 1964–1973. [Google Scholar] [CrossRef] [PubMed]
- Todd, T.W. Age Changes in the Pubic Bone. VIII. Roentgenographic Differentiation. Am. J. Phys. Anthropol. 1930, 14, 255–271. [Google Scholar] [CrossRef]
- Walker, R.A.; Lovejoy, C.O. Radiographic Changes in the Clavicle and Proximal Femur and Their Use in the Determination of Skeletal Age at Death. Am. J. Phys. Anthropol. 1985, 68, 67–78. [Google Scholar] [CrossRef] [PubMed]
- Gehring, K.D.; Haffner, H.T.; Weber, D.; Graw, M. Investigations on the Reliability of Determining an Individual’s Age from the Proximal Femur. HOMO-J. Comp. Hum. Biol. 2002, 52, 214–220. [Google Scholar] [CrossRef] [PubMed]
- De Froidmont, S.; Grabherr, S.; Vaucher, P.; De Cesare, M.; Egger, C.; Papageorgopoulou, C.; Roth, V.; Morand, G.; Mangin, P.; Uldin, T. Virtual Anthropology: A Comparison between the Performance of Conventional X-ray and MDCT in Investigating the Trabecular Structure of Long Bones. Forensic Sci. Int. 2013, 225, 53–59. [Google Scholar] [CrossRef]
- Acsádi, G.Y.; Nemeskéri, J. History of Human Life Span and Mortality; Akadémiai Kiadó: Budapest, Hungary, 1970; Volume 7. [Google Scholar]
- Benito, M.; Sánchez, J.A.; Codinha, S. Age-at-Death Estimation Based on Radiological and Image Analysis Methods in Clavicle in a Current Spanish Population. Int. J. Legal Med. 2014, 128, 523–533. [Google Scholar] [CrossRef]
- Fernández Castillo, R.; López Ruiz, M.C. Assessment of Age and Sex by Means of DXA Bone Densitometry: Application in Forensic Anthropology. Forensic Sci. Int. 2011, 209, 53–58. [Google Scholar] [CrossRef]
- Macchiarelli, R.; Bondioli, L. Linear Densitometry and Digital Image Processing of Proximal Femur Radiographs: Implications for Archaeological and Forensic Anthropology. Am. J. Phys. Anthropol. 1994, 93, 109–122. [Google Scholar] [CrossRef]
- Botha, D.; Lynnerup, N.; Steyn, M. Age Estimation Using Bone Mineral Density in South Africans. Forensic Sci. Int. 2019, 297, 307–314. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, L.; Hao, Y.; Wang, Z.; Wang, M.; Ge, S. Analysis of Trabecular Distribution of the Proximal Femur in Patients with Fragility Fractures. BMC Musculoskelet. Disord. 2013, 14, 130. [Google Scholar] [CrossRef]
- Petaros, A.; Caplova, Z.; Verna, E.; Adalian, P.; Baccino, E.; de Boer, H.H.; Cunha, E.; Ekizoglu, O.; Ferreira, M.T.; Fracasso, T.; et al. Technical Note: The Forensic Anthropology Society of Europe (FASE) Map of Identified Osteological Collections. Forensic Sci. Int. 2021, 328, 110995. [Google Scholar] [CrossRef] [PubMed]
- Cunha, E.; Wasterlain, S. The Coimbra Identified Osteological Collections. In Skeletal Series in Their Socioeconomic Context; Grupe, G., Peters, J., Eds.; M. Leidorf: Rahden/Westphalia, Germany, 2007; Volume 5, pp. 23–33. [Google Scholar]
- Kucheryavski, S.; Belyaev, I.; Fominykh, S. Estimation of Age in Forensic Medicine Using Multivariate Approach to Image Analysis. Chemom. Intell. Lab. Syst. 2009, 97, 39–45. [Google Scholar] [CrossRef]
- Turk, M.; Pentland, A. Eigenfaces for Recognition. J. Cogn. Neurosci. 1991, 3, 71–86. [Google Scholar] [CrossRef] [PubMed]
- Bentley, J.L. Multidimensional Binary Search Trees Used for Associative Searching. Commun. ACM 1975, 18, 509–517. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference and Prediction; Springer: New York, NY, USA, 2009; ISBN 978-0-387-84857-0. [Google Scholar]
- Witten, I.H.; Frank, E.; Hall, M.A.; Pal, C.J. Data Mining: Practical Machine Learning Tools and Techniques; Elsevier: Amsterdam, The Netherlands, 2016; ISBN 9780128042915. [Google Scholar]
- Mays, S. The Archaeology of Human Bones; Routledge: London, UK, 2021. [Google Scholar]
- Curate, F.; Albuquerque, A.; Ferreira, I.; Cunha, E. Sex Estimation with the Total Area of the Proximal Femur: A Densitometric Approach. Forensic Sci. Int. 2017, 275, 110–116. [Google Scholar] [CrossRef]
- Curate, F.; d’Oliveira Coelho, J.; Gonçalves, D.; Coelho, C.; Ferreira, M.T.; Navega, D.; Cunha, E. A Method for Sex Estimation Using the Proximal Femur. Forensic Sci. Int. 2016, 266, 579.e1–579.e7. [Google Scholar] [CrossRef]
- Christensen, A.M.; Leslie, W.D.; Baim, S. Ancestral Differences in Femoral Neck Axis Length: Possible Implications for Forensic Anthropological Analyses. Forensic Sci. Int. 2014, 236, 193.e1–193.e4. [Google Scholar] [CrossRef]
- Mendonça, M.C. de Estimation of Height from the Length of Long Bones in a Portuguese Adult Population. Am. J. Phys. Anthropol. 2000, 112, 39–48. [Google Scholar] [CrossRef]
- Kranioti, E.F.; Vorniotakis, N.; Galiatsou, C.; Işcan, M.Y.; Michalodimitrakis, M. Sex Identification and Software Development Using Digital Femoral Head Radiographs. Forensic Sci. Int. 2009, 189, 113.e1–113.e7. [Google Scholar] [CrossRef]
- Curate, F.; Albuquerque, A.; Cunha, E.M. Age at Death Estimation Using Bone Densitometry: Testing the Fernández Castillo and López Ruiz Method in Two Documented Skeletal Samples from Portugal. Forensic Sci. Int. 2013, 226, 296.e1–296.e6. [Google Scholar] [CrossRef]
- Martins, R.; Oliveira, P.E.; Schmitt, A. Estimation of Age at Death from the Pubic Symphysis and the Auricular Surface of the Ilium Using a Smoothing Procedure. Forensic Sci. Int. 2012, 219, 287.e1–287.e7. [Google Scholar] [CrossRef] [PubMed]
- Kotěrová, A.; Velemínská, J.; Cunha, E.; Brůžek, J. A Validation Study of the Stoyanova et Al. Method (2017) for Age-at-Death Estimation Quantifying the 3D Pubic Symphyseal Surface of Adult Males of European Populations. Int. J. Legal Med. 2019, 133, 603–612. [Google Scholar] [CrossRef] [PubMed]
- San Millán, M.; Rissech, C.; Turbón, D. A Test of Suchey-Brooks (Pubic Symphysis) and Buckberry-Chamberlain (Auricular Surface) Methods on an Identified Spanish Sample: Paleodemographic Implications. J. Archaeol. Sci. 2013, 40, 1743–1751. [Google Scholar] [CrossRef]
- White, T.; Black, M.; Folkens, P. Human Osteology; Academic Press: Amsterdam, The Netherlands, 2012; ISBN 9780123741349. [Google Scholar]
- Kotěrová, A.; Navega, D.; Štepanovský, M.; Buk, Z.; Brůžek, J.; Cunha, E. Age Estimation of Adult Human Remains from Hip Bones Using Advanced Methods. Forensic Sci. Int. 2018, 287, 163–175. [Google Scholar] [CrossRef]
- MacDonald, H.M.; Nishiyama, K.K.; Kang, J.; Hanley, D.A.; Boyd, S.K. Age-Related Patterns of Trabecular and Cortical Bone Loss Differ between Sexes and Skeletal Sites: A Population-Based HR-PQCT Study. J. Bone Miner. Res. 2011, 26, 50–62. [Google Scholar] [CrossRef]
- Khosla, S.; Riggs, B.L.; Atkinson, E.J.; Oberg, A.L.; McDaniel, L.J.; Holets, M.; Peterson, J.M.; Melton, L.J. Effects of Sex and Age on Bone Microstructure at the Ultradistal Radius: A Population-Based Noninvasive In Vivo Assessment. J. Bone Miner. Res. 2006, 21, 124–131. [Google Scholar] [CrossRef]
- Masset, C. Age Estimation Based on Cranial Sutures. In Age Markers in the Human Skeleton; Iscan, M.Y., Ed.; CC Thomas: Springfield, IL, USA, 1989; pp. 71–103. [Google Scholar]
- Bonnick, S.L.; Lewis, L.A. Bone Densitometry for Technologists, 3rd ed.; Human Press: Tottowa, NJ, USA, 2013; ISBN 9781461436256. [Google Scholar]
- d’Oliveira Coelho, J.; Curate, F.; Navega, D. Osteomics: Decision Support Systems for Forensic Anthropologists. In Statistics and Probability in Forensic Anthropology; Obertová, Z., Stewart, A., Cattaneo, C., Eds.; Academic Press: London, UK, 2020; pp. 259–273. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Navega, D.; Ferreira, M.T.; Curate, F. Eigenfemora—Age-at-Death Estimation in the Proximal Femur through an Image Processing Approach. Forensic Sci. 2024, 4, 1-11. https://doi.org/10.3390/forensicsci4010001
Navega D, Ferreira MT, Curate F. Eigenfemora—Age-at-Death Estimation in the Proximal Femur through an Image Processing Approach. Forensic Sciences. 2024; 4(1):1-11. https://doi.org/10.3390/forensicsci4010001
Chicago/Turabian StyleNavega, David, Maria Teresa Ferreira, and Francisco Curate. 2024. "Eigenfemora—Age-at-Death Estimation in the Proximal Femur through an Image Processing Approach" Forensic Sciences 4, no. 1: 1-11. https://doi.org/10.3390/forensicsci4010001
APA StyleNavega, D., Ferreira, M. T., & Curate, F. (2024). Eigenfemora—Age-at-Death Estimation in the Proximal Femur through an Image Processing Approach. Forensic Sciences, 4(1), 1-11. https://doi.org/10.3390/forensicsci4010001






