Electromyography-Based Human-in-the-Loop Bayesian Optimization to Assist Free Leg Swinging

Abstract

Background/Objectives: The manual tuning of exoskeleton control parameters is tedious and often ineffective for adapting to individual users. Human-in-the-loop (HIL) optimization offers an automated approach, but existing methods typically rely on metabolic cost, which requires prolonged data collection times of at least 60 s. Surface electromyography (EMG) signals, as an alternative, enable faster optimization with reduced data acquisition times. Methods: This study develops a rapid EMG-based HIL Bayesian optimization framework to tune hip exoskeleton controllers for assisting free leg swinging. Eight participants are asked to perform leg swinging at two frequencies with assistance from a hip exoskeleton. EMG signals from four sensors, representing muscle activity during forward and backward swings, are dynamically processed into cost functions. Bayesian optimization with Gaussian processes tunes four controller parameters using an expected improvement acquisition function. Optimization outcomes are validated against no device, zero torque, and general control baselines. Results: Optimization converges within an average of 142 s with a standard deviation of 24 s across all participants. The controller yields muscle activity reductions of 16.1% (p < 0.001) compared to no device, 21.7% (p < 0.001) versus zero torque, and 15.1% (p < 0.001) versus general control. EMG-based tuning is faster than metabolic-cost-based methods and perceived as less effortful, with Borg scale reductions of up to 39.5%. Conclusions: EMG-based HIL optimization significantly enhances controller tuning speed and effectiveness, demonstrating its potential for scalable and user-specific exoskeleton applications.

1. Introduction

Despite several examples of moderate energy reduction improvements in the realm of assistive exoskeletons, most devices still cannot fully account for high inter-subject variability in physiological responses [1,2,3,4,5,6,7]. Slight differences in exoskeleton actuation can significantly affect how users benefit from the assistance. Therefore, more thorough individualized control tuning can achieve better assistance to reduce the effort required to perform certain activities such as walking [8,9,10,11,12,13,14]. The ever-increasing demand for wearable robotics makes manual tuning of control parameters for each individual time-consuming and often strenuous [11,15,16,17]. With human-in-the-loop (HIL) technology, a paradigm that eliminates the need for expert intervention and extensive research hours, optimal parameters are automatically identified and tuned in real-time via physiological signals [8,11,14,18].

While several HIL optimization methods have shown success [2,8,17,18,19], they commonly rely on metabolic cost—a measure with a prolonged acquisition time [20,21,22]. Data measurements for metabolic cost often adapt slowly [12], estimations require substantial historical data [23], and signal readings are influenced by complex neurocognitive factors [21]. Due to these factors, traditional metabolic cost calculations may require 4–6 min of data per condition [2,19]. Some alternatives explore accelerating this process by estimating metabolic cost steady state. However, metabolic cost estimations typically demand one to two minutes of data per evaluation [20]. Since thorough optimization requires the evaluation of several conditions, the acquisition time aggregates to a lengthy procedure, allowing the user preference to shift before optimization completion [8,14]. A faster promising alternative is surface electromyography (EMG), a non-invasive measure of muscle activity voltage.

The integration of EMG and exoskeletons is not a novel concept; EMG signal input has been used for modulating control in exoskeletons for several decades [22,24]. While most implementations focus on volitional control of upper body prosthetics and orthotics, some devices employ EMG-control to assist the lower body [22,25]. Studies even demonstrate the successful use of EMG signals to optimally tune walking exoskeleton controllers [8,17]. However, while several studies, including those referenced here and others [8,17], demonstrate the potential of EMG signals as an objective metric in HIL optimization, challenges such as signal noise, poor repeatability, local metric insights, and the influence of muscle fatigue remain underexplored [26,27]. Fatigue can alter EMG signal characteristics over time, potentially affecting optimization reliability. To mitigate this, we focus on short-duration optimization windows and employ efficient optimization strategies to minimize prolonged exertion, reducing the impact of fatigue on signal consistency. Despite these drawbacks, EMG offers a shorter acquisition time, lower discomfort for subjects, and the ability to reflect reductions in energy economy effectively [26,28,29,30]. Therefore, improving the harnessing of this physiological metric has the potential to significantly reduce the time required for current hardware optimization methods.

We employ Bayesian optimization to improve the sample efficiency of our HIL optimization approach. We select Bayesian optimization for its noise tolerance, ability to quickly optimize physiological signals, and documented history of successful outcomes in HIL optimization [18,30,31].

The focus of this work centers on assisting stationary leg-swinging. Leg swinging is a pivotal component of walking and the hip is a natural contender as the joint to target, given its crucial contribution of up to 45% of the mechanical power during the walking gait cycle [1,32]. However, walking is typically analyzed as a whole, focusing on both the stance and swing phases simultaneously, which can mask the specific effects that exoskeleton assistance has on muscle activation during leg swinging alone [1,32]. Therefore, by isolating and optimizing leg-swinging, we aim to develop more targeted and efficient control tuning that can later be integrated with stance phase optimization for full gait cycle assistance.

While EMG-based tuning frameworks exist, they often suffer from high signal noise, inconsistent optimization convergence, and lengthy calibration times. Our approach addresses these limitations by integrating a dynamic EMG processing pipeline with Bayesian optimization, enabling faster convergence, improved repeatability, and enhanced signal stability. In this work, we optimize the control parameters of a self-contained, semi-rigid hip exoskeleton with one degree of freedom (hip flexion and extension) to assist leg swinging at two distinct swing frequencies. Figure 1 provides an overview of our methods. The key contributions of this study are (1) the development of a novel EMG-based HIL optimization framework that combines Bayesian optimization with dynamic EMG processing, providing a robust and efficient approach to tuning assistance controllers across varying conditions; (2) a substantial reduction in tuning time, achieving optimization in as little as 15 s per condition—outperforming both metabolic cost-based approaches and previous EMG-based methods; and (3) validation of the optimized controllers, demonstrating significant reductions in muscle activity (EMG) compared to baseline conditions, confirming the effectiveness of the tuned controllers in enhancing assistance.

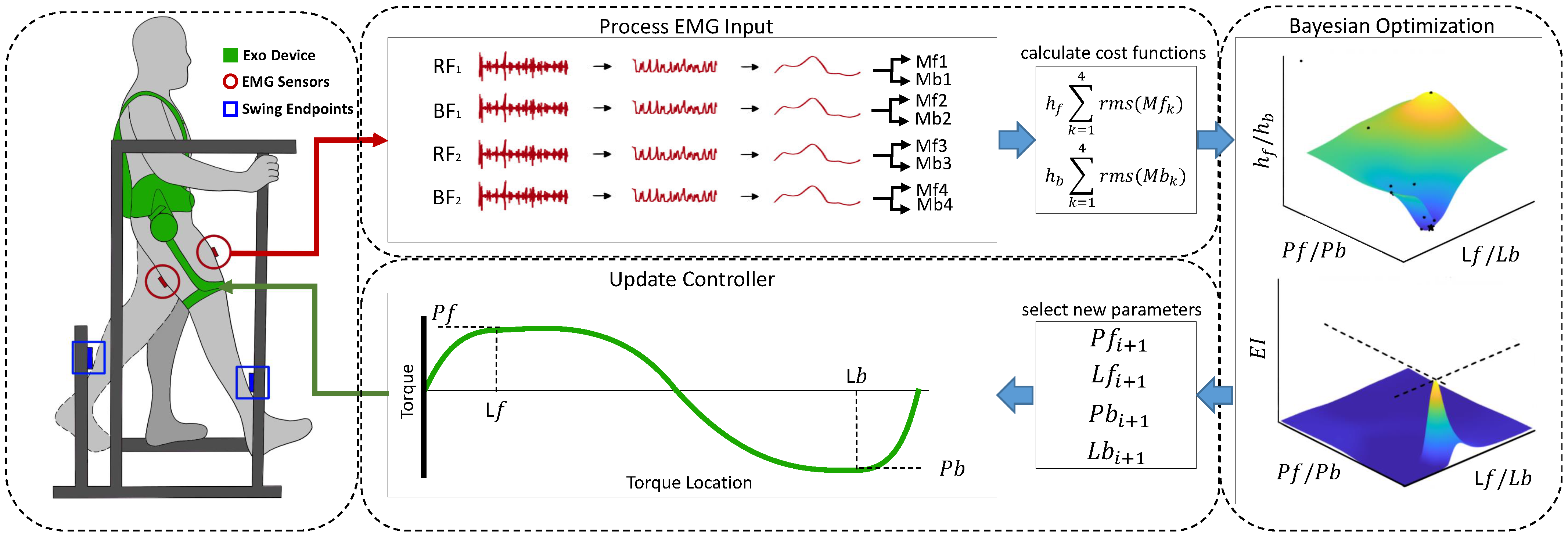
2. Materials and Methods

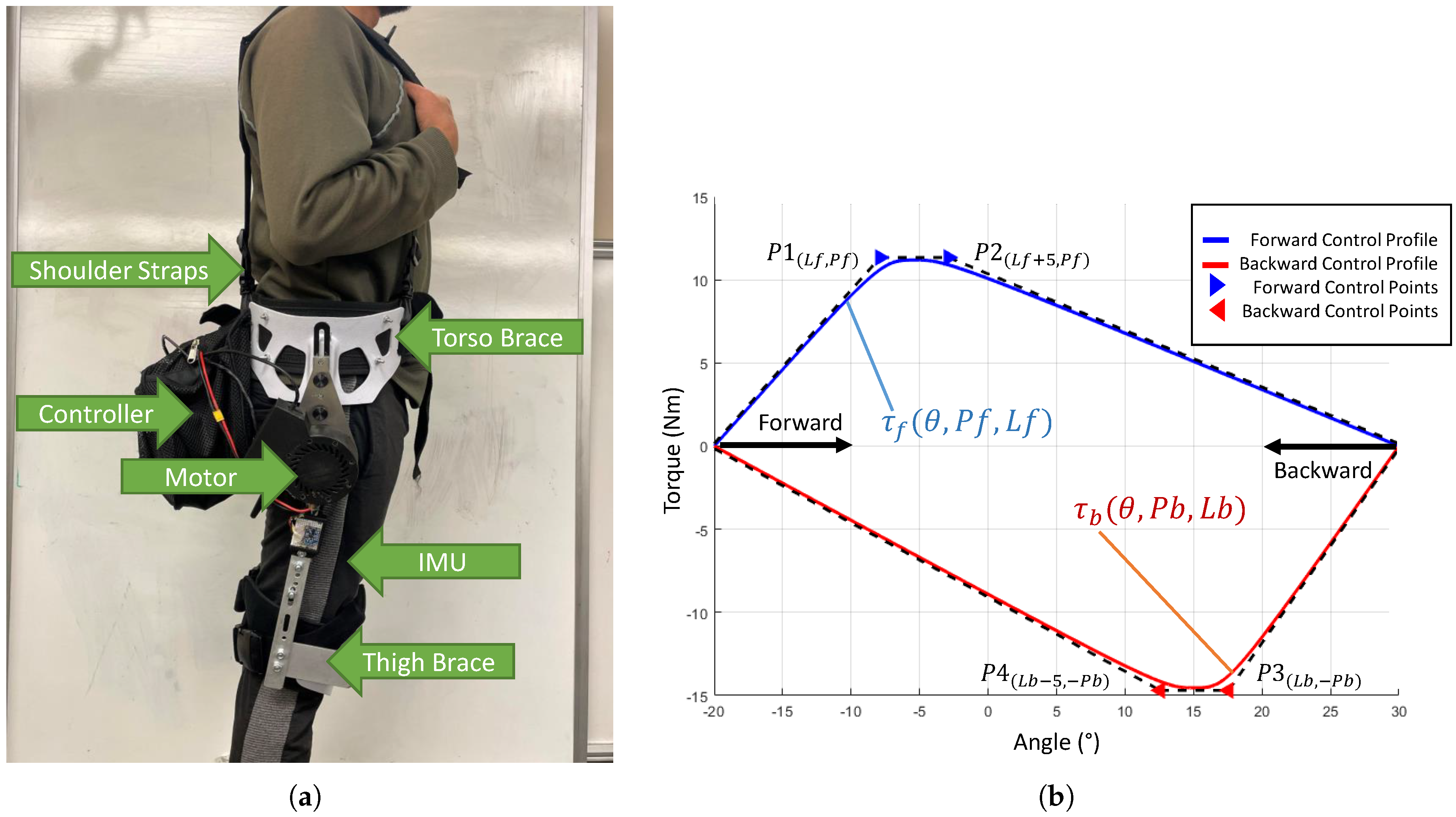
2.1. Hip Exoskeleton Device

A custom hip exoskeleton was used in this study to assist hip flexion and extension (Figure 2a). It features a 24 V brushless DC (BLDC) motor (AK70-10 T motor [CubeMars, Nanchang, Jiangxi Province, China]) capable of delivering a peak torque of 25 Nm and a nominal torque of 8 Nm. The exoskeleton is secured on the user by a series of straps (shoulder, leg, and belt) and minimal rigid components (plastic braces and aluminum links).The actuation is provided in a quasi-direct manner with an open-loop torque controller that allows backdriveability.

Preliminary tests comparing the motor encoder and an inertial measurement unit (IMU) (Adafruit BNO055 [Adafruit, Brooklyn, New York, NY, USA], close-loop triaxial 16-bit gyroscope, 100 Hz reading frequency) outputs under no-torque conditions showed negligible differences; however, under assistance, encoder readings were adversely affected by motor torque interacting with the user’s leg. We approximated hip orientation by measuring the thigh angle relative to the vertical using IMU-derived Euler angles, assuming an upright torso. The sensor is calibrated at initialization by defining the vertical as the zero position. The hip exoskeleton also contains elements to prevent injury and discomfort. These features include hard stops at the end of the range of motion, between −30° (extension/posterior) and 90° (flexion/anterior), to prevent over-extension beyond the comfortable range of motion of the human anatomy, two emergency stop buttons (one to stop the torque and the other to shut down the device), and integrated safety checks in the code to ensure the torque magnitude does not exceed 25 Nm.

The control operates on two levels: high-level control occurs within Python 3.9.2 on a Raspberry Pi 4 [Raspberry Pi Ltd., Pencoed, Wales]. This controller replicates torque shapes identified as effective in a prior study [33], employing cubic Bezier curves to define torque magnitude versus angle. These curves, comprising four points in a two-dimensional plane across the swing phase (Figure 2b), require eight inputs: location and magnitude coordinates for each point. The Bezier curves afford flexibility in torque profile shaping without explicit analytic definition.

In this study, the control inputs are further simplified by spacing control points 5° apart and equalizing their magnitudes, reducing the inputs from eight to four. This controller type has shown promising assistance profiles previously [33]. Leg swing control is divided into forward and backward directions, managed separately by a finite state machine (FSM). State transitions are initiated based on changes in angular velocity as detected by the IMU. To preserve natural swing dynamics, the controller is designed to apply only assistive torque that leads to positive work in either direction. Specifically, when the swing’s angular velocity is positive (i.e., in the anterior direction), the controller applies a strictly positive torque (also in the anterior direction); conversely, when the velocity is negative, it applies a strictly negative torque. The high-level control signals are updated and sent to the low-level motor controller with a set bandwidth of 100 Hz. The low-level motor control occurs at the motor, where high-level commands are transmitted via the CAN bus protocol to the integrated motor board at a frequency of 1 MHz.

2.2. EMG Data

2.2.1. Sensor Placement and MVC Determination

The surface EMG data were collected using Trigno sensors (Delsys, MA, USA), placed on the rectus femoris (RF) and biceps femoris (BF) of each leg at a sampling frequency of 1778 Hz. Additionally, the angle orientation data are collected from the same sensors at 148 Hz. These angle data are not used for real-time control but are collected solely for post-processing purposes to align the EMG data with orientation data during cost function development. To ensure consistency and comparability, the placement of sensors follow the standardized guidelines provided by the Surface Electromyography for the Non-Invasive Assessment of Muscles project [34]. Consistent sensor placement and MVC normalization play a crucial role in reducing inter-trial variability, ensuring that EMG-based cost functions remain stable throughout the optimization process. This step enhances the repeatability of the Bayesian optimization framework by minimizing fluctuations in signal intensity due to minor sensor misalignment, an issue commonly observed in prior EMG-based tuning methods. The RF MVC is measured during a seated knee extension against fixed resistance, and the biceps femoris MVC is assessed during a seated knee flexion. Each MVC trial lasts three seconds and is repeated two times, with rest intervals to prevent fatigue. The highest recorded value from these trials is used for normalization.

2.2.2. Signal Preprocessing

The EMG data from the four sensors are processed in MATLAB 2019b using a pipeline optimized for signal-to-noise ratio, as determined in a pilot study. To improve signal stability and reduce artifacts, we implement a multi-stage preprocessing pipeline that dynamically adapts to noise levels. Unlike previous EMG-based tuning methods that rely on fixed filtering parameters, our approach integrates outlier detection and adaptive interpolation. The first step involves band pass filtering the raw EMG signals between 20 Hz and 450 Hz to eliminate low-frequency noise and high-frequency interference.

Next, an outlier detection algorithm is applied to handle artifacts caused by motion or electrical interference. Extreme values exceeding three standard deviations from the mean are replaced using modified Akima cubic Hermite interpolation [35]. This step improves the reliability of the signal without distorting the physiological envelope, ensuring clean data for subsequent optimization (Figure 3a).

2.2.3. Signal Rectification and Dynamic Smoothing

After filtering and artifact removal, the EMG signals are rectified by taking the absolute value of the signal and subtracting the mean of the non-rectified values to account for any DC offset (Figure 3a). A three-step dynamic smoothing process is then applied:

• A moving max filter with a window size of up to 50 data points (less than 0.25% of the total dataset length) is used to highlight signal peaks.
• A discretization filter reduces the resolution of the data using bin sizes between 10 and 30.
• A moving average filter with a window size of up to 400 data points (∼1.6% of the dataset length) smooths the overall signal (Figure 3b).

These values are selected using an optimization process that maximizes the signal to noise ratio (SNR) of the EMG data. The calculation for SNR is determined by Equation (1).

After this, the signals are normalized by dividing each sensor’s output by its corresponding MVC value, allowing the four signals to be combined for further analysis (Figure 3b).

$$\mathrm{SNR}=10·{log}_{10}\left({\displaystyle \frac{P_{\mathrm{signal}}}{P_{\mathrm{noise}}}}\right)$$

(1)

2.2.4. Angle and Velocity Data Integration

The angle data collected from the sensors are linearly interpolated to match the frequency of the EMG data. These interpolated data are differentiated with respect to time to compute velocity. The velocity data are then used to split the EMG signals into forward and backward swing datasets (Figure 3c).

2.2.5. Epoching and Cost Function Calculation

The forward and backward swing datasets are segmented into epochs and averaged to create a single representative signal for each swing phase. This process is repeated for the EMG data collected from the four sensors (RF and BF of the swing and stance legs) under two different swing frequencies (slow and fast). As a result, eight distinct signals are produced: four sensors × two swing frequencies.

For subsequent analysis, these eight representations are used to calculate two cost functions: one for the forward swing and one for the backward swing. Each cost function is derived by summing the root mean squared (RMS) values of the four EMG signals relevant to that swing phase (Equation (2)).

$$h^d=\sum _{n=1}^4\mathrm{rms}\left(M_n^d\right)$$

(2)

Here, $d=f$ represents data associated with the forward direction, and $d=b$ represents data associated with the backward direction. The EMG data from the muscle models for the RF and BF of the swing leg, as well as the RF and BF of the stance leg, are represented as $M_1^d,M_2^d,M_3^d,M_4^d$, respectively. This process is applied to both slow-swing and fast-swing datasets.

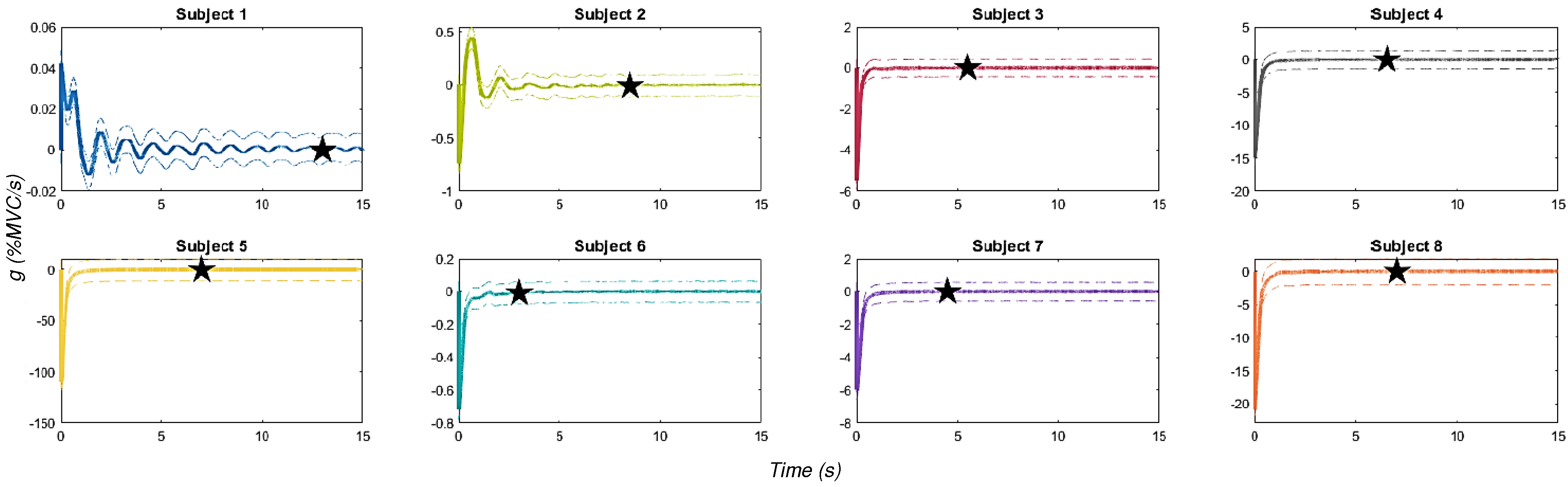
2.2.6. Data Convergence

To ensure the reliability of the EMG data for subsequent analysis, it was essential to determine when the signals reached a steady state. The steady state is defined as the point where the rate of change of the processed EMG signal became negligible, indicating consistent muscle activity over time.

The steady-state condition is analyzed by computing a running average of the EMG signal and monitoring the rate of change over successive time windows. Specifically,

• A running average ($R_i$) at time i is calculated for each sensor using the formula

  $$R_i={\displaystyle \frac{1}{i}}\sum _{j=1}^i{E}_j,$$

  (3)

  where $E_j$ represents the signal values at sample j.
• The rate of change ($g_i$) of the running average is computed using a forward difference method:

  $$g_i=\sum _{k=1}^4(R_{k,i+1}-R_{k,i}),$$

  (4)

  where $R_{k,i}$ denotes the running average of the k-th EMG signal at time i.
• These rates of change are aggregated into a single vector g. To analyze the stability of the signal, we segment this vector into windows using a partition method, with a window size w, based on a sampling frequency of 2 Hz. This frequency is chosen to balance refined detection (minimal lag) and an ample search window:

  $$B_i=\left[\begin{array}{cccc}{g}_{(i-1)w+1}& g_{(i-1)w+2}& \dots & g_{iw}\end{array}\right]$$

  (5)
• To identify the steady-state point, the rate of change is analyzed within overlapping time windows. Statistical methods, such as a two-sample z-test, are used to compare the mean rates of change between consecutive windows:

  $$H_0:\mu \left(B_i\right)=\mu \left(B_{i-1}\right),$$

  (6)

  where $B_i$ and $B_{i-1}$ represent the rate of change in the current and previous windows, respectively.
• A p-value of 0.95 is used to confirm no significant difference in the rates of change between consecutive windows. When this condition is met, the signal is considered to have reached a steady state.

The steady-state time is then determined to be the time at which this criterion is satisfied. The steady state is reached under 15 s for all participants, ensuring sufficient reliability for subsequent processing.

2.3. Experimental Protocol

A one-day protocol is conducted with eight healthy participants (age: 26.3 ± 3.2 years; weight: 64.6 ± 3.47 kg; height: 165.33 ± 11.13 cm, male: 5, female: 3). The subjects are asked to swing their right leg while their upper torso is supported by a custom rigid structure. The structure restricts the leg swing within a desired angle range (−20° to 30° from the vertical) using bumpers. Two swing frequencies, corresponding with normal walking frequencies [36], are tested (0.67 Hz and 0.83 Hz). These frequencies are encouraged via the use of a metronome, which provides the audible cue at which to make contact with each bumper. The participants are instructed to swing their leg at the beat of the metronome such that they make gentle contact with each bumper at each beat (Figure 1). To account for two contacts per swing, the metronome is played at twice the desired swing frequency. A work-to-rest ratio of 1:2 is kept consistent throughout the experiment to reduce the effects of fatigue.

The three-hour experiment consists of four main sections: acclimation, parameter optimization, and validation.

2.3.1. Acclimation

During the acclimation section, subjects are exposed to nine different parameter sets for each swing frequency. The parameter sets are selected using a Latin hypercube sampling (LHS) to provide an even distribution of the parameter space. Each parameter set is supplied for 30-s trials in clusters of three before allowing rest. This results in three slow-frequency clusters and three fast-frequency clusters, each followed by a rest period of 90 s. The main focus of this section is to allow participants to learn how to interact with the assistance provided by the device before tuning.

2.3.2. HIL Optimization

We utilize Bayesian optimization as a robust method to identify the optimal set of parameters when the objective function is noisy and expensive to evaluate. This approach involves constructing a probabilistic surrogate model of the objective function that combines prior assumptions about the function with observed data (posterior updates). The surrogate model predicts the objective function’s behavior and incorporates uncertainty, allowing efficient exploration and exploitation of the search space. By leveraging this surrogate model, Bayesian optimization predicts outcomes for different parameter settings and selects the next parameter to evaluate using an acquisition function that balances exploration (trying new settings) and exploitation (utilizing the best-known settings) [31].

In this study, the surrogate model used is a Gaussian process (GP), a versatile non-parametric approach for modeling distributions over functions. A GP is characterized by a mean function, which represents the expected value of the function, and a covariance function (or kernel), which captures the relationships and dependencies between input points in the parameter space. For simplicity, the prior mean function is assumed to be zero, implying no strong prior belief about the function’s values before observing data. The covariance function used in this study is the automatic relevance determination (ARD) squared exponential kernel, which encodes the similarity between points based on their distance while adjusting for the varying importance of each dimension in the input space. The acquisition function employed is the expected improvement (EI) function, which quantifies the potential improvement of the objective function over the best-known value. This function strategically selects the next parameter set to evaluate by maximizing the trade-off between exploration (favoring uncertain areas) and exploitation (favoring areas with high predicted values).

The human-in-the-loop Bayesian optimization procedure involves a maximum of 12 trials for each swing frequency, each lasting 15 s. Both swing frequencies are optimized concurrently within the same run, with the slower frequency sampled first, followed by a 10-s rest period and then the faster frequency.

The initial four trials are initialization trials that sample the parameter space to establish a baseline before the Bayesian optimization begins selecting new parameter sets. The optimization is conducted for up to eight trials, tuning two parameters for both forward and backward swing controllers simultaneously. This results in two controllers being tuned, each with two phases (forward and backward) for both slow and fast frequencies.

Convergence is defined as the same parameter set producing the best-performing controller three times within an allowable variation of ±10%. If convergence is not achieved within the maximum number of iterations, the experiment continues until all parameter sets converge. The optimal controller is determined as the best-performing parameter set estimated by the Bayesian algorithm.

2.3.3. Validation

Following the identification of the optimal parameter set, its performance is evaluated against three baselines:

• No exoskeleton (NE), where the subject performs free swinging.
• Zero actuation (ZA), where the subject wears the device but it remains unpowered.
• General control (GC), where the subject receives assistance from a predefined intuition controller supplying a magnitude of torque equivalent to the mean of the possible torque values at the beginning of each half swing.

The performance of the optimal and baseline conditions for each swing frequency is tested three times. During each iteration, a performance metric equivalent to the cost function (Equation (2)) is calculated.

$$\%\mathrm{\Delta }=100\left({\displaystyle \frac{{\mu }_{\mathrm{optimal}}-{\mu }_{\mathrm{baseline}}}{{\mu }_{\mathrm{baseline}}}}\right)$$

(7)

Each condition is represented by the mean value of the three observations. The percent change between the optimal mean (${\mu }_{\mathrm{optimal}}$) and the mean of each baseline (${\mu }_{\mathrm{baseline}}$) is then calculated (Equation (7)).

Data collection and processing for each trial follow the same protocol as the tuning trials. Any outliers in the data are identified and replaced with the center value of the data if they deviate by more than three standard deviations from the mean.

The statistical analysis between two conditions is paired. Since the data from most conditions are not normally distributed (Shapiro–Wilk test, p < 0.05), a non-parametric Wilcoxon test is used to assess the statistical significance of the comparison [37]. The null hypothesis assumes that the average percent change between the optimal and a particular baseline is zero, with a significance level of p < 0.05.

Additionally, each subject’s perceived effort is rated according to Borg’s scale. While subjective, the Borg scale has been shown to correlate well with physiological measures such as heart rate, lactate levels, and oxygen consumption. This makes it a reliable complement to the EMG objective measurements in assessing the effectiveness and impact of the exoskeleton [38].

3. Results

This section presents the experimental outcomes, including steady-state signal behavior, optimal controller performance compared to baseline conditions, subjective effort perceptions (via the Borg scale), and optimization process efficiency. Collectively, these results validate the effectiveness of the proposed Bayesian optimization framework in improving EMG-based cost function performance.

To ensure the reliability of the EMG data, the steady-state behavior was analyzed. Figure 4 illustrates the steady-state time average for each subject, demonstrating that the rate of change of a running average of the summed EMG data consistently converges within 15 s across all trials. This result confirms the stability of the EMG signal during the experimental conditions.

The optimal controller (OP) outperformed all baseline conditions on average (Figure 5). For the slow swing, OP reduced muscle activity by 15.2% (p $<{10}^{-7}$) compared to the no device condition and by 19.7% (p $<{10}^{-4}$) compared to the zero torque condition. Additionally, the OP reduced muscle activity by 14.5% (p $<{10}^{-4}$) compared to the general controller. For the fast swing, OP significantly reduced muscle activity compared to the no device and zero torque conditions by 17.0% (p $<{10}^{-4}$) and 23.6% (p $<{10}^{-4}$), respectively, and by 15.6% (p = 0.0015) compared to the fast swing general controller. The optimal controller profiles for all subjects are shown in Figure 6.

In terms of Borg scale values, the optimal controller is perceived to lower effort compared to most baselines. The percent change in mean Borg values between the optimal and each baseline condition is shown in

Table 1. Borg value comparison against baselines for validation.

Baseline	Opt. Slow (% Change)	Opt. Fast (% Change)
No Device	−26.0%	−14.4%
Zero Assistance	−39.5%	−26.8%
General Control	−18.5%	4.9%

, calculated using Equation (7).

The Bayesian optimization framework identified a preferred parameter set within an average of 9.5 trials (SD = 1.87). Early stop conditions were met for seven of the eight subjects, confirming the efficiency of the optimization process. For the remaining subject, all but one parameter (Lb) converged, suggesting a strong but incomplete preference by the acquisition function. Figure 7 illustrates optimization landscapes for a sample subject, highlighting the parameter tuning process.

4. Discussion

The optimization process demonstrates a strong ability to tune quickly and effectively, resulting in a significant reduction in muscle activity compared to all baselines. This outcome establishes the importance of tuning, as the optimal controller outperformed arbitrary assistance. The reduction in muscle activity is very likely attributed to the proper timing provided by the controller, which reduces the load on these muscles during critical phases of the leg swing. By delivering targeted assistance, the controller minimizes the energy required for muscle contraction, improving efficiency and reducing fatigue. These results highlight the necessity of fine-tuning controllers for individual users to achieve maximal benefit, especially in tasks involving repetitive motion.

The use of EMG data for tuning further validates its role as an effective and rapid alternative to metabolic cost, particularly given the challenges of metabolic measurements in real-time applications. The study’s ability to achieve tuning in as little as 15 s, compared to 60 s with traditional metabolic-cost-based methods, represents a significant advancement in human-in-the-loop optimization [18]. The reduced tuning time is particularly important in clinical or real-world settings, where prolonged optimization sessions can lead to user discomfort or fatigue.

Unlike previous EMG-based tuning frameworks [39], which often require extensive calibration and may struggle with signal stability, our method integrates a refined EMG preprocessing pipeline with Bayesian optimization to enhance repeatability and efficiency. By dynamically processing EMG signals into a cost function and leveraging Gaussian processes, we achieve robust optimization within an average of 142 s—substantially faster than traditional EMG-based tuning approaches, which typically require close to twice as long signal averaging periods or more iterative fine-tuning. This novel framework accelerates tuning and also ensures more reliable controller adaptation across different conditions.

The Borg scale results add another layer of validation to the optimization process by reflecting subjective user experience. The noticeable reduction in perceived effort (Table 1) show that the assistance from the optimal controller provided a noticeable aid while swinging aligns with the objective EMG data. This reinforces the conclusion that the optimized controller provides effective assistance. The significant decrease in perceived effort compared to baseline conditions suggests that users benefit not only physiologically but also experientially from the tuned exoskeleton assistance. These results emphasize the importance of optimizing assistive devices for both performance and comfort, as user satisfaction plays a crucial role in the long-term adoption of wearable technology.

Despite the promising results, limitations should be noted. The reliance on EMG as the sole physiological metric introduces potential variability due to factors such as signal noise and electrode placement. Although the data processing methods effectively mitigate some of these issues, the inherent noisiness of EMG signals suggests that future work should incorporate additional validation metrics to cross-check the findings. Furthermore, investigating the long-term effectiveness of the optimal controller was not addressed in this study. While this study focuses on stationary leg swinging, more dynamic activities such as walking, running, or squatting should be explored to fully understand the exoskeleton’s capabilities in more demanding real-world applications. Investigating how these findings translate to full movement cycle optimization would be an important step toward developing more comprehensive assistive devices. Moreover, the size of the subject pool restricts the generalizability of the results, as individual variations in muscle response and gait patterns could influence the outcomes. A larger, more diverse sample size would allow for more robust conclusions and better correlation analysis.

While the use of an IMU was necessary to overcome encoder instability due to mechanical backlash and compliance, it limits the control frequency to 100 Hz. This trade-off constitutes a notable limitation, especially for more dynamic activities, that warrants further investigation.

5. Conclusions

This study presents an EMG-based Bayesian optimization framework that significantly enhances the speed and reliability of exoskeleton controller tuning. Unlike prior EMG-based tuning methods, our approach integrates a dynamic EMG processing pipeline with Bayesian optimization, enabling faster convergence, improved signal stability, and reduced calibration times. The results demonstrate that optimization can be achieved in as little as 15 s per condition, substantially outperforming traditional metabolic-cost-based approaches and previous EMG-based methods.

Beyond methodological advancements, this work has practical implications for real-time exoskeleton control, particularly in applications requiring adaptive assistance strategies. The efficiency of this tuning framework makes it suitable for clinical rehabilitation settings, assistive robotics, and personalized exoskeleton control, where rapid adaptation is crucial for user comfort and performance.

Future work will explore extending this optimization approach to dynamic locomotion tasks, such as walking and running, to assess its effectiveness beyond stationary leg swinging. Additionally, integrating additional physiological metrics, such as joint torque or metabolic cost estimation, may further enhance the robustness of the optimization process. Investigating the long-term adaptability of optimized controllers over extended use will also be an important next step toward real-world implementation.

By refining and validating rapid EMG-based optimization, this study contributes to the broader goal of developing intelligent, user-adaptive exoskeletons that improve human mobility with minimal manual intervention.