Machine Learning for Modeling Wildfire Susceptibility at the State Level: An Example from Arkansas, USA
Abstract
1. Introduction
2. Materials and Methods
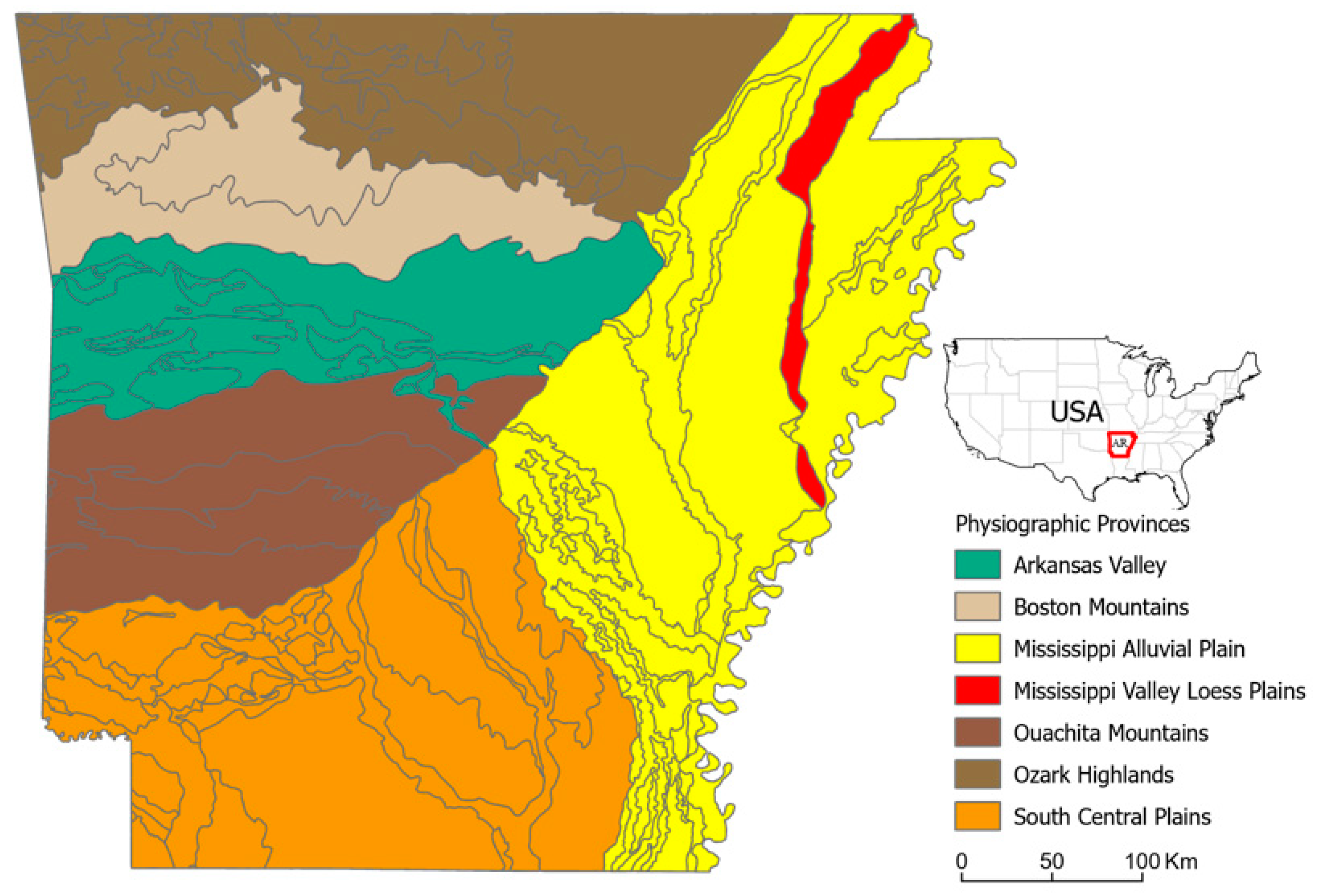
2.1. Study Area
2.2. Data Acquisition and Processing
2.3. OLS and GWR Analyses
2.4. RF Classification
3. Results and Discussions
3.1. OLS and GWR Outputs
3.2. RF Outputs
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chuvieco, E.; Aguado, I.; Dimitrakopoulos, A.P. Conversion of fuel moisture content values to ignition potential for integrated fire danger assessment. Can. J. For. Res. 2004, 34, 2284–2293. [Google Scholar] [CrossRef]
- Dickson, B.G.; Prather, J.W.; Xu, Y.; Hampton, H.M.; Aumack, E.N.; Sisk, T.D. Mapping the probability of large fire occurrence in northern Arizona, USA. Landsc. Ecol. 2006, 21, 747–761. [Google Scholar] [CrossRef]
- Dlamini, W.M. A Bayesian belief network analysis of factors influencing wildfire occurrence in Swaziland. Environ. Model. Softw. 2010, 25, 199–208. [Google Scholar] [CrossRef]
- Eugenio, F.C.; dos Santos, A.R.; Fiedler, N.C.; Ribeiro, G.A.; da Silva, A.G.; dos Santos, Á.B.; Paneto, G.G.; Schettino, V.R. Applying GIS to develop a model for forest fire risk: A case study in Espírito Santo, Brazil. J. Environ. Manag. 2016, 173, 65–71. [Google Scholar] [CrossRef]
- Hong, H.; Jaafari, A.; Zenner, E.K. Predicting spatial patterns of wildfire susceptibility in the Huichang County, China: An integrated model to analysis of landscape indicators. Ecol. Indic. 2019, 101, 878–891. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Beheshtirad, M.; Pradhan, B. A comparative assessment of prediction capabilities of modified analytical hierarchy process (M-AHP) and Mamdani fuzzy logic models using Netcad-GIS for forest fire susceptibility mapping. Geomat. Nat. Hazards Risk 2016, 7, 861–885. [Google Scholar] [CrossRef]
- Chang, Z.; Du, Z.; Zhang, F.; Huang, F.; Chen, J.; Li, W.; Guo, Z. Landslide Susceptibility Prediction Based on Remote Sensing Images and GIS: Comparisons of Supervised and Unsupervised Machine Learning Models. Remote Sens. 2020, 12, 502. [Google Scholar] [CrossRef]
- Wang, Z.; Lai, C.; Chen, X.; Yang, B.; Zhao, S.; Bai, X. Flood hazard risk assessment model based on random forest. J. Hydrol. 2015, 527, 1130–1141. [Google Scholar] [CrossRef]
- Rouet-Leduc, B.; Hulbert, C.; Lubbers, N.; Barros, K.; Humphreys, C.J.; Johnson, P.A. Machine Learning Predicts Laboratory Earthquakes. Geophys. Res. Lett. 2017, 44, 9276–9282. [Google Scholar] [CrossRef]
- Taalab, K.; Cheng, T.; Zhang, Y. Mapping landslide susceptibility and types using Random Forest. Big Earth Data 2018, 2, 159–178. [Google Scholar] [CrossRef]
- Park, H.; Kim, K.; Lee, D.K. Prediction of Severe Drought Area Based on Random Forest: Using Satellite Image and Topography Data. Water 2019, 11, 705. [Google Scholar] [CrossRef]
- Jaafari, A.; Pourghasemi, H.R. Factors influencing regional-scale wildfire probability in Iran: An application of random forest and support vector machine. In Spatial Modeling in GIS and R for Earth and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2019; pp. 607–619. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Gholamnia, K.; Gudiyangada Nachappa, T.; Ghorbanzadeh, O.; Blaschke, T. Comparisons of Diverse Machine Learning Approaches for Wildfire Susceptibility Mapping. Symmetry 2020, 12, 604. [Google Scholar] [CrossRef]
- McKenzie, D.; Peterson, D.L.; Agee, J.K. Fire Frequency in the Interior Columbia River Basin: Building Regional Models from Fire History Data. Ecol. Appl. 2000, 10, 1497–1516. [Google Scholar] [CrossRef]
- Amatulli, G.; Rodrigues, M.J.; Trombetti, M.; Lovreglio, R. Assessing Long-Term Fire Risk at Local Scale by Means of Decision Tree Technique. J. Geophys. Res Biogeosci. 2006, 111. [Google Scholar] [CrossRef]
- Lozano, F.J.; Suárez-Seoane, S.; Kelly, M.; Luis, E. A Multi-Scale Approach for Modeling Fire Occurrence Probability Using Satellite Data and Classification Trees: A Case Study in a Mountainous Mediterranean Region. Remote. Sens. Environ. 2008, 112, 708–719. [Google Scholar] [CrossRef]
- Oliveira, S.; Oehler, F.; San-Miguel-Ayanz, J.; Camia, A.; Pereira, J.M.C. Modeling spatial patterns of fire occurrence in Mediterranean Europe using Multiple Regression and Random Forest. For. Ecol. Manag. 2012, 275, 117–129. [Google Scholar] [CrossRef]
- Rodrigues, M.; de la Riva, J. An insight into machine-learning algorithms to model human-caused wildfire occurrence. Environ. Model. Softw. 2014, 57, 192–201. [Google Scholar] [CrossRef]
- Song, C.; Kwan, M.-P.; Song, W.; Zhu, J. A Comparison between Spatial Econometric Models and Random Forest for Modeling Fire Occurrence. Sustainability 2017, 9, 819. [Google Scholar] [CrossRef]
- Ouedraogo, I.; Defourny, P.; Vanclooster, M. Application of random forest regression and comparison of its performance to multiple linear regression in modeling groundwater nitrate concentration at the African continent scale. Appl. Hydrogeol. 2018, 27, 1081–1098. [Google Scholar] [CrossRef]
- Chowdhury, E.H.; Hassan, Q.K. Use of Remote Sensing-Derived Variables in Developing a Forest Fire Danger Forecasting System. Nat. Hazards 2013, 67, 321–334. [Google Scholar] [CrossRef]
- Aldersley, A.; Murray, S.J.; Cornell, S. Global and regional analysis of climate and human drivers of wildfire. Sci. Total Environ. 2011, 409, 3472–3481. [Google Scholar] [CrossRef]
- Parisien, M.-A.; Snetsinger, S.; Greenberg, J.; Nelson, C.R.; Schoennagel, T.; Dobrowski, S.; Moritz, M.A. Spatial variability in wildfire probability across the western United States. Int. J. Wildland Fire 2012, 21, 313–327. [Google Scholar] [CrossRef]
- Rodrigues, M.; Jiménez-Ruano, A.; Peña-Angulo, D.; de la Riva, J. A comprehensive spatial-temporal analysis of driving factors of human-caused wildfires in Spain using Geographically Weighted Logistic Regression. J. Environ. Manag. 2018, 225, 177–192. [Google Scholar] [CrossRef]
- Syphard, A.D.; Radeloff, V.C.; Keuler, N.S.; Taylor, R.S.; Hawbaker, T.; Stewart, S.I.; Clayton, M.K. Predicting spatial patterns of fire on a southern California landscape. Int. J. Wildland Fire 2008, 17, 602–613. [Google Scholar] [CrossRef]
- Yang, J.; Weisberg, P.J.; Dilts, T.E.; Loudermilk, E.L.; Scheller, R.M.; Stanton, A.; Skinner, C. Predicting wildfire occurrence distribution with spatial point process models and its uncertainty assessment: A case study in the Lake Tahoe Basin, USA. Int. J. Wildland Fire 2015, 24, 380–390. [Google Scholar] [CrossRef]
- Carlson, J.D.; Burgan, R.E.; Engle, D.M.; Greenfield, J.R. The Oklahoma Fire Danger Model: An operational tool for mesoscale fire danger rating in Oklahoma. Int. J. Wildland Fire 2002, 11, 183–191. [Google Scholar] [CrossRef]
- Reid, A.M.; Fuhlendorf, S.D.; Weir, J.R. Weather Variables Affecting Oklahoma Wildfires. Rangel. Ecol. Manag. 2010, 63, 599–603. [Google Scholar] [CrossRef]
- Weir, J.R.; Reid, A.M.; Fuhlendorf, S.D. Wildfires in Oklahoma; Oklahoma State University: Stillwater, OK, USA, 2012. [Google Scholar]
- Gorte, R.; Economics, H. The Rising Cost of Wildfire Protection. 2013. Available online: https://www.baileyhealthyforests.org/wp-content/uploads/2013/12/fire-costs-background-report.pdf (accessed on 27 January 2022).
- Balch, J.K.; Schoennagel, T.; Williams, A.P.; Abatzoglou, J.T.; Cattau, M.E.; Mietkiewicz, N.P.; St Denis, L.A. Switching on the Big Burn of 2017. Fire 2018, 1, 17. [Google Scholar] [CrossRef]
- Arpaci, A.; Malowerschnig, B.; Sass, O.; Vacik, H. Using multi variate data mining techniques for estimating fire susceptibility of Tyrolean forests. Appl. Geogr. 2014, 53, 258–270. [Google Scholar] [CrossRef]
- Nowak, D.J.; Greenfield, E.J. US Urban Forest Statistics, Values, and Projections. J. For. 2018, 116, 164–177. [Google Scholar] [CrossRef]
- Hodgdon, B.; Tyrrell, M. Literature review: An annotated bibliography on family forest owners. In GISF Research Paper, 2; Yale University: New Haven, CT, USA, 2003. [Google Scholar]
- Clutter, M.; Mendell, B.; Newman, D.; Wear, D.; Greis, J. Strategic Factors Driving Timberland Ownership Changes in the US South; United States Department of Agriculture: Washington, DC, USA, 2003. [Google Scholar]
- Pelkki, M.H. An Economic Assessment of Arkansas’ Forest Industries: Challenges and Opportunities for the 21st Century; Arkansas Agricultural Experiment Station: Fayetteville, AR, USA, 2005. [Google Scholar]
- He, W.; Goodkind, D.; Kowal, P. International Population Reports. In An Aging World: 2015; US Census Bureau: Suitland, MD, USA, 2016. [Google Scholar]
- Rowden, K.W.; Aly, M.H. GIS-based regression modeling of the extreme weather patterns in Arkansas, USA. Geoenviron. Disasters 2018, 5, 6. [Google Scholar] [CrossRef][Green Version]
- Thornton, P.E.; Thornton, M.M.; Mayer, B.W.; Wilhelmi, N.; Wei, Y.; Devarakonda, R.; Cook, R.B. Daymet: Annual Climate Summaries on a 1-km Grid for North America, 2nd ed.; ORNL DAAC: Oak Ridge, TN, USA, 2018.
- Stephenson, N. Actual evapotranspiration and deficit: Biologically meaningful correlates of vegetation distribution across spatial scales. J. Biogeogr. 1998, 25, 855–870. [Google Scholar] [CrossRef]
- Littell, J.S.; McKenzie, D.; Peterson, D.L.; Westerling, A.L. Climate and wildfire area burned in western US ecoprovinces, 1916–2003. Ecol. Appl. 2009, 19, 1003–1021. [Google Scholar] [CrossRef]
- Miller, J.D.; Skinner, C.N.; Safford, H.D.; Knapp, E.E.; Ramirez, C.M. Trends and causes of severity, size, and number of fires in northwestern California, USA. Ecol. Appl. 2012, 22, 184–203. [Google Scholar] [CrossRef]
- Miller, C.; Plucinski, M.; Sullivan, A.; Stephenson, A.; Huston, C.; Charman, K.; Prakash, M.; Dunstall, S. Electrically caused wildfires in Victoria, Australia are over-represented when fire danger is elevated. Landsc. Urban Plan. 2017, 167, 267–274. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis, 5th ed.; John Wiley & Sons: Chicester, UK, 2013; Available online: http://uark.summon.serialssolutions.com/2.0.0/link/0/eLvHCXMwdV3PS8MwFH7M7TLxoNPhr0nPQkvbrPlxGsxt3YRexPtIm9SDUGGrsD_fl6RxIPMYEhISkpfvJd_7HgBJozj8YxNqKtOSS1HHVVWJWnJeJmg0p0okQiurq50XZLlgr2u66EHhQ2Psj2FHU4y8rTz-pcrdZ2ib7DvGZeSiAWbKAVz0bvAQnaFLFmd9GMw3-Tz3uw09i5SKI1hIEFhwTqlNJ5Qg0GeEik4UypczQ5WWNoWLv4JWlzDQJi7hCnq6GcF58Su3uh_B0EBGp7h8Dc8bQz5XThU2aL8CdDdxOwdv-sNxXpvAK5HcwGS1fH9Zh2a0bfeSsy2JwOkQcSBjuJCGAd-0NlJO3ULApLY3TYKYblqzWKisrDJOpBZMpZLfwfh0Z_f_VTzAMLXJH8yDwyP02923nrgFeOoW8wfsm4i3 (accessed on 27 January 2022).
- Gösset, W.S. The probable error of a mean. Biometrika 1908, 6, 1–25. [Google Scholar]
- Brunsdon, C.; Aitkin, M.; Fotheringham, S.; Charlton, M. A comparison of random coefficient modelling and geographically weighted regression for spatially non-stationary regression problems. Geogr. Environ. Model. 1999, 3, 47–62. [Google Scholar]
- Páez, A.; Uchida, T.; Miyamoto, K. A general framework for estimation and inference of geographically weighted regression models: 1. Location-specific kernel bandwidths and a test for locational heterogeneity. Environ. Plan. A 2002, 34, 733–754. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Hanham, R.; Spiker, J.S. Urban sprawl detection using satellite imagery and geographically weighted regression. In Geo-Spatial Technologies in Urban Environments; Springer: Berlin/Heidelberg, Germany, 2005; pp. 137–151. [Google Scholar]
- Zhang, L.; Bi, H.; Cheng, P.; Davis, C.J. Modeling spatial variation in tree diameter–height relationships. For. Ecol. Manag. 2004, 189, 317–329. [Google Scholar] [CrossRef]
- Petter, S.; Straub, D.; Rai, A. Specifying Formative Constructs in Information Systems Research. MIS Q. 2007, 31, 623–656. [Google Scholar] [CrossRef]
- Cenfetelli, R.T.; Bassellier, G. Interpretation of formative measurement in information systems research. MIS Q. 2009, 33, 689–707. [Google Scholar] [CrossRef]
- Hair, J.F. Multivariate Data Analysis; Prentice Hall: Hoboken, NJ, USA, 2009. [Google Scholar]
- Kline, R.B. Principles and Practice of Structural Equation Modeling; Guilford Publications: New York, NY, USA, 2015. [Google Scholar]
- Kane, V.R.; Cansler, C.A.; Povak, N.; Kane, J.T.; McGaughey, R.J.; Lutz, J.; Churchill, D.J.; North, M.P. Mixed severity fire effects within the Rim fire: Relative importance of local climate, fire weather, topography, and forest structure. For. Ecol. Manag. 2015, 358, 62–79. [Google Scholar] [CrossRef]
- Dimitrakopoulos, A.P.; Mitsopoulos, I.D.; Gatoulas, K. Assessing ignition probability and moisture of extinction in a Mediterranean grass fuel. Int. J. Wildland Fire 2010, 19, 29–34. [Google Scholar] [CrossRef]
- Abatzoglou, J.T.; Kolden, C.A. Relationships between climate and macroscale area burned in the western United States. Int. J. Wildland Fire 2013, 22, 1003–1020. [Google Scholar] [CrossRef]
- Bartsch, A.; Balzter, H.; George, C. The influence of regional surface soil moisture anomalies on forest fires in Siberia observed from satellites. Environ. Res. Lett. 2009, 4, 045021. [Google Scholar] [CrossRef]
- Collins, B.M.; Omi, P.N.; Chapman, P.L. Regional relationships between climate and wildfire-burned area in the Interior West, USA. Can. J. For. Res. 2006, 36, 699–709. [Google Scholar] [CrossRef]
- Drever, C.R.; Drever, M.C.; Messier, C.; Bergeron, Y.; Flannigan, M. Fire and the relative roles of weather, climate and landscape characteristics in the Great Lakes-St. Lawrence forest of Canada. J. Veg. Sci. 2008, 19, 57–66. [Google Scholar] [CrossRef]





| Variable | Coefficient | StdError | t-Statistic | Probability | Robust_SE | Robust_t | Robust_Pr | VIF |
|---|---|---|---|---|---|---|---|---|
| Intercept | −10.14432 | 1.357473 | −7.472948 | 0.0000 * | 1.226492 | −8.271007 | 0.0000 * | …….. |
| Slope | 0.082004 | 0.028799 | 2.847436 | 0.0044 * | 0.028678 | 2.859514 | 0.0043 * | 2.8997 |
| SM | −0.016795 | 0.001446 | −11.61456 | 0.0000 * | 0.001380 | −12.17155 | 0.0000 * | 5.5536 |
| DEL | −0.000018 | 0.000004 | −4.012207 | 0.0001 * | 0.000004 | −4.424301 | 0.0000 * | 1.3836 |
| PCP | 0.044053 | 0.002921 | 15.08416 | 0.0000 * | 0.003131 | 14.070245 | 0.0000 * | 4.5952 |
| CA | −0.000002 | 0.000000 | −5.89363 | 0.0000 * | 0.000000 | −5.629685 | 0.0000 * | 2.3833 |
| Tmax | 0.347790 | 0.061850 | 5.623101 | 0.0000 * | 0.055513 | 6.264970 | 0.0000 * | 5.1519 |
| PET | −0.368855 | 0.047081 | −7.83445 | 0.0000 * | 0.043862 | −8.409510 | 0.0000 * | 5.7289 |
| DEF | 0.672038 | 0.063530 | 10.57824 | 0.0000 * | 0.064860 | 10.361411 | 0.0000 * | 1.9731 |
| PDSI | 0.381437 | 0.105376 | 3.619785 | 0.0003 * | 0.108099 | 3.528603 | 0.0004 * | 2.9396 |
| RLD | 0.018232 | 0.001874 | −9.73089 | 0.0000 * | 0.002036 | −8.956737 | 0.0000 * | 2.1991 |
| POH | 0.000042 | 0.000002 | 20.82940 | 0.0000 * | 0.000002 | 19.82122 | 0.0000 * | 2.3023 |
| POT | 0.000054 | 0.000003 | 16.68192 | 0.0000 * | 0.000003 | 16.33329 | 0.0000 * | 7.4380 |
| POS | 0.000020 | 0.000005 | 3.657684 | 0.0003 * | 0.000005 | 4.250684 | 0.0000 * | 2.0090 |
| WUI | 0.000040 | 0.000006 | 7.108861 | 0.0000 * | 0.000006 | 6.419036 | 0.0000 * | 2.3549 |
| POB | 0.000058 | 0.000026 | 2.251220 | 0.0244 * | 0.000011 | 5.354982 | 0.0000 * | 1.0427 |
| OLS Results | GWR Results | ||
|---|---|---|---|
| Adjusted R-squared | 0.505702 | Adjusted R-squared | 0.8703 |
| Joint Wald Statistic | 2888.262 | Multiple R-squared | 0.8941 |
| Koenker (BP) Statistic | 120.5529 | Sigma-Squared | 0.3408 |
| Jarque–Bera Statistic | 72.17902 | Sigma-Squared MLE | 0.2783 |
| Akaike Information Criterion | 8572.895 | Akaike Information Criterion | 5171.2 |
| Variable | Importance | % |
|---|---|---|
| PET | 4,497,387.15 | 22 |
| SM | 3,508,886.60 | 17 |
| PDSI | 2,466,707.62 | 12 |
| PCP | 2,082,161.71 | 10 |
| POS | 1,830,527.78 | 9 |
| CA | 1,689,034.18 | 8 |
| Slope | 1,023,721.58 | 5 |
| POH | 841,701.740 | 4 |
| Tmax | 754,822.330 | 4 |
| POT | 690,317.750 | 3 |
| RLD | 417,814.530 | 2 |
| WUI | 255,724.120 | 1 |
| DEL | 216,439.310 | 1 |
| POB | 188,394.610 | 1 |
| DEF | 53,002.1900 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saim, A.A.; Aly, M.H. Machine Learning for Modeling Wildfire Susceptibility at the State Level: An Example from Arkansas, USA. Geographies 2022, 2, 31-47. https://doi.org/10.3390/geographies2010004
Saim AA, Aly MH. Machine Learning for Modeling Wildfire Susceptibility at the State Level: An Example from Arkansas, USA. Geographies. 2022; 2(1):31-47. https://doi.org/10.3390/geographies2010004
Chicago/Turabian StyleSaim, Abdullah Al, and Mohamed H. Aly. 2022. "Machine Learning for Modeling Wildfire Susceptibility at the State Level: An Example from Arkansas, USA" Geographies 2, no. 1: 31-47. https://doi.org/10.3390/geographies2010004
APA StyleSaim, A. A., & Aly, M. H. (2022). Machine Learning for Modeling Wildfire Susceptibility at the State Level: An Example from Arkansas, USA. Geographies, 2(1), 31-47. https://doi.org/10.3390/geographies2010004





