Seasonal, Decadal, and El Niño-Southern Oscillation-Related Trends and Anomalies in Rainfall and Dry Spells during the Agricultural Season in Central Malawi
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Locations
2.2. Rainfall Data
3. Methods
3.1. Rainfall Indices
3.2. Statistical and Trend Analysis
4. Results
4.1. Variability and Trend Analysis of Rainfall and Dry Spell Events
4.1.1. Wet Events
4.1.2. Dry Events
4.1.3. Onset, End and Length of the Growing Season
4.2. Seasonal Rainfall Departures
4.3. Decadal Epochs of Rainfall
4.4. ENSO-Induced Rainfall Anomalies
Relationship between ENSO Events and Extreme Rainfall Events
5. Discussion
5.1. Seasonal Rainfall
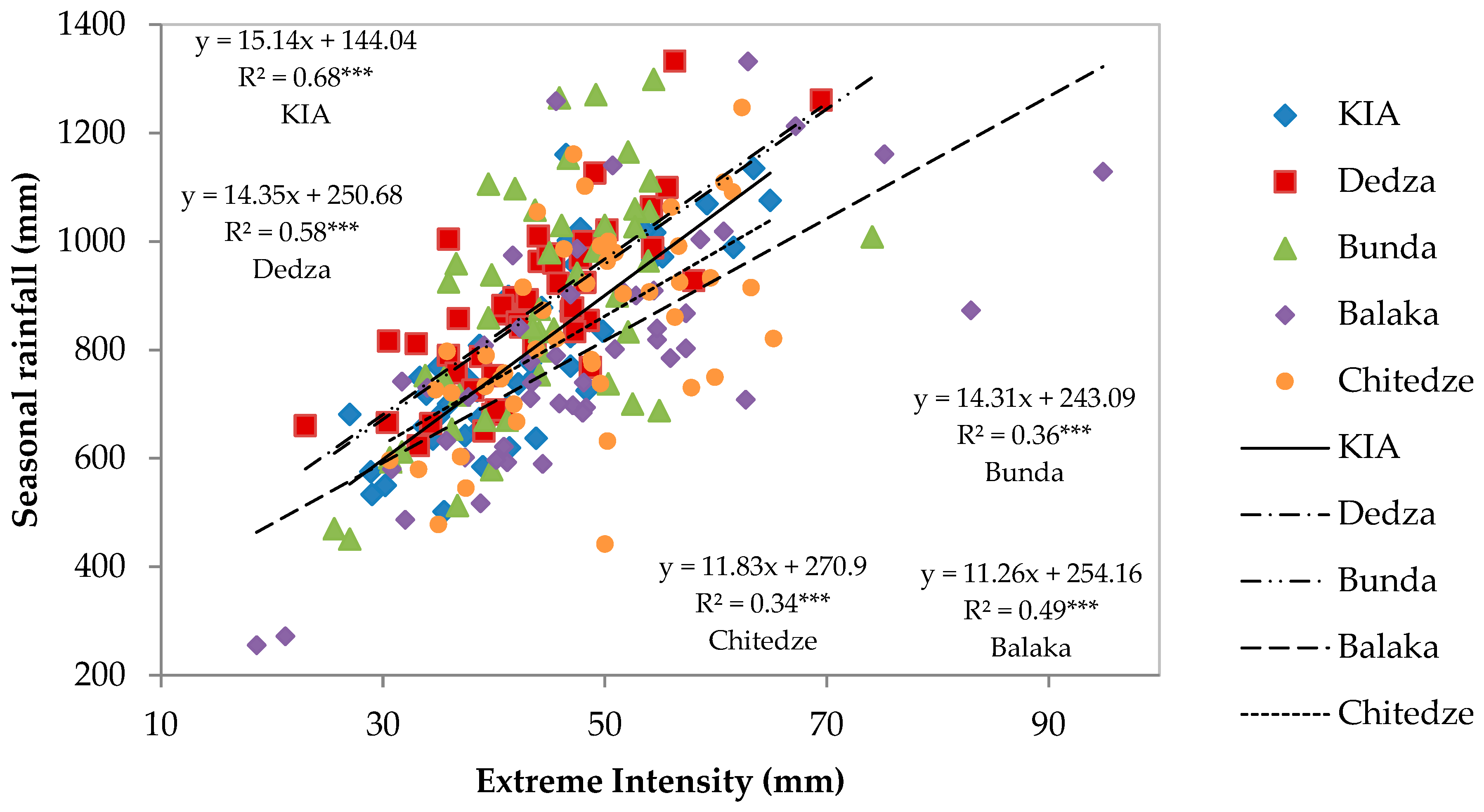
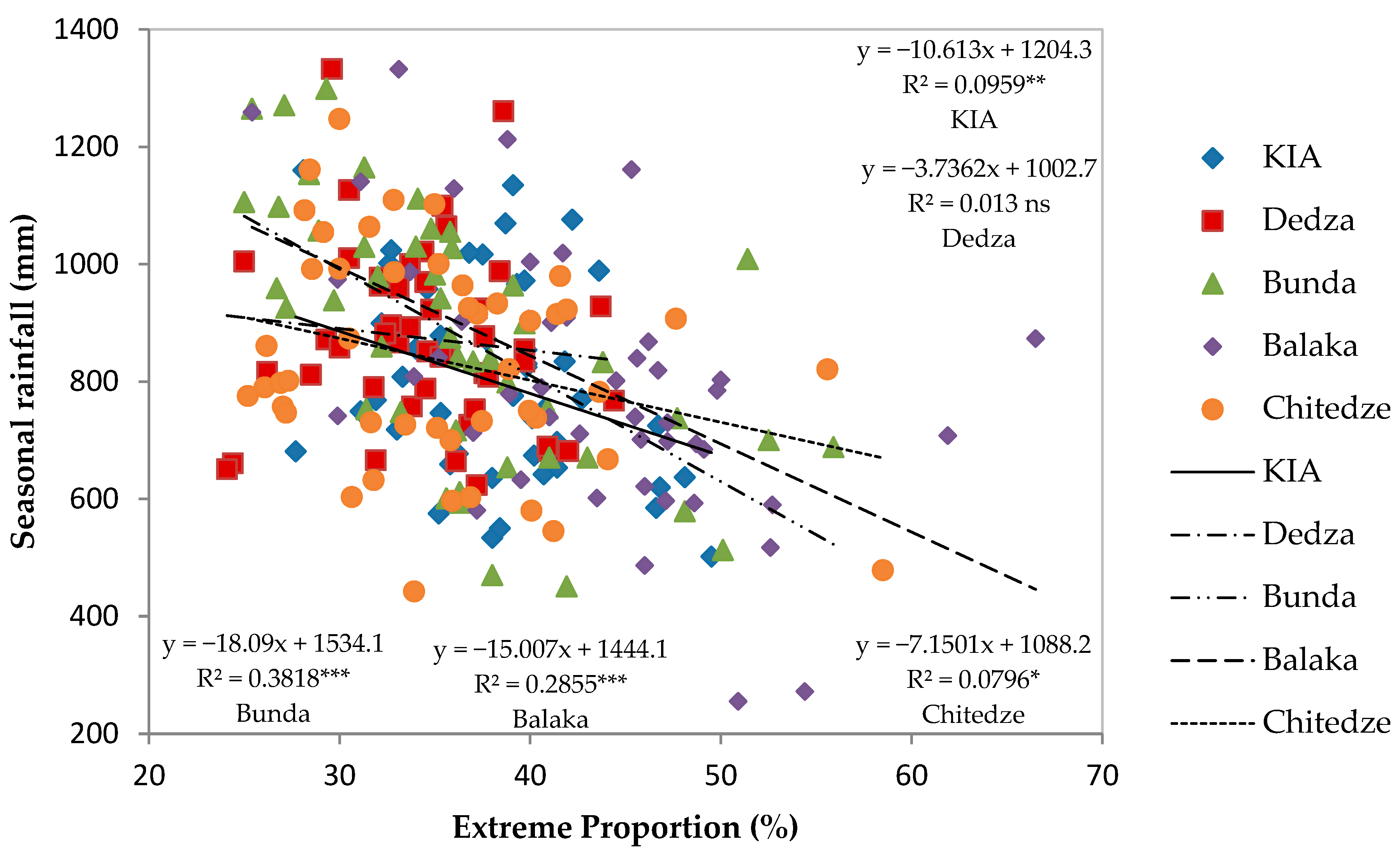
5.2. Extreme Rainfall Events
5.3. Dry Days and Spells
5.4. Seasonal and Decadal Rainfall Departures
5.5. ENSO-Induced Rainfall Anomalies
5.6. Onset, Cessation and Length of Growing Season
5.7. Location Inferences
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mzezewa, J.; Gwata, E.T. The nature of rainfall at a typical semi-arid tropical ecotope in Southern Africa and options for sustainable crop production. In Crop Production Technologies; Sharma, P., Ed.; IntechOpen: London, UK, 2012; pp. 93–112. Available online: https://www.intechopen.com/chapters/25581 (accessed on 22 January 2014).
- Kosgei, J.R.; Jewitt, G.P.W.; Kongo, V.M.; Lorentz, S.A. The influence of tillage on field scale water fluxes and maize yields in semi-arid environments: A case study of Potshini catchment, South Africa. Phys. Chem. Earth 2007, 32, 1117–1126. [Google Scholar] [CrossRef]
- Mwafulirwa, N.D. Climate Variability and Predictability in Tropical Southern Africa with a Focus on Dry Spells over Malawi. Master’s Thesis, Department of Geography and Environmental Studies, University of Zululand, Zululand, South Africa, 1999; p. 179. [Google Scholar]
- Silva, T.R.B.F.; Santos, C.A.C.; Silva, D.J.F.; Santos, C.A.G.; da Silva, R.M.; de Brito, J.I.B. Climate Indices-Based Analysis of Rainfall Spatiotemporal Variability in Pernambuco State, Brazil. Water 2022, 14, 2190. [Google Scholar] [CrossRef]
- McSweeney, C.; New, M.; Lizcano, G. UNDP Climate Change Country Profiles, Malawi; Technical Report; United Nations Development Programme: New York, NY, USA, 2012; pp. 1–27. [Google Scholar] [CrossRef]
- Ngongondo, C.S.; Xu, C.Y.; Gottschalk, L.; Alemaw, B. Evaluation of spatial and temporal characteristics of rainfall in Malawi: A case of data scarce region. Theor. Appl. Climatol. 2011, 106, 79–93. [Google Scholar] [CrossRef]
- Simelton, E.; Quinn, C.H.; Batisani, N.; Dougill, A.J.; Dyer, J.C.; Fraser, E.D.G.; Mkwambisi, D.D.; Sallu, S.M.; Stringer, L.C. Is rainfall really changing? Farmers’ perceptions, meteorological data and policy implications. Clim. Dev. 2013, 5, 123–138. [Google Scholar] [CrossRef]
- Nicholson, S.E.; Klotter, D.; Chavula, G. A detailed rainfall climatology for Malawi, Southern Africa. Int. J. Climatol. 2014, 34, 315–325. [Google Scholar] [CrossRef]
- Vincent, K.; Andrew, J.; Dougill, A.J.; Mkwambisi, D.D.; Cull, T.; Stringer, L.C.; Chanika, D. Analysis of Existing Weather and Climate Information for Malawi. 2014. Available online: http://kulima.com/wp-content/uploads/2011/03/Analysis-of-existing-weather-and-climate-information-for-Malawi-final-with-disclaimer.pdf (accessed on 18 January 2021).
- Siderius, C.; Kolusu, S.R.; Todd, M.C.; Bhave, A.; Dougill, A.J.; Reason, C.J.; Mkwambisi, D.D.; Kashaigili, J.J.; Pardoe, J.; Harou, J.J.; et al. Climate variability affects water-energy-food infrastructure performance in East Africa. One Earth 2021, 4, 397–410. [Google Scholar] [CrossRef]
- Zulu, L. Existing Research and Knowledge on Impacts of Climate Variability and Change on Agriculture and Communities in Malawi; Malawi Report No. 9; Global Center for Food Systems Innovation, Michigan State University: East Lansing, MI, USA, 2017. [Google Scholar] [CrossRef]
- Ziervogel, G.A.; Cartwright, A.; Adejuwon, T.J.; Zermoglio, F.; Shale, M.; Smith, B. Climate Change and Adaptation in African Agriculture; Stockholm Environment Institute, Rockefeller Foundation: Stockholm, Sweden, 2008; Available online: https://www.sei.org/publications/climate-change-adaptation-african-agriculture/ (accessed on 11 October 2011).
- Kruger, A.C. The influence of the decadal-scale variability of summer rainfall on the impact of El Niño and La Niña events in South Africa. Int. J. Climatol. 1999, 19, 59–68. [Google Scholar] [CrossRef]
- Alexander, F.; Nyasulu, M. Diagnosis of wet and dry events and its associated atmospheric circulation anomaly over Malawi, Southeast Africa. Dyn. Atmos. Ocean. 2021, 94, 101221. [Google Scholar] [CrossRef]
- Lüdecke, H.-J.; Lüning, S.; Müller-Plath, G.; Wallace, M.G. Decadal and multidecadal natural variability of African rainfall. J. Hydrol. Reg. Stud. 2021, 34, 100795. [Google Scholar] [CrossRef]
- Likoya, E.; Birch, C.E.; Chapman, S.; Dougill, A.J. Austral summer droughts and their driving mechanisms in observations and present-day climate simulations over Malawi. Int. J. Climatol. 2023, 43, 5154–5176. [Google Scholar] [CrossRef]
- Cook, B.I.; Slinski, W.A.K.; Shukla, S.; McNally, A. Investigating the strength and variability of El Niño–Southern oscillation teleconnections to hydroclimate and maize yields in Southern and East Africa. J. Hydrometeorol. 2024, 25, 257–275. [Google Scholar] [CrossRef]
- Ngongondo, C.S.; Alemaw, B.; Xu, C.; Chirwa, T.; Tallaksen, L.M. Regional frequency analysis of rainfall extremes in southern Malawi using the index rainfall and L-moments approaches. Stoch. Env. Res. Risk A 2011, 25, 939–955. [Google Scholar] [CrossRef]
- Almazroui, M.; Dambul, R.; Islam, M.N.; Jones, P.D. Principal components-based regionalization of the Saudi Arabian climate. Int. J. Climatol. 2015, 35, 2555–2573. [Google Scholar] [CrossRef]
- Haylock, M.; Nicholls, N. Trends in extreme rainfall indices for an updated high-quality data set for Australia, 1910–1998. Int. J. Climatol. 2000, 20, 1533–1541. [Google Scholar] [CrossRef]
- Tadross, M.A.; Hewitson, B.C.; Usman, M.T. The interannual variability of the onset of the maize growing season over South Africa and Zimbabwe. J. Clim. 2005, 18, 3356–3372. [Google Scholar] [CrossRef]
- Kiely, G. Climate change in Ireland from precipitation and stream-flow observations. Adv. Water Resour. 1999, 23, 141–151. [Google Scholar] [CrossRef]
- Burn, D.H.; Hag Elnur, M.A. Detection of hydrologic trends and variability. J. Hydrol. 2002, 55, 107–122. [Google Scholar] [CrossRef]
- Haghtalab, N.; Moore, N.J.; Ngongondo, C. Spatio-temporal analysis of rainfall variability and seasonality in Malawi. Reg. Environ. Chang. 2019, 19, 2041–2054. [Google Scholar] [CrossRef]
- Moore, N.; Breeze, V.; Deindorfer, H.; Nejadhashemi, A.P.; Adhikari, U.; Herman, M.; Messina, J.; Peter, B.; Frake, A.; Devisser, M.H. Climate Trends, Hydrologic Modeling, and Land Use Analysis in Malawi; Malawi Report No. 006; Global Center for Food Systems Innovation, Michigan State University: East Lansing, MI, USA, 2016. Available online: https://pdf.usaid.gov/pdf_docs/PA00XDT1R.pdf (accessed on 18 November 2020).
- Jury, M.R.; Mwafulirwa, N.D. Climate variability in Malawi, Part 1: Dry summers, statistical associations and predictability. Int. J. Climatol. 2002, 22, 1289–1302. [Google Scholar] [CrossRef]
- Lorkeers, A.J.M.; Venema, J.H. Land Resources Appraised of Lilongwe Agricultural Development Division; DP/MLW/5/011. GOM/UNDP/FAO Field Document No. 24; Land Resources Evaluation Project AG: Lilongwe, Malawi, 1991. [Google Scholar]
- Fiwa, L. Improving Rainfed Cereal Production and Water Productivity in Malawi, Modelling Field Management Options in Response to Current and Future Climatic Conditions. Ph.D. Dissertation, KU Leuven, Leuven, Belgium, 2015; p. 185. Available online: https://lirias.kuleuven.be/bitstream/123456789/493765/1/Lameck_FIWA.pdf (accessed on 11 January 2016).
- Libanda, B.; Zheng, M.; Banda, N. Variability of extreme wet events over Malawi. Geogr. Pannonica 2017, 21, 212–223. [Google Scholar] [CrossRef]
- WMO (World Meteorological Organization). Analyzing Long Time Series of Hydrological Data with Respect to Climate Variability; WCAP-3, WMO/TD No. 224; WMO: Geneva, Switzerland, 1988; p. 12. [Google Scholar]
- WMO (World Meteorological Organization). Guidelines on Analysis of Extremes in a Changing Climate in Support of Informed Decisions for Adaptation; WCDMP-No. 72; Climate Data and Monitoring: Geneva, Switzerland, 2009. [Google Scholar]
- Lettenmaier, D.P.; Wood, E.F.; Wallis, J.R. Hydro-climatological trends in the continental United States, 1948–1988. J. Clim. 1994, 7, 586–607. [Google Scholar] [CrossRef]
- Alexander, L.V.; Zhang, X.; Peterson, T.C.; Caesar, J.; Gleason, B.; Klein Tank, A.M.G.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F.; et al. Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. 2006, 111, D5. [Google Scholar] [CrossRef]
- Peterson, T.C. Climate change indices. WMO Bull. 2005, 54, 83–86. [Google Scholar]
- Kimaro, T.A.; Sibande, H. Trends of rainfall and maize productivity in Malawi. Tanzan. J. Eng. Technol. 2008, 2, 72–82. [Google Scholar] [CrossRef]
- Usman, M.T.; Reason, C.J.C. Dry spell frequencies and their variability over southern Africa. Clim. Res. 2004, 26, 199–211. [Google Scholar] [CrossRef]
- Stern, R.D.; Cooper, P.J.M. Assessing climate risk and climate change using rainfall data—A case study from Zambia. Exp. Agr. 2011, 47, 241–266. [Google Scholar] [CrossRef]
- Costa, A.C.; Soares, A. Trends in extreme precipitation indices derived from a daily rainfall database for the South of Portugal. Int. J. Climatol. 2008, 29, 1956–1975. [Google Scholar] [CrossRef]
- Onyutha, C. Statistical uncertainty in hydrometeorological trend analyses. Adv. Meteorol. 2016, 2016, 8701617. [Google Scholar] [CrossRef]
- Kisaka, M.O.; Mucheru-Muna, M.; Ngetich, F.K.; Mugwe, J.N.; Mugendi, D.; Mairura, F. Rainfall variability, drought characterization, and efficacy of rainfall data reconstruction: Case of Eastern Kenya. Adv. Meteorol. 2015, 2015, 380404. [Google Scholar] [CrossRef]
- Saidi, H.; Ciampittiello, M.; Dresti, C.; Ghiglieri, G. Observed variability and trends in extreme rainfall indices and Peaks-Over-Threshold series. Hydrol. Earth Syst. Sci. Discuss. 2013, 10, 6049–6079. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Raes, D.; Willems, P.; GBaguidi, F. RAINBOW—A software package for analyzing data and testing the homogeneity of historical data sets. In Proceedings of the 4th International Workshop on ‘Sustainable Management of Marginal Drylands’, Islamabad, Pakistan, 27–31 January 2006; Available online: https://iupware.be/wp-content/uploads/2016/03/rainbow_manual.pdf (accessed on 18 March 2009).
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Burn, D.H.; Cunderlik, J.; Pietroniro, A. Climatic influences on streamflow timing in the headwaters of the Mackenzie River Basin. J. Hydrol. 2008, 352, 225–238. [Google Scholar] [CrossRef]
- Queenie, K.Y.; Yip, K.Y.; Burn, D.H.H.; Seglenieks, F.; Pietroniro, A.; Soulis, E.D.D. Climate impacts on hydrological variables in the Mackenzie River Basin. Can. Water Resour. J. 2013, 37, 209–230. [Google Scholar] [CrossRef]
- Blain, G.C. The influence of nonlinear trends on the power of the trend-free pre-whitening approach. Acta Sci. Agric. Maringá 2015, 37, 21–28. [Google Scholar] [CrossRef]
- Hirsch, R.M.; Slack, J.R.; Smith, R.A. Techniques for trend assessment for monthly water quality data. Water Resour. Res. 1982, 18, 107–121. [Google Scholar] [CrossRef]
- Rustum, R.; Adeloye, A.J.; Mwale, F. Spatial and temporal trend analysis of long term rainfall records in data-poor catchments with missing data, a case study of Lower Shire floodplain in Malawi for the period 1953–2010. J. Hydrol. Earth Syst. Sci. Discuss. 2010. in preprint. [Google Scholar] [CrossRef]
- Lawson, M.P.; Balling, R.C.; Peters, A.J.; Rundquist, D.C. Spatial analysis of secular temperature fluctuations. J. Climatol. 1981, 1, 325–332. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C. Extreme rainfall (R20mm, Rx5day) in Yangtze–Huai, China, in June–July 2016: The role of ENSO and anthropogenic climate change. Am. Meteorol. Soc. 2016, 20, S102–S106. [Google Scholar] [CrossRef]
- Cairns, J.E.; Hellin, J.; Sonder, K.; Araus, J.L.; MacRobert, J.F.; Thierfelder, C.; Prasanna, B.M. Adapting maize production to climate change in sub-Saharan Africa. Food Sec. 2013, 5, 345–360. [Google Scholar] [CrossRef]
- Tadeyo, E.; Chen, D.; Ayugi, B.; Yao, C. Characterization of spatio-temporal trends and periodicity of precipitation over Malawi during 1979–2015. Atmosphere 2020, 11, 891. [Google Scholar] [CrossRef]
- Hudson, D.A.; Jones, R.G. Simulations of Present-Day and Future Climate over Southern Africa Using Hadam3h; Hadley Centre Technical Note 38; Met Office, Hadley Centre for Climate Prediction and Research: Bracknell, UK, 2002. Available online: https://digital.nmla.metoffice.gov.uk/download/file/IO_295593b0-2895-4122-92cc-8b475bf82377 (accessed on 28 June 2011).
- Clay, E.; Bohn, L.; Blanco de Armas, E.; Kabambe, S.; Tchale, H. Malawi and Southern Africa: Climatic Variability and Economic Performance; Disaster Management Facility, Working Paper Series No. 7; World Bank: Washington, DC, USA, 2003; Available online: http://documents.worldbank.org/curated/en/391461468774612214/Malawi-and-Southern-Africa-climatic-variability-and-economic-performance (accessed on 28 June 2011).
- Stroosnijder, L. Modifying land management in order to improve efficiency of rainwater use in the African highlands. Soil Till. Res. 2009, 103, 247–256. [Google Scholar] [CrossRef]
- New, M.; Hewitson, B.; Stephenson, D.B.; Tsiga, A.; Kruger, A.; Manhique, A.; Gomez, B.; Coelho, C.A.S.; Masisi, D.N.; Kululanga, E.; et al. Evidence of trends in daily climate extremes over Southern and West Africa. J. Geophys. Res. 2006, 111, D14. [Google Scholar] [CrossRef]
- Mkandawire, M. Investigating Dry Spells in Malawi during the Rainfall Season. Master’s Thesis, Department of Meteorology, University of Nairobi, Nairobi, Kenya, 2014. Available online: http://erepository.uonbi.ac.ke/bitstream/handle/11295/95428/Mkandawire_Investigating%20dry%20spells%20in%20Malawi%20during%20the%20rainfall%20season?sequence=1 (accessed on 22 September 2014).
- Chimimba, E.G.; Ngongondo, C.; Li, C.; Minoungou, B.; Maurice Monjerezi, M.; Eneya, L. Characterisation of dry spells for agricultural applications in Malawi. SN Appl. Sci. 2023, 5, 199. [Google Scholar] [CrossRef]
- Barron, J.; Rockstrom, J.; Gichuki, F.; Hatibu, N. Dry spell occurrence and potential impact on maize yields: Rainfall analysis and simple water balance modelling for semi-arid farming systems in Kenya and Tanzania. Agric. For. Meteorol. 2003, 117, 23–37. [Google Scholar] [CrossRef]
- Mathugama, S.C.; Peiris, T.S.G. Critical evaluation of dry spell research. Int. J. Basic Appl. Sci. 2011, 11, 153–160. [Google Scholar]
- Dieppois, B.; Poh, B.; Rouault, M.; New, M.; Lawler, D.; Keenlyside, N. Interannual to interdecadal variability of winter and summer southern African rainfall, and their teleconnections. J. Geophys. Res. Atmos. 2016, 121, 6215–6239. [Google Scholar] [CrossRef]
- Dai, A. Increasing drought under global warming in observations and models. Nat. Clim. Chang. 2013, 3, 52–58. [Google Scholar] [CrossRef]
- Ngongondo, C.; Xu, C.Y.; Tallaksen, L.M.; Alemaw, B. Observed and simulated changes in the water balance components over Malawi, during 1971–2000. Quat. Int. 2015, 369, 7–16. [Google Scholar] [CrossRef]
- Hurrell, J.W.; Delworth, T.L.; Danabasoglu, G.; Drange, H.; Drinkwater, K.; Griffies, S.; Holbrook, N.; Kirtman, B.; Keenlyside, N.; Latif, M.; et al. Decadal climate prediction: Opportunities and challenges. In Proceedings of the Oceanobs’09: Sustained Ocean Observations and Information for Society, Venice, Italy, 21–25 September 2009; Volume 6, p. 23. [Google Scholar] [CrossRef]
- Nicholson, S.E.; Selato, J.C. The influence of La Nina on African rainfall. Int. J. Climatol. 2000, 20, 1761–1776. [Google Scholar] [CrossRef]
- Pomposi, C.; Funk, C.; Shukla, S.; Harrison, L.; Magadzire, T. Distinguishing southern Africa precipitation response by strength of El Niño events and implications for decision-making. Environ. Res. Lett. 2018, 13, 074015. [Google Scholar] [CrossRef]
- Kane, R.P. Periodicities, ENSO effects and trends of some South African rainfall series: An update. S. Afr. J. Sci. 2009, 105, 199–207. [Google Scholar] [CrossRef]
- Rembold, F.; Meroni, M.; Urbano, F.; Csak, G.; Kerdiles, H.; Perez-Hoyos, A.; Lemoine, G.; Negre, T. A new global early warning system to detect anomaly hot spots of agricultural production for food security analysis. Agric. Syst. 2019, 168, 247–257. [Google Scholar] [CrossRef]
- Thulu, F.G.D.; Katengeza, E.W.; Mkandawire, M. Rainfall trends for El Niño seasons over Malawi from 1970 to 2016 and its impact on crop yield and hydropower Generation. Int. J. Sci. Res. Pub. 2017, 7, 96–104. [Google Scholar] [CrossRef]
- Setimela, P.; Gasura, E.; Thierfelder, C.; Zaman-Allah, M.; Cairns, J.E.; Boddupalli, P.M. When the going gets tough: Performance of stress tolerant maize during the 2015/16 (El Niño) and 2016/17 (La Niña) season in southern Africa. Agric. Ecosyst. Environ. 2018, 268, 79–89. [Google Scholar] [CrossRef]
- Tadross, M.; Suarez, P.; Lotsch, A.; Hachigonta, S.; Mdoka, M.; Unganai, L.; Lucio, F.; Kamdonyo, D.; Muchinda, M. Growing-season rainfall and scenarios of future change in southeast Africa: Implications for cultivating maize. Clim. Res. 2009, 40, 147–161. [Google Scholar] [CrossRef]
- Ngongondo, C.; Tallaksen, L.M.; Xu, C.-Y. Growing season length and rainfall extremes analysis in Malawi. IAHS Publ. 2014, 363, 361–366. Available online: https://www.researchgate.net/publication/270574754_Growing_season_length_and_rainfall_extremes_analysis_in_Malawi (accessed on 18 January 2021).
- Sutcliffe, C.; Dougill, A.J.; Quinn, C.H. Evidence and perceptions of rainfall change in Malawi: Do maize cultivar choices enhance climate change adaptation in sub-Saharan Africa? Reg. Environ. Chang. 2016, 16, 1215–1224. [Google Scholar] [CrossRef]
- Vizy, E.K.; Cook, K.H.; Chimphamba, J.; McCusker, B. Projected changes in Malawi’s growing season. Clim. Dyn. 2015, 45, 1673–1698. [Google Scholar] [CrossRef]
- Stroosnijder, L.; Hoogmoed, W.B. Crust formation on sandy soils in the Sahel II. Tillage and its effects on the water balance. Soil Till. Res. 1984, 4, 321–337. [Google Scholar] [CrossRef]


| No. | Station Name/Type | WMO ID | Latitude (S) | Longitude (E) | Altitude (MASL) | Mean Annual Temperature (°C) | Mean Annual Rainfall (mm) |
|---|---|---|---|---|---|---|---|
| 1 | Balaka, gauge | - | 14°98′ | 34°97′ | 625 | 25 | 801 |
| 2 | Dedza, reference | 67,689 | 14°32′ | 34°25′ | 1590 | 16 | 970 |
| 3 | Bunda, gauge | - | 14°18′ | 33°77′ | 1118 | 21 | 1030 |
| 4 | Chitedze, reference | 67,585 | 13°97′ | 33°63′ | 1149 | 20 | 868 |
| 5 | KIA, synoptic | 67,586 | 13°78′ | 33°78′ | 1229 | 21 | 944 |
| Index Name | Description | Units |
|---|---|---|
| Threshold indices | ||
| Wet days (WD) | Seasonal total number of wet days (DP > 0.85 mm) | Days |
| Dry days (DD) | Seasonal total number of dry days (DP < 0.85 mm) | Days |
| Onset of growing season (OGS) | First occasion from 1 November with 20 mm or more of rain within a 3-day period and no dry spell exceeding 10 days in the following 30 days | Date |
| End of growing season (EGS) | Last day before May 30 that accumulated 10 mm or more rainfall | Date |
| Duration indices | ||
| Wet spell/pentad (WP) | Five consecutive days with more than 4.25 mm of rainfall | Number |
| Dry spell (DS) | Five consecutive days with less than 4.25 mm of rainfall | Number |
| Growing season length (GSL) | Date of the beginning to the date of ending of the growing season | Days |
| Absolute indices | ||
| Maximum 1-day rainfall (Rx1day) | Seasonal maximum precipitation in 1 day | mm |
| Maximum 5-day rainfall (Rx5day) | Seasonal maximum precipitation in five consecutive days | mm |
| Percentile-based indices | ||
| Extreme intensity (RXI) | Average intensity of events greater than or equal to the 1961–2007 mean 95th percentile of the wet days | mm |
| Extreme frequency (RXF) | Number of days in the season with rainfall exceeding the 1961–2007 mean 95th percentile of the wet days | Days |
| Extreme percent (RXP) | Proportion of total seasonal rainfall from all events above the average long-term (1961–2007) mean 95th percentile of the wet days | % |
| Other indices | ||
| Seasonal rainfall (PCPTOT) | Seasonal total precipitation from wet days (DP ≥ 0.85 mm) | Mm |
| Rainfall Indices (Seasonal) | Balaka | Dedza | Bunda | Chitedze | KIA | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SE | CV | Mean | SE | CV | Mean | SE | CV | Mean | SE | CV | Mean | SE | CV | |
| Seasonal rainfall (mm) | 795.3 | 33.64 | 0.29 | 878.0 | 23.05 | 0.18 | 872.0 | 30.53 | 0.24 | 835.1 | 26.80 | 0.22 | 793.6 | 24.31 | 0.21 |
| Number of wet days | 49.0 | 2.07 | 0.29 | 68.0 | 1.69 | 0.17 | 59.0 | 1.98 | 0.23 | 62.0 | 1.72 | 0.19 | 60.0 | 1.31 | 0.15 |
| Number of wet pentads | 2.2 | 0.07 | 0.23 | 4.7 | 0.16 | 0.24 | 2.7 | 0.09 | 0.24 | 3.3 | 0.26 | 0.54 | 3.0 | 0.10 | 0.22 |
| Max 1-day rainfall (mm) | 72.1 | 3.37 | 0.32 | 69.9 | 3.16 | 0.31 | 64.2 | 2.81 | 0.30 | 71.5 | 2.92 | 0.28 | 66.0 | 3.37 | 0.35 |
| Max 5-day rainfall (mm) | 104.0 | 9.40 | 0.62 | 118.5 | 7.26 | 0.42 | 91.0 | 7.03 | 0.53 | 106.4 | 5.43 | 0.35 | 108.8 | 7.14 | 0.45 |
| Extreme intensity (mm) | 48.2 | 2.04 | 0.29 | 43.4 | 1.20 | 0.19 | 44.2 | 1.29 | 0.20 | 47.7 | 1.32 | 0.19 | 43.3 | 1.33 | 0.21 |
| Extreme frequency (days) | 2.8 | 0.13 | 0.32 | 2.7 | 0.13 | 0.33 | 2.9 | 0.15 | 0.36 | 2.6 | 0.11 | 0.30 | 2.9 | 0.13 | 0.30 |
| Extreme percent (%) | 43.1 | 1.19 | 0.19 | 34.4 | 0.70 | 0.14 | 35.8 | 1.31 | 0.25 | 35.4 | 1.03 | 0.20 | 38.2 | 0.72 | 0.13 |
| Number of dry days | 82.0 | 2.75 | 0.23 | 59.0 | 2.24 | 0.26 | 75.0 | 2.63 | 0.24 | 63.0 | 2.66 | 0.29 | 61.0 | 2.85 | 0.32 |
| 5 days dry spells a | 1.6 | 0.12 | 0.53 | 1.8 | 0.13 | 0.48 | 2.0 | 0.14 | 0.47 | 1.5 | 0.09 | 0.39 | 1.8 | 0.13 | 0.48 |
| 6 to 10 days dry spells | 7.4 | 0.18 | 0.17 | 7.4 | 0.19 | 0.18 | 7.6 | 0.20 | 0.18 | 7.7 | 0.21 | 0.19 | 7.6 | 0.19 | 0.17 |
| 11 to 15 days dry spells | 12.6 | 0.18 | 0.10 | 12.4 | 0.18 | 0.10 | 12.7 | 0.24 | 0.13 | 12.8 | 0.21 | 0.11 | 12.6 | 0.18 | 0.10 |
| >15 days dry spells | 20.1 | 0.67 | 0.23 | 18.2 | 0.45 | 0.17 | 20.2 | 0.53 | 0.18 | 17.8 | 0.34 | 0.13 | 19.4 | 0.57 | 0.20 |
| Rainfall and Dry Spell Indices | Kendall’s Tau | ||||
|---|---|---|---|---|---|
| Balaka | Dedza | Bunda | Chitedze | KIA | |
| Seasonal rainfall (PRCPTOT, mm) | 0.065 ** | 0.015 | −0.188 *** | −0.010 | 0.057 |
| Wet days (WD) | −0.225 *** | −0.144 ** | −0.188 *** | −0.214 *** | −0.059 |
| Wet pentads (WP) | −0.207 | −0.138 | −0.001 | −0.129 | 0.173 |
| Max 1-day rainfall (Rx1day, mm) | 0.174 | 0.134 | −0.070 | −0.029 | 0.077 |
| Max 5-day rainfall (Rx5day, mm) | 0.029 | 0.111 | −0.040 | 0.040 | 0.150 |
| Extreme intensity (RXI, mm) | 0.157 | 0.031 | −0.050 | 0.188 *** | 0.064 |
| Extreme frequency (RXF, days) | 0.054 | 0.308 ** | −0.070 | 0.100 | 0.020 |
| Extreme percent (RXP, %) | 0.119 | 0.192 | 0.231 ** | −0.181 *** | 0.008 |
| Dry days | 0.000 | 0.078 | −0.028 | −0.168 *** | −0.094 |
| 5-day dry spells (5 DS) | 0.012 | 0.158 | −0.093 | 0.146 | −0.025 |
| 6 to 10 days dry spells (6–10 DS) | −0.038 | −0.228 ** | 0.013 | 0.017 | −0.149 |
| 11to15 days of dry spells (11–15 DS) | 0.063 | −0.218 | −0.025 | −0.122 | −0.360 ** |
| >15 days of dry spells (>15 DS) | 0.161 | 0.068 | 0.131 | −0.210 * | 0.129 |
| Start of the season (days) | 0.114 | 0.007 | 0.130 | 0.157 | 0.054 |
| End of season (days) | −0.108 | −0.216 ** | −0.076 | −0.279 ** | −0.148 |
| Growing season length (GSL, days) | −0.197 *** | −0.178 ** | −0.187 *** | −0.338 *** | −0.117 ** |
| Seasonal Characteristics a | Balaka | Dedza | Bunda | Chitedze | KIA |
|---|---|---|---|---|---|
| Growing season length (days) | 134 (0.17) | 136 (0.17) | 137 (0.16) | 134 (0.17) | 129 (0.17) |
| Start of the growing season | |||||
| Earliest date | 01 Nov | 05 Nov | 01 Nov | 2 Nov | 26 Oct |
| Median start date | 23 Nov (15) | 27 Nov (14) | 22 Nov (15) | 25 Nov (15) | 24 Nov (15) |
| Most delayed date | 1 Jan | 03 Jan | 01 Jan | 11 Jan | 30 Dec |
| End of the growing season | |||||
| Earliest date | 23 Feb | 03 Mar | 21 Feb | 27 Feb | 04 Mar |
| Median end date | 14 Apr (19) | 15 Apr (21) | 09 Apr (21) | 10 Apr (20) | 07 Apr (20) |
| Most delayed date | 26 May | 27 May | 24 May | 27 May | 25 May |
| Period | Balaka | Dedza | Bunda | Chitedze | KIA | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | tk | Mean | tk | Mean | tk | Mean | tk | Mean | tk | |
| 1961–1970 | 746.4 | −0.72 | 818.5 | −1.24 | 894.8 | 0.38 | 813.9 | −0.41 | 762.5 | −0.64 |
| 1971–1980 | 817.5 | 0.33 | 895.4 | 0.38 | 1018.3 | 2.02 ** | 870.5 | 0.67 | 832.7 | 0.80 |
| 1981–1990 | 820.6 | 0.38 | 975.0 | 1.84 * | 877.0 | 0.08 | 866.8 | 0.60 | 779.3 | −0.30 |
| 1991–2000 | 790.6 | −0.07 | 827.3 | −1.08 | 794.2 | −1.23 | 791.8 | −0.81 | 792.0 | −0.03 |
| 2001–2007 | 804.2 | 0.10 | 872.4 | −0.10 | 734.5 | −1.55 | 831.1 | −0.06 | 804.8 | 0.19 |
| Indices | Spearman’s Rho | ||||
|---|---|---|---|---|---|
| KIA | Chitedze | Bunda | Dedza | Balaka | |
| RX1day | 0.22 * | 0.10 ns | 0.08 ns | −0.04 ns | 0.11 ns |
| RX5day | 0.28 ** | 0.02 ns | 0.09 ns | 0.04 ns | −0.03 ns |
| RXF | 0.13 ns | −0.18 ns | −0.06 ns | −0.10 ns | 0.15 ns |
| RXI | 0.23 * | 0.07 ns | 0.02 ns | −0.10 ns | 0.01 ns |
| RXP | 0.20 * | −0.12 ns | 0.10 ns | −0.12 ns | 0.02 ns |
| 5 days DS | 0.07 ns | 0.06 ns | −0.08 ns | −0.17 ns | −0.16 ns |
| 6–10 days DS | −0.01 ns | −0.05 ns | −0.13 ns | 0.18 ns | −0.12 ns |
| 11–15 days DS | −0.02 ns | 0.00 ns | 0.07 ns | 0.01 ns | 0.01 ns |
| >15 days DS | −0.12 ns | −0.15 ns | −0.03 ns | −0.14 ns | 0.04 ns |
| Index and Statistic | KIA | Chitedze | Bunda | Dedza | Balaka | |
|---|---|---|---|---|---|---|
| RX1day | Y | 4.55x + 65.80 | −0.67x + 71.55 | 6.36x + 63.69 | −0.62x + 69.88 | 0.98x + 72.07 |
| R2 | 0.0275 | 0.0008 | 0.0776 | 0.0006 | 0.0013 | |
| RX5day | Y | 11.66x + 108.38 | −0.20x + 106.41 | 4.35x + 90.87 | 0.91x + 118.43 | −6.08x + 104.18 |
| R2 | 0.0407 | 0.00002 | 0.0058 | 0.0003 | 0.0064 | |
| RXF | Y | 0.21x + 2.78 | −0.12x + 2.43 | −0.11x + 2.94 | −0.17x + 2.60 | 0.25x + 2.71 |
| R2 | 0.0089 | 0.004 | 0.002 | 0.0075 | 0.0124 | |
| RXI | Y | 2.05x + 43.18 | 0.92x + 47.65 | 1.05x + 44.12 | −0.99x + 43.48 | −0.63x + 48.24 |
| R2 | 0.0367 | 0.0076 | 0.0099 | 0.0107 | 0.0014 | |
| RXP | Y | 1.05x + 38.18 | −1.15x + 35.45 | 1.36x + 36.39 | −0.72x + 34.47 | −0.15x + 43.13 |
| R2 | 0.0332 | 0.0181 | 0.0246 | 0.0169 | 0.0003 | |
| 5 DS | Y | 0.50x +6.36 | 0.09x + 6.17 | −0.61x + 6.51 | −1.18x + 6.43 | −1.11x + 6.53 |
| R2 | 0.0063 | 0.0004 | 0.0073 | 0.0325 | 0.0356 | |
| 6–10 DS | Y | −1.27x + 17.41 | −0.79x + 19.33 | −2.52x + 21.41 | 2.44x + 16.46 | −1.84x + 23.41 |
| R2 | 0.007 | 0.004 | 0.0235 | 0.0288 | 0.011 | |
| 11–15 DS | Y | −1.24x + 3.81 | −0.69x + 8.00 | 1.48x + 8.63 | 0.17x + 6.40 | −0.78x + 11.38 |
| R2 | 0.0323 | 0.0031 | 0.013 | 0.0004 | 0.0033 | |
| >15 DS | Y | −1.33x + 7.11 | −2.08x + 4.32 | −0.95x + 6.74 | −1.62x + 3.55 | 1.48x + 10.67 |
| R2 | 0.0134 | 0.0419 | 0.0056 | 0.0347 | 0.0135 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mloza Banda, M.L.; Cornelis, W.; Mloza Banda, H.R. Seasonal, Decadal, and El Niño-Southern Oscillation-Related Trends and Anomalies in Rainfall and Dry Spells during the Agricultural Season in Central Malawi. Geographies 2024, 4, 563-582. https://doi.org/10.3390/geographies4030030
Mloza Banda ML, Cornelis W, Mloza Banda HR. Seasonal, Decadal, and El Niño-Southern Oscillation-Related Trends and Anomalies in Rainfall and Dry Spells during the Agricultural Season in Central Malawi. Geographies. 2024; 4(3):563-582. https://doi.org/10.3390/geographies4030030
Chicago/Turabian StyleMloza Banda, Medrina Linda, Wim Cornelis, and Henry R. Mloza Banda. 2024. "Seasonal, Decadal, and El Niño-Southern Oscillation-Related Trends and Anomalies in Rainfall and Dry Spells during the Agricultural Season in Central Malawi" Geographies 4, no. 3: 563-582. https://doi.org/10.3390/geographies4030030
APA StyleMloza Banda, M. L., Cornelis, W., & Mloza Banda, H. R. (2024). Seasonal, Decadal, and El Niño-Southern Oscillation-Related Trends and Anomalies in Rainfall and Dry Spells during the Agricultural Season in Central Malawi. Geographies, 4(3), 563-582. https://doi.org/10.3390/geographies4030030






