A Review of Sand–Clay Mixture and Soil–Structure Interface Direct Shear Test
Abstract
:1. General Introduction
2. The Role of Clay on the Mechanical Behavior of Sand–Clay Mixtures
2.1. State of the Art of the Mechanical Behavior of Sand–Clay Mixtures
2.1.1. Definition of Sand–Clay Mixture
2.1.2. Experimental Studies on Sand–Clay Mixtures’ Mechanical Behavior
2.2. Influence Factors on the Mechanical Response of Sand–Clay Mixtures
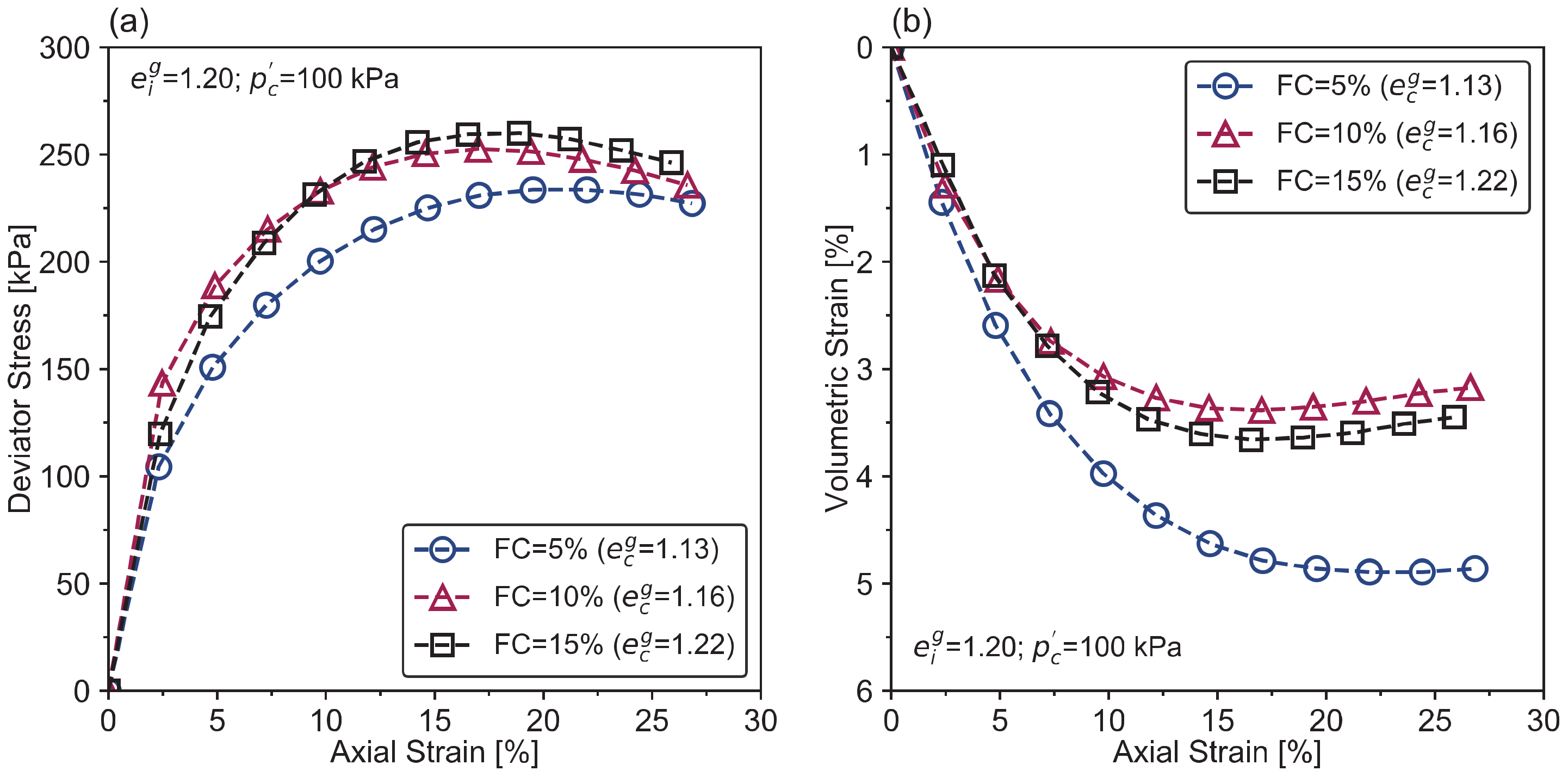
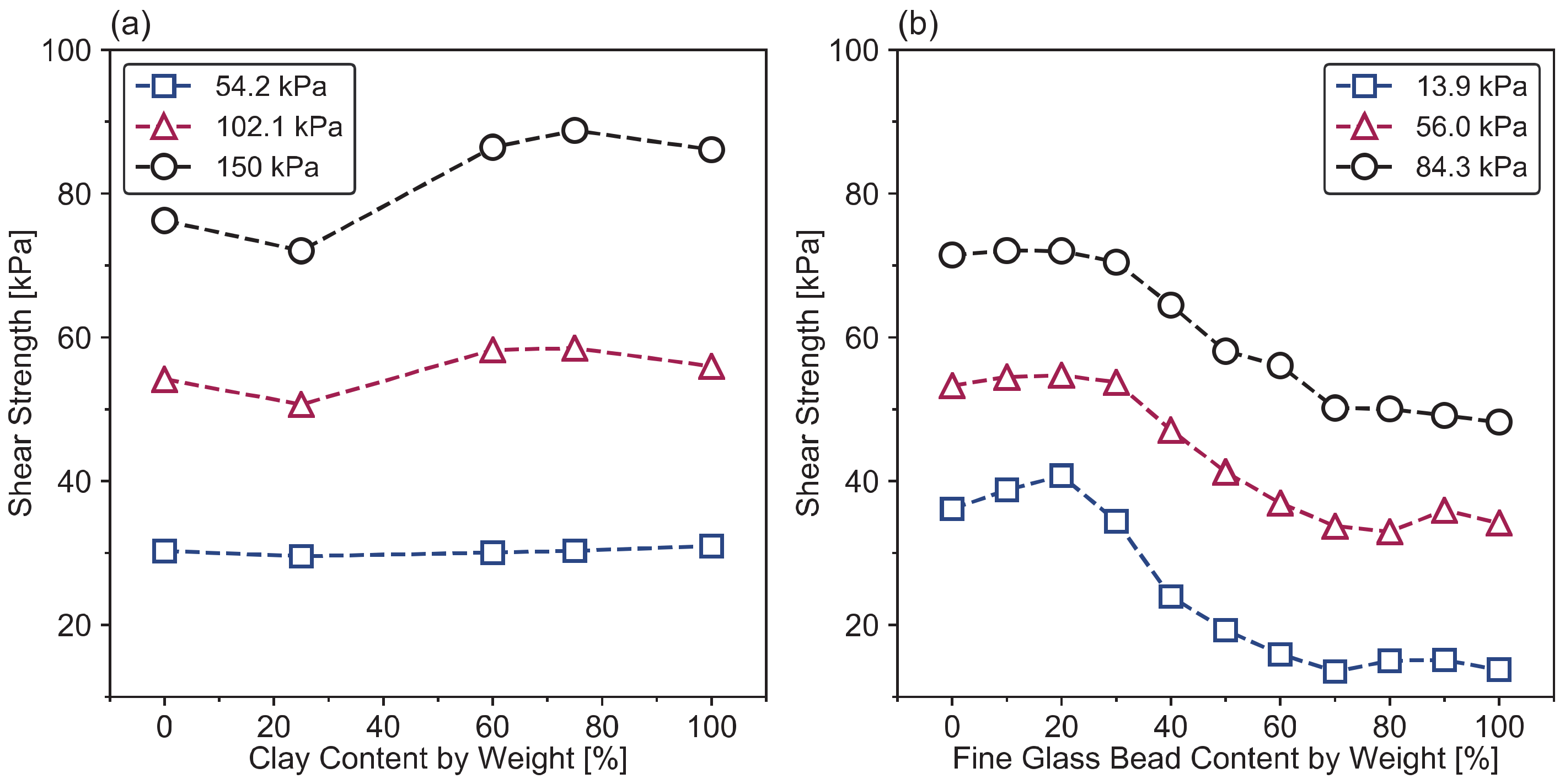
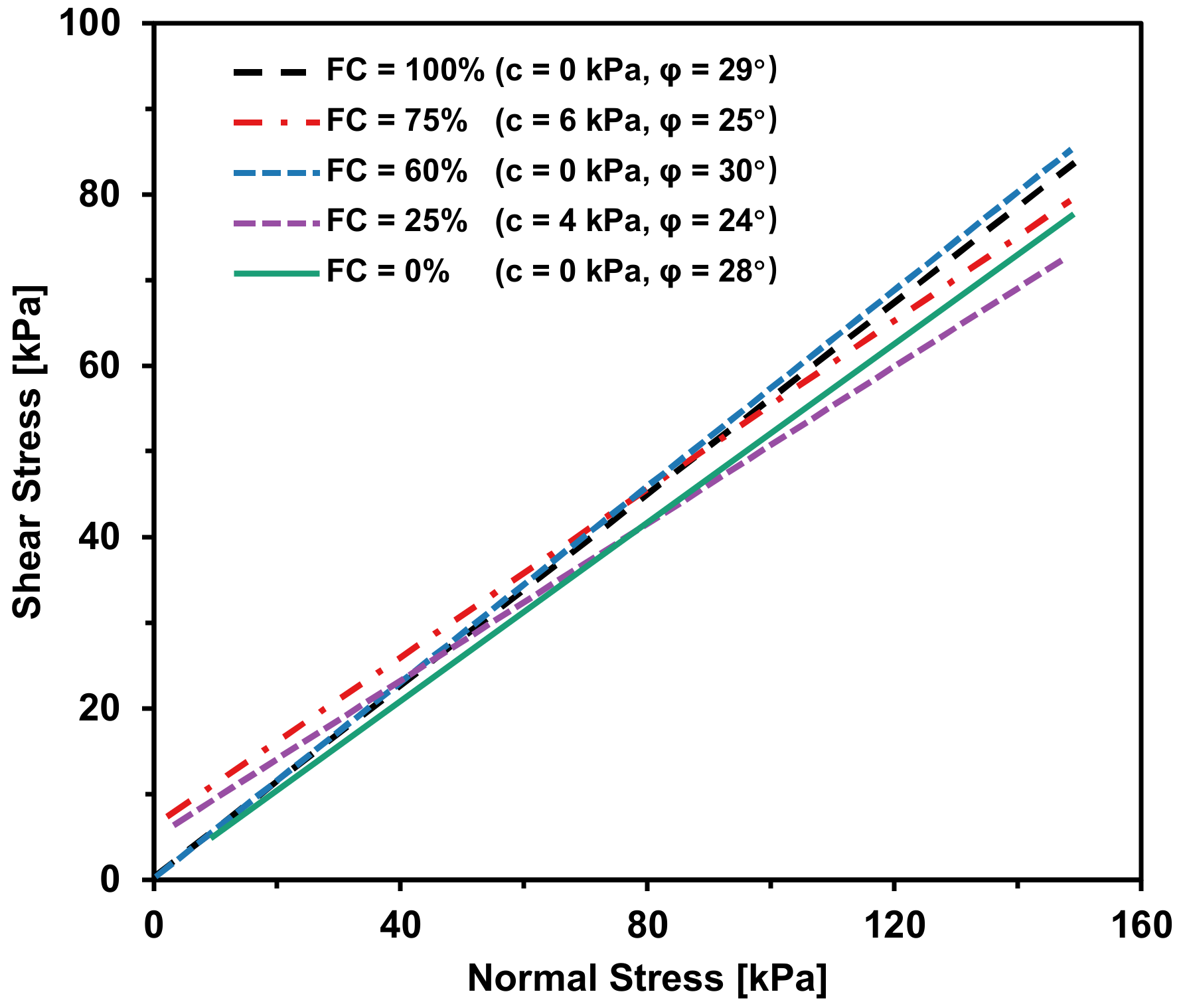
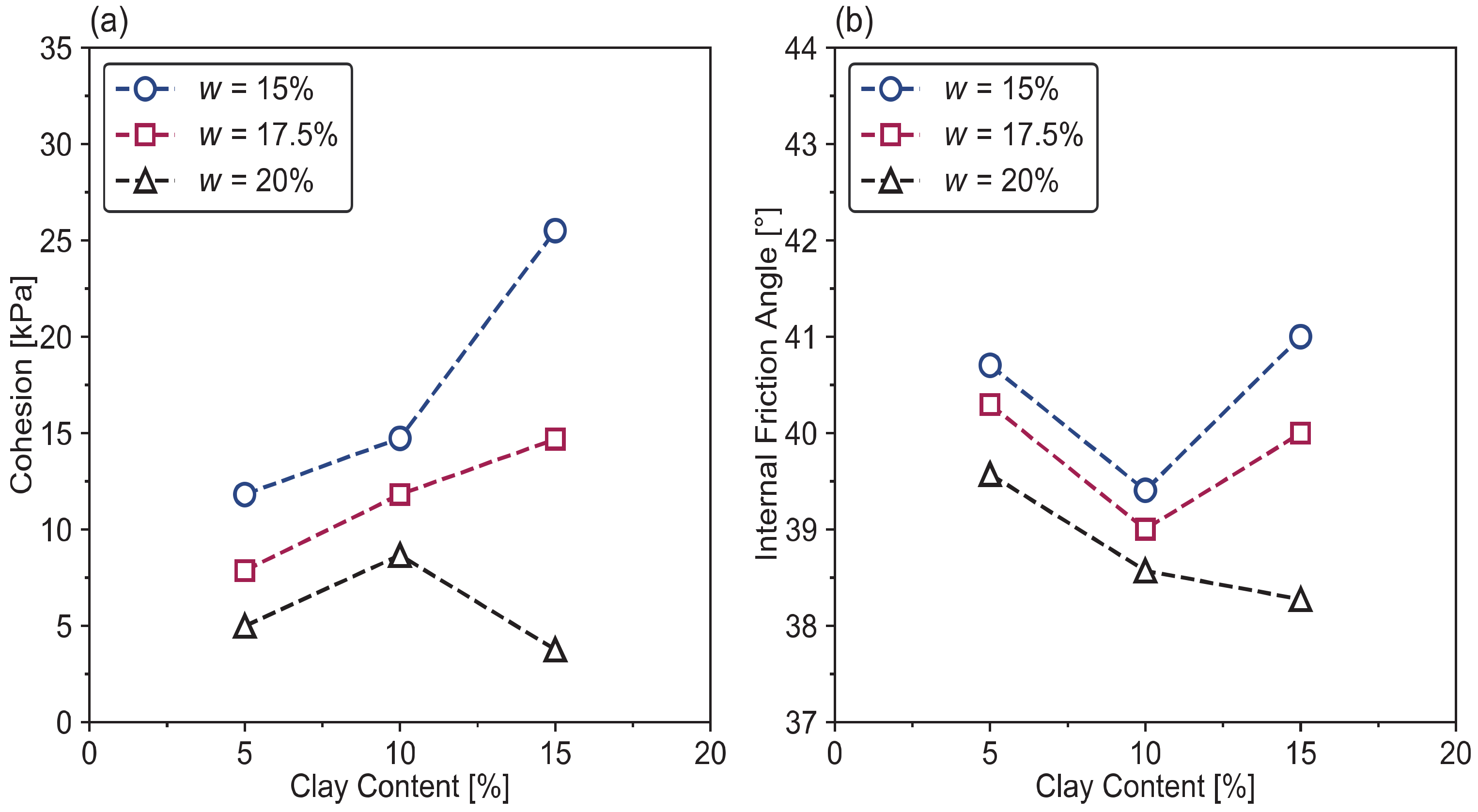
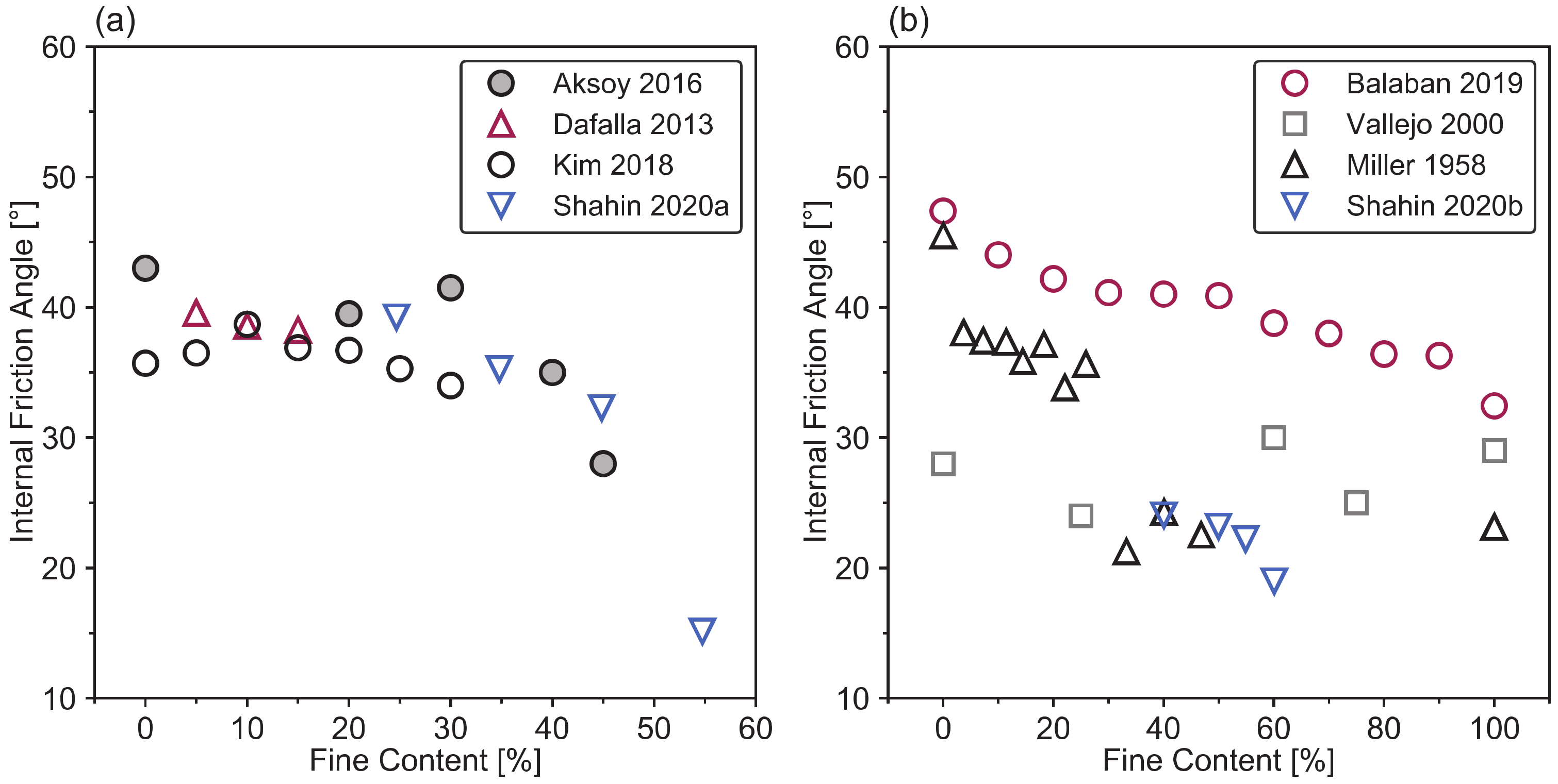
2.2.1. Fines Content
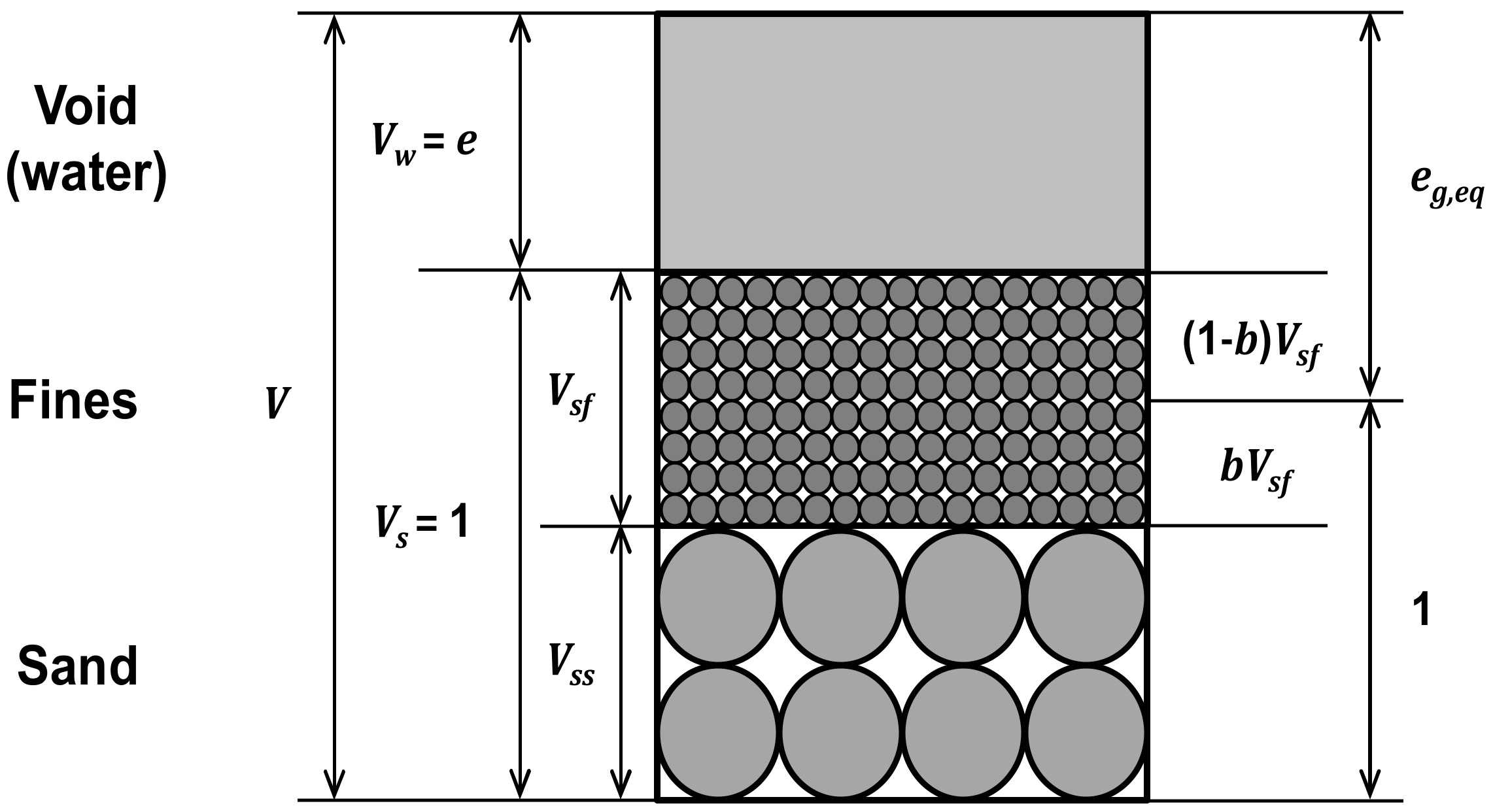
2.2.2. Intergranular and Interfine Void Ratios
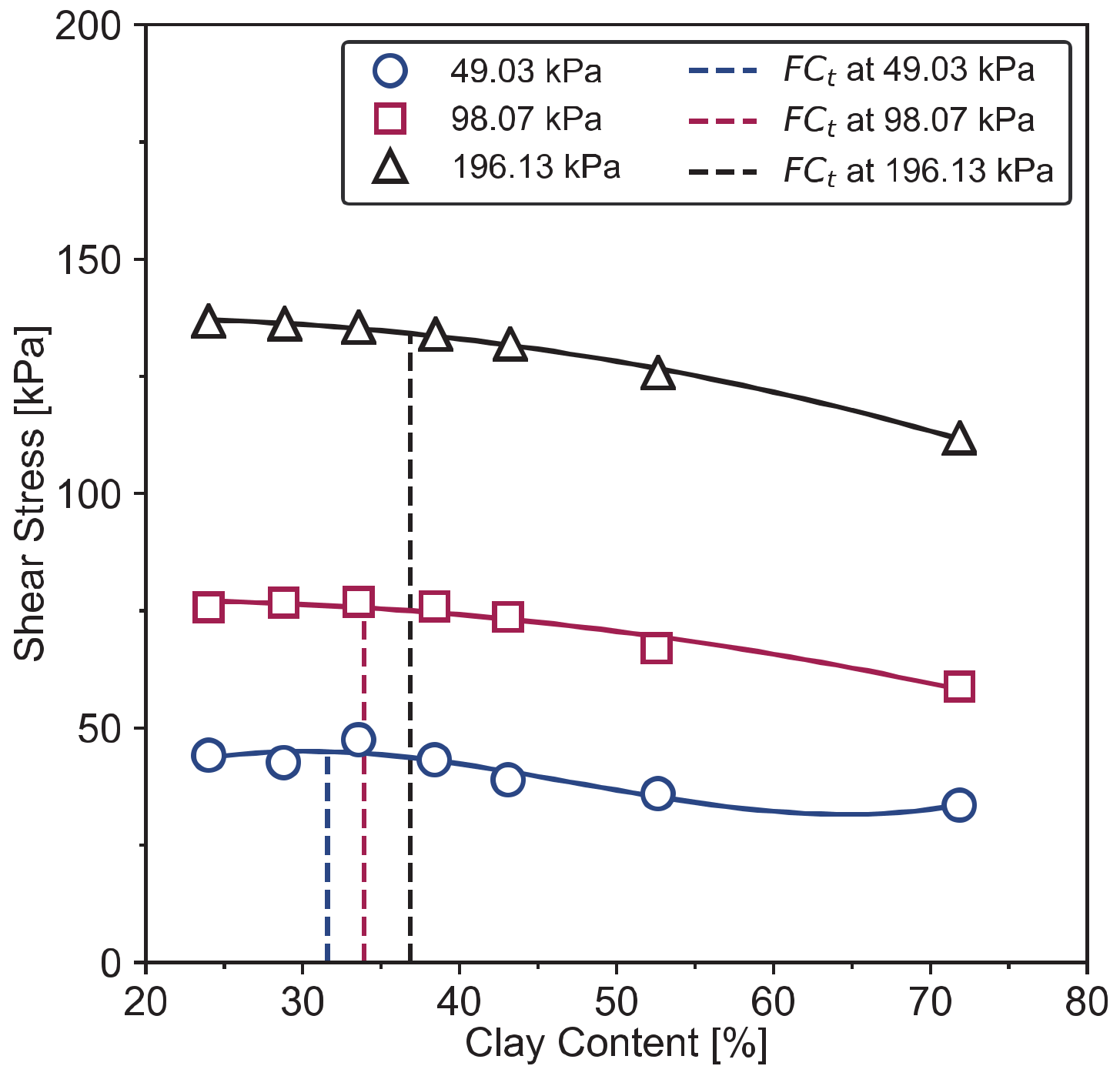
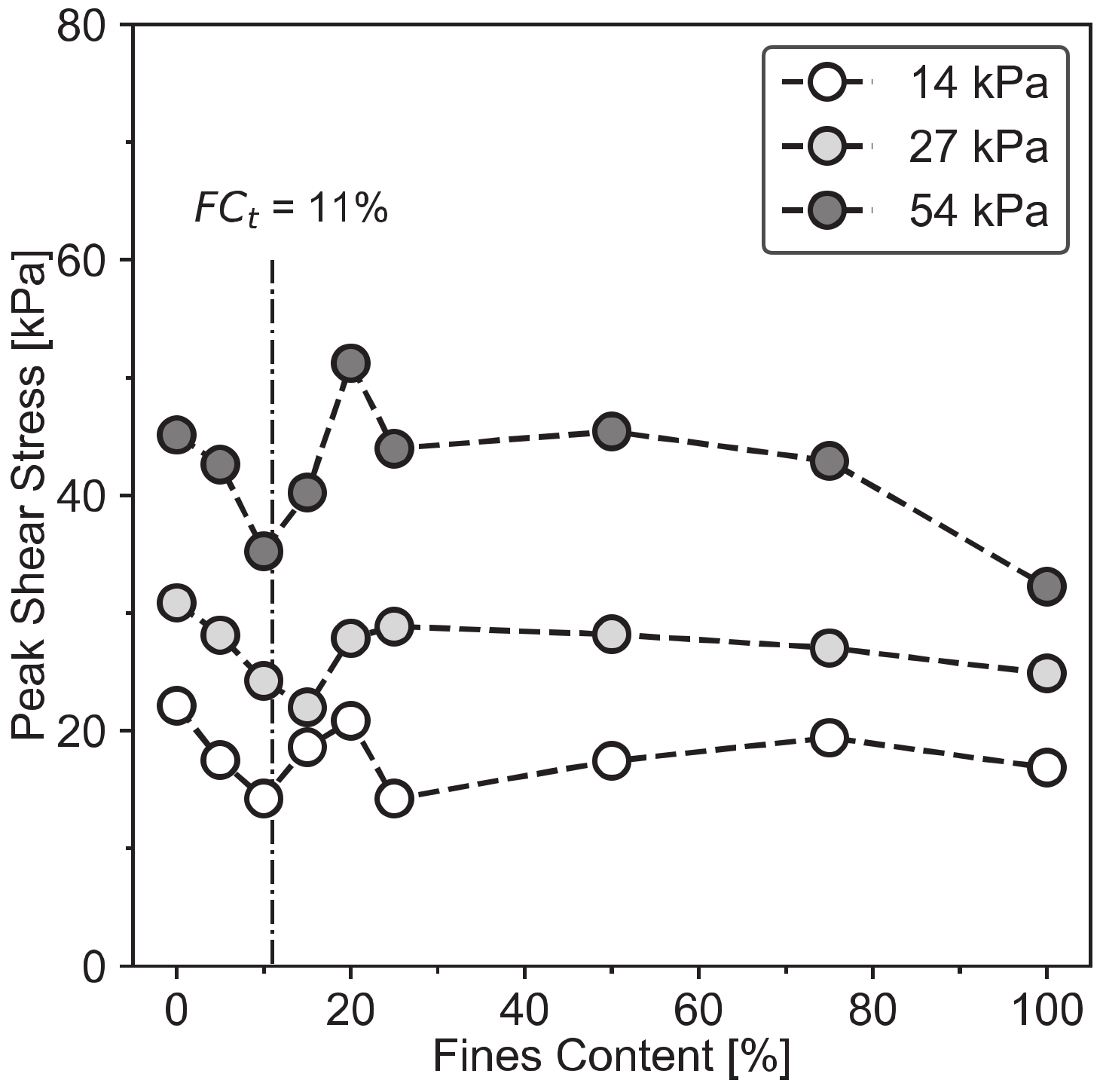
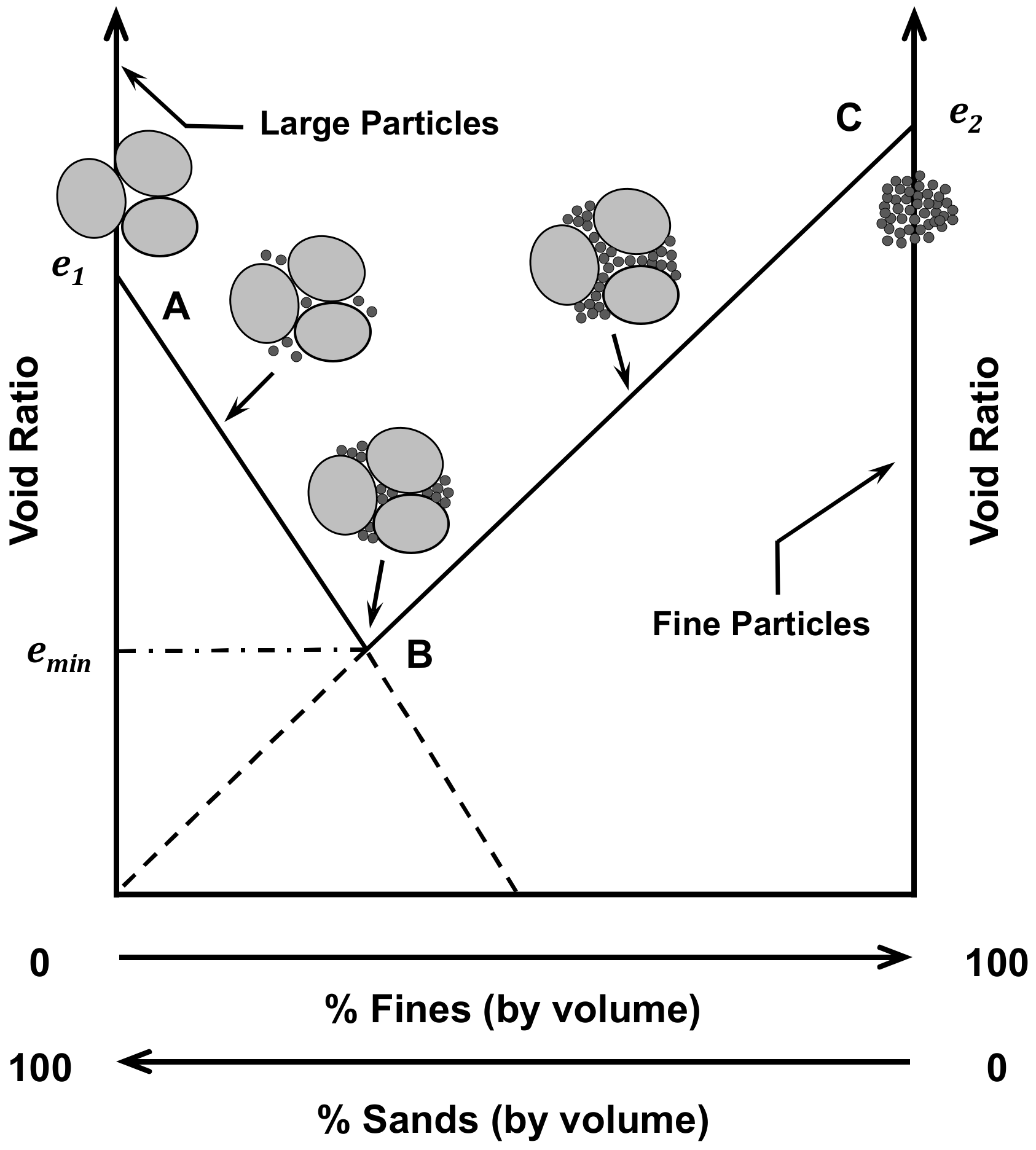
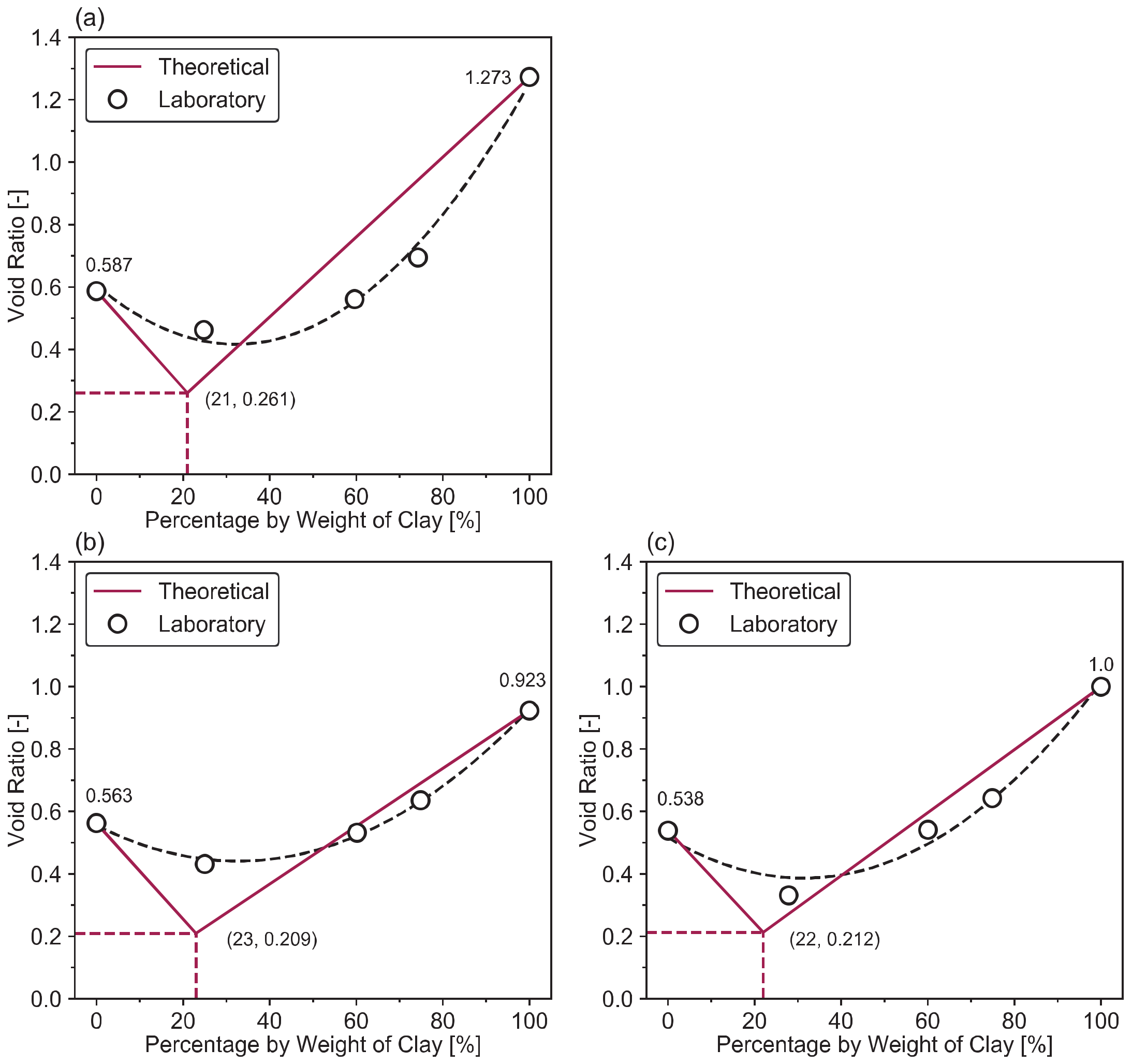
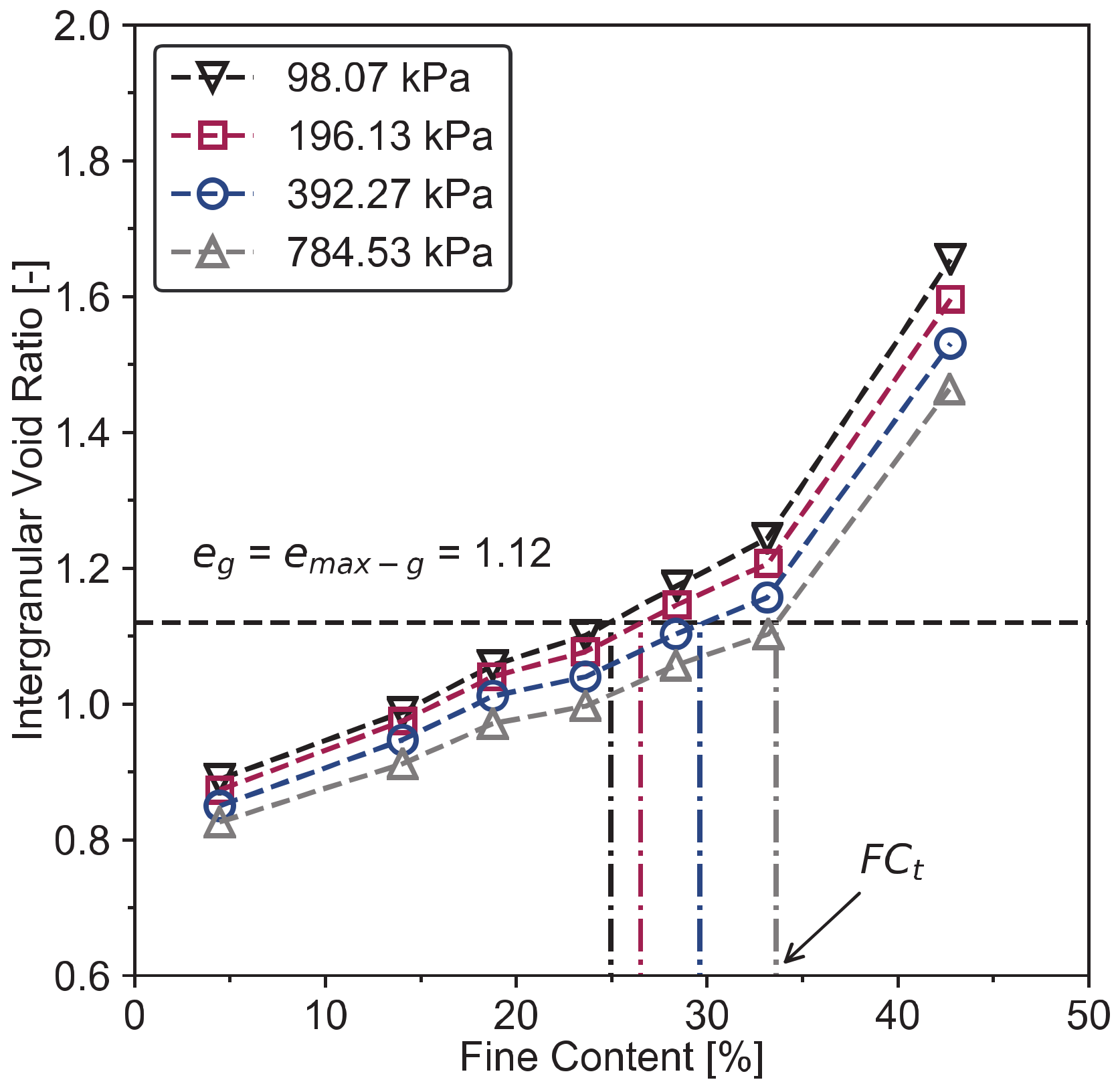
2.2.3. Transitional Fines Content (FCt)
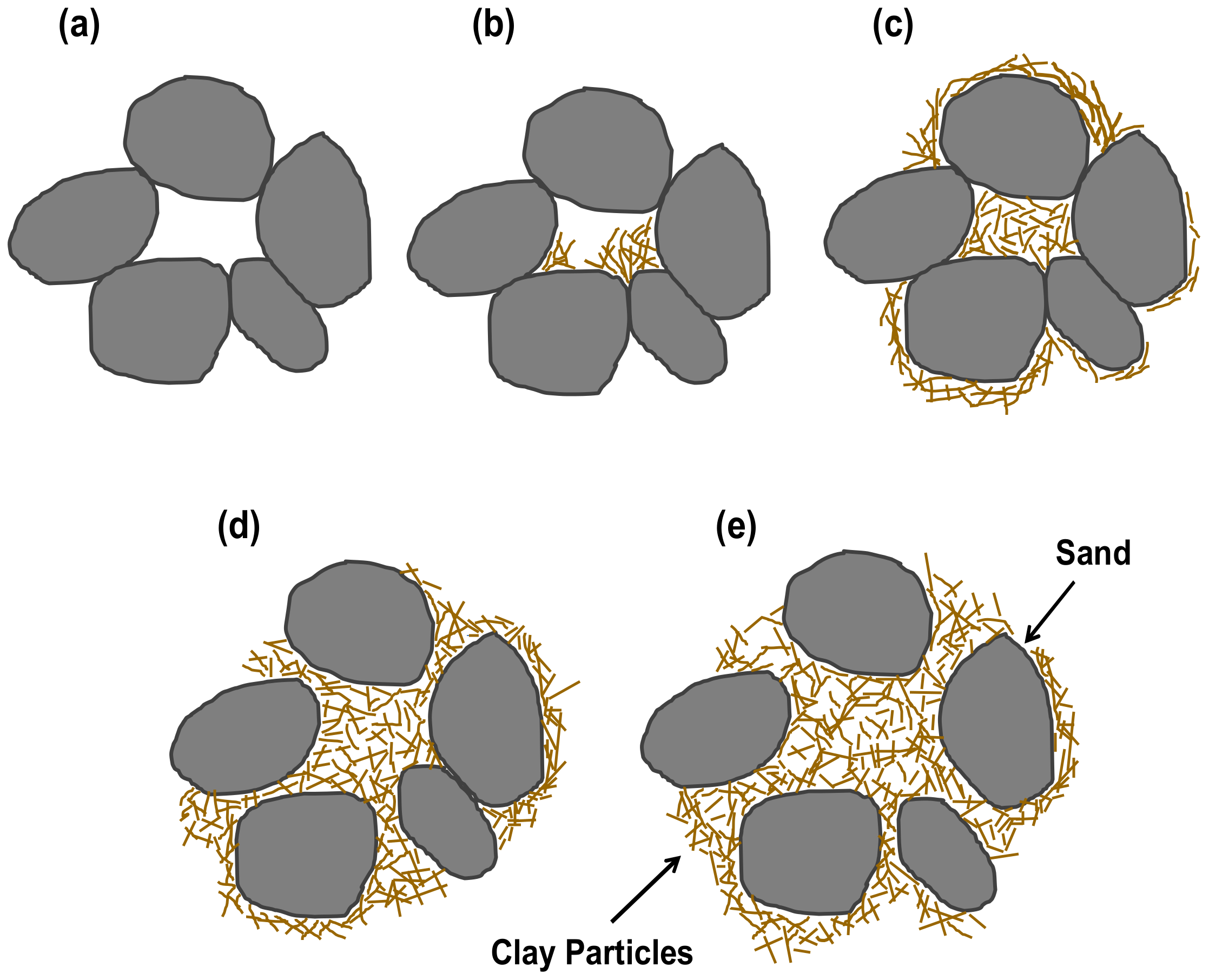
2.2.4. Microstructure of Sand–Clay Mixture
2.3. Concluding Remarks
- The mechanical behavior of the sand–clay mixture depends on the clay fraction. At low clay content it is mainly sand-controlled; at high clay content, it is primarily clay-controlled, while in the middle range of clay content, i.e., the transitional zone, the sand–clay mixture’s responses are not clear.
- Various factors control the mechanical behavior of sand–clay mixture, e.g., intergranular void ratio, water content, global void ratio, and density, which are always related to the clay fraction.
3. Interface Direct Shear Test
3.1. Introduction
3.2. Interface Direct Shear Test
3.2.1. Basic Knowledge
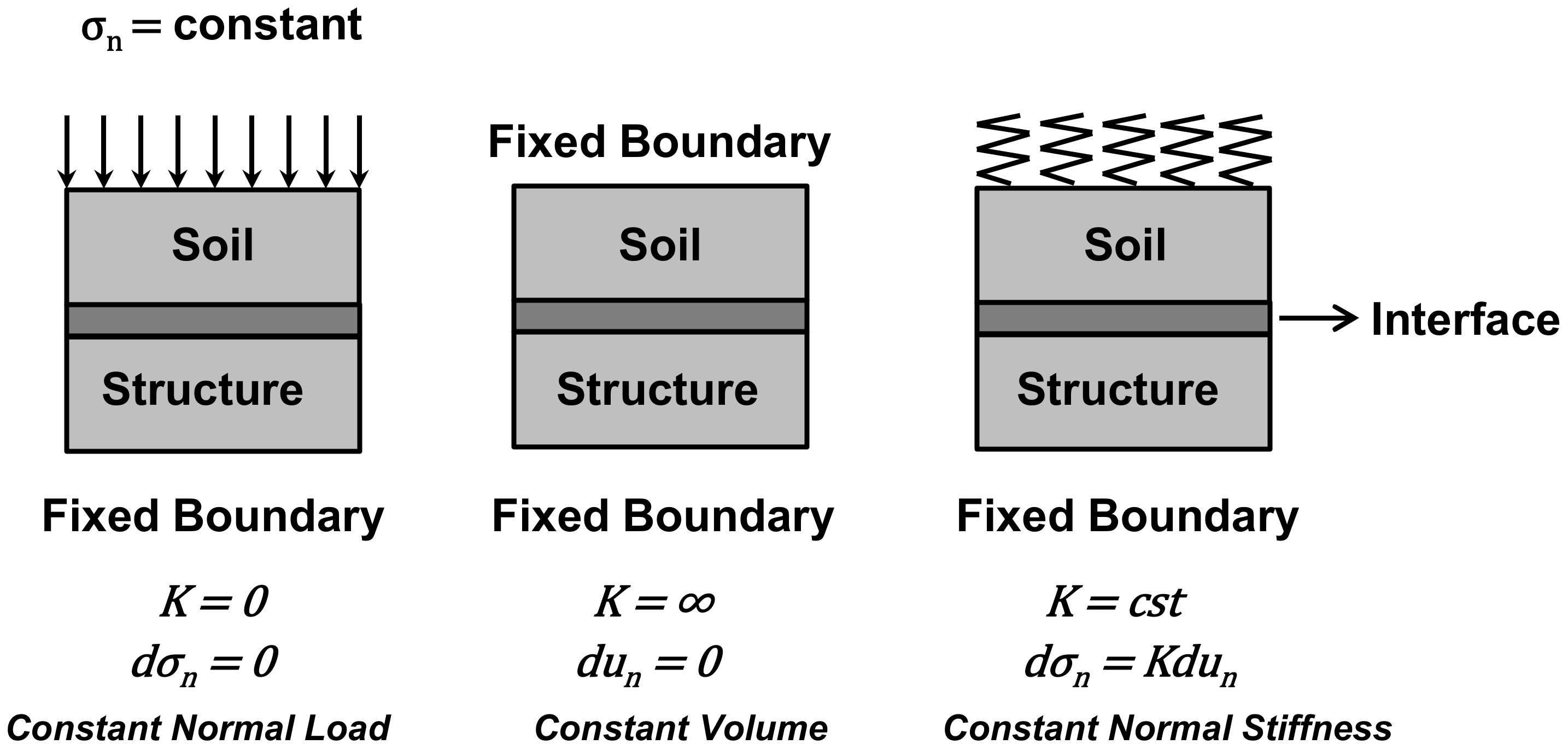
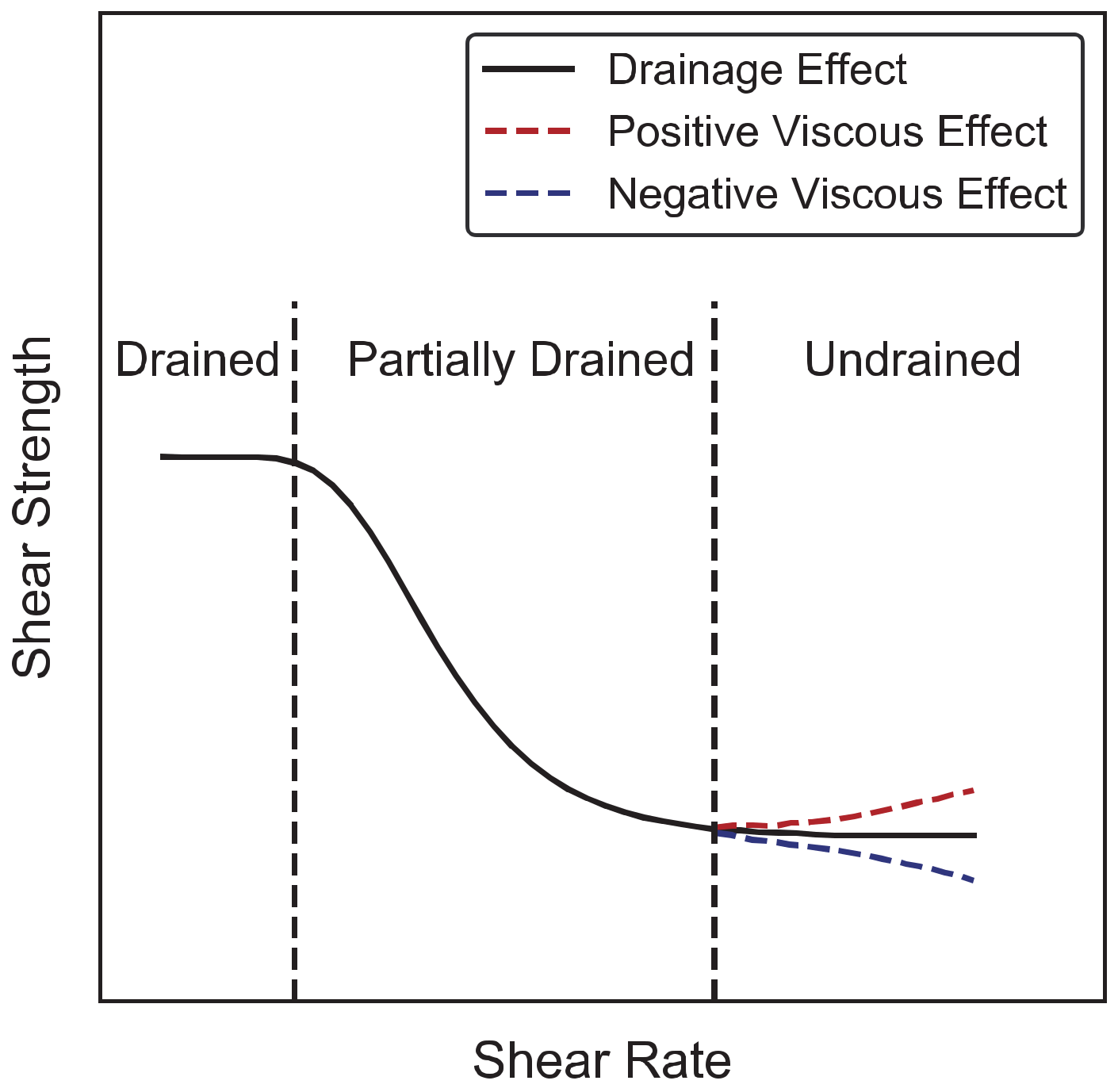
3.2.2. Boundary Conditions
- Constant Normal Load (CNL): The normal stress remains constant during the shearing stage of the interface direct shear test. In this case: , , .
- Constant Volume (CV) or Constant Normal Height (CNH): The normal stress changes during the interface shearing, and no normal displacement is allowed in the upper part of the interface element. In this case: , , .
- Constant Normal Stiffness (CNS): The normal stress changes proportionally to the elastic stiffness of the surrounding soil during the interface shear test. In this case: constant, , .
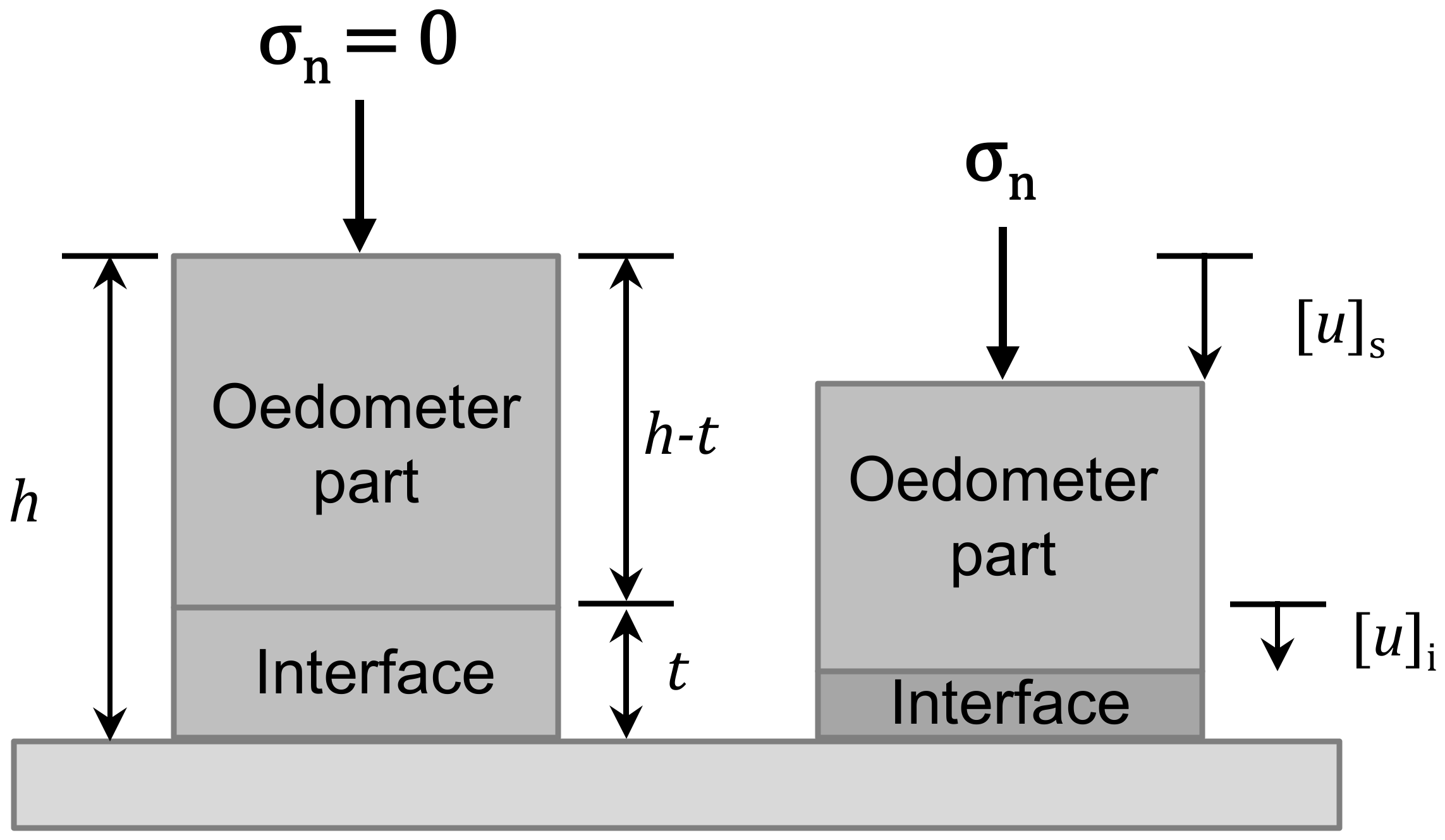
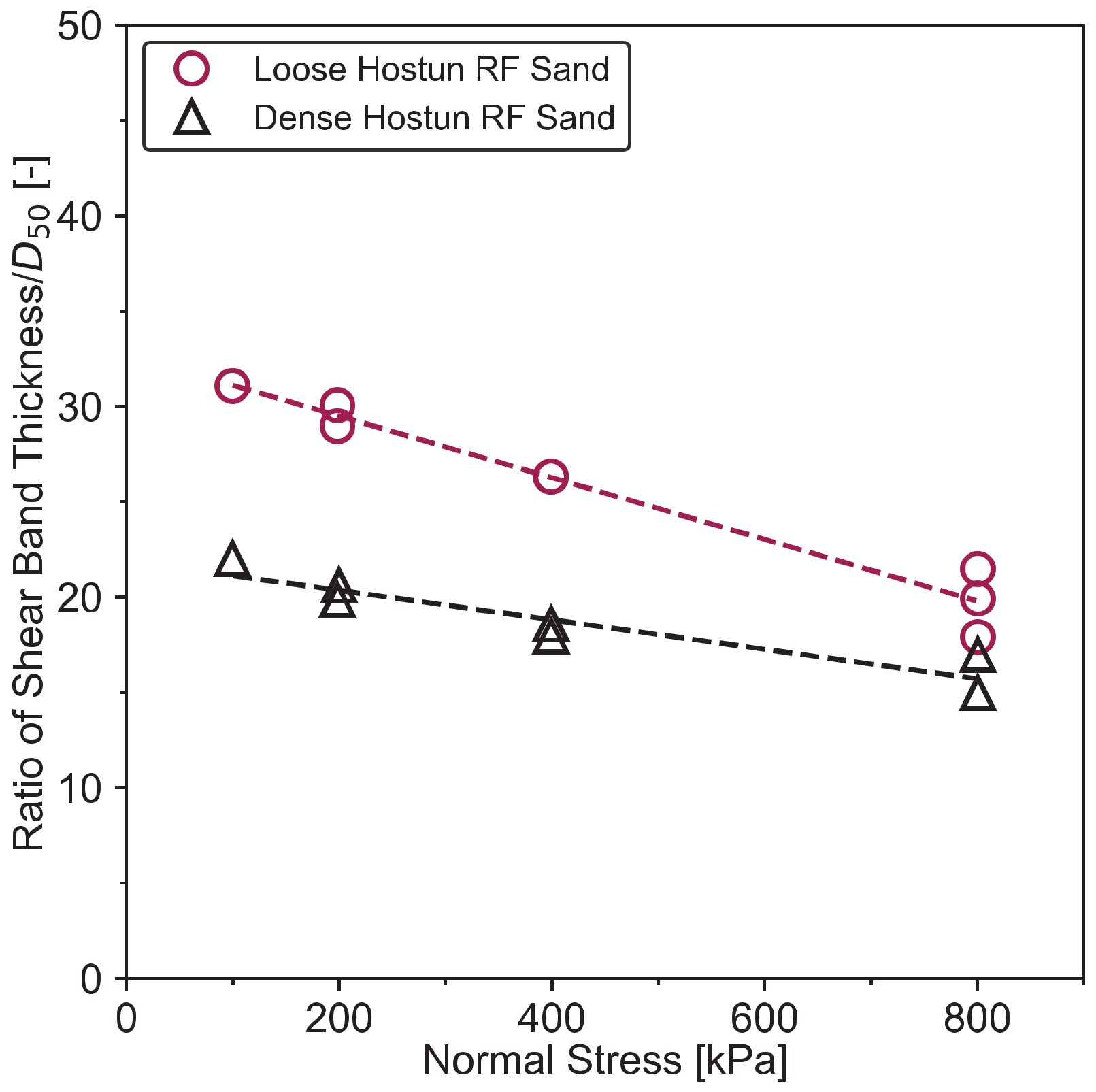
3.2.3. Interface Thickness
3.3. Influence Factors on the Mechanical Behavior of the Soil–Structure Interface
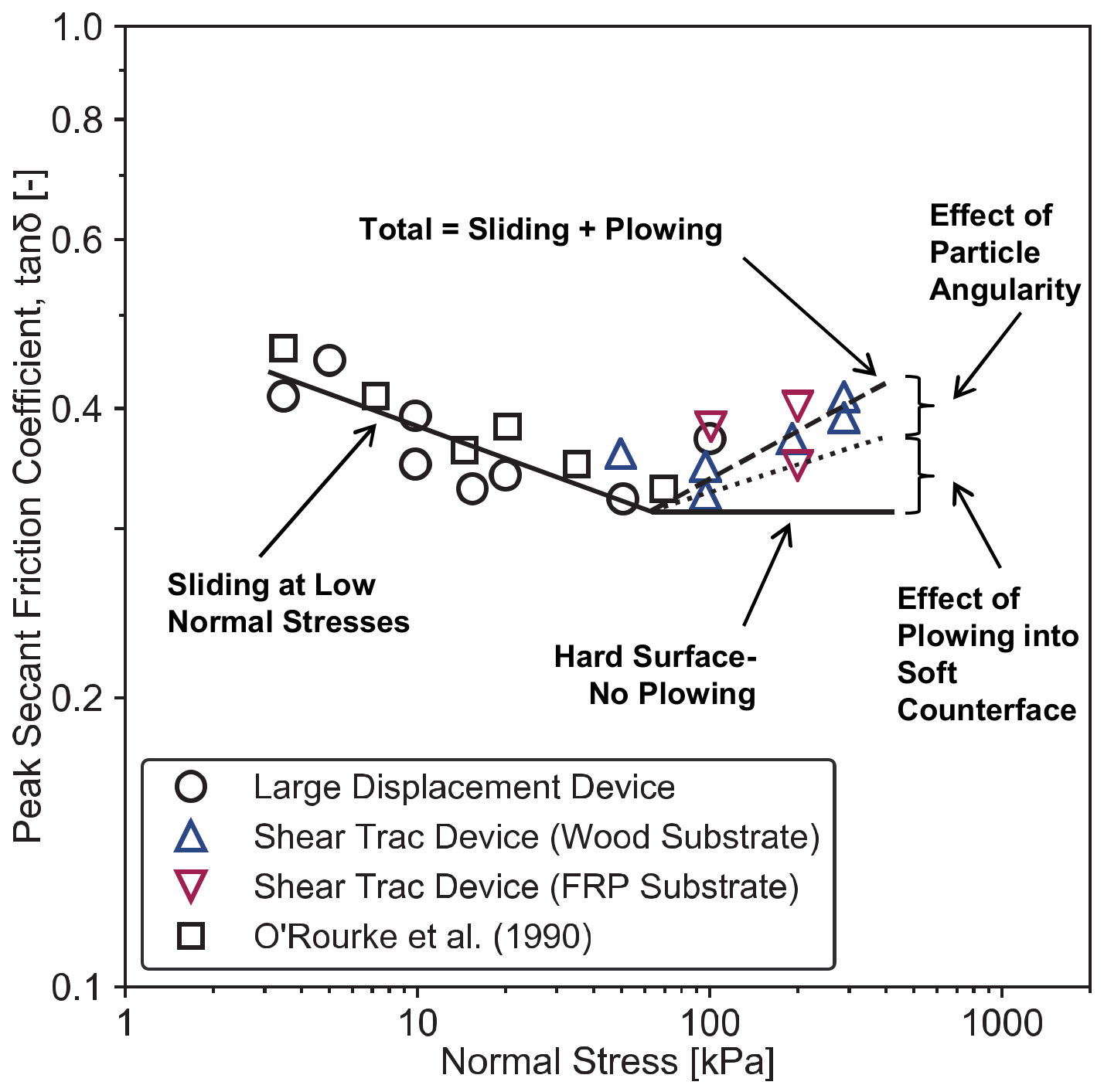
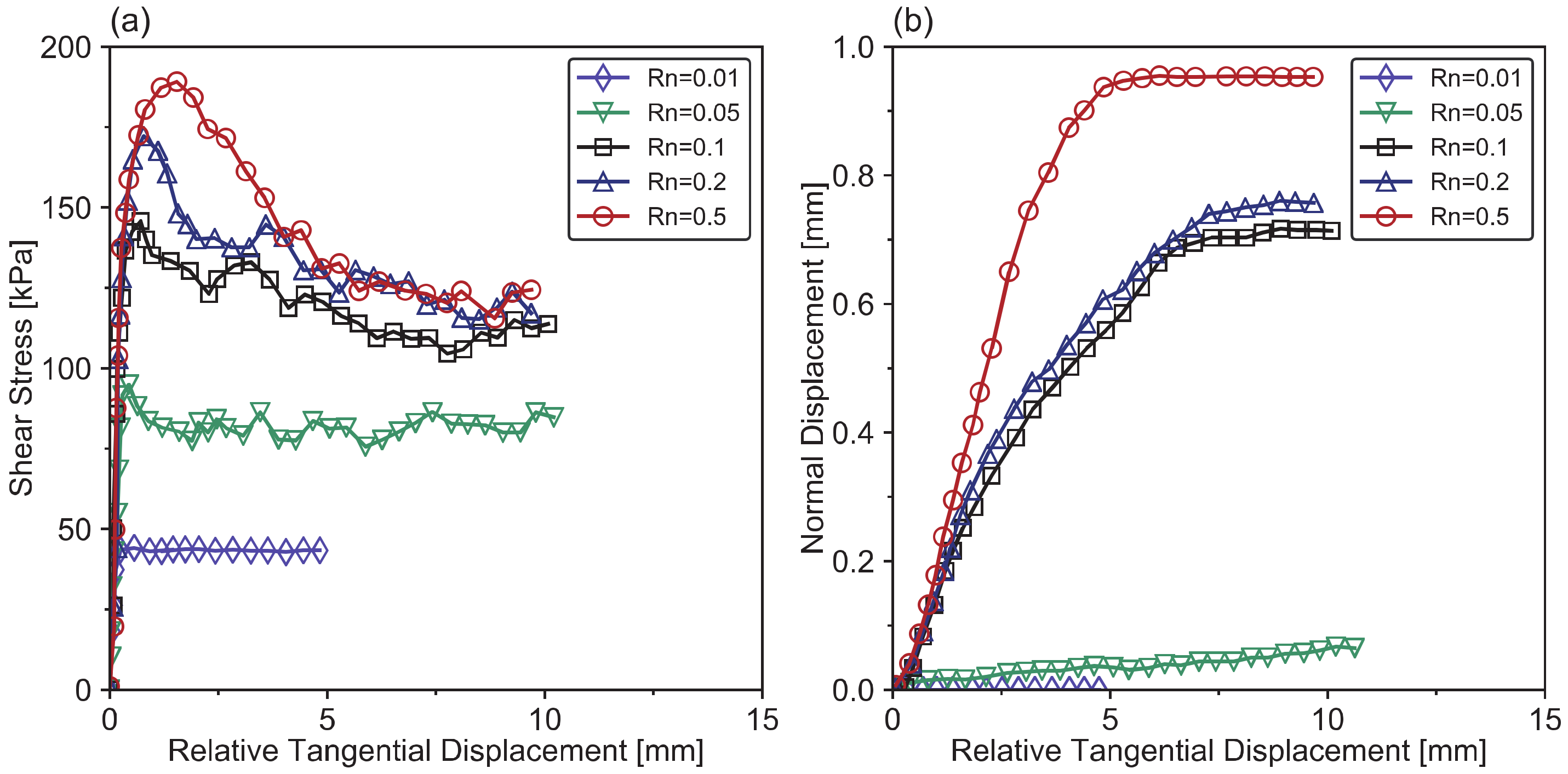
3.3.1. Effect of Normal Stress
3.3.2. Effect of Soil Density
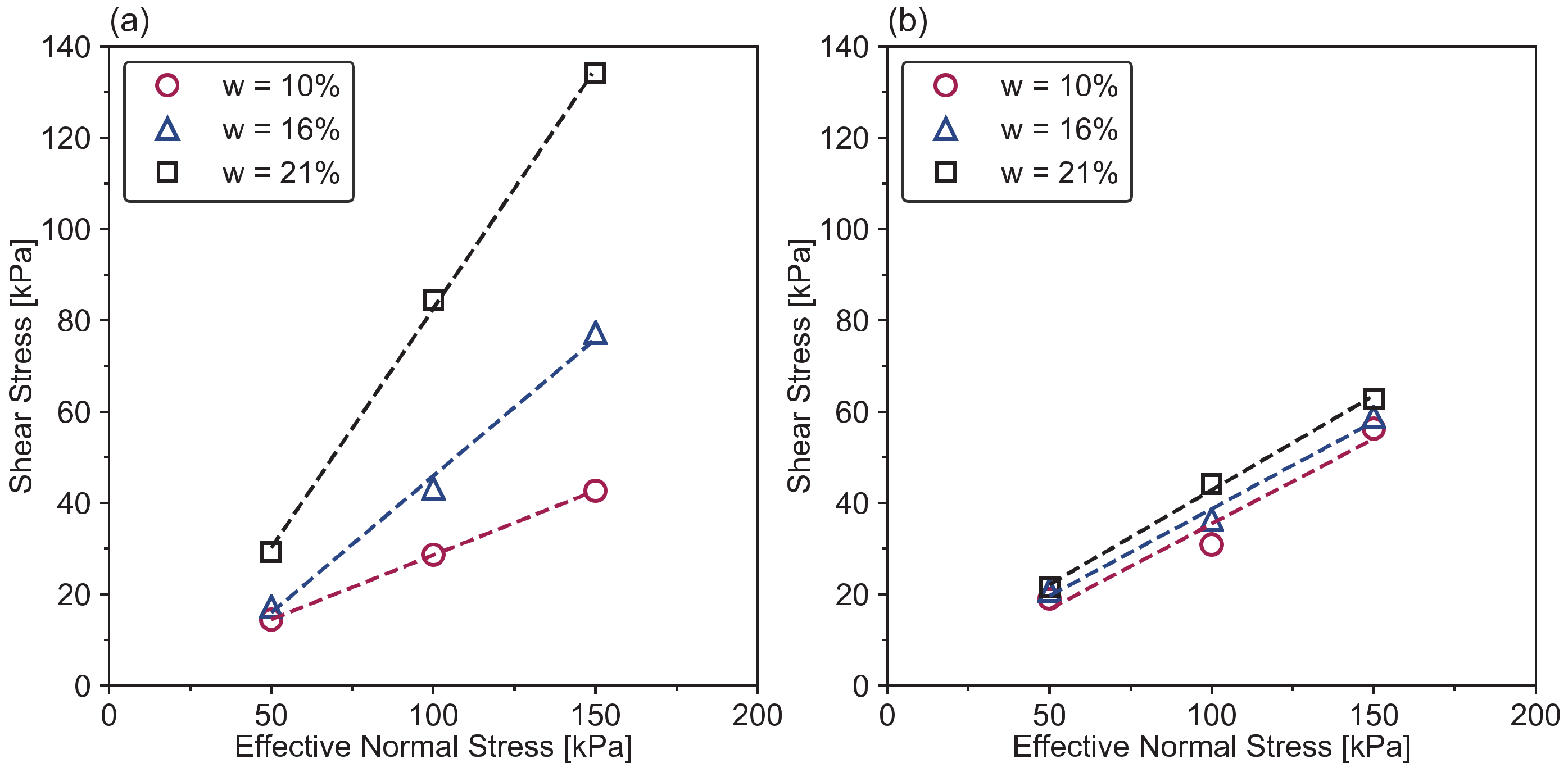
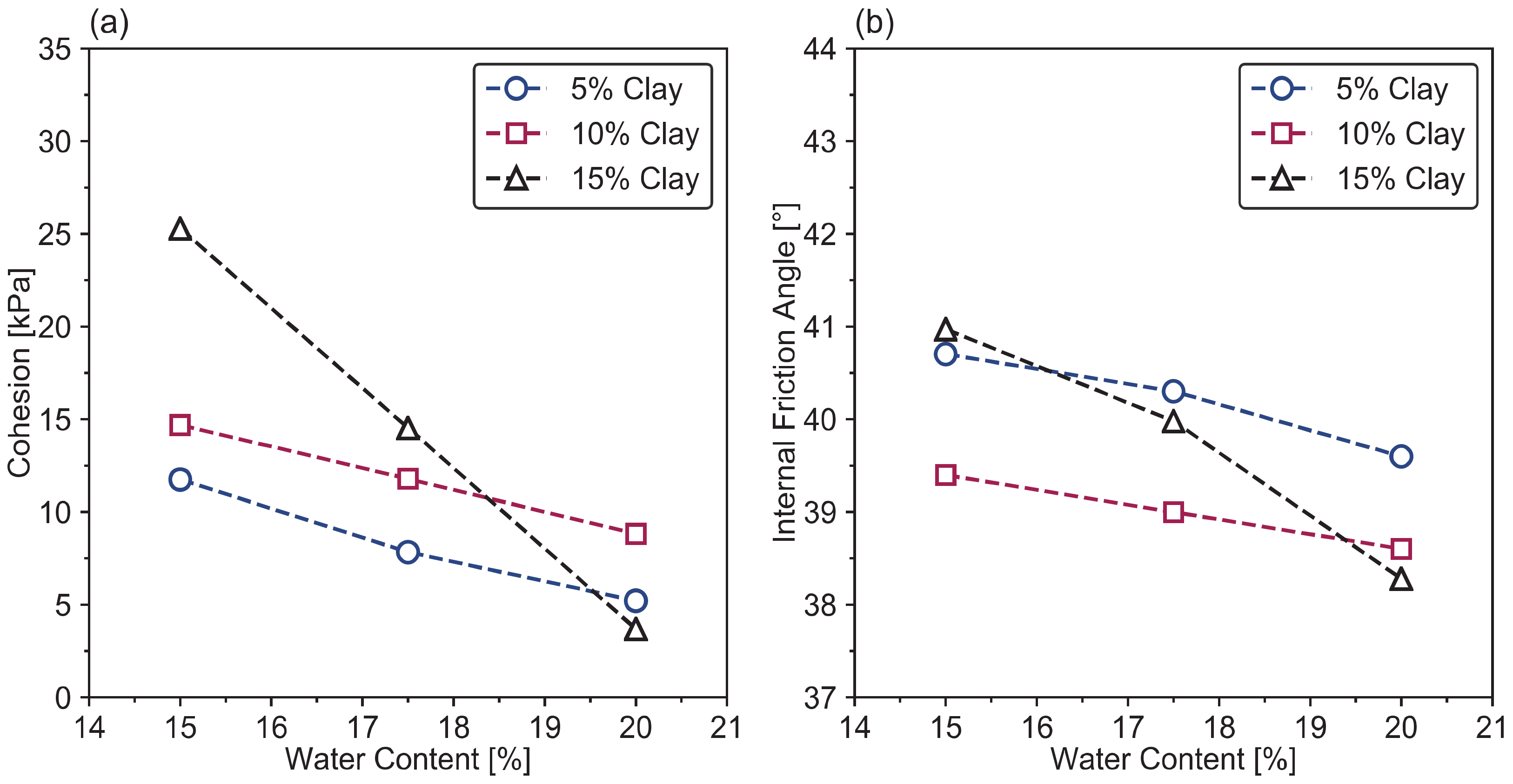
3.3.3. Effect of Water Content
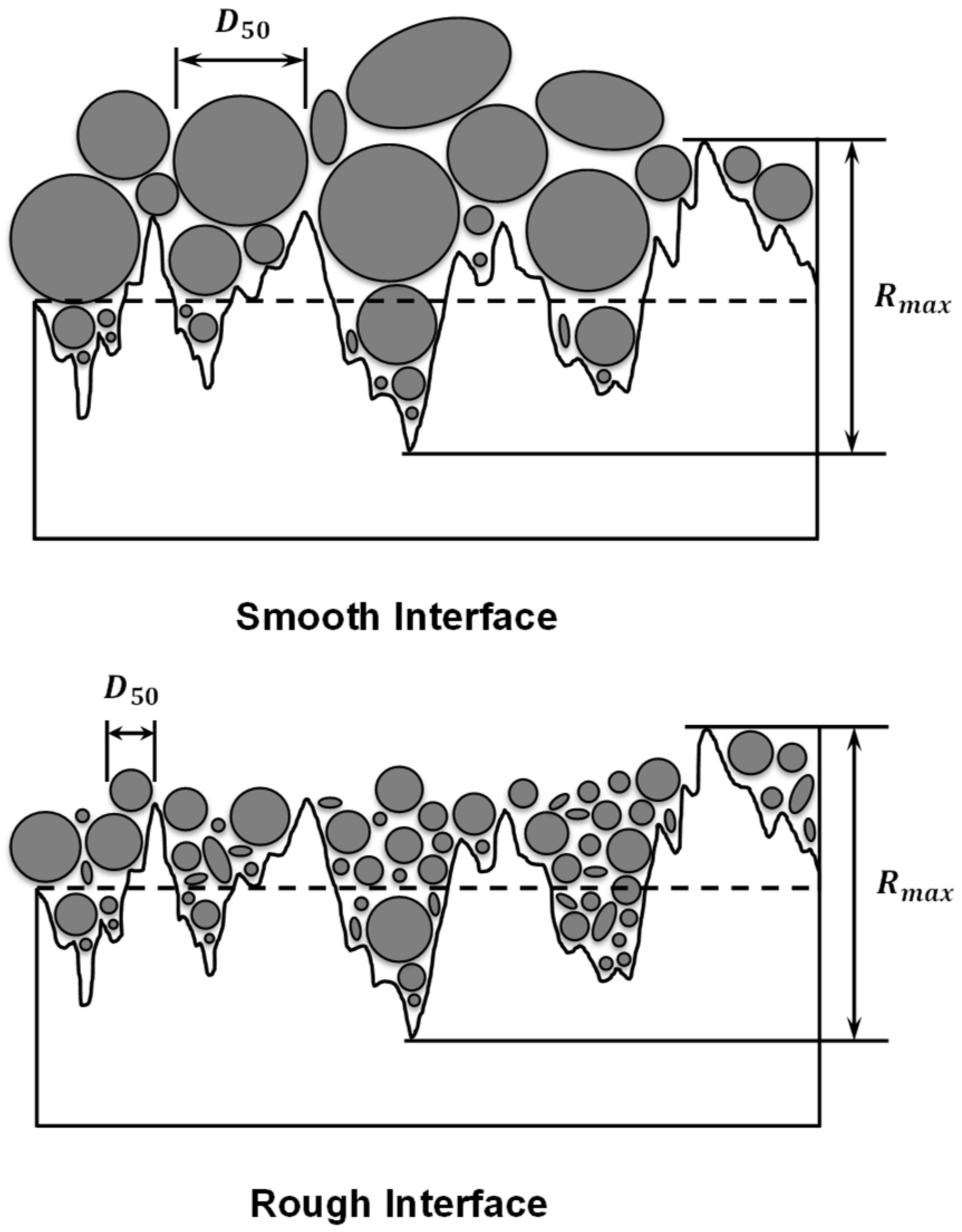
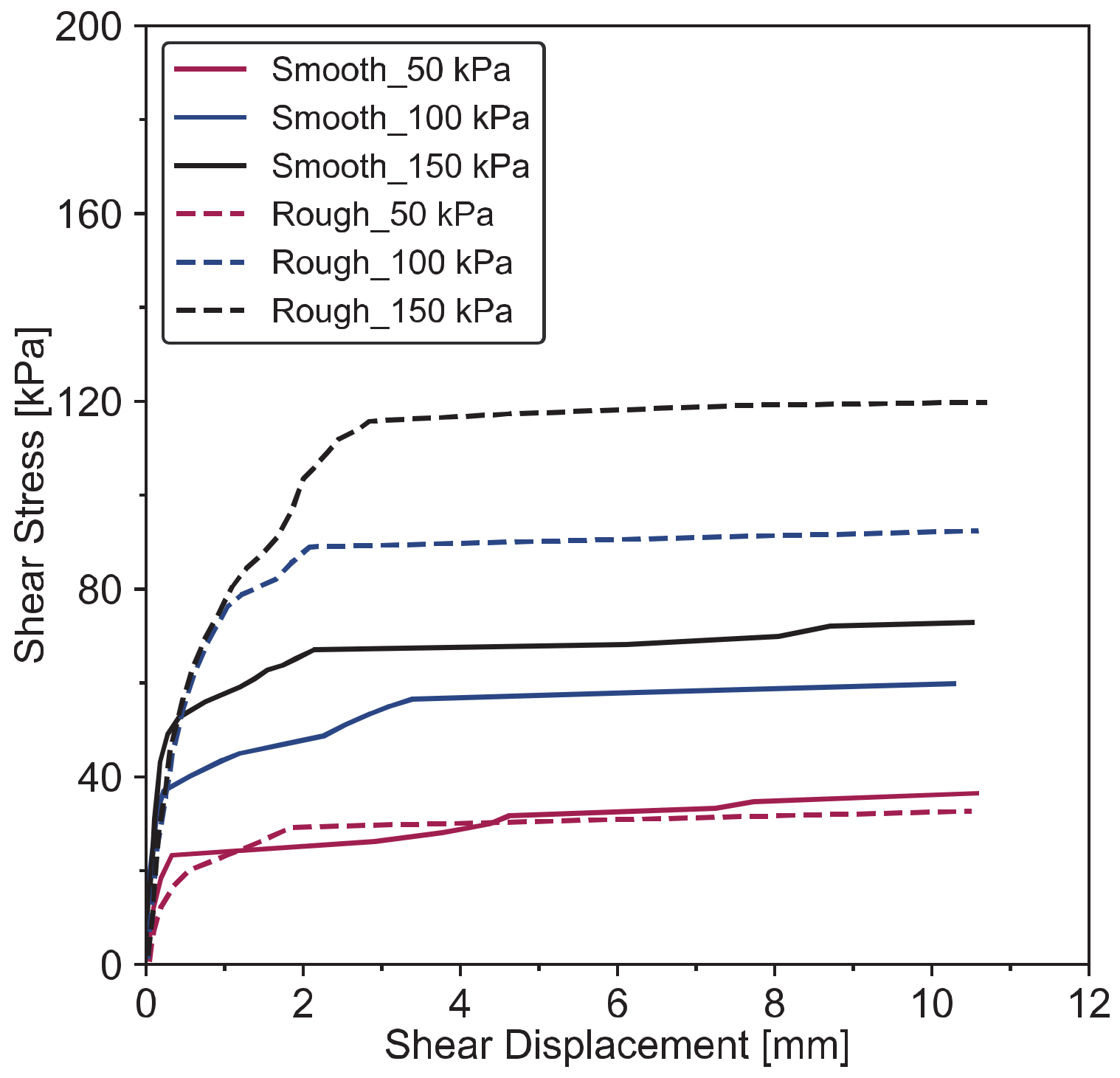
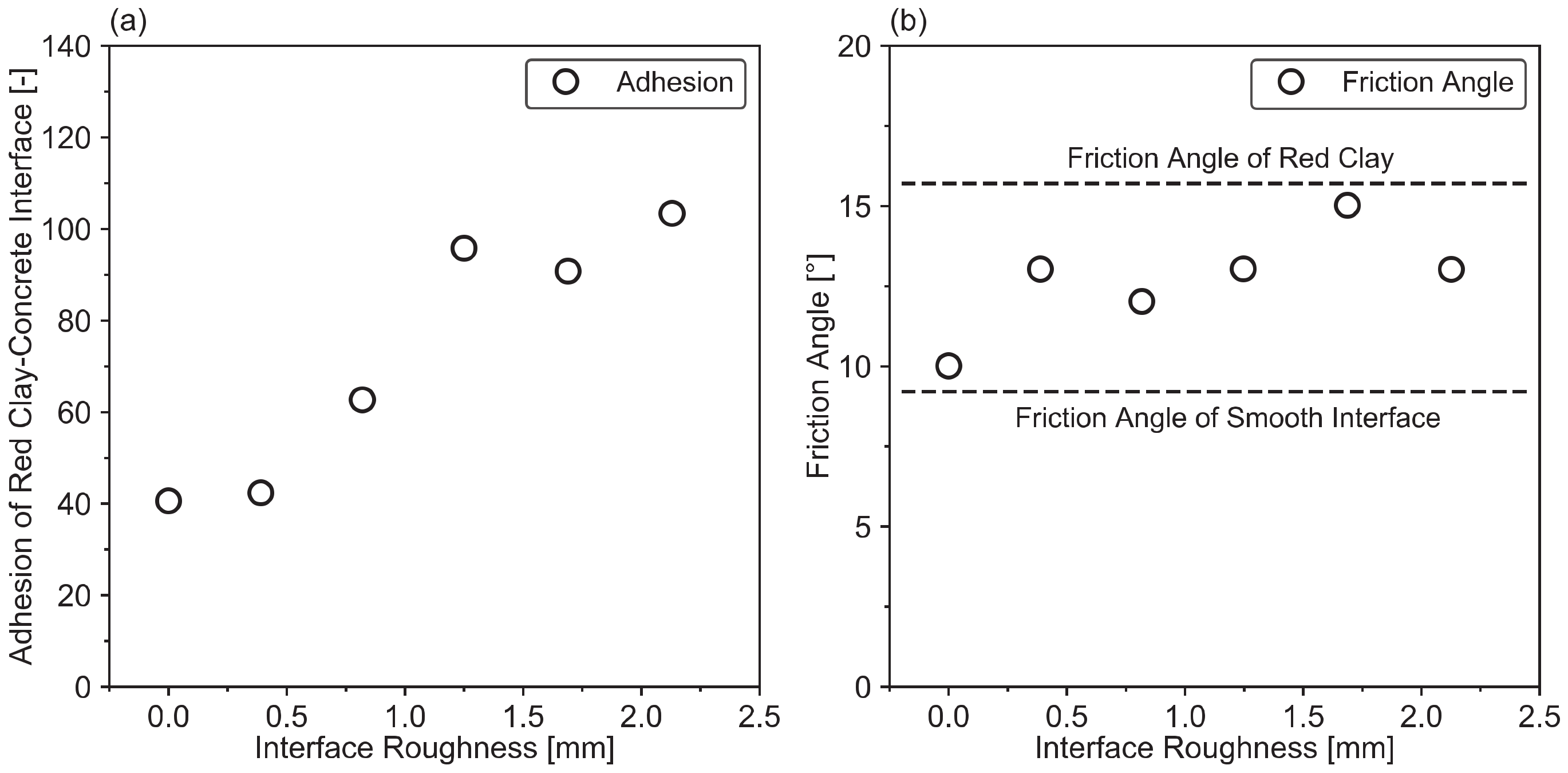
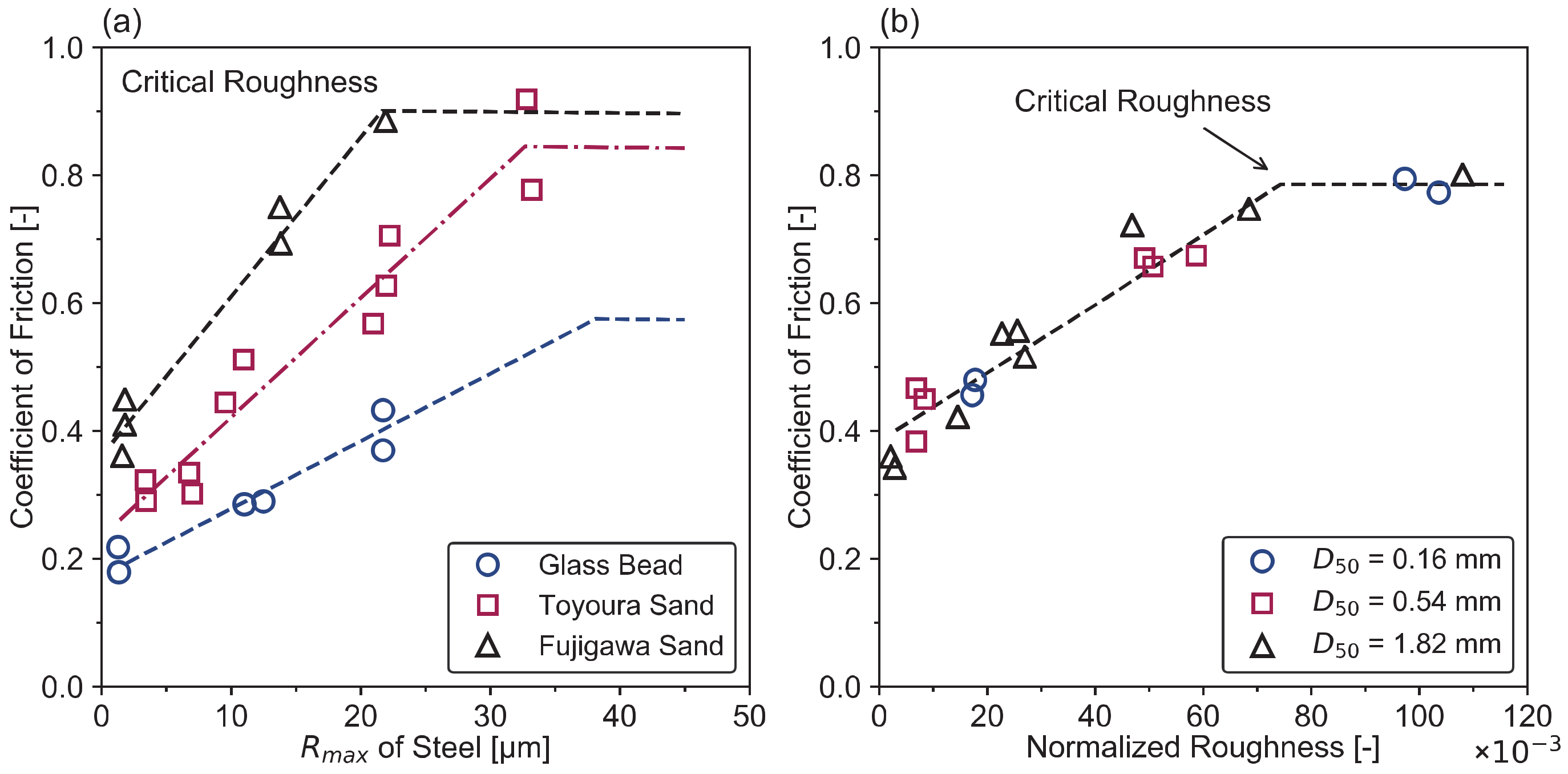
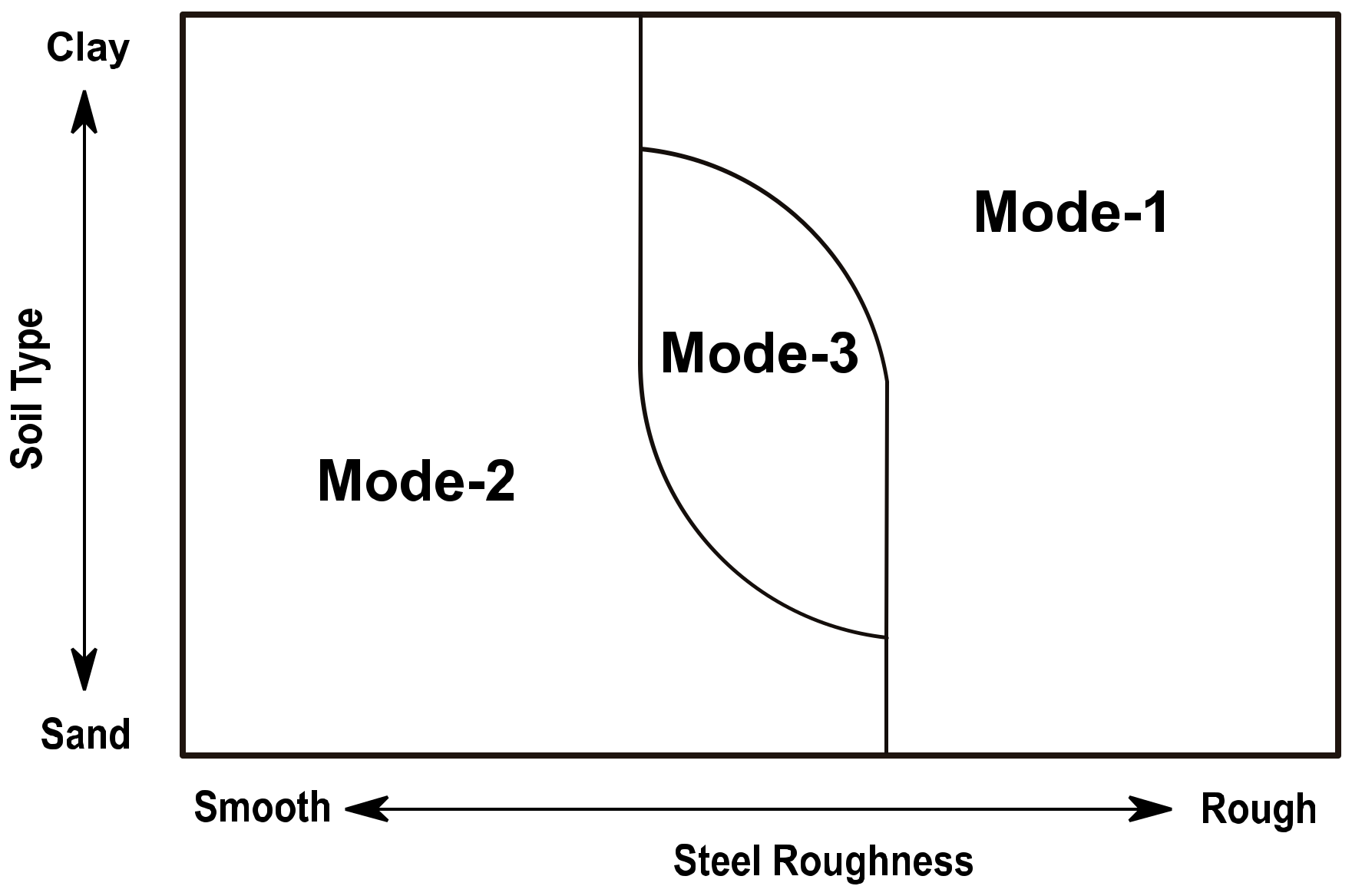
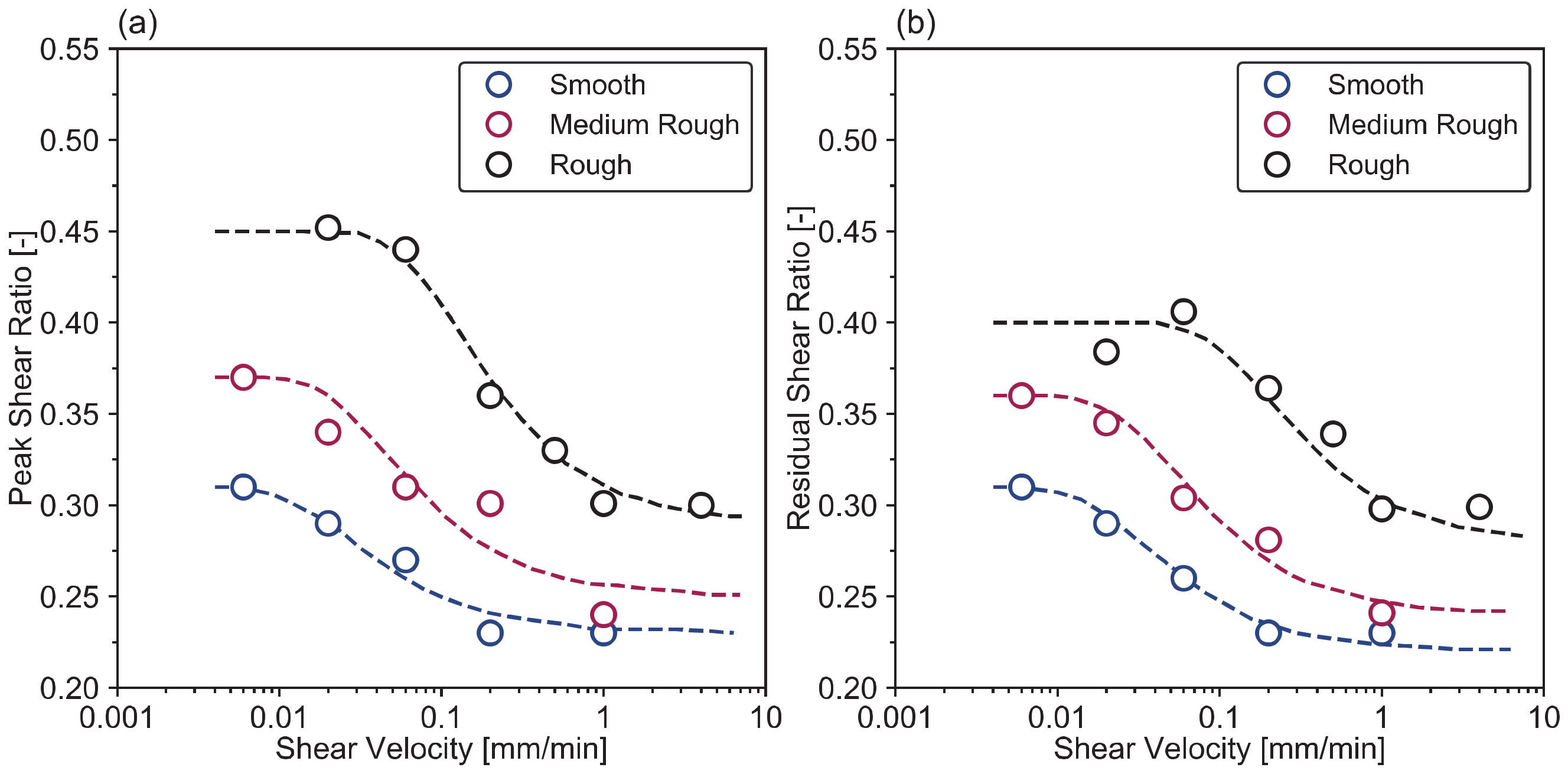
3.3.4. Influence of Interface Roughness
- Mode-1: The interface is rough; hence, shear failure occurs in the soil body.
- Mode-2: The interface is smooth, and full sliding occurs along with the interface.
- Mode-3: The shear failure and sliding occur simultaneously at the interface part.
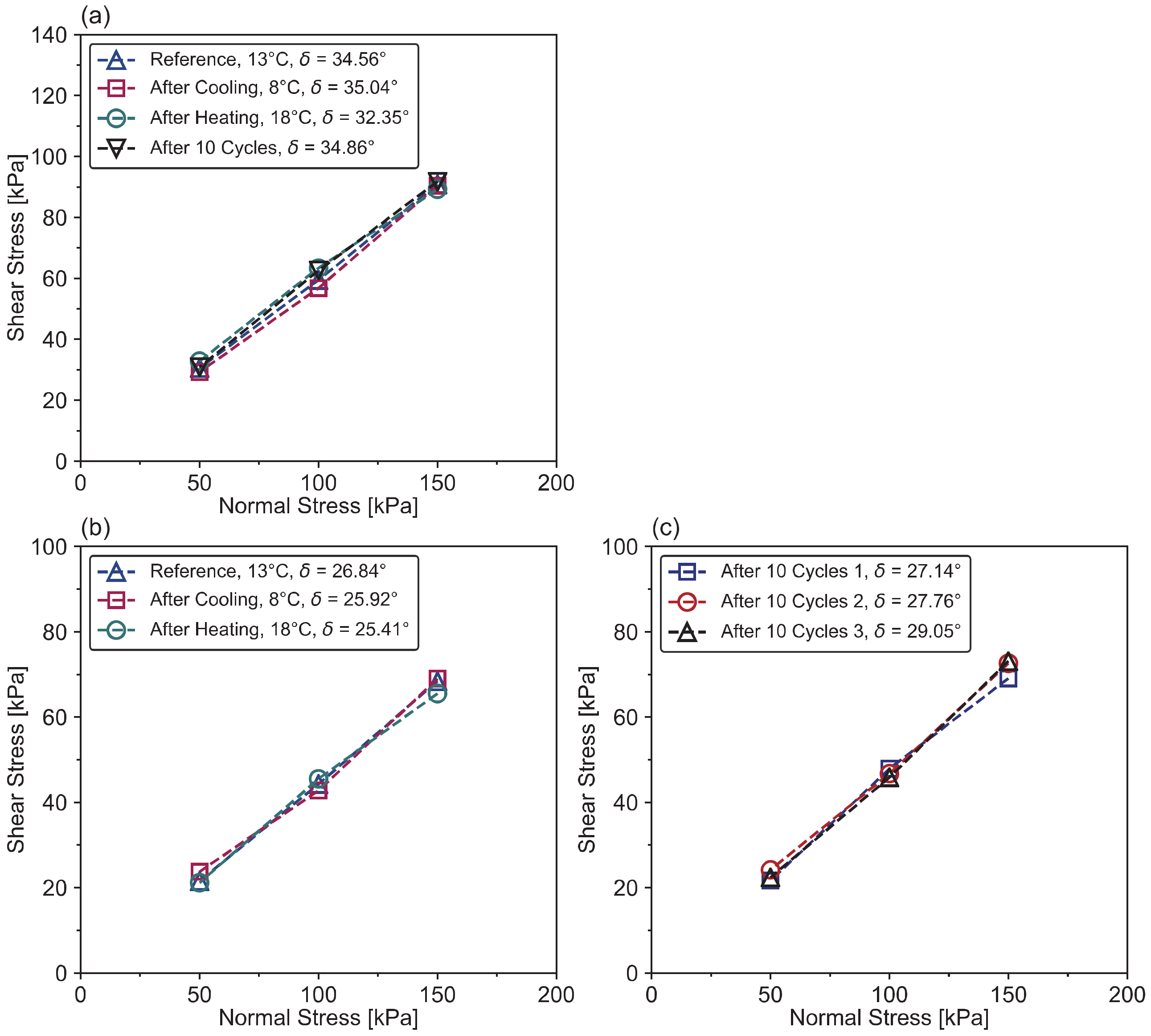
- For silica sand–structure or carbonate sand–structure interfaces, the shear behavior of the interface is not sensitive to thermal changes (for example, 8 °C~18 °C in Vasilescu [7]), which is confirmed by the fact that the friction angle of the sand–structure remains almost constant.
- For clay–structure interfaces, heating increases the shear strength of the interface and the cohesion between the two materials; this may be attributed to the thermal consolidation caused by heating [2,163]. Additionally, when the clay–structure interfaces are tested under drained conditions, a volumetric contraction is usually observed, agreeing with the typical behavior of NC clays. This can be explained by the fact that contraction is accompanied by loss of moisture of the soil. Attention should be paid, however, to the fact that the temperature range studied (typical of geothermal engineering) is not too high (e.g., 5 °C, 20 °C, and 40 °C in Yavari et al. [19]; −18 °C~20 °C in Xiao et al. [163]; 20 °C and 60 °C in Di Donna et al. [2]).
3.4. Particle Movement during Shearing
3.5. Interface Direct Shear Tests on Sand–Clay Mixture
4. Conclusions
- The mechanical behavior of the sand–clay mixture depends on the clay fraction, i.e., the changes of texture of sand–clay mixture functions of the clay content.
- Various factors that have relation to the clay fraction control the mechanical behavior of the sand–clay mixture (e.g., intergranular void ratio, water content, global void ratio, density).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abed, Y.; Bouzid, D.A.; Bhattacharya, S.; Aissa, M.H. Static impedance functions for monopiles supporting offshore wind turbines in nonhomogeneous soils-emphasis on soil/monopile interface characteristics. Earthq. Struct. 2016, 10, 1143–1179. [Google Scholar] [CrossRef]
- Di Donna, A.; Ferrari, A.; Laloui, L. Experimental investigations of the soil-concrete interface: Physical mechanisms, cyclic mobilization, and behaviour at different temperatures. Can. Geotech. J. 2016, 53, 659–672. [Google Scholar] [CrossRef]
- Dixon, D.; Gray, M.; Baumgartner, P.; Rigby, G. Pressures Acting on Waste Containers in Bentonite-Based Materials. In Proceedings of the International Conference on Radioactive Waste Management, Winnipeg, MB, Canada, 7–11 September 1986. [Google Scholar]
- Dupray, F.; François, B.; Laloui, L. Analysis of the FEBEX multi-barrier system including thermoplasticity of unsaturated bentonite. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 399–422. [Google Scholar] [CrossRef]
- Gens, A.; Guimaraes, L.d.N.; Garcia-Molina, A.; Alonso, E. Factors controlling rock-clay buffer interaction in a radioactive waste repository. Eng. Geol. 2002, 64, 297–308. [Google Scholar] [CrossRef] [Green Version]
- Laloui, L.; Sutman, M. Experimental investigation of energy piles: From laboratory to field testing. Geomech. Energy Environ. 2020, 27, 100214. [Google Scholar] [CrossRef]
- Vasilescu, A.-R. Design and Execution of Energy Piles: Validation by In-Situ and Laboratory Experiments. Ph.D. Thesis, École Centrale de Nantes, Nantes, France, 7 August 2019. [Google Scholar]
- Vasilescu, R.; Yin, K.; Fauchille, A.-L.; Kotronis, P.; Dano, C.; Manirakiza, R.; Gotteland, P. Influence of Thermal Cycles on the Deformation of Soil-Pile Interface in Energy Piles. In Proceedings of the E3S Web of Conferences, Glasgow, UK, 25 June 2019; p. 13004. [Google Scholar]
- Yu, Q.; Yin, K.; Ma, J.; Shimada, H. Vertical Shaft Support Improvement Studies by Strata Grouting at Aquifer Zone. Adv. Civ. Eng. 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- DeJong, J.T.; Randolph, M.F.; White, D.J. Interface load transfer degradation during cyclic loading: A microscale investigation. Soils Found. 2003, 43, 81–93. [Google Scholar] [CrossRef] [Green Version]
- Hu, L.; Pu, J. Testing and modeling of soil-structure interface. J. Geotech. Geoenviron. Eng. 2004, 130, 851–860. [Google Scholar] [CrossRef]
- Pra-ai, S. Behaviour of Soil-Structure Interfaces Subjected to a Large Number of Cycles. Application to Piles. Ph.D. Thesis, Université de Grenoble, Grenoble, France, 2013. [Google Scholar]
- Pra-ai, S.; Boulon, M. Soil-structure cyclic direct shear tests: A new interpretation of the direct shear experiment and its application to a series of cyclic tests. Acta Geotech. 2017, 12, 107–127. [Google Scholar] [CrossRef]
- Tovar-Valencia, R.D.; Galvis-Castro, A.; Salgado, R.; Prezzi, M. Effect of surface roughness on the shaft resistance of displacement model piles in sand. J. Geotech. Geoenviron. Eng. 2018, 144, 04017120. [Google Scholar] [CrossRef]
- Maghsoodi, S. Thermo-Mechanical Behavior of Soil-Structure Interface under Monotonic and Cyclic Loads in the Context of Energy Geostructures. Ph.D. Thesis, Université de Lorraine, Nancy, France, 2020. [Google Scholar]
- Rouaiguia, A. Residual shear strength of clay-structure interfaces. Int. J. Civ. Environ. Eng. 2010, 10, 6–18. [Google Scholar]
- Maghsoodi, S.; Cuisinier, O.; Masrouri, F. Thermal effects on mechanical behaviour of soil-structure interface. Can. Geotech. J. 2020, 57, 32–47. [Google Scholar] [CrossRef] [Green Version]
- Vasilescu, A.R.; Fauchille, A.-L.; Dano, C.; Kotronis, P.; Manirakiza, R.; Gotteland, P. Impact of Temperature Cycles at Soil-Concrete Interface for Energy Piles. In Proceedings of the International Symposium on Energy Geotechnics, Lausanne, Switzerland, 25–28 September 2018; pp. 35–42. [Google Scholar]
- Yavari, N.; Tang, A.M.; Pereira, J.-M.; Hassen, G. Effect of temperature on the shear strength of soils and the soil-structure interface. Can. Geotech. J. 2016, 53, 1186–1194. [Google Scholar] [CrossRef]
- Yazdani, S.; Helwany, S.; Olgun, G. Influence of temperature on soil-pile interface shear strength. Geomech. Energy Environ. 2019, 18, 69–78. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, J.; Xiao, Y.; Li, J. Effect of roughness on shear behavior of red clay-concrete interface in large-scale direct shear tests. Can. Geotech. J. 2015, 52, 1122–1135. [Google Scholar] [CrossRef]
- Li, C.; Kong, G.; Liu, H.; Abuel-Naga, H. Effect of temperature on behaviour of red clay-structure interface. Can. Geotech. J. 2019, 56, 126–134. [Google Scholar] [CrossRef]
- Liu, F.-Y.; Wang, P.; Geng, X.-y.; Wang, J.; Lin, X. Cyclic and post-cyclic behaviour from sand-geogrid interface large-scale direct shear tests. Geosynth. Int. 2016, 23, 129–139. [Google Scholar] [CrossRef]
- Martinez, A.; Stutz, H.H. Rate effects on the interface shear behaviour of normally and overconsolidated clay. Géotechnique 2019, 69, 801–815. [Google Scholar] [CrossRef]
- Sayeed, M.; Ramaiah, B.J.; Rawal, A. Interface shear characteristics of jute/polypropylene hybrid nonwoven geotextiles and sand using large size direct shear test. Geotext. Geomembr. 2014, 42, 63–68. [Google Scholar] [CrossRef]
- ASTM-D2487. Classification of Soils for Engineering Purposes (Unified Soil Classification System); ASTM International: West Conshohocken, PA, USA, 1992. [Google Scholar]
- Kim, U.-G.; Zhuang, L.; Kim, D.; Lee, J. Evaluation of cyclic shear strength of mixtures with sand and different types of fines. Mar. Georesources Geotechnol. 2017, 35, 447–455. [Google Scholar] [CrossRef]
- Bennett, R.; Hulbert, M. Clay Microstructure; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Kenney, T. Residual Strengths of Mineral Mixtures; Norges Geotekniske Institutt: Oslo, Norway, 1977; pp. 21–26. [Google Scholar]
- Mitchell, J.K.; Soga, K. Fundamentals of Soil Behavior; John Wiley & Sons: New York, NY, USA, 2005; Volume 3. [Google Scholar]
- Muir Wood, D.; Kumar, G. Experimental observations of behaviour of heterogeneous soils. Mech. Cohesive-Frict. Mater. 2000, 5, 373–398. [Google Scholar] [CrossRef]
- Thevanayagam, S.; Shenthan, T.; Mohan, S.; Liang, J. Undrained fragility of clean sands, silty sands, and sandy silts. J. Geotech. Geoenviron. Eng. 2002, 128, 849–859. [Google Scholar] [CrossRef]
- Lupini, J.F.; Skinner, A.E.; Vaughan, P.R. The drained residual strength of cohesive soils. Géotechnique 1981, 31, 181–213. [Google Scholar] [CrossRef]
- Cabalar, A.F.; Mustafa, W.S. Behaviour of sand-clay mixtures for road pavement subgrade. Int. J. Pavement Eng. 2017, 18, 714–726. [Google Scholar] [CrossRef]
- Graham, J.; Oswell, J.; Gray, M. The effective stress concept in saturated sand-clay buffer. Can. Geotech. J. 1992, 29, 1033–1043. [Google Scholar] [CrossRef]
- Graham, J.; Saadat, F.; Gray, M.; Dixon, D.; Zhang, Q.-Y. Strength and volume change behaviour of a sand-bentonite mixture. Can. Geotech. J. 1989, 26, 292–305. [Google Scholar] [CrossRef]
- Graham, J.; Sunn, B.; Gray, M. Strength and Volume Change Characteristics of a Sand-Bentonite Buffer. Available online: https://inis.iaea.org/collection/NCLCollectionStore/_Public/22/004/22004854.pdf?r=1 (accessed on 5 May 2021).
- Havens, J.H.; Goodwin, W.A. Clay Mineralogy and Soil Stabilization. 1951. Available online: https://uknowledge.uky.edu/ktc_researchreports/1346 (accessed on 5 May 2021).
- Kim, D.; Nam, B.H.; Youn, H. Effect of clay content on the shear strength of clay-sand mixture. Int. J. Geo-Eng. 2018, 9, 19. [Google Scholar] [CrossRef]
- Lade, P.V.; Liggio, C.; Yamamuro, J.A. Effects of non-plastic fines on minimum and maximum void ratios of sand. Geotech. Test. J. 1998, 21, 336–347. [Google Scholar]
- Miller, E.A.; Sowers, G.F. The strength characteristics of soil-aggregate mixtures & discussion. Highw. Res. Board Bull. 1958, 183, 16–32. [Google Scholar]
- Vallejo, L.E.; Mawby, R. Porosity influence on the shear strength of granular material-clay mixtures. Eng. Geol. 2000, 58, 125–136. [Google Scholar] [CrossRef]
- Cekerevac, C.; Laloui, L. Experimental study of thermal effects on the mechanical behaviour of a clay. Int. J. Numer. Anal. methods Geomech. 2004, 28, 209–228. [Google Scholar] [CrossRef]
- Esrig, M.I. Some temperature effects on soil compressibility and pore water pressure. Spec. Rep. 1969, 231. Available online: https://onlinepubs.trb.org/Onlinepubs/sr/sr103/103-022.pdf (accessed on 5 May 2021).
- Georgiannou, V.; Burland, J.; Hight, D. The undrained behaviour of clayey sands in triaxial compression and extension. Geotechnique 1990, 40, 431–449. [Google Scholar] [CrossRef]
- Hammad, T.; Fleureau, J.-M.; Hattab, M. Kaolin/montmorillonite mixtures behaviour on oedometric path and microstructural variations. Eur. J. Environ. Civ. Eng. 2013, 17, 826–840. [Google Scholar] [CrossRef]
- Hattab, M.; Hammad, T.; Fleureau, J.-M. Internal friction angle variation in a kaolin/montmorillonite clay mix and microstructural identification. Géotechnique 2015, 65, 1–11. [Google Scholar] [CrossRef]
- Hong, P.; Pereira, J.-M.; Tang, A.M.; Cui, Y.-J. On some advanced thermo-mechanical models for saturated clays. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 2952–2971. [Google Scholar] [CrossRef]
- Lingnau, B.; Graham, J.; Yarechewski, D.; Tanaka, N.; Gray, M. Effects of temperature on strength and compressibility of sand-bentonite buffer. Eng. Geol. 1996, 41, 103–115. [Google Scholar] [CrossRef]
- Monkul, M.M.; Ozden, G. Compressional behavior of clayey sand and transition fines content. Eng. Geol. 2007, 89, 195–205. [Google Scholar] [CrossRef]
- Namdar, A. Kaolinite thermal evaluation in geotechnical engineering. Adv. Nat. Appl. Sci. 2011, 5, 85–92. [Google Scholar]
- Paaswell, R.E. Temperature effects on clay soil consolidation. J. Soil Mech. Found. Div. 1967, 93, 9–22. [Google Scholar] [CrossRef]
- Polidori, E. Relationship between the Atterberg limits and clay content. Soils Found. 2007, 47, 887–896. [Google Scholar] [CrossRef] [Green Version]
- Wei, X.; Hattab, M.; Fleureau, J.-M.; Hu, R. Micro-macro-experimental study of two clayey materials on drying paths. Bull. Eng. Geol. Environ. 2013, 72, 495–508. [Google Scholar] [CrossRef]
- Fattah, M.Y.; Al-Lami, A.H. Behavior and characteristics of compacted expansive unsaturated bentonite-sand mixture. J. Rock Mech. Geotech. Eng. 2016, 8, 629–639. [Google Scholar] [CrossRef] [Green Version]
- Kacprzak, G.; Boutin, C.; Doanh, T. Permeability of sand-clay mixtures. Arch. Civ. Eng. 2010, 56, 299–320. [Google Scholar] [CrossRef]
- Gray, M.; Cheung, S.; Dixon, D. Swelling pressures of compacted bentonite/sand mixtures. MRS Online Proc. Libr. Arch. 1984, 44. [Google Scholar] [CrossRef]
- Revil, A.; Grauls, D.; Brévart, O. Mechanical compaction of sand/clay mixtures. J. Geophys. Res. Solid Earth 2002, 107, ECV 11–1. [Google Scholar] [CrossRef]
- Simpson, D.; Evans, T. Behavioral thresholds in mixtures of sand and kaolinite clay. J. Geotech. Geoenviron. Eng. 2016, 142, 04015073. [Google Scholar] [CrossRef]
- Dafalla, M.A. Effects of clay and moisture content on direct shear tests for clay-sand mixtures. Adv. Mater. Sci. Eng. 2013, 2013, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Krim, A.; Arab, A.; Chemam, M.; Brahim, A.; Sadek, M.; Shahrour, I. Experimental study on the liquefaction resistance of sand-clay mixtures: Effect of clay content and grading characteristics. Mar. Georesources Geotechnol. 2019, 37, 129–141. [Google Scholar] [CrossRef]
- Mollins, L.; Stewart, D.; Cousens, T. Drained strength of bentonite-enhanced sand. Geotechnique 1999, 49, 523–528. [Google Scholar] [CrossRef] [Green Version]
- Nagaraj, H. Influence of gradation and proportion of sand on stress-strain behavior of clay-sand mixtures. Int. J. Geo-Eng. 2016, 7, 19. [Google Scholar] [CrossRef] [Green Version]
- Dash, H.; Sitharam, T. Undrained monotonic response of sand-silt mixtures: Effect of nonplastic fines. Geomech. Geoeng. Int. J. 2011, 6, 47–58. [Google Scholar] [CrossRef]
- Cabalar, A.; Hasan, R. Compressional behaviour of various size/shape sand-clay mixtures with different pore fluids. Eng. Geol. 2013, 164, 36–49. [Google Scholar] [CrossRef]
- Cabalar, A.F.; Mustafa, W.S. Fall cone tests on clay-sand mixtures. Eng. Geol. 2015, 192, 154–165. [Google Scholar] [CrossRef]
- Peters, J.F.; Berney IV, E.S. Percolation threshold of sand-clay binary mixtures. J. Geotech. Geoenviron. Eng. 2010, 136, 310–318. [Google Scholar] [CrossRef]
- Khan, F.S.; Azam, S.; Raghunandan, M.E.; Clark, R. Compressive strength of compacted clay-sand mixes. Adv. Mater. Sci. Eng. 2014, 2014, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Azam, S. Study on the swelling behaviour of blended clay–sand soils. Geotech. Geol. Eng. 2007, 25, 369–381. [Google Scholar] [CrossRef]
- Saada, A.; Townsend, F. State of the art: Laboratory strength testing of soils. In Laboratory Shear Strength of Soil; ASTM International: West Conshohocken, PA, USA, 1981. [Google Scholar]
- Thevanayagam, S. Effect of fines and confining stress on undrained shear strength of silty sands. J. Geotech. Geoenviron. Eng. 1998, 124, 479–491. [Google Scholar] [CrossRef]
- Benahmed, N.; Nguyen, T.K.; Hicher, P.Y.; Nicolas, M. An experimental investigation into the effects of low plastic fines content on the behaviour of sand/silt mixtures. Eur. J. Environ. Civ. Eng. 2015, 19, 109–128. [Google Scholar] [CrossRef]
- Balaban, E.; Smejda, A.; Onur, M. An Experimental Study on Shear Strength Behavior of Soils Under Low Confining Pressure. In Proceedings of the 4th World Congress on Civil, Structural, and Environmental Engineering, Rome, Italy, 7–9 April 2019; pp. 1–8. [Google Scholar]
- Vallejo, L.E. Interpretation of the limits in shear strength in binary granular mixtures. Can. Geotech. J. 2001, 38, 1097–1104. [Google Scholar] [CrossRef]
- Cabalar, A.F. The effects of fines on the behaviour of a sand mixture. Geotech. Geol. Eng. 2011, 29, 91–100. [Google Scholar] [CrossRef]
- Kumar, G.; Wood, D.M. Mechanical Behaviour of Mixtures of Kaolin and Coarse Sand. In Proceedings of the IUTAM Symposium on Mechanics of Granular and Porous Materials, Cambridge, UK, 15–17 July 1996; pp. 57–68. [Google Scholar]
- Holtz, W. Triaxial Shear Characteristics of Clayey Gravel Soils; US Bureau of Reclamation: Washington, DC, USA, 1961.
- Kurata, S.; Fujishita, T. Research on the engineering properties of sand-clay mixtures. Rep. Port Harb. Res. Inst. 1961, 11, 389–424. [Google Scholar]
- Marsal, R.; Fuentes de la Rosa, A. Mechanical properties of rockfill soil mixtures. In Proceedings of the Transactions of the 12th International Congress on Large Dams, Mexico City, Mexico, 29 March–2 April 1976; pp. 179–209. [Google Scholar]
- Paduana, J.A. The Effect of Type and Amount of Clay on the Strength and Creep Characteristics of Clay-Sand Mixtures. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1966. [Google Scholar]
- Schlosser, F.; Long, N.-T. Recent results in French research on reinforced earth. J. Constr. Div. 1974, 100, 223–237. [Google Scholar] [CrossRef]
- Chu, J.; Leong, W. Effect of fines on instability behaviour of loose sand. Geotechnique 2002, 52, 751–755. [Google Scholar] [CrossRef]
- Monkul, M.M.; Ozden, G. Effect of Intergranular Void Ratio on One-Dimensional Compression Behavior. In Proceedings of the International Conference on Problematic Soils, Famagusta, Cyprus, 25–27 May 2005; p. 27. [Google Scholar]
- Kuerbis, R.; Negussey, D.; Vaid, Y.P. Effect of Gradation and Fines Content on the Undrained Response of Sand. Geotech. Spec. Publ. 1988, 330–345. [Google Scholar]
- Salgado, R.; Bandini, P.; Karim, A. Shear strength and stiffness of silty sand. J. Geotech. Geoenviron. Eng. 2000, 126, 451–462. [Google Scholar] [CrossRef]
- Yang, J.; Wei, L.; Dai, B. State variables for silty sands: Global void ratio or skeleton void ratio? Soils Found. 2015, 55, 99–111. [Google Scholar] [CrossRef] [Green Version]
- Cabalar, A.F.; Demir, S. Fall-cone testing of unsaturated sand-clay mixtures. Proc. Inst. Civ. Eng. Geotech. Eng. 2019, 172, 432–441. [Google Scholar] [CrossRef]
- Zuo, L.; Baudet, B.A. Determination of the transitional fines content of sand-non plastic fines mixtures. Soils Found. 2015, 55, 213–219. [Google Scholar] [CrossRef]
- Thevanayagam, S.; Mohan, S. Intergranular state variables and stress-strain behaviour of silty sands. Geotechnique 2000, 50, 1–23. [Google Scholar] [CrossRef]
- ASTM-D4254-16. Standard Test Methods for Minimum Index Density and Unit Weight of Soils and Calculation of Relative Density; ASTM International: West Conshohocken, PA, USA, 2016. [Google Scholar]
- Nova, R. Soil Mechanics; Wiley Online Library: Hoboken, NJ, USA, 2010. [Google Scholar]
- Bahadori, H.; Ghalandarzadeh, A.; Towhata, I. Effect of non plastic silt on the anisotropic behavior of sand. Soils Found. 2008, 48, 531–545. [Google Scholar] [CrossRef] [Green Version]
- Lupogo, K. Effect of fines mineralogy on the oedometric compressional behavior of sandy soils. J. Civ. Eng. Constr. Technol. 2013, 4, 232–238. [Google Scholar]
- Hazirbaba, K. Pore Pressure Generation Characteristics of Sands and Silty Sands: A Strain Approach. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2005. [Google Scholar]
- Polito, C.P. The Effects of Non-Plastic and Plastic Fines on the Liquefaction of Sandy Soils; Virginia Polytechnic Institute and State University: Blacksburg, VA, USA, 1999. [Google Scholar]
- Delage, P. A microstructure approach to the sensitivity and compressibility of some Eastern Canada sensitive clays. Géotechnique 2010, 60, 353. [Google Scholar] [CrossRef]
- Morgenstern, N.; Tchalenko, J. Microscopic structures in kaolin subjected to direct shear. Geotechnique 1967, 17, 309–328. [Google Scholar] [CrossRef]
- Ural, N. The Importance of Clay in Geotechnical Engineering. In Current Topics in the Utilization of Clay in Industrial and Medical Applications; InTech Open: Rijeka, Croatia, 2018; p. 83. [Google Scholar]
- Yin, K.; Fauchille, A.-L.; Othmani, K.; Sciarra, G.; Kotronis, P.; Benoit, Y.; Bertrand, F.; Branchu, S. Influence of sample preparation on the multi scale structure of sand-clay mixtures. In Proceedings of the E3S Web of Conferences, Glasgow, UK, 25 June 2019; p. 01007. [Google Scholar]
- Yamamuro, J.A.; Wood, F.M. Effect of depositional method on the undrained behavior and microstructure of sand with silt. Soil Dyn. Earthq. Eng. 2004, 24, 751–760. [Google Scholar] [CrossRef]
- Shaker, A.; Elkady, T. Hydraulic performance of sand-clay mixtures: Soil fabric perspective. Géotechnique Lett. 2015, 5, 198–204. [Google Scholar] [CrossRef]
- Carraro, J.A.H.; Prezzi, M.; Salgado, R. Shear strength and stiffness of sands containing plastic or nonplastic fines. J. Geotech. Geoenviron. Eng. 2009, 135, 1167–1178. [Google Scholar] [CrossRef]
- Di Donna, A. Thermo-Mechanical Aspects of Energy Piles. Ph.D. Thesis, École Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland, 2014. [Google Scholar]
- Maghsoodi, S.; Cuisinier, O.; Masrouri, F. Effect of Temperature on the Cyclic Behavior of Clay-Structure Interface. J. Geotech. Geoenviron. Eng. 2020, 146, 04020103. [Google Scholar] [CrossRef]
- Porcino, D.; Fioravante, V.; Ghionna, V.N.; Pedroni, S. Interface behavior of sands from constant normal stiffness direct shear tests. Geotech. Test. J. 2003, 26, 289–301. [Google Scholar]
- Xiao, S.; Suleiman, M.T.; Al-Khawaja, M. Investigation of effects of temperature cycles on soil-concrete interface behavior using direct shear tests. Soils Found. 2019, 59, 1213–1227. [Google Scholar] [CrossRef]
- Boukpeti, N.; White, D.J. Interface shear box tests for assessing axial pipe-soil resistance. Géotechnique 2017, 67, 18–30. [Google Scholar] [CrossRef] [Green Version]
- Martinez, A.; Frost, J. The influence of surface roughness form on the strength of sand-structure interfaces. Géotechnique Lett. 2017, 7, 104–111. [Google Scholar] [CrossRef]
- Xiao, S.; Suleiman, M.T.; Elzeiny, R.; Xie, H.; Al-Khawaja, M. Soil-concrete interface properties subjected to temperature changes and cycles using direct shear tests. Geotech. Front. 2017, 175–183. [Google Scholar] [CrossRef]
- Boulon, M. Basic features of soil structure interface behaviour. Comput. Geotech. 1989, 7, 115–131. [Google Scholar] [CrossRef]
- Potyondy, J.G. Skin friction between various soils and construction materials. Geotechnique 1961, 11, 339–353. [Google Scholar] [CrossRef]
- Airey, D.W.; Al-Douri, R.H.; Poulos, H.G. Estimation of pile friction degradation from shearbox tests. Geotech. Test. J. 1992, 15, 388–392. [Google Scholar]
- Desai, C.; Drumm, E.; Zaman, M. Cyclic testing and modeling of interfaces. J. Geotech. Eng. 1985, 111, 793–815. [Google Scholar] [CrossRef]
- David Frost, J.; Martinez, A. Interface Shear Response of JSC-1A, GRC-3, and JSC-Mars1 Regolith Simulants. J. Aerosp. Eng. 2018, 31, 04018003. [Google Scholar] [CrossRef]
- Mortara, G.; Mangiola, A.; Ghionna, V.N. Cyclic shear stress degradation and post-cyclic behaviour from sand–steel interface direct shear tests. Can. Geotech. J. 2007, 44, 739–752. [Google Scholar] [CrossRef]
- Shakir, R.; Zhu, J. Behavior of compacted clay-concrete interface. Front. Arch. Civ. Eng. China 2009, 3, 85–92. [Google Scholar] [CrossRef]
- Tabucanon, J.T.; Airey, D.W.; Poulos, H.G. Pile skin friction in sands from constant normal stiffness tests. Geotech. Test. J. 1995, 18, 350–364. [Google Scholar]
- Tsubakihara, Y.; Kishida, H. Frictional behaviour between normally consolidated clay and steel by two direct shear type apparatuses. Soils Found. 1993, 33, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Lehane, B.M.; Jardine, R.; Bond, A.J.; Frank, R. Mechanisms of shaft friction in sand from instrumented pile tests. J. Geotech. Eng. 1993, 119, 19–35. [Google Scholar] [CrossRef]
- Wernick, E. Skin Friction of Cylindrical Anchors in Noncohesive Soils. In Proceedings of the Symposium on Soil Reinforcing and Stabilising Techniques, Sydney, Australia, 16–19 October 1978; pp. 201–219. [Google Scholar]
- Boulon, M.; Foray, P. Physical and Numerical Simulation of Lateral Shaft Friction along Offshore Piles in Sand. In Proceedings of the 3rd International Conference on Numerical Methods in Offshore Piling, Nantes, France, 21–22 May 1986; pp. 127–147. [Google Scholar]
- DeJong, J.T.; White, D.J.; Randolph, M.F. Microscale observation and modeling of soil-structure interface behavior using particle image velocimetry. Soils Found. 2006, 46, 15–28. [Google Scholar] [CrossRef] [Green Version]
- White, D.J. An Investigation into the Behaviour of Pressed-In Piles. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2002. [Google Scholar]
- Yuan, B.; Xu, K.; Wang, Y.; Chen, R.; Luo, Q. Investigation of deflection of a laterally loaded pile and soil deformation using the PIV technique. Int. J. Geomech. 2017, 17, 04016138. [Google Scholar] [CrossRef]
- Take, W.A. Thirty-Sixth Canadian Geotechnical Colloquium: Advances in visualization of geotechnical processes through digital image correlation. Can. Geotech. J. 2015, 52, 1199–1220. [Google Scholar] [CrossRef]
- Tehrani, F.; Han, F.; Salgado, R.; Prezzi, M.; Tovar, R.; Castro, A. Effect of surface roughness on the shaft resistance of non-displacement piles embedded in sand. Géotechnique 2016, 66, 386–400. [Google Scholar] [CrossRef]
- Martinez, A.; Frost, J.D.; Hebeler, G.L. Experimental study of shear zones formed at sand/steel interfaces in axial and torsional axisymmetric tests. Geotech. Test. J. 2015, 38, 409–426. [Google Scholar] [CrossRef]
- Uesugi, M.; Kishida, H.; Tsubakihara, Y. Behavior of sand particles in sand-steel friction. Soils Found. 1988, 28, 107–118. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Zhang, J.-M. Monotonic and cyclic tests of interface between structure and gravelly soil. Soils Found. 2006, 46, 505–518. [Google Scholar] [CrossRef] [Green Version]
- Hammad, W.I. Modélisation Non Linéaire et Étude Expérimentale des Bandes de Cisaillement dans les Sables. Ph.D. Thesis, Univeristy of Grenoble, Grenoble, France, 1991. [Google Scholar]
- Hoteit, N. Contribution à L’étude du Comportement D’interface Sable-Inclusion et Application au Frottement Apparent. Ph.D. Thesis, Grenoble INPG, Grenoble, France, 1990. [Google Scholar]
- Hu, L.; Pu, J.L. Application of damage model for soil-structure interface. Comput. Geotech. 2003, 30, 165–183. [Google Scholar] [CrossRef]
- Lemos, L.J.L.; Vaughan, P.R. Clay-interface shear resistance. Géotechnique 2000, 50, 55–64. [Google Scholar] [CrossRef]
- Taha, A.; Fall, M. Shear behavior of sensitive marine clay-concrete interfaces. J. Geotech. Geoenviron. Eng. 2013, 139, 644–650. [Google Scholar] [CrossRef]
- Fleming, I.; Sharma, J.; Jogi, M. Shear strength of geomembrane-soil interface under unsaturated conditions. Geotext. Geomembr. 2006, 24, 274–284. [Google Scholar] [CrossRef]
- Frost, J.; DeJong, J.; Recalde, M. Shear failure behavior of granular–continuum interfaces. Eng. Fract. Mech. 2002, 69, 2029–2048. [Google Scholar] [CrossRef]
- Martinez, A.; Frost, J. Particle-scale effects on global axial and torsional interface shear behavior. Int. J. Numer. Anal. Methods Geomech. 2017, 41, 400–421. [Google Scholar] [CrossRef]
- Tomlinson, M. Some effects of pile driving on skin friction. In Behaviour of Piles; Thomas Telford Publishing: London, UK, 1971; pp. 107–114. [Google Scholar]
- Dove, J.E.; Frost, J.D. Peak friction behavior of smooth geomembrane-particle interfaces. J. Geotech. Geoenviron. Eng. 1999, 125, 544–555. [Google Scholar] [CrossRef]
- Martinez, A.; Palumbo, S. Anisotropic shear behavior of soil-structure interfaces: Bio-inspiration from snake skin. IFCEE 2018 2018, 94–104. [Google Scholar] [CrossRef]
- DeJong, J.T.; Westgate, Z.J. Role of initial state, material properties, and confinement condition on local and global soil-structure interface behavior. J. Geotech. Geoenviron. Eng. 2009, 135, 1646–1660. [Google Scholar] [CrossRef]
- Fioravante, V.; Ghionna, V.N.; Pedroni, S.; Porcino, D. A constant normal stiffness direct shear box for soil-solid interface tests. Riv. Ital. Geotec. 1999, 33, 7–22. [Google Scholar]
- Su, J. Advancing Multi-Scale Modeling of Penetrometer Insertion in Granular Materials. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2019. [Google Scholar]
- O’rourke, T.; Druschel, S.; Netravali, A. Shear strength characteristics of sand-polymer interfaces. J. Geotech. Eng. 1990, 116, 451–469. [Google Scholar] [CrossRef]
- Zhang, M.; Sang, S.; Wang, Y.; Bai, X. Factors Influencing the Mechanical Characteristics of a Pile-Soil Interface in Clay Soil. Front. Earth Sci. 2019, 7, 364. [Google Scholar] [CrossRef]
- Uesugi, M.; Kishida, H. Influential factors of friction between steel and dry sands. Soils Found. 1986, 26, 33–46. [Google Scholar] [CrossRef] [Green Version]
- Uesugi, M.; Kishida, H. Frictional resistance at yield between dry sand and mild steel. Soils Found. 1986, 26, 139–149. [Google Scholar] [CrossRef] [Green Version]
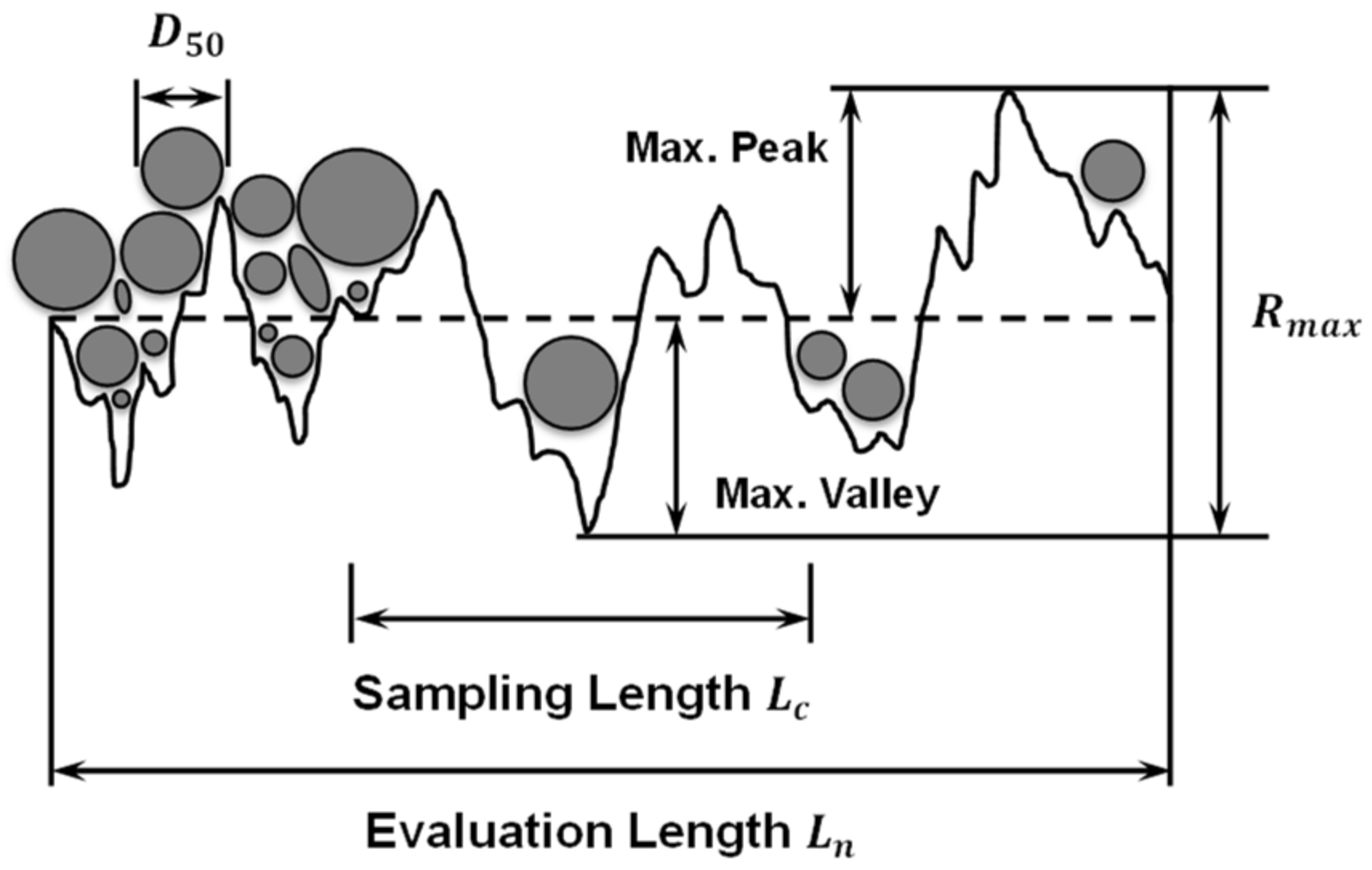
- Gadelmawla, E.; Koura, M.; Maksoud, T.; Elewa, I.; Soliman, H. Roughness parameters. J. Mater. Process. Technol. 2002, 123, 133–145. [Google Scholar] [CrossRef]
- International Organization for Standardization. 4287-Geometrical Product Specifications (GPS)-Surface Texture: Profile Method-Terms, Definitions and Surface Texture Parameters; International Organization for Standardization: Geneva, Switzerland, 1997. [Google Scholar]
- D’Aguiar, S.C.; Modaressi-Farahmand-Razavi, A.; Dos Santos, J.A.; Lopez-Caballero, F. Elastoplastic constitutive modelling of soil-structure interfaces under monotonic and cyclic loading. Comput. Geotech. 2011, 38, 430–447. [Google Scholar] [CrossRef]
- Yin, K.; Liu, J.; Lin, J.; Vasilescu, A.-R.; Othmani, K.; Di Filippo, E. Interface Direct Shear Tests on JEZ-1 Mars Regolith Simulant. Appl. Sci. 2021, 11, 7052. [Google Scholar] [CrossRef]
- Tsubakihara, Y.; Kishida, H.; Nishiyama, T. Friction between cohesive soils and steel. Soils Found. 1993, 33, 145–156. [Google Scholar] [CrossRef] [Green Version]
- Subba Rao, K.; Rao, K.; Allam, M.; Robinson, R. Interfacial friction between sands and solid surfaces. Proc. Inst. Civ. Eng. Geotech. Eng. 1998, 131, 75–82. [Google Scholar] [CrossRef]
- Maghsoodi, S.; Cuisinier, O.; Masrouri, F. Thermo-Mechanical Behaviour of Clay-Structure Interface. In Proceedings of the E3S Web of Conferences, Glasgow, UK, 25 June 2019; p. 10002. [Google Scholar]
- Uesugi, M.; Kishida, H.; Tsubakihara, Y. Friction between sand and steel under repeated loading. Soils Found. 1989, 29, 127–137. [Google Scholar] [CrossRef] [Green Version]
- Wang, D. Investigating the Thermal and Thermo-Mechanical Performances of Geothermal Heat Exchanger with Spiral-Tubes. Ph.D. Thesis, The Hong Kong Polytechnic University, Hong Kong, 2016. [Google Scholar]
- Littleton, I. An experimental study of the adhesion between clay and steel. J. Terramechanics 1976, 13, 141–152. [Google Scholar] [CrossRef]
- Nanda, S.; Sivakumar, V.; Hoyer, P.; Bradshaw, A.; Gavin, K.; Gerkus, H.; Jalilvand, S.; Gilbert, R.; Doherty, P.; Fanning, J. Effects of strain rates on the undrained shear strength of kaolin. Geotech. Test. J. 2017, 40, 951–962. [Google Scholar] [CrossRef]
- Scaringi, G.; Di Maio, C. Influence of displacement rate on residual shear strength of clays. Procedia Earth Planet. Sci. 2016, 16, 137–145. [Google Scholar] [CrossRef] [Green Version]
- Sorensen, K.K.; Baudet, B.; Simpson, B. Influence of structure on the time-dependent behaviour of a stiff sedimentary clay. Géotechnique 2007, 57, 113–124. [Google Scholar] [CrossRef] [Green Version]
- White, D.; O’Loughlin, C.; Stark, N.; Chow, S.H. Free Fall Penetrometer Tests in Sand: Determining the Equivalent Static Resistance. In Cone Penetration Testing 2018, Proceedings of the 4th International Symposium on Cone Penetration Testing, Delft, The Netherlands, 21–22 June 2018; CRC Press: London, UK; pp. 695–701.
- Xiao, S.; Suleiman, M.T.; McCartney, J.S. Shear Behavior of Silty Soil and Soil-Structure Interface under Temperature Effects. In Proceedings of the Geo-Congress 2014: Geo-Characterization and Modeling for Sustainability, Atlanta, GA, USA, 23–26 February 2014; pp. 4105–4114. [Google Scholar]
- Xiao, S.; Suleiman, M.T.; Naito, C.; Al-Khawaja, M. Modified-thermal borehole shear test device and testing procedure to investigate the soil-structure interaction of energy piles. Geotech. Test. J. 2017, 40, 1043–1056. [Google Scholar] [CrossRef]
- Guler, M.; Edil, T.B.; Bosscher, P.J. Measurement of particle movement in granular soils using image analysis. J. Comput. Civ. Eng. 1999, 13, 116–122. [Google Scholar] [CrossRef]
- Zhang, G.; Liang, D.; Zhang, J.-M. Image analysis measurement of soil particle movement during a soil-structure interface test. Comput. Geotech. 2006, 33, 248–259. [Google Scholar] [CrossRef]
- Song, Z.; Konietzky, H.; Cai, X. Modulus degradation of concrete exposed to compressive fatigue loading: Insights from lab testing. Struct. Eng. Mech. 2021, 78, 3. [Google Scholar]
- Kwak, T.-Y.; Park, K.-H.; Kim, J.; Chung, C.-K.; Baek, S.-H. Shear Band Characterization of Clayey Soils with Particle Image Velocimetry. Appl. Sci. 2020, 10, 1139. [Google Scholar] [CrossRef] [Green Version]
- Dudoignon, P.; Pantet, A.; Carrara, L.; Velde, B. Macro-micro measurement of particle arrangement in sheared kaolinitic matrices. Géotechnique 2001, 51, 493–499. [Google Scholar] [CrossRef]
- Hattab, M.; Fleureau, J.-M. Experimental study of kaolin particle orientation mechanism. Géotechnique 2010, 60, 323. [Google Scholar] [CrossRef]
- Hicher, P.; Wahyudi, H.; Tessier, D. Microstructural analysis of strain localisation in clay. Comput. Geotech. 1994, 16, 205–222. [Google Scholar] [CrossRef]
- Hicher, P.Y.; Wahyudi, H.; Tessier, D. Microstructural analysis of inherent and induced anisotropy in clay. Mech. Cohesive-Frict. Mater. 2000, 5, 341–371. [Google Scholar] [CrossRef]
- Sachan, A. Variation in geometric arrangement of particles in kaolinite clay due to shear deformation using SEM technique. Curr. Sci. 2007, 93, 515–522. [Google Scholar]
- Sivakumar, V.; Doran, I.; Graham, J. Particle orientation and its influence on the mechanical behaviour of isotropically consolidated reconstituted clay. Eng. Geol. 2002, 66, 197–209. [Google Scholar] [CrossRef]
- Meunier, A. Clays; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Shahin, M.; Khan, M.M.H.; Bari, M.N. A Disaster Resilient Road: Effects of Fines on Density and Shear Strength of Sands. Int. J. Transp. Eng. Technol. 2020, 6, 38. [Google Scholar] [CrossRef]
- Yin, K.; Liu, J.; Vasilescu, A.-R.; Di Filippo, E.; Othmani, K. A Procedure to Prepare Sand–Clay Mixture Samples for Soil–Structure Interface Direct Shear Tests. Appl. Sci. 2021, 11, 5337. [Google Scholar] [CrossRef]
- Aksoy, H.; Inal, E.; Gor, M. Skin Friction between Soil and Pile Materials. In Proceedings of the 12th International Congress on Advances in Civil Engineering, Istanbul, Turkey, 21–23 September 2016. [Google Scholar]
- Li, L.; Fall, M.; Fang, K. Shear behavior at interface between compacted clay liner–geomembrane under freeze-thaw cycles. Cold Reg. Sci. Technol. 2020, 172, 103006. [Google Scholar] [CrossRef]
- Yin, K.; Fauchille, A.-L.; Di Filippo, E.; Othmani, K.; Branchu, S.; Sciarra, G.; Kotronis, P. The influence of mixing orders on the microstructure of artificially prepared sand-clay mixtures. Adv. Mater. Sci. Eng. 2021, 2021, 1–15. [Google Scholar]

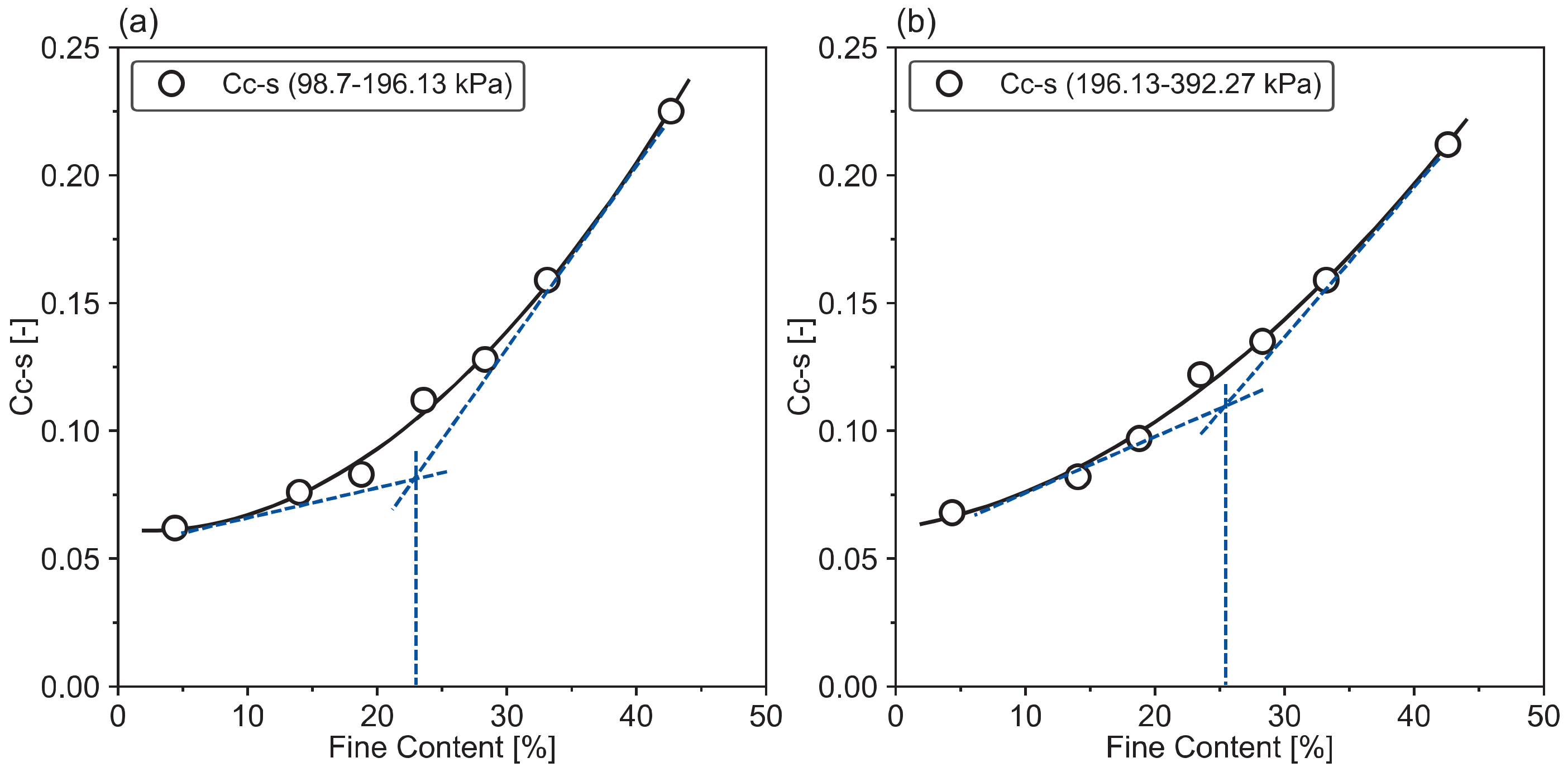
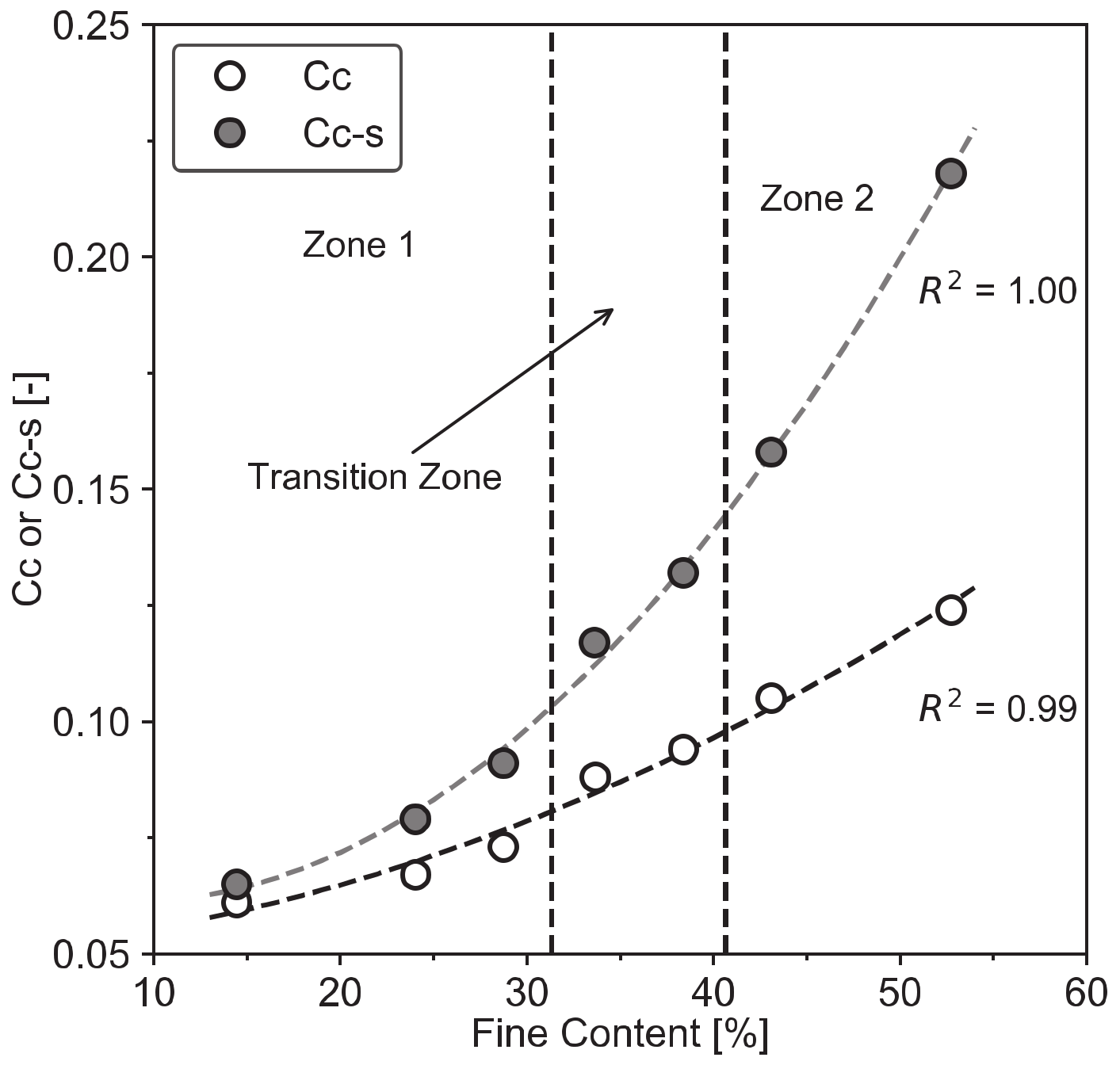
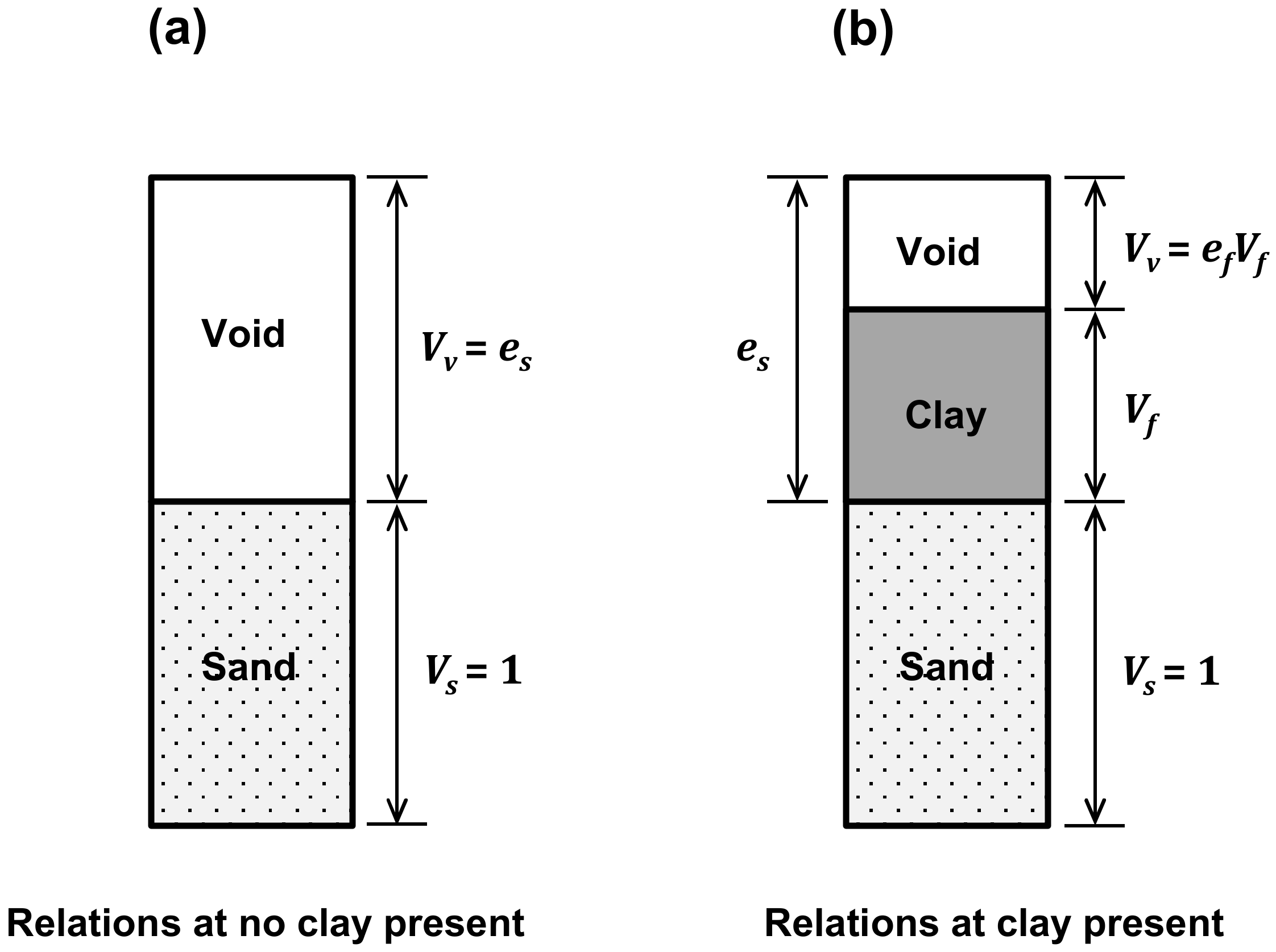
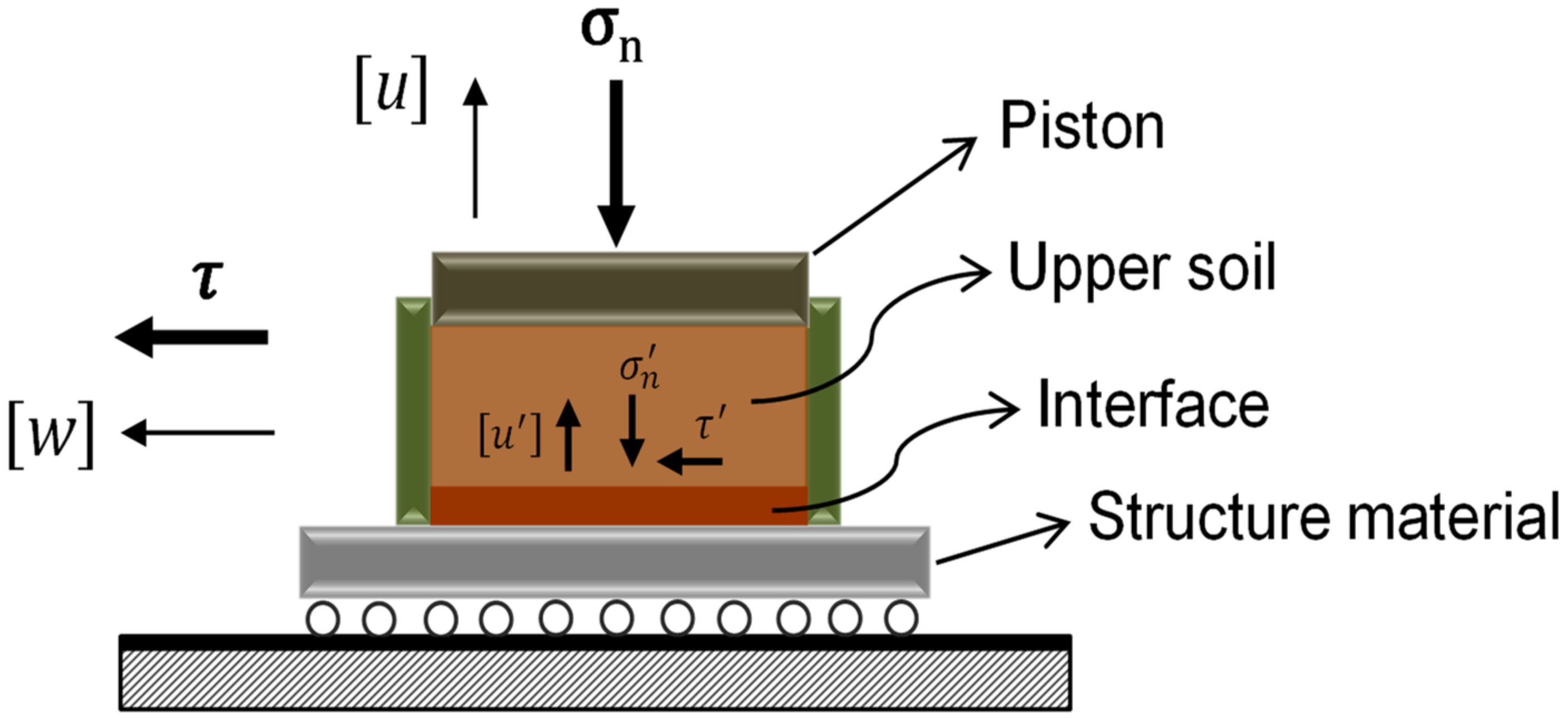










| Percentage of Clay in the Mixture (%) | |||||
|---|---|---|---|---|---|
| Mixture | Test Type | Sand-Controlled | Controlled by Both | Clay-Controlled | Reference |
| Gravel–clay | Triaxial test | <15 | 15~30 | >30 | Marsal (1976) |
| Gravel–clay | Triaxial test | <35 | 35~50 | >50 | Holtz (1961) |
| Sand–clay | Triaxial test | <30 | 30~50 | >50 | Paduana (1966) |
| Sand–clay | Triaxial test | <20 | 20~30 | >30 | Georgianou et al., (1990) |
| Sand–clay | Ring shear | <13 | 13~47 | >47 | Lupini et al., (1981) |
| Sand–clay | Direct shear | <20 | 20~38 | >38 | Kurata and Fujishita (1961) |
| Sand–clay | Direct shear | <20 | 20~50 | >50 | Schloser and Long (1974) |
| Glass beads–clay | Direct shear | <40 | 40~60 | >60 | Schloser and Long (1974) |
| Sand–clay | Direct shear | <25 | 25~60 | >60 | Vallejo (2000) |
| Sand–clay | Triaxial test | <30 | 30~40 | >40 | Kumar 1997 |
| Sand–clay | Triaxial test | <35 | 35~40 | >40 | Wood 2000 |
| Sand–clay | Direct shear | <19~34 | - | >19~34 | Monkul 2007 |
| Sand–fine sand | Direct shear | <11 | - | >11 | Cabalar 2011 |
| Average values | - | <24.6 | 24.6~40.9 | >40.9 | - |
| Reference | Soil | Structure | Test Type | Interface Thickness |
|---|---|---|---|---|
| Uesugi 1988 | sand | steel | direct shear test | 5 D50 |
| DeJong et al., 2003 | sand | aluminum plate | direct shear test | 5~8 D50 |
| Hu 2002, 2004 | quartz sand | steel plate | direct shear test | 5 D50 |
| Frost et al., 2002 | sand | geomembrane | direct shear test | 2~6 D50 |
| Zhang 2006 | gravel | steel | direct shear test | 5~6 D50 |
| Pra-ai 2017 | Fontainebleau sand | steel plate | direct shear test | 10~12 D50 |
| Tehrani 2016 | sand | brass model pile | axial load test | 3.2~4.2 D50 (D50 = 0.65 mm) |
| Martinez 2017 | sand | steel sleeves | cone penetration test | 5~7 D50 |
| Valencia 2018 | sand | brass model pile | tensile load test | 1.7 to 2.4 mm (D50 = 0.62 mm) |
| Reference | Soil | Structure | Test Type | Interface Thickness |
|---|---|---|---|---|
| Martinez 2018 | kaolin clay | steel | direct shear test | about 0.25 mm (D50 is unknown) |
| Yavari 2016 | kaolin clay | concrete plate | direct shear test | less than 1 mm (D50 is 0.8 μm) |
| Di Donna 2016 | illite clay | concrete | direct shear test | unknown |
| Maghsoodi 2019 | kaolin clay | steel | direct shear test | unknown |
| Chen 2015 | red clay | concrete | direct shear test | unknown |
| Tiwari 2010 | sand/silty sand/elastic silt/lean clay | concrete/steel /wood | direct shear test | unknown |
| Tiwari 2013 | sand/silty sand/elastic silt/lean clay | concrete/steel /wood | direct shear test | unknown |
| Aksoy 2016 | sand–clay mixture | steel/wood | direct shear test | unknown |
| Yazdani 2019 | kaolin clay | concrete | direct shear test | unknown |
| Rmax (mm) | Sand: D50 = 0.5 mm | Clay: D50 = 0.002 mm | ||
|---|---|---|---|---|
| Rn | Surface | Rn | Surface | |
| 0.001 | 0.002 | Smooth | 0.5 | Medium |
| 0.06 | 0.12 | Medium | 30 | High |
| 0.1 | 0.2 | High | - | - |
| Test Description | Effective Friction Angle (°) | Cohesion or Adhesion (kPa) |
|---|---|---|
| 6 °C, soil | 29 | 37.9 |
| 21 °C, soil | 25 | 35.5 |
| 6 °C, soil–concrete interface | 32 | 3.1 |
| 21 °C, soil–concrete interface | 32 | 7.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, K.; Fauchille, A.-L.; Di Filippo, E.; Kotronis, P.; Sciarra, G. A Review of Sand–Clay Mixture and Soil–Structure Interface Direct Shear Test. Geotechnics 2021, 1, 260-306. https://doi.org/10.3390/geotechnics1020014
Yin K, Fauchille A-L, Di Filippo E, Kotronis P, Sciarra G. A Review of Sand–Clay Mixture and Soil–Structure Interface Direct Shear Test. Geotechnics. 2021; 1(2):260-306. https://doi.org/10.3390/geotechnics1020014
Chicago/Turabian StyleYin, Kexin, Anne-Laure Fauchille, Eugenia Di Filippo, Panagiotis Kotronis, and Giulio Sciarra. 2021. "A Review of Sand–Clay Mixture and Soil–Structure Interface Direct Shear Test" Geotechnics 1, no. 2: 260-306. https://doi.org/10.3390/geotechnics1020014
APA StyleYin, K., Fauchille, A.-L., Di Filippo, E., Kotronis, P., & Sciarra, G. (2021). A Review of Sand–Clay Mixture and Soil–Structure Interface Direct Shear Test. Geotechnics, 1(2), 260-306. https://doi.org/10.3390/geotechnics1020014






