Chemo-Mechanical Couplings at Granular Contact: The Effect of Mineral Dissolution and Precipitation across the Scales
Abstract
:1. Introduction
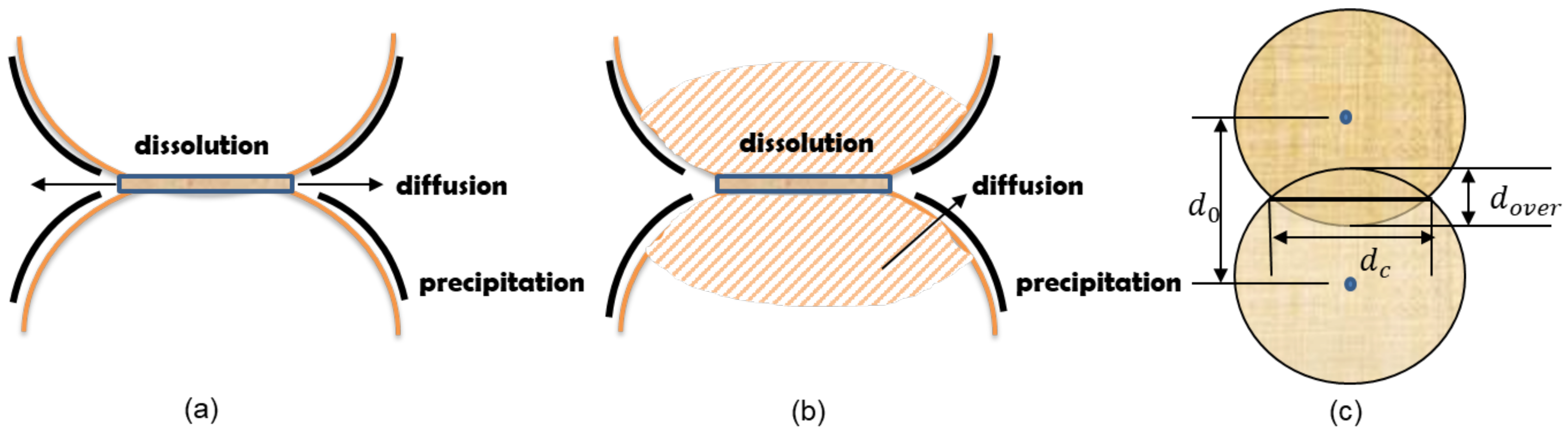
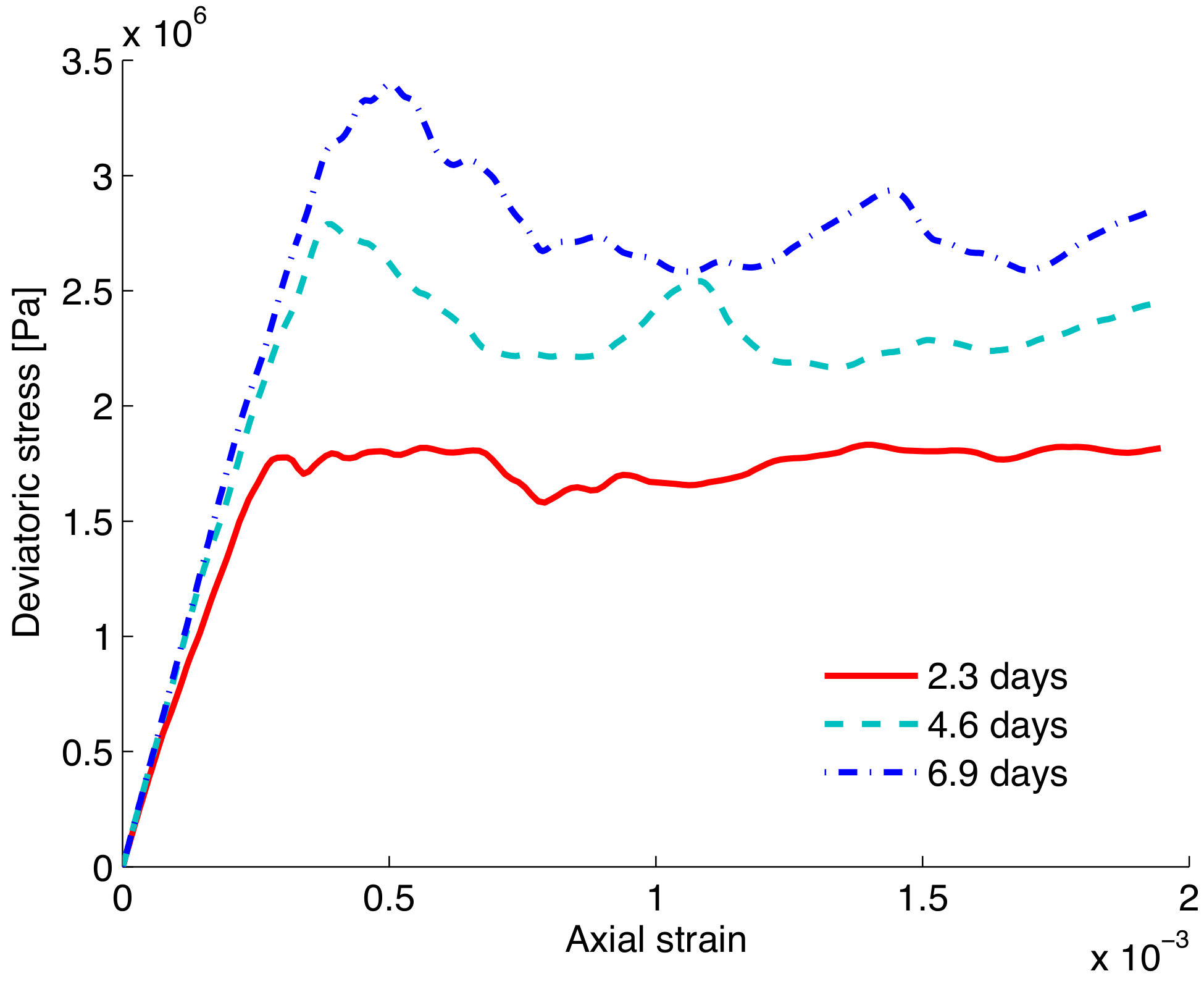
2. Mineral Dissolution under Highly Stressed Granular Contact
2.1. Geomechanical Background
2.2. Kinetic Rate Laws for Geochemical Reactions
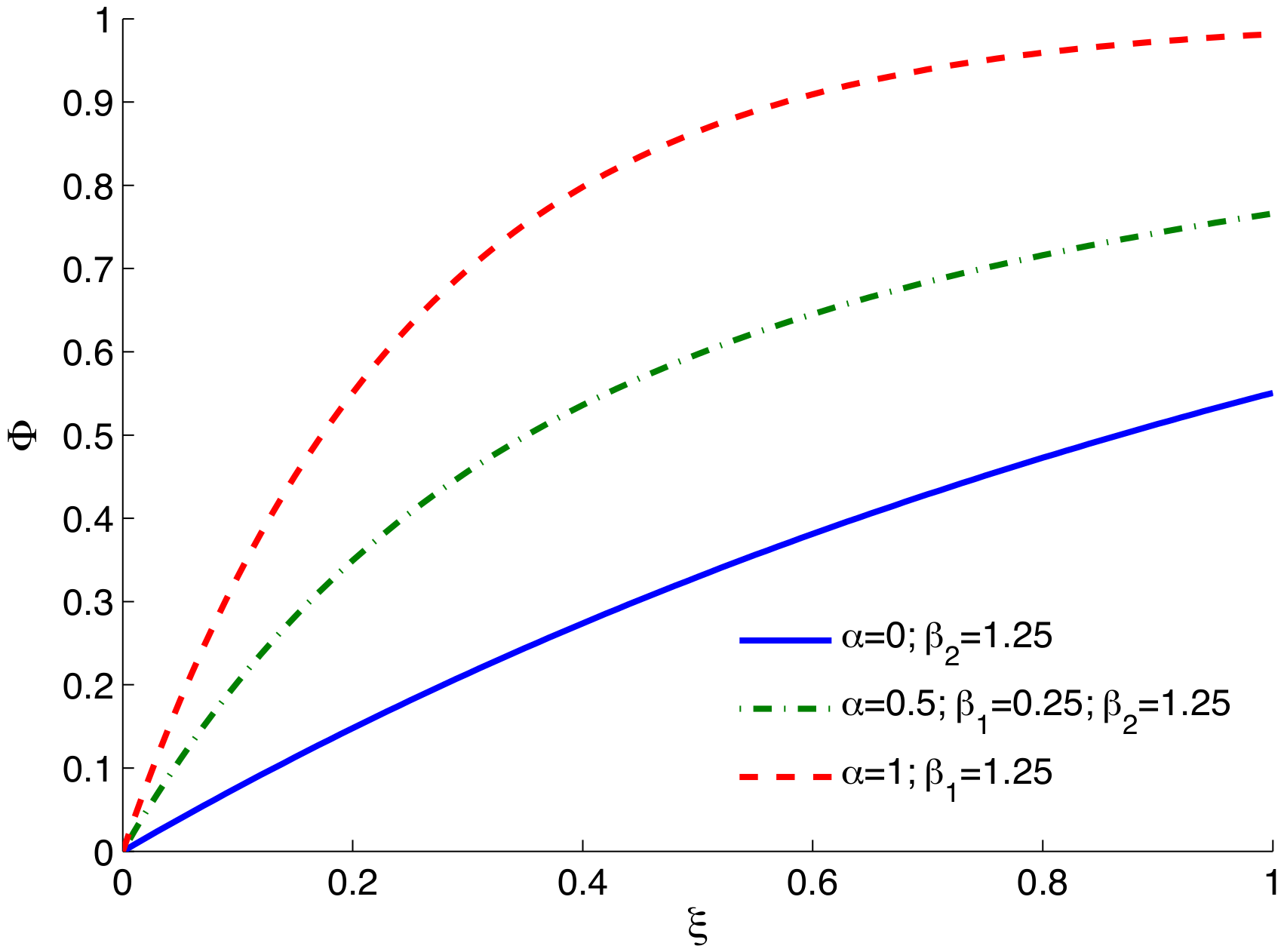
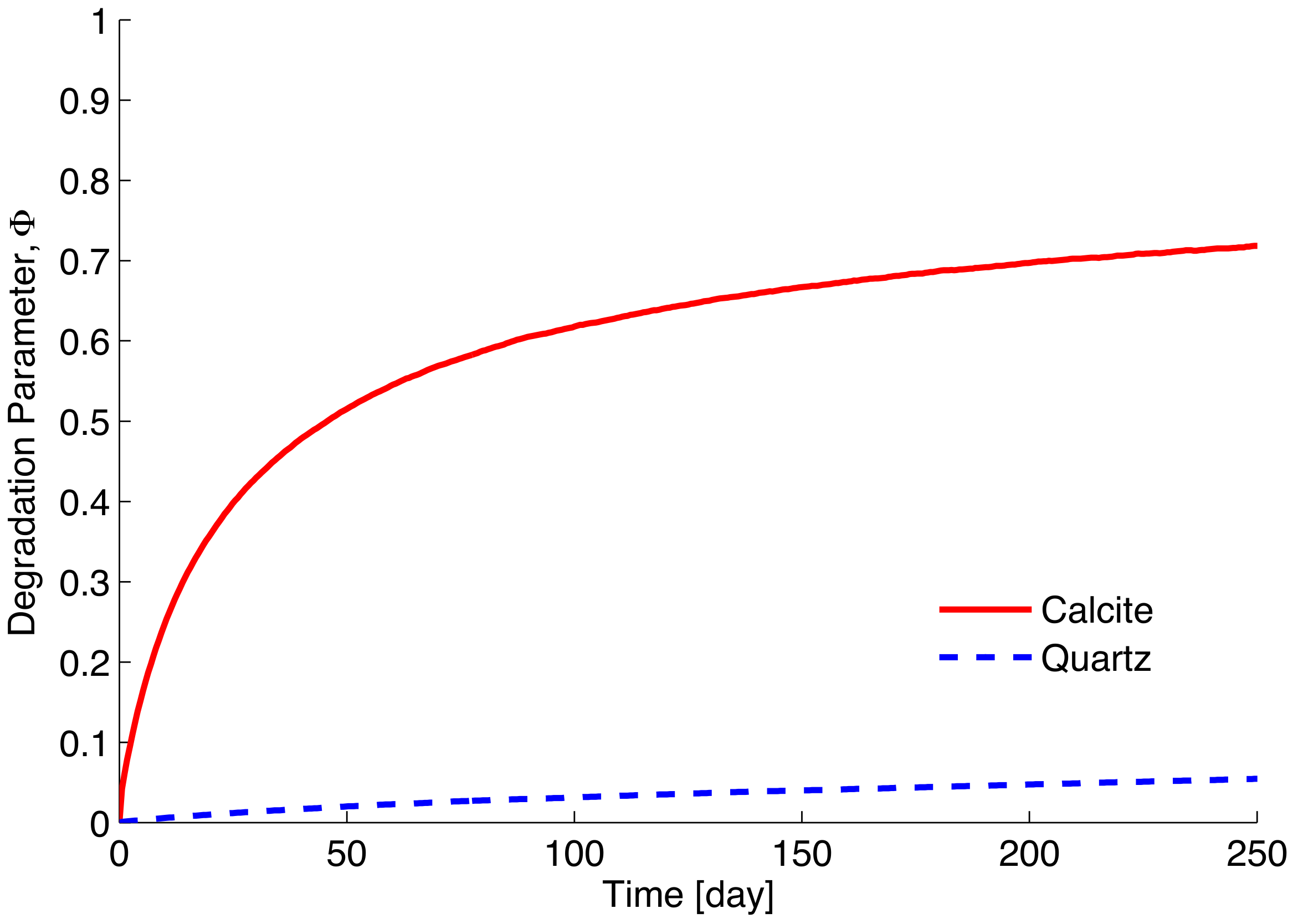
2.3. Numerical Results
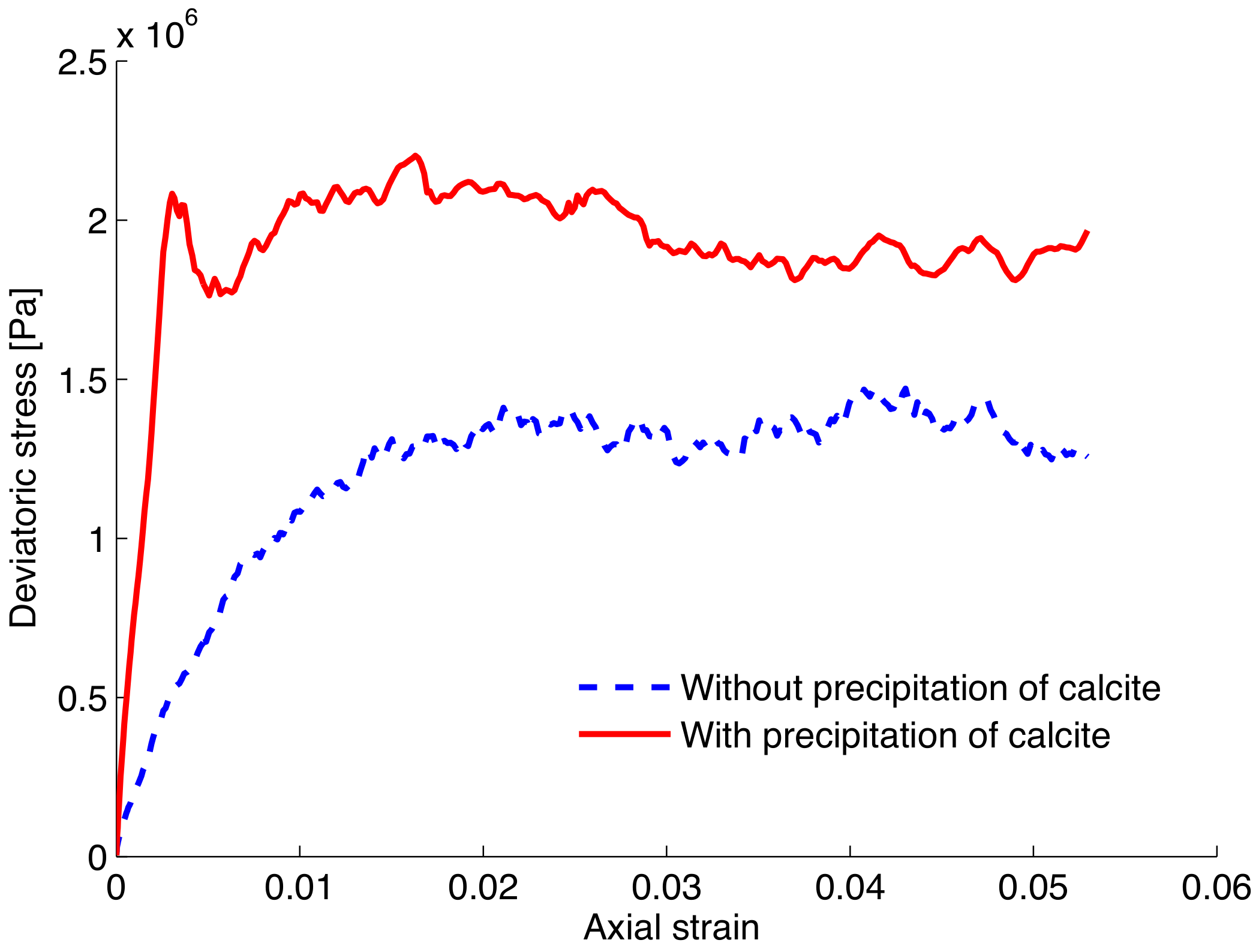
3. Microbially Induced Calcite Mineral Precipitation
3.1. Mechanisms and Mathematical Formulations
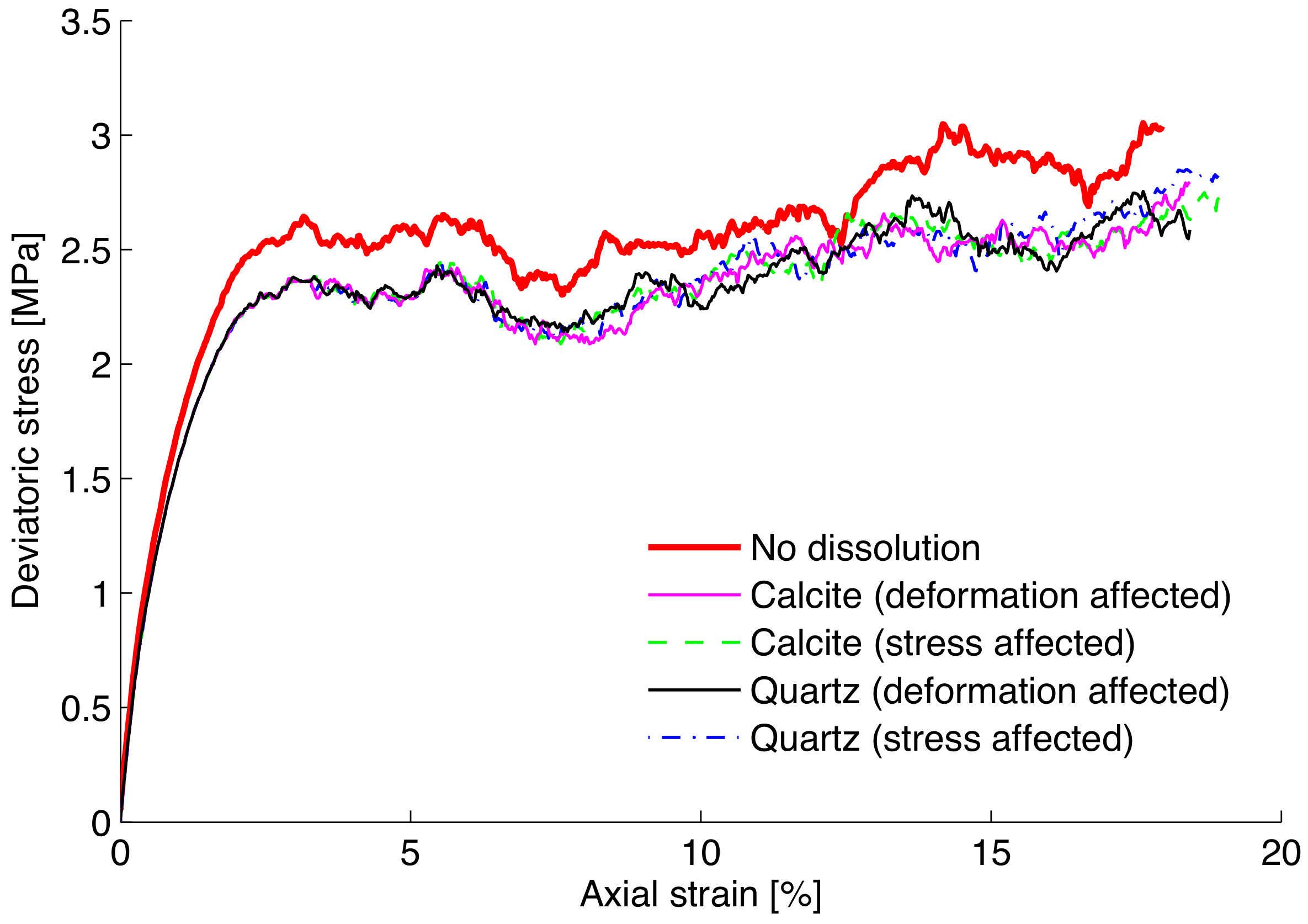
3.2. Numerical Simulations
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hueckel, T.; Cassiani, G.; Fan, T.; Pellegrino, A.; Fioravante, V. Aging of oil/gas-bearing sediments, their compressibility, and subsidence. J. Geotech. Geoenv. Eng. ASCE 2001, 127, 926–938. [Google Scholar] [CrossRef]
- Hueckel, T.; Hu, L.B. Feedback mechanisms in chemo-mechanical multi-scale modeling of soil and sediment compaction. Comput. Geotech. 2009, 36, 934–943. [Google Scholar] [CrossRef]
- Ciantia, M.O.; Castellanza, R.; Di Prisco, C. Experimental study on the water-induced weakening of calcarenites. Rock Mech. Rock Eng. 2015, 48, 441–461. [Google Scholar] [CrossRef]
- Nova, R.; Castellanza, R.; Tamagnini, C. A constitutive model for bonded geomaterials subject to mechanical and/or chemical degradation. Int. J. Numer. Anal. Methods Geomech. 2003, 27, 705–732. [Google Scholar] [CrossRef]
- Zhao, Y.; Cui, P.; Hu, L.B.; Hueckel, T. Multi-scale chemo-mechanical analysis of the slip surface of landslides in the Three Gorges. China. Sci. China Ser. E Technol. Sci. 2011, 54, 1757–1765. [Google Scholar] [CrossRef]
- Zhang, M.; McSaveney, M.J. Is air pollution causing landslide in China? Earth Planet. Sci. Lett. 2018, 481, 284–289. [Google Scholar] [CrossRef]
- Puppala, A.J.; Intharasombat, N.; Vempati, R.K. Experimental studies on ettringite-induced heaving in soils. J. Geotech. Eng. 2005, 131, 325–337. [Google Scholar] [CrossRef]
- Wang, Z.; Sigdel, P.; Hu, L. Chemo-mechanical interactions in the ettringite induced expansion of sulfate-bearing soils. Geosciences 2019, 9, 375. [Google Scholar] [CrossRef] [Green Version]
- Shalev, E.; Lyakhovsky, V.; Yechieli, Y. Salt dissolution and sinkhole formation along the Dead Sea shore. J. Geophys. Res. Solid Earth 2006, 111, B03102. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.S.; Kwon, S.K.; Sanchez, M.; Cho, G.C. Geological storage of high level nuclear waste. KSCE J. Civ. Eng. 2011, 15, 721–737. [Google Scholar] [CrossRef]
- Rutqvist, J. The geomechanics of CO2 storage in deep sedimentary formations. Geotech. Geol. Eng. 2012, 30, 525–551. [Google Scholar] [CrossRef] [Green Version]
- Hu, M.M.; Hueckel, T. Environmentally enhanced crack propagation in a chemically degrading isotropic shale. Geotechnique 2013, 63, 313–321. [Google Scholar] [CrossRef] [Green Version]
- DeJong, J.T.; Mortensen, B.M.; Martinez, B.C.; Nelson, D.C. Bio-mediated soil improvement. Ecol. Eng. 2010, 36, 197–210. [Google Scholar] [CrossRef]
- Weyl, P.K. Pressure solution and the force of crystallization—A phenomenological theory. J. Geophys. Res. 1959, 64, 20012025. [Google Scholar] [CrossRef]
- Elliott, D. Diffusion flow laws in metamorphic rocks. Geol. Soc. Am. Bull. 1973, 84, 2645–2664. [Google Scholar] [CrossRef]
- Rutter, E.H. The kinetics of rock deformation by pressure solution. Philos. Trans. R. Soc. Lond. Ser. A 1976, 283, 203–219. [Google Scholar]
- Ghoussoub, J.; Leroy, Y.M. Solid-fluid phase transformation within grain boundaries during compaction by pressure solution. J. Mech. Phys. Solids 2001, 49, 2385–2430. [Google Scholar] [CrossRef] [Green Version]
- Pietruszczak, S.; Lydzba, D.; Shao, J.F. Modelling of deformation response and chemo-mechanical coupling in chalk. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 997–1018. [Google Scholar] [CrossRef]
- Hu, L.B.; Hueckel, T. Coupled chemo-mechanics of intergranular contact: Toward a three-scale model. Comput. Geotech. 2007, 34, 306–327. [Google Scholar] [CrossRef]
- Cha, M.; Santamarina, J. C. Hydro-chemo-mechanical coupling in sediments: Localized mineral dissolution. Geomech. Energy Environ. 2016, 7, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Hueckel, T. Chemo-plasticity of clays subjected to stress and flow of a single contaminant. Int. J. Numer. Anal. Methods Geomech. 1997, 21, 43–72. [Google Scholar] [CrossRef]
- Coussy, O. Poromechanics; Wiley: New York, NY, USA, 2004. [Google Scholar]
- Tada, R.; Siever, R. Pressure solution during diagenesis: A review. Annu. Rev. Earth Planet. Sci. 1987, 17, 89–118. [Google Scholar] [CrossRef]
- Raj, R.; Chyung, C.K. Solution-precipitation creep in glass ceramics. Acta Metall. 1981, 29, 159–166. [Google Scholar] [CrossRef]
- Spiers, C.J.; Schutjens, P.M.T.M. Densification of crystalline aggregates by fluid phase diffusional creep. In Deformation Processes in Minerals, Ceramics and Rock; Meridith, P.G., Barber, D., Eds.; Unwin Hyman: London, UK, 1990; pp. 334–353. [Google Scholar]
- Denisov, N.Y.; Reltov, B.F. The influence of certain processes on the strength of soils. In Proceedings of the 5th International Conference on Soil Mechanics and Foundation Engineering, Paris, France, 17–22 July 1961; pp. 75–78. [Google Scholar]
- Baxter, C.D.P.; Mitchell, J.K. Experimental study on the aging of sands. J. Geotech. Geoenv. Eng. ASCE 2004, 130, 1051–1062. [Google Scholar] [CrossRef] [Green Version]
- Pingitore, N.E. The role of diffusion during carbonate diagenesis. J. Sediment. Res. 1982, 52, 27–39. [Google Scholar]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Yasuhara, H.; Elsworth, D.; Polak, A. A mechanistic model for compaction of granular aggregates moderated by pressure solution. J. Geophys. Res. 2003, 108, 2530. [Google Scholar] [CrossRef]
- Zhang, X.; Spiers, C.J. Compaction of granular calcite by pressure solution at room temperature and effects of pore fluid chemistry. Int. J. Rock Mech. Min. Sci. 2005, 42, 950–960. [Google Scholar] [CrossRef]
- Lydzba, D.; Pietruszczak, S.; Shao, J.F. Intergranual pressure solution in chalk: A multiscale approach. Comput. Geotech. 2007, 34, 291–305. [Google Scholar] [CrossRef]
- Shimizu, I. Kinetics of pressure solution creep in quartz: Theoretical considerations. Tectonophysics 1995, 245, 121–134. [Google Scholar] [CrossRef]
- Rimstidt, J.D.; Barnes, D.L. The kinetics of silica water reaction. Geochim. Cosmoch. Acta 1980, 44, 1683–1699. [Google Scholar] [CrossRef]
- Itasca. PFC2D User’s Guide; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 2008. [Google Scholar]
- Utili, S.; Nova, R. DEM analysis of bonded granular geomaterials. Int. J. Numer. Anal. Methods Geomech. 2008, 32, 1997–2031. [Google Scholar] [CrossRef]
- Kuhn, M.; Mitchell, J.K. Modelling of soil creep with the discrete element method. Eng. Comput. 1992, 9, 277–287. [Google Scholar] [CrossRef]
- Wang, Y.H.; Xu, D.; Tsui, K.Y. Discrete element modeling of contact creep and aging in sand. J. Geotech. Geoenv. Eng. 2008, 134, 1407–1411. [Google Scholar] [CrossRef]
- Kwok, C.Y.; Bolton, M.D. DEM simulations of thermally activated creep in soils. Geotechnique 2010, 60, 425–433. [Google Scholar] [CrossRef] [Green Version]
- DeJong, J.T.; Fritzges, M.B.; Nusslein, K. Microbially induced cementation to control sand response to undrained shear. J. Geotech. Geoenv. Eng. ASCE 2006, 132, 1381–1392. [Google Scholar] [CrossRef]
- Whiffin, V.S.; Van Paassen, L.A.; Harkes, M.P. Microbial carbonate precipitation as a soil improvement technique. Geomicrobiol. J. 2007, 24, 417–423. [Google Scholar] [CrossRef]
- Van Paassen, L.A.; Daza, C.M.; Staal, M.; Sorokin, D.Y.; Van der Zonb, W.; Van Loosdrecht, M.C. Potential Soil Reinforcement by Biological Denitrification. Ecol. Eng. 2010, 36, 168–175. [Google Scholar] [CrossRef]
- Chou, C.; Seagren, E.A.; Aydilek, A.H.; Lai, M. Biocalcification of Sand through Ureolysis. J. Geotech. Geoenv. Eng. ASCE 2011, 137, 1179–1189. [Google Scholar] [CrossRef] [Green Version]
- Barkouki, T.H.; Martinez, B.C.; Mortensen, B.M.; Weathers, T.S.; DeJong, J.T.; Spycher, N.F.; Ginn, T.R.; Smith, R.W.; Fujita, Y. Forward and inverse bio-geochemical modeling of microbially induced calcite precipitation in half-meter column experiments. Transp. Porous Media 2012, 90, 23–39. [Google Scholar] [CrossRef]
- Martinez, B.C.; DeJong, J.T.; Mortensen, B.M.; Barkouki, T.H.; Ginn, T.R.; Hunt, C.; Tanyu, B.; Major, D. Experimental optimization of microbial induced carbonate precipitation. J. Geotech. Geoenv. Eng. ASCE 2013, 139, 587–598. [Google Scholar] [CrossRef]
- Montoya, B.M.; DeJong, J.T.; Boulanger, R.W. Seismic response of liquefiable sand improved by microbial induced calcite precipitation. Geotechnique 2013, 63, 302–313. [Google Scholar] [CrossRef]
- Feng, K.; Montoya, B.M.; Evans, T.M. Numerical investigation of microbial induced cemented sand mechanical behavior. In ASCE Geotechnical Special Publication 234: Geo-Characterization and Modeling for Sustainability; Abu Farsakh, M., Yu, X., Hoyos, L.R., Eds.; American Society of Civil Engineers: Reston, VA, USA, 2014; pp. 644–1653. [Google Scholar]
- Panthi, S.; Soltanpour, Y.; Hu, L.B. Multi-scale modelling of enhanced dissolution and deformation of geomaterials: A Discrete Element approach. In ASCE Geotechnical Special Publication 236: Soil Behavior and Geomechanics; Zhang, X., Chu, J., Bulut, R., Eds.; American Society of Civil Engineers: Reston, VA, USA, 2014; pp. 502–511. [Google Scholar]
- Van Wijngaarden, W.K.; Vermolen, F.J.; Van Meurs, G.A.M.; Vuik, C. Modelling biogrout: A new ground improvement method based on microbial-induced carbonate precipitation. Transp. Porous Media 2011, 87, 397–420. [Google Scholar] [CrossRef] [Green Version]
- Fauriel, S.; Laloui, L. A bio-chemo-hydro-mechanical model for microbially induced calcite precipitation in soils. Comput. Geotech. 2012, 46, 104–120. [Google Scholar] [CrossRef]
- Akimana, R.M.; Seo, Y.; Li, L.; Howard, L.; Dewoolkar, M.; Hu, L.B. Exploring X-ray Computed Tomography characterization and reactive transport modelling of Microbially Induced Calcite Precipitation in sandy soils. In ASCE Geotechnical Special Publication 269: Sustainability and Resiliency in Geotechnical Engineering; Zekkos, D., Farid, A., De, A., Reddy, K.R., Yesiller, N., Eds.; American Society of Civil Engineers: Reston, VA, USA, 2016; pp. 62–71. [Google Scholar]
- Al Qabany, A.; Mortensen, B.; Martinez, B.; Soga, K.; DeJong, J. Microbial carbonate precipitation: Correlation of S-wave velocity with calcite precipitation. In ASCE Geotechnical Special Publication 211: Advances in Geotechnical Engineering; Han, J., Alzamora, D.E., Eds.; American Society of Civil Engineers: Reston, VA, USA, 2011; pp. 3993–4001. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bista, H.; Panthi, S.; Hu, L. Chemo-Mechanical Couplings at Granular Contact: The Effect of Mineral Dissolution and Precipitation across the Scales. Geotechnics 2022, 2, 158-170. https://doi.org/10.3390/geotechnics2010007
Bista H, Panthi S, Hu L. Chemo-Mechanical Couplings at Granular Contact: The Effect of Mineral Dissolution and Precipitation across the Scales. Geotechnics. 2022; 2(1):158-170. https://doi.org/10.3390/geotechnics2010007
Chicago/Turabian StyleBista, Hemanta, Sadrish Panthi, and Liangbo Hu. 2022. "Chemo-Mechanical Couplings at Granular Contact: The Effect of Mineral Dissolution and Precipitation across the Scales" Geotechnics 2, no. 1: 158-170. https://doi.org/10.3390/geotechnics2010007
APA StyleBista, H., Panthi, S., & Hu, L. (2022). Chemo-Mechanical Couplings at Granular Contact: The Effect of Mineral Dissolution and Precipitation across the Scales. Geotechnics, 2(1), 158-170. https://doi.org/10.3390/geotechnics2010007




