A Neural Network Model for Estimation of Failure Stresses and Strains in Cohesive Soils
Abstract
:1. Introduction
2. Feed forward Neural Networks
3. Numerical Formulation and Material Constitutive Model
4. Numerical Model Implementation
5. Numerical Modeling Results and NN Model Development
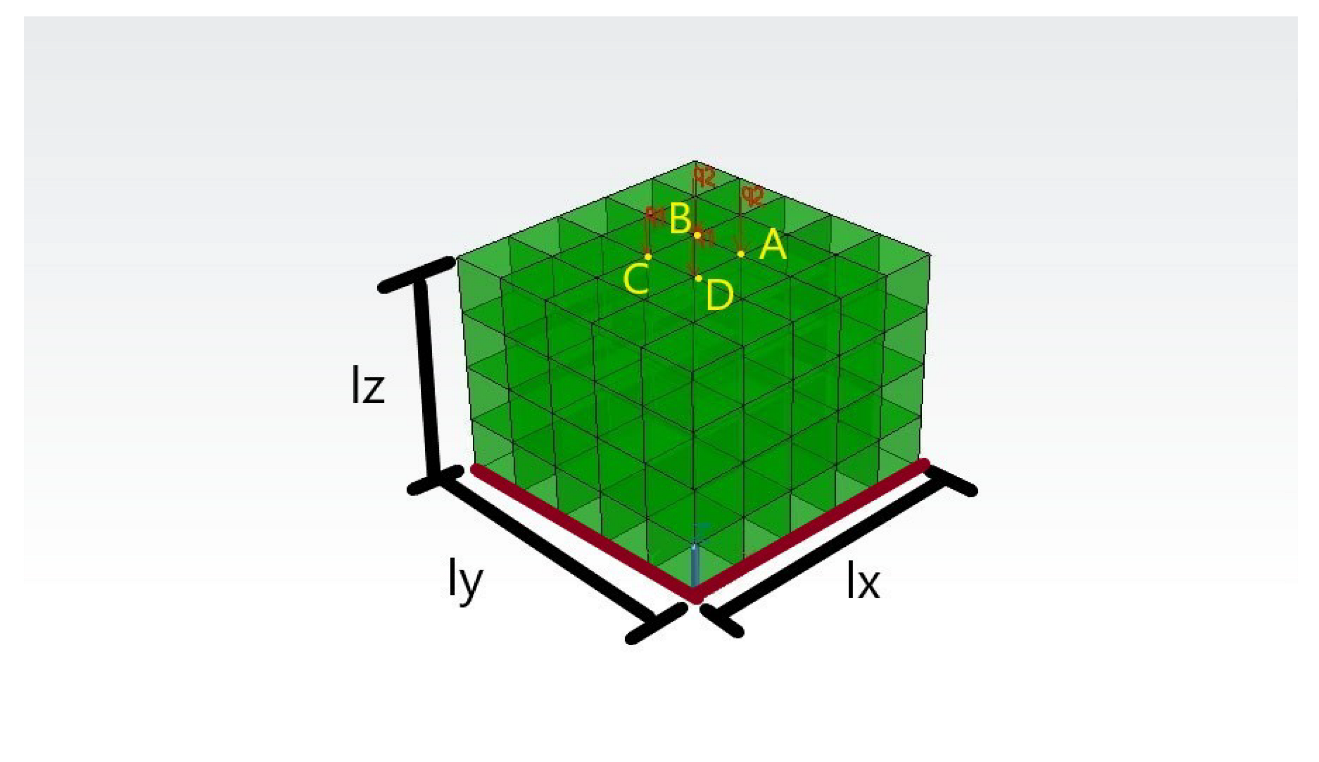
5.1. Description of the Numerical Simulations
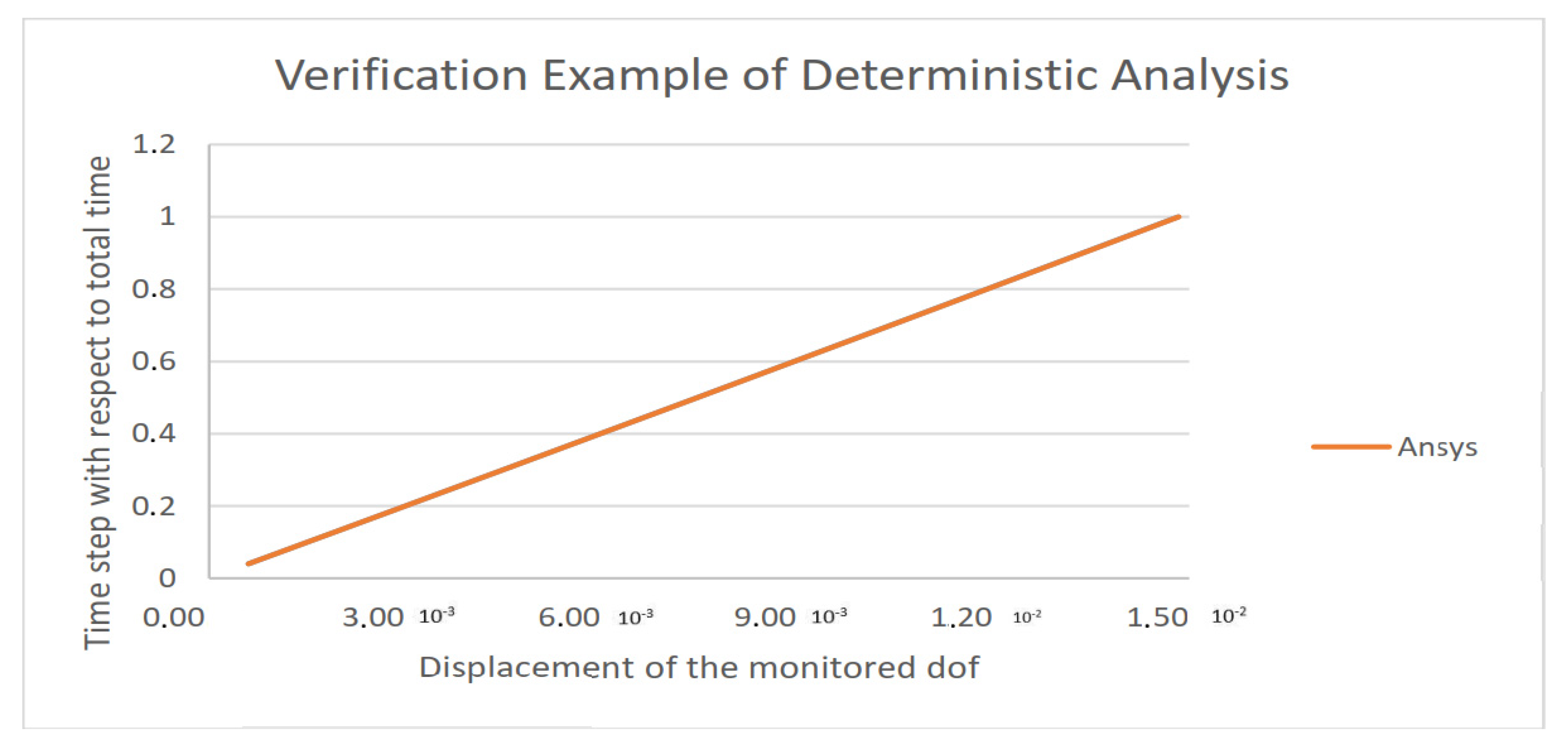
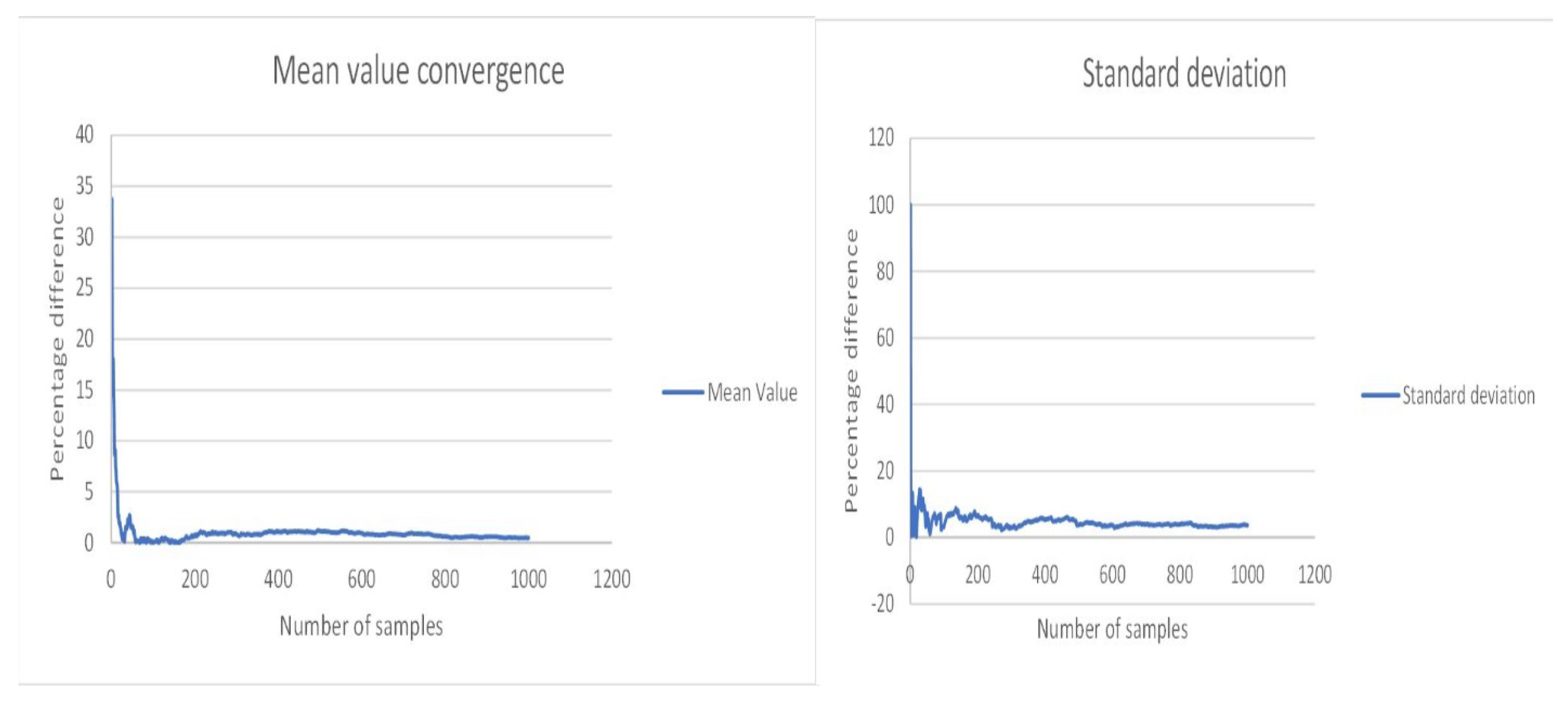
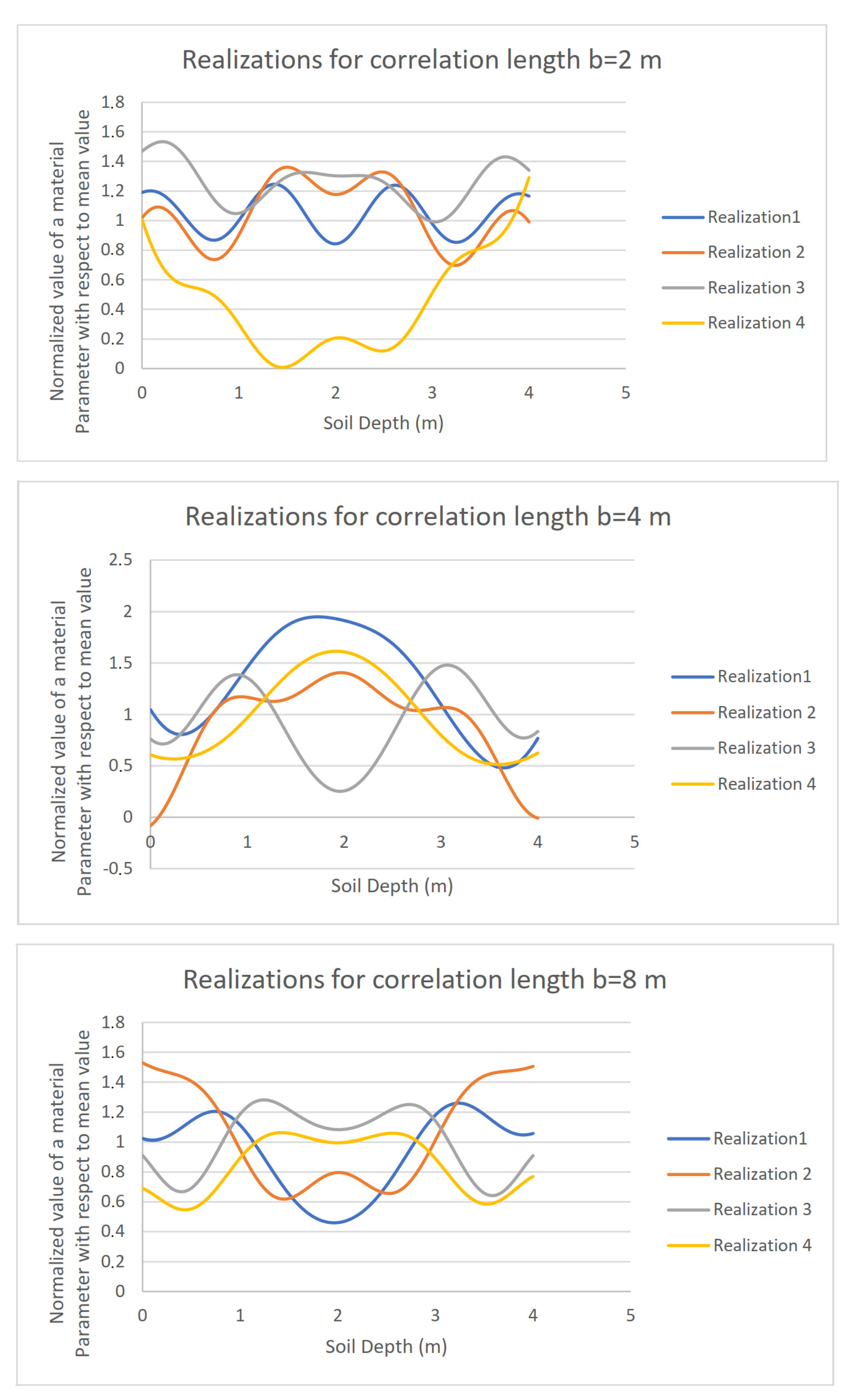
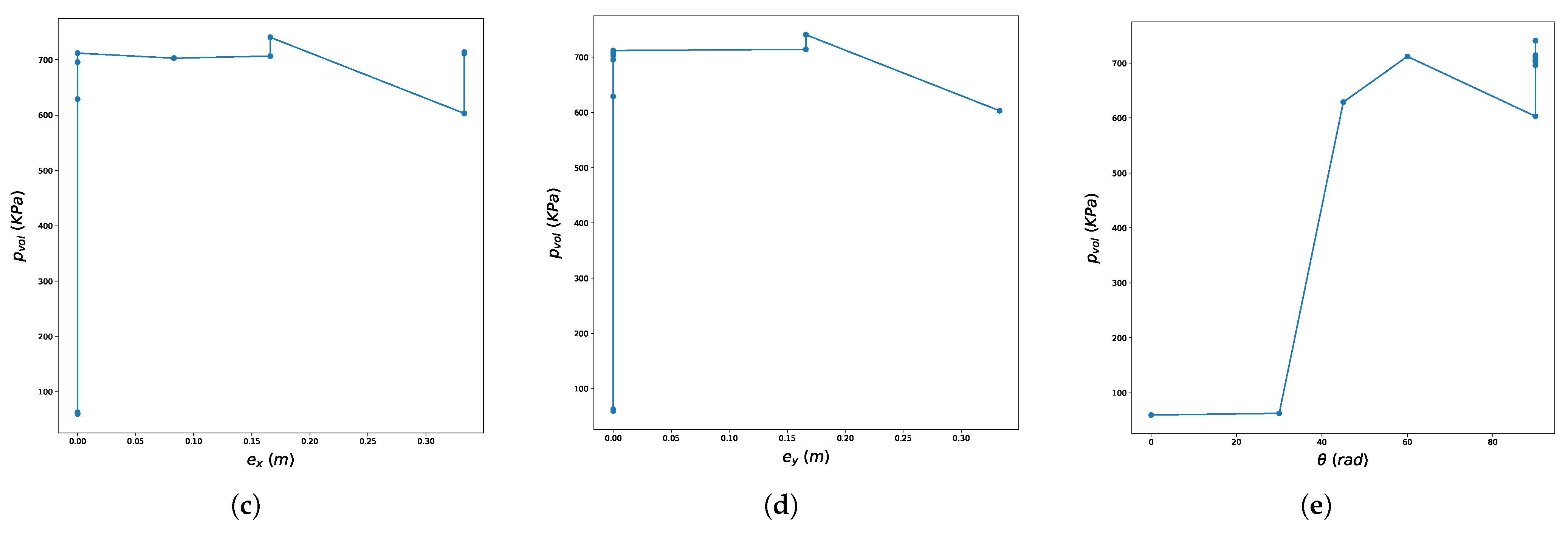
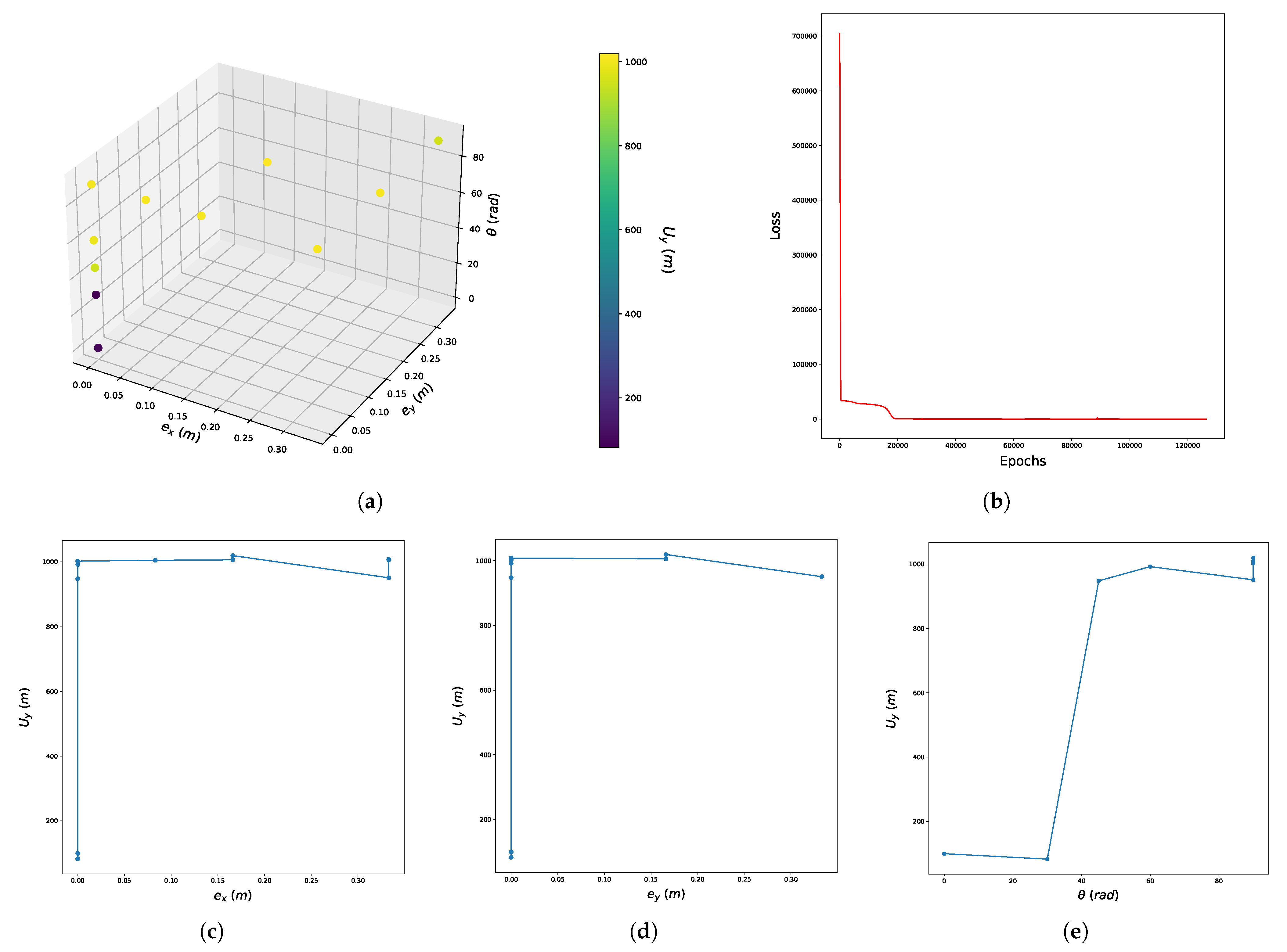
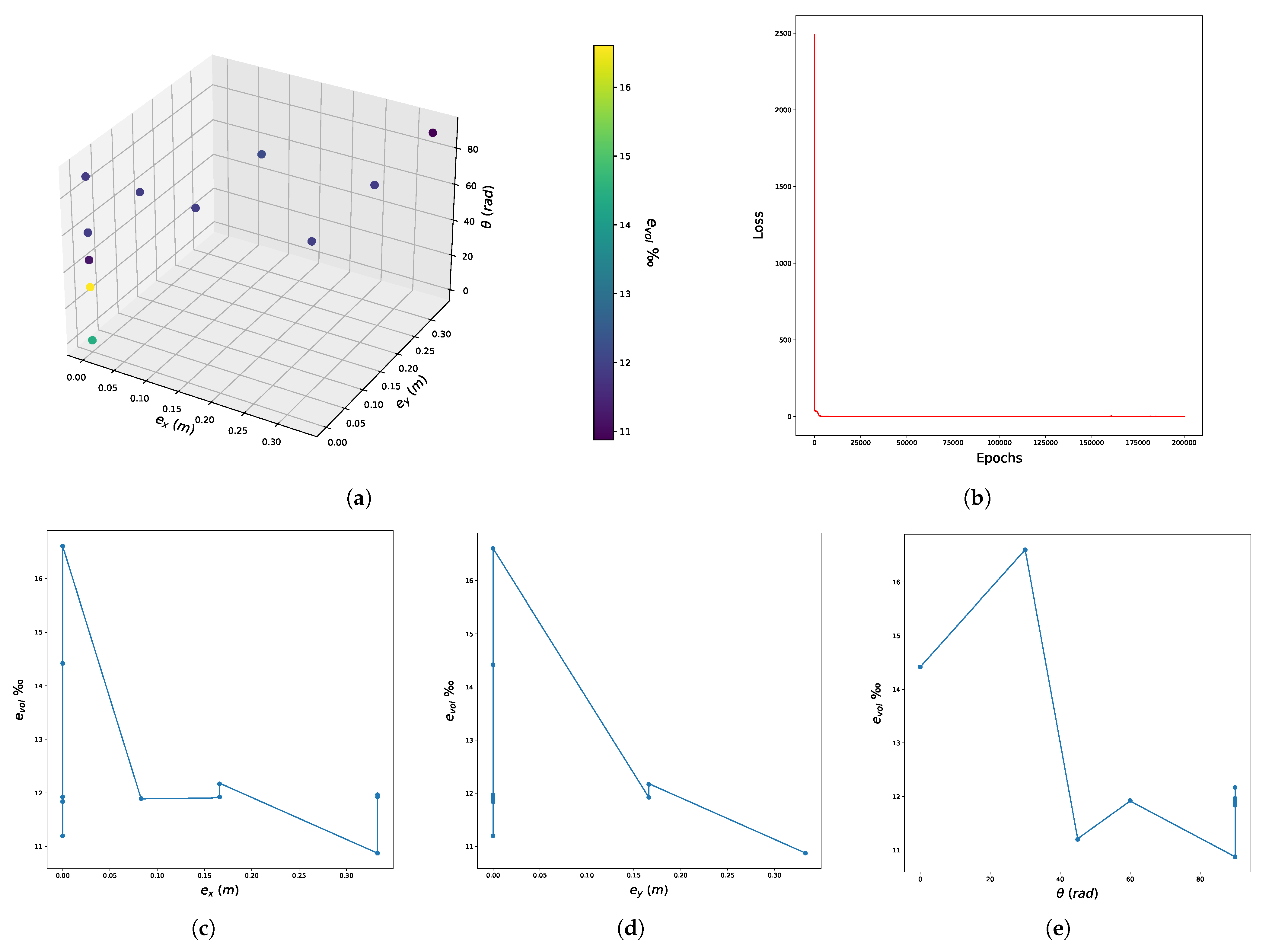
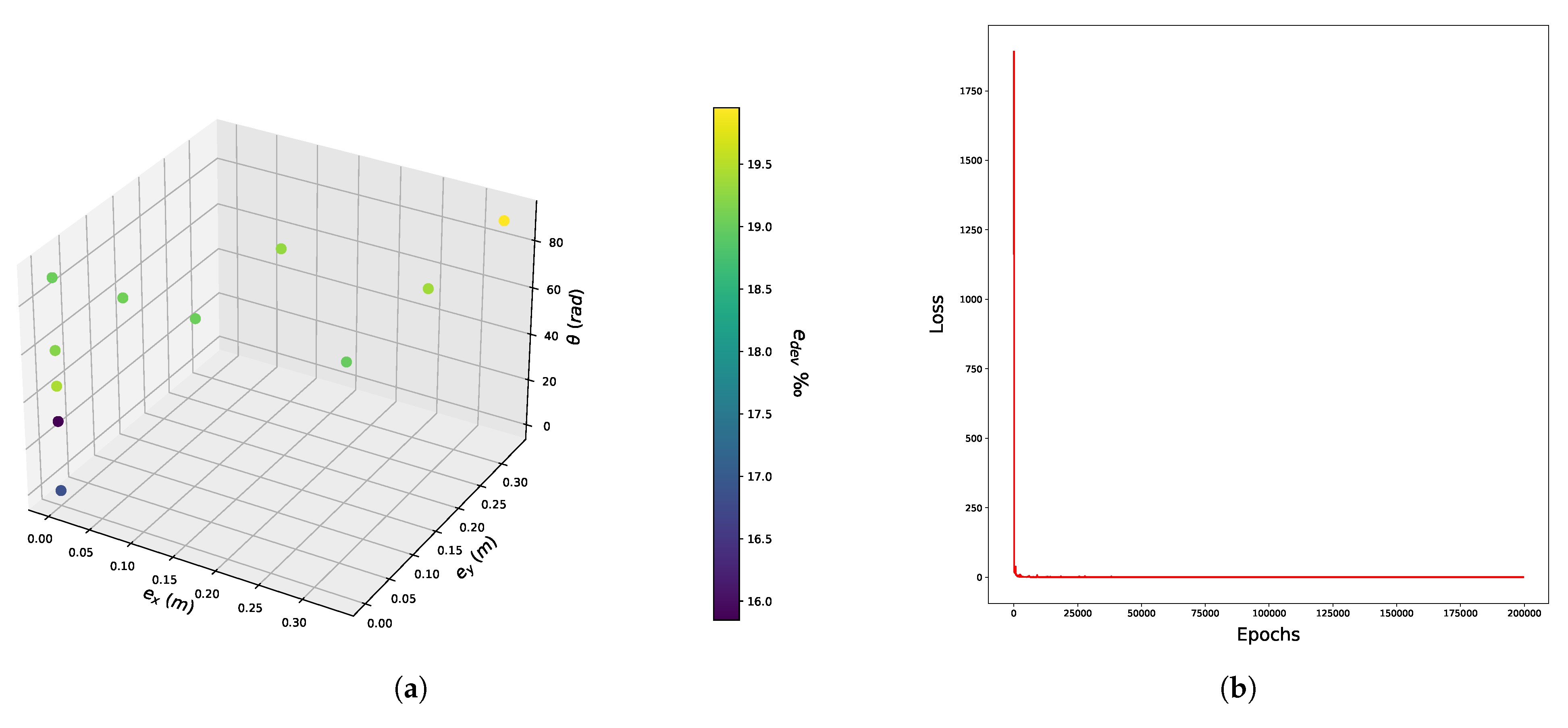
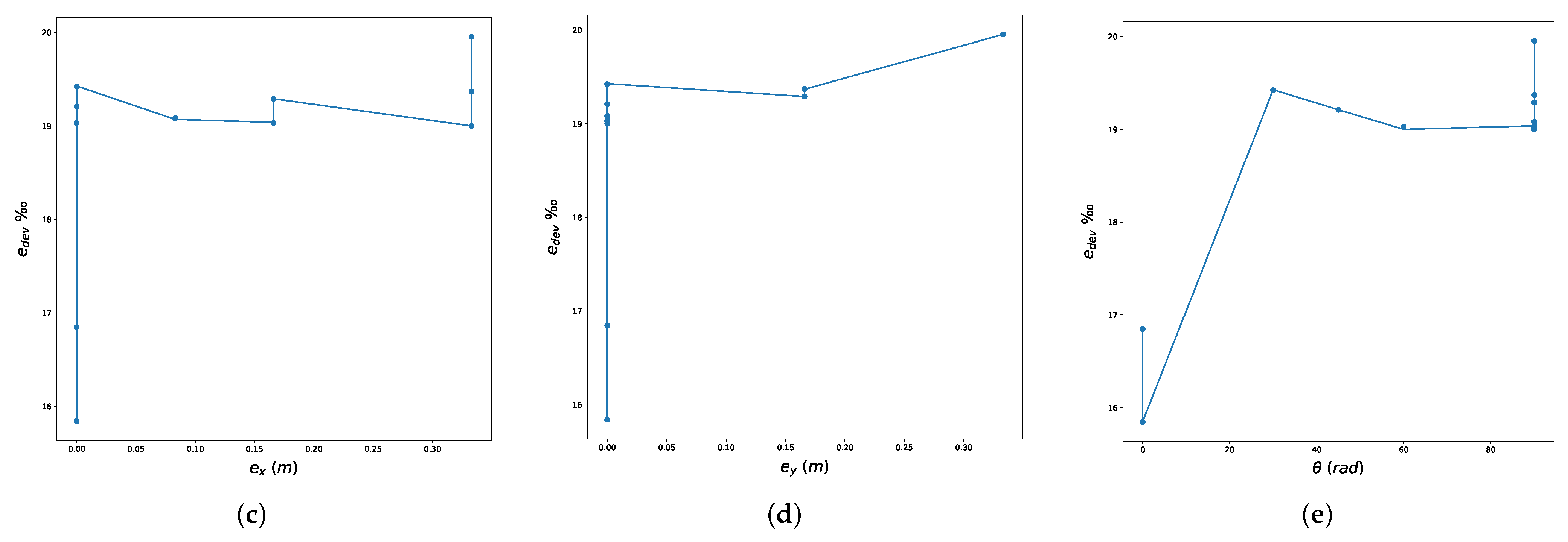
5.2. Presentation of the Results-Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Friction variables | |
| Friction variable indicating the influence of possible vertical load in the lateral direction of the foundation | |
| Friction variable indicating the influence of the cohesion of the soil | |
| Friction variable indicating the influence of the settlement dimensions | |
| alongside the total weight of the soil | |
| Shape variables | |
| Shape variable indicating the influence of possible vertical load in the lateral direction of the foundation | |
| Shape variable indicating the influence of the cohesion of the soil | |
| Shape variable indicating the influence of the settlement dimensions | |
| alongside the total weight of the soil | |
| Compressibility factor | |
| c | Critical state line inclination |
| k | Permeability in units |
| Friction angle | |
| Total mass matrix | |
| Total damping matrix | |
| Total stiffness matrix | |
| Solid skeleton mass matrix | |
| Density of the soil | |
| Deformation matrix | |
| Elasticity matrix | |
| Solid skeleton damping matrix | |
| Solid skeleton stiffness matrix | |
| Unity matrix | |
| Loading vector | |
| Matrix of permeability in units | |
| Shape functions for pore pressure | |
| Shape functions for displacements | |
| Saturation matrix | |
| Coupling matrix | |
| Permeability matrix | |
| Equivalent forces due to external loading | |
| Q | Variable for combining the influence of bulk moduli of fluid and solid skeleton in |
| porous problems | |
| Total stress tensor | |
| Deviatoric component of the stress tensor | |
| Hydrostatic component of the stress tensor | |
| a | Halfsize of the Bond Strength Envelope |
| Deviatoric component of the stress point of the center of the Plastic Yield Envelope | |
| Hydrostatic component of the stress point of the center of the Plastic Yield Envelope | |
| Similarity factor between the Plastic Yield Envelope and Bond Strength Envelope | |
| Generalized elliptic envelope | |
| Plastic Yield Envelope (PYE) | |
| F | Bond Strength Envelope (BSE) |
| Specific volume of the soil | |
| q | Von Mises stress |
| e | Deviatoric strain measure |
| Deviatoric component of the strain tensor | |
| f | Random function |
| Value of the random function at nodal points | |
| Shape functions | |
| Total number of shape functions | |
| Truncated normal PDF | |
| Standard normal PDF | |
| Standard normal CDF | |
| Standard deviation of the random variable before truncation | |
| A, B, | Normalized coordinates of the subspace of the truncated PDF |
| limits and x | |
| Karhunen Loeve random field | |
| Number of subintervals in the Latin Hypercube Sampling | |
| Mean value of the random field | |
| Random vector created with Latin Hypercube Sampling | |
| , , | Total number of eigenvalues and eigenfunctions |
| , respectively | |
| b | Correlation length |
| Covariance function | |
| Load factor causing failure of the body at exactly the time that ends | |
| the rampload function | |
| T | Time at which the rampload function ends |
| Symmetrization factor of the stochastic process | |
| Trial load factor of step n causing failure | |
| Time of failure at the generalized load factor | |
| Maximum trial load factor which causes safety | |
| Initial trial load factor causing failure | |
| Initial trial load factor which causes safety | |
| Equivalent forces of the shallow foundation | |
| Eccentricity | |
| Dimensions of the total finite element mesh | |
| Geostatic stresses in vertical direction and directions x and y, respectively | |
| Inclination of isotropic compression line for the respective normally | |
| consolidated clay | |
| Initial halfsize of the ellipse | |
| Residual halfsize of the ellipse | |
| OCR | Overconsolidation ratio |
| G | Shear modulus |
| Bulk modulus | |
| Specific weight | |
| Initial specific volume of the soil | |
| Displacement vector in direction x | |
| Compressibility factor at depth=0 | |
| Compressibility factor at maximum depth | |
| Ratio of the compressibility factors measured at depth=0 and at maximum depth | |
| Mean value of ratio R | |
| Compressibility factor at maximum depth when the ratio R has its mean value | |
| Linear distribution over depth for the compressibility factor | |
| Constant distribution over depth for the compressibility factor | |
| Mean value of | |
| Random variable case for the critical state line inclination | |
| Deterministic case for the critical state line inclination | |
| Mean value of the friction angle | |
| Standard deviation of the friction angle | |
| Mean value of the permeability | |
| Coefficient of variation of the friction angle | |
| Mean value of the compressibility factor in the random field representation | |
| Mean value of the critical state line inclination in the random field representation | |
| Mean value of the permeability in the random field representation | |
| Standard deviation of the compressibility factor in the random field | |
| representation | |
| Standard deviation of the critical state line inclination in the random field | |
| representation | |
| Standard deviation of the permeability in the random field representation | |
| Mean values of the results | |
| Coefficient of variation of the results | |
| M | Maximum values of the results |
| Minimum values of the results | |
| N | Total settlement force |
| Horizontal displacement at failure | |
| Vertical displacement at failure | |
| Volumetric stress at failure | |
| Von Mises stress at failure | |
| Volumetric strain at failure | |
| Deviatoric strain at failure | |
| Percentage plastic volumetric strains at failure | |
| Percentage plastic deviatoric strains at failure |
References
- Terzaghi, K.V. Theoretical Soil Mechanics; Wiley and Sons: Hoboken, NJ, USA, 1966. [Google Scholar]
- Michalowski, R.L. An Estimate of the Influence of Soil Weight on Bearing Capacity Using Limit Analysis. Soils Found. 1997, 37, 57–64. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Michalowski, R.L. Upper-bound load estimates on square and rectangular footings. Geotechnique 2001, 51, 787–798. [Google Scholar] [CrossRef]
- Martin, C. Exact bearing capacity calculations using the method of characteristics. In Proceedings of the 11th International Conference IACMAG, Graz, Austria, 19–24 June 2005. [Google Scholar]
- Rao, P.; Liu, Y.; Cui, J. Bearing capacity of strip footings on two-layered clay under combined loading. Comput. Geotech. 2015, 69, 210–218. [Google Scholar] [CrossRef]
- Zafeirakos, A.; Gerolymos, N. Bearing strength surface for bridge caisson foundations in frictional soil under combined loading. Acta Geotech. 2016, 11, 1189–1208. [Google Scholar] [CrossRef]
- Zhou, H.; Zheng, G.; Yin, X.; Jia, R.; Yang, X. The bearing capacity and failure mechanism of a vertically loaded strip footing placed on the top of slopes. Comput. Geotech. 2018, 94, 12–21. [Google Scholar] [CrossRef]
- Naderi, E.; Asakereh, A.; Dehghani, M. Bearing Capacity of Strip Footing on Clay Slope Reinforced with Stone Columns. Arab. J. Sci. Eng. 2018, 43, 5559–5572. [Google Scholar] [CrossRef]
- Sultana, P.; Dey, A.K. Estimation of Ultimate Bearing Capacity of Footings on Soft Clay from Plate Load Test Data Considering Variability. Indian Geotech. J. 2019, 49, 170–183. [Google Scholar] [CrossRef]
- Papadopoulou, K.; Gazetas, G. Shape Effects on Bearing Capacity of Footings on Two-Layered Clay. Geotech. Geol. Eng. 2020, 38, 1347–1370. [Google Scholar] [CrossRef]
- Fu, D.; Zhang, Y.; Yan, Y. Bearing capacity of a side-rounded suction caisson foundation under general loading in clay. Comput. Geotech. 2020, 123, 103543. [Google Scholar] [CrossRef]
- Li, S.; Yu, J.; Huang, M.; Leung, G. Upper bound analysis of rectangular surface footings on clay with linearly increasing strength. Comput. Geotech. 2021, 129, 103896. [Google Scholar] [CrossRef]
- Karhunen, K. Uber lineare Methoden in der Wahrscheinlichkeitsrechnung. Ann. Acad. Sci. Fenn. 1947, 37, 1–79. [Google Scholar]
- Ghanem, R.; Spanos, D. Stochastic Finite Elements: A Spectral Approach; Springer: Berlin/Heidelberg, Germany, 1991; Volume 1, pp. 1–214. [Google Scholar] [CrossRef]
- Papadrakakis, M.; Papadopoulos, V. Robust and efficient methods for the stochastic finite element analysis using Monte Carlo simulation. Comput. Methods Appl. Mech. Eng. 1996, 134, 325–340. [Google Scholar] [CrossRef]
- Matthies, H.G.; Brenner, C.E.; Butcher, G.; Soares, C.G. Uncertainties in probabilistic numerical analysis of structures and solids- Stochastic finite elements. Struct. Saf. 1997, 19, 283–336. [Google Scholar] [CrossRef]
- Assimaki, D.; Pecker, A.; Popescu, R.; Prevost, J. Effects of spatial variabilty of soil properties on surface ground motion. J. Earthq. Eng. 2003, 7, 1–44. [Google Scholar] [CrossRef]
- Popescu, R.; Deodatis, G.; Nobahar, A. Effects of random heterogeneity of soil properties on bearing capacity. Probabilistic Eng. Mech. 2005, 20, 324–341. [Google Scholar] [CrossRef]
- Sett, K.; Jeremic, B. Probabilistic elasto-plasticity: Solution and verification in 1D. Acta Geotech. 2007, 2, 211–220. [Google Scholar] [CrossRef]
- Meftah, F.; Dal-Pont, S.; Schrefler, B.A. A three-dimensional staggered finite element approach for random parametric modeling of thermo-hygral coupled phenomena in porous media. Int. J. Numer. Anal. Methods Geomech. 2012, 36, 574–596. [Google Scholar] [CrossRef]
- Li, D.Q.; Qi, X.H.; Cao, Z.J.; Tang, X.S.; Zhou, W.; Phoon, K.K.; Zhou, C.B. Reliability analysis of strip footing considering spatially variable undrained shear strength that linearly increases with depth. Soils Found. 2015, 55, 866–880. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Sun, Q.; Miao, H.; Li, J. Nonlinear stochastic seismic analysis of buried pipeline systems. Soil Dyn. Earthq. Eng. 2015, 74, 69–78. [Google Scholar] [CrossRef]
- Ali, A.; Lyamin, A.; Huang, J.; Li, J.; Cassidy, M.; Sloan, S. Probabilistic stability assessment using adaptive limit analysis and random fields. Acta Geotech. 2017, 12, 937–948. [Google Scholar] [CrossRef]
- Brantson, E.T.; Ju, B.; Wu, D.; Gyan, P.S. Stochastic porous media modeling and high-resolution schemes for numerical simulation of subsurface immiscible fluid flow transport. Acta Geophys. 2018, 66, 243–266. [Google Scholar] [CrossRef]
- Chwała, M. Undrained bearing capacity of spatially random soil for rectangular footings. Soils Found. 2019, 59, 1508–1521. [Google Scholar] [CrossRef]
- Olsson, A.; Sandberg, G.; Dahlblom, O. On Latin hypercube sampling for structural reliability analysis. Struct. Saf. 2003, 25, 47–68. [Google Scholar] [CrossRef]
- Simoes, J.; Neves, L.; Antao, A.; Guerra, N. Reliability assessment of shallow foundations on undrained soils considering soil spatial variability. Comput. Geotech. 2020, 119, 103369. [Google Scholar] [CrossRef]
- Savvides, A.; Papadrakakis, M. A computational study on the uncertainty quantification of failure of clays with a modified Cam-Clay yield criterion. Springer Nat. Appl. Sci. 2021, 3, 659. [Google Scholar] [CrossRef]
- Savvides, A.; Papadrakakis, M. Probabilistic Failure Estimation of an Oblique Loaded Footing Settlement on Cohesive Geomaterials with a Modified Cam Clay Material Yield Function. Geotechnics 2021, 1, 347–384. [Google Scholar] [CrossRef]
- Savvides, A.; Papadrakakis, M. Uncertainty Quantification of Failure of Shallow Foundation on Clayey Soils with a Modified Cam-Clay Yield Criterion and Stochastic FEM. Geotechnics 2022, 2, 348–384. [Google Scholar] [CrossRef]
- Savvides, A. Stochastic Failure of a Double Eccentricity Footing Settlement on Cohesive Soils with a Modified Cam Clay Yield Surface. Transp. Porous Media 2022, 141, 499–560. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Misyris, G.S.; Venzke, A.; Chatzivasileiadis, S. Physics-Informed Neural Networks for Power Systems. arXiv 2020, arXiv:1911.03737. [Google Scholar]
- Desai, S.; Mattheakis, M.; Joy, H.; Protopapas, P.; Roberts, S. One-Shot Transfer Learning of Physics-Informed Neural Networks. arXiv 2021, arXiv:2110.11286. [Google Scholar]
- Ramabathiran, A.A.; Ramachandran, P. SPINN: Sparse, Physics-based, and partially Interpretable Neural Networks for PDEs. arXiv 2021, arXiv:2102.13037. [Google Scholar] [CrossRef]
- Leung, W.T.; Lin, G.; Zhang, Z. Nh-pinn: Neural homogenization based physics-informed neural network for multiscale problems. arXiv 2021, arXiv:2108.12942. [Google Scholar] [CrossRef]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 2015, arXiv:1603.04467. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the Advances in Neural Information Processing Systems 32 (NeurIPS 2019): Annual Conference on Neural Information Processing Systems 2019, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Kharazmi, E.; Zhang, Z.; Karniadakis, G.E. hp-VPINNs: Variational physics-informed neural networks with domain decomposition. Comput. Methods Appl. Mech. Eng. 2021, 374, 113547. [Google Scholar] [CrossRef]
- Meng, X.; Li, Z.; Zhang, D.; Karniadakis, G.E. PPINN: Parareal physics-informed neural network for time-dependent PDEs. Comput. Methods Appl. Mech. Eng. 2020, 370, 113250. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Karniadakis, G.E. Extended Physics-Informed Neural Networks (XPINNs): A Generalized Space-Time Domain Decomposition Based Deep Learning Framework for Nonlinear Partial Differential Equations. Comput. Phys. 2020, 28, 2002–2041. [Google Scholar] [CrossRef]
- Zhou, W.H.; Garg, A.; Garg, A. Study of the volumetric water content based on density, suction and initial water content. Measurement 2016, 94, 531–537. [Google Scholar] [CrossRef]
- Zhang, P.; Yin, Z.Y.; Jin, Y.F.; Chan, T.H.T. A novel hybrid surrogate intelligent model for creep index prediction based on particle swarm optimization and random forest. Eng. Geol. 2020, 265, 105328. [Google Scholar] [CrossRef]
- Zhang, P.; Yin, Z.Y.; Jin, Y.F.; Chan, T.H.T.; Gao, F.P. Intelligent modelling of clay compressibility using hybrid meta-heuristic and machine learning algorithms. Geosci. Front. 2021, 12, 441–452. [Google Scholar] [CrossRef]
- Zhang, N.S.; Zhou, S.L.; Xu, A.; Shuang, Y. Investigation on Performance of Neural Networks Using Quadratic Relative Error Cost Function. IEEE Access 2019, 7, 106642–106652. [Google Scholar] [CrossRef]
- Zhang, P.; Qi, C.; Sun, X.; Fang, H.; Huang, Y. Bending behaviors of the in-plane bidirectional functionally graded piezoelectric material plates. Mech. Adv. Mater. Struct. 2020, 29, 1925–1945. [Google Scholar] [CrossRef]
- Njock, P.G.A.; Shen, S.L.; Zhou, A.; Lyu, H.M. Evaluation of soil liquefaction using AI technology incorporating a coupled ENN/ t-SNE model. Soil Dyn. Earthq. Eng. 2020, 130, 105988. [Google Scholar] [CrossRef]
- Chen, R.P.; Zhang, P.; Kang, X.; Zhong, Z.Q.; Liu, Y.; Wu, H.N. Prediction of maximum surface settlement caused by earth pressure balance (EPB) shield tunneling with ANN methods. Soils Found. 2019, 59, 284–295. [Google Scholar] [CrossRef]
- Chen, R.; Zhang, P.; Wu, H.; Wang, Z.; Zhong, Z. Prediction of shield tunneling-induced ground settlement using machine learning techniques. Front. Struct. Civ. Eng. 2019, 13, 1363–1378. [Google Scholar] [CrossRef]
- Elbaz, K.; Shen, S.L.; Zhou, A.; Yuan, D.J.; Xu, Y.S. Optimization of EPB Shield Performance with Adaptive Neuro-Fuzzy Inference System and Genetic Algorithm. Appl. Sci. 2019, 9, 780. [Google Scholar] [CrossRef] [Green Version]
- Elbaz, K.; Shen, S.L.; Zhou, A.; Yin, Z.; Lyu, H.M. Prediction of Disc Cutter Life During Shield Tunneling with AI via the Incorporation of a Genetic Algorithm into a GMDH-Type Neural Network. Engineering 2021, 7, 238–251. [Google Scholar] [CrossRef]
- Zhang, P.; Chen, R.P.; Wu, H.N. Real-time analysis and regulation of EPB shield steering using Random Forest. Autom. Constr. 2019, 106, 102860. [Google Scholar] [CrossRef]
- Zhang, P.; Wu, H.N.; Chen, R.P.; Chan, T.H.T. Hybrid meta-heuristic and machine learning algorithms for tunneling-induced settlement prediction: A comparative study. Tunn. Undergr. Space Technol. 2020, 99, 103383. [Google Scholar] [CrossRef]
- Huang, F.; Huang, J.; Jiang, S.; Zhou, C. Landslide displacement prediction based on multivariate chaotic model and extreme learning machine. Eng. Geol. 2017, 218, 173–186. [Google Scholar] [CrossRef]
- Yang, B.; Lacasse, S.; Liu, Z. Time series analysis and long short-term memory neural network to predict landslide displacement. Landslides 2019, 16, 677–694. [Google Scholar] [CrossRef]
- Zhang, P.; Yin, Z.Y.; Zheng, Y.; Gao, F.P. A LSTM surrogate modelling approach for caisson foundations. Ocean. Eng. 2020, 204, 107263. [Google Scholar] [CrossRef]
- Liu, Z.; Gilbert, G.; Cepeda, J.M.; Lysdahl, A.O.K.; Piciullo, L.; Hefre, H.; Lacasse, S. Modelling of shallow landslides with machine learning algorithms. Geosci. Front. 2021, 12, 385–393. [Google Scholar] [CrossRef]
- Wu, Z.; Wei, R.; Chu, Z.; Liu, Q. Real-time rock mass condition prediction with TBM tunneling big data using a novel rock–machine mutual feedback perception method. J. Rock Mech. Geotech. Eng. 2021, 13, 1311–1325. [Google Scholar] [CrossRef]
- Wu, C.; Hong, L.; Wang, L.; Zhangd, R.; Pijushe, S.; Zhang, W. Prediction of wall deflection induced by braced excavation in spatially variable soils via convolutional neural network. Gondwana Res. 2022. [Google Scholar] [CrossRef]
- Zhang, W.; Gu, X.; Tang, L.; Yin, Y.; Liu, D.; Zhang, Y. Application of machine learning, deep learning and optimization algorithms in geoengineering and geoscience: Comprehensive review and future challenge. Gondwana Res. 2022, 109, 1–17. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, N.; Zheng, Q.; Xu, Y.S. Real-time prediction of shield moving trajectory during tunnelling using GRU deep neural network. Acta Geotech. 2022, 17, 1167–1182. [Google Scholar] [CrossRef]
- Kavvadas, M.; Amorosi, A. A constitutive model for structured soils. Geotechnique 2000, 50, 263–273. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. A method for stochastic optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar]
- Fletcher, R. Practical Methods of Optimization; Wiley and Sons: Hoboken, NJ, USA, 1987. [Google Scholar]
- Zienkiewicz, O.C.; Chan, A.H.C.; Pastor, M.; Schrefler, B.A.; Shiomi, T. Computational Geomechanics with Special Reference to Earthquake Engineering; Wiley: Chichester, UK, 1999; Volume 1, pp. 17–49. [Google Scholar]
- Biot, M.A. General theory of three dimensional consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Lewis, R.W.; Schrefler, B.A. The Finite Element Method in the Deformation and Consolidation of Porous Media; Wiley and Sons: Hoboken, NJ, USA, 1988; Volume 1, pp. 1–508. [Google Scholar] [CrossRef]
- Borja, R.; Lee, S. Cam-Clay plasticity, Part 1: Implicit integration of elasto-plastic constitutive relations. Comput. Methods Appl. Mech. Eng. 1990, 78, 49–72. [Google Scholar] [CrossRef]
- Borja, R. Cam-Clay plasticity, Part 2: Implicit integration of constitutive equation based on a nonlinear elastic stress predictor. Comput. Methods Appl. Mech. Eng. 1991, 88, 225–240. [Google Scholar] [CrossRef]
- Kalos, A. Investigation of the nonlinear time-dependent soil behavior. PhD Diss. NTUA 2014, 1, 193–236. [Google Scholar]
- Vrakas, A. On the computational applicability of the modified Cam-clay model on the ‘dry’ side. Comput. Geotech. 2018, 94, 214–230. [Google Scholar] [CrossRef]
- Melenk, J.M.; Babuska, I. The partition of unity finite element method: Basic theory and applications. Comput. Methods Appl. Mech. Eng. 1996, 139, 289–314. [Google Scholar] [CrossRef] [Green Version]
- Szabo, B.; Babuska, I. Intoduction to Finite Element Analysis. Formulation, Verification and Validation; Wiley Series in Computational Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 1, pp. 1–382. [Google Scholar] [CrossRef]
- Stickle, M.M.; Yague, A.; Pastor, M. Free Finite Element Approach for Saturated Porous Media: Consolidation. Math. Probl. Eng. 2016, 2016, 4256079. [Google Scholar] [CrossRef]


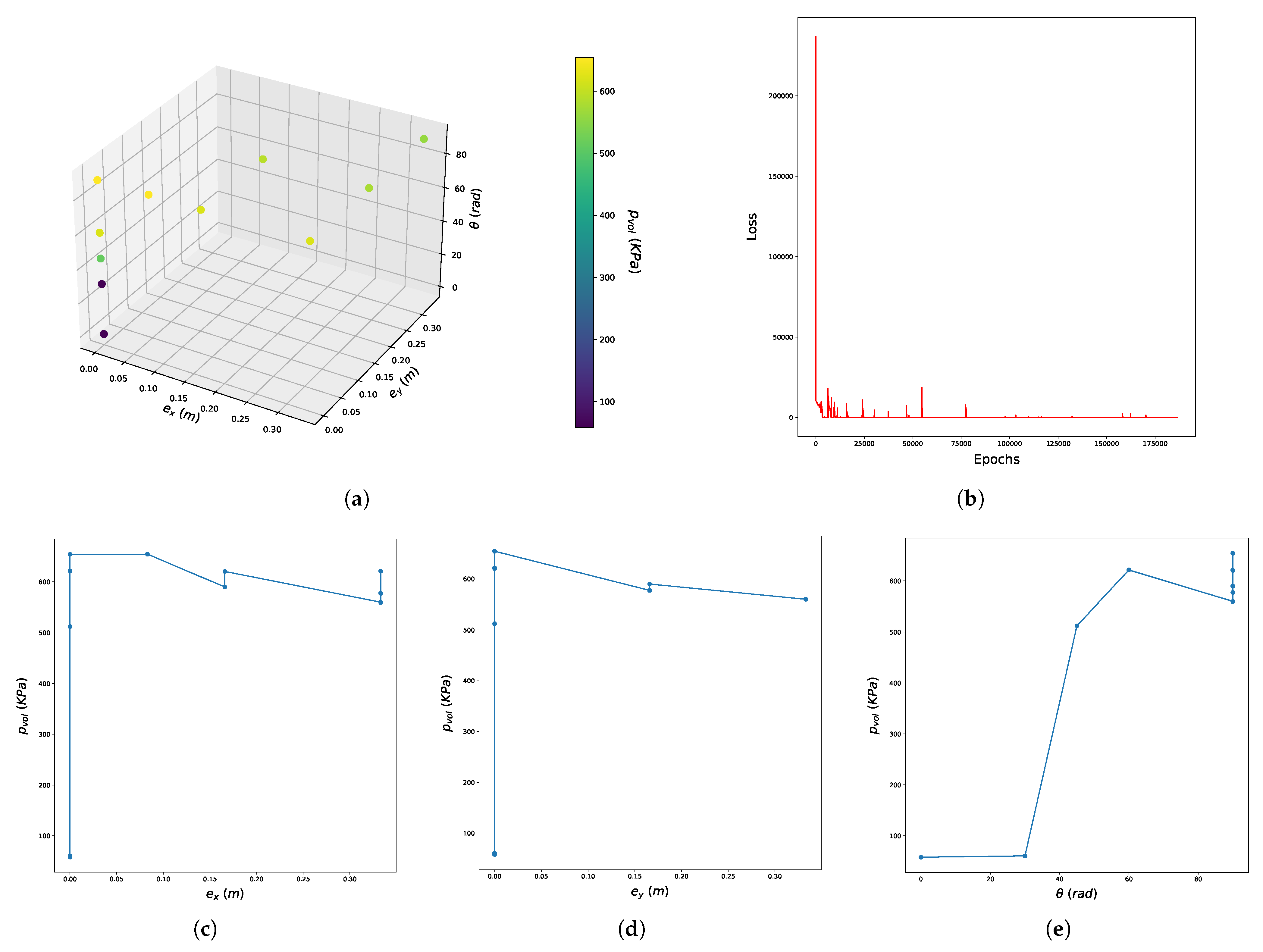
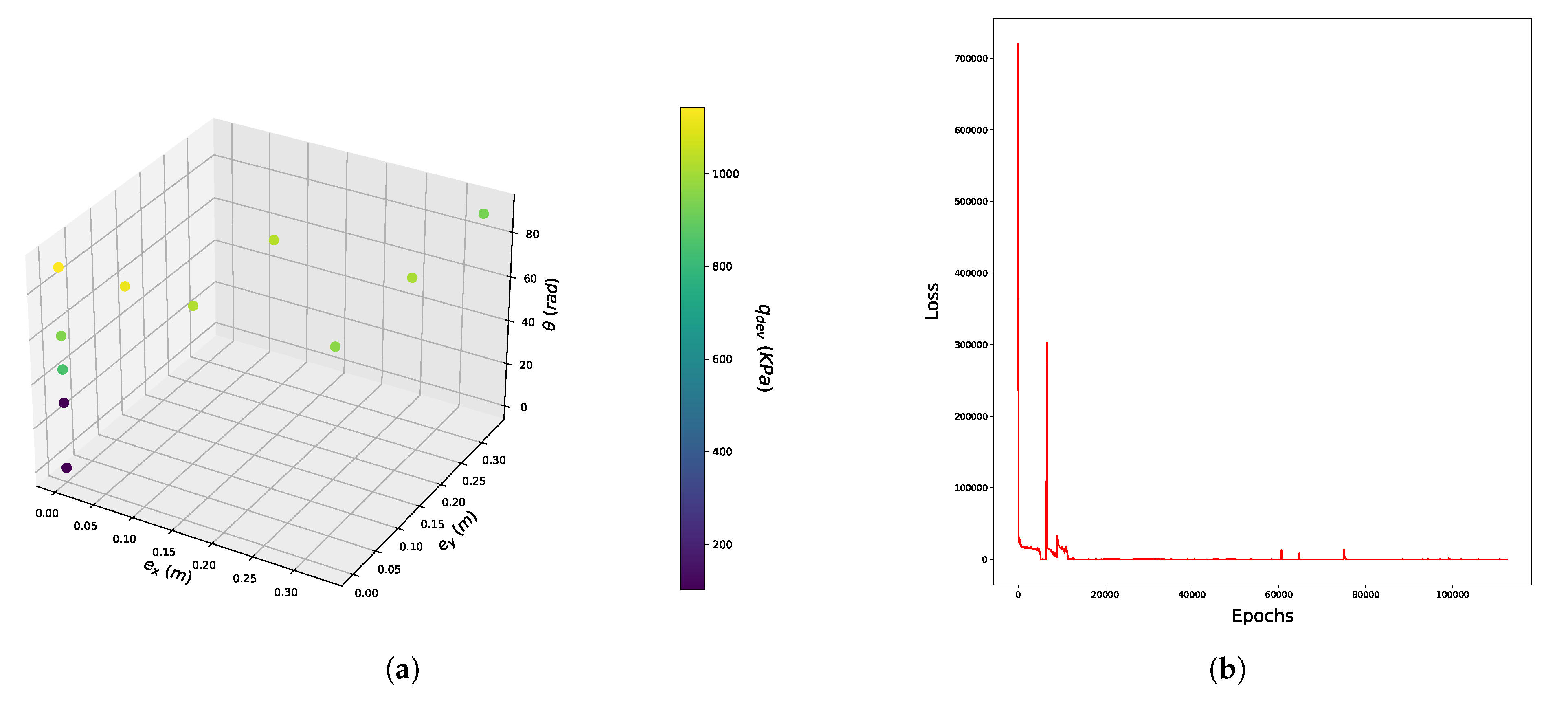
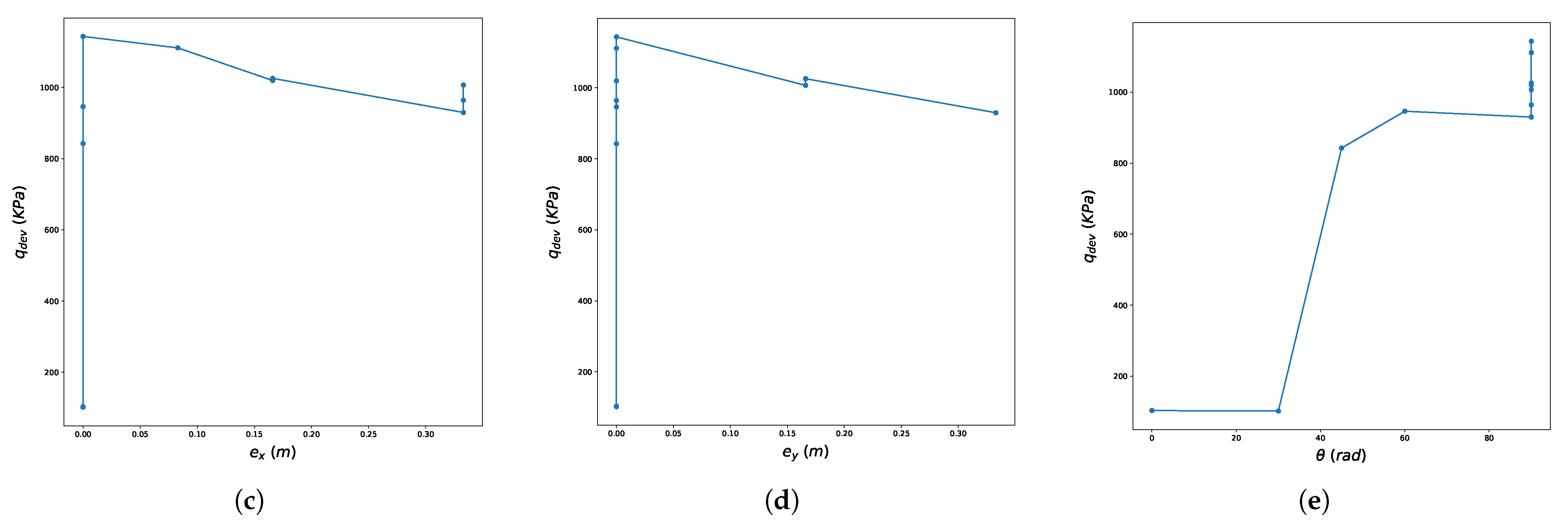
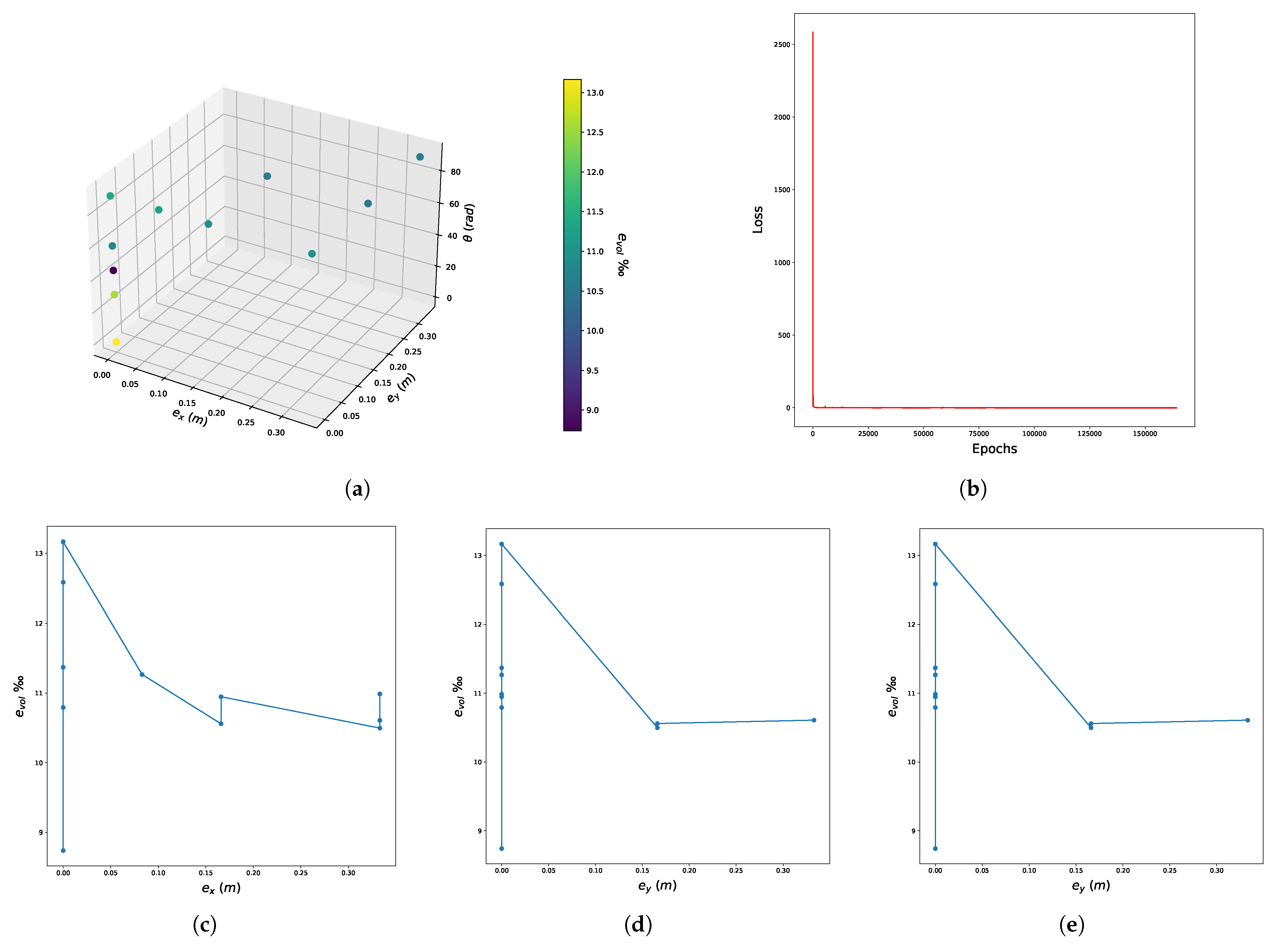


| c | Abbreviation-NN Number | |
|---|---|---|
| Linear | Random | ---d1 |
| Linear | Deterministic | ---d2 |
| Constant | Random | ---d3 |
| Constant | Deterministic | ---d4 |
| c | k | Abbreviation-NN Number | |
|---|---|---|---|
| Constant | Random | Deterministic | --- |
| Constant | Random | Random | --- |
| Constant | Deterministic | Random | --- |
| Constant | Deterministic | Deterministic | --- |
| Linear | Random | Deterministic | --- |
| Linear | Random | Random | --- |
| Linear | Deterministic | Random | --- |
| Linear | Deterministic | Deterministic | --- |
| Random Field, b = 2 | Random Field, b = 2 | Random Field, b = 2 | --- |
| Random Field, b = 4 | Random Field, b = 4 | Random Field, b = 4 | --- |
| Random Field, b = 8 | Random Field, b = 8 | Random Field, b = 8 | --- |
| NeurNet and Number | # of Epochs | Loss |
|---|---|---|
| 130,900 | ||
| 138,000 | ||
| NeurNet and Number | # of Epochs | Loss |
|---|---|---|
| 161,400 | ||
| 493,000 | ||
| NeurNet and Number | # of Epochs | Loss |
|---|---|---|
| 116,100 | ||
| 50,000 | ||
| 143,300 | ||
| 65,200 |
| NeurNet | # of Epochs | Loss |
|---|---|---|
| 159,400 | ||
| 200,000 | ||
| 200,000 | ||
| 199,600 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Savvides, A.-A.; Papadopoulos, L. A Neural Network Model for Estimation of Failure Stresses and Strains in Cohesive Soils. Geotechnics 2022, 2, 1084-1108. https://doi.org/10.3390/geotechnics2040051
Savvides A-A, Papadopoulos L. A Neural Network Model for Estimation of Failure Stresses and Strains in Cohesive Soils. Geotechnics. 2022; 2(4):1084-1108. https://doi.org/10.3390/geotechnics2040051
Chicago/Turabian StyleSavvides, Ambrosios-Antonios, and Leonidas Papadopoulos. 2022. "A Neural Network Model for Estimation of Failure Stresses and Strains in Cohesive Soils" Geotechnics 2, no. 4: 1084-1108. https://doi.org/10.3390/geotechnics2040051
APA StyleSavvides, A.-A., & Papadopoulos, L. (2022). A Neural Network Model for Estimation of Failure Stresses and Strains in Cohesive Soils. Geotechnics, 2(4), 1084-1108. https://doi.org/10.3390/geotechnics2040051








