Effect of the Field-Stress State on the Subgrade Resilient Modulus for Pavement Rutting and IRI
Abstract
:1. Introduction
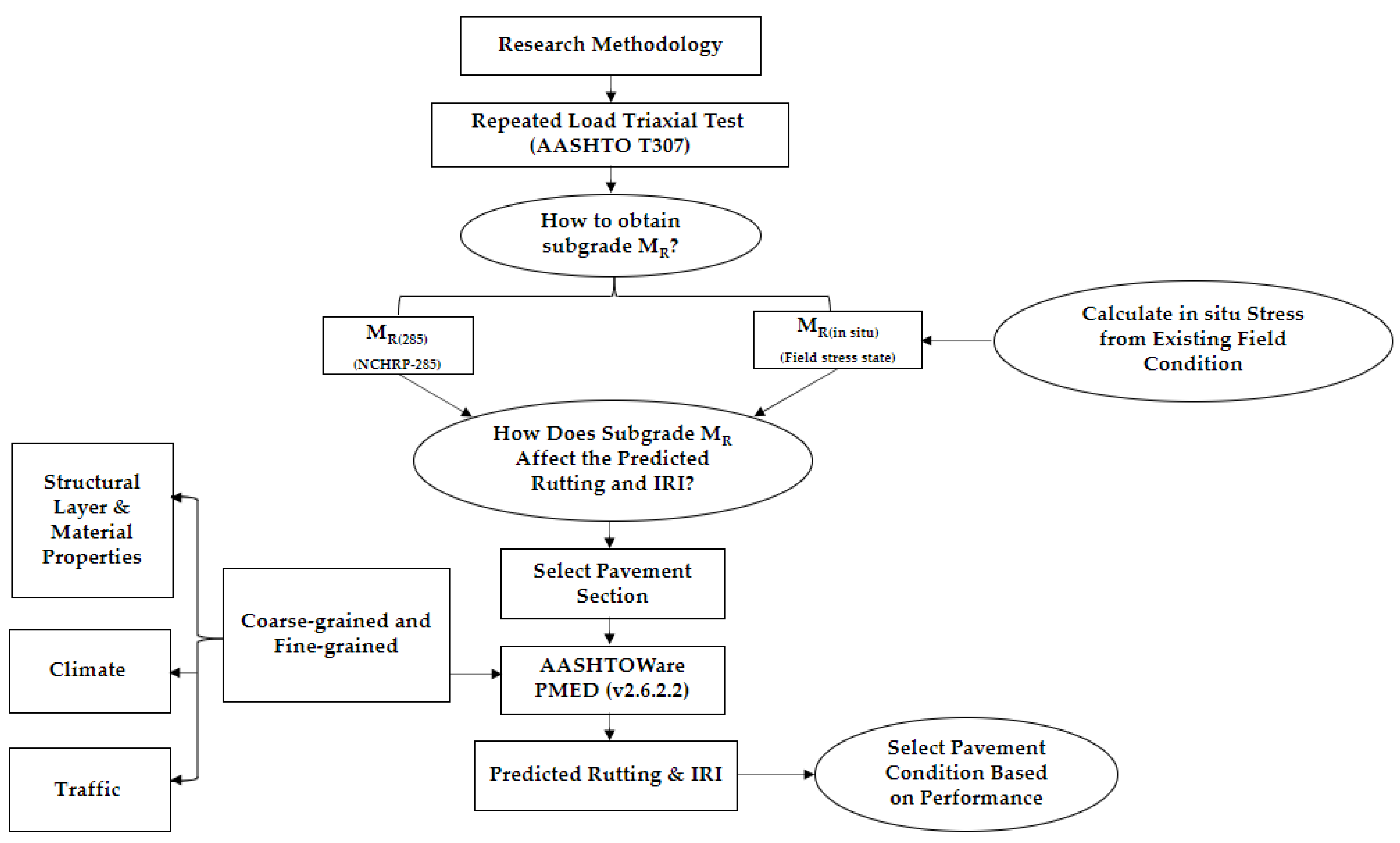
2. Research Questions and Objectives
- What is the effect of the stress conditions on the calculated MR for subgrade soil?
- How does the subgrade MR affect the predicted rutting and IRI?
- Is it possible to classify pavement conditions based on predicted and measured pavement performance?
- Task 1: Conduct Repeated Load Triaxial Test (RLTT) as per AASHTO T307 (AASHTO 2017) for coarse-grained and fine-grained samples.
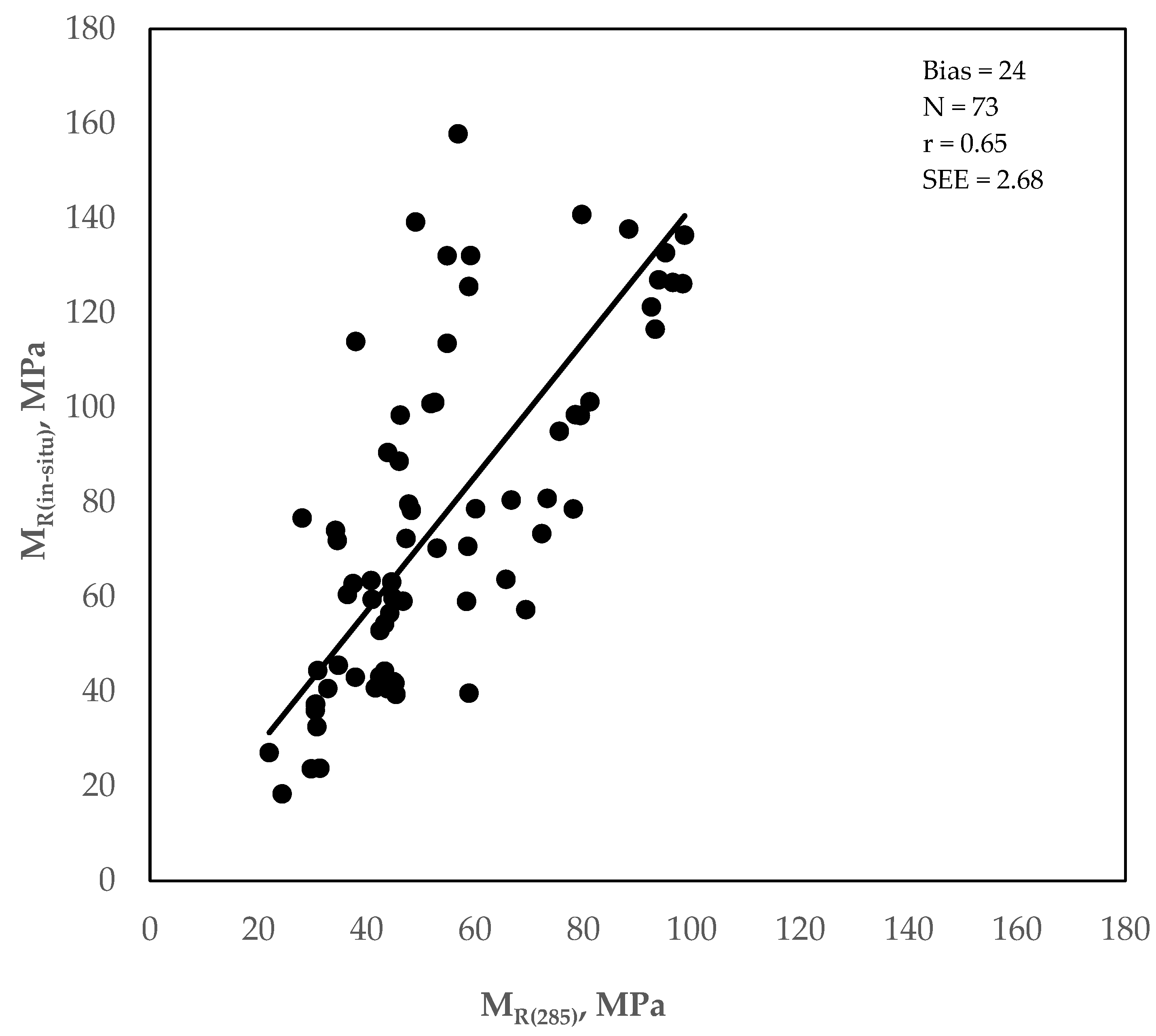
- Task 2: Obtain laboratory-measured MR (MR(285)) as per NCHRP-285 [38] and in situ MR (MR(in situ)) using field-stress conditions. Establish a linear relationship between the MR(285) and MR(in situ) and estimate the Pearson product-moment correlation coefficient (r). The value of r can range from 0.0, indicating no relationship between the two variables, to positive or negative 1.0, indicating a strong linear relationship between the two variables. Bias and Standard Error of Estimate (SEE) were also calculated.
- Task 3: Predict rutting and IRI using MEPDG and compare them with field-measured values. Classify the pavement conditions as “Good”, “Fair”, and “Poor” as per FHWA guidelines [39] for rutting and IRI.
3. Research Methodology
3.1. Pavement Profile Layer Information
| Site ID | BH | Asphalt Core | Base Layer | Subgrade Layer | ||||
|---|---|---|---|---|---|---|---|---|
| Thickness (cm) | Unit Weight γ1 (kN/m3) | Thickness (cm) | Unit Weight γ2 a (kN/m3) | Thickness (cm) | Unit weight γ3 b (kN/m3) | |||
| Core 1 (Hole A) | Core 2 (Hole B) | |||||||
| B278 | B278-1 | 17.7 | 18.2 | STB = 22.3 ITB = 22.6 BTA = 22.8 | 15.2 | 20.3 | 15.4 | 16.8 |
| B278-2 | 19.1 | 19.1 | 16.5 | 16.5 | 16.9 | |||
| B278-3 | 15.2 | 15.2 | 17.8 | 17.3 | 17.6 | |||
| L72 | L72-1 | 16.5 | 16.5 | 10.2 | 22.2 | 16.2 | 16.9 | |
| L72-2 | 16.8 | 16.8 | 12.7 | 15.7 | 16.9 | |||
| L72-3 | 36.8 | 35.6 | No base | 16.3 | 16.9 | |||
| L72-4 | 17.8 | 17.8 | 12.7 | 16.5 | 16.9 | |||
| L72-5 | 16.5 | 15.2 | 11.4 | 17.0 | 17.4 | |||
| L72-6 | 17.8 | 17.8 | 10.2 | 16.2 | 16.9 | |||
| L72-7 | 29.2 | 25.4 | No base | 16.2 | 16.9 | |||
| L72-8 | 25.4 | 25.4 | No base | 17.3 | 18.4 | |||
| L72-9 | 27.3 | 26.0 | No base | 17.4 | 18.4 | |||
| L72-10 | 29.2 | 25.4 | No base | 17.3 | 18.4 | |||
| L72-11 | 29.8 | 27.9 | No base | 16.7 | 17.3 | |||
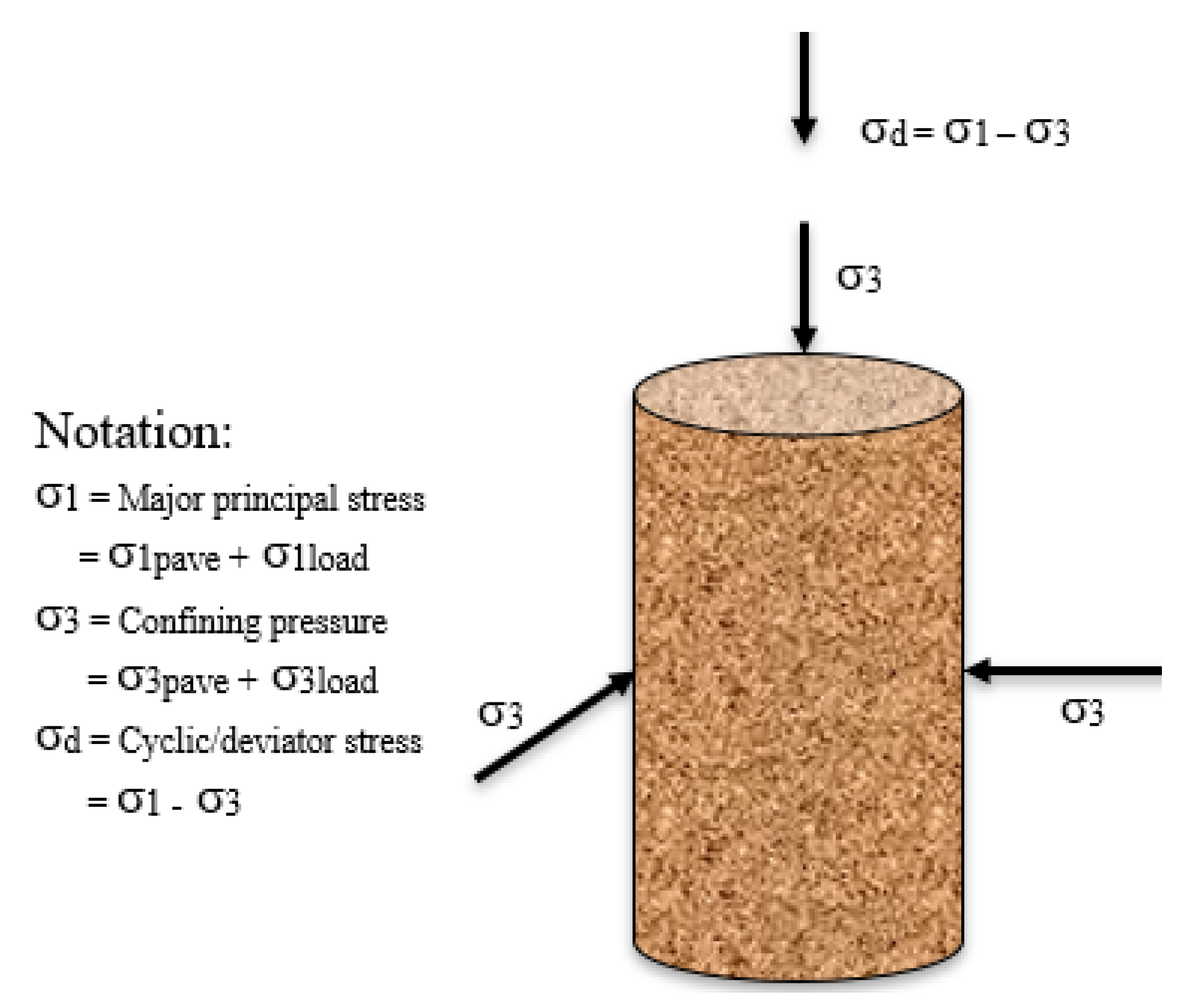
3.2. Resilient Modulus Tests
- Pa = atmospheric pressure (101.1 kPa)
- k1, , and = model parameters
- θ = bulk stress = (σ1 + σ2 + σ3)
- σ1, σ2, and σ3 = principal stresses and
- τoct = octahedral shear stress
- =
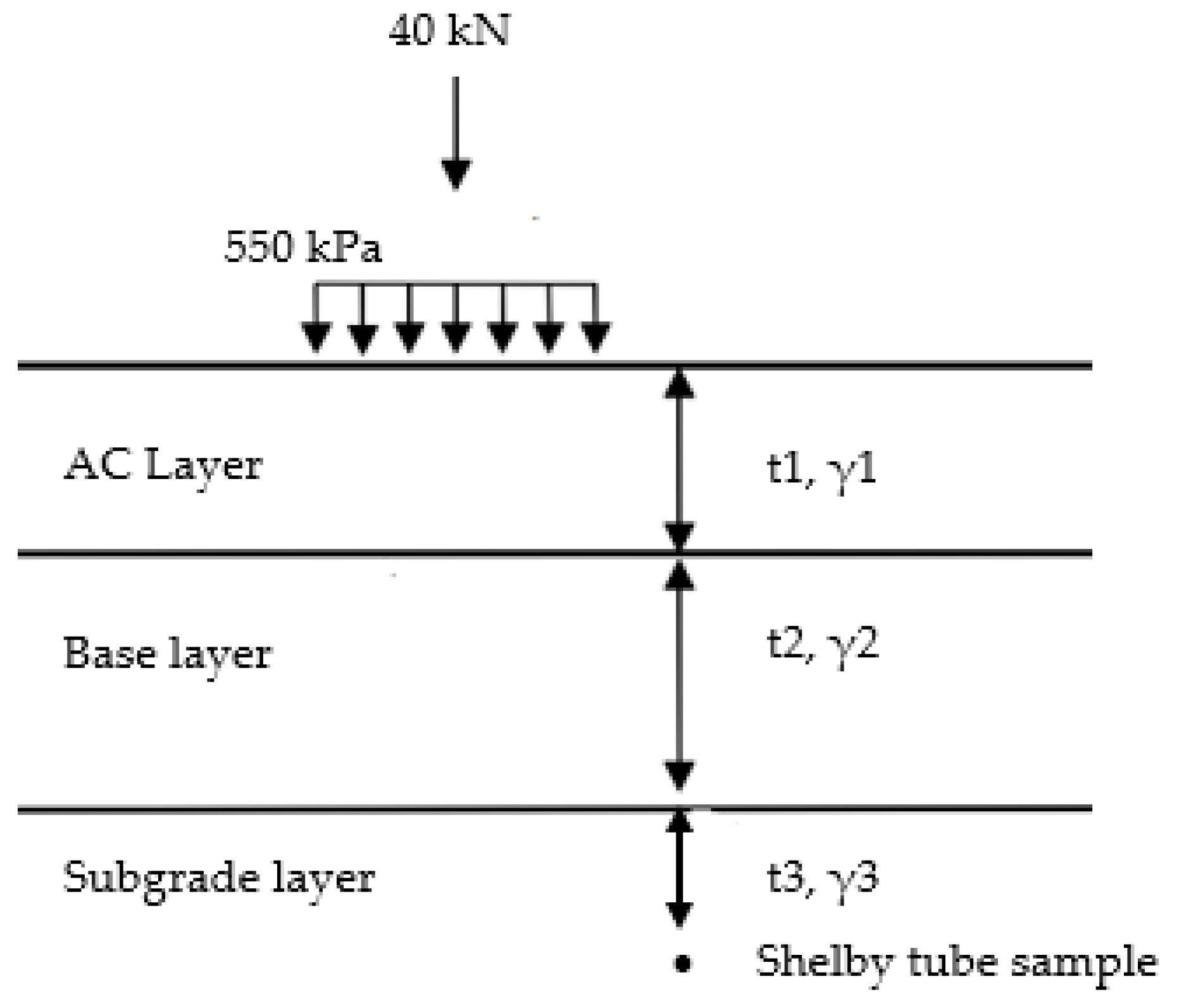
3.3. Calculate In Situ Stress for the Existing Pavement Section
3.4. Pavement Input Parameters
3.5. Threshold Values for Pavement Rutting and IRI
4. Results
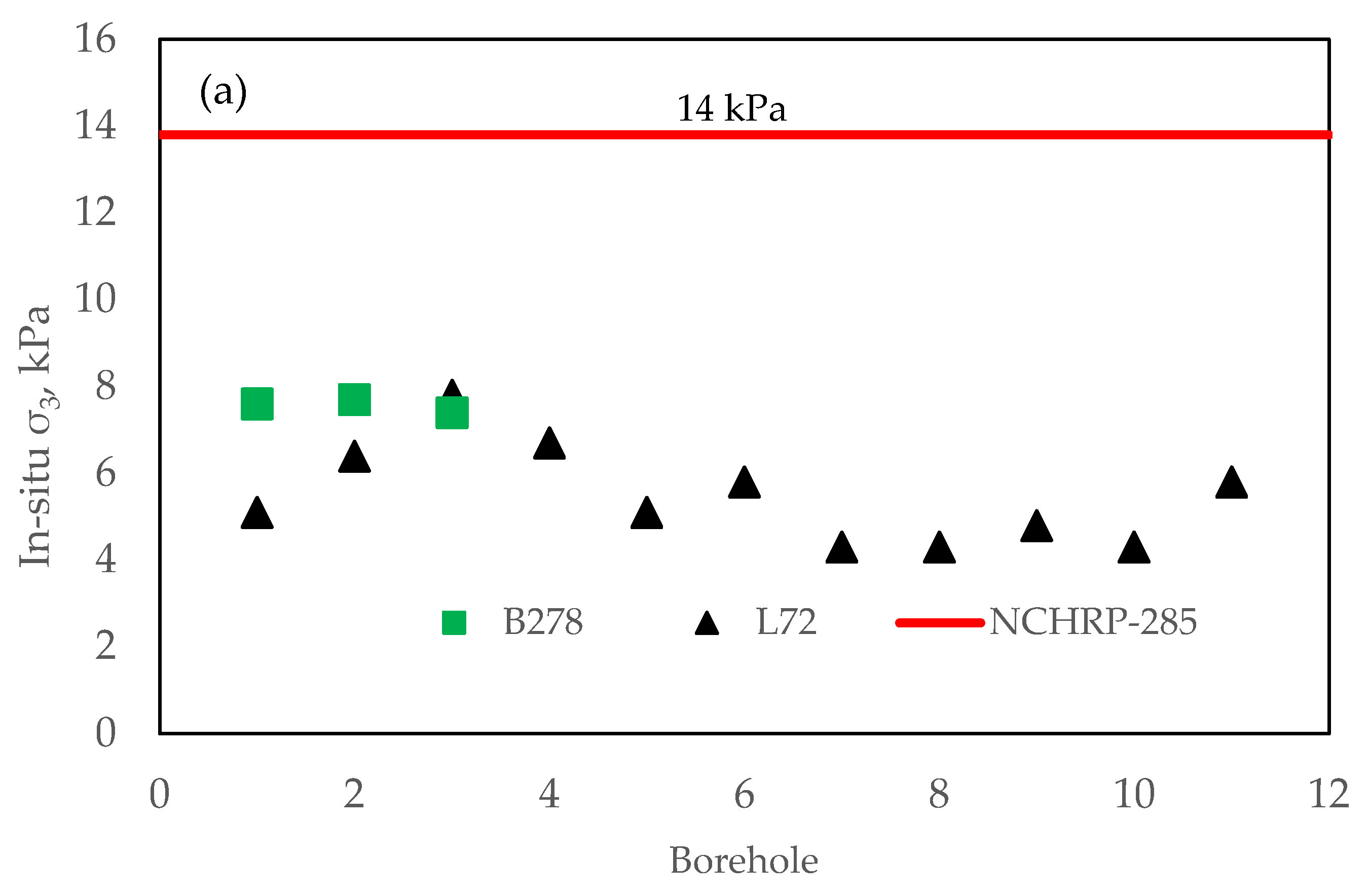
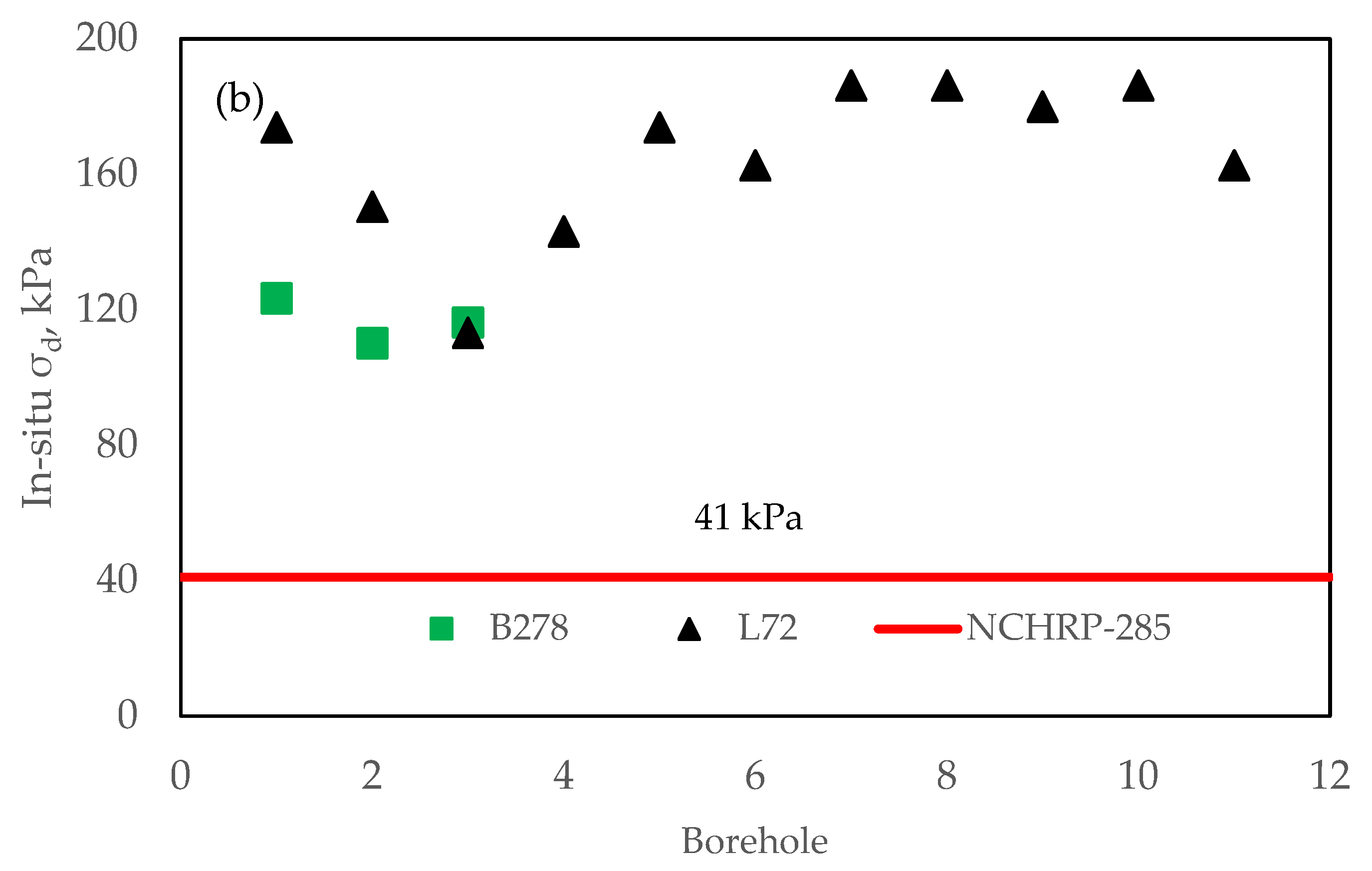
4.1. Effect of In Situ Stress
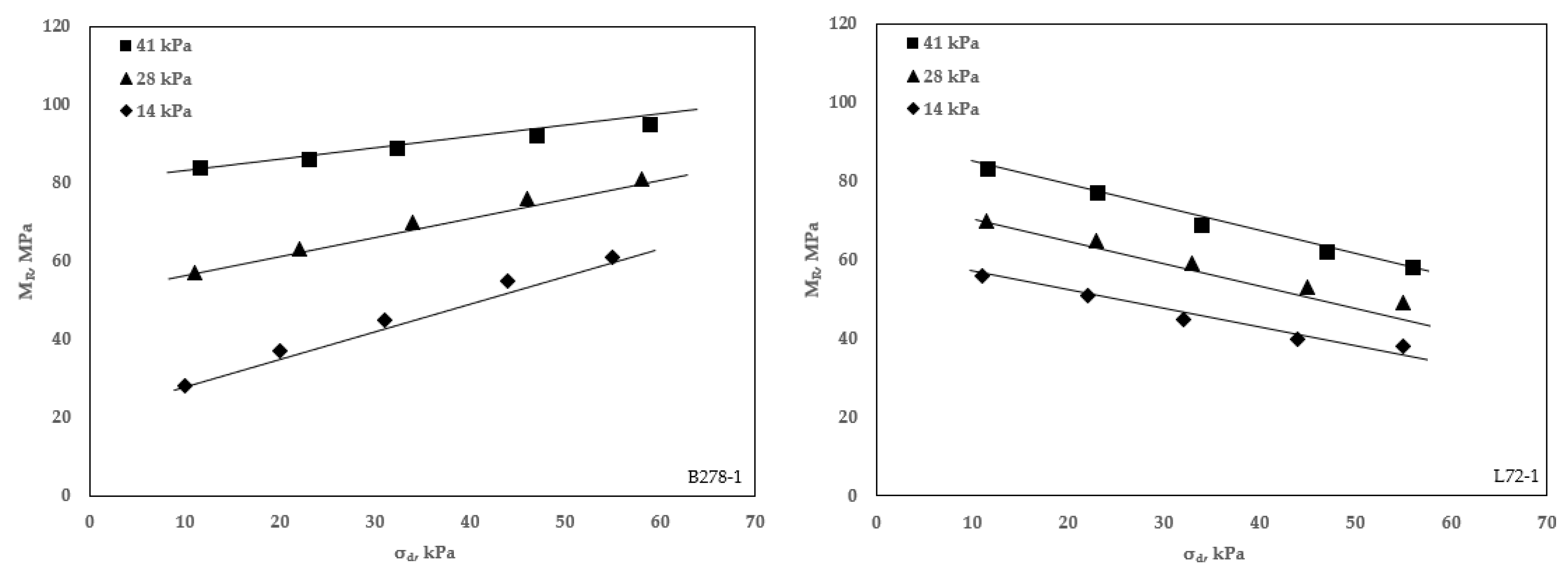
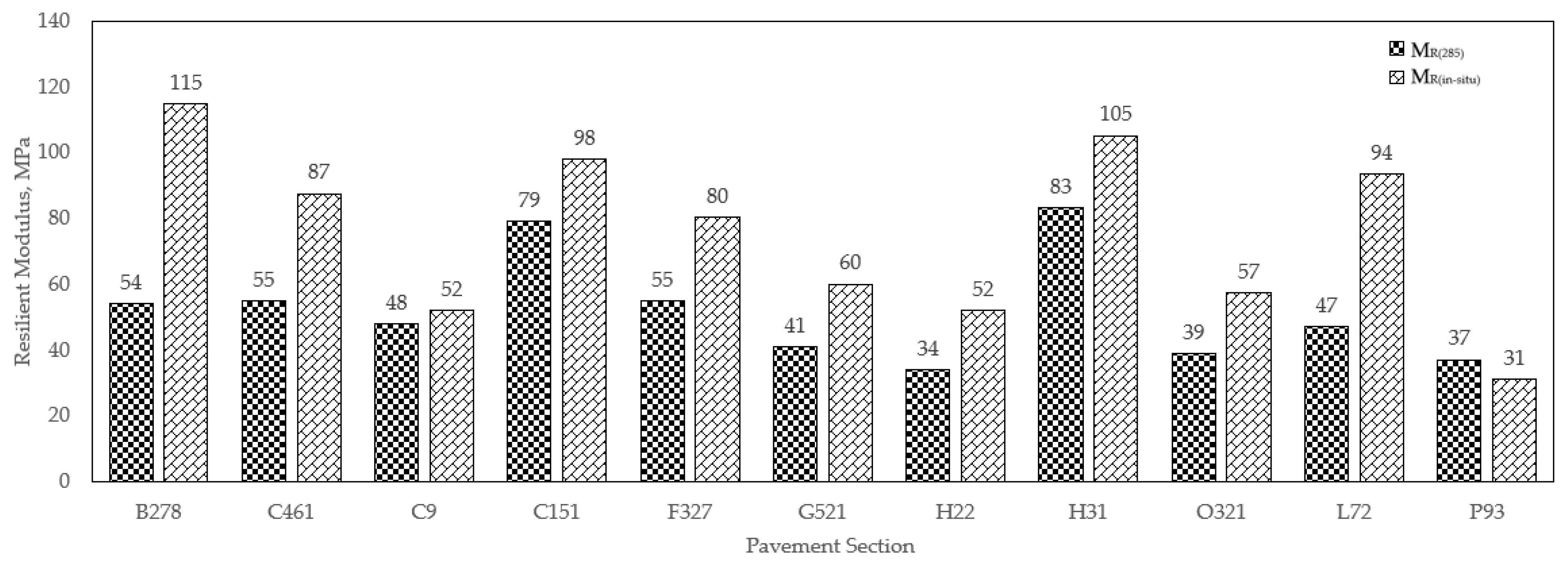
4.2. Resilient Modulus Test Result
4.3. Effect of Subgrade MR for Predicting Rutting and IRI
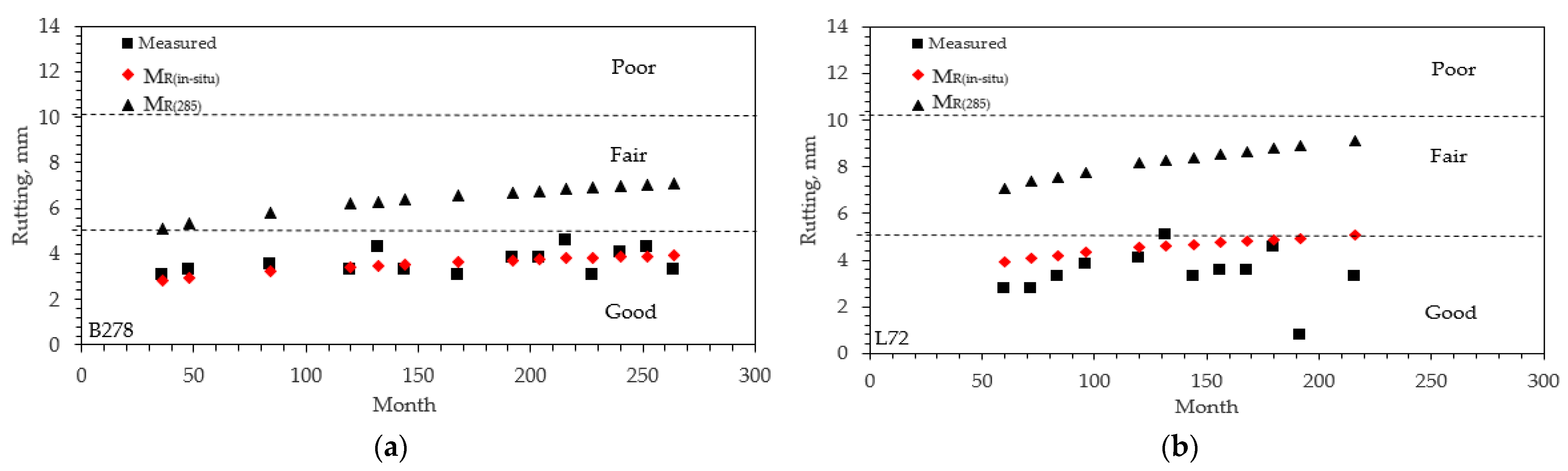
- For segment B278-1, the predicted rutting using MR(in situ) increased from 3 to 4.9 mm with pavement age. These values indicate that the pavement is in “Good” condition for this period. The field-measured values have a similar magnitude and would also indicate that the pavement is in “Good” condition.
- The predicted rutting using MR(285) ranged from 5 to 7 mm, which is higher than predicted using MR(in situ) and indicates the pavement is in “Fair” condition. This is not in agreement with the “Good” rating from the field-measured values.
- Similar results were observed for segment L72-1, shown in Figure 9b. Furthermore, the predicted rutting for L72-1 using MR(285) indicates a “Fair” condition from 60 months to 216 months (18 years), whereas a “Fair” condition is not reached until 216 months (18 years) for the rutting predicted using MR(in situ).
- The initial IRI predicted for segment B278-1 is 1689 mm/km for MR(in situ) and 2533 mm/km for MR(285). Both values indicate that the pavement is in “Fair” condition.
- Using MR(285), the predicted IRI indicates that the B278-1 pavement is in “Poor” condition after 80 months, whereas using MR(in situ), the pavement is rated as “Fair” for the duration of the time studied.
- At 240 months, the predicted IRI of B278-1 was 2257 mm/km (“Fair” condition) for MR(in situ), but 3385 mm/km (“Poor” condition) for MR(285). That means the MR(285) predicted an IRI that was 1.5 times higher than predicted using the MR(in situ).
- The measured IRI values for B278-1 were between those predicted by MR(285) and MR(in situ). The measured values corresponded to an initial rating of “Fair” up to 192 months and “Poor” thereafter.
- For section L72-1, the predicted IRI using MR(in situ) was 1277 mm/km at 60 months and increased to 1671 mm/km at 216 months. Thus, this segment is initially rated as “Good” and then rated as “Fair” after 156 months. In contrast, when MR(285) is used, the predicted IRI is equal to 1915 mm/km at 60 months and increases to 2507 mm/km with a “Fair” rating for the duration studied.
- The measured IRIs for segment L72-1 were in between those predicted by MR(285). and MR(in situ)as they were for B278-1. At 216 months, the predicted IRI of L72-1 was 1671 mm/km (“Fair” condition) for MR(in situ), whereas 2507 mm/km (“Fair” condition) for MR(285). That means the MR(285) predicted an IRI that was 1.5 times higher than predicted using the MR(in situ).
5. Summary of Findings and Conclusions
- Based on the resilient modulus test results, the MR of coarse-grained soil increases with increasing deviator stress. In contrast, the MR of fine-grained soil decreases with increasing deviator stress because of the “stress hardening” and “stress softening” behavior for coarse-grained and fine-grained soil, respectively.
- Rutting: Both sections were classified as “Fair” using the MR found from NCHRP-285, whereas they were classified as “Good” employing the MR calculated using the in situ stress state. The reason is that the in situ stress significantly affects the calculation of subgrade MR and, subsequently, the use of MR in the rutting prediction. The predictions using MR(in situ) were in close agreement with the field-measured values.
- IRI: For both sections, the predicted IRI using MR(in situ) was 33% less than the IRI predicted using MR(285). Section B278-1 was classified as “Fair” using the MR found from the in situ stress state, whereas it was rated as “Poor” using the MR calculated using the NCHRP-285. Similarly, the section of L72-1 was classified as “Fair” for the duration studied for MR(285). In contrast, it was initially classified as “Good”, and it is rated as “Fair” after 150 months of using MR(in situ). The predicted IRI was approximately 17% (average) less than in the field-measured values when the MR(in situ) was used, whereas 21% was overpredicted using MR(285).
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- AASHTO. Guide for Design of Pavement Structures; AASHTO: Washington, DC, USA, 1993. [Google Scholar]
- AASHTO. Mechanistic-Empirical Pavement Design Guide: A Manual of Practice, 2nd ed.; AASHTO: Washington, DC, USA, 2015. [Google Scholar]
- AASHTO. Mechanistic-Empirical Pavement Design Guide: A Manual of Practice, 3rd ed.; AASHTO: Washington, DC, USA, 2020. [Google Scholar]
- Seed, H.B.; Chan, C.K.; Lee, C.E. Resilience Characteristics of Subgrade Soils and their Relations to Fatigue Failures in Asphalt Pavements. In Proceedings of the International Conference on the Structural Design of Asphalt Pavements, Ann Arbor, MI, USA, 20–24 August 1962; pp. 77–113. [Google Scholar]
- Brown, S.F. Soil Mechanics in Pavement Engineering, 36th Rankine Lecture of the British Geotechnical Society. Geotechnique 1996, 46, 383–426. [Google Scholar] [CrossRef]
- Ng, K.; Henrichs, Z.R.; Ksaibati, K.; Wulff, S.S. Measurement and Estimation of the Resilient Modulus of Subgrade Materials for Mechanistic-Empirical Pavement Design Guide in Wyoming. In Proceedings of the Transportation Research Board Annual Meeting, Washington, DC, USA, 10–14 January 2016; pp. 1–17. [Google Scholar]
- Brown, S.F. Repeated Load Testing of a Granular Material. J. Geotech. Eng. Div. 1974, 100, 825–841. [Google Scholar] [CrossRef]
- Burczyk, J.M.; Ksaibati KSprecher, R.A.; Farrar, M.J. Factors Influencing Determination of a Subgrade Resilient Modulus Value. In Transportation Research Record 1462; Transportation Research Board, National Research Council: Washington, DC, USA, 1995; pp. 72–78. [Google Scholar]
- Burmister, D.M. The Theory of Stresses and Displacements in Layered Systems and Application to the Design of Airport Runways. Highway Research Board; National Research Council: Washington, DC, USA, 1943; Volume 23, pp. 125–148. [Google Scholar]
- Ng, K.; Hellrung, D.; Ksaibati, K.; Wulff, S.S. Systematic back-calculation protocol and prediction of resilient modulus for MEPDG. IJPE 2018, 19, 62–74. [Google Scholar] [CrossRef]
- AASHTO T 307; Standard Method of Test for Determining the Resilient Modulus of Soils and Aggregate Materials. AASHTO: Washington, DC, USA, 2017.
- Puppala, A.; Mohammad, L.; Allen, A. Engineering Behavior of Lime-Treated Louisiana Subgrade Soil. Transp. Res. Rec. J. Transp. Res. Board 1996, 1546, 24–31. [Google Scholar] [CrossRef]
- Puppala, A.J. Estimating Stiffness of Subgrade and Unbound Materials for Pavement Design; Transportation Research Board: Washington, DC, USA, 2008. [Google Scholar]
- Han, Z.; Vanapalli, S.K. State-of-the-Art: Prediction of Resilient Modulus of Unsaturated Subgrade Soils. Int. J. Geomech. 2016, 16, 04015104. [Google Scholar] [CrossRef]
- Islam, K.M.; Gassman, S.; Rahman, M.M. Field and laboratory characterization of subgrade resilient modulus for pavement mechanistic-empirical pavement design guide application. TRB 2020, 2674, 921–930. [Google Scholar] [CrossRef]
- Rahman, M.M.; Islam, K.M.; Gassman, S. Estimation of resilient modulus for coarse-grained subgrade soils from quick shear tests for mechanistic-empirical pavement designs. Designs 2019, 3, 48. [Google Scholar] [CrossRef]
- Islam, K.M.; Gassman, S.L. Influence of subgrade resilient modulus selection methodology on AASHTOWare pavement ME design. In Geo-Congress; ASCE: Charlotte, North Carolina, 2022; pp. 192–204. [Google Scholar]
- Rahman, M.M.; Gassman, S.L.; Islam, K.M. Effect of Moisture Content on Subgrade Soils Resilient Modulus for Predicting Pavement Rutting. Geosciences 2023, 13, 103. [Google Scholar] [CrossRef]
- Seed, H.; Mitry FMonosmith, C.; Chan, C. Prediction of Pavement Deflection From Laboratory Repeated Load Tests. In Report No. 35; NCHRP, Transportation Research Board: Washington, DC, USA, 1967. [Google Scholar]
- Yao, Y.; Zheng, J.; Zhang, J.; Peng, J.; Li, J. Model for predicting resilient modulus of unsaturated subgrade soils in south China. KSCE J. Civ. Eng. 2018, 22, 2089–2098. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, J.; Zeng, L.; Li, J.; Li, F. Rapid estimation of resilient modulus of subgrade soils using performance-related soil properties. Int. J. Pavement Eng. 2021, 22, 732–739. [Google Scholar] [CrossRef]
- Tamošiūnas, T.; Skuodis, Š. Predictive Stress Modeling of Resilient Modulus in Sandy Subgrade Soils. Infrastructures 2023, 8, 29. [Google Scholar] [CrossRef]
- Kumar, P.; Puppala, A.J.; Tingle, J.S.; Chakraborty, S.; Congress, S.S.C. Resilient Characteristics of Polymer Emulsion-Treated Sandy Soil. Transp. Res. Rec. 2022, 2676, 526–538. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, J.; Liu, W.; Lu, W. Predicting resilient modulus of fine-grained subgrade soils considering relative compaction and matric suction. Road Mater. Pavement Des. 2021, 22, 703–715. [Google Scholar] [CrossRef]
- Kim, S.S.; Pahno, S.; Durham, S.A.; Yang, J.; Chorzepa, M.G. Prediction of Resilient Modulus From the Laboratory Testing of Sandy Soils (No. FHWA-GA-19-1725); Department of Transportation. Office of Performance-Based Management & Research: Atlanta, GA, USA, 2019; Georgia DOT Research project 17–25, Final Report.
- Mohammad, L.N.; Huang BPuppala, A.J.; Allen, A. Regression Model for Resilient Modulus of Subgrade Soils. Transp. Res. Rec. J. Transp. Res. Board 1999, 1687, 47–54. [Google Scholar] [CrossRef]
- Bhuvaneshwari, S.; Robinson, R.G.; Gandhi, S.R. Resilient Modulus of Lime Treated Expansive Soil. Geotech. Geol. Eng. 2018, 37, 305–315. [Google Scholar] [CrossRef]
- Islam, K.M.; Gassman, S.L. Predicting Flexible Pavement Distress and IRI Considering Subgrade Resilient Modulus of Fine-Grained Soils Using MEPDG. Materials 2023, 16, 1126. [Google Scholar] [CrossRef] [PubMed]
- Rada, G.; Witczak, M.W. Comprehensive Evaluation of Laboratory Resilient Moduli Results for Granular Materials. In Transportation Research Record 810; TRB, National Research Council: Washington, DC, USA, 1981; pp. 23–33. [Google Scholar]
- Buchanan, S. Resilient modulus: What, Why, and How? 2007. Available online: https://www.vulcaninnovations.com/public/pdf/2-Resilient-Modulus-Buchanan.pdf (accessed on 1 February 2023).
- Drumm, E.C.; Boateng-Poku, Y.; Johnson Pierce, T. Estimation of subgrade resilient modulus from standard tests. J. Geotech. Eng. 1990, 116, 774–789. [Google Scholar] [CrossRef]
- Kumar, A.; George, V. Effect of soil parameters on resilient modulus using cyclic tri-axial tests on lateritic subgrade soils from Dakshina Kannada, India. Geotech. Geol. Eng. 2018, 36, 3987–4000. [Google Scholar] [CrossRef]
- Maher, A.; Bennert, T.; Gucunski, N.; Papp, W.J., Jr. Resilient Modulus Properties of New Jersey Subgrade Soils (No. FHWA NJ 2000-01); FHWA NJ 2000-01, Final Report; TRIS, USDOT, STATEDOT: Washington, DC, USA, 2000. [Google Scholar]
- Kim, D.; Siddiki, N.Z. Simplification of resilient modulus testing for subgrades. Jt. TRP 2006, 265, IN/JTRP-2005/23. Available online: https://docs.lib.purdue.edu/cgi/viewcontent.cgi?article=1736&context=jtrp (accessed on 1 February 2023).
- Witzack, M.; Qi, X.; Mirza, M.W. Use of Nonlinear Subgrade Modulus in AASHTO Design Procedures. J. Transp. Eng. 1995, 121, 273–282. [Google Scholar]
- Yau, A.; Von Quintus, H. Study of LTPP Laboratory Resilient Modulus Test Data and Response Characteristics; Report No. FHWA-RD-02-051; Federal Highway Administration: McLean, VA, USA, 2002.
- Zaman, M.; Chen, D.-H.; Laguros, J. Resilient Modulus of Granular Materials. J. Transp. Eng. 1994, 120, 967–988. [Google Scholar] [CrossRef]
- NCHRP-285. Laboratory Determination of Resilient Modulus for Flexible Pavement Design; Research Results Digest, Issue Number 14; Transportation Research Board: Washington, DC, USA, 2004; 486p. [Google Scholar]
- Fesearal Highway Administration (FHWA). Pavement Performance Measures and Forecasting and The Effects of Maintenance and Rehabilitation Strategy on Treatment Effectiveness, Chapter 3, 2015. Available online: https://www.fhwa.dot.gov/publications/research/infrastructure/pavements/ltpp/17095/004.cfm (accessed on 1 February 2023).
- Amirkhanian, S.N.; Corley, M. Characterization of Bases and Subbases for AASHTO ME Pavement Design (No. FHWA-SC-21-01); Tech Report; South Carolina. Dept. of Transportation. Office of Materials and Research, Tri-County Technical College: Pendleton, UC, USA, 2021. [Google Scholar]
- Hurley, C.D. Asphalt Pavement Evaluation to Support the Calibration of the AASHTO MEPDG for South Carolina Conditions. Master Thesis, Clemson University, Clemson, SC, USA, 2019. ProQuest LLC, Ann Arbor, MI 48106-1346. [Google Scholar]
- NCHRP-1-37; Guide for Mechanistic-Empirical Design of New and Rehabilitated Pavement Structures-Final Report. Transportation Research Board: Washington, DC, USA, 2004.
- Huang, Y.H. Pavement Analysis and Design; Prentice Hall, Inc.: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
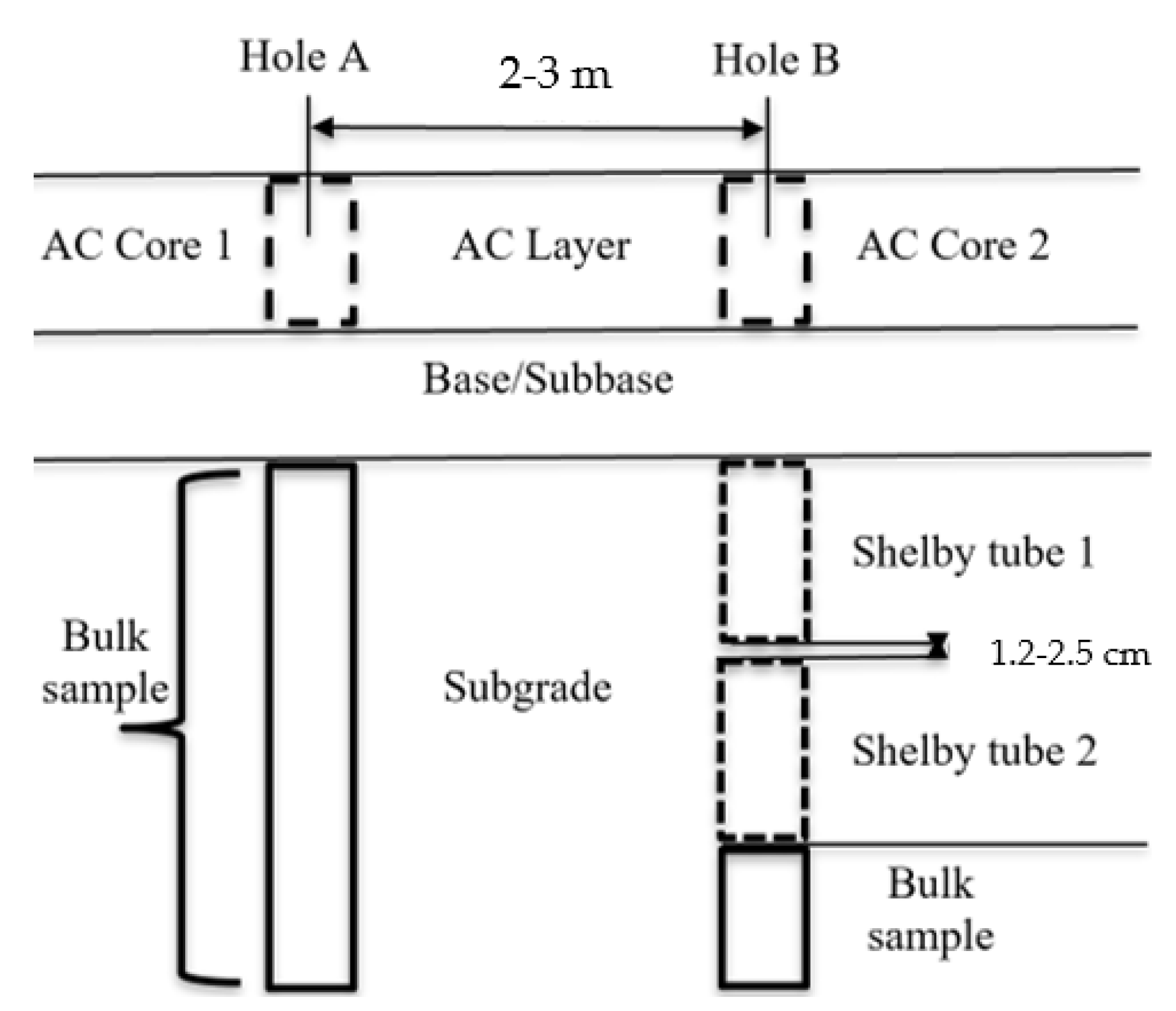


| Site ID | Construction Finish Year | Length of Section (km) | Number of Coring Locations with Shelby Tube Samples |
|---|---|---|---|
| B278 | 1998 | 2.6 | 3 |
| C461 | 1996 | 4.0 | 3 |
| C9 | 1999 | 3.0 | 3 |
| C151 | 1999 | 8.7 | 10 |
| F327 | 1992 | 7.9 | 6 |
| G521 | 2003 | 4.8 | 7 |
| H22 | 2001 | 1.6 | 3 |
| H31 | 2005 | 6.4 | 9 |
| O321 | 2004 | 9.8 | 13 |
| L72 | 2002 | 9.8 | 11 |
| P93 | 2001 | 1.9 | 5 |
| Site ID | BH | Field Stress from Pavement (kPa) | Field Stress from Loading (kPa) | Total σ1 (kPa) | Total σ3 (kPa) | σd (kPa) | ϴ (kPa) | ||
|---|---|---|---|---|---|---|---|---|---|
| σ1pave | σ3pave | σ1load | σ3load | ||||||
| B278 | B278-1 | 7.6 | 3.8 | 123.3 | 3.8 | 130.9 | 7.6 | 123.3 | 146.0 |
| B278-2 | 7.7 | 3.8 | 110.1 | 3.9 | 117.8 | 7.7 | 110.1 | 133.2 | |
| B278-3 | 7.1 | 3.6 | 116.4 | 3.8 | 123.6 | 7.4 | 116.2 | 138.4 | |
| L72 | L72-1 | 5.8 | 2.9 | 173.2 | 2.2 | 178.9 | 5.1 | 173.8 | 189.2 |
| L72-2 | 6.4 | 3.2 | 150.4 | 3.2 | 156.8 | 6.4 | 150.4 | 169.6 | |
| L72-3 | 7.8 | 3.9 | 113.2 | 3.9 | 121.0 | 7.8 | 113.2 | 136.5 | |
| L72-4 | 6.6 | 3.3 | 143.2 | 3.4 | 149.8 | 6.7 | 143.1 | 163.2 | |
| L72-5 | 5.8 | 2.9 | 173.2 | 2.2 | 178.9 | 5.1 | 173.8 | 189.2 | |
| L72-6 | 6.1 | 3.0 | 162.3 | 2.8 | 168.4 | 5.8 | 162.6 | 180.0 | |
| L72-7 | 5.6 | 2.8 | 185.0 | 1.5 | 190.6 | 4.3 | 186.2 | 199.2 | |
| L72-8 | 5.6 | 2.8 | 185.0 | 1.5 | 190.6 | 4.3 | 186.2 | 199.2 | |
| L72-9 | 5.7 | 2.9 | 178.9 | 1.9 | 184.7 | 4.8 | 179.9 | 194.2 | |
| L72-10 | 5.6 | 2.8 | 185.0 | 1.5 | 190.6 | 4.3 | 186.2 | 199.2 | |
| L72-11 | 6.1 | 3.1 | 162.3 | 2.8 | 168.5 | 5.8 | 162.6 | 180.1 | |
| Site ID | BH | k1 | k2 | k3 | MR(285) (MPa) | MR (in-situ) (MPa) | Initial IRI (mm/km) |
|---|---|---|---|---|---|---|---|
| B278 | B278-1 | 520 | 0.923 | 1.281 | 55 | 132 | 1831 * |
| B278-2 | 530 | 0.899 | 1.582 | 59 | 132 | 1752 * | |
| B278-3 | 555 | 0.934 | 0.131 | 48 | 80 | 1484 | |
| L72 | L72-1 | 483 | 0.923 | 1.281 | 51 | 186 | 1121 |
| L72-2 | 413 | 1.154 | 0.769 | 38 | 114 | 963 | |
| L72-3 | 430 | 0.913 | 1.082 | 44 | 90 | 821 | |
| L72-4 | 470 | 0.933 | 1.230 | 49 | 139 | 616 * | |
| L72-5 | 871 | 0.440 | −1.815 | 59 | 40 | 1073 | |
| L72-6 | 690 | 0.228 | 1.010 | 80 | 141 | 1184 | |
| L72-7 | 455 | 0.228 | 1.010 | 53 | 101 | 1247 | |
| L72-8 | 445 | 0.219 | 1.052 | 52 | 101 | 1263 | |
| L72-9 | 405 | 0.789 | −0.714 | 31 | 44 | 1042 | |
| L72-10 | 427 | 0.792 | −1.100 | 31 | 37 | 1042 | |
| L72-11 | 438 | 0.821 | −1.210 | 31 | 36 | 1042 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Islam, K.M.; Gassman, S.L. Effect of the Field-Stress State on the Subgrade Resilient Modulus for Pavement Rutting and IRI. Geotechnics 2023, 3, 360-374. https://doi.org/10.3390/geotechnics3020021
Islam KM, Gassman SL. Effect of the Field-Stress State on the Subgrade Resilient Modulus for Pavement Rutting and IRI. Geotechnics. 2023; 3(2):360-374. https://doi.org/10.3390/geotechnics3020021
Chicago/Turabian StyleIslam, Kazi Moinul, and Sarah L. Gassman. 2023. "Effect of the Field-Stress State on the Subgrade Resilient Modulus for Pavement Rutting and IRI" Geotechnics 3, no. 2: 360-374. https://doi.org/10.3390/geotechnics3020021
APA StyleIslam, K. M., & Gassman, S. L. (2023). Effect of the Field-Stress State on the Subgrade Resilient Modulus for Pavement Rutting and IRI. Geotechnics, 3(2), 360-374. https://doi.org/10.3390/geotechnics3020021





