Meta-Material Layout for the Blast Protection of Above-Ground Steel Pipes
Abstract
:1. Introduction
2. Background
2.1. Simplification of the Analytical Simulation Model for the Calculation of Band-Gaps
2.2. Blast Loading
Blast Loading Time Parameters
3. Methodology and Materials
3.1. Periodic Materials Theory
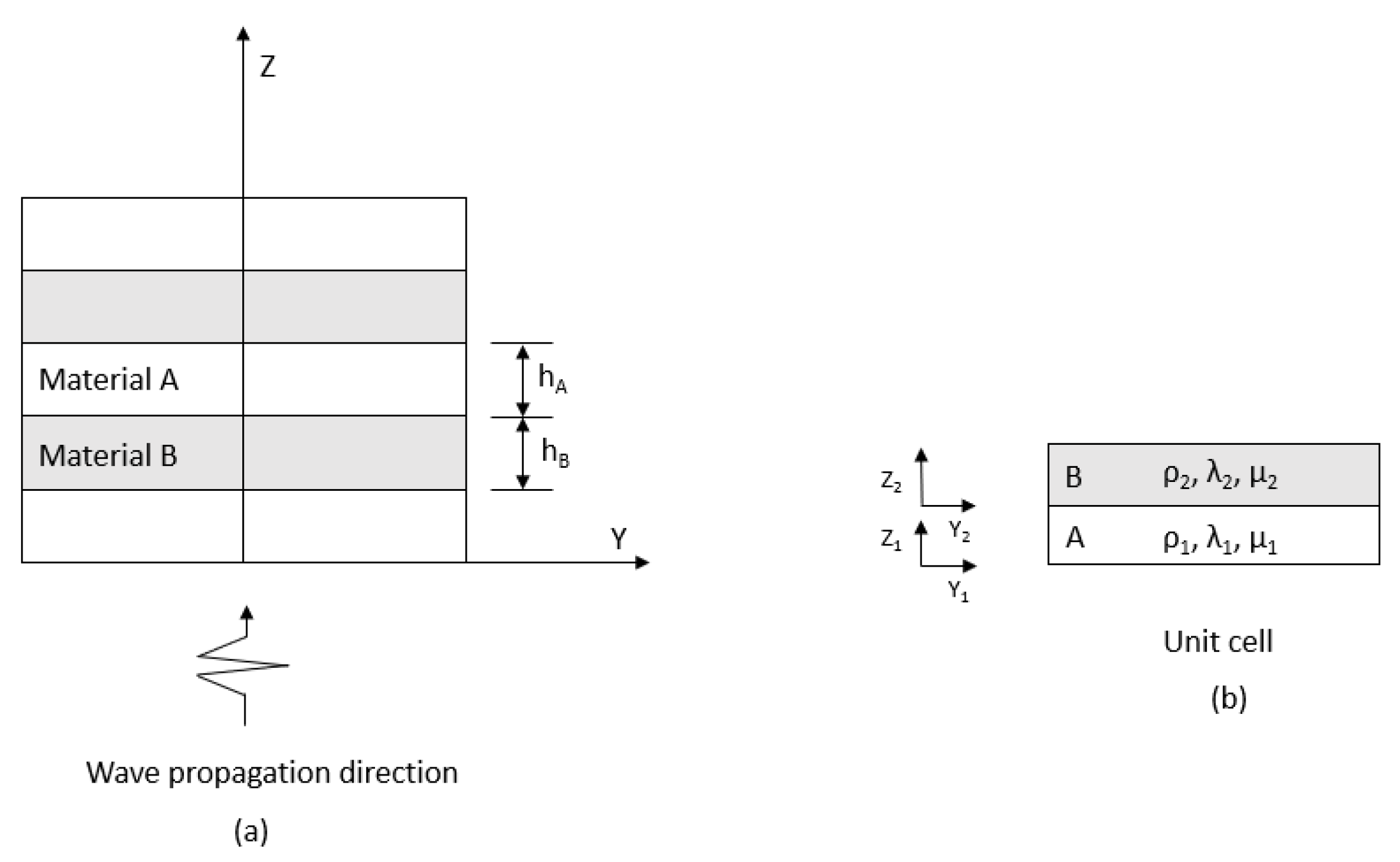
3.2. Materials and Layout Structure
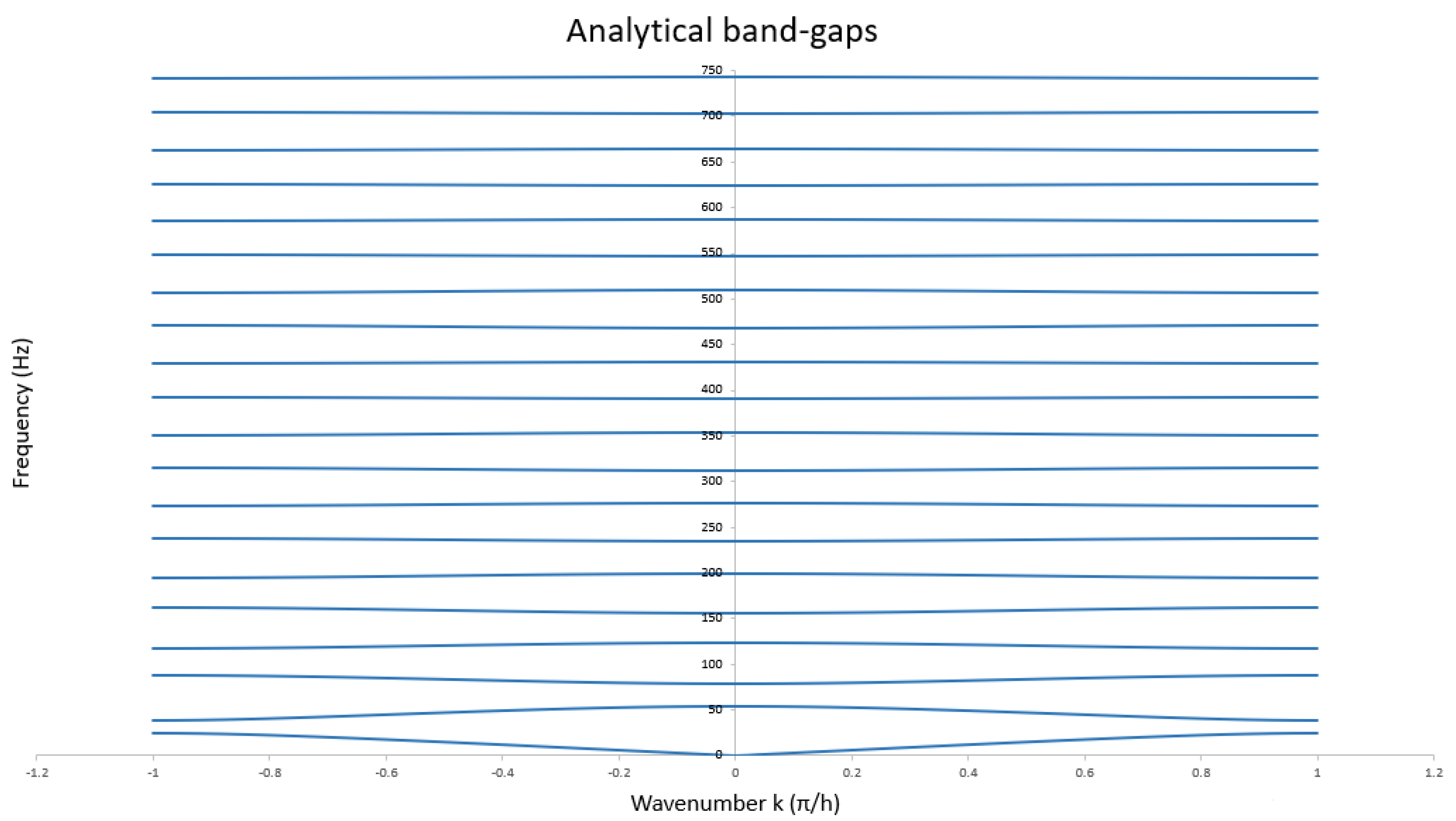
3.3. Analytical Calculation of the Band-Gaps
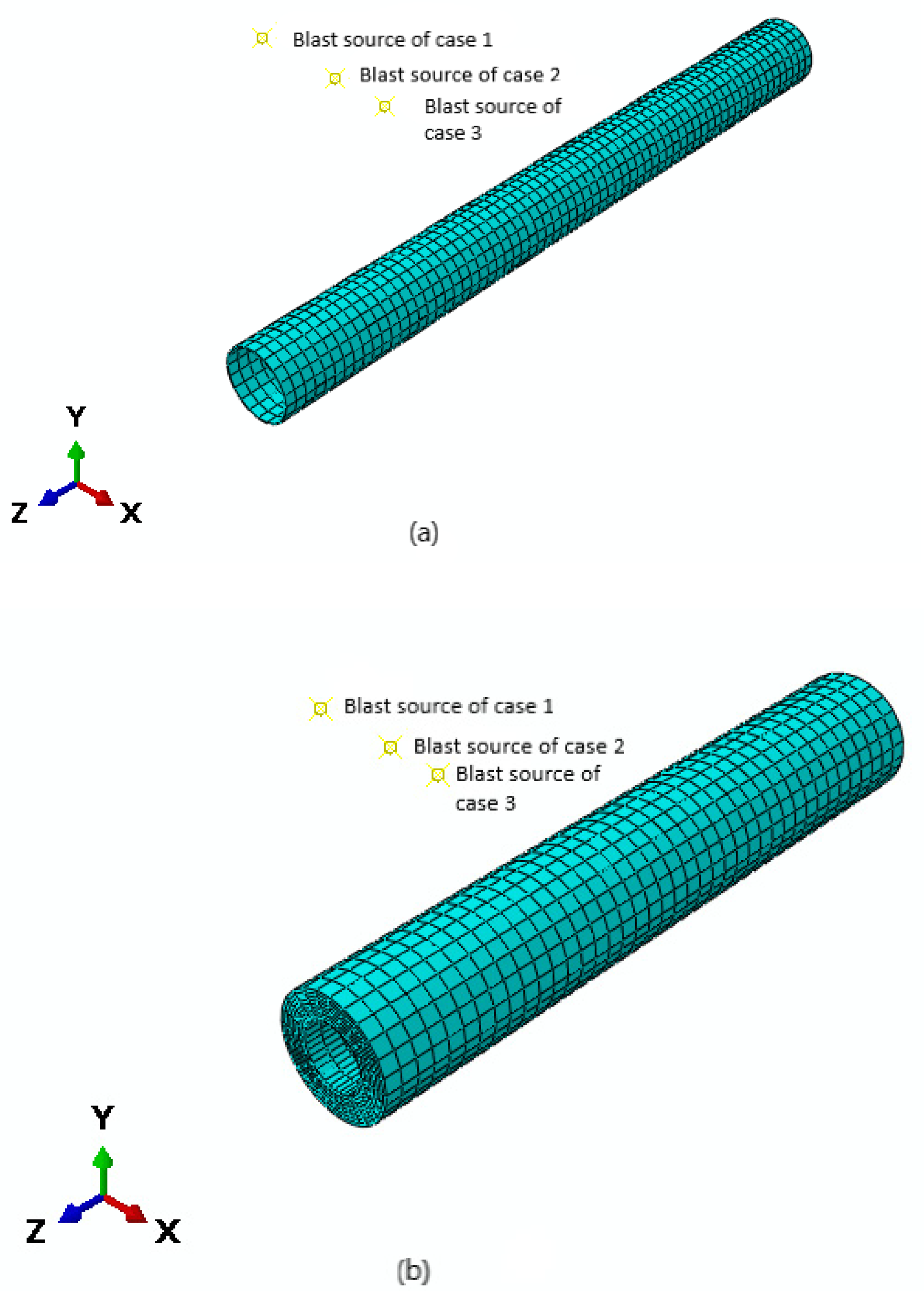
3.4. Definition of the Explosion Case Scenarios
4. Finite Element Modeling
5. Results
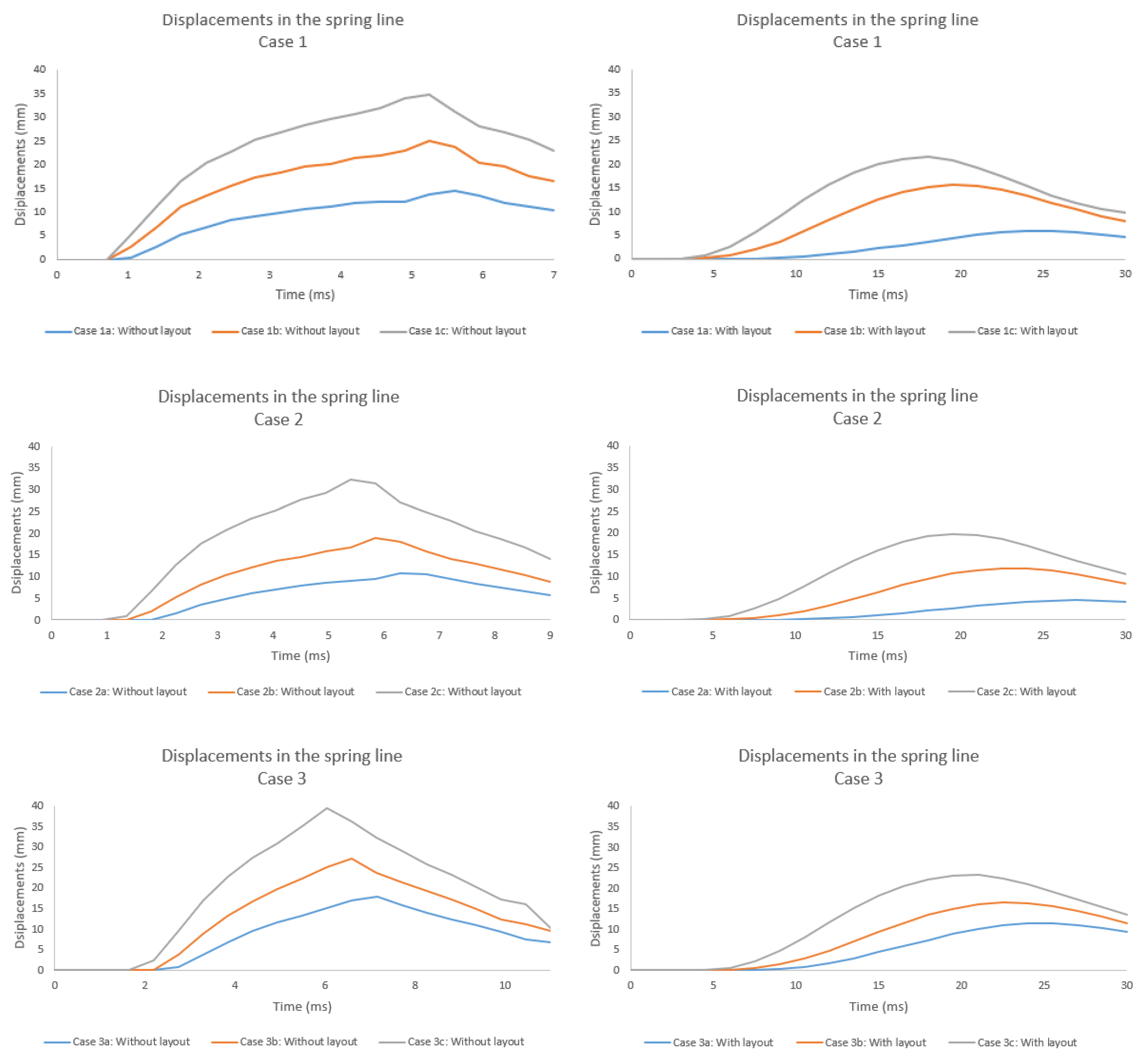
5.1. Displacements in the Pipe Spring Line
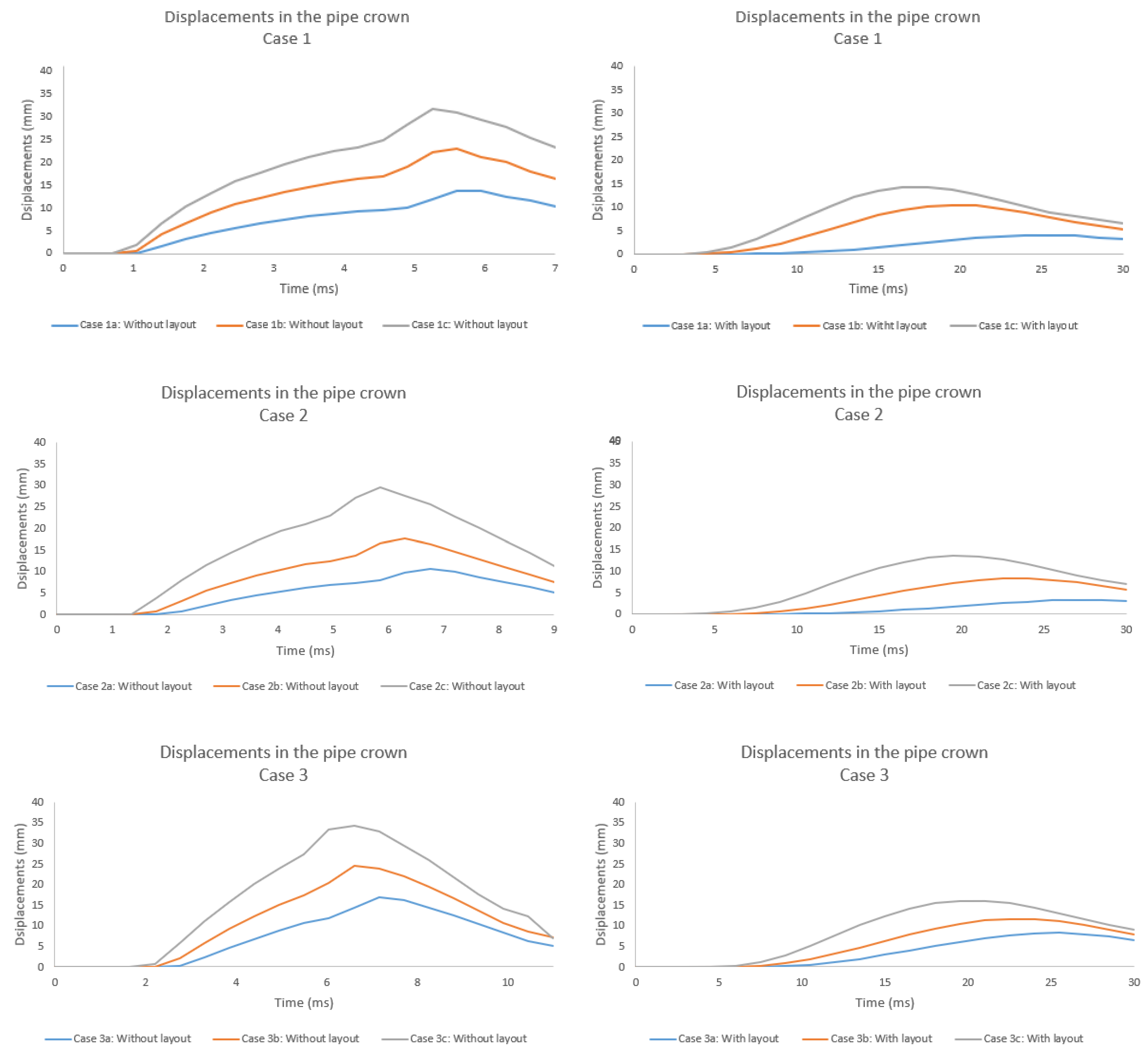
5.2. Displacements in the Pipe Crown
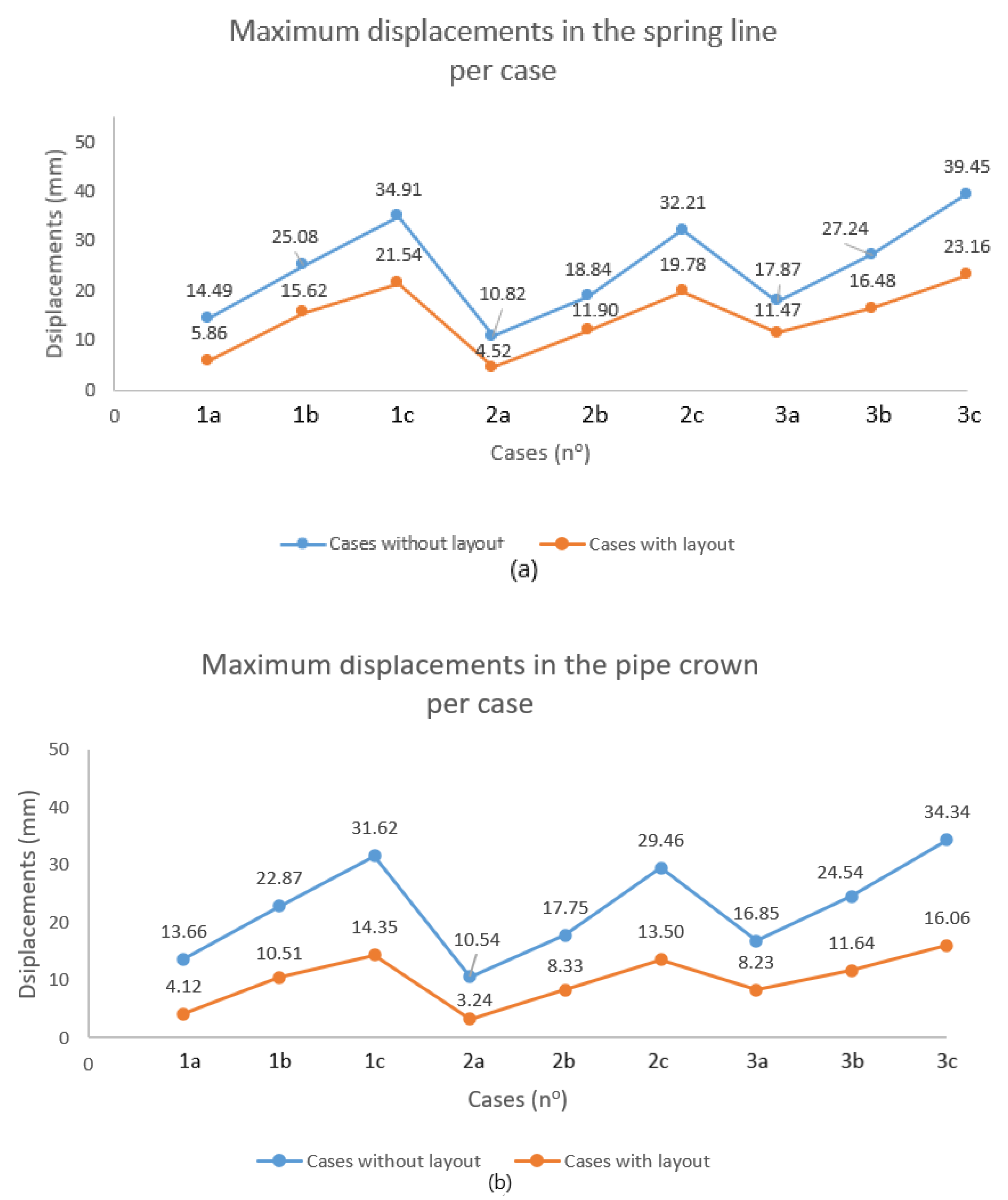
5.3. Maximum Displacements
6. Conclusions
7. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Resilience Framework of, U.S. Department of Homeland Security. 2018. Available online: https://www.dhs.gov/sites/default/files/publications/dhs_resilience_framework_july_2018_508.pdf (accessed on 20 April 2023).
- Proposal for a Directive of the European Parliament and of the Council on the Resilience of Critical Entities. 2020. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX%3A52020PC0829 (accessed on 20 April 2023).
- Directive (EU) 2016/1148 of the European Parliament and of the Council of 6 July 2016 Concerning Measures for a High Common Level of Security of Network and Information Systems across the Union. 2016. Available online: https://eur-lex.europa.eu/eli/dir/2016/1148/oj (accessed on 20 April 2023).
- Sun, T.C.; Huang, G.L.; Huang, H.H. On the negative effective mass density in acoustic metamaterials. Int. J. Eng. Sci. 2009, 47, 610–617. [Google Scholar]
- Sun, T.C.; Huang, H.H. Wave attenuation mechanism in an acoustic metamaterial with negative effective mass density. New J. Phys. 2009, 11, 013003. [Google Scholar]
- US Department of Energy. Development of Seismic Isolation Systems Using Periodic Materials; University of Houston: Houston, TX, USA, 2014. [Google Scholar]
- Shi, Z.; Cheng, Z.; Wen-Kai, L. Dispersion Differences and Consistency of Artificial Periodic Structures. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2017, 64, 1591–1598. [Google Scholar] [CrossRef]
- Shi, Z.; Cheng, Z.; Xiang, H. Seismic isolation foundations with effective attenuation zones. Soil Dyn. Earthq. Eng. 2014, 57, 143–151. [Google Scholar] [CrossRef]
- Liu, X.; Ren, Y.; Song, X. Combined Attenuation Zones of Combined Layered Periodic Foundations. Appl. Sci. 2021, 11, 7114. [Google Scholar] [CrossRef]
- Xiang, H.J.; Shi, Z.F.; Wang, S.J.; Mo, Y.L. Periodic materials-based vibration attenuation in layered foundations: Experimental validation. Smart Mater. Struct. 2012, 21, 112003. [Google Scholar] [CrossRef]
- Mo, Y.L.; Shi, Z.; Tang, Y.; Menq, F.; Cheng, Z.; Laskar, A.; Yan, Y. Seismic isolation of two-dimensional periodic foundations. J. Appl. Phys. 2014, 116, 044908. [Google Scholar]
- Mo, Y.L.; Shi, Z.; Tang, Y.; Menq, F.; Cheng, Z.; Yan, Y. Three dimensional periodic foundations for base seismic isolation. Smart Mater. Struct. 2015, 24, 075006. [Google Scholar]
- Cheng, Z.; Shi, Z.; Palermo, A.; Xiang, H.; Guo, W.; Marzani, A. Seismic vibrations attenuation via damped layered periodic foundations. Eng. Struct. 2020, 211, 110427. [Google Scholar] [CrossRef]
- Cheng, Z.; Shi, Z. Composite periodic foundation and its application for seismic isolation. Earthq. Eng. Struct. Dyn. 2018, 47, 925–944. [Google Scholar] [CrossRef]
- Cheng, Z.; Shi, Z.; Lin, W. Wave Dispersion Analysis of Multi-story Frame Building Structures Using the Periodic Structure Theory. Soil Dyn. Earthq. Eng. 2018, 106, 215–230. [Google Scholar] [CrossRef]
- Jai, S.; Shaik, V.S.A.; Alam, A.; Laskar, A. Application of innovative one-dimensional periodic isolation systems for seismic response reduction of bridges. Adv. Struct. Eng. 2019, 23, 1397–1412. [Google Scholar] [CrossRef]
- Agguzzi, G.; Martakis, P.; Dertimanis, K.V.; Colombi, A.; Chatzi, N.E. Nonlinear periodic foundations for seismic protection: Practical design, realistic evaluation, and stability considerations. Soil Dyn. Earthq. Eng. 2021, 150, 106934. [Google Scholar]
- Bursi, S.O.; Basone, F.; Wenzel, M.; Fossetti, M. Finite locally resonant Meta-foundations for the seismic protection of fuel storage tanks. Earthq. Eng. Struct. Dyn. 2018, 48, 232–252. [Google Scholar]
- Khodakarami, M.I.; Farajian, M.; Sharafi, P. Effect of Meta-Foundation on the Seismic Responses of Liquid Storage Tanks. Appl. Sci. 2022, 12, 2514. [Google Scholar]
- Bursi, S.O.; Basone, F.; Wenzel, M. Design of a Metamaterial-Based Foundation for Fuel Storage Tanks and Experimental Evaluation of Its Effect on a Connected Pipeline System. J. Press. Vessel Technol. 2019, 142, 021903. [Google Scholar]
- Zhou, P.; Wan, S.; Wang, X.; Fu, J.; Shen, L. Novel periodic pile barriers in saturated soil and applications to propagation attenuation of shear plane waves. Comput. Geotech. 2022, 150, 104925. [Google Scholar] [CrossRef]
- Shi, Z.; Cheng, Z.; Wu, J. Numerical Evaluation of the Effectiveness of Periodic Wave Barriers in Pre-stressed Saturated Soil. J. Vib. Eng. Technol. 2022. [Google Scholar] [CrossRef]
- Meng, L.; Shi, Z.; Cheng, Z. Vibration mitigation in saturated soil by periodic pile barriers. Comput. Geotech. 2021, 117, 103251. [Google Scholar] [CrossRef]
- Meng, L.; Shi, Z.; Cheng, Z. Filtering property of periodic pile barriers under moving loads. Comput. Geotech. 2021, 136, 104244. [Google Scholar] [CrossRef]
- Pu, X.; Shi, Z. Periodic pile barriers for Rayleigh wave isolation in a poroelastic half-space. Soil Dyn. Earthq. Eng. 2019, 121, 75–86. [Google Scholar] [CrossRef]
- Zhou, J.; Pu, X.; Shi, Z. Attenuation Characteristics of Plane Waves by Metabarriers with Negative Parameters. In Advances in Transportation Geotechnics IV, 1st ed.; Tutumluer, E., Nazaria, S., Al-Qadi, I., Issam, I.A., Eds.; Springer: Cham, Switzerland, 2022; pp. 987–997. [Google Scholar]
- Zhou, J.; Cheng, Z.; Shi, Z. Vibration Reduction Performance of a Periodic Layered Slab Track. In Advances in Environmental Vibration and Transportation Geodynamics, 1st ed.; Tutumluer, E., Chen, X., Xiao, Y., Eds.; Springer: Singapore, 2020; pp. 779–791. [Google Scholar] [CrossRef]
- Pu, X.; Shi, Z. Broadband surface wave attenuation in periodic trench barriers. J. Sound Vib. 2020, 468, 115130. [Google Scholar] [CrossRef]
- Yuan, L.; Cai, Z.; Jiang, H.; Ma, T.; Du, J.; Wang, J. SH wave propagation in a periodic cement-based piezoelectric layered barrier. Mech. Adv. Mater. Struct. 2022, 29, 4902–4910. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, W.; Wu, Z.; Dai, Y.; Li, Y.; Zhou, A. Study on Vibration Isolation Effect of Periodic Pile Arrangement on Subway Ground. IOP Conf. Ser. Earth Environ. Sci. 2020, 455, 012152. [Google Scholar] [CrossRef]
- Zhou, J.; Gao, Y.; Shi, Z. A Simplified Analytical Method for Detuning Periodic Pile Barriers. J. Appl. Comput. Mech. 2022, 8, 1480–1487. [Google Scholar] [CrossRef]
- Liu, C.X.; Yu, G.L. Deep learning-based topology design of periodic barrier for full-mode waves. Constr. Build. Mater. 2022, 314, 125579. [Google Scholar] [CrossRef]
- Mitchell, S.J. Metaconcrete: Engineered Aggregates for Enhanced Dynamic Performance. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2016. [Google Scholar]
- Pandolfi, A.; Ortiz, M.; Bricolla, D. Experimental Validation of Metaconcrete Blast Mitigation Properties. J. Appl. Mech. 2019, 84, 031001. [Google Scholar]
- Pandolfi, A.; Ortiz, M.; Bricolla, D.; Cuni, M.; Juli, D.A. Experimental Validation of the Attenuation Properties in the Sonic Range of Metaconcrete Containing Two Types of Resonant Inclusions. Exp. Mech. 2020, 61, 515–532. [Google Scholar]
- Kettenbeil, C.; Ravichandran, G. Experimental investigation of the dynamic behavior of metaconcrete. Int. J. Impact Eng. 2018, 11, 199–207. [Google Scholar] [CrossRef]
- Liu, Y.; An, X.; Chen, H.; Fan, H. Vibration attenuation of finite-size Metaconcrete: Mechanism, prediction and verification. Compos. Part A Appl. Sci. Manuf. 2021, 143, 106294. [Google Scholar] [CrossRef]
- Xu, C.; Hao, H.; Pham, M.T.; Bi, K.; Chen, W. Static mechanical properties and stress wave attenuation of metaconcrete subjected to impulsive loading. Eng. Struct. 2022, 263, 114382. [Google Scholar] [CrossRef]
- Hao, H.; Hao, Y.; Jin, H.; Chen, W. Predicting the Response of Locally Resonant Concrete Structure under Blast Load. Constr. Build. Mater. 2020, 252, 118920. [Google Scholar]
- Hao, H.; Huang, Z.; Jin, H.; Cheng, X.; Chen, W. Dynamic Response of Metaconcrete Beam Under Blast Load. Int. J. Struct. Stab. Dyn. 2023, 2350178. [Google Scholar] [CrossRef]
- Hao, H.; Pham, M.T.; Bi, K.; Cheng, X. Experimental and numerical assessment of stress wave attenuation of metaconcrete rods subjected to impulsive loads. Int. J. Impact Eng. 2022, 159, 104052. [Google Scholar] [CrossRef]
- Hao, H.; Cheng, X.; Chen, W. The influence of design parameters of engineered aggregate in Metaconcrete on bandgap region. J. Mech. Phys. Solids 2022, 139, 103929. [Google Scholar]
- Hao, H.; Jin, H.; Chen, W.; Cheng, X. Effect of enhanced coating layer on the bandgap characteristics and response of metaconcrete. Mech. Adv. Mater. Struct. 2023, 30, 175–188. [Google Scholar] [CrossRef]
- Zhang, E.; Zhao, H.; Iu, G.; Chen, P.; Yang, H. Design and evaluation of dual-resonant aggregates metaconcrete. Lat. Am. J. Solids Struct. 2023, 20, e479. [Google Scholar] [CrossRef]
- Tran, P.; Nguyen-Van, V.; Peng, C.; Hazell, P.J.; Lee, L.; Nguyen-Xuan, H. Performance of meta concrete panels subjected to explosive load: Numerical investigations. Struct. Concr. 2023. [Google Scholar] [CrossRef]
- Tarlochan, F. Sandwich Structures for Energy Absorption Applications. Materials 2021, 14, 4731. [Google Scholar] [CrossRef]
- Ngo, T.; Bohara, P.R.; Linforth, S.; Nguyen, T.; Ghazlan, A. Dual-mechanism auxetic-core protective sandwich structure under blast loading. Compos. Struct. 2022, 299, 116088. [Google Scholar] [CrossRef]
- Li, Z.; Chen, W.; Hao, H. Blast mitigation performance of cladding using Square Dome-shape Kirigami folded structure as core. Int. J. Mech. Sci. 2018, 145, 83–95. [Google Scholar] [CrossRef]
- Vo, N.; Hao, H.; Pham, M.T.; Bi, K.; Chen, W. Impact Load Mitigation of Meta-panels with Single Local Resonator. Eng. Struct. 2022, 265, 114528. [Google Scholar] [CrossRef]
- Hao, H.; Vo, N.; Bi, K.; Pham, T.; Chen, W. Stress Wave Mitigation Properties of Dual meta-Panels against Blast Loads. Int. J. Impact Eng. 2021, 154, 103877. [Google Scholar]
- Hao, H.; Vo, H.N.; Bi, K.; Pham, M.T.; Chen, W.; Bi, K.; Ha, N.S. Blast resistant enhancement of meta-panels using multiple types of resonators. Int. J. Mech. Sci. 2022, 215, 106965. [Google Scholar]
- Fan, H.; He, H. Dynamic theory of sandwich meta-panel under blast load. Eur. J. Mech./Solids 2022, 94, 104599. [Google Scholar]
- Vo, N.; Pham, M.T.; Hao, H.; Bi, K.; Chen, W. Experimental and Numerical Validation of Impact Mitigation Capability of Meta-panels. Int. J. Mech. Sci. 2022, 231, 107591. [Google Scholar] [CrossRef]
- Fan, H.; He, H. Explosion vibration mitigation of meta-plate with mass–spring metastructures. Extrem. Mech. Lett. 2021, 42, 101108. [Google Scholar]
- Li, Q.Q.; He, C.H.; Li, E.; Liu, P.; Lin, Y.X.; Wu, Y. Design of resonant structures in resin matrix to mitigate the blast wave with a very wide frequency range. Smart Mater. Struct. 2020, 29, 045042. [Google Scholar] [CrossRef]
- Huang, G.; Xu, X.; Gang, X.; Yangyang, C.; Wen, J.; Barnhart, V.M. A nonlinear dissipative elastic metamaterial for broadband wave mitigation. Int. J. Mech. Sci. 2019, 164, 105159. [Google Scholar]
- Huang, G.; Chen, H.; Chen, Y.Y.; Barnhart, V.M. Elastic Metamaterials for Blast Wave Impact Mitigation. In Blast Mitigation Strategies in Marine Composite and Sandwich Structures, 1st ed.; Rajapakse, Y., Gopalakrishnan, S., Eds.; Springer: Singapore, 2018; pp. 357–375. [Google Scholar] [CrossRef]
- Tan, T.K.; Huang, H.H.; Sun, T.C. Blast-wave impact mitigation using negative effective mass density concept of elastic metamaterials. Int. J. Impact Eng. 2014, 64, 20–29. [Google Scholar] [CrossRef]
- Yang, J.; Kim, E.; Hwang, Y.H.; Shul, W.C. Impact and blast mitigation using locally resonant woodpile metamaterials. Int. J. Impact Eng. 2017, 101, 24–31. [Google Scholar]
- Kontogeorgos, M.; Fuggini, C. Meta-Material Layout for the Protection of Buried Steel Pipes against Surface Explosion. Geotechnics 2022, 2, 427–440. [Google Scholar] [CrossRef]
- Hernández-Báez, A.; Torres, E.S.; Amaya-Gomez, R.; Pradilla, D. Oil Onshore Pipeline Quantitative Risk Assessment under Fire and Explosion Scenarios. Processes 2023, 11, 557. [Google Scholar] [CrossRef]
- Cheng, L.; Ma, L.; Li, M. Quantitative risk analysis of urban natural gas pipeline networks using geographical information systems. J. Loss Prev. Process Ind. 2013, 26, 1183–1192. [Google Scholar]
- Pourtaghi, G.; Kouhpaee, H.; Esmaeili, R.; Gholamnia, R.; Jabbari, M. Risk assessment of fire, explosion and release of toxic gas of Siri–Assalouyeh sour gas pipeline using fuzzy analytical hierarchy process. Heliyon 2021, 7, e07835. [Google Scholar]
- Piccinelli, R.; Krausmann, E. Analysis of natech risk for pipelines: A review. In Joint Research Centre Scientific and Policy Reports; Publications Office of the European Union: Luxembourg, 2013. [Google Scholar]
- Girgin, S.; Krausmann, E. Historical analysis of U.S. onshore hazardous liquid pipeline accidents triggered by natural hazards. J. Loss Prev. Process Ind. 2016, 40, 578–590. [Google Scholar] [CrossRef]
- Hao, H.; Zhang, X. Challenges of Effective Blast Protection of Buildings. In Engineering for Extremes, 1st ed.; Rosowsky, D.V., Stewart, G.M., Eds.; Springer: Cham, Switzerland, 2021; pp. 93–117. [Google Scholar] [CrossRef]
- Hao, H.; Hao, Y.; Jin, H.; Chen, W. Review of the current practices in blast-resistant analysis and design of concrete structures. Adv. Struct. Eng. 2016, 19, 1193–1223. [Google Scholar] [CrossRef]
- Unified Facilities Criteria. Structures to Resist the Effects of Accidental Explosions, 1st ed.; U.S. Army Corps of Engineers, Naval Facilities Engineering Command, Air Force Civil Engineer Support Agency: Washington, DC, USA, 2008. [Google Scholar]
- Oliveira, V.D.; Rana, S.; Fangueiro, R.; Pichandi, S. Fibrous and composite materials for blast protection of structural elements-A state-of-the-art review. J. Reinf. Plast. Compos. 2014, 32, 1477–1500. [Google Scholar] [CrossRef]
- Salih, Y.A.; Abdulla, A.I.; Jomaa’h, M.M. Impact Resistance of GFRP Reinforced Concrete One-Way Slabs. Inf. Sci. Lett. 2022, 11, 1267–1275. [Google Scholar]
- Xie, Z.; Duan, Z.; Guo, Y.; Li, X.; Zen, J. Behavior of Fiber-Reinforced Polymer-Confined High-Strength Concrete under Split-Hopkinson Pressure Bar (SHPB) Impact Compression. Appl. Sci. 2019, 9, 2830. [Google Scholar] [CrossRef] [Green Version]
- Adhikary, S.D.; Goswami, A. Retrofitting materials for enhanced blast performance of Structures: Recent advancement and challenges ahead. Constr. Build. Mater. 2019, 204, 224–243. [Google Scholar]
- Kovacs, T.; Nyikes, Z.; Figuli, L. Application of High Energy Absorbing Materials for Blast Protection. Acta Mater. Transylvanica 2018, 1, 93–96. [Google Scholar] [CrossRef]
- Ha, S.N.; Marundrury, S.S.; Pham, T.; Pournasiri, E.; Shi, F.; Hao, H. Effect of grounded blast furnace slag and rice husk ash on performance of ultra-high-performance concrete (UHPC) subjected to impact loading. Constr. Build. Mater. 2022, 329, 127213. [Google Scholar] [CrossRef]
- Wei, J.; Li, J.; Wu, C.; Liu, Z.X.; Fang, J. Impact resistance of ultra-high-performance concrete strengthened reinforced concrete beams. Int. J. Impact Eng. 2021, 158, 104023. [Google Scholar] [CrossRef]
- Zeng, J.; Long, T. Compressive Behavior of FRP Grid-Reinforced UHPC Tubular Columns. Polymers 2022, 14, 125. [Google Scholar] [CrossRef]
- Mohammadi, Y.; Sadeghian, A.; Shaghaghi, T.M.; Taghipoor, H. Performance Assessment of Hybrid Fibre-Reinforced Concrete (FRC) under Low-Speed Impact: Experimental Analysis and Optimized Mixture. Shock Vib. 2023, 2023, 7110987. [Google Scholar] [CrossRef]
- Si, Z.; Liu, F.; Pan, J.; Dong, H. Research on Impact Resistance of Reinforced Concrete Beams Strengthened with Carbon Fiber Reinforced Polymer Grid and Engineered Cementitious Composites. Polymers 2022, 14, 1951. [Google Scholar] [CrossRef]
- Do, V.T.; Pham, T.; Gehl, A.; Hao, H.; Nguyen, T.P. Impact Responses of Precast Hollow Reinforced Concrete Beams with Prestress Tendons using High-Fidelity Physics-Based Simulations. Eng. Fail. Anal. 2021, 131, 729–742. [Google Scholar] [CrossRef]
- Yan, X.; Lin, C.; Liu, X.; Zheng, T.; Shi, S.; Mao, H. Numerical and Analytical Investigations of the Impact Resistance of Partially Precast Concrete Beams Strengthened with Bonded Steel Plates. Buildings 2023, 13, 696. [Google Scholar] [CrossRef]
- Mao, H.; Yan, X.; Zong, C.; Lin, C. Numerical Analysis of the Impact Resistance of Partially Precast Concrete Beams and Prediction of the Displacement Response. KSCE J. Civ. Eng. 2023, 27, 2058–2072. [Google Scholar] [CrossRef]
- Xue, S.; Hao, H.; Hao, Y. Numerical evaluation of the impact performance of precast concrete segmental columns and strengthening techniques. Eng. Struct. 2021, 244, 112725. [Google Scholar] [CrossRef]
- Huang, Z.; Chen, W.; Tran, T.T.; Pham, T.; Hao, H.; Chen, Z.; Elchalakani, M. Experimental and Numerical Study on Concrete Beams Reinforced with Basalt FRP Bars under Static and Impact Loads. Compos. Struct. 2021, 263, e386–e395. [Google Scholar] [CrossRef]
- Zhang, X.; Hao, H.; Li, C.; Do, V.T. Experimental study on the behavior of precast segmental column with domed shear key and unbonded post-Tensioning tendon under impact loading. Eng. Struct. 2018, 173, 589–605. [Google Scholar] [CrossRef]
- Mao, H.; Yan, X.; Zong, C.; Lin, C.; Liu, X. Experimental Research on Impact Resistance of Partially Precast Concrete Beams. KSCE J. Civ. Eng. 2023, 26, 4038–4051. [Google Scholar] [CrossRef]
- Kheyroddin, A.; Arshadi, H.; Ahadi, M.R.; Taban, G.; Kioumarsi, M. The impact resistance of Fiber-Reinforced concrete with polypropylene fibers and GFRP wrapping. Mater. Proc. 2021, 45, 5433–5438. [Google Scholar] [CrossRef]
- Wang, W.; Mo, Z.; Chouw, N.; Xu, Z.D. Impact resistance of flax FRP fully wrapped coconut fibre reinforced concrete beams and shear contribution of FRP. Constr. Build. Mater. 2023, 392, 131922. [Google Scholar] [CrossRef]
- Zhang, X.; Hao, H. Improved Impact Resistant Capacity of Segmental Column with Fibre Reinforced Polymer Wrap. Int. J. Impact Eng. 2018, 125, 117–133. [Google Scholar] [CrossRef]
- Quek, J.; Liu, C.; Musngi, J.V.; Malalasekara, P.B. A comparison of finite element simulation and experimental results from reinforced concrete columns wrapped with fibre-reinforced polymer subjected to blast loading. Int. J. Comput. Methods Exp. Meas. 2020, 8, 233–242. [Google Scholar] [CrossRef]
- Olarewaju, J.; Kameswara Rao, N.S.V.; Mannan, M.A. Blast Effects on Underground Pipes. Electron. J. Geotech. Eng. 2010, 15, 645–658. [Google Scholar]
- Ngo, T.; Mendis, P.; Gupta, A.; Ramsay, J. Blast loading and blast effects on structures—Overview. EJSE Spec. Issue: Load. Struct. 2007, 1, 76–91. [Google Scholar] [CrossRef]
- Shirbhate, P.A.; Goel, M.D. A Critical Review of Blast Wave Parameters and Approaches for Blast Load Mitigation. Arch. Comput. Methods Eng. 2020, 28, 1713–1730. [Google Scholar] [CrossRef]
- Department of Defense. Unified Facilities Criteria: Structures to Resist the Effects of Accidental Explosions; UFC 3-340-02; Department of Defense: Washington, DC, USA, 2008. [Google Scholar]
- Solomos, G.; Karlos, V. JRC Technical Reports: Calculation of Blast Loads for Application to Structural Components, 1st ed.; Publications Office of the European Union: Luxembourg, 2008. [Google Scholar]
- Anirban, D.; Zimmie, Τ. Effects of Surface Explosion on Underground Tunnel and Potential Mitigation Measures. Transp. Infrastruct. Geotechnol. 2016, 3, 74–90. [Google Scholar]
- US Nuclear Regulatory Commission. Characterizing Explosive Effects on Underground Structures; Office of Nuclear Security and Incident Response: San Antonio, TX, USA, 2014. [Google Scholar]
- Ibrahim, E.Y.; Nabil, M. Finite Element Analysis of Pile Foundations Under Surface Blast Loads. In Proceedings of the 13th International Conference on Damage Assessment of Structures, Porto, Portugal, 9–10 July 2019; Wahab, M.A., Ed.; Springer Nature: Singapore, 2020; pp. 446–460. [Google Scholar]



| Properties | Material 1 Polyurethane Foam | Material 2 Rubber |
|---|---|---|
| Density ρ (kg/m3) | 900 | 1300 |
| Young’s Modulus E (Pa) | 1.47 × 108 | 58,000 |
| Poisson’s ration ν | 0.42 | 0.463 |
| Attenuation Zone No. | Frequency Range (Hz) |
|---|---|
| 1 | 24.27–39.03 |
| 2 | 53.69–78.06 |
| 3 | 87.74–117.10 |
| 4 | 124.13–156.13 |
| 5 | 161.61–195.17 |
| 6 | 199.64–234.20 |
| 7 | 237.98–273.23 |
| 8 | 276.52–312.27 |
| 9 | 315.17–351.30 |
| 10 | 353.91–390.33 |
| 11 | 392.70–429.37 |
| 12 | 431.54–468.40 |
| 13 | 470.42–507.43 |
| 14 | 509.32–546.46 |
| 15 | 548.24–585.49 |
| 16 | 587.17–624.52 |
| 17 | 626.12–663.55 |
| 18 | 665.08–702.58 |
| 19 | 704.05–741.61 |
| Case No. | Subcase | TNT Charge (kg) | Distance from Pipe (m) | Z (m/kg 0.333) | ttot = tA + to (ms) |
|---|---|---|---|---|---|
| 1 | a | 50 | 2.50 | 0.68 | 4.79 |
| b | 100 | 2.50 | 0.54 | 2.18 | |
| c | 150 | 2.50 | 0.47 | 2.23 | |
| 2 | a | 50 | 3.50 | 0.95 | 8.44 |
| b | 100 | 3.50 | 0.75 | 7.57 | |
| c | 200 | 3.50 | 0.60 | 4.09 | |
| 3 | a | 150 | 5.00 | 0.94 | 10.33 |
| b | 250 | 5.00 | 0.79 | 9.76 | |
| c | 400 | 5.00 | 0.68 | 8.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kontogeorgos, M.; Fuggini, C. Meta-Material Layout for the Blast Protection of Above-Ground Steel Pipes. Geotechnics 2023, 3, 584-600. https://doi.org/10.3390/geotechnics3030032
Kontogeorgos M, Fuggini C. Meta-Material Layout for the Blast Protection of Above-Ground Steel Pipes. Geotechnics. 2023; 3(3):584-600. https://doi.org/10.3390/geotechnics3030032
Chicago/Turabian StyleKontogeorgos, Miltiadis, and Clemente Fuggini. 2023. "Meta-Material Layout for the Blast Protection of Above-Ground Steel Pipes" Geotechnics 3, no. 3: 584-600. https://doi.org/10.3390/geotechnics3030032





