Advancements in Understanding Interface Friction: A Combined Experimental and Machine Learning Approach Using Multiple Linear and Random Forest Regressions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material
2.2. Methods
3. Results and Discussion
3.1. Internal versus Interface Friction
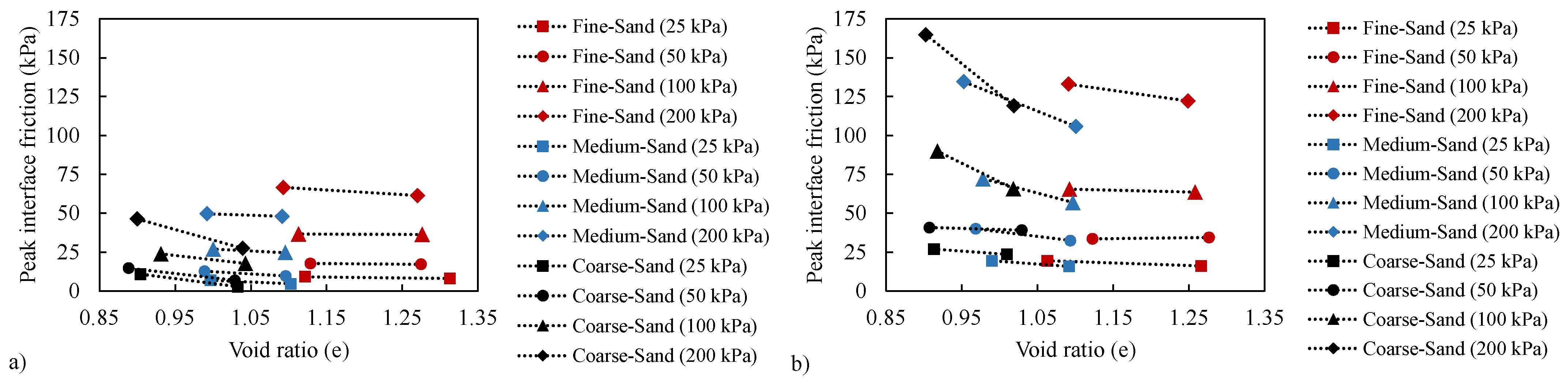
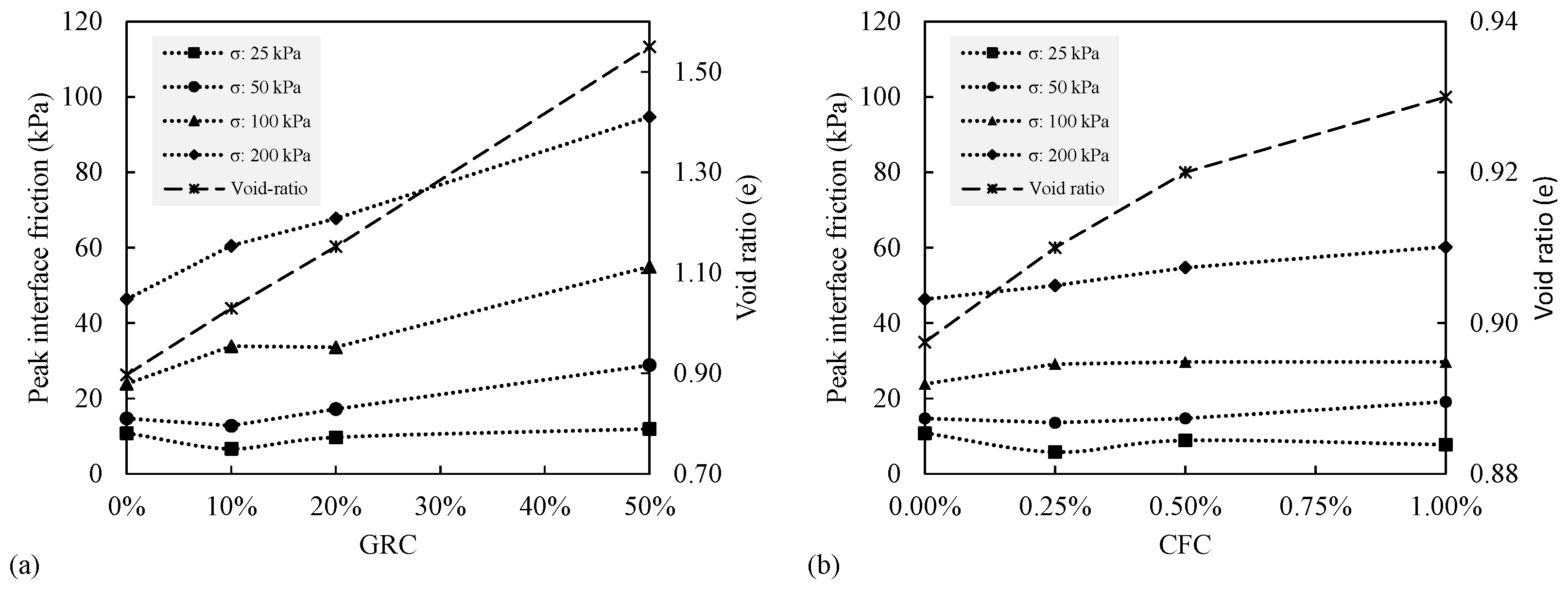
3.2. Void Ratio Impact
3.3. Peak Interface Friction
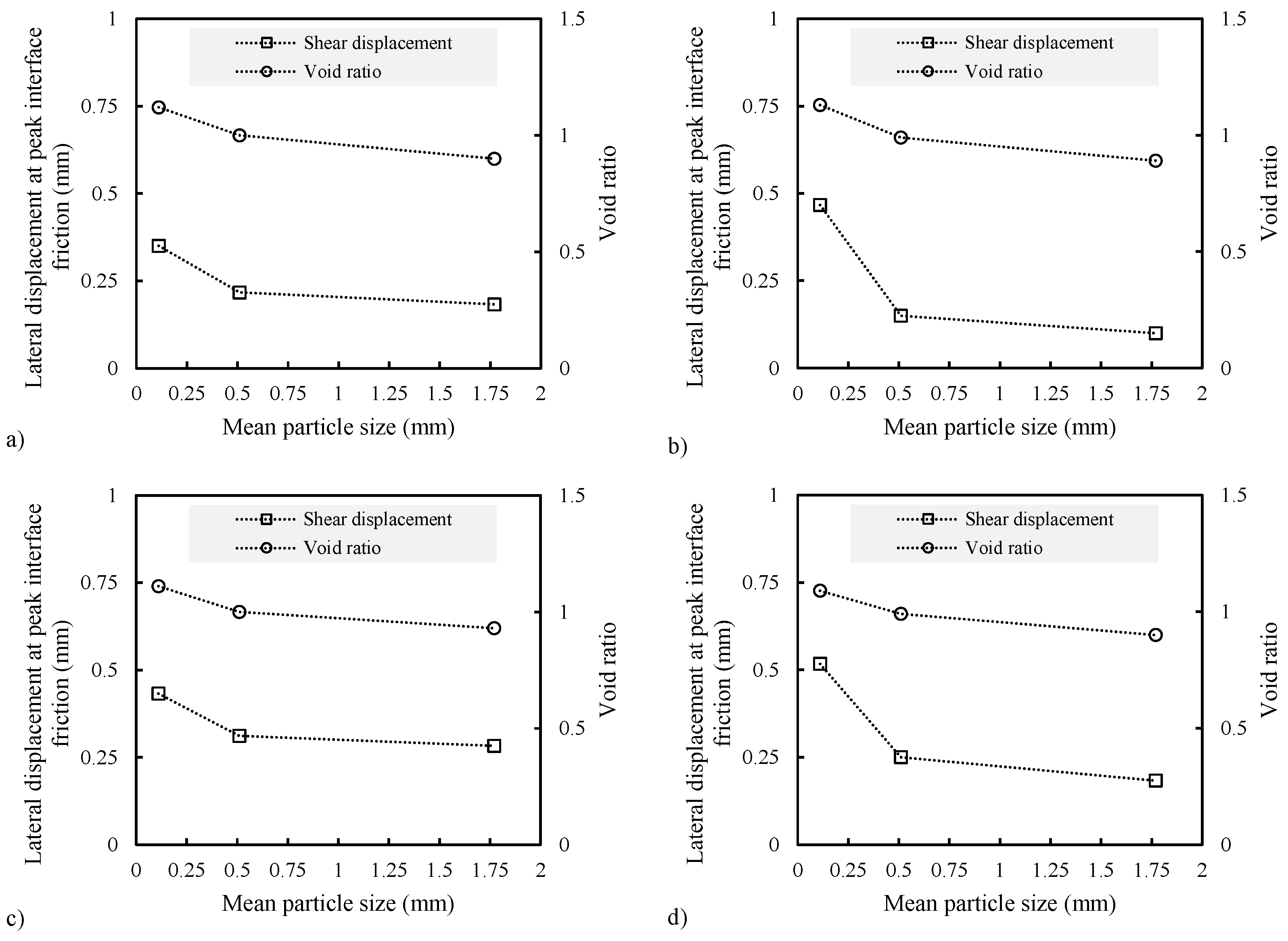
3.4. Lateral Displacement versus Peak Interface Friction
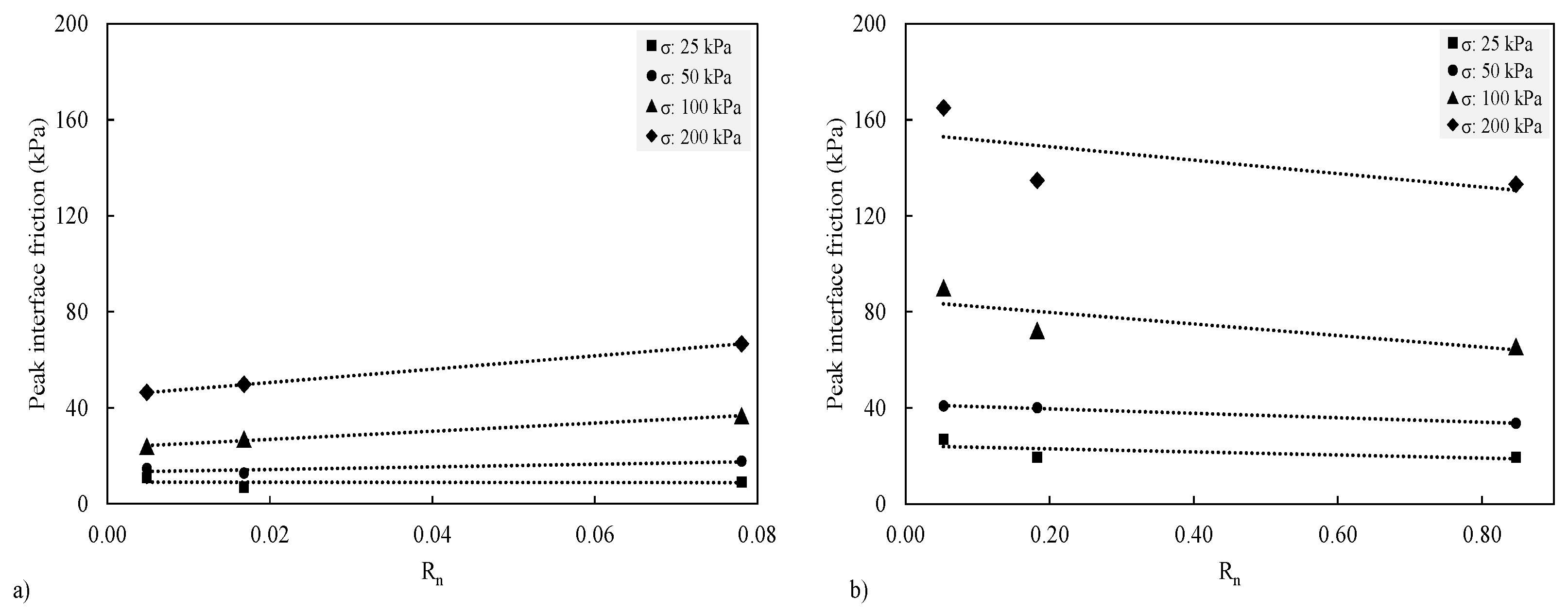
3.5. Normalise Roughness
3.6. Sand–Recycled Material/Steel Interface
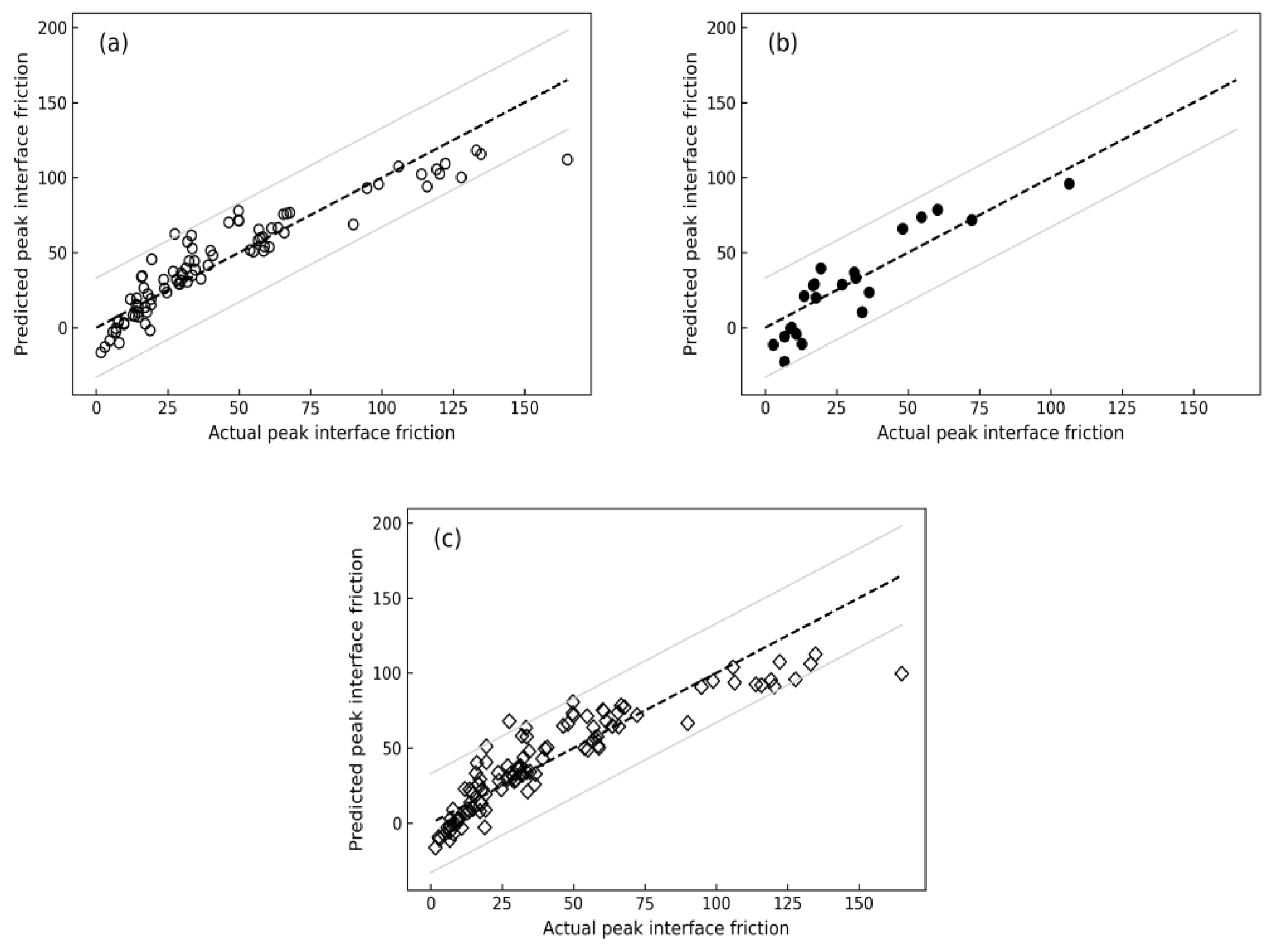
3.7. Multiple Linear Regression
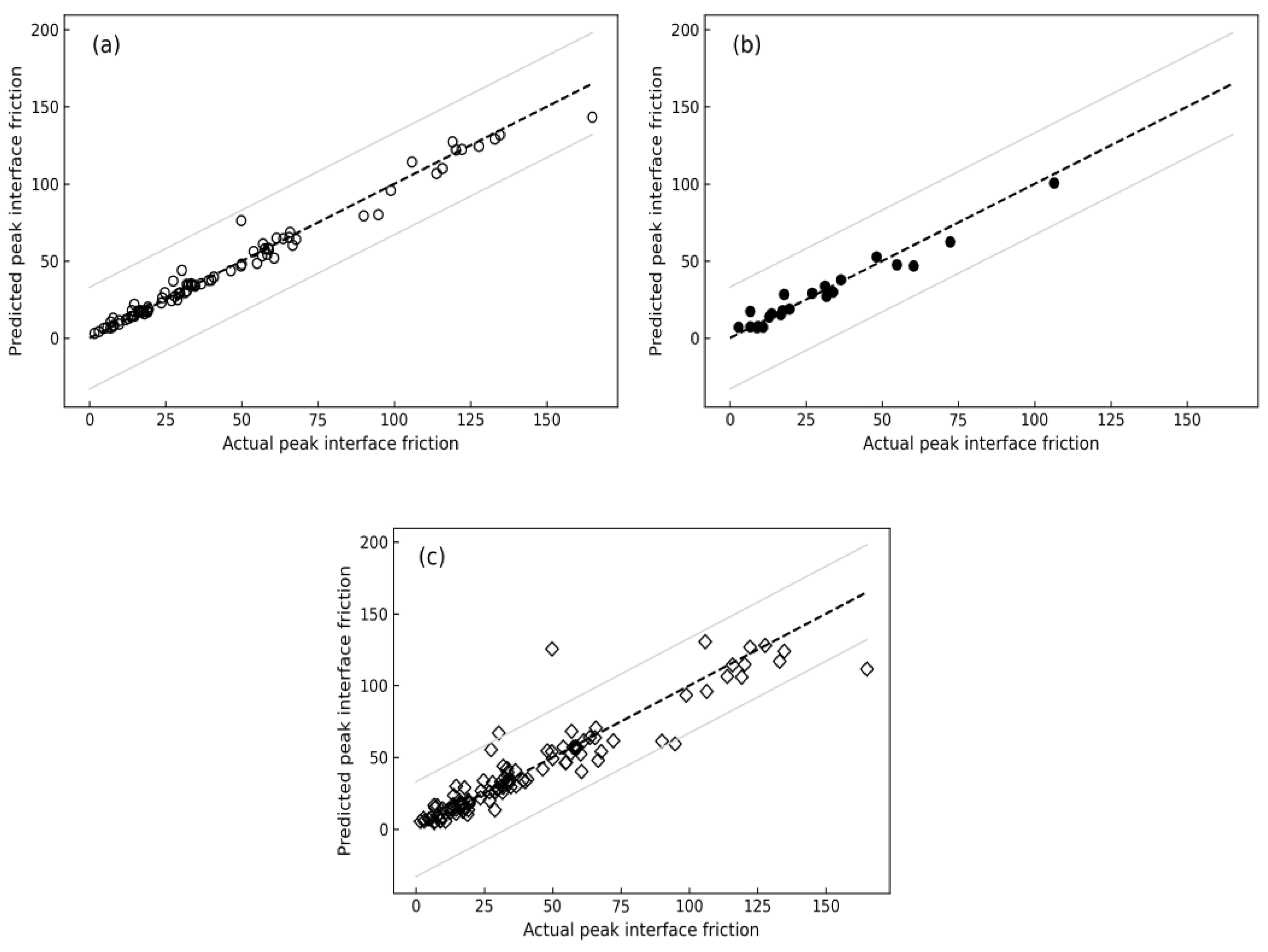
3.8. Random Forest Regression
3.9. Method Comparison
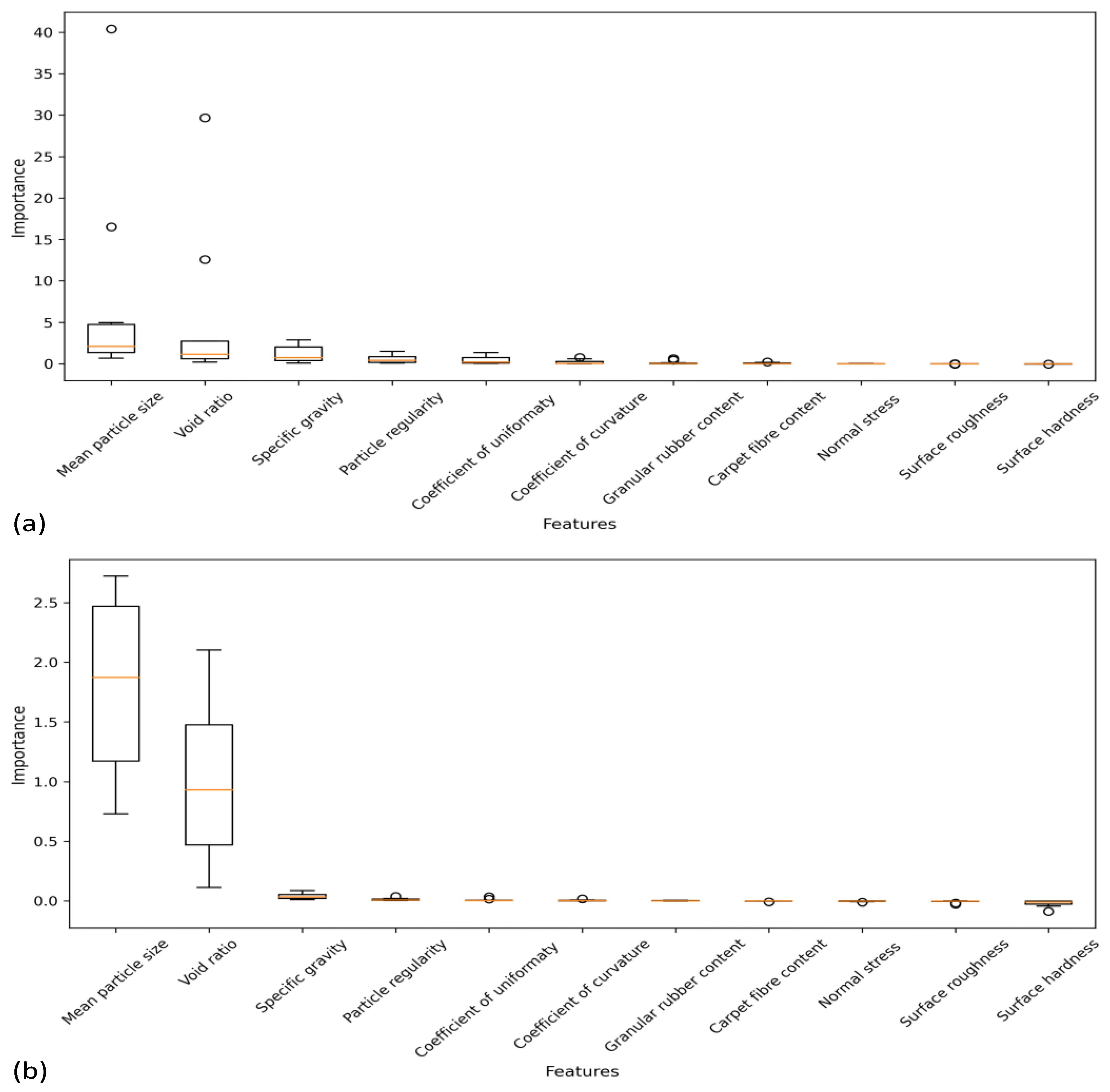
3.10. Importance of Features
4. Conclusions
- An increase in sample density leads to higher interface friction by reducing the void ratio, which, in turn, increases the contact surface and enhances friction.
- The shear strength of the sand markedly exceeds the peak interface friction shown at both the sand/smooth steel and sand/rough steel interfaces.
- Coarse sand specimens attain their peak interface frictional resistance with less lateral deformation than medium and fine-grained sands.
- The inclusion of recycled material into sand enhances its interface friction. Mixtures of sand and granular rubber show a significant enhancement in peak interface friction, while mixtures with carpet fibre show a slight enhancement.
- The machine learning findings validate the efficacy of both MLR and RFR models in predicting the peak interface friction, with the latter outperforming the former in terms of accuracy.
- The application of 10-fold cross-validation reveals that mean particle size and void ratio are the most significant input features.
- Future research should consider various input parameters, including soil type, sand–rubber size ratio, carpet fibre size ratio, moisture content, temperature, shear rate, and stress history as well as the incorporation of hybrid machine learning techniques.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| D50 | Mean particle size |
| e | Void ratio |
| Gs | Specific gravity |
| ⍴r | Particle regularity |
| Cu | Coefficient of uniformity |
| Cc | Coefficient of curvature |
| GRC | Granular rubber content |
| GR | Granular rubber |
| CFC | Carpet fibre content |
| CF | Carpet fibre |
| σn | Normal stress |
| Rt | Surface roughness |
| HD | Surface hardness |
| ML | Machine learning |
| MLR | Multiple linear regression |
| RFR | Random forest regression |
| τ | Interface friction |
| τp | Peak interface friction |
| μ | Interface friction coefficient |
| Rn | Normalised roughness |
Appendix A
| # | D50 (mm) | e | Gs | ρr | Cu | Cc | GRC (%) | CFC (%) | σn (kPa) | Rt (µm) | HD | τp (kPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.11 | 1.313 | 2.70 | 0.454 | 1.45 | 0.96 | 0 | 0.00 | 25 | 0.009 | 150 | 8.06 |
| 2 | 0.11 | 1.275 | 2.70 | 0.454 | 1.45 | 0.96 | 0 | 0.00 | 50 | 0.009 | 150 | 17.22 |
| 3 | 0.11 | 1.276 | 2.70 | 0.454 | 1.45 | 0.96 | 0 | 0.00 | 100 | 0.009 | 150 | 36.39 |
| 4 | 0.11 | 1.270 | 2.70 | 0.454 | 1.45 | 0.96 | 0 | 0.00 | 200 | 0.009 | 150 | 61.39 |
| 5 | 0.51 | 1.103 | 2.66 | 0.392 | 1.20 | 0.97 | 0 | 0.00 | 25 | 0.009 | 150 | 4.72 |
| 6 | 0.51 | 1.096 | 2.66 | 0.392 | 1.20 | 0.97 | 0 | 0.00 | 50 | 0.009 | 150 | 9.72 |
| 7 | 0.51 | 1.096 | 2.66 | 0.392 | 1.20 | 0.97 | 0 | 0.00 | 100 | 0.009 | 150 | 24.72 |
| 8 | 0.51 | 1.092 | 2.66 | 0.392 | 1.20 | 0.97 | 0 | 0.00 | 200 | 0.009 | 150 | 48.06 |
| 9 | 1.77 | 1.033 | 2.66 | 0.410 | 1.45 | 0.96 | 0 | 0.00 | 25 | 0.009 | 150 | 2.78 |
| 10 | 1.77 | 1.029 | 2.66 | 0.410 | 1.45 | 0.96 | 0 | 0.00 | 50 | 0.009 | 150 | 6.94 |
| 11 | 1.77 | 1.043 | 2.66 | 0.410 | 1.45 | 0.96 | 0 | 0.00 | 100 | 0.009 | 150 | 17.78 |
| 12 | 1.77 | 1.039 | 2.66 | 0.410 | 1.45 | 0.96 | 0 | 0.00 | 200 | 0.009 | 150 | 27.50 |
| 13 | 0.89 | 0.710 | 2.45 | 1.000 | 1.44 | 0.96 | 0 | 0.00 | 25 | 0.009 | 150 | 1.67 |
| 14 | 0.89 | 0.710 | 2.45 | 1.000 | 1.44 | 0.96 | 0 | 0.00 | 50 | 0.009 | 150 | 6.67 |
| 15 | 0.89 | 0.708 | 2.45 | 1.000 | 1.44 | 0.96 | 0 | 0.00 | 100 | 0.009 | 150 | 13.89 |
| 16 | 0.89 | 0.716 | 2.45 | 1.000 | 1.44 | 0.96 | 0 | 0.00 | 200 | 0.009 | 150 | 31.94 |
| 17 | 0.11 | 1.122 | 2.70 | 0.454 | 1.45 | 0.96 | 0 | 0.00 | 25 | 0.009 | 150 | 9.17 |
| 18 | 0.11 | 1.129 | 2.70 | 0.454 | 1.45 | 0.96 | 0 | 0.00 | 50 | 0.009 | 150 | 17.78 |
| 19 | 0.11 | 1.113 | 2.70 | 0.454 | 1.45 | 0.96 | 0 | 0.00 | 100 | 0.009 | 150 | 36.67 |
| 20 | 0.11 | 1.093 | 2.70 | 0.454 | 1.45 | 0.96 | 0 | 0.00 | 200 | 0.009 | 150 | 66.67 |
| 21 | 0.51 | 0.997 | 2.66 | 0.392 | 1.20 | 0.97 | 0 | 0.00 | 25 | 0.009 | 150 | 6.94 |
| 22 | 0.51 | 0.989 | 2.66 | 0.392 | 1.20 | 0.97 | 0 | 0.00 | 50 | 0.009 | 150 | 12.78 |
| 23 | 0.51 | 1.000 | 2.66 | 0.392 | 1.20 | 0.97 | 0 | 0.00 | 100 | 0.009 | 150 | 26.94 |
| 24 | 0.51 | 0.992 | 2.66 | 0.392 | 1.20 | 0.97 | 0 | 0.00 | 200 | 0.009 | 150 | 49.72 |
| 25 | 1.77 | 0.904 | 2.66 | 0.410 | 1.45 | 0.96 | 0 | 0.00 | 25 | 0.009 | 150 | 10.83 |
| 26 | 1.77 | 0.889 | 2.66 | 0.410 | 1.45 | 0.96 | 0 | 0.00 | 50 | 0.009 | 150 | 14.72 |
| 27 | 1.77 | 0.931 | 2.66 | 0.410 | 1.45 | 0.96 | 0 | 0.00 | 100 | 0.009 | 150 | 23.89 |
| 28 | 1.77 | 0.900 | 2.66 | 0.410 | 1.45 | 0.96 | 0 | 0.00 | 200 | 0.009 | 150 | 46.39 |
| 29 | 0.89 | 0.645 | 2.45 | 1.000 | 1.44 | 0.96 | 0 | 0.00 | 25 | 0.009 | 150 | 3.06 |
| 30 | 0.89 | 0.636 | 2.45 | 1.000 | 1.44 | 0.96 | 0 | 0.00 | 50 | 0.009 | 150 | 18.89 |
| 31 | 0.89 | 0.641 | 2.45 | 1.000 | 1.44 | 0.96 | 0 | 0.00 | 100 | 0.009 | 150 | 19.17 |
| 32 | 0.89 | 0.640 | 2.45 | 1.000 | 1.44 | 0.96 | 0 | 0.00 | 200 | 0.009 | 150 | 33.33 |
| 33 | 0.11 | 1.266 | 2.70 | 0.454 | 1.45 | 0.96 | 0 | 0.00 | 25 | 0.093 | 150 | 16.11 |
| 34 | 0.11 | 1.276 | 2.70 | 0.454 | 1.45 | 0.96 | 0 | 0.00 | 50 | 0.093 | 150 | 34.44 |
| 35 | 0.11 | 1.258 | 2.70 | 0.454 | 1.45 | 0.96 | 0 | 0.00 | 100 | 0.093 | 150 | 63.61 |
| 36 | 0.11 | 1.249 | 2.70 | 0.454 | 1.45 | 0.96 | 0 | 0.00 | 200 | 0.093 | 150 | 122.22 |
| 37 | 0.51 | 1.092 | 2.66 | 0.392 | 1.20 | 0.97 | 0 | 0.00 | 25 | 0.093 | 150 | 15.83 |
| 38 | 0.51 | 1.094 | 2.66 | 0.392 | 1.20 | 0.97 | 0 | 0.00 | 50 | 0.093 | 150 | 32.50 |
| 39 | 0.51 | 1.097 | 2.66 | 0.392 | 1.20 | 0.97 | 0 | 0.00 | 100 | 0.093 | 150 | 56.94 |
| 40 | 0.51 | 1.101 | 2.66 | 0.392 | 1.20 | 0.97 | 0 | 0.00 | 200 | 0.093 | 150 | 105.83 |
| 41 | 1.77 | 1.010 | 2.66 | 0.410 | 1.45 | 0.96 | 0 | 0.00 | 25 | 0.093 | 150 | 23.61 |
| 42 | 1.77 | 1.029 | 2.66 | 0.410 | 1.45 | 0.96 | 0 | 0.00 | 50 | 0.093 | 150 | 39.17 |
| 43 | 1.77 | 1.018 | 2.66 | 0.410 | 1.45 | 0.96 | 0 | 0.00 | 100 | 0.093 | 150 | 65.83 |
| 44 | 1.77 | 1.019 | 2.66 | 0.410 | 1.45 | 0.96 | 0 | 0.00 | 200 | 0.093 | 150 | 119.17 |
| 45 | 0.89 | 0.691 | 2.45 | 1.000 | 1.44 | 0.96 | 0 | 0.00 | 25 | 0.093 | 150 | 16.67 |
| 46 | 0.89 | 0.697 | 2.45 | 1.000 | 1.44 | 0.96 | 0 | 0.00 | 50 | 0.093 | 150 | 31.11 |
| 47 | 0.89 | 0.693 | 2.45 | 1.000 | 1.44 | 0.96 | 0 | 0.00 | 100 | 0.093 | 150 | 56.67 |
| 48 | 0.89 | 0.698 | 2.45 | 1.000 | 1.44 | 0.96 | 0 | 0.00 | 200 | 0.093 | 150 | 127.78 |
| 49 | 0.11 | 1.063 | 2.70 | 0.454 | 1.45 | 0.96 | 0 | 0.00 | 25 | 0.093 | 150 | 19.44 |
| 50 | 0.11 | 1.123 | 2.70 | 0.454 | 1.45 | 0.96 | 0 | 0.00 | 50 | 0.093 | 150 | 33.61 |
| 51 | 0.11 | 1.092 | 2.70 | 0.454 | 1.45 | 0.96 | 0 | 0.00 | 100 | 0.093 | 150 | 65.56 |
| 52 | 0.11 | 1.091 | 2.70 | 0.454 | 1.45 | 0.96 | 0 | 0.00 | 200 | 0.093 | 150 | 133.06 |
| 53 | 0.51 | 0.990 | 2.66 | 0.392 | 1.20 | 0.97 | 0 | 0.00 | 25 | 0.093 | 150 | 19.44 |
| 54 | 0.51 | 0.968 | 2.66 | 0.392 | 1.20 | 0.97 | 0 | 0.00 | 50 | 0.093 | 150 | 40.00 |
| 55 | 0.51 | 0.978 | 2.66 | 0.392 | 1.20 | 0.97 | 0 | 0.00 | 100 | 0.093 | 150 | 72.22 |
| 56 | 0.51 | 0.952 | 2.66 | 0.392 | 1.20 | 0.97 | 0 | 0.00 | 200 | 0.093 | 150 | 134.72 |
| 57 | 1.77 | 0.913 | 2.66 | 0.410 | 1.45 | 0.96 | 0 | 0.00 | 25 | 0.093 | 150 | 26.94 |
| 58 | 1.77 | 0.907 | 2.66 | 0.410 | 1.45 | 0.96 | 0 | 0.00 | 50 | 0.093 | 150 | 40.83 |
| 59 | 1.77 | 0.918 | 2.66 | 0.410 | 1.45 | 0.96 | 0 | 0.00 | 100 | 0.093 | 150 | 90.00 |
| 60 | 1.77 | 0.902 | 2.66 | 0.410 | 1.45 | 0.96 | 0 | 0.00 | 200 | 0.093 | 150 | 165.00 |
| 61 | 0.89 | 0.645 | 2.45 | 1.000 | 1.44 | 0.96 | 0 | 0.00 | 25 | 0.093 | 150 | 17.22 |
| 62 | 0.89 | 0.665 | 2.45 | 1.000 | 1.44 | 0.96 | 0 | 0.00 | 50 | 0.093 | 150 | 34.72 |
| 63 | 0.89 | 0.654 | 2.45 | 1.000 | 1.44 | 0.96 | 0 | 0.00 | 100 | 0.093 | 150 | 58.33 |
| 64 | 0.89 | 0.655 | 2.45 | 1.000 | 1.44 | 0.96 | 0 | 0.00 | 200 | 0.093 | 150 | 120.28 |
| 65 | 0.11 | 1.307 | 2.70 | 0.454 | 1.45 | 0.96 | 0 | 0.00 | 25 | 0.019 | 89 | 14.17 |
| 66 | 0.11 | 1.300 | 2.70 | 0.454 | 1.45 | 0.96 | 0 | 0.00 | 50 | 0.019 | 89 | 31.94 |
| 67 | 0.11 | 1.309 | 2.70 | 0.454 | 1.45 | 0.96 | 0 | 0.00 | 100 | 0.019 | 89 | 58.61 |
| 68 | 0.11 | 1.300 | 2.70 | 0.454 | 1.45 | 0.96 | 0 | 0.00 | 200 | 0.019 | 89 | 115.83 |
| 69 | 0.23 | 1.152 | 2.69 | 0.427 | 1.45 | 0.96 | 0 | 0.00 | 25 | 0.019 | 89 | 16.67 |
| 70 | 0.23 | 1.139 | 2.69 | 0.427 | 1.45 | 0.96 | 0 | 0.00 | 50 | 0.019 | 89 | 31.39 |
| 71 | 0.23 | 1.158 | 2.69 | 0.427 | 1.45 | 0.96 | 0 | 0.00 | 100 | 0.019 | 89 | 57.50 |
| 72 | 0.23 | 1.153 | 2.69 | 0.427 | 1.45 | 0.96 | 0 | 0.00 | 200 | 0.019 | 89 | 113.89 |
| 73 | 0.51 | 1.075 | 2.66 | 0.392 | 1.20 | 0.97 | 0 | 0.00 | 25 | 0.019 | 89 | 18.06 |
| 74 | 0.51 | 1.068 | 2.66 | 0.392 | 1.20 | 0.97 | 0 | 0.00 | 50 | 0.019 | 89 | 31.67 |
| 75 | 0.51 | 1.073 | 2.66 | 0.392 | 1.20 | 0.97 | 0 | 0.00 | 100 | 0.019 | 89 | 58.89 |
| 76 | 0.51 | 1.083 | 2.66 | 0.392 | 1.20 | 0.97 | 0 | 0.00 | 200 | 0.019 | 89 | 106.39 |
| 77 | 1.77 | 0.980 | 2.66 | 0.410 | 1.45 | 0.96 | 0 | 0.00 | 25 | 0.019 | 89 | 13.61 |
| 78 | 1.77 | 0.975 | 2.66 | 0.410 | 1.45 | 0.96 | 0 | 0.00 | 50 | 0.019 | 89 | 28.06 |
| 79 | 1.77 | 1.002 | 2.66 | 0.410 | 1.45 | 0.96 | 0 | 0.00 | 100 | 0.019 | 89 | 53.89 |
| 80 | 1.77 | 0.972 | 2.66 | 0.410 | 1.45 | 0.96 | 0 | 0.00 | 200 | 0.019 | 89 | 98.89 |
| 81 | 1.77 | 0.700 | 2.45 | 1.000 | 1.45 | 0.96 | 0 | 0.00 | 25 | 0.019 | 89 | 7.78 |
| 82 | 1.77 | 0.700 | 2.45 | 1.000 | 1.45 | 0.96 | 0 | 0.00 | 50 | 0.019 | 89 | 14.70 |
| 83 | 1.77 | 0.710 | 2.45 | 1.000 | 1.45 | 0.96 | 0 | 0.00 | 100 | 0.019 | 89 | 30.30 |
| 84 | 1.77 | 0.700 | 2.45 | 1.000 | 1.45 | 0.96 | 0 | 0.00 | 200 | 0.019 | 89 | 49.80 |
| 85 | 1.70 | 1.050 | 2.50 | 0.406 | 1.56 | 0.96 | 10 | 0.00 | 25 | 0.009 | 150 | 6.68 |
| 86 | 1.70 | 1.030 | 2.50 | 0.406 | 1.56 | 0.96 | 10 | 0.00 | 50 | 0.009 | 150 | 12.80 |
| 87 | 1.70 | 1.030 | 2.50 | 0.406 | 1.56 | 0.96 | 10 | 0.00 | 100 | 0.009 | 150 | 33.90 |
| 88 | 1.70 | 1.010 | 2.50 | 0.406 | 1.56 | 0.96 | 10 | 0.00 | 200 | 0.009 | 150 | 60.60 |
| 89 | 1.62 | 1.150 | 2.34 | 0.402 | 3.45 | 1.94 | 20 | 0.00 | 25 | 0.009 | 150 | 9.73 |
| 90 | 1.62 | 1.150 | 2.34 | 0.402 | 3.45 | 1.94 | 20 | 0.00 | 50 | 0.009 | 150 | 17.20 |
| 91 | 1.62 | 1.150 | 2.34 | 0.402 | 3.45 | 1.94 | 20 | 0.00 | 100 | 0.009 | 150 | 33.60 |
| 92 | 1.62 | 1.160 | 2.34 | 0.402 | 3.45 | 1.94 | 20 | 0.00 | 200 | 0.009 | 150 | 67.80 |
| 93 | 1.18 | 1.490 | 1.87 | 0.390 | 4.93 | 0.84 | 50 | 0.00 | 25 | 0.009 | 150 | 11.95 |
| 94 | 1.18 | 1.490 | 1.87 | 0.390 | 4.93 | 0.84 | 50 | 0.00 | 50 | 0.009 | 150 | 28.90 |
| 95 | 1.18 | 1.490 | 1.87 | 0.390 | 4.93 | 0.84 | 50 | 0.00 | 100 | 0.009 | 150 | 55.00 |
| 96 | 1.18 | 1.490 | 1.87 | 0.390 | 4.93 | 0.84 | 50 | 0.00 | 200 | 0.009 | 150 | 94.80 |
| 97 | 1.77 | 0.920 | 2.66 | 0.410 | 1.45 | 0.96 | 0 | 0.25 | 25 | 0.009 | 150 | 5.83 |
| 98 | 1.77 | 0.920 | 2.66 | 0.410 | 1.45 | 0.96 | 0 | 0.25 | 50 | 0.009 | 150 | 13.61 |
| 99 | 1.77 | 0.920 | 2.66 | 0.410 | 1.45 | 0.96 | 0 | 0.25 | 100 | 0.009 | 150 | 29.17 |
| 100 | 1.77 | 0.920 | 2.66 | 0.410 | 1.45 | 0.96 | 0 | 0.25 | 200 | 0.009 | 150 | 50.00 |
| 101 | 1.77 | 0.915 | 2.65 | 0.410 | 1.45 | 0.96 | 0 | 0.50 | 25 | 0.009 | 150 | 8.89 |
| 102 | 1.77 | 0.915 | 2.65 | 0.410 | 1.45 | 0.96 | 0 | 0.50 | 50 | 0.009 | 150 | 14.72 |
| 103 | 1.77 | 0.915 | 2.65 | 0.410 | 1.45 | 0.96 | 0 | 0.50 | 100 | 0.009 | 150 | 29.72 |
| 104 | 1.77 | 0.915 | 2.65 | 0.410 | 1.45 | 0.96 | 0 | 0.50 | 200 | 0.009 | 150 | 54.72 |
| 105 | 1.77 | 0.907 | 2.65 | 0.410 | 1.45 | 0.96 | 0 | 1.00 | 25 | 0.009 | 150 | 7.78 |
| 106 | 1.77 | 0.907 | 2.65 | 0.410 | 1.45 | 0.96 | 0 | 1.00 | 50 | 0.009 | 150 | 19.17 |
| 107 | 1.77 | 0.907 | 2.65 | 0.410 | 1.45 | 0.96 | 0 | 1.00 | 100 | 0.009 | 150 | 29.72 |
| 108 | 1.77 | 0.907 | 2.65 | 0.410 | 1.45 | 0.96 | 0 | 1.00 | 200 | 0.009 | 150 | 60.28 |
References
- Dove, J.E.; Frost, J.D. Peak Friction Behavior of Smooth Geomembrane-Particle Interfaces. J. Geotech. Geoenviron. Eng. 1999, 125, 544–555. [Google Scholar] [CrossRef]
- Su, L.-J.; Zhou, W.-H.; Chen, W.-B.; Jie, X. Effects of relative roughness and mean particle size on the shear strength of sand-steel interface. Measurement 2018, 122, 339–346. [Google Scholar] [CrossRef]
- Dove, J.E.; Frost, J.D.; Han, J.; Bachus, R.C. The Influence of Geomembrane Surface Roughness on Interface Strength. In Proceedings of the Geosynthetics ’97, Long Beach, CA, USA, 11–13 March 1997. [Google Scholar]
- Vaid, Y.; Rinne, N. Geomembrane coefficients of interface friction. Geosynth. Int. 1995, 2, 309–325. [Google Scholar] [CrossRef]
- Frost, J.; Han, J. Behavior of interfaces between fiber-reinforced polymers and sands. J. Geotech. Geoenviron. Eng. 1999, 125, 633–640. [Google Scholar] [CrossRef]
- Vangla, P.; Latha Gali, M. Effect of particle size of sand and surface asperities of reinforcement on their interface shear behaviour. Geotext. Geomembr. 2016, 44, 254–268. [Google Scholar] [CrossRef]
- Ward, H.C. Profile Characterization. In Rough Surfaces, 1st ed.; Thomas, T.R., Ed.; Longman: London, UK, 1982; p. 261. [Google Scholar]
- Kishida, H.; Uesugi, M. Tests of the interface between sand and steel in the simple shear apparatus. Géotechnique 1987, 37, 45–52. [Google Scholar] [CrossRef]
- Shaia, H.A.; Abuel-Naga, H.M. On the normalized relative roughness for soil-fiber reinforced polymer interface shear behaviour. Lowl. Technol. Int. 2014, 16, 9–13. [Google Scholar] [CrossRef]
- Abuel-Naga, H.; Shaia, H.; Bouazza, A. Effect of surface roughness and hardness of Continuum materials on interface shear strength of granular materials. J. Test. Eval. 2017, 46, 826–831. [Google Scholar] [CrossRef]
- Daghistani, F.; Abuel-Naga, H. Evaluating the Influence of Sand Particle Morphology on Shear Strength: A Comparison of Experimental and Machine Learning Approaches. Appl. Sci. 2023, 13, 8160. [Google Scholar] [CrossRef]
- Zhang, P.; Yin, Z.-Y.; Jin, Y.-F.; Liu, X.-F. Modelling the mechanical behaviour of soils using machine learning algorithms with explicit formulations. Acta Geotech. 2021, 17, 1403–1422. [Google Scholar] [CrossRef]
- Yu, H.; Taleghani, A.D.; Al Balushi, F.; Wang, H. Machine learning for rock mechanics problems; an insight. Front. Mech. Eng. 2022, 8, 1003170. [Google Scholar] [CrossRef]
- Daghistani, F.; Baghbani, A.; Abuel Naga, H.; Faradonbeh, R.S. Internal Friction Angle of Cohesionless Binary Mixture Sand–Granular Rubber Using Experimental Study and Machine Learning. Geosciences 2023, 13, 197. [Google Scholar] [CrossRef]
- Saad, A.H.; Nahazanan, H.; Yusuf, B.; Toha, S.F.; Alnuaim, A.; El-Mouchi, A.; Elseknidy, M.; Mohammed, A.A. A Systematic Review of Machine Learning Techniques and Applications in Soil Improvement Using Green Materials. Sustainability 2023, 15, 9738. [Google Scholar] [CrossRef]
- Zarei, C.; Sihag, P.; Rahimi, L. Prediction of Undrained Shear Strength of Crushed Tire Mixture with Fine-Grained Soil by using Machine Learning Approaches. Res. Sq. 2021. [Google Scholar] [CrossRef]
- Qi, C.; Fourie, A.; Chen, Q.; Zhang, Q. A strength prediction model using artificial intelligence for recycling waste tailings as cemented paste backfill. J. Clean. Prod. 2018, 183, 566–578. [Google Scholar] [CrossRef]
- Ahmad, A.; Farooq, F.; Ostrowski, K.A.; Śliwa-Wieczorek, K.; Czarnecki, S. Application of Novel Machine Learning Techniques for Predicting the Surface Chloride Concentration in Concrete Containing Waste Material. Materials 2021, 14, 2297. [Google Scholar] [CrossRef] [PubMed]
- Asteris, P.G.; Koopialipoor, M.; Armaghani, D.J.; Kotsonis, E.A.; Lourenço, P.B. Prediction of cement-based mortars compressive strength using machine learning techniques. Neural Comput. Appl. 2021, 33, 13089–13121. [Google Scholar] [CrossRef]
- Cevallos, S.; Jerves, A.X.; Mital, U.; Medina, D.A.; Quinteros, V.S.; Mulas, M.; Torgersrud, Ø. Towards a more accurate characterization of granular media 2.0: Involving AI in the process. Comput. Geotech. 2023, 160, 105510. [Google Scholar] [CrossRef]
- Jain, P.; Chhabra, H.; Chauhan, U.; Prakash, K.; Samant, P.; Singh, D.K.; Soliman, M.S.; Islam, M.T. Machine Learning Techniques for Predicting Metamaterial Microwave Absorption Performance: A Comparison. IEEE Access 2023, 11, 128774–128783. [Google Scholar] [CrossRef]
- Mital, U.; Andrade, J.E. Bridging length scales in granular materials using convolutional neural networks. Comput. Part. Mech. 2022, 9, 221–235. [Google Scholar] [CrossRef]
- Zhang, P.; Yin, Z.-Y.; Chen, Q. Image-based 3D reconstruction of granular grains via hybrid algorithm and level set with convolution kernel. J. Geotech. Geoenviron. Eng. 2022, 148, 04022021. [Google Scholar] [CrossRef]
- AS1289.3.6.1; Method of Testing Soils for Engineering Purposes—Soil Classification. Australian Standard: Sydney, Australia, 2009.
- AS1774.19; The Determination of Sieve Analysis and Moisture Content. Australian Standard: Sydney, Australia, 2003.
- AS1289.6.2.2; Soil Strength and Consolidation Tests—Determination of Shear Strength of a Soil—Direct Shear Test Using a Shear Box. Standards Australia: Sydney, Australia, 2020.
- Senthen Amuthan, M.; Boominathan, A.; Banerjee, S. Density and Shear Strength of Particulate Rubber Mixed with Sand and Fly Ash. J. Mater. Civ. Eng. 2018, 30, 04018136. [Google Scholar] [CrossRef]
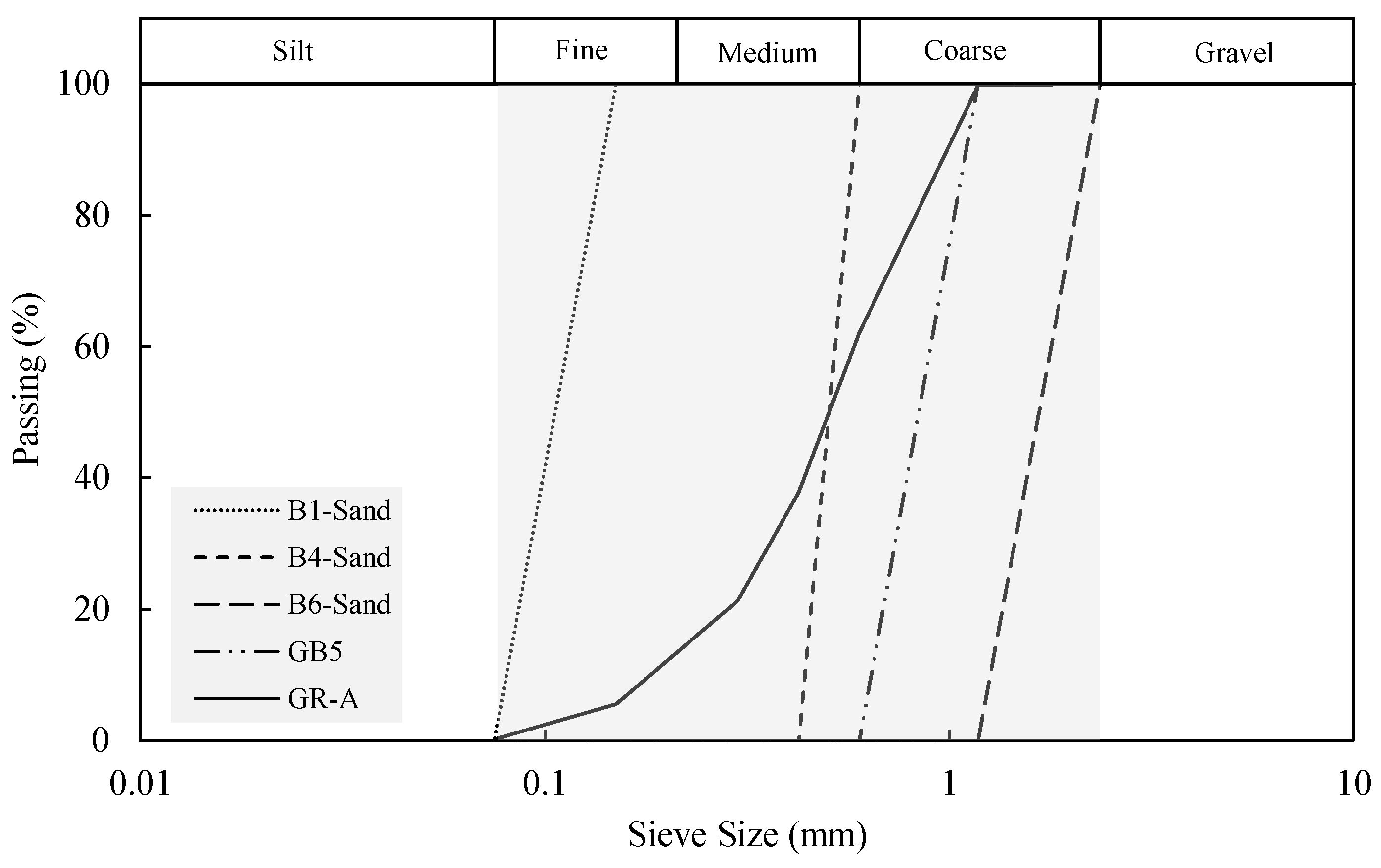





| Granular Material | D50 (mm) | Cu | Cc | Gs | |
|---|---|---|---|---|---|
| B1-Sand | 0.11 | 1.45 | 0.96 | 2.70 | 0.454 |
| B4-Sand | 0.51 | 1.20 | 0.97 | 2.66 | 0.392 |
| B6-Sand | 1.77 | 1.45 | 0.96 | 2.66 | 0.410 |
| GB5 | 0.89 | 1.44 | 0.96 | 2.45 | 1 |
| GR-A | 0.51 | 3.04 | 1.19 | 1.08 | 0.37 |
| Tested Material | Rt (µm) | HD |
|---|---|---|
| Smooth steel | 8.588 | 150 |
| Rough steel | 93.163 | 150 |
| Aluminium | 18.919 | 89 |
| Type | Sand–Rubber Mixture |
|---|---|
| Nblows | 5 |
| Nlayers | 1 |
| Whammer (kN) | 0.026 |
| Hdrop (m) | 0.30 |
| Vmold (m3) | 0.000082 |
| Total Energy (kJ) | 475.61 |
| Feature | Description |
|---|---|
| D50 | This feature presents the average diameter of the granular particles, which influences the contact area and interlocking with the continuum surface. |
| e | This feature presents the ratio of the volume of voids to the volume of solids in the granular material, which affects the density and packing of the particles. |
| Gs | This feature presents the ratio of the density of the granular material to the density of water, which reflects the mineral composition and porosity of the particles. |
| ρr | This feature presents the degree of deviation of the particle shape from a perfect sphere, which affects the frictional resistance and rolling behaviour of the particles |
| Cu | This feature presents the ratio of the particle size corresponding to 60% passing in the sieve analysis to the particle size corresponding to 10% passing, which indicates the gradation and sorting of the granular material. |
| Cc | This feature presents the ratio of the square of the particle size corresponding to 30% passing in the sieve analysis to the product of the particle sizes corresponding to 10% and 60% passing, which indicates the shape of the particle size distribution curve. |
| GRC | This feature presents the percentage of granular rubber added to the sand by dry weight, which modifies the properties of the sand such as void ratio, specific gravity, and particle regularity. |
| CFC | This feature presents the percentage of carpet fibre added to the sand by dry weight, which modifies the properties of the sand such as void ratio, specific gravity, and particle regularity. |
| σn | This feature presents the normal force per unit area applied on the granular material at the interface with the continuum surface, which influences the shear strength and frictional resistance of the interface |
| Rt | This feature presents the relative vertical distance along a surface profile between the highest peak and lowest valley, which indicates the texture and asperity of the continuum surface |
| HD | This feature presents the ability of the continuum surface to resist plastic deformation from a standardised force, which reflects the material and stiffness of the continuum surface |
| σn (kPa) | Sand Only (kPa) | Sand/Smooth Steel (kPa) | Sand/Rough Steel (kPa) | |
|---|---|---|---|---|
| Fine sand (D50: 0.11) | 25 | 23.33 | 9.17 | 19.44 |
| 50 | 40 | 17.78 | 33.61 | |
| 100 | 73.89 | 36.67 | 65.56 | |
| 200 | 138.33 | 66.67 | 133.06 | |
| Medium sand (D50: 0.51) | 25 | 31.94 | 6.94 | 19.44 |
| 50 | 54.72 | 12.78 | 40 | |
| 100 | 94.17 | 26.94 | 72.22 | |
| 200 | 164.72 | 49.72 | 134.72 | |
| Coarse sand (D50: 1.77) | 25 | 48.06 | 10.83 | 26.94 |
| 50 | 88.89 | 14.72 | 40.83 | |
| 100 | 118.61 | 23.89 | 90 | |
| 200 | 227.22 | 46.39 | 165 |
| Phase | Parameter | Value |
|---|---|---|
| Train and Test Sets | test_size | 0.2 |
| random_state | 0 | |
| KFold Cross-Validation | n_splits | 10 |
| random_state | 0 | |
| shuffle | True | |
| Feature Importance Estimation | n_repeats | 10 |
| Visualisation | start_point | 0 |
| boundary_shift | 20% |
| Training Database | Testing Database | 10-Fold CV | |
|---|---|---|---|
| Observations | 86 | 22 | 108 |
| MAE | 10.20 | 12.59 | 11.22 |
| RMSE | 13.79 | 14.73 | 15.16 |
| RMSLE | 0.49 | 0.88 | - |
| R² | 0.86 | 0.65 | 0.81 |
| Phase | Parameter | Value |
|---|---|---|
| Train and Test Sets | test_size | 0.2 |
| random_state | 0 | |
| KFold Cross-Validation | n_splits | 10 |
| random_state | 0 | |
| shuffle | True | |
| Model | n_estimators | 100 |
| random_state | 0 | |
| Visualisation | start_point | 0 |
| boundary_shift | 20% |
| Training Database | Testing Database | 10-Fold CV | |
|---|---|---|---|
| Observations | 86 | 22 | 108 |
| MAE | 3.20 | 4.30 | 7.16 |
| RMSE | 5.43 | 5.65 | 12.81 |
| RMSLE | 0.12 | 0.27 | 0.31 |
| R² | 0.98 | 0.95 | 0.87 |
| Multiple Linear Regression | Random Forest Regression | |||||
|---|---|---|---|---|---|---|
| Training Data | Testing Data | 10-Fold CV | Training Data | Testing Data | 10-Fold CV | |
| Observation | 86 | 22 | 108 | 86 | 22 | 108 |
| MAE | 10.20 | 12.59 | 11.22 | 3.20 | 4.30 | 7.16 |
| RMSE | 13.79 | 14.73 | 15.16 | 5.43 | 5.65 | 12.81 |
| RMSLE | 0.49 | 0.88 | - | 0.12 | 0.27 | 0.31 |
| R2 | 0.86 | 0.65 | 0.81 | 0.98 | 0.95 | 0.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daghistani, F.; Abuel-Naga, H. Advancements in Understanding Interface Friction: A Combined Experimental and Machine Learning Approach Using Multiple Linear and Random Forest Regressions. Geotechnics 2024, 4, 109-126. https://doi.org/10.3390/geotechnics4010006
Daghistani F, Abuel-Naga H. Advancements in Understanding Interface Friction: A Combined Experimental and Machine Learning Approach Using Multiple Linear and Random Forest Regressions. Geotechnics. 2024; 4(1):109-126. https://doi.org/10.3390/geotechnics4010006
Chicago/Turabian StyleDaghistani, Firas, and Hossam Abuel-Naga. 2024. "Advancements in Understanding Interface Friction: A Combined Experimental and Machine Learning Approach Using Multiple Linear and Random Forest Regressions" Geotechnics 4, no. 1: 109-126. https://doi.org/10.3390/geotechnics4010006
APA StyleDaghistani, F., & Abuel-Naga, H. (2024). Advancements in Understanding Interface Friction: A Combined Experimental and Machine Learning Approach Using Multiple Linear and Random Forest Regressions. Geotechnics, 4(1), 109-126. https://doi.org/10.3390/geotechnics4010006







