Static and Dynamic Cone Penetrometer Tests for Babolsar Sand Parameters via Physical Modeling

Abstract

Field tests are the most suitable method to determine geotechnical parameters. Owing to some restrictions in field tests, physical modeling has been widely accepted as a proper method to define mathematical correlations among geotechnical parameters. This study investigates correlations between parameters derived from cone penetrometer tests. The tests were performed in a cylindrical chamber with a height and diameter of 1000 mm to minimize the boundary effect. Coastal poorly graded sand sampled from the Babolsar region, adjacent to the Caspian Sea, was used. Some correlations among geotechnical parameters, including cone resistance, dynamic cone resistance, dynamic penetration index, modulus of elasticity, internal friction angle, and relative density, are presented. All correlations were categorized into three main categories: soil stiffness, penetration strength, and geotechnical parameters. The results had reasonable accuracy and precision. The average R² value of the obtained results was approximately 94. The investigations into the inherent CPT also indicated that the strength parameter had more accuracy than stiffness and other sand parameters. Specifically, the R² value for the correlation between the results of various penetration tests, considered strength parameters, averaged 97. In contrast, the R² value for the correlation between the elasticity modulus and cone penetration test results was 86.

1. Introduction

Soil investigations [1] are of great importance in geotechnical analysis and design. Also, the accuracy of soil characteristics has a profound effect on structural design and the prediction of a structure’s lifetime [2,3]. There are a lot of methods for determining soil characteristics, which are generally divided into three main categories. These include laboratory tests, in situ tests, and geophysical tests [4].

In situ tests provide more accurate data in comparison with the other two methods, and this is due to the evaluation of intact soil [5,6]. In other words, soil disturbance and the evaluation of limited amounts of soil samples are crucial problems in laboratory tests, and these problems have a significant effect on investigations regarding sandy soils. One of the best in situ tests is the cone penetrometer test conducted using two types of static and dynamic methods [4,7].

CPT is one of the best methods for evaluating the mechanical parameters of sandy soils [8,9,10,11]. It also has been widely used in offshore and onshore environments to characterize and investigate the behavior of soil [12,13]. There are lots of correlations between CPT results and density [14,15,16,17], elasticity module [18,19,20], friction angle [21,22,23], and other mechanical parameters of soils [24,25]. This apparatus is one of the appropriate pieces of equipment used for the estimation of soil mechanical characteristics and soil classification, using the cone resistance and the sleeve friction resistance [10,26,27]. Moreover, research has shown a direct nonlinear relationship between the normalized cone resistance and the friction angle [16]. However, the cone penetration test (CPT) device has some disadvantages, including limited availability, the need for a large space for operation, and high costs. Consequently, it is not always feasible for small projects or locations with restricted access. In such cases, simpler methods are needed to obtain the necessary parameters. One alternative is the dynamic cone penetration test (DCPT), which, due to its penetrative inherence, can somewhat replicate CPT results, particularly for shallow penetrations, making it more suitable for smaller projects.

The dynamic cone penetrometer (DCP) test is typically used to determine the California bearing ratio test (CBR) for road bases [28,29]. The DCP test can also measure the other mechanical parameters of soils, such as elastic modulus, axial compression capacity of cohesionless soils, and shear resistance [30,31]. The other advantages of this test are its small dimensions, low weight, and convenient movability. Using the results of this test, many soil strength and stiffness parameters can be accurately determined, which significantly reduces both project costs and completion time.

This research focuses on predicting the strength and stiffness parameters of sandy soils (specifically Babolsar sand) using results from cone penetration tests (CPTs), dynamic cone penetration tests (DCPs), and plate load tests. It also estimates the cone resistance from CPTs using dynamic cone penetration results. Overall, in this study, 24 physical modeling tests were conducted at four different relative densities. Laboratory tests were performed in a chamber with a diameter and height of 1000 mm to minimize boundary condition errors. To enhance sample accuracy and result repeatability, the dry deposition method was used. This study provides correlation relationships between the results of the CPT, DCPT, and PLT. Based on these test results, the strength and stiffness parameters of the sand were predicted. Finally, to validate the results, some of the findings from this research were compared with studies conducted by other researchers.

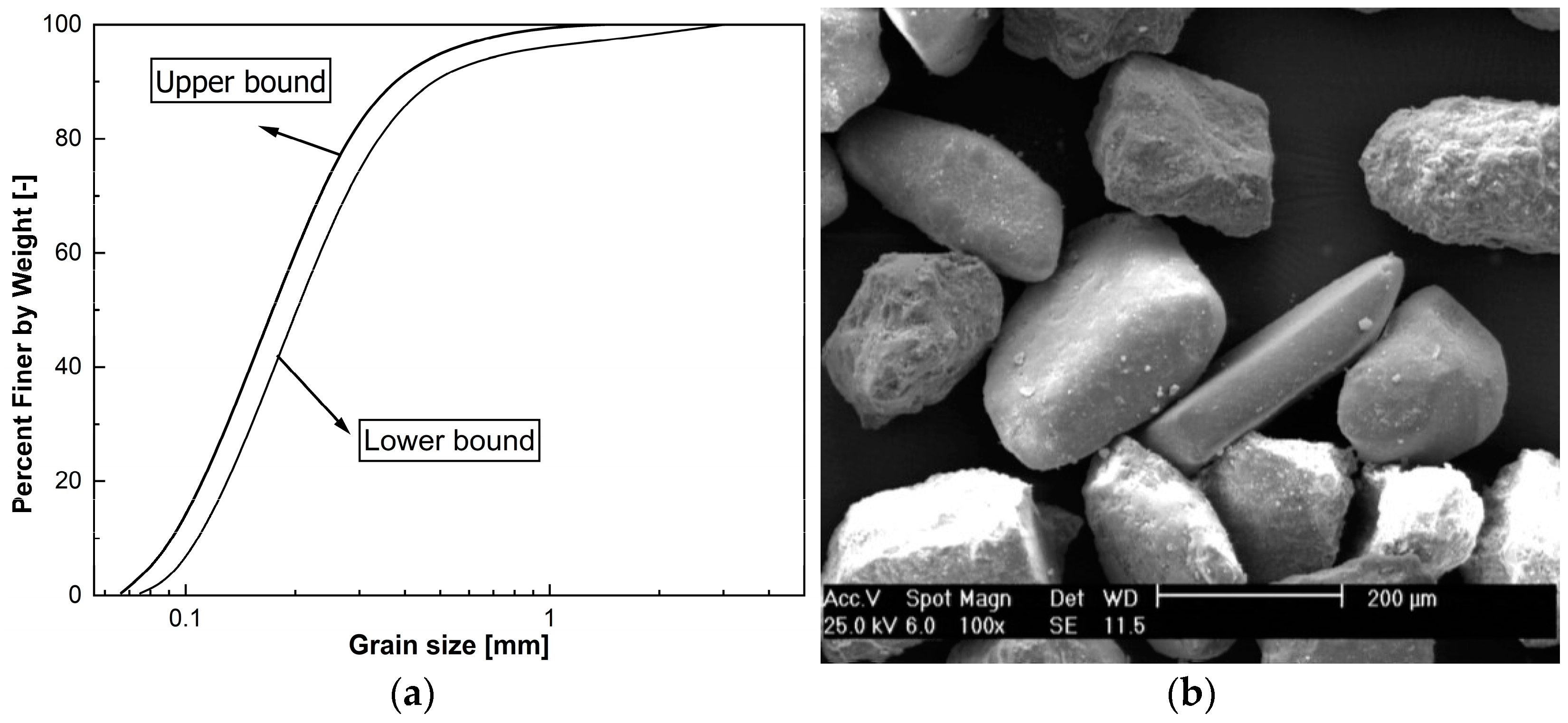
2. Materials

Babolsar sand collected from the coasts of the Caspian Sea in the north of Iran was used. Babolsar, positioned near a significant commercial port, is located at coordinates 36°42′02″ N, 52°39′00″ E, and is approximately 10 m below the free water level [32]. Regarding ASTM D6913 [33], in the unified classification method, it is classified as the SP (poorly graded soil) category. Soil sample gradation is shown in Figure 1a, and a scanning electron microscope image of sand is shown in Figure 1b. Triaxial test shear apparatus with dimensions of 7 mm produced by MTM Co. (Yangon, Myanmar) was used to measure the internal friction angle of sand, in which the friction angles were 29, 32.5, 36.5, and 41.2 degrees for loose (${\mathrm{D}}_{\mathrm{r}}\approx 20\%$), medium-dense (${\mathrm{D}}_{\mathrm{r}}\approx 40\%$), dense (${\mathrm{D}}_{\mathrm{r}}\approx 60\%$), and very dense (${\mathrm{D}}_{\mathrm{r}}\approx 85\%$) soil, respectively. Other soil parameters are also listed in

Table 1. The index properties of Babolsar sand.

Parameter	Value	Standard Reference
${\mathrm{D}}_{50} \left(\mathrm{mm}\right)$ 1	0.18	ASTM D6913 [33]
${\mathrm{e}}_{\max } \left(-\right)$ 2	0.876	ASTM D4253 [34]
${\mathrm{e}}_{\min }\left(-\right)$ 3	0.637	ASTM D4254 [35]
${\mathrm{\gamma }}_{\mathrm{d},\max } \left({\displaystyle \raisebox{1ex}{$\mathrm{kN}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{m}}^3$}\right.}\right)$ 4	17.0	ASTM D4254 [35]
${\mathrm{\gamma }}_{\mathrm{d},\min } \left({\displaystyle \raisebox{1ex}{$\mathrm{kN}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{m}}^3$}\right.}\right)$ 5	14.82	ASTM D4253 [34]
${\mathrm{G}}_{\mathrm{s}} \left(-\right)$ 6	2.78	ASTM D854 [36]
${\mathrm{C}}_{\mathrm{u}} \left(-\right)$ 7	1.22	ASTM D6913 [33]
${\mathrm{C}}_{\mathrm{c}} \left(-\right)$ 8	1.67	ASTM D6913 [33]
${\omega }_{\mathrm{opt}} \left(\%\right)$ 9	11	ASTM D698 [37]

¹ Diameter for 50% finer by weight, ² maximum void ratio, ³ minimum void ratio, ⁴ maximum dry density, ⁵ minimum dry density, ⁶ specific gravity, ⁷ coefficient of uniformity, ⁸ coefficient of curvature, ⁹ optimum water content.

.

3. Methods

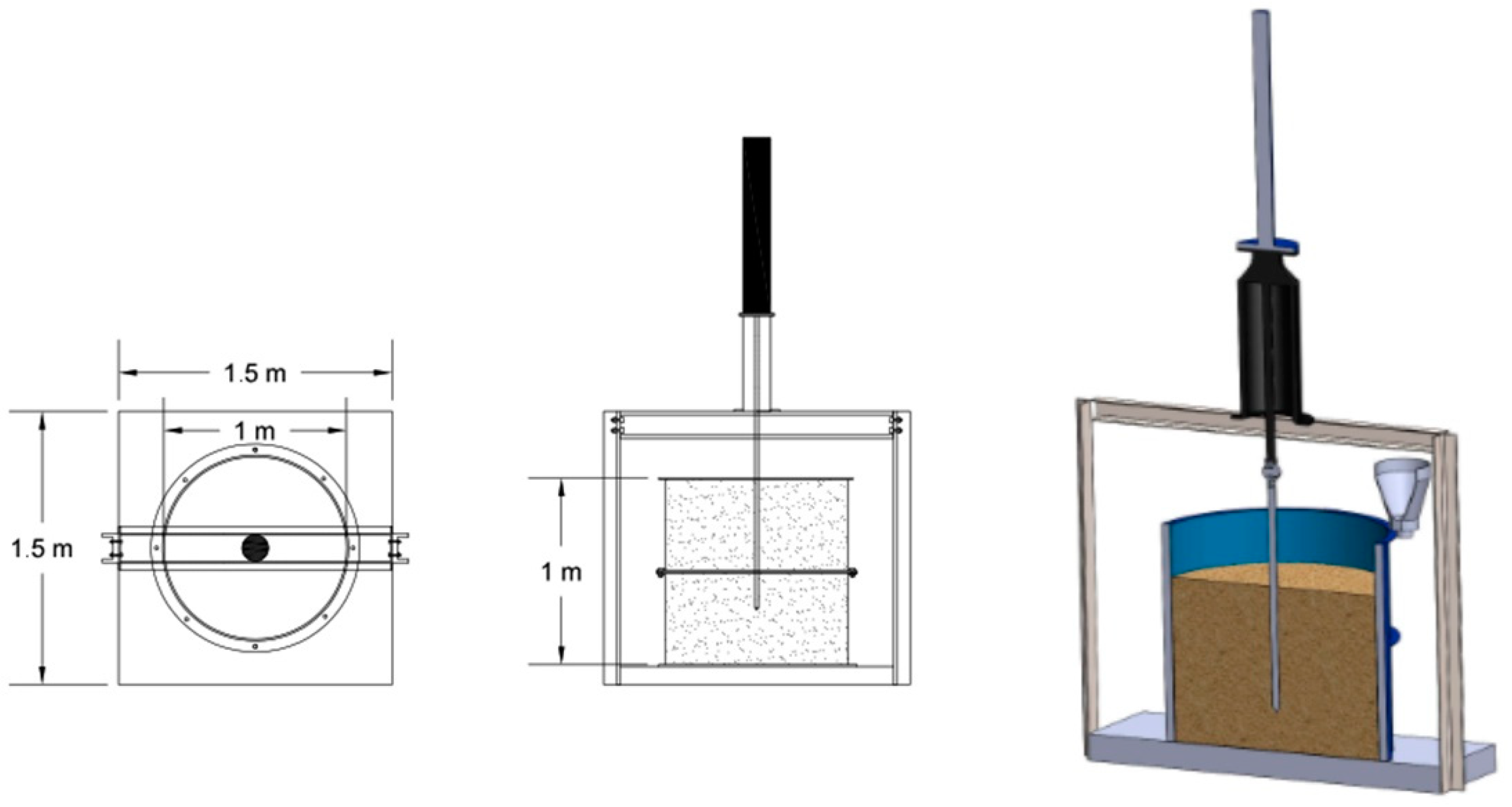
3.1. Soil Preparation and 1 g Chamber

The tests were carried out in a simple chamber (1 g) with a diameter and a height of 1000 mm. It was made of steel with several stiffeners to have a rigid wall (Figure 2). Since the boundary condition is a paramount factor in the finite element and physical modeling, the diameter of the chamber was designed and built large enough to minimize the boundary condition effect [30,38]. Abu-Farsakh et al. determined that a minimum distance of 225 mm between the cone and the edge of the testing chamber is necessary to mitigate the effects of the mold’s side walls [28]. Mohammadi et al. further observed that, as the relative density (Dr) increases, the influence of the side walls becomes more pronounced. However, this effect becomes negligible in molds with a diameter exceeding 500 mm. Additionally, maintaining a 250 mm distance between the cone and the mold edge is sufficient to completely eliminate the boundary condition effect [38].

The samples were constructed using the dry sedimentation method. In this method, the sand sample retains its natural moisture and is assumed to be dry [39,40]. Thus, first, the soil weight for specific density was measured for a height of 5 cm. Next, the soil was weighed and poured into a funnel. The funnel’s tip had a fixed level from the sample surface. Then, the valve located at the funnel’s end was opened, and the soil started pouring into the chamber, as illustrated in Figure 3a. In low densities, fixing the funnel’s height/level from the sample’s surface was enough for constructing the soil sample. However, it was required to compact the soil sample in higher densities after the pouring process. The soil compaction process was performed by placing lumber 15 mm thickness on the soil sample and ramming it until the considered soil density was reached, as shown in Figure 3b. As presented in Figure 3c; to have an accurate density, it is essential to check the soil level during the compaction process. Afterward, all aforementioned steps were repeated to add new layers to the sample. The new layers were added to reach the desired height of the soil sample, which was 1000 mm.

3.2. Laboratory Investigations (CPT, DCP, and PLT)

The laboratory investigations conducted in this study were divided into two main categories, including physical modeling in a 1g chamber and small-scale soil test investigations. The executed physical modeling consisted of static CPT, dynamic CPT, and a plate load test (PLT). The element test investigations consisted of relative soil density determination tests, triaxial tests, and specific gravity of soil solids. All the tests were performed at least two times to verify the process and results.

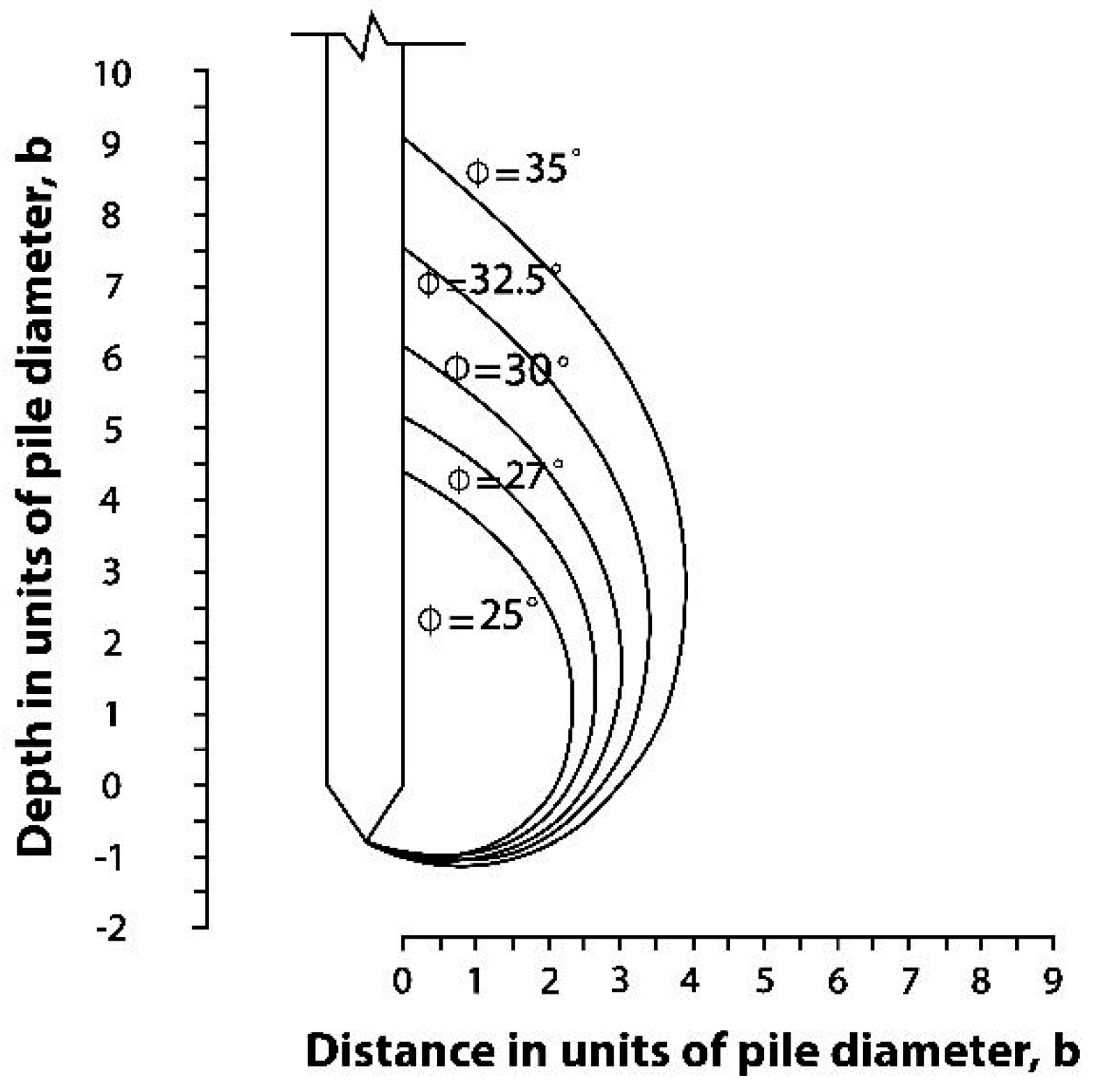
3.2.1. Static Cone Penetration Test (CPT)

According to ASTM D5778 [41], the static cone penetrometer consisted of a cone with a cross area of 1000 mm² (35.7 mm diameter) and a frictional part with an area of 15,000 mm². This device penetrates soil at a constant pace of 20 mm/s, produced by a hydraulic jack with a 1000 mm stroke. Then, the cone resistance and sleeve frictional resistance are measured continuously using existing sensors at constant time intervals.

The cone, which was used in this research, was constructed based on the ASTM D5778 [41] standard and consisted of four main parts, including the friction sleeve, inner part, conical tip, and the guiding bar. The conical tip and the sleeve part are in contact with the soil; thus, they were constructed of 420 stainless steels with high abrasion resistance and high enduring ability from corrosion. The inner part was built from 7075 aluminum for its high elasticity module and low-yielding stress point. This type of aluminum characteristic makes it capable of tolerating considerable strain, and this feature increases the accuracy of sensing and measurements. The cone-bearing capacity and sleeve friction resistance were measured separately using strain gauges at two height levels. Four different strain gauges were mounted at each point to increase the accuracy of the data reading. Two vertical and two horizontal strain gauges had 180 inclinations in relevance to each other, and they were attached to the inner bar. During calibration, the sensors showed completely linear responses, with a reading sensitivity of 2 N. The penetration depth was measured with a depth gauge accurate to 0.1 mm, ensuring minimal measurement error. The strain gauges’ attachment points and the CPT schematic shape are shown in Figure 4.

3.2.2. Dynamic Cone Penetration Test (DCP)

Dynamic CPT is one of the most practical tests for road construction works and the determination of soil parameters in shallow penetration (1–2 m). Regarding the ASTM D6951 [42] standard, it consists of a cone with a 20 mm diameter with a tip angle of 60 degrees with respect to the horizon. This device penetrates the soil using an 8 kg hammer, which falls from a height of 575 mm and has 45 J theoretical driving energy. A bar with a 16 mm diameter was used to convey the whole hammer’s energy to the cone and reduce the soil-bar interaction effect in the penetration process [38].

The diameter of the chamber may cause some errors in the simulation process for a boundary condition effect; thus, a chamber with a diameter of 1000 mm was chosen to minimize the boundary condition effect as it is the best diameter for this type of sandy soil. Some researchers reported that, with an increase in the soil density ratio, there is an increase in the required diameter of the chamber for simulation [28,38]. However, 500 mm is the minimum required diameter for minimizing the boundary condition effect. In this test, the results are indicated with a factor named the dynamic penetration index (DPI), which is equal to the penetration depth per specific blow [43].

$$\mathrm{DPI}={\displaystyle \frac{{\mathrm{P}}_{\mathrm{i}+1}-{\mathrm{P}}_{\mathrm{i}}}{{\mathrm{B}}_{\mathrm{i}+1}-{\mathrm{B}}_{\mathrm{i}}}}$$

(1)

where DPI = DCP index (${\displaystyle \raisebox{1ex}{$\mathrm{mm}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{blow}$}\right.}$), P = penetration at i or i + 1 hammer drops (mm), and B = blow count. The weighted averaging method, which could be considered one of the best averaging methods, was utilized to calculate the DCP results at each level and determine soil parameters. It is formulated as follows:

$${\mathrm{DPI}}_{\mathrm{ave}}={\displaystyle \frac{1}{\mathrm{H}}}{\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{i}=\mathrm{n}}\left[{\left(\mathrm{DPI}\right)}_{\mathrm{i}}\times {\left(\mathrm{Z}\right)}_{\mathrm{i}}\right]$$

(2)

where Z is the penetration distance per blow set and H is the overall penetration depth of interest. Furthermore, another functional method for analyzing DCP data is converting it to the dynamic tip resistance (dynamic cone resistance, ${\mathrm{q}}_{\mathrm{d}}$). The amount of cone penetration energy directly relates to the hammer ramming energy; hence, if this energy is enough, the soil will fail, and the cone will penetrate. The penetration depth for each hammer ramming is a function of soil stiffness. The hammer’s ramming energy could be calculated by knowing that the hammer’s weight and fall height are constant and determined. Therefore, the penetration depth would decrease with soil stiffness and density increment. The tip’s dynamic resistance (${\mathrm{q}}_{\mathrm{d}}$) in the sandy soils was a function of the test condition and apparatus geometry. The Dutch formula is commonly used for the calculation of ${\mathrm{q}}_{\mathrm{d}}$ [44]:

$${\mathrm{q}}_{\mathrm{d}}={\displaystyle \frac{1}{\mathrm{A}}}\times \left({\displaystyle \frac{\mathrm{KE}}{\mathrm{X}}}\right)\times \left({\displaystyle \frac{\mathrm{M}}{\mathrm{M}+\mathrm{P}}}\right)$$

(3)

where A = cross-sectional area of the cone, KE = imparted kinetic energy, X = incremental penetration (${\displaystyle \raisebox{1ex}{$\mathrm{mm}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{blow}$}\right.}$), M = mass of the hammer, and P = mass of the penetrometer.

3.2.3. Plate Load Test

The plate load test was utilized to measure the soil’s bearing capacity. The PLT results, which are helpful for shallow foundation design, represent the soil’s bearing capacity and determine its compressibility. They could also be used to evaluate flexible and rigid pavements. The direct result of this test is the load-movement curve, which is drawn from measurements of the load on a rigid plate and its movement at pre-determined levels. The base reaction coefficient and elastic modulus of soil can be derived from the load-movement curve by using the theory of elasticity [18].

One of the most important deformability parameters that is highly useful for designing shallow foundations in structures and road construction projects is the elastic modulus. It is common to derive this parameter using the plate load test results [45,46]. The elastic modulus is defined as the slope of the (initial) linear part of the vertical stress–settlement curve derived from PLT.

According to ASTM D1195 [47], the plate should behave as a rigid body, so standards recommend a minimum plate thickness of 1 inch (25.4 mm). Its diameter should also be in the range of 6 to 30 inches (152–762 mm). In this study, a steel plate with a 250 mm diameter and 24.5 mm thickness was used. The load was applied to the plate using a 150 KN hydraulic jack. The applied load and plate movement were measured with an S-shaped load cell placed under the hydraulic jack and three-micrometer gauges with 0.001 mm accuracy, respectively. The micrometer gauges were placed at a 120-degree angle with respect to one another on the plate load.

4. Results

In this section, the derived results from the abovementioned experiments are compared and evaluated. Finally, the relationship or correlations between different mechanical characteristics of Babolsar sand is presented.

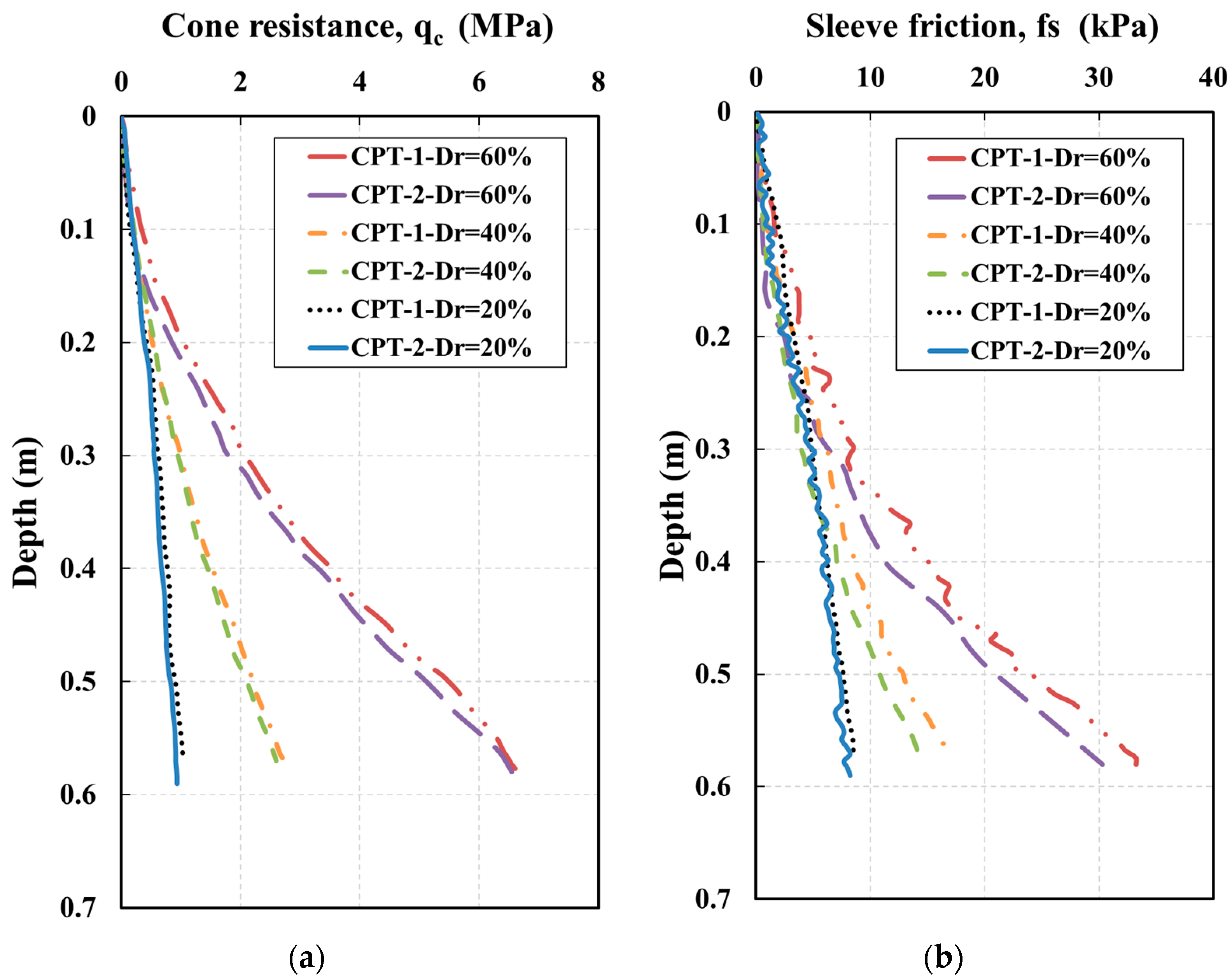
4.1. Repeatability of Tests

Several tests were performed to ensure the potential for repeatability and accuracy of the results. In this study, the static cone penetrometer test in different densities was performed twice, and the results were acceptable; therefore, it was considered to have high repeatability (Figure 5).

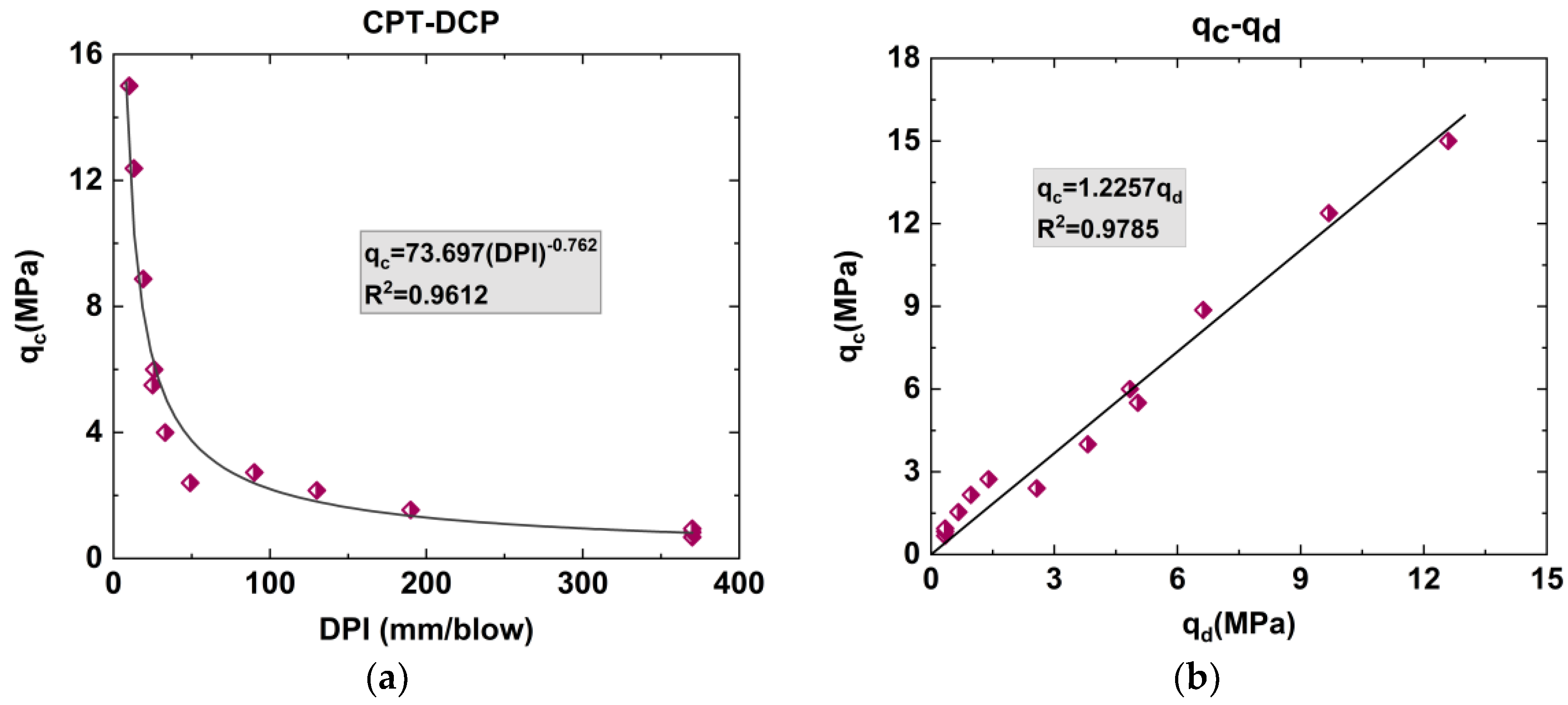
4.2. CPT Cone Resistance ($q_c$) vs. DCP Cone Resistance ($q_d$) and DCP Penetration Index (DPI)

One of the best approaches for determining soil strength parameters and soil layer profiles in sandy soils is the cone penetrometer test. However, DCP is a practical choice since it can be used in less accessible areas and is inexpensive. Due to its applicability and benefits, finding correlations between CPT and DCP results has attracted researchers’ attention. These correlations may help engineers and researchers to find desired geotechnical parameters of sands and help them to better predict their behavior. There was a non-linear relationship between these two parameters, and the value of q_c decreases with an increase in DPI. High DPI values in low-density sands are expected because, at low relative densities, the larger voids between particles reduce their interaction, leading to lower sand resistance to penetration. This leads to lower sand resistance against penetration, causing a greater penetration depth with each strike of DCP. On the other hand, in high-density soils, a significant change in soil density is not expected upon the initial strike of DCP. Thus, low DPI values could be justified in dense soils, i.e., the ${\mathrm{q}}_{\mathrm{c}}$-DPI correlation could be defined as a typical reciprocal function (Figure 6a).

Da Fonseca introduced the Ke factor value as a ratio of ${\mathrm{q}}_{\mathrm{c}}$ to ${\mathrm{q}}_{\mathrm{d}}$ [45]:

$${\mathrm{K}}_{\mathrm{e}}={\displaystyle \frac{{\mathrm{q}}_{\mathrm{c}}}{{\mathrm{q}}_{\mathrm{d}}}}$$

(4)

The ${\mathrm{K}}_{\mathrm{e}}$ values proposed by different researchers are listed in Table 2:

Table 2. Summary of correlation between q_d and q_c in earlier studies.

Reference	${\mathbf{K}}_{\mathbf{e}}$
Da Fonseca [48]	1
Dos Santos and Bicalho [49]	1.3–2.5
Rios et al. [50]	0.87–1.85
Kodicherla and Nandyala [51]	1.12

Table 2. Summary of correlation between q_d and q_c in earlier studies.

Reference	${\mathbf{K}}_{\mathbf{e}}$
Da Fonseca [48]	1
Dos Santos and Bicalho [49]	1.3–2.5
Rios et al. [50]	0.87–1.85
Kodicherla and Nandyala [51]	1.12

$${\mathrm{q}}_{\mathrm{c}}=73.70\times {\mathrm{DPI}}^{-0.762}$$

(5)

$${\mathrm{q}}_{\mathrm{c}}=1.225\times {\mathrm{q}}_{\mathrm{d}}$$

(6)

As shown in Figure 6, the results of both tests had a strong correlation with a high coefficient of determination (R²). This was due to the fact that both tests were penetration-type tests, and in both of them, the soil shear bands formed completely during the penetration. In other words, both of them had the same nature. Where DPI = DCP index (${\displaystyle \raisebox{1ex}{$\mathrm{mm}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{blow}$}\right.}$), ${\mathrm{q}}_{\mathrm{c}}$ = cone resistance (MPa), and ${\mathrm{q}}_{\mathrm{d}}$ = dynamic cone resistance (MPa). As shown in Figure 6, the results of both tests had a strong correlation with a high coefficient of determination (R²). This was due to the fact that both tests were penetration-type tests, and in both of them, the soil shear bands formed completely during the penetration. In other words, both of them had the same nature.

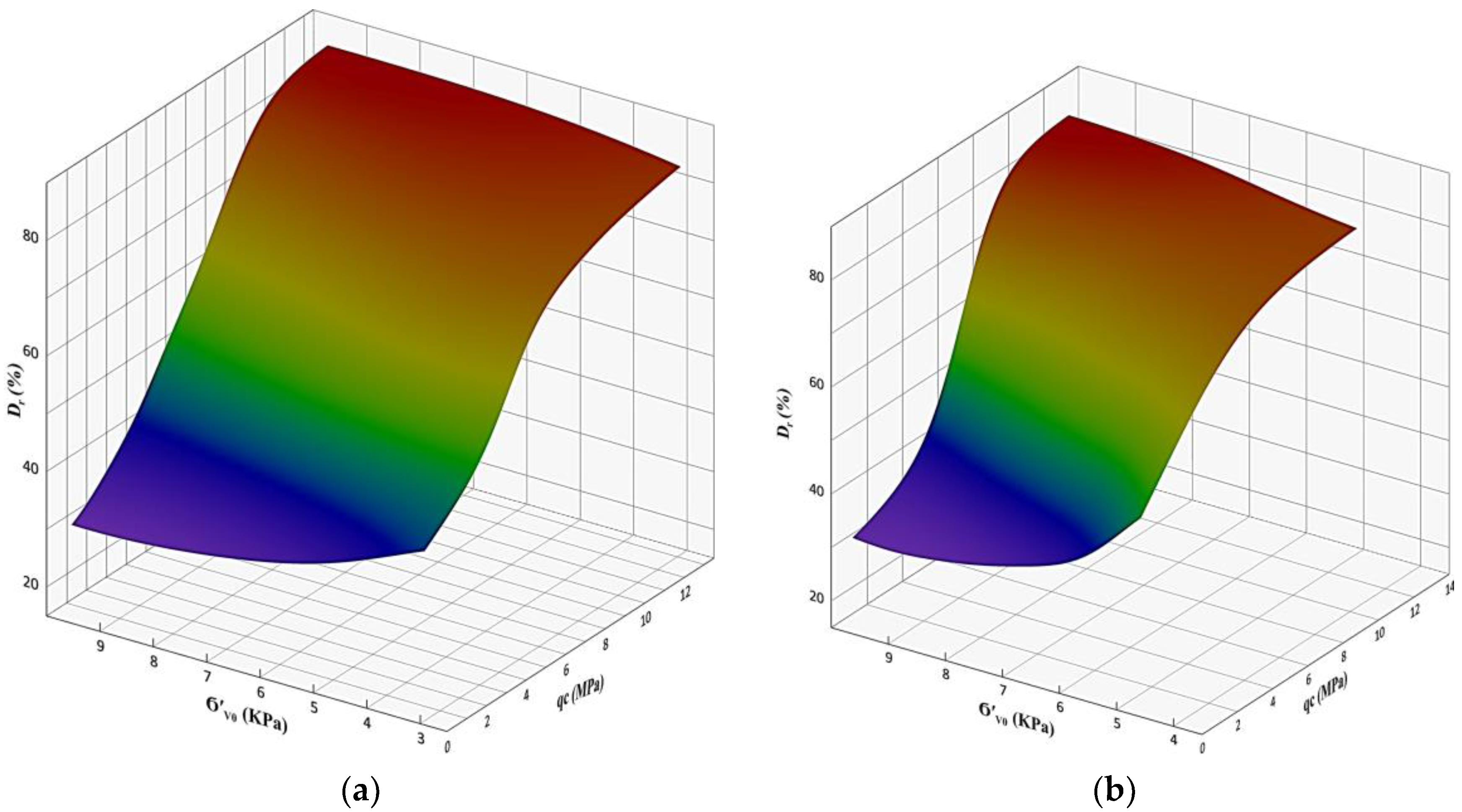
4.3. Relative Density (Dr (%)) vs. CPT Cone Resistance ($q_c$) and DCP Cone Resistance ($q_d$)

Relative density is one of the most paramount and very applicable strength parameters of sands as it has a direct impact on soil direct shear strength. Moreover, the CPT is a common and applicable method for determining the relative density of sandy soils. Most studies have shown the logarithmic relationship between the two parameters. Schmertmann introduced the correlation between Dr and ${\mathrm{q}}_{\mathrm{c}}$ [52]:

$$\mathrm{Dr}\left(\%\right)={\displaystyle \frac{100}{{\mathrm{C}}_2}}\ln \left({\displaystyle \frac{{\mathrm{q}}_{\mathrm{c}}\left(\mathrm{MPa}\right)}{{\mathrm{C}}_0{\left({\mathrm{\sigma }}_{\mathrm{vc}}^{\prime }\right)}^{{\mathrm{C}}_1}}}\right)$$

(7)

where ${\mathrm{C}}_0,{ \mathrm{C}}_1,{\mathrm{and} \mathrm{C}}_2$ are empirical fitting parameters, and ${\mathrm{\sigma }}_{\mathrm{vc}}^{\prime }$ = initial effective vertical stress. Many studies have been carried out to determine the values of these factors in calibration chambers. Some of them are listed in

Table 3. Summary of correlation parameters suggested by earlier studies for fitting Equation (7).

Sand	${\mathbf{C}}_0$	${\mathbf{C}}_1$	${\mathbf{C}}_2$	Reference
Several NC sands	2.91	0.700	0.050	[52]
Ticino	2.41	0.550	0.157
Hokksund	3.29	0.530	0.086
Ticino	2.90	0.550	0.140	[53]
Ticino, Toyoura, Hokksund	3.10	0.500	0.175
Ottawa sand	2.55	0.612	0.119	[54]

:

Regarding the results of this research, the C₀, C₁, and C₂ values were 0.025, 1.37, and 3.9, respectively (Figure 7a). The proposed correlation is reasonably accurate; thus, the difference in the values of the factors from previous researchers’ investigations is justifiable because of the difference in soil structure.

Equation (8) calculates the Dr value from ${\mathrm{q}}_{\mathrm{d}}$. This correlation is the same as the Dr–${\mathrm{q}}_{\mathrm{c}}$ correlation, and only constant multiplying factors have different values. The proposed C₀, C₁, and C₂ values in this equation are 0.021, 0.85, and 5.28, respectively (Figure 7b).

$$\mathrm{Dr}\left(\%\right)={\displaystyle \frac{100}{5.28}}\ln \left({\displaystyle \frac{{\mathrm{q}}_{\mathrm{d}}\left(\mathrm{MPa}\right)}{0.021{\left({\mathrm{\sigma }}_{\mathrm{vc}}^{\prime }\right)}^{0.85}}}\right)$$

(8)

4.4. Comparisons and Discussions

In order to verify the accuracy of the results, static and dynamic cone penetration tests were performed, and the results of these two tests were compared with the values of the modulus of elasticity obtained from the plate load test. The comparison of the results is presented in the following three separate sections.

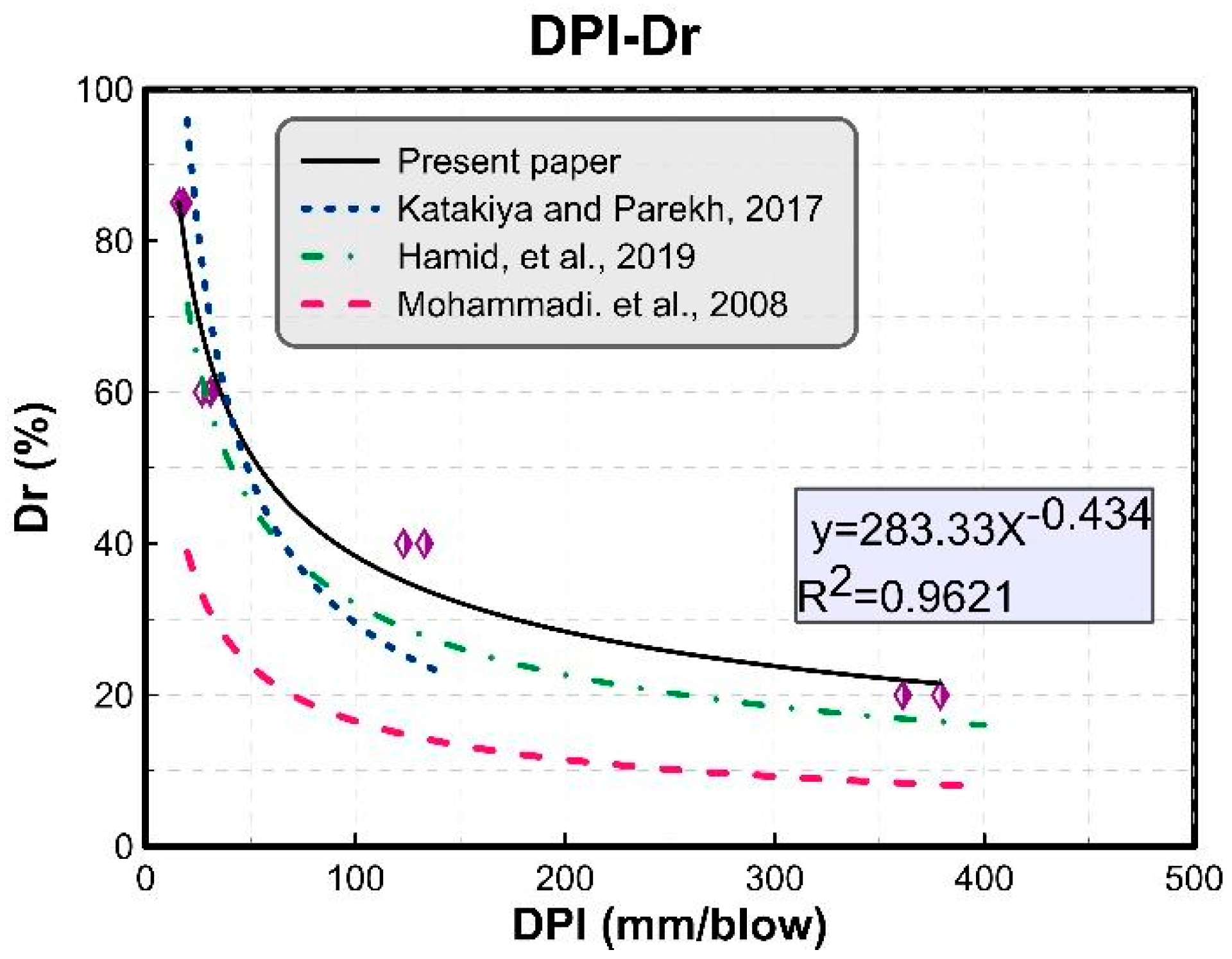
4.5. Comparisons, DCP Penetration Index (DPI) versus Relative Density (Dr %)

As mentioned above, the relative density has a direct relation with the direct shear test result in sands. The cone penetration value per hit is also a function of the shear strength of sands. Thus, the cone penetration value per hit (DPI factor) is dependent on Dr, and these two parameters have an inverse relationship [38,55,56]. Figure 8 shows the correlation curve derived from this research (Equation (9)).

$$\mathrm{Dr}\left(\%\right)=283.33\times {\left(\mathrm{DPI}\right)}^{-0.0434}$$

(9)

4.6. Friction Angle ($\phi$) versus CPT Cone Resistance ($q_c$) and DCP Cone Resistance ($q_d$)

Several investigations have been conducted by previous researchers to determine the soil internal friction angle of clean sands, and the basis of all these methods is the bearing capacity theory, cavity expansion theory, and empirical methods, which are based on calibration chamber tests. Most of these correlations are empirical and derived from laboratory tests on the calibration chamber [9]. Many correlations have been introduced to find internal friction angles from ${\mathrm{q}}_{\mathrm{c}}$ so far [22].

The general failure in soil could be formulated by assuming logarithmic spiral failure zones and is represented by the following expression (Equation (10)) [10]:

$$\mathrm{r}={\mathrm{r}}_0{\left(\mathrm{e}\right)}^{\mathrm{\theta }\mathrm{tng}\mathrm{\phi }}$$

(10)

where ${\mathrm{r}}_0$ is the radius of the logarithmic spiral for $\mathrm{\theta }=0$ (assumed equal to the penetrometer diameter), $\mathrm{\theta }$ is the angle between a radius and ${\mathrm{r}}_0$, and $\mathrm{\phi }$ is the angle between the radius and the normal at that point on the spiral (assumed equal to the friction angle of the soil).

Figure 9 depicts the rupture surface with different soil’s internal friction angles, $\mathrm{\phi }$. A higher $\mathrm{\phi }$ would require higher shear force and would have a higher rupture surface. Therefore, the internal friction angle of soil has an effect and correlation with the tip cone resistance.

Some correlations between $\mathrm{\phi }$ and ${\mathrm{q}}_{\mathrm{c}}$ are presented in

Table 4. Summary of correlation between $\mathrm{\phi }$ and ${\mathrm{q}}_{\mathrm{c}}$ by earlier studies.

Reference	Equation
[9]	$$\tan \left({\mathrm{\phi }}^{\prime }\right)={\displaystyle \frac{1}{2.62}}\left(\log {\displaystyle \frac{{\mathrm{q}}_{\mathrm{c}}}{{\mathrm{\sigma }}_{\mathrm{v}0}^{\prime }}}+0.29\right)$$
[57]	$${\mathrm{\phi }}^{\prime }=17.6+11\log {\mathrm{q}}_{\mathrm{t}1}$$
[58]	$${\mathrm{\phi }}^{\prime }={25}^{°}\times {\left({\mathrm{q}}_{\mathrm{t}1}\right)}^{0.1}$$
[59]	$${\mathrm{\phi }}^{\prime }=9^{°}+6.25\ln \left({\displaystyle \frac{{\mathrm{q}}_{\mathrm{t}}}{{\mathrm{\sigma }}_{\mathrm{h}0}^{\prime }}}\right)$$
[60]	$${\mathrm{\phi }}^{\prime }={15.6}^{°}\times {\left({\displaystyle \frac{{\mathrm{q}}_{\mathrm{t}}}{{\mathrm{\sigma }}_{\mathrm{h}0}^{\prime }}}\right)}^{0.171}$$
[61]	$${\mathrm{q}}_{\mathrm{c}}=\left[\left({\mathrm{N}}_{\mathrm{q}}-1\right)\left({\mathrm{\sigma }}_{\mathrm{v}0}^{\prime }+{\displaystyle \frac{{\mathrm{C}}^{\prime }}{\tan {\mathrm{\phi }}^{\prime }}}\right)\right]+{\mathrm{\sigma }}_{\mathrm{v}0}$$
[20]	$$\begin{gathered} \mathrm{C}+0.000780\left(1-\sin \mathrm{\phi }\right){\mathrm{\sigma }}_{\mathrm{vc}}^{\prime }\tan \left({\displaystyle \frac{2}{3}}\mathrm{\phi }\right)\left[{\displaystyle \frac{{\mathrm{q}}_{\mathrm{c}}-\left(\frac{{\mathrm{\sigma }}_{\mathrm{v}0}-2{\mathrm{\sigma }}_{\mathrm{h}0}}{3}\right)}{\left(\frac{{\mathrm{\sigma }}_{\mathrm{v}0}^{\prime }-2{\mathrm{\sigma }}_{\mathrm{h}0}^{\prime }}{3}\right)}}\right]={\mathrm{f}}_{\mathrm{s}} \\ \left({\tan }^2\left({\displaystyle \frac{\mathrm{\pi }}{4}}+{\displaystyle \frac{\mathrm{\phi }}{2}}\right){\mathrm{e}}^{\mathrm{\pi }\mathrm{an}\mathrm{\phi }}-1\right)\mathrm{C}\times \cot \mathrm{\phi }+\overline{\mathrm{q}}\times {\tan }^2\left({\displaystyle \frac{\mathrm{\pi }}{4}}+{\displaystyle \frac{\mathrm{\phi }}{2}}\right){\mathrm{e}}^{\mathrm{\pi }\mathrm{an}\mathrm{\phi }} \\ +\mathrm{\gamma }\mathrm{B}\left[{\tan }^2\left({\displaystyle \frac{\mathrm{\pi }}{4}}+{\displaystyle \frac{\mathrm{\phi }}{2}}\right){\mathrm{e}}^{\mathrm{\pi }\mathrm{an}\mathrm{\phi }}+1\right]\tan \mathrm{\phi }={\mathrm{q}}_{\mathrm{E}}+{\mathrm{N}}_{\mathrm{u}}\Delta \mathrm{U} \end{gathered}$$

${\mathrm{N}}_{\mathrm{q}}=\left({\displaystyle \frac{{\mathrm{q}}_{\mathrm{c}}-{\mathrm{\sigma }}_{\mathrm{v}0}}{{\mathrm{\sigma }}_{\mathrm{v}0}^{\prime }}}\right)+1$: bearing capacity factor, ${\mathrm{q}}_{\mathrm{t}1}={\displaystyle \frac{\raisebox{1ex}{${\mathrm{q}}_{\mathrm{t}}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{P}}_{\mathrm{atm}}$}\right.}{{\left(\raisebox{1ex}{${\mathrm{\sigma }}_{\mathrm{v}0}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{P}}_{\mathrm{atm}}$}\right.\right)}^{0.5}}}$: Stress-normalized cone resistance, ${\mathrm{\sigma }}_{\mathrm{v}0}^{\prime }$: effective vertical stress, ${\mathrm{\sigma }}_{\mathrm{v}0}$: total vertical stress, ${\mathrm{\sigma }}_{\mathrm{h}0}$: total horizontal stress, ${\mathrm{\sigma }}_{\mathrm{h}0}^{\prime }$: effective horizontal stress, ${\mathrm{P}}_0$: effective surcharge stress, ${\mathrm{q}}_{\mathrm{c}}$: measurement cone resistance, ${\mathrm{q}}_{\mathrm{t}}$: total cone tip resistance, and ${\mathrm{q}}_{\mathrm{c}\left(\mathrm{MCPT}\right)}$: measurement cone resistance for a cone with $2{ \mathrm{cm}}^2$ area.

. These correlations were derived from finite element simulations and laboratory and field test data, and most were based on physical modeling tests.

The suggested equation is plotted and presented in Figure 10a. The suggested curves by previous researchers were used to verify the presented results [57,58].

Also, Figure 10b shows the internal friction angle of soil versus the normalized cone resistance of DCP (${\mathrm{q}}_{\mathrm{d}1}$). As can be seen, there is a logarithmic correlation between these two parameters. The normalized cone resistance of the dynamic cone penetrometer (DCP) was determined in the same way as the normalized cone resistance of CPT (Equations (11) and (12)).

$$\mathrm{\phi }={14.069}^{°}+4.977\ln \left({\mathrm{q}}_{\mathrm{t}1}\right)$$

(11)

$$\mathrm{\phi }={19.756}^{°}+3.603\ln \left({\mathrm{q}}_{\mathrm{d}1}\right)$$

(12)

${\mathrm{q}}_{\mathrm{d}1}={\displaystyle \frac{\raisebox{1ex}{${\mathrm{q}}_{\mathrm{t}}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{P}}_{\mathrm{atm}}$}\right.}{{\left(\raisebox{1ex}{${\mathrm{\sigma }}_{\mathrm{v}0}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{P}}_{\mathrm{atm}}$}\right.\right)}^{0.5}}}$: Stress-normalized dynamic cone resistance.

During cone penetration tests, data is continuously collected, and tip resistance is affected by the effective vertical stress, which changes with depth. For this reason, the cone resistance in the equation is normalized relative to the vertical stress. Therefore, the friction angle was determined using cone penetration test data from depths where stress measurement sensors were positioned. This approach was selected because the vertical and horizontal stress measurements at these depths were more accurate, while interpolation was required for other locations. As a result, the data points on the graph were fewer in number and spaced out.

4.7. Friction Angle versus DCP Penetration Index (DPI)

The shear strength of the soil is dependent on the internal friction angle, and there is a direct relation between these two [62,63,64]. The value of cone resistance in DCP will increase with an increment in soil shear strength. Therefore, there is a reverse correlation between DPI and φ [38,55]. The best-proposed correlation between these parameters, which was derived from this research, is presented in Figure 11 (Equation (13)):

$$\mathrm{\phi }=53.841\times {\left(\mathrm{DPI}\right)}^{-0.105}$$

(13)

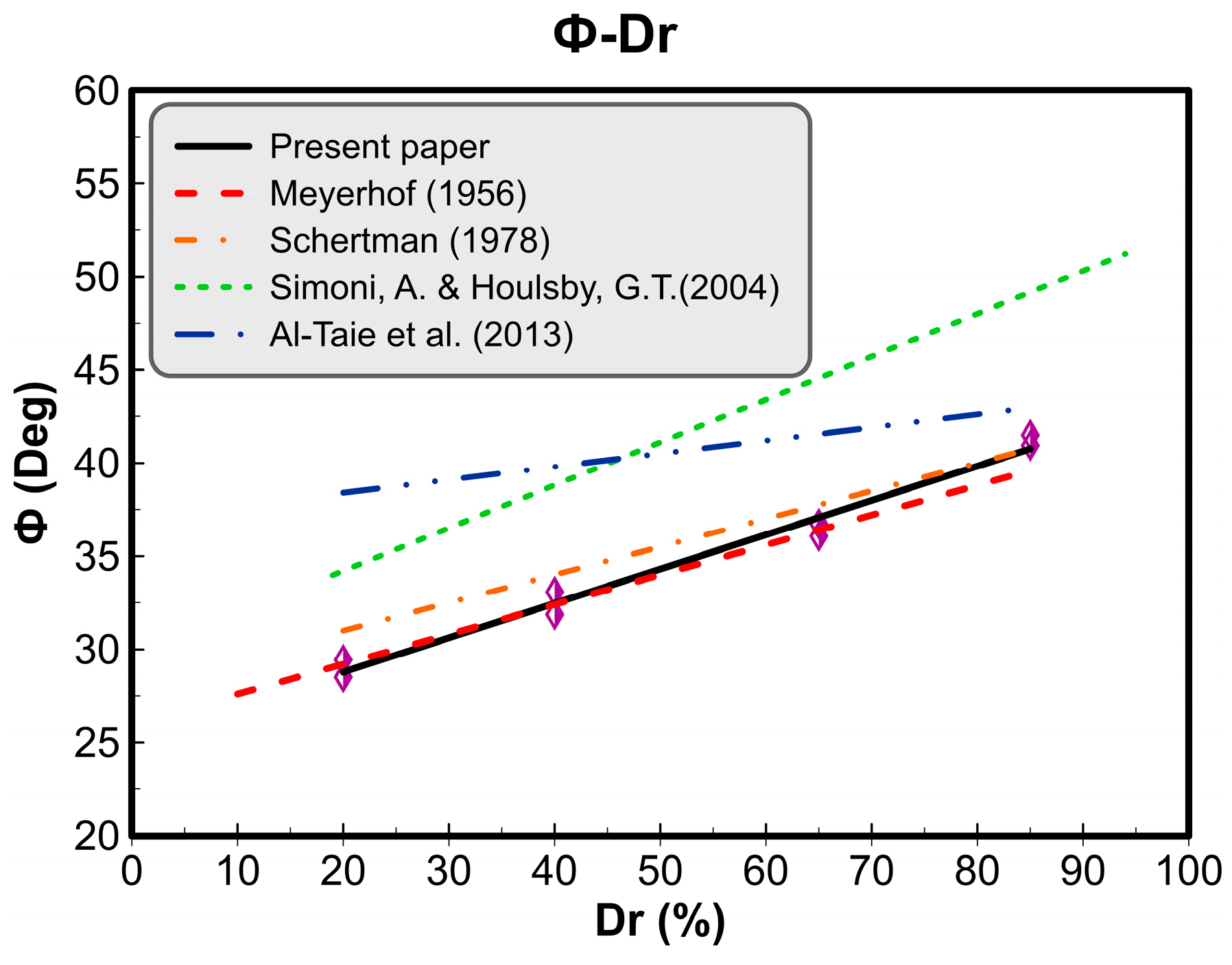
4.8. Friction Angle versus Relative Density (Dr (%))

The internal friction angle of sands is highly dependent on the interaction between soil particles [65,66]. The friction angle of granular soil is not a material constant, but depends on the relative density and pressure level [67,68]. Moroto defined the peak $\mathrm{\phi }$ (at failure) of soil as a function of “granular material characteristics” and “particle characteristics” [69]. Granular material characteristics are generally related to relative density (Dr). Particle characteristics mainly represent the intrinsic characteristics of soil particles, such as roundness R and the uniformity of the particles.

Hence, there is a direct relationship between φ and Dr %. The proposed correlation by previous investigations, which were based on empirical data, has a linear relationship of $\mathrm{\phi }=\mathrm{a}+\mathrm{bDr}$ proposed by Schmertmann [52], Simoni and Houlsby [70], Meyerhof [71], Al-Taie et al. [72], and Mohammadi et al. [38].

The suggested correlation based on the test results in this study was also linear. Figure 12 shows different correlations and their values (Equation (14)).

$$\mathrm{\phi }=0.184\times \mathrm{Dr}+25.09$$

(14)

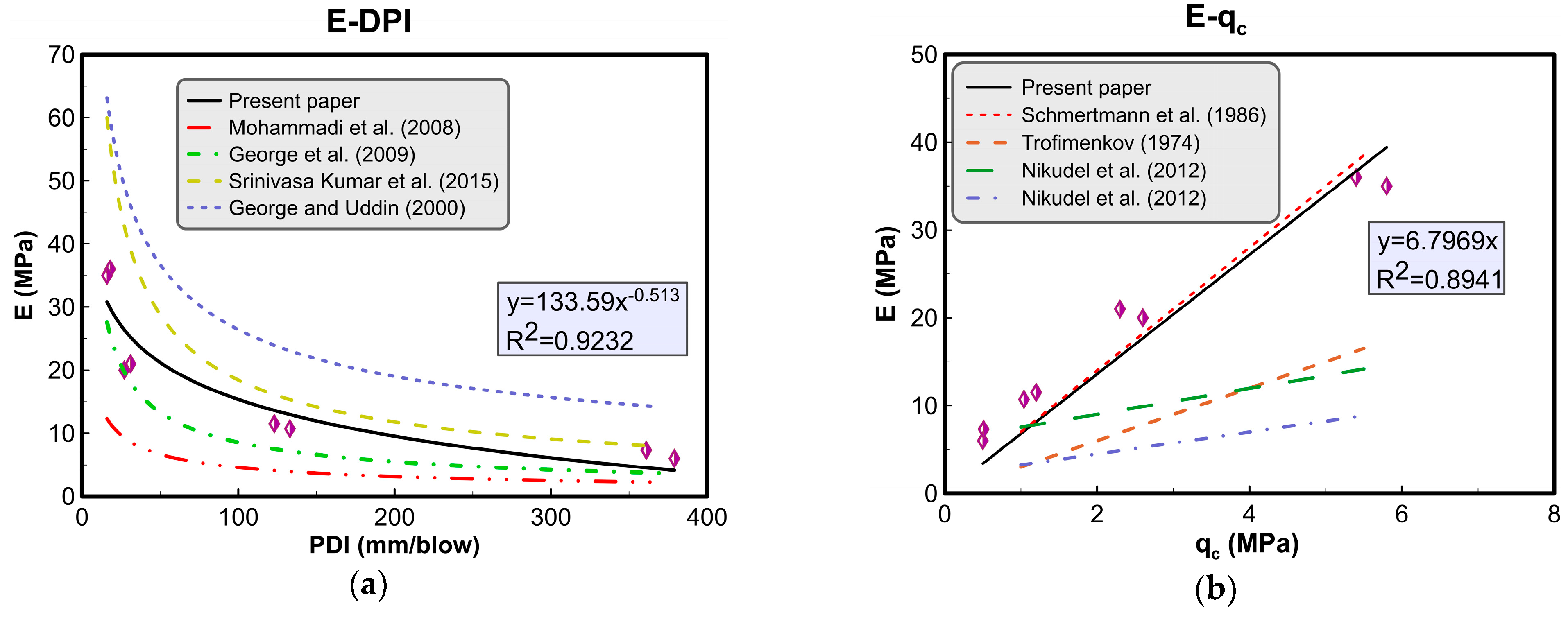
4.9. Modulus of Elasticity (E) versus Dynamic and Static Cone Penetration Test Parameters

The modulus of elasticity is a suitable parameter for expressing soil strength in civil works on roads and is also applicable in soil behavior analytical models. This parameter can be derived from different in situ tests. One of the popular in situ tests for elasticity modulus determination is the plate load test (PLT), but there is some difficulty in measuring the reaction load and determining the elasticity modulus in less accessible sites. Thus, finding a correlation between DPI and PLT might be suitable for this purpose [73,74,75]. The best correlation between DPI and E (derived from PLT) is presented in Figure 13a.

The PLT is not feasible or an economical choice for deep soil characterization projects. Therefore, there is a need for a correlation between other in situ tests and the elasticity modulus or PLT results. Many studies have been performed by different researchers to find the best correlation between E and q_c [23,76,77,78]. The best correlations between E (derived from PLT) and ${\mathrm{q}}_{\mathrm{c}}$ (derived from CPT), as well as q_d (derived from DCP), are presented in Equations (15), (16) and (17), respectively (Figure 13b)

$$\mathrm{E}=133.59\times {\left(\mathrm{DPI}\right)}^{-0.513}$$

(15)

$$\mathrm{E}=6.797{\mathrm{q}}_{\mathrm{c}}$$

(16)

$$\mathrm{E}=4.839{\mathrm{q}}_{\mathrm{d}}$$

(17)

Ultimately, all of the correlations that were evaluated and obtained in this paper are listed in

Table 5. Summary of correlations presented in current research.

No.	Parameters	Equations	Determination Coefficient $({\mathbf{R}}^2$)
1	${\mathrm{q}}_{\mathrm{c}}-\mathrm{D}\mathrm{P}\mathrm{I}$	${\mathrm{q}}_{\mathrm{c}}=73.70\times \mathrm{D}\mathrm{P}{\mathrm{I}}^{-0.762}$	0.96
2	${\mathrm{q}}_{\mathrm{c}}-{\mathrm{q}}_{\mathrm{d}}$	${\mathrm{q}}_{\mathrm{c}}=1.225\times {\mathrm{q}}_{\mathrm{d}}$	0.98
3	$\mathrm{D}\mathrm{r}-{\mathrm{q}}_{\mathrm{c}}$	$\mathrm{D}\mathrm{r}\left(\%\right)={\displaystyle \frac{100}{5.28}}\mathrm{l}\mathrm{n}\left({\displaystyle \frac{{\mathrm{q}}_{\mathrm{d}}\left(\mathrm{M}\mathrm{P}\mathrm{a}\right)}{0.021{\left({\mathrm{\sigma }}_{\mathrm{v}\mathrm{c}}^{\prime }\right)}^{0.85}}}\right)$	0.96
4	$\mathrm{D}\mathrm{r}-{\mathrm{q}}_{\mathrm{d}}$	$\mathrm{D}\mathrm{r}\left(\%\right)={\displaystyle \frac{100}{3.9}}\mathrm{l}\mathrm{n}\left({\displaystyle \frac{{\mathrm{q}}_{\mathrm{c}}\left(\mathrm{M}\mathrm{P}\mathrm{a}\right)}{0.025{\left({\mathrm{\sigma }}_{\mathrm{v}\mathrm{c}}^{\prime }\right)}^{1.37}}}\right)$	0.95
5	$\mathrm{D}\mathrm{r}-\mathrm{D}\mathrm{P}\mathrm{I}$	$\mathrm{D}\mathrm{r}\left(\%\right)=283.33\times {\left(\mathrm{D}\mathrm{P}\mathrm{I}\right)}^{-0.0434}$	0.96
6	$\mathrm{\phi }-{\mathrm{q}}_{\mathrm{c}}$	$\mathrm{\phi }={14.069}^{°}+4.977\ln \left({\mathrm{q}}_{\mathrm{t}1}\right)$	0.96
7	$\mathrm{\phi }-{\mathrm{q}}_{\mathrm{d}}$	$\mathrm{\phi }={19.756}^{°}+3.603\ln \left({\mathrm{q}}_{\mathrm{d}1}\right)$	0.95
8	$\mathrm{\phi }-\mathrm{D}\mathrm{P}\mathrm{I}$	$\mathrm{\phi }=53.841\times {\left(\mathrm{D}\mathrm{P}\mathrm{I}\right)}^{-0.105}$	0.97
9	$\mathrm{\phi }-\mathrm{D}\mathrm{r}$	$\mathrm{\phi }=0.184\times \mathrm{D}\mathrm{r}+25.09$	0.97
10	$\mathrm{E}-\mathrm{D}\mathrm{P}\mathrm{I}$	$\mathrm{E}=133.59\times {\left(\mathrm{D}\mathrm{P}\mathrm{I}\right)}^{-0.513}$	0.92
11	$\mathrm{E}-{\mathrm{q}}_{\mathrm{c}}$	$\mathrm{E}=6.797{\mathrm{q}}_{\mathrm{c}}$	0.89
12	$\mathrm{E}-{\mathrm{q}}_{\mathrm{d}}$	$\mathrm{E}=4.839{\mathrm{q}}_{\mathrm{d}}$	0.84

. As can be seen, the R² factor (coefficient of determination) had a reasonable value in all of the correlations.

4.10. Practical Implications

A critical aspect of engineering research involves assessing a study’s practical, economic, and environmental implications and loading impacts [79]. This research primarily aims to predict the strength and stiffness parameters of sandy soils through three tests: CPT, DCP, and PLT. By enhancing the accuracy of these predictions, this study seeks to optimize design processes, reducing costs and execution time while minimizing material usage in engineering projects, ultimately leading to a lower environmental impact.

Furthermore, this research explores the potential of using the dynamic cone penetration test to estimate the parameters typically obtained from CPT and PLT. This approach is particularly advantageous in engineering projects, as the dynamic cone penetration test is more compact, easier to perform in confined or restricted-access areas, and significantly lowers geotechnical investigation costs. Unlike the CPT and PLT, the dynamic cone penetration test is widely available and easily accessible.

5. Conclusions

In this study, existing correlations between the strength and geotechnical parameters of Babolsar sand were evaluated by performing DCP, CPT, and PLT tests. In total, 24 physical modeling tests were performed, including 8 CPT tests, 8 DCP tests, 8 PLT tests, and 24 triaxial tests for the determination of the soil internal friction angle. In this research, Babolsar sand was used, and all of the samples were constructed using the dry sedimentation method in a chamber with a 700 mm diameter and 1000 mm height. The outcome of this study, which is the correlation between different geotechnical and mechanical parameters of Babolsar sand, is presented in Table 5.

The main conclusions are listed below:

• An increase in the relative density value increases the interaction between soil particles; due to this phenomenon, the internal friction angle value is also increased. The results showed that there is a linear relationship between these two parameters;
• The cone resistance is increased in both CPT and DCP tests by an increase in the internal friction angle and relative density, and there is a logarithmic correlation between these two;
• An increase in the soil’s relative density increases the cone resistance in both CPT and DCP tests, and there is a linear correlation between these two parameters. In addition, under the same condition, the DPI factor value had an inverse correlation with cone resistance;
• The elasticity modulus is a suitable geotechnical parameter for determining soil stiffness in sandy soils. The cone resistance value in both CPT and DCP tests is increased linearly by an increase in the elasticity modulus of sands. There was also a nonlinear correlation between the DPI factor and these two parameters;
• The dynamic and static penetration tests had the same nature, and the soil shear bands formed completely during the penetration. The correlations between the parameters of both tests had a high coefficient of determination (R²) and accuracy. On the other hand, the plate load test measured stiffness and no shear band formed. Therefore, the correlation between PLT and CPT parameters had lower R² values.