Seismic Behavior of Retaining Walls: A Critical Review of Experimental and Numerical Findings

Abstract

For reliable seismic design of earth-retaining structures, it is critical to accurately assess the magnitude and distribution of dynamic earth pressures. Over the years, numerous experimental and numerical studies have sought to clarify the complex soil–structure interactions in backfill–wall systems under seismic loads. This article expands on an earlier review by the authors of analytical and field performance studies addressing the seismic behavior of retaining walls. Despite extensive research, there is still no consensus on a standardized seismic evaluation method or on the necessity of including seismic loads in the design of retaining structures. This review critically examines notable experimental and numerical findings on dynamic lateral earth pressure, highlighting that the current design practices cannot be generally applied to all types of retaining structures. More importantly, these practices often rely on experimental data extrapolated beyond their original applicability.

1. Introduction

Retaining walls are critical structures that provide lateral support to soil masses and are extensively used in hilly areas, transportation infrastructure, underground constructions, the mining sector, and military applications. Accurately estimating lateral earth pressure is fundamental for assessing the stability of these structures, particularly in seismically active areas. The behavior of soil during an earthquake is intricate, involving nonlinear soil properties, soil liquefaction potential, soil–structure interaction (SSI) effects, and the transient nature of seismic loading. Evaluating seismic earth pressure on retaining structures is a challenging SSI issue that must consider various factors, including the characteristics of input motions (such as amplitude, frequency, directivity, and duration), the responses of both backfill and foundation soil, and the properties of the wall (such as strength and stiffness).

The pioneering work of Okabe [1] and Mononobe and Matsuo [2], known as the Mononobe–Okabe (M-O) method, introduced a pseudostatic approach to estimate seismic earth pressure by extending Coulomb’s [3] static earth pressure theory. Despite several limitations, this method remains popular in current practice largely because of its simplicity. Subsequently, numerous researchers [4,5,6,7,8,9,10,11,12,13,14] have modified and extended the M-O approach, proposing new analytical solutions for determining seismic earth pressure. These solutions often rely on simplified assumptions that might not accurately represent the true seismic response of the wall–soil system and show noticeable disparity from the observed field performance of retaining structures [15,16,17,18,19]. Over the years, physical model tests, including 1-g shaking table tests [2,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54] and dynamic centrifuge tests [18,19,55,56,57,58,59,60,61,62,63,64,65,66,67], have been conducted to calculate seismic active and passive earth thrust on various types of retaining walls.

Additionally, since the 1970s, numerical techniques have been employed to validate seismic design methods and provide new perspectives into the problem of seismic earth pressures on retaining walls, including finite element (FE) methods [18,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93] and finite difference (FD) methods [94,95,96,97,98,99,100,101,102]. In recent decades, advancements in seismology, soil dynamics, and earthquake engineering have significantly improved our understanding of wall–soil interactions during earthquakes. With improvements to computational capabilities, advanced numerical models have become more feasible and manageable, enabling more adequate procedures for design and assessment. Importantly, advancements in computational techniques and numerical modeling have allowed for more sophisticated SSI analyses, incorporating nonlinear soil behavior and more realistic representations of seismic loading. These advanced constitutive soil models can provide more accurate predictions of dynamic earth pressures. However, even with these advanced techniques, uncertainties and assumptions still exist. The accuracy of numerical models heavily relies on input parameters, soil property characterizations, and understanding dynamic system behaviors. Validating these models through field observations and laboratory testing is essential for improving their reliability.

Despite extensive research on seismic earth pressures behind retaining walls via analytical, experimental, numerical, and field studies, discrepancies between different methods persist, highlighting the need for continued investigation. This article builds on an earlier review by the authors (Khan et al. [15]) of analytical and field performance studies in this area. This detailed review of key experimental and numerical studies on the seismic performance of retaining walls demonstrates the necessity for further research. Specifically, integrating experimental data with advanced numerical simulations and generating an extensive field performance database are crucial for refining our understanding of seismic earth pressures and enhancing the design and resilience of retaining structures.

2. Physical Model Testing

Early analytical solutions for dynamic thrust on gravity walls proposed by Okabe [1] were based on simplified assumptions, which prompted additional experimentation to validate these solutions. Generally, these studies can be categorized into two main types: (1) 1-g shaking table tests and (2) dynamic centrifuge testing. Mononobe and Matsuo [2] originally conducted shaking table experiments on small-scale wall models, which, together with Okabe’s [1] solution, laid the foundation for the M-O method. Later, several investigators performed similar experiments using shaking tables and dynamic centrifuges, exploring different model configurations and shaking mechanisms. A detailed summary of significant advancements on this subject from 1960–1980 can be found in [103,104,105,106].

Shaking table experiments have been the primary choice for model testing because of the availability of shaking tables and the ease of model construction. In these experiments, the model walls are usually securely attached to the base of the shaking platform. However, dynamic centrifuge experiments, though more recent and less common, involve models that are either attached to the centrifuge base or directly founded on soil. Centrifuge testing provides consistent scaling of critical parameters and is relatively efficient in terms of time and cost. These experiments aim to improve the understanding of the seismic behavior of retaining structures, increasing their preference for model testing. Both the shaking table and centrifuge tests have utilized sinusoidal and earthquake excitations.

2.1. 1-g Shaking Table Experiments

Over the years, numerous shaking table experiments have been carried out to study the dynamic responses of retaining walls [2,20,21,22,23,24,25,31,42,49,50,51,52,53,54]. However, these studies have utilized very small-scale models, and their findings have displayed varying levels of consistency with theoretical estimates [18]. Shaking table tests using small-scale models have encountered several limitations, such as difficulties in accurately scaling soil strength and stiffness of retaining structures under 1-g conditions. Additionally, due to constraints related to the dimensions and capacities of shaking tables, the model walls were often directly fastened to the base of the model container, essentially founded on rigid bedrock. Moreover, because comprehensive earthquake data were lacking at the time, sinusoidal excitations were employed as input motions [107].

Pioneering research on seismic earth pressure on gravity walls was initiated by Mononobe and Matsuo [2] using a shaking table. Their initial setup involved a stiff base container placed on rails, propelled by a unique cone-shaped drum winch attached to the base of the container via a crankshaft. This design enabled the direct use of sinusoidal input motion with a linearly varying frequency. Later, Mononobe and Matsuo [20] replaced the shaking table with a “swing” to induce seismic vibrations during their experiments. To isolate the earth pressure induced only by soil action, they considered wall inertia and deducted it from the recorded resultant pressure. Subsequently, Jacobsen [31] and Matsuo [42] adopted similar setups, utilizing a rigid box under sinusoidal excitations. They reported that for a peak ground acceleration (PGA) of up to $0.4\mathrm{g}$, the measured maximum earth pressure magnitude agreed well with the M-O solution. However, unlike the M-O method, they observed that the resultant dynamic thrust acted at a height of ${\displaystyle \frac{2H}{3}}$ above the base of the wall. The introduction of hydraulically operated shaking tables enabled more extensive testing on small-scale models [21,23,24,25,49,50,51,52,53,108]. Their findings generally supported the M-O predictions. A detailed compilation of these studies and their findings is available in [105,106]. Matsuzawa et al. [109] examined the findings of previous shaking table tests to determine the dynamic water pressures on stiff retaining walls. They suggested a M-O-based design methodology, including factors such as permeability, wall movement modes, and backfill geometry. Ishibashi et al. [26] examined the impact of water in the sandy and cohesive backfill of rigid, nonyielding walls during earthquakes via 1-D shaking table tests. Richards et al. [27] developed an analytical procedure to calculate the threshold accelerations required to initiate movement in gravity-wall bridge abutments during seismic events. They validated their analysis through shaking table tests on small-scale bridge abutment model walls with different interface conditions between the wall, foundation, backfill, and bridge deck, all subjected to seismic excitations. Their study revealed that the measured threshold accelerations closely matched the theoretical predictions. Koseki et al. [28] improved the M-O method after conducting shaking table and tilting tests on a $0.53\mathrm{m}$ tall wall. Their refined approach accounted for strain localization in the backfill soil along an existing active failure wedge. Both the experimental and analytical findings indicated that the failure plane created by the initial active failure wedge could influence the subsequent development of earth pressure until the seismic intensity was high enough to create a new, deeper secondary failure wedge in the denser adjacent backfill.

Ling et al. [29,30], Wilson [32], Watanabe et al. [33,34], and Mock and Cheng [35,36] incorporated seismic excitations into their shaking table experiments. Ling et al. [29,30] conducted shaking table tests on 2.8-m-high geosynthetic-reinforced soil modular block (GRS-MB) retaining walls with sandy and silty sand backfill. They observed minimal wall deformation and horizontal acceleration amplification during moderate earthquake motions ($\mathrm{PGA}=0.4\mathrm{g}$). Under higher intensity seismic motions ($\mathrm{PGA}=0.86\mathrm{g}$), they noted only slight deformation and horizontal acceleration amplification. They reported that increasing the reinforcement length of the top layer from 2.05 to $2.52\mathrm{m}$ and reducing the vertical reinforcement spacing from 0.6 to $0.4\mathrm{m}$ significantly reduced the displacement of the wall facing. Additionally, the presence of unsaturated conditions in the silty sand backfill further reduced facing displacements under earthquake loading.

Wilson [32] conducted full-scale shaking table tests to investigate the force–displacement relationship and seismic earth pressure on bridge abutment walls with cohesive backfill under both at-rest and passive initial conditions. The model consisted of a $2.13\mathrm{m}$ high and $0.2\mathrm{m}$ thick reinforced concrete wall positioned on a $0.47\mathrm{m}$ box above a $2.15\mathrm{m}$ backfill (Figure 1). The tests showed that for at-rest conditions and $\mathrm{PGA}\le 0.66\mathrm{g}$, the resultant dynamic earth pressure remained relatively low, primarily driven by wall inertia. However, as the PGA approached $1\mathrm{g}$, the resultant dynamic earth pressure increased significantly. The study revealed that the low resultant seismic soil pressure at a lower PGA was influenced by the high stiffness and cohesiveness of the backfill, the wall’s limited height, the capacity of the wall movement (translation and rotation) away from the backfill, and the compatibility of deformation at the soil–wall interface. However, the tests revealed that under passive initial conditions and $\mathrm{PGA}\le 0.66\mathrm{g}$, the resultant seismic earth pressure increased the overall thrust by approximately 5% of the maximum static passive pressure. The overall thrust increased by almost 30% for higher PGA values.

Watanabe et al. [33,34] investigated the dynamic earth pressure distribution along the height of a gravity wall divided into three sections: two outer segments and a central core plate connected to load cells. Sand was used as the backfill material, and the wall was constructed on either a thin gravel layer or sand, ensuring that sliding failure occurred before overturning. Inertial loads from the plates were measured and considered in the load cell data analysis to calculate the resultant seismic soil pressure. On the basis of experimental results, an analysis procedure involving the calculation of a critical yield acceleration was proposed to evaluate stability against sliding or overturning via a pseudostatic approach. The M-O equation was then applied with this yield acceleration to determine the maximum total seismic thrust. The study revealed that while the total seismic thrust increased with increasing PGA, the thrust was limited to this maximum value. Ultimately, the design loads were recommended on the basis of the wall’s stability rather than the characteristics of the seismic excitation [107].

Mock and Cheng [35] investigated the dynamic behavior of semi-gravity cantilever T-shaped walls with and without a sound wall via full-scale shaking table tests using a slightly cohesive backfill. In the tests without sound walls, the resultant seismic earth pressure aligned with the M-O results, and the resultant thrust acted at approximately ${\displaystyle \frac{H}{3}}$. However, adding a sound wall increased the seismic pressure in the upper 60–70% of the wall, creating a nonlinear pressure distribution and shifting the application point to approximately ${\displaystyle \frac{H}{2}}$. The authors observed that the M-O method lacked sufficient accuracy in estimating seismic earth pressure for the various earthquake records studied, particularly for the retaining wall with a sound wall. Consequently, they recommended further investigation to evaluate the design implications of using the M-O method for such retaining wall configurations [36]. Figure 2 shows the experimental configuration employed by Mock and Cheng [35] in their shaking table experiments.

Krishna and Latha [37] examined the dynamic behavior of model reinforced earth walls with wrapped facing via shaking table tests. They reported that alterations in the input earthquake motion characteristics, rebar spacing, and applied surcharge pressure all had a substantial impact on the seismic performance of these walls. Models with greater rebar spacing showed higher acceleration amplification factors. Furthermore, face deformations were more pronounced at low-frequency vibrations, lower surcharge pressures, fewer layers of rebars, and elevated base accelerations. Ertugrul and Trandafir [38] reported shaking table test results on small-scale cantilever wall models subjected to sinusoidal excitations, including geofoam inclusions. Their results highlighted the significant impact of wall flexibility on dynamic earth pressures. Dynamic earth pressure coefficients calculated using the Steedman and Zeng [5] method closely aligned with test results for models with lower flexibility ratios. Additionally, the inclusion of deformable materials reduced residual post-earthquake wall stresses, thereby improving the overall post-seismic wall stability. Fox et al. [39] performed shaking table experiments on a 6.1-m-high GRS-MB wall with reinforcements placed at vertical intervals of $0.6\mathrm{m}$. The wall was subjected to various earthquake and sinusoidal excitations. The study revealed that while the wall itself sustained moderate damage, the backfill soil exhibited significant cracking. Latha and Santhanakumar [40] performed shaking table experiments on GRS walls and observed that increasing the relative density of the backfill soil greatly reduced the lateral facing displacements and settlements in the reinforced fill.

Yang et al. [41,43] and Zhu et al. [44] carried out large-scale model shaking table tests to study how the stiffness of foundation soil beneath gravity walls impacted seismic earth pressure. Their findings revealed that higher foundation soil stiffness resulted in reduced seismic thrust behind the wall. Kloukinas et al. [45] studied the seismic behavior of cantilever walls with dry silica sand backfill via theoretical studies and shaking table experiments. Their theoretical approach encompassed limit analysis and wave-propagation techniques, addressing various factors such as strength, inertia, movement, and deformation compatibility. The shaking table tests included various combinations of wall designs, soil arrangements and input motions. The authors concluded that the experimental results aligned well with the theoretical predictions, thereby improving the understanding of the intricate mechanics involved in the problem.

Wilson and Elgamal [46] performed extensive large-scale shaking table experiments on a small-scale cantilever model walls with cohesive backfill. Their results demonstrated that the M-O method, which disregards the influence of backfill cohesion, significantly overestimates dynamic soil pressures. Nakajima et al. [47] examined the influence of backfill cohesion on dynamic earth pressure via shaking table tests. The authors observed (1) increased shear strength along the backfill failure plane, (2) greater shear resistance at the wall–backfill interface, and (3) the presence of a nonactive earth pressure zone in the upper backfill region. Yünkül and Gürbüz [48] studied the dynamic response of gravity walls with inclined backside and inclined backfill. Their shaking table tests on a $0.75\mathrm{m}$ high model wall under sinusoidal excitations revealed that pseudostatic limit-state methods overestimate dynamic thrusts and fail to accurately capture the seismic responses of gravity walls, as they ignore inertial forces and phase differences. Additionally, the tests suggested that dynamic thrusts on the wall could be disregarded up to a PGA of $0.2\mathrm{g}$.

Although the scaled 1-g shaking table tests by Mononobe and Matsuo [2] were pioneering in evaluating the seismic response of gravity walls, their applicability is limited. The findings from these scaled model experiments, which used frictional materials, cannot be directly applied to full-scale (prototype) structures due to the stress-dependent nature of material properties. Therefore, the Mononobe and Matsuo [2] experiments are specifically relevant to the tested geometry and materials of model walls up to $1.8\mathrm{m}$ in height with relatively loose, cohesionless backfill. Following their work, several researchers conducted similar 1-g shaking table experiments on small-scale models with various configurations and shaking mechanisms [21,22,23,24,25,31,42,49,50,51,52,53,54]. These studies generally concluded that the M-O method provides a reasonable estimate of the total resultant thrust but suggested that the application point should be higher than ${\displaystyle \frac{H}{3}}$. However, as with the Mononobe and Matsuo [2] experiments, the precision and utility of 1-g shaking table tests were constrained because of the difficulties in replicating in situ stress conditions, particularly for granular backfills. Importantly, ground motion amplifications and the increase in earth pressure with height documented in these studies were significantly influenced by the specific design of the shaking table container and the characteristics of the sand, which may not necessarily reflect a realistic field response.

Kloukinas et al. [45] reported in their shaking table experiments that the wall–soil system transitions between active and passive states during seismic excitation. This observation contrasts with the conclusions of other researchers [23,24,25,42,50,108], who maintained that the wall–soil system remains in an active state only. Shaking table experiments by Wilson [32], Watanabe et al. [33,34], and Mock and Cheng [35] included seismic excitations and offered valuable insights into dynamic SSI mechanisms. Specifically, Watanabe et al. [33,34] identified the development of a phase difference between wall inertia forces and the dynamic thrust increment, with this phase difference approaching $180°$ for input accelerations below 0.30 g and decreasing for higher accelerations. Additionally, full-scale shaking table tests by Wilson [110] demonstrated that the influence of the dynamic thrust increment on the total active thrust was negligible for $\mathrm{PGA}\le 0.66\mathrm{g}$.

Although the shaking table experiments of Wilson [32] and Mock and Cheng [35] are commendable, neither study adequately addressed the scaling of their models relative to model scaling relationships or properly considered soil properties in that context. A fundamental drawback of 1-g shaking table experiments, regardless of the model size, involves complex scaling issues. Typically, earthquake motions are often applied directly from field data, maintaining identical amplitudes and frequencies. Moreover, the soil often exhibits rigid plastic behavior at low confining stress due to the dependence of soil strength and stiffness on the confining stress, making it difficult to scale the results to prototype dimensions [61]. Wilson [110] addressed the impact of short wall height, emphasizing the challenges associated with low confining stress. Additionally, boundary effects present significant challenges, as the proximity between the model structure and the rigid container boundary often fails to replicate free-field conditions effectively, as observed by Mock and Cheng [35]. Despite these constraints, analytical solution developers have extrapolated the observed behavior beyond their applicable range, frequently criticizing the original M-O solution as inadequate. This critique is unsurprising, given that similar limitations affected all the models [107].

Table 1. Summary of significant 1-g shaking table experiments for seismic earth pressures.

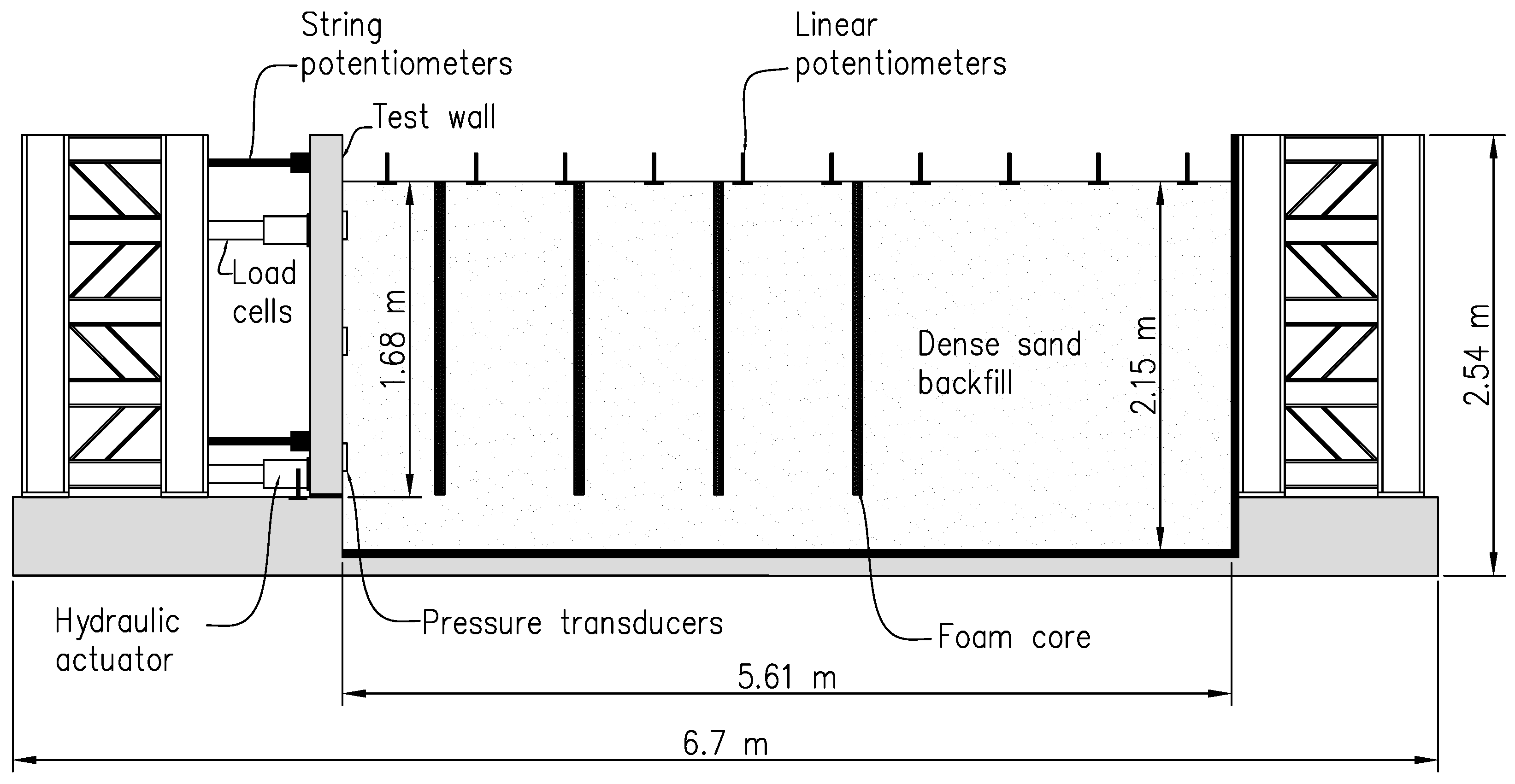
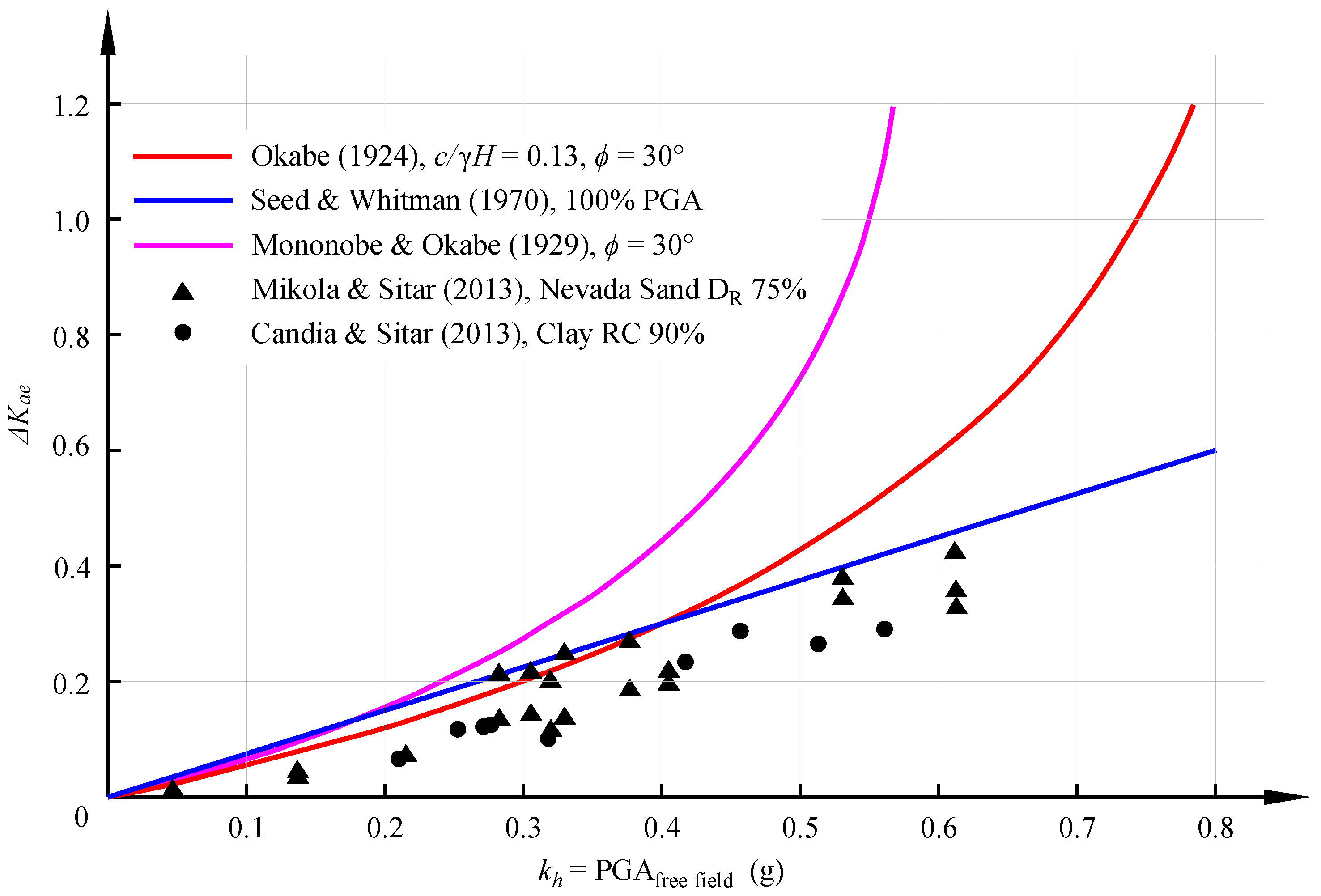
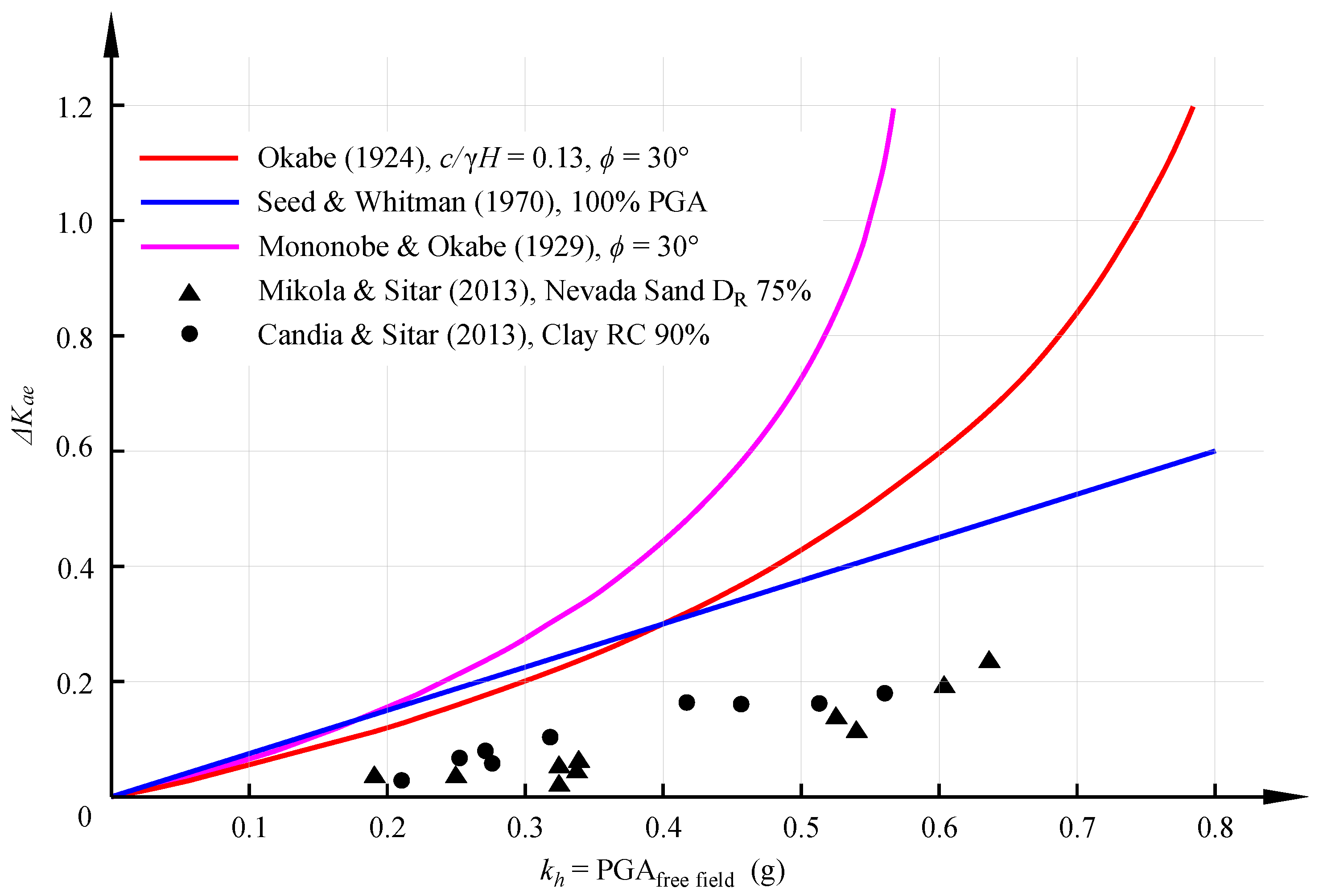
Researchers	Problem Studied	Wall Height (m)	Nature of Shaking	Major Findings
Mononobe and Matsuo (1929) [2]	Gravity wall, dry sand backfill.	1.2–1.8	Sinusoidalexcitations	The resultant dynamic thrust acts at ${\displaystyle \frac{H}{3}}$ above the wall base.
Jacobsen (1939) [31]	Flexible walls, dry sand backfill.	0.91	Sinusoidalexcitations	Results agree reasonably with the M-O method, but dynamic thrust acts at ${\displaystyle \frac{2H}{3}}$ above the wall base.
Matsuo and Ohara (1960) [50]	Quay walls (Fixed and movable type), dry and saturated sand backfill.	0.4	Sinusoidalexcitations	Amplitude of pressure change is substantial at ${\displaystyle \frac{H}{2}}$ for rigid walls. For flexible walls, the maximum pressure amplitude diminishes as the displacement falls below a specific threshold.
Niwa (1960) [52]	Large-scale gravity wall model, sand backfill.	3	Sinusoidalexcitations	Both translational and rocking components made up the wall’s vibration amplitude.
Ichihara and Matsuzawa (1973) [21]	Movable wall, dry sand backfill.	0.55	Sinusoidalexcitations	The dynamic responses are governed by the magnitude and mode of wall movements and the amplitude of input acceleration.
Sherif and Fang (1984) [108]	Rigid wall, dry silica sand backfill.	1	Steady sinusoidal motion	Dynamic pressure distribution was nonlinear. Resultant dynamic thrust acts at $0.55H$ above the wall base.
Ishibashi and Fang (1987) [25]	Rigid wall, dry silica sand backfill.	1.2	Sinusoidalexcitations	Dynamic pressure distribution was nonlinear. Resultant dynamic thrust acts at 0.47–0.53H above the wall base for any wall movement mode if $k_h\le 0.45$.
Ishibashi et al. (1994) [26]	Rigid walls, sandy and cohesive saturated backfill.	0.6–1.2	Sinusoidalexcitations	Resultant hydrodynamic pressure and resultant total dynamic pressure act at $0.6H$ from the bottom of the backfill.
Koseki et al. (1998) [28]	Gravity wall, cantilever wall, leaning-type wall, dry sand backfill.	0.53	Sinusoidalexcitations	Overturning with tilting of the wall face was observed as the major failure mode.
Watanabe et al. (2003, 2011) [33,34]	Gravity wall, cantilever wall, leaning-type wall, dry sand backfill.	0.53	Modified typical earthquake motions	Overturning was the major failure pattern observed in all retaining wall models.
Ling et al.(2005, 2012) [29,30]	GRS-MB walls, dry sand and silty sand backfill.	2.8	Typical earthquake motions	GRS-MB walls performed well under moderate to strong shaking.
Krishna and Latha (2007) [37]	GRS walls, dry sand backfill	0.6	Sinusoidalexcitations	Overturning was the major deformation mode.
Wilson (2009, 2015) [32,46]	Bridge abutment wall, silty sand backfill	2.13	Modified typical earthquake motions	The tests revealed that under at-rest conditions and $\mathrm{PGA}\le 0.66\mathrm{g}$, the resultant dynamic soil pressure remained relatively minimal. However, as the PGA approached $1\mathrm{g}$, the resultant dynamic pressure became notably significant.
Mock and Cheng (2011, 2014) [35,36]	Cantilever walls with and without sound wall, silty sand backfill.	1.83–3.66	Typical earthquake motions	Without sound walls, test results agree with the M-O predictions, with the resultant seismic pressure acting on approximately ${\displaystyle \frac{H}{3}}$. With sound walls, test results show nonlinear pressure distribution and the resultant seismic pressure shifting to about ${\displaystyle \frac{H}{2}}$.
Ertugrul and Trandafir (2014) [38]	Cantilever wall, cohesionless granular backfill with geofoam.	0.75	Harmonicexcitations	Test results highlighted the significant impact of wall flexibility on seismic earth pressures. Tests on models with lower flexibility ratios closely matched the seismic coefficients computed by Steedman and Zeng [5].
Yang et al.(2015, 2018) [41,43]	Gravity walls, granite sand backfill.	1.6	Scaled modified typical earthquake motions	Test results indicated that higher foundation soil stiffness resulted in reduced seismic thrust behind the wall.
Kloukinas et al. (2015) [45]	Cantilever wall, dry silica sand backfill.	0.6	Harmonic excitations and modified typical earthquake motions	The experimental findings validate the stress-limit analysis predictions, suggesting that the pseudostatic stability analysis is effective for both harmonic and seismic excitations.
Nakajima et al. (2021) [47]	Gravity wall, cohesive and cohesionless backfill.	0.6	Sinusoidalexcitations	Results indicated increased shear strength along the backfill failure plane; greater shear resistance at the wall–backfill interface; and the presence of a nonactive earth pressure zone in the upper backfill region.
Yünkül andGürbüz (2023) [48]	Gravity walls, dry silica sand backfill.	0.75	Sinusoidalexcitations	Dynamic thrusts on the wall could be disregarded up to a PGA of $0.2\mathrm{g}$. Test results indicated that pseudostatic limit–state methods overestimated the dynamic thrusts.

presents a summary of significant 1-g shaking table experiments for seismic earth pressures.

2.2. Dynamic Centrifuge Experiments

Numerous researchers have carried out dynamic centrifuge tests on model walls with input accelerations exceeding $1\mathrm{g}$ [18,19,55,56,57,58,59,60,61,62,63,64,65,66,67]. These experiments offer several advantages over 1-g shaking table tests, such as the following: (a) Accurate scaling of the stress–strain behavior of soil, enabling the model to replicate prototype conditions; (b) the ability to position the model far from boundaries, close to free field conditions; (c) the possibility for the retaining structure to be underlain by a soil deposit rather than resting directly on the container base; and (d) the reasonable scaling of input motions from recorded data [107]. Detailed discussions on centrifuge scaling laws can be found in Kutter [111]. Nevertheless, dynamic centrifuge experiments also have certain limitations: the gravity field increases with depth; frequency characteristics of the input motions can be captured only by means of highly sensitive instruments; and a stationary benchmark is lacking due to unwanted vibrations in the loading frame resulting from dynamic soil–wall interactions. This issue becomes prominent in the presence of mass asymmetry within the soil [57].

Giarlelis and Mylonakis [112] conducted a comparative analysis of shaking table and dynamic centrifuge tests against limit–state methods and elastic methods proposed by Veletsos and Younan [113,114,115]. They reported that inconsistencies in the dynamic soil pressure distribution and the resultant application point among different methods could be attributed to the wall and foundation flexibility. In the reviewed experimental studies, the soil–wall systems were not classified as “rigid” when accounting for this flexibility. Notably, the shaking table experimental results aligned more closely with the limit–state solutions, whereas the centrifuge experiment results were more consistent with the elastic solutions. This difference was attributed to the higher accuracy in scaling achieved by centrifuge experiments.

The earliest centrifuge study investigating the dynamic behavior of cantilever walls with dry medium-dense sand backfill was carried out by Ortiz et al. [61]. Their findings showed a general agreement between the peak dynamic pressures and the M-O predictions, with the resultant dynamic thrust positioned at approximately ${\displaystyle \frac{H}{3}}$ above the base of the wall. Bolton and Steedman [60,62] examined the seismic response of a microconcrete and aluminum cantilever wall model supporting dry sand backfill via centrifuge tests. The walls, which were firmly connected to the loading frame, underwent sinusoidal excitations up to $0.22\mathrm{g}$. The resultant dynamic load was found to act at ${\displaystyle \frac{H}{3}}$ above the wall base, aligning with the M-O outcomes, highlighting the necessity of considering wall inertial forces to accurately determine seismic earth pressures.

Steedman [116] conducted centrifuge experiments on cantilever walls with dry sand backfill, observing that seismic thrusts matched the M-O predictions; however, the results suggested that the application point should be ${\displaystyle \frac{H}{2}}$ above the wall base. Steedman and Zeng [5] subsequently re-examined the outcomes of Bolton and Steedman [62] experiments and determined that the measured dynamic forces aligned with the M-O predictions, albeit with a nontriangular pressure distribution. Insights from Zeng’s [63] centrifuge tests led Steedman and Zeng [5] to highlight the importance of accounting for the amplification and phase change of input motion, stressing that variations in backfill acceleration influenced the dynamic pressure distribution. Consequently, they suggested that the application point of the dynamic load should be positioned at ${\displaystyle \frac{H}{2}}$ above the base of the wall.

Stadler [65] performed centrifuge tests on cantilever walls fixed to a container with a dry, medium-dense sand backfill, observing that the total soil pressure exhibited a triangular distribution with depth, whereas the dynamic soil pressure ranged from triangular to rectangular shapes. Additionally, Stadler [65] proposed that employing a fraction (20–70%) of the original PGA in the M-O equation resulted in forces that aligned well with measured values. Dewoolkar et al. [66] performed dynamic centrifuge experiments on fixed-base cantilever walls with saturated cohesionless backfills, using sinusoidal excitation with varying amplitudes reaching $0.7\mathrm{g}$. They reported that dynamic earth pressures were proportional to the excess pore pressure in the backfill but independent of the wall stiffness. The dynamic pressure distribution varied from triangular to inverted triangular, and the resultant dynamic thrust position fluctuated between 0.6–0.8H from the wall top. Additionally, a significant increase in earth pressure exceeding M-O predictions was noted when the backfill soil underwent liquefaction.

Saito et al. [67] modeled a gravity-type wall retaining dry, dense sand to predict the wall displacements. The dynamic centrifuge test employed sinusoidal excitations with an amplitude of $0.4\mathrm{g}$ and a frequency of 1.5 Hz. The experimental results revealed that the wall experienced a permanent displacement of $1.4\mathrm{m}$ and a rotation $4°$ away from the backfill soil. Matsuo et al. [55] performed centrifuge tests on gravity-type walls with different embedment depths, using a design analogous to the shaking table studies of Watanabe et al. [33,34], featuring two outer sections and a central core plate section coupled to the load cells. They applied sinusoidal excitation for 20 cycles and with amplitudes up to $0.7\mathrm{g}$. The findings showed that the dynamic active pressure remained relatively constant regardless of the applied base acceleration during wall sliding. The measured dynamic soil pressures were lower than the M-O predictions. Importantly, wall embedment significantly improved the seismic stability.

Nakamura [56] performed centrifuge model tests on gravity walls using both harmonic and earthquake excitations. The results indicated that the computed dynamic soil pressure was lower than the values predicted by the M-O method. Furthermore, it was observed that the inertial forces acting on the wall and backfill did not consistently occur simultaneously, challenging a fundamental assumption of the M-O method. Additionally, the total earth pressure distribution was observed to be nonlinear, time-dependent, and influenced by the characteristics of the applied input motion, deviating from the M-O theory. Al-Atik and Sitar [18] carried out centrifuge model experiments to evaluate the seismic response of stiff and flexible U-shaped cantilever walls retaining dry, medium-dense sand backfill. Their findings revealed that seismic soil pressure increases linearly with depth and can be approximated by a triangular distribution, with the resultant dynamic thrust positioned at ${\displaystyle \frac{H}{3}}$ above the wall base. Notably, seismic soil pressures and inertial forces did not occur simultaneously. Al-Atik and Sitar [18] concluded that the M-O method overestimates seismic soil pressures and suggested that it can be ignored on cantilever walls for a PGA below $0.4\mathrm{g}$. Their conclusions were consistent with those of Clough and Fragaszy [117], who posited that cantilever walls designed with cohesionless backfill can withstand dynamic loads at PGAs up to $0.4\mathrm{g}$.

Mikola et al. [19] conducted centrifuge tests on cantilever and basement walls with dry, medium-dense sand backfill, finding that the dynamic earth pressure increases with depth and thrust acts at approximately $0.33H$ above the base, which is lower than the 0.5–0.6H recommended by most contemporary design codes. They also reported that the Seed and Whitman [103] method accurately estimates upper-bound loads for nonyielding walls but underestimates for free-standing walls. The study revealed that the M-O method is conservative and that cantilever walls with sufficient static safety factor can withstand a PGA of up to $0.4\mathrm{g}$, which is consistent with the Clough and Fragaszy [117] findings. Candia and Sitar [97] conducted similar tests to examine the effects of soil cohesion on the dynamic earth pressure.

Figure 3 and Figure 4 present centrifuge data from Mikola and Sitar [96] on cohesionless soil and Candia and Sitar [97] on compacted silty clay plotted against the peak free-field acceleration at the maximum wall moment. For stiff walls in cohesionless soil, the M-O solution and the Seed and Whitman [103] approximation provide a reasonable upper-bound, approximately one-third of Wood’s [79] solution for rigid walls. Cohesion has minimal impact, with silty clay backfill yielding results near or below the average of the data values. Dynamic earth pressure coefficients for cantilever walls are significantly lower than those of conventional design procedures, with no significant distinction between cohesive and cohesionless backfill, potentially because of experimental constraints. Seed and Whitman [103] proposed that well-designed gravity walls perform effectively for $\mathrm{PGA}\le 0.3\mathrm{g}$ without seismic-specific designs, supported by data showing minimal seismic earth pressure coefficients below this threshold, which is consistent with Al-Atik and Sitar [18] and Sitar et al. [118]. Wagner and Sitar [58] conducted similar centrifuge tests with rigid and flexible cantilever walls and deep stiff walls retaining cohesive and cohesionless soils. They concluded that the M-O method is a reasonable upper-bound for rigid walls, whereas flexible walls experience much lower loads than predicted. For deep embedded walls, dynamic loads do not increase continuously with depth and represent only a small portion of the total load.

Jo et al. [59] conducted centrifuge tests to study the dynamic behavior of variable-height inverted T-shaped stiff cantilever walls with dry, medium-dense sand backfill under earthquake and sinusoidal excitations. Their results indicated that the dynamic earth pressure varied over time and exhibited a triangular distribution, differing from Seed and Whitman’s [103] inverted-triangle interpretation. The dynamic thrust was located approximately $0.33H$ above the wall base. The study revealed that the M-O method underestimated dynamic earth pressure for walls with a prototype height of $5.4\mathrm{m}$ but overestimated it for those with a height of $10.4\mathrm{m}$. Importantly, the phase difference between the wall and soil significantly influenced the magnitude and distribution of seismic pressure. The maximum moment in the wall stem occurred when seismic acceleration acted towards the backfill, placing the wall–soil system in an active state.

Early centrifuge experiments undertaken by Ortiz et al. [61], Bolton and Steedman [60,62], Zeng [63], Steedman and Zeng [64], and Stadler [65] and Dewoolkar et al. [66] studied models retaining walls with both dry and saturated granular backfills. Notably, these early studies, which were constrained by payload capacity, typically employed sinusoidal excitations and pressure cells for evaluating the dynamic soil pressures on the walls. While many of these studies reported a general concordance between the maximum dynamic pressures and the M-O predictions, uncertainty remained about the exact point of application of the seismic thrust.

Importantly, Nakamura [56] and Al-Atik and Sitar [18] observed through centrifuge experiments that retaining wall–backfill systems can exhibit both active and passive states under dynamic excitations. Nakamura [56] highlighted the significant influence of the phase difference between the backfill soil and the retaining wall on dynamic earth pressure. Although Ortiz et al. [61] and Nakamura [56] identified nonlinear dynamic earth pressure distributions, Stadler [65], Sitar and Al-Atik [119], and Mikola et al. [19] reported that these distributions could be reasonably approximated as linear. Similarly, centrifuge tests by Sitar and coworkers [16,18,118,119,120,121] revealed a notable phase difference between wall inertia and earth thrust during strong motions for both yielding and nonyielding cantilever walls.

Candia et al. [57] identified notable differences between measured and anticipated dynamic earth pressures. Traditional design practices assume that seismic earth pressures increase toward the surface, influenced by scaling limitations and the setup of typical 1-g shaking tables, where the structures are mounted on a rigid base. However, Candia et al. [57] found through their centrifuge experiments that seismic earth pressure increases almost linearly with depth when the basement and cantilever walls are founded on soil rather than a rigid base. Additionally, they reported that the dynamic earth pressure is unrelated to cohesion, contrary to analytical studies by Rao and Choudhury [122], Shukla et al. [123], Shukla and Habibi [124] and Shukla and Zahid [125].

The differences between theoretical predictions and experimental observations of seismic earth pressure and wall displacement arise from several interrelated factors rooted in idealized assumptions and practical limitations. Theoretical models, such as the M-O method and modified pseudo-dynamic approaches, often assume rigid walls, homogeneous cohesionless soils, and linear-elastic soil behavior, which neglect critical realistic SSI complexities. For instance, resonance effects, where earth pressure theoretically increases at specific frequencies, are rarely replicated in experiments due to scaling distortions in centrifuge tests or 1-g shaking table experiments. These models also ignore important SSIs, such as the wall flexibility and foundation compliance, which analytical studies show reduce dynamic pressures. Additionally, cohesion in backfill or layered backfills in experiments introduce unaccounted shear strength variations, while turbulence or incomplete saturation during testing disrupts cohesion mobilization, screening theoretical trends such as reduced active pressure under moderate shaking.

Experimental limitations further exacerbate these gaps. Small-scale models fail to replicate prototype stress conditions, altering wave propagation, damping ratios, and phase relationships between soil and wall motion. Sensor inaccuracies and noise in high amplitude shaking environments obscure transient pressure measurements, particularly near failure surfaces. For example, dynamic centrifuge studies reveal progressive soil strength degradation under cyclic loading, a phenomenon rigid-plastic theoretical models fail to capture. Similarly, damping ratios are often arbitrarily assigned in experiments, diverging from site-specific conditions. These issues are compounded by boundary condition simplifications, such as rigid wall assumptions in shaking tables, which overestimate pressures compared to flexible-wall numerical simulations.

To bridge these gaps, it is recommended to integrate advanced numerical models to calibrate experiments, ensuring scaling laws and boundary conditions align with theoretical assumptions. In addition, frequency-sweep tests and high-resolution sensor networks could isolate resonance effects and reduce measurement noise. Full-scale centrifuge tests with realistic SSI and soil heterogeneity are also critical to validate the modified pseudo-dynamic methods. While challenges persist in capturing nonlinear soil behavior and pore pressure effects, such advancements agree to reconcile theory with experimental outcomes, improving the reliability of seismic design of retaining structures.

Table 2. Summary of significant dynamic centrifuge experiments for seismic earth pressures.

Researchers	Problem Studied	Wall Height (m)	Nature of Shaking	Major Findings
Ortiz et al. (1983) [61]	Cantilever walls, dry sand backfill.	0.11	Earthquake-likemotions	Results agree reasonably with the M-O predictions and dynamic resultant positioned at approximately ${\displaystyle \frac{H}{3}}$ above the wall base. Inertial forces were not explicitly considered.
Bolton and Steedman (1982, 1984) [60,62]	Cantilever walls, dry sand backfill.	0.20	Sinusoidalexcitations	The resultant dynamic load was found to act at ${\displaystyle \frac{H}{3}}$ above the wall base, consistent with the M-O outcomes. Significance of wall inertial forces was considered.
Stadler (1996) [65]	Cantilever walls, dry sand backfill.	0.23	Sinusoidalexcitations	Total earth pressure exhibited a triangular distribution with depth, while dynamic pressure ranged from triangular to rectangular shapes.
Saito et al. (1999) [67]	Gravity walls, dry sand backfill.	0.30	Sinusoidalexcitations	From the experiments, it was revealed that the wall experienced a permanent displacement of $1.4\mathrm{m}$ and a rotation $4°$ away from the backfill soil.
Dewoolkar et al. (2001) [66]	Cantilever walls, saturated sand backfill.	0.25	Sinusoidalexcitations	The resultant dynamic thrust acts at 0.6–0.8H from the wall top. Dynamic pressure distribution varies from triangular to inverted triangular.
Matsuo et al. (2002) [55]	Gravity walls, dry sand backfill.	0.30	Sinusoidalexcitations	The measured dynamic soil pressures were lower than the M-O predictions. Importantly, wall embedment significantly improved the seismic stability.
Nakamura (2006) [56]	Gravity walls, dry sand backfill.	0.30	Sinusoidal and earthquake excitations	Phase relation exists between the wall inertia force and dynamic thrust increment. Total earth pressure distribution was observed to be nonlinear, time-dependent, and influenced by the characteristics of the applied input motion.
Al-Atik and Sitar (2010) [18]	Cantilever walls, dry sand backfill.	0.18	Scaled modified typical earthquake motions	The resultant dynamic thrust acts at ${\displaystyle \frac{H}{3}}$ above the wall base. The M-O method overestimated seismic earth pressures and suggested that it can be ignored on cantilever walls for PGAs below $0.4\mathrm{g}$.
Mikola et al. (2016) [19]	Cantilever walls, basement walls, dry sand backfill.	0.18	Typical earthquake motions	Dynamic earth pressure increases with depth, and the resultant dynamic load acts at $\approx 0.3H$ above the wall base. Cantilever walls could withstand PGA up to $0.4\mathrm{g}$.
Candia et al. (2016) [57]	Cantilever walls, basement walls, dry sand backfill.	0.18	Typical earthquake motions	Seismic earth pressure increases nearly linearly with depth when basement and cantilever walls are supported by soil, instead of being anchored to a rigid base. Dynamic earth pressure is unrelated to cohesion.
Wagner and Sitar (2016) [58]	Cantilever walls, deep stiff wall, cohesionless and cohesive backfill.	0.18–0.38	Typical earthquake motions	The M-O method is a reasonable upper-bound for rigid walls, while flexible walls experience much lower loads than predicted. For deep embedded walls, dynamic loads do not increase continuously with depth and represent only a small portion of the total load.
Jo et al. (2017) [59]	Cantilever walls, dry sand backfill.	0.11–0.22	Sinusoidal and earthquake excitations	The resultant seismic load is positioned at $\approx 0.33H$ above the wall base. The phase difference between the wall and soil significantly affects the magnitude and distribution of seismic soil pressure. The maximum wall stem moment was found to occur when seismic acceleration was directed towards the backfill soil.

provides a summary of significant dynamic centrifuge experiments for seismic earth pressures.

3. Numerical Studies

Numerical methods, including the FE and FD approaches, have been employed since the 1970s (e.g., Clough and Duncan [68], Wood [79], Nadim and Whitman [87]) to evaluate the static and earthquake-induced pressures on retaining structures. These methods have undergone validation with actual case studies and data from physical model tests; however, their predictive ability is still contentious, especially for regions experiencing high PGAs. Various computer programs such as PLAXIS, ABAQUS, FLAC, and ANSYS, among others, have been applied to conduct numerical analyses on retaining wall–soil interaction problems. When appropriately calibrated, numerical analyses, in conjunction with experimental and analytical studies, have proven to be invaluable tools for addressing challenges such as irregular geometry, complex kinematic wall constraints, inhomogeneous soil conditions, elastoplastic behavior of backfill, and realistic seismic ground motions. However, notably, the outcomes of numerical analyses are highly contingent on the accurate selection of soil and interface parameters. This section discusses the numerical methods used to analyze seismic earth pressure problem in retaining structures.

Clough and Duncan [68] utilized the FE method to model the wall–backfill interface for static analyses. Their study considered various modes of wall movement (translation, rotation, or a combination) and different levels of wall roughness (perfectly rough or smooth), thereby providing a more accurate depiction of the interface. They calculated the static earth pressures, showing good alignment with classical limit–state theory, albeit with some nonlinearity influenced by wall deformation modes. The residual displacements were consistent with Terzaghi’s [126] experimental findings. Wood [79] performed a FE study to analyze the earthquake behavior of nonyielding walls, assuming homogeneous, linear elastic soil. The analysis considered the soil–wall bonding and varying soil stiffness. The results indicated that the interface conditions (smooth or bonded wall) did not significantly impact the frequency response or earth pressure distribution.

Nadim and Whitman [87] conducted FE analysis to examine the earthquake behavior of gravity walls. Their study incorporated a predefined failure surface within the backfill, applied a secant shear modulus to account for large strain behavior and incorporated frictional slip elements at the interface between the wall and the soil. Their research revealed that the amplification of wall displacements is significantly influenced by the ratio between the predominant earthquake frequency and the natural frequency of the backfill. Seed and Duncan [88] formulated an extensive FE analysis program called ’SSCOMP’ for assessing SSIs, compaction-induced earth pressures, and deformations. This program underwent validation through various case studies that focused on the placement and compaction of soil in layers, as demonstrated by Seed and Duncan [89].

Siddharthan and Maragakis [90] employed the FE method to model flexible cantilever walls supporting dry sand, considering the nonlinear hysteretic behavior of the soil, as well as changes in lateral stresses and volume associated with grain slip induced by cyclic loads. The impacts of relative soil density and wall flexibility were studied on the dynamic response of the wall. They reported that the maximum wall moments decreased with increasing relative soil density and increased wall flexibility. Additionally, the comparison between the bending moments calculated by the FE model and those computed by Seed and Whitman [103] demonstrated that the latter produced conservative values. Alampalli and Elgamal [127] proposed a numerical model that incorporated the compatibility between the wall mode shapes and the surrounding backfill soil. Their findings demonstrated that wall flexibility influences the dynamic earth pressure distribution. Madabhushi and Zeng [91] utilized SWANDYNE FE code to model the dynamic performance of gravity walls, finding good agreement between the predicted displacements and centrifuge test results for both dry and saturated conditions.

Al-Homoud and Whitman [92] used FE code (FLEX) to investigate gravity walls retaining and founded on dry sand. They validated their analytical model by comparing the FE predictions with centrifuge test outcomes, achieving satisfactory agreement. The study revealed that various displacement modes could occur for these retaining walls, with outward tilting being a dominant type, often accompanied by permanent tilting after shaking. Wu and Finn [93] studied different shear modulus distributions in backfill by simulating a rigid wall on a rigid base via FE modeling. They used an approximate method to express the resultant dynamic pressure as a function of the ratio between the cyclic frequency of the earthquake and the fundamental cyclic frequency of the retaining wall–backfill system. Their findings were consistent with the results from related studies (Wu [128]; Finn et al. [129]; Wu and Finn [130]). The authors concluded that the Wood’s [79] solution should be applied only when the cyclic frequency of the excitation significantly differs from that of the wall–soil system.

Gazetas et al. [69] utilized FEs to simulate the response of flexible walls subjected to short-duration and impulsive base excitations. They incorporated both linear and nonlinear soil models, and their results indicated that accounting for factors such as wall and foundation flexibility, soil yielding, and relative wall–backfill movement reduced the seismic impact on the walls. The findings aligned with the observed resilient performance of these walls during earthquakes. Ostadan [131] introduced a straightforward approach to forecast the maximum dynamic earth pressures on rigid building walls resting on a rigid foundation, via a single-degree-of-freedom system. This method considered kinematic SSI effects, in situ nonlinear dynamic soil properties, and the frequency contents of an earthquake. However, the solution did not consider the inertia effect of the superstructure on the dynamic earth pressure. The solutions derived from this method fall between the lower-bound M-O solution and the upper-bound Wood’s [79] solution, making Ostadan’s [131] approach valuable for providing a speedy and conservative estimate of the dynamic earth pressure distribution. However, a realistic structural system would likely have a lower application point for the equivalent lateral force.

Psarropoulos et al. [70] employed ABAQUS FE software to examine seismic earth pressures on rigid and flexible nonsliding retaining walls. Their study aimed to validate the assumptions underlying Veletsos and Younan’s [115] analytical solution and assess its applicability. The versatility of the FE method allows for considering more realistic scenarios that are challenging for analytical solutions, such as the inclusion of backfill soil heterogeneity and translational foundation flexibility. The numerical study demonstrated convergence with the Wood’s [79] solution for a rigid wall fixed at its base and with Veletsos and Younan’s [115] solution for a wall exhibiting rotational flexibility about its base. The authors contended that assuming complete bonding at the wall–soil interface might lead to inaccuracies, especially at the ground surface where unrealistic tensile stresses may develop. Nevertheless, they noted a reduction in such tensile stresses when a heterogeneous soil is considered in the model.

Pathmanathan et al. [71] conducted nonlinear FE analyses using the DIANA computer program on concrete cantilever walls retaining dry granular backfill. The objective was to specifically evaluate seismic earth pressures and wall displacements under various seismic excitations. The study revealed that pressures exerted on the wall stem surpassed predictions by the M-O method, potentially attributed to the relative flexibility of the structural wedge and the nonmonolithic motion of the driving soil wedge. The authors cautioned that the conclusions drawn from their study might not be applicable to retaining structures with different geometries or material properties. They suggested further research to establish more general conclusions regarding the suitability of the M-O method in assessing seismic earth pressures on cantilever walls.

Madabhushi and Zeng [72] conducted dynamic centrifuge experiments and numerical simulations using the SWANDYNE FE program to investigate the earthquake response of cantilever walls retaining both dry and saturated sand backfills. Their results revealed a significant increase in wall moments during seismic shaking for both backfill conditions. Following shaking, residual wall moments were significantly greater than those observed under static loading. Wall failure was primarily linked to liquefaction in the backfill soil, causing pronounced outward wall movement and uneven backfill subsidence. Numerical simulations reasonably captured the main characteristics observed in the centrifuge tests, with slightly better accuracy in modeling dry backfill compared with saturated backfill. Jung and Bobet [73] extended the work of Veletsos and Younan [115] by including vertical and horizontal translational springs at the base in their analysis using the ABAQUS FE code. Through extensive parametric studies, they determined that the dynamic response was strongly influenced by the wall’s translational, bending, and rotational flexibilities, whereas vertical translation had a negligible effect. Additionally, they reported that rigid walls with rigid foundations are subjected to greater seismic soil pressures than flexible walls with softer foundations.

Green et al. [95] employed the FLAC code to assess the dynamic response of cantilever walls, comparing their findings with predictions from the M-O method for seismic earth pressures and the Newmark sliding block [132] method for permanent wall displacements. Dynamic earth pressures aligned with M-O predictions at low acceleration levels but exceeded these predictions as accelerations increased. This discrepancy was attributed to the flexibility of the cantilever wall system and the nonmonolithic motion of the driving wedge. Permanent wall displacements were consistent with the Newmark’s method [132]. Additionally, Green et al. [95] identified a key divergence between the critical load scenarios for structural design and global stability, challenging the conventional assumption that they are identical. Specifically, the critical load scenario for global stability occurred when $k_h$ was directed away from the backfill, whereas the critical load scenario for structural design occurred when $k_h$ was directed towards the backfill.

Al-Atik and Sitar [18] utilized the FE code OpenSees, while Mikola and Sitar [96] employed the FD code FLAC to simulate both yielding and nonyielding walls retaining and founded on sand. They calibrated their models using centrifuge experiments. Similarly, Candia and Sitar [97] utilized the FD code FLAC to model the same walls examined by Mikola and Sitar [96] but retaining and founded on clay. Their objective was to examine the impact of cohesive backfill on seismic soil pressure. These investigations collectively demonstrated that when a constitutive soil model is employed in numerical simulations and calibrated against centrifuge test data, a numerical model could accurately capture the main characteristics of a soil–wall system. Callisto and Soccodato [98] investigated the earthquake behavior of embedded cantilever walls in dry medium-dense soil using the FD code FLAC with a nonlinear hysteretic model and a Mohr-Coulomb failure criterion. The retaining wall was designed with a pseudostatic method with a small seismic coefficient, and recorded seismic signals were applied at the bedrock level in the numerical simulations.

Athanasopoulos-Zekkos et al. [74] performed numerical simulations using the dynamic PLAXIS FE code to analyze the seismic response of gravity walls, validating the dynamic centrifuge results reported by Nakamura [56]. Their research highlighted that the dynamic earth thrust was reduced because of the phase shift between the peak earth thrust and the wall inertia forces. Trandafir and Ertugrul [75] conducted dynamic FE analysis to assess the impact of expanded polystyrene (EPS) geofoam on the seismic performance of gravity walls. They investigated the behavior of walls with and without an EPS panel between the wall and the retained soil, focusing on the dynamic thrust and wall displacements. Their findings showed that an EPS panel reduced permanent displacements caused by earthquakes. Similarly, Tiznado and Rodríguez-Roa [76] conducted 2D dynamic FE analyses to evaluate the performance of gravity walls on cohesionless soils and revealed that permanent wall displacements were significantly influenced by earthquake amplification effects in the soil.

Ibrahim [77] utilized the PLAXIS FE code to analyze the displacement of gravity walls retaining and founded on dense sand subjected to various historical earthquakes. The results revealed that seismic wall displacements either matched or exceeded the corresponding pseudostatic values. Gravity walls with inclined positive back slopes experienced greater total sliding and rotational displacements compared to those with vertical back walls. Additionally, when the ratio of the wall height to the foundation width was less than 1.4, seismic sliding predominates, and rotation is minimal. However, for higher ratios, the wall became more flexible, resulting in increased rotation, ultimately resulting in overturning and failure when the ratio reached 1.8. Taiebat et al. [99] performed nonlinear dynamic analyses using the FLAC FD code to assess the response of basement walls designed according to the M-O method, with a PGA of $0.46\mathrm{g}$ as required by the Canadian national building code. Their findings indicated that using a PGA of $0.46\mathrm{g}$ for basement wall design based on the M-O method was overly conservative. They suggested that a PGA of 50–60% would provide acceptable performance in terms of the drift ratio. These results aligned with those of previous studies by Al-Atik and Sitar [18] and Lew et al. [16], which were based on dynamic centrifuge experiments.

Gazetas et al. [78] employed FE codes (ABAQUS and PLAXIS) to simulate anchored sheet-pile walls utilizing nonlinear soil models. To address the small-strain stiffness nonlinearity in seismic analysis, they employed an advanced hardening soil model suitable for this purpose [133,134]. The study determined that pseudostatic methods are inappropriate for dynamic SSI, and although Beam-on-Winkler foundation models are better at representing interaction, they fail to accurately model concentrated plastic deformation. The researchers concluded that well-established FE codes can realistically estimate loads and displacements but noted that their numerical models lacked validation through a case history or a physical model. Cakir [80] utilized FE analyses with ANSYS to study how varying backfill properties affect the dynamic response of a cantilever wall, considering backfill and subsoil interactions. A three-dimensional FE model was used to simulate the structural wall and backfill–foundation system, accounting for the nonlinear hysteretic soil behavior, increased lateral stresses, and volumetric changes due to cyclic loads. Special interface elements were included between the backfill and the wall to facilitate sliding and accommodate debonding/recontact behavior. The study emphasized that the dynamic response of cantilever walls can significantly change due to backfill interactions, highlighting the importance of considering these interactions in their design.

Osouli and Zamiran [100] carried out numerical simulations via FLAC FD code to study the earthquake response of cantilever walls with cohesive backfill. Through numerical simulations validated against documented centrifuge tests performed by Candia et al. [57], the study analyzed various seismic events, including Kobe, Loma Prieta, and Chi-Chi, with different PGAs. The results revealed notable differences in the dynamic earth thrust coefficients and the points of action between walls with cohesive sandy backfill and those with cohesionless backfill. For weak to moderate ground motions ($\mathrm{PGA}\le 0.45\mathrm{g}$), the study suggested selecting the dynamic thrust for walls with cohesive sandy backfill at 50–75% of the Seed and Whitman [103] correlation, acting approximately at ${\displaystyle \frac{H}{4}}$ above the wall base. Conversely, for PGAs exceeding $0.45\mathrm{g}$, similar seismic responses were recommended for both backfill types. In this context, they suggested that the dynamic thrust for cohesive sandy backfill should be 75–100% of the Seed and Whitman [103] prediction, with thrust acting at ${\displaystyle \frac{H}{3}}$ above the wall base.

Bakr and Ahmad [81] utilized the PLAXIS FE code to introduce original design charts correlating dynamic earth pressure with the gravity wall displacement. They reported that dynamic active earth pressure is unaffected by earthquake excitations and is independent of wall movement during earthquakes. However, wall movement significantly affects the dynamic passive load. The numerical results indicated that the pseudo-dynamic methods tend to overestimate seismic earth pressure compared to the M-O method. Conti and Caputo [101] employed the FLAC FD code to analyze the dynamic response of cantilever walls, focusing on the suitability of the M-O method for such structures and the potential phase difference between the maximum earth thrust and inertia forces, which are critical for seismic design considerations. Their numerical findings indicated that the maximum earth thrust on the wall stem aligns with the maximum bending moment when the inertia forces act away from the backfill.

Bakr et al. [82] employed the PLAXIS FE code to investigate the impact of dynamic earth pressure on the structural and global stability of a cantilever wall. They also examined the deformation behavior of the wall–backfill system and the significance of natural frequency in stability analysis. The authors identified a difference in the critical load states for structural and global stability. Specifically, structural stability is most critical when the maximum acceleration is directed towards the backfill and the excitation frequency closely matches the wall’s natural frequency. Conversely, global stability is most critical when maximum acceleration occurs with minimal frequency content. Additionally, the natural frequency of the wall does not affect the global stability. However, while the shaking duration impacts the global stability, it does not affect the structural stability of the wall.

Tiwari and Lam [83] used the FE code ABAQUS to examine the earthquake behavior of cantilever walls with crushed rocks as backfill. They reported that the backfill near the stem and the heel slab significantly influences its seismic response. Kitsis et al. [84] extended the work of Athanasopoulos-Zekkos et al. [74] by considering cohesion in the backfill and investigating the seismic behavior of gravity walls via a dynamic PLAXIS FE code. Their numerical results revealed that introducing even a small to moderate amount of cohesion in the backfill significantly enhanced the seismic kinematic response of the wall–soil system compared to cohesionless backfill. Specifically, they observed a 60% reduction in lateral wall displacements, a 40% decrease in rotation, and reduced or eliminated backfill settlements with cohesive backfills. However, the impact of cohesive backfill on dynamic thrust can vary, ranging from beneficial to neutral or even adverse compared with cohesionless backfill. The authors noted that only low levels of cohesion (5 kPa to 15 kPa) in the backfill might positively influence the dynamic response of the system.

Singh et al. [85] utilized the PLAXIS FE code in a numerical study to examine seismic active earth pressure acting on gravity walls with cohesionless backfill. Their findings indicated that the total active earth thrust decreases as the PGA increases to approximately $0.55\mathrm{g}$, after which it begins to increase for higher PGA values. This behavior was attributed to the reduced wall–soil interaction caused by the prevailing overturning effects up to a PGA of $0.55\mathrm{g}$. Beyond this threshold, the formation of failure wedges contributes to the observed increase in total active earth thrust. Tsantilas et al. [86] utilized the FE code ABAQUS to study the dynamic behavior of a U-shaped basement wall and an inverted T-shaped cantilever wall with a shear key, within a dry sand stratum. They validated their numerical findings against dynamic centrifuge experiments of Mikola and Sitar [96] using typical earthquake motions. The study focused on earth pressures behind walls, with the parametric analysis indicating that predicting these pressures is complex. However, importantly, the pressures could align in magnitude and distribution with either the M-O or the Veletsos and Younan [113,114,115] solutions, contingent upon factors such as wall displacement constraints, base rotational flexibility, and excitation intensity.

In recent years, there has been a paradigm shift toward the use of advanced numerical techniques to gain deeper insights into the dynamic behavior of retaining walls. Numerical methods such as FE and FD have been extensively applied in analyzing retaining structures, thus providing invaluable insights into the key mechanisms governing dynamic earth pressure due to their ability to model complex nonlinear dynamic SSI behavior. However, the outcomes of such numerical analyses heavily depend on various modeling aspects, particularly the choice of soil and interface parameters, necessitating thorough calibration against experimental data for reliability. Although these techniques have been validated using real case studies and experimental data, their predictive accuracy continue to be a topic of debate, particularly in regions with high PGAs. Moreover, numerical studies have shown alignment with analytical solutions and indicated that adding plasticity and permitting permanent deformation might further reduce the dynamic earth pressure on walls.

Numerical predictions show no consistent trend in calculating dynamic earth pressure and its distribution. Several researchers [18,19,57,81,90,99] have found that the M-O method does not accurately represent the earthquake behavior of retaining wall–backfill systems. Studies [18,19,57,74] have highlighted that dynamic earth pressure is notably affected by the phase difference between maximum earth thrust and wall inertia forces. Some studies [19,57,90] argue that the system stays in an active state, whereas others [18,71,95] suggest that it may switch between active and passive states during a seismic event. Regarding pressure distribution, researchers [18,19,57] have proposed linear distribution, which contradicts with centrifuge test findings [56,61] that observed nonlinear distribution. These inconsistencies highlight the complexity of seismic earth pressure problems, making it one of the most challenging aspects of SSI.

The reliability of linear or nonlinear earth pressure distributions in retaining wall design depends on alignment between analysis methods and real-field conditions. At low PGA levels ($0.1–0.3\mathrm{g}$), linear pressure distributions dominate, aligning with simplified methods like the M-O approach. These methods work well for rigid walls in dry, homogeneous soils, where soil behavior remains largely elastic. However, scaling limitations in 1-g shaking table experiments (e.g., amplified damping) and idealized assumptions in simulations (e.g., ignoring pore pressure) can lead to inaccuracies. At moderate PGA ($0.3–0.6\mathrm{g}$), nonlinear effects emerge due to soil yielding, partial liquefaction, or flexible wall interactions. Dynamic centrifuge tests and advanced numerical models become critical here, as they capture layered soils, wall flexibility, and pore pressure effects.

For high PGA (≥0.6 g), extreme nonlinearities like liquefaction, soil–structure separation, and resonance necessitate high-g centrifuge tests and specialized constitutive models (e.g., PM4Sand for liquefaction). These scenarios often produce parabolic pressure profiles that experiments may underestimate due to sensor noise, while simulations risk overprediction if boundary conditions are oversimplified. Reliability hinges on matching methods to specific conditions: rigid walls in dry soils at low PGA favor M-O or 1-g tests, while flexible walls in saturated or liquefiable soils at high PGA require centrifuges coupled with advanced numerical frameworks. Hybrid validation–calibrating simulations with experimental data–bridges gaps in scaling and soil nonlinearity.

Engineers must prioritize site-specific analyses, combining physical testing and computational models (for pore pressure and SSI). This approach ensures safer designs in earthquake-prone regions, balancing theoretical consistency with real-world complexity. Ultimately, aligning PGA levels with appropriate methodologies–and cross-validating results–enhances the seismic resilience of retaining structures.

Yielding retaining walls align with analytical predictions during earthquakes by mobilizing active earth pressures, but nonyielding walls exhibit inconsistencies between numerical and experimental results due to their limited displacement, which prevents full stress redistribution. For nonyielding walls, numerical models often oversimplify soil behavior (e.g., using Mohr-Coulomb constitutive model) and assume static pressure distributions, while physical model experiments reveal shifted thrust application points higher or lower than theoretical 0.33–0.5H caused by dynamic SSI, seismic wave propagation effects, and wall flexure. These discrepancies arise from numerical limitations in capturing cyclic degradation, pore pressure dynamics, and multidirectional shaking, as well as experimental scaling artifacts (e.g., boundary interference, stress-level distortions). To resolve this, advanced constitutive models and hybrid validation frameworks are recommended to better replicate field-scale SSI and improve seismic thrust predictions for rigid walls.

The existing literature primarily addresses the assessment of dynamic soil pressure for gravity-type retaining walls, with less focus on cantilever-type retaining walls. Despite their fundamentally different behaviors, gravity walls are rigid, whereas cantilever walls are flexible. According to numerical modeling by Green et al. [95] and shaking table studies by Kloukinas et al. [45], the critical loading scenario for the seismic design of cantilever walls occurs when seismic acceleration is directed away from the backfill, inducing a passive earth pressure state. In contrast, centrifuge studies by Jo et al. [59] indicated that such a condition occurs when seismic acceleration is oriented towards the backfill, leading to an active earth pressure state. Proper identification of the critical loading condition is essential for effective retaining wall design, but the literature shows conflicting results on this matter.

Table 3. Summary of significant numerical studies for seismic earth pressures.

Researchers	Problem Studied	Constitutive Model	Nature of Shaking	Major Findings
Wood (1973) [79]	Rigid wall, elastic uniform soil backfill, Finite elements.	Linear elastic model.	Harmonic base excitations	The results indicated that the interface conditions did not significantly impact the seismic response of rigid walls.
Nadim and Whitman (1983) [87]	Gravity wall, dry backfill, 2D FEmodel.	Elastic model with adjusted dynamic soil properties.	Sinusoidal and typical earthquake motions	The amplification of wall displacements is significantly influenced by the ratio between the predominant earthquake frequency and the natural frequency of the backfill.
Al-Homoud and Whitman(1999) [92]	Gravity wall, cohesionless backfill, 2D FE analyses using FLEX code.	Viscous cap model.	Sinusoidal and typical earthquake motions	Various displacement modes are possible with outward tilting being a dominant mode for these walls, often accompanied by certain permanent outward tilting after shaking.
Psarropoulos et al. (2005) [70]	Gravity and cantilever walls, homogenous and inhomogeneous backfill, 2D FE analyses using ABAQUS code.	Viscoelastic soil model, beam elements for the wall.	Harmonic excitations	The authors noted a decrease in earth pressure for highly flexible walls due to the soil inhomogeneity.
Madabhushi and Zeng (2007) [72]	Cantilever wall, cohesionless backfill, FE analyses using SWANDYNE code.	Modified Mohr-Coulomb soil model and P-Z Mark III soil model, linear elastic model for the wall.	Typical earthquake motions	The failure of the wall was attributed to liquefaction of the backfill soil.
Green et al. (2008) [95]	Cantilever wall, cohesionless backfill, 2D FD analyses using FLAC code.	Mohr-Coulomb model for soil, elastic beam elements for wall.	Sinusoidalexcitations	Dynamic earth pressures aligned with M-O predictions at low acceleration levels but exceeded these predictions as accelerations increased.
Al-Atik and Sitar (2010) [18]	Cantilever walls (open channel structures), cohesionless backfill, 2D FE analyses using OpenSees code.	Pressure dependent multiyield soil model, elastic beam/column elements for open channel structures.	Typical earthquake motions	Peak dynamic earth pressures can be represented using a triangular distribution.
Tiznado and Rodríguez-Roa (2011) [76]	Gravity wall, cohesionless backfill, 2D FE analyses using PLAXIS code.	Hardening soil model with small-strain, linear elastic model for the wall.	Typical earthquake motions	Seismic amplification influences both foundation soil and backfill, markedly affecting wall displacements.
Mikola and Sitar (2013) [96]	Basement and cantilever walls, cohesionless backfill, 2D FD analyses using FLAC code.	UBCHYST model for soil, linear elastic beam elements for the walls.	Typical earthquake motions	The estimated seismic earth pressures agree with centrifuge test data and are significantly lower than those derived analytically using both the M-O and the Seed and Whitman methods.
Candia and Sitar (2013) [97]	Basement and cantilever walls, cohesive backfill, 2D FD analyses using FLAC code.	UBCHYST model for soil, linear elastic beam elements for the walls.	Typical earthquake motions	Peak horizontal pressure on the walls can be estimated linearly, with the resultant located between 0.35–0.45H for basement walls and 0.35–0.40H for cantilever walls.
Athanasopoulos-Zekkos et al. (2013) [74]	Gravity wall, cohesionless backfill, 2D FE analyses using PLAXIS code.	Mohr-Coulomb model for soil, linear elastic model for the wall.	Typical earthquake motions	The dynamic earth thrust was reduced due to the phase shift between the peak earth thrust and the wall inertia forces.
Ibrahim (2014) [77]	Gravity wall, cohesionless backfill, 2D FE analyses using PLAXIS code.	Mohr-Coulomb model for soil, linear elastic model for the wall.	Typical earthquake motions	Gravity walls with inclined positive back slopes experienced greater total sliding and rotational displacements than those with vertical back walls.
Osouli and Zamiran (2017) [100]	Cantilever wall, cohesive backfill, 2D FD analyses using FLAC code.	UBCHYST model for soil, beam structural elements with elastic behavior for the wall.	Typical earthquake motions	For $\mathrm{PGA}\le 0.45\mathrm{g}$, seismic thrust on walls with cohesive backfill can be 50–75% of Seed and Whitman’s [103] correlation, acting at ${\displaystyle \frac{H}{4}}$ above the base. For $\mathrm{PGA}>0.45\mathrm{g}$, it is 75–100%, acting at ${\displaystyle \frac{H}{3}}$ above the base.
Bakr and Ahmad (2018) [81]	Gravity wall, cohesionless backfill, 2D FE analyses using PLAXIS code.	Hardening soil model with small-strain, linear viscoelastic model for the wall.	Sinusoidalexcitations	Wall movement notably affects the dynamic passive thrust. The numerical results indicated that the pseudo-dynamic methods tend to overestimate seismic earth pressure when compared to the M-O method.
Conti and Caputo (2019) [101]	Cantilever wall, cohesionless backfill, nonlinear explicit FD analyses using FLAC code.	Mohr-Coulomb material model for soil, Elastic beam elements for wall and elastic–perfectly plastic interfaces.	Typical earthquake motions	The maximum earth thrust on the wall stem aligns with the maximum bending moment when the inertia forces act away from the backfill.
Bakr et al. (2019) [82]	Cantilever wall, cohesionless backfill, 2D FE analyses using PLAXIS code.	Hardening soil model with small-strain, linear viscoelastic model for the wall.	Typical earthquake motions	The structural stability of the cantilever wall relies significantly on its natural frequency relative to the earthquake frequency content. In contrast, global stability seems unaffected by this factor.
Tiwari and Lam (2021) [83]	Cantilever wall, crushed rocks back-fill, 2D FE analyses using ABAQUS code.	Mohr-Coulomb model for soil, linear elastic model for the wall.	Sinusoidalexcitations	The backfill near the wall stem and the heel slab significantly influences its seismic response.
Kitsis et al. (2022) [84]	Gravity wall, cohesive backfill, 2D FE analyses using PLAXIS code.	Mohr-Coulomb model for soil, linear elastic model for the wall.	Sinusoidal and earthquake excitations	Small values of backfill cohesion (5 kPa to 15 kPa) might positively influence the dynamic response of the wall–backfill system.
Singh et al. (2023) [85]	Gravity wall, cohesionless backfill, 2D FE analyses using PLAXIS code.	Hardening soil model with small-strain, linear elastic model for the wall.	Typical earthquake motions	For $\mathrm{PGA}\le 0.55\mathrm{g}$, total active earth thrust decreases, and it increases for $\mathrm{PGA}>0.55\mathrm{g}$.
Tsantilas et al. (2024) [86]	Basement wall, invered T-shaped cantilever wall, dry sand backfill, 2D FE analyses using ABAQUS code.	Refined plasticity constitutive soil model [135].	Typical earthquake motions	The numerically obtained earth pressures depend on several factors such as wall displacement constraints, base rotational flexibility, and excitation intensity.

presents a summary of significant numerical studies for seismic earth pressures.

4. Conclusions

This critical review analyzed the seismic performance of retaining walls on the basis of experimental and numerical findings. The comprehensive analysis reveals several key insights and ongoing challenges in understanding and predicting the behavior of retaining walls during seismic events. This area has garnered significant attention from researchers, government agencies, and commercial enterprises. Given the vast number of possible backfill conditions and wall geometries, the review concentrates on notable past efforts relevant to this area of study.

The physical model tests reviewed above have (1) generally validated the M-O solution and its extension by Seed and Whitman as an upper-bound for the behavior of yielding structures; (2) consistently shown that yielding retaining structures maintain an active state during seismic events; (3) highlighted ongoing disagreements regarding the distribution of earth pressures along the wall height; (4) demonstrated a pronounced phase difference between the maximum dynamic earth thrust and wall inertia forces across various earthquake intensities in both yielding and nonyielding structures; and (5) offered critical insights and observations on permanent wall displacements caused by earthquakes.

The outcomes of the numerical analyses discussed above have (1) shown that there is no definitive trend for evaluating the magnitude and distribution of seismic earth pressures; (2) highlighted a lack of agreement on the state of the wall–soil system during earthquakes for yielding structures; (3) emphasized the significant impact of wall movement modes on the magnitude and distribution of earth pressures; (4) validated the effectiveness of elastic solutions in accounting for wall and foundation flexibility; (5) established the phase correlation between the wall inertia force and seismic thrust increment; and (6) documented the development of residual earth pressures and displacements post-shaking.

Both experimental and numerical approaches have strengths and limitations. Experimental methods offer valuable real-world data and observations; however, they are often constrained by scale and scope. Numerical simulations, on the other hand, allow for extensive parametric studies and the exploration of complex scenarios, but they require accurate input parameters and validation against empirical data.

In summary, although significant progress has been made in comprehending the seismic behavior of retaining walls, this review underscores the necessity for further research to address the inconsistencies among various methods. More comprehensive studies incorporating a wider range of wall geometries, backfill conditions, and seismic intensities are needed to develop more unified and reliable predictive models. Future studies should focus on integrating experimental data with advanced numerical simulations in addition to an extensive field performance database to refine our understanding of dynamic earth pressures and improve the design and resilience of retaining structures.