The Effect of Failure Criteria on Liquefaction and Pore Pressure Prediction in Non-Plastic Soils †
Abstract
1. Introduction
2. Background
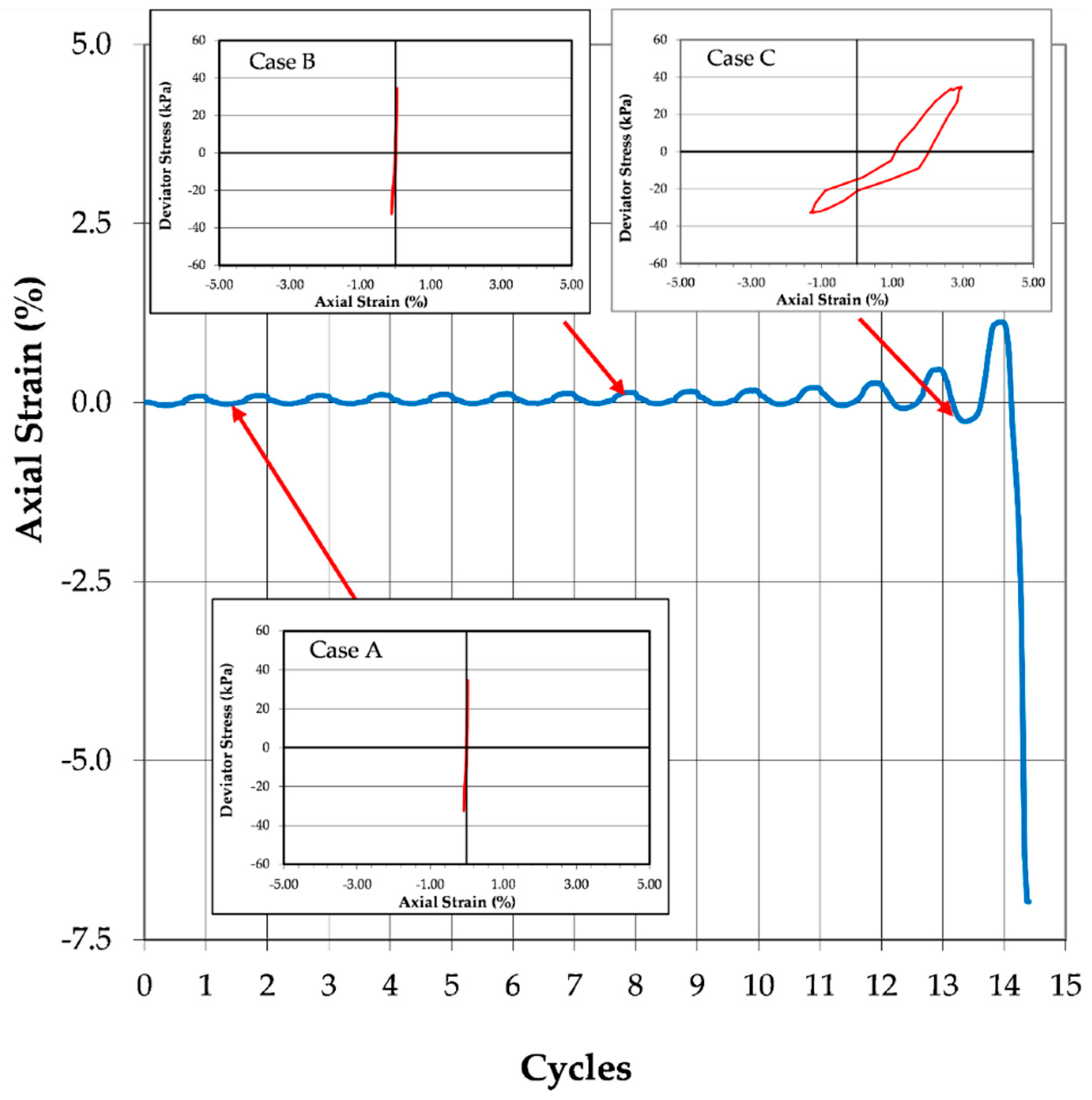
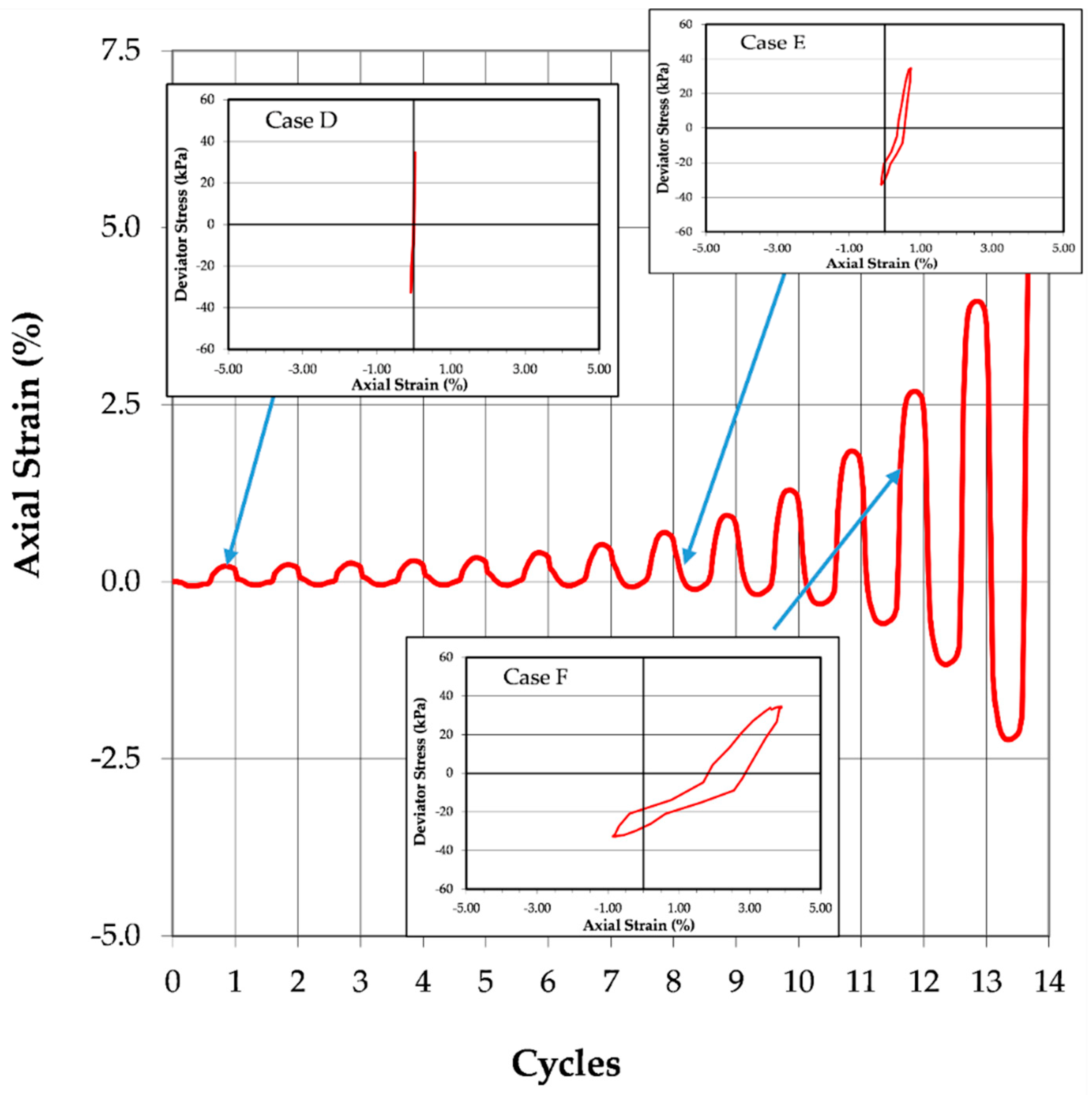
2.1. Modes of Liquefaction Failure
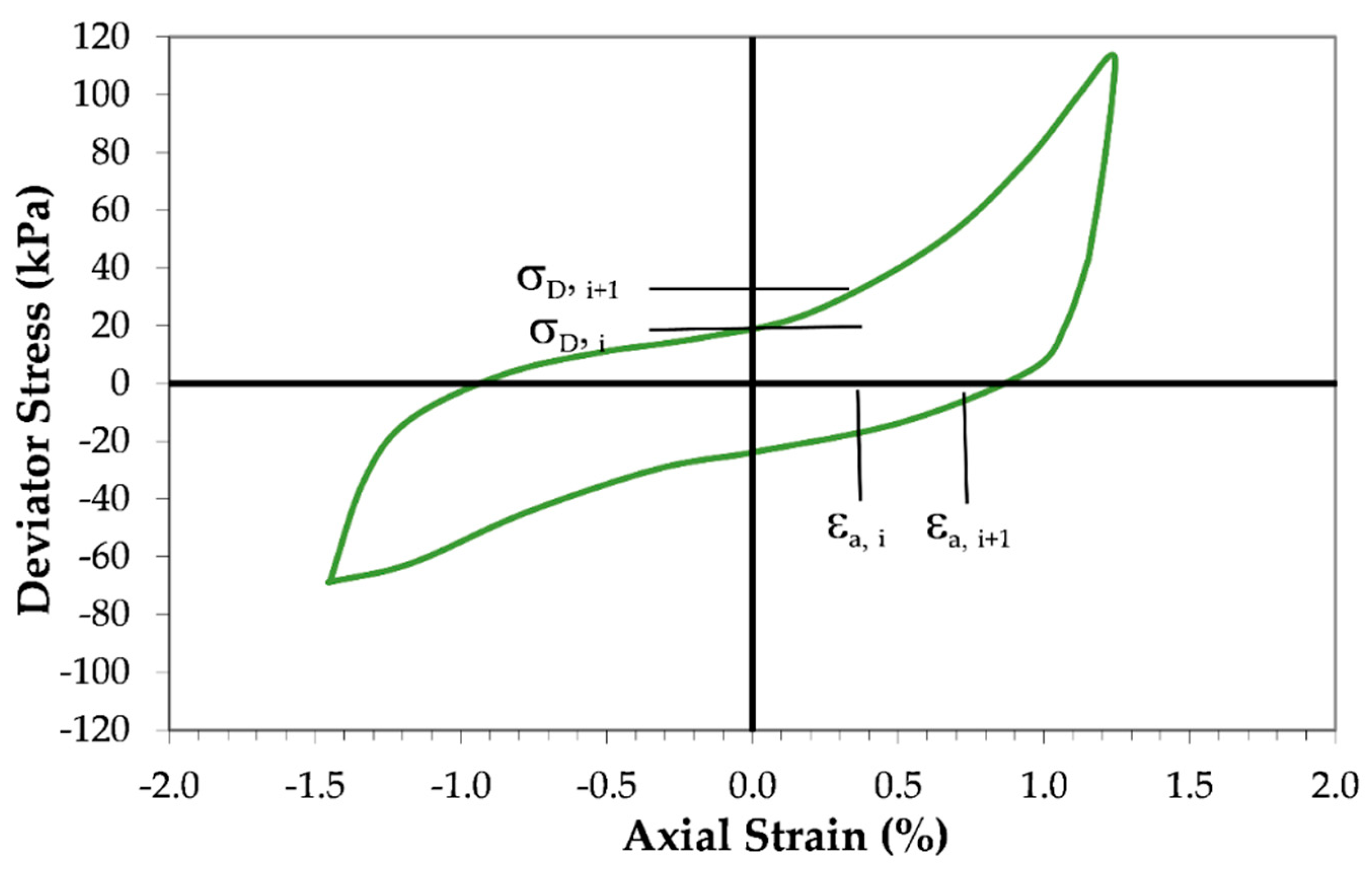
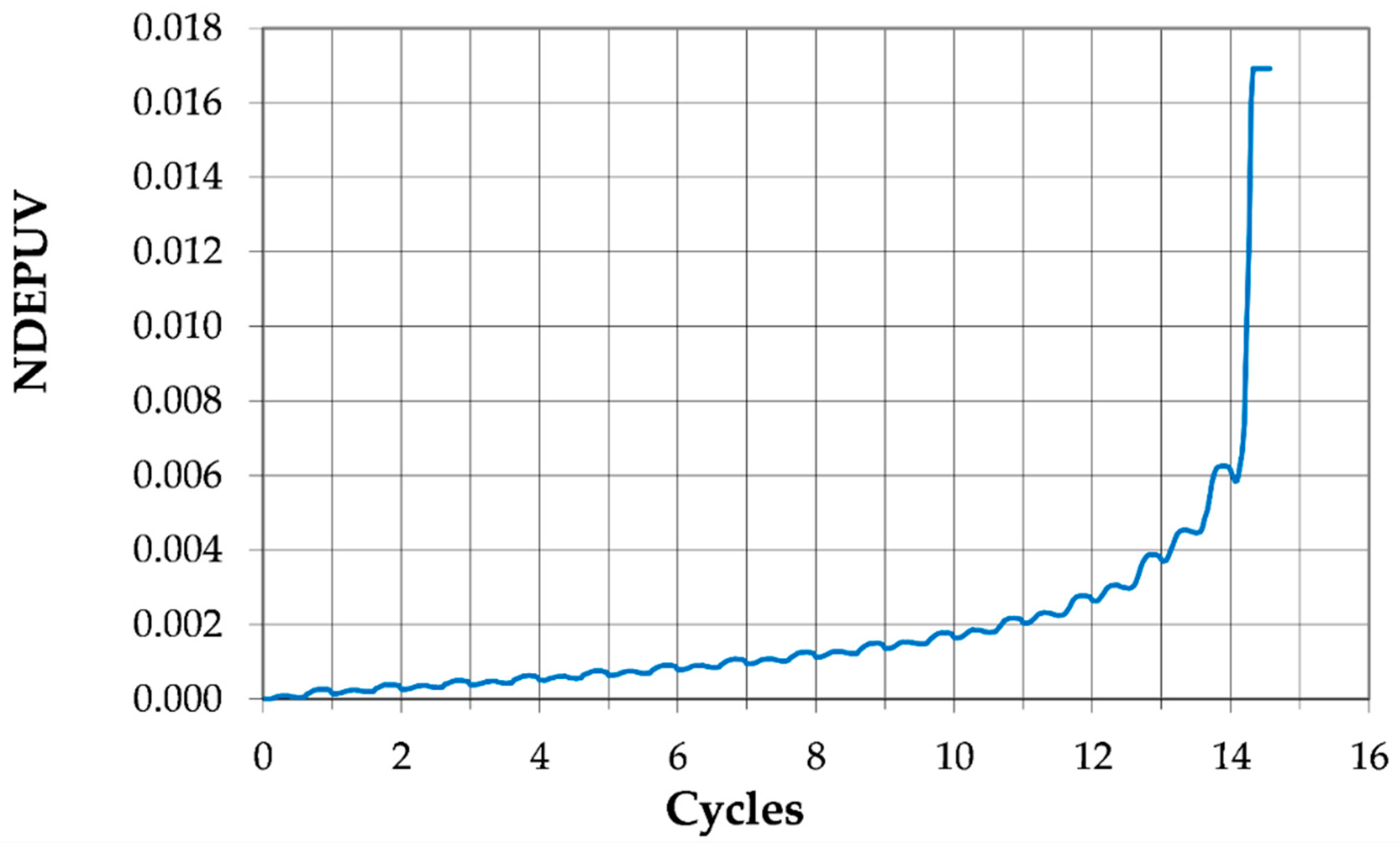
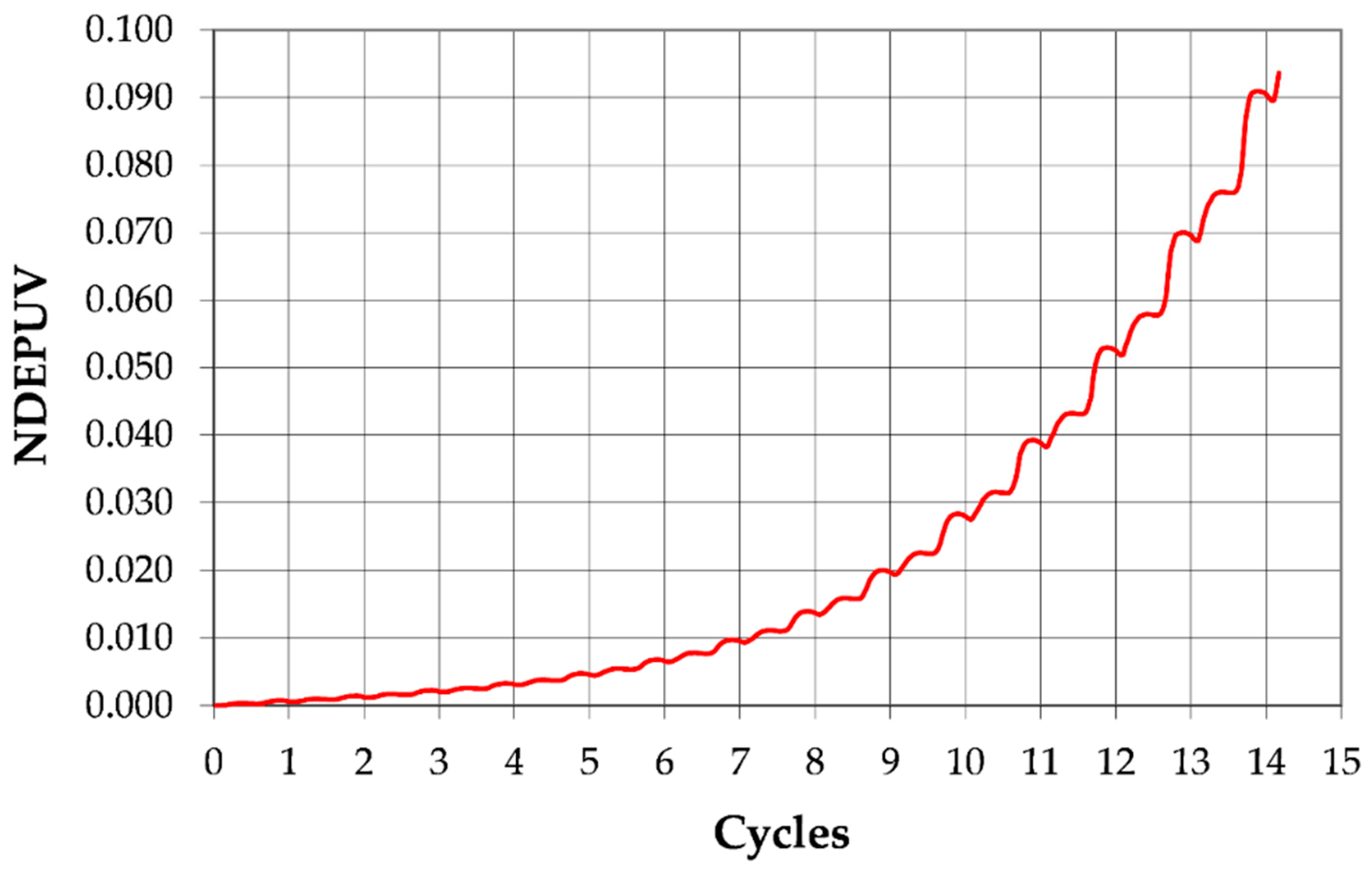
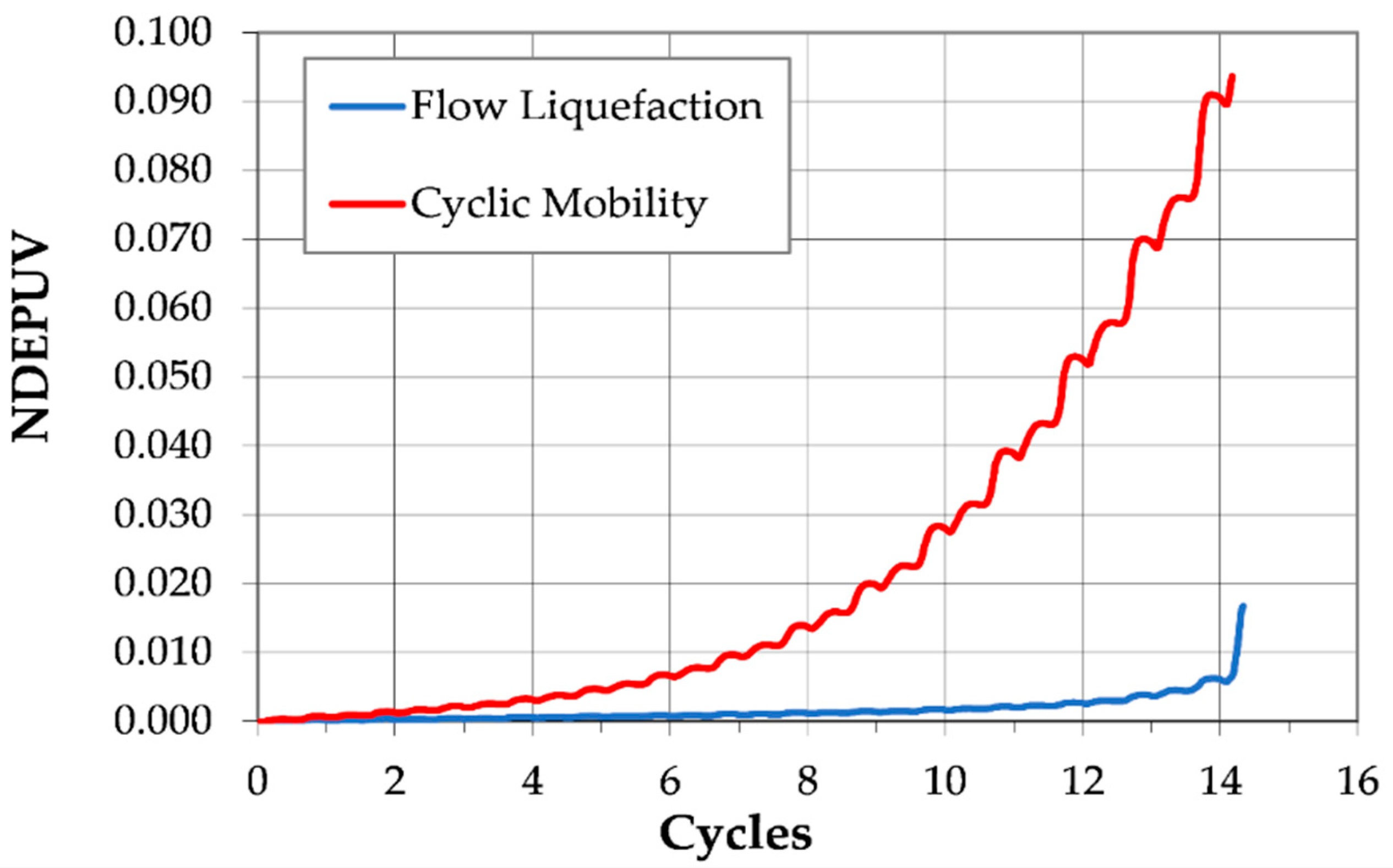
2.2. Normalized Dissipated Energy per Unit Volume
3. Laboratory Testing Program
3.1. Soils Tested
3.2. Soil Mixtures
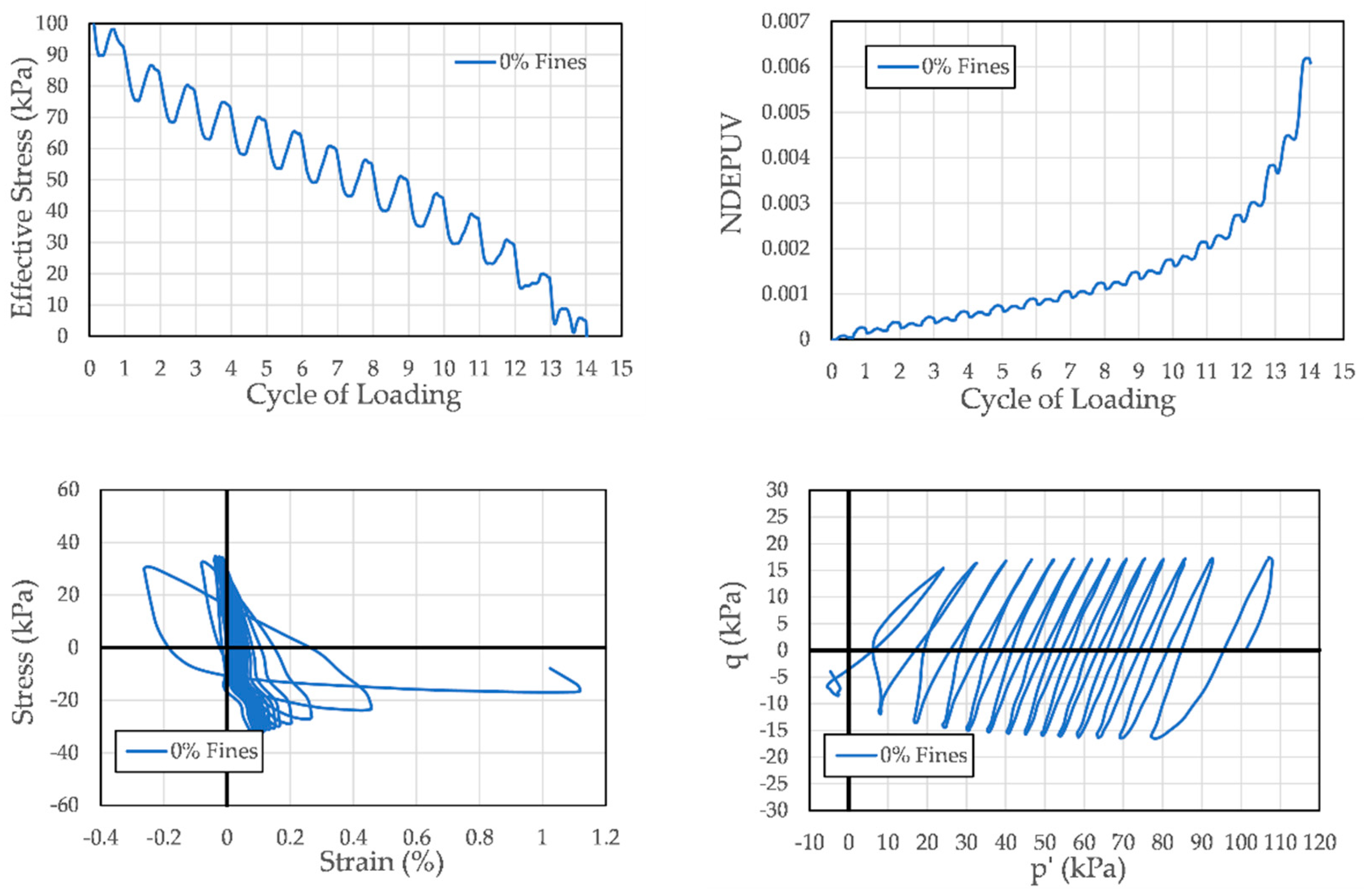
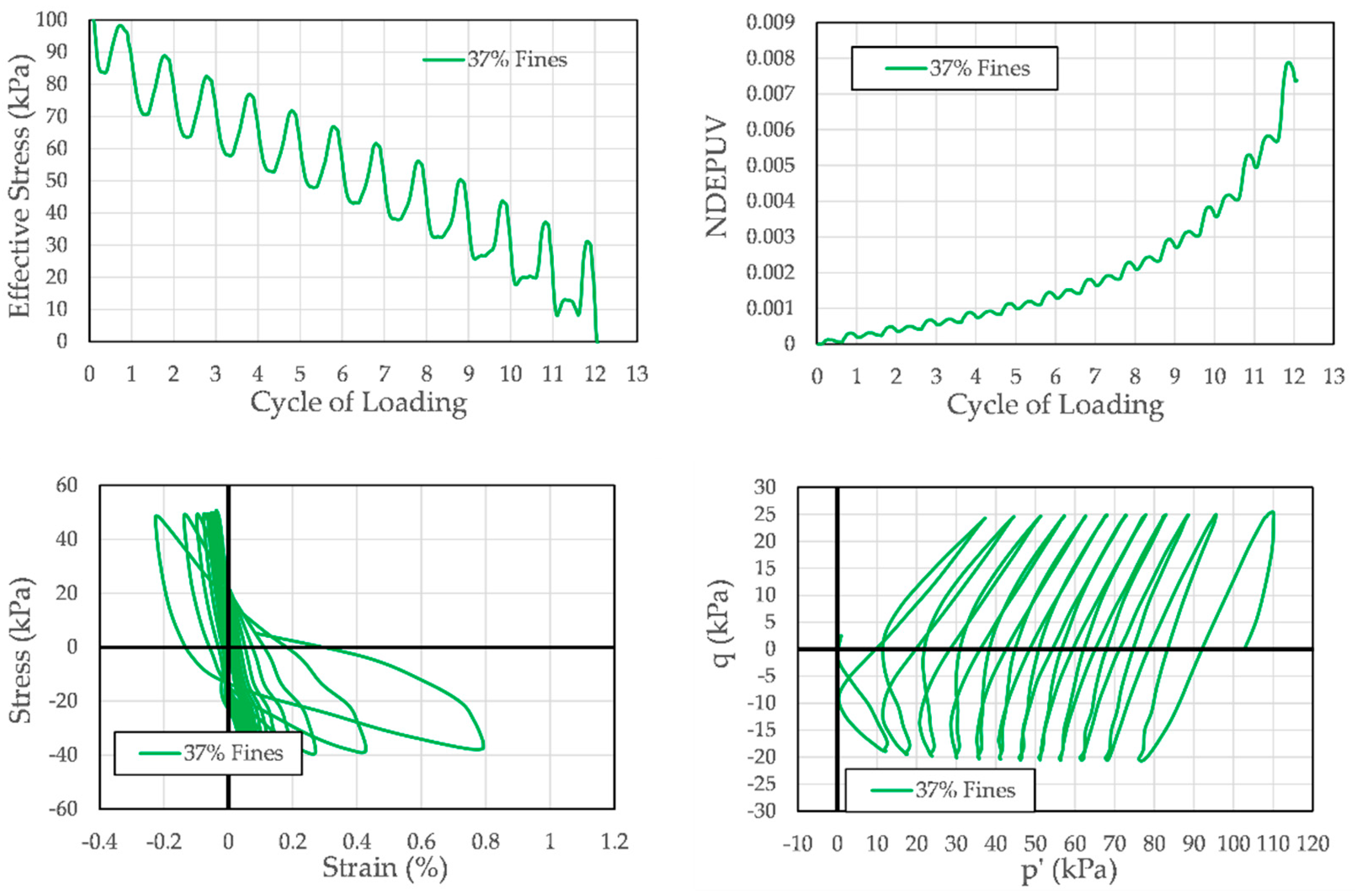
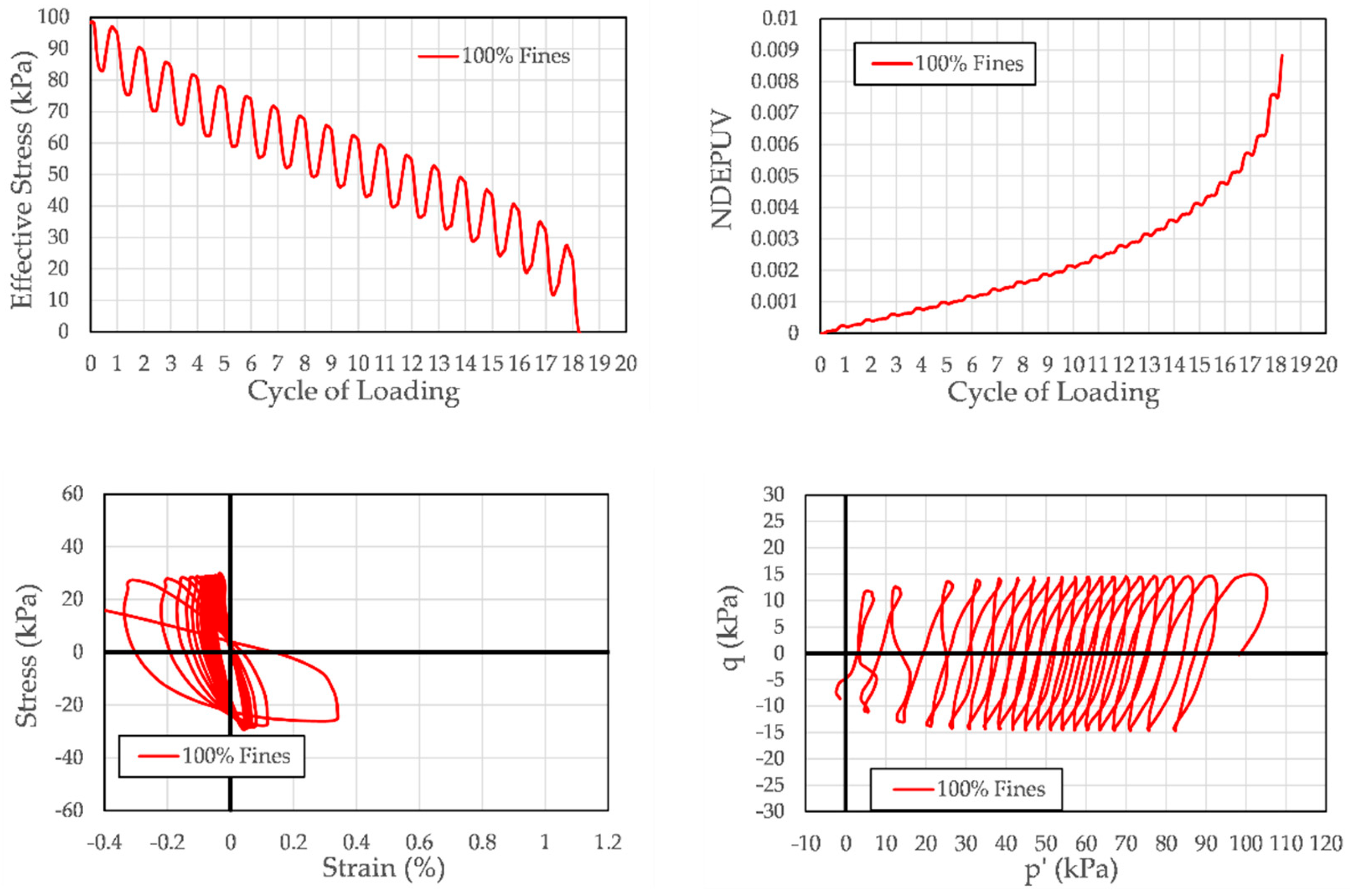
3.3. Cyclic Triaxial Testing
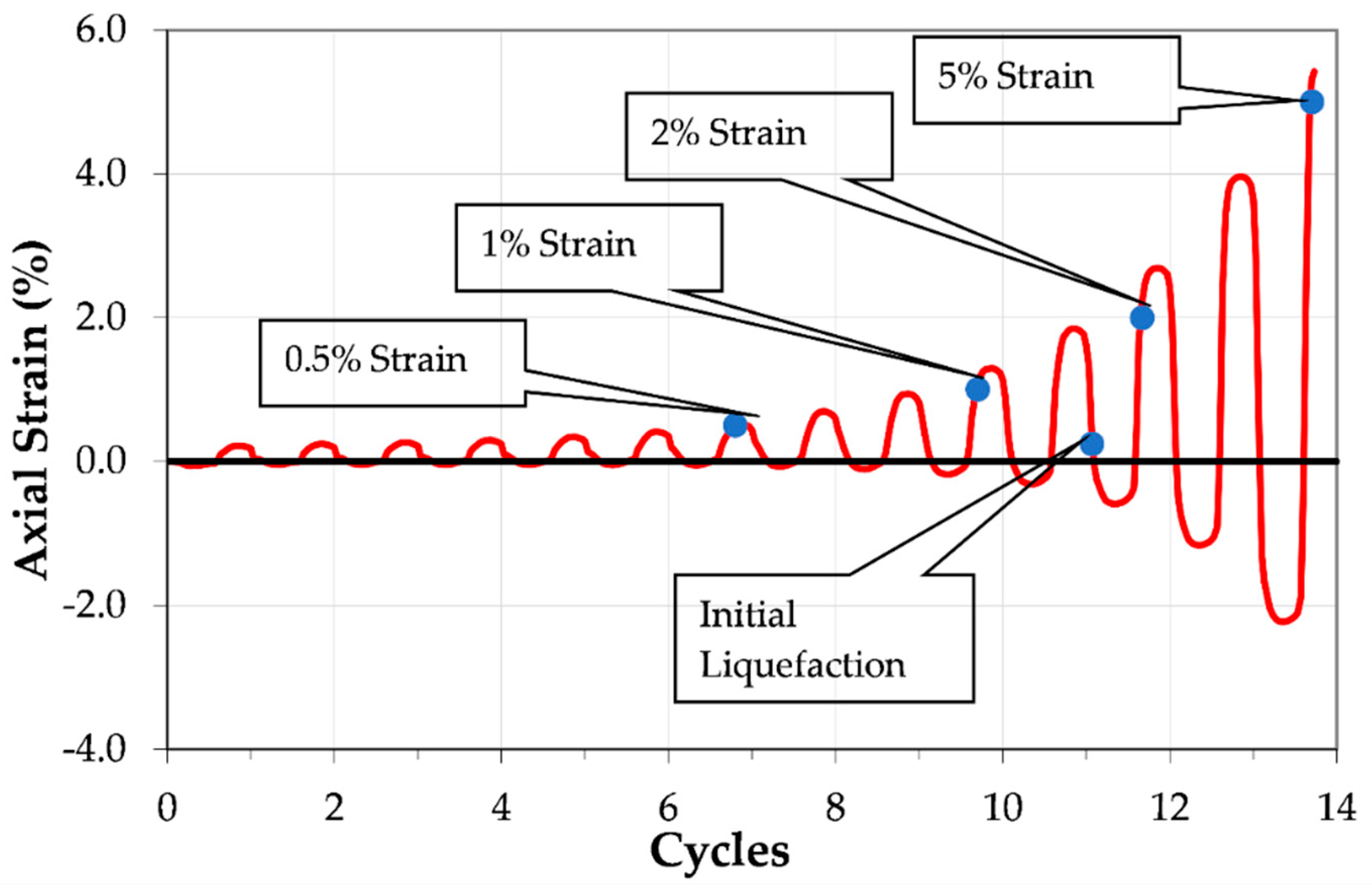
- Stress-based criterion: The stress-based liquefaction criterion used was initial liquefaction. Initial liquefaction was defined as occurring when the effective stress acting on the specimen reached 0 kPa. This corresponds to a pore pressure ratio, ru, of 1.0, where ru is the ratio of the excess pore pressure that has been generated in the specimen during cyclic loading to the initial effective confining stress.
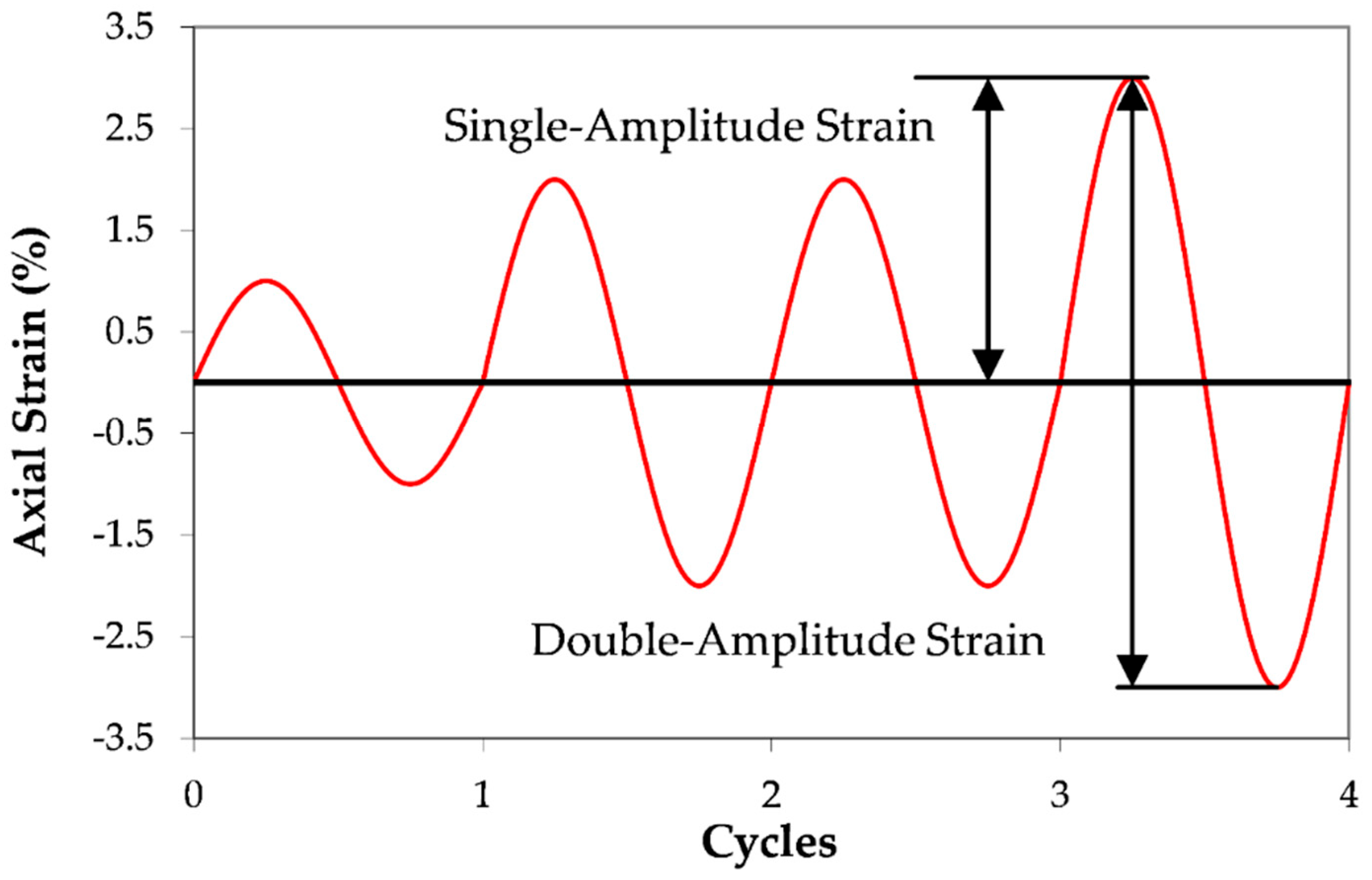
- Strain-based criteria: Liquefaction was also defined at four strain thresholds—0.5%, 1%, 2%, and 5% single-amplitude axial strain—in either extension or compression.
- Flow liquefaction failure: Specimens reaching initial liquefaction within 5% of the number of cycles of loading required to obtain 0.5% axial strain. For example, if a specimen reached 0.5% axial strain in 10.0 cycles of loading, it would be deemed to have experienced flow liquefaction if it achieved initial liquefaction (i.e., zero effective stress) between 9.5 and 10.5 cycles of loading.
- Cyclic mobility failure: Specimens requiring more than 5% of the number of cycles of loading required to obtain 0.5% axial strain to reach initial liquefaction after attaining 0.5% axial strain.
4. Discussion
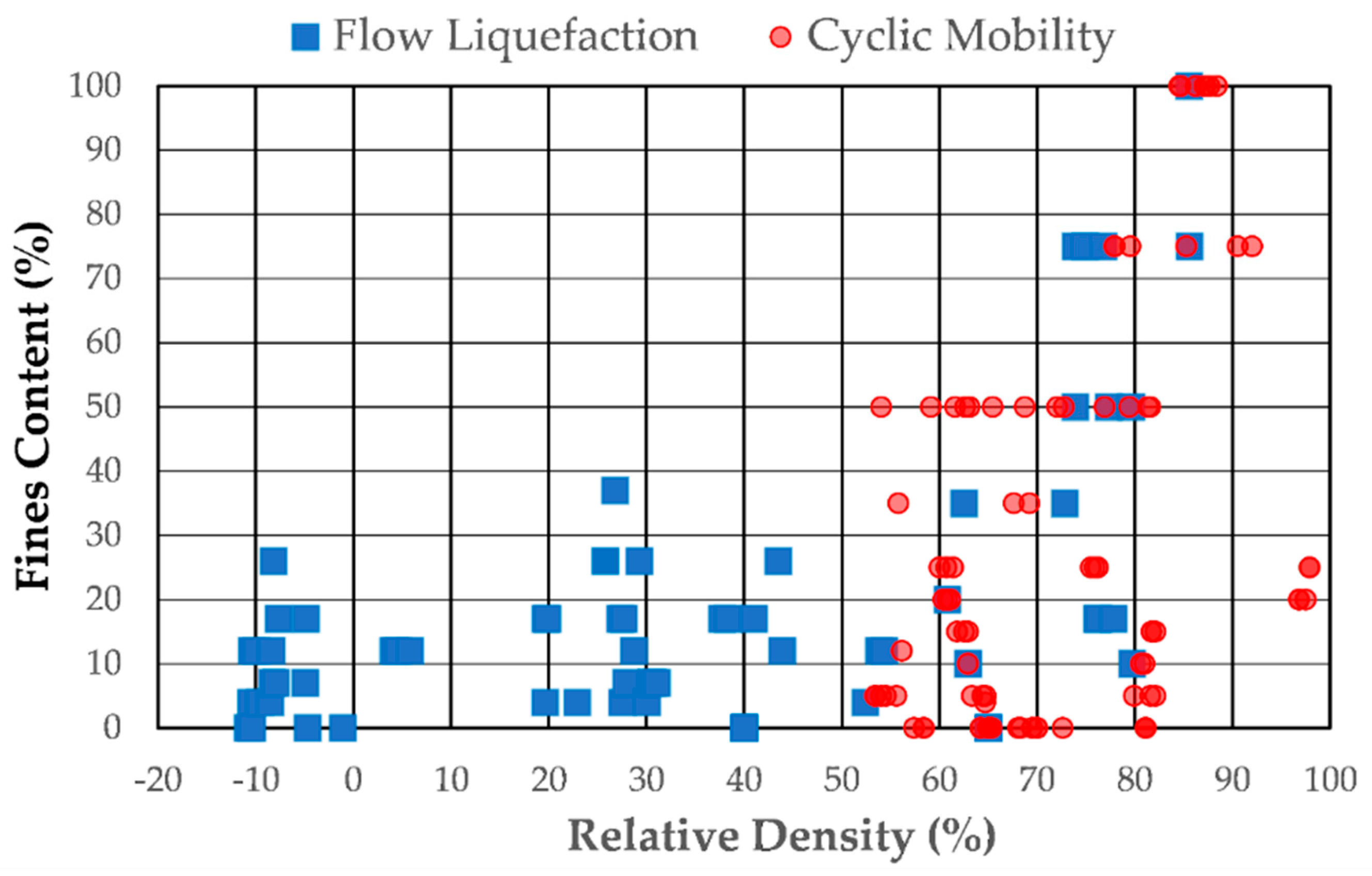
4.1. Effect on Relative Density
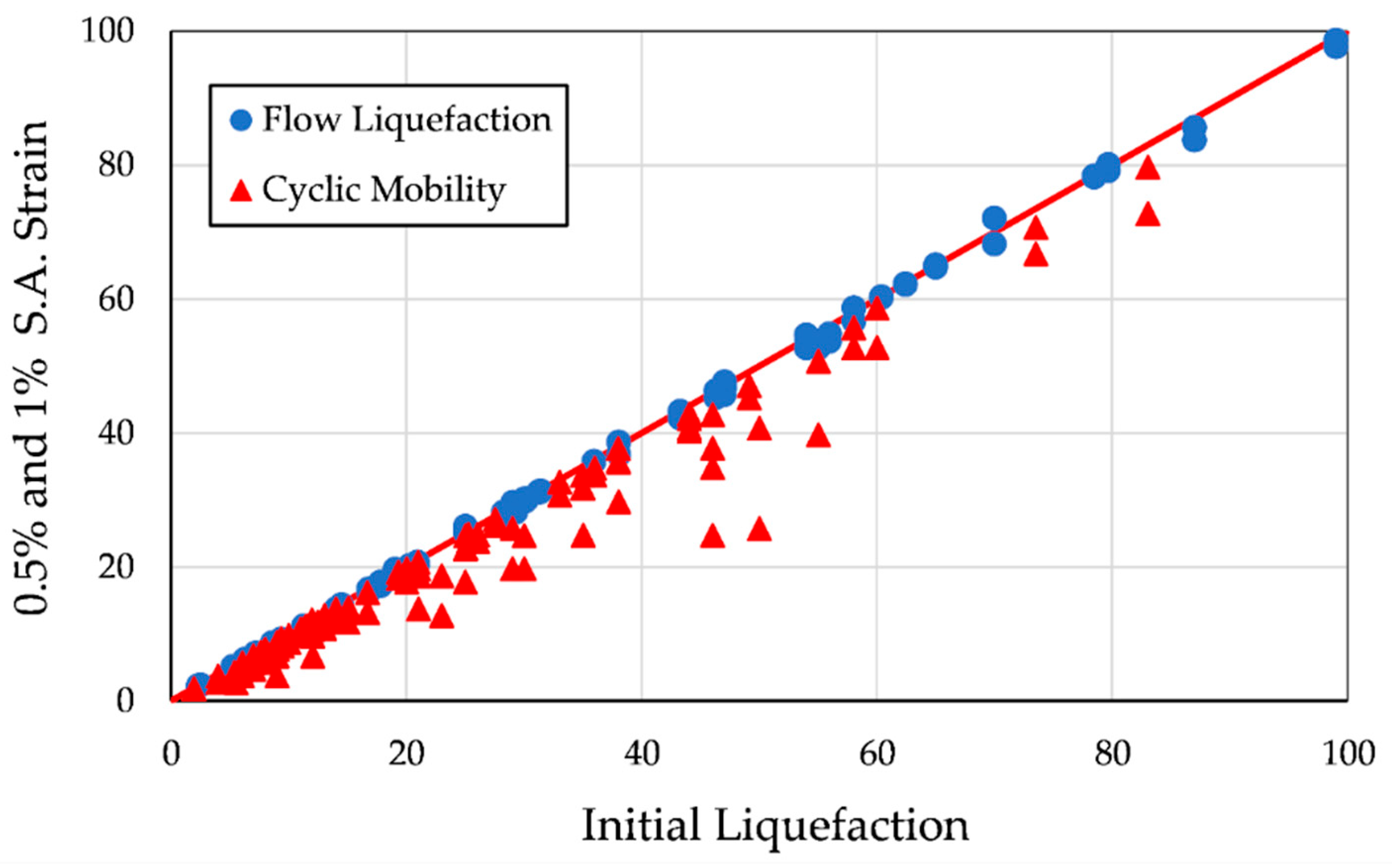
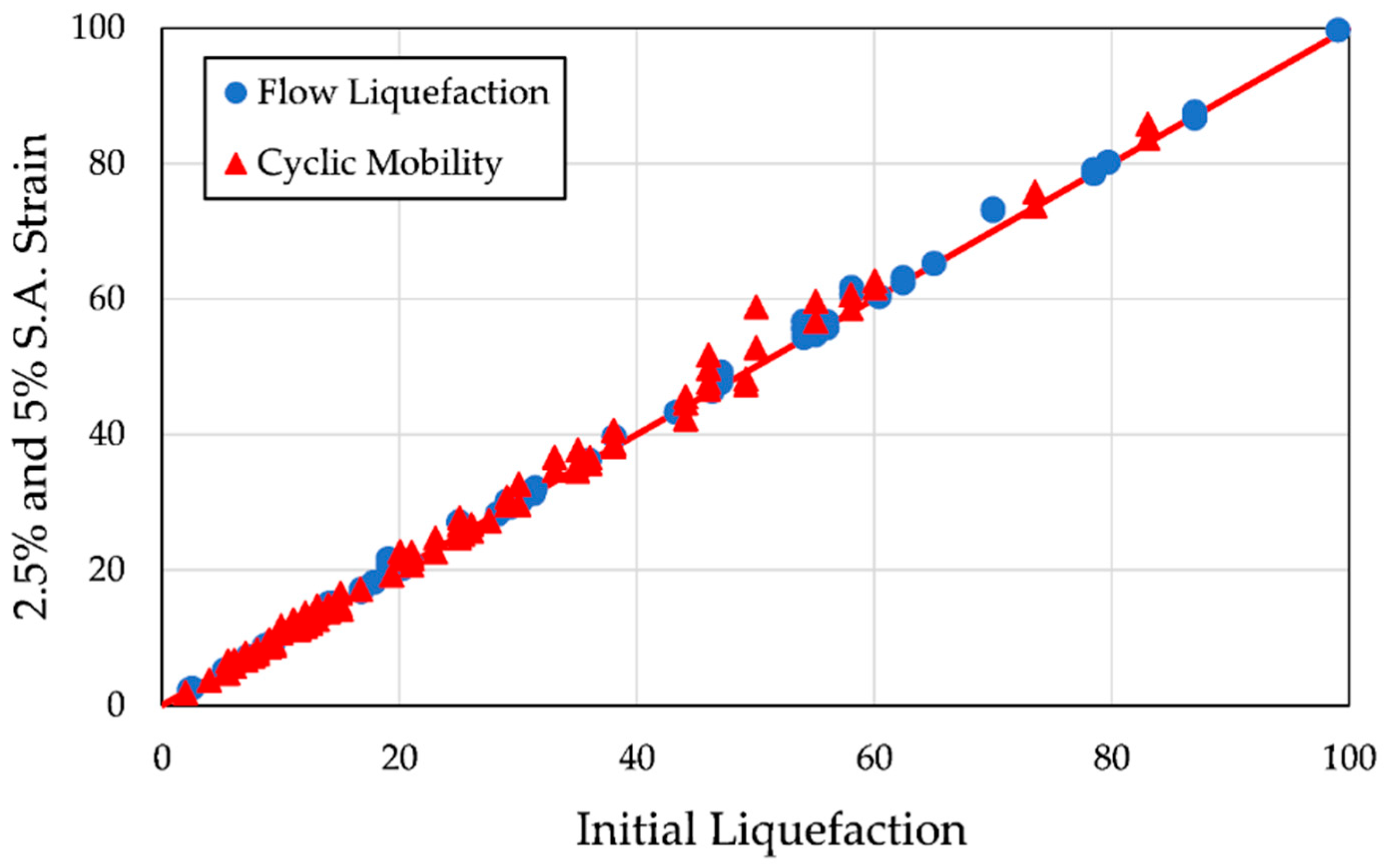
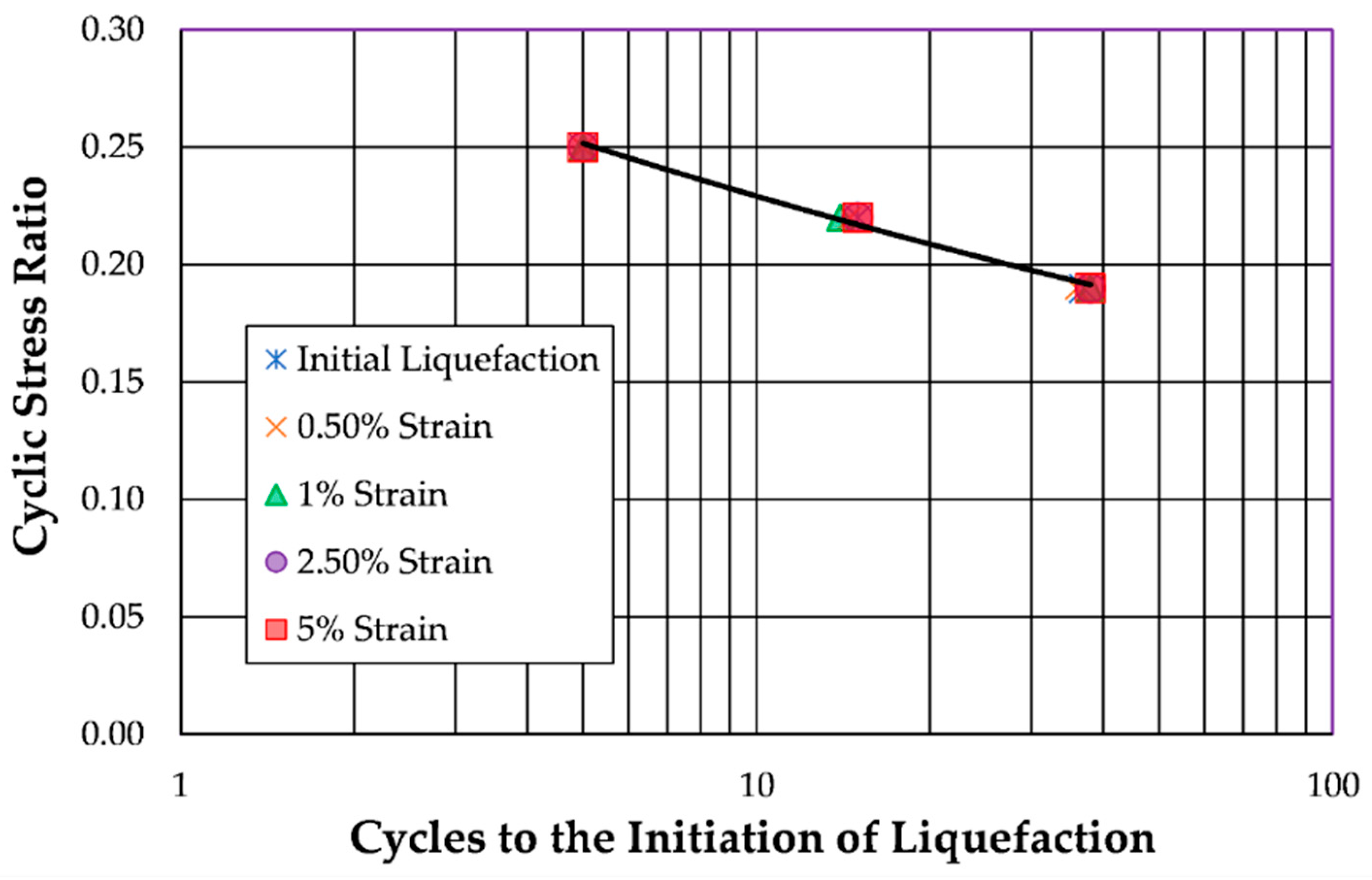
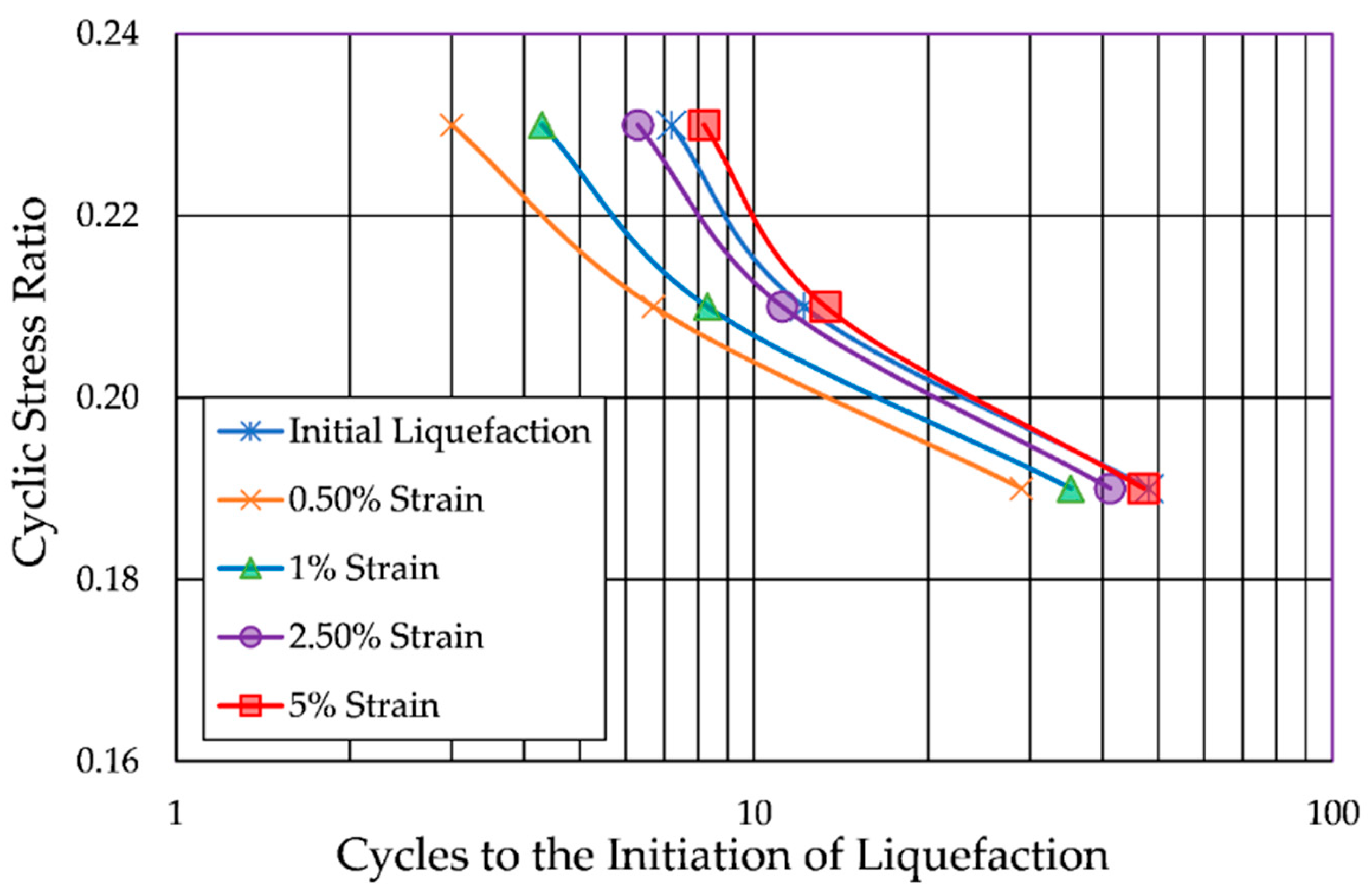
4.2. Effect of Failure Criteria on the Number of Cycles Required to Trigger Liquefaction
4.3. Cyclic Resistance of Soils Undergoing Flow Liquefaction
4.4. Cyclic Resistance of Soils Undergoing Cyclic Mobility
4.5. Dissipated Energy in Specimens Subjected to Flow Liquefaction and Cyclic Mobility
5. Conclusions
- The most critical factor influencing the interpretation of cyclic triaxial test results is whether the soil undergoes flow liquefaction or cyclic mobility. The difference between the two behaviors is critical, because flow liquefaction results in sudden, large, permanent displacements of the soil mass. Conversely, cyclic mobility typically results in little, if any, permanent deformation of the soil mass.
- Relative density is the primary determinant of whether a soil experiences flow liquefaction or cyclic mobility. Soils with relative densities below 50% consistently underwent flow liquefaction, whereas 82% of soils with relative densities above 50% exhibited cyclic mobility. The influence of non-plastic fines content on failure mode susceptibility was found to be minimal.
- For soils susceptible to flow liquefaction, the choice of liquefaction criterion is relatively insignificant, because the rapid strain development causes all criteria to yield similar cycle counts for liquefaction initiation.
- For soils susceptible to cyclic mobility, the choice of liquefaction criterion is crucial, as the gradual accumulation of strain leads to significant variations in the number of cycles required for liquefaction initiation.
- Soils that undergo flow liquefaction require much less energy dissipation to trigger liquefaction, with the majority of their energy loss coming during the final, large, permanent displacement that accompanies initial liquefaction.
- Soils that undergo cyclic mobility require more energy to achieve a state of zero effective stress than specimens that undergo flow liquefaction. This is because these specimens undergo large biaxial straining without ever achieving the large, permanent, monotonic displacement that accompanies flow liquefaction.
- When choosing a liquefaction criterion for a cyclic triaxial test, it is recommended that either initial liquefaction or a minimum of 2.5% single-amplitude axial strain be chosen. These criteria will ensure a more accurate prediction of pore pressure generation if the test results are used to determine the input parameters for pore pressure generation models.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Seed, H.B.; Lee, K.L. Liquefaction of Saturated Sands During Cyclic Loading. J. Soil Mech. Found. Div. 1966, 92, 105–134. [Google Scholar] [CrossRef]
- Lee, K.L.; Seed, H.B. Cyclic Stress Conditions Causing Liquefaction of Sand. J. Soil Mech. Found. Div. 1967, 93, 47–70. [Google Scholar] [CrossRef]
- Castro, G. Liquefaction of Sands. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, 1969. [Google Scholar]
- Salvatore, N.; Pizzi, A.; Rollins, K.M.; Pagliaroli, A.; Amoroso, S. Liquefaction assessment of gravelly soils: The role of in situ and laboratory geotechnical tests through the case study of the Sulmona basin (Central Italy). Ital. J. Geosci. 2022, 141, 216–229. [Google Scholar] [CrossRef]
- Kumar, D.R.; Samui, P.; Burman, A. Suitability assessment of the best liquefaction analysis procedure based on SPT data. Multiscale Multidiscip. Model. Exp. Des. 2023, 6, 319–329. [Google Scholar] [CrossRef]
- Ntritsos, N.; Cubrinovski, M. A CPT-based effective stress analysis procedure for liquefaction assessment. Soil Dyn. Earthq. Eng. 2020, 131, 106063. [Google Scholar] [CrossRef]
- ASTM D5311/D5311M-13; Standard Test Method for Load Controlled Cyclic Triaxial Strength of Soil. ASTM International: West Conshohocken, PA, USA, 2013. Available online: www.astm.org (accessed on 11 March 2025).
- Polito, C. The Effects of Non-Plastic and Plastic Fines on the Liquefaction of Sandy Soils. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 10 December 1999. [Google Scholar]
- Askari, F.; Dabiri, R.; Shafiee, A.; Jafari, M. Liquefaction resistance of sand-silt mixtures using laboratory-based shear wave velocity. Int. J. Civ. Eng. 2011, 9, 135–144. [Google Scholar]
- Khashila, M.; Hussien, C.M.; Karray, M. On the Dynamic Soil Behavior under Triaxial and Simple Shear Modes. Int. J. Geomech. 2021, 21, 8. [Google Scholar] [CrossRef]
- Gobbi, S.; Reiffsteck, P.; Lenti, L.; d’Avila, M.P.S.; Semblat, J.F. Liquefaction triggering in silty sands: Effects of non-plastic fines and mixture-packing conditions. Acta Geotech. 2022, 17, 391–410. [Google Scholar] [CrossRef]
- Janalizadeh Choobbasti, A.; Selatahneh, H.; Karimi Petanlar, M. Effect of fines on liquefaction resistance of sand. Innov. Infrastruct. Solut. 2020, 5, 87. [Google Scholar] [CrossRef]
- Enomoto, T. Liquefaction and post-liquefaction properties of sand-silt mixtures and undisturbed silty sands. Soils Found. 2019, 59, 2311–2323. [Google Scholar] [CrossRef]
- El Ghoraiby, M.; Park, H.; Manzari, M. Stress-strain behavior and liquefaction strength characteristics of Ottawa F65 sand. Soil Dyn. Earthq. Eng. 2020, 138, 106292. [Google Scholar] [CrossRef]
- Nong, Z.-Z.; Park, S.-S.; Lee, D.-E. Comparison of sand liquefaction in cyclic triaxial and simple shear tests. Soils Found. 2021, 61, 1071–1085. [Google Scholar] [CrossRef]
- Ni, X.-Q.; Zhang, Z.; Ye, B.; Zhang, S. Unique relation between pore water pressure generated at the first loading cycle and liquefaction resistance. Eng. Geol. 2022, 296, 106476. [Google Scholar] [CrossRef]
- Sze, H.; Yang, J. Failure Modes of Sand in Undrained Cyclic Loading: Impact of Sample Preparation. J. Geotech. Geoenviron. Eng. 2014, 140, 152–169. [Google Scholar] [CrossRef]
- Green, R.A.; Mitchell, J.K.; Polito, C.P. An energy-based pore pressure generation model for cohesionless soils. In Proceedings of the John Booker Memorial Symposium—Developments in Theoretical Geomechanics, Sydney, NSW, Australia, 16–17 November 2000; Balkema: Rotterdam, The Netherlands, 2000; pp. 383–390. [Google Scholar]
- Nemat-Nasser, S.; Shokooh, A. A Unified Approach to Densification and Liquefaction of Cohesionless Sand in Cyclic Shearing. Can. Geotech. J. 1979, 16, 659–678. [Google Scholar] [CrossRef]
- Berrill, J.B.; Davis, R.O. Energy Dissipation and Seismic Liquefaction of Sands: Revised Model. Soils Found. 1985, 25, 106–118. [Google Scholar] [CrossRef] [PubMed]
- Figueroa, J.; Saada, A.; Liang, L.; Dahisaria, N. Evaluation of Soil Liquefaction by Energy Principles. J. Geotech. Eng. 1994, 120, 1554–1569. [Google Scholar] [CrossRef]
- Baziar, M.H.; Shahnazari, H.; Sharafi, H. A laboratory study on the pore pressure generation model for Firouzkooh silty sands using hollow torsional test. Int. J. Civ. Eng. 2011, 9, 126–134. [Google Scholar]
- Jafarian, Y.; Towhata, I.; Baziar, M.H.; Noorzad, A.; Bahmanpour, A. Strain energy-based evaluation of liquefaction and residual pore water pressure in sands using cyclic torsional shear experiments. Dyn. Earthq. Eng. 2012, 35, 13–28. [Google Scholar] [CrossRef]
- Kokusho, T. Liquefaction Potential Evaluation: Energy-Based Method Compared to Stress-Based Method. In Proceedings of the Seventh International Conference on Case Histories in Geotechnical Engineering, Chicago, IL, USA, 29 April–4 May 2013. [Google Scholar]
- Green, R.A. Energy-Based Evaluation and Remediation of Liquefiable Soils. Ph.D. Thesis, Department of Civil Engineering, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2001. [Google Scholar]
- Silver, M.L. Laboratory Triaxial Testing Procedures To Determine The Cyclic Strength of Soils. NUREG-0031; National Technical Information Service: Springfield, VA, USA, 1977. [Google Scholar]
- Ladd, R.S. Preparing Test Specimens Using Undercompaction. Geotech. Test. J. 1978, 1, 16–23. [Google Scholar] [CrossRef]
- Seed, H.B.; Idriss, I.M. Ground Motions and Soil Liquefaction During Earthquakes; Earthquake Engineering Research Institute: Berkeley, CA, USA, 1982; p. 134. Available online: http://catalog.hathitrust.org/api/volumes/oclc/9388022.html (accessed on 20 March 2025).


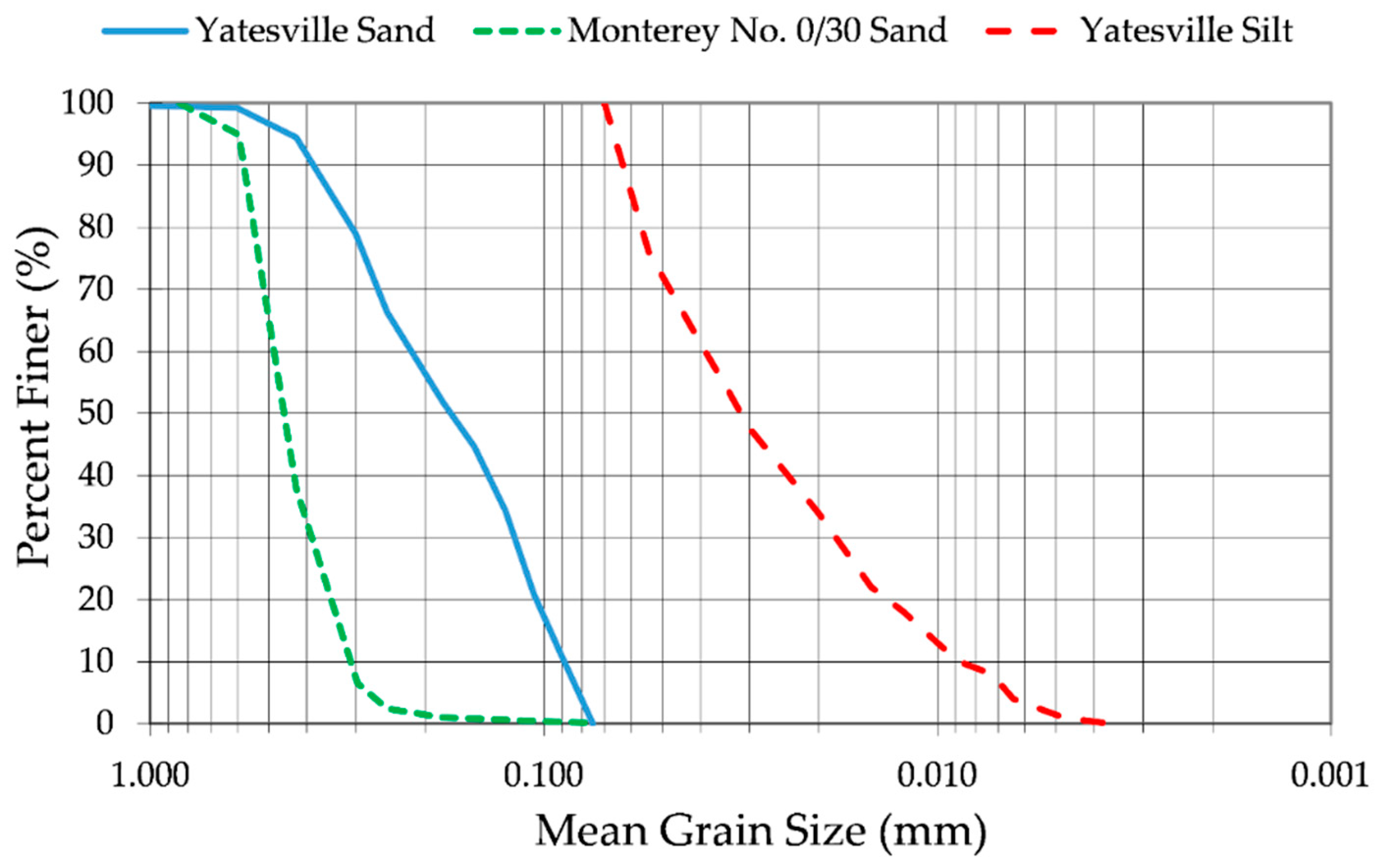


| Yatesville Sand | Monterey 0/30 Sand | Yatesville Silt | |
|---|---|---|---|
| USCS Classification | SP | SP | ML |
| Specific Gravity, Gs | 2.72 | 2.65 | 2.78 |
| Median Grain Size, D50 (mm) | 0.18 | 0.43 | 0.03 |
| Coefficient of Uniformity, Cu | 2.4 | 1.5 | 4.4 |
| Coefficient of Curvature, Cc | 0.77 | 1.04 | 0.93 |
| Maximum Index Void Ratio | 0.972 | 0.821 | 1.723 |
| Minimum Index Void Ratio | 0.653 | 0.631 | 0.727 |
| Liquid Limit, LL | Not Measured | Not Measured | Not Determinable |
| Plastic Limit, PL | Not Measured | Not Measured | Not Determinable |
| Plasticity Index, PI | Not Measured | Not Measured | 0 |
| Silt Content (%) | ||||||||
|---|---|---|---|---|---|---|---|---|
| 4 | 7 | 12 | 17 | 26 | 37 | 50 | 75 | |
| USCS Classification | SP | SP-SM | SP-SM | SM | SM | SM | SM | ML |
| Specific Gravity, Gs | 2.72 | 2.72 | 2.73 | 2.73 | 2.73 | 2.74 | 2.75 | 2.76 |
| Median Grain Size, D50 (mm) | 0.17 | 0.16 | 0.17 | 0.17 | 0.17 | 0.15 | 0.06 | 0.03 |
| Coefficient of Uniformity, Cu | 2.6 | 3.5 | 4.5 | 6.6 | 8.7 | 13.3 | 7.2 | 2.6 |
| Coefficient of Curvature, Cc | 0.75 | 0.91 | 1.10 | 1.10 | 0.62 | 0.80 | 0.87 | 0.75 |
| Maximum Index Void Ratio | 0.911 | 0.872 | 0.840 | 0.802 | 0.728 | 0.684 | 1.031 | 1.314 |
| Minimum Index Void Ratio | 0.609 | 0.528 | 0.517 | 0.502 | 0.483 | 0.397 | 0.423 | 0.591 |
| Silt Content (%) | ||||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 15 | 20 | 25 | 35 | 50 | 75 | |
| USCS Classification | SP | SP-SM | SP-SM | SM | SM | SM | SM | ML |
| Specific Gravity, Gs | 2.66 | 2.66 | 2.67 | 2.67 | 2.68 | 2.69 | 2.71 | 2.74 |
| Median Grain Size, D50 (mm) | 0.43 | 0.43 | 0.43 | 0.43 | 0.40 | 0.36 | 0.07 | 0.05 |
| Coefficient of Uniformity, Cu | 1.7 | 2.2 | 11.5 | 17.0 | 25.3 | 38.5 | 21.3 | 6.2 |
| Coefficient of Curvature, Cc | 1.07 | 1.39 | 6.47 | 8.40 | 10.73 | 0.72 | 0.52 | 2.95 |
| Maximum Index Void Ratio | 0.755 | 0.702 | 0.670 | 0.627 | 0.625 | 0.690 | 0.973 | 1.139 |
| Minimum Index Void Ratio | 0.566 | 0.470 | 0.419 | 0.344 | 0.335 | 0.378 | 0.418 | 0.579 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polito, C.P. The Effect of Failure Criteria on Liquefaction and Pore Pressure Prediction in Non-Plastic Soils. Geotechnics 2025, 5, 27. https://doi.org/10.3390/geotechnics5020027
Polito CP. The Effect of Failure Criteria on Liquefaction and Pore Pressure Prediction in Non-Plastic Soils. Geotechnics. 2025; 5(2):27. https://doi.org/10.3390/geotechnics5020027
Chicago/Turabian StylePolito, Carmine P. 2025. "The Effect of Failure Criteria on Liquefaction and Pore Pressure Prediction in Non-Plastic Soils" Geotechnics 5, no. 2: 27. https://doi.org/10.3390/geotechnics5020027
APA StylePolito, C. P. (2025). The Effect of Failure Criteria on Liquefaction and Pore Pressure Prediction in Non-Plastic Soils. Geotechnics, 5(2), 27. https://doi.org/10.3390/geotechnics5020027








