Thermodynamic Assessment of the AF–CrF3 (A = Li, Na, K) and CrF2–CrF3 Systems
Abstract
:1. Introduction
2. Literature Review
2.1. Structural Data
2.2. Thermodynamic Data
| Compound | (298.15 K) | (298.15 K) | (T/K)/(J·K−1·mol−1) = a + b·T + c·T2 + d·T−2 + e·T3 | T(K) | Ref. | ||||
|---|---|---|---|---|---|---|---|---|---|
| (kJ·mol−1) | (J·K−1·mol−1) | a | b | c | d | e | |||
| LiF(Cr) | −616.931 | 35.66 | 43.30898 | 0.016312168 | 5.0470398 × 10−7 | −569123.6 | 298.15−2500 | [30] | |
| LiF(l) | −598.654 | 42.96 | 64.183 | - | - | - | - | 298.15–6000 | [30] |
| NaF(Cr) | −576.650 | 51.21 | 47.630 | 0.01479 | - | −464300 | - | 298.15–2500 | [30] |
| NaF(l) | −557.730 | 52.75 | 72.989 | - | - | - | - | 298.15–6000 | [30] |
| KF(Cr) | −568.606 | 66.55 | 68.757414 | −0.057756882 | 7.5404856 × 10−5 | −766718.34 | −2.3885627 × 10−8 | 298.15−2000 | [30] |
| KF(l) | −554.374 | 67.77 | 71.965 | - | - | - | - | 298.15–6000 | [30] |
| CrF2(Cr) | −781.8 | 86.87 | 76.68345 | 0.0105410 | −1.386756 × 10−9 | −1338373 | - | 298.15–1167 | [26,27] |
| CrF2(l) | −764.692 | 86.308 | 100 | - | - | - | - | 1167–4000 | [25,26,27] |
| CrF3(Cr) | −1160.0 | 93.88 | 75.86301 | 0.0404446 | −4.20805 × 10−6 | −782870 | - | 298.15–1100 | [25,26,27] |
| CrF3(Cr) | - | - | 226.552 | −0.0870137 | 2.020701 × 10−5 | −49199760 | - | 1100–1698 | [26,27] |
| CrF3(l) | −1125.281 | 83.0567 | 130 | - | - | - | - | 1698–2500 | [26,27] |
| Cr2F5(Cr) | −1950.8 | 181.0 | 152.54646 | 0.05098565 | −4.20944 × 10−6 | −2121243 | - | 298.15–6000 | [26], this work |
| Li3CrF6(Cr) | −3070.0 | 210.6 | 205.78995 | 0.089381104 | −2.69393806 × 10−6 | −2490240.8 | - | 298.15–1100 | [26], this work |
| Li3CrF6(Cr) | - | - | 356.47894 | −0.038077196 | 2.172112194 × 10−5 | −50907130.8 | - | 1100−3000 | [26], this work |
| NaCrF4(Cr) | −1777.5 | 156.2 | 123.49301 | 0.0552346 | −4.20805 × 10−6 | −1247170 | - | 298.15–3000 | [26], this work |
| α—Na3CrF6(Cr) | −2935.9 | 314.5 | 218.75301 | 0.0848146 | −4.20805 × 10−6 | −2175770 | - | 298.15–913 | [26], this work |
| β—Na3CrF6(Cr) | −2925.4 | 326.3 | 218.75301 | 0.0848146 | −4.20805 × 10−6 | −2175770 | - | 913–3000 | [26], this work |
| Na5Cr3F14(Cr) | −6545.65 | 584.2 | 465.739030 | 0.1952838 | −1.262415 × 10−5 | −4670110 | - | 298.15–3000 | [26], this work |
| α—KCrF4(Cr) | −1772.8 | 181.9 | 144.620424 | −0.017312282 | 7.1196806 × 10−5 | −1549588.34 | −2.3885627 × 10−8 | 298.15–1066 | [26], this work |
| β—KCrF4(Cr) | −1768.8 | 185.9 | 144.620424 | −0.017312282 | 7.1196806 × 10−5 | −1549588.34 | −2.3885627 × 10−8 | 1066–3000 | [26], this work |
| K2CrF5(Cr) | −2378.6 | 251.0 | 213.377838 | −0.075069164 | 1.4660166 × 10−4 | −2316306.68 | −4.7771254 × 10−8 | 298.15–3000 | [26], this work |
| K2Cr5F17(Cr) | −7067.5 | 632.8 | 516.829878 | 0.086709236 | 1.2976946 × 10−4 | −5447786.68 | −4.7771254 × 10−8 | 298.15–3000 | [26], this work |
| α—K3CrF6(Cr) | −2941.2 | 338.5 | 282.135252 | −0.132826046 | 2.2200652 × 10−4 | −3083025.02 | −7.1656881 × 10−8 | 298.15−499 | [26], this work |
| β—K3CrF6(Cr) | −2925.0 | 371.3 | 282.135252 | −0.132826046 | 2.2200652 × 10−4 | −3083025.02 | −7.1656881 × 10−8 | 499–3000 | [26], this work |
2.3. Phase Diagram Data
2.3.1. CrF2−CrF3 System
2.3.2. AF−CrF3 (A = Li, Na, K) Binary Systems
3. Thermodynamic Modelling
3.1. Gibbs Energies of Pure Compounds
3.2. Solid Solutions
3.3. Liquid Solution
4. Results and Discussion
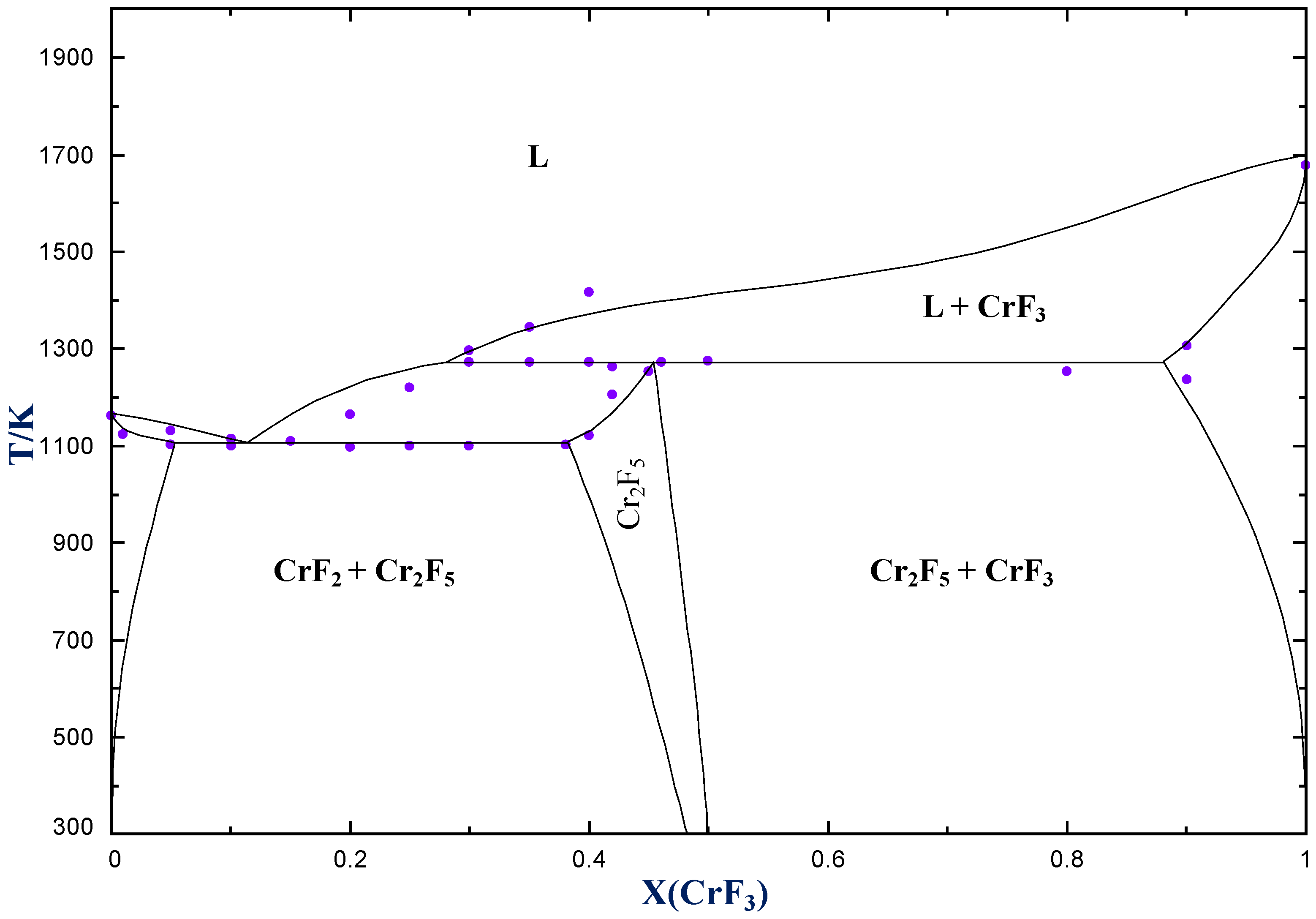
4.1. CrF2–CrF3
4.2. AF–CrF3 (A = Li, Na, K)
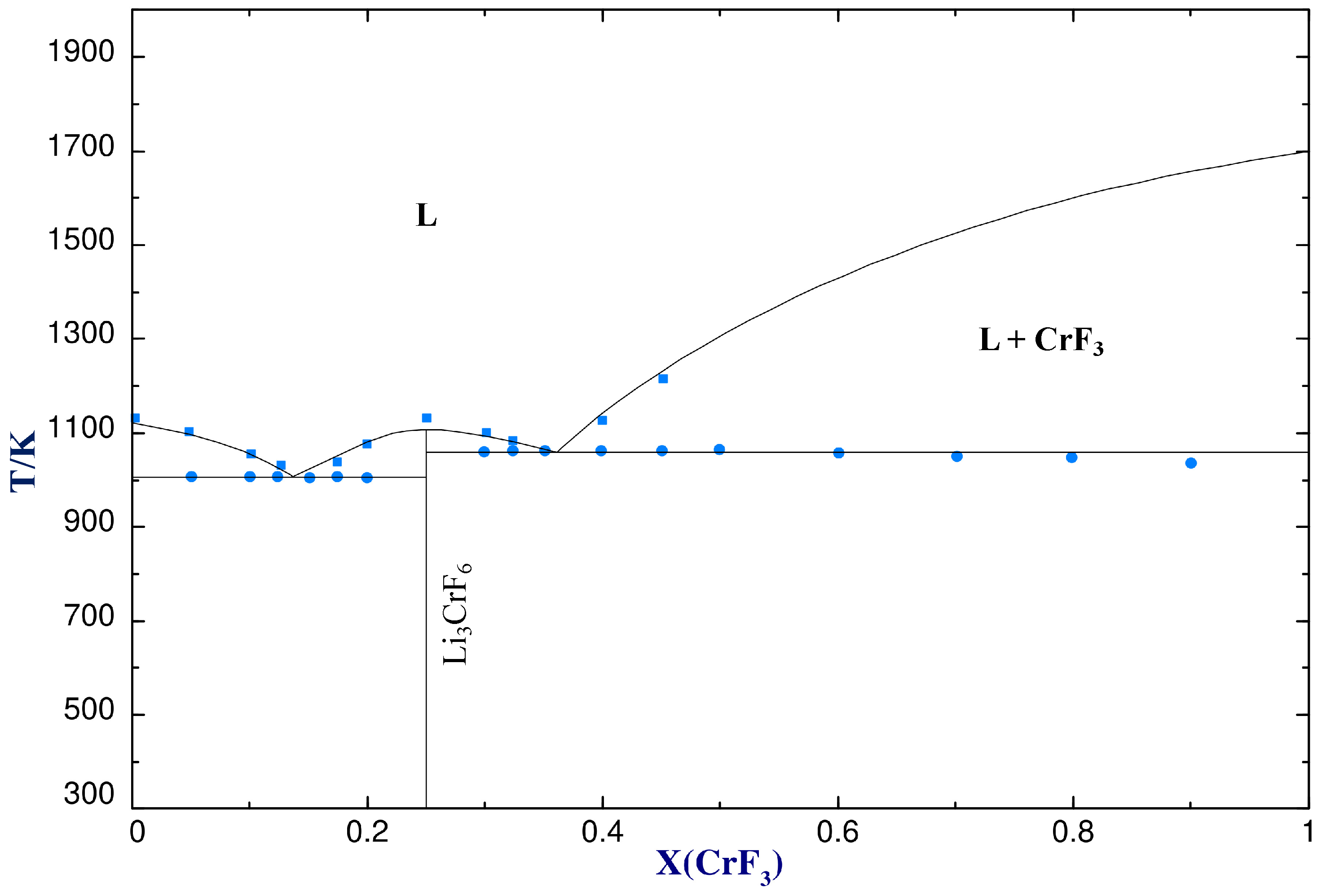
4.2.1. LiF−CrF3
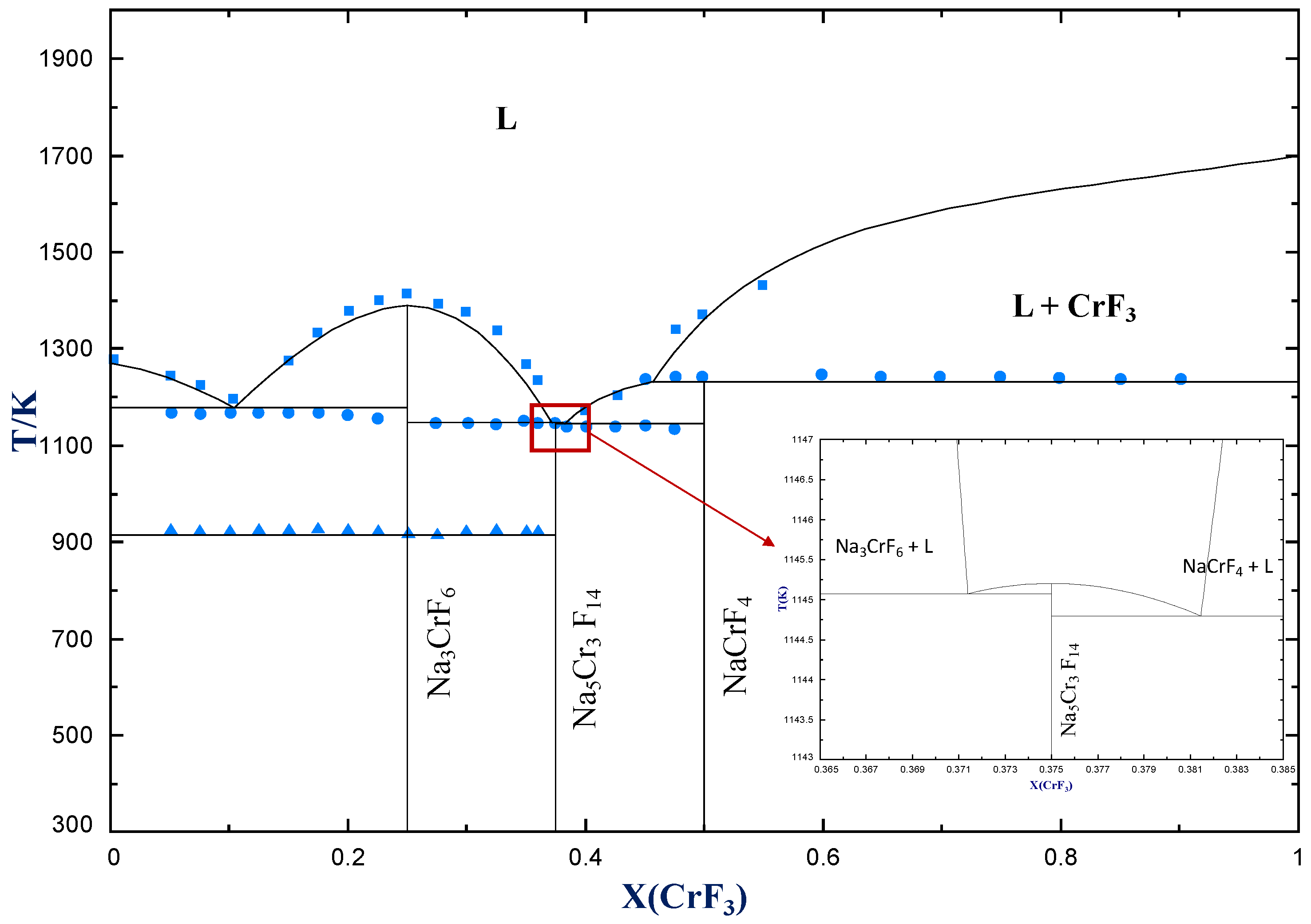
4.2.2. NaF−CrF3
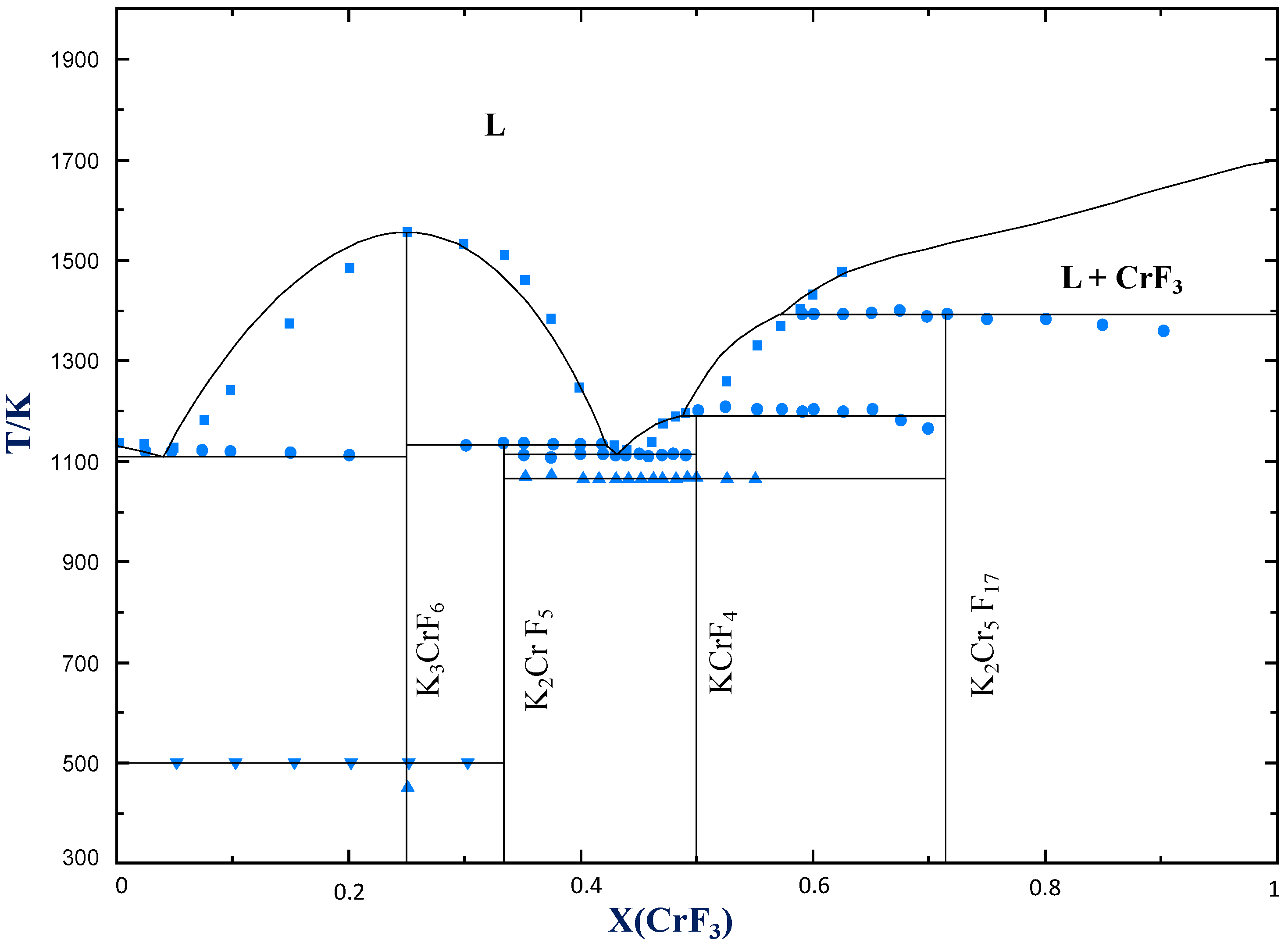
4.2.3. KF−CrF3
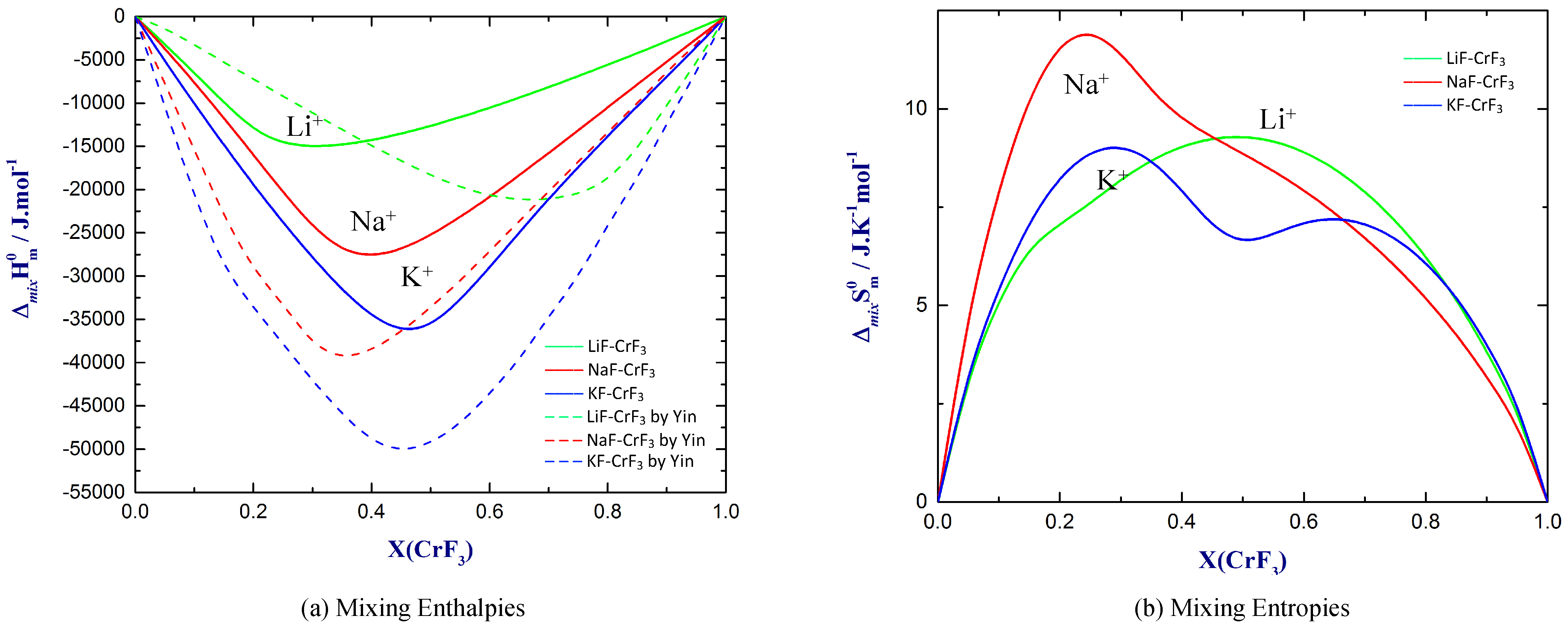
4.3. Excess Properties
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kelly, J.E. Generation IV International Forum: A decade of progress through international cooperation. Prog. Nucl. Energy 2014, 77, 240–246. [Google Scholar] [CrossRef]
- Tosolin, A.; Souček, P.; Beneš, O.; Vigier, J.-F.; Luzzi, L.; Konings, R.J.M. Synthesis of plutonium trifluoride by hydro-fluorination and novel thermodynamic data for the PuF3–LiF system. J. Nucl. Mater. 2018, 508, 319–328. [Google Scholar] [CrossRef]
- Beneš, O.; Konings, R.J.M. Comprehensive Nuclear Materials; Konings, R.J.M., Ed.; Elsevier: Oxford, UK, 2012; Chapter 3.13; pp. 359–389. [Google Scholar]
- Liu, J.; Huang, H.; Liu, R.; Zhu, Z.; Lei, Q.; Liu, A.; Li, Y. Corrosion of Cr in Molten Salts with different Fluoroacidity in the presence of CrF3. Corros. Sci. 2020, 169, 108636. [Google Scholar] [CrossRef]
- Bettis, E.S.; Cottrell, W.B.; Mann, E.R.; Meem, J.L.; Whitman, G.D. The Aircraft Reactor Experiment—Operation. Nucl. Sci. Eng. 1957, 2, 841–853. [Google Scholar] [CrossRef]
- Delpech, S.; Cabet, C.; Slim, C.; Picard, G.S. Molten Fluorides for Nuclear Applications. Mater. Today 2010, 13, 34–41. [Google Scholar] [CrossRef]
- Olson, L.C.; Ambrosek, J.W.; Sridharan, K.; Anderson, M.H.; Allen, T.R. Materials Corrosion in Molten LiF–NaF–KF salt. J. Fluor. Chem. 2009, 130, 67–73. [Google Scholar] [CrossRef]
- Sabharwall, P.; Ebner, M.; Sohal, M.; Sharpe, P.; Anderson, M.H.; Allen, T.R. Molten Salts for High Temperature Reactors: University of Wisconsin Molten Salt Corrosion and Flow Loop Experiments—Issues Identified and Path Forward; (Idaho National Laboratory (INL/EXT-10-18090)); Idaho National Laboratory: Idaho Falls, ID, USA, 2010. [Google Scholar]
- Tyagi, A.K.; Köhler, J. Preparation, Magnetic Properties and Structure of β-Li3CrF6. Mater. Res. Bull. 2000, 35, 135–141. [Google Scholar] [CrossRef]
- Massa, W.; Rüdorff, W. α-Li3MeF6 and β-Li3MeF6 compounds. Z. Naturforsch. B 1971, 26, 1216–1218. [Google Scholar] [CrossRef]
- Knoke, G. Kristallstrukturbestimmungen an den Verbindungen NaCrF4, CsCrF4 und Cs4Cr5F19 Sowie Weitere Untersuchungen an Ternären Chrom(III)fluoriden. Doctoral Dissertation, Marburg, Germany, 1977. [Google Scholar]
- García-Fernández, P.; Moreno, M.; Aramburu, J.A. Electrostatic Control of Orbital Ordering in Noncubic Crystals. J. Phys. Chem. C 2014, 118, 7554–7561. [Google Scholar] [CrossRef]
- Brunton, G. The Crystal structure of Na3CrF6. Mater. Res. Bull. 1969, 4, 621–626. [Google Scholar] [CrossRef]
- Le Bail, A.; Mercier, A.-M. Distorted chiolite crystal structures of α-Na5M3F14 (M = Cr, Fe, Ga) studied by X-ray powder diffraction. Powd. Diff. 2003, 18, 128–134. [Google Scholar] [CrossRef]
- De Kozak, A. Les systèmes CrF3–MF(M = Li, Na ou K). C. R. Acad. Sci. Paris 1969, C, 416–418. [Google Scholar]
- Lacorre, P.; Leblanc, M.; Pannetier, J.; Ferey, G. Ordered magnetic frustration: XV. Re-examination of the magnetic structure of α–KCrF4. J. Magn. Magn. Mater. 1991, 94, 337–341. [Google Scholar] [CrossRef]
- Manaka, H.; Etoh, T.; Honda, Y.; Iwashita, N.; Ogata, K.; Terada, N.; Hisamatsu, T.; Ito, M.; Narumi, Y.; Kondo, A.; et al. Effects of Geometrical Spin Frustration on Triangular Spin Tubes Formed in CsCrF4 and α–KCrF4. J. Phys. Soc. Jpn. 2011, 80, 084714. [Google Scholar] [CrossRef]
- Sassoye, C.; de Kozak, A. Crystal Structure and Thermal Behaviour of K2[CrF5·H2O]. Z. Anorg. Allg. Chem. 2006, 632, 445–448. [Google Scholar] [CrossRef]
- de Kozak, A. Thèse de Doctorat ès Sciences, Univ. Paris VI, Paris, France, 1970. Rev. Chim. Min. 1971, 8, 301–337. [Google Scholar]
- Baran, M.; Szymczak, H.; Wardzyński, W.; Wanklyn, B.M. EPR and optical absorption spectra of K2Cr5F17 monocrystals. Phys. Status Solidi B 1978, 90, K59–K61. [Google Scholar] [CrossRef]
- De Kozak, A.; Samouël, M. Le Système ternaire NaF-ZnF2–CrF3. I. Étude radiocristallographique. Triangulation. J. Less Common Met. 1975, 40, 185–193. [Google Scholar] [CrossRef]
- Boo, W.O.J.; Stout, J.W. Heat capacity and entropy of CuF2 and CrF2 from 10 to 300 K. Anomalies associated with magnetic ordering and evaluation of magnetic contributions to the heat capacity. J. Chem. Phys. 1979, 71, 9–16. [Google Scholar] [CrossRef]
- Sturm, B.J. Phase equilibria in the system chromium (II) fluoride-chromium (III) fluoride. Inorg. Chem. 1962, 1, 665–672. [Google Scholar] [CrossRef]
- Miranday, J.P.; Ferey, G.; Jacoboni, C.; Dance, J.M.; Tressaud, A.; De Pape, R. Croissance cristalline, polymorphisme et propriétés magnétiques de Na5Cr3F14. Rev. Chim. Miner. 1975, 12, 187–192. [Google Scholar]
- Hansen, W.N.; Griffel, M. Heat Capacities of CrF3 and CrCl3 from 15 to 300 °K. J. Chem. Phys. 1958, 28, 902–907. [Google Scholar] [CrossRef]
- Iorish, V.S.; Aristova, N.M.; Bergman, G.A.; Gorohov, L.N.; Gusarov, A.V.; Yezhov, Y.S.; Kulikov, A.N.; Osina, E.L.; Shenyavskaya, E.A.; Handamirova, N.E.; et al. Thermodynamic Properties of Substances; Publishing House Nauka: Moscow, Russia, 1978. [Google Scholar]
- Ansara, I.; Sundman, B. The Scientific Group Thermodata Europe (SGTE). In Computer Handling Determination of Data; Elsevier Science Pub. Co.: Amsterdam, The Netherlands, 1987; pp. 154–158. [Google Scholar]
- Yin, H.; Wang, K.; Xie, L.; Han, H.; Wang, W. Thermodynamic Modeling of KF–CrF3 Binary System. Chem. Res. Chin. Univ. 2015, 31, 461–465. [Google Scholar] [CrossRef]
- Yin, H.; Zhang, P.; An, X.; Cheng, J.; Li, X.; Wu, S.; Wu, X.; Liu, W.; Xie, L. Thermodynamic modeling of LiF-NaF-KF-CrF3 system. J. Fluor. Chem. 2018, 209, 6–13. [Google Scholar] [CrossRef]
- Chase, M.W., Jr.; Curnutt, J.L.; Downey, J.R., Jr.; McDonald, R.A.; Syverud, A.N.; Valenzuela, E.A. JANAF Thermochemical Tables. J. Phys. Chem. Ref. Data 1998, 11, 695–940. [Google Scholar] [CrossRef] [Green Version]
- Tressaud, A.; Dance, J.M.; Ravez, J.; Portier, J.; Hagenmuller, P.; Goodenough, J.B. Crystal chemistry and magnetic properties of CrIIBIIIF5 compounds. Mater. Res. Bull. 1973, 8, 1467–1477. [Google Scholar] [CrossRef]
- Kattner, U.R.; Seifert, H.J.; Lukas, H.L. Integrated Computational Materials Engineering, CALPHAD. Calphad 2010, 34, 385–386. [Google Scholar] [CrossRef]
- Chang, Y.A.; Chen, S.; Zhang, F.; Yan, X.; Xie, F.; Schmid-Fetzer, R.; Alan Oates, W. Phase diagram calculation: Past, present and future. Prog. Mater. Sci. 2004, 49, 313–345. [Google Scholar] [CrossRef]
- Bale, C.W.; Chartrand, P.; Degterov, S.A.; Eriksson, G.; Hack, K.; Mahfoud, R.B.; Melançon, J.; Pelton, A.D.; Petersen, S. FactSage thermochemical software and databases. Calphad 2002, 26, 189–228. [Google Scholar] [CrossRef]
- Leitner, J.; Vonka, P.; Sedmidubsky, D.; Svoboda, P. Application of Neumann–Kopp rule for the estimation of heat capacity of mixed oxides. Thermochim. Acta 2010, 497, 7–13. [Google Scholar] [CrossRef]
- Pelton, A.D.; Degterov, S.A.; Eriksson, G.; Robelin, C.; Dessureault, Y. The modified quasichemical model I–binary solutions. Metall. Mater. Trans. B 2000, 31, 651–659. [Google Scholar] [CrossRef]
- Beneš, O.; Beilmann, M.; Konings, R.J.M. Thermodynamic assessment of the LiF–NaF–ThF4–UF4 system. J. Nucl. Mater. 2010, 405, 186–198. [Google Scholar] [CrossRef]
- Hong, K.C.; Kleppa, O.J. Thermochemistry of the Liquid Mixtures of the Alkaline Earth Fluorides with Alkali Fluorides. J. Chem. Thermodyn. 1978, 8, 31–36. [Google Scholar] [CrossRef]
- Capelli, E.; Beneš, O.; Beilmann, M.; Konings, R.J.M. Thermodynamic investigation of the LiF–ThF4 system. J. Chem. Thermodyn. 2013, 58, 110–116. [Google Scholar] [CrossRef]
- Ocadiz-Flores, J.; Gheribi, A.E.; Vlieland, J.; de Haas, D.; Dardenne, K.; Rothe, J.; Konings, R.J.M.; Smith, A.L. Examination of the short-range structure of molten salts: ThF4, UF4, and related alkali actinide fluoride systems. Phys. Chem. Chem. Phys. 2021, 23, 11091–11103. [Google Scholar] [CrossRef]
- Ocadiz-Flores, J.A.; Capelli, E.; Raison, P.E.; Konings, R.J.M.; Smith, A.L. Thermodynamic assessment of the LiF-NiF2, NaF-NiF2 and KF-NiF2 systems. J. Chem. Thermodyn. 2018, 121, 17–26. [Google Scholar] [CrossRef]

| Compound | Symmetry | Space Group | a(Å) | b(Å) | c(Å) | (°) | Ref. |
|---|---|---|---|---|---|---|---|
| α—Li3CrF6 | Monoclinic | C2/c | 14.4058(10) | 8.6006(4) | 10.0122(6) | 94.714(5) | [9,10] |
| β—Li3CrF6 | Orthorhombic | Pna21 | 9.5796(1) | 8.4071(1) | 4.9793(7) | 90 | [9,10] |
| α—NaCrF4 | Monoclinic | P2/c | 7.862(2) | 5.328(2) | 7.406(2) | 101.65(4) | [11] |
| β—NaCrF4 | Tetragonal | P4/mmm * | 15.330(5) | 5.330(5) | 6.279(3) | 90 | [12] |
| Na3CrF6 | Monoclinic | P2/c | 5.46(1) | 5.68(1) | 7.88(1) | 90 | [13] |
| α—Na5Cr3F14 | Monoclinic | P2/c | 10.5096(3) | 7.2253(2) | 7.2713(2) | 90.6753(7) | [14] |
| β—Na5Cr3F14 | Orthorhombic | C222 | 10.49(1) | 10.19(1) | 10.21(1) | 90 | [15] |
| γ—Na5Cr3F14 | Tetragonal | P422 | 7.32(2) | 7.32(2) | 10.24(2) | 90 | [15] |
| KCrF4 | Orthorhombic | Pnma | 15.761(10) | 7.448(5) | 18.361(11) | 90 | [16,17] |
| K2CrF5 | Orthorhombic | Pbcn | 7.334(2) | 12.804(4) | 20.151(5) | 90 | [18] |
| K2Cr5F17 | Orthorhombic | Pmmm * | 12.56(1) | 7.25(1) | 7.36(1) | 90 | [19,20] |
| γ—K3CrF6 | Cubic | 8.66(1) | 8.66(1) | 8.66(1) | 90 | [19] |
| A | B | |||
|---|---|---|---|---|
| Li+ | Li+ | 6 | 6 | 3 |
| Na+ | Na+ | 6 | 6 | 3 |
| K+ | K+ | 6 | 6 | 3 |
| Cr2+ | Cr3+ | 6 | 6 | 2.4 |
| Li+ | Cr3+ | 2 | 6 | 2 |
| Na+ | Cr3+ | 4 | 6 | 2.7 |
| K+ | Cr3+ | 6 | 6 | 3 |
| Equilibrium | Invariant Reaction | This Study (calc.) | Sturm et al. [23] | ||
|---|---|---|---|---|---|
| X(CrF3) | T/K | X(CrF3) | T/K | ||
| Eutectic | CrF2(cr) + Cr2F5(cr) = L | 0.115 | 1104 | 0.14 * | 1103 ± 5 |
| Peritectic | Cr2F5(ss) = CrF3(cr) + L | 0.28 | 1271 | 0.29 | 1272 ± 5 |
| Equilibrium | Invariant Reaction | This Study (calc.) | De Kozak [15] | Yin et al. (calc.) [29] | |||
|---|---|---|---|---|---|---|---|
| X(CrF3) | T/K | X(CrF3) | T/K | X(CrF3) | T/K | ||
| Eutectic | LiF(cr) + Li3CrF6(cr) = L | 0.136 | 1008 | 0.15 | 1003 | 0.148 | 1003 |
| Congruent melting | Li3CrF6(cr) = L | 0.25 | 1111 | 0.25 | 1129 | 0.25 | 1125 |
| Eutectic | Li3CrF6(cr) + CrF3(cr) = L | 0.363 | 1062 | 0.35 | 1059 | 0.354 | 1058 |
| Equilibrium | Invariant Reaction | This Study (calc.) | De Kozak [15] | Yin et al. (calc.) [29] | |||
|---|---|---|---|---|---|---|---|
| X(CrF3) | T/K | X(CrF3) | T/K | X(CrF3) | T/K | ||
| Eutectic | NaF(cr) + Na3CrF6(cr) = L | 0.106 | 1175 | 0.123 | 1166 | 0.114 | 1162 |
| Congruent melting | Na3CrF6(cr) = L | 0.25 | 1385 | 0.25 | 1413 | 0.25 | 1416 |
| Eutectic | Na5Cr3F14(cr) + Na3CrF6 = L | 0.371 | 1145 | - | - | 0.367 | 1142 |
| Congruent melting | Na5Cr3F14(cr) = L | 0.375 | 1145 | - | - | 0.375 | 1142 |
| Eutectic | Na5Cr3F14(cr) + NaCrF4 = L | 0.381 | 1144 | - | - | 0.383 | 1141 |
| Peritectic | NaCrF4(cr) = L + CrF3(cr) | 0.5 | 1232 | 0.5 | 1234 | 0.5 | 1239 |
| Equilibrium | Invariant Reaction | This Study (calc.) | De Kozak [15] | Yin et al. (calc.) [29] | |||
|---|---|---|---|---|---|---|---|
| X(CrF3) | T/K | X(CrF3) | T/K | X(CrF3) | T/K | ||
| Eutectic | KF(cr) + K3CrF6(cr) = L | 0.041 | 1108 | 0.048 | 1115 | 0.045 | 1113 |
| Congruent melting | K3CrF6(cr) = L | 0.25 | 1553 | 0.25 | 1553 | 0.25 | 1548 |
| Peritectic | K2CrF5(cr) = K3CrF6(cr) + L | 0.333 | 1130 | 0.333 | 1133 | 0.333 | 1135 |
| Eutectic | K2CrF5(cr) + KCrF4(cr) = L | 0.432 | 1112 | 0.45 | 1112 | 0.426 | 1107 |
| Peritectic | KCrF4(cr)= K2Cr5F17(cr) + L | 0.50 | 1191 | 0.50 | 1200 | 0.50 | 1195 |
| Peritectic | K2Cr5F17(cr) = L + CrF3(cr) | 0.714 | 1390 | 0.714 | 1390 | 0.714 | 1388 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dumaire, T.; Konings, R.J.M.; Smith, A.L. Thermodynamic Assessment of the AF–CrF3 (A = Li, Na, K) and CrF2–CrF3 Systems. Thermo 2021, 1, 205-219. https://doi.org/10.3390/thermo1020014
Dumaire T, Konings RJM, Smith AL. Thermodynamic Assessment of the AF–CrF3 (A = Li, Na, K) and CrF2–CrF3 Systems. Thermo. 2021; 1(2):205-219. https://doi.org/10.3390/thermo1020014
Chicago/Turabian StyleDumaire, Thomas, Rudy J. M. Konings, and Anna Louise Smith. 2021. "Thermodynamic Assessment of the AF–CrF3 (A = Li, Na, K) and CrF2–CrF3 Systems" Thermo 1, no. 2: 205-219. https://doi.org/10.3390/thermo1020014
APA StyleDumaire, T., Konings, R. J. M., & Smith, A. L. (2021). Thermodynamic Assessment of the AF–CrF3 (A = Li, Na, K) and CrF2–CrF3 Systems. Thermo, 1(2), 205-219. https://doi.org/10.3390/thermo1020014






